| Issue |
A&A
Volume 599, March 2017
|
|
|---|---|---|
| Article Number | A74 | |
| Number of page(s) | 10 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201629757 | |
| Published online | 02 March 2017 | |
Measuring diffuse interstellar bands with cool stars
Improved line lists to model background stellar spectra⋆
GEPI, Observatoire de Paris, PSL Research University, CNRS, Université Paris-Diderot, Sorbonne Paris Cité, Place Jules Janssen, 92195 Meudon, France
e-mail: ana.monreal-ibero@obspm.fr; rosine.lallement@obspm.fr
Received: 20 September 2016
Accepted: 1 December 2016
Context. Diffuse stellar bands (DIBs) are ubiquitous in stellar spectra. Traditionally, they have been studied through their extraction from hot (early-type) stars because of their smooth continuum. In an era in which there are several ongoing or planned massive Galactic surveys using multi-object spectrographs, cool (late-type) stars constitute an appealing set of targets. However, from the technical point of view, the extraction of DIBs in their spectra is more challenging because of the complexity of the continuum.
Aims. In this contribution we provide the community with an improved set of stellar lines in the spectral regions associated with the strong DIBs at λ6196.0, λ6269.8, λ6283.8, and λ6379.3. These lines allow for the creation of better stellar synthetic spectra, reproducing the background emission and a more accurate extraction of the magnitudes associated with a given DIB (e.g., equivalent width, radial velocity).
Methods. The Sun and Arcturus were used as representative examples of dwarf and giant stars, respectively. A high quality spectrum for each of them was modeled using TURBOSPECTRUM and the Vienna Atomic Line Database (VALD) stellar line list. The oscillator strength log (gf) and wavelength of specific lines were modified to create synthetic spectra in which the residuals in both the Sun and Arcturus were minimized.
Results. The TURBOSPECTRUM synthetic spectra, based on improved line lists, reproduce the observed spectra for the Sun and Arcturus in the mentioned spectral ranges with greater accuracy. Residuals between the synthetic and observed spectra are always 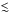 10%, which is much better than residuals with previously existing options. We tested the new line lists with some characteristic spectra from a variety of stars, including both giant and dwarf stars, and under different degrees of extinction. As occurred with the Sun and Arcturus, residuals in the fits used to extract the DIB information are smaller when using synthetic spectra made with the updated line lists. Tables with the updated parameters are provided to the community.
10%, which is much better than residuals with previously existing options. We tested the new line lists with some characteristic spectra from a variety of stars, including both giant and dwarf stars, and under different degrees of extinction. As occurred with the Sun and Arcturus, residuals in the fits used to extract the DIB information are smaller when using synthetic spectra made with the updated line lists. Tables with the updated parameters are provided to the community.
Key words: ISM: lines and bands / ISM: structure / stars: late-type
© ESO, 2017
1. Introduction
Stellar spectra may display some nonstellar weak absorption features of unknown origin associated with one or several clouds of interstellar medium (ISM) in their line of sight. These are the so-called diffuse interstellar bands (DIBs; see Herbig 1995; Sarre 2006, for a review). They were already noticed around the early 20s by Heger (see McCall & Griffin 2013, for a revision of the history of the DIBs discovery) and their interstellar origin was established in the 30s (Merrill 1934, 1936).
Today, we know more than 400 of these features (e.g., Galazutdinov et al. 2000; Hobbs et al. 2009). Most of them are seen in the optical with some additional DIBs clearly identified in the near-infrared (Joblin et al. 1990; Foing & Ehrenfreund 1994; Cox et al. 2014; Hamano et al. 2016) and a few proposed candidates in the near-UV (Bhatt & Cami 2015). Also, DIBs seem omnipresent. Even if the vast majority of DIB research is restricted to our Galaxy, they have been detected in many kind of extragalactic sources, such as the Magellanic Clouds, M31, M33 in the Local Group (Ehrenfreund et al. 2002; Welty et al. 2006; Cordiner et al. 2008, 2011; Cox et al. 2007; van Loon et al. 2013), nearby reddened galaxies (Ritchey & Wallerstein 2015), dusty starburst galaxies (Heckman & Lehnert 2000; Monreal-Ibero et al. 2015b), quasars (e.g., Lawton et al. 2008), and supernovae (Sollerman et al. 2005; Phillips et al. 2013).
Still, almost one century after their discovery, the nature of their carriers (i.e., the agent that originates these features) remains a mystery (see Fulara & Krełowski 2000, and references therein). Among the possible carrier candidates, one can find hydrocarbon chains (e.g., Maier et al. 2004), polycyclic aromatic hydrocarbons (PAHs; e.g., Salama et al. 1996; Kokkin et al. 2008), or fullerenes (Iglesias-Groth 2007; Sassara et al. 2001). In general, carbon seems to be involved. Particularly promising in this regard is the recent confirmation in the laboratory of C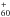 as the carrier of the two DIBs at 9577 and 9632 Å (Campbell et al. 2015), confirming an earlier proposal by Foing & Ehrenfreund (1994).
as the carrier of the two DIBs at 9577 and 9632 Å (Campbell et al. 2015), confirming an earlier proposal by Foing & Ehrenfreund (1994).
Not all the DIBs vary in unison. Instead, DIBs are grouped in families. Different pairs of DIBs show a range in the degree of correlation when their strengths (as traced by their equivalent widths) are compared, with DIBs in the same family having larger degrees of correlation (e.g., Cami et al. 1997; Friedman et al. 2011; Xiang et al. 2012). More noteworthy, although the degree of correlation between DIB equivalent width and the column density of molecular hydrogen, N(H2), is very variable and depends on the feature under consideration, DIBs present good correlations with the amount of neutral hydrogen along a given line of sight, the extinction, and the interstellar Na I D and Ca H&K lines (e.g., Herbig 1993; Friedman et al. 2011; Lan et al. 2015; Baron et al. 2015). Thus, irrespective of the actual nature of carrier(s), DIBs can be used as tools to infer properties of the 3D structure of the ISM.
Traditionally, investigations on the nature of the DIBs and their relation with the ISM in general are carried out using hot (early-type) star spectra since they are brighter and present a spectrum dominated by a smooth, featureless continuum. However, DIBs seem sensitive to the radiation field of these stars (Vos et al. 2011; Dahlstrom et al. 2013; Cordiner et al. 2013) and, therefore, hot stars are not the optimal targets to prove the typical conditions of the general ISM of our Galaxy. In fact, Raimond et al. (2012) showed how using cooler target star correlations between DIBs (and reddening) improve, confirming that the radiation field of UV bright stars has a significant influence on the DIB strength. Moreover, hot stars are not automatically abundant in a given region of interest. An alternative strategy would be the use of extragalactic spectra (Lan et al. 2015; Baron et al. 2015). Although these spectra in principle have lower quality in terms of signal-to-noise ratio and spectral resolution, they are also much more numerous and, thus, DIBs can be detected through stacking of similar spectra in terms of extinction and location.
A last option would be using the information carried in the spectra of cool stars since they are much more abundant and prove less extreme conditions of the ISM in terms of radiation field. Specifically, thanks to the advent of multi-object spectrographs, we live in an epoch where large spectroscopic surveys offer the possibility of conducting surveys at Galactic scales. Encouraging results in this direction have been presented by most of the ongoing surveys, such as SDSS (Yuan & Liu 2012), RAVE (Munari et al. 2008; Kos et al. 2014), and Gaia-ESO (Puspitarini et al. 2015) in the optical, as well as SDSS-III APOGEE (Zasowski et al. 2015; Elyajouri et al. 2016) in the infrared. The role of DIBs as tools to gain insight into the Galactic ISM structure will become even more prominent in the forthcoming years now that the Gaia satellite provides a 3D map of the Galaxy, including accurate positions of about one billion stars and hence line of sight directions. Also, with a spectrograph at a resolving power of ~11 500 (Katz et al. 2004), it will provide accurate measurements of the DIB at λ8621. Likewise several foreseen, highly multiplexed MOSs (e.g., WEAVE@WHT, Dalton et al. 2014; MOONS@VLT, Cirasuolo et al. 2014, 4MOST@VISTA, de Jong et al. 2014) will provide an immense amount of cool star spectra. These collections of data will constitute rich material for DIBs (and ISM, in general) research and, therefore, as preparatory work, it is necessary and timely to revisit and improve the existing methods for extraction of the information associated with the DIBs.
One strategy to reproduce (and get rid of) the stellar component would be the use of synthetic stellar models, (e.g., Destree et al. 2007). With this idea in mind, Chen et al. (2013) developed a method to automatically fit the spectra to a combination of a stellar synthetic spectrum, the atmospheric transmission, and a given DIB empirical profile. This method was applied later on by Puspitarini et al. (2015) to study the variation of the DIBs as a function of the distance along the LOS and to study the DIB-extinction relationship in different regions of the Milky Way. Both works pointed out a difficulty with this approach: some of the stellar features were not properly reproduced by the synthetic spectral modeling, thus adding uncertainty to the derivation of the magnitudes associated with a given DIB of interest. This point has also been raised recently by Kohl et al. (2016) who, after a careful modeling of the stellar emission in the vicinity of the DIB at λ5780, found no significant DIB absorption in any of their target stars and attributed the differences between modeled and observed spectra to inaccuracies in the stellar atmospheric modeling rather than to DIB absorption. In this investigation, we aim to improve that modeling by revisiting the stellar line lists in the spectral regions associated with some of the strongest DIBs.
Section 2 presents the observational data that were used to improve and test the line lists, and describes our criteria to select the spectral ranges that we plan to improve. Section 3 describes our working strategy and provides a list of modified stellar lines. Some examples illustrating the improvements for extraction of DIB parameters are included in Sect. 4. Our main conclusions are summarized in Sect. 5.
2. Observational data
We used two sets of data. The first data set is made out of two high quality spectra of the Sun and Arcturus and were used to improve the line lists. The second data set was used to evaluate the quality of the modeling using the new list. In the following, details about both sets are presented.
2.1. The Sun and Arcturus spectra
The solar observations are based on 50 solar Fourier transform spectrometer (FTS) scans taken by James Brault and Larry Testerman at Kitt Peak between 1981 and 1984. The spectral resolving power is δλ/λ ~ 300 000. The signal-to-noise ratio (S/N) is on the order of 3000 around 625 nm. Details on the spectra can be found in Kurucz (2005).
The spectrum of Arcturus was downloaded from the UVES-POP database (Bagnulo et al. 2003)1. Its resolution is about 80 000, as it was acquired with a 0.̋5 slit.
2.2. The test spectra
For this evaluation we intentionally chose a data set representative of current observing programs with 8 m class telescopes. We selected eight spectra from the ESO data archive to test the modeling of the stellar background emission. The observing programs they belong to aim to measure the metallicity of open cluster members (Santos et al. 2009, 2012). In order to test a variety of conditions, the spectra correspond to both giants (like Arcturus) and dwarfs (like the Sun) and suffer from extinction in different degrees. All of these spectra were obtained with the UVES spectrograph (Dekker et al. 2000) at the VLT, but with a diversity of spectral resolutions. All the spectra cover from 4780 to 6805 Å. In Table 1 we compile the utilized spectra and their relevant instrumental characteristics.
Test spectra.
2.3. Studied spectral ranges
In this contribution we focus on the spectral ranges of a reduced but relevant set of DIBs. As starting point, we used the list of DIBs presented in Table 1 of Puspitarini et al. (2013) and restricted our study to those DIBs included in the spectral range used by the Gaia-ESO survey to observe bright late-type stars. Specifically, this survey uses the UVES spectrograph in its DIC1/580 nm setting for this purpose, covering from 4760 Å to 6840 Å. Additionally, we required the DIBs to be relatively strong. That means having not only large equivalent width (EW) but also small full width at half maximum (FWHM). Using the results by Hobbs et al. (2008) for HD 204827 as reference, we restricted to those DIBs with EW(mÅ)/FWHM(Å) > 60. Also, a good pre-existing model of the DIB profile is needed. We used the templates empirically derived by Raimond et al. (2012) and Puspitarini et al. (2013), who averaged several FEROS (R ~ 48 000) spectra of early-type (B-A5) stars. Because of their empirical nature, these templates take possible asymmetries in bands and blending with neighboring ISM features into account. We excluded λ6445.3 since the model needed further improvements (see Fig. 6. in Puspitarini et al. 2013). In this way, the final list of DIBs of interest includes λ6196.0, λ6269.8, λ6283.8, λ6379.3, and λ6613.6. For typical ISM velocities this last feature is strongly blended with a set of stellar lines at λ6614.4 Å (Fe i) and 6613.7 Å (Fe i and Y ii), which are particularly difficult to reproduce with the simple strategy described in Sect. 3. Therefore, we decide not to consider this DIB at this stage and envision a more refined strategy for this range in the future. Finally, the fitting procedure needs some continuum toward the blue and red of the DIB under analysis, and DIBs trace ISM at a certain velocity (and therefore can appear blue- and redshifted in the spectra). Having taken all this into account, we selected the following three spectral ranges for inspection: 6186–6214 Å, 6259–6303 Å, and 6369–6389 Å.
The first spectral range is also needed when analyzing the λλ6203.0, 6204.5 blend. This is particularly interesting since the relative intensities of the DIBs in the blend do not vary in accord, pointing toward a different origin (Porceddu et al. 1991). Since these two DIBs did not fulfill our criterion of EW(mÅ)/FWHM(Å) (λ6204.5 is particularly broad), they are not tested here. However, studies on this blend based on late-type star spectra may equally benefit from the line list provided here.
Also, the second spectral range is infested with a series of strong absorption telluric features between ~6275 Å and ~6303 Å, which are caused mainly by O2 in the atmosphere (but also water vapor). Before tuning the stellar line list, the spectra of the Sun and Arcturus were corrected from this telluric absorption using TAPAS2 (Bertaux et al. 2014).
Stellar parameters for Sun and Arcturus.
 |
Fig. 1 Comparison of the modeled spectra of the Sun (left) and Arcturus (right). Each panel contains two graphics. In the main (upper) panel, the black line indicates the observed spectrum. The red and blue lines show the modeled spectrum using the original and improved line list, respectively. For the sake of clarity, these two lines have been offset by −0.10 and −0.05 in the y-axis. In the complementary (lower) panel, the residuals (data – model) using both line lists are shown. Finally, the profiles for the DIBs that motivated the corrections presented here and a putative cloud at v = 0 km s-1 are included for reference. |
3. Toward optimized line lists
The stellar line lists were improved by comparing synthetic spectra with the observed spectra for the Sun and Arcturus described in Sect. 2.1. For that, we utilized the radiative transfer code TURBOSPECTRUM (Alvarez & Plez 1998; Plez 2012), which requires a model with the stellar atmosphere structure. For the Sun, we utilized one of the native models from the grid of MARCS models for late-type stars (Gustafsson et al. 2008), while for Arcturus we interpolated using a code provided by T. Masseron3. Additionally, basic stellar parameters and the geometry of the atmosphere needed to be provided. Utilized parameters for both stars are listed in Table 2. The last input for TURBOSPECTRUM is a list with the physical parameters of the lines that we intend to tune. We used as starting point those provided by the Vienna Atomic Line Database (VALD-3)4 (Ryabchikova et al. 2015). With this, two initial synthetic spectra were created and degraded to an effective resolution that takes the broadening due to rotation and turbulence of the stars into account. Utilized values are shown in the last column of Table 2.
The synthetic spectra using TURBOSPECTRUM and the original VALD-3 line list are shown in Fig. 1 in red. A quick inspection of this figure is enough to state that several spectral features are not properly modeled with residuals with absolute values 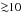 %. In most of those cases, the equivalent width of the stellar line is overestimated. Some examples have already been noticed (see, e.g., a residual at ~6609.5 Å in Fig. 2 of Puspitarini et al. 2015).
%. In most of those cases, the equivalent width of the stellar line is overestimated. Some examples have already been noticed (see, e.g., a residual at ~6609.5 Å in Fig. 2 of Puspitarini et al. 2015).
We modified the VALD-3 line list with the spirit of keeping the tuning as simple as possible. Thus, we allowed ourselves to modify only the oscillator strength (log (gf)) and, exceptionally, the wavelength of the line. In those few cases in which we did not identify a line responsible for a given feature, we created a new line by replicating a nearby Fe I or Fe II line at the wavelength of the feature that we intended to reproduce. This is reasonable strategy since iron lines are ubiquitous and iron is good proxy for the star metallicity. Finally, in those cases in which a different log (gf) was required to minimize the residuals for the Sun and for Arcturus, we adopted an intermediate value for log (gf) as a compromise. This is a pragmatic approach that is valid for our goals (i.e., get rid of the stellar spectra without necessarily having a deep understanding of the stellar physics). Synthetic spectra using TURBOSPECTRUM and our modified line lists are shown in blue in Fig. 1. Even if there are still some low-level residuals, typically 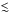 10%, these synthetic spectra clearly beat those created with the TURBOSPECTRUM code together with the original VALD-3 line list.
10%, these synthetic spectra clearly beat those created with the TURBOSPECTRUM code together with the original VALD-3 line list.
Table 3, which contains the means, standard deviations, and medians of the residuals in each subplot of Fig. 1, offers a more quantitative way of comparing all two options. By looking at the standard deviations of the residuals, it is clear that TURBOSPECTRUM models using the updated line lists are much better than those using the original line lists. Since the residuals that matter most are those within the relatively narrow wavelength ranges that only include each DIB plus some limited continuum to either side, we also estimated the local standard deviation, in 2 Å-wide bins, for both the Sun and Arcturus. As occurred with the global standard deviations, these were comparable or smaller when using the updated line lists than when using the original line lists.
The updated line lists are the main outcome of this contribution and they are provided in Tables 4 to 6. In the following section, we show some examples of their applicability for DIB extraction.
Residual statistics for the Sun and Arcturus.
Modified stellar lines in the 6186−6214 Å spectral range.
Modified stellar lines in the 6259−6303 Å spectral range.
Modified stellar lines in the 6369−6389 Å spectral range.
4. Extraction of DIB using the new line lists
Stellar parameters for the test stars.
We tested our updated line lists using the UVES spectra presented in Sect. 2.2. A thorough description of the strategy to measure the DIB equivalent widths can be found in Puspitarini et al. (2013) and Monreal-Ibero et al. (2015a) and is not repeated here. In short, the spectra are modeled as the product of a series of functions that reproduce the stellar absorption features, stellar global continuum, interstellar absorption (i.e., the DIB), and telluric transmission. The DIBs were expected to be weak, especially along the sight lines with low reddening. Thus, additional constraints were needed to make the fits converge. Specifically, we impose limits on the expected velocities for the DIBs, based on the direction of the sky and the results for H i (Brand & Blitz 1993; Kalberla et al. 2010). Each UVES spectrum was fitted twice. The only brick that we changed in these two fits was the function representing the stellar absorption features. In both cases we used TURBOSPECTRUM to create the synthetic stellar spectrum, but we used either the original VALD-3 stellar line lists or included our updates. The identical stellar parameters that we used to create both models are listed in Table 7. Also, we set [α/ Fe] = 0.0 and we assumed a plane-parallel geometry for the dwarf stars and a spherical geometry for the giants.
The derived DIB parameters, both equivalent width and velocity, for the eight test spectra are presented in Table 8. Reported errors for the equivalent widths take two components into account. The first component is the formal 1-sigma statistical errors associated with the fit. The second component is an estimation of the uncertainty associated with the reported stellar parameters (Teff, log g, and metallicity). For that, in those cases in which the band could be strongly blended with a strong stellar line, the fit was performed two times: without any mask and masking this contaminating line. The difference between the equivalent widths derived from these two fits is an estimation of the uncertainty from that, and as such, was added to the error budget. In those cases where the fit did not converge (i.e., the estimated DIB velocity reached the imposed limits), we estimated an upper limit for a possible DIB using the standard deviation of the residuals and typical width of the DIB. Regarding the reported errors in the velocities, these include only the formal 1-sigma statistical errors associated with the fit.
The most relevant result that one can extract from Table 8 is that the χ2 is smaller when using the synthetic spectra generated with the new line list most of the time, supporting the use of the corrections provided in Sect. 3. Besides, even in the few cases in which the χ2 is comparable, lines in the proximity of the DIB are better reproduced when using the improved line list and only a few lines at the edge of the spectral range under consideration have relatively important residuals. This is visualized in a graphical manner in Figs. 2 to 5, which show the residuals for the fits of the eight stars when using the original (red) and updated (blue) line lists. These last residuals are 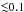 for the dwarf star spectra. Regarding the giant stars, the residuals are slightly larger than 0.1 only for a few lines in the spectral range of the DIB at λ6196.0. These lines are particularly susceptible to further improvements and have been marked in Table 4 with an asterisk. The determination of the log (gf) and central wavelength can change depending on the stars used for calibration (e.g., convection inside the star may have an effect on the central wavelength of a given stellar line; see Molaro & Monai 2012). Thus, small additional adjustments in both log (gf) and the central wavelength, using additional calibration stars, can further improve the modeling of these lines.
for the dwarf star spectra. Regarding the giant stars, the residuals are slightly larger than 0.1 only for a few lines in the spectral range of the DIB at λ6196.0. These lines are particularly susceptible to further improvements and have been marked in Table 4 with an asterisk. The determination of the log (gf) and central wavelength can change depending on the stars used for calibration (e.g., convection inside the star may have an effect on the central wavelength of a given stellar line; see Molaro & Monai 2012). Thus, small additional adjustments in both log (gf) and the central wavelength, using additional calibration stars, can further improve the modeling of these lines.
Not every DIB was detected in every spectrum. This is not surprising, given the covered range of stellar extinctions (see Table 1). The DIB that was detected in a larger number of spectra is that at λ6283.8. The derived equivalent widths are smaller when using the updated line list in all cases but IC4651AM4226. This is very much in line with the result by Kohl et al. (2016) for the DIB at λ5780 who, after carefully quantifying the stellar absorption in some spectra with previously reported ISM absorption, did not find hints of DIB detection and highlight the importance of adequately reproducing the stellar spectrum.
DIB measurements for the test stars.
The other DIBs were only detected in some of the stars. To give an idea of the relative importance of all the different components playing a role (different ISM absorptions, stellar spectrum, etc.), we show the fits for the four DIBs in NGC6705_No1111 in Fig. 6. This is both a giant and a relatively high-metallicity star. This implies that stellar absorptions are particularly strong here, and thus this is representative of one of the most difficult examples that one might find in a putative future exploitation of MOS spectra for ISM studies. All these points are equally applicable to the other star in the cluster, i.e., NGC 6705_No1184. In particular, the fitting algorithm was able to identify an excess of absorption at the position for the DIB at λ6269. However, this line is strongly blended with three stellar lines at ~λ6268 (Ti i, V i, and Fe i), which might prevent an accurate determination of the DIB centroid (i.e., velocity) and explain the differences in velocity with respect to the DIB at λ6283.8. Alternatively, small uncertainties in the automatic reduction of the archive data by the ESO pipeline (e.g., local issues with flat-fielding and fringing) could play a role in the determination of the centroid of large features, as is the case of the DIB at λ6283.8. A final source of uncertainty, regarding the velocities, is the structure in velocity for the ISM itself along the line of sight. Since our goal here is testing the line lists, not the fitting technique, we used the simple approach of reproducing the ISM absorptions by one single component (i.e., one cloud). However, this is not necessarily true. For example, in the direction of NGC 6705, H i observations show the existence of at least two clouds at very different velocities (Kalberla et al. 2010). The simplicity of a fit using only one component coupled with differences in the physical conditions between these clouds might also explain the velocities differences observed between the different DIBs.
 |
Fig. 2 Comparison of the fit residuals for the DIB at λ6196.0 Å. Dwarf test stars are in the left column, while giant stars are in the right column. Red lines indicate the synthetic spectra using the original line list and blue lines indicate those with the improved line list, as in Fig. 1. |
All in all, the line list corrections provided here offer the possibility of making better use of the colossal amount of cold star spectra generated in the forthcoming years for DIB research. From the technical point of view, the most promising DIB, is that at λ6283.8. Armed with a good fitting algorithm, an accurate synthetic stellar spectrum (such as the spectrum that can be generated using this updated line list) and appropriate tools for good telluric corrections, such as TAPAS here, but also, for example, Molecfit (Smette et al. 2015), researchers will be able to extract plenty of material that will help to constrain the structure of the Galactic ISM. However, given the dependence of this DIB with the environment, additional information coming from, for example, other DIBs will be desirable and certainly feasible in the light of sights with higher extinction.
 |
Fig. 6 NGC 6705_No1111 as an example of fit in the spectral region for each DIB. Total spectra are represented with solid lines as follows: black – observed spectra; red – fit with original line list; blue – fit with updated line list. Components associated with the modeled DIBs are shown with long-dashed violet and orange lines, while the synthetic spectra as created by TURBOSPECTRUM appear as green short-dashed lines. |
5. Summary and conclusions
In this paper we improve the extraction of the parameters associated with the DIBs in the spectra of cool stars by providing updated line lists in three spectral ranges associated with the four strong DIBs at λ6196.0, λ6269.8, λ6283.8, and λ6379.3. For that we tuned the log (gf) (and occasionally the central wavelength) of the stellar lines and created synthetic spectra with TURBOSPECTRUM for the Sun and Arcturus, which minimized the residuals for both stars when comparing synthetic and observed spectra.
The final stellar synthetic spectra with the improved line lists reproduce the observed spectra for these stars with greater accuracy. The global standard deviation for the residual in a given spectral range when using TURBOSPECTRUM with the updated line lists are typically about half of those using the original lists, and with local residuals ~<10%, for both stars. We tested our updated line lists with a set of UVES spectra for eight stars both, dwarf and giants, which suffer from different amounts of extinction. The quality of the fit, as characterized by the χ2, was better when using our updated line lists, and thus we offer them to the community.
Despite the general improvement of the models, discrepancies remain between the radial velocities measured for the λ6283.8 DIB and for the other DIBs. However, based on a similar fitting method radial velocities were consistently measured in the spectra of the Gaia-ESO Survey at high optical extinctions (AV ~ 1 mag; see Figs. 8, 9, 12, 14, and 16 by Puspitarini et al. 2015). The examples chosen here (lower extinction toward metallic giant stars) are much more challenging and our results strongly suggest that additional work needs to be performed either to improve the updated atomic data, or the profiles of the theoretical stellar lines to reach the high degree of precision (a few percent) that will allow us to derive reliable radial velocity in these more challenging cases.
Here, we have focused on the improvement of the stellar modeling in three specific spectral ranges, corresponding to four strong DIBs. Inaccuracies in the stellar atmospheric modeling have already been identified in other spectral ranges of interest for ISM research, as that associated with the DIBs at λ5780 and λ5797 (Kohl et al. 2016). Given the value of the ratio between these two DIBs as a tracer of the characteristics of the environment (i.e., radiation field Cami et al. 1997; Vos et al. 2011; Cordiner et al. 2013), there is a strong motivation for a similar work to that presented here for this spectral range. Likewise, the DIB at λ6614 is relatively strong and, as such, the creation of synthetic spectra in this spectral range should be contemplated. However, a preliminary exploration of this range, which is not discussed here, points toward a need for a more delicate approach, where for some stellar lines additional parameters other than log (gf) should be tuned and effects like departures from LTE should be explored. These updated line lists together with the enormous data base that will be generated in the forthcoming years will offer an extraordinary opportunity to learn about the nature and statistical properties of DIBs. Likewise, their suitability as probes of the properties of the ISM (e.g., distribution, excitation, etc.) will be significantly enhanced. In particular, the assigned value for the foreground extinction affects the determination of the stellar parameters (e.g., effective temperature and metallicity). The DIBs, with their capacity to act as independent estimators of the extinction, will play a fundamental role in constraining this value.
Acknowledgments
We thank Piercarlo Bonifacio and Elisabetta Caffau for useful advice about the focus of this work and the use of TURBOSPECTRUM. We also thank Monique Spite for allowing us to use her piece of code that puts the Vald-3 line lists in a format that is adequate for TURBOSPECTRUM and with whom we shared stimulating discussions regarding the work presented here. We also thank the referee for the useful comments that have significantly improved the first submitted version of this paper. We acknowledge support from Agence Nationale de la Recherche through the STILISM project (ANR-12-BS05-0016-02). This work has made use of the VALD database, operated at Uppsala University, the Institute of Astronomy RAS in Moscow, and the University of Vienna. This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.
References
- Alvarez, R., & Plez, B. 1998, A&A, 330, 1109 [NASA ADS] [Google Scholar]
- Bagnulo, S., Jehin, E., Ledoux, C., et al. 2003, The Messenger, 114, 10 [NASA ADS] [Google Scholar]
- Baron, D., Poznanski, D., Watson, D., Yao, Y., & Prochaska, J. X. 2015, MNRAS, 447, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Bertaux, J. L., Lallement, R., Ferron, S., Boonne, C., & Bodichon, R. 2014, A&A, 564, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bhatt, N. H., & Cami, J. 2015, ApJS, 216, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Brand, J., & Blitz, L. 1993, A&A, 275, 67 [NASA ADS] [Google Scholar]
- Cami, J., Sonnentrucker, P., Ehrenfreund, P., & Foing, B. H. 1997, A&A, 326, 822 [NASA ADS] [Google Scholar]
- Campbell, E. K., Holz, M., Gerlich, D., & Maier, J. P. 2015, Nature, 523, 322 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Chen, H.-C., Lallement, R., Babusiaux, C., et al. 2013, A&A, 550, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cirasuolo, M., Afonso, J., Carollo, M., et al. 2014, in Ground-based and Airborne Instrumentation for Astronomy V, Proc. SPIE, 9147, 91470 [Google Scholar]
- Cordiner, M. A., Smith, K. T., Cox, N. L. J., et al. 2008, A&A, 492, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cordiner, M. A., Cox, N. L. J., Evans, C. J., et al. 2011, ApJ, 726, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Cordiner, M. A., Fossey, S. J., Smith, A. M., & Sarre, P. J. 2013, ApJ, 764, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, N. L. J., Cordiner, M. A., Ehrenfreund, P., et al. 2007, A&A, 470, 941 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cox, N. L. J., Cami, J., Kaper, L., et al. 2014, A&A, 569, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dahlstrom, J., York, D. G., Welty, D. E., et al. 2013, ApJ, 773, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Dalton, G., Trager, S., Abrams, D. C., et al. 2014, in Ground-based and Airborne Instrumentation for Astronomy V, Proc. SPIE, 9147, 91470 [Google Scholar]
- de Jong, R. S., Barden, S., Bellido-Tirado, O., et al. 2014, in Ground-based and Airborne Instrumentation for Astronomy V, Proc. SPIE, 9147, 91470 [Google Scholar]
- Dekker, H., D’Odorico, S., Kaufer, A., Delabre, B., & Kotzlowski, H. 2000, in Optical and IR Telescope Instrumentation and Detectors, eds. M. Iye, & A. F. Moorwood, SPIE Conf. Ser., 4008, 534 [Google Scholar]
- Destree, J. D., Snow, T. P., & Eriksson, K. 2007, ApJ, 664, 909 [NASA ADS] [CrossRef] [Google Scholar]
- Ehrenfreund, P., Cami, J., Jiménez-Vicente, J., et al. 2002, ApJ, 576, L117 [NASA ADS] [CrossRef] [Google Scholar]
- Elyajouri, M., Monreal-Ibero, A., Remy, Q., & Lallement, R. 2016, ApJS, 225, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Foing, B. H., & Ehrenfreund, P. 1994, Nature, 369, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Friedman, S. D., York, D. G., McCall, B. J., et al. 2011, ApJ, 727, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Fulara, J., & Krełowski, J. 2000, New Astron. Rev., 44, 581 [Google Scholar]
- Galazutdinov, G. A., Musaev, F. A., Krełowski, J., & Walker, G. A. H. 2000, PASP, 112, 648 [NASA ADS] [CrossRef] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hamano, S., Kobayashi, N., Kondo, S., et al. 2016, ApJ, 821, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Heckman, T. M., & Lehnert, M. D. 2000, ApJ, 537, 690 [NASA ADS] [CrossRef] [Google Scholar]
- Heger, M. L. 1922, Lick Observatory Bulletin, 10, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Herbig, G. H. 1993, ApJ, 407, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Herbig, G. H. 1995, ARA&A, 33, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Hobbs, L. M., York, D. G., Snow, T. P., et al. 2008, ApJ, 680, 1256 [NASA ADS] [CrossRef] [Google Scholar]
- Hobbs, L. M., York, D. G., Thorburn, J. A., et al. 2009, ApJ, 705, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias-Groth, S. 2007, ApJ, 661, L167 [NASA ADS] [CrossRef] [Google Scholar]
- Joblin, C., D’Hendecourt, L., Leger, A., & Maillard, J. P. 1990, Nature, 346, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Jofré, P., Heiter, U., Soubiran, C., et al. 2014, A&A, 564, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalberla, P. M. W., McClure-Griffiths, N. M., Pisano, D. J., et al. 2010, A&A, 521, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Katz, D., Munari, U., Cropper, M., et al. 2004, MNRAS, 354, 1223 [NASA ADS] [CrossRef] [Google Scholar]
- Kharchenko, N. V., Piskunov, A. E., Röser, S., Schilbach, E., & Scholz, R.-D. 2005, A&A, 438, 1163 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Kohl, S., Czesla, S., & Schmitt, J. H. M. M. 2016, A&A, 591, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kokkin, D. L., Troy, T. P., Nakajima, M., et al. 2008, ApJ, 681, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Kos, J., Zwitter, T., Wyse, R., et al. 2014, Science, 345, 791 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kurucz, R. L. 2005, Mem. Soc. Astron. It. Suppl., 8, 189 [Google Scholar]
- Lan, T.-W., Ménard, B., & Zhu, G. 2015, MNRAS, 452, 3629 [Google Scholar]
- Lawton, B., Churchill, C. W., York, B. A., et al. 2008, AJ, 136, 994 [NASA ADS] [CrossRef] [Google Scholar]
- Maier, J. P., Walker, G. A. H., & Bohlender, D. A. 2004, ApJ, 602, 286 [NASA ADS] [CrossRef] [Google Scholar]
- McCall, B. J., & Griffin, R. E. 2013, ed. M. Berry, in Proc. Roy. Soc. A, 469, 20120604 [Google Scholar]
- Merrill, P. W. 1934, PASP, 46, 206 [NASA ADS] [CrossRef] [Google Scholar]
- Merrill, P. W. 1936, ApJ, 83, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Molaro, P., & Monai, S. 2012, A&A, 544, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Monreal-Ibero, A., Lallement, R., Puspitarini, L., Bonifacio, P., & Monaco, L. 2015a, Mem. Soc. Astron. It., 86, 527 [NASA ADS] [Google Scholar]
- Monreal-Ibero, A., Weilbacher, P. M., Wendt, M., et al. 2015b, A&A, 576, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Munari, U., Tomasella, L., Fiorucci, M., et al. 2008, A&A, 488, 969 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pandey, A. K., Sandhu, T. S., Sagar, R., & Battinelli, P. 2010, MNRAS, 403, 1491 [NASA ADS] [CrossRef] [Google Scholar]
- Phillips, M. M., Simon, J. D., Morrell, N., et al. 2013, ApJ, 779, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Plez, B. 2012, Turbospectrum: Code for spectral synthesis, Astrophysics Source Code Library [Google Scholar]
- Porceddu, I., Benvenuti, P., & Krelowski, J. 1991, A&A, 248, 188 [NASA ADS] [Google Scholar]
- Puspitarini, L., Lallement, R., & Chen, H.-C. 2013, A&A, 555, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Puspitarini, L., Lallement, R., Babusiaux, C., et al. 2015, A&A, 573, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raimond, S., Lallement, R., Vergely, J. L., Babusiaux, C., & Eyer, L. 2012, A&A, 544, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ritchey, A. M., & Wallerstein, G. 2015, PASP, 127, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Ryabchikova, T., Piskunov, N., Kurucz, R. L., et al. 2015, Phys. Scr, 90, 054005 [NASA ADS] [CrossRef] [Google Scholar]
- Salama, F., Bakes, E. L. O., Allamandola, L. J., & Tielens, A. G. G. M. 1996, ApJ, 458, 621 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Santos, N. C., Lovis, C., Pace, G., Melendez, J., & Naef, D. 2009, A&A, 493, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Lovis, C., Melendez, J., et al. 2012, A&A, 538, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sarre, P. J. 2006, J. Mol. Spectrosc., 238, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Sassara, A., Zerza, G., Chergui, M., & Leach, S. 2001, ApJS, 135, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Smette, A., Sana, H., Noll, S., et al. 2015, A&A, 576, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sollerman, J., Cox, N., Mattila, S., et al. 2005, A&A, 429, 559 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sousa, S. G., Santos, N. C., Mayor, M., et al. 2008, A&A, 487, 373 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- van Loon, J. T., Bailey, M., Tatton, B. L., et al. 2013, A&A, 550, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vos, D. A. I., Cox, N. L. J., Kaper, L., Spaans, M., & Ehrenfreund, P. 2011, A&A, 533, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Welty, D. E., Federman, S. R., Gredel, R., Thorburn, J. A., & Lambert, D. L. 2006, ApJS, 165, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Xiang, F., Liu, Z., & Yang, X. 2012, PASJ, 64, 31 [NASA ADS] [Google Scholar]
- Yuan, H. B., & Liu, X. W. 2012, MNRAS, 425, 1763 [NASA ADS] [CrossRef] [Google Scholar]
- Zasowski, G., Ménard, B., Bizyaev, D., et al. 2015, ApJ, 798, 35 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Comparison of the modeled spectra of the Sun (left) and Arcturus (right). Each panel contains two graphics. In the main (upper) panel, the black line indicates the observed spectrum. The red and blue lines show the modeled spectrum using the original and improved line list, respectively. For the sake of clarity, these two lines have been offset by −0.10 and −0.05 in the y-axis. In the complementary (lower) panel, the residuals (data – model) using both line lists are shown. Finally, the profiles for the DIBs that motivated the corrections presented here and a putative cloud at v = 0 km s-1 are included for reference. |
| In the text | |
 |
Fig. 2 Comparison of the fit residuals for the DIB at λ6196.0 Å. Dwarf test stars are in the left column, while giant stars are in the right column. Red lines indicate the synthetic spectra using the original line list and blue lines indicate those with the improved line list, as in Fig. 1. |
| In the text | |
 |
Fig. 3 Same as for Fig. 2 but for the DIB at λ6269.8 Å. |
| In the text | |
 |
Fig. 4 Same as for Fig. 2 but for the DIB at λ6283.8 Å. |
| In the text | |
 |
Fig. 5 Same as for Fig. 2 but for the DIB at λ6379.3 Å. |
| In the text | |
 |
Fig. 6 NGC 6705_No1111 as an example of fit in the spectral region for each DIB. Total spectra are represented with solid lines as follows: black – observed spectra; red – fit with original line list; blue – fit with updated line list. Components associated with the modeled DIBs are shown with long-dashed violet and orange lines, while the synthetic spectra as created by TURBOSPECTRUM appear as green short-dashed lines. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


