| Issue |
A&A
Volume 599, March 2017
|
|
|---|---|---|
| Article Number | A69 | |
| Number of page(s) | 10 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201629747 | |
| Published online | 02 March 2017 | |
Supergranulation and multiscale flows in the solar photosphere
Global observations vs. a theory of anisotropic turbulent convection
1 Université de Toulouse, UPS-OMP, IRAP, 31400 Toulouse, France
e-mail: frincon@irap.omp.eu
2 CNRS; IRAP; 14 avenue Édouard Belin, 31400 Toulouse, France
3 The Rudolf Peierls Centre for Theoretical Physics, University of Oxford, 1 Keble Road, Oxford, OX1 3NP, UK
4 Merton College, Oxford OX1 4JD, UK
Received: 19 September 2016
Accepted: 24 December 2016
The Sun provides us with the only spatially well-resolved astrophysical example of turbulent thermal convection. While various aspects of solar photospheric turbulence, such as granulation (one-Megameter horizontal scale), are well understood, the questions of the physical origin and dynamical organization of larger-scale flows, such as the 30-Megameters supergranulation and flows deep in the solar convection zone, remain largely open in spite of their importance for solar dynamics and magnetism. Here, we present a new critical global observational characterization of multiscale photospheric flows and subsequently formulate an anisotropic extension of the Bolgiano-Obukhov theory of hydrodynamic stratified turbulence that may explain several of their distinctive dynamical properties. Our combined analysis suggests that photospheric flows in the horizontal range of scales between supergranulation and granulation have a typical vertical correlation scale of 2.5 to 4 Megameters and operate in a strongly anisotropic, self-similar, nonlinear, buoyant dynamical regime. While the theory remains speculative at this stage, it lends itself to quantitative comparisons with future high-resolution acoustic tomography of subsurface layers and advanced numerical models. Such a validation exercise may also lead to new insights into the asymptotic dynamical regimes in which other, unresolved turbulent anisotropic astrophysical fluid systems supporting waves or instabilities operate.
Key words: Sun: photosphere / Sun: interior / convection / turbulence / instabilities
© ESO, 2017
1. Introduction
The solar photosphere is the stage of many spectacular (magneto-)hydrodynamic phenomena and it provides us with a unique observationally well-resolved example of strongly nonlinear thermal convection, one of the most common fluid instabilities and transport processes encountered in nature and astrophysics (Kupka et al. 2007). While some aspects of solar thermal turbulence, such as granulation, are now well understood (Nordlund et al. 2009), we still lack definitive answers to many important questions, such as how the turbulence organizes on large scales, and how it interacts with and amplifies magnetic fields or transports quantities such as angular momentum or magnetic flux (Miesch 2005; Charbonneau 2014).
The most direct observational characterization of flows connected to the solar convection zone at scales larger than the granulation has been achieved through measurements of Doppler-projected velocities at the photospheric level. In particular, even a simple visual inspection of Doppler images of the quiet Sun clearly reveals the pattern of supergranulation flow “cells”, whose trademark signature is a peak around ℓ ~ 120−130 (35 Megameters, Mm) in the spherical-harmonics energy spectrum of Doppler-projected velocities (Hathaway et al. 2000, 2015; Williams et al. 2014). The physical origin of this supergranulation is widely debated (Rieutord & Rincon 2010). In particular, while the idea that supergranulation-scale flows may just be a manifestation of some form of thermal convection has a long history, it has often been dismissed due to the seeming lack of photometric intensity contrast at the same scales (Langfellner et al. 2016). Besides, there is as yet no general consensus on local helioseismic estimates of the amplitude, depth and structure of subsurface flows on this scale (Nordlund et al. 2009; Rieutord & Rincon 2010; Gizon et al. 2010; Švanda et al. 2013; Švanda 2015; DeGrave et al. 2014) – or in fact on any scale larger than that (see, e.g., Hanasoge et al. 2012; Gizon & Birch 2012; Hanasoge et al. 2016; Greer et al. 2015, 2016; Toomre & Thompson 2015). Numerical simulations of the problem have, until recently, also been quite limited. While their results have not led to clear-cut results and conclusions (see reviews by Miesch 2005; Nordlund et al. 2009; Rieutord & Rincon 2010), many of them suggest that meso- to supergranulation-scale flows have a convective (buoyant) origin (e.g., Rincon et al. 2005; Lord et al. 2014; Cossette & Rast 2016).
In this article, we attempt to make further progress on this problem using the high-quality observations of the solar photosphere provided by the Solar Dynamics Observatory (SDO) and a new theoretical analysis. In Sect. 2, we present a global observational analysis of multiscale photospheric vector flows reconstructed from quasi-full disc Doppler and photometric data from SDO using a tracking technique. This analysis subsequently leads us in Sect. 3 to formulate a theory of anisotropic turbulent convection that may explain several distinctive dynamical properties of these flows. As further argued in Sect. 4, the combined results consistently suggest that photospheric flows in the horizontal range of scales in between supergranulation and granulation operate in a strongly anisotropic, self-similar, buoyant dynamical regime. Connections between these results and earlier work, as well as future perspectives, are discussed in Sect. 5. The main text of the article is focused on results. The technical details of the data processing and analysis are provided in the two Appendices.
2. Observations
Our observational analysis is based on 24 h of uninterrupted high-resolution white-light intensity and Doppler observations of the entire solar disc by the HMI instrument aboard the SDO satellite (Scherrer et al. 2012; Schou et al. 2012). The data was obtained on October 8, 2010 starting at 14:00:00 UTC, one of the quietest periods of solar activity since the launch of SDO. Our analysis is distinct and independent of the recent studies by Williams et al. (2014), Langfellner et al. (2015), Hathaway et al. (2015), and both confirms and extends some of their results.
2.1. Data analysis
2.1.1. Velocity field reconstruction
Our first objective is to reconstruct the three components (ur,uθ,uϕ) of the photospheric vector velocity field in the angular degree range 20 <ℓ< 850 from available observations. To this end, we perform a coherent structure tracking analysis (CST, Roudier et al. 2012) of photometric structures such as granules. This technique provides us with the projection of the photospheric velocity field (ux,uy) onto the plane of the sky/CCD matrix (Fig. 1). We can then combine the results with Doppler data, which provides the out-of-plane component uz of the velocity field, to calculate the full vector velocity field at the surface in solar spherical coordinates,  where B0 = 6.3° is the heliographic latitude of the central point of the solar disc at the time of observation. The reduction and filtering of the raw photometric and Doppler data required to build a consistent data set for (ux,uy,uz) is described in detail in Appendix A.
where B0 = 6.3° is the heliographic latitude of the central point of the solar disc at the time of observation. The reduction and filtering of the raw photometric and Doppler data required to build a consistent data set for (ux,uy,uz) is described in detail in Appendix A.
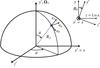 |
Fig. 1 Coordinate systems used in the reconstruction of the 3D photospheric velocity field. |
2.1.2. Spherical-harmonics analysis
The reconstructed vector field u(θ,ϕ) = (ur,uθ,uϕ) is expanded in terms of vector spherical harmonics as 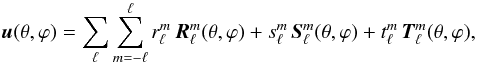 (4)where
(4)where 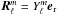 ,
, 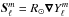 , and
, and 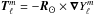 . The spectral coefficients
. The spectral coefficients 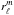 describe the radial flow component, and the coefficients
describe the radial flow component, and the coefficients 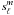 and
and 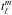 describe the spheroidal (divergent) and toroidal (vortical) parts of the horizontal flow components, respectively. Global maps of the horizontal divergence and radial vorticity at the surface are obtained by mapping back
describe the spheroidal (divergent) and toroidal (vortical) parts of the horizontal flow components, respectively. Global maps of the horizontal divergence and radial vorticity at the surface are obtained by mapping back 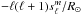 and
and 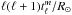 to physical space. The corresponding one-dimensional radial, spheroidal and toroidal energy spectra are given by
to physical space. The corresponding one-dimensional radial, spheroidal and toroidal energy spectra are given by 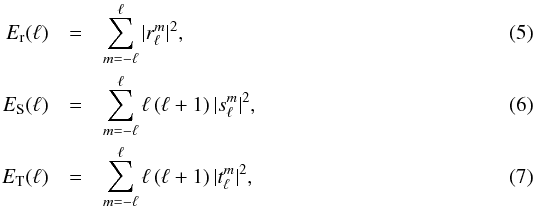 respectively. The ℓ(ℓ + 1) prefactors in ES and ET result from the definition of the spheroidal and toroidal vector spherical harmonics basis vectors.
respectively. The ℓ(ℓ + 1) prefactors in ES and ET result from the definition of the spheroidal and toroidal vector spherical harmonics basis vectors.
The technical aspects of the harmonic-transforms procedure of SDO/HMI data are described in detail in Appendix B. Here, it suffices to mention that the data must first be apodized because we only see one side of the Sun, and we must eliminate near-limb regions where the CST analysis is not reliable. Besides, as will be shown below, the radial component of the flow is very weak and can only be tentatively determined using data close to the disc center to limit contamination by the intrinsic algorithmic noise of the CST in the deprojection process. We therefore use an apodizing window with a 15° opening heliocentric angle from the disc center to compute the spectra of the radial and line-of-sight (Doppler) velocity fields, and a window with a 60° opening angle to compute the spectra of the horizontal velocity field. The general mathematical definition of these windows is provided in Eq. (B.5).
 |
Fig. 2 a)Left: quasi-full-disc map of the horizontal divergence |
2.2. Results
2.2.1. Velocity field maps
Figure 2 shows maps of the horizontal divergence field ∇h·uh and vertical vorticity field 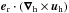 derived from a single snapshot of the 30-min-averaged horizontal surface velocity field (uθ,uϕ) using the spherical-harmonics spheroidal-toroidal decomposition into divergent and vortical motions. The pattern is dominated by supergranulation, whose divergent morphology is revealed in the close-up panel using a line-integral convolution technique highlighting horizontal-flow Lagrangian trajectories (Cabral & Leedom 1993). The vortical component of the flow is significantly weaker than the divergent component, as indicated by the associated rate of strains reported in the color bars (and further demonstrated in the spectral analysis presented below). Figure 3 shows a local map in the same disc-center zone of the 24h-averaged ur, superimposed with horizontal flows averaged over the same time scale. There is a noticeable correlation between the weak upflows (downflows) and horizontal divergences (convergences) at the supergranulation scale.
derived from a single snapshot of the 30-min-averaged horizontal surface velocity field (uθ,uϕ) using the spherical-harmonics spheroidal-toroidal decomposition into divergent and vortical motions. The pattern is dominated by supergranulation, whose divergent morphology is revealed in the close-up panel using a line-integral convolution technique highlighting horizontal-flow Lagrangian trajectories (Cabral & Leedom 1993). The vortical component of the flow is significantly weaker than the divergent component, as indicated by the associated rate of strains reported in the color bars (and further demonstrated in the spectral analysis presented below). Figure 3 shows a local map in the same disc-center zone of the 24h-averaged ur, superimposed with horizontal flows averaged over the same time scale. There is a noticeable correlation between the weak upflows (downflows) and horizontal divergences (convergences) at the supergranulation scale.
 |
Fig. 3 Local map at the disc center of the 24h-averaged radial (color contours) and horizontal spheroidal flow components (arrow field). |
2.2.2. Energy spectra
Figure 4 shows the spherical-harmonics radial, spheroidal and toroidal energy spectra Er(ℓ), ES(ℓ), and ET(ℓ) of the 30-min-averaged velocity-field components. The horizontal divergent component is energetically dominant at all scales probed: the corresponding spheroidal spectrum ES(ℓ) exhibits a clear peak at the supergranulation scale ℓ ~ 120, corresponding to a typical rms flow velocity of 400 m s-1. The rms radial flow is 20−30 m s-1 at ℓ ~ 120. The spectra of the different flow components behave differently for ℓ > 120: the spheroidal ES(ℓ) and radial Er(ℓ) spectra respectively decay and increase with decreasing scale, while the toroidal spectrum ET(ℓ) is almost flat. The exact shapes of the weaker and noisier Er(ℓ) and ET(ℓ) are moderately sensitive to the processing and averaging of the data, but the general trend described here is robust (as explained in Appendix A.2, it is very difficult to separate the Doppler contributions of the large-scale spectral tail of granulation from those of the radial component of the large-scale motions otherwise detected by the CST. Consequently, and while we did our best to remove the large-scale contribution of granulation from the Doppler data, our results for Er(ℓ) in the range 120 < ℓ < 500 still probably slightly overestimate the actual amplitude of the radial component of flows not associated with granulation. We also find that Er(ℓ) lies somewhere between ℓ1/2 and ℓ power laws, depending on the exact filtering procedure applied to the Doppler signal). The spectral falloff at ℓ > 500 is due to the intrinsic 2.5–5 Mm CST spatial resolution down to which the vector-field reconstruction was performed. The different power laws that these apparently self-similar spectra follow for ℓ < 500 will be discussed in Sects. 3.3 and 4.3.
 |
Fig. 4 Spherical-harmonics energy spectra (see Eqs. (5)–(7)) of maps of the 30-min-averaged (top) velocity field derived from the joint CST-Doppler analysis. The thin lines indicate different possible spectral slopes (see Sect. 3). Vertical dashed line: ℓ = 120. Inset: vertical scale estimate. |
2.2.3. Vertical correlation scale
Finally, we estimate the typical vertical correlation scale λr of these subsonic flows as a function of horizontal scale λh = 2π/kh (or of the angular degree ℓ = khR⊙). This can be obtained from the mass conservation relation 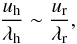 (8)where uh and ur are the horizontal and vertical velocity fluctuations (because the medium is stratified, here λr serves as an a priori proxy notation for either the radial wavelength of the perturbations or the local density scale height, whichever one is smaller). We therefore define
(8)where uh and ur are the horizontal and vertical velocity fluctuations (because the medium is stratified, here λr serves as an a priori proxy notation for either the radial wavelength of the perturbations or the local density scale height, whichever one is smaller). We therefore define 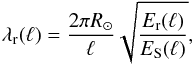 (9)and plot this quantity in Fig. 4 (inset) for 30 <ℓ< 500. Remarkably, the typical vertical correlation scale does not vary significantly in the range 120 <ℓ< 500 ([9,35] Mm), that is λr ~ [2.5,4] Mm. Considering the uncertainties in the determination of Er discussed in Sect. 2.2.2, this scale estimate should probably be considered as an upper bound rather than as an exact value. Overall, this scale appears to be comparable with the density scale height Hρ ≃ [1,2] Mm below the surface, but is somewhat deeper than the granulation thermal boundary layer (Nordlund et al. 2009).
(9)and plot this quantity in Fig. 4 (inset) for 30 <ℓ< 500. Remarkably, the typical vertical correlation scale does not vary significantly in the range 120 <ℓ< 500 ([9,35] Mm), that is λr ~ [2.5,4] Mm. Considering the uncertainties in the determination of Er discussed in Sect. 2.2.2, this scale estimate should probably be considered as an upper bound rather than as an exact value. Overall, this scale appears to be comparable with the density scale height Hρ ≃ [1,2] Mm below the surface, but is somewhat deeper than the granulation thermal boundary layer (Nordlund et al. 2009).
2.3. Main conclusions
The observational analysis presented above leads us to the following conclusions.
-
(i)
The flow in the range 120 <ℓ< 500 is characterized by divergent (convergent) horizontal flows correlated with upflows (downflows). This predominantly cell-like morphology of the flow suggests that the dynamics in that range of scales is dominated by buoyancy forces.
-
(ii)
The ratio of uh to ur suggests that motions are strongly anisotropic (λr ≪ λh) and strongly feel the effects of stratification, with the vertical correlation scale of order the density scale height.
-
(iii)
The significant energy content of horizontal motions and their spectral break at the supergranulation scale, followed by the apparent power-law decay of their spectrum at smaller horizontal scales, suggest that supergranulation corresponds to the largest buoyancy-driven scale of the system, below which some form of nonlinear cascade takes place.
3. Theoretical considerations
Let us now attempt a theory of anisotropic turbulent convection that could explain these observations. As argued by Rincon (2007), a good starting point is the Bolgiano-Obukhov (BO59, see Oboukhov 1959; Bolgiano 1962) phenomenology, which is based on the following assumptions: (i) a constant spectral flux of buoyancy fluctuations follows from the temperature/energy equation; (ii) a balance between the inertial and buoyancy terms in the momentum equation; and (iii) isotropy of motions. BO59 predicts a k− 7/5 thermal spectrum, and a steep k− 11/5 velocity spectrum. For the Sun, the latter is ruled out by Fig. 4 for 120 < ℓ < 500. This is not very surprising because, while the first two BO59 assumptions make sense in the present context, the isotropy assumption must manifestly be false because λr ≪ λh (see Sect. 2.2.3).
More generally, we point out that the isotropic BO59 scaling laws are not observed either in simulations of Rayleigh-Bénard convection with order-unity vertical to horizontal aspect ratio (Rincon 2006, 2007; Kumar et al. 2014). While the conclusions of these previous studies apply to the regime kH > 1 (where k is an isotropic wave number), they do not appear to be directly applicable to the strongly anisotropic regime khH ≪ 1 characteristic of the astrophysical problem investigated in the present paper. In any case, in what follows, we only use the phenomenology of the original isotropic BO59 theory as a physical motivation to derive distinct anisotropic scaling laws for the largely unexplored “long horizontal wavelength” regime khH ≪ 1.
3.1. Theoretical framework
An anisotropic generalization of BO59 may be derived from the following set of dynamical equations valid in the Boussinesq and anelastic limits: 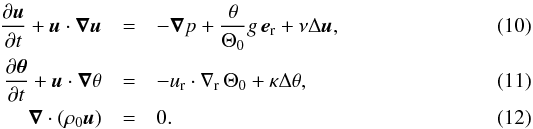 Here ρ0 is the mean density, u denotes velocity perturbations, p denotes pressure fluctuations divided by ρ0, Θ = Θ0 + θ is the actual temperature in the Boussinesq limit, and the potential temperature (Pρ− γ)1 /γ in the anelastic limit, Θ0(r) is its horizontally averaged part and θ its fluctuations around this average, ν is the kinematic viscosity, κ is the thermal diffusivity (κ ≫ ν in the Sun), and g = −ger is the acceleration of gravity.
Here ρ0 is the mean density, u denotes velocity perturbations, p denotes pressure fluctuations divided by ρ0, Θ = Θ0 + θ is the actual temperature in the Boussinesq limit, and the potential temperature (Pρ− γ)1 /γ in the anelastic limit, Θ0(r) is its horizontally averaged part and θ its fluctuations around this average, ν is the kinematic viscosity, κ is the thermal diffusivity (κ ≫ ν in the Sun), and g = −ger is the acceleration of gravity.
3.2. Phenomenology of anisotropic turbulent convection
The solar convection zone underneath the thin thermal boundary layer at the surface is in the strongly nonlinear convection regime, so its thermodynamic profile is very close to adiabatic and Θ0 is almost independent of r. We may then argue that the thermal injection term on the r.h.s. of Eq. (11) is small compared to the nonlinear advection term on the l.h.s.. Similarly to the Kolmogorov phenomenology in hydrodynamics (K41, see, e.g., Davidson 2004), which postulates a constant flux of kinetic energy in the inertial range (δu3/λ ~ const.), the dynamics in this “thermal-inertial” regime is characterized by a constant flux of θ variance from scale to scale: 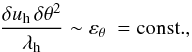 (13)where εθ = ⟨κ | ∇δθ | 2⟩ is the (time) average dissipation rate of thermal fluctuations (equal to their injection rate) and δ denotes increments of fluctuations between two points separated by a horizontal separation vector λh at a constant radial coordinate. Equation (13) effectively corresponds to BO59 assumption (i). This can, in fact, also be formalized on the basis of Yaglom’s exact law for dissipative scalars (Monin & Yaglom 1971; Rincon 2006), which Eq. (11) obviously satisfies if ∇rΘ0 = 0. Similarly to BO59 assumption (ii), we seek a buoyancy-dominated dynamical regime balancing the inertial and buoyancy terms in Eq. (10), but we drop the isotropy assumption, expecting instead that λr ≪ λh. The result of this is
(13)where εθ = ⟨κ | ∇δθ | 2⟩ is the (time) average dissipation rate of thermal fluctuations (equal to their injection rate) and δ denotes increments of fluctuations between two points separated by a horizontal separation vector λh at a constant radial coordinate. Equation (13) effectively corresponds to BO59 assumption (i). This can, in fact, also be formalized on the basis of Yaglom’s exact law for dissipative scalars (Monin & Yaglom 1971; Rincon 2006), which Eq. (11) obviously satisfies if ∇rΘ0 = 0. Similarly to BO59 assumption (ii), we seek a buoyancy-dominated dynamical regime balancing the inertial and buoyancy terms in Eq. (10), but we drop the isotropy assumption, expecting instead that λr ≪ λh. The result of this is 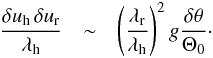 (14)The small (λr/λh)2 prefactor on the r.h.s. accounts for the partial cancellation of buoyancy by the pressure gradient in the vertical direction, as a result of the horizontal redistribution of buoyancy work by pressure forces (this prefactor also appears in the dispersion relation of gravity waves in the limit λr ≪ λh).
(14)The small (λr/λh)2 prefactor on the r.h.s. accounts for the partial cancellation of buoyancy by the pressure gradient in the vertical direction, as a result of the horizontal redistribution of buoyancy work by pressure forces (this prefactor also appears in the dispersion relation of gravity waves in the limit λr ≪ λh).
3.3. Scaling laws
Equations (13), (14), combined with the mass conservation relation Eq. (8), lead to the following self-similar scaling relations, 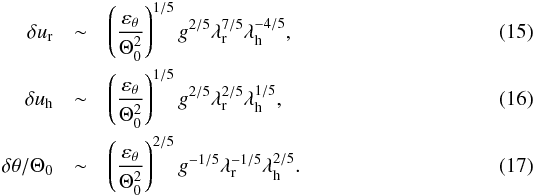 As a consistency check, we can see that the isotropic BO59 prediction δu ~ λ3/5, δθ ~ λ1/5 is recovered if we set λr = λh. Here however, we are instead interested in a strongly stratified regime in which the typical vertical scale height Hρ of the system is much smaller than λh. We therefore treat λr as a simple parameter equal to Hρ in Eqs. (15)–(17), as also suggested by our observational result of Sect. 2.2.3. Doing this results in the following power-law energy spectra as functions of horizontal wave number kh = ℓ/R⊙,
As a consistency check, we can see that the isotropic BO59 prediction δu ~ λ3/5, δθ ~ λ1/5 is recovered if we set λr = λh. Here however, we are instead interested in a strongly stratified regime in which the typical vertical scale height Hρ of the system is much smaller than λh. We therefore treat λr as a simple parameter equal to Hρ in Eqs. (15)–(17), as also suggested by our observational result of Sect. 2.2.3. Doing this results in the following power-law energy spectra as functions of horizontal wave number kh = ℓ/R⊙, 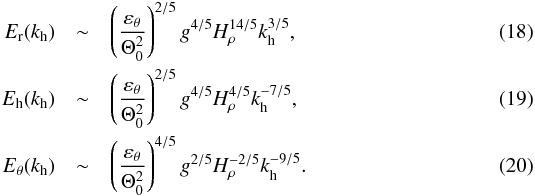 We note that in the regime khHρ ≪ 1, relevant to the astrophysics problem investigated here, these scalings are distinct from the classical isotropic BO59 prediction.
We note that in the regime khHρ ≪ 1, relevant to the astrophysics problem investigated here, these scalings are distinct from the classical isotropic BO59 prediction.
4. Comparison of theory with observations
4.1. Self-similar buoyant dynamics
Physically, the theory proposed above describes a situation in which buoyant thermal fluctuations stochastically injected through the surface boundary layer drive nonlinear anisotropic convective motions (plumes) in the adiabatic layer. By mixing these thermal fluctuations, turbulent velocity fluctuations drive a horizontal cascade of buoyancy down to thermal dissipative scales, resulting in statistically self-similar buoyant dynamics. This picture appears to be very much in line with the observed phenomenology of flows at scales larger than the granulation, notably the hierarchical, bubbling recurrent dynamics of “trees and families of fragmenting granules” documented by Roudier et al. (2003, 2009, 2016). The dynamics are “quasi-2D” in the sense that there is no refinement of the vertical scale as the horizontal cascade proceeds, but it is 3D in the sense that finite λr ~ Hρ is required to ensure mass conservation.
4.2. Spectral amplitudes vs. theoretical estimates
We now test for consistency between the observed spectral amplitudes and our theoretical scaling estimates derived by assuming that the observed fluctuations have a convective origin. A fit of the observed ES(ℓ) ~ Eh(kh) /R⊙ to Eq. (19) in the range 120 < ℓ < 500 for Hρ ≃ 2 Mm gives 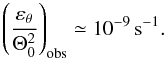 (21)On the other hand, a theoretical dimensional estimate of the same quantity can be obtained directly in terms of the solar luminosity L⊙ and internal structure of the Sun. The convective flux as a function of horizontal scale, as estimated from Eqs. (15)–(17), is
(21)On the other hand, a theoretical dimensional estimate of the same quantity can be obtained directly in terms of the solar luminosity L⊙ and internal structure of the Sun. The convective flux as a function of horizontal scale, as estimated from Eqs. (15)–(17), is 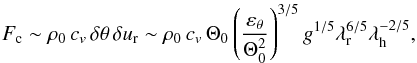 (22)where cv is the specific heat at constant volume. We see that this flux increases with decreasing horizontal scale (the horizontal kinetic energy, on the other hand, increases with increasing horizontal scale in this regime. This is a consequence of the different anisotropic scalings for ur and uh, and suggests that supergranulation-scale convection, while dominant in terms of horizontal kinetic energy, does not transport a significant fraction of the solar flux). However, this scaling theory is only applicable for λh ≫ λr. As λh becomes of the order of λr ~ Hρ, there should be a crossover to either the standard isotropic Bolgiano regime δu ~ λ3/5, δθ ~ λ1/5, or directly to the Kolmogorov regime δu ~ λ1/3, δθ ~ λ1/3 (Kumar et al. 2014). In both cases, the cascade proceeds in both horizontal and vertical directions, with Fc ~ λ4/5 for BO59 or Fc ~ λ2/3 for K41, that is, the convective flux decreases with decreasing scale λ. We therefore argue that the convective flux peaks at the isotropization scale λh ~ λr ~ Hρ, and require that Fc at this scale be of the order of the total solar flux,
(22)where cv is the specific heat at constant volume. We see that this flux increases with decreasing horizontal scale (the horizontal kinetic energy, on the other hand, increases with increasing horizontal scale in this regime. This is a consequence of the different anisotropic scalings for ur and uh, and suggests that supergranulation-scale convection, while dominant in terms of horizontal kinetic energy, does not transport a significant fraction of the solar flux). However, this scaling theory is only applicable for λh ≫ λr. As λh becomes of the order of λr ~ Hρ, there should be a crossover to either the standard isotropic Bolgiano regime δu ~ λ3/5, δθ ~ λ1/5, or directly to the Kolmogorov regime δu ~ λ1/3, δθ ~ λ1/3 (Kumar et al. 2014). In both cases, the cascade proceeds in both horizontal and vertical directions, with Fc ~ λ4/5 for BO59 or Fc ~ λ2/3 for K41, that is, the convective flux decreases with decreasing scale λ. We therefore argue that the convective flux peaks at the isotropization scale λh ~ λr ~ Hρ, and require that Fc at this scale be of the order of the total solar flux, 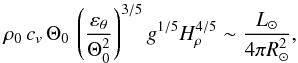 (23)where L⊙ ~ 3.8 × 1026 W is the solar luminosity. Using ρ0 ≃ 10-2 kg m-3, Θ0 ≃ 1.9 × 104 K, cv ≃ 105 J kg-1 K-1 (Stix 2004) and Hρ ≃ 2 Mm in Eq. (23), we obtain the theoretical estimate
(23)where L⊙ ~ 3.8 × 1026 W is the solar luminosity. Using ρ0 ≃ 10-2 kg m-3, Θ0 ≃ 1.9 × 104 K, cv ≃ 105 J kg-1 K-1 (Stix 2004) and Hρ ≃ 2 Mm in Eq. (23), we obtain the theoretical estimate 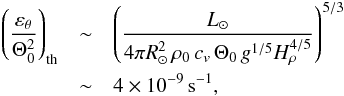 (24)which, given the approximate nature of the calculation and the neglect of geometric prefactors in Eqs. (15)–(17) and Eqs. (18)–(20), is relatively close to our observational estimate in Eq. (21) (this cascade time scale also appears to be similar to the typical plume thermal diffusion time scale in the Sun (Miesch 2005; Cossette & Rast 2016), that is, the “turbulent” diffusivity Hρδu(Hρ) at scale Hρ is of the order of the molecular diffusivity κ). Overall, the observed amplitudes therefore seem consistent with a convective origin of the turbulence. We note, finally, that if this estimate holds, then Eq. (17) suggests relative temperature fluctuations δθ/ Θ0 of approximately 1% at supergranulation scales in the first few Mm below the surface, consistent with helioseismic inferences (e.g., Duvall Jr et al. 1997).
(24)which, given the approximate nature of the calculation and the neglect of geometric prefactors in Eqs. (15)–(17) and Eqs. (18)–(20), is relatively close to our observational estimate in Eq. (21) (this cascade time scale also appears to be similar to the typical plume thermal diffusion time scale in the Sun (Miesch 2005; Cossette & Rast 2016), that is, the “turbulent” diffusivity Hρδu(Hρ) at scale Hρ is of the order of the molecular diffusivity κ). Overall, the observed amplitudes therefore seem consistent with a convective origin of the turbulence. We note, finally, that if this estimate holds, then Eq. (17) suggests relative temperature fluctuations δθ/ Θ0 of approximately 1% at supergranulation scales in the first few Mm below the surface, consistent with helioseismic inferences (e.g., Duvall Jr et al. 1997).
4.3. Spectral power laws
The horizontal spectral scaling laws predicted by our theory for the vertical and horizontal velocities, Er(ℓ) ~ Er(kh) /R⊙ ∝ ℓ3/5 (Eq. (18)) and ES(ℓ) ~ Eh(kh) /R⊙ ∝ ℓ− 7/5 (Eq. (19)), are broadly consistent with our observations, as shown in Fig. 4 by the power laws in the relevant range of scales. Different tentative scalings Eh(ℓ) ∝ ℓ− 5/3 and Er(ℓ) ∝ ℓ1/3, derived by naively postulating K41 scalings for the horizontal velocity field and using the mass conservation Eq. (8) with λr ~ Hρ to obtain the scaling of the vertical velocity component, are shown for comparison (dotted lines). Such scalings cannot be ruled out given the closeness of their spectral exponents to those of our theory and the aforementioned sensitivity in the determination of Er(ℓ) to the details of data processing. However, we see no reasonable physical argument as to why or how such an “anisotropic K41” regime would actually be realized in this environment, in contrast with the nonlinear buoyancy regime described above which naturally produces divergent horizontal motions at all scales (which are manifest in Figs. 2 and 3). At this stage, we do not have a theory for the scalings of the energy spectrum ET(ℓ) of the weaker horizontal toroidal velocity field, which seems to be only weakly coupled to the spheroidal divergent dynamics.
Finally, at even larger scales (ℓ< 120), beyond the supergranulation spectral break, our observational analysis shows a regime change to an intriguing ES(ℓ) ∝ ℓ2. This might be one of the first observations of a large-scale k2 pre-injection spectrum predicted by Saffman (1967). In theory, this spectrum is established as a result of long-range pressure correlations in turbulent flows in which fluid “eddies” have a random distribution of linear momentum (Davidson 2004), as opposed to a random distribution of angular momentum, which would instead result in a k4 spectrum (Batchelor & Proudman 1956). In the solar photosphere, such eddies could perhaps be associated with supergranulation cells and smaller-scale convective motions.
5. Discussion
We have presented a set of consistent arguments suggesting that turbulent flows at scales larger than granulation are a manifestation of statistically self-similar, strongly nonlinear convection in the bulk adiabatic layer below the solar surface. While the classic idea that supergranulation has a convective origin has usually been dismissed due to the seeming lack of photometric intensity contrast at the corresponding scales at the surface (Langfellner et al. 2016), helioseismology suggests that relative temperature fluctuations of approximately a few percent are present underneath the surface at such scales (Duvall Jr et al. 1997), in line with our calculation in Sect. 4.2. Besides, all existing large-scale simulations, including those with radiative transfer that do not display any “meso” or “super” scale intensity contrast at the surface, exhibit a strong buoyancy driving and flows at such scales in the bulk of the convective layer (e.g., Rincon et al. 2005; Nordlund et al. 2009; Bushby & Favier 2014; Lord et al. 2014; Cossette & Rast 2016, see also Rieutord & Rincon 2010, Fig. 12). Importantly, in these simulations, these scales are significantly larger than those of the most unstable linear modes of the system at rest, and the statistical order at such scales emerges dynamically in the nonlinear regime. If there are indeed significant thermal fluctuations associated with supergranulation-scale convection in the first few Mm below the surface, they may be blanketed by the thinner thermal granulation boundary layer, or could be optically thick due to the extreme dependence of opacities on temperature (Nordlund et al. 2009). Our theory also suggests that anisotropic supergranulation-scale convection, although it generates strong horizontal flows, does not significantly contribute to the transport of thermal energy due to the weakness of the radial component of the velocity field at such scales.
We do not have a quantitative answer as to what determines the spectral supergranulation break, and can only offer directions. Our theory predicts that thermal fluctuations increase with scale as Eθ(ℓ) ∝ ℓ− 9/5 in the nonlinear convection regime. However, there is a physical limit to how large such fluctuations can be, which could determine the maximum buoyant scale at which the self-similar scaling should break down. This limit should be related in some way to the maximum entropy fluctuations that can be injected into the adiabatic layer and, therefore, to the details of granulation and of the superadiabatic thermal boundary layer at the surface. This conclusion appears to be in line with the recent numerical simulations of this problem by Cossette & Rast (2016), which show that the thickness of the boundary layer has a strong effect on the energy-containing scale of the turbulent energy spectra. However, other physical explanations (e.g., Featherstone & Hindman 2016) cannot be ruled out at this stage.
Based on our experience with this data, the observational analysis and comparison with theory presented above are close to the limit of what is achievable with a combination of surface tracking and direct Doppler measurements given their disparate natures. Future progress will probably come from acoustic tomography (Toomre & Thompson 2015) and advanced numerical models. While somewhat speculative at this stage, our theory, including Eqs. (18)–(20), may soon be testable using such tools. An important question in this respect asks to what extent pristine power-law scalings derived from simple dynamical arguments can be realized in systems such as the photospheric transition region, where a variety of physical processes become intertwined.
The qualitative implications of such analyses could be wider than the solar context. They may notably provide us with fundamental insight into the structure of anisotropic turbulence in general (e.g., Nazarenko & Schekochihin 2011), as well as into turbulence in more distant, unresolved astrophysical systems supporting anisotropic waves or instabilities, such as stellar interiors (Zahn 2008; Miesch & Toomre 2009), galaxy clusters (Zhuravleva et al. 2014) and accretion discs (Walker et al. 2016).
Acknowledgments
This work is dedicated to the memory of Jean-Paul Zahn, a pioneer in astrophysical fluid dynamics research whose passion and work have been an invaluable source of inspiration to us.
We thank Nathanaël Schæffer for his assistance with the SHTns library, the SDO/HMI data provider JSOC, the SDO/HMI team members, in particular P. Scherrer, S. Couvidat and J. Schou for sharing information on the calibration and removal of systematics. This work was granted access to the HPC resources of CALMIP under allocation 2011-[P1115]. We also thank N. Renon for his assistance with the CST code parallelization. The work of A.A.S. was supported in part by grants from the UK STFC and EPSRC. F.R. and A.A.S. thank the Wolfgang Pauli Institute, Vienna, for its hospitality.
References
- Batchelor, G. K., & Proudman, I. 1956, Phil. Trans. R. Soc. Lond., Ser. A, 248, 369 [Google Scholar]
- Bolgiano, R. 1962, J. Geophys. Res., 67, 3015 [Google Scholar]
- Bushby, P. J., & Favier, B. 2014, A&A, 562, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cabral, B., & Leedom, L. C. 1993, in Proc. 20th Annual Conference on Computer Graphics and Interactive Techniques, SIGGRAPH ’93 (New York: ACM), 263 [Google Scholar]
- Charbonneau, P. 2014, ARA&A, 52, 251 [Google Scholar]
- Cossette, J.-F., & Rast, M. P. 2016, EpJ, 829, L17 [Google Scholar]
- Davidson, P. A. 2004, Turbulence (Oxford University Press) [Google Scholar]
- DeGrave, K., Jackiewicz, J., & Rempel, M. 2014, ApJ, 788, 127 [Google Scholar]
- Duvall Jr, T. L., Kosovichev, A. G., Scherrer, P. H., et al. 1997, Sol. Phys., 170, 63 [Google Scholar]
- Featherstone, N. A., & Hindman, B. W. 2016, ApJ, 830, L15 [Google Scholar]
- Gizon, L., & Birch, A. C. 2012, Proc. Natl. Acad. Sci., 109, 11896 [Google Scholar]
- Gizon, L., Birch, A. C., & Spruit, H. C. 2010, ARA&A, 48, 289 [Google Scholar]
- Greer, B. J., Hindman, B. W., Featherstone, N. A., & Toomre, J. 2015, ApJ, 803, L17 [Google Scholar]
- Greer, B. J., Hindman, B. W., & Toomre, J. 2016, ApJ, 824, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Hanasoge, S., Gizon, L., & Sreenivasan, K. R. 2016, Annu. Rev. Fluid Mech., 48, 191 [Google Scholar]
- Hanasoge, S. M., Duvall, T. L., & Sreenivasan, K. R. 2012, Proc. Natl. Acad. Sci., 109, 11928 [Google Scholar]
- Hathaway, D. H. 1992, Sol. Phys., 137, 15 [Google Scholar]
- Hathaway, D. H., Beck, J. G., Bogart, R. S., et al. 2000, Sol. Phys., 193, 299 [Google Scholar]
- Hathaway, D. H., Teil, T., Norton, A. A., & Kitiashvili, I. 2015, ApJ, 811, 105 [Google Scholar]
- Howe, R., & Thompson, M. J. 1998, A&AS, 131, 539 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kumar, A., Chatterjee, A. G., & Verma, M. K. 2014, Phys. Rev. E, 90, 023016 [Google Scholar]
- Kupka, F., Roxburgh, I., & Chan, K. L. 2007, Convection in Astrophysics, IAU Symp., 239 [Google Scholar]
- Langfellner, J., Gizon, L., & Birch, A. C. 2015, A&A, 581, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Langfellner, J., Birch, A. C., & Gizon, L. 2016, A&A, 596, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lord, J. W., Cameron, R. H., Rast, M. P., Rempel, M., & Roudier, T. 2014, ApJ, 793, 24 [Google Scholar]
- Miesch, M. S. 2005, Liv. Rev. Sol. Phys., 2, 1 [Google Scholar]
- Miesch, M. S., & Toomre, J. 2009, Annu. Rev. Fluid Mech., 41, 317 [Google Scholar]
- Monin, A. S., & Yaglom, A. M. 1971, Statistical Fluid Mechanics: Mechanics of Turbulence (MIT Press), 770 [Google Scholar]
- Nazarenko, S. V., & Schekochihin, A. A. 2011, J. Fluid Mech., 677, 134 [Google Scholar]
- Nordlund, Å., Stein, R. F., & Asplund, M. 2009, Liv. Rev. Sol. Phys., 6, 2 [Google Scholar]
- Oboukhov, A. M. 1959, Dokl. Akad. Nauk. SSR, 125, 1246 [Google Scholar]
- Rieutord, M., & Rincon, F. 2010, Liv. Rev. Sol. Phys., 7, 2 [Google Scholar]
- Rieutord, M., Roudier, T., Roques, S., & Ducottet, C. 2007, A&A, 471, 687 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rincon, F. 2006, J. Fluid Mech., 563, 43 [Google Scholar]
- Rincon, F. 2007, in Convection in Astrophysics, eds. F. Kupka, I. Roxburgh, & K. L. Chan, IAU Symp., 239, 58 [Google Scholar]
- Rincon, F., Lignières, F., & Rieutord, M. 2005, A&A, 430, L57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roudier, T., Lignières, F., Rieutord, M., Brandt, P. N., & Malherbe, J. M. 2003, A&A, 409, 299 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roudier, T., Rieutord, M., Brito, D., et al. 2009, A&A, 495, 945 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roudier, T., Rieutord, M., Malherbe, J. M., et al. 2012, A&A, 540, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roudier, T., Rieutord, M., Prat, V., et al. 2013, A&A, 552, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roudier, T., Malherbe, J. M., Rieutord, M., & Frank, Z. 2016, A&A, 590, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saffman, P. G. 1967, J. Fluid Mech., 27, 581 [Google Scholar]
- Schaeffer, N. 2013, Geophys. Geosyst., 14, 751 [Google Scholar]
- Scherrer, P. H., Schou, J., Bush, R. I., et al. 2012, Sol. Phys., 275, 207 [Google Scholar]
- Schou, J., & Brown, T. M. 1994, A&AS, 107, 541 [NASA ADS] [Google Scholar]
- Schou, J., Scherrer, P. H., Bush, R. I., et al. 2012, Sol. Phys., 275, 229 [Google Scholar]
- Stix, M. 2004, The Sun: an introduction (Berlin: Springer) [Google Scholar]
- Toomre, J., & Thompson, M. J. 2015, Space Sci. Rev., 196, 1 [Google Scholar]
- Švanda, M. 2015, A&A, 575, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Švanda, M., Roudier, T., Rieutord, M., Burston, R., & Gizon, L. 2013, ApJ, 771, 32 [Google Scholar]
- Walker, J., Lesur, G., & Boldyrev, S. 2016, MNRAS, 457, L39 [Google Scholar]
- Williams, P. E., Pesnell, W. D., Beck, J. G., & Lee, S. 2014, Sol. Phys., 289, 11 [Google Scholar]
- Zahn, J.-P. 2008, in The Art of Modeling Stars in the 21st Century, eds. L. Deng, & K. L. Chan, IAU Symp., 252, 47 [Google Scholar]
- Zhuravleva, I., Churazov, E., Schekochihin, A. A., et al. 2014, Nature, 515, 85 [Google Scholar]
Appendix A: Photospheric velocity field reconstruction
Appendix A.1: Data reduction
In order to obtain (ux,uy,uz) needed for the reconstruction of the three components of the photospheric velocity field in Eqs. (1)–(3), we used raw 4096 × 4096 HMI photometric and Doppler images with a 0.5′′ pixel size (~360 km) every δt = 45 s.
Appendix A.1.1: Reorientation and derotation of images
All the images were first reoriented using the SDO CROTA2 fits header keyword to have the solar north pole pointing “up” (y > 0 corresponds to the northern hemisphere), and derotated’ and aligned to avoid rotational smearing. We used the following rotation profile adjusted from the raw Doppler data averaged over the 24 h of observations: 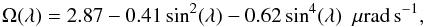 (A.1)where λ = π/ 2−θ is the latitude.
(A.1)where λ = π/ 2−θ is the latitude.
Appendix A.1.2: Coherent structure tracking (CST) analysis
Starting with a sequence of intensity images, the CST algorithm (Rieutord et al. 2007; Roudier et al. 2012, 2013) determines the projection (ux, uy) in the CCD plane of the photospheric Eulerian velocity field by following the trajectories of many individual intensity structures such as granules during their entire “life” (the period of time, typically a few minutes, during which a structure remains a coherent, single object that does not split or merge). The average velocity of each structure is computed from its total displacement over this time interval, and supersonic velocities (larger than 7 km s-1) are rejected. The velocities obtained this way are irregularly spaced on the field of view, and the last part of the procedure consists in approximating the results by the best differentiable Eulerian field fitting the data, using a multi-resolution wavelet analysis (Rieutord et al. 2007). Applying this procedure to the SDO/HMI data set, we obtained a sequence of 5862 velocity-field maps with a temporal resolution of 30 min and a spatial resolution of 2.5 Mm (3.5′′, or 7 HMI pixels, corresponding to a maximum angular degree ℓ ~ 850). We further removed the (x,y) velocity signal associated with the satellite motion 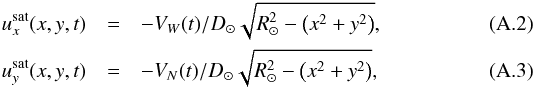 where D⊙ is the distance from the satellite to the Sun, and VW and VN are the westwards and northwards components of the satellite peculiar velocity (given in the data file’s headers). We finally found it necessary to filter out all the signal at spherical harmonics ℓ < 20, as the latter is polluted by systematic large-scale velocity-field residuals associated with imperfect corrections of the rotation, satellite motions, plages regions, and artificial large-scale drifts imprinted by the CST analysis itself far from disc center (Roudier et al. 2013). This filtering was performed in the spherical-harmonics space by means of the harmonic-transform machinery described Appendix B.
where D⊙ is the distance from the satellite to the Sun, and VW and VN are the westwards and northwards components of the satellite peculiar velocity (given in the data file’s headers). We finally found it necessary to filter out all the signal at spherical harmonics ℓ < 20, as the latter is polluted by systematic large-scale velocity-field residuals associated with imperfect corrections of the rotation, satellite motions, plages regions, and artificial large-scale drifts imprinted by the CST analysis itself far from disc center (Roudier et al. 2013). This filtering was performed in the spherical-harmonics space by means of the harmonic-transform machinery described Appendix B.
Appendix A.1.3: Doppler data analysis
Dopplergrams map the out-of-plane (line-of-sight, l.o.s.) component of the photospheric velocity field. The SDO/HMI convention is that uDop is taken as positive when the flow is away from the observer, so that the out-of-plane velocity towards the observer is uz ≃ −uDop (Fig. 1). This equality is only approximate because of the inclination between the actual l.o.s and the ez unit vector due to the finite distance between the Earth and the Sun. This effect is taken into account to eliminate the global rotational satellite motion signals, but is otherwise negligible. We first substracted the rotational Doppler shift 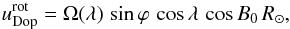 (A.4)where Ω(λ) is given in Eq. (A.1), and the Doppler shift associated with the satellite motion
(A.4)where Ω(λ) is given in Eq. (A.1), and the Doppler shift associated with the satellite motion 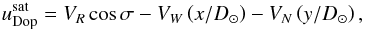 (A.5)where
(A.5)where 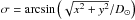 . The images were subsequently “derotated” in the same way as the white-light images and further corrected from a polynomial radial limbshift function adjusted from ring averages of two hours of data taken at different heliocentric angles from disc center ρ,
. The images were subsequently “derotated” in the same way as the white-light images and further corrected from a polynomial radial limbshift function adjusted from ring averages of two hours of data taken at different heliocentric angles from disc center ρ, 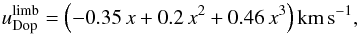 (A.6)where x = 1−cosρ and
(A.6)where x = 1−cosρ and 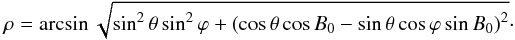 (A.7)Since the 5862 velocity-field maps derived from the CST have a 2.5 Mm spatial resolution, we then downsampled the 40962 Dopplergrams to 5862, keeping only one point out of seven in each direction, and averaged over 30-min periods to obtain an effective sequence of maps of uz, with the same spatial and temporal resolution as that of the (ux,uy) maps derived from CST.
(A.7)Since the 5862 velocity-field maps derived from the CST have a 2.5 Mm spatial resolution, we then downsampled the 40962 Dopplergrams to 5862, keeping only one point out of seven in each direction, and averaged over 30-min periods to obtain an effective sequence of maps of uz, with the same spatial and temporal resolution as that of the (ux,uy) maps derived from CST.
Appendix A.2: Noise analysis and ℓ-ν filtering
While the raw CST signal is not sensitive to solar oscillations or granulation, it is contaminated by an undesirable intrinsic algorithmic noise that can, to some extent, be removed via ℓ-ν filtering using the harmonic-transform machinery described in Appendix B. The ℓ-ν diagram of the x-component of the raw CST velocity field computed from 24 h of data is shown in Fig. A.1 (top – the y-component behaves similarly). The main signal (red bump) is contaminated by a white-noise-in-time component in the form of a vertical white stripe. To remove this noise, we filtered out all the data at frequencies larger than those given by the filtering envelope (also shown in the figure): 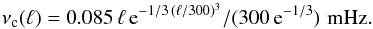 (A.8)The ℓ-ν diagram of the Doppler signal (first downgraded to the 586 × 586 CST resolution) for the same range of frequencies is shown in Fig. A.1 (bottom; the high-frequency part, not shown here, contains the usual p-mode ridges). The spectral support of the turbulent Doppler signal appears to be somewhat different from that of the CST. In particular, there is a fairly large, relatively high-frequency component in the 300 < ℓ < 800 range (in white in the figure), which we attribute to the large-scale spectral tail of granulation and which is not captured by the CST. Note that the decrease of this signal at the smallest scales represented is due to the coarse-graining associated with the downgrade of the Doppler maps to the CST resolution.
(A.8)The ℓ-ν diagram of the Doppler signal (first downgraded to the 586 × 586 CST resolution) for the same range of frequencies is shown in Fig. A.1 (bottom; the high-frequency part, not shown here, contains the usual p-mode ridges). The spectral support of the turbulent Doppler signal appears to be somewhat different from that of the CST. In particular, there is a fairly large, relatively high-frequency component in the 300 < ℓ < 800 range (in white in the figure), which we attribute to the large-scale spectral tail of granulation and which is not captured by the CST. Note that the decrease of this signal at the smallest scales represented is due to the coarse-graining associated with the downgrade of the Doppler maps to the CST resolution.
The presence of this extra signal component in the Doppler data but not in the CST implies that the two raw signals cannot naively be mixed in the 3D-velocity-field reconstruction in Eqs. (1)–(3), as this would lead to spurious cross-talk between the different field components. In our view, the most consistent way to proceed is, therefore, to apply the same ℓ-ν filtering envelope (A.8) to both Doppler and CST fields. While it is imperfect and does not totally remove the granulation tail contribution from the large-scale signal, this procedure focuses the analysis on large-scale motions inferred from the CST, limits the risk of cross-analysing signals of different physical origin, and makes it possible to extract the weak supergranulation-scale ur signal from the Doppler data out of the strong large-scale tail of the surface granulation dynamics. This filtering also entirely removes the solar oscillation signal from the Doppler data.
Finally, we found it necessary to discard the residual signal in the spherical harmonics ℓ < 20 because of the presence of significant instrumental systematics in the 2010 SDO data (priv. comm. by Couvidat, Scherrer, Schou, see also Hathaway et al. 2015).
 |
Fig. A.1 Distribution of power in the ℓ-ν plane for a 24-h sequence of ux signal derived from the CST (top) and SDO/HMI Doppler signal (bottom). The dashed line marks the filtering envelope (A.8). The color-scale from blue to red is identical on both plots and extends over five orders of magnitude. |
Appendix B: Harmonic-analysis technique
Appendix B.1: Harmonic transforms and spectra
Any sufficiently smooth scalar field ψ(θ,ϕ) on the sphere can be expanded in terms of spherical harmonics as 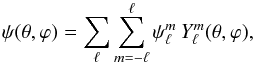 (B.1)where
(B.1)where 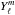 is the orthonormalized spherical harmonic of degree ℓ and azimuthal wavenumber m, and
is the orthonormalized spherical harmonic of degree ℓ and azimuthal wavenumber m, and 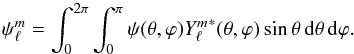 (B.2)The one-dimensional energy spectrum of ψ is defined as
(B.2)The one-dimensional energy spectrum of ψ is defined as 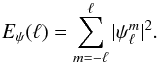 (B.3)This decomposition can be generalized to vector fields, as explained in the main article; we refer to Eq. (4). The rest of this Appendix describes the procedure used to compute the harmonic transforms of scalar and vector fields derived from SDO/HMI data sets.
(B.3)This decomposition can be generalized to vector fields, as explained in the main article; we refer to Eq. (4). The rest of this Appendix describes the procedure used to compute the harmonic transforms of scalar and vector fields derived from SDO/HMI data sets.
Appendix B.2: Data interpolation on a Gauss-Legendre-Fourier grid
Spherical-harmonics transforms of all fields are computed using Gauss-Legendre quadrature coupled to a Fast-Fourier-Transform algorithm in the azimuthal direction. This requires the knowledge of the field on a two-dimensional (2D) Gauss-Legendre-Fourier (GLF) grid of size Nθ × Nϕ of polar angles corresponding to Gauss nodes θn(0 <θn<π,1 ≤ n ≤ Nθ), and equally-spaced longitudes ϕp = 2πp/Nϕ (with 0 ≤ p<Nϕ; by convention, ϕ = 0 is the central meridian of the visible disc, ϕ = π/ 2 is the eastern limb and ϕ = −π/ 2 is the western limb). However, our fields are originally available on a 5862 Cartesian 2D grid. Therefore, interpolation from the original Cartesian grid to a GLF grid is a prerequisite. To carry it out, we choose a spectral resolution (Nθ,Nϕ), compute the Cartesian coordinates of the corresponding GLF grid in the plane of the sky/CCD, and interpolate the field on the original, regular Cartesian grid to these coordinates using the RectBivariateSpline function of the Python module scipy.interpolate. A similar, reverse interpolation procedure is used to reproject fields manipulated in spectral space from the GLF grid to the original “observation” grid. This is, for instance, required to obtain the divergence field on this grid.
Appendix B.3: Estimator of spectral coefficients
An apodizing window W(θ,ϕ) must be applied to the data in order to deal with the fact that we only see one side of the Sun, and to eliminate near-limb regions where the CST analysis is unreliable due to projection effects. We use the estimator 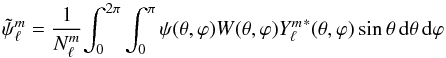 (B.4)to obtain the spectral coefficients
(B.4)to obtain the spectral coefficients 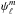 of a scalar field ψ known on a limited area (see Hathaway 1992, for a similar definition; the harmonic coefficients of vector fields can be estimated similarly). The normalization coefficients
of a scalar field ψ known on a limited area (see Hathaway 1992, for a similar definition; the harmonic coefficients of vector fields can be estimated similarly). The normalization coefficients 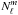 are functionally dependent on the apodizing window, and can be defined in different ways (see next paragraph). The integral in the numerator of Eq. (B.4), or its generalization to the vector case, are computed from the discrete data sets interpolated on the GLF grid using the python interface of the SHTns library (Schaeffer 2013). The tilde notation for the estimators of the spectral coefficients is dropped in the text to simplify notations.
are functionally dependent on the apodizing window, and can be defined in different ways (see next paragraph). The integral in the numerator of Eq. (B.4), or its generalization to the vector case, are computed from the discrete data sets interpolated on the GLF grid using the python interface of the SHTns library (Schaeffer 2013). The tilde notation for the estimators of the spectral coefficients is dropped in the text to simplify notations.
Appendix B.4: Apodizing and normalization issues
Dealing with data on a limited area, or apodizing it, introduces leakage between different harmonics. In helioseismology, this leakage can partly be alleviated by separating the oscillatory components of the signal according to their discrete temporal frequencies (Schou & Brown 1994; Howe & Thompson 1998). However, this approach cannot be used here because the flows that we analyze are characterized by a continuum of time scales. As a result, leakage cannot be eliminated and can notably lead to overestimating the magnitude of the flow.
The results of a detailed technical analysis including careful tests and validations using synthetic data (not presented here but available on request) show that a sensible approach to estimate accurately the spectral coefficients in our problem is to use a “ρ (heliocentric angle from disc center) window” function, ![\appendix \setcounter{section}{2} \begin{equation} \label{eq:rhomask} W(\rho)=\left[\frac{1}{2}\left(1-\tanh S\left(\frac{\rho-\rho_{\rm c}}{\rho_{\rm c}}\right)\right)\right]^n, \end{equation}](/articles/aa/full_html/2017/03/aa29747-16/aa29747-16-eq185.png) (B.5)where S is a smoothing parameter, ρc is the critical heliocentric angle from disc center above which the apodization becomes significant, and integer n parametrizes the sharpness of the fall-off of the window function. We adopt an “energy-conserving” normalization, which consists in directly calibrating the coefficients
(B.5)where S is a smoothing parameter, ρc is the critical heliocentric angle from disc center above which the apodization becomes significant, and integer n parametrizes the sharpness of the fall-off of the window function. We adopt an “energy-conserving” normalization, which consists in directly calibrating the coefficients ![\hbox{$\Nlm[W]$}](/articles/aa/full_html/2017/03/aa29747-16/aa29747-16-eq189.png) introduced in Eq. (B.4) once and for all based on a comparison between the (known) analytical spectra of a few test synthetic scalar fields defined over the whole sphere on the one hand, and the spectra obtained through a (unrenormalized) harmonic analysis of the apodized versions of the same fields on the other hand. For the family of W given by Eq. (B.5), we found that using a normalization factor independent of ℓ and m is appropriate. Most importantly, although this strategy does not entirely eliminate the leakage problem, it does alleviate that of overestimating the spectral amplitude.
introduced in Eq. (B.4) once and for all based on a comparison between the (known) analytical spectra of a few test synthetic scalar fields defined over the whole sphere on the one hand, and the spectra obtained through a (unrenormalized) harmonic analysis of the apodized versions of the same fields on the other hand. For the family of W given by Eq. (B.5), we found that using a normalization factor independent of ℓ and m is appropriate. Most importantly, although this strategy does not entirely eliminate the leakage problem, it does alleviate that of overestimating the spectral amplitude.
Appendix B.5: Harmonic-analysis parameters
All the results of the paper involving a harmonic analysis were computed for a resolution (Nθ,Nϕ) = (846,1728), corresponding to ℓmax = mmax = 845. This resolution was determined using the Nyquist criterion applied to the 5862 CST grid resolution of ~ 2.5 Mm. We used the window function ![\appendix \setcounter{section}{2} \begin{equation} \label{eq:window60} W_{60}(\rho)=\left[\frac{1}{2}\left(1-\tanh 5\left(\frac{\rho-\pi/3}{\pi/3}\right)\right)\right]^6, \end{equation}](/articles/aa/full_html/2017/03/aa29747-16/aa29747-16-eq194.png) (B.6)which apodizes the field sharply at angular distances from disc center larger than ρc = 60°, and the same window with a narrower opening ρc = 15°. The normalization of the harmonic spectra of the apodized data is based on the energy-conserving normalization introduced above, with
(B.6)which apodizes the field sharply at angular distances from disc center larger than ρc = 60°, and the same window with a narrower opening ρc = 15°. The normalization of the harmonic spectra of the apodized data is based on the energy-conserving normalization introduced above, with ![\hbox{$\Nlm[W_{60}]=0.36$}](/articles/aa/full_html/2017/03/aa29747-16/aa29747-16-eq197.png) for all ℓ and m.
for all ℓ and m.
All Figures
 |
Fig. 1 Coordinate systems used in the reconstruction of the 3D photospheric velocity field. |
| In the text | |
 |
Fig. 2 a)Left: quasi-full-disc map of the horizontal divergence |
| In the text | |
 |
Fig. 3 Local map at the disc center of the 24h-averaged radial (color contours) and horizontal spheroidal flow components (arrow field). |
| In the text | |
 |
Fig. 4 Spherical-harmonics energy spectra (see Eqs. (5)–(7)) of maps of the 30-min-averaged (top) velocity field derived from the joint CST-Doppler analysis. The thin lines indicate different possible spectral slopes (see Sect. 3). Vertical dashed line: ℓ = 120. Inset: vertical scale estimate. |
| In the text | |
 |
Fig. A.1 Distribution of power in the ℓ-ν plane for a 24-h sequence of ux signal derived from the CST (top) and SDO/HMI Doppler signal (bottom). The dashed line marks the filtering envelope (A.8). The color-scale from blue to red is identical on both plots and extends over five orders of magnitude. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


