| Issue |
A&A
Volume 599, March 2017
|
|
|---|---|---|
| Article Number | A6 | |
| Number of page(s) | 11 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201629745 | |
| Published online | 20 February 2017 | |
New analytical solutions for chemical evolution models: characterizing the population of star-forming and passive galaxies
1 Dipartimento di Fisica, Sezione di Astronomia, Università di Trieste, via G.B. Tiepolo 11, 34131 Trieste, Italy
e-mail: spitoni@oats.inaf.it
2 INAF Osservatorio Astronomico di Trieste, via G.B. Tiepolo 11, 34131 Trieste, Italy
Received: 19 September 2016
Accepted: 4 November 2016
Context. Analytical models of chemical evolution, including inflow and outflow of gas, are important tools for studying how the metal content in galaxies evolves as a function of time.
Aims. We present new analytical solutions for the evolution of the gas mass, total mass, and metallicity of a galactic system when a decaying exponential infall rate of gas and galactic winds are assumed. We apply our model to characterize a sample of local star-forming and passive galaxies from the Sloan Digital Sky Survey data, with the aim of reproducing their observed mass-metallicity relation.
Methods. We derived how the two populations of star-forming and passive galaxies differ in their particular distribution of ages, formation timescales, infall masses, and mass loading factors.
Results. We find that the local passive galaxies are, on average, older and assembled on shorter typical timescales than the local star-forming galaxies; on the other hand, the star-forming galaxies with higher masses generally show older ages and longer typical formation timescales compared than star-forming galaxies with lower masses. The local star-forming galaxies experience stronger galactic winds than the passive galaxy population. Exploring the effect of assuming different initial mass functions in our model, we show that to reproduce the observed mass-metallicity relation, stronger winds are requested if the initial mass function is top-heavy. Finally, our analytical models predict the assumed sample of local galaxies to lie on a tight surface in the 3D space defined by stellar metallicity, star formation rate, and stellar mass, in agreement with the well-known fundamental relation from adopting gas-phase metallicity.
Conclusions. By using a new analytical model of chemical evolution, we characterize an ensemble of SDSS galaxies in terms of their infall timescales, infall masses, and mass loading factors. Local passive galaxies are, on average, older and assembled on shorter typical timescales than the local star-forming galaxies. Moreover, the local star-forming galaxies show stronger galactic winds than the passive galaxy population. Finally, we find that the fundamental relation between metallicity, mass, and star formation rate for these local galaxies is still valid when adopting the average galaxy stellar metallicity.
Key words: galaxies: abundances / galaxies: evolution / galaxies: ISM
© ESO, 2017
1. Introduction
Chemical evolution of galaxies studies how subsequent stellar generations and gas flows alter the chemical composition of the galaxy interstellar medium (ISM) to give rise to the present-day observed chemical abundance pattern of galaxies. In this respect, the galaxy star formation and gas mass assembly histories play a major role, together with the assumed initial mass function (IMF) and stellar nucleosynthetic yields. Chemical evolution is an essential ingredient in the broader framework of galactic archeology, which aims at constraining and recovering the formation and evolution of galaxies, starting from the observed chemical, dynamical, and photometric properties of their member stars at the present time.
Simple analytical models of chemical evolution have previously enabled deriving analytical functions for the metallicity evolution of a stellar system. We assume a constant IMF and complete mixing of the various chemical species within the ISM of a galaxy at any time of its evolution. Finally, a further fundamental hypothesis is to retain the instantaneous recycling approximation (IRA): all the stars with mass m ≥ 1 M⊙ instantaneously die as they form, whereas all the stars with m< 1 M⊙ have infinite lifetimes. This type of models still represents a useful tool for tracing the metallicity evolution of galaxies, but only when the abundance of chemical elements produced on typical short timescales is considered. An example of such a chemical element is given by oxygen, which incidentally represents the best proxy for the total metallicity of the galaxy ISM. Pioneering works in this field are considered those of Schmidt (1963); Searle & Sargent (1972); Tinsley (1974); and Pagel & Patchett (1975).
To build a realistic analytical model for the galaxy chemical evolution, gas flows must be included in the set of differential equations to be solved because galaxies do not evolve as closed boxes. Analytical and semi-analytical solutions for models including infall and outflow of gas have been known for at least 30 yr (see, for example, Chiosi 1980; Clayton & Pantelaki 1986, 1993; Pagel & Patchett 1975; Hartwick 1976; Clayton 1988; Twarog 1980; Edmunds 1990; Erb 2008; Recchi & Kroupa 2015; Kudritzki et al. 2015). Moreover, solutions have also been found later with radial gas flows, provided a particular gas velocity profile is assumed in the equations (see Lacey & Fall 1985; Edmunds & Greenhow 1995; Martinelli 1998; Portinari & Chiosi 2000; Spitoni & Matteucci 2011; Pezzulli & Fraternali 2015). A summary of some of the most frequently used analytical solutions for the metallicity evolution of a system with different prescriptions for inflows and outflows of gas can be found in Recchi et al. (2008) and Spitoni et al. (2010).
Recently, Spitoni (2015) presented an analytical solution for the evolution of the metallicity of a galaxy in presence of environmental effects. In this work, a galaxy suffers the infall of enriched gas from another evolving galactic system, with the metallicity of the infalling material evolving according to the metallicity evolution of the companion galaxy, hence with chemical abundances variable in time.
More recently, Weinberg et al. (2016) showed chemical analytical solutions with different prescriptions for the star formation rate (SFR) analyzing constant, exponential, or linear-exponential star formation histories.
To solve the set of differential equations for the gas mass, total mass, and metallicity of the galaxy and hence obtain analytical solutions for these quantities, some of the previous works in the literature (see, for example, Matteucci & Chiosi 1983; Matteucci 2001, 2012) assumed an infall rate of gas that is directly proportional to the SFR over the entire galaxy evolution. This assumption is not physical, and it represents a strong simplification in analytical models. Nevertheless, by exploring the effects of different prescriptions for the infall term in the equations, the final predicted physical properties of the galaxy have been found to not deviate substantially from the case of a generic exponential infall law (Recchi et al. 2008). The infall of gas that follows an exponential law is a fundamental assumption adopted in most of the detailed numerical chemical evolution models in which IRA is relaxed. Chemical evolution models of our Galaxy (Chiappini et al. 1997; Romano et al. 2010; Brusadin et al. 2013; Micali et al. 2013) assume that the various different stellar components formed through different separated accretion episodes of gas, with the accretion rate of each episode obeying to a decaying exponential law. Colavitti et al. (2008) reported that the two-infall model of Chiappini et al. (1997) is qualitatively in agreement with results of the GADGET2 (Springel 2005) cosmological hydrodynamical simulations when the standard cosmological parameters from WMAP three-years (Spergel et al. 2007) are assumed, namely Ω0 = 0.275, Ωλ = 0.725, and Ωb = 0.041.
We here present the results of an analytical chemical evolution model in which a decaying exponential infall rate of gas is assumed as a function of time; we show that analytical solutions for the evolution of the galaxy metallicity, gas mass, and total mass can be found under this assumption. Furthermore, we apply our model to investigate and explain the observed mass-metallicity relation (MZ relation, hereafter), as derived in a sample of galaxies from the Sloan Digital Sky Survey (SDSS) by Peng et al. (2015). We extend and update the methods and results obtained by Spitoni et al. (2010), which reproduced the observed MZ relation in 27 730 local SDSS star-forming galaxies (Kewley & Ellison 2008) with an analytical model of chemical evolution. In particular, we aim at characterizing the two distinct MZ relations that Peng et al. (2015) derived for the local actively star-forming (we refer to them as star-forming) galaxies and the passively evolving (passive) galaxies. A tight relation between the stellar mass and the gas-phase metallicity such as displayed by a large sample of galaxies like the one provided by the SDSS can be used to constrain the various fundamental parameters playing a role in any galaxy formation theory: the infall timescale, wind loading factor parameters, infall mass values, and the star formation efficiencies.
On the one hand, the analytical model of Spitoni et al. (2010) assumed both the gas outflow rate and the gas infall rate to be directly proportional to the galaxy SFR; when this simplifying assumption is made, the analytical solution for the metallicity of the system does not explicitly depend upon the time variable, which indeed turns out to be hidden in the galaxy gas mass fraction entering in the equations.
Furthermore, Kudritzki et al. (2015) assumed constant ratios of galactic wind mass-loss and accretion mass gain to SFR in the IRA approximation. They investigated the radially averaged metallicity distribution of the ISM of a sample of 20 local star-forming disk galaxies by means of analytical chemical evolution model.
On the other hand, in this work, we show that when a decaying exponential infall law is assumed, the analytical solution for the evolution of the galaxy metallicity explicitly depends upon the time variable; this fact will allow us to also provide an estimate for the age of the galaxies and characterize them in terms of their infall timescale.
Mannucci et al. (2010) added a further dimension to the observed MZ relation of local galaxies; in particular, they found that local galaxies place themselves on a tight surface in the 3D space defined by gas phase metallicity, SFR, and stellar mass, with a small residual dispersion of about 0.05 dex and hence showing an underlying fundamental relation. In this work, we test whether our new analytical model is able to recover a similar fundamental relation for the local population of passive and star-forming galaxies.
Our paper is organized as follows. In Sect. 2, after summarizing the basic assumptions of our chemical evolution model, we present the new analytical solutions for the galaxy metallicity, gas mass, and total mass. In Sect. 3 we discuss the observed MZ relation in the population of local passive and star-forming galaxies by Peng et al. (2015) and present the method we employ to reproduce it. In Sect. 4 we present the methods used to reproduce the MZ relation with the new analytical solutions. In Sect. 5 we report our results, and in Sect. 6, we discuss whether the population of galaxies drawn by our new analytical model are predicted to follow the fundamental relation of Mannucci et al. (2010). Finally, our conclusions are drawn in Sect. 7.
2. Model
In this section we present new analytical solutions for the evolution of the metallicity, gas mass, and total mass of galaxies in the framework of simple models of chemical evolution where an exponential infall of gas is assumed. We summarize the basic assumptions of our model and show the system of differential equations that are to be solved. We show the new analytical solution and explore the effect of varying the main free parameters of our model.
2.1. Basic assumptions
The main assumptions of the simple model (Tinsley 1980) are as follows:
-
1.
The IMF is constant in time and space, which means that everygalaxy stellar generation hosts stars with a mass sampling auniversal distribution, regardless of the age, metallicity, andbirthplace of the stellar generation.
-
2.
The gas is well mixed at any time of the galaxy evolution (instantaneous mixing approximation).
-
3.
Stars with mass m ≥ 1 M⊙ die instantaneously, as soon as they form (IRA), while stars with mass m< 1 M⊙ have infinite lifetimes.
By making these simplifying assumptions, we can derive analytical formulas for the evolution of the main galaxy physical properties, such as the metallicity Z, SFR, gas, and stellar mass; the two following quantities appear in the various differential equations: 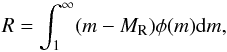 (1)which represents the so-called returned mass fraction, where φ(m) is the IMF and MR is the mass of the stellar remnant, and
(1)which represents the so-called returned mass fraction, where φ(m) is the IMF and MR is the mass of the stellar remnant, and 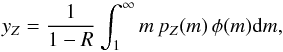 (2)which represents the so-called yield per stellar generation, with pZ(m) being the fraction of the newly produced and ejected metals by a star of mass m. The values of yZ and R for different IMFs are taken from Vincenzo et al. (2016), who also showed that the effect of metallicity on these quantities is minor compared to the adopted IMF and set of stellar yields. The IMF is defined in the stellar mass range 0.1–100 M⊙. In particular, we assume average values over metallicity from Table 2 of Vincenzo et al. (2016), corresponding to the compilation of stellar yields of Romano et al. (2010).
(2)which represents the so-called yield per stellar generation, with pZ(m) being the fraction of the newly produced and ejected metals by a star of mass m. The values of yZ and R for different IMFs are taken from Vincenzo et al. (2016), who also showed that the effect of metallicity on these quantities is minor compared to the adopted IMF and set of stellar yields. The IMF is defined in the stellar mass range 0.1–100 M⊙. In particular, we assume average values over metallicity from Table 2 of Vincenzo et al. (2016), corresponding to the compilation of stellar yields of Romano et al. (2010).
In our model we explore the effect of the two following IMFs:
-
1.
Chabrier (2003; which is similar toKroupa 2001), for which we obtain a return massfraction R = 0.441, a yield of metals per stellar generation yZ = 0.0631, and a yield of oxygen per stellar generation yO = 0.0407;
-
2.
Salpeter (1955), for which R = 0.287, yZ = 0.0301, and yO = 0.018.
We assume for the SFR a linear Schmidt (1959) law of the following form: 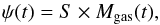 (3)where Mgas(t) is the galaxy gas mass at the time t, and S is the so-called star formation efficiency (SFE), a free parameter of our model that is measured in Gyr-1.
(3)where Mgas(t) is the galaxy gas mass at the time t, and S is the so-called star formation efficiency (SFE), a free parameter of our model that is measured in Gyr-1.
The infall model is taken from Chiosi (1980) and the rate is assumed to obey the following decaying exponential law: 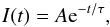 (4)where τ is the so-called infall timescale, which determines the typical timescale over which the galaxy is assumed to assemble, and A is a constant constrained by the total infall gas mass (Minf) by the following equation:
(4)where τ is the so-called infall timescale, which determines the typical timescale over which the galaxy is assumed to assemble, and A is a constant constrained by the total infall gas mass (Minf) by the following equation: 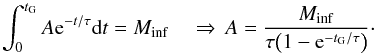 (5)With Eq. (5) we impose that the integral of the infall rate over the entire galaxy lifetime is the total gas infall mass, Minf. We assume the galactic lifetime to be tG = 14 Gyr.
(5)With Eq. (5) we impose that the integral of the infall rate over the entire galaxy lifetime is the total gas infall mass, Minf. We assume the galactic lifetime to be tG = 14 Gyr.
In our model, we also take into account outflow gas episodes in galaxies. The outflow rate is assumed to be proportional to the SFR in the galaxy (see Matteucci 2012; Matteucci & Chiosi 1983): 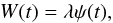 (6)with the wind parameter λ being a dimensionless quantity. We are aware that in our study galactic winds are treated in a simple way. On the other hand, Recchi & Hensler (2013) showed that the pure galactic wind mass-loss depends on the gas stratification: we can obtain various wind strengths and different mass loading factors for the same SFR. However, Eq. (6) has been used in almost all the chemical evolution models in the literature up to now (see Vincenzo et al. 2014; Recchi et al. 2008; Lanfranchi et al. 2008).
(6)with the wind parameter λ being a dimensionless quantity. We are aware that in our study galactic winds are treated in a simple way. On the other hand, Recchi & Hensler (2013) showed that the pure galactic wind mass-loss depends on the gas stratification: we can obtain various wind strengths and different mass loading factors for the same SFR. However, Eq. (6) has been used in almost all the chemical evolution models in the literature up to now (see Vincenzo et al. 2014; Recchi et al. 2008; Lanfranchi et al. 2008).
2.2. Set of differential equations
The set of differential equations we have to solve to characterise the evolution of the galaxy total mass, gas mass, and metallicity is the following: ![\begin{equation} \begin{cases} \dot{M}_\mathrm{tot}(t) = A {\rm e}^{-t/{\tau}} -\lambda \psi(t) & \\[7pt] \dot{M}_\mathrm{gas}(t) = -\big(1 - R \big) \psi(t) + A {\rm e}^{-t/{\tau}}- \lambda \psi(t) & \\[7pt] \dot{M}_Z(t) = \big(-Z(t)+y_z \big)\big(1-R\big) \psi(t) -\lambda Z(t) \psi(t) + Z_\mathrm{inf} A {\rm e}^{-t/{\tau}}, \label{system1} \end{cases} \end{equation}](/articles/aa/full_html/2017/03/aa29745-16/aa29745-16-eq38.png) (7)where Mtot and Mgas are the total mass and the gas mass of the galaxy, respectively; Z = MZ/Mgas represents the gas metallicity of the system, and Zinf the metallicity of the infalling gas. The total stellar mass of the system can be retrieved by means of the following formula: M⋆(t) = Mtot(t)−Mgas(t).
(7)where Mtot and Mgas are the total mass and the gas mass of the galaxy, respectively; Z = MZ/Mgas represents the gas metallicity of the system, and Zinf the metallicity of the infalling gas. The total stellar mass of the system can be retrieved by means of the following formula: M⋆(t) = Mtot(t)−Mgas(t).
By recalling that MZ = Z × Mgas, if we differentiate the latter with respect to time and then combine the second and the third equations in the system of Eq. (7), the temporal evolution of the gas metallicity, Z, obeys the following differential equation: 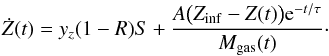 (8)By assuming Zinf = 0, the second term in the right-hand side of Eq. (8) is responsible for a dilution of the metal content within the galaxy ISM as the infall rate of gas proceeds.
(8)By assuming Zinf = 0, the second term in the right-hand side of Eq. (8) is responsible for a dilution of the metal content within the galaxy ISM as the infall rate of gas proceeds.
2.3. Analytical solutions
In this section, we present the analytical solutions for the system of Eq. (7) and show the effects on Mgas(t), Mtot(t), and Z(t) caused by the variation of the adopted IMF and wind parameter λ.
We assume for Eq. (7) the following initial conditions:
-
1.
At t = 0, we assume Mtot(0) = Mgas(0) ≪ Minf. To integrate Eq. (7), an initial gas mass different from zero is required; we consider it as negligible with respect to the infall mass.
-
2.
The metallicity of the gas infall is constant: Zinf = 0.
-
3.
The metallicity of the galaxy is primordial at the formation of the galaxy: Z(0) = Zinf = 0.
The solution for the gas mass is ![\begin{equation} M_\mathrm{gas}(t)= {\rm e}^{-\alpha t} \left( \frac{ A \left[ {\rm e}^{-t/\tau + \alpha t} - 1 \right] \tau }{ \alpha \tau - 1} + M_\mathrm{gas}(0) \right), \end{equation}](/articles/aa/full_html/2017/03/aa29745-16/aa29745-16-eq52.png) (9)while the total galaxy mass (Mgas(t) + M⋆(t)) evolves according to the following formula:
(9)while the total galaxy mass (Mgas(t) + M⋆(t)) evolves according to the following formula: 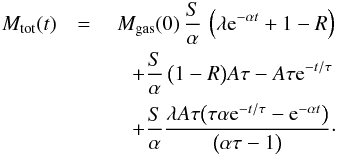 Finally, the solution for the galaxy gas-phase metallicity is
Finally, the solution for the galaxy gas-phase metallicity is ![\begin{eqnarray*} Z(t) &=& \frac{y_z S\big( 1-R \big)}{ \alpha \tau-1} \\ &&\quad \times \frac{M_\mathrm{gas}(0) t \big( \alpha \tau - 1 \big)^2+ A \tau\big[t - \tau (1 + \alpha t) + \tau {\rm e}^{\alpha t -t/\tau} \big] } { A \tau \big({\rm e}^{\alpha t -t/\tau} -1\big) + M_\mathrm{gas}(0)\big( \alpha \tau-1\big) }\cdot \end{eqnarray*}](/articles/aa/full_html/2017/03/aa29745-16/aa29745-16-eq55.png) In these equations, we have defined the parameter α as follows:
In these equations, we have defined the parameter α as follows: 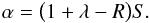 (10)We note that when we consider the case without infall mass (Minf = 0, and hence A = 0) and without winds (λ = 0), we recover the closed-box solution. We have with these assumptions that
(10)We note that when we consider the case without infall mass (Minf = 0, and hence A = 0) and without winds (λ = 0), we recover the closed-box solution. We have with these assumptions that 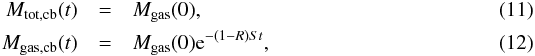 and
and 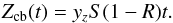 (13)Mtot,cb(t), Mgas,cb(t), and Zcb(t) are exactly the solutions of the closed-box model reported in Spitoni (2015) for the total mass, gas mass, and metallicity of the gas, respectively.
(13)Mtot,cb(t), Mgas,cb(t), and Zcb(t) are exactly the solutions of the closed-box model reported in Spitoni (2015) for the total mass, gas mass, and metallicity of the gas, respectively.
 |
Fig. 1 Effects of galactic winds. We show in both panels the predicted evolution in time of the galaxy gas mass Mgas (gray dashed lines), stellar mass M⋆ (blue dotted lines), and total mass Mtot = Mgas + M⋆ (red solid lines). The model assumes an exponential infall law with timescale τ = 2 Gyr and infall mass Minf = 1010M⊙, and an SFE S = 1 Gyr-1. Left panel: model without galactic winds (λ = 0); right panel: model with wind parameter λ = 0.5. |
In Fig. 1 we show how Mgas, M⋆ and Mtot evolve when we assume an infall timescale τ = 2 Gyr, infall mass Minf = 1010M⊙, and SFE S = 1 Gyr-1. A model with wind parameter λ = 0.5 (right panel) is compared with a model without outflow (left panel). As the time tends to tG, both models predict the total galaxy gas mass to be zero and hence the stellar mass to approach the galaxy total mass. In the model without galactic winds, M⋆(tG) ≈ Mtot(tG) = Minf, while in the model with outflow we find that M⋆(tG) ≈ Mtot(tG) <Minf, since the galaxy loses a substantial fraction of its total infall mass in the intergalactic medium (IGM) because of the galactic winds. The shape of the temporal evolution of the galaxy SFR can be retrieved from the behavior of Mgas(t), since we assume them to be proportional between each other.
 |
Fig. 2 Effect of varying the wind parameter λ on the time evolution of the metallicity Z. The model assumes an exponential infall law with timescale τ = 2 Gyr and infall mass Minf = 1010M⊙, and an SFE S = 1 Gyr-1. In the left panel we show the results of models with a Salpeter (1955) IMF, while in the right panel a Chabrier (2003) IMF is assumed. |
In Fig. 2 we show how the gas metallicity Z is predicted to evolve with time when we assume different wind parameters, λ. The right panel shows the results of models with a Chabrier (2003) IMF, while the left panel shows models with a Salpeter (1955) IMF. All the models assume Minf = 1010M⊙, τ = 2 Gyr, and S = 1 Gyr-1. The figure clearly shows that as the wind parameter λ increases, the galaxy metallicity is predicted to saturate at progressively earlier epochs toward always lower metallicities. Interestingly, the assumption of a Chabrier (2003) IMF causes an enhanced chemical enrichment of the galaxy ISM. At any galactic time, the gas metallicity with a Chabrier (2003) IMF is about twice higher than the metallicity with a Salpeter (1955) IMF, which is due to the large portion of massive stars in the Chabrier (2003) IMF. As expected, the choice of the IMF has a strong effect on the metallicity evolution of a galactic system.
3. MZ relation of the SDSS sample of star-forming and passive galaxies
By analyzing a sample of local galaxies from SDSS data, Peng et al. (2015) were able to separate the local population of actively star-forming and gas-rich galaxies from the passive and gas-poor galaxies. In Fig. 3 we report the data by Peng et al. (2015), showing that these two populations of galaxies present distinct relations in the MZ plane, with the passive galaxies having on average higher stellar metallicities than the star-forming galaxies.
For a given stellar mass, there is a gap in metallicity between the two galaxy populations, which is observed to diminish as the stellar mass increases. At M⋆ ≈ 1011M⊙ and beyond, star-forming and passive galaxies share almost the same average stellar metallicities. In Fig. 3 we also show the fits of the passive and star-forming sequences by means of third-order polynomial functions that we use in this paper.
 |
Fig. 3 Observed uncertainties of the MZ relations for star-forming and passive galaxies by Peng et al. (2015) are reported with blue lines. We show with orange lines the third-order polynomial fits for the passive and star-forming galaxies adopted in this article. |
To explain the observed MZ relation of the star-forming and passive galaxy populations in the SDSS data, Peng et al. (2015) suggested that galaxies ceased to accrete gas from the outside and kept forming stars only by exhausting the remaining available cold gas reservoir within their potential well. In this way, as soon as the galaxy is strangulated and stops accreting gas, the concentration of metals in the galaxy can steeply increase, and similarly the metallicity of all the subsequent stellar generations rises. The average time needed for star-forming galaxies to reach the high-metallicity stripe of passive galaxies in the MZ relation is predicted by Peng et al. (2015) to be on the order of ~4 Gyr.
We do not invoke any a priori strangulation scenario and aim at reproducing the two observed sequences of star-forming and passive galaxies by using our new analytical model with an exponential infall law and by varying the important parameters of galaxy evolution. In particular, we characterize the local SDSS galaxies in terms of their age, infall timescale of formation, infall mass, and wind parameter.
4. Methods
For the MZ relation, Peng et al. (2015) adopted the average stellar metallicity, Z⋆(t); we recover this quantity from our models by averaging the gas metallicity of each galaxy in the following way: 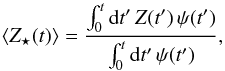 (14)where the metallicity of the various galaxy stellar populations is weighted with the total number of stars formed with that metallicity (the latter quantity is directly proportional to the SFR). This expression represents the so-called mass-weighted average metallicity of all the stellar populations ever born in the galaxy (see Pagel 1997).
(14)where the metallicity of the various galaxy stellar populations is weighted with the total number of stars formed with that metallicity (the latter quantity is directly proportional to the SFR). This expression represents the so-called mass-weighted average metallicity of all the stellar populations ever born in the galaxy (see Pagel 1997).
4.1. Passive galaxies
To define a galaxy as passive, we adopt the following criterium introduced by Fossati et al. (2015), which takes into account the galaxy specific SFR (sSFR), that is, the SFR per unit galaxy stellar mass: 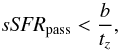 (15)where b is the birthrate parameter b = SFR/ ⟨SFR⟩ as defined by Sandage (1986), and tz is the age of the Universe at redshift z. As in Fossati et al. (2015), we assume the value proposed by Franx et al. (2008): b = 0.3.
(15)where b is the birthrate parameter b = SFR/ ⟨SFR⟩ as defined by Sandage (1986), and tz is the age of the Universe at redshift z. As in Fossati et al. (2015), we assume the value proposed by Franx et al. (2008): b = 0.3.
Since the SDSS sample of galaxies considered by Peng et al. (2015) has an average redshift ⟨z⟩ = 0.05, the passive galaxy population is characterized by sSFRpass < 2.29 × 10-11 yr-1.
4.2. Star-forming galaxies
For star-forming galaxies, we adopt the following scaling relation between μ⋆ and M⋆ found by Boselli et al. (2014) for a sample of the Herschel Reference Survey SDSS galaxies: 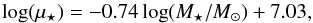 (16)where μ⋆ is the ratio between Mgas and M⋆: μ⋆ = Mgas/M⋆. Molecular gas masses are estimated from the H-band luminosity-dependent conversion factor of Boselli et al. (2002), while the galaxy stellar masses are derived from the galaxy i-band luminosities by assuming a Chabrier (2003) IMF and using the g−i color-dependent stellar mass-to-light ratio relation from Zibetti et al. (2009).
(16)where μ⋆ is the ratio between Mgas and M⋆: μ⋆ = Mgas/M⋆. Molecular gas masses are estimated from the H-band luminosity-dependent conversion factor of Boselli et al. (2002), while the galaxy stellar masses are derived from the galaxy i-band luminosities by assuming a Chabrier (2003) IMF and using the g−i color-dependent stellar mass-to-light ratio relation from Zibetti et al. (2009).
A further scaling relation found by Boselli et al. (2014) is the following relation between the typical galaxy gas depletion timescale, τgas, and the galaxy stellar mass: 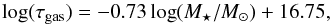 (17)where τgas = Mgas/SFR is defined as the inverse of our SFE, namely τgas = 1 /S. According to Eq. (17), galaxies with higher stellar mass would consume their available gas mass on progressively shorter typical timescales if only star formation activity were taking place in the galaxy; this means that larger galaxies are expected to experience, on average, higher SFEs (see Matteucci 2012). We adopt Eq. (17) to constrain the galaxy SFE (which is kept fixed during the galaxy evolution), given an initial value for the galaxy infall mass, Minf.
(17)where τgas = Mgas/SFR is defined as the inverse of our SFE, namely τgas = 1 /S. According to Eq. (17), galaxies with higher stellar mass would consume their available gas mass on progressively shorter typical timescales if only star formation activity were taking place in the galaxy; this means that larger galaxies are expected to experience, on average, higher SFEs (see Matteucci 2012). We adopt Eq. (17) to constrain the galaxy SFE (which is kept fixed during the galaxy evolution), given an initial value for the galaxy infall mass, Minf.
Principal characteristics of the computed passive and star-forming galaxies.
4.3. Summary of the free parameters and constraints
The free parameters entering in the analytical solutions of our chemical evolution model are the following:
-
1.
the infall timescale τ;
-
2.
the infall mass Minf;
-
3.
the wind parameter λ.
We created a set of chemical evolution models by varying these free parameters with a very fine resolution. The assumed infall timescale τ spans the range between 0.1 and 8 Gyr, with a resolution of the grid values of Δτ = 0.05 Gyr. The wind parameter λ is defined between 0 and 10, with a resolution of Δλ = 0.5. The infall masses are in the range between 105.5 and 1012.5M⊙.
The SFE is determined by means of Eq. (17), where M⋆ is replaced with Minf. We cannot vary the SFE of the galaxy according to its stellar mass, since the system of Eq. (7) is solved by keeping the SFE constant.
The observational constraints that we assume to characterize the star-forming and passive populations of galaxies in the SDSS sample of Peng et al. (2015) are the following:
-
1.
Our models for passive and star-forming galaxieshave average stellar metallicities defined such that| log (Z⋆,mod)−log (Z⋆,obs) | < 0.001 dex, where Z⋆,mod are computed with Eq. (14) and Z⋆,obs are the stellar metallicities obtained with the fit reported in Fig. 3 for the observed values by Peng et al. (2015).
-
2.
Our models for star-forming galaxies have |μ⋆,mod−μ⋆,obs| < 0.001, where μ⋆,obs are computed by means of Eq. (16).
-
3.
Our models for passive galaxies must have sSFRmod,passive< 2.29 × 10-11 yr-1, where sSFRmod is the predicted specific SFR.
-
4.
Our models for star-forming galaxies must have sSFRmod,star−forming > 2.29 × 10-11 yr-1.
In this way, we are able to select and distinguish which chemical evolution model best represents the sample of Peng et al. (2015). We follow the chemical evolution of our entire galaxy sample with a fixed time resolution Δt = 0.0065 Gyr. The ages of all star-forming and passive galaxies are defined as the galactic time when all the observational constraints for a given population are fulfilled.
 |
Fig. 4 Upper panels: MZ relation by Peng et al. (2015) (fitted by third-order polynomial functions shown in Fig. 3) for passive and star-forming galaxies. We reproduce it using the new analytical solution presented in this paper and vary different parameter models. In this figure we focus on the timescale parameter τ, and the color code indicates different τ values of the computed galaxies that reside along the MZ relations. In the left panel we adopt a Chabrier (2003) IMF, whereas in the right panel the Salpeter (1955) IMF is assumed. Lower panels: distribution of the predicted passive galaxies (red histogram) and star-forming galaxies (blue histogram) that reproduced the MZ relation in terms of the timescale parameter τ with a Chabrier (2003) IMF (left panel) and a Salpeter (1955) IMF (right panel). |
 |
Fig. 5 Upper panels: as in Fig. 4, but here, the color code indicates different ages of the galaxies that reproduce the MZ relations. Lower panels: distribution of the predicted passive galaxies (red histogram) and star-forming galaxies (blue histogram) that reproduced the MZ relation in terms of the age of galaxies. In the left panel we adopt a Chabrier (2003) IMF, whereas in the right panel we show the results assuming a Salpeter (1955) IMF. |
 |
Fig. 6 Upper panels: as in Fig. 4, but here, the color code indicates different wind parameters λ of the galaxies that reproduce the MZ relations. Lower panels: distribution of the predicted passive galaxies (red histogram) and star-forming galaxies (blue histogram) that reproduced the MZ relation in terms of the wind parameter λ of galaxies. In the left panel we adopt a Chabrier (2003) IMF, whereas in the right panel a Salpeter (1955) IMF is adopted. |
 |
Fig. 7 Upper panels: as in Fig. 4 but here, the color code indicates different infall mass Minf of the galaxies which reproduce the MZ relations. Lower panels: distribution of the predicted passive galaxies (red histogram) and star-forming galaxies (blue histogram) which reproduced the MZ relation in terms of infall mass Minf of galaxies. In the left panel we adopt a Chabrier (2003) IMF, whereas in the right one the Salpeter (1955) one. |
 |
Fig. 8 Upper panels: simulated passive and star-forming galaxies that are able to reproduce the MZ relations of Peng et al. (2015) in the 3D plot to test a more general relation between stellar M∗, average stellar metallicity Z, and the SFR using a Chabrier (2003; left panel) and a Salpeter IMF (right panel). Lower panels: 2D projection in the M∗- SFR plane. |
As stressed before, we study the case of primordial infall of gas (i.e., Zinf = 0). Although Lehner et al. (2013) studied the circumgalactic medium of galaxies and recently demonstrated that metal-enriched infalls occur, previous papers (Tosi 1988; Matteucci 2012) have shown that an infall enriched with metallicity Z ≤ 0.4 Z⊙ does not produce differences in the evolution of the solar neighborhood. Moreover, assuming an infall with a metallicity higher than 0.4 Z⊙ requires very specific situations. Recently, Spitoni et al. (2016) considered the effects of an enriched infall of gas with the same chemical abundances as the matter ejected and/or stripped from dwarf satellites of the Milky Way on the chemical evolution of the Galactic halo. We found that α elements are only slightly affected by such an enriched infall of gas.
5. Results
In this section we present our results concerning the characterization of the local passive and star-forming galaxies of the SDSS sample of Peng et al. (2015), by making use of the new analytical solutions presented in Sect. 2.3 in the presence of an exponential infall of gas. We remark on the fact that we selected the best chemical evolution models characterizing the SDSS sample of Peng et al. (2015) by imposing the set of constraints presented in the previous Sect. 4.3 and by varying all the free parameters simultaneously.
In Table 1 we summarize the main results of our work. We report the range of values spanned by the main free parameters of our models to reproduce the observed MZ relation of the local star-forming and passive galaxies. For each parameter we also report the value within which 75 per cent of the galaxies are expected to reside. We show in Table 1 our results for both the Salpeter (1955) and the Chabrier (2003) IMFs. A fundamental quantity that we can predict is the age distribution of the passive and star-forming galaxy SDSS population, corresponding to the second row in the table.
We assume that galaxies can form at different times, and by age we mean the galaxy evolutionary time, namely the difference between the time corresponding to redshift z = ⟨0.05⟩ and the formation epoch.
To better visualize our results, in Figs. 4–7 we show how local star-forming and passive galaxies are expected to be distributed in the MZ relation (upper panels) and in relative number (lower panels) for different values of the infall timescale, age, wind parameter, and infall mass, respectively. In the lower panels of the figures we indicate with N/Ntot the ratio between the number of the computed star-forming (or passive) galaxies in the considered bins of infall timescale, age, wind parameter, and infall mass values over the total number of the computed star-forming (passive) galaxies. The plots on the left correspond to our results with a Chabrier (2003) IMF, while on the right we show our results with a Salpeter (1955) IMF.
Figure 4 shows that our models for the local passive galaxies are characterized by shorter typical formation timescales than the star-forming galaxies. This is mainly due to the requirement of very low sSFRs for these galaxies at the present time. Therefore, they had the time to consume or remove most of their total infall gas mass through the star formation activity or galactic wind. The short typical formation timescales also enhance the star formation activity and hence the metal production in the earliest epochs of the galaxy evolution. According to the predictions of our models, local passive galaxies are currently undergoing the declining, fading phase of their SFR evolution.
In our analytical model of chemical evolution, the IMF only enters in the calculation of the yield of metals per stellar generation and the returned mass fraction. Top-heavy IMFs determine higher yields of metals per stellar generation and hence a more effective chemical enrichment of the galaxy ISM, fixed all the other model parameters. Therefore, passive galaxies with a top-heavy IMF that reach their relatively high observed stellar metallicity are on average characterized by longer formation timescales (a less intensive SFR at early times). We find that when we assume the Salpeter (1955) IMF, the distribution of the formation timescales of passive galaxies is narrower than when we assume a Chabrier (2003) IMF, which contains a larger number of massive stars. We find that almost 75 per cent of all passive galaxies are expected to assemble on τ ≤ 1.8 Gyr with a Salpeter (1955) IMF, while this time is τ ≤ 2.4 Gyr with a Chabrier (2003) IMF (see also Table 1).
In Fig. 4 we show the results of our models for the age distribution of local galaxies. Our main result is that passive galaxies are on average much older than the star-forming galaxies. The passive galaxies need a longer evolution to exhaust their total reservoir of gas, as described before, and to be observed as quiescent objects at the present time.
In the case of star-forming galaxies the star-forming galaxies with higher mass generally show older ages and longer typical formation timescales than star-forming galaxies with lower masses.
To reach their higher observed stellar metallicities with respect to the less massive galaxies, the more massive galaxies must be older. On the other hand, longer formation timescales can ensure more massive galaxies to be still observed as star forming at the present time, since large amounts of gas may be still available for star formation at later epochs.
Peng et al. (2015) were able to also derive luminosity-weighted stellar ages for their galaxy sample. Their main finding is that passive galaxies are on average about 4 Gyr older than the star-forming galaxies, with this difference remaining almost constant when considering different bins for the galaxy stellar mass.
Considering the difference between the median age values of our computed star-forming and passive galaxies, we find that our results are in agreement with the data by Peng et al. (2015). With the Chabrier (2003) IMF, we find that the median stellar ages for star-forming and passive galaxy are 0.9 Gyr and 5.1 Gyr, respectively; therefore the Δ age = 4.2 Gyr. We find a larger difference between the median ages when we adopt the Salpeter (1955) IMF; in this case, the median stellar ages for star-forming and passive galaxies are 2.1 Gyr and 7.5 Gyr, respectively; therefore Δ age = 5.4 Gyr.
Models of galaxies with a top-heavy IMF are expected to need less time to reach their relatively high observed stellar metallicity because of the chemical enrichment, which is driven by a larger number of massive stars; the minimum age we found for passive galaxies with the Chabrier (2003) IMF is 0.6 Gyr, much younger than the value we found using the Salpeter (1955) IMF (1.8 Gyr).
In Fig. 6 we present our results for the distribution of the wind parameter, λ, associated with our best models for the star-forming and passive galaxy populations of the SDSS sample of Peng et al. (2015). According to our results, the population of galaxies that suffer more prominent wind episodes are the star-forming galaxies. To reproduce the observed average stellar metallicity of star-forming galaxies at lower stellar mass, stronger winds are needed. On the other hand, the wind parameter, λ, is predicted to decrease toward star-forming galactic systems with higher stellar mass. In summary, the observed MZ relation can be well reproduced by assuming a variable mass-loading factor, which increases when passing from more massive to less massive galactic systems. This conclusion has been discussed by several authors in the past (see, for example, Spitoni et al. 2010, and references therein). This correlation between the mass-loading factor, λ, and the galaxy stellar mass is also valid for passive galaxies, although the galactic winds for these systems are predicted to be much weaker than for the star-forming galaxies.
The IMF choice can also affect the typical values of the wind parameter that best reproduce the observed MZ relation. Our best models for low-mass and metal-poor star-forming galaxies with a Salpeter (1955) IMF require weaker galactic winds than similar models with a Chabrier (2003) IMF, which predict a faster and hence more effective chemical enrichment of the galaxy ISM. Table 1 and Fig. 6 show that the distribution of the wind parameters for star-forming galaxies with a Salpeter (1955) IMF span the range 0 ≲ λ ≲ 5.8, and the 75% of star-forming galaxies are expected to have λ ≲ 2.25, while the models of star-forming galaxies with a Chabrier (2003) IMF span the range 0.6 ≲ λ ≲ 10.2, and the 75% of star-forming galaxies are expected to have λ ≲ 5.3.
At variance with Peng et al. (2015), our models fit the data when galactic winds occur during the entire galaxy evolution.
 |
Fig. 9 Stellar metallicity as a function of the SFR for the computed star-forming and passive galaxies. The color code indicates the stellar mass. In the upper panel model results with a Salpeter (1955) IMF are drawn, and in the lower panel a Chabrier (2003) IMF is adopted. |
In Fig. 7 we show our results for the distribution of the infall mass of our best models for the local population of star-forming and passive galaxies. We find that passive galaxies are characterized by lower infall masses than the star-forming galaxies. Passive galaxies in the Local Universe must be characterized by very low sSFRs, which can be obtained in the framework of our analytical model with an exponential infall of gas by assuming low infall gas masses together with short typical timescales (as we discussed above for the passive population). In this way, nearly most of the infall gas mass is converted into stars at the later epochs of the galaxy evolution. Typical values of the infall mass of our best models for the passive and star-forming galaxies can be found in Table 1.
The results for the infall mass distribution of the local population of star-forming and passive galaxies are strongly affected by the adopted IMF. Higher infall masses are required with a Chabrier (2003) IMF. We recall here that we assumed a primordial infall of gas. Because a top-heavy IMF leads to a more efficient chemical enrichment than a Salpeter (1955) IMF, a stronger dilution of metals and therefore higher infall masses are required to obtain the observed MZ relation.
6. Predicted fundamental relation of the local star-forming and passive galaxies
In this section, we analyze the correlations that local galaxies are predicted to show by our chemical evolution model in the 3D space defined by stellar mass, gas-phase metallicity, and SFR. Mannucci et al. (2010) showed that local galaxies lie on a tight surface in such a space and named the resulting correlation the “fundamental relation”, implying that it is valid at all redshifts.
Since we do not possess gas-phase metallicities for the passive galaxies in the sample of Peng et al. (2015), we use the average galaxy stellar metallicity instead of the gas-phase metallicity to study the MZ relation. The gas metallicity is typically higher than the stellar one for evolved galactic systems. Our results are shown in Fig. 8, where we show that local star-forming and passive galaxies lie on a tight surface when considering their stellar mass, M⋆, mass-weighted stellar metallicity, ⟨Z⋆⟩, and SFR. The projection of this 3D diagram onto the M⋆-Z⋆ place gives rise to the MZ relation that we discussed in the previous sections. Figure 8 shows that the two populations of galaxies are separated by a discontinuity that is due to the different metallicity distributions of star-forming and passive objects.
The discontinuity is also visible in Fig. 9, where we show the projection of the predicted fundamental relation onto the Z⋆-SFR plane. In this figure, the color-coding corresponds to the galaxy stellar mass. The local galaxy populations are predicted to show a similar trend as the one presented by Mannucci et al. (2010, see the right panel of their Fig. 1), where higher stellar masses are found for galaxies with higher SFRs and metallicities.
7. Conclusions
We have developed a new analytical model of chemical evolution, in which an exponential infall of gas and galactic winds are assumed. We applied this model to reproduce the observed MZ relation for local SDSS galaxies (Peng et al. 2015); in particular, we characterized the populations of gas-rich and star-forming and passive (gas-poor and quiescent) galaxies, by showing how their ages, formation timescales, mass-loading factors and infall masses must relate to each other. Finally, we analyzed the fundamental relation for these local galaxies in the 3D space, defined by stellar mass, average stellar metallicity, and SFR. Our main conclusions can be summarized as follows:
-
1.
We assume that all galaxies form by gas accretion with anexponential law. We find that passive galaxies are characterizedby shorter typical formation timescales and are older objects thanthe star-forming galaxies.
-
2.
Galactic winds in star-forming galaxies are found on average to be stronger than in passive galaxies. The intensity of the galactic winds depends on the adopted IMF, with the higher values of the mass-loading factor corresponding to top-heavy IMFs. This is a consequence of the fact that top-heavy IMFs lead to a more efficient metal enrichment of the galaxy ISM than bottom-heavy IMFs.
-
3.
The observed MZ relation of Peng et al. (2015) can be reproduced by our models without invoking any strangulation effects. This is because the assumption of an exponential infall of gas, also coupled to galactic winds, naturally reduces the gas accretion after the assumed infall timescale, hence mimics the effect of strangulation. Nevertheless, we conclude that strangulation is not the main physical mechanism driving the transition of galaxies toward the passive evolution.
-
4.
We have shown that our models for star-forming and passive galaxies imply that they obey the so-called fundamental relation of Mannucci et al. (2010), which a is more general relation between stellar mass, metallicity, and SFR. The fundamental relation of Mannucci et al. (2010) adopts the gas-phase metallicity, and we find that it is still valid when adopting the average galaxy stellar metallicity (M⋆-SFR-Z⋆).
Acknowledgments
We thank the anonymous referee for the suggestions that improved the paper. The work was supported by PRIN MIUR 2010-2011, project “The Chemical and dynamical Evolution of the Milky Way and Local Group Galaxies”, prot. 2010LY5N2T.
References
- Boselli, A., Lequeux, J., & Gavazzi, G. 2002, A&A, 384, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boselli, A., Cortese, L., Boquien, M., et al. 2014, A&A, 564, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brusadin, G., Matteucci, F., & Romano, D. 2013, A&A, 554, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Chiappini, C., Matteucci, F., & Gratton, R. 1997, ApJ, 477, 765 [NASA ADS] [CrossRef] [Google Scholar]
- Chiosi, C. 1980, A&A, 83, 206 [NASA ADS] [Google Scholar]
- Clayton, D. D. 1988, MNRAS, 234, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Clayton, D. D., & Pantelaki, I. 1986, ApJ, 307, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Clayton, D. D., & Pantelaki, I. 1993, Phys. Rep., 227, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Colavitti, E., Matteucci, F., & Murante, G. 2008, A&A, 483, 401 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Edmunds, M. G. 1990, MNRAS, 246, 678 [NASA ADS] [Google Scholar]
- Edmunds, M. G., & Greenhow, R. M. 1995, MNRAS, 272, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Erb, D. K. 2008, ApJ, 674, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Fossati, M., Wilman, D. J., Fontanot, F., et al. 2015, MNRAS, 446, 2582 [NASA ADS] [CrossRef] [Google Scholar]
- Franx, M., van Dokkum, P. G., Förster Schreiber, N. M., et al. 2008, ApJ, 688, 770 [NASA ADS] [CrossRef] [Google Scholar]
- Hartwick, F. D. A. 1976, ApJ, 209, 418 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., & Ellison, S. L. 2008, ApJ, 681, 1183 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Kudritzki, R.-P., Ho, I.-T., Schruba, A., et al. 2015, MNRAS, 450, 342 [Google Scholar]
- Lacey, C. G., & Fall, M. 1985, ApJ, 290, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Lanfranchi, G. A., Matteucci, F., & Cescutti, G. 2008, A&A, 481, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lehner, N., Howk, J. C., Tripp, T. M., et al. 2013, ApJ, 770, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Mannucci, F., Cresci, G., Maiolino, R., Marconi, A., & Gnerucci, A. 2010, MNRAS, 408, 2115 [NASA ADS] [CrossRef] [Google Scholar]
- Martinelli, A. 1998, A&A, 335, 847 [NASA ADS] [Google Scholar]
- Matteucci, F. 2001, The Chemical Evolution of the Galaxy, ASSL (Kluwer Academic Publisher) [Google Scholar]
- Matteucci F. 2012, Chemical Evolution of Galaxies (Berlin: Springer-Verlag) [Google Scholar]
- Matteucci, F., & Chiosi, C. 1983, A&A, 123, 121 [NASA ADS] [Google Scholar]
- Micali, A., Matteucci, F., & Romano, D. 2013, MNRAS, 436, 1648 [NASA ADS] [CrossRef] [Google Scholar]
- Pagel B. E. J. 1997, in Nucleosynthesis and Chemical Evolution of Galaxies, ed. E. J. P. Bernard (Cambridge: Cambridge Univ. Press), 392 [Google Scholar]
- Pagel, B. E. J., & Patchett, B. E. 1975, MNRAS, 172, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, Y., Maiolino, R., & Cochrane, R. 2015, Nature, 521, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Pezzulli, G., & Fraternali, F. 2015, MNRAS, 455, 2308 [Google Scholar]
- Portinari, L., & Chiosi, C. 2000, A&A, 355, 929 [NASA ADS] [Google Scholar]
- Recchi, S., & Kroupa, P. 2015, MNRAS, 446, 4168 [NASA ADS] [CrossRef] [Google Scholar]
- Recchi, S., & Hensler, G. 2013, A&A, 551, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Recchi, S., Spitoni, E., Matteucci, F., & Lanfranchi, G. A. 2008, A&A, 489, 555 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Romano, D., Karakas, A. I., Tosi, M., & Matteucci, F. 2010, A&A, 522, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Sandage, A. 1986, A&A, 161, 89 [NASA ADS] [Google Scholar]
- Schmidt, M. 1959, ApJ, 129, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, M. 1963, ApJ, 137, 758 [NASA ADS] [CrossRef] [Google Scholar]
- Searle, L., & Sargent, W. L. W. 1972, ApJ, 173, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Spergel, D. N., Bean, R., Dor, O., et al. 2007, ApJS, 170, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Spitoni, E. 2015, MNRAS, 451, 1090 [NASA ADS] [CrossRef] [Google Scholar]
- Spitoni, E., & Matteucci, F. 2011, A&A, 531, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spitoni, E., Calura, F., Matteucci, F., & Recchi, S. 2010, A&A, 514, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spitoni, E., Vincenzo, F., Matteucci, F., & Romano, D. 2016, MNRAS, 458, 2541 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V. 2005, MNRAS, 364, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Tinsley, B. M., 1974, ApJ, 192, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Tinsley, B. M. 1980, Fundamentals of Cosmic Physics, 5, 287 [Google Scholar]
- Tosi, M. 1988, A&A, 197, 33 [NASA ADS] [Google Scholar]
- Twarog, B. A. 1980, ApJ, 242, 242 [NASA ADS] [CrossRef] [Google Scholar]
- Vincenzo, F., Matteucci, F., Vattakunnel, S., & Lanfranchi, G. A. 2014, MNRAS, 441, 2815 [NASA ADS] [CrossRef] [Google Scholar]
- Vincenzo, F., Matteucci, F., Belfiore, F., & Maiolino, R. 2016, MNRAS, 455, 4183 [NASA ADS] [CrossRef] [Google Scholar]
- Weinberg, D. H., Andrews, B. H., & Freudenburg, J. 2016, ApJ, submitted, [arXiv:1604.07435] [Google Scholar]
- Zibetti, S., Charlot, S., & Rix, F. 2009, MNRAS, 400, 1181 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Effects of galactic winds. We show in both panels the predicted evolution in time of the galaxy gas mass Mgas (gray dashed lines), stellar mass M⋆ (blue dotted lines), and total mass Mtot = Mgas + M⋆ (red solid lines). The model assumes an exponential infall law with timescale τ = 2 Gyr and infall mass Minf = 1010M⊙, and an SFE S = 1 Gyr-1. Left panel: model without galactic winds (λ = 0); right panel: model with wind parameter λ = 0.5. |
| In the text | |
 |
Fig. 2 Effect of varying the wind parameter λ on the time evolution of the metallicity Z. The model assumes an exponential infall law with timescale τ = 2 Gyr and infall mass Minf = 1010M⊙, and an SFE S = 1 Gyr-1. In the left panel we show the results of models with a Salpeter (1955) IMF, while in the right panel a Chabrier (2003) IMF is assumed. |
| In the text | |
 |
Fig. 3 Observed uncertainties of the MZ relations for star-forming and passive galaxies by Peng et al. (2015) are reported with blue lines. We show with orange lines the third-order polynomial fits for the passive and star-forming galaxies adopted in this article. |
| In the text | |
 |
Fig. 4 Upper panels: MZ relation by Peng et al. (2015) (fitted by third-order polynomial functions shown in Fig. 3) for passive and star-forming galaxies. We reproduce it using the new analytical solution presented in this paper and vary different parameter models. In this figure we focus on the timescale parameter τ, and the color code indicates different τ values of the computed galaxies that reside along the MZ relations. In the left panel we adopt a Chabrier (2003) IMF, whereas in the right panel the Salpeter (1955) IMF is assumed. Lower panels: distribution of the predicted passive galaxies (red histogram) and star-forming galaxies (blue histogram) that reproduced the MZ relation in terms of the timescale parameter τ with a Chabrier (2003) IMF (left panel) and a Salpeter (1955) IMF (right panel). |
| In the text | |
 |
Fig. 5 Upper panels: as in Fig. 4, but here, the color code indicates different ages of the galaxies that reproduce the MZ relations. Lower panels: distribution of the predicted passive galaxies (red histogram) and star-forming galaxies (blue histogram) that reproduced the MZ relation in terms of the age of galaxies. In the left panel we adopt a Chabrier (2003) IMF, whereas in the right panel we show the results assuming a Salpeter (1955) IMF. |
| In the text | |
 |
Fig. 6 Upper panels: as in Fig. 4, but here, the color code indicates different wind parameters λ of the galaxies that reproduce the MZ relations. Lower panels: distribution of the predicted passive galaxies (red histogram) and star-forming galaxies (blue histogram) that reproduced the MZ relation in terms of the wind parameter λ of galaxies. In the left panel we adopt a Chabrier (2003) IMF, whereas in the right panel a Salpeter (1955) IMF is adopted. |
| In the text | |
 |
Fig. 7 Upper panels: as in Fig. 4 but here, the color code indicates different infall mass Minf of the galaxies which reproduce the MZ relations. Lower panels: distribution of the predicted passive galaxies (red histogram) and star-forming galaxies (blue histogram) which reproduced the MZ relation in terms of infall mass Minf of galaxies. In the left panel we adopt a Chabrier (2003) IMF, whereas in the right one the Salpeter (1955) one. |
| In the text | |
 |
Fig. 8 Upper panels: simulated passive and star-forming galaxies that are able to reproduce the MZ relations of Peng et al. (2015) in the 3D plot to test a more general relation between stellar M∗, average stellar metallicity Z, and the SFR using a Chabrier (2003; left panel) and a Salpeter IMF (right panel). Lower panels: 2D projection in the M∗- SFR plane. |
| In the text | |
 |
Fig. 9 Stellar metallicity as a function of the SFR for the computed star-forming and passive galaxies. The color code indicates the stellar mass. In the upper panel model results with a Salpeter (1955) IMF are drawn, and in the lower panel a Chabrier (2003) IMF is adopted. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


