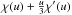| Issue |
A&A
Volume 599, March 2017
|
|
|---|---|---|
| Article Number | A5 | |
| Number of page(s) | 16 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201629692 | |
| Published online | 20 February 2017 | |
Constructing stable 3D hydrodynamical models of giant stars
1 Heidelberger Institut für Theoretische Studien, Schloss-Wolfsbrunnenweg 35, 69118 Heidelberg, Germany
e-mail: sebastian.ohlmann@h-its.org
2 Institut für Theoretische Physik und Astrophysik, Universität Würzburg, Emil-Fischer-Str. 31, 97074 Würzburg, Germany
3 Zentrum für Astronomie der Universität Heidelberg, Institut für theoretische Astrophysik, Philosophenweg 12, 69120 Heidelberg, Germany
4 Zentrum für Astronomie der Universität Heidelberg, Astronomisches Recheninstitut, Mönchhofstr. 12–14, 69120 Heidelberg, Germany
Received: 12 September 2016
Accepted: 28 November 2016
Hydrodynamical simulations of stellar interactions require stable models of stars as initial conditions. Such initial models, however, are difficult to construct for giant stars because of the wide range in spatial scales of the hydrostatic equilibrium and in dynamical timescales between the core and the envelope of the giant. They are needed for, e.g., modeling the common envelope phase where a giant envelope encompasses both the giant core and a companion star. Here, we present a new method of approximating and reconstructing giant profiles from a stellar evolution code to produce stable models for multi-dimensional hydrodynamical simulations. We determine typical stellar stratification profiles with the one-dimensional stellar evolution code mesa. After an appropriate mapping, hydrodynamical simulations are conducted using the moving-mesh code arepo. The giant profiles are approximated by replacing the core of the giant with a point mass and by constructing a suitable continuation of the profile to the center. Different reconstruction methods are tested that can specifically control the convective behaviour of the model. After mapping to a grid, a relaxation procedure that includes damping of spurious velocities yields stable models in three-dimensional hydrodynamical simulations. Initially convectively stable configurations lead to stable hydrodynamical models while for stratifications that are convectively unstable in the stellar evolution code, simulations recover the convective behaviour of the initial model and show large convective plumes with Mach numbers up to 0.8. Examples are shown for a 2 M⊙ red giant and a 0.67 M⊙ asymptotic giant branch star. A detailed analysis shows that the improved method reliably provides stable models of giant envelopes that can be used as initial conditions for subsequent hydrodynamical simulations of stellar interactions involving giant stars.
Key words: hydrodynamics / methods: numerical / stars: general
© ESO, 2017
1. Introduction
Dynamical interactions of stars can be modelled with hydrodynamical simulations. Most systems examined so far consist of rather compact stars, such as collisions of main sequence (MS) stars as a model for blue stragglers (e.g., Benz & Hills 1987; Lombardi et al. 1996; Sills et al. 2001) or mergers of compact objects, i.e., white dwarfs (WDs), neutron stars (NSs), and black holes (see the review by Rosswog 2015). These compact object mergers may lead to a wide variety of phenomena, such as Type Ia supernovae from merging WDs (e.g., Pakmor et al. 2013), or gravitational wave emission from neutron star mergers (e.g., Bauswein et al. 2016). An important interaction of more extended giant stars is the common envelope (CE) phase. During this phase, the envelope of the primary giant star is shared by the core of the giant and the companion star. Gravitational binding energy is released and drives the ejection of the envelope. The result of this phase is either a close binary or a merger of the stellar cores (for a recent review, see Ivanova et al. 2013). The CE phase is needed to explain the evolution of stellar systems towards, e.g., close WD and MS binaries (Schreiber & Gänsicke 2003; Zorotovic et al. 2010), double WDs (Han et al. 1995; Nelemans et al. 2001), and Type Ia supernovae (Iben & Tutukov 1984; Ruiter et al. 2009; Toonen et al. 2012).
To conduct hydrodynamical simulations of these stellar interactions, stable models of stars are needed as initial conditions. In 1D stellar evolution approaches, the assumption of hydrostatic equilibrium is usually part of the equations that are solved. For a 3D hydrodynamics code, however, hydrostatic equilibrium is a special solution of the more general equations that is not explicitely enforced; it can be easily disturbed by mismatches between the discretizations of pressure and gravity. For more compact stars, such as MS stars, WDs, or NSs, the representation of their global hydrostatic structure causes no particular problems because they span a small range of temporal and spatial scales only. The difficulty in modeling WD or NS interactions lies in the additional physics that is needed, as, e.g., a degenerate equation of state, nuclear burning, or general relativity. It is, however, harder to obtain stable models of giant stars because their hydrostatic equilibrium encompass a wide range of scales in time and space and because their envelope is usually only loosely bound. Thus, giant structures need to be approximated for use in hydrodynamical simulations.
In recent years, numerical representations of giant structures have mainly been used for modeling the dynamical spiral-in of a companion into a giant envelope during a CE phase. Hydrodynamical simulations use either a discretization on computational grids (Sandquist et al. 1998, 2000; Ricker & Taam 2008, 2012; Passy et al. 2012; Ohlmann et al. 2016a,b; Staff et al. 2016a,b; Iaconi et al. 2017) or smoothed particle hydrodynamics (SPH, Passy et al. 2012; Nandez et al. 2014, 2015). As an approximation to the giant structure, the core of the giant is usually replaced by a point mass and the remaining envelope profile is mapped to the grid without modifications (e.g., Sandquist et al. 1998, 2000; Passy et al. 2012; Staff et al. 2016a,b; Iaconi et al. 2017). This procedure leads to mismatches in the hydrostatic equilibrium of the envelope, resulting in spurious velocity fluctuations that have to be damped away. The resulting giant profile has to be stable for several dynamical timescales to ensure that modeling the spiral-in is not dominated by spurious artifacts. However, the procedures of approximating the giant profile, mapping it to the hydrodynamical grid and subsequently relaxing it have not been analyzed in detail so far.
In this paper, we present a novel method of approximating and reconstructing giant profiles and show that they can be mapped to and relaxed in multi-dimensional hydrodynamical simulations. This procedure leads to stable giant envelopes that can reliably be used for hydrodynamical simulations of the CE phase. Similar to previous approaches, the core of the giant is replaced by a point mass with a softened gravitational potential. Instead of a simple mapping, however, the profile of the giant envelope is reconstructed by integrating the hydrostatic equilibrium, taking into account the self-gravity of the gas and the gravity of the point mass. This way, the reconstruction does not depend on the grid resolution, and it can specifically control the convective behaviour of the profile. Using a relaxation procedure that damps out spurious velocities, models are obtained in hydrodynamical simulations that are stable over several dynamical timescales. They are then used as initial conditions for simulations of the CE phase, such as those presented in Ohlmann et al. (2016a,b).
The structure of the paper is as follows: we introduce the numerical methods in Sect. 2. Approximations to giant structures and reconstruction methods are explained in Sect. 3. Results from hydrodynamical simulations are presented in Sect. 4. After a discussion (Sect. 5), we conclude in Sect. 6.
2. Numerical methods
The hydrodynamical simulations presented in this paper are carried out using the moving-mesh code arepo (Springel 2010). It solves the Euler equations with a finite volume approach on an unstructured, moving Voronoi mesh. Moreover, the mesh can be adaptively refined on arbitrary criteria; here, we employ this capability to ensure a similar cell mass on average. A tree method solves for the self-gravity of the gas. The numerical method has recently been updated to ensure second order convergence on arbitrary moving meshes (Pakmor et al. 2016). As equation of state, either an ideal gas equation of state (EOS) for a monoatomic gas with γ = 5/3 is utilized or the OPAL EOS (Rogers et al. 1996; Rogers & Nayfonov 2002), which incorporates the ionization state of the medium and also radiation pressure. Radiative transport is not included in our calculations.
The stellar evolution code mesa (Paxton et al. 2011, 2013, 2015) is used in version 6208 to create stellar models in various evolutionary stages. We set the metallicity to Z = 0.02 and use standard settings otherwise, i.e., the Reimers prescription with η = 0.5 for red giant (RG) winds (Reimers 1975) and the Blöcker prescription with η = 0.1 for asymptotic giant branch (AGB) winds (Blöcker 1995). These values are the same as in Paxton et al. (2013, see there for further information and references.
2.1. Computational grids
Because arepo solves the hydrodynamics equations on an unstructured grid, we have the freedom to adapt the grid to the problem at hand. Different types of initial grids are implemented:
-
Regular cubic grids.
-
Nested cubic grids, where for each level of nesting the inner half of the grid in each direction (i.e. an eighth of the total volume) is replaced by a grid with double the resolution and half the grid spacing of the original level.
-
An adaptive cubic grid, where the grid is built in spherical shells tracking the mass distribution of the star to create approximately equal-mass cells. Given the mass profile m(r) of the star and the mass of cells mcell, the shells are constructed as follows: for each inner radius r1, we compute an outer radius r2 and the grid spacing a using conditions on the mass of the shell,
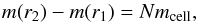 (1)and on the volume of the shell,
(1)and on the volume of the shell, 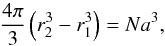 (2)where N is the number of cells in the shell. As an additional constraint, we impose that the width of the shell is a multiple of the grid spacing,
(2)where N is the number of cells in the shell. As an additional constraint, we impose that the width of the shell is a multiple of the grid spacing, 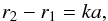 (3)where we usually choose k = 5. These equations are solved subsequently for each shell to yield r2, a, and N. In each shell, grid points are placed on a cubic grid with spacing a, where only the points with radii between r1 and r2 are considered.
(3)where we usually choose k = 5. These equations are solved subsequently for each shell to yield r2, a, and N. In each shell, grid points are placed on a cubic grid with spacing a, where only the points with radii between r1 and r2 are considered. -
A HEALPix grid with spherical shells tracking the mass profile of the star, where the cells are distributed in each shell according to the HEALPix tesselation (Górski et al. 2005) similar to the distribution of SPH particles by Pakmor et al. (2012). We deviate slightly from their scheme as we are not bound to strictly equal-mass cells compared to particles in SPH simulations. In each shell ranging from a given radius r1 to r2, we distribute
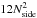 cells using the algorithm of Górski et al. (2005), where Nside denotes the number of divisions of a base pixel in the HEALPix algorithm. Thereby, it is ensured that the cells are symmetric and have approximately a mass of mcell,0. The cells have a radial diameter of Δrr = r2−r1, whereas the lateral diameter can be computed by multiplying the midpoint (r1 + r2)/2 by the angular resolution θ of the shell (Górski et al. 2005),
cells using the algorithm of Górski et al. (2005), where Nside denotes the number of divisions of a base pixel in the HEALPix algorithm. Thereby, it is ensured that the cells are symmetric and have approximately a mass of mcell,0. The cells have a radial diameter of Δrr = r2−r1, whereas the lateral diameter can be computed by multiplying the midpoint (r1 + r2)/2 by the angular resolution θ of the shell (Górski et al. 2005), 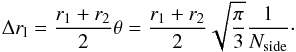 (4)Let the symmetry factor S be S = Δrr/ Δrl, which is one for symmetric cells. By imposing S = 1, r2 can be computed for different values of Nside. We then chose the radius for which the resulting cell mass,
(4)Let the symmetry factor S be S = Δrr/ Δrl, which is one for symmetric cells. By imposing S = 1, r2 can be computed for different values of Nside. We then chose the radius for which the resulting cell mass, 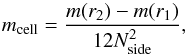 (5)is closest to the given cell mass mcell,0. To avoid large jumps in this quantity, it is limited by
(5)is closest to the given cell mass mcell,0. To avoid large jumps in this quantity, it is limited by 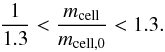 (6)If the mass limit is enforced for a shell (i.e., when condition (6) is violated), the number Nside is used for which log (S) is closest to zero (i.e., the most symmetric cells are chosen). To resolve the steep gradients near the surface of the star, the mass limit is not enforced for radii larger than 95% of the radius of the star. The positions of the cells on each sphere are computed according to the HEALPix algorithm that needs a coordinate system. This system is rotated randomly in space for each shell to avoid grid orientation effects.
(6)If the mass limit is enforced for a shell (i.e., when condition (6) is violated), the number Nside is used for which log (S) is closest to zero (i.e., the most symmetric cells are chosen). To resolve the steep gradients near the surface of the star, the mass limit is not enforced for radii larger than 95% of the radius of the star. The positions of the cells on each sphere are computed according to the HEALPix algorithm that needs a coordinate system. This system is rotated randomly in space for each shell to avoid grid orientation effects.
For each grid, the density and pressure profiles were continued outside the stellar surface at sufficiently low values to emulate the vacuum there in a numerically feasible way. For the adaptive cubic and HEALPix grids, a face-centered cubic grid was added in the outer part to sample the vacuum values in the rest of the box. The box size is chosen to be four times as large as the radius of the corresponding stellar model. Periodic boundary conditions are employed, because no outflows are expected and the boundary is far enough away. Tests with larger boxes did not show different results.
Because arepo uses an adaptive and moving mesh, the choice of the initial grid does not significantly influence the simulations (at least if it is not too coarse in the beginning); after a few time steps, the configuration is similar for each initial grid (see Sect. 4.2.4). If the mesh remains static, however, mass-adaptive meshes are superior to regular meshes. Except for three simulations discussed in Sect. 4.2.4, the HEALPix grid is used for all simulations presented in this paper.
2.2. Mapping stellar structures onto a grid
The initial conditions for hydrodynamical simulations are generated by mapping a one-dimensional, spherically symmetric profile from the stellar evolution code onto the grid used by the hydrodynamics code. In a finite volume method, as also employed by arepo, the average values of the conserved quantities are stored in each cell. Thus, we integrate over spherical shells when using the HEALPix grid to compute the averages of density and internal energy from the stellar evolution profile; these are then used as input values for the hydrodynamics code. It is also possible to integrate over the pressure and compute the internal energy from the EOS. This method may reproduce the hydrostatic equilibrium slightly better, but we found the differences to be very small (≲1% in most parts of the envelope), hence, we use the internal energy from integrating over the shells.
For the other grids, it is more difficult to compute integrals over the cell volumes because the geometry of the Voronoi mesh has to be known. The integral can be approximated by taking the value of the spherically symmetric function at the radius that is given by the center of mass of the cell. Since the cubic grids are mostly regular (except at the interface between nested levels in the nested grid or between adjacent spherical layers in the adaptive mesh), this can also be approximated by the value computed at the mesh-generating point of the cell. Thus, for all other grids besides the HEALPix grid, the value of the density and internal energy are taken at the position of the mesh-generating point of the corresponding cell. The differences in the simulations between the grids, however, are small due to using an adaptive and moving mesh (see Sect. 4.2.4).
2.3. Relaxation procedure
Mapping spherically symmetric stellar models to multi-dimensional hydrodynamical grids introduces discretization errors in the hydrostatic equilibrium. This is primarily due to discretizing the pressure term differently from the gravitational term in the numerical scheme: pressure enters through flux computations in the finite volume scheme whereas gravity is computed point-wise in the tree method. An additional source of error is the interpolation from the high-resolution stellar profile to the coarser hydrodynamical grid. Thus, errors in the hydrostatic equilibrium are introduced leading to spurious velocities.
The magnitude of the velocity fluctuations caused by resolution effects can be estimated for a simple one-dimensional example of an isothermal atmosphere with pressure scale height H. This analytical estimate assumes that the velocities are zero initially and yields the amplitude of velocity fluctuations after one timestep of the numerical scheme. For the atmosphere, the update of the momentum can be computed according to the finite volume scheme: the discrete pressure is expanded into a Taylor series in the grid spacing δ, where the first order term cancels the gravitational source term. The higher order terms depend on the numerical flux function, i.e., on the Riemann solver and on the reconstruction. For the arepo scheme, these terms lead to spurious velocities that can be expressed in terms of the Mach number M for the first part of a time step as (for details of the computation, see Appendix A)  (7)where γ is the adiabatic index and CCFL the Courant-Friedrichs-Levy constant that appears in the stability constraint for the time step Δt = CCFLδ/cs. Although this result is strictly only valid in the one-dimensional case, it gives a lower limit for the resolution that is needed also in multi-dimensional simulations to avoid velocity fluctuations due to the spatial discretization.
(7)where γ is the adiabatic index and CCFL the Courant-Friedrichs-Levy constant that appears in the stability constraint for the time step Δt = CCFLδ/cs. Although this result is strictly only valid in the one-dimensional case, it gives a lower limit for the resolution that is needed also in multi-dimensional simulations to avoid velocity fluctuations due to the spatial discretization.
Thus, to stabilize a hydrostatic atmosphere down to Mach numbers of 0.01 (0.001), one pressure scale height has to be resolved with at least 3.2 (6.8) cells (assuming γ = 5/3 and CCFL = 0.4). This is of course only a necessary but not a sufficient condition for reaching the corresponding amplitude of Mach number fluctuations. We ensure that all our initial models fulfill this criterion and have sufficient resolution per pressure scale height.
Even if the resolution requirement is met, other sources of numerical error (e.g., interpolation error, errors from the gravity solver) still introduce spurious velocity fluctuations. Thus, an appropriate relaxation procedure is necessary when mapping stellar models to hydrodynamical grids: the velocity fluctuations have to be damped. This can be reached by adding a term in the momentum equation proportional to 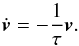 (8)It damps the velocities on a timescale τ. The time discretization is the same as for the rest of the scheme, and Eq. (8) is simply added as an additional source term.
(8)It damps the velocities on a timescale τ. The time discretization is the same as for the rest of the scheme, and Eq. (8) is simply added as an additional source term.
The value of the damping timescale is essential for reaching stable models, especially for dilute giant envelopes that encompass many timescales. The following scheme, based on Pakmor et al. (2012) and Rosswog et al. (2004), proved to produce stable models: the physical time of the whole relaxation run is chosen to be 10tdyn where the dynamical timescale tdyn can either be the sound crossing time or the free-fall timescale (which are usually of similar order); we use the sound crossing time of the stellar models. For the value of the damping timescale, we use a small value τ1 = tdyn/ 10 in the beginning that is subsequently increased to τ2 = tdyn (i.e., the damping is decreased) according to 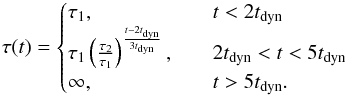 (9)The exponential form ensures that the temporal change of the damping timescale is proportional to the damping timescale itself. This means that damping on longer timescales (i.e., a larger value of τ) is also applied for a longer time. Taking τ2 on the order of the dynamical timescale is necessary to suppress pulsations that typically occur on this timescale. After 5tdyn, the damping is disabled and the system is evolved for another 5tdyn to ensure that the stellar model is stable in hydrodynamical simulations without damping.
(9)The exponential form ensures that the temporal change of the damping timescale is proportional to the damping timescale itself. This means that damping on longer timescales (i.e., a larger value of τ) is also applied for a longer time. Taking τ2 on the order of the dynamical timescale is necessary to suppress pulsations that typically occur on this timescale. After 5tdyn, the damping is disabled and the system is evolved for another 5tdyn to ensure that the stellar model is stable in hydrodynamical simulations without damping.
3. Stellar structures
3.1. Spatial structure of stars
 |
Fig. 1 Hertzsprung-Russell diagram for the evolution of a 2 M⊙ star using mesa. Different evolutionary phases are marked for which the profiles are shown in Fig. 2. |
 |
Fig. 2 Profiles of pressure p and pressure derivative dp/ dr plotted over the relative radius r/R, where R is the stellar radius of the corresponding profile. Shown are different evolutionary states for a ZAMS of 2 M⊙ and an isothermal WD of 0.6 M⊙. |
In hydrodynamical simulations the Euler equations are discretized in space and time; thus, it is important to analyze the spatial structure of the stars that are to be mapped to the computational grid. As an example, we compare stellar profiles at different evolutionary stages for a model with a zero-age main sequence (ZAMS) mass of 2 M⊙, which is evolved until the first thermal pulse on the AGB using mesa. The evolution of the model is shown in a Hertzsprung-Russell diagram in Fig. 1, where different evolutionary points are marked for which the pressure profiles are given in Fig. 2. For comparison, a profile of the interior of a cold, isothermal 0.6 M⊙ carbon-oxygen WD with T = 5 × 105 K is shown as well. This model was set up by integrating the hydrostatic equilibrium equations with the Helmholtz equation of state (Timmes & Swesty 2000) starting from a central density of 3.2 × 106 g cm-3.
In Fig. 2, the profiles of the pressure and its spatial derivative are compared as functions of relative radius r/R, where R is the stellar radius of the corresponding model. The models show the usual behaviour: the core of the star contracts while its envelope expands when it evolves away from the MS. During core He burning on the horizontal branch (HB), the core expands and the envelope contracts slightly. On the AGB, the envelope expands even further than on the first red giant branch (RGB) and the maximum pressure in the core rises. The RGB and AGB profiles are similar, especially in the outer parts. The pressure profiles (Fig. 2, upper panel) show that the range in scales in radius and pressure increases drastically during the evolution. In the relative radius, it increases from roughly one to two decades for the MS model to five decades for the AGB model. The pressure derivative (Fig. 2, lower panel) shows a linear behaviour for r → 0, which is expected from expanding the stellar structure equations about the origin. To obtain stable models, the profile has to be resolved to the scale where the pressure derivative decreases linearly; otherwise a cusp in the pressure would be introduced at the origin, leading to spurious velocities. Resolving these scales is computationally not feasible for more evolved stellar structures with current numerical techniques.
Thus, approximations are needed to model giant profiles in hydrodynamical simulations – as opposed to MS and WD models, which can be mapped to a hydrodynamical simulation without approximations due to the smaller range in scales.
 |
Fig. 3 Approximate gravitational acceleration (left) and corresponding density for the modified Lane-Emden equation (right). The left panel shows uχ(u) (χ from Eq. (10)) compared to a Newtonian acceleration of a point mass (−1 /u2). Above u = 1, both functions coincide by construction. The right panel shows |
3.2. Approximations to giant profiles
Giant profiles are approximated here by replacing the core of the giant by a point mass that interacts only gravitationally with the envelope. Gravitation-only particles have been implemented in arepo for modeling dark matter (Springel 2010). Their gravitational acceleration is given by a spline function (Springel 2010, see also their Fig. 15) 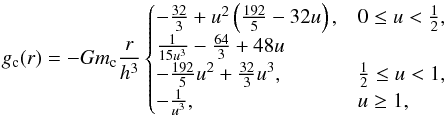 (10)where u = r/h, h is the softening length of the interaction, and mc is the mass of the particle representing the core. One advantage of this functional form is that it reduces exactly to the Newtonian acceleration outside the softening radius (i.e., for r>h) while still avoiding the singularity at r = 0. For radii smaller than h, gravity is modified; thus, the stellar profile of the giant is cut out and has to be replaced by a suitable function in this central region. Throughout this paper, we choose gc as given by Eq. (10), but the method can also be used for other functional forms of gc.
(10)where u = r/h, h is the softening length of the interaction, and mc is the mass of the particle representing the core. One advantage of this functional form is that it reduces exactly to the Newtonian acceleration outside the softening radius (i.e., for r>h) while still avoiding the singularity at r = 0. For radii smaller than h, gravity is modified; thus, the stellar profile of the giant is cut out and has to be replaced by a suitable function in this central region. Throughout this paper, we choose gc as given by Eq. (10), but the method can also be used for other functional forms of gc.
To integrate the giant profiles including the gravitation of the point mass, the stellar structure equations are modified, 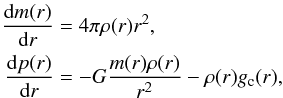 (11)where gc is the core acceleration given in Eq. (10), m denotes the integrated envelope mass (without the core mass), ρ the density of the gas, and p the pressure. Thus, the self-gravity of the gas as well as the gravity of the core is taken into account; the function ρ(r) still has to be specified.
(11)where gc is the core acceleration given in Eq. (10), m denotes the integrated envelope mass (without the core mass), ρ the density of the gas, and p the pressure. Thus, the self-gravity of the gas as well as the gravity of the core is taken into account; the function ρ(r) still has to be specified.
To create a stellar profile from the center of the star to the surface, the profile is continued from the cut radius h inwards to replace the original profile in the central region. The requirements for this continuation are that it should be smooth, lead to a similar profile when mapped into the hydrodynamics code and thus should be aware of the presence of the gravitational force of the core.
 |
Fig. 4 Comparison of density (upper left), pressure (upper right), internal energy (lower left) and derivative of pressure (lower right) for a 2 M⊙ RG with a ~ 0.4 M⊙ He core. Shown is the original profile from the mesa stellar evolution code as well as approximate profiles for cut radii of 1%, 5%, and 10% of the total radius. The approximate profiles were computed using a polytropic index of n = 3 for the interior part. |
To obtain continuations that fulfill these requirements, we introduce a modified Lane-Emden equation (cf., e.g., Kippenhahn et al. 2012 for a discussion of the Lane-Emden equation) that can be derived by combining the modified stellar structure Eqs. (11) to yield 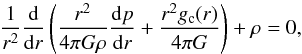 (12)where gc is the gravitational force of the core given by Eq. (10). One can now introduce a polytropic relation
(12)where gc is the gravitational force of the core given by Eq. (10). One can now introduce a polytropic relation 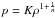 (with K denoting the polytropic constant, and n the polytropic index), and ρ = ρ0θn with the polytropic temperature θ and the central gas density ρ0, and a scaled radius
(with K denoting the polytropic constant, and n the polytropic index), and ρ = ρ0θn with the polytropic temperature θ and the central gas density ρ0, and a scaled radius 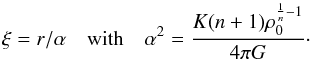 (13)Inserting these relations into Eq. (12) yields the well-known Lane-Emden equation, with an additional term that accounts for the core,
(13)Inserting these relations into Eq. (12) yields the well-known Lane-Emden equation, with an additional term that accounts for the core, 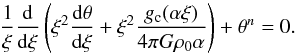 (14)By introducing a new function χ,
(14)By introducing a new function χ, 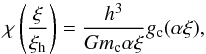 (15)where ξh = h/α is the non-dimensional radius at which the profile is cut, Eq. (14) can be written as
(15)where ξh = h/α is the non-dimensional radius at which the profile is cut, Eq. (14) can be written as 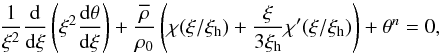 (16)where
(16)where 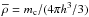 can be interpreted as a mean density of the core (i.e., the core mass spread out in a sphere of radius h). The function uχ(u) can be seen as a dimensionless form of the gravitational acceleration in Eq. (10) and is compared in Fig. 3 (left panel) to the original Newtonian acceleration 1 /u2. The interesting point is that the gravitational force of the core appears as an additional density term that depends on the ratio of the mean density of the core to the central density of the polytropic solution. This can be seen even more clearly when converting Eq. (16) into two first-order ODEs that can be used for integrating,
can be interpreted as a mean density of the core (i.e., the core mass spread out in a sphere of radius h). The function uχ(u) can be seen as a dimensionless form of the gravitational acceleration in Eq. (10) and is compared in Fig. 3 (left panel) to the original Newtonian acceleration 1 /u2. The interesting point is that the gravitational force of the core appears as an additional density term that depends on the ratio of the mean density of the core to the central density of the polytropic solution. This can be seen even more clearly when converting Eq. (16) into two first-order ODEs that can be used for integrating, 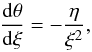 (17)
(17)![\begin{equation} \frac{\diff\eta}{\diff\xi} = \xi^2 \left[ \theta^n + \frac{\overline{\rho}}{\rho_0} \left( \chi(\xi/\xi_{\rm h}) + \frac{\xi}{3\xi_{\rm h}} \chi'(\xi/\xi_{\rm h}) \right) \right], \label{eq:laneemdensplit2} \end{equation}](/articles/aa/full_html/2017/03/aa29692-16/aa29692-16-eq94.png) (18)where η is the non-dimensional mass and where the initial conditions are given by η(0) = 0, θ(0) = 1. The original Lane-Emden equation does not feature the second term in the brackets of Eq. (18). This term in the mass integration corresponds to an additional density source caused by the core particle. Thus, assuming a smoothed gravitational force for the core as given in Eq. (10) is similar to smearing out the mass of the core inside a sphere of radius h with a density profile as shown in Fig. 3 (right panel).
(18)where η is the non-dimensional mass and where the initial conditions are given by η(0) = 0, θ(0) = 1. The original Lane-Emden equation does not feature the second term in the brackets of Eq. (18). This term in the mass integration corresponds to an additional density source caused by the core particle. Thus, assuming a smoothed gravitational force for the core as given in Eq. (10) is similar to smearing out the mass of the core inside a sphere of radius h with a density profile as shown in Fig. 3 (right panel).
The solution of this modified Lane-Emden equation now depends not only on the polytropic index n, but also on the parameters 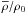 , ξh, and on the form of the function χ. For χ given by Eq. (15) the corresponding term in Eq. (16) reduces to zero for ξ>ξh, i.e., in the outer part. Thus, the modified Lane-Emden equation is reduced to the usual Lane-Emden equation in this region. The behaviour of the solution in the inner part (ξ<ξh) depends on the ratio
, ξh, and on the form of the function χ. For χ given by Eq. (15) the corresponding term in Eq. (16) reduces to zero for ξ>ξh, i.e., in the outer part. Thus, the modified Lane-Emden equation is reduced to the usual Lane-Emden equation in this region. The behaviour of the solution in the inner part (ξ<ξh) depends on the ratio 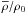 . For
. For 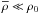 , the first term in the brackets in Eq. (18) dominates and the impact of the modification is small. The density resulting from smearing out the point mass,
, the first term in the brackets in Eq. (18) dominates and the impact of the modification is small. The density resulting from smearing out the point mass, 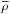 , can be neglected compared to the central gas density, ρ0 and the solution is similar to the solution of the Lane-Emden equation. In the opposite case,
, can be neglected compared to the central gas density, ρ0 and the solution is similar to the solution of the Lane-Emden equation. In the opposite case, 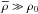 , the second term in the brackets in Eq. (18) dominates and the contribution of the gas density is negligible in the inner part for integrating the solution. Hence, the gas mass in the interior part is negligible compared to the mass of the core, and the solution differs from the normal Lane-Emden equation. This is usually the case for the models presented in this paper.
, the second term in the brackets in Eq. (18) dominates and the contribution of the gas density is negligible in the inner part for integrating the solution. Hence, the gas mass in the interior part is negligible compared to the mass of the core, and the solution differs from the normal Lane-Emden equation. This is usually the case for the models presented in this paper.
The solutions of the modified Lane-Emden equation show the same behaviour for convective stability as the solutions of the original Lane-Emden equation: the Schwarzschild criterion yields convective stability for 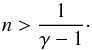 (19)For an adiabatic index γ = 5/3 corresponding to an ideal monoatomic gas, this yields n > 3/2 for convectively stable stratifications.
(19)For an adiabatic index γ = 5/3 corresponding to an ideal monoatomic gas, this yields n > 3/2 for convectively stable stratifications.
To obtain a smooth transition to a stellar profile at a certain radius, the solution of the modified Lane-Emden equation can be fitted to yield the corresponding density and its derivative: the integration of Eqs. (17) and (18) yields the function 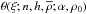 , where the parameters n,h, and
, where the parameters n,h, and 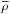 are given. The density
are given. The density 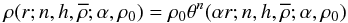 (20)can be used to fit the parameters α and ρ0 such that the density and its derivative are matched at the transition radius. This has been implemented using a non-linear root finder.
(20)can be used to fit the parameters α and ρ0 such that the density and its derivative are matched at the transition radius. This has been implemented using a non-linear root finder.
A few examples for such approximate stellar profiles are shown in Fig. 4 for a 2 M⊙ RG with a ~ 0.4 M⊙ He core (the RG model in Fig. 1) for different core cutoff radii. In this example, a polytropic index of n = 3 is used for the modified Lane-Emden solution in the interior part that was fitted to the profile. For the integration of the hydrostatic equilibrium of the profile, the OPAL equation of state (Rogers et al. 1996; Rogers & Nayfonov 2002) was used that is identical to the equation of state used by mesa in this ρ-T regime. The plots show that the stellar profile is reproduced very well in the outer part at radii larger than the cut radius for the important thermodynamic quantities. The connection to the inner part of the modified Lane-Emden solutions is smooth, as expected. Moreover, the derivative of the pressure (Fig. 4, lower right) shows linear behaviour for r → 0, which is important for ensuring hydrostatic equilibrium at the center of the star.
 |
Fig. 5 Comparison of different integration methods for a 2 M⊙ RG using the OPAL equation of state. The profile was cut at 5% of the stellar radius. Shown are the density ρ (upper left), the pressure p (upper right), the internal energy u (lower left), and the difference between the gradient ∇ and the adiabatic gradient ∇ad (lower right). |
3.3. Reconstructing stellar profiles
To use a stellar profile from a stellar evolution code in a multi-dimensional hydrodynamics code, the stellar structure equations have to be integrated when employing a different equation of state or approximate profiles such as described in the previous section. Especially for a different equation of state, some of the thermodynamic quantities will deviate. In this case, different reconstruction methods can be utilized to recover specific properties of the models.
Usually, the density is taken from the stellar profile for integrating the stellar structure equations: given ρ(r) as function of the radius, one can easily integrate 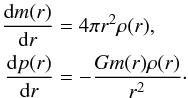 (21)This ensures that density, mass, and pressure profiles equal the values from the stellar evolution code. However, the values of the internal energy, entropy, sound speed, temperature gradients and other quantities may differ compared to the stellar evolution code. Thus, regions of convective stability or instability are not necessarily recovered correctly.
(21)This ensures that density, mass, and pressure profiles equal the values from the stellar evolution code. However, the values of the internal energy, entropy, sound speed, temperature gradients and other quantities may differ compared to the stellar evolution code. Thus, regions of convective stability or instability are not necessarily recovered correctly.
To conserve the convective stability or instability of the profile in different regions, the difference ∇−∇ad between the temperature gradient and the adiabatic gradient can be integrated in an alternative way1. To this end, a third equation for the temperature has to be added that is integrated along with the other equations, 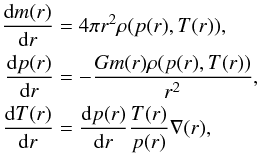 (22)where the temperature gradient is
(22)where the temperature gradient is 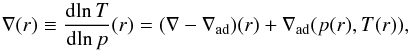 (23)and ∇ad is the adiabatic gradient given by the equation of state. This method ensures that the difference ∇−∇ad remains the same with respect to the corresponding equation of state. Hence, the criterion for convective stability will be fulfilled in the same regions of the stellar profile. This method, however, may change the mass profile of the star and thus also its radius and total mass. Hence, the quantities that one wants to preserve when mapping to a hydrodynamics code decide on the method to use.
(23)and ∇ad is the adiabatic gradient given by the equation of state. This method ensures that the difference ∇−∇ad remains the same with respect to the corresponding equation of state. Hence, the criterion for convective stability will be fulfilled in the same regions of the stellar profile. This method, however, may change the mass profile of the star and thus also its radius and total mass. Hence, the quantities that one wants to preserve when mapping to a hydrodynamics code decide on the method to use.
 |
Fig. 6 Comparison of different integration methods for a 2 M⊙ RG using an ideal equation of state. The profile was cut at 5% of the stellar radius. The panels show the same quantities as in Fig. 5. |
When employing the same equation of state in the stellar evolution code and in the hydrodynamics code, both integration methods yield the same result. This is demonstrated in Fig. 5 for a 2 M⊙ RG that was cut at 5% of the stellar radius. The figure shows the density ρ, the pressure p, the internal energy u, and the difference between the gradient ∇ and the adiabatic gradient ∇ad for the profile from mesa and reconstructed profiles using ρ or ∇−∇ad as given quantities. As one can see, both methods yield almost the same result.
However, using an ideal gas EOS for the reconstruction yields different profiles, as shown for the 2 M⊙ RG in Fig. 6. The deviations in the resulting stellar profiles is larger for extended giant profiles because the difference between the ideal gas equation of state and the OPAL equation of state is larger for lower densities and temperatures, where recombination plays an important role. When reconstructing using the density (red dashed line in Fig. 6), the profiles of density and pressure are recovered accurately, while the internal energy is smaller in the outer parts of the envelope. Moreover, ∇−∇ad< 0 for most parts of the envelope which means that the envelope is convectively stable when using this profile for mapping to the hydrodynamics code in contradiction to the original profile. The largest deviation can be seen in the outer part, where the two dips in the profile of ∇−∇ad correspond to the ionization zones of He and H. This model can also be reconstructed using ∇−∇ad (Fig. 6, yellow dotted line), reproducing the convectively unstable behaviour of the envelope for radii larger than the cut radius. However, the profile constructed in this way is smaller in radius by 18% and in gas mass by 27% (without core) because of the steeper adiabatic gradient.
Overview of RG relaxation runs.
Apart from reproducing stellar models for a different equation of state, the reconstruction method for ∇−∇ad also allows the generation of stellar profiles for use in the hydrodynamics code that can artificially be made convectively unstable or stable by adding or subtracting a constant in Eq. (23). The stratification of a convective envelope, e.g., is nearly adiabatic. Changing ∇ by a small amount (0.01–0.05, i.e., about 2.5% to 12.5% of the ideal gas adiabatic gradient of 0.4) leads to a convectively stable stratification. Since the temperature gradient is now shallower than in the original profile, the envelope will be larger in radius and mass.
As an example, this reconstruction method is applied to the same 2 M⊙ RG model in Fig. 5 (green dash-dotted line), with ∇ being decreased by 0.05. Starting the integration from the center, this results in a model with a convectively stable envelope because ∇ < ∇ad there. However, the mass distribution deviates from the original profile: the model is 61% larger in radius and 88% larger in mass (without core mass). The spike visible in ∇−∇ad is located at the surface of the original model and due to the gradient indicating super-adiabicity in the very surface layers. This, however, affects only a small part of the profile that cannot be resolved in the hydrodynamical simulations and can thus be neglected. Although the mass profile changes using this reconstruction method, these models can be used for testing the numerical stability in the hydrodynamical simulation (because convective motions should be absent) while still having similar density and pressure profiles.
4. Stable models in hydrodynamical simulations
4.1. Stability criteria
After creating the initial radial profiles – either by taking the stellar evolution data directly or by applying approximations – they are mapped to a three-dimensional grid to conduct hydrodynamical simulations. Discretization errors resulting from the mapping or from the numerical scheme lead to velocity fluctuations that may in turn lead to an unstable representation of the stellar model. In this case, instabilities may emerge with large, potentially also non-symmetric, spurious velocities resulting in expanded profiles or pulsating envelopes.
The objective is thus to arrive at stable representations of stellar models in hydrodynamical simulations. It is, however, difficult to define stringent criteria on stability since inherent, convective motions are present in convectively unstable envelopes, and hence the hydrostatic equilibrium cannot be fulfilled exactly. For Mach numbers that are not too large (≲ 0.1), a stationary state should result with only small deviations from the hydrostatic equilibrium.
We require that after several dynamical time scales the following approximate conditions are met in the hydrodynamical simulations:
-
1.
The deviations from the initial pressure and density profilesshould be small.
-
2.
Both sides of the hydrostatic equilibrium equation, ∇p = −ρ∇Φ, should compensate each other.
-
3.
For convectively stable profiles, the Mach numbers in the model should be small compared to the Mach numbers expected in the problem.
-
4.
For convectively unstable models, a stationary state should be reached.
-
5.
To exclude the presence of pulsations, the potential energy of the system should be constant.
To allow the hydrodynamics code to relax the initial profile to a stable representation, sufficient numerical resolution is required and a damping scheme is employed (see Sect. 2.3).
4.2. RG models
The relaxation procedure as outlined in Sect. 2.3 is now applied to RG structures to show that stable representations can be obtained reliably. Since the space of stellar model parameters as well as numerical parameters is huge, only a subset can be tested. To this end, a suite of 14 simulations was run for an initial model of a 2 M⊙ RG in the middle of the first giant branch (the same as in Fig. 1). A summary of the simulations is presented in Table 1. In the following, we discuss how well the original star is reproduced in terms of the mechanical structure (i.e., density and pressure distributions) but also regarding convectively stable or unstable layers.
4.2.1. Convectively stable atmospheres
The envelope of the 2 M⊙ RG is convectively unstable and should thus show convective motions. The magnitude of these velocities can be quite substantial: the Mach number according to mixing-length theory as computed by mesa ranges up to 0.5 in the outermost layers. When setting up such an initial model, it is thus difficult to judge whether velocities are due to convective motions or whether they are numerical artifacts caused by the numerical scheme. Hence, the magnitude of spurious velocities introduced by the numerical method is best studied for convectively stable stars. We created a set of four artificial, convectively stable models (model F, model G, model H, model I; see Table 1) by reconstructing the 2 M⊙ RG model using a temperature gradient shifted by a small amount for convective stability and using the OPAL EOS, the same as in mesa (in this ρ-T regime). This way, models are created for which the density and pressure structure resembles the initial stellar profile (see Fig. 5). The shift of 0.02 (0.05) corresponds to 5% (12.5%) of the adiabatic gradient for a value of 0.4 in the deeper interior. The flatter temperature gradient, however, leads to more extended profiles with more mass (Table 1 and Fig. 5).
For the convectively stable model H, the Mach number and density distributions are shown in Fig. 7, and the hydrostatic equilibrium in Fig. 8. As required for a stable model, the density profile follows the initial profile closely (Fig. 7, lower panel). In the central part, it decreases by about 10%, and at the surface, the very steep initial gradient cannot be fully resolved, hence, a slight expansion occurs. After the damping is switched off at 5tdyn = 47.3 d, the profile does not expand further. The Mach numbers are zero initially, increase during the relaxation run, and level off at the end of the run (Fig. 7, upper panel). The model stays very subsonic with Mach numbers below 0.05 in the inner part and less than 0.01 in most parts of the envelope. Near the surface, the Mach numbers increase again up to 0.1. In the background regions outside of the star, large spurious fluctuations occur. Because densities are low in these regions, however, the fluctuations are unimportant for the evolution of the stellar model (this also occurs for most of the other simulations). The mean Mach number over the whole grid is 0.009. The Mach numbers during the damping phase (at 18.9 d) are largest near the surface and at the radius where the core is connected to the envelope, i.e., at the softening length of its gravitational interaction. From these regions, the fluctuations disperse slowly into other regions of the envelope (compare red and yellow lines in Fig. 7, upper panel; five dynamical timescales lie in between those profiles). An important point here is that the Mach numbers introduced during a relaxation run in a convectively stable model (about 0.01) are much smaller than those encountered in convectively unstable models (e.g., model A). Hence, the convective motions seen in those models should not be affected by the imperfect stabilization of the hydrostatic equilibrium.
 |
Fig. 7 Mach number and density profile for model H. The top panel shows the Mach number at different times during the relaxation run, the bottom panel shows the density at the same times. Both quantities were radially binned and averaged in shells. This model should be convectively stable. |
 |
Fig. 8 Hydrostatic equilibrium for model H. The top panel shows the two sides of the hydrostatic equilibrium, |∇p| and ρ|g| at different times during the relaxation run. The bottom panel shows the relative error in the hydrostatic equilibrium. All quantities were radially binned and averaged in shells. This model should be convectively stable. |
The hydrostatic equilibrium for model H is shown in Fig. 8. Both terms that should cancel in hydrostatic equilibrium are indeed very similar and constant over time (Fig. 8, upper panel); small changes can be seen in the center (correlated to the decrease in density there) and near the surface due to the expansion. The error in the hydrostatic equilibrium is shown in Fig. 8 (lower panel). Initially, it is roughly 2% throughout the envelope, but it decreases during the relaxation run as the model converges to a hydrostatic equilibrium that is stable in the hydrodynamical simulation. The decrease is largest between 3 R⊙ and 40 R⊙ where most of the mass of the envelope is located. The mean error of the hydrostatic equilibrium over the whole grid computed for this model is 8 × 10-3 and hence, the final model fulfills the hydrostatic equilibrium to better than a per cent on average.
The density profile is constant in time after disabling the damping and the Mach number is small. This indicates that no pulsation is present, which is confirmed by the potential energy showing very small fluctuations <1% after the initial expansion. Pulsations would cause regular changes in the potential energy with a period of the dynamical timescale (about 9 d for this model). The initial expansion causes a small decrease of the potential energy by 2% to 3% (for all models). After this, the relative difference stays below 1% for all models in Table 1. Moreover, the error in the total energy is roughly 1% for all models except model C (about 3%) due to its lower resolution. Thus, none of the models show significant pulsations.
Combining all these results, we conclude that we are able to generate a model that stays in hydrostatic equilibrium for a convectively stable profile. For model G with a lower resolution, the results are very similar, only the mean error in the hydrostatic equilibrium, 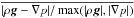 , is slightly larger with 1.3%. For the model with a smaller core cutoff radius, model F, the error in the hydrostatic equilibrium is similar (1.4%), but the resulting mean Mach number is larger: 0.02 instead of 0.01. Since the generation of the spurious velocities starts at the boundary of the core, this indicates that higher resolutions are needed to stabilize models with smaller core cutoff radii. The model that is farther away from the threshold to convective instability, model I, shows a similar hydrostatic equilibrium error and even lower Mach numbers with a mean of 0.005. Thus, spurious motions are even smaller for this model.
, is slightly larger with 1.3%. For the model with a smaller core cutoff radius, model F, the error in the hydrostatic equilibrium is similar (1.4%), but the resulting mean Mach number is larger: 0.02 instead of 0.01. Since the generation of the spurious velocities starts at the boundary of the core, this indicates that higher resolutions are needed to stabilize models with smaller core cutoff radii. The model that is farther away from the threshold to convective instability, model I, shows a similar hydrostatic equilibrium error and even lower Mach numbers with a mean of 0.005. Thus, spurious motions are even smaller for this model.
4.2.2. Convectively unstable atmospheres
The method proposed here is able to reproduce convectively stable profiles with Mach number fluctuations below 0.02. Thus, modeling convectively unstable profiles should not be influenced by these velocities if the expected Mach number of the convective motions is larger.
As an example of a convectively unstable model, we study model A that is similar to model H studied in the previous section, but is reconstructed using the density profile with the OPAL EOS (the same as in the mesa code in this regime) and thus reproduces the convective behaviour of the original 2 M⊙ model. The thermal timescale of this stellar model is 3400 yr, much longer than the dynamic or sound crossing time (9.4 d). It is also much longer than the time covered by simulations of binary interactions using this giant, which is of the order of a few years. Thus, the impact of radiative transfer should be small, at least in the initial phase of the binary simulations.
 |
Fig. 9 Mach number and density profile for model A. The top panel shows the Mach number at different times during the relaxation run, the bottom panel shows the density at the same times. Both quantities were radially binned and averaged in shells. Moreover, the profile from the mesa model is plotted. This model should be convectively unstable. |
 |
Fig. 10 Comparison of Mach number distributions for model H (left panel) and model A (right panel). Model H should be convectively stable, model A convectively unstable. The low-density region outside the stars (large cells) shows spurious Mach number fluctuations. |
The Mach number and density profiles are plotted in Fig. 9 together with those of the original mesa model. The density profile (lower panel) reproduces the original profile quite well throughout the envelope and differs only in the inner part, where it was cut off, and near the surface, where it expands slightly. The difference becomes significant only below ρ ≈ 10-7 g cm-3 and as the transition to the ambient medium is gradual, the definition of a new radius would be ambiguous. Although convective motions are present, the density profile changes only slightly near the surface after the damping is disabled and is nearly stationary in the rest of the envelope.
The Mach number (Fig. 9, upper panel) evolves from a state similar to the non-convective model in the beginning (cf. Fig. 7, upper panel) to a state with a Mach number between 0.1 and 0.2 throughout the envelope. The mean Mach number in this model is 0.12. This indicates that convective motions develop and dominate the flow in the envelope. The stratification of the envelope is only marginally unstable, and the convective motions are triggered by spurious velocity fluctuations. Outside of the star, spurious Mach number fluctuations can be seen similar to the non-convective model. Compared to the Mach number of convective motions according to the mixing-length theory as computed by mesa, the Mach numbers in the hydrodynamical model are much higher in most parts of the envelope. The increase of the Mach number near the surface, however, is similar in both the mesa model and our hydrodynamical model and is due to the decrease in sound speed in the outer layers. The kinetic energy due to the convective motions in this model is 1% of the total energy. This value is similar for the other convective models in Table 1 whereas for the non-convective models, the kinetic energy is due to numerical fluctuations and amounts to values between 0.01% and 0.1% of the total energy.
The Mach number distribution in the x-y plane is compared in Fig. 10 for the non-convective model H (left panel) and for the convective model A (right panel). Both simulations show spurious fluctuations in the outer region that is discretized in coarse cells2. The non-convective model (left panel) shows Mach numbers up to 0.05 only near the center and near the surface, as also seen in the radial profile (Fig. 7, upper panel). For the convective model (Fig. 10, right panel), a complex flow pattern emerges after the damping is turned off. It shows large plumes near the surface where the Mach number can reach values up to 0.5 and features updrafts and downdrafts during its evolution. Thus, the convectively unstable model A develops a convective pattern that can be followed in the hydrodynamical simulation. The global convective timescale for this model is 58 d (as estimated from integrating over averaged convective velocities), and the total time of the relaxation run is 94 d (ten times the dynamical timescale). Thus, the second half of the run, where no damping is applied, covers roughly one convective timescale, so the development of convection is expected during the run. Although we cannot reproduce a steady state of the convective flow field, the large-scale convective motions are recovered. These contain most of the kinetic energy and thus potentially have the largest impact on the evolution of the binary system.
The agreement in the hydrostatic equilibrium is not expected to be perfect due to the convective motions in the envelope. The mean deviation for this model is 2.7% and thus a factor of 3 larger than in the non-convective case (cf. Table 1), but still on the per cent level. This indicates that the dynamic motions induced by convection lead to changes in ρ and increase the mismatch of terms in the hydrostatic equilibrium, i.e., between pressure gradient and gravity.
Thus, convective envelopes of RG models can be reproduced for which a stationary density structure results that follows the original model. Furthermore, the model still approximately fulfills the hydrostatic equilibrium at the per cent level and shows convective motions as expected in the envelope.
4.2.3. Equation of state
All hydrodynamical simulations of CE phases published so far use an ideal gas EOS with constant γ for the hydrodynamics – except for the SPH simulations by Nandez et al. (2015) and Nandez & Ivanova (2016). Since stellar evolution codes usually employ an EOS that accounts for the ionization state of the plasma, the stellar profile has different thermodynamic properties when using an ideal gas EOS. As shown in Sect. 3.3 (cf. Fig. 6), this leads to changes in the convective stability. The thermodynamic structure and the convective behaviour can only be reproduced using the same (or a very similar) EOS.
Model J of our simulation suite was set up by reconstructing the stellar profile of the 2 M⊙ RG using the density profile and an ideal gas EOS with γ = 5/3. According to the stellar evolution code (that uses the OPAL EOS), this model has a deep convective envelope. However, the reconstruction with the ideal gas EOS leads to a convectively stable stratification (cf. Fig. 6). This is reproduced by model J; it does not develop convective motions: the mean Mach number remains as low as 6 × 10-3 and the mean error in the hydrostatic equilibrium is 1.3% (see Table 1). In this respect, the model is very similar to the artificially stabilized model G at the same resolution. Thus, mapping the density and pressure profile of this model from the stellar evolution code to the hydrodynamics code and using an ideal EOS results in a suppression of convective motions that should be present in the convective envelope.
To recover the convective properties of the stellar model, one can reconstruct ∇−∇ad, i.e., the difference to the adiabatic gradient (see Sect. 3.3). Setting this to zero for the reconstruction yields an adiabatic stratification that is convectively unstable. Although the stratification is only marginally unstable, spurious velocity fluctuations due to mismatches in the discretization of the hydrostatic equilibrium trigger the onset of convective motions in the envelope. Since this reconstruction method leads to a shallower temperature gradient, a smaller envelope results with less mass (see Fig. 6 and model K in Table 1). The relaxation run for model K shows convective motions, as expected for a convectively unstable model: the mean Mach number is 0.045 and the mean hydrostatic equilibrium error 1.6%. The mean Mach number is smaller than for the models reconstructed using the OPAL EOS which have a mean Mach number of about 0.12 (model A and model B, see Table 1). This is probably due to the different stratification.
Hence, the expected behaviour of initial stellar profiles can be reproduced also using an ideal EOS. The convective envelope of the giant, however, is expected to be convectively stable (as opposed to the original mesa model) when reconstructing the profile with an ideal EOS. Thus, to generate stellar models for the hydrodynamical simulations that show the correct convective behaviour, the same equation of state has to be used as in the stellar evolution code.
4.2.4. Numerical parameters
The construction of the initial models is influenced by the choice of the parameters resolution, core cutoff radius, and grid type.
To study the convergence behaviour of the simulations, the convectively stable model created by reconstructing the profile of ∇ with a shift of 0.02 was run in two resolutions: with 5 × 105 cells (model G) and with 2 × 106 cells (model H). For these models, the mean Mach number fluctuations are similar (9.6 × 10-3 vs. 9.1 × 10-3). The mean error in the hydrostatic equilibrium decreases by a factor of 1.6 which corresponds to the increase in resolution by a factor of 4 in number of cells which roughly means a factor of 41/3 ≈ 1.6 in average spatial resolution; hence, the error decreases to first order with the mean linear cell size. The convectively unstable model reconstructed using the density profile and the OPAL EOS was run in three resolutions (see Table 1): with 105 cells (model C), with 5 × 105 cells (model B), and with 2 × 106 cells (model A). At the lowest resolution, the mean Mach number (0.075) was smaller than for the other resolutions (0.12 for both); the errors in the hydrostatic equilibrium are similar and probably dominated by the presence of convective motions. Since the two highest resolutions show very similar properties, we conclude that the resolution of the convective motions is converged when using more than 5 × 105 cells.
The properties of simulations using different core cutoff radii are quite similar (compare model B, model D, model E), although for a large radius (10%, model E), the mean Mach number is slightly smaller. Decreasing the core cutoff radius is a goal for CE simulations because in this way, a larger fraction of the envelope can be reproduced on the grid. For convectively stable models, the model with a smaller core cutoff radius (model F, core is 2% of radius) shows a larger value of the mean Mach number by a factor of 2 than the model G (core is 5% of radius). Here, probably a higher resolution is needed to resolve the hydrostatic equilibrium better where the largest pressure gradients occur, namely at the boundary between core and envelope.
Overview of AGB relaxation runs.
All simulations presented so far used as initial grid configuration spherical shells with cells distributed on these shells according to the HEALPix distribution (cf. Sect. 2.1). Simulations similar to model B have been also carried out for different initial grids: model L using a cubic grid, model M using a cubic adaptive grid, and model N using a cubic nested grid (see Table 1). However, because a moving mesh is employed with an adaptive refinement ensuring similar cell masses, the difference between these simulations is small and the influence of the initial grid is negligible. This is, however, not true for static meshes: tests on static meshes show that the mass-adaptive grids result in better equilibria since they reflect the symmetry and allow for high spatial resolution in the center.
4.3. AGB models
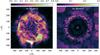 |
Fig. 11 Comparison of Mach number distributions for model O (left panel) and model P (right panel). Model O should be convectively unstable, model P convectively stable. |
 |
Fig. 12 Comparison of density distributions for model O (left panel) and model P (right panel). Model O should be convectively unstable, model P convectively stable. |
In addition to the 2 M⊙ RG model presented in the previous section, a 0.68 M⊙ AGB star (from a ZAMS model of 1 M⊙) is used as a second example. Its luminosity is 2400 L⊙, the dynamical timescale is 75 d, and the thermal timescale is 27 yr. The stellar model was set up using the OPAL EOS and the ideal EOS (Table 2). Both models were reconstructed using the density and mapped to a HEALPix grid with 5 × 105 cells. Similar to the 2 M⊙ RG model, the AGB model using the ideal EOS is expected to be convectively stable in most parts of the envelope (except near the surface and in a zone at a radius of about 80 R⊙), whereas the model using the OPAL EOS should be convectively unstable throughout the envelope.
This behaviour is indeed reproduced by our simulations: the mean Mach number in the convectively unstable model O is 0.2, whereas it is about 0.02 for the convectively stable model P. Moreover, the distribution of the Mach number in the x-y plane (Fig. 11) shows convective motions and large plumes with Mach numbers up to 0.8 for model O (left panel). Model P (right panel) shows only small Mach numbers in the envelope that are located in the central region, near the surface, and in a shell at approximately the radius (≈ 80 R⊙) that is expected to be convectively unstable.
Model P also shows a spherical density distribution following the original mesa model (Fig. 12, right panel) and the mean error of the hydrostatic equilibrium is about 2%. Hence, this model is still in a good hydrostatic equilibrium. Model O, however, shows a very dynamic behaviour: the convective cells are comparable to the size of the star and lead to a non-spherical density distribution that is also more extended compared to the original mesa model (Fig. 12, left panel).
The total runtime of the relaxation covers 750 d, i.e., roughly 2 yr. This is only one order of magnitude smaller than the thermal timescale; thus, radiative transfer may be important for binary simulations that cover longer time spans.
5. Discussion
5.1. Comparison to other setups used in simulations of the CE phase
Hydrodynamical simulations of the CE phase with grid codes have employed two strategies of dealing with the wide range of scales in giant profiles up to now: either the core is replaced by a point mass that interacts only gravitationally, similar to the method proposed in this paper (e.g. Sandquist et al. 1998, 2000; Passy et al. 2012; Staff et al. 2016a,b; Iaconi et al. 2017), or the core is represented by a cloud of particles for which the density is mapped to the grid for computing gravity (cloud-in-cell method, Ricker & Taam 2008, 2012). Both types of simulations did not employ a continuation of the profile below a certain radius, but simply mapped the one-dimensional profile to the grid, with the center of the star being in the center of a grid cell. This implies cutting the profile of the giant at a certain radius that depends on the resolution; moreover, the central part of the mapped profile is not in hydrostatic equilibrium, leading to velocity fluctuations. Hence, usually a strong damping is employed, reducing the velocities by about a factor of two each timestep. This implies damping on a timescale of the order of the timestep.
In contrast, the method proposed in this paper leads to a one-dimensional profile that can be mapped to the hydrodynamical grid independent of its resolution. Furthermore, the damping timescale can be chosen to be a tenth of the dynamical timescale (i.e., much larger than a timestep, see Eq. (9)), which damps sound waves on a physical timescale, allowing the profile to settle to an equilibrium. The damping can be made weaker with this method because the one-dimensional profile incorporates the gravitational force of the point mass and leads to a stable hydrostatic equilibrium after it is mapped to the grid. Thus, only slight distortions are generated, leading to small velocity fluctuations that can easily be damped away.
Moreover, grid simulations have up to now employed an ideal gas EOS that usually leads to convectively stable envelopes although the envelope of the giant is convectively unstable in the stellar evolution code (cf. model J in Table 1). Using a similar EOS in the hydrodynamical simulations as in the stellar evolution code, the convective behaviour of the model can be reproduced in our simulations. The reconstruction method using the temperature gradient (see Eq. (22)) can also be used to specifically generate models that are convectively stable or unstable, although this may lead to differences in the mechanical structure. If using a different EOS in the hydrodynamics code than in the stellar evolution code (e.g., an ideal gas EOS), either the mechanical profile of the star can be reproduced (i.e., density and pressure profiles) or its convective behaviour, but not both. In previous simulations, only the mechanical structure was recovered. With the method proposed here, however, it is possible to choose which properties of the stellar model are reproduced.
5.2. AGB models
The AGB models show rather violent behaviour with high Mach numbers up to 0.8 and with large convective cells, resulting in a dynamic structure that is not spherically symmetric. This behaviour is similar to what is seen in the radiation hydrodynamical simulations by Freytag & Höfner (2008) and Freytag et al. (2012). Their code uses a Cartesian grid, fixes the gravitational field, and includes non-local radiative transport. Moreover, energy is inserted in the interior with a magnitude corresponding to the core luminosity that drives convection. The simulations display a complex dynamical behaviour with large convective cells and shocks in the envelope. Although we do not include radiative transport, the convective motions in the envelope look qualitatively similar in our models. These, however, are tailored to be used as initial models for binary interactions that include self-gravity.
6. Conclusions
To study hydrodynamical interactions involving giant stars – such as CE phases – initial conditions for the hydrodynamical simulations have to be generated from the stellar evolution model. In this paper, a new method is presented to reliably create approximate models of giants that can be used for this purpose.
The profiles of giants are approximated by replacing the core with a point mass to limit the range in spatial and temporal scales such that hydrodynamical simulations are computationally feasible. The profile is continued to the stellar center by solving a modified Lane-Emden equation, a method that does not depend on the resolution of the grid in the hydrodynamical simulation. When using a different EOS in the hydrodynamical simulation than that in the stellar evolution code, the thermodynamic properties change. An improved reconstruction method is proposed that allows to recover either the mechanical properties (i.e., the density and pressure profiles) or the convective behaviour of the envelope. When using the same EOS, both methods yield the same profile as in the stellar evolution calculation.
These reconstructed profiles of giant envelopes are then mapped onto an unstructured grid for hydrodynamical simulations. To reach a stable model, a relaxation procedure is utilized: spurious velocity fluctuations are damped on a timescale related to the dynamical timescale of the giant. Several criteria are checked to assess the stability of the envelope: the profiles of density and pressure should remain similar to the original ones; the hydrostatic equilibrium should be maintained; the Mach number should be small for a convectively stable envelope, and a steady state should develop for a convectively unstable envelope; no pulsations should be present. It is shown that these criteria are fulfilled for the examples of a 2 M⊙ RGB and a 0.68 M⊙ AGB star; extending these simulations to other masses and evolutionary stages is straightforward. The examples show that convectively stable envelopes can be reproduced reliably, where the convective stability can be controlled by the reconstruction method. Convectively unstable envelopes develop fluid motions with profiles similar to the stellar evolution models.
The method proposed here improves on previous hydrodynamics studies (Sandquist et al. 1998, 2000; Ricker & Taam 2008, 2012; Passy et al. 2012; Staff et al. 2016a,b; Iaconi et al. 2017), by generating approximate profiles that do not depend on the grid resolution and by allowing to control the convective behaviour of the envelope by the reconstruction method. Also, the relaxation procedure is shown to generate giant envelopes that remain stable for several dynamical timescales.
Stable giant envelopes as modeled here can be used as initial conditions for hydrodynamical simulations of the CE phase (Ohlmann et al. 2016a,b), but might also be used to study mass transfer in binary systems or other dynamical phenomena involving giant envelopes.
This idea was originally proposed by Edelmann et al. (2016), although with fixed gravity.
If pi is taken as the average over cell i, the result remains the same for constant reconstruction. For linear reconstruction, the constant in Eq. (7) changes from 1/12 to 7/72, i.e., by roughly 20%. The order of magnitude and the scaling with δ/H stays the same.
Acknowledgments
The work of S.T.O. was supported by Studienstiftung des deutschen Volkes and by the graduate school GRK 1147 at University Würzburg. S.T.O. and F.K.R. acknowledge support by the DAAD/Go8 German-Australian exchange program. R.P. and V.S. acknowledge support by the European Research Council under ERC-StG grant EXAGAL-308037. S.T.O., F.K.R., R.P., and V.S. were supported by the Klaus Tschira Foundation. Parts of this work were performed on the computational resource ForHLR I funded by the Ministry of Science, Research and the Arts Baden-Württemberg and DFG (“Deutsche Forschungsgemeinschaft”). For data processing and plotting, NumPy and SciPy (Oliphant 2007), IPython (Pérez & Granger 2007), and Matplotlib (Hunter 2007) were used. We thank the anonymous referee for helpful comments.
References
- Bauswein, A., Stergioulas, N., & Janka, H.-T. 2016, Eur. Phys. J. A, 52, 56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benz, W., & Hills, J. G. 1987, ApJ, 323, 614 [NASA ADS] [CrossRef] [Google Scholar]
- Blöcker, T. 1995, A&A, 297, 727 [NASA ADS] [Google Scholar]
- Edelmann, P. V. F., Röpke, F. K., Hirschi, R., Georgy, C., & Jones, S. 2016, A&A, submitted [Google Scholar]
- Freytag, B., & Höfner, S. 2008, A&A, 483, 571 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Freytag, B., Steffen, M., Ludwig, H.-G., et al. 2012, J. Comput. Phys., 231, 919 [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z., Podsiadlowski, P., & Eggleton, P. P. 1995, MNRAS, 272, 800 [NASA ADS] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [Google Scholar]
- Iaconi, R., Reichardt, T., Staff, J., et al. 2017, MNRAS, 464, 4028 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, Jr., I., & Tutukov, A. V. 1984, ApJS, 54, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Ivanova, N., Justham, S., Chen, X., et al. 2013, A&ARv, 21, 59 [Google Scholar]
- Kippenhahn, R., Weigert, A., & Weiss, A. 2012, Stellar Structure and Evolution (Berlin, Heidelberg: Springer-Verlag) [Google Scholar]
- Lombardi, Jr., J. C., Rasio, F. A., & Shapiro, S. L. 1996, ApJ, 468, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Nandez, J. L. A., & Ivanova, N. 2016, MNRAS, 460, 3992 [NASA ADS] [CrossRef] [Google Scholar]
- Nandez, J. L. A., Ivanova, N., & Lombardi, Jr., J. C. 2014, ApJ, 786, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Nandez, J. L. A., Ivanova, N., & Lombardi, J. C. 2015, MNRAS, 450, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Nelemans, G., Yungelson, L. R., Portegies Zwart, S. F., & Verbunt, F. 2001, A&A, 365, 491 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ohlmann, S. T., Röpke, F. K., Pakmor, R., & Springel, V. 2016a, ApJ, 816, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Ohlmann, S. T., Röpke, F. K., Pakmor, R., Springel, V., & Müller, E. 2016b, MNRAS, 462, L121 [NASA ADS] [CrossRef] [Google Scholar]
- Oliphant, T. E. 2007, Comput. Sci. Eng., 9, 10 [CrossRef] [PubMed] [Google Scholar]
- Pakmor, R., Edelmann, P., Röpke, F. K., & Hillebrandt, W. 2012, MNRAS, 424, 2222 [NASA ADS] [CrossRef] [Google Scholar]
- Pakmor, R., Kromer, M., Taubenberger, S., & Springel, V. 2013, ApJ, 770, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Pakmor, R., Springel, V., Bauer, A., et al. 2016, MNRAS, 455, 1134 [NASA ADS] [CrossRef] [Google Scholar]
- Passy, J.-C., De Marco, O., Fryer, C. L., et al. 2012, ApJ, 744, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
- Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
- Pérez, F., & Granger, B. E. 2007, Comput. Sci. Eng., 9, 21 [Google Scholar]
- Reimers, D. 1975, Mem. Soc. Roy. Sci. Liège, 8, 369 [Google Scholar]
- Ricker, P. M., & Taam, R. E. 2008, ApJ, 672, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Ricker, P. M., & Taam, R. E. 2012, ApJ, 746, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, F. J., & Nayfonov, A. 2002, ApJ, 576, 1064 [Google Scholar]
- Rogers, F. J., Swenson, F. J., & Iglesias, C. A. 1996, ApJ, 456, 902 [NASA ADS] [CrossRef] [Google Scholar]
- Rosswog, S. 2015, Liv. Rev. Comput. Astrophys., 1, 109 [Google Scholar]
- Rosswog, S., Speith, R., & Wynn, G. A. 2004, MNRAS, 351, 1121 [NASA ADS] [CrossRef] [Google Scholar]
- Ruiter, A. J., Belczynski, K., & Fryer, C. 2009, ApJ, 699, 2026 [NASA ADS] [CrossRef] [Google Scholar]
- Sandquist, E. L., Taam, R. E., Chen, X., Bodenheimer, P., & Burkert, A. 1998, ApJ, 500, 909 [NASA ADS] [CrossRef] [Google Scholar]
- Sandquist, E. L., Taam, R. E., & Burkert, A. 2000, ApJ, 533, 984 [NASA ADS] [CrossRef] [Google Scholar]
- Schreiber, M. R., & Gänsicke, B. T. 2003, A&A, 406, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sills, A., Faber, J. A., Lombardi, Jr., J. C., Rasio, F. A., & Warren, A. R. 2001, ApJ, 548, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V. 2010, MNRAS, 401, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Staff, J. E., De Marco, O., Macdonald, D., et al. 2016a, MNRAS, 455, 3511 [NASA ADS] [CrossRef] [Google Scholar]
- Staff, J. E., De Marco, O., Wood, P., Galaviz, P., & Passy, J.-C. 2016b, MNRAS, 458, 832 [NASA ADS] [CrossRef] [Google Scholar]
- Timmes, F. X., & Swesty, F. D. 2000, ApJS, 126, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Toonen, S., Nelemans, G., & Portegies Zwart, S. 2012, A&A, 546, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Toro, E. F. 2009, Riemann Solvers and Numerical Methods for Fluid Dynamics: A Practical Introduction (Berlin, Heidelberg: Springer) [Google Scholar]
- Toro, E. F., Spruce, M., & Speares, W. 1994, Shock waves, 4, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Zingale, M., Dursi, L. J., ZuHone, J., et al. 2002, ApJS, 143, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Zorotovic, M., Schreiber, M. R., Gänsicke, B. T., & Nebot Gómez-Morán, A. 2010, A&A, 520, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Derivation of Mach number fluctuations
The magnitude of the velocity fluctuations introduced by the spatial discretization can be computed for the arepo scheme as follows. For an overview of numerical hydrodynamics and an in-depth explanation of Godunov schemes and Riemann solvers, see the book by Toro (2009).
The initial condition is chosen as an isothermal atmosphere given in z direction as p(z) = p0exp(−z/H) and ρ(z) = ρ0exp(−z/H), with H denoting the pressure scale height. We assume an ideal equation of state. The gravitational acceleration is constant and given by 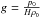 . The speed of sound is also constant and given by
. The speed of sound is also constant and given by 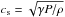 . The grid is assumed to be equidistant with grid spacing δ. We use the HLLC solver (Toro et al. 1994) to compute the Riemann problems at the cell interfaces.
. The grid is assumed to be equidistant with grid spacing δ. We use the HLLC solver (Toro et al. 1994) to compute the Riemann problems at the cell interfaces.
For this setup, the update of the conserved quantities Ui for cell i reads for a simple forward Euler time step (from time tn to tn + 1 = tn + Δt): 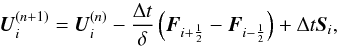 (A.1)where
(A.1)where  denotes the flux over the left (right) cell boundary and Si = (0,ρig,ρigvi)⊺ is the gravitational source term (ρi: density, vi: velocity).
denotes the flux over the left (right) cell boundary and Si = (0,ρig,ρigvi)⊺ is the gravitational source term (ρi: density, vi: velocity).
For the initial conditions given here, the velocity is zero and for each Riemann problem, pL>pR (L: left interface, R: right interface). Thus, the fluxes are computed for the subsonic L∗ region of the HLLC solver (Toro et al. 1994) as 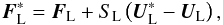 (A.2)where SL is the left wave speed and
(A.2)where SL is the left wave speed and  the solution of the Riemann problem in the L∗ region. FL is the Euler flux computed with the values at the left interface. Plugging in the solution of the Riemann problem as given in Toro et al. (1994) for zero velocities (vL = vR = 0) yields for the momentum flux
the solution of the Riemann problem in the L∗ region. FL is the Euler flux computed with the values at the left interface. Plugging in the solution of the Riemann problem as given in Toro et al. (1994) for zero velocities (vL = vR = 0) yields for the momentum flux 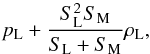 (A.3)where SM denotes the velocity of the contact discontinuity. This flux can now be combined with Eq. (A.1) to compute the update of the momentum,
(A.3)where SM denotes the velocity of the contact discontinuity. This flux can now be combined with Eq. (A.1) to compute the update of the momentum, 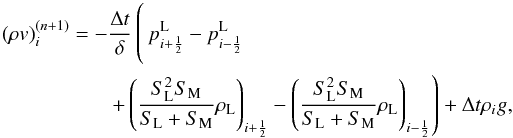 (A.4)where v(n) = 0 is assumed. To obtain the magnitude of velocity fluctuations caused by the spatial discretization, a reconstruction has to be chosen. For constant reconstruction,
(A.4)where v(n) = 0 is assumed. To obtain the magnitude of velocity fluctuations caused by the spatial discretization, a reconstruction has to be chosen. For constant reconstruction, 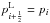 holds, whereas for linear reconstruction a central finite difference for the derivative is employed which yields
holds, whereas for linear reconstruction a central finite difference for the derivative is employed which yields 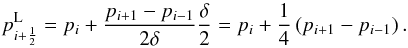 (A.5)After inserting the reconstruction into Eq. (A.4), pressure and density are expanded into a Taylor series around cell i and only the highest order terms are retained. For this expansion, we assume that the value pi represents the pressure at xi and not the average over cell i, which is the usual interpretation, because we use the same procedure in the setup of our simulations3. For better comparison between different initial values, the resulting Mach number M = v/cs is computed. The first order term in the expansion cancels out the gravitational source term, but for constant reconstruction, Mach number fluctuations are of the order of (δ/H)2. For linear reconstruction, this order vanishes as well and we obtain Eq. (7).
(A.5)After inserting the reconstruction into Eq. (A.4), pressure and density are expanded into a Taylor series around cell i and only the highest order terms are retained. For this expansion, we assume that the value pi represents the pressure at xi and not the average over cell i, which is the usual interpretation, because we use the same procedure in the setup of our simulations3. For better comparison between different initial values, the resulting Mach number M = v/cs is computed. The first order term in the expansion cancels out the gravitational source term, but for constant reconstruction, Mach number fluctuations are of the order of (δ/H)2. For linear reconstruction, this order vanishes as well and we obtain Eq. (7).
A similar derivation was done by Zingale et al. (2002, Sect. 3.1), but for a PPM scheme in the context of mapping hydrostatic profiles into the AMR code FLASH. For their scheme, they find a coefficient of 5/24 and the same order of the error, similar to our findings.
All Tables
All Figures
 |
Fig. 1 Hertzsprung-Russell diagram for the evolution of a 2 M⊙ star using mesa. Different evolutionary phases are marked for which the profiles are shown in Fig. 2. |
| In the text | |
 |
Fig. 2 Profiles of pressure p and pressure derivative dp/ dr plotted over the relative radius r/R, where R is the stellar radius of the corresponding profile. Shown are different evolutionary states for a ZAMS of 2 M⊙ and an isothermal WD of 0.6 M⊙. |
| In the text | |
 |
Fig. 3 Approximate gravitational acceleration (left) and corresponding density for the modified Lane-Emden equation (right). The left panel shows uχ(u) (χ from Eq. (10)) compared to a Newtonian acceleration of a point mass (−1 /u2). Above u = 1, both functions coincide by construction. The right panel shows |
| In the text | |
 |
Fig. 4 Comparison of density (upper left), pressure (upper right), internal energy (lower left) and derivative of pressure (lower right) for a 2 M⊙ RG with a ~ 0.4 M⊙ He core. Shown is the original profile from the mesa stellar evolution code as well as approximate profiles for cut radii of 1%, 5%, and 10% of the total radius. The approximate profiles were computed using a polytropic index of n = 3 for the interior part. |
| In the text | |
 |
Fig. 5 Comparison of different integration methods for a 2 M⊙ RG using the OPAL equation of state. The profile was cut at 5% of the stellar radius. Shown are the density ρ (upper left), the pressure p (upper right), the internal energy u (lower left), and the difference between the gradient ∇ and the adiabatic gradient ∇ad (lower right). |
| In the text | |
 |
Fig. 6 Comparison of different integration methods for a 2 M⊙ RG using an ideal equation of state. The profile was cut at 5% of the stellar radius. The panels show the same quantities as in Fig. 5. |
| In the text | |
 |
Fig. 7 Mach number and density profile for model H. The top panel shows the Mach number at different times during the relaxation run, the bottom panel shows the density at the same times. Both quantities were radially binned and averaged in shells. This model should be convectively stable. |
| In the text | |
 |
Fig. 8 Hydrostatic equilibrium for model H. The top panel shows the two sides of the hydrostatic equilibrium, |∇p| and ρ|g| at different times during the relaxation run. The bottom panel shows the relative error in the hydrostatic equilibrium. All quantities were radially binned and averaged in shells. This model should be convectively stable. |
| In the text | |
 |
Fig. 9 Mach number and density profile for model A. The top panel shows the Mach number at different times during the relaxation run, the bottom panel shows the density at the same times. Both quantities were radially binned and averaged in shells. Moreover, the profile from the mesa model is plotted. This model should be convectively unstable. |
| In the text | |
 |
Fig. 10 Comparison of Mach number distributions for model H (left panel) and model A (right panel). Model H should be convectively stable, model A convectively unstable. The low-density region outside the stars (large cells) shows spurious Mach number fluctuations. |
| In the text | |
 |
Fig. 11 Comparison of Mach number distributions for model O (left panel) and model P (right panel). Model O should be convectively unstable, model P convectively stable. |
| In the text | |
 |
Fig. 12 Comparison of density distributions for model O (left panel) and model P (right panel). Model O should be convectively unstable, model P convectively stable. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.