| Issue |
A&A
Volume 599, March 2017
|
|
|---|---|---|
| Article Number | A106 | |
| Number of page(s) | 15 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201526885 | |
| Published online | 08 March 2017 | |
Redshift-space distortions of galaxies, clusters, and AGN
Testing how the accuracy of growth rate measurements depends on scales and sample selections
1 Dipartimento di Fisica e Astronomia - Università di Bologna, viale Berti Pichat 6/2, 40127 Bologna, Italy
e-mail: federico.marulli3@unibo.it
2 INAF–Osservatorio Astronomico di Bologna, via Ranzani 1, 40127 Bologna, Italy
3 INFN–Sezione di Bologna, viale Berti Pichat 6/2, 40127 Bologna, Italy
4 Department of Physics, Ludwig-Maximilians-Universität, Scheinerstr. 1, 81679 München, Germany
5 Max-Planck-Institut für Astrophysik, Karl-Schwarzschild Strasse 1, 85748 Garching bei München, Germany
Received: 3 July 2015
Accepted: 8 December 2016
Aims. Redshift-space clustering anisotropies caused by cosmic peculiar velocities provide a powerful probe to test the gravity theory on large scales. However, to extract unbiased physical constraints, the clustering pattern has to be modelled accurately, taking into account the effects of non-linear dynamics at small scales, and properly describing the link between the selected cosmic tracers and the underlying dark matter field.
Methods. We used a large hydrodynamic simulation to investigate how the systematic error on the linear growth rate, f, caused by model uncertainties, depends on sample selections and co-moving scales. Specifically, we measured the redshift-space two-point correlation function of mock samples of galaxies, galaxy clusters and active galactic nuclei, extracted from the Magneticum simulation, in the redshift range 0.2 ≤ z ≤ 2, and adopting different sample selections. We estimated fσ8 by modelling both the monopole and the full two-dimensional anisotropic clustering, using the dispersion model.
Results. We find that the systematic error on fσ8 depends significantly on the range of scales considered for the fit. If the latter is kept fixed, the error depends on both redshift and sample selection due to the scale-dependent impact of non-linearities if not properly modelled. Concurrently, we show that it is possible to achieve almost unbiased constraints on fσ8 provided that the analysis is restricted to a proper range of scales that depends non-trivially on the properties of the sample. This can have a strong impact on multiple tracer analyses, and when combining catalogues selected at different redshifts.
Key words: cosmology: theory / cosmology: observations / dark matter / dark energy / large-scale structure of Universe
© ESO, 2017
1. Introduction
The dynamics of the Universe is shaped by the gravity force. The understanding of gravity is thus key to unveiling the nature of the Universe and its cosmological evolution. After almost one century from its original formulation, Einstein’s general relativity (GR) is still the dominant theory for describing gravity. However, despite its lasting experimental successes, some fundamental open issues are motivating challenging efforts aimed at searching for possible expansions or radically alternative models (Amendola et al. 2013). First of all, GR is not a quantum field theory and cannot be reconciled with the principles of quantum mechanics. Secondly, an increasingly large amount of astronomical observations cannot be explained by GR and baryonic matter alone, requiring the introduction of a never-observed form of dark matter (DM, Zwicky 1937). Finally, independent cosmological observations provide indisputable evidence for an accelerated expansion of the Universe, requiring the introduction of another dark component, generally dubbed dark energy (DE), when interpreted in the GR framework (Riess et al. 1998; Perlmutter et al. 1999). Whether GR provides a reliable description of the large scale structure of the Universe, and thus the latter is dominated by unknown dark components, or, on the contrary, such a gravity theory has to be corrected, or even abandoned, is one of the key questions of modern physics and cosmology.
One of the most effective ways to test the gravity theory on large scales, that is, where DM and DE arise, is to exploit the apparent anisotropies observed in galaxy maps; the so-called redshift-space distortions (RSD, Kaiser 1987; Hamilton 1998). Indeed, by modelling redshift-space clustering anisotropies, it is possible to constrain the linear growth rate of cosmic structures, f ≡ dlog δ/ dlog a, where a is the dimensionless scale factor and δ the linear fractional density perturbation, provided that the galaxy bias is known. The first RSD measurements were exploited primarily to estimate the mean matter density, ΩM, that can be derived directly from f(z) when a gravity model is assumed (Peacock et al. 2001; Hawkins et al. 2003). Later, Guzzo et al. (2008) and Zhang et al. (2008) showed that RSD can be effectively used to discriminate between DE and modified gravity scenarios. RSD thus started to be considered as a powerful probe of gravity, and several applications to galaxy redshift surveys followed rapidly, both in the local Universe and at larger redshifts, up to z ~ 1, such as 6dFGS (Beutler et al. 2012), SDSS (Samushia et al. 2012; Chuang & Wang 2013; Chuang et al. 2013), WiggleZ (Blake et al. 2012; Contreras et al. 2013), VIPERS (de la Torre et al. 2013), and BOSS (Tojeiro et al. 2012; Reid et al. 2012, 2014).
All of the above measurements have been obtained from large galaxy redshift surveys. The first tentative studies are starting to also consider different tracers, but results are still strongly affected by statistical uncertainties due to the paucity of the catalogues used. Thanks to the wealth of observational data now available, or expected in the near future, for instance from the ESA Euclid mission1 (Laureijs et al. 2011), the NASA Wide Field Infrared Space Telescope (WFIRST) mission2 (Spergel et al. 2013), and the extended Roentgen Survey with an Imaging Telescope Array (eROSITA) satellite mission3 (Merloni et al. 2012), it will soon become possible to apply these methodologies on both cluster and active galactic nuclei (AGN) catalogues. Galaxy clusters are the biggest collapsed structures in the Universe. They appear more strongly biased than galaxies, that is, their clustering signal is higher. Moreover, they are relatively unaffected by non-linear dynamics on small scales. This could help in modelling RSD in their clustering pattern, as the effect of small scale incoherent motions that generate the so-called fingers-of-God pattern, is substantially less severe relative to the galaxy clustering case, also improving the cosmological constraints that can be extracted from baryon acoustic oscillations (Veropalumbo et al. 2014). The main drawback is the low density of galaxy cluster samples and the fact that these sources can only be reliably detected at relatively small redshifts. On the other hand, AGN can be detected from up to very large distances. Powered by accreting supermassive black holes hosted at their centres, their extreme luminosities make them optimal tracers to investigate the largest scales of the Universe, and thus its cosmological evolution (see e.g. Marulli et al. 2008, 2009; Bonoli et al. 2009, and references therein).
The aim of this paper is to investigate the accuracy of the so-called dispersion model (described in Sect. 3) as a function of co-moving scales and sample selection. To achieve this goal, we exploit realistic mock samples of galaxies, galaxy clusters and AGN extracted from the Magneticum hydrodynamic simulation, at six snapshots in the range 0.2 ≤ z ≤ 2. We adopt a similar methodology as in Bianchi et al. (2012), though substantially extending that analysis. Specifically, i) in line with the majority of recent studies, we investigate the systematic errors of fσ8, instead of β; ii) we consider different kinds of realistic mock tracers, instead of solely DM haloes; iii) we analyse the dependency of the errors as a function of redshift; and iv) as a function of different sample selections. In agreement with previous investigations (see e.g. Bianchi et al. 2012; Mohammad et al. 2016), we find that the approximate modelisation of non-linear dynamics provided by the dispersion model introduces systematic errors on fσ8 measurements that depend non-trivially on the redshift and bias of the tracers. On the other hand, as we demonstrate here, it is possible to substantially reduce the systematic errors on fσ8 provided that the fit is restricted to a proper range of scales that depends on sample selection. An alternative investigation of the impact of the galaxy sample selection function on the ability to test GR with RSD was carried out recently by Hearin (2015), analysing the small-scale effects of the assembly bias in velocity space.
The software that we implemented to perform all the analyses presented in this paper can be freely downloaded4. It consists of a set of C++ libraries that can be used for several astronomical calculations, in particular to measure the two-point correlation function and to model RSD (CosmoBolognaLib, Marulli et al. 2016). We also provide the full documentation for these libraries, and some example codes that explain how to use them.
The paper is organised as follows. In Sect. 2 we describe the Magneticum simulation used to construct mock samples of galaxies, clusters and AGN, whose main properties are reported in Appendix A. In Sects. 3 and 4 we present the formalism used to model RSD and to measure the two-point correlation function in redshift-space mock catalogues, respectively. The results of our analyses are presented in Sect. 5. In Sect. 7 we summarise our conclusions. Finally, in the Appendices B and C we discuss the tests performed to investigate the robustness of the methods applied in our analysis.
2. The Magneticum simulation
The most direct way to investigate systematic errors in linear growth rate measurements from RSD is to exploit large numerical simulations and to apply to them the same methodologies used for real data. As our goal is to study the effects of different sample selections, we make use of realistic mock catalogues of different cosmic tracers. Specifically, we analyse galaxy, cluster and AGN mock catalogues extracted from the hydrodynamic Magneticum simulation5 (Dolag et al., in prep.).
This simulation is based on the parallel cosmological TreePM-SPH code P-GADGET3 (Springel 2005). The code uses an entropy-conserving formulation of smoothed-particle hydrodynamics (SPH; Springel & Hernquist 2002) and follows the gas using a low-viscosity SPH scheme to properly track turbulence (Dolag et al. 2005). It also allows a treatment of radiative cooling and heating from a uniform time-dependent ultraviolet background and star formation with the associated feedback processes. The latter is based on a sub-resolution model for the multi-phase structure of the interstellar medium (ISM; Springel & Hernquist 2003a).
Radiative cooling rates are computed by following the same procedure presented by Wiersma et al. (2009). We account for the presence of the cosmic microwave background and of ultraviolet/X-ray background radiation from quasars and galaxies, as computed by Haardt & Madau (2001). The contributions to cooling from each one of the 11 elements, H, He, C, N, O, Ne, Mg, Si, S, Ca and Fe, have been pre-computed using the publicly available CLOUDY photoionisation code (Ferland et al. 1998) for an optically thin gas in photoionisation equilibrium.
In the multiphase model for star formation (Springel & Hernquist 2003b), the ISM is treated as a two-phase medium where clouds of cold gas form from cooling of hot gas and are embedded in the hot gas phase assuming pressure equilibrium whenever gas particles are above a given threshold density. The hot gas within the multiphase model is heated by supernovae and can evaporate the cold clouds. A certain fraction of massive stars (10%) is assumed to explode as supernovae type II (SNII). The released energy by SNII (1051 erg) is modelled to trigger galactic winds with the mass-loading rate being proportional to the star-formation rate to obtain a resulting wind velocity of vwind = 350 km s-1. Our simulation also includes a detailed model of chemical evolution according to Tornatore et al. (2007). Metals are produced by SNII, by supernovae type Ia (SNIa) and by intermediate- and low-mass stars in the asymptotic giant branch (AGB). Metals and energy are released by stars of different mass by properly accounting for mass-dependent lifetimes, with a lifetime function according to Padovani & Matteucci (1993), the metallicity-dependent stellar yields by Woosley & Weaver (1995) for SNII, the yields by van den Hoek & Groenewegen (1997) for AGB stars and the yields by Thielemann et al. (2003) for SNIa. Stars of different mass are initially distributed according to a Chabrier initial-mass function (Chabrier 2003).
Most importantly, the Magneticum simulation also includes a prescription for black-hole growth and for feedback from AGN. As for star formation, the accretion onto black holes and the associated feedback adopts a sub-resolution model. Black holes are represented by collisionless “sink particles” that can grow in mass by accreting gas from their environments or by merging with other black holes. Our implementation is based on the model presented in Springel et al. (2005) and Di Matteo et al. (2005), including the same modifications as in the study of Fabjan et al. (2010) and some new, minor changes, as described in Hirschmann et al. (2014).
The black hole (BH) gas accretion rate, ṀBH, is estimated by using the Bondi-Hoyle-Lyttleton approximation (Hoyle & Lyttleton 1939; Bondi & Hoyle 1944; Bondi 1952): 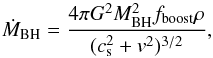 (1)where ρ and cs are the density and the sound speed of the surrounding (ISM) gas, respectively, fboost is a boost factor for the density, which is typically set to 100, and v is the velocity of the black hole relative to the surrounding gas. The black hole accretion is always limited to the Eddington rate. The radiated bolometric luminosity, Lbol, is related to the black-hole-accretion rate by
(1)where ρ and cs are the density and the sound speed of the surrounding (ISM) gas, respectively, fboost is a boost factor for the density, which is typically set to 100, and v is the velocity of the black hole relative to the surrounding gas. The black hole accretion is always limited to the Eddington rate. The radiated bolometric luminosity, Lbol, is related to the black-hole-accretion rate by 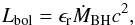 (2)where ϵr is the radiative efficiency, for which we adopt a fixed value of 0.1, standardly assumed for a radiatively efficient accretion disk onto a non-rapidly spinning black hole according to Shakura & Sunyaev (1973; see also, Springel 2005; Di Matteo et al. 2005).
(2)where ϵr is the radiative efficiency, for which we adopt a fixed value of 0.1, standardly assumed for a radiatively efficient accretion disk onto a non-rapidly spinning black hole according to Shakura & Sunyaev (1973; see also, Springel 2005; Di Matteo et al. 2005).
The simulation covers a cosmological volume with periodic boundary conditions initially occupied by an equal number of 15263 gas and DM particles, with relative masses that reflect the global baryon fraction, Ωb/ΩM. The box side is 896h-1 Mpc. The cosmological model adopted is a spatially flat ΛCDM Universe with matter density ΩM = 0.272, baryon density Ωb = 0.0456, power spectrum normalisation σ8 = 0.809, and Hubble constant H0 = 70.4 km s-1 Mpc-1, chosen to match the seven-year Wilkinson Microwave Anisotropy Probe (WMPA7, Komatsu et al. 2011). More details on the Magneticum simulation and the derived mock catalogues can be found in Hirschmann et al. (2014), Saro et al. (2014), Bocquet et al. (2016).
Firstly, the following section describes our analysis of large samples of mock galaxies, clusters and AGN selected in stellar mass, cluster mass and BH mass, respectively. Then, we consider several sub-samples with different selections, as reported in Tables A.1–A.3 (see Sect. 5).
3. Redshift-space distortions
To construct redshift-space mock catalogues, we adopt the same methodology used in Bianchi et al. (2012) and Marulli et al. (2011, 2012a,b). Here we provide a brief description. We consider a local virtual observer at z = 0, and place the centre of each snapshot of the Magneticum simulation at a co-moving distance, Dc, corresponding to its redshift, that is: 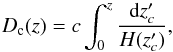 (3)where c is the speed of light, and the Hubble expansion rate is:
(3)where c is the speed of light, and the Hubble expansion rate is: ![\begin{eqnarray} H(z) &= &H_0\left[\hspace*{-22.5mm}\phantom{\left(3\int_0^z\frac{1+w(z)}{1+z}\right)}\Omega_{\rm M}(1+z)^3+\Omega_{\rm k}(1+z)^2\right. \nonumber\\ &&\left.\quad +\,\Omega_{\rm DE} \exp\left(3\int_0^z\frac{1+w(z)}{1+z}\right)\right]^{0.5}, \label{eq:HubbleFull} \end{eqnarray}](/articles/aa/full_html/2017/03/aa26885-15/aa26885-15-eq38.png) (4)where Ωk = 1−ΩM−ΩDE, w(z) is the DE equation of state, and the contribution of radiation is assumed negligible. In our case: Ωk = 1, w(z) = 1, so ΩDE ≡ ΩΛ = 1−ΩM and the Hubble expansion rate reduces to:
(4)where Ωk = 1−ΩM−ΩDE, w(z) is the DE equation of state, and the contribution of radiation is assumed negligible. In our case: Ωk = 1, w(z) = 1, so ΩDE ≡ ΩΛ = 1−ΩM and the Hubble expansion rate reduces to: ![\begin{equation} H(z) = H_0\left[\Omega_{\rm M}(1+z)^3+\Omega_{\Lambda}\right] . \label{eq:Hubble} \end{equation}](/articles/aa/full_html/2017/03/aa26885-15/aa26885-15-eq44.png) (5)To estimate the distribution of mock sources in redshift-space, we then transform the co-moving coordinates of each object into angular positions and observed redshifts. The latter are computed as follows:
(5)To estimate the distribution of mock sources in redshift-space, we then transform the co-moving coordinates of each object into angular positions and observed redshifts. The latter are computed as follows: 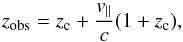 (6)where zc is the cosmological redshift due to the Hubble recession velocity at the co-moving distance of the object and v∥ is the line-of-sight component of its centre of mass velocity. In this analysis, we do not include either errors in the observed redshift, or geometric distortions caused by an incorrect assumption of the background cosmology (see Marulli et al. 2012b, for more details).
(6)where zc is the cosmological redshift due to the Hubble recession velocity at the co-moving distance of the object and v∥ is the line-of-sight component of its centre of mass velocity. In this analysis, we do not include either errors in the observed redshift, or geometric distortions caused by an incorrect assumption of the background cosmology (see Marulli et al. 2012b, for more details).
In the linear regime, the velocity field can be determined from the density field, and the amplitude of RSD is proportional to the parameter β, defined as follows: 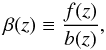 (7)where the linear growth rate, f, can be approximated in most cosmological frameworks as:
(7)where the linear growth rate, f, can be approximated in most cosmological frameworks as: 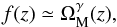 (8)with γ ≃ 0.545 in ΛCDM. The linear bias factor can be estimated as:
(8)with γ ≃ 0.545 in ΛCDM. The linear bias factor can be estimated as: 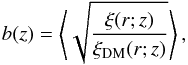 (9)where the mean is computed at sufficiently large scales at which non-linear effects can be neglected.
(9)where the mean is computed at sufficiently large scales at which non-linear effects can be neglected.
In the linear regime, the redshift-space two-point correlation function can be written as follows: 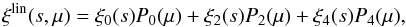 (10)where μ ≡ cosθ = s∥/s is the cosine of the angle between the separation vector and the line of sight,
(10)where μ ≡ cosθ = s∥/s is the cosine of the angle between the separation vector and the line of sight, 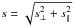 , and Pl are the Legendre polynomials (Kaiser 1987; Lilje & Efstathiou 1989; McGill 1990; Hamilton 1992; Fisher et al. 1994). Eq. (10) is derived in the distant-observer approximation, that is reasonable at the scales considered in this analysis. The multipoles of ξ(s⊥,s∥) are:
, and Pl are the Legendre polynomials (Kaiser 1987; Lilje & Efstathiou 1989; McGill 1990; Hamilton 1992; Fisher et al. 1994). Eq. (10) is derived in the distant-observer approximation, that is reasonable at the scales considered in this analysis. The multipoles of ξ(s⊥,s∥) are: ![% subequation 1457 0 \begin{eqnarray} \xi_0(s) & = &\left(1+ \frac{2}{3}\beta + \frac{1}{5}\beta^2 \right) \cdot \xi(r) \label{eq:xi0_1} \\ & = & \left[(b\sigma_8)^2 + \frac{2}{3} f\sigma_8 \cdot b\sigma_8 + \frac{1}{5}(f\sigma_8)^2 \right] \cdot \frac{\xi_{\rm DM}(r)}{\sigma_8^2}, \label{eq:xi0_2} \end{eqnarray}](/articles/aa/full_html/2017/03/aa26885-15/aa26885-15-eq57.png)
![% subequation 1471 0 \begin{eqnarray} \xi_2(s) & = &\left(\frac{4}{3}\beta + \frac{4}{7}\beta^2\right)\left[\xi(r)-\overline{\xi}(r)\right] \label{eq:xi2_1} \\ & = &\left[\frac{4}{3}f\sigma_8 \cdot b\sigma_8 + \frac{4}{7}(f\sigma_8)^2\right]\left[\frac{\xi_{\rm DM}(r)}{\sigma_8^2}-\frac{\overline{\xi}_{\rm DM}(r)}{\sigma_8^2}\right], \label{eq:xi2_2} \end{eqnarray}](/articles/aa/full_html/2017/03/aa26885-15/aa26885-15-eq58.png)
![% subequation 1487 0 \begin{eqnarray} \xi_4(s) & = &\frac{8}{35}\beta^2\left[\xi(r) + \frac{5}{2}\overline{\xi}(r) -\frac{7}{2}\overline{\overline{\xi}}(r)\right] \label{eq:xi4_1} \\ & = &\frac{8}{35}(f\sigma_8)^2\left[\frac{\xi_{\rm DM}(r)}{\sigma_8^2} + \frac{5}{2}\frac{\overline{\xi}_{\rm DM}(r)}{\sigma_8^2} -\frac{7}{2}\frac{\overline{\overline{\xi}}_{\rm DM}(r)}{\sigma_8^2} \right], \label{eq:xi4_2} \end{eqnarray}](/articles/aa/full_html/2017/03/aa26885-15/aa26885-15-eq59.png) where ξ(r) and ξDM(r) are the real-space undistorted correlation functions of tracers and DM, respectively, whereas the barred functions are:
where ξ(r) and ξDM(r) are the real-space undistorted correlation functions of tracers and DM, respectively, whereas the barred functions are: ![\begin{eqnarray} \overline{\xi}_{\rm DM}(r) &\equiv& \frac{3}{r^3}\int^r_0{\rm d}r'\xi_{\rm DM}(r')r'{^2}, \label{eq:xi_} \\[3mm] \overline{\overline{\xi}}_{\rm DM}(r) &\equiv& \frac{5}{r^5}\int^r_0{\rm d}r'\xi_{\rm DM}(r')r'{^4} . \label{eq:xi__} \end{eqnarray}](/articles/aa/full_html/2017/03/aa26885-15/aa26885-15-eq62.png) Equations (11b)–(13b) are derived from Eqs. (11a)–(13a) respectively, using Eq. (7). In this analysis, ξDM(r) is estimated by Fourier transforming the linear power spectrum computed with the software CAMB (Lewis & Bridle 2002) for the cosmological model considered here. We could alternatively measure the DM correlation function directly from the snapshots of the simulation. However, by using CAMB, we can substantially reduce the computational time, we get a smooth model with no errors due to measurements and, more importantly, we can closely mimic the analysis we would have done with real data.
Equations (11b)–(13b) are derived from Eqs. (11a)–(13a) respectively, using Eq. (7). In this analysis, ξDM(r) is estimated by Fourier transforming the linear power spectrum computed with the software CAMB (Lewis & Bridle 2002) for the cosmological model considered here. We could alternatively measure the DM correlation function directly from the snapshots of the simulation. However, by using CAMB, we can substantially reduce the computational time, we get a smooth model with no errors due to measurements and, more importantly, we can closely mimic the analysis we would have done with real data.
Equation (10) is an effective description of RSD only at large scales, where non-linear effects are negligible (but see e.g. Scoccimarro 2004; Taruya et al. 2010; Seljak & McDonald 2011; Wang et al. 2014, for a more accurate modelling). An empirical model that can account for both linear and non-linear dynamics is the so-called dispersion model (Peacock & Dodds 1996; Peebles 1980; Davis & Peebles 1983) that describes the redshift-space correlation function as a convolution of the linearly-distorted correlation with the distribution function of pairwise velocities, f(v): 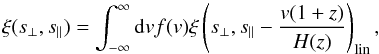 (16)where the pairwise velocity v is expressed in physical coordinates.
(16)where the pairwise velocity v is expressed in physical coordinates.
Since we are not considering redshift errors, we use the exponential form for f(v) (Marulli et al. 2012b), namely: 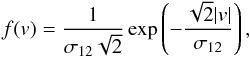 (17)(Davis & Peebles 1983; Fisher et al. 1994; Zurek et al. 1994). The quantity σ12 can be interpreted as the dispersion in the pairwise random peculiar velocities, and is assumed to be independent of pair separations.
(17)(Davis & Peebles 1983; Fisher et al. 1994; Zurek et al. 1994). The quantity σ12 can be interpreted as the dispersion in the pairwise random peculiar velocities, and is assumed to be independent of pair separations.
The dispersion model given by Eqs. (10)–(17) depends on three free quantities, fσ8, bσ8 and σ12 (since 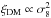 ), and on the reference background cosmology used both to convert angles and redshifts into distances and to estimate the real-space DM two-point correlation function. This model has been widely used in the past years to estimate the linear growth rate both in configuration space, that is by modelling ξ(s⊥,s∥) or its multipoles (e.g. Peacock et al. 2001; Hawkins et al. 2003; Guzzo et al. 2008; Ross et al. 2007; Cabré & Gaztañaga 2009a,b; Contreras et al. 2013) and in Fourier space, by modelling the power spectrum (e.g. Percival et al. 2004; Tegmark et al. 2004; Blake et al. 2011). In this analysis, we investigate the accuracy of the dispersion model in configuration space, while alternative RSD models will be analysed in an upcoming paper.
), and on the reference background cosmology used both to convert angles and redshifts into distances and to estimate the real-space DM two-point correlation function. This model has been widely used in the past years to estimate the linear growth rate both in configuration space, that is by modelling ξ(s⊥,s∥) or its multipoles (e.g. Peacock et al. 2001; Hawkins et al. 2003; Guzzo et al. 2008; Ross et al. 2007; Cabré & Gaztañaga 2009a,b; Contreras et al. 2013) and in Fourier space, by modelling the power spectrum (e.g. Percival et al. 2004; Tegmark et al. 2004; Blake et al. 2011). In this analysis, we investigate the accuracy of the dispersion model in configuration space, while alternative RSD models will be analysed in an upcoming paper.
4. Methodology
The aim of this work is to test widely-used statistical methods for modelling RSD and to extract constraints on the linear growth rate. Thus, we use methodologies that can be applied directly to real data. Nevertheless, we do not consider any specific mock catalogue, in order to keep our analysis general, that is, not restricted to any specific real survey. To measure the two-point correlation functions of our mock samples, we make use of the Landy & Szalay (1993) estimator: 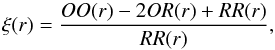 (18)where OO(r), OR(r) and RR(r) are the fractions of object–object, object–random and random–random pairs, with spatial separation r, in the range [r−δr/ 2,r + δr/ 2], where δr is the bin size. The random catalogues are constructed to be three times larger than the associated mock samples. As we are considering mock catalogues in cubic boxes, with no geometrical selection effects and periodic conditions, we could easily estimate the two-point correlation function directly from the density field, or compute the random counts analytically. Nevertheless, we prefer to use the Landy & Szalay (1993) estimator to more closely mimic the analysis of real data, as stressed before. In any case, this choice does not impact the results of our analysis. Moreover, as we verified, the number of random objects used in this work is large enough to have no significant effect on our measurements (see Appendix B). We compute the correlation functions up to a maximum scale of r = 50h-1 Mpc, both in the parallel and perpendicular directions. As we have verified with a sub-set of mocks, going to higher scales does not change our results, as the constraints on fσ8 are mainly determined by the RSD signal at smaller scales.
(18)where OO(r), OR(r) and RR(r) are the fractions of object–object, object–random and random–random pairs, with spatial separation r, in the range [r−δr/ 2,r + δr/ 2], where δr is the bin size. The random catalogues are constructed to be three times larger than the associated mock samples. As we are considering mock catalogues in cubic boxes, with no geometrical selection effects and periodic conditions, we could easily estimate the two-point correlation function directly from the density field, or compute the random counts analytically. Nevertheless, we prefer to use the Landy & Szalay (1993) estimator to more closely mimic the analysis of real data, as stressed before. In any case, this choice does not impact the results of our analysis. Moreover, as we verified, the number of random objects used in this work is large enough to have no significant effect on our measurements (see Appendix B). We compute the correlation functions up to a maximum scale of r = 50h-1 Mpc, both in the parallel and perpendicular directions. As we have verified with a sub-set of mocks, going to higher scales does not change our results, as the constraints on fσ8 are mainly determined by the RSD signal at smaller scales.
To model RSD and extract constraints on fσ8, we exploit the model given by Eqs. (10)–(17). We consider two case studies. The first consists of modelling only the monopole of the redshift-space two-point correlation function at large scales, via Eq. (11b), that is in the Kaiser limit, assuming that the non-linear effects can be neglected at these scales. In this case, the bσ8 factor has to be fixed a priori. When analysing real catalogues, this factor can be determined either directly with the deprojection technique (see e.g. Marulli et al. 2012b), or from the three-point correlation function (see e.g. Moresco et al. 2014), or by combining clustering and lensing measurements (see e.g. Sereno et al. 2015). To minimise the uncertainties and systematics possibly present in the above methods, we derive bσ8 directly from the real-space two-point correlation functions of our mock tracers, through Eq. (9), while the DM correlation is obtained by Fourier transforming the linear CAMB power spectrum, fixing σ8 at the value of the Magneticum simulation.
The second method considered in this work consists of fully exploiting the redshift-space two-dimensional anisotropic correlation function ξ(s⊥,s∥) . An alternative approach would be to use the multipole moments of the correlation function. The advantage is that this reduces the number of observables, thus helping in the computation of the covariance matrix (e.g. de la Torre et al. 2013; Petracca et al. 2016). However, we are not mimicking any real redshift survey here. Thus, a detailed treatment of the statistical errors is not necessary for the purposes of the present paper that focuses instead on the systematic uncertainties caused by a poor modelisation of non-linear effects. Therefore, we use diagonal covariance matrices only, whose elements are estimated analytically from Poisson statistics. As discussed in Bianchi et al. (2012), the effect on growth rate measurements caused by assuming negligible off-diagonal elements in the covariance matrix is small (of the order of only a few percent in that analysis), thanks to the large volumes of the mock samples with respect to the scales used for the parameter estimations. Appendix C provides some further tests, using the mock samples analysed in this work, that appear in overall agreement with the Bianchi et al. (2012) conclusions (see also Petracca et al. 2016). Moreover, to investigate the accuracy of the dispersion model as a function of scales, it is more convenient to exploit ξ(s⊥,s∥) . Indeed, following this approach, we can explore the full r∥−r⊥ plane, searching for the optimal region to be used to minimise model uncertainties.
 |
Fig. 1 Ratio between the redshift-space and real-space two-point spherically averaged correlation functions, ξ(s) /ξ(r), at z = 0.2, for galaxies with log (MSTAR [h-1M⊙]) > 10 (top panel), clusters with log (M500 [h-1M⊙]) > 13 (central panel), and AGN with log (MBH [h-1M⊙]) > 6.3 (bottom panel). The redshift-space correlation functions have been measured directly from the simulation, while the real-space ones have been either measured from the simulation (red dots), or derived from the CAMB power spectrum (blue squares). The error bars represent the statistical noise as prescribed by Mo et al. (1992). The black solid lines show the expected values of ξ(s) /ξ(r) at large scales predicted by Eq. (11b). The dotted blue and dashed red lines are the best-fit ratios estimated from the blue and red points, respectively. |
5. Results
In this section, we present our main results obtained from mock samples of three different tracers – galaxies, clusters and AGN – using the two approaches described in Sect. 4. For each catalogue, we analyse six snapshots corresponding to the redshifts z = { 0.2,0.52,0.72,1,1.5,2 }. Moreover, at each redshift we consider different sample selections. In total, we analyse 270 mock catalogues, whose main properties, including the number of objects in each sample, are reported in Tables A.1–A.3, and in Fig. A.1.
 |
Fig. 2 Top panel: best-fit values of f(z)σ8(z) for galaxies with log (MSTAR [h-1M⊙]) > 10 (red dots), clusters with log (M500 [h-1M⊙]) > 13 (blue squares) and AGN with log (MBH [h-1M⊙]) > 6.3 (green diamonds), obtained with the method described in Sect. 5.1. The black line shows the function ΩM(z)0.545·σ8(z), where ΩM(z) and σ8(z) are the known values of the simulation. Bottom panel: percentage systematic errors on f(z)σ8(z), [(fσ8)measured−(fσ8)simulation] /(fσ8)simulation·100, that is, the percentage differences between the points and the black line shown in the top panel. The error bars have been estimated with Eq. (19). The values reported have been slightly shifted for visual clarity. To guide the eyes, the light and grey shaded areas highlight the 5% and 10% error regions, respectively. |
5.1. The linear growth rate from the clustering monopole
We begin analysing the spherically averaged two-point correlation function – the clustering monopole – at large linear scales. The aim of this exercise is to investigate the accuracy of the RSD model in the simplest case possible, that is, in the so-called Kaiser limit.
Figure 1 shows the ratio between the redshift-space and real-space two-point correlation functions, ξ(s) /ξ(r). Specifically, we show here the results obtained at z = 0.2 for galaxies with log (MSTAR [h-1M⊙]) > 10, clusters with log (M500 [h-1M⊙]) > 13 and AGN with log (MBH [h-1M⊙]) > 6.3, as reported by the labels. These correspond to the upper left samples reported in Tables A.1–A.3. Results obtained from the other mock samples are similar, but more scattered due to the lower densities. The redshift-space correlation functions have been measured directly from the simulation through the procedure described in Sect. 4. The real-space correlation functions were estimated in two different ways. They were either measured directly from the simulation, or they were derived from the linear CAMB power spectrum assuming a linear bias factor. The differences at small scales, r ≲ 5h-1 Mpc, between the ratios computed with the measured (blue squares) and CAMB (red dots) real-space correlation functions are due to non-linear effects. We verified that using the non-linear CAMB power spectrum, via the HALOFIT routine (Smith et al. 2003), does not fully remove the discrepancy. Nevertheless, as we model the large scale clustering here, this has no effect on our results. On the other hand, the small discrepancies at scales r ≳ 40h-1 Mpc can introduce systematic errors. These are, however, smaller than the estimated uncertainties. The error bars in Fig. 1 show the statistical Poisson noise (Mo et al. 1992). Scales larger than 60h-1 Mpc, not shown in the plot, are too noisy to affect the fit. More specifically, we verified that a convenient scale range for achieving robust results is 10 <r [h-1 Mpc] < 50. The black solid lines show the expected values of ξ(s) /ξ(r) at large scales, as predicted by Eq. (11b).
By modelling the clustering ratio, ξ(s) /ξ(r), via Eq. (11a), it is possible to estimate the factor β. We do this by measuring both ξ(s) and ξ(r) from the simulation. The result is shown by the dotted blue lines in Fig. 1. Instead, to estimate fσ8 from the monopole of the two-point correlation function, we use Eq. (11b). In this case, the factor bσ8 has to be fixed. This requires estimation of the real-space two-point correlation function of the DM. As described above, we obtain the latter by Fourier transforming the CAMB power spectrum. Moreover, to estimate the mean linear bias, a range of scales must be chosen in Eq. (9). We compute the linear bias in the range 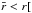 h-1 Mpc] < 50, where
h-1 Mpc] < 50, where 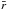 is a free parameter that sets the minimum scale beyond which the bias is relatively scale-independent. Such a minimum scale depends on redshift and sample selection, and was estimated for each sample considered. The dashed red lines are the best-fit ratios estimated with this method.
is a free parameter that sets the minimum scale beyond which the bias is relatively scale-independent. Such a minimum scale depends on redshift and sample selection, and was estimated for each sample considered. The dashed red lines are the best-fit ratios estimated with this method.
 |
Fig. 3 Iso-correlation contours of the redshift-space two-point correlation function, corresponding to the values ξ(s⊥,s∥) = [0.05,0.1,0.2,0.4,1,3], for galaxies with log (MSTAR [h-1M⊙] ) > 10, at z = 0.2 (black contours). The dot-dashed green and solid red contours show the best-fit model given by Eq. (16), with the real-space correlation function ξ(r) measured from the simulation, and estimated from the CAMB power spectrum, respectively. The blue dashed contours show the linear best-fit model given by Eq. (10) with the CAMB real-space correlation function. |
As can be seen by comparing red and blue lines, the two methods provide concordant results, both of them in agreement with the expectations. Indeed, the real-space correlation function provided by CAMB and assuming a linear bias is in reasonable agreement with the one measured directly from the simulation.
The constraints on fσ8 as a function of redshift are shown in the upper panel of Fig. 2. As in Fig. 1, we show the results obtained for galaxies with log (MSTAR [h-1M⊙] ) > 10, clusters with log (M500 [h-1M⊙] ) > 13 and AGN with log (MBH [h-1M⊙] ) > 6.3. The black line shows the function ΩM(z)0.545·σ8(z), where ΩM(z) and σ8(z) are the values of the Magneticum simulation. In the lower panel, we show the percentage systematic errors on fσ8, defined as [(fσ8)measured−(fσ8)simulation] /(fσ8)simulation·100. The error bars have been estimated by propagating on fσ8 the β errors provided by the scaling formula presented in Bianchi et al. (2012), that gives the statistical errors as a function of bias, b, volume, V, and density, n: 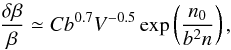 (19)where n0 = 1.7 × 10-4h3 Mpc-3 and C = 4.9 × 102h-1.5 Mpc1.5. In this case, these error bars have to be considered as lower limits only, as the scaling formula has been calibrated based on fits of the full two-dimensional anisotropic correlation function ξ(s⊥,s∥) . Moreover, they have been computed in different scale ranges and with Friends-of-Friends DM haloes, differently from this analysis, where we consider tracers hosted in DM sub-haloes. Using the full covariance matrix in this statistical analysis does not change our conclusions, as shown in Appendix C.
(19)where n0 = 1.7 × 10-4h3 Mpc-3 and C = 4.9 × 102h-1.5 Mpc1.5. In this case, these error bars have to be considered as lower limits only, as the scaling formula has been calibrated based on fits of the full two-dimensional anisotropic correlation function ξ(s⊥,s∥) . Moreover, they have been computed in different scale ranges and with Friends-of-Friends DM haloes, differently from this analysis, where we consider tracers hosted in DM sub-haloes. Using the full covariance matrix in this statistical analysis does not change our conclusions, as shown in Appendix C.
As demonstrated by Figs. 1 and 2, it is indeed possible to achieve almost unbiased constraints on fσ8 from the monopole of the two-point correlation function, at all redshifts considered, and for both galaxies, clusters and AGN, provided that the linear bias is estimated at sufficiently large scales. The advantage of this method is the minimal number of free parameters necessary for the modelisation. However, the linear bias has to be assumed, or measured from other probes.
5.2. The linear growth rate from the anisotropic 2D clustering
To extract all possible information from the redshift-space two-point correlation function, the anisotropic correlation ξ(s⊥,s∥) or, alternatively, all the relevant multipoles, have to be modelled. As discussed in Sect. 4, we consider the first approach. Differently from the analysis of Sect. 5.1, here we can jointly constrain the two terms fσ8 and bσ8. In this section we investigate the accuracy of the constraints on fσ8 provided by the dispersion model, as a function of sample selection, with bσ8 and σ12 as free parameters.
5.2.1. Galaxies
Here we begin presenting our results for the galaxy mock samples. The black lines of Fig. 3 show the iso-correlation contours of the redshift-space two-point correlation function, ξ(s⊥,s∥) , for galaxies with log (MSTAR [h-1M⊙] ) > 10, at z = 0.2. The other lines are the best-fit models obtained with three different methods. The dot-dashed green lines are obtained by using the full non-linear dispersion model given by Eq. (16), with the real-space correlation function ξ(r) measured directly from the simulation. The blue dashed and red solid contours are obtained with ξ(r) estimated from the CAMB power spectrum, and by fitting the linear model given by Eq. (10) and the non-linear one by Eq. (16), respectively. The fitting is carried out in the scale ranges 3 <r⊥ [h-1 Mpc] < 35 and 3 <r∥ [h-1 Mpc] < 35.
As one can see, while all three models provide a good description of the anisotropic clustering at scales larger than ~5 h-1 Mpc, none of them can accurately reproduce the fingers-of-God pattern at small scales. This is expected for the blue contours obtained without modelling the non-linear dynamics. For the other two cases, the discrepancy is due to the insufficiently accurate description of non-linearities provided by the dispersion model. We verified that the minimum scales considered for the fit had a negligible impact on the fingers-of-God shape, that is, we find the same results even considering scales smaller that 3 h-1 Mpc in the fit. The green contours appear in better agreement with the measurements at small scales, due to the fact that the real-space correlation function is measured from the mock catalogue. The model corresponding to the green contours provides constraints on β, not on fσ8. We show it here only to highlight the differences at small scales between the dispersion model estimated with ξ(r) measured from the simulation, and the one with ξ(r) from the linear CAMB power spectrum, assuming a linear scale-independent bias.
 |
Fig. 4 Top panel of the upper window: best-fit values of f(z)σ8(z) for galaxies with log (MSTAR [h-1M⊙] ) > 10. The open and solid blue squares show the values obtained by fitting the data with the models given by Eqs. (10) and (16), respectively, in the scale ranges 3 <r⊥ [h-1 Mpc] < 35 and 3 <r∥ [h-1 Mpc] < 35. The open and solid red dots have been obtained with the method described in Sect. 5.2.1, fitting the data with the models given by Eqs. (10) and (16), respectively. The black line shows the function ΩM(z)0.545·σ8(z), where ΩM(z) and σ8(z) are the known values of the simulation. For comparison, the grey dots show a set of recent observational measurements from galaxy surveys (see Sect. 5.2.1). Bottom panel of the upper window: percentage systematic errors on f(z)σ8(z), defined as [(fσ8)measured−(fσ8)simulation] /(fσ8)simulation·100, that is, the percentage differences between the points and the black line shown in the top panel. To guide the eyes, the light and grey shaded areas highlight the 5% and 10% error regions. Lower window: best-fit values of |
The best-fit values of fσ8 as a function of redshift are shown in the top panel of the upper window of Fig. 4. The open and solid blue squares show the values obtained by fitting the data with the models given by Eqs. (10) and (16), respectively, that is, they correspond to the blue and red contours of Fig. 3 (at z = 0.2). The bottom panel of the upper window shows the percentage systematic errors on fσ8, that is, [(fσ8)measured−(fσ8)simulation] /(fσ8)simulation·100.
As can be seen, the resulting best-fit values of fσ8 are strongly biased with respect to the true ones, with a systematic error that depends on the redshift. At z = 0.2, we get an underestimation of ~10 (20) % with the non-linear (linear) dispersion model; at z = 1 the error reduces to ~5 (8)%, while at z = 2 we get an overestimation of ~20%, with both linear and non-linear modelling. This result is in relative agreement with that found by Bianchi et al. (2012) at z = 1, although the two analyses are not directly comparable, as Bianchi et al. (2012) considered a sample of Friends-of-Friends DM haloes, slightly affected by fingers-of-God. As expected, the convolution given by Eq. (16) reduces the systematic error on fσ8, especially at low redshifts. However, it does not totally remove the discrepancies, in agreement with previous findings (e.g. Mohammad et al. 2016, and references therein). For comparison, the grey dots of Fig. 4 show a set of recent observational measurements of fσ8 from large galaxy surveys: 6dFGS at z = 0.067 (Beutler et al. 2012); SDSS(DR7) Luminous Red Galaxies at z = 0.25,0.37 (Samushia et al. 2012) from scales lower than 60 and 200h-1 Mpc; BOSS at z = 0.3,0.57,0.6 (Tojeiro et al. 2012; Reid et al. 2012); WiggleZ at z = 0.44,0.6,0.73 (Blake et al. 2012); and VIPERS at z = 0.8 (de la Torre et al. 2013). These results were obtained using different RSD models, most of them more accurate than the dispersion model considered in this work. Nevertheless, many of these measurements underestimate fσ8 with respect to GR+ΛCDM predictions (see e.g. Macaulay et al. 2013). In line with our findings, this could be explained, at least partially, by model uncertainties still present in the more sophisticated RSD models considered.
The direct way to reduce these systematic errors is to improve the modelisation of RSD at non-linear scales (see e.g. Scoccimarro 2004; Taruya et al. 2010; Seljak & McDonald 2011; Wang et al. 2014; de la Torre et al. 2013). Here we explore a different approach, investigating the dependency of the systematic error on the co-moving scales considered in the analysis. In the following plots, we show the results obtained by repeating our fitting procedure for different values of the minimum perpendicular separation and the maximum parallel separation used in the fit, that is,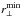 and
and 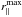 . By increasing the value of
. By increasing the value of 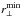 , we can cut the region more affected by fingers-of-God anisotropies, while by reducing
, we can cut the region more affected by fingers-of-God anisotropies, while by reducing 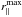 , we avoid the region more affected by shot noise. As we verified, also changing
, we avoid the region more affected by shot noise. As we verified, also changing 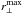 and
and 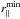 , or adopting different scale selection criteria, does not significantly affect the results. The aim here is to search for optimal regions in this plane to possibly achieve unbiased constraints. As non-linear dynamics impact on different scales for different redshifts and biases of the tracers, we expect that the best values of
, or adopting different scale selection criteria, does not significantly affect the results. The aim here is to search for optimal regions in this plane to possibly achieve unbiased constraints. As non-linear dynamics impact on different scales for different redshifts and biases of the tracers, we expect that the best values of 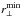 and
and 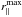 , that is, the ones that minimise systematic errors, will be different for different sample selections.
, that is, the ones that minimise systematic errors, will be different for different sample selections.
The results of this analysis are shown in Fig. 4 with open and solid red dots, obtained by fitting the data with the model given by Eqs. (10) and (16), respectively, that is, by considering either the linear or the non-linear RSD model. We explore the ranges ![\hbox{$5<r_\perp^{\rm min}[h^{-1}\,\mbox{Mpc}]<20$}](/articles/aa/full_html/2017/03/aa26885-15/aa26885-15-eq127.png) and
and ![\hbox{$15<r_\parallel^{\rm max}[h^{-1}\,\mbox{Mpc}]<35$}](/articles/aa/full_html/2017/03/aa26885-15/aa26885-15-eq128.png) , highlighted by the grey areas in the bottom panels of the lower window of Fig. 4. Specifically, we consider a 10 × 10 grid in the
, highlighted by the grey areas in the bottom panels of the lower window of Fig. 4. Specifically, we consider a 10 × 10 grid in the 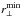 ,
, 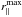 plane. The best-fit values of
plane. The best-fit values of 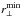 and
and 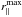 , shown in the bottom panels of the lower window, are the ones that minimise the systematic error on fσ8. The ranges considered are large enough to achieve systematic errors on fσ8 lower than ~5%. Indeed, for proper values of
, shown in the bottom panels of the lower window, are the ones that minimise the systematic error on fσ8. The ranges considered are large enough to achieve systematic errors on fσ8 lower than ~5%. Indeed, for proper values of 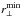 and
and 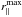 , it is possible to significantly reduce the systematic error on fσ8 at all redshifts, without having to improve the treatment of non-linearities. The error bars have been estimated using the scaling formula given by Eq. (19).
, it is possible to significantly reduce the systematic error on fσ8 at all redshifts, without having to improve the treatment of non-linearities. The error bars have been estimated using the scaling formula given by Eq. (19).
Both the linear and non-linear dispersion models provide similar results when 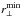 and
and 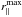 are kept free. In other words, it seems more convenient simply to not consider the scales where non-linear effects have a non-negligible impact, rather than to try modelling them with the empirical description provided by Eq. (16).
are kept free. In other words, it seems more convenient simply to not consider the scales where non-linear effects have a non-negligible impact, rather than to try modelling them with the empirical description provided by Eq. (16).
These results show that i) it is possible to significantly reduce the systematics in RSD constraints, even with the dispersion model, by cutting the 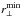 ,
, 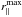 plane conveniently; and ii) the optimal
plane conveniently; and ii) the optimal 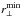 ,
, 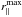 range depends on sample selection and thus cannot be simply fixed in multi-tracer analyses. As can be seen in Fig. 4, we do not find any clear trend of
range depends on sample selection and thus cannot be simply fixed in multi-tracer analyses. As can be seen in Fig. 4, we do not find any clear trend of 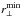 and
and 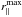 as a function of redshift, as it would be expected if the systematics were caused by non-linearities. This is possibly caused by the insufficiently large volumes considered. The analysis of larger data sets, that we defer to future work, will hopefully clarify this point.
as a function of redshift, as it would be expected if the systematics were caused by non-linearities. This is possibly caused by the insufficiently large volumes considered. The analysis of larger data sets, that we defer to future work, will hopefully clarify this point.
For completeness, we then apply our method to several sub-samples with different selections. Specifically, we consider galaxy catalogues selected in stellar mass, MSTAR, g-band absolute magnitude, Mg and star formation rate (SFR). The selection thresholds considered and the number of galaxies in each sample are reported in Table A.1. The percentage systematic errors on fσ8 are reported in Fig. 5 as a function of redshift and sample selections, as indicated by the labels. The result is quite remarkable: it is indeed possible to get almost unbiased constraints on fσ8 with the dispersion model, independent of sample selections, provided that 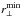 and
and 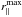 are chosen conveniently. For the largest galaxy sample shown in Fig. 2, the preferred value of
are chosen conveniently. For the largest galaxy sample shown in Fig. 2, the preferred value of 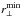 is ~15 h-1 Mpc at low and high redshifts, and ~5 h-1 Mpc around z = 1, while
is ~15 h-1 Mpc at low and high redshifts, and ~5 h-1 Mpc around z = 1, while 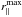 is ~15 h-1 Mpc at low redshifts, and increases up to ~35 h-1 Mpc at z = 2. Again, we do not find any clear trend of
is ~15 h-1 Mpc at low redshifts, and increases up to ~35 h-1 Mpc at z = 2. Again, we do not find any clear trend of 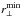 and
and 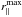 as a function of redshift or sample bias.
as a function of redshift or sample bias.
 |
Fig. 5 Percentage systematic errors on f(z)σ8(z) for galaxies, [(fσ8)measured-(fσ8)simulation] /(fσ8)simulation·100, as a function of redshift and sample selections, as indicated by the labels. S1−S5 refer to the five selection thresholds reported in Tables A.1–A.3, for the different tracers and properties used for the selection. |
Overall, all of these results show that our modelling of RSD is mostly sensitive to the lower fitting cut-off, depending on how the tracers relate to the underlying mass. Indeed, the effect of the different selections considered here is simply to select sub-samples of haloes of different masses (hence bias) hosting the observed galaxies. As noted above, this has to be considered in multi-tracer analyses, where a single sample selection might introduce systematics.
 |
Fig. 6 Iso-correlation contours of the redshift-space two-point correlation function, corresponding to the values ξ(s⊥,s∥) = [0.2,0.4,1,3], for clusters with log (M500 [h-1M⊙] ) > 13, at z = 0.2 (black contours). The other contours are as in Fig. 3. |
5.2.2. Galaxy groups and clusters
In this section, we perform the same analysis presented in Sect. 5.2.1 on the mock samples of galaxy groups and clusters. To simplify the discussion, in the following we use the term “clusters” to refer to all of these objects; though the less massive ones should be considered as galaxy groups, or simply haloes, from an observational perspective (see Table A.2).
 |
Fig. 7 Best-fit values of f(z)σ8(z) for clusters with log (M500 [h-1M⊙]) > 13. All the symbols are as in Fig. 4. |
 |
Fig. 8 Percentage systematic errors on f(z)σ8(z) for clusters, as a function of redshift and sample selections. All the symbols are as in Fig. 5. |
Figure 6 shows the iso-correlation contours of the redshift-space two-point correlation function of clusters with log (M500 [h-1M⊙]) > 13, at z = 0.2. The other contours are the best-fit models, as in Fig. 3. As can be seen, the fingers-of-God anisotropies are almost absent, differently from the galaxy correlation function shown in Fig. 3, due to the lower values of non-linear motions of clusters at small scales. This makes the convolution of Eq. (16) negligible, as can be seen by comparing the dashed blue and solid red lines. Interestingly, when the real-space correlation function ξ(r) is measured from the mocks (green contours), the dispersion model fails to match the small-scale clustering shape. This is primarily caused by the paucity of the cluster sample. Due to the low number of cluster pairs at small separations, the small-scale clustering cannot be estimated accurately, thus introducing systematic errors in the model. On the contrary, when ξ(r) is estimated from CAMB, the small-scale clustering shape can be accurately described. For visual clarity, we have only shown here the iso-correlation contours down to ξ(s⊥,s∥) = 0.2, as for lower values they appear too scattered.
 |
Fig. 9 Iso-correlation contours of the redshift-space two-point correlation function, corresponding to the values ξ(s⊥,s∥) = [0.1,0.2,0.4,1,3], for AGN with log (MBH [h-1M⊙]) > 6.3, at z = 0.2 (black contours). The other contours show the best-fit models, as in Fig. 3. |
 |
Fig. 10 Best-fit values of f(z)σ8(z) for AGN with log (MBH [h-1M⊙] ) > 6.3. All the symbols are as in Fig. 4. |
Figure 7 shows the best-fit values of fσ8 as a function of redshift. In contrast with what we found with galaxies, the constraints on the linear growth rate obtained in the scale ranges 3 <r⊥ [h-1 Mpc] < 35 and 3 <r∥ [h-1 Mpc] < 35 (blue squares) appear severely overestimated at all redshifts, independently from the dispersion model used (linear or non-linear). To investigate how these systematics depend on the scale range considered in the fit, we repeated the same analysis described in Sect. 5.2.1, keeping free the parameters 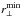 and
and 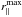 . The result is shown by the red dots in Fig. 7. As one can see, we are able to substantially reduce the systematics on fσ8 at all redshifts. This was obtained by cutting the small perpendicular separations, limiting the analysis to r⊥ ≳ 20h-1 Mpc, as shown in the lower window of Fig. 7.
. The result is shown by the red dots in Fig. 7. As one can see, we are able to substantially reduce the systematics on fσ8 at all redshifts. This was obtained by cutting the small perpendicular separations, limiting the analysis to r⊥ ≳ 20h-1 Mpc, as shown in the lower window of Fig. 7.
These results appear in overall agreement with what was previously found by Bianchi et al. (2012), where systematic errors become positive for DM halo masses larger than 1013h-1M⊙, that is, for group masses and above. This represents a nice confirmation, not related to the specific simulation or halo/cluster selection, but only to the dynamics of haloes of large masses.
Then, we consider several cluster sub-samples selected in mass, M500, temperature, T500 and luminosity, L500, whose main properties are reported in Table A.2. M500, T500 and L500 are, respectively, the mass, the temperature and the luminosity enclosed within a sphere of radius r500c, in which the mean matter density is equal to 500 times the critical density ρcrit(z) = 3H2(z)/8πG, where H(z) is the Hubble parameter. Figure 8 shows the percentage systematic errors on fσ8 as a function of redshift and sample selections. For the largest samples analysed, we do not get any significant bias on fσ8, similarly to what we found with galaxies. However, when selecting too few objects, the results appear quite scattered, though without systematic trends. Indeed, the advantages resulting from the low fingers-of-God anisotropies compensate with the paucity of cluster pairs at small scales. Summarising, it seems possible to get unbiased constraints on the linear growth rate from the RSD of galaxy clusters, but the cluster sample has to be sufficiently numerous.
5.2.3. AGN
Finally, we analyse the AGN mock samples. The results are shown in Figs. 9–11, and are analogous to the plots presented in the previous two sections for galaxies and clusters. As expected, we find similar results to the ones found with galaxies. Differently from the cluster case, the fingers-of-God are clearly evident in the AGN correlation function, and not accurately described by the dispersion model, as can be seen in Fig. 9. Nevertheless, the convolution of Eq. (16) significantly helps in reducing the systematic error on fσ8, even more than was found when analysing the galaxy sample, as evident by comparing Figs. 3 and 9. Also in this case, it is possible to get almost unbiased constraints on fσ8 at all redshifts and for the different selections considered, provided that the analysis is restricted to 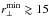 h-1 Mpc and
h-1 Mpc and 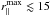 h-1 Mpc. Specifically, we considered AGN catalogues selected in BH mass, MBH, bolometric luminosity, Lbol, and Eddington factor, fEdd, as reported in Table A.3. Only the AGN samples with the lower number of objects analysed here (cyan points in Fig. 11) are not large enough to provide robust constraints on fσ8.
h-1 Mpc. Specifically, we considered AGN catalogues selected in BH mass, MBH, bolometric luminosity, Lbol, and Eddington factor, fEdd, as reported in Table A.3. Only the AGN samples with the lower number of objects analysed here (cyan points in Fig. 11) are not large enough to provide robust constraints on fσ8.
6. Discussion
The results presented in this paper extend the previous work by Bianchi et al. (2012), who analysed mock samples of DM haloes at z = 1. One of the main differences with respect to that work is that here we used galaxy, cluster and AGN simulated catalogues that are more directly comparable to observational samples. Moreover, we investigated the systematic errors of fσ8 instead of β, and extended the analysis to different redshifts and sample selections. The use of these simulated objects as test particles provides a better treatment of non-linearities in small-scale dynamics that translates to a more realistic description of the fingers-of-God in the redshift-space galaxy and AGN clustering, as can be seen in Figs. 3 and 9. On the other hand, the selected cluster samples are more similar to the DM halo samples analysed by Bianchi et al. (2012), as expected, with fingers-of-God anisotropies almost absent, as shown in Fig. 6. Nevertheless, the Magneticum samples provide cluster properties that allowed us to apply more realistic selections.
 |
Fig. 11 Percentage systematic errors on f(z)σ8(z) for AGN, as a function of redshift and sample selections. All the symbols are as in Fig. 5. |
One of the main results found by Bianchi et al. (2012) is that, when using the dispersion model, the systematic errors on the linear growth rate are positive for DM haloes with masses lower than ~1013h-1M⊙, and negative otherwise (see also Okumura & Jing 2011; Marulli et al. 2012b). Our findings reinforce these conclusions. Indeed, regardless of the specific selections considered, the overall trends of our systematic errors depend ultimately on the mass of the DM haloes hosting the selected tracers.
Moreover, extending the Bianchi et al. (2012) analysis, we investigated how the systematic errors depend on the co-moving scales considered. Our main finding is that it is possible to substantially reduce the systematic errors at all redshifts and selections by restricting the analysis in a proper subregion of the r⊥−r∥ plane. The latter depends on the properties of the selected objects, specifically on the mass of the host halo, due to the difficulties in modelling the non-Gaussian nature of the velocity probability density function of the tracers.
7. Conclusions
Clustering anisotropies in redshift-space are one of the most effective probes to test Einstein’s General Relativity on large scales. Though only galaxy samples have been considered so far for these analyses, other astronomical tracers, such as clusters and AGN, will be used in the near future, aimed at maximising the dynamic and redshift ranges where one can constrain the linear growth rate of cosmic structures. In particular, clusters of galaxies can be efficiently used to probe the low-redshift Universe. Their large bias and low velocity dispersion at small scales make them optimal tracers for large-scale structure analyses (Sereno et al. 2015; Veropalumbo et al. 2014, 2016). On the other hand, AGN samples can be exploited to push the GR test on larger redshifts.
In this work, we made use of both galaxy, cluster and AGN mock samples extracted from the Magneticum, a cosmological hydrodinamic simulation of the standard ΛCDM Universe, to investigate the accuracy of the widely used dispersion model as a function of scale and sample selection. Instead of analysing the clustering multipoles, we preferred to extract fσ8 constraints from the monopole only, or from the full 2D anisotropic correlation ξ(s⊥,s∥) . This allowed us to explore the r⊥−r∥ plane, aimed at finding the optimal range of scales to minimise systematic uncertainties.
The main results of this analysis are the following.
-
It is possible to achieve almost unbiased constraints on fσ8 by modelling the large-scale monopole of the two-point correlation function with the Kaiser limit of the dispersion model (Eq. (11b)), provided that the linear bias factor bσ8 is known. The latter has to be estimated at sufficiently large scales to avoid non-linearities. With real data, the linear bias can be estimated either with the de-projection technique, or from the three-point correlation function, or by combining clustering and lensing measurements (see the discussion in Sect. 4).
-
When higher multipoles are considered, fσ8 and bσ8 can be jointly constrained and the statistical error on fσ8 substantially reduced (see e.g. de la Torre et al. 2013; Petracca et al. 2016). However, systematic errors can arise if non-linearities are not treated accurately, such as with the dispersion model (Eqs. (10)–(17)). On the other hand, the analysis shown in this paper demonstrates that it is still possible to reduce the systematic errors on fσ8 if the range of scales used to model RSD is chosen appropriately. The latter depends on the properties of the tracers. We do not find however any clear prescription to relate these scale ranges to the sample properties.
-
If the linear growth rate is estimated from the RSD of either galaxies or AGN, the value of fσ8 will be underestimated at z ≲ 1, and overestimated at larger redshifts, when the fit is performed in the fixed range of scales 3 <r⊥,r∥ [h-1 Mpc] < 35. With
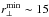 h-1 Mpc and
h-1 Mpc and 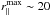 h-1 Mpc, we get almost unbiased constraints. However, the proper values of
h-1 Mpc, we get almost unbiased constraints. However, the proper values of 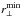 and
and 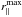 depend on sample selection, and should be fixed differently for each sample analysed, calibrating the analysis using specific mock catalogues.
depend on sample selection, and should be fixed differently for each sample analysed, calibrating the analysis using specific mock catalogues. -
If the RSD of galaxy groups and clusters are modelled in the range of scales 3 <r⊥,r∥ [h-1 Mpc] < 35, the value of fσ8 is severely overestimated at all redshifts. The results at z = 1 appear in overall agreement with those of Bianchi et al. (2012). The systematic error can be reduced if the fit is performed at larger scales, as expected due to the low number of cluster pairs at small separations. Specifically, with
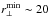 h-1 Mpc, we get unbiased constraints, but only for the densest group samples. The paucity of the most massive cluster samples does not allow us to obtain robust results.
h-1 Mpc, we get unbiased constraints, but only for the densest group samples. The paucity of the most massive cluster samples does not allow us to obtain robust results.
To summarise, as the dispersion model cannot accurately describe the non-linear motions at small scales, the constraints on fσ8 can be biased. At the present time, it is difficult to include model uncertainties in these kind of analyses, and even more difficult to improve the RSD modelling at small scales (see e.g. de la Torre & Guzzo 2012; Bianchi et al. 2015, and references therein). Instead of trying to improve the model, in this analysis, we investigated how the systematic errors on the linear growth rate caused by model uncertainties depend on the co-moving scales considered. As we have shown, in order to reduce these systematics it is necessary to restrict the analysis to a proper subregion of the r⊥−r∥ plane. More specifically, we found that it is enough to choose a proper value for 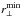 and
and 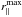 . Indeed, as we verified, also changing
. Indeed, as we verified, also changing 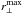 and
and 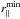 does not significantly affect the results.
does not significantly affect the results.
Overall, we find that in order to reduce the systematics in the fσ8 measurements, it is more convenient to simply not consider the small scales where non-linear effects significantly distort the clustering shape, rather than to try modelling them with the empirical description provided by the dispersion model given by Eq. (16). The drawback of this approach is that it inevitably increases the statistical error on fσ8. Moreover, the r⊥−r∥ region to be selected depends on the properties of the tracers, and should be determined using suitable mock catalogues. On the other hand, without a sufficiently accurate modelisation of non-linear dynamics at small scales, this approach is the only one that can achieve unbiased constraints.
This can have a non-negligible impact on multiple tracer analyses (see e.g. McDonald & Seljak 2009; Blake et al. 2013; Marín et al. 2016, and references therein) if the RSD are modelled at small non-linear scales with the dispersion model. To avoid different systematic errors on the linear growth rate estimated from the small-scale RSD of different tracers, the r⊥−r∥ plane analysed should be different for each sample. On the other hand, in multiple tracer techniques that require analysis of different samples at the same scales, it is necessary to limit the analysis at large enough scales where systematic errors are lower than statistical errors for all the different tracers. And the same when joining together different redshifts, where RSD constraints can be differently biased.
Acknowledgments
We acknowledge support from the grants ASI/INAF No. I/023/12/0 “Attività relative alla fase B2/C per la missione Euclid” and MIUR PRIN 2010–2011 “The dark Universe and the cosmic evolution of baryons: from current surveys to Euclid”. L.M. acknowledges financial contributions from contracts and PRIN INAF 2012 “The Universe in the box: multiscale simulations of cosmic structure”. K.D. acknowledges support from the DFG Cluster of Excellence “Origin and Structure of the Universe”. We are especially grateful for the support by M. Petkova through the Computational Center for Particle and Astrophysics (C2PAP). Computations were performed at the “Leibniz-Rechenzentrum” with CPU time assigned to the Project “pr86re”, as well as at the “Rechenzentrum der Max-Planck- Gesellschaft” at the “Max-Planck-Institut für Plasmaphysik” with CPU time assigned to the “Max-Planck-Institut für Astrophysik”. Information on the Magneticum Pathfinder project is available online6. Finally, we thank the referee for several useful suggestions that improved the presentation of our results.
References
- Amendola, L., Appleby, S., Bacon, D., et al. 2013, Liv. Rev. Rel., 16, 6 [Google Scholar]
- Beutler, F., Blake, C., Colless, M., et al. 2012, MNRAS, 423, 3430 [NASA ADS] [CrossRef] [Google Scholar]
- Bianchi, D., Guzzo, L., Branchini, E., et al. 2012, MNRAS, 427, 2420 [NASA ADS] [CrossRef] [Google Scholar]
- Bianchi, D., Chiesa, M., & Guzzo, L. 2015, MNRAS, 446, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Blake, C., Brough, S., Colless, M., et al. 2011, MNRAS, 415, 2876 [NASA ADS] [CrossRef] [Google Scholar]
- Blake, C., Brough, S., Colless, M., et al. 2012, MNRAS, 425, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Blake, C., Baldry, I. K., Bland-Hawthorn, J., et al. 2013, MNRAS, 436, 3089 [NASA ADS] [CrossRef] [Google Scholar]
- Bocquet, S., Saro, A., Dolag, K., & Mohr, J. J. 2016, MNRAS, 456, 2361 [Google Scholar]
- Bondi, H. 1952, MNRAS, 112, 195 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Bondi, H., & Hoyle, F. 1944, MNRAS, 104, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Bonoli, S., Marulli, F., Springel, V., et al. 2009, MNRAS, 396, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Cabré, A., & Gaztañaga, E. 2009a, MNRAS, 393, 1183 [NASA ADS] [CrossRef] [Google Scholar]
- Cabré, A., & Gaztañaga, E. 2009b, MNRAS, 396, 1119 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Chuang, C.-H., & Wang, Y. 2013, MNRAS, 435, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Chuang, C.-H., Prada, F., Cuesta, A. J., et al. 2013, MNRAS, 433, 3559 [NASA ADS] [CrossRef] [Google Scholar]
- Contreras, C., Blake, C., Poole, G. B., et al. 2013, MNRAS, 430, 924 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, M., & Peebles, P. J. E. 1983, ApJ, 267, 465 [NASA ADS] [CrossRef] [Google Scholar]
- de la Torre, S., & Guzzo, L. 2012, MNRAS, 427, 327 [NASA ADS] [CrossRef] [Google Scholar]
- de la Torre, S., Guzzo, L., Peacock, J. A., et al. 2013, A&A, 557, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Matteo, T., Springel, V., & Hernquist, L. 2005, Nature, 433, 604 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Dolag, K., Vazza, F., Brunetti, G., & Tormen, G. 2005, MNRAS, 364, 753 [NASA ADS] [CrossRef] [Google Scholar]
- Fabjan, D., Borgani, S., Tornatore, L., et al. 2010, MNRAS, 401, 1670 [NASA ADS] [CrossRef] [Google Scholar]
- Ferland, G. J., Korista, K. T., Verner, D. A., et al. 1998, PASP, 110, 761 [Google Scholar]
- Fisher, K. B., Scharf, C. A., & Lahav, O. 1994, MNRAS, 266, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Guzzo, L., Pierleoni, M., Meneux, B., et al. 2008, Nature, 451, 541 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Haardt, F., & Madau, P. 2001, in Clusters of Galaxies and the High Redshift Universe Observed in X-rays, eds. D. M. Neumann, & J. T. V. Tran, 64 [Google Scholar]
- Hamilton, A. J. S. 1992, ApJ, 385, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Hamilton, A. J. S. 1998, in The Evolving Universe, ed. D. Hamilton, Astrophys. Space Sci. Libr., 231, 185 [Google Scholar]
- Hawkins, E., Maddox, S., Cole, S., et al. 2003, MNRAS, 346, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Hearin, A. P. 2015, MNRAS, 451, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Hirschmann, M., Dolag, K., Saro, A., et al. 2014, MNRAS, 442, 2304 [NASA ADS] [CrossRef] [Google Scholar]
- Hoyle, F., & Lyttleton, R. A. 1939, Proc. Cambridge Phil. Soc., 35, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, N. 1987, MNRAS, 227, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E., Smith, K. M., Dunkley, J., et al. 2011, ApJS, 192, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Landy, S. D., & Szalay, A. S. 1993, ApJ, 412, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Laureijs, R., Amiaux, J., Arduini, S., et al. 2011, ArXiv e-prints [arXiv:1110.3193] [Google Scholar]
- Lewis, A., & Bridle, S. 2002, Phys. Rev. D, 66, 103511 [NASA ADS] [CrossRef] [Google Scholar]
- Lilje, P. B., & Efstathiou, G. 1989, MNRAS, 236, 851 [NASA ADS] [CrossRef] [Google Scholar]
- Macaulay, E., Wehus, I. K., & Eriksen, H. K. 2013, Phys. Rev. Lett., 111, 161301 [NASA ADS] [CrossRef] [Google Scholar]
- Marín, F. A., Beutler, F., Blake, C., et al. 2016, MNRAS, 455, 4046 [NASA ADS] [CrossRef] [Google Scholar]
- Marulli, F., Bonoli, S., Branchini, E., Moscardini, L., & Springel, V. 2008, MNRAS, 385, 1846 [NASA ADS] [CrossRef] [Google Scholar]
- Marulli, F., Bonoli, S., Branchini, E., et al. 2009, MNRAS, 396, 1404 [NASA ADS] [CrossRef] [Google Scholar]
- Marulli, F., Carbone, C., Viel, M., Moscardini, L., & Cimatti, A. 2011, MNRAS, 418, 346 [NASA ADS] [CrossRef] [Google Scholar]
- Marulli, F., Baldi, M., & Moscardini, L. 2012a, MNRAS, 420, 2377 [NASA ADS] [CrossRef] [Google Scholar]
- Marulli, F., Bianchi, D., Branchini, E., et al. 2012b, MNRAS, 426, 2566 [NASA ADS] [CrossRef] [Google Scholar]
- Marulli, F., Veropalumbo, A., & Moresco, M. 2016, Astron. Comput., 14, 35 [NASA ADS] [CrossRef] [Google Scholar]
- McDonald, P., & Seljak, U. 2009, J. Cosmol. Astropart. Phys., 10, 7 [Google Scholar]
- McGill, C. 1990, MNRAS, 242, 428 [NASA ADS] [CrossRef] [Google Scholar]
- Merloni, A., Predehl, P., Becker, W., et al. 2012, ArXiv e-prints, [arXiv:1209.3114] [Google Scholar]
- Mo, H. J., Jing, Y. P., & Boerner, G. 1992, ApJ, 392, 452 [NASA ADS] [CrossRef] [Google Scholar]
- Mohammad, F. G., de la Torre, S., Bianchi, D., Guzzo, L., & Peacock, J. A. 2016, MNRAS, 458, 1948 [NASA ADS] [CrossRef] [Google Scholar]
- Moresco, M., Marulli, F., Baldi, M., Moscardini, L., & Cimatti, A. 2014, MNRAS, 443, 2874 [NASA ADS] [CrossRef] [Google Scholar]
- Okumura, T., & Jing, Y. P. 2011, ApJ, 726, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Padovani, P., & Matteucci, F. 1993, ApJ, 416, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Peacock, J. A., & Dodds, S. J. 1996, MNRAS, 280, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Peacock, J. A., Cole, S., Norberg, P., et al. 2001, Nature, 410, 169 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Peebles, P. J. E. 1980, The Large-Scale Structure of the Universe (Princeton, N.J., Princeton University Press) [Google Scholar]
- Percival, W. J., Burkey, D., Heavens, A., et al. 2004, MNRAS, 353, 1201 [NASA ADS] [CrossRef] [Google Scholar]
- Perlmutter, S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Petracca, F., Marulli, F., Moscardini, L., et al. 2016, MNRAS, 462, 4208 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, B. A., Samushia, L., White, M., et al. 2012, MNRAS, 426, 2719 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, B. A., Seo, H.-J., Leauthaud, A., Tinker, J. L., & White, M. 2014, MNRAS, 444, 476 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Ross, N. P., da Ângela, J., Shanks, T., et al. 2007, MNRAS, 381, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Samushia, L., Percival, W. J., & Raccanelli, A. 2012, MNRAS, 420, 2102 [NASA ADS] [CrossRef] [Google Scholar]
- Saro, A., Liu, J., Mohr, J. J., et al. 2014, MNRAS, 440, 2610 [NASA ADS] [CrossRef] [Google Scholar]
- Scoccimarro, R. 2004, Phys. Rev. D, 70, 083007 [NASA ADS] [CrossRef] [Google Scholar]
- Seljak, U., & McDonald, P. 2011, J. Cosmol. Astropart. Phys., 11, 39 [Google Scholar]
- Sereno, M., Veropalumbo, A., Marulli, F., et al. 2015, MNRAS, 449, 4147 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Smith, R. E., Peacock, J. A., Jenkins, A., et al. 2003, MNRAS, 341, 1311 [NASA ADS] [CrossRef] [Google Scholar]
- Spergel, D., Gehrels, N., Breckinridge, J., et al. 2013, ArXiv e-prints [arXiv:1305.5422] [Google Scholar]
- Springel, V. 2005, MNRAS, 364, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., & Hernquist, L. 2002, MNRAS, 333, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., & Hernquist, L. 2003a, MNRAS, 339, 289 [Google Scholar]
- Springel, V., & Hernquist, L. 2003b, MNRAS, 339, 312 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., White, S. D. M., Jenkins, A., et al. 2005, Nature, 435, 629 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Taruya, A., Nishimichi, T., & Saito, S. 2010, Phys. Rev. D, 82, 063522 [NASA ADS] [CrossRef] [Google Scholar]
- Tegmark, M., Blanton, M. R., Strauss, M. A., et al. 2004, ApJ, 606, 702 [NASA ADS] [CrossRef] [Google Scholar]
- Thielemann, F.-K., Argast, D., Brachwitz, F., et al. 2003, Nucl. Phys. A, 718, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Tojeiro, R., Percival, W. J., Brinkmann, J., et al. 2012, MNRAS, 424, 2339 [NASA ADS] [CrossRef] [Google Scholar]
- Tornatore, L., Borgani, S., Dolag, K., & Matteucci, F. 2007, MNRAS, 382, 1050 [NASA ADS] [CrossRef] [Google Scholar]
- van den Hoek, L. B., & Groenewegen, M. A. T. 1997, A&AS, 123, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Veropalumbo, A., Marulli, F., Moscardini, L., Moresco, M., & Cimatti, A. 2014, MNRAS, 442, 3275 [NASA ADS] [CrossRef] [Google Scholar]
- Veropalumbo, A., Marulli, F., Moscardini, L., Moresco, M., & Cimatti, A. 2016, MNRAS, 458, 1909 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, L., Reid, B., & White, M. 2014, MNRAS, 437, 588 [NASA ADS] [CrossRef] [Google Scholar]
- Wiersma, R. P. C., Schaye, J., & Smith, B. D. 2009, MNRAS, 393, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., & Weaver, T. A. 1995, ApJS, 101, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, H., Yu, H., Noh, H., & Zhu, Z.-H. 2008, Phys. Lett. B, 665, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Zurek, W. H., Quinn, P. J., Salmon, J. K., & Warren, M. S. 1994, ApJ, 431, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Zwicky, F. 1937, ApJ, 86, 217 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Main properties of the selected samples
Main properties of the samples of galaxies analysed in the paper.
Main properties of the samples of galaxy groups and clusters analysed in the paper.
Main properties of the samples of AGN analysed in the paper.
Tables A.1–A.3 report the main properties of the mock samples analysed in this work. We consider only integral catalogues. The min and max quantities reported in the Tables are the minimum and maximum thresholds used for the selections, while median is the median of the sample distributions. As can be seen, we adopt suitable sample selections to have a minimum of approximately 50 000 objects in the smallest galaxy samples, and approximately 10 000 objects in the smallest cluster and AGN samples. As an illustrative example, Fig. A.1 shows the number of mock galaxies, clusters and AGN as a function of redshift, for three different selections, as indicated by the labels.
 |
Fig. A.1 The number of mock galaxies (red dots), clusters (blue squares) and AGN (green diamonds) as a function of redshift, for the three selections: Gs1, Cl1, Af1 (see Tables A.1–A.3). |
Appendix B: Effect of random catalogue number densities
 |
Fig. B.1 Ratio Δξ/σξ as a function of scales obtained from the sample of mock galaxies at z = 0.2, where |
We test the impact of our assumptions in constructing the random catalogues by repeating the full statistical analysis on a subset of the mock samples, using random catalogues with different number densities. Figure B.1 shows an example case obtained from the sample of mock galaxies at z = 0.2. The lines show the ratio Δξ/σξ as a function of scales, where 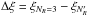 , with NR being the ratio between the number of random objects and galaxies, and σξ is the estimated statistical uncertainty. The different lines refer to the values
, with NR being the ratio between the number of random objects and galaxies, and σξ is the estimated statistical uncertainty. The different lines refer to the values 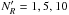 . The effect of different random number densities on the measured correlation functions is marginal, considering the estimated uncertainties. As verified, the net effect on the final RSD constraints is also negligible.
. The effect of different random number densities on the measured correlation functions is marginal, considering the estimated uncertainties. As verified, the net effect on the final RSD constraints is also negligible.
Appendix C: Effect of covariance matrix approximations
 |
Fig. C.1 Difference between fσ8 measurements obtained with diagonal Poisson errors and by considering the full covariance matrix assessed with either the jackknife (solid lines) or the bootstrap (dashed lines) techniques, divided by the 1σ uncertainty on fσ8, as a function of redshift. Red, blue and green symbols refer to galaxy, cluster and AGN samples, respectively. |
All the results presented in this paper have been obtained by assuming Poisson errors in clustering measurements and by neglecting the off-diagonal elements of the covariance matrix. Both of these approximations can introduce systematic errors in the inferred cosmological constraints. However, as we verified, they do not significantly impact our present conclusions, introducing only marginal differences in the final obtained constraints, considering the estimated uncertainties. Figure C.1 shows the difference in the fσ8 measurements obtained with diagonal Poisson errors and by considering the full covariance matrix assessed with either jackknife or bootstrap techniques, divided by the 1σ uncertainty on fσ8. We use 125 jackknife/bootstrap mock realisations to compute the covariance matrices (see Veropalumbo et al. 2016, for more details on the used methods and codes). As can be seen, the effect of assuming negligible off-diagonal elements in the covariance matrix is not statistically significant. Moreover, the off-diagonal elements in the covariance matrix can introduce systematics and spurious scatter in the inferred cosmological constraints, if not properly estimated with a sufficiently large number of mocks. The above considerations motivated our choice of neglecting off-diagonal terms in the analyses presented in this paper, in line with previous similar works (see e.g. Bianchi et al. 2015; Petracca et al. 2016).
All Tables
Main properties of the samples of galaxy groups and clusters analysed in the paper.
All Figures
 |
Fig. 1 Ratio between the redshift-space and real-space two-point spherically averaged correlation functions, ξ(s) /ξ(r), at z = 0.2, for galaxies with log (MSTAR [h-1M⊙]) > 10 (top panel), clusters with log (M500 [h-1M⊙]) > 13 (central panel), and AGN with log (MBH [h-1M⊙]) > 6.3 (bottom panel). The redshift-space correlation functions have been measured directly from the simulation, while the real-space ones have been either measured from the simulation (red dots), or derived from the CAMB power spectrum (blue squares). The error bars represent the statistical noise as prescribed by Mo et al. (1992). The black solid lines show the expected values of ξ(s) /ξ(r) at large scales predicted by Eq. (11b). The dotted blue and dashed red lines are the best-fit ratios estimated from the blue and red points, respectively. |
| In the text | |
 |
Fig. 2 Top panel: best-fit values of f(z)σ8(z) for galaxies with log (MSTAR [h-1M⊙]) > 10 (red dots), clusters with log (M500 [h-1M⊙]) > 13 (blue squares) and AGN with log (MBH [h-1M⊙]) > 6.3 (green diamonds), obtained with the method described in Sect. 5.1. The black line shows the function ΩM(z)0.545·σ8(z), where ΩM(z) and σ8(z) are the known values of the simulation. Bottom panel: percentage systematic errors on f(z)σ8(z), [(fσ8)measured−(fσ8)simulation] /(fσ8)simulation·100, that is, the percentage differences between the points and the black line shown in the top panel. The error bars have been estimated with Eq. (19). The values reported have been slightly shifted for visual clarity. To guide the eyes, the light and grey shaded areas highlight the 5% and 10% error regions, respectively. |
| In the text | |
 |
Fig. 3 Iso-correlation contours of the redshift-space two-point correlation function, corresponding to the values ξ(s⊥,s∥) = [0.05,0.1,0.2,0.4,1,3], for galaxies with log (MSTAR [h-1M⊙] ) > 10, at z = 0.2 (black contours). The dot-dashed green and solid red contours show the best-fit model given by Eq. (16), with the real-space correlation function ξ(r) measured from the simulation, and estimated from the CAMB power spectrum, respectively. The blue dashed contours show the linear best-fit model given by Eq. (10) with the CAMB real-space correlation function. |
| In the text | |
 |
Fig. 4 Top panel of the upper window: best-fit values of f(z)σ8(z) for galaxies with log (MSTAR [h-1M⊙] ) > 10. The open and solid blue squares show the values obtained by fitting the data with the models given by Eqs. (10) and (16), respectively, in the scale ranges 3 <r⊥ [h-1 Mpc] < 35 and 3 <r∥ [h-1 Mpc] < 35. The open and solid red dots have been obtained with the method described in Sect. 5.2.1, fitting the data with the models given by Eqs. (10) and (16), respectively. The black line shows the function ΩM(z)0.545·σ8(z), where ΩM(z) and σ8(z) are the known values of the simulation. For comparison, the grey dots show a set of recent observational measurements from galaxy surveys (see Sect. 5.2.1). Bottom panel of the upper window: percentage systematic errors on f(z)σ8(z), defined as [(fσ8)measured−(fσ8)simulation] /(fσ8)simulation·100, that is, the percentage differences between the points and the black line shown in the top panel. To guide the eyes, the light and grey shaded areas highlight the 5% and 10% error regions. Lower window: best-fit values of |
| In the text | |
 |
Fig. 5 Percentage systematic errors on f(z)σ8(z) for galaxies, [(fσ8)measured-(fσ8)simulation] /(fσ8)simulation·100, as a function of redshift and sample selections, as indicated by the labels. S1−S5 refer to the five selection thresholds reported in Tables A.1–A.3, for the different tracers and properties used for the selection. |
| In the text | |
 |
Fig. 6 Iso-correlation contours of the redshift-space two-point correlation function, corresponding to the values ξ(s⊥,s∥) = [0.2,0.4,1,3], for clusters with log (M500 [h-1M⊙] ) > 13, at z = 0.2 (black contours). The other contours are as in Fig. 3. |
| In the text | |
 |
Fig. 7 Best-fit values of f(z)σ8(z) for clusters with log (M500 [h-1M⊙]) > 13. All the symbols are as in Fig. 4. |
| In the text | |
 |
Fig. 8 Percentage systematic errors on f(z)σ8(z) for clusters, as a function of redshift and sample selections. All the symbols are as in Fig. 5. |
| In the text | |
 |
Fig. 9 Iso-correlation contours of the redshift-space two-point correlation function, corresponding to the values ξ(s⊥,s∥) = [0.1,0.2,0.4,1,3], for AGN with log (MBH [h-1M⊙]) > 6.3, at z = 0.2 (black contours). The other contours show the best-fit models, as in Fig. 3. |
| In the text | |
 |
Fig. 10 Best-fit values of f(z)σ8(z) for AGN with log (MBH [h-1M⊙] ) > 6.3. All the symbols are as in Fig. 4. |
| In the text | |
 |
Fig. 11 Percentage systematic errors on f(z)σ8(z) for AGN, as a function of redshift and sample selections. All the symbols are as in Fig. 5. |
| In the text | |
 |
Fig. A.1 The number of mock galaxies (red dots), clusters (blue squares) and AGN (green diamonds) as a function of redshift, for the three selections: Gs1, Cl1, Af1 (see Tables A.1–A.3). |
| In the text | |
 |
Fig. B.1 Ratio Δξ/σξ as a function of scales obtained from the sample of mock galaxies at z = 0.2, where |
| In the text | |
 |
Fig. C.1 Difference between fσ8 measurements obtained with diagonal Poisson errors and by considering the full covariance matrix assessed with either the jackknife (solid lines) or the bootstrap (dashed lines) techniques, divided by the 1σ uncertainty on fσ8, as a function of redshift. Red, blue and green symbols refer to galaxy, cluster and AGN samples, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


