| Issue |
A&A
Volume 598, February 2017
|
|
|---|---|---|
| Article Number | A24 | |
| Number of page(s) | 8 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201629609 | |
| Published online | 26 January 2017 | |
On the fast magnetic rotator regime of stellar winds⋆
University of Vienna, Department of Astrophysics, Türkenschanzstrasse 17, 1180 Vienna, Austria
e-mail: colin.johnstone@univie.ac.at
Received: 29 August 2016
Accepted: 7 October 2016
Aims. We study the acceleration of the stellar winds of rapidly rotating low mass stars and the transition between the slow magnetic rotator and fast magnetic rotator regimes. We aim to understand the properties of stellar winds in the fast magnetic rotator regime and the effects of magneto-centrifugal forces on wind speeds and mass loss rates.
Methods. We extend a solar wind model to 1D magnetohydrodynamic simulations of the winds of rotating stars. We test two assumptions for how to scale the wind temperature to other stars and assume the mass loss rate scales as 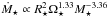 , in the unsaturated regime, as estimated from observed rotational evolution.
, in the unsaturated regime, as estimated from observed rotational evolution.
Results. For 1.0 M⊙ stars, the winds can be accelerated to several thousand km s-1, and the effects of magneto-centrifugal forces are much weaker for lower mass stars. We find that the different assumptions for how to scale the wind temperature to other stars lead to significantly different mass loss rates for the rapid rotators. If we assume a constant temperature, the mass loss rates of solar mass stars do not saturate at rapid rotation, which we show to be inconsistent with observed rotational evolution. If we assume the wind temperatures scale positively with rotation, the mass loss rates are only influenced significantly at rotation rates above ~ 75 Ω⊙. We suggest that models with increasing wind speed for more rapid rotators are preferable to those that assume a constant wind speed. If this conclusion is confirmed by more sophisticated wind modelling. it might provide an interesting observational constraint on the properties of stellar winds.
Key words: solar wind / stars: rotation / stars: solar-type / stars: winds, outflows / stars: magnetic field / stars: evolution
All of the codes and output data used in this paper can be downloaded from https://zenodo.org/record/160052#.V_y6drWkVC1 or obtained by contacting the author.
© ESO, 2017
1. Introduction
The solar wind accelerates because of a combination of thermal pressure gradients and pressure from waves propagating through the wind (Cranmer et al. 2007; Cranmer 2009). For the winds of rapid rotators, a further mechanism is important. Due to the fast rotation and the stellar magnetic field, the wind is accelerated by magneto-centrifugal forces (Belcher & MacGregor 1976). For the most rapid rotators, the winds can reach speeds of several thousand km s-1. The rotation rates at which magneto-centrifugal forces are important are determined by the stellar magnetic field strength and the contributions of the other acceleration mechanisms (Holzwarth & Jardine 2007).
All these effects are important given the influence of stellar winds on the atmospheric evolution of planets. Stellar winds can cause planetary atmospheres to lose mass (Kislyakova et al. 2013) and can potentially change atmospheric chemistry and even the surface climate (Airapetian et al. 2016). At young ages, low-mass stars show a large spread in rotation rates which quickly converge as stars spin down (Gallet & Bouvier 2013). A subset of stars go through phases of extremely rapid rotation, with rotation rates exceeding 100 times that of the Sun (Hartman et al. 2010). The magnetic activity of such stars evolve significantly differently from their slowly rotating counterparts (Johnstone et al. 2015a; Tu et al. 2015) which can be important for the evolution of a planet’s atmosphere (Johnstone et al. 2015c).
The basic mathematical theory for the equatorial winds of rotating magnetised stars was developed by Weber & Davis (1967). Belcher & MacGregor (1976) defined two regimes: the slow magnetic rotator (SMR) regime and the fast magnetic rotator (FMR) regime. In the SMR regime, magneto-centrifugal forces are negligible; in the FMR regime, they can be the dominant process determining the velocity of the wind. Extremely rapid rotators can enter the centrifugal magnetic rotator (CMR) regime when the equatorial corotation radius, Rco, is in the subsonic part of the wind; in the CMR regime, the mass flux in the wind is massively enhanced by magneto-centrifugal effects. When Rco is smaller than the stellar radius, the star breaks apart.
The aim of this paper is similar to those of Belcher & MacGregor (1976), though we use improved understandings of the solar wind, the magnetic fields of Sun-like stars, wind mass loss rates, and stellar rotational evolution; we also apply a 1D magnetohydrodynamic (MHD) solar wind model. In Sect. 2, we describe our wind model; in Sect. 3, we consider the different assumptions about wind temperature on the mass loss and spin-down of rapid rotators; in Sect. 4, we study the properties of winds in the FMR regime and the transition between the SMR and FMR regimes; in Sect. 5, we discuss our results.
2. Wind model
2.1. MHD code
Our 1D MHD wind model is based on the hydrodynamic model developed by Johnstone et al. (2015b) and is described in detail in their Sect 3.1 and Appendix A. The model is solved using the Versatile Advection Code (VAC) developed by Tóth (1996). It is common in stellar wind models to assume that the thermal pressure, p, and density, ρ, are related by a polytropic equation of state, such that p = Kρα. In our model, we take α = 1.05 when r< 15 R⊙ and α = 1.51 when r< 25 R⊙. Between 15 and 25 R⊙, we assume α varies between these values linearly. In Johnstone et al. (2015b), the radial structures of our model were verified against measured values of the real solar wind, both close to the Sun and far away.
In this paper, we extend the model to take into account magnetic fields and stellar rotation. We therefore use the MHD physics model in VAC, modified to take into account the spatial variations in α. In addition, we include momentum source terms for centrifugal and Coriolis forces. We hold Br constant throughout the simulation domain, as is necessary in 1D MHD. At the lower boundary, we hold the density, ρ, constant and allow Bφ to vary with no constraints; the radial velocity component, Vr, in the first grid point is set to be equal to the value in the second grid point and Vφ at the lower boundary is set such that the velocity and magnetic field vectors are parallel. At the upper boundary, we assume zero spatial gradients in all quantities.
We start the simulations with a simple isothermal Parker wind solution (Parker 1958) for Vr at all radii. The initial density structure is calculated based on mass conservation (i.e. ρVrr2 = const.) and the radial magnetic field is calculated from Br(r) = B⋆(r/R⋆)-2, where B⋆ is the assumed radial magnetic field at the stellar surface. Both Vφ and Bφ are zero everywhere in the initial conditions. Early in the simulation, a non-physical shock propagates through the domain and the simulation quickly relaxes to its final state. The simulations are performed on a grid of 500 cells extending from the stellar surface to 1 AU. The sizes of each grid cell increase linearly from the stellar surface to the outer boundary, with the final grid point being 100 times larger than the first.
2.2. Validation of code
To verify our simulations, we run models for isothermal winds (i.e. α = 1 everywhere) with different rotation rates and compare the results to solutions of the analytic model of Weber & Davis (1967). The method we use to solve the Weber-Davis (WD) model is described in Appendix A.
For the MHD simulations, we assume at the base of the wind (i.e. at the stellar surface), a proton number density of 107 cm-3, a wind temperature of 2 MK, and a radial magnetic field of 1 G. We run simulations with stellar rotation rates of 1 Ω⊙, 25 Ω⊙, 50 Ω⊙, and 100 Ω⊙. For the analytic models, the only difference is that we use the mass loss rates from the MHD simulations as an input instead of the base density. This is necessary because the analytic model requires the mass flux as an input. In Fig. 1, we compare the radial structures of Vr and Vφ from both methods and find excellent agreements. There are similarly good agreements in other wind parameters, and also for simulations with stronger magnetic fields.
 |
Fig. 1 Figure comparing the velocity structures of isothermal winds simulated using our numerical MHD model (solid lines) and using the analytic Weber-Davis model (circles) for different rotation rates. |
2.3. Application to stars
We scale our solar wind model to other stars based on their masses and rotation rates. This is similar to the approach taken by Holzwarth & Jardine (2007), and more recently using 3D MHD models by Réville et al. (2016). For the radius and luminosity, we simply assume 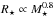 and
and 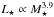 . Since we are interested in winds in the equatorial plane, we consider only the slow component of the solar wind. The three parameters in our model are the temperature, density, and magnetic field strength at the base of the wind. For the current solar wind, these were determined by Johnstone et al. (2015b) to be 1.8 MK and 2.6 × 107 cm-3 for the temperature and proton density respectively. We assume a base magnetic field of 0.54 G, as justified in Sect. 4.3 of Johnstone et al. (2015b); this value takes into account the fact that we assume Br ∝ r-2 everywhere, whereas in reality, Br decreases faster with r within the closed corona.
. Since we are interested in winds in the equatorial plane, we consider only the slow component of the solar wind. The three parameters in our model are the temperature, density, and magnetic field strength at the base of the wind. For the current solar wind, these were determined by Johnstone et al. (2015b) to be 1.8 MK and 2.6 × 107 cm-3 for the temperature and proton density respectively. We assume a base magnetic field of 0.54 G, as justified in Sect. 4.3 of Johnstone et al. (2015b); this value takes into account the fact that we assume Br ∝ r-2 everywhere, whereas in reality, Br decreases faster with r within the closed corona.
We assume that the wind temperature scales linearly with coronal temperature, which is known to depend strongly on X-ray activity (Schmitt 1997; Güdel et al. 1997). We use the relation derived by Johnstone & Güdel (2015) for the coronal average temperature, 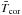 , in MK as a function of X-ray surface flux FX, in erg s-1 cm-2:
, in MK as a function of X-ray surface flux FX, in erg s-1 cm-2: 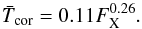 (1)To get FX as a function of stellar mass and rotation rate, we use the empirical relation derived by Wright et al. (2011). The result is that winds are hotter for more rapidly rotating stars until FX, and therefore
(1)To get FX as a function of stellar mass and rotation rate, we use the empirical relation derived by Wright et al. (2011). The result is that winds are hotter for more rapidly rotating stars until FX, and therefore 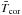 , saturates. Saturation takes place at lower Ω⋆ for lower-mass stars. The above model was called Model A by Johnstone et al. (2015b). In the same paper, Johnstone et al. (2015b) considered a separate assumption, which they called Model B. In this model, they assumed, as in Matt et al. (2012), that the sound speed at the base of the wind is a constant fraction of the surface escape velocity. The wind temperature in this model is approximately the same for all stars. Johnstone et al. (2015b) showed that these two models can lead to very different wind properties. In Sect. 3, we test both models and describe why we prefer Model A to Model B.
, saturates. Saturation takes place at lower Ω⋆ for lower-mass stars. The above model was called Model A by Johnstone et al. (2015b). In the same paper, Johnstone et al. (2015b) considered a separate assumption, which they called Model B. In this model, they assumed, as in Matt et al. (2012), that the sound speed at the base of the wind is a constant fraction of the surface escape velocity. The wind temperature in this model is approximately the same for all stars. Johnstone et al. (2015b) showed that these two models can lead to very different wind properties. In Sect. 3, we test both models and describe why we prefer Model A to Model B.
Once the wind temperature has been set, to get the base density, we choose the value that gives us the desired mass loss rate. We estimate a star’s mass loss rate using 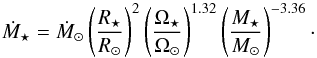 (2)This relation was derived by Johnstone et al. (2015a) by fitting the free parameters in a rotational evolution model to the observational constraints. A similar relation was derived using similar methods by Matt et al. (2015). To scale the magnetic field to other stars, we assume that
(2)This relation was derived by Johnstone et al. (2015a) by fitting the free parameters in a rotational evolution model to the observational constraints. A similar relation was derived using similar methods by Matt et al. (2015). To scale the magnetic field to other stars, we assume that  (3)where τ⋆ and τ⊙ are the stellar and solar convective turnover times. This is based on the analysis of measured stellar global magnetic field strengths by Vidotto et al. (2014). For the convective turnover times, we use the relation derived by Wright et al. (2011). In Eqs. (2) and (3), when Ω⋆ is greater than the saturation rotation rate, Ωsat, we assume the Ω⋆ dependence saturates, and replace Ω⋆ with Ωsat. The saturation rotation rate is given by
(3)where τ⋆ and τ⊙ are the stellar and solar convective turnover times. This is based on the analysis of measured stellar global magnetic field strengths by Vidotto et al. (2014). For the convective turnover times, we use the relation derived by Wright et al. (2011). In Eqs. (2) and (3), when Ω⋆ is greater than the saturation rotation rate, Ωsat, we assume the Ω⋆ dependence saturates, and replace Ω⋆ with Ωsat. The saturation rotation rate is given by 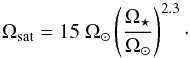 (4)This was estimated by Johnstone et al. (2015a) from fitting a stellar rotational evolution model to observations.
(4)This was estimated by Johnstone et al. (2015a) from fitting a stellar rotational evolution model to observations.
Another effect that we take into account is the increase in the equatorial radii of rapid rotators due to centrifugal effects. To calculate the equatorial radius, we numerically solve 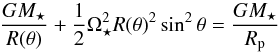 (5)where R(θ) is the stellar radius at colatitude θ and Rp is the polar radius (see e.g. Eq. (2.10) of Maeder 2009). This equation simply states that the effective gravitational potential is uniform over the stellar surface. For simplicity, we assume Rp = R⋆, i.e. the polar radius is the radius the entire star would have in the absence of rotation1. Taking the bulging of the star into account is important for the winds of very rapid rotators and is essential for calculating the break up rotation rate.
(5)where R(θ) is the stellar radius at colatitude θ and Rp is the polar radius (see e.g. Eq. (2.10) of Maeder 2009). This equation simply states that the effective gravitational potential is uniform over the stellar surface. For simplicity, we assume Rp = R⋆, i.e. the polar radius is the radius the entire star would have in the absence of rotation1. Taking the bulging of the star into account is important for the winds of very rapid rotators and is essential for calculating the break up rotation rate.
 |
Fig. 2 Wind mass loss rate against rotation rate for both Model A and Model B for solar mass stars. In both cases, Ṁ⋆ follows Eq. (2) in the unsaturated regime and is then allowed to vary freely in the saturated regime. The filled circles show individual simulations. |
3. Wind temperature: constraints from rotational evolution
In this section, we consider the different influences of Model A and Model B on the mass loss rates of solar mass stars. The importance of these models is not that either is likely to be correct, but that they represent different possibilities for how wind acceleration changes with the activity level of the star. Model A represents cases in which the winds of more active stars are faster than the winds of less active stars, either because they are hotter or because of stronger acceleration from waves, or a combination of the two. An example of this is the model used by Airapetian et al. (2016). Model B represents the case where the wind speeds are constant, and the mass loss rates change only because of changes in the densities. Examples of this assumption can be found in Wood et al. (2002) and Cranmer & Saar (2011).
In Fig. 2, we show the dependence of mass loss rate on stellar rotation rate for both Model A and Model B. In the unsaturated regime, we force the mass loss rate to increase according to 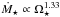 , as estimated from observed stellar rotational evolution (Johnstone et al. 2015a). In the saturated regime, we hold constant the base density, temperature, and radial field, and Ṁ⋆ is allowed to change as a result of the changes in the centrifugal and Lorentz forces. We therefore have in Model A a higher base temperature and a lower base density than in Model B, for all models except for the current solar wind case. Both models are by definition identical for the current Sun.
, as estimated from observed stellar rotational evolution (Johnstone et al. 2015a). In the saturated regime, we hold constant the base density, temperature, and radial field, and Ṁ⋆ is allowed to change as a result of the changes in the centrifugal and Lorentz forces. We therefore have in Model A a higher base temperature and a lower base density than in Model B, for all models except for the current solar wind case. Both models are by definition identical for the current Sun.
We find that at rapid rotation, Model A and Model B lead to significantly different mass loss rates. In Model A, Ṁ⋆ saturates at the saturation threshold (15 Ω⊙) and remains approximately constant until ~ 100 Ω⊙ when it then begins to increase rapidly with faster rotation. In Model B, the mass loss rate never saturates and continues to increase with increasing rotation rate at approximately the same rate as in the unsaturated regime.
This difference is caused by the different acceleration profiles of the winds in the two models and the important fact that the mass loss rates in winds are determined by what happens in the lower parts of the wind where the material is subsonic and subalfvénic. The wind speeds at 1 AU and the radii of the sonic points as functions of the rotation rate are shown in Fig. 3. In Model A, the winds of more rapidly rotating stars accelerate faster and therefore become supersonic closer to the stellar surface. The increasing centrifugal and Lorentz forces acting on the winds have a smaller effect on the mass loss rate since they are primarily significant at larger radii. In Model B, since the wind temperatures remain constant, the sonic point remains far from the stellar surface at almost all rotation rates, so the centrifugal and Lorentz forces are significant in the subsonic wind. The result is that even if the primary driving mechanisms of the winds saturate, Ṁ⋆ still increases quickly with rotation because of magneto-centrifugal acceleration.
 |
Fig. 3 Rotational dependence of the wind speed at 1 AU (upper-panel) and radius of the sonic point (lower-panel) for Model A and Model B. The filled circles show individual simulations. |
 |
Fig. 4 Rotational evolution between 100 Myr and 1 Gyr of a solar mass star with a rotation rate at 100 Myr of 70 Ω⊙. The blue and green lines show the evolutions with and without sautation of Ṁ⋆ at 15 Ω⊙. These correspond approximately to the Ṁ⋆–Ω⋆ relations for Model A and Model B shown in Fig. 2. |
It is interesting to consider stellar rotational evolution since spin-down is a direct consequence of stellar winds and is well constrained observationally (Bouvier et al. 2014). We can describe the spin-down rate of a star as 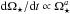 . In the unsaturated regime, a ≈ 3, and in the saturated regime, a ≈ 1 (Matt et al. 2015). The wind torque law found by Matt et al. (2012) approximately implies that
. In the unsaturated regime, a ≈ 3, and in the saturated regime, a ≈ 1 (Matt et al. 2015). The wind torque law found by Matt et al. (2012) approximately implies that 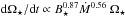 . Inserting the Ω⋆ dependences of Ṁ⋆ from Eq. (2) and B⋆ from Eq. (3) gives a ≈ 2.89, as expected for the unsaturated regime. In the saturated regime, we instead get a ≈ 1 if both Ṁ⋆ and B⋆ saturate, and a ≈ 1.74 if only B⋆ saturates, suggesting that Ṁ⋆ saturation is observationally necessary. This is further illustrated in Fig. 4 where we show the rotational evolution of a solar mass star with a 100 Myr rotation rate of 70 Ω⊙. This corresponds to the 90th percentile of the rotation distribution at this age. We use the rotational evolution model described in Johnstone et al. (2015a) to evolve the star’s rotation until 1 Gyr assuming saturation of Ṁ⋆ (blue line) and no saturation of Ṁ⋆ (green line). The red triangles show the observed 90th percentile at different ages, which are clearly better fitted by the blue line. The necessity of Ṁ⋆ saturation would likely be even clearer if we considered the rotational evolution of rapid rotators before 100 Myr. We can conclude from these considerations that the Ṁ⋆–Ω⋆ relation shown in Fig. 2 for Model B is not consistent with the observed rotational evolution of rapid rotators.
. Inserting the Ω⋆ dependences of Ṁ⋆ from Eq. (2) and B⋆ from Eq. (3) gives a ≈ 2.89, as expected for the unsaturated regime. In the saturated regime, we instead get a ≈ 1 if both Ṁ⋆ and B⋆ saturate, and a ≈ 1.74 if only B⋆ saturates, suggesting that Ṁ⋆ saturation is observationally necessary. This is further illustrated in Fig. 4 where we show the rotational evolution of a solar mass star with a 100 Myr rotation rate of 70 Ω⊙. This corresponds to the 90th percentile of the rotation distribution at this age. We use the rotational evolution model described in Johnstone et al. (2015a) to evolve the star’s rotation until 1 Gyr assuming saturation of Ṁ⋆ (blue line) and no saturation of Ṁ⋆ (green line). The red triangles show the observed 90th percentile at different ages, which are clearly better fitted by the blue line. The necessity of Ṁ⋆ saturation would likely be even clearer if we considered the rotational evolution of rapid rotators before 100 Myr. We can conclude from these considerations that the Ṁ⋆–Ω⋆ relation shown in Fig. 2 for Model B is not consistent with the observed rotational evolution of rapid rotators.
 |
Fig. 5 Wind properties for stars with masses of 0.5 M⊙ (left-column) and 1.0 M⊙ (right-column) for different rotation rates. Note the different scales on the y-axes in the two columns. |
 |
Fig. 6 Radial variations in the forces that cause acceleration in our wind model; these are the four terms on the RHS of Eq. (6). Both cases are for solar mass stars. |
4. Results: stellar winds in the FMR regime
We now consider only Model A for calculating wind temperatures. In Fig. 5, we show the wind densities, and radial and azimuthal speeds for 0.5 M⊙ and 1.0 M⊙ stars with a wide range of rotation rates.
In the 1.0 M⊙ case, the wind has the acceleration profile of the current solar wind, with a radial outflow velocity at 1 AU of 400 km s-1 and an azimuthal velocity of 0.5 km s-1. Going to faster rotation, the winds accelerate to higher speeds due to their higher temperatures, with a speed of about 1300 km s-1 for stars rotating at 15 Ω⊙. This is entirely due to increased thermal acceleration. At this point, the wind driving saturates and the radial outflow speed depends only weakly on rotation until ~ 50 Ω⊙, where magneto-centrifugal wind acceleration becomes significant. At more rapid rotation, the wind speed depends strongly on Ω⋆. At 50 Ω⊙, the wind has a Vr at 1 AU of 1800 km s-1, and at 100 Ω⊙, this value is 2600 km s-1 In all cases, the azimuthal component of the wind velocity, which is strongly Ω⋆-dependent, peaks close to the star and then decreases to insignificant values by 1 AU.
The acceleration of the solution is described by 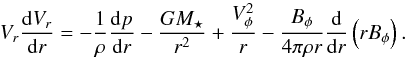 (6)This is Eq. (9.18) of Lamers & Cassinelli (1999). The terms on the RHS correspond to each of the forces that influence the radial acceleration of the wind; from left to right, they are the thermal pressure gradient, gravity, the centrifugal force, and the radial component of the Lorentz force. In the absence of stellar rotation and/or the magnetic field, the final two terms are zero and the equation corresponds to the model of Parker (1958). We show in Fig. 6 each of these terms as a function of radius for rotation rates of 1 Ω⋆ and 50 Ω⋆. For the 1 Ω⋆ case, the centrifugal and Lorentz force terms are negligible at all radii. For the 50 Ω⋆ case, the centrifugal term is negligible, but the Lorentz force is stronger than the thermal pressure term beyond 0.2 AU. Since the wind is already supersonic at 0.2 AU, Ṁ⋆ is still determined by the thermal acceleration.
(6)This is Eq. (9.18) of Lamers & Cassinelli (1999). The terms on the RHS correspond to each of the forces that influence the radial acceleration of the wind; from left to right, they are the thermal pressure gradient, gravity, the centrifugal force, and the radial component of the Lorentz force. In the absence of stellar rotation and/or the magnetic field, the final two terms are zero and the equation corresponds to the model of Parker (1958). We show in Fig. 6 each of these terms as a function of radius for rotation rates of 1 Ω⋆ and 50 Ω⋆. For the 1 Ω⋆ case, the centrifugal and Lorentz force terms are negligible at all radii. For the 50 Ω⋆ case, the centrifugal term is negligible, but the Lorentz force is stronger than the thermal pressure term beyond 0.2 AU. Since the wind is already supersonic at 0.2 AU, Ṁ⋆ is still determined by the thermal acceleration.
 |
Fig. 7 Mass loss rate (upper-panel) and radial outflow speed (lower-panel) as a function of rotation for three stellar masses. The small circles show the individual simulations and the vertical dashed lines show the saturation thresholds. |
The wind acceleration in the 0.5 M⊙ case, shown in Fig. 5, leads to much slower winds for the rapid rotators. The 1 AU wind speed for the 100 Ω⊙ case is 1200 km s-1, which is half that of the 1.0 M⊙ case. To understand this, consider the Michel velocity (Michel 1969) which can be used as an estimate of the wind outflow speed far from the star in the FMR regime (Belcher & MacGregor 1976). The Michel velocity is given by 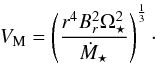 (7)Since Br ∝ r-2, this is a constant throughout the wind. At rapid rotation, due to the lower saturation threshold, Ṁ⋆ and B⋆ are lower for lower mass stars in our model. These two almost cancel each other out, leading to only a small effect on VM. The main reason for the lower wind speeds of lower mass stars is that Br at large radii is lower, due not to the weaker field at the stellar surface, but due to the smaller stellar radius, since Br(r) = B⋆(r/R⋆)-2. The dependences of Ṁ⋆ and Vr at 1 AU on Ω⋆ can be clearly seen in Fig. 7.
(7)Since Br ∝ r-2, this is a constant throughout the wind. At rapid rotation, due to the lower saturation threshold, Ṁ⋆ and B⋆ are lower for lower mass stars in our model. These two almost cancel each other out, leading to only a small effect on VM. The main reason for the lower wind speeds of lower mass stars is that Br at large radii is lower, due not to the weaker field at the stellar surface, but due to the smaller stellar radius, since Br(r) = B⋆(r/R⋆)-2. The dependences of Ṁ⋆ and Vr at 1 AU on Ω⋆ can be clearly seen in Fig. 7.
5. Conclusions
In this paper, we study the winds of rapidly rotating stars using recent knowledge of stellar magnetic fields. We show that solar mass stars rotating at 100 Ω⊙ have winds with speeds of ~ 2500 km s-1. Such rapid rotators have be seen in young stellar clusters (e.g. Hartman et al. 2010), and it is possible that the Sun was once rotating at such a rate. Even greater wind speeds should be expected given that we use only average magnetic field strengths, and in reality, the global magnetic field of a star will vary over a large range. We should expect that as the global fields of stars vary, both stochastically and cyclically, the winds speeds will vary in response. Given the influence that stellar winds can have one the atmospheric evolution of planetary atmospheres, understanding the properties of stellar winds in the FMR regime can be important for our understanding of the atmospheric evolution of the solar system terrestrial planets.
Based on the solar relation between flares and coronal mass ejections (CMEs), and the high flare activity of active stars, it has been suggested that the winds of active stars are dominated by CMEs (Aarnio et al. 2012; Drake et al. 2013), though their actual existence is still unclear (Leitzinger et al. 2014). The influences on highly time-dependent CME winds of the magneto-centrifugal forces of rapid rotators is currently unexplored.
Probably the most important problem in the study of stellar winds of low mass stars is the lack of direct observational constraints on wind properties. Indirect methods include measuring astrospheric Lyα absorption (Wood et al. 2014), getting upper limits on radio emission from winds (Gaidos et al. 2000), fitting stellar rotational evolution (Matt et al. 2015), and the analysis of planetary transits (Kislyakova et al. 2014). The most important result in this paper is the suggestion that assumptions for the wind speeds of rapid rotators can be tested using rotational evolution. If we assume that wind speeds are the same for stars with different activity levels, we find almost no saturation of the mass loss rate at fast rotation. The lack of saturation is likely inconsistent with observed rotational evolution, meaning that this could be an indirect observational constraint on stellar wind properties. Specifically, the winds of more rapidly rotating stars need to be faster so that they become supersonic closer to the stellar surface; if this does not happen, magneto-centrifugal acceleration can significantly influence the mass loss rate, causing the most rapidly rotating stars to spin down faster than is observed.
This argument needs to be explored with more complex and internally consistent models before it can be made with any certainty. The 1D equatorial model that we use here will overestimate the increase in Ṁ⋆ due to magneto-centrifugal effects, which should be fixed by applying 2D and 3D MHD models. Such models will also be able to take into account the meridional components of the velocity, and meridional gradients in all quantities (i.e. ∂/∂θ terms), which are ignored in the Weber-Davis model (Suess & Nerney 1973). Given the lack of observational constraints on the winds of low mass stars, if these results can be confirmed by more sophisticated theoretical work, it could provide an important constraint on future stellar wind models.
Based on Fig. 2.7 of Maeder (2009), we expect this assumption to be accurate, with only a few percent difference between Rp and R⋆.
For this, we use the optimize.root() function of the SciPy package (Jones et al. 2001). For finding the slow point, optimize.root() required a good initial guess, which we make by eye.
Acknowledgments
C.P.J. acknowledges the support of the FWF NFN project S116601-N16 “Pathways to Habitability: From Disks to Active Stars, Planets and Life”, and the related FWF NFN subproject S116604-N16. This publication is supported by the Austrian Science Fund (FWF).
References
- Aarnio, A. N., Matt, S. P., & Stassun, K. G. 2012, ApJ, 760, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Airapetian, V. S., Glocer, A., Gronoff, G., Hébrard, E., & Danchi, W. 2016, Nature Geoscience, 9, 452 [Google Scholar]
- Belcher, J. W., & MacGregor, K. B. 1976, ApJ, 210, 498 [NASA ADS] [CrossRef] [Google Scholar]
- Bouvier, J., Matt, S. P., Mohanty, S., et al. 2014, Protostars and Planets VI, 433 [Google Scholar]
- Cranmer, S. R. 2009, Liv. Rev. Sol. Phys., 6, 3 [Google Scholar]
- Cranmer, S. R., & Saar, S. H. 2011, ApJ, 741, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Cranmer, S. R., van Ballegooijen, A. A., & Edgar, R. J. 2007, ApJS, 171, 520 [Google Scholar]
- Drake, J. J., Cohen, O., Yashiro, S., & Gopalswamy, N. 2013, ApJ, 764, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Gaidos, E. J., Güdel, M., & Blake, G. A. 2000, Geophys. Res. Lett., 27, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Gallet, F., & Bouvier, J. 2013, A&A, 556, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Güdel, M., Guinan, E. F., & Skinner, S. L. 1997, ApJ, 483, 947 [NASA ADS] [CrossRef] [Google Scholar]
- Hartman, J. D., Bakos, G. Á., Kovács, G., & Noyes, R. W. 2010, MNRAS, 408, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Holzwarth, V., & Jardine, M. 2007, A&A, 463, 11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johnstone, C. P., & Güdel, M. 2015, A&A, 578, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johnstone, C. P., Güdel, M., Brott, I., & Lüftinger, T. 2015a, A&A, 577, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johnstone, C. P., Güdel, M., Lüftinger, T., Toth, G., & Brott, I. 2015b, A&A, 577, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johnstone, C. P., Güdel, M., Stökl, A., et al. 2015c, ApJ, 815, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, E., Oliphant, T., Peterson, P., et al. 2001 SciPy: Open source scientific tools for Python (Online, accessed 2016-08-10) [Google Scholar]
- Kislyakova, K. G., Lammer, H., Holmström, M., et al. 2013, Astrobiology, 13, 1030 [NASA ADS] [CrossRef] [Google Scholar]
- Kislyakova, K. G., Holmström, M., Lammer, H., Odert, P., & Khodachenko, M. L. 2014, Science, 346, 981 [NASA ADS] [CrossRef] [Google Scholar]
- Lamers, H. J. G. L. M., & Cassinelli, J. P. 1999. in Introduction to Stellar Winds, (Cambridge, UK: Cambridge Unuversity Press) 452 [Google Scholar]
- Leitzinger, M., Odert, P., Greimel, R., et al. 2014, MNRAS, 443, 898 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A. 2009, in Physics, Formation and Evolution of Rotating Stars (Springer) [Google Scholar]
- Matt, S. P., MacGregor, K. B., Pinsonneault, M. H., & Greene, T. P. 2012, ApJ, 754, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Matt, S. P., Brun, A. S., Baraffe, I., Bouvier, J., & Chabrier, G. 2015, ApJ, 799, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Michel, F. C. 1969, ApJ, 158, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1958, ApJ, 128, 664 [Google Scholar]
- Preusse, S., Kopp, A., Büchner, J., & Motschmann, U. 2005, A&A, 434, 1191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Réville, V., Folsom, C. P., Strugarek, A., & Brun, A. S. 2016, ApJ, 832, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Schmitt, J. H. M. M. 1997, A&A, 318, 215 [NASA ADS] [Google Scholar]
- Suess, S. T., & Nerney, S. F. 1973, ApJ, 184, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Tóth, G. 1996, Astrophys. Lett. Commun., 34, 245 [NASA ADS] [Google Scholar]
- Tu, L., Johnstone, C. P., Güdel, M., & Lammer, H. 2015, A&A, 577, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vidotto, A. A., Gregory, S. G., Jardine, M., et al. 2014, MNRAS, 441, 2361 [NASA ADS] [CrossRef] [Google Scholar]
- Weber, E. J., & Davis, Jr., L. 1967, ApJ, 148, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Wood, B. E., Müller, H.-R., Zank, G. P., & Linsky, J. L. 2002, ApJ, 574, 412 [NASA ADS] [CrossRef] [Google Scholar]
- Wood, B. E., Müller, H.-R., Redfield, S., & Edelman, E. 2014, ApJ, 781, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, N. J., Drake, J. J., Mamajek, E. E., & Henry, G. W. 2011, ApJ, 743, 48 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Solving the Weber-Davis (WD) model
To solve the isothermal WD model, we use the method described by Preusse et al. (2005). The six input parameters are the wind temperature, Twind, the radial field at the star, Br,⋆, and the stellar mass, M⋆, radius, R⋆, and rotation rate, Ω⋆. From these parameters, the radial structures of the wind density, velocity, and magnetic field can be derived.
Unlike the wind model of Parker (1958), which has one critical radius at the sonic point, the WD model has three critical points. This can be seen from Eq. (9.73) of Lamers & Cassinelli (1999) for the radial gradient in the radial component of the wind velocity, Vr: 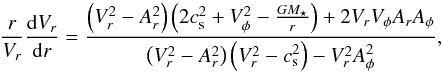 (A.1)where Vφ is the azimuthal component of the wind velocity in the non-rotating frame of reference,
(A.1)where Vφ is the azimuthal component of the wind velocity in the non-rotating frame of reference, 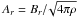 and
and 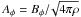 are the radial and azimuthal components of the Alfvén velocity at a given r, and cs is the sound speed. At a given radius, Vφ and Aφ are given by
are the radial and azimuthal components of the Alfvén velocity at a given r, and cs is the sound speed. At a given radius, Vφ and Aφ are given by 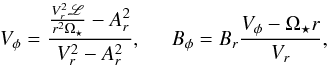 (A.2)where L is defined below. The denominator of the RHS of Eq. (A.1) vanishes when
(A.2)where L is defined below. The denominator of the RHS of Eq. (A.1) vanishes when ![\appendix \setcounter{section}{1} \begin{equation} V_r^2 = V_{r,{\rm s}}^2 = \frac{1}{2} \left[ c_{\rm s}^2 + |\boldsymbol{A}|^2 - \sqrt{ (c_{\rm s}^2 + |\boldsymbol{A}|^2)^2 - 4 c_{\rm s}^2 A_r^2 } \right], \end{equation}](/articles/aa/full_html/2017/02/aa29609-16/aa29609-16-eq85.png) (A.3)and when
(A.3)and when ![\appendix \setcounter{section}{1} \begin{equation} V_r^2 = V_{r,f}^2 = \frac{1}{2} \left[ c_{\rm s}^2 + |\boldsymbol{A}|^2 + \sqrt{ (c_{\rm s}^2 + |\boldsymbol{A}|^2)^2 - 4 c_{\rm s}^2 A_r^2 } \right], \end{equation}](/articles/aa/full_html/2017/02/aa29609-16/aa29609-16-eq86.png) (A.4)where
(A.4)where 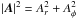 . Specifically, this is where Vr is equal to the radial component of either the slow or the fast magnetosonic wave velocities, given by Vr,s and Vr,f. At these points, the numerator and denominator of the RHS of Eq. (A.1) simultaneously vanish. These two points are the slow and fast points. The third critical point is the Alfvén point, at radius rA, where Vr = Ar, which is between the slow and fast points.
. Specifically, this is where Vr is equal to the radial component of either the slow or the fast magnetosonic wave velocities, given by Vr,s and Vr,f. At these points, the numerator and denominator of the RHS of Eq. (A.1) simultaneously vanish. These two points are the slow and fast points. The third critical point is the Alfvén point, at radius rA, where Vr = Ar, which is between the slow and fast points.
It is convenient to define x = r/rA and u = Vr/VA, where VA = Vr(rA) = Ar(rA) is the radial wind speed at the Alfvén point, and rewrite the equation for dVr/ dr as ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{eqn:dVrdrNormed} &&\left[ 1 - \frac{\mathscr{V}}{u^2} + \mathscr{W} \frac{x^2 \left( 1 - x^2 \right)^2 }{(1-x^2 u)^3} \right] x^2 u \frac{{\rm d}u}{{\rm d}x} = \nonumber\\ &&~~~~~~2 \mathscr{V} x - \mathscr{U} + \mathscr{W} \left[ \frac{x^3 \left( 1 - u \right)^2}{\left(1-x^2u \right)^2} + \frac{2 x^3 u \left( 1 - u \right) \left( 1 - x^2 \right)}{\left(1-x^2u \right)^3} \right] \end{eqnarray}](/articles/aa/full_html/2017/02/aa29609-16/aa29609-16-eq96.png) (A.5)where U, V, and W are constants given by
(A.5)where U, V, and W are constants given by 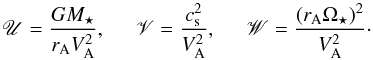 (A.6)These are Eqs. (9.67) and (9.68) of Lamers & Cassinelli (1999). It is also convenient to define three more constants in the wind representing mass and magnetic fluxes, and the specific angular momentum:
(A.6)These are Eqs. (9.67) and (9.68) of Lamers & Cassinelli (1999). It is also convenient to define three more constants in the wind representing mass and magnetic fluxes, and the specific angular momentum: 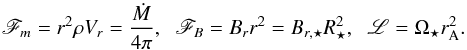 (A.7)As in Preusse et al. (2005), integrating Eq. (A.5) gives
(A.7)As in Preusse et al. (2005), integrating Eq. (A.5) gives 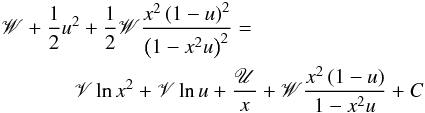 (A.8)where C is the constant of integration. This equation can easily by solved numerically to get Vr at all radii when the values of C, rA, and VA are known. As in Preusse et al. (2005), we find these values by searching for the value of V that gives the correct wind solution.
(A.8)where C is the constant of integration. This equation can easily by solved numerically to get Vr at all radii when the values of C, rA, and VA are known. As in Preusse et al. (2005), we find these values by searching for the value of V that gives the correct wind solution.
For each guess of V, we first calculate the corresponding VA and rA values from Eq. (A.7) and 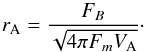 (A.9)From these, we get U, W, and L. Then, we find the values of r and Vr where the nominator and denominator of Eq. (A.1) simultaneously vanish.2 One of these points is where r<rA and Vr<VA and corresponds to the slow point, and the other is where r>rA and Vr>VA and corresponds to the fast point. We then use Eq. (A.8) to calculate C at the slow and fast points. We start by taking an initial guess of V and search for the value of V at which C is the same at the slow and fast points. With the correct value of V, we then solve Eq. (A.8) numerically to get Vr(r), then use Fm and FB to get ρ(r) and Br(r), and finally Eq. (A.2) to get Vφ(r) and Bφ(r).
(A.9)From these, we get U, W, and L. Then, we find the values of r and Vr where the nominator and denominator of Eq. (A.1) simultaneously vanish.2 One of these points is where r<rA and Vr<VA and corresponds to the slow point, and the other is where r>rA and Vr>VA and corresponds to the fast point. We then use Eq. (A.8) to calculate C at the slow and fast points. We start by taking an initial guess of V and search for the value of V at which C is the same at the slow and fast points. With the correct value of V, we then solve Eq. (A.8) numerically to get Vr(r), then use Fm and FB to get ρ(r) and Br(r), and finally Eq. (A.2) to get Vφ(r) and Bφ(r).
All Figures
 |
Fig. 1 Figure comparing the velocity structures of isothermal winds simulated using our numerical MHD model (solid lines) and using the analytic Weber-Davis model (circles) for different rotation rates. |
| In the text | |
 |
Fig. 2 Wind mass loss rate against rotation rate for both Model A and Model B for solar mass stars. In both cases, Ṁ⋆ follows Eq. (2) in the unsaturated regime and is then allowed to vary freely in the saturated regime. The filled circles show individual simulations. |
| In the text | |
 |
Fig. 3 Rotational dependence of the wind speed at 1 AU (upper-panel) and radius of the sonic point (lower-panel) for Model A and Model B. The filled circles show individual simulations. |
| In the text | |
 |
Fig. 4 Rotational evolution between 100 Myr and 1 Gyr of a solar mass star with a rotation rate at 100 Myr of 70 Ω⊙. The blue and green lines show the evolutions with and without sautation of Ṁ⋆ at 15 Ω⊙. These correspond approximately to the Ṁ⋆–Ω⋆ relations for Model A and Model B shown in Fig. 2. |
| In the text | |
 |
Fig. 5 Wind properties for stars with masses of 0.5 M⊙ (left-column) and 1.0 M⊙ (right-column) for different rotation rates. Note the different scales on the y-axes in the two columns. |
| In the text | |
 |
Fig. 6 Radial variations in the forces that cause acceleration in our wind model; these are the four terms on the RHS of Eq. (6). Both cases are for solar mass stars. |
| In the text | |
 |
Fig. 7 Mass loss rate (upper-panel) and radial outflow speed (lower-panel) as a function of rotation for three stellar masses. The small circles show the individual simulations and the vertical dashed lines show the saturation thresholds. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


