| Issue |
A&A
Volume 598, February 2017
|
|
|---|---|---|
| Article Number | A110 | |
| Number of page(s) | 15 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201629374 | |
| Published online | 09 February 2017 | |
Secular orbital evolution of Jupiter family comets
1 P.A.S. Space Research Centre, Bartycka 18A, 00-716 Warszawa, Poland
e-mail: wajer@cbk.waw.pl
2 Dept. of Physics and Astronomy, Uppsala University, Box 516, 75120 Uppsala, Sweden
3 IAPS-INAF, via Fosso del Cavaliere 100, 00133 Roma, Italy
4 IFAC-CNR, Via Madonna del Piano 10, 50019 Sesto Fiorentino (FI), Italy
5 Département Lagrange, University of Nice – Sophia Antipolis, CNRS, Observatoire de la Côte d’Azur, 06300 Nice, France
Received: 22 July 2016
Accepted: 16 November 2016
Context. The issue of the long term dynamics of Jupiter family comets (JFCs) involves uncertain assumptions about the physical evolution and lifetimes of these comets. Contrary to what is often assumed, real effects of secular dynamics cannot be excluded and therefore merit investigation.
Aims. We use a random sample of late heavy bombardment cometary projectiles to study the long-term dynamics of JFCs by a Monte Carlo approach. In a steady-state picture of the Jupiter family, we investigate the orbital distribution of JFCs, including rarely visited domains like retrograde orbits or orbits within the outer parts of the asteroid main belt.
Methods. We integrate 100 000 objects over a maximum of 100 000 orbital revolutions including the Sun, a comet, and four giant planets. Considering the steady-state number of JFCs to be proportional to the total time spent in the respective orbital domain, we derive the capture rate based on observed JFCs with small perihelia and large nuclei. We consider a purely dynamical model and one where the nuclei are eroded by ice sublimation.
Results. The JFC inclination distribution is incompatible with our erosional model. This may imply that a new type of comet evolution model is necessary. Considering that comets may live for a long time, we show that JFCs can evolve into retrograde orbits as well as asteroidal orbits in the outer main belt or Cybele regions. The steady-state capture rate into the Jupiter family is consistent with ~1 × 109 scattered disk objects with diameters D > 2 km.
Conclusions. Our excited scattered disk makes it difficult to explain the JFC inclination distribution, unless the physical evolution of JFCs is more intricate than assumed in standard, erosional models. Independent of this, the population size of the Jupiter family is consistent with a relatively low-mass scattered disk.
Key words: comets: general / celestial mechanics
© ESO, 2017
1. Introduction
The dynamics of Jupiter family comets (JFCs) is a topic of long-standing importance in celestial mechanics and solar system science. Most of the literature can be divided in to two categories: the tracing of orbital motions of individual JFCs over short or long periods of time by accurate integrations, and Monte Carlo simulations of the orbital evolution of large samples of fictitious JFCs over even longer periods. This literature is too rich to be reviewed here, so we give only a few examples.
Comprehensive catalogues presenting data on the orbital evolutions of individual JFCs appeared several decades ago (e.g. Carusi et al. 1985; Belyaev et al. 1986). These were based on the use of the relatively slow computers of that time, but the limitation to a time frame of several centuries is consistent with the short Lyapunov times of JFCs in general (Tancredi 1995). The number of known JFCs is now a few times larger, and new kinds of orbits have appeared, which were not known in the 1980s. However, there is no recent catalogue where the full sample of JFCs is presented in a similar way.
As long as the aim is to provide reliable data on these orbital evolutions, there is no use in extending the integrations over ~104 yr or more. Therefore, secular effects have to be studied using the statistics of large samples of fictitious objects. However, while many papers have dealt with relevant Monte Carlo simulations, they have concentrated on other aspects than the secular dynamics of JFCs. The main topic has been the statistical relation between the Jupiter family and its source populations, in particular the Edgeworth-Kuiper belt or the scattered disk (Levison & Duncan 1997; Volk & Malhotra 2008; Di Sisto et al. 2009). A very important goal was to place constraints on the lifetimes of JFCs to determine the steady-state capture rate into the Jupiter family in view of its observed population characteristics. These lifetimes have been found to be very short (Levison & Duncan 1997) and, therefore, very little attention has been paid to secular dynamics, which remain largely unexplored. We note that some insight into the secular dynamics of Halley-type comets was reached in a paper by Bailey & Emel’yanenko (1996), but this has not been followed up by any similar study of JFCs.
We have undertaken a massive set of long-term orbital integrations for JFCs within a project devoted to clarifying the cometary contribution to the late heavy bombardment. The use of the results for that purpose is described in a companion paper (Rickman et al. 2017, hereafter Paper II). Here we concentrate on the dynamics by studying several problems that concern secular behaviour. One is how JFCs may evolve to occupy different kinds of untypical orbits and how frequently this occurs in view of possibly explaining some interesting, observed objects. Another is to characterize the dynamical lifetimes and the interplay between the Jupiter family and its neighbouring populations, like Centaurs and Halley-type comets. For reference, we consider the results of neglecting physical evolution (purely dynamical model) but concentrate on those obtained by including the mass loss due to ice sublimation and dust outflow (erosional model). An important outcome is a new determination of the average physico-dynamical lifetimes of JFCs in different kinds of orbits, and a corresponding derivation of the steady-state capture rate into the Jupiter family.
In Sects. 2 and 3, we describe how we construct our basic sample of orbital evolutions for the JFCs in terms of initial orbits and integrations, respectively. Section 4 is devoted to lifetimes and end states, neglecting the physical erosion effects. In Sect. 5, we investigate the residence times in different ranges of perihelion distance, as well as the steady-state capture rate for the Jupiter family – both with and without the effects of surface erosion. We also consider the distributions of inclinations, nuclear sizes, and ages in the steady-state Jupiter family. In Sect. 6, we present our results on the production of retrograde comets within the Jupiter family. Section 7 explores the production of Encke-like objects by orbital deflection of JFCs at close encounters with terrestrial planets and, in Sect. 8, we study the incursions of JFCs into the outer asteroid belt plus the Cybele and Hilda regions. We discuss our results and draw our conclusions in Sect. 9.
2. Initial orbits
The transfer of cometary objects into inner planet-crossing orbits as a consequence of giant planet migration that was caused by the dynamical instability of the Nice Model was simulated by Brož et al. (2013) in an attempt to place constraints on the cometary flux through the asteroid Main Belt. From these calculations we have access to a complete sample of orbital elements for 6014 fictitious objects that arrived for the first time into perihelion distances that were less than 3.9 au. These came from an initial sample of 27 000 objects in the trans-planetary disk, thus representing 22% thereof. A small fraction had very large semi-major axes or very high inclinations, but we decided to exclude those from our study.
Our criterion was to include only orbits with period P< 20 yr and Tisserand parameter TJ> 2 with respect to Jupiter. A total of 820 orbits were thus excluded, out of which more than 99% had P> 20 yr and about 19% had P> 200 yr. This left us with 5194 orbits, and from these we deleted a randomly chosen set of 194 to arrive at a final sample consisting of 5000 initial orbits. Figure 1 shows the distributions of semi-major axes (a), perihelion distances (q), inclinations (i), and Tisserand parameters (TJ) for the finally retained sample.
 |
Fig. 1 Histograms of initial elements for the 5000 orbits used in this study. In the four panels we show the semi-major axes (upper left), perihelion distances (upper right), inclinations (lower left), and jovian Tisserand parameters (lower right). |
The cutoff at P = 20 yr is clearly seen in the a distribution, while at TJ = 2 the frequency is already close to zero. The a distribution features gaps at the 2:1, 3:2, and 1:1 mean motion resonances with Jupiter. These occur because the dumping of results in the Brož et al. (2013) integrations was not done at every orbit. Hence the orbits that we use are not strictly the first ones with q < 3.9 au. This means that objects captured into resonant orbits at close encounters may have left the resonance during a following encounter. In addition, there may be stable regions at the resonances that are not at all populated by close encounters.
The q distribution shows the predominance of values not far from the considered limit at 3.9 au. Direct captures into much smaller perihelion distances are rare, and less than 6% of our orbits have q < 2 au. The i distribution looks similar to that of the present Jupiter family, which is not unexpected since the dynamical origin of the objects is similar in both cases. The Tisserand parameters are rarely below 2.4 and peak in the range 2.8−3.0. As in the present Jupiter family, a small fraction (6%) are found between 3.0 and 3.1.
Finally, each of the 5000 sets of elements (a,q,i) had to be associated with angular elements (Ω,ω,M) corresponding to the longitude of the ascending node, argument of perihelion, and mean anomaly at the epoch, respectively. The actual values of these parameters were not known to us, and we applied a cloning technique, whereby 20 sets of random, uniformly distributed values on the interval [0,2π] were chosen for each (a,q,i) combination. Hence, in total, our initial sample consisted of 100 000 orbits.
3. Orbital integrations
Our dynamical model consists of the Sun, four giant planets – all treated as point masses – and the cometary object, which is treated as punctual and massless. Masses and radii of the former are taken from the JPL DE424 ephemeris1, whereby the solar mass is increased by the masses of the four terrestrial planets and the Moon. Only the Newtonian gravitational force is considered. The initial conditions for the heliocentric motions of the planets are also taken from DE424, and the same epoch is used for the cometary initial orbits. The use of current orbits for the giant planets means that we study a dynamical system essentially equivalent to that of today’s JFCs, and we can hence use the outputs of our integrations as relevant to current JFC dynamics.
The equations of motion for the six-body problem (Sun + four planets + test object) were integrated into a barycentric, ecliptic reference frame, and all the input and output elements for the test objects are heliocentric and ecliptic. The osculation epoch of the output elements is typically within one week of the actual perihelion time and, thus, our fundamental data base for JFC dynamics consists of the full set of osculating orbital elements near the perihelion passages of our test objects. We allow each test object to perform a maximum of 100 000 revolutions around the Sun, but the integrations were ended prematurely in case the test object reached a semi-major axis of more than 1000 au, reached an eccentricity exceeding 0.9999, or collides with the Sun or a planet. Information on end states and lifetimes is given in Sect. 4.
We used the classic Radau integrator RA15 (Everhart 1985). This works to 15th order. We kept 19 terms in the series and specified nine significant digits and an internal accuracy of 1 × 10-12. This method serves well for integrations of cometary orbits, since the time step is automatically adjusted at close encounters to keep the specified accuracy. Though not symplectic, it thus practically conserves the energy of the system, and we verified that the relative change of this energy oscillates between 10-13 and 10-12 in absolute value.
In Fig. 2, we show bivariate distributions of orbital elements at the first and last (100 000th) perihelion passages in the (a,e) and (a,i) planes for the 4418 surviving comets. These share the property of having entered into relatively stable orbits, where they are likely to spend a long time. The red dots indicate the initial orbits and other colours show the final ones, split into different ranges of TJ. In the left-hand panels, the semi-major axis extends to the maximum value of 7.36 au for the initial orbits, while the right-hand panels show larger values up to 100 au for the final orbits.
 |
Fig. 2 Distributions of initial and final orbital elements for surviving comets. Upper panels: eccentricity vs. semi-major axis; lower panels: inclination vs. semi-major axis; left panels: periods below 20 yr; right panels: periods above 20 yr. Red dots show initial orbits. For the final orbits, sky-blue dots indicate TJ < 2, dark blue dots indicate 2 < TJ < 3, and green dots indicate TJ > 3. |
The regions populated by final orbits in these parametric planes are, in order of increasing semi-major axis: the Jupiter family with some concentration around the 2:1 resonance, the Hilda and Thule-type mean motion resonances (3:2 and 4:3), the quasi-Trojan orbits (1:1 resonance), and the Centaur and scattered disk populations shown in the right-hand panels.
Several interesting features can be seen. One is the excitation of inclinations that takes place during the 100 000 orbits, thereby leaving some surviving comets on high-inclination and even retrograde orbits. These are particularly common for the smaller semi-major axes (left-hand panels). These type of evolutions are the subject of Sect. 6. Another remarkable feature – already noted in earlier papers that will be cited below – is that the long lives of the survivors have allowed many of them to diffuse in jovian Tisserand parameter, not only into TJ < 2, as in the cases just mentioned, but also into TJ > 3. The latter phenomenon causes comets to intrude into orbital domains that are classically considered to belong to asteroids. Particularly evident is a group of survivors at the 5:2 resonance with Jupiter reaching eccentricities down to 0.2 and aphelion distances down to 3.4 au. The general phenomenon is caused by resonant interactions with Jupiter and will be analyzed in Sect. 8.
4. End states and lifetimes
The cumulative distribution of survival times for our entire sample of comets is shown in Fig. 3. The median lifetime is ~6400 revolutions, and the quartiles are at ~2500, and ~16 000 revolutions. The 4418 final survivors after 100 000 revolutions correspond to 4.4%. As mentioned, these survivors have to avoid both considered end states: (a) ejection or diffusion into orbits with a > 1000 au; (b) collision with the Sun or a giant planet.
We checked for collisions with great care. At each close encounter, we surveyed the distance between the comet and the nearby massive body at each RA15 substep, and a collision was registered only if this distance decreased below the physical radius of the body. Some grazing impacts may thus have been missed, but the step size is carefully monitored by the RA15 code so the trajectory is densely sampled. The risk of missing an impact is therefore very small. In total, we found that 2.6% of our comets (2628) experienced collisions and, of these, 736 involved the Sun, 1698 involved Jupiter, 192 involved Saturn, and two involved Uranus. There was no collision with Neptune. We note that many close encounters would have implied a risk of tidal break-up owing to the passage inside the Roche limit, but this risk is difficult to evaluate, and we chose to let the comets survive intact.
From the numbers given above, we infer that 93% of the comets (to be precise, 92 954) experienced the ejection/diffusion end state, so this is by far the dominant fate of the comets. While, in some cases, the comets may return to orbits with a < 1000 au, we think that the return to actual Jupiter family orbits is very unlikely. At the moment when this end state was reached, the majority (64%) were Jupiter-crossing in the sense of q < 5.5 au, while the rest got ejected from Centaur or scattered disk orbits. In terms of the jovian Tisserand parameter, about 80% had 2 < TJ < 3, while the rest were mainly of Centaur or scattered disk type with TJ > 3.
In fact, while none of our initial orbits were of Centaur type, we found that about 75% of the comets made at least one excursion into the Centaur population. We define this by q > 5.5 au and a < 30.1 au. More than 60% spent at least 100 orbits there, and about 40% spent at least 1000 orbits. Transits in both directions were common; Jupiter family comets becoming Centaurs or Centaurs being captured into the Jupiter family. The same comet may experience this repeatedly during its evolution.
 |
Fig. 3 Cumulative fraction of comets in our entire sample with dynamical lifetimes exceeding the given number of orbits. |
Numbers of comets in our integrated sample, divided into three different ranges of jovian Tisserand parameter, concerning both the starting orbits and the orbits at the end of the integrations.
In Table 1, we summarize our results concerning the stability of the jovian Tisserand parameter. Transitions across the imposed borders at TJ = 2 and TJ = 3 are seen to occur quite frequently – this was illustrated for the special case of survivors in Fig. 2. Here we see that comets starting with TJ > 3 are vulnerable to transits into the TJ < 3 range. Comets starting with 2 < TJ < 3 are more stable, but about 18% of these evolve into TJ > 3 and less than 2% into TJ < 2. There is an apparent discrepancy between our results and the relative stability of the Tisserand parameter found by Levison & Duncan (1997). The simple explanation is that the statistics shown in Table 1 is derived by neglecting physical evolution, while Levison & Duncan concluded that the TJ < 2 comets (referred to as Halley Type Comets, HTCs) found in their simulation had made the transitions too late to be still visible.
There are two kinds of orbits with TJ > 3, which get occupied by comets in our sample. One kind has semi-major axes around 3 au and low inclinations; these are pushed into decreasing eccentricities by resonances, thus gaining angular momentum and evolving into TJ > 3. The other is under the control of Saturn, Uranus or Neptune, belonging to the Centaur or scattered disk populations with perihelia significantly outside Jupiter’s orbit. As long as the inclinations stay reasonably low, these objects have TJ > 3. Both groups can be identified in Fig. 2 – the first one in the left hand panels, and the second one mainly in the right hand panels. Although they seem about equally populated among the survivors, in total the Centaur and scattered disk group contains 98% of the end states and the inner group only 2%.
5. Steady-state Jupiter family
For some purposes, we may put all the orbital revolutions performed by comets into a common pool and regard the currently observed Jupiter family as a random sample from this pool. This means that we assume the Jupiter family to be in a steady state, statistically speaking, and the chronology of the computed evolutions is of no relevance.
We will now derive some results for such a steady-state Jupiter family, using two assumptions. In one case we disregard all the effects of physical evolution of the comet nuclei like we did in Sect. 4. In the other case we consider the nuclei to shrink monotonously to smaller radii by surface erosion, and a criterion of radius R > 1 km is usually imposed for the steady-state Jupiter family.
5.1. Capture rate and perihelion distance
With the steady-state assumption, the average number of JFCs residing in any domain of the parametric space (a,q,i) at any particular time is proportional to the total time spent by our sample comets inside that domain. In Table 2, we present our results concerning the distribution of perihelion distance in the Jupiter family. For this purpose we only consider those orbits in our data base, that have TJ > 2 as the criterion for JFCs. We accumulate the periods of all these orbits within different ranges of q. We also include the distribution of the minimum values qmin reached by the individual comets in orbits with TJ > 2. The latter distribution is shown graphically in Fig. 4.
For different distances (d) from the Sun, we list the relative numbers of steady-state JFCs (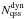 ) with q < d, and the relative numbers (
) with q < d, and the relative numbers (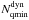 ) of JFCs that penetrate at least once inside d during their orbital evolutions.
) of JFCs that penetrate at least once inside d during their orbital evolutions.
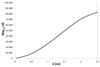 |
Fig. 4 Cumulative distribution of the minimum perihelion distances reached by the comets in our sample, assuming unlimited physical lifetimes. |
The data presented in Table 2 and Fig. 4 correspond to the assumption that the nuclear radii of comets remain constant, so that the comets have unlimited lifetimes. We find that the steady-state distribution of q is steeper than that of qmin. Relative to the number of comets with perihelia within 1.5 au, only 6.6% have perihelia within 0.5 au. On the other hand, about 17% of the comets with qmin < 1.5 au attain qmin < 0.5 au. The erosional model and its results – also included in the table – is described in Sect. 5.2.
We also estimate the required capture rate into the Jupiter family to maintain its current population in a steady state. For this we use literature values for the number of observed or observable objects. We first deal with the assumption of unlimited physical lifetimes, which deviates from earlier practice, where JFCs were assumed to end their visible lifetimes either abruptly (Levison & Duncan 1997) or gradually, in terms of a fading law (Brasser & Wang 2015). It is beyond the scope of this paper to discuss the rationale for or against such a visibility function. By neglecting it, we overestimate the observable lifetimes, but we will make another estimate allowing for the effects of erosion in Sect. 5.2. In addition, we explicitly account for comet dormancy as follows:
Comets are known to exist in a dormant state, where the activity may be sealed by a refractory surface layer (Kresák 1987; Jewitt 2004). Hence, when using our integrated orbits, we have to take into account that these may belong to either active or dormant comets. We concentrate on perihelion distances below 1.5 au since, otherwise, the observed samples would be far from complete. Di Sisto et al. (2009) listed 17 active JFCs in these types of orbits and nuclear diameters D > 2 km and corrected for incompleteness by stating the total number to be 25 ± 5.
Whitman et al. (2006) listed 17 near-Earth objects (q < 1.3 au) with D > 2 km in JFC-like orbits, which may be mostly or entirely dormant comets. Also, there are close to 1 000 NEOs with D > 1 km (Mainzer et al. 2014), and if their CSD index is −1.5 (Bottke et al. 2002), ~300 have D > 2 km. If 6% of these are of cometary origin (Bottke et al. 2002), we may take the number of dormant JFCs with q < 1.3 au to be about 18. Di Sisto et al. (2009) estimated only 10 ± 2 active JFCs when restricting the perihelion range to q < 1.3 au, and this may indicate a dormant/active ratio around two. When applying this, we find 75 ± 15 JFCs with q < 1.5 au and D > 2 km by merging the active and dormant objects.
We find that, for all the 83 013 JFCs that came to perihelia within 2.5 au, the total time spent with q < 1.5 au is T = 7.41 × 108 yr, corresponding to an average of 8.93 kyr per comet. Dividing the above number by this lifetime, we estimate that the steady-state capture rate into the visible Jupiter family (q < 2.5 AU) is (8.4 ± 1.7) × 10-3 comets per yr with D > 2 km (i.e., 0.7−1.0 comets per century). Let us now estimate how the steady-state capture rate and JFC orbital distribution are affected by the erosion of the nuclei.
5.2. Effects of surface erosion
Our simple model of cometary activity considers this to be caused by free surface sublimation of H2O ice and accompanying release of an equal mass of refractories (dust) into space. We use a thermal model that treats the nucleus as a rotating ice-dust sphere, where the whole surface is covered by an equal fraction of exposed ice. It takes into account the absorption of sunlight, thermal emission, heat conduction and water ice sublimation. The insolation varies with cometocentric latitude, heliocentric distance (r) and the diurnal cycle. We solve the heat diffusion equation with two boundary conditions: the surface energy balance and the insulating condition for the interior of the nucleus. The scheme of the thermal model is essentially the same as developed by Froeschlé & Rickman (1986) and Rickman & Froeschlé (1986).
The thermal emissivity is taken as 0.95, the rotation period of the nucleus is assumed to be 12 h, and we use a low thermal inertia (20 W s1/2 m-2 K-1). Seasonal effects are avoided by taking the spin axis as perpendicular to the orbital plane. We hence get the H2O-free sublimation flux as a function of r in the form of an interpolation table ranging from 0.3 to 6 au (the perihelion and aphelion distances of the modelled comet). For smaller distances we use a r-2 extrapolation. By means of these results, we integrate the sublimation flux over an arbitrary orbit using the true anomaly as an integration variable. As explained in Paper II, we scale this flux by a factor of 0.05 to account for the average level of activity of JFCs.
Thus, we compute the accumulated amount of mass loss per unit surface area over an entire orbital revolution for any given combination of orbital elements (a,e). Using an assumed cometary density of 500 kg m-3, the thickness of the lost surface layer is obtained. For any orbit in our data base we may add up the lost thicknesses for all the preceding orbital revolutions by the same comet with significant sublimation, and hence we get an estimate of the total, accumulated erosion depth E that occurred from the time the comet entered its initial orbit.
If we consider, as above, all the orbits in our data base with q < 2.5 au and TJ > 2. We thus have a large set of orbits (i = 1,...,N), each characterized by two quantities: the erosion depth Ei and the period Pi. For a comet with a certain orbit to have nuclear radius R > 1 km, it must have been captured as a co-called parent comet, with an initial radius Ro > 1 km + Ei. We use a power law with index −α for the cumulative radius distribution of the initial comets, and we consider a standard capture rate of comets with Ro > 1 km. Therefore, we compute a weight factor 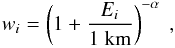 (1)which signifies that the orbit in question is shared by 1 /wi comets, captured with Ro> 1 km. Each of these thus has a corresponding residence time equal to wiPi.
(1)which signifies that the orbit in question is shared by 1 /wi comets, captured with Ro> 1 km. Each of these thus has a corresponding residence time equal to wiPi.
In Sect. 5.1, we computed the total residence times T spent by our sample comets in different ranges of perihelion distance by adding all the relevant orbital periods Pi from our data base. This was the basis for the relative population numbers listed in Table 2 under label 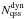 . Generally, we can define the total residence time by
. Generally, we can define the total residence time by 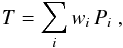 (2)and the numbers
(2)and the numbers 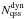 were obtained by putting wi ≡ 1. Now we include two more lines in Table 2 labeled
were obtained by putting wi ≡ 1. Now we include two more lines in Table 2 labeled 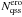 , where we use wi from Eq. (1) as found with α = 1.5 and 2.5. These values bracket the likely range of the CSD slope for JFCs according to published literature (Morbidelli & Rickman 2015). The effect of erosion is very clear. Comets with smaller perihelion distances, in general, have larger erosion depths, thus requiring larger parent comets, which reduces their number. Therefore, the steady-state number of JFCs with q< 2.5 au is from 4.95 to 5.6 times the number with q< 1.5 au, when erosion is accounted for, compared to 3.6 times without erosion.
, where we use wi from Eq. (1) as found with α = 1.5 and 2.5. These values bracket the likely range of the CSD slope for JFCs according to published literature (Morbidelli & Rickman 2015). The effect of erosion is very clear. Comets with smaller perihelion distances, in general, have larger erosion depths, thus requiring larger parent comets, which reduces their number. Therefore, the steady-state number of JFCs with q< 2.5 au is from 4.95 to 5.6 times the number with q< 1.5 au, when erosion is accounted for, compared to 3.6 times without erosion.
Finally, we have to update our estimate of the steady-state capture rate of JFCs by including the erosion. We still consider the whole set of orbits with q< 1.5 au, now using the parameters Ei and Pi. The total residence time of comets with q< 1.5 au is now found from Eq. (2) with the relevant wi. It is found to be T = 1.83 × 108 yr for α = 1.5 and T = 1.15 × 108 yr for α = 2.5. These numbers translate into an effective lifetime per comet, captured with Ro> 1 km, of 2.20 kyr and 1.39 kyr, respectively. Thus, we now estimate a higher capture rate of 3.4 ± 0.7 or 5.4 ± 1.1 comets per century with D> 2 km, corresponding to the two α values.
Di Sisto et al. (2009) report a mean lifetime of 1.335 kyr for JFCs with Ro> 1 km and q< 1.5 au, using the model of physical evolution that they found to give the best fit to observed JFC orbits. This involves rapid destruction owing to a very high rate of splits, in addition to a contribution by ice sublimation, where the latter is similar to our model. Comparison of our results is not straightforward as a result of several differences in assumptions and procedures. However, our lifetimes are clearly longer (as expected), since the values given above are averages over all comets that entered into orbits with q< 2.5 au. According to Table 2, these comets are 1.683 times as numerous as those considered by Di Sisto et al., so our lifetimes should be multiplied by this number to make the averages comparable.
5.3. Inclinations
Levison & Duncan (1997) compared the inclination distribution of the observed JFCs with that of the captured comets resulting from their simulations. They then found that a reasonable agreement required the assumption of limited visible lifetimes for the simulated comets (see Sect. 5.4). This prompts us to make a similar investigation based on our results.
We have used the JFC nuclear radius determinations by Tancredi et al. (2006) to find our observed sample. Ideally, we wanted JFCs with q< 2.5 au and D> 2 km, but to get a sufficient sample size, we were forced to include comets with D> 1.6 km – this gave a sample of 69 comets. Their cumulative inclination distribution is compared with three curves derived from our simulations.
In one case we use the whole sample of 100 000 orbital evolutions, and we select the comets with qmin< 2.5 au. For each of these we record the value of the inclination for the first orbit with q< 2.5 au and 2 <TJ< 3, in case such an orbit exists. This yields the initial inclination distribution of the visible JFCs in the sense of Levison & Duncan (1997).
In the second case, we obtain the steady-state JFC inclination distribution disregarding physical evolution in the same way that we derived the distribution of perihelion distances in Sect. 5.1, using the total residence times in different inclination bins without weighting the orbits. In the third case we do the same with the erosional model by using the products wiPi, where wi is now found from 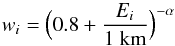 (3)to adhere to the same radius limit as for the observed sample. This yields the steady-state JFC inclination distribution, when the erosional effects are taken into account.
(3)to adhere to the same radius limit as for the observed sample. This yields the steady-state JFC inclination distribution, when the erosional effects are taken into account.
 |
Fig. 5 Cumulative JFC inclination distributions. The red diamonds refer to observed JFCs with D> 1.6 km. The green curve shows the initial distribution of JFCs with q< 2.5 au. The blue curve shows the steady-state distribution excluding erosion, and the orange and cyan curves show the same, including erosion, using α = 1.5 and 2.5, respectively. |
In Fig. 5, we present the mentioned comparison. The result is very striking. The observations are very well fitted by the extreme option of choosing only the initial, visible orbits, while all the other models fail. Since we know that the Jupiter family gets dynamically heated with time owing to the scattering at close encounters with Jupiter, we can only conclude that the parameters of the model we employ would have to be tweaked to the extreme to fit the observed inclination distribution of JFCs.
The reason that Levison & Duncan (1997) found a good fit by assuming the lifetimes of their modelled JFCs to be limited to a maximum of 12 000 yr, thus allowing the comets to survive for many hundred orbits (while we find essentially vanishing lifetimes) is that they used a very flat version of the scattered disk, while we use a version that is much more excited. In fact, our comets arrive into the visible Jupiter family with an initial inclination distribution that is already very close to that of the observed comets (see Fig. 1). Very little further dynamical heating is thus allowed.
The question is, is this conclusion realistic? One consequence would be that the JFC lifetimes are extremely short. We saw in Sect. 5.2 that the average lifetime in the erosional model is about 2000 yr depending on α. Since we apparently need much shorter lifetimes, the required capture rate for the observed Jupiter family is very large, and it is far from clear that this is consistent with a reasonable mass of the scattered disk (cf. Brasser & Morbidelli 2013).
We find it likely that the erosional model, like any model with a monotonously decreasing visibility function, is oversimplified. If one would use an alternative model including temporary deactivation or dormancy of comets with rejuvenations occurring by mantle blow-off in connection with strong jovian perturbations (Rickman et al. 1991), it seems possible that the observed JFCs are not as young as they appear – they could be recently reactivated by downward jumps of the perihelion distance. In which case, they would have a natural tendency to favour low inclinations. However, this is just a suggestion, which remains to be confirmed or rejected by further studies.
5.4. Ages and sizes
The above-described erosion depths were derived using all the revolutions previous to each particular orbit, counting from the start of the integrations. Meanwhile, when analysing the capture of comets into the Jupiter family, the usual assumption is that those comets are fresh by the time they first enter into perihelion distances smaller than 2.5 au. Therefore, in principle, we may have overestimated the erosion depths and hence also the capture rate. However, we have verified that the amounts of erosion before the first entry into q< 2.5 au are indeed negligible.
In the classical paper by Levison & Duncan (1997), the authors found that the orbital distribution of the Jupiter family in their capture simulations had an optimum fit to that of the observed JFCs if they considered the comets to be visible only for 12 000 yr after the first entry into q< 2.5 au. This can be considered as the maximum age of JFCs according to their results. The erosion model that we apply in fact leads to an age distribution for our steady-state Jupiter family and to an orbital distribution that may or may not agree with observations. However, we emphasize that it was not chosen to produce a good fit to the orbits. It reduces the ages and limits the lifetimes, but it is not a realistic model for the actual physical evolution. In our opinion, formulating such a model remains a task for the future.
In comparison with Levison & Duncan (1997), we calculated the JFC age distribution in the following way. We consider comets with q< 1.5 au and R> 1 km. Each relevant orbit in the pool resulting from our integrations has an age Ai, which we compute by adding all the orbital periods previously spent with q< 2.5 au. The distributions shown in Fig. 6 are age histograms, where each orbit of the pool contributes by wi = 1 for no erosion and by its actual value of wi according to Eq. (1) for each of the two erosional models.
 |
Fig. 6 Histogram representing the distribution of ages (see main text) of steady-state Jupiter family comets with q< 1.5 au and nuclear radii larger than 1 km. The age scale is artificially cut at 125 kyr for clarity. For each bin, we show the number of orbits in our integrated sample satisfying the above criteria. |
 |
Fig. 7 Number of revolutions in retrograde orbits found in all our integrations, as a function of (a,q) in the left-hand panels and (a,i) in the right-hand panels. The top panels show the uncorrected numbers based on the dynamical evolutions, while the lower panels show the effective numbers corresponding to eroded nuclei of radii larger than 0.1 km. |
The decrease in the numbers with increasing age is a natural consequence of the loss of comets; in the model with no erosion, this is due to dynamical effects, while the physical losses dominate in the other two models. The age distribution for the first model clearly demonstrates the drastic effect of imposing an age limit at 12 kyr (Levison & Duncan 1997). The median age in this case is as large as 37.4 kyr. We also see that our erosional model yields age distributions in better agreement with the Levison & Duncan (1997) limit. In this case, the median age is 16.8 kyr for α = 1.5 and 12.2 kyr for α = 2.5. Still, most comets are older than the maximum allowed age according to Levison & Duncan.
When using the erosional model, we have to pay attention to the fact that the size distribution for the JFCs may differ from that of their source population because of the physical evolution of the nuclei. We have investigated this and the analysis is presented in Paper II. The basic result is that the JFCs have a somewhat shallower size distribution than their precursors have at the moment, when they reach q< 3.9 au. The difference of the power-law index amounts to about 0.2−0.3 for the slopes under consideration, which is in agreement with an earlier estimate by Weissman & Lowry (2003). Thus, the α values that we use for the initial comets appear to be slightly too small. However, in view of the uncertainty over the real JFC α value, we do not attach much importance to this deviation.
6. Production of retrograde JFCs
Figure 2 displays 12 comets that evolved into retrograde orbits and stayed retrograde until the 100 000th revolution. In total, 417 comets performed at least one revolution with i> 90°. In many cases, only single or just a few revolutions in marginally retrograde orbits were performed, but we looked specifically for sequences comprising at least ten retrograde revolutions, where the maximum inclination was at least 95°. Calling these retrograde visits, we count 514 of them, and no more than nine are performed by any single comet.
The majority of the retrograde visits occurred after the comets had completed a large fraction of 100 000 revolutions. These comets therefore differ from the average comets by their longevity (see Fig. 3). This means that erosion may play an important role in the evolution of retrograde comets (see below). Moreover, we find that most of the 417 comets had their integrations ended by collisions with the Sun: 299 in total, whereof 177 were still retrograde, and 122 had returned to prograde orbits. In addition to the 12 retrograde survivors, 25 retrograde comets became survivors in the prograde state. The rest were lost prematurely by ejection or diffusion, mainly in the prograde state.
 |
Fig. 8 Double histogram showing, in red, the distribution of initial inclinations of the 417 retrograde comets and, in blue, that of the whole sample of 5000 starting orbits. |
In Fig. 7, we show the distributions of (a,q) and (a,i) for the nearly 1.9 million revolutions in retrograde orbits performed by the 417 comets. We show both the unweighted distributions and those corrected for erosion. The retrograde comets are seen to be distributed more or less like the Jupiter family in the (a,q) plane. In fact, some retrograde orbits exist beyond the 12 au limit of the diagram, including a few that are even found close to the orbit of 1P/Halley.
There is a concentration of orbits near the 1:1 resonance with Jupiter, especially at very high eccentricities, but orbits near the 2:1 and 3:2 resonances are relatively rare. The main concentration of unweighted, retrograde orbits is found at the smallest semi-major axes on either side of the 2:1 gap. These orbits are strictly limited to high eccentricities and aphelion distances Q> 5 au. As a consequence, the perihelion distances are small.
For this reason and owing to the long timescales, the comets are very vulnerable to physical destruction. This fact is clearly illustrated by making a comparison with the effective numbers shown in the lower panels. The latter numbers have been derived for a steady-state population with radii ranging all the way down to 0.1 km by modifying Eq. (1) with α = 1.5. Obviously, the weight factors are very small because the comets have undergone extensive erosion and their parents must have been very large.
This fact was noted by Di Sisto et al. (2009), who find a few transitions into retrograde orbits for their JFC sample, however none of these comets survived the assumed physical destruction effects long enough to actually become retrograde. Some similar transitions were also found by Levison & Duncan (1997), but like all the HTCs produced in their simulation (see above), these retrograde comets would no longer be visible. The reason why we also show the unweighted orbital distribution is to highlight the importance of the physical evolution, while keeping in mind that the way this works in reality is still not fully known.
By calculating the sum of all the retrograde orbital periods, we find that, neglecting erosion, the steady-state number of retrograde JFCs2 with D> 2 km is 0.02 times the total number with q< 1.5 au and similar sizes, i.e., about 1.5. Including erosion, and using α = 1.5, we obtain only about 0.3 comets down to a limiting radius of 0.1 km. If we use α = 2.5, the number is even smaller. Hence, in the framework of our erosion model, we do not expect any retrograde comet to exist of the kind we have discussed.
In the JPL Small Body Database3, at the time of writing, three comets with periods less than 20 yr and retrograde orbits are listed – 333P/LINEAR, P/2006 R1 (Siding Spring) and P/2013 AL76 (Catalina). Their inclinations are about 132°, 160° and 145°, respectively. The first-mentioned object may have a nuclear radius of a few km, while the others appear to have sub-km nuclei. According to our above prediction, they would likely be HTCs by origin, but this suggestion would also need to be verified. No firm verdict on their origin is possible, until the realism of our erosion model is confirmed, and the evolution of HTCs is scrutinized in a way similar to the present scrutiny of JFCs.
With regard to the dynamics of JFCs transiting into retrograde orbits, in Fig. 8 we show the relative distributions of initial inclinations for the 417 retrograde comets and the whole sample of 5000 original orbits. A certain preference for high initial inclinations of comets that become retrograde can be noticed, but evolutions starting from very low inclinations are not excluded.
Greenstreet et al. (2012) find by long-term integrations that NEAs sometimes transit into retrograde orbits and, to some extent, our results for JFCs can be compared to theirs for NEAs. These authors integrated fictitious asteroids from Main Belt resonant sources until becoming NEAs (q< 1.3 AU) and further on until removal from the system. They showed that, in the majority of cases, the transitions into retrograde orbits involved NEAs temporarily placed in the 3:1 and 4:1 mean motion resonances (MMRs) with Jupiter. The mechanism was not fully elucidated, but the objects were said to transit from a large amplitude, prograde Kozai cycle into another large amplitude, retrograde Kozai cycle by a continuous crossing of the i = 90° limit.
In Fig. 9, we plot the semi-major axis vs. the eccentricity of our retrograde JFCs at the last perihelion before their retrograde visits. It is obvious that our comets do not behave like the NEAs at all. At the moment they transit, they are always beyond the 3:1 resonance, and they show no affinity for the main MMRs. The two trends exhibited by this diagram are that the transit orbits are always Jupiter crossing, and that high eccentricities are favoured.
 |
Fig. 9 The eccentricities (e) and semi-major axes (a) of 514 JFC orbits immediately preceding retrograde visits. The tangency curves with respect to Jupiter’s current orbit are shown as full-drawn curves for Q = 4.95 au and q = 5.45 au, and vertical dashed lines indicate the main MMRs with respect to Jupiter. |
Since most of the orbits in question have high eccentricities and inclinations, the Jupiter-crossing property does not guarantee the possibility of close encounters with the planet. To evaluate this possibility, the best tool is the MOID, i.e., the minimum orbit intersection distance (ℳ), by the method of Wiśniowski & Rickman (2013). Our integration output does not allow us to immediately calculate the real MOIDs in retrospect, so we use an approximate analysis. We calculate the MOID (ℳo) between each comet orbit and a circular orbit with aJ = 5.2028 au in the ecliptic plane. This is enough to give a first indication about the role of close encounters in triggering the flips into retrograde orbits.
The results are shown in Fig. 10. We see a clear concentration to very small values, which certainly would not have existed, unless the flips were caused by close encounters with Jupiter. For the 514 retrograde visits we find 320 cases of ℳo< 0.25 au, which means that the true MOID with Jupiter’s eccentric orbit could be close to zero. We take this to indicate a significant fraction of close encounters with Jupiter providing the final gateway into retrograde orbits. However, 72 retrograde visits start with ℳo> 1 au, showing that in another significant fraction of cases, close encounters are not involved.
 |
Fig. 10 The MOID values of 514 JFC orbits immediately preceding retrograde visits with respect to a circular jovian orbit in the ecliptic plane. These are referred to as ℳo in the text. |
A full analysis of the dynamics of prograde-retrograde transitions of JFCs is deferred to a future paper, but we now offer a preliminary discussion, based on visual inspection of diagrams that show the long-term evolutions of orbital elements for JFCs with retrograde visits. A few such diagrams are shown in Fig. 11. Two comets are shown, both of them starting out from low inclinations. They display two routes into high-inclination, eventually retrograde orbits. On the one hand, we recognize the action of secular resonances, whereby the inclination and eccentricity are pumped up during the time the nodal or apsidal lines are locked in resonance with Jupiter or Saturn. On the other hand, we also see jumps caused by close encounters, whereby the inclination suddenly increases substantially, and the semi-major axis undergoes a sudden decrease. Obviously, the two mechanisms may collaborate in causing flips from prograde into retrograde orbits, because each of them may bring a comet from a low to a high inclination, thus facilitating the job for the other one to bring about the final flip. Of course, the dynamics is reversible, so that transitions from retrograde into prograde orbits also occur.
 |
Fig. 11 Temporal evolutions of orbital elements for two comets that made significant visits into retrograde orbits, using the number of orbits as time variable. The time frames cover several thousand orbits before the comets become retrograde and significantly less afterwards. Two panels are shown for each comet: the upper panel exhibits the semi-major axis a (au), the eccentricity e, the inclination i and the argument of perihelion ω, while the lower panel shows the quantity Lz = (1−e2)1/2cosi, expressing the vertical component of the angular momentum, and the critical arguments of the ν16 and ν5 secular resonances. The colour codings are shown to the right. Angles are labelled on the left and the other quantities on the right. |
Let us provide some more details about Fig. 11. The upper two panels show a comet, which initially had i = 7°. After 8000 revolutions, its inclination has increased substantially but remains smaller than 50°. Soon thereafter, the ν5 resonance causes an increase of the eccentricity, assisted by a close encounter with Jupiter during revolution No. 8471. After two minima caused by a Kozai cycle, the inclination starts climbing along with the eccentricity owing to simultaneous ν5 and ν16 resonances. Another close encounter with Jupiter during the 10 124th revolution kicks the eccentricity to nearly unity and starts a series of Kozai cycles, which lasts for thousands of revolutions. The eccentricity remains very high, and the maxima of the inclination reach ever higher values due to the ν16 resonance. A close encounter with Jupiter initiates a short retrograde visit, which is ended by another close encounter shortly before the comet collides with the Sun.
The lower two panels of Fig. 11 show a comet that initially had i = 19°. Largely because of the ν16 resonance, its inclination is almost 60° after 25 000 revolutions. During the following 4000 revolutions, there is a secular increase of eccentricity and decrease of inclination, related to the ν5, ν16 and Kozai resonances. Many close encounters add an important element of chaos to these evolutions. The most noteworthy of these occur during revolutions Nos. 29 340−29 342 and 29 625. The first brings the eccentricity to near unity. The second throws the comet from i = 6.1° to i = 133.7°, while decreasing the semi-major axis from 4.8 to 3.9 AU. The comet stays retrograde for thousands of revolutions afterwards.
7. Production of Encke-like objects
We now briefly describe and discuss an experiment that we performed to investigate the origin of objects in orbits similar to that of comet 2P/Encke, which are decoupled from close-encounter interactions with Jupiter. In their comprehensive study, Levison et al. (2006) find the action by terrestrial planets to work quantitatively through the orbital deflections caused by close encounters with Mars, the Earth, or Venus, combined with the action of the ν6 resonance to further decrease the perihelion distance. In our very extensive set of orbital integrations we could not include the terrestrial planets as gravitating objects in the N-body code. As a consequence, our dynamical model – as it stands – does not provide the transfer routes that may account for Encke-like objects. We then opted for a simulation of orbital deflections by terrestrial planets through Monte Carlo sampling, focussing on very close encounters.
We took the near-perihelion osculating elements for the comet orbit and the associated sets of planetary elements (see Paper II), and we computed the MOID for each comet-planet pair. From this computation, we also know the unperturbed approach velocity in case of a close encounter, and we can thus compute the collisional radius of the planet (Rcoll). In the case of ℳ < 5 Rcoll, there is a chance of an extremely close encounter with impact parameter Rcoll< ℐ < 5 Rcoll, and we evaluated the probability of such an encounter using the MOID method (Rickman et al. 2014).
There are about 230 000 such cases in total for the 100 000 comets, when followed throughout their dynamical histories and counting all the terrestrial planets as deflecting agents. To limit ourselves to a reasonable number of deflections, we randomly selected ~10% of the cases for further study. With a random, linear sampling of the timing of the encounter, we selected a random value of ℐ (with a square root distribution) on the interval [Rcoll,5 Rcoll]. The approach velocity vector is fully known, and we picked a random aiming point in the b-plane (Greenberg et al. 1988) at distance ℐ from the origin. We then applied the so-called matched conic section method (Everhart 1969) to calculate the deflection of the comet orbit owing to the attraction of the planet.
After deflection, the objects were integrated further, possibly until the 100 000th revolution in the usual six-body system, which includes the giant planets, but excludes the others. No further check for close encounters with terrestrial planets was made for the deflected comets. In Fig. 12, we present the resulting steady-state orbital distribution of these comets in the (Q,q) plane. The contributing comets have been weighted by their individual deflection probabilities. We limit this plot to the Encke-like domain defined by Levison et al. (2006).
 |
Fig. 12 Steady-state distribution of Encke-like comets over the parametric (Q,q) plane as found by our simulations. The arbitrary colour scale, as given on the right hand side, denotes the relative number of comets per cell in the diagram. |
The diagram exhibits a wide-spread fine structure in the form of resonant stripes, where comets have experienced secular eccentricity pumping. This sometimes goes in the direction of circularizing the orbits, but very often leads into the sungrazing end state. This structure would be smeared out in the plot by Levison et al. (2006; their Fig. 1b) but, most likely, in reality it does not exist. The small nudges given to the comets in their integrations would inhibit the long-term action of these resonances in most cases (see Valsecchi et al. 1995), while we introduced the artefact of leaving the comets entirely in the hands of the giant planets.
We find that deflected comets get dynamically ejected only if their starting semi-major axis is larger than 2.6 au. For smaller values, if Jupiter-crossing occurs, it is only for very high eccentricity, so encounters are rare and inefficient in changing the orbits. In these cases, collision with the Sun is very likely, and many of the survivors are “saved by the bell”, since our integrations stop after 100 000 revolutions. Looking at the statistics of end states for the deflected comets, we find a remarkably high probability (more than 12%) of collision with the Sun, and most of these belong to the above-mentioned category.
We derived the steady-state number of comets in the Encke-like domain and made a comparison with the results of Levison et al. (2006), which are quite different. In fact, using our first approximation to the transfer mechanism, we predict only 1/40 of the number of Encke-like comets found by Levison et al. (2006). Thus, our method is severely lacking in transfer efficiency, and several reasons for this are easily identifiable.
First, consider the limitation caused by cutting the integrations to a total of 100 000 revolutions. Compare this to the example provided by Levison et al. (2006) of a comet meeting their requirement for an Encke-like comet. Before this happens, the comet spends a million years (roughly 250 000 orbits) in a decoupled state waiting for the completion of its transfer. If this situation is typical, we missed most of the transfers by stopping the integrations too early. Moreover, as in the case mentioned, most transfers may require several interventions by terrestrial planets – something that our procedure forbids.
It is true that more than one encounter as close as those that we modelled is not likely to occur for the same object. However, significant perturbations may be caused by the more distant and more frequent encounters that our procedure neglects. The main reason for the inefficiency of our transfer model appears to be the premature cutting of the integrations and the limitation to the closest encounters, which are too rare to have a large effect.
If we had integrated all the comets until ejection or collision, some more deflections would have occurred. However, the increase would not be large, as seen from the fact that more than 80% of the deflections that we followed up by further integrations happened before the 50 000th revolution. In fact, only about 4% of the initial comets survive for 100 000 revolutions. We have to conclude that, while some parts of comet dynamics – especially involving close encounters with Jupiter – rely heavily on the far tails of the perturbation distribution (Everhart 1969; Froeschlé & Rickman 1981; Zhou et al. 2002), the current problem is different. The transfer of JFCs into Encke-like orbits is a slow process, likely involving several decisive events plus a background of small nudges caused by the terrestrial planets, and our simulations cannot deal realistically with these dynamics.
8. Incursions into asteroidal orbits
In Fig. 2, we could see that some of the survivors, during their 100 000th revolutions, reached low eccentricities and aphelion distances significantly less than 4 au. Some of them had thus become interlopers into the outer parts of the asteroid main belt and the Cybele region. We now have a closer look at this behaviour throughout the integrations, bearing in mind that it is a question of temporary episodes spent with the relevant type of orbits. The survivors represent only those episodes that happened to last until the integrations were ended.
 |
Fig. 13 Left-hand panel: number of revolutions spent by our sample comets per unit area in the asteroidal parts of the (a,e) plane, plotted according to an arbitrary colour scale shown on the right. Right-hand panel: same area of the (a,e) plane, cut into small cells for which the total number of comet orbital revolutions within the cell, as listed, is plotted using the colour scale shown on the right. Only cells occupied by at least two asteroids in the MPC database are plotted. |
The left-hand panel of Fig. 13 shows a zoom into the relevant region of the (a,e) plane, where the total number of revolutions spent per unit area is represented by an arbitrary colour scale, taking into consideration our entire sample without regard to physical lifetimes. The upper right part of the diagram is heavily populated and represents a low-eccentricity part of what is usually called the Jupiter family. We also see finger-like, vertical extensions of lower number density for a < 3.2 au, sometimes reaching down to nearly circular orbits. For larger semi-major axes these extensions are more ubiquitous and merge into wider bands that reach down to e ≈ 0. Two notable extensions occur at the 4:7 and 3:5 MMRs (mean motion resonances) at 3.58 and 3.70 au of semi-major axis, respectively.
The most conspicuous fingers appear to be associated with the 8:3, 5:2, 7:3, and 9:4 MMRs and Kirkwood gaps (from left to right). However, we believe these to be spurious for the following reason: we had a closer look at the comets that entered into low-eccentricity orbits – e < 0.25 in the first two cases and e < 0.15 in the last two cases. In total, there were 25 of this type of comet, but these were clones of only five initial comets from the (Brož et al. 2013) integrations. All of these had their initial orbits very close to the resonance centres in terms of semi-major axis. Unfortunately, as mentioned in Sect. 2, we did not have access to the angular elements of these orbits and were thus forced to select random values. In particular, the mean longitudes were picked with a uniform probability distribution on [0,2π]. However, all the five perihelion distances are small enough to make sure that close encounters with Jupiter had caused major perturbations during the last revolution preceding our initial orbits. This places a constraint on the mean longitude, which our procedure did not respect. Thus, we conclude that our 25 comets were placed in stable, resonant orbits that the real comets would not have achieved. This made them experience strong eccentricity pumping, which caused the fingers seen in the figure, but this behaviour is unlikely to be shared by real comets.
The same cannot be said about the comets beyond the 2:1 resonance. We have investigated a small sample of comets that entered into low-eccentricity orbits (e < 0.10) in the semi-major axis range of the Cybele group, which we took to be a ∈ [3.3,3.6] au. This includes part of the 2:1 resonance gap of JFCs (Vaghi & Rickman 1982), but this gap refers to the usual, high-eccentricity JFC orbits, while we are interested in the very rare excursions into Cybele-type, asteroidal orbits. The comets of our sample mostly start out in chaotic orbits like usual JFCs, but later on get trapped in a MMR (usually, the 4:7 MMR), which leads to eccentricity-pumping and temporary capture into asteroidal orbits. However, there is also a notable number of comets that are put into a stable resonance from the very beginning and are brought into the Cybele region by this resonance. We deem these cases to be suspect for the same reason described above for the Kirkwood gap visitors. On the other hand, those that start in chaotic orbits are free to go wherever they can in phase space, like JFCs in general, and we cannot argue that these evolutions would not be shared by real comets.
In the right-hand panel of Fig. 13, we show the same orbital domain as in the left-hand panel but somewhat differently. We cut the domain into cells of dimension 0.005 au × 0.002, and we selected all such cells that contain at least two asteroids of the IAU/MPC database4. For these cells, we plot the number of comet orbital revolutions in the same sample as for the left-hand panel, using a different colour scale. Requiring two asteroids rather than one, three or any other small number is to some extent an arbitrary choice, but it is related to the cell size. If we used larger cells, we would not resolve the dynamical structures equally well. Moreover, by excluding cells with single asteroids, we focus on the area with a significant, true asteroid population, and we avoid contamination by scattered “asteroids in cometary orbits” (Hahn & Rickman 1985), which are likely of cometary origin.
Thus, we now see a picture of the number density of “comets in asteroidal orbits” in the sense that there are real, observed asteroids with essentially the same values of a and e. The left half of the diagram exhibits the spurious cometary intruders into the Kirkwood gaps, while the right half shows the same for the Cybele and Hilda groups. By far, the largest number of comets is found in the Hilda region. A significant population is also formed by the spurious comets, to which we also add those near the 13:6 and 2:1 resonances, while the Cybele region is sparsely populated.
We have calculated the steady-state number of comets in the coloured cells of Fig. 13 (right-hand panel) by comparing the residence times with those corresponding to the observed Jupiter family, similar to what we did for the retrograde comets in Sect. 6 and for Encke-like comets in Sect. 7. Our result is about 12 Hilda-type comets, including both active and dormant states with D> 2 km, assuming that the dormant/active ratio is the same and using infinite physical lifetimes. For the Cybele region, this number is about 0.03. If we include erosion, we obtain 1.6–2.8 Hilda-type comets and <0.004 Cybele comets in the same size interval. The observed number of quasi-Hilda comets, first discussed by Kresák (1972), is roughly consistent with our estimate. Comets in Cybele group orbits are unlikely to exist at any random time, even considering smaller sizes, although occasionally one such comet might exist.
9. Discussion and conclusions
The first question to ask is, how well does our fictitious comet sample represent the real Jupiter family? It is clear that there must be some deviations, because the real Jupiter family is not completely known owing to the well known discovery biasses and uncertainties over the physical evolution of the nuclei. Our approach is a common one, namely, to depart from an assumed parent population that may be thought to represent reality. We then need to discuss the possible reasons why our assumptions may be skewed and what influence this may have on our conclusions.
Our initial orbit sample was described in Sect. 2. It is derived from dynamical simulations by Brož et al. (2013), who refer to the delivery of trans-neptunian disk objects into the inner solar system during the planet migration phase in the Nice Model. This involves two possible problems. One question is whether the structure of the disk, at the time in question, is identical to that of the current scattered disk. The other is if the dynamical transfer in the case of migrating giant planets is similar enough to the one that today’s JFCs are experiencing. Unfortunately, we have to leave these questions essentially unanswered. However, we note that our sample is based on an excited disk, which has undergone viscous stirring (Levison et al. 2011), leaving the orbits significantly inclined with respect to the ecliptic. The current scattered disk should then be at least as excited (Brasser & Morbidelli 2013). We think that this gives our investigation an advantage over the classical work by Levison & Duncan (1997), which used a more flattened scattered disk as the source of the JFCs.
There is one more problem that may be just as serious. Even though the scattered disk is likely the most important source of JFCs, it has not yet been fully proven that it is the only one. Emel’yanenko et al. (2005) argue that the Oort Cloud provides a significant contribution as well, and Brasser et al. (2012) find that high-inclination Centaurs are mostly likely derived from the Oort Cloud, which implies that these comets can also reach into the short-period comet population. Meanwhile, our assumption is that all the comets come from the scattered disk, so our JFCs are strictly limited to this particular origin.
Moreover, we made a down-selection of objects from the Brož et al. (2013) study, whereby comets arriving into orbits with q< 3.9 au were only included if their orbital periods were less than 20 yr and their jovian Tisserand parameters were TJ> 2. Thereby, we cut away almost 14% of all comets entering into the inner solar system. The question thus arises, if these excluded comets would have evolved differently to those that we chose to include.
The fundamental parameter in this respect is TJ. The excluded comets almost always have TJ between 2 and 3, but their distribution peaks near 2.6, which is markedly different from the included comets (lower right panel of Fig. 1). Furthermore, the largest value is less than 2.8, and the median is as low as 2.56. From this we conclude that our sample of orbital evolutions differs significantly from what we would have, if no comets were excluded. However, the difference is not drastic and we may rightly claim that our results cover a large majority of JFCs in a first approximation.
The next issue concerns our modelling of physical evolutionary effects and erosional lifetimes. This is not the main scope of this paper and we have limited ourselves to a simplistic approach based on H2O free sublimation. In an attempt to simulate the H2O production rates of observed JFCs, we used a crude scaling so that the mass-loss rate is 5% of the rate for an entirely free-sublimating nucleus. We apply the same scaling factor without distinction for all nuclear radii and all perihelion distances. It is quite likely that this implies significant error bars in the results. These uncertainties are difficult to estimate quantitatively, but one contributing item is the fact that reasonably accurate measurements of gas production rates and nuclear radii for the same comet do not exist in large numbers. In addition, the set of activity levels thus determined may be biassed to an unknown degree in favour of the highly active nuclei and, in any case, the observations cover only comets with perihelion distances q ≲ 2 au.
It is often claimed that the long-term erosion of JFC nuclei is dominated by randomly occurring, macroscopic disintegrations (usually called splitting) rather than ice sublimation (Di Sisto et al. 2009; Belton 2015). This means that the lifetimes could be much smaller than we estimate. However, there are large discrepancies between the different estimates and we prefer to leave the mechanism unmodelled. We shall return to this problem below. In addition, comets are known to undergo tidal splitting at encounters deep within the Roche zone of the Sun or a planet, but we did not include this phenomenon into our model. In all likelihood, this decision did not bias our results significantly.
In terms of end states and dynamical lifetimes, our comets behave similarly to the visible comets (q < 2.5 au) of Levison & Duncan (1997). Planetary collisions occur with roughly equal probability, and the vast majority of the comets experience ejection into hyperbolic orbits or diffusion into a > 1000 au. Our survivor category, including 4.4% of the comets, may be an artefact of our decision to cut the integrations after 100 000 revolutions. These too would most likely be ejected in the very long run.
The approach that we take in this paper concerning the orbital evolution of JFCs is to find out, first, what may happen during 100 000 revolutions in the absence of nucleus erosion, and then how this picture is modified under the assumptions of our erosional model. Our motivation is that we do not regard this model as carved in stone. We have already commented on the substantial error bars likely involved, and we believe that infinite lifetimes – although an extreme assumption – may serve well to show what can actually be achieved by secular orbital evolution, at least for large comet nuclei that survive for a very long time.
In this spirit, we have shown how JFCs may transit across the TJ = 2 and TJ = 3 limits repeatedly as a statistically significant phenomenon. We observe both an interchange between JFC and Centaur orbits, and temporary visits into retrograde orbits or orbits typical of the outer main belt asteroids and Hildas. These may be regarded as extreme features of the dynamical heating process that all JFCs are bound to undergo. With the aid of our erosional model we can observe, how this heating is quenched by introducing finite, physical lifetimes.
An obvious example is provided by the retrograde comets as illustrated by Fig. 7. We have shown that the most common retrograde orbits have very small perihelion distances and we have provided two examples of comets, which spent a long time in such special orbits before turning retrograde (Fig. 11). Clearly, this must have significant consequences when erosion is included. Indeed, in a steady-state model, retrograde comets originating as JFCs would be expected to exist if there was no erosion, but not when erosion is accounted for. However, given the uncertainties over the actual physical evolution of JFCs, it cannot be excluded that the three observed retrograde comets in otherwise JFC-like orbits may be true native JFCs rather than Halley-type interlopers. Another, related example is comet 96P/Machholz 1, which has an inclination near 60° and is involved in a Kozai cycle that may eventually imply its destruction by plunging into the Sun (Bailey et al. 1992). With a Tisserand parameter of 1.94, this is formally a Halley-type comet with a record-low semi-major axis, but judging from our results, it may also be a native JFC, which has had time to evolve into its current dynamical state.
The issue of comet lifetimes is highlighted by the results shown in Fig. 5. This demonstrates that a good fit to the observed JFC inclination distribution cannot be achieved by our steady-state models, no matter if erosion is included or not. A good fit is only obtained for the very first orbits performed by our sample comets in the respective perihelion distance range (q < 2.5 au). A priori, this would seem to imply that JFCs have to disappear almost immediately after becoming visible, which is in stark contrast to the result by Levison & Duncan (1997), who found that visible JFCs may survive up to 12 kyr without conflict with the observed inclination distribution. With our erosional model we find the typical ages of steady-state JFCs to be in reasonable agreement with this limit, but the fit to the inclination distribution is very poor.
We interpret this to be due to the disk providing the source of our comets being more excited than the scattered disk used by Levison & Duncan (1997). Consequently, we have to face the problem of extremely short lifetimes, which may in fact be at odds with what is known about the past orbital evolutions of JFCs. If so, invoking an extremely quick destruction of JFCs, for instance in the shape of a furious disintegration rate, is not an adequate solution. We have therefore suggested exploring an alternative approach in terms of a new model of physical evolution, where the visibility of comets is no longer a monotonously decreasing function of time.
The salient feature of this type of scenario is that the observed JFCs would represent a biassed selection out of a much larger JFC population, where the majority are hiding as dormant or low-active objects. The selection criterion would be a recent close encounter with Jupiter causing a so-called capture into a lower perihelion distance, causing a return from dormancy by dust mantle blow-off. In turn, the requirement of this type of an encounter would favour the low-inclination orbits, so that the observed JFCs might imitate fresh and newly captured comets rather than actually being such.
Hence, the JFC lifetimes could be much longer than they appear, and our erosional model may also have underestimated these lifetimes by underestimating the number of dormant or low-active comets. This would allow secular dynamical effects to play a larger role, but it would not affect the steady-state capture rate into the Jupiter family from the source population – in our case, the scattered disk. The increased lifetimes would be compensated for an increased number of unobserved, quasi-dormant JFCs. In fact, limits to this number may follow from analyses of NEA search programs and their discovery biasses (Bottke et al. 2002; Whitman et al. 2006).
In this paper, we have made some estimates of the steady-state capture rate of JFCs. Our method is to build a model of a steady-state Jupiter family with an arbitrary scale from our orbital integration output, and then to scale this model to the observed number of JFCs. When doing this for the erosional model, we calculate the accumulated, previous erosion depth for each current orbit, thus associating each comet of a given size with the necessary size of its ultimate parent. Assuming a size distribution for the initial nuclei, this allows us to put weights on the different orbital revolutions before scaling to observed numbers.
We found that 83% of our initial comets became visible in the sense of reaching q< 2.5 au. This explains the rough agreement between our collisional rates and those of Levison & Duncan (1997). For all these comets, the average time spent with q< 1.5 au was found to be 8.93 kyr in the model with infinite physical lifetimes. Scaling to the estimated number of JFCs with q< 1.5 au and nuclear diameter D> 2 km, we found the necessary capture rate to be 0.7–1.0 comets per century in this size range. Using the erosional model including its weighting procedure, we found a corresponding capture rate of roughly 3–6 comets per century.
This capture rate can be translated into a required number of scattered disk objects (SDOs) by (1) assuming that SDOs are the only source of JFCs; (2) using values for the escape rate of SDOs and the transfer efficiency into the Jupiter family upon this type of escape. Both values can be taken from previous simulations. They are heavily dependent on how the disk was modelled in those simulations, which introduces some uncertainty into the results. If we trust the classical paper by Duncan & Levison (1997), the combined, intrinsic rate of transfer into the Jupiter family is about 8 × 10-9 per century. In their case, the estimated number of visible JFCs was 500 and the average lifetime was ≃10 kyr, thus implying a capture rate of about five comets per century. Dividing this by the intrinsic transfer rate, we obtain 6 × 108 as the necessary number of SDOs.
According to Brasser & Morbidelli (2013), the size limit of total absolute magnitude HT< 9 used by Duncan & Levison (1997) is in rough agreement with the nuclear diameter limit (D> 2 km) that we used. Thus, our capture rates are in mutual agreement. The same holds for the number of SDOs, as long as we neglect an Oort Cloud contribution to the JFCs as Levison & Duncan (1997) did. We note, however, that Brasser & Morbidelli (2013) found a lower SDO escape rate than Duncan & Levison (1997), which would raise the number of SDOs to about 1 × 109.
We finally note our finding regarding the origin of Encke-like comets. We explored one mechanism of production of this type of comets, namely, extremely close encounters with terrestrial planets that cause major changes of orbital energy, by which comets can be directly emplaced into the Encke-like domain. We also neglected further perturbations by terrestrial planets after these deflections occurred. This was found to be a very inefficient way to produce Encke-like comets, compared with the much more realistic dynamical model of Levison et al. (2006). On the one hand, the much more frequent, smaller nudges provided by more distant encounters with terrestrial planets must offer another important way to decouple comets from Jupiter’s influence. On the other hand, by leaving the decoupled comets in the hands of the giant planets, we made them too vulnerable to collisions with the Sun via secular eccentricity pumping.
Acknowledgments
This work was supported by the Polish National Science Center under Grant No. 2011/01/B/ST9/05442. H.R. was also supported by Grant No. 74/10:2 of the Swedish National Space Board. The paper benefitted from valuable comments by the referee, Romina Di Sisto, which are gratefully acknowledged.
References
- Bailey, M. E., & Emel’yanenko, V. V. 1996, MNRAS, 278, 1087 [NASA ADS] [CrossRef] [Google Scholar]
- Bailey, M. E., Chambers, J. E., & Hahn, G. 1992, A&A, 257, 315 [NASA ADS] [Google Scholar]
- Belton, M. J. S. 2015, Icarus, 245, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Belyaev, N. A., Kresák, L. K., Pittikh, E., & Pushkarev, A. 1986, Catalogue of short-period comets − Katalog korotkoperiodicheskikh komet (Bratislava: SAV) [Google Scholar]
- Bottke, W. F., Morbidelli, A., Jedicke, R., et al. 2002, Icarus, 156, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Brasser, R., & Morbidelli, A. 2013, Icarus, 225, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Brasser, R., & Wang, J.-H. 2015, A&A, 573, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brasser, R., Schwamb, M. E., Lykawka, P. S., & Gomes, R. S. 2012, MNRAS, 420, 3396 [NASA ADS] [CrossRef] [Google Scholar]
- Brož, M., Morbidelli, A., Bottke, W. F., et al. 2013, A&A, 551, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carusi, A., Kresák, L., Perozzi, E., & Valsecchi, G. B. 1985, Long-term evolution of short-period comets (Bristol: Adam Hilger) [Google Scholar]
- Di Sisto, R. P., Fernández, J. A., & Brunini, A. 2009, Icarus, 203, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Duncan, M. J., & Levison, H. F. 1997, Science, 276, 1670 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Emel’yanenko, V. V., Asher, D. J., & Bailey, M. E. 2005, MNRAS, 361, 1345 [NASA ADS] [CrossRef] [Google Scholar]
- Everhart, E. 1969, AJ, 74, 735 [NASA ADS] [CrossRef] [Google Scholar]
- Everhart, E. 1985, in Dynamics of Comets: Their Origin and Evolution, eds. A. Carusi, & G. B. Valsecchi (Dordrecht: Reidel), Astrophys. Space Sci. Lib., 115, 185 [Google Scholar]
- Froeschlé, C., & Rickman, H. 1981, Icarus, 46, 400 [NASA ADS] [CrossRef] [Google Scholar]
- Froeschlé, C., & Rickman, H. 1986, A&A, 170, 145 [NASA ADS] [Google Scholar]
- Greenberg, R., Carusi, A., & Valsecchi, G. B. 1988, Icarus, 75, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Greenstreet, S., Gladman, B., Ngo, H., Granvik, M., & Larson, S. 2012, ApJ, 749, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Hahn, G., & Rickman, H. 1985, Icarus, 61, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Jewitt, D. C. 2004, in Comets II, eds. M. C. Festou, H. U. Keller, & H. A. Weaver (Tucson: Univ. Arizona), 659 [Google Scholar]
- Kresák, L. 1972, in The Motion, Evolution of Orbits, and Origin of Comets, eds. G. A. Chebotarev, E. I. Kazimirchak-Polonskaia, & B. G. Marsden, IAU Symp., 45, 503 [Google Scholar]
- Kresák, L. 1987, A&A, 187, 906 [NASA ADS] [Google Scholar]
- Levison, H. F., & Duncan, M. J. 1997, Icarus, 127, 13 [Google Scholar]
- Levison, H. F., Terrell, D., Wiegert, P. A., Dones, L., & Duncan, M. J. 2006, Icarus, 182, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Levison, H. F., Morbidelli, A., Tsiganis, K., Nesvorný, D., & Gomes, R. 2011, AJ, 142, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Mainzer, A., Bauer, J., Grav, T., et al. 2014, ApJ, 784, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Morbidelli, A., & Rickman, H. 2015, A&A, 583, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rickman, H., & Froeschlé, C. 1986, A&A, 170, 161 [NASA ADS] [Google Scholar]
- Rickman, H., Kamel, L., Froeschlé, C., & Festou, M. C. 1991, AJ, 102, 1446 [NASA ADS] [CrossRef] [Google Scholar]
- Rickman, H., Wiśniowski, T., Wajer, P., Gabryszewski, R., & Valsecchi, G. B. 2014, A&A, 569, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rickman, H., Wiśniowski, T., Gabryszewski, R., et al. 2017, A&A, 598, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tancredi, G. 1995, A&A, 299, 288 [NASA ADS] [Google Scholar]
- Tancredi, G., Fernández, J. A., Rickman, H., & Licandro, J. 2006, Icarus, 182, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Vaghi, S., & Rickman, H. 1982, in Sun and Planetary System, eds. W. Fricke, & G. Teleki, Astrophys. Space Sci. Lib., 96, 391 [Google Scholar]
- Valsecchi, G. B., Morbidelli, A., Gonczi, R., Farinella, P., & Froeschlé, C. 1995, Icarus, 118, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Volk, K., & Malhotra, R. 2008, ApJ, 687, 714 [NASA ADS] [CrossRef] [Google Scholar]
- Weissman, P. R., & Lowry, S. C. 2003, in Lunar and Planetary Science Conf., 34, 2003 [Google Scholar]
- Whitman, K., Morbidelli, A., & Jedicke, R. 2006, Icarus, 183, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Wiśniowski, T., & Rickman, H. 2013, Acta Astron., 63, 293 [NASA ADS] [Google Scholar]
- Zhou, J.-L., Sun, Y.-S., & Zhou, L.-Y. 2002, Celest. Mech. Dyn. Astron., 84, 409 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Numbers of comets in our integrated sample, divided into three different ranges of jovian Tisserand parameter, concerning both the starting orbits and the orbits at the end of the integrations.
For different distances (d) from the Sun, we list the relative numbers of steady-state JFCs (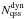 ) with q < d, and the relative numbers (
) with q < d, and the relative numbers (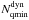 ) of JFCs that penetrate at least once inside d during their orbital evolutions.
) of JFCs that penetrate at least once inside d during their orbital evolutions.
All Figures
 |
Fig. 1 Histograms of initial elements for the 5000 orbits used in this study. In the four panels we show the semi-major axes (upper left), perihelion distances (upper right), inclinations (lower left), and jovian Tisserand parameters (lower right). |
| In the text | |
 |
Fig. 2 Distributions of initial and final orbital elements for surviving comets. Upper panels: eccentricity vs. semi-major axis; lower panels: inclination vs. semi-major axis; left panels: periods below 20 yr; right panels: periods above 20 yr. Red dots show initial orbits. For the final orbits, sky-blue dots indicate TJ < 2, dark blue dots indicate 2 < TJ < 3, and green dots indicate TJ > 3. |
| In the text | |
 |
Fig. 3 Cumulative fraction of comets in our entire sample with dynamical lifetimes exceeding the given number of orbits. |
| In the text | |
 |
Fig. 4 Cumulative distribution of the minimum perihelion distances reached by the comets in our sample, assuming unlimited physical lifetimes. |
| In the text | |
 |
Fig. 5 Cumulative JFC inclination distributions. The red diamonds refer to observed JFCs with D> 1.6 km. The green curve shows the initial distribution of JFCs with q< 2.5 au. The blue curve shows the steady-state distribution excluding erosion, and the orange and cyan curves show the same, including erosion, using α = 1.5 and 2.5, respectively. |
| In the text | |
 |
Fig. 6 Histogram representing the distribution of ages (see main text) of steady-state Jupiter family comets with q< 1.5 au and nuclear radii larger than 1 km. The age scale is artificially cut at 125 kyr for clarity. For each bin, we show the number of orbits in our integrated sample satisfying the above criteria. |
| In the text | |
 |
Fig. 7 Number of revolutions in retrograde orbits found in all our integrations, as a function of (a,q) in the left-hand panels and (a,i) in the right-hand panels. The top panels show the uncorrected numbers based on the dynamical evolutions, while the lower panels show the effective numbers corresponding to eroded nuclei of radii larger than 0.1 km. |
| In the text | |
 |
Fig. 8 Double histogram showing, in red, the distribution of initial inclinations of the 417 retrograde comets and, in blue, that of the whole sample of 5000 starting orbits. |
| In the text | |
 |
Fig. 9 The eccentricities (e) and semi-major axes (a) of 514 JFC orbits immediately preceding retrograde visits. The tangency curves with respect to Jupiter’s current orbit are shown as full-drawn curves for Q = 4.95 au and q = 5.45 au, and vertical dashed lines indicate the main MMRs with respect to Jupiter. |
| In the text | |
 |
Fig. 10 The MOID values of 514 JFC orbits immediately preceding retrograde visits with respect to a circular jovian orbit in the ecliptic plane. These are referred to as ℳo in the text. |
| In the text | |
 |
Fig. 11 Temporal evolutions of orbital elements for two comets that made significant visits into retrograde orbits, using the number of orbits as time variable. The time frames cover several thousand orbits before the comets become retrograde and significantly less afterwards. Two panels are shown for each comet: the upper panel exhibits the semi-major axis a (au), the eccentricity e, the inclination i and the argument of perihelion ω, while the lower panel shows the quantity Lz = (1−e2)1/2cosi, expressing the vertical component of the angular momentum, and the critical arguments of the ν16 and ν5 secular resonances. The colour codings are shown to the right. Angles are labelled on the left and the other quantities on the right. |
| In the text | |
 |
Fig. 12 Steady-state distribution of Encke-like comets over the parametric (Q,q) plane as found by our simulations. The arbitrary colour scale, as given on the right hand side, denotes the relative number of comets per cell in the diagram. |
| In the text | |
 |
Fig. 13 Left-hand panel: number of revolutions spent by our sample comets per unit area in the asteroidal parts of the (a,e) plane, plotted according to an arbitrary colour scale shown on the right. Right-hand panel: same area of the (a,e) plane, cut into small cells for which the total number of comet orbital revolutions within the cell, as listed, is plotted using the colour scale shown on the right. Only cells occupied by at least two asteroids in the MPC database are plotted. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


