| Issue |
A&A
Volume 597, January 2017
|
|
|---|---|---|
| Article Number | A129 | |
| Number of page(s) | 18 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201629125 | |
| Published online | 17 January 2017 | |
Establishing binarity amongst Galactic RV Tauri stars with a disc⋆,⋆⋆
1 Instituut voor Sterrenkunde (IvS), KU Leuven, Celestijnenlaan 200D, 3001 Leuven, Belgium
e-mail: rajeev@ster.kuleuven.be
2 Institut d’Astronomie et d’Astrophysique, Université Libre de Bruxelles, CP 226, Boulevard du Triomphe, 1050 Bruxelles, Belgium
Received: 14 June 2016
Accepted: 30 September 2016
Context. Over the last few decades it has become more evident that binarity is a prevalent phenomenon amongst RV Tauri stars with a disc. This study is a contribution to comprehend the role of binarity upon late stages of stellar evolution.
Aims. In this paper we determine the binary status of six Galactic RV Tauri stars, namely DY Ori, EP Lyr, HP Lyr, IRAS 17038−4815, IRAS 09144−4933, and TW Cam, which are surrounded by a dusty disc. The radial velocities are contaminated by high-amplitude pulsations. We disentangle the pulsations from the orbital signal in order to determine accurate orbital parameters. We also place them on the HR diagram, thereby establishing their evolutionary nature.
Methods. We used high-resolution spectroscopic time series obtained from the HERMES and CORALIE spectrographs mounted on the Flemish Mercator and Swiss Leonhard Euler Telescopes, respectively. An updated ASAS/AAVSO photometric time series is analysed to complement the spectroscopic pulsation search and to clean the radial velocities from the pulsations. The pulsation-cleaned orbits are fitted with a Keplerian model to determine the spectroscopic orbital parameters. We also calibrated a PLC relationship using type II cepheids in the LMC and apply the relation to our Galactic sample to obtain accurate distances and hence luminosities.
Results. All six of the Galactic RV Tauri stars included in this study are binaries with orbital periods ranging between ~650 and 1700 days and with eccentricities between 0.2 and 0.6. The mass functions range between 0.08 to 0.55 M⊙ which points to an unevolved low-mass companion. In the photometric time series we detect a long-term variation on the timescale of the orbital period for IRAS 17038−4815, IRAS 09144−4933, and TW Cam. Our derived stellar luminosities indicate that all except DY Ori and EP Lyr are post-AGB stars. DY Ori and EP Lyr are likely examples of the recently discovered dusty post-RGB stars.
Conclusions. The orbital parameters strongly suggest that the evolution of these stars was interrupted by a strong phase of binary interaction during or even prior to the AGB. The observed eccentricities and long orbital periods among these stars provide a challenge to the standard theory of binary evolution.
Key words: stars: variables: Cepheids / binaries: spectroscopic / stars: AGB and post-AGB / circumstellar matter / stars: distances / stars: chemically peculiar
Based on observations made with the Flemish Mercator Telescope and the Swiss Leonhard Euler Telescope.
Radial velocity tables are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/597/A129
© ESO, 2017
1. Introduction
RV Tauri stars are a group of luminous radial pulsators that occupy the high-luminosity end of the population II cepheid instability strip. They were classified as post-asymptotic giant branch (post-AGB) stars by Jura (1986) because of their observational properties. They occupy the F, G, or K spectral classes, they are highly luminous, and many of them have an infrared excess (IR-excess) which indicates the presence of circumstellar material.
RV Tauri stars are characterised and defined by their light curves that show alternating deep and shallow minima. The period between two successive minima is typically between 20 and 75 days and is called the fundamental period. The time between two successive deep minima has a range typically twice that of the fundamental period and is very often termed the formal period. These stars occupy the higher period range among the population II cepheids (Wallerstein 2002). As yet, there is no definite characterisation of the photometric wavering related to the pulsations of RV Tauri stars. Some objects display a very distinct alternation of shallow and deep minima, while for others the light curves are less stable and are more semi-periodic. Nevertheless, it is now widely accepted that most of the RV Tauri stars can be subdivided photometrically in two groups based on their long term variability: the RVa and RVb types. The RVa type stars have a constant mean magnitude, while the RVb types vary slowly in mean magnitude with a long secondary period of around 600 to 2600 days (Pollard et al. 1996).
In contrast to the photometric classification based primarily on the light variability, a spectroscopic classification of RV Tauri stars was presented in Preston et al. (1963). Three distinct spectroscopic groups were defined: those with spectral types G or K (RVA); those with spectral types Fp(R), weak lines in their spectra, and strong CN and CH bands (RVB); and those like RVB but with little or no trace of CN bands (RVC).
About 23% of the 126 RV Tauri stars known in the Galaxy (see GCVS: Samus et al. 2009), exhibit an IR-excess in their spectral energy distribution (SED), as is illustrated with an example in Fig. 1. Colour−colour plots made on the basis of infrared surveys like the Infra-Red Astronomical Satellite (IRAS) and the Wide-field Infrared Survey Explorer (WISE) have enabled a classification of these excesses.
 |
Fig. 1 Example of the SED of TW Cam; a RV Tauri star surrounded by a disc. The red line shows the fit with a photospheric model atmosphere. The clear broad IR-excess can already be seen at a wavelength of ~2 μm, indicative of a dusty disc. |
Lloyd Evans (1985) showed that RV Tauri stars occupy a specific region in the IRAS colour-colour plot: the RV Tauri box. A more in-depth study by Gezer et al. (2015) explores the WISE colour-colour plot and compares Galactic RV Tauri stars with a reference sample of Galactic post-AGB stars in relation to their IR properties, binary status, and chemical abundances. They found that a large fraction of the Galactic RV Tauri stars have the same infrared properties as the reference stars with a known disc. Bujarrabal et al. (2015) and Hillen et al. (2015) confirmed that RV Tauri stars which have a broad IR-excess, mimicking that of post-AGB stars, indeed have a circumbinary disc by proving the disc-like structure around the RV Tauri star, AC Her. The discs are all found around binary systems, hence these RV Tauri stars are likely binaries as well.
Over the past few decades, it has become clear that the photospheres of many post-AGB and RV Tauri stars show chemical anomalies, the so-called depletion phenomenon. Refractory elements with high condensation temperature (e.g. Si, Ti, and Fe) are under-abundant, while volatile elements with lower condensation temperature (e.g. C, N, O and Zn) are found to be over-abundant or close to solar abundances (Giridhar et al. 1994, 1998, 2000; Van Winckel et al. 1998; Maas et al. 2005).
A well-accepted explanation for this anomaly is given by Waters et al. (1992), in terms of selective re-accretion of gas from the circumbinary environment, while the dust remains stable at the sublimation radius as a consequence of radiation pressure. This idea is confirmed by the observation that a large fraction of depleted stars are surrounded by a disc (Gezer et al. 2015). Van Winckel et al. (1995) showed that the extremely depleted iron-deficient post-AGB stars HR 4049 (Lambert et al. 1988; Waelkens et al. 1991a), HD 44179, HD 52961 (Waelkens et al. 1991b), and BD+39°4926 (Kodaira et al. 1970) are actually binaries.
There is growing evidence that binarity is a needed condition for disc formation or conversely, a Keplerian disc around a post-AGB system implies that it is a binary. Van Winckel et al. (2009) studied a sample of six post-AGB stars which are low-amplitude pulsators with a disc and found them all to be binaries. They provide a good indication that the disc-binarity correlation is indeed bona fide among post-AGB stars. Is this also the case for RV Tauri stars with disc-like IR-excesses?
At present, there are six confirmed binaries in a sample of 126 known Galactic RV Tauri stars, namely, U Mon (Pollard & Cottrell 1995; Pollard et al. 1997), IW Car (Pollard et al. 1997), AC Her (Van Winckel et al. 1998), ENTra (Van Winckel et al. 1999), SX Cen (Maas et al. 2002), and RU Cen (Maas et al. 2002). The low fraction of confirmed spectroscopic binaries is very likely an observational bias, which is strengthened by the difficulty in tracing orbital motion in high-amplitude pulsators. Another reason is the presence of shocks in the photospheres, causing line-splitting and line profile variability in the spectra, which again makes the orbit hard to detect.
This paper is a contribution to comprehending the disc-binarity connection amongst RV Tauri stars. In Sect. 2 we describe the sample of RV Tauri stars presented in this study, together with the photometric and spectroscopic data. Section 3 exhibits our photometric analysis including the pulsations, SEDs, and PLC relationship. The method used to obtain pulsation-cleaned orbits leading to the spectroscopic results are described in Sect. 4. In Sect. 5 we discuss our results and their implications, and we conclude in Sect. 6.
2. Sample selection and data overview
2.1. Sample
Of the 126 Galactic RV Tauri stars (Samus et al. 2009), 23 objects with a near IR-excess, are part of the ongoing High Efficiency and Resolution Mercator Echelle Spectrograph (HERMES) radial velocity monitoring program. We selected RV Tauri stars from that sample which are not yet known to be binaries and which had sufficient data coverage for a radial velocity study. The mentioned selection criteria resulted in a sample of six Galactic RV Tauri stars listed in Table 1.
Since the monitoring programme is carried out by relatively small telescopes, we are observationally limited towards bright objects with a mean V-mag ≲ 13.
2.1.1. DY Ori
Schmidt et al. (1995) studied the pulsations of DY Ori and they showed that it is a photometric RV Tauri variable but of an unknown type, with a pulsation period of 60 ± 8 days. The analysis was based on only 21 V-Band photometric observations from the General Catalogue of Variable Stars (GCVS).
One of the first optical spectral analyses of this object was presented by Evans (1985), after which it was classified as an RV Tauri spectroscopic type B based on the system of Preston et al. (1963). Gonzalez et al. (1997) carried out a detailed abundance analysis of field RV Tauri stars and DY Ori was found to have a highly depleted photosphere and to be very iron-poor with an [Fe/H] of −2.3 ± 0.11 dex. Gonzalez et al. (1997) also estimated the effective temperature of DY Ori as Teff = 6000 K using spectra at a phase just after maximum light.
Our sample of Galactic RV Tauri stars.
2.1.2. EP Lyr
EP Lyr was first found to be variable by Schneller (1931). Much interest in the object was gained in the early 1960s with the work of Wenzel (1961), who claimed that it is a β Lyrae-type eclipsing binary with a long period. Later investigations by Preston et al. (1963) and Wachmann (1968) proved this claim to be wrong. EP Lyr was classified as an RVb photometric type by Kholopov et al. (1985) under the suspicion that the mean brightness underwent long-term variations. After the work of Zsoldos (1995), it became clear that EP Lyr is of an RVa type with a pulsation period of 83.46 days and no remarkable long-term photometric variability.
A synthetic spectrum analysis of EP Lyr by Wahlgren (1992) reported an effective temperature of 5250 K, log g of 1.5, and [Fe/H] of −1.7 dex. Gonzalez et al. (1997) carried out an abundance study of EP Lyr in which they better constrained the Teff, log g, and [Fe/H] based on the Fe-line (see Table 1). They also found that the star is very metal-poor, rich in oxygen, and very depleted. The effective temperature of EP Lyr shows large changes across the pulsation phase from 5500 K up to even 7000 K (Gonzalez et al. 1997). This results in a spectral type change from G5 to A4. Based on the spectroscopic classification of Preston et al. (1963), EP Lyr is classified as an RVB spectroscopic type.
2.1.3. HP Lyr
One of the first variability studies of this object includes the work of Erleksova (1971). They showed that its O−C diagram contain many period instabilities with abrupt changes from 0.001P to 0.01P on a scale of 20 to 100 pulsation cycles. HP Lyr has been termed a long-period variable in the literature owing to its high pulsation fundamental period of 69.35 days and a formal period of 138.7 days (Graczyk et al. 2002). Graczyk et al. (2002) also showed one important feature of this star: the pulsation period is variable with at least a 1% change in 20 years. On the other hand, it does not show any long-term variability in its mean V-mag and so it is classified as a photometric RVa type.
HP Lyr is of an RVB spectroscopic type based on the classification of Preston et al. (1963). The star shows a few peculiarities in the RV Tauri class; it was reported as probably the hottest known RV Tauri variable by Graczyk et al. (2002) with a mean effective temperature of 7700 K. A spectral analysis of HP Lyr by Giridhar et al. (2005) resulted in a Teff of 6300 K.
This object might be one where the dust-gas separation is most apparent. Figure 4 of Giridhar et al. (2005) shows a tight correlation between different chemical species with respect to solar abundance and the condensation temperature, TC. Elements like C, N, and O are close to solar abundance and high condensation temperature elements like Ti, Al, and Sc are highly under-abundant.
2.1.4. IRAS 17038−4815
Although it is a genuine RV Tauri star, IRAS 17038−4815 has recieved little attention in past decades. It has a high-amplitude pulsation of ~1.6 mag in the V-band and a photometric fundamental period of 38 days, with a formal period of 76 days (Maas 2003). Kiss et al. (2007) classifies it as an RVa photometric type based on the only found period of 75.9 ± 1.9 days in the ASAS photometric time series.
The strong CN and CH bands in its spectrum make it a genuine RVB spectroscopic type. Maas et al. (2005) derive an effective temperature of 4750 K and a metallicity of [Fe/H] = −1.5 dex, indicating a depleted atmosphere.
The preliminary orbit of IRAS 17038−4815 was already published by Van Winckel (2007). They found a pulsation period of 37.95 days, which was cleaned from the orbit to obtain an orbital period of 1381 ± 16 days and eccentricity of 0.56 ± 0.05.
2.1.5. IRAS 09144−4933
A recent variability study of IRAS 09144−4933 is presented in the work of Kiss et al. (2007). They analysed the ASAS photometry and estimated a pulsation period of 93 ± 2 days. The fit to their pulsation data is not very clear and the ASAS data itself seem to have a lot of scatter. This object might be either too faint for pulsations to be detected by the ASAS instrument or a relatively low-amplitude pulsator. We note that this star is the faintest in our sample with a mean V-mag of ~13.8.
IRAS 09144−4933 is of a G0 spectral class with an effective temperature of 5750 K and a metallicity, [Fe/H] = −0.5 dex. These parameters are derived assuming a plane parallel local thermodynamic equilibrium (LTE) atmosphere (Maas et al. 2005). The elements with a high condensation temperature of ~1500 K are either moderately depleted or not at all. Maas et al. (2005) also reports that most s-process elements, except for Ba, Ti, and Sc, are under-abundant.
2.1.6. TW Cam
Preston et al. (1963) first reported an 85-day photometric pulsation period using GCVS data. Later, Zsoldos & Kollath (1991) reported a fundamental period of 43 days together with an 86-day formal period. Over the last few decades, it has become clear that these two periods are the dominant ones in the photometry of TW Cam. The star was reported as an RVa type by (Giridhar et al. 2000).
TW Cam was classified as an RVA spectroscopic type by Preston et al. (1963). Giridhar et al. (2000) derived stellar model parameters for TW Cam from the Fe-lines and showed that it is mildly depleted with an [Fe/H] of −0.5 dex. They also constrain an effective temperature of 4800 K from the Fe-line analyses. It therefore belongs to the spectral type G3.
2.2. Photometric data
We present an updated V-band photometric analysis based on the All Sky Automated Survey (ASAS, Pojmanski 2002) to study the pulsations for all objects except for TW Cam and HP Lyr, for which data from the American Association of Variable Star Observers (AAVSO)1 were used.
ASAS is an ongoing long-term photometric monitoring that maps the sky south of δ = +28° consisting of two observing sites namely, Las Campanas Observatory (Chile) and Haleakala (Maui). Each site is equipped with two wide-field instruments which can observe simultaneously in the V and I-band. The instrument is very well-suited for sources with a maiximum V-band brightness of 14 mag. To date, the ASAS catalogue consists of more than 267 260 V-band frames that have imaged a total of around 20 million stars brighter than 14 mag. Around 50 000 of them are seen to be variable.
We gathered ASAS data by querying the ASAS Catalogue of Variable Stars (ACVS)2 and the ASAS All Star Catalogue (AASC)3. Each time series from ASAS is partitioned by its observed field. Most of the data in our analysis were obtained using the ASAS-3 configuration with a wide-field (8.8° × 8.8°) CCD camera.
The critical PSF sampling is not reached by the instrument and therefore the pipeline data-reduction routine approximates the aperture photometry into five different aperture size measurements which range from 2 pixels to 6 pixels. The ASAS guidelines recommend a preferred aperture size for every magnitude bin and we limited our photometric analysis to the A-grade data quality.
Table 2 outlines our photometric dataset. Column 2 represents the number of photometric data points, Col. 3 gives the source of the data, Col. 4 displays the ASAS aperture size used for each star, and the last column denotes the span of the time series.
Characteristics of the photometric dataset.
2.3. Spectroscopic data
High-resolution spectroscopic data for DY Ori, EP Lyr, HP Lyr, and TW Cam were obtained using the HERMES spectrograph mounted on the 1.2 m Mercator telescope at the Roque de los Muchachos Observatory, La Palma. HERMES is a fibre-fed spectrograph operating in a temperature-controlled environment to ensure good wavelength stability and excellent throughput. The fibre has an aperture of 2.5 arcsec on-sky and the high resolution is reached via a two-sliced image slicer which is made to resemble a slit. It is built to have minimum light loss despite the high resolution. A star with a V-band magnitude of 10th has a signal-to-noise ratio (S/N) of 110 at 550 nm over an hour exposure with an average seeing condition. The spectrograph obtains 55 orders with a resolution of R = 85 000 corresponding to 3.5 km s-1 and a high spectral coverage of 377−900 nm in a single exposure. Once the observing night ends, the data are reduced through a dedicated pipeline tailored to ensure efficient data reduction (see Raskin et al. 2011, for details).
The spectroscopic data for the targets in the southern hemisphere, IRAS 17048−4815 and IRAS 09144−4933, were obtained from the 1.2 m Swiss Leonhard Euler Telescope located at La Silla observatory. The telescope is equipped with a fibre-fed echelle spectrograph (CORALIE), containing 68 orders with a broad wavelength range of 390 nm to 680 nm. CORALIE can deliver a high resolving power of 50 000 at 550 nm (Queloz et al. 1999). The spectrograph is fed by two fibres, one of which is the science fibre and the other is a reference fibre. The science fibre has a diameter of 2 arcsec on-sky with a double scrambler device for the input illumination to be more stable and the reference fibre is used for the calibration lamp. The data are automatically reduced by software that provides the measurement of radial velocities via a cross-correlation method (see Baranne et al. 1979, 1996, for details).
Table 3 outlines our spectroscopic dataset: the original number of epochs per target (Noriginal), the number of epochs with not good enough S/N in the spectra (Nbad), the number of spectra related to shocks (Nshocks, see Sect. 4.2), and the final number of spectra that were considered good enough to be used for the orbital analysis (Nused = Noriginal−Nbad−Nshocks). The span of the spectroscopic time series is denoted △ T in the last column of Table 3. It is important to note here that the minimum S/N in the spectra below which any radial velocity was treated as bad data due to poor weather conditions was set to 20.
Characteristics of the spectroscopic dataset (see text).
3. Photometric analysis and the PLC relation
3.1. Pulsation analysis
The main aim of this research is to probe the binary status of our sample of RV Tauri stars with a disc. However, these are high-amplitude pulsators. In some cases (e.g. low-inclined orbital planes) the pulsations might even drown the orbital motions in the radial velocity amplitude. To better constrain the orbital parameters of the binary system, the radial velocity variations induced by the pulsations should be cleaned from the observed radial velocities.
Pulsation periods derived from the photometric and spectroscopic time series.
 |
Fig. 2 Photometric phase plot of DY Ori, EP Lyr, and HP Lyr, folded on a formal period of 60.8 days, 83.2 days, and 136.8 days, respectively. The horizontal solid black line is the mean Vmag. |
 |
Fig. 3 Photometric phase plot of IRAS 17038−4815 and TW Cam folded on a formal period of 75.9 days and 86.1 days, respectively. The horizontal solid black line is the mean Vmag. |
The original photometric data was first checked for any extreme outliers and these points were excluded by imposing a sigma clipping to any flux value beyond ~4σ from the mean. We then carried out a pulsation analysis in the photometric time series to obtain the dominant pulsation frequencies. We limit ourselves to a S/N of ~4 in the analysis of the frequency spectrum. This S/N is, in principle, the accepted critical value below which it is not possible to distinguish signal from noise (Breger et al. 1993). The photometric pulsation periods are used to disentangle the pulsations from the original radial velocity data. However, the cycle-to-cycle variability in the pulsations also induces a signal in the radial velocities which is hard to correct for.
The pre-whitening procedure involves finding the dominant peak frequency using the Lomb-Scargle method (Scargle 1982). The fit parameters associated with the dominant frequency is fit using a sinusoidal function and then subtracted from the original data to find the next significant peak frequency in the residuals. This process is repeated until the S/N stop-criterion is reached. The pulsation frequencies obtained above the S/N criterion are listed in Table 4. We used the fundamental period (P0) obtained after the pre-whitening process to fold the data on the formal period (P1 = 2 × P0). The phased pulsation periods are shown in Figs. 2 and 3.
The pulsation periods derived for DY Ori, EP Lyr, HP Lyr, and TW Cam are consistent with what has been presented in the literature (see references in Table 4). In the case of EP Lyr, we also consider the frequency peak with S/N = 3.8, corresponding to a pulsation period of 41.6 days, as a real signal (as quoted in the literature).
The RVb nature of IRAS 17038−4815, IRAS 09144−4933, and TW Cam are confirmed by the long-term photometric variation in the light curves on the timescale of the orbital period (see italicised numbers in Col. 3 of Table 4). No long-term photometric variability is seen in the time series of DY Ori extending over ~2500 days (~2 × Porb). We therefore classify it as an RVa photometric type.
Figure 4 displays the time series of the photometric pulsations. We note that we did not include the pulsation time series of IRAS 09144−4933 in Fig. 4 because the main period detected in the light curves is the orbital period (P = 1758 days, see Table 4). Two putative pulsation periods of 85 and 50 days are detected only slightly above the S/N criterion (see Table 4), but the scatter in the data is too large to obtain a good fit to the pulsations.
 |
Fig. 4 Time series of the pulsations using ASAS and AAVSO photometric data. Here we mainly display their pulsational nature and not the long-term variability. The solid red line is the pulsation model fit to the photometric time series and the horizontal solid black line is the mean Vmag. |
3.2. Spectral energy distribution
We model the SEDs of the stars using photometric data available from different catalogues listed in Tables B.1 to B.6. The fit itself is done using a parameter-grid search to obtain the optimised Kurucz model (Kurucz 1979) parameters using a χ2 minimisation method (see Degroote et al. 2011 for details). We used initial model atmosphere parameters, Teff and [Fe/H], based on the values found in the literature (see Table 1). We note that the [Fe/H] was kept fixed in the SED fit to the values found in the literature. Since the Teff changes significantly during the pulsation cycle, we account for the Teff range during the pulsation cycle by allowing the effective temperature to vary by 10% of its value. An example of the fitted SED for DY Ori is shown in Fig. 5 and the rest of the SEDs are displayed in Appendix A.
From the SEDs we obtain the total extinction E(B−V) towards the star and the results are illustrated in Table 5. We assume in this process that the colour excess is due to interstellar and circumstellar reddening. We also assume that the circumstellar component follows the same extinction law. The errors in E(B−V) are computed using a Monte Carlo method on the photometric SED data whereby a random number generator was used to scramble the original SED data points within one standard deviation creating 100 000 randomised SED fits of the same structure. The errors were then computed by taking the standard deviation of the parameters linked to each SED fit.
The main challenge in building SEDs for strong pulsators like RV Tauri stars is that the photometric flux changes considerably from one phase to another. The way to compensate for this would be to obtain similarly phased data. As these data are not available, we restricted our fit to the photometry we retrieved which includes all available phases.
3.3. Period-luminosity-colour (PLC) relationship and distances
One of the main advantages that pulsating type II cepheids offer is that they allow us to constrain the distances and hence luminosities via a period-luminosity (P−L) relation. The Magellanic clouds have proven to be particularly useful in the calibration of the P−L relation for population II cepheids mainly because they are close enough for reasonably bright apparent magnitudes of the stars and distant enough to approximate their distance as the same. Some of the P−L relationship studies of the population II cepheids in the Galactic globular clusters, Small Magellanic Cloud (SMC), and Large Magellanic Cloud (LMC) are included in the works of Nemec et al. (1994); Alcock et al. (1998) and Ripepi et al. (2015).
 |
Fig. 5 SED of DY Ori. The red line is the stellar photosphere fitted using a Kurucz model and the black line is the dereddened model. |
Distances and luminosities of the Galactic sample, derived using the PLC relationship.
Since the luminosity of a star is dependent on two variables, the radius and effective temperature, we expect the luminosity of a type II cepheid to be better constrained using a colour and period relation. Indeed, this proves to be the case since the PLC relationship is generally tighter than the P−L relation. We calibrate the PLC relation in the LMC and apply it to our Galactic stars, assuming there is no metallicity dependency of the relation.
The amount of extinction towards a star plays an important role in obtaining a well-calibrated PLC relation. To circumvent and minimise reddening effects, we do not use the V- and I-band apparent magnitudes independently, but rather the Wesenheit index (Ngeow & Kanbur 2005), which is a combination of the two. The Wesenheit index is reddening-free and is defined as 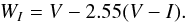 (1)The reddening-free Wesenheit index can also be written in terms of the intrinsic values of the same variables (van den Bergh & Hagen 1968; Madore 1976, 1982):
(1)The reddening-free Wesenheit index can also be written in terms of the intrinsic values of the same variables (van den Bergh & Hagen 1968; Madore 1976, 1982): 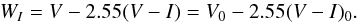 (2)The PLC relation is constructed based on publicly available data4 (Soszyński et al. 2008). These are data from the OGLE-III observations carried out using the 1.3 m Warsaw telescope at Las Campanas Observatory in Chile. Stars with either a missing I-band photometry or Fourier coefficient (φ31) were not included. This lead to a final list of 187 LMC type II Cepheids. We decided to recalibrate the PLC relation using a broader log (P) range of 0.001
(2)The PLC relation is constructed based on publicly available data4 (Soszyński et al. 2008). These are data from the OGLE-III observations carried out using the 1.3 m Warsaw telescope at Las Campanas Observatory in Chile. Stars with either a missing I-band photometry or Fourier coefficient (φ31) were not included. This lead to a final list of 187 LMC type II Cepheids. We decided to recalibrate the PLC relation using a broader log (P) range of 0.001 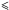 Log (P)
Log (P) 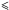 1.83, available for a bigger sample of type II Cepheids compared to the smaller sample and a narrower log (P) range of 0.9
1.83, available for a bigger sample of type II Cepheids compared to the smaller sample and a narrower log (P) range of 0.9 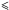 log (P)
log (P) 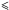 1.75 studied by Alcock et al. (1998).
1.75 studied by Alcock et al. (1998).
We used the mean I-band, mean V-band, and periods with their associated uncertainties to obtain the quantity V0−2.55(V−I)0 for each log (P) value. A significant reduction in scatter in the Wesenheit plane is seen (Fig. 6). This supports the fact that the stars in the sample are affected by a considerable amount of reddening. The few outliers in the Wesenheit plane in the W Vir regime are due to the peculiar W Vir stars (pW Vir; marked with Cyan star symbols). Other outliers in the BL Her region could possibly be attributed to either eclipsing type II Cepheids or anomalous type II Cepheids which are different from the W Vir, pW Vir, BL Her, and RV Tauri stars (for more details, see Soszyński et al. 2008).
Our results for the BL Her and W Vir types agree with the results of Matsunaga et al. (2009) which show that these two types of population II cepheids are colinear in the P−L plane. We notice a larger scatter in the quantity V0−2.55(V−I)0 and an upward “bending” of the relation for the longer periods (>20 days) in the RV Tauri star regime. This can be attributed to extinction by circumstellar dust. It is more apparent in the J- and Ks-band, as these bands are more contaminated by thermal emission of the hot dust (e.g. Matsunaga et al. 2009; Ripepi et al. 2015). To optimise our PLC relationship, we excluded the objects with circumstellar dust in a linear regression analysis. The red star symbols in Fig. 6 identify the highly reddened RV Tauri stars in the LMC.
We made use of the extinction law (AI/AV) by Cardelli et al. (1989) to obtain the intrinsic (V−I)0 from the individual (V−I) values of each star in the LMC. We assumed a mean reddening towards the LMC of E(V−I) = 0.09 ± 0.07 (Haschke et al. 2011) consistent with the mean E(V−I) of population II Cepheids in the LMC by Ripepi et al. (2015). A linear regression in Log (P) against the quantity V0−(V−I)0 yields the following PLC relation for the intrinsic apparent magnitude (V0) of the population II cepheids: 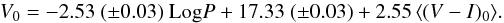 (3)Adopting a distance modulus to the LMC of 18.5 (Walker 2012), we compute the absolute magnitudes of the population II cepheids in the LMC as
(3)Adopting a distance modulus to the LMC of 18.5 (Walker 2012), we compute the absolute magnitudes of the population II cepheids in the LMC as 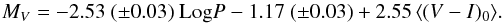 (4)Based on 30 LMC type II Cepheids, Alcock et al. (1998) derived a steeper slope of −2.95 ± 0.12 and a higher zero-point offset of 17.89 ± 0.2 in Eq. (3). The PLC relation for the population II cepheids in the LMC is shown in Fig. 6.
(4)Based on 30 LMC type II Cepheids, Alcock et al. (1998) derived a steeper slope of −2.95 ± 0.12 and a higher zero-point offset of 17.89 ± 0.2 in Eq. (3). The PLC relation for the population II cepheids in the LMC is shown in Fig. 6.
It is straightforward to derive the distances to our Galactic targets using the absolute magnitudes from the PLC relationship. However, it is still necessary to take into account the amount of extinction, E(B−V), towards the stars. The individual E(B−V) values of our Galactic sample were obtained by computing a SED Kurucz model and applying an amount of reddening to match the observed values. We used a value for the total to selective Galactic extinction, Rv, of 3.1 (Weingartner & Draine 2001) to obtain the amount of extinction Av towards each star in our sample and hence the reddening-corrected distances. The luminosities were then computed using the distances and the total integrated flux below the dereddened SED model. The results are outlined in Table 5.
The error in the distances and hence the luminosities is a combined error in the absolute magnitude obtained from the PLC and the uncertainty in the amount of reddening.
 |
Fig. 6 Top: apparent V-band magnitude (mv). Bottom: reddening-free Wesenheit magnitudes for population II cepheids in the LMC. |
4. Spectroscopic results
4.1. Radial velocities
The individual radial velocities are obtained by cross-correlating the reduced spectra with a predefined software mask adapted for a given object type. A typical mask contains a large set of distinct spectral lines for a given stellar spectral type.
We made use of a F0 and a G2 mask for HP Lyr and TW Cam, respectively. Depending on S/N quality criterion, a typical number of lines used is 1200 for both masks and both stars. We only used lines obtained in spectral orders between 54 and 74 (477−655 nm), which are typically the spectral orders with the highest S/N and without strong telluric contamination.
Being very depleted, the spectra of DY Ori and EP Lyr do not show many photospheric lines. These are the two stars in the sample for which a mask adapted to their photospheric anomalies, had to be constructed. This is done by plotting a spectrum with high overall photon count and identifying the main stellar lines present. The mask is then a linelist containing the rest wavelengths of the stellar lines identified. The mask for DY Ori and EP Lyr contain 72 stellar lines covering a wavelength range of 434.2−746.8 nm. We outline here that a spectrum with an overall good S/N does not necessarily point to a good S/N in the cross-correlation function (CCF). The main factor describing the S/N in the CCF is how optimised the cross-correlation mask is.
The radial velocities for IRAS 17038−4815 and IRAS 09144−4933 from CORALIE are derived in the same way as the HERMES data using a mask suited for a star of spectral type G2.
Each radial velocity point itself is computed by fitting a Gaussian to the cross-correlation function and computing the mean of the fit. The error in each radial velocity data point is then one standard deviation of the Gaussian fit. The data points with a bad S/N in the CCF were discarded, even after using an optimised mask, as they are most likely related to spectra taken in poor weather conditions. The S/N criterion in the CCF below which the data was treated as “bad” was different from star to star.
4.2. Shocks
The atmospheres of RV Tauri stars are known to show differential motion in their line forming layers. Thus, it is possible at certain phases that two waves are moving towards each other, creating shock regions. A study by Fadeiev (1984) showed that indeed in very luminous stars, pulsations exist in the form of standing waves only in the innermost layers, while in the outer layers the waves get transformed into running waves. These shocks leave an observational signature in the spectrum of the star in the form of a distorted stellar line profile. A good example tracing the impact moment of the two waves is the appearance of the He I-5856 line, as in the case of RU Cen (e.g. Maas et al. 2002). Baird (1982) also mentions the apparition of the He I-5856 as emission in the spectrum of AC Her at certain phases in the pulsation. The He I emission line can only be produced by a violent event, i.e. a shock in the atmosphere of RU Cen.
One very prominent signature of the shock is also seen in the Hα profile at certain phases. Pollard et al. (1997) showed an increased emission at given phases consistent with the passage of two shocks waves through the photosphere.
The CCF profile is the mean profile of the stellar lines cross-correlated with the mask. Therefore, these shock events are seen as distortion in the mean CCF profile at certain phases in the pulsation cycle (e.g. Gillet et al. 1990). A double peak is seen when the differential motion has a significant velocity difference. An example of such a situation is shown in Fig. 7.
The velocities related to these distorted CCF profiles are identified and eliminated in our orbital analysis. They are still plotted as “zero-velocity red dots” indicating at which phases in the pulsation cycle they occur (see middle panels of Figs. 8 to 13).
 |
Fig. 7 Top: example of a CCF profile unaffected by shock for TW Cam. Bottom: mean CCF profile of the cross-correlated stellar lines in the spectrum with a double peak; a blue shifted and a redshifted peak indicative of two layers moving towards each other. |
4.3. Pulsation cleaned orbits
To obtain the uncontaminated orbital velocities, we first fit the original radial velocities with a Keplerian orbital model using a non-linear least-squares method. We obtain the starting parameters of the fit by a minimisation method. An eccentric orbital model (model 1) is constructed using the orbital period found in the periodogram. We then compute a second eccentric model (model 2) after a least-squares minimisation. After each non-linear least-squares fit, the variance reduction number is computed to compare model 1 and model 2. The iteration continues until there is no significant change between two subsequent variance reduction values.
The residuals to the fit are then pre-whitened to find other periodicities which now trace the pulsations. The pulsation periods found above a S/N of 4 are cross-checked with the ones found in the photometry. If they match, the residuals are then fit with the formal period and two overtones for all except HP Lyr and IRAS 17038−4815 where one overtone was used. The pulsation fit is then subtracted from the original radial velocity data to obtain a pulsation-cleaned orbit. The cleaned orbit was then fit with a Keplerian model to extract accurate orbital parameters. This procedure was repeated for all the stars in our sample.
The errors in the orbital parameters were computed using a Monte Carlo method on the radial velocity data points. A random number generator was used to scramble the data points with a mean value corresponding to the radial velocity value and a scaled standard deviation to match a fit with a χ2 value of ~1. This was done because the purely intrinsic uncertainties in the individual radial velocities were too small compared to the scatter in the data. One thousand randomised Keplerian fits of the same structure were obtained for each star, and errors were then computed by taking the standard deviation of the parameters linked to each Keplerian fit.
The main result is that the six stars in our sample are indeed binaries with orbital periods ranging from 654 to 1683 days. We have demonstrated that in the case of strong pulsators, it is a prime factor to clean the radial velocities from the pulsation signals in order pin down the orbital parameters as accurately as possible. The original orbits, the spectroscopic pulsation fit, and the pulsation-cleaned orbits are shown in Figs. 8 to 13. We note that the horizontal black lines in the fit (top and bottom panels of Figs. 8 to 13) are the systemic velocities which are outlined in Table 6 as γ. The grey shaded regions in the residuals represent a standard deviation of 3-σ. We display the individual binary orbital parameters in Table 6.
 |
Fig. 8 Top: original radial velocity data of DY Ori fitted with a Keplerian orbit folded on an orbital period of 1244 d and eccentricity of 0.3. Middle: pulsations in the radial velocity folded on a period of 60.8 d. The red squares and the purple shaded region display the positions in the phase plot where the shocks occur. Bottom: pulsation cleaned orbit folded on a period of 1230 d with an eccentricity of 0.2. |
 |
Fig. 9 Top: original radial velocity data of TW Cam fitted with a Keplerian orbit folded on an orbital period of 655 d and eccentricity of 0.3. Middle: pulsations in the radial velocity folded on a period of 86.4 d. The red squares and the purple shaded region display the positions in the phase plot where the shocks occur. Bottom: pulsation cleaned orbit folded on a period of 654 d with an eccentricity of 0.2. |
 |
Fig. 10 Top: original radial velocity data of EP Lyr fitted with a Keplerian orbit folded on an orbital period of 1080 d and eccentricity of 0.6. Middle: pulsations in the radial velocity folded on a period of 83.2 d. The red squares and the purple shaded region display the positions in the phase plot where the shocks occur. Bottom: pulsation cleaned orbit folded on a period of 1066 d with an eccentricity of 0.6. |
 |
Fig. 11 Top: original radial velocity data of HP Lyr fitted with a Keplerian orbit folded on an orbital period of 1650 d and eccentricity of 0.2. Middle: pulsations in the radial velocity folded on a period of 136 d. The red squares and the purple shaded region display the positions in the phase plot where the shocks occur. Bottom: pulsation cleaned orbit folded on a period of 1631 d with an eccentricity of 0.17. |
 |
Fig. 12 Top: original radial velocity data of IRAS 09144−4933 fitted with a Keplerian orbit folded on an orbital period of 1640 d and eccentricity of 0.4. Middle: pulsations in the radial velocity folded on a period of 100 d. The red squares and the purple shaded region display the position in the phase plot where the shocks occur. Bottom: pulsation cleaned orbit folded on a period of 1683 d with an eccentricity of 0.45. |
 |
Fig. 13 Top: original radial velocity data of IRAS 17038−4815 fitted with a Keplerian orbit folded on an orbital period of 1393 d and eccentricity of 0.6. Middle: pulsations in the radial velocity folded on a period of 37.3 d. The red squares and the purple shaded region display the position in the phase plot where the shocks occur. Bottom: pulsation cleaned orbit folded on a period of 1386 d with an eccentricity of 0.57. |
5. Discussion
5.1. Luminosities and evolutionary stage
The pulsations of the stars have been profitably used to obtain their luminosities via the PLC relation of the population II cepheids in the LMC. The big sample of LMC population II cepheids used to derive the PLC relation allowed us to better constrain the uncertainties in the slope and the intercept of the regression than the sample presented in the previous study of Alcock et al. (1998). We derive the V-band absolute magnitudes as MV = −2.53 Log (P) (± 0.03) − 1.17 (± 0.03) + 2.55 ⟨(V−I)0⟩. The slope of our PLC, −2.53 ± 0.03, is found to be slightly less steep than the value of −2.95± 0.12 given by Alcock et al. (1998). We also find a slightly more negative value of −1.17 ± 0.03 for the intercept than the value of −0.61 ± 0.2 calculated by Alcock et al. (1998). Our sample of Galactic objects are found in the ~2 to 7 kpc vicinity. Using these distances we obtained their luminosities. Assuming the tip of the RGB to be at a luminosity of ~2500 L⊙ (Kamath et al. 2016), all stars but DY Ori and EP Lyr can be classified as post-AGB candidates.
Recent surveys in the SMC and LMC enabled the discovery of a new class of dusty objects termed as “post-RGB” objects (Kamath et al. 2015, 2016). These are evolved, dusty objects with mid-IR-excesses and stellar parameters mimicking that of post-AGB stars, except that they have lower luminosities (100−2500L⊙) than expected for a post-AGB star. So far there are 42 of these objects known in the SMC and 119 in the LMC. These stars evolve off the RGB much earlier than we expect from a standard single-star evolution scenario. This is very likely the consequence of a strong binary interaction process already occurring on the RGB. The stellar parameters and luminosities of DY Ori and EP Lyr classify them as post-RGB stars. We therefore note that these two stars are the first Galactic counterparts of the newly discovered post-RGB stars in the Magellanic clouds.
In our sample, DY Ori has the lowest luminosity with a pulsation period of 30.4 days. If we consider the RV Tauri stars in the LMC, the lowest pulsation period is found to be that of OGLE-LMC-T2CEP-016, with a pulsation period of ~20.3 ± 1 days (Soszyński et al. 2008). This period translates into a luminosity of 1040 ± 40 L⊙ based on our PLC relation. This is an indication that RV Tauri stars with circumstellar dust can occupy even the low-luminosity regime in the HR diagram making them post-RGB objects (see Fig. 14).
 |
Fig. 14 Position of the Galactic RV Tauri stars on the HRD. The dark lines are evolutionary tracks from Bertelli et al. (2009). The red dashed line shows the RGB-tip at 2500 L⊙. The positions of TW Cam and IRAS 17038-4815 nearly coincide here. |
5.2. Long orbital periods and eccentricities
5.2.1. Long orbital periods
The orbital periods for our sample ranges from 650 days to 1680 days. In Table 7 (Cols. 2 and 3, respectively), we list the total orbital separation (a1 + a2) at periastron (ap) and apastron passage (aap) for two different inclinations of 90° and 60°. We used the Eggleton formula (Eggleton 1983) to estimate the effective Roche lobe radius of the primary star at periastron (RRLp) and apastron (RRLap) passage (see Cols. 6 and 7). In Col. 8 we list the radius of a star of the same luminosity, “evolved back” to the RGB or AGB phase, assuming an effective temperature of 3500 K.
The high values of the Roche lobe filling factor shown in the last column of Table 7 suggest that these stars should have interacted owing to a RLOF (roche lobe over flow) event at an earlier stage of their evolution. More evidence for a RLOF event is motivated by circumstellar material observed at this stage of their evolution. A non-conservative mass transfer event on the AGB, which causes mass to be transferred through the 2nd and 3rd Lagrangian points, is expected in our sample. This serves as a logical explanation for the presence of a CB disc. The mentioned evidence suggests that a RLOF scenario was a likely occurrence in these systems and consequently lead to an orbital shrinkage.
Derived orbital parameters for the pulsation-cleaned orbits.
It is striking that, despite the evidence for a history of Roche lobe overfilling, none of the systems encountered a dramatic spiral-in. Such a stable RLOF was already proposed by Tout & Eggleton (1988) and Han et al. (1995). This occurs when the mass-ratio is reversed prior to RLOF as a result of a tidally enhanced wind mass-loss of the primary.
The systems described here are surrounded by likely Keplerian dusty circumstellar discs which store angular momentum (e.g. Bujarrabal et al. 2015). There is enough observational evidence that the inner rim of the disc starts already at the dust sublimation radius (~3−5 AU) for our targets (De Ruyter et al. 2006; Hillen et al. 2016). The orbital separations shown in Table 6 suggest that the stellar components are close to the disc inner rim at apastron passage. This indicates a disc-binary interaction is very probable whereby angular momentum can be imparted from the binary system to the disc. It is outside the scope of this paper to investigate this, but it seems that the presence of a circumbinary disc has an important impact on the orbital evolution of these systems. This will be included in our future research.
5.2.2. Eccentricities
The eccentricities of the orbits range between 0.2 and 0.6. The non-zero eccentricities are striking. Indeed, tides are expected to circularise the orbits very efficiently when the size of the star reaches the Roche lobe radius (e.g. Zahn 1977, 1989). The orbital parameters we derive suggest that the eccentricity is maintained or increased (pumped) by some mechanism.
A few eccentricity-pumping mechanisms have been proposed to explain the e−log (P) distribution displayed by many long-period binaries with high eccentricites. The systems include sdB binaries (Vos et al. 2015), barium stars (Pols et al. 2003; Izzard et al. 2010), CH stars (McClure & Woodsworth 1990), and CEMP stars (Abate et al. 2015). The mechanisms involved are a tidally enhanced wind mass loss (Tout & Eggleton 1988), an enhanced mass loss at periastron by a RLOF (Soker 2000), eccentricity pumping by the CB disc (Dermine et al. 2013), and pumping induced by a wind-RLOF (Bonačić Marinović et al. 2008).
An eccentricity-pumping event by the CB disc could possibly explain some of the observed eccentricities in our sample of RV Tauri stars. Evidence for a disc-binary interaction is provided by the strongly depleted atmospheres among the RV Tauri stars with a disc (e.g. Gezer et al. 2015; Maas et al. 2005). The discrepancies between the above-mentioned proposed models and the observed eccentricities urges studies that go further into the question of eccentricity pumping via mass-transfer between the stars, disc-binary interaction, and other input physics not yet taken into account.
5.3. RVb, inclinations and nature of companion
We have used an updated ASAS/AAVSO photometry to study the pulsational variability with an extended coverage for the RV Tauri stars. The immediate results include an improved knowledge of their pulsational characteristics and brightness modulations throughout the orbit.
We reveal the RVb photometric nature of IRAS 17038−4815, IRAS 09144−4933, and TW Cam and the RVa photometric type of DY Ori. The long-term periodic change in the RVbs (see Table 4) of the order of the orbital period provides good evidence that the variability is associated with variable extinction through the circumstellar dust. Our results therefore further support the arguments of Waelkens et al. (1991b) and Waelkens & Mayor (1993). The RVb “phenomenon” offers a way to place constraints on the orbital inclinations of the binaries. However, there are two important factors which need to be taken into account when predicting the inclinations solely based on their RVb nature: the inner radius of the disc and the scale-height of the disc.
Generally, the inner radius of post-AGB discs is located at the dust sublimation radius (De Ruyter et al. 2006; Hillen et al. 2016, and in prep.), with AC Her being the exception (Hillen et al. 2015, and in prep.). Furthermore, the SEDs indicate that a large amount of the stellar luminosity is converted into IR-emission indicating a significant scale-height. In these cases it could well be possible that the observers’ lines of sight even graze the disc at inclinations lower than 70°. A detailed investigation of these two factors is beyond the scope of this study and we assumed a minimum orbital inclination of 70° for the RVb types.
Given that these are wide binaries, the inclinations must be significantly higher than 0° to induce a noticeable radial velocity shift. Also, for inclinations below 35°, we find improbably high values for the mass of the companion (m2) under the assumption that the primary is of 0.6 M⊙ (e.g. Weidemann 1990). These values allow us to put a lower limit of ~35° and an upper limit of 60° for the orbital inclination of the RVas.
The spectra are dominated by the highly luminous primary star and no signature of the companion is seen in the spectra. These stars are, therefore, single-lined spectroscopic binaries.
The mass functions range from 0.08 to 0.55, which translates into a minimum mass range of 0.5 to 1.2 M⊙ (displayed in Table 7) for the companion, assuming a mass of 0.6 M⊙ for the primary and an edge-on inclination. The minimum masses of the companion offer two possibilities of their nature: a low-luminosity white dwarf (WD) or an unevolved low-mass main sequence star.
We argue that the companion is not likely a WD for two reasons:
-
Considering the mass of a white dwarf is well constrained at~0.6 ± 0.1 M⊙ (e.g. Weidemann 1990). Our lower mass limit of the companion almost rules out this possibility. We note here that HP Lyr still qualifies to have a WD secondary based on a minimum companion mass of ~0.5 M⊙.
-
A compact white dwarf companion would have accreted mass from the primary most probably causing the system to show symbiotic activity.
Radii of the stars and roche lobe parameters.
6. Conclusions
We have used high-resolution spectroscopic data from the HERMES and CORALIE spectrographs to probe the binary status of a sample of six Galactic RV Tauri stars with a disc. All of them are binaries and we therefore extend the sample of known binary RV Tauri stars with a disc from 6 to 12.
We present a novel PLC relationship calibrated using data for 187 type II cepheids in the LMC available from Soszyński et al. (2008). The PLC was used to obtain accurate distances and hence luminosities of our sample of Galactic RV Tauri stars. The luminosities of HP Lyr, IRAS 17038−4815, IRAS 09144−4933, and TW Cam suggest that they are post-AGB stars. The lower luminosities of DY Ori and EP Lyr show that these objects have evolved off the RGB, making them dusty post-RGB objects. According to theory, these stars should have experienced a spiral-in event and have a circularised orbit at this stage. The observed long orbital periods and eccentricities indicate that these binary systems do not follow standard binary evolution models.
The stars included in this study, show mild to highly depleted photospheres; a consequence of re-accretion of gas from the disc. Together with the disc-binarity correlation, the link between binarity and depletion is extended.
Long-term variations in the photometric time series of the order of the orbital period is detected for IRAS 17038−4815, IRAS 09144−4933, and TW Cam. This enabled us to classify them as RVb photometric types and consequently place constraints on their orbital inclinations and the mass of their companions. We also prove the RVa nature of DY Ori: there is no significant long-term variation seen in its photometric time series.
Acknowledgments
This research has been carried out based on observations made using the Mercator Telescope, operated on the island of La Palma by the Flemish Community, situated at the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrof´isica de Canarias. We used data from the HERMES spectrograph, supported by the Fund for Scientific Research of Flanders (FWO), the Research Council of K.U. Leuven, the Fonds National Recherches Scientific (FNRS), the Royal Observatory of Belgium, the Observatoire de Genève, Switzerland, and the Thringer Landessternwarte Tautenburg, Germany. This research has been conducted based on funding from the Research Council of K.U. Leuven and was partially funded by the Belgian Science Policy Office under contract BR/143/A2/STARLAB. In this study we also included data from the Swiss Leonhard Euler 1.2 m Telescope located at the Haute Provence Observatory in La Silla. We used the following internet-based resources: NASA Astrophysics Data System for bibliographic services; Simbad; the VizieR online catalogue operated by CDS; and the ASAS and AAVSO photometric databases. R.M. thanks Brent Miszalski, Shazrene Mohamed, Peter Wood, and Jonas Debosscher for their helpful comments and inputs. The authors thank the anonymous referee for the valuable comments which helped in improving the paper.
References
- Abate, C., Pols, O. R., Karakas, A. I., & Izzard, R. G. 2015, A&A, 576, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alcock, C., Allsman, R. A., Alves, D. R., et al. 1998, AJ, 115, 1921 [NASA ADS] [CrossRef] [Google Scholar]
- Baird, S. R. 1982, PASP, 94, 850 [NASA ADS] [CrossRef] [Google Scholar]
- Baranne, A., Mayor, M., & Poncet, J. L. 1979, Vist. Astron., 23, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Baranne, A., Queloz, D., Mayor, M., et al. 1996, A&AS, 119, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertelli, G., Nasi, E., Girardi, L., & Marigo, P. 2009, A&A, 508, 355 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonačić Marinović, A. A., Glebbeek, E., & Pols, O. R. 2008, A&A, 480, 797 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Breger, M., Stich, J., Garrido, R., et al. 1993, A&A, 271, 482 [NASA ADS] [Google Scholar]
- Bujarrabal, V., Castro-Carrizo, A., Alcolea, J., & Van Winckel, H. 2015, A&A, 575, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- De Ruyter, S., Van Winckel, H., Maas, T., et al. 2006, A&A, 448, 641 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Degroote, P., Acke, B., Samadi, R., et al. 2011, A&A, 536, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dermine, T., Izzard, R. G., Jorissen, A., & Van Winckel, H. 2013, A&A, 551, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eggleton, P. P. 1983, ApJ, 268, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Erleksova, G. E. 1971, Peremennye Zvezdy, 18, 53 [NASA ADS] [Google Scholar]
- Evans, T. L. 1985, MNRAS, 217, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Fadeiev, I. A. 1984, Ap&SS, 100, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Gezer, I., Van Winckel, H., Bozkurt, Z., et al. 2015, MNRAS, 453, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Gillet, D., Burki, G., & Duquennoy, A. 1990, A&A, 237, 159 [NASA ADS] [Google Scholar]
- Giridhar, S., Rao, N. K., & Lambert, D. L. 1994, ApJ, 437, 476 [NASA ADS] [CrossRef] [Google Scholar]
- Giridhar, S., Lambert, D. L., & Gonzalez, G. 1998, ApJ, 509, 366 [NASA ADS] [CrossRef] [Google Scholar]
- Giridhar, S., Lambert, D. L., & Gonzalez, G. 2000, ApJ, 531, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Giridhar, S., Lambert, D. L., Reddy, B. E., Gonzalez, G., & Yong, D. 2005, ApJ, 627, 432 [NASA ADS] [CrossRef] [Google Scholar]
- Gonzalez, G., Lambert, D. L., & Giridhar, S. 1997, ApJ, 479, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Graczyk, D., Mikolajewski, M., Leedjarv, L., et al. 2002, Acta Astron., 52, 293 [NASA ADS] [Google Scholar]
- Han, Z., Eggleton, P. P., Podsiadlowski, P., & Tout, C. A. 1995, MNRAS, 277, 1443 [NASA ADS] [CrossRef] [Google Scholar]
- Haschke, R., Grebel, E. K., & Duffau, S. 2011, AJ, 141, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Hillen, M., de Vries, B. L., Menu, J., et al. 2015, A&A, 578, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hillen, M., Kluska, J., Le Bouquin, J.-B., et al. 2016, A&A, 588, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Izzard, R. G., Dermine, T., & Church, R. P. 2010, A&A, 523, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jura, M. 1986, ApJ, 309, 732 [NASA ADS] [CrossRef] [Google Scholar]
- Kamath, D., Wood, P. R., & Van Winckel, H. 2015, MNRAS, 454, 1468 [NASA ADS] [CrossRef] [Google Scholar]
- Kamath, D., Wood, P. R., Van Winckel, H., & Nie, J. D. 2016, A&A, 586, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kholopov, P. N., Samus, N. N., Kazarovets, E. V., & Perova, N. B. 1985, Information Bulletin on Variable Stars, 2681, 1 [NASA ADS] [Google Scholar]
- Kiss, L. L., Derekas, A., Szabó, G. M., Bedding, T. R., & Szabados, L. 2007, MNRAS, 375, 1338 [NASA ADS] [CrossRef] [Google Scholar]
- Kodaira, K., Greenstein, J. L., & Oke, J. B. 1970, ApJ, 159, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Kurucz, R. L. 1979, ApJS, 40, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Lambert, D. L., Hinkle, K. H., & Luck, R. E. 1988, ApJ, 333, 917 [NASA ADS] [CrossRef] [Google Scholar]
- Lloyd Evans, T. 1985, MNRAS, 217, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Maas, T. 2003, Ph.D. Thesis, Katholieke Universiteit Leuven, Belgium [Google Scholar]
- Maas, T., Van Winckel, H., & Waelkens, C. 2002, A&A, 386, 504 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maas, T., Van Winckel, H., & Lloyd Evans, T. 2005, A&A, 429, 297 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Madore, B. F. 1976, MNRAS, 177, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Madore, B. F. 1982, ApJ, 253, 575 [NASA ADS] [CrossRef] [Google Scholar]
- Matsunaga, N., Feast, M. W., & Menzies, J. W. 2009, in AIP Conf. Ser. 1170, eds. J. A. Guzik, & P. A. Bradley, 96 [Google Scholar]
- McClure, R. D., & Woodsworth, A. W. 1990, ApJ, 352, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Nemec, J. M., Nemec, A. F. L., & Lutz, T. E. 1994, AJ, 108, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Ngeow, C.-C., & Kanbur, S. M. 2005, MNRAS, 360, 1033 [NASA ADS] [CrossRef] [Google Scholar]
- Pojmanski, G. 2002, Acta Astron., 52, 397 [NASA ADS] [Google Scholar]
- Pollard, K. H., & Cottrell, P. L. 1995, in IAU Colloq. 155, Astrophysical Applications of Stellar Pulsation, ASP Conf. Ser., 83, 409 [NASA ADS] [Google Scholar]
- Pollard, K. R., Cottrell, P. L., Kilmartin, P. M., & Gilmore, A. C. 1996, MNRAS, 279, 949 [NASA ADS] [Google Scholar]
- Pollard, K. R., Cottrell, P. L., Lawson, W. A., Albrow, M. D., & Tobin, W. 1997, MNRAS, 286, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Pols, O. R., Karakas, A. I., Lattanzio, J. C., & Tout, C. A. 2003, in ASP Conf. Ser. 303, eds. R. L. M. Corradi, J. Mikolajewska, & T. J. Mahoney, 290 [Google Scholar]
- Preston, G. W., Krzeminski, W., Smak, J., & Williams, J. A. 1963, ApJ, 137, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Queloz, D., Casse, M., & Mayor, M. 1999, in IAU Colloq. 170, Precise Stellar Radial Velocities, eds. J. B. Hearnshaw, & C. D. Scarfe, ASP Conf. Ser. 185, 13 [Google Scholar]
- Raskin, G., van Winckel, H., Hensberge, H., et al. 2011, A&A, 526, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ripepi, V., Moretti, M. I., Marconi, M., et al. 2015, MNRAS, 446, 3034 [NASA ADS] [CrossRef] [Google Scholar]
- Samus, N. N., Kazarovets, E. V., Pastukhova, E. N., Tsvetkova, T. M., & Durlevich, O. V. 2009, PASP, 121, 1378 [NASA ADS] [CrossRef] [Google Scholar]
- Scargle, J. D. 1982, ApJ, 263, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, E. G., Chab, J. R., & Reiswig, D. E. 1995, AJ, 109, 1239 [NASA ADS] [CrossRef] [Google Scholar]
- Schneller, H. 1931, Astron. Nachr., 243, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Soker, N. 2000, A&A, 357, 557 [NASA ADS] [Google Scholar]
- Soszyński, I., Udalski, A., Szymański, M. K., et al. 2008, Acta Astron., 58, 293 [NASA ADS] [Google Scholar]
- Tout, C. A., & Eggleton, P. P. 1988, MNRAS, 231, 823 [NASA ADS] [CrossRef] [Google Scholar]
- van den Bergh, S., & Hagen, G. L. 1968, AJ, 73, 569 [NASA ADS] [CrossRef] [Google Scholar]
- Van Winckel, H. 2007, Baltic Astr., 16, 112 [Google Scholar]
- Van Winckel, H., Waelkens, C., & Waters, L. B. F. M. 1995, A&A, 293, L25 [NASA ADS] [Google Scholar]
- Van Winckel, H., Waelkens, C., Waters, L. B. F. M., et al. 1998, A&A, 336, L17 [NASA ADS] [Google Scholar]
- Van Winckel, H., Waelkens, C., Fernie, J. D., & Waters, L. B. F. M. 1999, A&A, 343, 202 [NASA ADS] [Google Scholar]
- Van Winckel, H., Lloyd Evans, T., Briquet, M., et al. 2009, A&A, 505, 1221 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vos, J., Østensen, R. H., Marchant, P., & Van Winckel, H. 2015, A&A, 579, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wachmann, A. A. 1968, Astronomische Abhandlungen der Hamburger Sternwarte, 8, 105 [NASA ADS] [Google Scholar]
- Waelkens, C., & Mayor, M. 1993, in Luminous High-Latitude Stars, ASP Conf. Ser., 45, 318 [NASA ADS] [Google Scholar]
- Waelkens, C., Lamers, H. J. G. L. M., Waters, L. B. F. M., et al. 1991a, A&A, 242, 433 [NASA ADS] [Google Scholar]
- Waelkens, C., Van Winckel, H., Bogaert, E., & Trams, N. R. 1991b, A&A, 251, 495 [NASA ADS] [Google Scholar]
- Wahlgren, G. M. 1992, AJ, 104, 1174 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, A. R. 2012, Ap&SS, 341, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Wallerstein, G. 2002, PASP, 114, 689 [NASA ADS] [CrossRef] [Google Scholar]
- Waters, L. B. F. M., Trams, N. R., & Waelkens, C. 1992, A&A, 262, L37 [NASA ADS] [Google Scholar]
- Weidemann, V. 1990, ARA&A, 28, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Wenzel, W. 1961, Information Bulletin on Variable Stars, 1, 1 [NASA ADS] [Google Scholar]
- Zahn, J.-P. 1977, A&A, 57, 383 [NASA ADS] [Google Scholar]
- Zahn, J.-P. 1989, A&A, 220, 112 [NASA ADS] [Google Scholar]
- Zsoldos, E. 1995, A&A, 296, 122 [NASA ADS] [Google Scholar]
- Zsoldos, E., & Kollath, Z. 1991, Ap&SS, 181, 251 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Spectral energy distributions
 |
Fig. A.1 SED of EP Lyr. The red line is the stellar photosphere fitted using a Kurucz model and the black line is the dereddened model. |
 |
Fig. A.2 SED of HP Lyr. The red line is the stellar photosphere fitted using a Kurucz model and the black line is the dereddened model. |
 |
Fig. A.3 SED of IRAS 17038−4815. The red line is the stellar photosphere fitted using a Kurucz model and the black line is the dereddened model. |
 |
Fig. A.4 SED of IRAS 09144−4933. The red line is the stellar photosphere fitted using a Kurucz model and the black line is the dereddened model. |
 |
Fig. A.5 SED of TW Cam. The red line is the stellar photosphere fitted using a Kurucz model and the black line is the dereddened model. |
Appendix B: SED photometry
Photometric bands used to construct the SED of DY Ori.
Photometric bands used to construct the SED of EP Lyr.
Photometric bands used to construct the SED of HP Lyr.
Photometric bands used to construct the SED of IRAS 17038−4815.
Photometric bands used to construct the SED of IRAS 09144−4933.
Photometric bands used to construct the SED of TW Cam.
All Tables
Distances and luminosities of the Galactic sample, derived using the PLC relationship.
All Figures
 |
Fig. 1 Example of the SED of TW Cam; a RV Tauri star surrounded by a disc. The red line shows the fit with a photospheric model atmosphere. The clear broad IR-excess can already be seen at a wavelength of ~2 μm, indicative of a dusty disc. |
| In the text | |
 |
Fig. 2 Photometric phase plot of DY Ori, EP Lyr, and HP Lyr, folded on a formal period of 60.8 days, 83.2 days, and 136.8 days, respectively. The horizontal solid black line is the mean Vmag. |
| In the text | |
 |
Fig. 3 Photometric phase plot of IRAS 17038−4815 and TW Cam folded on a formal period of 75.9 days and 86.1 days, respectively. The horizontal solid black line is the mean Vmag. |
| In the text | |
 |
Fig. 4 Time series of the pulsations using ASAS and AAVSO photometric data. Here we mainly display their pulsational nature and not the long-term variability. The solid red line is the pulsation model fit to the photometric time series and the horizontal solid black line is the mean Vmag. |
| In the text | |
 |
Fig. 5 SED of DY Ori. The red line is the stellar photosphere fitted using a Kurucz model and the black line is the dereddened model. |
| In the text | |
 |
Fig. 6 Top: apparent V-band magnitude (mv). Bottom: reddening-free Wesenheit magnitudes for population II cepheids in the LMC. |
| In the text | |
 |
Fig. 7 Top: example of a CCF profile unaffected by shock for TW Cam. Bottom: mean CCF profile of the cross-correlated stellar lines in the spectrum with a double peak; a blue shifted and a redshifted peak indicative of two layers moving towards each other. |
| In the text | |
 |
Fig. 8 Top: original radial velocity data of DY Ori fitted with a Keplerian orbit folded on an orbital period of 1244 d and eccentricity of 0.3. Middle: pulsations in the radial velocity folded on a period of 60.8 d. The red squares and the purple shaded region display the positions in the phase plot where the shocks occur. Bottom: pulsation cleaned orbit folded on a period of 1230 d with an eccentricity of 0.2. |
| In the text | |
 |
Fig. 9 Top: original radial velocity data of TW Cam fitted with a Keplerian orbit folded on an orbital period of 655 d and eccentricity of 0.3. Middle: pulsations in the radial velocity folded on a period of 86.4 d. The red squares and the purple shaded region display the positions in the phase plot where the shocks occur. Bottom: pulsation cleaned orbit folded on a period of 654 d with an eccentricity of 0.2. |
| In the text | |
 |
Fig. 10 Top: original radial velocity data of EP Lyr fitted with a Keplerian orbit folded on an orbital period of 1080 d and eccentricity of 0.6. Middle: pulsations in the radial velocity folded on a period of 83.2 d. The red squares and the purple shaded region display the positions in the phase plot where the shocks occur. Bottom: pulsation cleaned orbit folded on a period of 1066 d with an eccentricity of 0.6. |
| In the text | |
 |
Fig. 11 Top: original radial velocity data of HP Lyr fitted with a Keplerian orbit folded on an orbital period of 1650 d and eccentricity of 0.2. Middle: pulsations in the radial velocity folded on a period of 136 d. The red squares and the purple shaded region display the positions in the phase plot where the shocks occur. Bottom: pulsation cleaned orbit folded on a period of 1631 d with an eccentricity of 0.17. |
| In the text | |
 |
Fig. 12 Top: original radial velocity data of IRAS 09144−4933 fitted with a Keplerian orbit folded on an orbital period of 1640 d and eccentricity of 0.4. Middle: pulsations in the radial velocity folded on a period of 100 d. The red squares and the purple shaded region display the position in the phase plot where the shocks occur. Bottom: pulsation cleaned orbit folded on a period of 1683 d with an eccentricity of 0.45. |
| In the text | |
 |
Fig. 13 Top: original radial velocity data of IRAS 17038−4815 fitted with a Keplerian orbit folded on an orbital period of 1393 d and eccentricity of 0.6. Middle: pulsations in the radial velocity folded on a period of 37.3 d. The red squares and the purple shaded region display the position in the phase plot where the shocks occur. Bottom: pulsation cleaned orbit folded on a period of 1386 d with an eccentricity of 0.57. |
| In the text | |
 |
Fig. 14 Position of the Galactic RV Tauri stars on the HRD. The dark lines are evolutionary tracks from Bertelli et al. (2009). The red dashed line shows the RGB-tip at 2500 L⊙. The positions of TW Cam and IRAS 17038-4815 nearly coincide here. |
| In the text | |
 |
Fig. A.1 SED of EP Lyr. The red line is the stellar photosphere fitted using a Kurucz model and the black line is the dereddened model. |
| In the text | |
 |
Fig. A.2 SED of HP Lyr. The red line is the stellar photosphere fitted using a Kurucz model and the black line is the dereddened model. |
| In the text | |
 |
Fig. A.3 SED of IRAS 17038−4815. The red line is the stellar photosphere fitted using a Kurucz model and the black line is the dereddened model. |
| In the text | |
 |
Fig. A.4 SED of IRAS 09144−4933. The red line is the stellar photosphere fitted using a Kurucz model and the black line is the dereddened model. |
| In the text | |
 |
Fig. A.5 SED of TW Cam. The red line is the stellar photosphere fitted using a Kurucz model and the black line is the dereddened model. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


