| Issue |
A&A
Volume 597, January 2017
|
|
|---|---|---|
| Article Number | A37 | |
| Number of page(s) | 16 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201628708 | |
| Published online | 20 December 2016 | |
A generalized Bayesian inference method for constraining the interiors of super Earths and sub-Neptunes
1 Physics Institute, University of Bern, Sidlerstrasse 5, 3012 Bern, Switzerland
e-mail: caroline.dorn@space.unibe.ch
2 Institute of Geophysics, ETH Zürich, Sonneggstrasse 5, 8092 Zürich, Switzerland
3 Department of Geosciences, Raymond & Beverly Sackler Faculty of Exact Sciences, Tel Aviv University, 69978 Tel Aviv, Israel
4 Royal Observatory of Belgium, Earth Rotation and Space Geodesy, 1180 Bruxelles, Belgium
Received: 13 April 2016
Accepted: 26 August 2016
Aims. We aim to present a generalized Bayesian inference method for constraining interiors of super Earths and sub-Neptunes. Our methodology succeeds in quantifying the degeneracy and correlation of structural parameters for high dimensional parameter spaces. Specifically, we identify what constraints can be placed on composition and thickness of core, mantle, ice, ocean, and atmospheric layers given observations of mass, radius, and bulk refractory abundance constraints (Fe, Mg, Si) from observations of the host star’s photospheric composition.
Methods. We employed a full probabilistic Bayesian inference analysis that formally accounts for observational and model uncertainties. Using a Markov chain Monte Carlo technique, we computed joint and marginal posterior probability distributions for all structural parameters of interest. We included state-of-the-art structural models based on self-consistent thermodynamics of core, mantle, high-pressure ice, and liquid water. Furthermore, we tested and compared two different atmospheric models that are tailored for modeling thick and thin atmospheres, respectively.
Results. First, we validate our method against Neptune. Second, we apply it to synthetic exoplanets of fixed mass and determine the effect on interior structure and composition when (1) radius; (2) atmospheric model; (3) data uncertainties; (4) semi-major axes; (5) atmospheric composition (i.e., a priori assumption of enriched envelopes versus pure H/He envelopes); and (6) prior distributions are varied.
Conclusions. Our main conclusions are: (1) given available data, the range of possible interior structures is large; quantification of the degeneracy of possible interiors is therefore indispensable for meaningful planet characterization. (2) Our method predicts models that agree with independent estimates of Neptune’s interior. (3) Increasing the precision in mass and radius leads to much improved constraints on ice mass fraction, size of rocky interior, but little improvement in the composition of the gas layer, whereas an increase in the precision of stellar abundances enables to better constrain mantle composition and relative core size; (4) for thick atmospheres, the choice of atmospheric model can have significant influence on interior predictions, including the rocky and icy interior. The preferred atmospheric model is determined by envelope mass. This study provides a methodology for rigorously analyzing general interior structures of exoplanets which may help to understand how exoplanet interior types are distributed among star systems. This study is relevant in the interpretation of future data from missions such as TESS, CHEOPS, and PLATO.
Key words: methods: statistical / planets and satellites: interiors / stars: abundances / planets and satellites: composition / planets and satellites: atmospheres / methods: analytical
© ESO, 2016
1. Introduction
The characterization of planet interiors is one of the main foci of current exoplanetary science. For the characterization of super Earths and sub-Neptunes, we mostly rely on mass and radius measurements. Direct measurements of atmospheres are, thus far, mostly limited to transiting hot Jupiters and a few Sub-Neptunes (Iyer et al. 2016), with the exception of super Earth 55 Cnc E (Tsiaras et al. 2016; Demory et al. 2016). For interior characterization, common practice is the use of mass-radius-plots where mass and radius of exoplanets are compared to synthetically computed interior models (e.g., Sotin et al. 2007; Seager et al. 2007; Fortney et al. 2007; Dressing et al. 2015; Howe et al. 2014). However, it is difficult to know (1) how well one interior model compares with the generally large number of other possible interior scenarios that also fit data and (2) which structural parameters can actually be constrained by the observations. Thus, this approach fails to address the degeneracy problem that is, that different interior models can have identical mass and radius. In order to draw meaningful conclusions about an exoplanet’s interior it is therefore necessary to account for this inherent degeneracy (e.g., Rogers & Seager 2010; Schmitt et al. 2014; Carter et al. 2012; Weiss et al. 2016; Dorn et al. 2015).
The Bayesian analysis of Rogers & Seager (2010) to exoplanets of three to four parameters was generalized for purely rocky exoplanets by Dorn et al. (2015). Here, we extend the full probabilistic analysis of Dorn et al. (2015) to more general interior structures by including volatile elements in form of icy layers, oceans, and atmospheres. The previous work of Rogers & Seager (2010) uses a grid search method which calls for strong a priori assumptions on structure and composition of exoplanets to significantly reduce the parameter space. However, the number of parameters that affect mass and radius is large (e.g., it comprises composition and size of core, mantle, ice layers, and gas, as well as internal energy). Here, we present a generalized Bayesian inference scheme that incorporates the following aspects:
-
Our method is applicable to a wide range of planet-types,including rocky super Earths and sub-Neptunes.
-
We employ a full probabilistic Bayesian inference analysis using a Markov chain Monte Carlo (McMC) technique to constrain core size, mantle thickness and composition, mass of water-ice, and key characteristics of the atmosphere (e.g., mass, intrinsic luminosity, composition).
-
We test two different atmospheric models, tailored to thick and thin atmospheres, that account for enrichments in elements heavier than H and He.
-
We employ state-of-the-art modeling to compute interior structure based on self-consistent thermodynamics for a pure iron core, a silicate mantle, high-pressure ice, water ocean, and atmosphere (to some extent).
-
Compared to previous work of Rogers & Seager (2010), our scheme can also be used for high dimensional parameter spaces.
Besides mass and radius estimates, additional constraints are crucial to reduce model degeneracy (e.g., Dorn et al. 2015; Grasset et al. 2009). Dorn et al. (2015) demonstrate that the use of relative bulk abundance constraints of Fe/Si and Mg/Si taken from the host star (henceforth referred to as abundance constraints) leads to much improved constraints on core size and mantle composition in the case of purely rocky exoplanets. The validity of a direct correlation between stellar and planetary relative bulk abundances is suggested by observational solar system studies and planet formation models (Carter et al. 2012; Lodders 2003; Drake & Righter 2002; McDonough & Sun 1995; Bond et al. 2010; Elser et al. 2012; Johnson et al. 2012; Thiabaud et al. 2015). Here, we also assume solar bulk abundance constraints based on spectroscopic measurements (Lodders 2003).
Our generalized interior structure model is based on previous studies of mass-radius relations. Generally, H2O in liquid and high-pressure ice form (e.g., Valencia et al. 2007a; Seager et al. 2007), and H2-He atmospheres (e.g., Rogers et al. 2011; Fortney et al. 2007) are considered. Although it would not be surprising if the compositional diversity of ices and atmospheres exceeds the one found in the solar system (e.g., Newsom 1995), the few observational data on exoplanets limit us to relatively simple planetary interior models.
The structural parameters that we investigate include: (1) internal energy, mass, and composition of the gas layer; (2) mass and temperature of the ice layer; (3) mantle size and composition; and (4) core size. For present purposes, we assume a general planetary structure consisting of a pure iron core, a silicate mantle, a water ice layer and an atmosphere. To compute the resultant density profile for the purpose of estimating mass and radius, we follow Dorn et al. (2015) and assume hydrostatic equilibrium coupled with a thermodynamic approach based on Gibbs free-energy minimization and Equation-of-State (EoS) modeling.
In this study, we wish to quantify the influence of the following parameters on predicted interior structure and composition: (1) planet radius; (2) data uncertainty (e.g., mass, radius, bulk abundances); (3) semi-major axis; (4) atmospheric model; (5) atmospheric composition (i.e., a priori assumption of enriched envelopes versus pure H/He envelopes); and (6) prior distributions. In a companion paper (Dorn et al. 2017), we present results on the application of our proposed method to six exoplanets (HD 219134b, Kepler-10b, Kepler-93b, CoRoT-7b, 55 Cnc e, and HD 97658b) for which spectroscopic measurement of their host star’s photospheres are available (Hinkel et al. 2014).
The outine of this study is as follows: we describe the iterative inference scheme (Sect. 2.1), model parameters (Sect. 2.2), data (Sect. 2.3), and the forward model (Sect. 2.4). In Sect. 3, we validate our method against Neptune and present results for different synthetic planet cases. In Sects. 4 and 5, we discuss results and conclude.
2. Methodology
2.1. Bayesian inference
We employ a Bayesian method to compute the posterior probability density function (pdf) for each model parameter m from data d and prior information. According to Bayes’ theorem, the posterior distribution p(m | d) for a fixed model parameterization, conditional on data, is proportional to prior information p(m) on model parameters and the likelihood function L(m | d), which can be interpreted in probabilistic terms as a measure of how well a given model fits data: 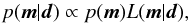 (1)and
(1)and 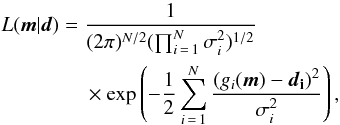 (2)where N is the total number of data points, and σi is the estimated error on the ith datum. In practice, the posterior distribution can not be derived analytically; instead we employ McMC simulation that samples the prior parameter space and evaluates the distance of the response of each candidate model to data. Finally, we use the Metropolis-Hastings algorithm to efficiently explore the posterior distribution.
(2)where N is the total number of data points, and σi is the estimated error on the ith datum. In practice, the posterior distribution can not be derived analytically; instead we employ McMC simulation that samples the prior parameter space and evaluates the distance of the response of each candidate model to data. Finally, we use the Metropolis-Hastings algorithm to efficiently explore the posterior distribution.
Briefly, the inference strategy works as follows. An initial starting model is drawn randomly from the prior distribution. The posterior density of this model is calculated using Eqs. (1), (2). A new (candidate) model is subsequently created from a proposal distribution that is centered around the current model. Moving from the current to the new model is accepted with a probability that depends on their likelihood ratios (Mosegaard & Tarantola 1995). The method works iteratively and the samples that are generated with this approach are distributed according to the posterior distribution. We refer to Dorn et al. (2015) for more details.
The large number of models needed for the analysis requires very efficient computations. Presently, generating models of the internal structure of a planet takes on average 40−90 s of CPU time on a four quad-core AMD Opteron 8380 CPU node and 32 GB of RAM. Ten independent McMC chains were run. Burn-in periods (i.e., number of samples until stationary distribution has been reached) last on average some hundred samples. Convergence is reached when the effective length (actual length divided by the autocorrelation length) is large (>1000). In all, we analyzed some 105 models.
2.2. Model parameterization
Our exoplanet interior model consists of a layered sphere with an iron core surrounded by a silicate mantle, a water layer, and an atmosphere as illustrated in Fig. 1. We distinguish between two different atmospheric models: a radiative transfer model (model I) and a pressure scale-height model (model II). These models are discussed further in Sect. 2.4.4. The key characteristics of both models are parameterized in Table 1.
Summary of model parameters m.
 |
Fig. 1 Illustration of model parameterization. a) Model I parameters are core radius rcore, mantle composition c comprising the oxides Na2O-CaO-FeO-MgO-Al2O3-SiO2, mantle radius rmantle, mass of water mwater, mass of envelope menv, envelope Luminosity L, and envelope metallicity Zenv. b) Model II parameters are as for a), with atmosphere parameterized by pressure at the bottom of the atmosphere pbatm, number of scale-heights of opaque layers N, mean molecular weight μ, and a temperature-related parameter α. See Sect. 2.2 and Table 1 for more details. |
2.3. Data
The data d that we rely on are listed in Table 2.
Summary of data d.
Fe/Sibulk is the mass ratio between the mass of iron to silicate for the entire planet (core and mantle), whereas Fe/Simantle is only that which is contained in the mantle. Since all magnesium and silicate are in the mantle, Mg/Sibulk equals their mass ratio for the mantle Mg/Simantle. We use the stellar abundances (Fe/Sistar and Mg/Sistar) as a proxy for Fe/Sibulk and Mg/Sibulk. Similarly, we fix the absolute abundance of minor refractory elements (Na, Ca, and Al) in the mantle cminor to stellar values. Here, we consider solar estimates for Fe/Si and Mg/Si and associated uncertainties, as well as Na2O, CaO, and Al2O3 using the values of Lodders et al. (2009). Stellar radius, and stellar effective temperature are also fixed parameters. Because uncertainty on stellar radius is generally small compared to uncertainties on planet radius, we neglect possible correlations between both and fix stellar radius.
2.4. Structure model
Data d and model parameters m are linked by a physical model embodied by the forward operator g(·), 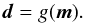 (3)For a given model m of the interior structure, mass M, radius R, and Fe/Sibulk are computed and compared with observed data d. The function g(m) combines thermodynamic, Equation-of-State (EoS), and atmospheric modeling as described in the following sections.
(3)For a given model m of the interior structure, mass M, radius R, and Fe/Sibulk are computed and compared with observed data d. The function g(m) combines thermodynamic, Equation-of-State (EoS), and atmospheric modeling as described in the following sections.
2.4.1. Iron core
In our model, we assume that the core is made of pure solid hcp (hexagonal close-packed) iron. Unlike in Earth’s core, we neglect light elements and nickel and disregard other iron polymorphs that stabilize at high temperatures. To compute the core density profile, we use an EoS for hcp iron provided by Bouchet et al. (2013). It is based on results obtained from ab initio molecular dynamics simulations for pressures up to 1500 GPa and temperatures up to about 15 000 K and is in good agreement with experimental data obtained at Earth’s core conditions. This extensive pressure-temperature (p-T) range allows for modeling rocky exoplanets up to ten Earth masses (M⊕). Throughout, we assume an adiabatic temperature profile.
2.4.2. Silicate mantle
Computing the mantle density profile is done in a manner analogous to Dorn et al. (2015). Equilibrium mineralogy and density are computed as a function of pressure, temperature, and bulk composition by Gibbs energy minimization (Connolly 2009) within the model chemical system Na2O-CaO-FeO-MgO-Al2O3-SiO2. For these calculations the pressure is obtained by integrating the load from the surface boundary condition. As in Dorn et al. (2015) we fix the thermal gradient in the mantle based on the adiabatic gradient of Earth’s mantle. The mantle surface temperature equals the maximum of either the temperature at the bottom of the water layer or 1600 K (usual reference temperature of the Earth). For this purpose, we adopt the thermodynamic formulation of Stixrude & Lithgow-Bertelloni (2005) and parameters given in Stixrude & Lithgow-Bertelloni (2011).
2.4.3. Water layer
Water has a rich phase diagram with a variety of structural transitions depending on temperature and pressure (e.g., French et al. 2009). In most of our planet realizations, temperatures in the water layer generally range from ~250 K to ~1000 K and pressures up to a few hundred GPa. In order to compute the density profile of the water layer, we follow Vazan et al. (2013), using a quotidian equation of state (QEoS), which combines the Cowan ion EoS with the Thomas-Fermi model for electrons and treats H2O as a mixture of atoms. This QEoS is in good agreement with the widely used ANEOS (Thompson & Lauson 1972) and SESAME EoS (Lyon & Johnson 1992). Above 44.3 GPa, we use the tabulated EoS from Seager et al. (2007) that is derived from DFT simulations and predict a gradual transformation from ice VIII to X. We assume an adiabatic thermal profile in the ice layer.
2.4.4. Atmospheric models
Previous works on mass-radius relationships are often restricted to pure H/He envelopes (e.g., Rogers & Seager 2010; Howe et al. 2014). However, the compositional diversity might be large (Newsom 1995) and significantly effect radius (e.g., Baraffe et al. 2008; Vazan et al. 2015). Here, we employ two different atmospheric models that account for enriched atmospheres (with the caveat of assuming ideal gas behavior). Model I solves the radiative transfer equation. This model assumes ideal gas behavior and accounts for the presence of H, He, C, and O. It considers opacities that are adapted to solar abundances (Lodders 2003). More detailed and complex calculation of absorption and emission coefficients that inherit self-consistent opacities, scattering, clouds, and non-equilibrium chemistry could theoretically also be taken into account. However, in practice, the sparseness of available data does not warrant a more sophisticated treatment. Mass and radius observations will only allow us to constrain key characteristics of the envelope. For comparison, we also employ a second atmospheric model II that calculates an isothermal atmosphere with a simple pressure model using the scale-height model. Model II is computationally very inexpensive. The validity of models I and II is roughly restricted to 0.01 > menv/M and 0.0001 > menv/M, respectively. Details on these limits are discussed in Sect. 3.2.2. Both models are described in the following.
Atmospheric model I:
relies on the atmospheric code presented in Venturini et al. (2015), which has been adapted to compute planetary radii. For a radius and mass of the solid interior, distance to star a, stellar effective temperature Tstar, stellar radius Rstar, planet envelope luminosity L, envelope metallicity Zenv, and envelope mass menv, we solve the equations of hydrostatic equilibrium, mass conservation, and energy transport. As in Venturini et al. (2015), we implement the CEA (Chemical Equilibrium with Applications) package (Gordon & McBride 1994) for the EoS, which performs chemical equilibrium calculations for an arbitrary gaseous mixture, including dissociation and ionization and assuming ideal gas behavior. We assume an envelope with an elemental composition of H, He, C, and O. We define the envelope metallicity as the mass fraction of C and O in the envelope, which can vary between 0 and 1. The reason to implement CEA and not a more sophisticated EoS (for example, one that can take into account degeneracy of free electrons) is simply because no such EoS exists for an arbitrary mixture of H, He, C, and O.
These chemical elements are fundamental because they allow for the formation of key atmospheric molecules such as H2O, CH4, CO2, and CO (Madhusudhan 2012; Lodders 2002; Visscher & Moses 2011; Heng & Lyons 2016). Moreover, effects of electron degeneracy pressure are important to compute radius of planets with massive envelopes. Even for the most extreme model realizations in this study where the mass fraction of the envelope is about 1% (for a planet of 7 M⊕), we expect the error to be less than 10% in radius.
For the energy transport, we adopt the model presented in Jin et al. (2014), where an irradiated atmosphere is assumed at the top of the gaseous envelope and for which the analytic irradiation model of Guillot et al. (2010) is adopted. This irradiation model assumes a semi-gray, globally averaged temperature profile. Specifically we are using an analytical solution of the radiative transfer equation in the two-stream approximation. This irradiation model assumes a semi-gray, global temperature-averaged profile (Guillot et al. 2010), for which optical depth τ is related to the infrared mean opacity (κth) by dτ/ dr = κthρ, where ρ is density.
For the temperature gradient of the irradiated atmosphere, we solve the radial derivative of Eq. (49) of Guillot et al. (2010): ![\begin{eqnarray} T^4& =& \frac{3 T_{\text{int}}^4 }{4} \left[\frac{2}{3} + \tau \right] + \frac{3 T_{\text{eq}}^4 }{4} \left[ \frac{2}{3} + \frac{2}{3 \gamma}\left\{1 + \left(\frac{\gamma \tau}{2} -1\right) {\rm e}^{-\gamma \tau} \right\} \right.\nonumber\\ && \quad \left. + \frac{2\gamma}{3} \bigg( 1 - \frac{\tau^2}{2} \bigg) E_2(\gamma \tau) \right] , \end{eqnarray}](/articles/aa/full_html/2017/01/aa28708-16/aa28708-16-eq49.png) (4)where γ = κv/κth is the ratio between visible and infrared opacity, Tint is the intrinsic temperature given by
(4)where γ = κv/κth is the ratio between visible and infrared opacity, Tint is the intrinsic temperature given by 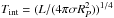 , and E2(γτ) is the exponential integral, defined by
, and E2(γτ) is the exponential integral, defined by 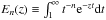 with n = 2. The boundary between the irradiated atmosphere and the envelope is set at
with n = 2. The boundary between the irradiated atmosphere and the envelope is set at 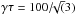 (Jin et al. 2014). For γτ larger than this, the usual Schwarzschild criterion to distinguish between convective and radiative layers is applied. That is, if the adiabatic temperature gradient is larger than the radiative one, the layer is stable against convection, and the radiative diffusion approximation is used for computing the temperature gradient:
(Jin et al. 2014). For γτ larger than this, the usual Schwarzschild criterion to distinguish between convective and radiative layers is applied. That is, if the adiabatic temperature gradient is larger than the radiative one, the layer is stable against convection, and the radiative diffusion approximation is used for computing the temperature gradient: 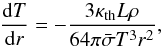 (5)where L is the intrinsic luminosity,
(5)where L is the intrinsic luminosity, 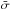 is the Stefan-Boltzmann constant. Since we do not perform evolutionary calculations, L is a model parameter (see Sect. 2.2). However, when the radiative gradient is larger than the adiabatic gradient, the layer is convective, and the temperature gradient is assumed to be adiabatic (which is computed with the EoS).
is the Stefan-Boltzmann constant. Since we do not perform evolutionary calculations, L is a model parameter (see Sect. 2.2). However, when the radiative gradient is larger than the adiabatic gradient, the layer is convective, and the temperature gradient is assumed to be adiabatic (which is computed with the EoS).
In Guillot et al. (2010), κth and κv (and therefore, γ) are free parameters. In order to reduce the number of free parameters, we use the prescription of Jin et al. (2014) who calibrate γ for different equilibrium temperatures in order to reproduce results from more sophisticated atmospheric models for which a wavelength-dependent opacity function is used while solving for radiative equilibrium (Parmentier et al. 2013; Fortney et al. 2008). We implement this calibration in our numerical scheme, that is we interpolate the values of γ for a given equilibrium temperature from Table 2 of Jin et al. (2014). In this way, without using detailed opacity calculations in the treatment of irradiation, we mimic the fundamental physics underlying atmospheric absorption and re-irradiation in a more simple (and numerically inexpensive) fashion. In order to compare the transit radius of a model realization with the measured radius from primary transits, we follow Guillot et al. (2010) and evaluate where the chord optical depth τch becomes 2/3.
Atmospheric model II:
assumes a simplified atmospheric model with a thin, isothermal atmosphere in hydrostatic equilibrium and ideal gas behavior, which is calculated using the scale-height model. For a given pressure pbatm, mean molecular weight μ, mean temperature (parameterized by α), number of scale heights of opaque layers N and a given solid interior we compute planet radius.
The scale-height H is the increase in altitude for which the pressure drops by a factor of e and can be expressed by 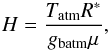 (6)where gbatm and Tatm are gravity at the bottom of the atmosphere and atmospheric temperature, respectively. R∗ is the universal gas constant (8.3144598 J mol-1 K-1) and μ the mean molecular weight. The pressure p at a given depth z is the result of weight of the overlying gas layers. The hydrostatic equilibrium equation gives:
(6)where gbatm and Tatm are gravity at the bottom of the atmosphere and atmospheric temperature, respectively. R∗ is the universal gas constant (8.3144598 J mol-1 K-1) and μ the mean molecular weight. The pressure p at a given depth z is the result of weight of the overlying gas layers. The hydrostatic equilibrium equation gives: 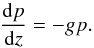 (7)With the assumption that gravity g is constant and using the EoS for ideal gas, the density ρ can be expressed as:
(7)With the assumption that gravity g is constant and using the EoS for ideal gas, the density ρ can be expressed as: 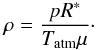 (8)The combination of the previous equations and the subsequent integration over pressure and altitude z (z = 0 where p = p0 and ρ = ρ0) leads to p = p0exp(−z/H) and ρ = ρ0exp(−z/H). The mass of the atmosphere matm is directly related to the pressure pbatm as:
(8)The combination of the previous equations and the subsequent integration over pressure and altitude z (z = 0 where p = p0 and ρ = ρ0) leads to p = p0exp(−z/H) and ρ = ρ0exp(−z/H). The mass of the atmosphere matm is directly related to the pressure pbatm as: 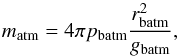 (9)where rbatm and pbatm are radius and pressure at the bottom of the atmosphere, respectively. The thickness of the opaque atmosphere layer zatm is:
(9)where rbatm and pbatm are radius and pressure at the bottom of the atmosphere, respectively. The thickness of the opaque atmosphere layer zatm is: 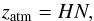 (10)where N is the number of opaque scale-heights H. The atmosphere’s constant temperature is defined as
(10)where N is the number of opaque scale-heights H. The atmosphere’s constant temperature is defined as 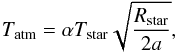 (11)where Rstar and Tstar are radius and effective temperature of the host star and a is semi-major axes. The factor α is a model parameter (see Sect. 2.2) and incorporates possible cooling and heating of the atmosphere, it can vary between 0 and αmax. There is an upper bound αmax, because there is a physical limit to the amount of warming by greenhouse gases. We approximate αmax for a moist (water-saturated) atmosphere (see Appendix A).
(11)where Rstar and Tstar are radius and effective temperature of the host star and a is semi-major axes. The factor α is a model parameter (see Sect. 2.2) and incorporates possible cooling and heating of the atmosphere, it can vary between 0 and αmax. There is an upper bound αmax, because there is a physical limit to the amount of warming by greenhouse gases. We approximate αmax for a moist (water-saturated) atmosphere (see Appendix A).
Generally, atmospheres can contain trace elements present at low pressures that have negligible contribution to the mass of the envelope but a significant contribution to the optical depth. In order to account for such effects, we use pbatm and N as independent parameters.
We have chosen to make model II very general, that is we decouple structure and transmissivity of the gas layer by distinguishing between μ and N. The equivalent procedure of this in model I would be to define opacities as free parameters. Model II has four compared to three degree of freedom in model I.
 |
Fig. 2 Sampled one-dimensional (1D) marginal posterior cdfs (blue) of model I parameters for Neptune: a) mass of envelope menv; b) envelope Luminosity L; c) mass of water mwater; d) mantle radius rmantle; e) core radius rcore; f) Fe/Simantle; g) Mg/Simantle. Prior and posterior nearly completely overlap in g). The envelope metallicity Zenv (not shown) is fixed, Zenv = 0. The prior cdfs are plotted in red. Gray area in plots a)−d) represent independent literature estimates (see main text). |
Prior model parameter ranges.
2.5. Prior information
Table 3 lists prior parameter distributions. The chosen prior parameters distributions are wide reflecting a conservative choice. Different priors are discussed in Sect. 3.3.
Prior bounds on Fe/Simantle and Mg/Simantle are linked to the stellar abundance constraints. Since all Si and Mg are assumed to be in the mantle, Mg/Sistar defines the prior on Mg/Simantle. We assume Mg/Sistar to be Gaussian distributed. Fe, on the other hand, is distributed between core and mantle. Thus, the bulk abundance constraint Fe/Sibulk (=Fe/Sistar) defines only the upper bound of the prior on Fe/Simantle. There is an additional numerical limitation that the absolute iron oxide abundance in the mantle cannot exceed 70%. For pbatm (model II), menv and L (model I), we assume the logarithm of these parameters to be uniformly distributed. The upper bound on the mass of the envelope in model I is set to 90% of the planet mass, which is roughly the scale of Saturn and possibly Jupiter. The range of luminosities L is chosen such that it embraces those of the Moon and Neptune. For model II, the mass of the envelope is parameterized through pbatm. Its prior upper bound is arbitrarily set to 1 GPa. At such high pressures, the atmosphere may no longer behave like a gas and the simplified pressure scale-height model becomes invalid (e.g., Andrews 2010). Only model realizations with pbatm well below 1 GPa can be used for further interpretation. The temperature-related parameter α uniformly varies between 0 and αmax, making up for possible cooling and heating of the atmosphere; αmax scales with surface gravity (see Appendix A).
An example of the influence of different priors on interior model predictions is discussed at the end of this study. Some examples are also shown in Rogers & Seager (2010). In a future study, we will address this problem in more detail.
3. Results
3.1. Method validation: Neptune
As in Dorn et al. (2015), we validate the methodology against solar system planets. Here, we compare with Neptune (M = 17.15M⊕ , R = 3.87R⊕ , where R⊕ is 1 Earth radius), the smallest volatile-rich solar system planet. For model I, we have restricted the gas envelope to a pure H/He gas layer (Zenv = 0) and use the more appropriate EoS of Saumon et al. (1995) for Neptune, since the (otherwise employed) assumption of ideal gas behavior can result in radius uncertainties larger than 10% for a gas mass fractions of a few percent. Although both atmospheric models I and II are not specifically tailored for Neptune, their application serve as a benchmark test and are not meant to provide new insights on Neptune’s interior.
For Neptune, geophysical data (gravitational and magnetic moments, solid-body rotation period, and heat flux) and atmospheric composition estimates are available that provide us with constraints on a possible three-component interior: (1) an outermost molecular envelope largely composed of H/He, (2) a weakly conducting ionic ocean of water, methane, and ammonia, and (3) a rocky central core (e.g., Soderlund et al. 2013; Podolak et al. 2000; Ness et al. 1989). The transition between outermost envelope and ocean is predicted to be around 0.8 R by Lee et al. (2006), whereas the transition from ocean to rock likely occurs below 0.3 R (Redmer 2011). The transitions are neither well determined (Podolak et al. 2000; Nettelmann et al. 2013) nor necessarly sharp (Helled et al. 2010). For a three-component structure of H/He, H2O, and SiO2, Helled et al. (2010) suggest an upper bound on the water mass fraction of 90% and an upper bound on the envelope mass fraction of 24%. If the ice/rock ratio is restricted to proto-solar, Hubbard et al. (1995) find that Neptune could consist of about 25% rock, 60−70% ice, and 5−15% gas by mass.
Data of synthetic planets.
 |
Fig. 3 Sampled two-dimensional (2D) marginal posterior pdfs (blue) of model I parameters for Neptune: a) mass of envelope menv and envelope Luminosity L; b) mass of water mwater and mantle radius rmantle. Gray areas represent independent literature estimates (see main text). |
Here, we use uncertainties of 1% on both the observed M and R, and 10% on the solar ratios Fe/Sistar and Mg/Sistar (Lodders 2003). Results for the two atmospheric models are shown in Figs. 2 and 4, respectively. The one-dimensional (1D) marginal posterior cumulative distribution function (cdf) for each model parameter (in blue) is plotted with the prior distribution (in red) and independent parameter estimates (gray areas). The cdf describes the probability of a model parameter m with a certain probability distribution to be less or equal to a given value of m. In addition, Fig. 3 shows the 2D marginal posterior pdfs for those model parameters of model I for which we have independent estimates. These plots suggest the following:
-
The interior structure of Neptune is constrained by the data.
Available independent parameter estimates (shown in gray) overlap with the blue posterior cdfs for menv, L, mwater, and rmantle (model I, Figs. 2 and 3); for model II (Fig. 4) this is only the case for matm (derived from pbatm and Eq. (9)), mwater and rmantle are over-and under-predicted, respectively.
With only mass, radius, and abundance constraints, our method (model I) predicts independent geophysical estimates of Neptune’s interior. Compared to independent estimates, our calculated confidence regions for the structural parameters are larger, since we rely on limited data:
-
The simplified pressure model II leads to an overestimation of mwater and underestimation of rmantle compared to model I. This is because the same radius fraction of gas results in different p-T boundary conditions for the ice layer for both models. The simplified pressure model II generally overestimates pbatm, which leads to an increase in water ice density. In order to fit the radius, the higher water ice density implies a larger mwater. At the same time, the mass contribution of the rocks needs to be reduced so as not to overestimate mass.
 |
Fig. 4 Sampled 1D marginal posterior cdfs (blue) of model II parameters for Neptune: a) pressure at bottom of atmosphere pbatm; b) atmospheric mass fraction matm/M (Eq. (9)); c) temperature-related parameter α; d) number of scale-heights of opaque layers N; e) mean molecular weight μ; f) mass of water mwater; g) mantle radius rmantle; h) core radius rcore; i) Fe/Simantle; j) Mg/Simantle. The prior cdfs are plotted in red. Gray areas in b), e), f) represent independent literature estimates (see main text). |
 |
Fig. 5 Masses and radii of synthetic planets (black dots, cases A−K), observed exoplanets (gray dots) from Dressing et al. (2015), and Earth and Venus. Planets are plotted against mass-radius curves of idealized compositions for which a surface temperature of 300 K has been assumed. Planet cases A−K are summarized in Table 4. |
3.2. Synthetic cases
Next, we apply our method to synthetic exoplanets. Application to actual observations is presented in a companion paper (Dorn et al. 2017). In this study, we emphasize instead the influence of the following parameters on interior predicitions: bulk density 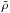 , data uncertainties, semi-major axis, atmospheric composition, and prior distributions. For the latter, we test the a priori assumption of enriched envelopes versus pure H/He envelopes. For all synthetic planets we assume M = 7M⊕, since the transition between rocky and non-rocky planets seems to occurr around this mass (e.g., Weiss & Marcy 2014; Rogers 2015). Table 4 lists all relevant data for the synthetic cases and Fig. 5 shows their masses and radii plotted against curves of idealized compositions. For all synthetic cases, we assume solar values for abundance constraints (Lodders 2003), stellar effective temperature and stellar radius of the Sun. In the following, we discuss these test cases.
, data uncertainties, semi-major axis, atmospheric composition, and prior distributions. For the latter, we test the a priori assumption of enriched envelopes versus pure H/He envelopes. For all synthetic planets we assume M = 7M⊕, since the transition between rocky and non-rocky planets seems to occurr around this mass (e.g., Weiss & Marcy 2014; Rogers 2015). Table 4 lists all relevant data for the synthetic cases and Fig. 5 shows their masses and radii plotted against curves of idealized compositions. For all synthetic cases, we assume solar values for abundance constraints (Lodders 2003), stellar effective temperature and stellar radius of the Sun. In the following, we discuss these test cases.
 |
Fig. 6 Sampled 1D marginal posterior cdfs of model I parameters for synthetic planet cases (A−D) of 7 M⊕ that vary in terms of radii: 1.7 R⊕ (A), 2.2 R⊕ (B), 2.6 R⊕ (C), 2.9 R⊕ (D); a) mass of envelope menv; b) envelope luminosity L; c) envelope metallicity Zenv; d) mass of water mwater; e) mantle radius rmantle; f) core radius rcore; g) Fe/Simantle; h) Mg/Simantle. |
 |
Fig. 7 Sampled 1D marginal posterior cdfs of model II parameters for synthetic planet cases (A−D) of 7 M⊕ that vary in terms of radii: 1.7 R⊕ (A), 2.2 R⊕ (B), 2.6 R⊕ (C), 2.9 R⊕ (D); a) pressure at bottom of atmosphere pbatm; b) atmospheric mean molecular weight μ; c) temperature-related parameter α; d) number of scale-heights of opaque layers N, e) mass of water mwater; f) mantle radius rmantle; g) core radius rcore; h) Fe/Simantle; i) Mg/Simantle. Depending on the case, the upper prior bound in c) differs, which is indicated by the vertical colored lines corresponding to the respective case. |
3.2.1. Influence of bulk density
Planets A, B, C, and D are assigned different radii (1.7, 2.2, 2.6, and 2.9 R⊕) and hence bulk densities 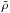 (Table 4). Uncertainties for mass and radius are assumed to be similar to the predicted uncertainties from the PLATO mission (Rauer et al. 2014), that is 5% and 2%, respectively. The influence of planet bulk density on retrieved parameters is shown in Figs. 6 and 7. We observe, as expected, that bulk density correlates positively with the size of the rocky interior rmantle, and correlates negatively with mass of water (mwater) and gas (menv). Core size and mantle composition (Figs. 6f−h and 7g−i) show only small variations, because they are constrained by the solar abundances.
(Table 4). Uncertainties for mass and radius are assumed to be similar to the predicted uncertainties from the PLATO mission (Rauer et al. 2014), that is 5% and 2%, respectively. The influence of planet bulk density on retrieved parameters is shown in Figs. 6 and 7. We observe, as expected, that bulk density correlates positively with the size of the rocky interior rmantle, and correlates negatively with mass of water (mwater) and gas (menv). Core size and mantle composition (Figs. 6f−h and 7g−i) show only small variations, because they are constrained by the solar abundances.
 |
Fig. 8 Sampled 2D marginal posterior pdfs of model I parameters for synthetic planet case C showing the correlation between: a) rcore and rmantle; b) rmantle and mwater; c) mwater and menv; d) menv, and Zenv; e) mwater and the averaged μ corresponding to Zenv. Those model realizations that explain the data within 1σ are plotted in blue. Samples in c), d) for which gas mass fractions menv/M > 0.01 are highlighted in green and should be taken with care. See main text for discussion of features B1 and B2. |
 |
Fig. 9 Sampled 2D marginal posterior pdfs of model II parameters for synthetic planet case C showing the correlation between: a) rcore and rmantle; b) rmantle and mwater; c) mwater and pbatm; d) pbatm, and μ; e) mwater and μ; f) mwater and α; g) mwater and N. Those model realizations that explain the data within 1σ are plotted in blue. Samples in c), d) for which gas mass fractions menv/M > 0.0001 are highlighted in green and should be taken with care. |
Among the parameters characterizing the gas layer for model I (Fig. 6), menv and Zenv are constrained by data, whereas envelope luminosity L is not. For the planet with the highest bulk density (case A) the gas layer contributes very little to planet radius, i.e., metallicity is high and/or menv is small. Case A is found with a 90% probability to have an atmosphere smaller in mass than Earth (10-7menv/M). Compared to high bulk density planets, low density planets can have gas of lower metallicity while gas mass fraction tends to be higher. For very low density planets (case D) when even pure water ice is not sufficient to explain radius, small menv are excluded as a result of which menv is larger than 10-5M with a probability of 90%.
The gas layer parameters for model II (Fig. 7) indicate that the number of opaque scale-heights N and temperature (parameterized by α) in the gas layer appear to be best constrained by data. The expected trend of a higher temperature (larger α) and an increased number of scale-heights that are needed to explain low bulk density planets is clearly visible (Figs. 7c and d). Mean molecular weight μ and pbatm are both weakly constrained for the high bulk density cases (A, B, and C). When pure water ice cannot compensate enough to fit radius (case D compared to the other cases) the gas layer moves to higher pressures pbatm, lower mean molecular weights, higher temperatures (α), and more scale-heights (Fig. 7 light green curve).
Although the use of both atmospheric models yield very similar parameter distributions for the rocky part of the planet, there are significant differences in mwater, particulary for the low density planets (cases C and D). This is because parameters related to gas and ice layers are those with the largest influence on planet radius. Hence differences in the atmospheric model affect the gas structure and in consequence the distribution of mwater. We will discuss these differences in more detail in the following.
 |
Fig. 10 Sampled 1D marginal posterior cdfs of model I parameters for synthetic planet cases B, E, F, G that vary in terms of data uncertainties. B is the reference case (σM = 0.05 M, σR = 0.02 R, 20% for both σFe/Sibulk and σMg/Sibulk), E has larger uncertainties in mass and radius (σM = 0.2 M, σR = 0.1 R), whereas F and G have larger uncertainties in the abundance constraints, 50% and 80%, respectively. a) Mass of envelope menv; b) envelope luminosity L; c) envelope metallicity Zenv; d) mass of water mwater; e) mantle radius rmantle; f) core radius rcore; g) Fe/Simantle; h)Mg/Simantle. The priors in g) and h) are not shown as not to overload the plot, because they differ among the cases. |
3.2.2. Influence of atmospheric model
Here, we take a closer look at the different parameter estimates for case C when using model I and II. We plot the sampled 2D marginal posterior distributions of model parameters in Figs. 8 and 9. Overall, the distributions show similar trends with clear differences for the rocky and icy interior depending on atmospheric model:
-
There is a strong correlation between mwater and menv inmodel I (Fig. 8). Formodel II, the corresponding correlation between mwaterand pbatm is weak. This reflects a higher degeneracy in the gas layerparameters for model II (more degrees offreedom).
-
For model II, strongest correlations with mwater are seen for μ and α among the gas parameters.
-
For model I compared to model II, rmantle tends to be larger (Figs. 8a and 9a).
-
There is a clear discrepancy in the estimated mwater between the two models. For model I, the minimum mwater is estimated to be about 0.1 M, whereas for model II it is 0.5 M.
Model II leads to the misinterpretation that relatively low-density planets (case C) require a massive ocean to explain mass and radius. This is in line with earlier conclusions suggesting that it is impossible to distinguish between a thick atmosphere and an ocean based on mass and radius alone (e.g., Adams et al. 2008). This is important in view of the different formation histories implied by either interpretation. The results show that the simplified pressure model II fails to explain thicker atmospheres and thereby overestimates the amount of water ice. This is because it does not account for energy transport and thus overestimates the pressure increase with atmospheric depth. Thicker atmospheres can in principle be realized, if temperatures (i.e., α) exceeding the prior range (αmax, Appendix A) would be allowed, implying a larger greenhouse effect. However, there is a physical upper limit, the Komabayashi-Ingersoll Limit (Komabayasi 1967; Ingersoll 1969), to the amount of outgoing long-wave radiation that can be absorbed and emitted by greenhouse gases that warm the atmosphere. More advanced modeling would be required to determine this upper limit for the studied cases, but this is outside of the scope of this study.
In the 2D plots (Figs. 8b and c) showing the correlation between rmantle and rcore, and rmantle and mwater, respectively, two “branches” (labeled B1 and B2) are visible (valid for massive atmospheres menv> 0.01 M ) which are characterized by:
-
B1:
mwater < 0.5 M,
Zenv < 0.02,
L > 1022.5 erg/s;
-
B2:
mwater> 0.5 M,
0.02 <Zenv< 1.0,
1018 erg/s < L < 1022.5 erg/s.
For gas envelopes of supersolar abundances (B2), self-gravity of massive gas layers leads to compressed envelopes. To fit radius in this case, a large mwater is required. For subsolar abundances and very high luminosities (B1), the envelopes are thick and make up for a large fraction of planet radius (>25%). However, a minimum mwater of 0.1 M appears to be required to fit radius. This is because we restrict the prior range on luminosity L to a maximum of 1023 erg/s (Neptune-like 1022.52 erg/s). If larger luminosities than the prior range were allowed, thicker gas layers with negligible ice mass fractions could be realized. This suggests that constraints on the luminosities would allow to partly lift the degeneracy between an ocean and a thick atmosphere. This will be investigated in more detail in the future.
We compare the planetary radii that are computed with both atmospheric models by using the calculated pressures and temperatures from model I (e.g., pressures at bottom and top of the gas layer and an averaged temperature) as input in model II for a rocky interior of 7 M⊕. For an envelope mass of menv> 10-3M⊕ (corresponding to pbatm≈ 1000 bar), the discrepancy in radius becomes comparable to the observed radius uncertainty of 2%. We note that the comparison of both models is sensitive to the choice of temperature averaging. Hence, for large bulk density planets with thin atmospheres (cases A and B), the choice of atmospheric model does not significantly affect estimates of the rocky and icy interior (Figs. 6 and 7), whereas it becomes relevant for relatively low-density planets (cases C and D).
For the cases studied here, we conclude that the more accurate representation of gas layer physics makes model I more favorable inspite of larger computational costs. In the case of thin atmospheres, model II is valid.
 |
Fig. 11 Sampled 1D marginal posterior cdfs of model II parameters for synthetic planet cases B, E, F, G that vary in terms of data uncertainties. B is the reference case (σM = 0.05 M, σR = 0.02 R, 20% for both σFe/Sibulk and σMg/Sibulk), E has larger uncertainties in mass and radius (σM = 0.2 M, σR = 0.1 R), whereas F and G have larger uncertainties in the abundance constraints, 50% and 80%, respectively. a) Pressure at bottom of atmosphere pbatm; b) atmospheric mean molecular weight μ; c) temperature-related parameter α; d) number of scale-heights of opaque layers N; e) mass of water mwater; f) mantle radius rmantle; g) core radius rcore; h) Fe/Simantle; i) Mg/Simantle. The priors in h) and i) are not shown as not to overload the plot, because they differ among the cases. |
3.2.3. Influence of data uncertainty
Here, we study the influence of data uncertainty on structural parameter estimation. As summarized in Table 4, we vary uncertainty in mass and radius between cases B (σM of 5%, σR of 2%) and E (σM of 20%, σR of 10%); we vary uncertainties on planet bulk abundances between cases B (20%), F (50%), and G (80%). All cases B, E, F, and G have the same bulk density of 3.62 g/cm3. The smallest chosen data uncertainties reflect those of high quality data similar to those expected from PLATO. Results are shown in Figs. 10 and 11. The results can be summarized as follows:
-
Mass and radius uncertainties mainly affect estimates of rmantle, mwater, and Zenv.For example, the retrieved confidence region for rmantle and mwater is three timeslarger in case E compared to case B(the 5% to 95% percentile range of rmantle for case E is0.28–0.73 R compared to 0.54−0.66 R in case B; similarly the range of mwater for case E is 0.08−0.93 M compared to 0.22−0.5 M in case B).
-
Mass and radius uncertainties do not significantly affect estimates of core and mantle composition, since they are conditioned to the same abundance constraints (cf. case B and E).
-
Reducing the uncertainties on the abundance constraints mainly improves the ability to constrain the mantle composition. For example, the 5% to 95% percentile ranges for Mg/Simantle in cases F and G are larger by a factor of 2.6 and 3.4 compared to case B, respectively.
-
Compared to the studied cases, the influence on determining core size is more pronounced for purely rocky planets as described by Dorn et al. (2015). Here, only moderate effects are seen for core size estimates, where the 5% to 95% percentile range of core size rcore is 30% larger for case G compared to B.
-
Uncertainties on the abundance constraints have only minor effects on estimates of rmantle and mwater. Between cases B and G, for example, the 50th percentile of mwater varies by up to 8%.
For the studied cases, mass and radius uncertainties are more important than uncertainties on Fe/Sibulk and Mg/Sibulk to constrain key structural parameters such as mwater and rmantle. This conclusion might vary depending on the actual planet mass and bulk density.
 |
Fig. 12 Sampled 1D marginal posterior cdfs of menv (model I) for the synthetic planets: case C at 1 AU, case H at 0.1 AU, case J at 1 AU, and case K at 0.1 AU. For cases J and K, the gas composition is restricted to pure H/He (Zenv = 0) using the EoS of Saumon et al. (1995). |
3.2.4. Influence of semi-major axes
The semi-major axis influences the energy budget available in the gas envelope and thereby the radius of the planet. Figure 12 demonstrates the effect of distance to the star on estimates of menv. For the same planet with a smaller semi-major axis (case H compared to C), the interior can be explained by a smaller menv and higher envelope metallicity Zenv, although the effect on Zenv is small (not shown). This result is intuitive, since a hotter gas envelope implies a lower gas density, which results in a larger radius. Thus, in order to compensate for a higher intrinsic luminosity while still fitting the radius, the gas mass must be smaller and/or more heavier elements need to be present. If only pure H/He gas layers are considered, the same trend for menv is observed (cases K and J in Fig. 12a). Compared to metal-rich envelopes, the restriction to pure H/He envelopes leads to smaller menv for the reason just discussed.
3.3. Influence of prior distribution
The results obtained by a Bayesian inference analysis are subject to the choice of prior, which, if not chosen carefully can lead to a significant imprint on parameters that are weakly constrained by data. In the following, we consider a number of different priors to illustrate this on a selected set of parameters that are sensed differently by the data considered here. We have singled out core size, which is largely determined by bulk abundances and mass, in addition to envelope metallicity and luminosity that are mainly constrained by radius and stellar irradiation.
Figure 13 illustrates the effect of different prior choices on estimated (posterior) core size rcore for a Neptune-sized planet. Here, we contrast a uniform prior in rcore with a uniform prior in rcore3 . A uniform prior in rcore gives more weight to smaller core sizes relative to a uniform prior in rcore3 . But since rcore3 is directly proportional to core mass it represents the more natural choice. The results indicate that the effect of the prior is negligible for the 50%-percentile of rcore. This is an example where the choice of prior is less significant.
 |
Fig. 13 Sampled 1D marginal posterior cdfs (blue) for different priors (red) of core size rcore for Neptune (applying model I). Distributions are depicted in dashed when the prior is uniform in rcore and solid when it is uniform in rcorercore3 . The latter is identical to Fig. 2e. |
Next, we investigate an example where the estimated parameter is only weakly constrained by data. This is, for example, the case for envelope metallicity Zenv. We compare a uniform prior in Zenv and in 1/Zenv for a case-C planet. A uniform prior in 1/Zenv is motivated by the fact that H and He are most abundant elements and that primary atmospheres are likely rich in H and He (e.g., Alibert et al. 2004). Also, the scale height of the gas layer correlates positively with 1/Zenv. The results are shown in Fig. 14 and illustrate that a uniform distribution in Zenv, relative to a uniform in 1/Zenv, gives more weight to larger envelope metallicities. This implies that we are favoring lighter-element atmospheres over heavier-elements. A uniform prior in Zenv may be more appropriate for secondary (outgassed) atmospheres, for which heavy element enrichment is a priori a more likely scenario.
Finally, we consider luminosity L. For purposes of illustration, we chose the following range 1022.52 ± 0.05 erg/s, which corresponds to the observed luminosity of Neptune. More generally, additional constraints such as infrared flux measurements would allow for a narrower prior range on luminosity. Figure 15 illustrates the effect of assuming different prior ranges on L in estimating gas mass fraction menv/M for the case of a Neptune-sized planet. The new prior range on L leads to an improved constraint on gas mass fraction of 0.05 <menv/M< 0.09 that better predicts independent geophysical estimates relative to the earlier determined range (0.01 <menv/M< 0.2), where a relative wide prior range was invoked (Table 3). In this example, the choice of prior has no significant effect on the 50%-percentile of menv/M.
From the above, we can conclude that the posterior distribution is mostly affected by the assumed prior distribution for those parameters that are weakly constrained by data. In summary, it should be emphasized that the choice of prior is not arbitrary but need to be based (whenever possible) on observations, laboratory measurements and/or theoretical considerations.
 |
Fig. 14 Sampled 1D marginal posterior cdfs (blue) for different priors (red) of envelope metallicity Zenv for case C (7 M⊕, 2.6 R⊕, applying model I). Distributions are depicted in dashed when the prior is uniform in Zenv and solid when it is uniform in 1/Zenv. The latter is identical to Fig. 6c. |
 |
Fig. 15 Sampled 1D marginal posterior cdfs (blue) for mwater assuming different priors on L for Neptune (applying model I). Solid blue line refer to wide prior range on L (1018−1023 erg/s), whereas dashed blue line refer to narrow prior range on L (1022.47−1022.57 erg/s). The former is identical to Fig. 2a. Gray area represent independent literature estimates (see main text). |
4. Discussion
Here, we have extended the method of Dorn et al. (2015) from purely rocky exoplanets to general exoplanet types that include volatile-rich layers in the form of water ice, oceans, and atmospheres. For the same data of mass, radius, and bulk abundance constraints, the degeneracy of core and mantle parameters is generally larger in planets of general structure than for purely rocky planets, since their contribution to mass and radius can in part be compensated by volatile material.
The key to constrain the structural parameters resides in the large density contrasts between rock, water, and gaseous layers. In other words, our ability to constrain interiors is because of the different data sensitivity of the various parameters. The abundance constraints couple core size with mantle size and composition. The relative sizes of core and mantle are thus determined by Fe/Sibulk. The mass of the planet mainly dictates the absolute size of the rocky part and the mass of water. Planetary radius meanwhile determines the characteristics of the envelope and the water layer.
The strength of the presented inference method is that it is modular, i.e., different interior structure models can be tested against each other. However, the applicability and informative value of the inference method is subject to imposed assumptions on the structure model. For example, the two tested atmospheric models differ in terms of complexity and general applicability.
Model I is more elaborate in that it calculates pressure-temperature profiles for a given composition while solving for hydrostatic equilibrium, mass conservation, and energy transport. But it is restricted to H, He, C, and O and it assumes equilibrium chemistry, ideal gas behavior, as well as prescribed opacities. The latter are fit to results of radiative equilibrium models that use a wavelength-dependent opacity function by Jin et al. (2014) for solar metallicities. In that regard, the opacities used are not self-consistent when non-solar metallicities are considered (Zenv≠ 0.02). Different values of opacities can lead to differences in radius by up to 5%. Models that compute line-by-line opacities with their corresponding atmospheric abundances should be performed in the future to compute planetary radii in a self-consistent way. The assumption of ideal gas behavior introduces a bias in radius for large atmospheric mass fractions, for example for a 1% menv/M planet atmosphere the difference in the radius between ideal gas and the Saumon et al. (1995) EoS (for H-He) can reach 10%.
Model II assumes an isothermal, homogeneous atmosphere and ideal gas behavior. Therefore, model II is strictly only valid in the case of thin atmospheres (menv≲ 10-3M⊕). While, future available spectroscopic measurements will allow to constrain the key characteristics of the atmosphere (Benneke & Seager 2012), it will be difficult to make use of these additional constraints when using the simplified atmospheric model II since isothermal temperatures are non-physical. However, in the case of thin atmospheres, model II has the advantage of being computationally inexpensive and very general in the way it is set up, i.e., it does not make assumptions about opacities but fully decouples structure and opacity of the atmosphere by distinguishing between μ and N, where N accounts for the effect of trace elements in the atmosphere that can have a big impact on opacity. Therefore, model II is especially useful for secondary atmospheres on small exoplanets, where the composition of the atmosphere can be very diverse. In comparison, model I uses prescribed opacities and thus neglects trace elements. Although not warranted here, it is possible to treat opacities in model I as free parameters to account for trace elements at the cost of increasing the number of parameters.
A further limitation of the structural model is the assumption of a pure iron core. If volatile elements in the core are negligible, this assumption leads to a systematic overestimation of core density and thus an underestimation of core size. In addition, we assume sub-solidus conditions in the rocky interior and a perfectly known EoS for all considered materials. Pressures and temperatures in the various planet cases considered here exceed the ranges that can be measured in the laboratory and while ab initio calculations could fill the gaps, these are not always available. Available EoS include some (mostly unquantifiable) uncertainty (see Connolly & Khan 2016, for detailed examples).
Here, we have used water as a proxy for the composition of the ice and ocean layers, but other compositions are also possible (e.g., CO, CO2, CH4, NH3). Water is often used as a proxy for ice, since (1) oxygen is more abundant than carbon and nitrogen in the universe, and (2) water condenses at higher temperatures than ammonia and methane.
5. Conclusions and outlook
We present a generalized inference method that enables us to make meaningful statements about the interior structure of observed exoplanets. Our full probabilistic Bayesian inference analysis formally accounts for data and model uncertainties, as well as model degeneracy. By employing a Markov chain Monte Carlo technique, we quantify the state of knowledge that can be obtained on composition and thickness of core, mantle, water ice, and gaseous layers for given data of mass, radius, and bulk abundance proxies for Fe/Sibulk and Mg/Sibulk obtained from spectroscopic measurements. We have built upon the work of Dorn et al. (2015) and extended the dimensionality of the interior characterization problem to include volatile elements in the form of gas, water ice and ocean. Our method succeeds at constraining planet interior structure even for high dimensional parameter spaces and thereby overcomes limitations of previous works on mass-radius relationship of exoplanets.
We have validated our method against Neptune. Using synthetic planets, we have determined how predictions on interior structure depend on various parameters: bulk density, data uncertainties, semi-major axes, atmospheric composition (i.e., a priori assumption of enriched envelopes versus pure H/He envelopes), and prior distributions. Furthermore, we have investigated two different atmosphere models and quantify how parameter estimates depend on the choice of the atmosphere model. We summarize our findings as follows:
-
It is possible to constrain core size, mantle size and composition,mass of water ice, and key characteristics of the gas layer (e.g.,internal energy, mass, composition), given observations of mass,radius, and bulk abundance proxies Fe/Sibulk and Mg/Sibulk taken from the host star.
-
A Bayesian analysis is key in order to rigorously analyse planetary interiors, as it formally accounts for data and model uncertainty, as well as the inherent degeneracy of the problem addressed here. The range of possible interior structures is large even for small data uncertainties. Our method is able to quantify the probability that a planet is rocky and/or volatile-rich.
-
Our method has been successfully validated against Neptune for which independent structure estimates based on geophysical data (e.g., gravitational and magnetic moments) are available.
-
Model parameters have different sensitivity to the various data. Constraints on bulk abundances Fe/Sibulk and Mg/Sibulk determine relative core size and mantle composition. Mass mostly determines the size of the rocky and icy interior, whereas radius mainly determines structure and composition of the gas and the water ice layers.
-
Increasing precision in mass and radius leads to a much better constrained ice mass fraction, size of rocky interior (confidence regions of mwater and rmantle in case B are three times smaller compared to case E), and some improvement on the composition of the gas layer, whereas an increase in precision of stellar refractory abundances enables improved constraints on mantle composition and relative core size.
-
We have proposed two different atmospheric models: model I solves for radiative transfer; whereas model II uses a simplified scale-height pressure model. Both models yield different insights about possible gas layer characteristics that are subject to prescribed assumptions. In particular, for thick atmospheres, we see a clear discrepancy between model I and II which result in different estimates of rock and ice layers. The validity of model II is strictly limited to thin atmospheres (menv≲ 10-3M⊕).
-
We have investigated the effect of prior distribution on estimated parameters and observed that the assumed prior distribution significantly affects the posterior distribution of those parameters, that are weakly constrained.
The method presented here is valuable for the interpretation of future data from space missions (TESS, CHEOPS, and PLATO) that aim at characterizing exoplanets through precise measurements of R and M. Improving measurement precision, however, is costly as it depends on observation time. Our method helps to quantify the scientific return that could be gained as data precision is increased. Moreover, our study is relevant for the understanding on how interior types are distributed among stars and the implications of these for planet formation.
Acknowledgments
This work was supported by the Swiss National Foundation under grant 15-144, the ERC grant 239605. It was in part carried out within the frame of the National Centre for Competence in Research PlanetS. We would like to thank James Connolly for informed discussions.
References
- Adams, E. R., Seager, S., & Elkins-Tanton, L. 2008, ApJ, 673, 1160 [NASA ADS] [CrossRef] [Google Scholar]
- Alibert, Y., Mordasini, C., & Benz, W. 2004, A&A, 417, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andrews, D. G. 2010, An introduction to atmospheric physics (Cambridge University Press) [Google Scholar]
- Baraffe, I., Chabrier, G., & Barman, T. 2008, A&A, 482, 315 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benneke, B., & Seager, S. 2012, ApJ, 753, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Bond, J. C., O’Brien, D. P., & Lauretta, D. S. 2010,ApJ, 715, 1050 [Google Scholar]
- Bouchet, J., Mazevet, S., Morard, G., Guyot, F., & Musella, R. 2013, Phys. Rev. B, 87, 094102 [NASA ADS] [CrossRef] [Google Scholar]
- Carter, J. A., Agol, E., Chaplin, W. J., et al. 2012, Science, 337, 556 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Connolly, J. A. D. 2009, Geochemistry, Geophysics, Geosystems, 10, Q10014 [Google Scholar]
- Connolly, J. A. D., & Khan, A. 2016, J. Geophys. Res., DOI:10.1002 [Google Scholar]
- Demory, B. O., Gillon, M., de Wit, J., et al. 2016, Nature [Google Scholar]
- Dorn, C., Khan, A., Heng, K., et al. 2015, A&A, 57, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dorn, C., Hinkel, N. R., & Venturini, J. 2017, A&A, 597, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drake, M. J., & Righter, K. 2002, Nature, 416, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Dressing, C. D., Charbonneau, D., Dumusque, X., et al. 2015, ApJ, 800, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Elser, S., Meyer, M. R., & Moore, B. 2012, Icarus, 221, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Fortney, J. J., Marley, M. S., & Barnes, J. W. 2007, ApJ, 659, 1661 [NASA ADS] [CrossRef] [Google Scholar]
- Fortney, J. J., Lodders, K., Marley, M. S., & Freedman, R. S. 2008, ApJ, 678, 1419 [NASA ADS] [CrossRef] [Google Scholar]
- French, M., Mattsson, T. R., Nettelmann, N., & Redmer, R. 2009, Phys. Rev. B, 79, 054107 [NASA ADS] [CrossRef] [Google Scholar]
- Goldblatt, C., & Watson, A. J. 2012,Phys. Eng. Sci., 370, 4197 [Google Scholar]
- Gordon, S., & McBride, B. 1994, Computer program for calculation of complex chemical equilibrium compositions and application (Cleveland, Ohio, Springfield, Va: National Aeronautics and Space Administration) [Google Scholar]
- Grasset, O., Schneider, J., & Sotin, C. 2009, ApJ, 693, 722 [NASA ADS] [CrossRef] [Google Scholar]
- Guillot, T. 2010, A&A, 520, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Helled, R., Anderson, J. D., Podolak, M., & Schubert, G. 2010, ApJ, 726, 15 [Google Scholar]
- Heng, K., & Lyons, J. R. 2016, ApJ, 817, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Hinkel, N. R., Timmes, F. X., Young, P. A., Pagano, M. D., & Turnbull, M. C. 2014, AJ, 148, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Howe, A. R., Burrows, A. S., & Verne, W. 2014, ApJ, 787, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Hubbard, W. B., Podolak, M., & Stevenson, D. J. 1995, Neptune and Triton, 109 [Google Scholar]
- Ingersoll, A. P. 1969, J. Atmosph. Sci., 26, 1191 [Google Scholar]
- Iyer, A. R., Swain, M. R., Zellem, R. T., et al. 2016, ApJ, 823, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Jin, S., Mordasini, C., Parmentier, V., et al. 2014, ApJ, 795, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, T. V., Mousis, O., Lunine, J. I., & Madhusudhan, N. 2012, ApJ, 757, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Komabayasi, M. 1967, J. Meteorolog. Soc. Japan, 45, 137 [Google Scholar]
- Lee, K. K., Benedetti, L. R., Jeanloz, R., et al. 2006, J. Chem. Phys., 125, 014701 [NASA ADS] [CrossRef] [Google Scholar]
- Lodders, K. 2003, ApJ, 591, 1220 [NASA ADS] [CrossRef] [Google Scholar]
- Lodders, K., & Fegley, B. 2002, Icarus, 155, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Lodders, K., Palme, H., & Gail, H. P. 2009, in Solar system (Heidelberg: Springer Berlin), 712 [Google Scholar]
- Lyon, S. P., & Johnson, J. D. 1992, LANL Rep. LA-UR-92-3407 (Los Alamos: LANL) [Google Scholar]
- Madhusudhan, N. 2012, ApJ, 758, 36 [NASA ADS] [CrossRef] [Google Scholar]
- McDonough, W. F., & Sun, S. S. 1995, Chem. Geo., 120, 223 [Google Scholar]
- Mosegaard, K., & Tarantola, A. 1995, J. Geophys. Res., 100, 12431 [NASA ADS] [CrossRef] [Google Scholar]
- Nettelmann, N., Helled, R., Fortney, J. J., & Redmer, R. 2013, Planet. Space Sci., 77, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Ness, N. F., Acuña, M. H., Burlaga, L. F., et al. 1989, Science, 246, 1473 [NASA ADS] [CrossRef] [Google Scholar]
- Newsom, H. E. 1995, Amer. Geophys. Union., 1, 159 [Google Scholar]
- Parmentier, V., Showman, A. P., & Lian, Y. 2013, A&A, 558, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Podolak, M., Podolak, J. I., & Marley, M. S. 2000, Planet. Space Sci., 48, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Rauer, H., Catala, C., Aerts, C., et al. 2014, Experimental Astronomy, 38, 249 [Google Scholar]
- Redmer, R., Mattsson, T. R., Nettelmann, N., & French, M. 2011, Icarus, 211, 798 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, L. A. 2015, ApJ, 801, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, L. A., & Seager, S. 2010, ApJ, 712, 974 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, L. A., Bodenheimer, P., Lissauer, J. J., & Seager, S. 2011, ApJ, 738, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Saumon, D., Chabrier, G., & Van Horn, H. M. 1995, ApJS, 99, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Schmitt, J. R., Agol, E., Deck, K. M., et al. 2014, ApJ, 795 [Google Scholar]
- Seager, S., Kuchner, M., Hier-Majumder, C. A., & Militzer, B. 2007, ApJ, 669, 1279 [NASA ADS] [CrossRef] [Google Scholar]
- Soderlund, K. M., Heimpel, M. H., King, E. M., & Aurnou, J. M. 2013, Icarus, 224, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Sotin, C., Grasset, O., & Mocquet, A. 2007, Icarus, 191, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Stixrude, L., & Lithgow-Bertelloni, C. 2005, Phys. Prop. Geophys. J. Int., 162, 610 [CrossRef] [Google Scholar]
- Stixrude, L., & Lithgow-Bertelloni, C. 2011, Geophys. J. Int., 184, 1180 [NASA ADS] [CrossRef] [Google Scholar]
- Tsiaras, A., Rocchetto, M., Waldmann, I. P., et al. 2016, ApJ, 820, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Thiabaud, A., Marboeuf, U., Alibert, Y., Leya, I., & Mezger, K. 2015, A&A, 580, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thompson, S. L., & Lauson, H. S. 1972, Improvements in the Chart D radiation-hydrodynamic CODE III: revised analytic equation of state: Albuquerque, N. Mex., USA, Sandia Laboratories, Report SC-RR-71-0714 [Google Scholar]
- Valencia, D., Sasselov, D. D., & O’Connell, R. J. 2007a, ApJ, 665, 1413 [NASA ADS] [CrossRef] [Google Scholar]
- Vazan, A., Kovetz, A., Podolak, M., & Helled, R. 2013, MNRAS, 1248 [Google Scholar]
- Vazan, A., Helled, R., Kovetz, A., & Podolak, M. 2015, ApJ, 803, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Venturini, J., Alibert, Y., Benz, W., & Ikoma, M. 2015, A&A, 576, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Visscher, C., & Moses, J. I. 2011, ApJ, 738, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Weiss, L. M., & Marcy, G. W. 2014, ApJ, 783, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Weiss, L. M., Rogers, L. A., Isaacson, H. T., et al. 2016, ApJ, 819, 83 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Approximation of αmax
There is a physical upper limit to the amount of warming by greenhouse gases. The Komabayashi-Ingersoll (KI) limit describes the maximum amount of radiation which can be transferred by a moist atmosphere, which occurs when the transparency τs of the atmosphere becomes very small, i.e., τs = τlimit.
For model II, this limit is represented by αmax and that we roughly approximate as follows: 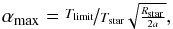 (A.1)where Rstar and Tstar are radius and effective temperature of the host star, a is semi-major axes, and Tlimit is:
(A.1)where Rstar and Tstar are radius and effective temperature of the host star, a is semi-major axes, and Tlimit is: 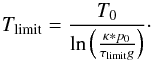 (A.2)
(A.2)
Here, T0 is the temperature at some vapor pressure p0 (here, we use p0 = 1 × 105 Pa and T0 = 373 K for water, (Goldblatt & Watson 2012)); κ and τlimit are opacity and optical depth at the KI limit, g is surface gravity. The fraction κ/τlimit is approximated for Earth (Tlimit ≈ 400 K) and is estimated to be 10-7 (in SI units). Thereby, Tlimit (Eq. (A.2)) scales with the surface gravity. This is a rough estimate for Tlimit and thus αmax. More advanced modeling would be required to better determine this limit, but this is outside of the scope of this study.
Equation (A.2) is derived from τs = κ ∗ ps/g and the Clausius-Clapeyron equation, that relates the surface pressure ps and temperature Ts: 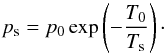 (A.3)
(A.3)
All Tables
All Figures
 |
Fig. 1 Illustration of model parameterization. a) Model I parameters are core radius rcore, mantle composition c comprising the oxides Na2O-CaO-FeO-MgO-Al2O3-SiO2, mantle radius rmantle, mass of water mwater, mass of envelope menv, envelope Luminosity L, and envelope metallicity Zenv. b) Model II parameters are as for a), with atmosphere parameterized by pressure at the bottom of the atmosphere pbatm, number of scale-heights of opaque layers N, mean molecular weight μ, and a temperature-related parameter α. See Sect. 2.2 and Table 1 for more details. |
| In the text | |
 |
Fig. 2 Sampled one-dimensional (1D) marginal posterior cdfs (blue) of model I parameters for Neptune: a) mass of envelope menv; b) envelope Luminosity L; c) mass of water mwater; d) mantle radius rmantle; e) core radius rcore; f) Fe/Simantle; g) Mg/Simantle. Prior and posterior nearly completely overlap in g). The envelope metallicity Zenv (not shown) is fixed, Zenv = 0. The prior cdfs are plotted in red. Gray area in plots a)−d) represent independent literature estimates (see main text). |
| In the text | |
 |
Fig. 3 Sampled two-dimensional (2D) marginal posterior pdfs (blue) of model I parameters for Neptune: a) mass of envelope menv and envelope Luminosity L; b) mass of water mwater and mantle radius rmantle. Gray areas represent independent literature estimates (see main text). |
| In the text | |
 |
Fig. 4 Sampled 1D marginal posterior cdfs (blue) of model II parameters for Neptune: a) pressure at bottom of atmosphere pbatm; b) atmospheric mass fraction matm/M (Eq. (9)); c) temperature-related parameter α; d) number of scale-heights of opaque layers N; e) mean molecular weight μ; f) mass of water mwater; g) mantle radius rmantle; h) core radius rcore; i) Fe/Simantle; j) Mg/Simantle. The prior cdfs are plotted in red. Gray areas in b), e), f) represent independent literature estimates (see main text). |
| In the text | |
 |
Fig. 5 Masses and radii of synthetic planets (black dots, cases A−K), observed exoplanets (gray dots) from Dressing et al. (2015), and Earth and Venus. Planets are plotted against mass-radius curves of idealized compositions for which a surface temperature of 300 K has been assumed. Planet cases A−K are summarized in Table 4. |
| In the text | |
 |
Fig. 6 Sampled 1D marginal posterior cdfs of model I parameters for synthetic planet cases (A−D) of 7 M⊕ that vary in terms of radii: 1.7 R⊕ (A), 2.2 R⊕ (B), 2.6 R⊕ (C), 2.9 R⊕ (D); a) mass of envelope menv; b) envelope luminosity L; c) envelope metallicity Zenv; d) mass of water mwater; e) mantle radius rmantle; f) core radius rcore; g) Fe/Simantle; h) Mg/Simantle. |
| In the text | |
 |
Fig. 7 Sampled 1D marginal posterior cdfs of model II parameters for synthetic planet cases (A−D) of 7 M⊕ that vary in terms of radii: 1.7 R⊕ (A), 2.2 R⊕ (B), 2.6 R⊕ (C), 2.9 R⊕ (D); a) pressure at bottom of atmosphere pbatm; b) atmospheric mean molecular weight μ; c) temperature-related parameter α; d) number of scale-heights of opaque layers N, e) mass of water mwater; f) mantle radius rmantle; g) core radius rcore; h) Fe/Simantle; i) Mg/Simantle. Depending on the case, the upper prior bound in c) differs, which is indicated by the vertical colored lines corresponding to the respective case. |
| In the text | |
 |
Fig. 8 Sampled 2D marginal posterior pdfs of model I parameters for synthetic planet case C showing the correlation between: a) rcore and rmantle; b) rmantle and mwater; c) mwater and menv; d) menv, and Zenv; e) mwater and the averaged μ corresponding to Zenv. Those model realizations that explain the data within 1σ are plotted in blue. Samples in c), d) for which gas mass fractions menv/M > 0.01 are highlighted in green and should be taken with care. See main text for discussion of features B1 and B2. |
| In the text | |
 |
Fig. 9 Sampled 2D marginal posterior pdfs of model II parameters for synthetic planet case C showing the correlation between: a) rcore and rmantle; b) rmantle and mwater; c) mwater and pbatm; d) pbatm, and μ; e) mwater and μ; f) mwater and α; g) mwater and N. Those model realizations that explain the data within 1σ are plotted in blue. Samples in c), d) for which gas mass fractions menv/M > 0.0001 are highlighted in green and should be taken with care. |
| In the text | |
 |
Fig. 10 Sampled 1D marginal posterior cdfs of model I parameters for synthetic planet cases B, E, F, G that vary in terms of data uncertainties. B is the reference case (σM = 0.05 M, σR = 0.02 R, 20% for both σFe/Sibulk and σMg/Sibulk), E has larger uncertainties in mass and radius (σM = 0.2 M, σR = 0.1 R), whereas F and G have larger uncertainties in the abundance constraints, 50% and 80%, respectively. a) Mass of envelope menv; b) envelope luminosity L; c) envelope metallicity Zenv; d) mass of water mwater; e) mantle radius rmantle; f) core radius rcore; g) Fe/Simantle; h)Mg/Simantle. The priors in g) and h) are not shown as not to overload the plot, because they differ among the cases. |
| In the text | |
 |
Fig. 11 Sampled 1D marginal posterior cdfs of model II parameters for synthetic planet cases B, E, F, G that vary in terms of data uncertainties. B is the reference case (σM = 0.05 M, σR = 0.02 R, 20% for both σFe/Sibulk and σMg/Sibulk), E has larger uncertainties in mass and radius (σM = 0.2 M, σR = 0.1 R), whereas F and G have larger uncertainties in the abundance constraints, 50% and 80%, respectively. a) Pressure at bottom of atmosphere pbatm; b) atmospheric mean molecular weight μ; c) temperature-related parameter α; d) number of scale-heights of opaque layers N; e) mass of water mwater; f) mantle radius rmantle; g) core radius rcore; h) Fe/Simantle; i) Mg/Simantle. The priors in h) and i) are not shown as not to overload the plot, because they differ among the cases. |
| In the text | |
 |
Fig. 12 Sampled 1D marginal posterior cdfs of menv (model I) for the synthetic planets: case C at 1 AU, case H at 0.1 AU, case J at 1 AU, and case K at 0.1 AU. For cases J and K, the gas composition is restricted to pure H/He (Zenv = 0) using the EoS of Saumon et al. (1995). |
| In the text | |
 |
Fig. 13 Sampled 1D marginal posterior cdfs (blue) for different priors (red) of core size rcore for Neptune (applying model I). Distributions are depicted in dashed when the prior is uniform in rcore and solid when it is uniform in rcorercore3 . The latter is identical to Fig. 2e. |
| In the text | |
 |
Fig. 14 Sampled 1D marginal posterior cdfs (blue) for different priors (red) of envelope metallicity Zenv for case C (7 M⊕, 2.6 R⊕, applying model I). Distributions are depicted in dashed when the prior is uniform in Zenv and solid when it is uniform in 1/Zenv. The latter is identical to Fig. 6c. |
| In the text | |
 |
Fig. 15 Sampled 1D marginal posterior cdfs (blue) for mwater assuming different priors on L for Neptune (applying model I). Solid blue line refer to wide prior range on L (1018−1023 erg/s), whereas dashed blue line refer to narrow prior range on L (1022.47−1022.57 erg/s). The former is identical to Fig. 2a. Gray area represent independent literature estimates (see main text). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


