| Issue |
A&A
Volume 596, December 2016
|
|
|---|---|---|
| Article Number | A34 | |
| Number of page(s) | 10 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201628767 | |
| Published online | 25 November 2016 | |
Transport of relativistic electrons at shocks in shell-type supernova remnants: diffusive and superdiffusive regimes
1 Dipartimento di Fisica, Università della Calabria, 87036 Rende, Italy
e-mail: silvia.perri@fis.unical.it
2 INAF, Osservatorio Astrofisico di Arcetri, Largo E. Fermi, 5, 50125 Firenze, Italy
e-mail: amato@arcetri.astro.it
Received: 22 April 2016
Accepted: 6 September 2016
Context. Understanding the transport properties of energetic particles in the presence of magnetic turbulence is crucial for interpreting observations of supernova remnants (SNR) and for assessing the cosmic-ray acceleration mechanism.
Aims. We aim at obtaining information on the transport regimes of energetic electrons upstream and downstream of SNR blast waves by studying the X-ray rims.
Methods. We considered emission profiles expected when synchrotron energy losses dominate, normal diffusion (typically causing an exponential decay), and superdiffusion (causing a power-law decay) for a spherically symmetric model. Then we compared the model profiles, projected on the plane of the sky, with Chandra observations of supernova (SN)1006 and Tycho’s SN.
Results. Our study shows that downstream of the blast wave the observed profile is exponentially cut-off due to synchrotron energy losses in the amplified and shock compressed magnetic field present. Upstream of the blast wave and close to the shock, the observed profile of SN1006 is well reproduced by electron diffusion in the Bohm regime. However, the long X-ray tail far upstream of the shock is better explained by considering a change in the energetic electrons’ transport regime, that appears to become superdiffusive and gives rise to a power law intensity profile on scales over which the magnetic field strength can be assumed to be constant. Similar results are obtained for Tycho, although in this case the nonlinear effects associated with particle acceleration appear to be stronger close to the shock.
Conclusions. The analysis of Chandra observations of the X-ray thin rims of SN1006 and of Tycho’s SN, SN 1572, can be well explained assuming normal diffusion in the vicinity of the blast wave and superdiffusion far upstream, similarly to what has been found for particles accelerated at interplanetary shocks. This suggests that anomalous transport is common in both interplanetary space and interstellar medium.
Key words: acceleration of particles / shock waves / ISM: supernova remnants
© ESO, 2016
1. Introduction
Supernova remnant (SNR) shocks are the most popular candidates for the acceleration of Galactic cosmic rays (CRs; e.g., Aharonian et al. 2004; Helder et al. 2012). The prevailing energization mechanism is thought to be diffusive shock acceleration (DSA; e.g., Bell 1978; Lee & Fisk 1982; Drury 1983; Amato 2014). This association has gained important observational support in recent years thanks to the data collected by X-ray telescopes such as Chandra and XMM-Newton and gamma-ray telescopes such as Fermi and AGILE, with the former instruments showing accelerated electrons with energies of up to tens of TeV (Reynolds et al. 2012; Vink 2012) and the latter highlighting for the first time the presence of relativistic protons in SNRs (Abdo et al. 2010a,b; Giuliani et al. 2011; Tavani et al. 2010). However, a number of questions on the details of the acceleration processes remain open (e.g., Balogh et al. 2013; Lagage & Cesarsky 1983; Reynolds et al. 2012; Helder et al. 2012; Amato 2014).
A distinctive feature of many SNRs are the very narrow rims of X-ray emission, which have been interpreted as caused by synchrotron radiation of ~TeV electrons (Bamba et al. 2005). For shell-type SNRs we can confidently assume that electron acceleration occurs at the blast wave produced by the SN ejecta (Achterberg et al. 1994; Green 2009; Morlino et al. 2010; Reynolds et al. 2012). The intense synchrotron emission observed as thin rims in many historical SNRs has suggested signficant magnetic field amplification (MFA) in the vicinity of the shock, with values ranging from 30–500μG (Reynolds et al. 2012; Ressler et al. 2014; Tran et al. 2015), to be compared with the typical magnetic field strength in the interstellar medium, which is ~3−6μG.
In principle, the thinness of the X-ray rims could be also due to effective magnetic field damping downstream of the shock instead of effective magnetic field amplification. In the first hypothesis, the width of the filaments would be determined by the length scale over which the magnetic field is damped and not be attributed to strong synchrotron losses, and the field strength could be moderate, without the need for amplification. Important studies in this respect were published by Rettig & Pohl (2012), who showed that it is possible to distinguish between damping and losses based on detailed spectral studies of the filaments. Very detailed studies were conducted on the filaments of SN1006 and Tycho’s SN by Ressler et al. (2014) and Tran et al. (2015), respectively. For SN1006, Ressler et al. (2014) showed that the shrinkage with energy of the filament width in X-rays is too rapid to result solely from magnetic field damping, and an MFA higher by a factor 10−50 with respect to the average value in the interstellar medium (ISM) is required. For Tycho’s SN, an even broader spectral study of the filaments were carried out by Tran et al. (2015), who considered both radio and X-ray emission. The conclusion of their analysis is that while damping must be at work on scales of about a few percent of the remnant radius to explain the radio and X-ray width of the rims, the implied field strength is between 50 and 400 μG, so that once again MFA must be operating.
This MFA is generally believed to be due to the backstreaming of cosmic-ray protons that are accelerated at the shocks (Skilling 1975; Bell 1978, 2004). In the upstream medium, the variation in the level of self-generated magnetic turbulence with distance from the shock and the associated variation in the particle diffusion coefficient have been explicitly taken into account in Bell’s pioneering work (Bell 1978). This was a preliminary calculation of how accelerated particles affect the environment of their acceleration site. More refined calculations followed, trying to fully address the strong nonlinearity of the problem of efficient particle acceleration at shocks (Drury 1983). All these efforts have led to the development of the theory of nonlinear diffusive shock acceleration (NLDSA), which in its current formulation includes many different aspects of the back-reaction of the acceleration process on the accelerator; see Amato (2014), for instance, for a recent review.
Important information on the particle transport and acceleration at SNR shocks can be inferred from the analysis of the spatial profiles of the X-ray emission. Bamba et al. (2003, 2005) estimated the width of the X-ray profiles of five historical SNRs by fitting the downstream emission profile with an empirical exponentially decaying function. These authors found that the scale length of the exponential is of about a few × 10-2 pc in the downstream of young remnants and a factor 2–4 larger in their upstream.
More recently, Helder et al. (2012) have fitted the downstream X-ray emission profiles of several remnants with an exponential decay in spherical geometry, taking the projection effects into account. These fits broadly agree with the observations, even though the observed downstream profiles appear to be steeper than the model profiles. Helder et al. (2012) stated that exponential decay over a width wd (typical of diffusive transport) or a uniform shell of radius wd (typical of advection dominated transport) can provide an equally good fit to the downstream, which indicates that the diffusion and advection length of the emitting particles must be very similar in these objects, as the authors discuss. No attempt is made in that work, or in the studies mentioned above (Ressler et al. 2014; Tran et al. 2015), to fit the upstream emission profile, while this can provide important information on the particle transport.
Such an attempt has been made instead by Morlino et al. (2010), for example, who showed that the observation of thin rims at SN1006 is consistent with the predictions of NLDSA, where accelerated particles are the primary sources of the turbulence that guarantees efficient scattering and acceleration to high energies. Morlino et al. (2010) also suggested an MFA upstream of the shock by a factor ~ 10.
One of the open questions related to the association between SNRs and CR acceleration has to do with the problem of achieving sufficiently high energies in SNRs (see Blasi 2013, and Amato 2014, for recent reviews of the open problems in the SNR-CR connection). The time available for particle acceleration is limited: typically by radiative losses when electrons are considered, and by the age or the size of the accelerator for protons and heavy nuclei. Within DSA theory, on the other hand, the acceleration time depends on how fast a particle of given energy can return to the shock front after each crossing, and hence, ultimately, on the transport properties of the fluid on both sides of the blast wave. Because of the difficulties faced by current models in explaining CR acceleration up to PeV energies (where the so-called knee in the CR spectrum is located and where the Galactic component of CRs is thought to end), it is appropriate to explore the possibility that different transport regimes than considered so far might be at work and help to solve the problem.
In this context, a number of studies, both numerical (Zimbardo et al. 2006; Pommois et al. 2007; Shalchi & Kourakis 2007; Tautz 2010; Lazarian & Yan 2014) and based on data analysis in the heliosphere (Perri & Zimbardo 2007, 2008, 2009a,b; Sugiyama & Shiota 2011; Trotta & Zimbardo 2011; Perri & Zimbardo 2015a), have shown that energetic particle transport in the presence of magnetic turbulence can be superdiffusive rather than diffusive. For nondiffusive transport, the mean square displacement of the particle grows nonlinearly in time, 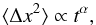 (1)with α ≠ 1 (Duffy et al. 1995; Kirk et al. 1996; Metzler & Klafter 2000, 2004). In particular, when α > 1, we have superdiffusion, and when α < 1 we have subdiffusion. Superdiffusion involves non-Gaussian statistics comprising power-law probability distributions, and in this framework the upstream time profile of energetic particles accelerated at an infinite planar shock is found to be a power law (Perri & Zimbardo 2007, 2008). Recently, Perri & Zimbardo (2012a) have included superdiffusive transport within a first-order Fermi acceleration process and found an energy spectral index for accelerated particles that depends not only on the shock compression ratio, but also on α. This has allowed them to derive energy spectra harder than those predicted by the standard DSA, and also shorter acceleration times (Perri et al. 2015; Perri & Zimbardo 2015a,b).
(1)with α ≠ 1 (Duffy et al. 1995; Kirk et al. 1996; Metzler & Klafter 2000, 2004). In particular, when α > 1, we have superdiffusion, and when α < 1 we have subdiffusion. Superdiffusion involves non-Gaussian statistics comprising power-law probability distributions, and in this framework the upstream time profile of energetic particles accelerated at an infinite planar shock is found to be a power law (Perri & Zimbardo 2007, 2008). Recently, Perri & Zimbardo (2012a) have included superdiffusive transport within a first-order Fermi acceleration process and found an energy spectral index for accelerated particles that depends not only on the shock compression ratio, but also on α. This has allowed them to derive energy spectra harder than those predicted by the standard DSA, and also shorter acceleration times (Perri et al. 2015; Perri & Zimbardo 2015a,b).
In this paper we determine whether the idea of superdiffusive transport is compatible with, or even favored by, observations of SNRs. Different fits to the observed X-ray intensity profiles are attempted, both within the framework of normal diffusive transport and in a scenario in which anomalous transport is important.
In Sect. 2 we describe the main properties of the emission profiles expected from energy loss and the different transport models, that is, normal and superdiffusive. In Sect. 3 we study and fit the X-ray emission profiles obtained by Chandra observations of the blast waves of SN1006 and Tycho’s SNR. In Sect. 4 we conclude, and a summary of the superdiffusion framework is given in Appendix A.
2. Modeling the SNR X-ray profiles
2.1. Synchrotron losses
Electron acceleration at SNR shocks is thought to be a loss-limited process, with the main loss mechanism being synchrotron radiation. The highest energy electrons in SNRs emit synchrotron radiation in the X-ray band. The spectral distribution of the synchrotron radiation has a dominant Fourier component at frequency ν0 ~ (eB⊥E2)/(6πm3c5), so that photons with typical energy Eγ = 1 keV are emitted by electrons with energies Ee = (22TeV)(B/ 100μG)− 1/2(Eγ/ 1 keV)1/2 (Parizot et al. 2006). These electrons lose energy through radiation at a rate (Rybicki-Lightman 1987) 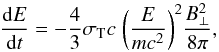 (2)where σT is the electron Thomson cross-section and B⊥ is the magnetic field perpendicular to the particle orbit. The implied synchrotron energy loss time is
(2)where σT is the electron Thomson cross-section and B⊥ is the magnetic field perpendicular to the particle orbit. The implied synchrotron energy loss time is 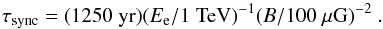 (3)Since these high-energy electrons cannot radiate energy for times longer than τsync, their emission is limited to narrow regions around the shock, detected as thin rims in the X-ray. The thickness of the rims obviously depends on how far from the shock electrons can travel in a time τsync and allows us to extract information on the particle transport regime.
(3)Since these high-energy electrons cannot radiate energy for times longer than τsync, their emission is limited to narrow regions around the shock, detected as thin rims in the X-ray. The thickness of the rims obviously depends on how far from the shock electrons can travel in a time τsync and allows us to extract information on the particle transport regime.
2.2. Geometrical modeling
We consider a simple one-dimensional, spherically symmetric model in which the synchrotron emissivity Sν only depends on the distance r from the shock along the radius of the SNR: 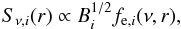 (4)where i = 1,2 denotes the upstream or downstream region, B is the total magnetic field, and fe is the electron distribution function. We then integrate the volume emissivity along the line of sight to obtain the emission profile to be compared with data:
(4)where i = 1,2 denotes the upstream or downstream region, B is the total magnetic field, and fe is the electron distribution function. We then integrate the volume emissivity along the line of sight to obtain the emission profile to be compared with data: 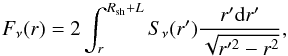 (5)where r′ is the spherical radius, r is the distance from the SNR center projected on the plane of the sky, Rsh is the radius of the blast wave, and L the relevant extent of the upstream region. For r′ > (<)Rsh we will have Sν = Sν,1(Sν,2).
(5)where r′ is the spherical radius, r is the distance from the SNR center projected on the plane of the sky, Rsh is the radius of the blast wave, and L the relevant extent of the upstream region. For r′ > (<)Rsh we will have Sν = Sν,1(Sν,2).
2.3. Particle spatial distributions
The transport of particles upstream and downstream of a planar shock can be described by the standard one-dimensional transport equation (Völk et al. 1981) ![\begin{eqnarray} \frac{\partial f_{\rm e}(E,x,t)}{\partial t}+V(x)\frac{\partial f_{\rm e}(E,x,t)}{\partial x}-\frac{p}{3}\frac{\partial f_{\rm e}(E,x,t)}{\partial p}\frac{\partial V(x)}{\partial x}=\nonumber \\ \frac{\partial}{\partial x}\biggl[D(E,x)\frac{\partial f_{\rm e}(E,x,t)}{\partial x}\biggr]-\frac{\partial}{\partial E} \left[\left(\frac{{\rm d}E}{{\rm d}t}\right) f_{\rm e}(E,x)\right] ,\label{transport} \end{eqnarray}](/articles/aa/full_html/2016/12/aa28767-16/aa28767-16-eq40.png) (6)where V is the fluid speed, p the particle momentum, and D(E,x) the diffusion coefficient. The last term on the RHS of Eq. (6) represents the particle energy losses. We search for stationary solutions (∂/∂t = 0) of Eq. (6) for constant (spatially independent) plasma speed V and diffusion coefficient D on both sides of the shock. As for the loss term, since the main contribution in our case comes from synchrotron losses, the term dE/ dt appearing in Eq. (6) can be written as in Eq. (2). Since we consider power-law distributions of particles, we can further simplify Eq. (6) by writing (e.g., Parizot et al. 2006)
(6)where V is the fluid speed, p the particle momentum, and D(E,x) the diffusion coefficient. The last term on the RHS of Eq. (6) represents the particle energy losses. We search for stationary solutions (∂/∂t = 0) of Eq. (6) for constant (spatially independent) plasma speed V and diffusion coefficient D on both sides of the shock. As for the loss term, since the main contribution in our case comes from synchrotron losses, the term dE/ dt appearing in Eq. (6) can be written as in Eq. (2). Since we consider power-law distributions of particles, we can further simplify Eq. (6) by writing (e.g., Parizot et al. 2006) ![\begin{equation} \frac{\partial}{\partial E}\left[\left(\frac{{\rm d}E}{{\rm d}t}\right) f_{\rm e}(E,x)\right] \approx \frac{f_{\rm e}(E,x)}{\tau_{\rm sync}} \cdot \label{simpleloss} \end{equation}](/articles/aa/full_html/2016/12/aa28767-16/aa28767-16-eq47.png) (7)This approximation can only be safely made for particle spectra steeper than E-2. For flatter spectra, this approximation misses the pile-up effect that arises when synchrotron losses are dominant. However, we here model the X-ray emission of two remnants, SN1006 and Tycho’s SN, both of which have steep underlying particle spectra inferred: ∝ E-2.2 for SN1006 (Ressler et al. 2014) and ∝ E-2.16 in Tycho’s SN (Tran et al. 2015). This approximation allows us to transform the original partial differential equation (Eq. (6)) into an ordinary differential equation. For a more general treatment of particle transport in SNRs, we refer to Rettig & Pohl (2012). Under our simplified assumptions (see also Parizot et al. 2006), the final equation for the evolution of the particle distribution function reads
(7)This approximation can only be safely made for particle spectra steeper than E-2. For flatter spectra, this approximation misses the pile-up effect that arises when synchrotron losses are dominant. However, we here model the X-ray emission of two remnants, SN1006 and Tycho’s SN, both of which have steep underlying particle spectra inferred: ∝ E-2.2 for SN1006 (Ressler et al. 2014) and ∝ E-2.16 in Tycho’s SN (Tran et al. 2015). This approximation allows us to transform the original partial differential equation (Eq. (6)) into an ordinary differential equation. For a more general treatment of particle transport in SNRs, we refer to Rettig & Pohl (2012). Under our simplified assumptions (see also Parizot et al. 2006), the final equation for the evolution of the particle distribution function reads 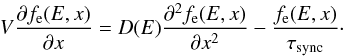 (8)We note that when the downstream magnetic field is not too strong, the electron energy loss is characterized by a loss time τsync that is not necessarily much shorter than the SNR age, so that the first term in Eq. (6), ∂fe/∂t, should be retained. From our analysis the downstream magnetic field for SN 1006 has been estimated to be about 36 μG, which corresponds to τsync ~ 231 yr versus a SNR age of 1000 yrs. Thus, Eq. (8) is to be considered only as a first approximation. Several solutions for the particle distribution functions can be found, depending on the dominance of one term with respect to the others in Eq. (8).
(8)We note that when the downstream magnetic field is not too strong, the electron energy loss is characterized by a loss time τsync that is not necessarily much shorter than the SNR age, so that the first term in Eq. (6), ∂fe/∂t, should be retained. From our analysis the downstream magnetic field for SN 1006 has been estimated to be about 36 μG, which corresponds to τsync ~ 231 yr versus a SNR age of 1000 yrs. Thus, Eq. (8) is to be considered only as a first approximation. Several solutions for the particle distribution functions can be found, depending on the dominance of one term with respect to the others in Eq. (8).
2.3.1. Downstream solutions
In the downstream, we expect losses to be non-negligible. Whether advection or diffusion dominates therefore depends on the particle energy and on the level of turbulence. The general solution of Eq. (8) reads ![\begin{eqnarray} &&f_{{\rm e},2}(E,x) = f_0\exp{(-x/\Delta R_2)}, \nonumber\\ &&\Delta R_2 = \frac{V_2\tau_{\rm syn}}{2}\left[1+\sqrt{\left(1+\frac{4D_2}{V_2^2\tau_{\rm syn}}\right)}\right], \label{downstream} \end{eqnarray}](/articles/aa/full_html/2016/12/aa28767-16/aa28767-16-eq55.png) (9)where V2 is the plasma speed downstream. Basically, the length ΔR2 is the size of the emitting region for each given particle energy, which is closely related to, but not exactly the same as, the size of the observed X-ray rims, with the difference due to projection effects (Parizot et al. 2006; Morlino et al. 2010). Furthermore, from Eq. (9) we can easily obtain two limiting cases, namely the regime in which advection dominates and the regime in which diffusion dominates. In the former case the electron spatial profile becomes fe,2(E,x) = f0exp(−x/ (V2τsyn)), while in the latter case we have
(9)where V2 is the plasma speed downstream. Basically, the length ΔR2 is the size of the emitting region for each given particle energy, which is closely related to, but not exactly the same as, the size of the observed X-ray rims, with the difference due to projection effects (Parizot et al. 2006; Morlino et al. 2010). Furthermore, from Eq. (9) we can easily obtain two limiting cases, namely the regime in which advection dominates and the regime in which diffusion dominates. In the former case the electron spatial profile becomes fe,2(E,x) = f0exp(−x/ (V2τsyn)), while in the latter case we have 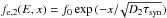 .
.
2.3.2. Upstream solutions
We now consider the upstream region, where the ambient magnetic field B1 is weaker than the downstream field B2 because of the compression at the shock. Assuming that the upstream field is approximately isotropic, as is expected in the case of strong turbulence, and since the magnetic field components perpendicular to the shock normal are compressed, the relation B2 = rBB1 with  and rc the shock compression ratio holds. This implies that synchrotron losses upstream are weaker by a factor
and rc the shock compression ratio holds. This implies that synchrotron losses upstream are weaker by a factor 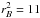 in a strong shock (rc = 4), as appropriate for the fast blast waves considered in the present work. As a first approximation, we neglect the loss term in Eq. (6) and obtain V∂fe,1(E,x) /∂x = D(E)∂2fe,1(E,x) /∂x2. In this simplified case, we obtain the standard diffusive solution for the particle profile for x< 0 (i.e., upstream, with the shock position at x = 0),
in a strong shock (rc = 4), as appropriate for the fast blast waves considered in the present work. As a first approximation, we neglect the loss term in Eq. (6) and obtain V∂fe,1(E,x) /∂x = D(E)∂2fe,1(E,x) /∂x2. In this simplified case, we obtain the standard diffusive solution for the particle profile for x< 0 (i.e., upstream, with the shock position at x = 0), 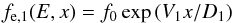 (10)(e.g., Drury 1983; Giacalone 2012).
(10)(e.g., Drury 1983; Giacalone 2012).
In reality, if SNRs are the primary sources of galactic CRs, as currently believed, then particle acceleration at the blast waves of young remnants, as we consider here, is expected to occur with a high efficiency: 10% or more of the kinetic energy of the explosion must be converted into accelerated particles. If this is the situation, the system is more appropriately described within the framework of NLDSA and the accelerated particles are the primary sources of the turbulence that guarantees efficient scattering and acceleration to high energies. In this scenario the magnetic turbulence can be generated by particles back-streaming in the upstream medium at super-Alfvénic speed (as observed in the ion foreshock of the Earth’s bow shock Perri et al. 2009), and the turbulence level will decrease with increasing distance from the shock front, since so does the particle density. While attempts at fitting the X-ray emission profiles of SN1006 and Tycho’s SN have been carried out within the latest and most well-developed models of NLDSA (see Morlino et al. 2010, for SN1006; and Morlino & Caprioli 2012, for Tycho’s SN), the simplest description of the problem, and one that predicts a power-law profile in the upstream, is the model described in the seminal paper by Bell (1978), which we consider here as a reference model. When we neglect the number density of diffuse galactic CRs, which is certainly a good approximation at the energies we are interested in (TeV or higher), and we also neglect energy losses (an assumption that can be checked a posteriori), we can write the spatial profile of the electron distribution function in perfect analogy with that of the hadronic CRs taking up most of the shock energy and driving the turbulence, 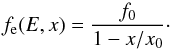 (11)In this expression f0 is the particle number density in phase space at the shock (x = 0) and
(11)In this expression f0 is the particle number density in phase space at the shock (x = 0) and 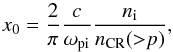 (12)where
(12)where 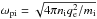 is the ion plasma frequency, ni is the number density of the upstream gas and nCR( >p) ≈ 4πp3f0(p) is the number of accelerated particles with momentum higher than p. When we assume an acceleration efficiency ξCR, namely that a fraction ξCR of the shock kinetic energy is transferred into accelerated particles, we can rewrite
is the ion plasma frequency, ni is the number density of the upstream gas and nCR( >p) ≈ 4πp3f0(p) is the number of accelerated particles with momentum higher than p. When we assume an acceleration efficiency ξCR, namely that a fraction ξCR of the shock kinetic energy is transferred into accelerated particles, we can rewrite 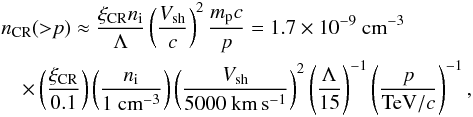 (13)where Λ = ln(pmax/pmin). It follows that x0, which also represents the diffusion scale upstream of the shock, x0(p) = D1(x = 0,p) /Vsh, can be estimated as
(13)where Λ = ln(pmax/pmin). It follows that x0, which also represents the diffusion scale upstream of the shock, x0(p) = D1(x = 0,p) /Vsh, can be estimated as 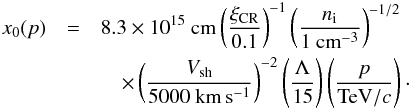 (14)On a scale comparable with x0(p), the density of particles of momentum >p starts to decrease. At the same time, the magnetic field will not be constant in the precursor, but will progressively decrease with the distance from the shock. Its strength is predicted to scale as
(14)On a scale comparable with x0(p), the density of particles of momentum >p starts to decrease. At the same time, the magnetic field will not be constant in the precursor, but will progressively decrease with the distance from the shock. Its strength is predicted to scale as 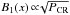 both within Bell’s description and within the framework of NLDSA (Amato & Blasi 2005, 2006), with PCR decreasing on the scale of the CR precursor Lprec ≈ D1(0,pmax) /Vsh = x0(pmax), where pmax is the highest energy at which the shock currently accelerates particles. The decrease in magnetic field strength with distance is slow, approximately
both within Bell’s description and within the framework of NLDSA (Amato & Blasi 2005, 2006), with PCR decreasing on the scale of the CR precursor Lprec ≈ D1(0,pmax) /Vsh = x0(pmax), where pmax is the highest energy at which the shock currently accelerates particles. The decrease in magnetic field strength with distance is slow, approximately 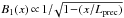 (see Eqs. (17) and (18) below), so that we neglect this effect here, taking
(see Eqs. (17) and (18) below), so that we neglect this effect here, taking 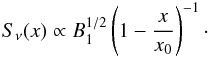 (15)Finally, a third scenario envisaged for particle propagation upstream of the shock is the possibility of anomalous transport far upstream, in particular superdiffusion. The motivation comes from recent studies of energetic electrons and protons accelerated at interplanetary shock waves (Perri & Zimbardo 2007, 2008, 2009a, 2012a, 2015a; Sugiyama & Shiota 2011). The analysis of particle profiles far upstream of these shocks has indicated superdiffusive particle propagation in the interplanetary space. This transport regime has been ascribed to an approximately constant low level of turbulence far from the shock front (Perri & Zimbardo 2012b). Furthermore, Perri & Zimbardo (2012b) analyzed magnetic field fluctuations upstream of the shocks at a timescale in resonance with energetic particles and reported the occurrence of a broad, scale-free distribution of particle scattering times τ, namely a non-negligible probability associated with very long τ.
(15)Finally, a third scenario envisaged for particle propagation upstream of the shock is the possibility of anomalous transport far upstream, in particular superdiffusion. The motivation comes from recent studies of energetic electrons and protons accelerated at interplanetary shock waves (Perri & Zimbardo 2007, 2008, 2009a, 2012a, 2015a; Sugiyama & Shiota 2011). The analysis of particle profiles far upstream of these shocks has indicated superdiffusive particle propagation in the interplanetary space. This transport regime has been ascribed to an approximately constant low level of turbulence far from the shock front (Perri & Zimbardo 2012b). Furthermore, Perri & Zimbardo (2012b) analyzed magnetic field fluctuations upstream of the shocks at a timescale in resonance with energetic particles and reported the occurrence of a broad, scale-free distribution of particle scattering times τ, namely a non-negligible probability associated with very long τ.
Numerical studies of full particle trajectories in magnetic turbulence have also shown that anomalous transport is found when the level of turbulence is weak (Pommois et al. 2007; Shalchi & Kourakis 2007; Gkioulidou et al. 2007), while transport is found to be diffusive for high turbulence levels.
We therefore conjectured a similar situation upstream of SNR shocks: far upstream, where the magnetic field fluctuations are substantially lower than in the ramp close to the shock front, the transport regime can be different from diffusive. Perri & Zimbardo (2007, 2008) derived a power-law particle time or spatial profile for particles accelerated at an infinite planar shock in the superdiffusive framework. This power-law profile has a slope a related to the exponent of superdiffusion α by a = 2−α (see Appendix A). It has been found that for superdiffusion the upstream power-law profile breaks at short distances from the shock, where it smoothly becomes a nearly flat function (this has been inferred from in situ spacecraft measurements and can be explained assuming the modified Gaussian propagator in Eq. (A.4) for superdiffusion close to the shock front; Perri & Zimbardo 2009b; Perri et al. 2015; Perri & Zimbardo 2015a). As mentioned above, if turbulence is efficiently created by the streaming particles in the vicinity of the shock, as the amplified magnetic fields inferred in SNRs suggest, then particle scattering is expected to be fast in the vicinity of the shock and to lead to normal diffusive transport. On the other hand, far away from the shock, there are not enough streaming particles for effective self-generation of the scattering turbulence and the transport might become anomalous, and in particular superdiffusive. We call this distance Lprec and treated it as a free parameter in the model. It is clear, however, that Lprec must be related with the distance at which the flux of particles of a given energy is no longer high enough for efficient growth of the magnetic field perturbations.
Assuming superdiffusion beyond Lprec, our particle distribution becomes 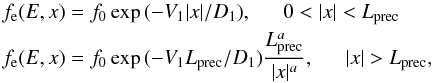 (16)where for simplicity we assumed an isotropic distribution function and directly matched the densities at x = Lprec. For normal diffusive transport caused by the interaction of particles with strong self-generated turbulence, assuming Bohm diffusion in a spatially constant magnetic field, we can determine the upstream electron emission profiles by estimating the magnetic field amplitude downstream of the shock B2 (one free parameter) and using the magnetic field compression ratio. Conversely, in the superdiffusive scenario the number of free parameters increases to three, since we need to fix the length Lprec that separates the regimes close upstream and far upstream, and the slope a of the power law.
(16)where for simplicity we assumed an isotropic distribution function and directly matched the densities at x = Lprec. For normal diffusive transport caused by the interaction of particles with strong self-generated turbulence, assuming Bohm diffusion in a spatially constant magnetic field, we can determine the upstream electron emission profiles by estimating the magnetic field amplitude downstream of the shock B2 (one free parameter) and using the magnetic field compression ratio. Conversely, in the superdiffusive scenario the number of free parameters increases to three, since we need to fix the length Lprec that separates the regimes close upstream and far upstream, and the slope a of the power law.
It is important to stress that in the superdiffusive regime Eq. (6) does not hold anymore and the normal diffusion coefficient D diverges (because the mean free path of particles diverges). The transport equation that describes the process is indeed a fractional diffusion-advection equation (see Metzler & Klafter 2000; Litvinenko & Effenberger 2014; Perri et al. 2015, for a complete discussion). More details on superdiffusion are given in Appendix A.
3. Analysis of remnants
Using the simplified models for the X-ray emission profiles described in Sect. 2, we reproduced the observed spatial profiles of two historical SNRs, SN1006 and Tycho’s SN. The emissivity was obtained from measurements within rectangular boxes that included the upstream and downstream regions around the blast wave of each remnant. The radial profile of SN1006 is described in Morlino et al. (2010) and was obtained from Chandra observations (dating 2008 June 24; ObsID. 9107; PI: Petre; see also Katsuda et al. 2009) of the northeastern limb of the remnant (see Fig. 1 in Morlino et al. 2010). It is obtained by averaging over a direction of a rectangle of 50 × 120 arcsec2. Tycho’s SN emission profile instead is extracted from Chandra observations of the western side of the remnant between 235″ and 270″ (the data are courtesy of Jacco Vink and were presented by Helder et al. 2012: 10% error bars were associated to the data points in that article). It should be noted that, differently from SN1006, some of the synchrotron filaments in Tycho’s SN are contaminated by thermal emission. This does not come from the shocked gas, whose contribution is shown to be very weak (Cassam-Chenaï et al. 2007), but from the supernova ejecta. The latter spatially overlap the filaments in some places, but as can be seen from Chandra images (see Fig. 1 in Tran et al. 2015, and also their discussion), this occurs mostly at the eastern side of the remnant, whereas filaments in the west, such as the one we consider, are rather clean.
 |
Fig. 1 Radial profile of the emission at 1 keV for the SN1006 remnant in logarithmic scale (asterisks). The thick red line corresponds to the model integrated along the line of sight for synchrotron-loss-dominated transport downstream, and diffusive transport upstream (test-particle regime). Upstream the profile decreases exponentially with a scale-length Ldiff = D1/Vsh (diffusion length). |
3.1. SN1006
SN1006 hosts a blast wave that is propagating with speed Vsh = 4330 km s-1 in an ambient interstellar medium with density ni = 0.05 cm-3 (Morlino et al. 2010). Assuming a distance d = 2.2 kpc (Helder et al. 2012), the radius of the remnant can be estimated to be Rsh ~ 10 pc.
We started our analysis of the remnant by fitting the downstream emissivity profile. We used Eq. (5) with the emissivity described according to Eq. (4) and fe,2(r) given by Eq. (9). The thickness ΔR2 only depends on the known downstream shock speed, which is V2 = Vsh/ 4, and on the unknown magnetic field strength B2, since we assumed particle diffusion according to Bohm’s scaling: D2 = 1/3(cEe/ (qeB2)), as expected for well-developed turbulence with high δB/B0. The best model profile is found for a magnetic field strength B2 = 36μG, which is within the range of values typically found in the literature (Parizot et al. 2006; Morlino et al. 2010; Ressler et al. 2014), even though in the low end (note that the value of B2 may change when considering different filaments around the blast wave).
For the upstream region, we first made the simple assumption of diffusive transport in the Bohm regime, with a spatially constant diffusion coefficient D1. The upstream magnetic field is 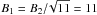 μG, and we verified that the time for energy loss τsyn is much longer than the diffusion time
μG, and we verified that the time for energy loss τsyn is much longer than the diffusion time 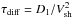 . In this regime Eq. (10) holds, so that the radial profile decays exponentially with a scale corresponding to the diffusion length Ldiff = D1/Vsh = 0.18 pc = 0.018Rsh. This model is plotted in Fig. 1 as a thick red line along with the normalized intensity profile of SN1006 as observed by Chandra in the X-rays (asterisks): the value of B2, which is the only free-parameter of the model, leads to a modeled intensity profile that closely resembles the observed profile, both downstream and in the shock ramp upstream (close upstream). A simple test-particle diffusive model therefore appears adequate to reproduce the brightest part of the emission profile.
. In this regime Eq. (10) holds, so that the radial profile decays exponentially with a scale corresponding to the diffusion length Ldiff = D1/Vsh = 0.18 pc = 0.018Rsh. This model is plotted in Fig. 1 as a thick red line along with the normalized intensity profile of SN1006 as observed by Chandra in the X-rays (asterisks): the value of B2, which is the only free-parameter of the model, leads to a modeled intensity profile that closely resembles the observed profile, both downstream and in the shock ramp upstream (close upstream). A simple test-particle diffusive model therefore appears adequate to reproduce the brightest part of the emission profile.
However, a purely exponential profile leaves the weaker but extended emission at larger distance from the shock in the upstream unexplained. A natural check to make is to verify whether the overall large-scale X-ray emission profile can be reasonably well fit by a power-law model for the spatial distribution of particles such as the one that results from Bell’s theory (Bell 1978), where the particle scattering is due to self-generated turbulence. We took the emissivity as in Eq. (15), with x0 to be calculated at the typical particle energy corresponding to 1 keV emission in the magnetic field immediately upstream of the shock. Within Bell’s model the magnetic field immediately upstream of the shock can be calculated based on the relation 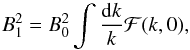 (17)where
(17)where 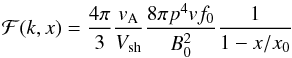 (18)and p(k) = eB0/ck through the resonance condition. The integration in Eq. (17) is readily transformed into an integral over the particles’ partial pressure and finally leads to (see, e.g., Amato & Blasi 2006)
(18)and p(k) = eB0/ck through the resonance condition. The integration in Eq. (17) is readily transformed into an integral over the particles’ partial pressure and finally leads to (see, e.g., Amato & Blasi 2006) 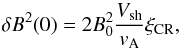 (19)which in our case corresponds to B1 ≈ 16(ξCR/ 0.1)μG, not far from our best value (B1 ≈ 11μG) based on the downstream emission profile. With this magnetic field the electrons emitting 1 keV photons have an energy Ee ~ 60 TeV and their diffusion length is x0 ~ 1.1 pc, which is one tenth of the SN1006 radius.
(19)which in our case corresponds to B1 ≈ 16(ξCR/ 0.1)μG, not far from our best value (B1 ≈ 11μG) based on the downstream emission profile. With this magnetic field the electrons emitting 1 keV photons have an energy Ee ~ 60 TeV and their diffusion length is x0 ~ 1.1 pc, which is one tenth of the SN1006 radius.
The line-of-sight integrated Bell profile, coming from Eq. (15), is shown in Fig. 2 as a dashed red line and decreases upstream much more slowly than the observed Chandra X-ray integrated emissivity. It is worth remarking that we assumed a constant upstream magnetic field B1, whereas the field is expected to decrease over the scale Lprec. We also tried to describe the data with different model parameters, but the result is that no good agreement between models and observations can be obtained with a single shape of the particle distribution fe(E,x), be it exponential or power law. Conversely, the data seem suggestive of a distribution function that has an exponential decrease with distance from the shock in the shock vicinity and a power-law decrease farther away. In terms of particle transport, this agrees very well with a picture in which diffusion dominates in the highly turbulent field close to the shock (Bell 1978; Achterberg et al. 1994; Morlino et al. 2010; Caprioli & Spitkovsky 2014), while superdiffusive transport occurs where the turbulence level decreases, in analogy with what has been found at interplanetary shocks (Perri & Zimbardo 2007, 2008, 2012b).
 |
Fig. 2 Radial profile of the emission at about 1 keV for the SN1006 remnant in logarithmic scale (asterisks). The thick red line corresponds to the model integrated along the line of sight for synchrotron-loss-dominated transport downstream, diffusive transport close upstream (as in Fig. 1), and superdiffusive transport far upstream (in the flatter tail of the profile). The dashed red line corresponds to the model integrated along the line of sight for synchrotron-loss-dominated transport downstream, and a profile following the modeling by Bell (1978) upstream. The profile refers to the filament shown in Fig.1 of Morlino et al. (2010). |
The decreased level of magnetic field fluctuations can lead to a change in the particle scattering time distribution and in the distribution of the particle jump lengths (Zumofen & Klafter 1993; Perri & Zimbardo 2012b). We tried to reproduce the observed upstream radial profile through Eq. (16), namely maintaining the Bohm diffusion in the ramp and assuming a power-law emissivity profile far upstream, as predicted by superdiffusion. Of course, as stated above, in this scenario the number of free parameters increases to three, namely B2, Lprec, and a. We fixed B1 as before, based on the downstream profile and on the assumption of a strong shock. For the other two parameters our best values are Lprec = 80 arcsec and a = 0.7. It is clear from Fig. 2 that the modeled intensity profile reproduces the data very well, therefore we now comment on the physical meaning of the values we found for our parameters. First of all, the index a< 1, corresponds to superdiffusive transport with an anomalous diffusion exponent α ≃ 1.3, as shown by Perri & Zimbardo (2007, 2008). Second, the angular extent of the precursor, given the assumed distance of the SNR (2.2 kpc), translates into a physical length Lprec = 0.85 pc, which roughly corresponds to the diffusion length Ldiff(300TeV) = D1(300TeV) /Vsh = 0.7 pc of particles with energy ≈ 300TeV for the given magnetic field strength and SNR expansion velocity. This value of the energy (approximatelyfive times that of the electrons emitting keV photons) is not far from that estimated for the maximum particle energy in this remnant (Berezhko et al. 2012). The emerging picture is therefore that of normal diffusive transport within a distance upstream of the shock on the order of Ldiff(Emax), over which the particles are still numerous enough to self-generate the turbulence for efficient scattering, and of anomalous superdiffusive transport at larger distances, where the turbulence level reaches values typical of the interstellar medium.
3.2. Tycho’s supernova
For Tycho’s SN we adopted a similar approach as we used for SN1006. Here the shock has a speed Vsh = 4579 km s-1 and is moving in a medium with density ni = 0.5 cm-3. The distance of the source was taken to be d = 3.3 kpc (Helder et al. 2012), so that the radius of the blast wave is Rsh ~ 3.9 pc. In this remnant very strong magnetic fields have been inferred, reaching values as high as 500μG (Parizot et al. 2006; Tran et al. 2015). We best reproduced the data with a downstream magnetic field B2 = 300μG, in agreement with the value reported by Morlino & Caprioli (2012).
Again, we first considered a profile that is appropriate to describe particles that diffuse with a spatially constant diffusion coefficient in the upstream and downstream. In spite of the great magnetic field strength derived from fitting the downstream, the upstream magnetic field (B1 ≈ 90μG, as derived from compression at a strong shock of a completely isotropic magnetic field, 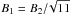 ) is not strong enough to cause relevant energy losses of the X-ray emitting particles over a timescale τdiff.
) is not strong enough to cause relevant energy losses of the X-ray emitting particles over a timescale τdiff.
 |
Fig. 3 Same as Fig. 1, but for Tycho’s SNR. The profile is the same as in Helder et al. (2012). The thick red line indicates the theoretical profile integrated along the line of sight, while the thick blue line is the theoretical profile convolved with the Chandra PSF. |
In Fig. 3 we report the radial emission profile (asterisks) of Tycho’s SNalong with the theoretical model (red line) and the theoretical model convolved with the point spread function (PSF) of Chandra (blue line), which corresponds to an angular resolution of 0.5 arcsec (Morlino & Caprioli 2012). While the downstream side is well reproduced by Eq. (9), the upstream ramp is not well described by diffusive transport with a spatially constant coefficient: this leads to a steeper decrease than observed. Even after convolution with the instrument PSF the discrepancy remained, which prompted us to seek alternative explanations.
The most natural guess is that nonlinear effects may be stronger in Tycho’s SN than in SN1006, as also suggested by the greater magnetic field strength and by previous studies (Morlino & Caprioli 2012). It is worth noticing, for example, that if MFA were only due to the resonant streaming instability (Eq. (19)), the value of the upstream magnetic field strength would imply that ξCR ≈ 0.9, namely a conversion efficiency of 90% of the shock kinetic energy into accelerated particles. Such a high efficiency is clearly unreasonable, and some other process must be at work to amplify the magnetic field, for example, the non-resonant streaming instability (Bell 2004).
However, we again considered a particle distribution following the theory of Bell (1978). The only parameter to be determined is the length-scale x0 at the energy of the emitting particles. Estimating x0 from Eq. (14) is just for comparison in this case, owing to the discrepancy between the value of B1 that derives from the theory by Bell (1978) and the one derived from observations: x0 corresponds to the diffusion length of particles of a given energy in the self-generated turbulence described by Eq. (18), which underestimates the magnetic field, however. We let x0 vary between 0.007 pc (corresponding to the diffusion length of particles emitting 1 keV photons in a 90μG magnetic field) and 0.1 pc, but in reality no good fit can be found for a model profile along the lines of Bell (1978): close to the shock the observed decrease is much faster than ∝ x-1 (as expected from Eq. (15)), while at larger distances the decrease is slower than the model prediction.
In addition, Tycho’s SN shows a flat tail of emission far upstream, which we investigated in the framework of superdiffusion. The emissivity resulting from Eq. (16) with Lprec = 2 arcsec, and a = 0.7 agrees well with the observed profile far upstream (see Fig. 4). Our best values correspond to Ldiff = 0.007pc = 0.0018Rsh for X-ray emitting particles, and Lprec = 0.03 pc. This value of Lprec corresponds to the diffusion length of particles with energy ≈ 200 TeV, which is not far from the maximum energy of protons in Tycho’s SN, as estimated by Morlino & Caprioli (2012), and also similar to what we have found for SN1006.
 |
Fig. 4 Same as Fig. 2, but for Tycho’s SNR. The thick red line indicates the theoretical profile integrated along the line of sight, while the thick blue line is the theoretical profile convolved with the Chandra PSF. |
4. Discussion and conclusions
We have considered the X-ray intensity profiles of the outer rims of two young supernova remnants, SN1006 and Tycho’s SN, and compared them to simple analytical models of particle transport in the presence of synchrotron energy losses. In particular, we set up a spherically symmetric model of the shock region and computed the intensity profile of X-ray emission along the radial direction (in the plane of sky) Fν(r) by integrating the volume emissivity Sν(r) along the line of sight. For the transport of relativistic electrons upstream of the shock, we considered three different models: normal diffusion with a spatially constant diffusion coefficient, normal diffusion with a diffusion coefficient that depends on distance from the shock as described by Bell (1978), where turbulence is self-generated by the accelerated protons streaming away from the shock, and finally the case of anomalous, superdiffusive transport, which yields a rather flat power-law density profile far upstream of the shock.
For SN1006, the downstream radial profile is well described within a scenario in which the transport is dominated by synchrotron losses in a magnetic field B2 ≃ 36μG, in agreement with previous estimates (Parizot et al. 2006; Morlino et al. 2010); for the upstream, the best description is found in terms of a combination of Bohm diffusion in a field 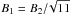 (the compression ratio of the shock rc = 4) close upstream, and superdiffusion far upstream, with the former explaining the ramp seen in the data, and the latter being at the origin of the extended flat tail of X-ray emission. We emphasize that it is not possible to reproduce the long upstream tail by an exponential or by a profile following Bell (1978). More generally, a single power-law profile seems unable to reproduce the entire upstream emission, near and far from the shock, and a profile following Bell (1978; ∝ x-1) is in any case too steep to represent the extended upstream tail: a flatter power law with slope a ≃ 0.7 is needed to fit the observations. This suggests that far upstream of the shock the transport of relativistic electrons is superdiffusive, with an anomalous diffusion exponent α = 2−a ≃ 1.3. We note that this value of α is consistent with those found in the heliosphere by Perri & Zimbardo (2007, 2008, 2009a). The change of transport regime from normal in the SNR upstream shock ramp to superdiffusive in the SNR upstream shock tail might arise because the turbulence level far upstream is weaker, and it is closer to that in the undisturbed interstellar medium. This is consistent with turbulent MFA in a region of size corresponding to the ramp thickness Lprec, and negligible self-generated turbulence at larger distances (Bell 1978, 2004; Amato 2014). Our best estimate of Lprec, based on observations, is fully compatible with its interpretation as the diffusion length of particles at the highest energy currently achieved in the remnant as estimated by Berezhko et al. (2012), Emax ~ 300 TeV.
(the compression ratio of the shock rc = 4) close upstream, and superdiffusion far upstream, with the former explaining the ramp seen in the data, and the latter being at the origin of the extended flat tail of X-ray emission. We emphasize that it is not possible to reproduce the long upstream tail by an exponential or by a profile following Bell (1978). More generally, a single power-law profile seems unable to reproduce the entire upstream emission, near and far from the shock, and a profile following Bell (1978; ∝ x-1) is in any case too steep to represent the extended upstream tail: a flatter power law with slope a ≃ 0.7 is needed to fit the observations. This suggests that far upstream of the shock the transport of relativistic electrons is superdiffusive, with an anomalous diffusion exponent α = 2−a ≃ 1.3. We note that this value of α is consistent with those found in the heliosphere by Perri & Zimbardo (2007, 2008, 2009a). The change of transport regime from normal in the SNR upstream shock ramp to superdiffusive in the SNR upstream shock tail might arise because the turbulence level far upstream is weaker, and it is closer to that in the undisturbed interstellar medium. This is consistent with turbulent MFA in a region of size corresponding to the ramp thickness Lprec, and negligible self-generated turbulence at larger distances (Bell 1978, 2004; Amato 2014). Our best estimate of Lprec, based on observations, is fully compatible with its interpretation as the diffusion length of particles at the highest energy currently achieved in the remnant as estimated by Berezhko et al. (2012), Emax ~ 300 TeV.
An analogous study was carried out for Tycho’s SN. We assumed an exponential profile in the downstream region due to synchrotron energy losses and in the upstream ramp region due to normal transport with the Bohm diffusion coefficient. However, in this case, it was not possible to obtain as good a fit of the emission profile as for SN1006. On the other hand, Tycho’s SN was shown by previous studies (Morlino & Caprioli 2012) to be one of the most effective particle accelerators in the Galaxy, so that a much stronger nonlinearity of the system is expected with respect to the case of SN1006, and it is not too surprising that simple test-particle modeling does not work too well. For the region farther upstream, we found that the emission can be well reproduced by a power-law profile with slope ≃ 0.7, corresponding to superdiffusion with an anomalous diffusion exponent α ≃ 1.3. Again, the size of the precursor, when physically interpreted as the diffusion length of particles that have been accelerated to the highest energy the system can currently achieve, is found to roughly agree with independent estimates of Emax found in the literature (Morlino & Caprioli 2012).
We would like to remark that, using very simple analytical models, we were able to describe the X-ray integrated emissivity in the downstream and upstream regions for two historical SNRs. In particular, the long flat X-ray tail observed in the two remnants at distances >Lprec is compatible with a change in the particle transport regime, from diffusive close to the shock to superdiffusive far from the shock. This result is similar to what has been found from the analysis of time profiles of energetic particles upstream of interplanetary shocks (Perri & Zimbardo 2007, 2009a, 2015a; Sugiyama & Shiota 2011; Zimbardo et al. 2012), and it is interesting to note that in many of these shock crossings the exponent of anomalous diffusion is close to α = 1.3, as found here for the SNRs. This similarity suggests that superdiffusion with α ≃ 1.3 is typical when the turbulence level is not too strong, for instance, δB/B0 ≤ 1, as in the solar wind. Furthermore, it is interesting to note that a method of analysis developed for space physics can be useful for the analysis of remote SNR data. By recalling the finding of superdiffusive electron transport in the Coma cluster of galaxies (Ragot & Kirk 1997), we may argue that superdiffusion in astrophysics is a relatively common process.
Acknowledgments
We thank G. Morlino and Jacco Vink for kindly providing us the data of the X-ray profile of SN1006 and Tycho’s SN. The authors acknowledge support from the International Space Science Institute (ISSI) in Bern, where part of this work was carried out, through the International Team No. 297 “Superdiffusive transport in space plasmas and its influence on energetic particle acceleration and propagation”. E.A. acknowledges support from the PRIN-INAF 2012 grant. This work has been supported by the Agenzia Spaziale Italiana under the contract ASI-INAF 2015-039-R.O “Missione M4 di ESA: Partecipazione Italiana alla fase di assessment della missione THOR”.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. (Fermi collaboration) 2010a, Science, 327, 1103 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. (Fermi collaboration) 2010b, ApJ, 712, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Achterberg, A., Blandford, R. D., & Reynolds, S. P. 1994, A&A, 281, 220 [NASA ADS] [Google Scholar]
- Aharonian, F. A., Akhperjanian, A. G., Aye, K.-M., et al. 2004, Nature, 432, 75 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Amato, E. 2014, Int. J. Mod. Phys. D, 23, 1430013 [Google Scholar]
- Amato, E., & Blasi, P. 2005, MNRAS, 364, L76 [NASA ADS] [Google Scholar]
- Amato, E., & Blasi, P. 2006, MNRAS, 371, 1251 [NASA ADS] [CrossRef] [Google Scholar]
- Balogh, A., Bykov, A., Lin, R. P., et al., 2013, in Particle acceleration in cosmic plasmas, Space Science Series of ISSI (New York: Springer) [Google Scholar]
- Bamba, A., Yamazaki, R., Ueno, M., & Koyama, K. 2003, ApJ, 589, 827 [NASA ADS] [CrossRef] [Google Scholar]
- Bamba, A., Yamazaki, R., Yoshida, T., Terasawa, T., & Koyama, K. 2005, ApJ, 621, 793 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, A. R. 1978, MNRAS, 182, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, A. R. 2004, MNRAS, 353, 550 [Google Scholar]
- Berezhko, E., Ksenofontov, L. T., & Volk, H. J. 2012, ApJ, 759, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Blasi, P. 2013, A&ARv, 21, 70 [Google Scholar]
- Blumen, A., Klafter, J., & Zumofen, G. 1990, Europhys. Lett., 13, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Caprioli, D., & Spitkovsky, A. 2014, ApJ, 794, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Cassam-Chenaï, G., Hughes, J. P., Ballet, J., & Decourchelle, A. 2007, ApJ, 665, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Drury, L. O’C., 1983, Rep. Prog. Phys., 46, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Duffy, P., Kirk, J.-G., Gallant, Y.-A., et al. 1995, A&A, 302, L21 [NASA ADS] [Google Scholar]
- Geisel, T., Nierwetberg, J., & Zacherl, A. 1985, Phys. Rev. Lett., 54, 616 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Giacalone, J. 2012, ApJ, 761, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Giuliani, A., Cardillo, M., Tavani, M., et al. 2011, ApJ, 742, 30 [Google Scholar]
- Gkioulidou, M., Zimbardo, G., Pommois, P., Veltri, P., & Vlahos, L. 2007, A&A, 462, 1113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Green, D. A. 2009, Bull. Astron. Soc. India, 37, 45 [Google Scholar]
- Helder, E. A., Vink, J., Bykov, A. M., et al. 2012, Space Sci. Rev., 173, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Katsuda, S., Petre, R., Long, K. S., et al. 2009, ApJ, 692, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Kirk, J. G., Duffy, P., & Gallant, Y. A. 1996, A&A, 314, 1010 [NASA ADS] [Google Scholar]
- Klafter, J., Blumen, A., & Shlesinger, M. F., 1987, Phys. Rev. A, 35, 7 [Google Scholar]
- Klafter, J., Shlesinger, M. F., & Zumofen, G. 1996, Phys. Today, 49, 33 [CrossRef] [Google Scholar]
- Lagage, P. O., & Cesarsky, C. J. 1983, A&A, 125, 249 [NASA ADS] [Google Scholar]
- Lazarian, A., & Yan, H. 2014, ApJ, 784, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, M. A., & Fisk, L. A. 1982, Space Sci. Rev., 32, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Litvinenko, Y. E., & Effenberger, F. 2014, ApJ, 796, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Metzler, R., & Klafter, J. 2000, Phys. Rep., 339, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Metzler, R., & Klafter, J. 2004, J. Phys. A: Math. Gen., 37, R161 [NASA ADS] [CrossRef] [Google Scholar]
- Morlino, G., & Caprioli, D. 2012, A&A, 538, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morlino, G., Amato, E., Blasi, P., & Caprioli, D. 2010, MNRAS, 405, L21 [NASA ADS] [Google Scholar]
- Parizot, E., Marcowith, A., Ballet, J., & Gallant, Y.-A. 2006, A&A, 453, 387 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perri, S., & Zimbardo, G. 2007, ApJ, 671, L177 [NASA ADS] [CrossRef] [Google Scholar]
- Perri, S., & Zimbardo, G. 2008, J. Geophys. Res., 113, A03107 [NASA ADS] [Google Scholar]
- Perri, S., & Zimbardo, G. 2009a, ApJ, 693, L118 [NASA ADS] [CrossRef] [Google Scholar]
- Perri, S., & Zimbardo, G. 2009b, Adv. Space Res., 44, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Perri, S., & Zimbardo, G. 2012a, ApJ, 750, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Perri, S., & Zimbardo, G. 2012b, ApJ, 754, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Perri, S., & Zimbardo, G. 2015a, ApJ, 815, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Perri, S., & Zimbardo, G. 2015b, J. Phys.: Conf. Ser., 642, 012020 [NASA ADS] [CrossRef] [Google Scholar]
- Perri, S., Yordanova, E., Carbone, V., et al. 2009, J. Geophys. Res., 114, A02102 [NASA ADS] [CrossRef] [Google Scholar]
- Perri, S., Zimbardo, G., Effenberger, F., & Fichtner, H. 2015, A&A, 578, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perrone, D., Dendy, R. O., Furno, I., et al. 2013, Space Sci. Rev., 187, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Pommois, P., Zimbardo, G., & Veltri, P. 2007, Phys. Plasmas, 14, 012311 [NASA ADS] [CrossRef] [Google Scholar]
- Ragot, B. R., & Kirk, J. G., 1997, A&A, 327, 432 [NASA ADS] [Google Scholar]
- Reynolds, S. P., Gaensler, B. M., & Bocchino, F. 2012, Space Sci. Rev., 166, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Ressler, S. M., Katsuda, S., Reynolds, S. P., et al. 2014, ApJ, 790, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Rettig, R., & Pohl, M. 2012, A&A, 545, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rybicki, G. B., & Lightman A. P. 2004, in Radiative Processes in Astrophysics (Wiley-VCH) [Google Scholar]
- Shalchi, A. 2011, Phys. Rev. E, 83, 046402 [NASA ADS] [CrossRef] [Google Scholar]
- Shalchi, A., & Kourakis, I. 2007, A&A, 470, 405 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shlesinger, M. F., Zaslavsky, G. M., & Klafter, J. 1993, Nature, 363, 31 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Skilling, F. 1975, MNRAS, 172, 557 [NASA ADS] [CrossRef] [Google Scholar]
- Sugiyama, T., & Shiota, D. 2011, ApJ, 731, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Tautz, R. C. 2010, Plasma Phys. Control Fusion, 52, 045016 [Google Scholar]
- Tavani, M., Giuliani, A., Chen, A. W., et al. (AGILE Collaboration) 2010, ApJ, 710, L151 [NASA ADS] [CrossRef] [Google Scholar]
- Tran, A., Williams, B. J., Petre, R., Ressler, S. M., & Reynolds, S. P. 2015, ApJ, 812, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Trotta, E. M., & Zimbardo, G. 2011, A&A, 530, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vink, J. 2012, A&ARv, 20, 49 [Google Scholar]
- Völk, H. J., Morfill, G. E., & Forman, M. A. 1981, ApJ, 249, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Zimbardo, G., & Perri, S. 2013, ApJ, 778, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Zimbardo, G., Pommois, P., & Veltri, P. 2006, ApJ, 109, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Zimbardo, G., Perri, S., Pommois, P., & Veltri, P. 2012, Adv. Space Res., 49, 1633 [NASA ADS] [CrossRef] [Google Scholar]
- Zimbardo, G., Amato, E., Bovet, A., et al. 2015, J. Plasma Phys., 81, 495810601 [CrossRef] [Google Scholar]
- Zumofen, G., & Klafter, J. 1993, Phys. Rev. E, 47, 2 [Google Scholar]
Appendix A: Synopsis of superdiffusive transport at collisionless shocks
In relation to the modeling and data analyses presented in Sects. 2 and 3, here we summarize the tools appropriate for describing superdiffusion. The results presented in this section were derived in previous papers (see Klafter et al. 1987, 1996; Zumofen & Klafter 1993; Metzler & Klafter 2000, 2004; Perri & Zimbardo 2007, 2008, 2012a; Perrone et al. 2013; Shlesinger et al. 1993). We considered transport only along one direction, namely x, as this is appropriate for our scopes, with x eventually denoting the distance from the shock (x = 0 is the shock position).
For normal diffusion, the diffusion coefficient can be obtained as the time integral of the Lagrangian velocity autocorrelation function, 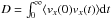 (e.g., Shalchi 2011). However, if the Lagrangian velocity autocorrelation function does not go fast to zero (i.e., exponentially), as in the presence of a power-law tailed function, for example, then the integral is diverging,
(e.g., Shalchi 2011). However, if the Lagrangian velocity autocorrelation function does not go fast to zero (i.e., exponentially), as in the presence of a power-law tailed function, for example, then the integral is diverging, 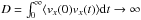 so that no time asymptotic diffusion coefficient can be defined. This divergence is related to long-range correlations in the velocity, that is, to a non-Markovian, non-local process. The divergence of D implies that the mean free path λ = 3D/v also diverges, since the particle speed v is finite. This requires a new approach to transport, which allows for non-Gaussian statistics. Of a number of possible tools (Perrone et al. 2013; Perri et al. 2015), we here discuss a probabilistic description involving Lévy walks. These are characterized by a probability ψ of making a free path, or jump, of length ℓ (forward or backward) in a time t given by Klafter et al. (1987)
so that no time asymptotic diffusion coefficient can be defined. This divergence is related to long-range correlations in the velocity, that is, to a non-Markovian, non-local process. The divergence of D implies that the mean free path λ = 3D/v also diverges, since the particle speed v is finite. This requires a new approach to transport, which allows for non-Gaussian statistics. Of a number of possible tools (Perrone et al. 2013; Perri et al. 2015), we here discuss a probabilistic description involving Lévy walks. These are characterized by a probability ψ of making a free path, or jump, of length ℓ (forward or backward) in a time t given by Klafter et al. (1987)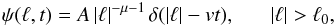 (A.1)where A is a normalization constant. The qualifying property of ψ is that for low values of μ, heavy power-law tails are obtained, which correspond to a non-negligible probability of very long jumps. It is important to have a coupling between jump length and jump duration, as expressed by the delta function, to ensure a constant, finite velocity. In the above expression, the power-law form only applies for | ℓ | >ℓ0, with ℓ0 a scale parameter. That is, ψ has a nonsingular, smooth behavior for ℓ → 0. It is readily verified that for μ< 2 the mean square value of ℓ, and hence the mean free path, diverges,
(A.1)where A is a normalization constant. The qualifying property of ψ is that for low values of μ, heavy power-law tails are obtained, which correspond to a non-negligible probability of very long jumps. It is important to have a coupling between jump length and jump duration, as expressed by the delta function, to ensure a constant, finite velocity. In the above expression, the power-law form only applies for | ℓ | >ℓ0, with ℓ0 a scale parameter. That is, ψ has a nonsingular, smooth behavior for ℓ → 0. It is readily verified that for μ< 2 the mean square value of ℓ, and hence the mean free path, diverges, 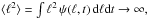 which means that the central limit theorem, leading to normal diffusion, is not applicable (e.g., Metzler & Klafter 2000). It can be shown that, to leading order, in the superdiffusive case, that is, for 1 <μ< 2, the mean square deviation is
which means that the central limit theorem, leading to normal diffusion, is not applicable (e.g., Metzler & Klafter 2000). It can be shown that, to leading order, in the superdiffusive case, that is, for 1 <μ< 2, the mean square deviation is 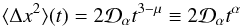 (A.2)(Geisel et al. 1985; Klafter et al. 1987; Zumofen & Klafter 1993; Zimbardo & Perri 2013).
(A.2)(Geisel et al. 1985; Klafter et al. 1987; Zumofen & Klafter 1993; Zimbardo & Perri 2013). 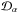 is the anomalous diffusion coefficient that has physical dimensions different from the normal diffusion coefficient D. More precisely (Zimbardo & Perri 2013; Perri et al. 2015; Perri & Zimbardo 2015a),
is the anomalous diffusion coefficient that has physical dimensions different from the normal diffusion coefficient D. More precisely (Zimbardo & Perri 2013; Perri et al. 2015; Perri & Zimbardo 2015a), 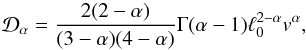 (A.3)where Γ is the Euler gamma function. Thus,
(A.3)where Γ is the Euler gamma function. Thus, 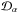 diverges for α → 1 and reaches zero for α → 2.
diverges for α → 1 and reaches zero for α → 2.
In addition, the probability distribution of particles P(x,t) of being at position x at time t (the propagator) is not Gaussian, as for normal diffusion, but it also has power-law tails. This can be obtained by solving a generalized Montroll-Weiss equation in Fourier-Laplace space (e.g., Zumofen & Klafter 1993; Zimbardo & Perri 2013). We introduce a scaling variable ξ = (x/ℓ0)/(t/t0)1 /μ, where the time t0 = ℓ0/v, being v the particle velocity; the scaling variable corresponds to the argument of the Gaussian for normal diffusion, and to the argument of the modified Gaussian in Eq. (A.4) below in the anomalous case. The generalized Montroll-Weiss equation can be solved analytically in two limits: for low values of the scaling variable ξ = (x/ℓ0)/(t/t0)1 /μ ≪ 1 we obtain a modified Gaussian, ![\appendix \setcounter{section}{1} \begin{eqnarray} P(x,t) \simeq {\frac{\Gamma((\mu+1)/\mu)} {\pi (Ct)^{1/\mu}}} \exp \left[-\frac{\Gamma(3/\mu)}{2\Gamma(1/\mu)} \left [{\frac{x}{(Ct)^{1/\mu}}}\right]^2 \right]\label{eqpropclose} \end{eqnarray}](/articles/aa/full_html/2016/12/aa28767-16/aa28767-16-eq199.png) (A.4)(see Zumofen & Klafter 1993; Zimbardo & Perri 2013). Conversely, for large distances, ξ ≫ 1 but | x | <vt, we obtain a power law,
(A.4)(see Zumofen & Klafter 1993; Zimbardo & Perri 2013). Conversely, for large distances, ξ ≫ 1 but | x | <vt, we obtain a power law, ![\appendix \setcounter{section}{1} \begin{equation} P(x,t) \simeq {\frac{\Gamma (\mu+1)} {\pi}} \sin \left [{\frac{\pi}{2}}\mu \right] {|C|} {\frac{t} {|x|^{\mu+1}}} , \label{eqpropxt} \end{equation}](/articles/aa/full_html/2016/12/aa28767-16/aa28767-16-eq202.png) (A.5)where Γ is Euler gamma function, and the C is a normalization constant (see Zumofen & Klafter 1993; Zimbardo & Perri 2013; Perri et al. 2015; Zimbardo et al. 2015)
(A.5)where Γ is Euler gamma function, and the C is a normalization constant (see Zumofen & Klafter 1993; Zimbardo & Perri 2013; Perri et al. 2015; Zimbardo et al. 2015) 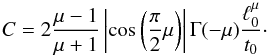 (A.6)The propagator reaches zero for x>vt (Blumen et al. 1990; Zumofen & Klafter 1993). The condition ξ = 1 fixes the matching between the two forms of the propagators in Eqs. (A.4) and (A.5).
(A.6)The propagator reaches zero for x>vt (Blumen et al. 1990; Zumofen & Klafter 1993). The condition ξ = 1 fixes the matching between the two forms of the propagators in Eqs. (A.4) and (A.5).
The propagator allows us to compute the density of particles of a given energy at any position in space and time as (e.g., Ragot & Kirk 1997) 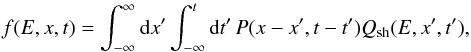 (A.7)where Qsh = Φ0(E)δ(x′−Vsht′) indicates the particle shock source, which moves with a speed Vsh. When we use the propagator for Lévy walks, the above expression allows us to obtain some of the most important modifications of the standard scenario due to superdiffusive transport. In particular, we can compute the particle distribution function far upstream of the shock, where the form (A.5) of the propagator applies, yielding
(A.7)where Qsh = Φ0(E)δ(x′−Vsht′) indicates the particle shock source, which moves with a speed Vsh. When we use the propagator for Lévy walks, the above expression allows us to obtain some of the most important modifications of the standard scenario due to superdiffusive transport. In particular, we can compute the particle distribution function far upstream of the shock, where the form (A.5) of the propagator applies, yielding 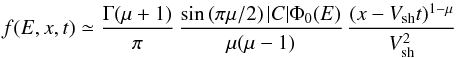 (A.8)(Perri & Zimbardo 2007, 2008). For remote observations such as those of SNRs, we may choose the observation time as t = 0, so that we have a power law in space with slope a = μ−1 < 1. This is markedly different from the predictions of normal diffusion, which yields an exponential profile upstream of the shock. As shown above, considering the varying level of Alfvén waves generated by cosmic rays streaming away from the shock, Bell (1978) obtained an energetic particle profile that is a power law with slope a = 1. However, superdiffusive transport yields a power-law profile even for constant turbulence level and constant transport properties (Perri & Zimbardo 2012b). Accordingly, an energetic particle power-law profile with 0 <a < 1 implies superdiffusive transport with α = 3−μ = 2−a. We may note that studying the precursor, that is, the upstream profile of energetic particles, is the most direct way to determine the transport properties perpendicular to the shock (once the upstream Vsh is known). For SNRs, we may directly fit the upstream synchrotron emission profiles (in this case we really “see” the spatial distribution of energetic particles).
(A.8)(Perri & Zimbardo 2007, 2008). For remote observations such as those of SNRs, we may choose the observation time as t = 0, so that we have a power law in space with slope a = μ−1 < 1. This is markedly different from the predictions of normal diffusion, which yields an exponential profile upstream of the shock. As shown above, considering the varying level of Alfvén waves generated by cosmic rays streaming away from the shock, Bell (1978) obtained an energetic particle profile that is a power law with slope a = 1. However, superdiffusive transport yields a power-law profile even for constant turbulence level and constant transport properties (Perri & Zimbardo 2012b). Accordingly, an energetic particle power-law profile with 0 <a < 1 implies superdiffusive transport with α = 3−μ = 2−a. We may note that studying the precursor, that is, the upstream profile of energetic particles, is the most direct way to determine the transport properties perpendicular to the shock (once the upstream Vsh is known). For SNRs, we may directly fit the upstream synchrotron emission profiles (in this case we really “see” the spatial distribution of energetic particles).
Other modifications of the diffusive shock acceleration scenario due to superdiffusive transport, concerning the energy spectral index of accelerated particles and the acceleration time, are described in Perri & Zimbardo (2012a, 2015a).
All Figures
 |
Fig. 1 Radial profile of the emission at 1 keV for the SN1006 remnant in logarithmic scale (asterisks). The thick red line corresponds to the model integrated along the line of sight for synchrotron-loss-dominated transport downstream, and diffusive transport upstream (test-particle regime). Upstream the profile decreases exponentially with a scale-length Ldiff = D1/Vsh (diffusion length). |
| In the text | |
 |
Fig. 2 Radial profile of the emission at about 1 keV for the SN1006 remnant in logarithmic scale (asterisks). The thick red line corresponds to the model integrated along the line of sight for synchrotron-loss-dominated transport downstream, diffusive transport close upstream (as in Fig. 1), and superdiffusive transport far upstream (in the flatter tail of the profile). The dashed red line corresponds to the model integrated along the line of sight for synchrotron-loss-dominated transport downstream, and a profile following the modeling by Bell (1978) upstream. The profile refers to the filament shown in Fig.1 of Morlino et al. (2010). |
| In the text | |
 |
Fig. 3 Same as Fig. 1, but for Tycho’s SNR. The profile is the same as in Helder et al. (2012). The thick red line indicates the theoretical profile integrated along the line of sight, while the thick blue line is the theoretical profile convolved with the Chandra PSF. |
| In the text | |
 |
Fig. 4 Same as Fig. 2, but for Tycho’s SNR. The thick red line indicates the theoretical profile integrated along the line of sight, while the thick blue line is the theoretical profile convolved with the Chandra PSF. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


