| Issue |
A&A
Volume 596, December 2016
|
|
|---|---|---|
| Article Number | A14 | |
| Number of page(s) | 33 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201526711 | |
| Published online | 21 November 2016 | |
The matter distribution in the local Universe as derived from galaxy groups in SDSS DR12 and 2MRS⋆
1 Department of Astrophysics, University of Vienna, Türkenschanzstraße 17, 1180 Vienna, Austria
e-mail: christoph.saulder@equinoxomega.net
2 European Southern Observatory, Karl-Schwarzschild-Straße 2, 85748 Garching bei München, Germany
3 Smithsonian Astrophysical Observatory, Harvard-Smithsonian Center for Astrophysics, 60 Garden St., MS09, Cambridge, MA 02138, USA
4 Sternberg Astronomical Institute, M.V. Lomonosov Moscow State University, 13 Universitetski prospect, 119992 Moscow, Russia
5 European Southern Observatory, Alonso de Córdova 3107, Vitacura, Casilla 19001, Santiago, Chile
Received: 9 June 2015
Accepted: 29 July 2016
Context. Friends-of-friends algorithms are a common tool to detect galaxy groups and clusters in large survey data. In order to be as precise as possible, they have to be carefully calibrated using mock catalogues.
Aims. We create an accurate and robust description of the matter distribution in the local Universe using the most up-to-date available data. This will provide the input for a specific cosmological test planned as follow-up to this work, and will be useful for general extragalactic and cosmological research.
Methods. We created a set of galaxy group catalogues based on the 2MRS and SDSS DR12 galaxy samples using a friends-of-friends based group finder algorithm. The algorithm was carefully calibrated and optimised on a new set of wide-angle mock catalogues from the Millennium simulation, in order to provide accurate total mass estimates of the galaxy groups taking into account the relevant observational biases in 2MRS and SDSS.
Results. We provide four different catalogues: (i) a 2MRS based group catalogue; (ii) an SDSS DR12 based group catalogue reaching out to a redshift z = 0.11 with stellar mass estimates for 70% of the galaxies; (iii) a catalogue providing additional fundamental plane distances for all groups of the SDSS catalogue that host elliptical galaxies; (iv) a catalogue of the mass distribution in the local Universe based on a combination of our 2MRS and SDSS catalogues.
Conclusions. While motivated by a specific cosmological test, three of the four catalogues that we produced are well suited to act as reference databases for a variety of extragalactic and cosmological science cases. Our catalogue of fundamental plane distances for SDSS groups provides further added value to this paper.
Key words: galaxies: clusters: general / galaxies: distances and redshifts / large-scale structure of Universe / galaxies: statistics
The full catalogues (Tables A.1 to A.8) are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/596/A14
© ESO, 2016
1. Introduction
Galaxy clusters and groups have been an important tool in extragalactic astronomy since the discovery of their nature. Zwicky (1933) used the internal dynamics of nearby clusters to postulate dark matter for the first time. Messier was the first to notice an overdensity of nebulae in the Virgo constellation (Biviano 2000) and thereby discovered the first galaxy cluster being unaware of its nature or the nature of the nebulae (galaxies). The investigation of galaxy clusters started shortly after the Great Debate, when it became established that the Universe contains other galaxies than our own. The first milestone was the discovery of dark matter in galaxy clusters (Zwicky 1933). The first significant cluster catalogues were produced by Abell (1958) and Zwicky et al. (1961). Starting with the pioneering work of Turner & Gott (1976) and heavily applied in Huchra & Geller (1982), Zeldovich et al. (1982) and Press & Davis (1982), the methods of finding clusters became more sophisticated and reproducible. The most common algorithm even up to the present day is the friend-of-friends (FoF) algorithm (Press & Davis 1982), although there are other techniques around (Yang et al. 2005; Gal 2006; Koester et al. 2007; Hao et al. 2010; Makarov & Karachentsev 2011; Muñoz-Cuartas & Müller 2012). Knebe et al. (2011) provide a comprehensive comparison between halo finder algorithms for simulated data. A detailed study on the optimization of cluster and group finders with a focus on FoF algorithms was performed by Eke et al. (2004a). Duarte & Mamon (2014, 2015) discuss the quality of FoF group finders and the impact of different linking lengths on the recovery of various group parameters. Efficient and reliable algorithms become crucially important, especially during the last decade and in the time of big data and surveys, such as 2MASS (Skrutskie et al. 2006), SDSS (Stoughton et al. 2002; Alam et al. 2015), 2dFGRS (Colless et al. 2001), 6dF Galaxy Survey (Jones et al. 2004, 2009), and GAMA (Driver et al. 2011). Information on galaxy grouping and clustering is important because it provides a laboratory to study the dependence of galaxy morphology on the environment (Einasto et al. 1974; Oemler 1974; Davis & Geller 1976; Dressler 1980; Postman & Geller 1984; Dressler et al. 1997; Goto et al. 2003; van der Wel et al. 2010; Wilman et al. 2011; Cappellari et al. 2011) or environmental influence on different properties of galaxies and groups (Huertas-Company et al. 2011; Luparello et al. 2013; Hearin et al. 2013; Hou et al. 2013; Yang et al. 2013; Wetzel et al. 2013; Budzynski et al. 2014; Einasto et al. 2014). It also provides a way to study the halo mass-luminosity relationship (Yang et al. 2009; Wake et al. 2011) and thereby helps us understand the dark matter distribution in the Universe.
Notable group and cluster catalogues besides those already mentioned are Turner & Gott (1976), Moore et al. (1993), Eke et al. (2004b), Gerke et al. (2005), Yang et al. (2007), Berlind et al. (2006), Brough et al. (2006), Crook et al. (2007), Knobel et al. (2009), Tempel et al. (2012, 2014)Nurmi et al. (2013), and Tully (2015). In our study, we will refer to all groups and clusters as groups independent of their sizes. This also includes individual galaxies to which we refer to as a group with just one member.
It is important to make a suitable choice for the linking length, which is the distance that defines which object is still a “friend” of others. Most FoF algorithms differ in the choice of scaling the linking length (Huchra & Geller 1982; Ramella et al. 1989; Nolthenius & White 1987; Moore et al. 1993; Robotham et al. 2011; Tempel et al. 2012), which is an important modification of all non-volume limited samples. In the way we implement the FoF algorithm of the group finder, we mainly follow Robotham et al. (2011) and use the corrected luminosity function of our sample for scaling.
Finally, it is crucial to calibrate the group finder on a set of mock catalogues to test its reliability. We created suitable mock catalogues using the Millennium simulation (Springel et al. 2005). When calculating the group catalogue, we paid specific attention that the mass in the considered volume matches the mass predicted by the cosmology. As discussed for various methods in Old et al. (2014, 2015), it is notoriously difficult to assign accurate masses for groups, especially if they are below 1014M⊙. The group catalogues which we obtained provide valuable insights into the matter distribution of the local Universe.
One of the motivations for this work is to obtain the basic dataset for a cosmological test, which was outlined in Saulder et al. (2012). In a follow-up paper we will elaborate the applications of the data for test and the full background (Saulder et al., in prep.). Hence, here we provide only essential details on that theory, in order to explain the motivation for our work. The tested theory, “timescape cosmology” (Wiltshire 2007), aims to explain the accelerated expansion of the Universe by backreactions due to General Relativity and the observed inhomogeneities in the Universe instead of introducing dark energy. The theory makes use of so-called “finite infinity” (FI) regions and their sizes are provided in this paper. The term was coined by Ellis (1984) and describes a matter horizon (Ellis & Stoeger 1987) of the particles that will eventually be bound. In our approach, we approximate the finite infinity regions with spheres of a mean density equal to the renormalized critical density (“true critical density” in Wiltshire 2007), which is slightly lower than the critical density in the Λ- cold dark matter (CDM) model.
This paper is structured as follows: in Sect. 2, we describe the samples, which we used for the group finder and its calibration. These calibrations are explained in detail in Sect. 3. The results of the group finder are provided in Sect. 4 and they are discussed and summarized in Sect. 5. In Sect. 6, we give brief conclusions. Appendices A to D provide additional information on calibrations used throughout the paper.
2. Galaxy samples
We used the 12th data release of the Sloan Digital Sky Survey (SDSS DR12, Alam et al. 2015) and the 2MASS Redshift Survey (2MRS, Huchra et al. 2012b), which is a spectroscopic follow-up survey of the Two Micron All Sky Survey (2MASS, Skrutskie et al. 2006), as our input observational data.
From the SDSS database, we retrieved data for 432 038 galaxies, which fulfilled the following set of criteria: spectroscopic detection, photometric and spectroscopic classification as galaxy (by the automatic pipeline), observed redshift between 0 and 0.1121, and the flag SpecObj.zWarning is zero. Additional constraints were applied later to further filter this raw dataset. We obtained the following parameters for all galaxies: photometric object ID, equatorial coordinates, galactic coordinates, spectroscopic redshift, Petrosian magnitudes in the g, r, and i band, their measurement errors, and extinction values based on Schlegel et al. (1998).
We used all 44 599 galaxies of table3.dat from 2MRS catalogue (Huchra et al. 2012a). We obtained the following parameters for these galaxies: 2MASS-ID, equatorial coordinates, galactic coordinates, extinction-corrected total extrapolated magnitudes in all three 2MASS bands (Ks, H, and J), their corresponding errors, and spectroscopic redshift (in km s-1), with its uncertainty.
In order to derive stellar masses for our catalogues, we also used additonal data from the Reference Catalog of Galaxy Spectral Energy Distributions (RCSED, Chilingarian et al. 2016), the UKIDSS survey (Lawrence et al. 2007), and the SIMBAD2 database.
We choose a large set of simulated data provided the Millennium simulation (Springel et al. 2005) in order to calibrate our group finder and properly assess potential observational biases.
Aside from the dark matter halos produced by its original run, the Millennium simulation database contains data from re-runs with updated cosmological parameters, semi-analytic models of galaxies, and the full particle information of a smaller run (called millimil).
Parameters of the Millennium simulation (original run and millimil(MM)).
Number of galaxies, number of FoF groups, and the percentage of all particles in these groups (with at least 20 particles) by a snapshot used, and corresponding redshifts.
Given that the cosmological parameters (see Table 1) used by the Millennium simulation in its original run (Springel et al. 2005) substantially deviate from the recently adopted values based on cosmic microwave background (CMB) data from the Planck satellite (Planck Collaboration I 2014) than reruns (Guo et al. 2013), which used WMAP7 cosmological parameters (Komatsu et al. 2011), it was appealing to use this rerun. However, for the reruns (Guo et al. 2013), the database of the Millennium simulation does not contain the friends-of-friends groups, which are required for a proper calibration of a group finder algorithm, but only the halos derived from them. Hence, we had to use the data from the original run.
For our group catalogue, we intended to reach up to a redshift of 0.11, which corresponds to the co-moving distance of about 323 Mpc/h100. Therefore, we had to obtain a cube of at least this side-length. Using our method to derive multiple mock catalogues (see the next section) from the dataset, we would ideally retrieve the full volume of the Millennium run (a cube with 500 Mpc/h100 side-length), but due to limitations in our available computational facilities, we had to restrict ourselves to a cube with the 400 Mpc/h100 side-length. To properly consider evolutionary effects, we obtained not only data from the last (present day) snapshot of the Millennium simulation, but also from all snapshots up-to (actually slightly beyond) the limiting redshift of our group catalogue. In the end, we received six cubes with a side-length of 400 Mpc/h100 for the latest snapshots (snapnum 63 (present day) to 58) of the Millennium simulation. The basic data is listed in Table 2. For the FoF-groups of these cubes, we obtained the following parameters: FoF-group ID number, co-moving coordinates, and number of particles in the FoF-group.
Because the Millennium simulation is a dark matter only simulation, all data on the luminous part of galaxies was derived from semi-analytic galaxy models with which the dark matter halos were populated. We used the semi-analytic models from Guo et al. (2011) created using the L-galaxies galaxy formation algorithm (Croton et al. 2006; De Lucia et al. 2006), and obtained the following list of parameters for all galaxies brighter than −15 mag in the SDSS r band in the previously defined cubes of the snapshots (see Table 2): galaxy ID, FoF-group ID number to which the galaxy belongs, co-moving coordinates, peculiar velocities, number of particles in the galaxy’s halo, and “dusty”3 absolute SDSS magnitudes for the g, r, and i band.
Less than half of the particles of the simulation are in FoF-groups (see Table 2). This is a cause for concern, because we aim to create a model of the local Universe, which provides a highly complete picture of the mass distribution. Full particle information on the original run of the Millennium simulation was not available to us (and would exceed our computational capacities anyway). However, for a smaller volume (see Table 1) of the millimil run (MM), the complete particle information as well as the FoF-groups are available in the Millennium simulation database. For the entire MM volume and the latest six snapshots (the same as for the original run) we obtained the following parameters for all FoF groups: FoF-group ID, Cartesian coordinates, number of particles in the FoF-group, and radius R200,NFW, within which the FoF group has an overdensity 200 times the critical density of the simulation when fitted by a NFW-profile. In addition to that, we received the same set of parameters of semi-analytical galaxy models as we did for the semi-analytical models in the original run using the same conditions as earlier for the entire MM volume. We also obtained the Cartesian coordinates for all particles of the latest snapshots of MM.
3. Description of the method
3.1. Processing observational data
We had to further process the data retrieved from SDSS and 2MRS in order to construct a dataset suitable for our group finder algorithm. The calibrations were largely the same for SDSS and 2MRS. Methodological differences are explained below.
The first step was to correct for the solar system motion relative to the CMB. We used the measurements from Hinshaw et al. (2009) and correct observed redshifts zobs applying a method explained in Saulder et al. (2013), Appendix A, but slightly updated using the redshift addition theorem (Davis & Scrimgeour 2014), to corrected redshifts zcor.
Afterwards, we corrected the observed SDSS magnitudes msdss for the Galactic foreground extinction according to Schlegel et al. (1998).
The 2MRS magnitudes obtained from the database were already corrected for galactic extinction. Hence, we could directly the observed 2MRS magnitudes as extinction-corrected magnitudes mcor.
In the next step, we calculated the extinction and K-corrected apparent magnitudes mapp using analytical polynomial approximations of K-corrections from Chilingarian et al. (2010) updated in Chilingarian & Zolotukhin (2012) for SDSS bands: 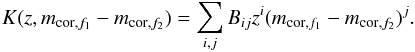 (1)We calculated the luminosity distance DL(zcor) following the equations (Hogg 1999):
(1)We calculated the luminosity distance DL(zcor) following the equations (Hogg 1999):
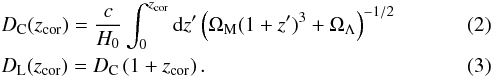 DC denotes for the co-moving distance. For consistency reasons, we used the values of the original Millennium simulation run for the cosmological parameters (see Table 1). We then computed K-corrected absolute magnitudes Mabs.
DC denotes for the co-moving distance. For consistency reasons, we used the values of the original Millennium simulation run for the cosmological parameters (see Table 1). We then computed K-corrected absolute magnitudes Mabs.
After these calibrations, finer cuts were applied on the SDSS and 2MRS datasets to make them compatible with the mock catalogues built in the next sub-section and directly usable for our group finder algorithm.
From the SDSS data, we removed all galaxies which fulfilled all of the following conditions: a corrected redshift zcor higher than 0.11 or lower than zero, an apparent magnitude mapp> 18.27 mag, 0.5 mag fainter than the official limiting magnitude in the r band of 17.77 mag (Strauss et al. 2002) (to clean the sample from poorly identified or misclassified objects), a measured magnitude error greater than 1 mag in the r or g band, and r band absolute magnitude Mabs fainter than −15 mag. Applying these cuts, our SDSS sample was reduced to 402 588 galaxies.
From the 2MRS data, we removed all objects for which no redshift information was provided. We also removed all galaxies which fulfilled the following set of conditions: a corrected redshift zcor lower than zero, an apparent magnitude mapp> 12.25 mag, 0.5 mag fainter than the official limiting magnitude in the Ks band of 11.75 mag (Huchra et al. 2012b), and Ks band absolute magnitude Mabs fainter than −18 mag. After these cuts, we ended up with a 2MRS sample of 43 508 galaxies.
3.2. Creating the mock catalogues
We constructed sets of mock catalogues each corresponding to both observational datasets and the “true” dark matter distribution based on the simulated data.
 |
Fig. 1 Projections of the distribution of galaxies in the SDSS mock catalogues and their overlaps. The fine green and red pixel in every plot show the projected (on the xy-plane) areas, where galaxies from two mock catalogues can be found, which belong to only one of the two catalogues. Yellow pixels indicate galaxies from both catalogues. The tiny blue crosses indicate galaxies that can be found in both catalogues in the same evolutionary stage (from the same redshift snapshot). Left panel: overlap of two mock catalogues whose coordinate origins are located in the neighbouring corners. Central panel: overlap of two mock catalogues whose origins are located in opposite corners, yet in the same plane (side of the cube). Right panel: overlap of two mock catalogues whose origins are located diagonally, opposite across the entire cube. |
 |
Fig. 2 Projections of the distribution of the galaxies in the 2MRS mock catalogues and their overlaps. Symbols as in Fig. 1. |
We created eight (largely) independent mock catalogues for the data cubes obtained from original run of the Millennium simulation using the following method. We put an observer into each of its 8 vertices4 and thereby obtained 8 different viewpoints, which became largely independent from each other once we included the Malmquist-bias into our calculations. These mock catalogues are not completely independent, because the brightest galaxies can be seen across the entire cube and, therefore, some of them are included in every mock catalogue (yet at different distances/redshifts and consequently at slightly differently evolutionary states). The overlaps of the different mock catalogues are illustrated in Figs. 1 and 2 for different geometrical arrangements between a set of two mock catalogues for the same survey. Depending on the distance between the corners, the overlap ranges from about nine percent to about a tenth of a percent for SDSS and always less than one percent for 2MRS5.
Prior to constructing the mock catalogues, there was one important issue to be considered: the data from Guo et al. (2011) does not contain 2MASS magnitudes. Therefore, we derived them from SDSS magnitudes using a colour transformation inspired by Bilir et al. (2008), which is provided in Appendix B.2.
The (dark matter) FoF groups are important for the calibration of the group finder algorithm. To avoid losing dark matter information on cut-off groups (edge-effect) in our sample, we moved the origin 10 Mpc/h100 inwards in all directions and we restricted “our view” to the first octant.
The cosmological redshift zcosmo was calculated from the co-moving distance DC by inverting Eq. (2). The co-moving distance itself was derived directly from the Cartesian coordinates of the Millennium simulation. The luminosity distance DL was obtained from the co-moving distance and the cosmological redshift using Eq. (3).
However, one does not directly observe the cosmological redshift, but a parameter, which we call the “observed” redshift zobs, which considers effects from peculiar motions and measurement uncertainties.
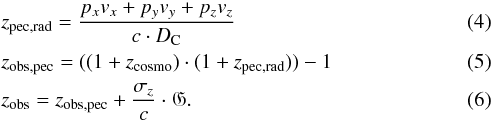 The projection of the peculiar motion vx, vy, and vz on the line of sight from the coordinate origin (view point) to the galaxy at the Cartesian coordinates px, py, and pz yielded the redshift zpec,rad of the radial component of the peculiar motion. We added it to the cosmological redshift using the theorem of Davis & Scrimgeour (2014). The redshift measurement uncertainty σz is about 30 km s-1 for SDSS and about 32 km s-1 for 2MRS. We use the symbol G to indicate a random Gaussian noise with a standard deviation σ of 1, which was implemented in our code using the function gasdev (Normal (Gaussian) Deviates) from Press et al. (1992).
The projection of the peculiar motion vx, vy, and vz on the line of sight from the coordinate origin (view point) to the galaxy at the Cartesian coordinates px, py, and pz yielded the redshift zpec,rad of the radial component of the peculiar motion. We added it to the cosmological redshift using the theorem of Davis & Scrimgeour (2014). The redshift measurement uncertainty σz is about 30 km s-1 for SDSS and about 32 km s-1 for 2MRS. We use the symbol G to indicate a random Gaussian noise with a standard deviation σ of 1, which was implemented in our code using the function gasdev (Normal (Gaussian) Deviates) from Press et al. (1992).
The absolute magnitudes Mabs from semi-analytic models were converted into apparent magnitudes mapp.
The magnitudes in the 2MRS catalogue were already corrected for extinction and the survey’s limiting magnitude was applied on the extinction corrected values. Consequently, we did not have to consider extinction for the 2MRS data.
However, we had to take extinction into account for mock catalogues which we compared to SDSS data. We used the reddening map of Schlegel et al. (1998) and multiplied the reddening coefficients of that map with the conversion factors listed in Stoughton et al. (2002) to obtain extinction values Amodel. To be more specific: only a part of the Schlegel map was used, which covers one eighth of the sky (the sky coverage of a single mock catalogue) and was at least 20 degrees away from the Galactic plane to reproduce a comparable extinction profile as the area covered SDSS. 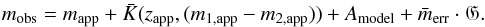 (7)Considering the extinction correction (for SDSS only), the mock K-correction
(7)Considering the extinction correction (for SDSS only), the mock K-correction  , and the photometric uncertainty to the apparent magnitude
, and the photometric uncertainty to the apparent magnitude 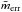 , we were able to calculate the observed magnitude mobs. The mock K-correction is explained in detail in Appendix C. The uncertainties in the Petrosian model magnitudes, which were used for the selection (limiting magnitude) of the spectroscopic sample of SDSS, were calculated using the uncertainties provided by the survey, which are 0.026 mag for the g band and 0.024 mag for the r band. The photometric uncertainties of 2MRS are 0.037 mag in the J band and 0.056 mag in the Ks band.
, we were able to calculate the observed magnitude mobs. The mock K-correction is explained in detail in Appendix C. The uncertainties in the Petrosian model magnitudes, which were used for the selection (limiting magnitude) of the spectroscopic sample of SDSS, were calculated using the uncertainties provided by the survey, which are 0.026 mag for the g band and 0.024 mag for the r band. The photometric uncertainties of 2MRS are 0.037 mag in the J band and 0.056 mag in the Ks band.
Observations do not directly yield 3D positions as we have in the simulated data, but a 2D projection on the sky plus a redshift. The equatorial coordinates α′ and δ′ were obtained by simple geometry: 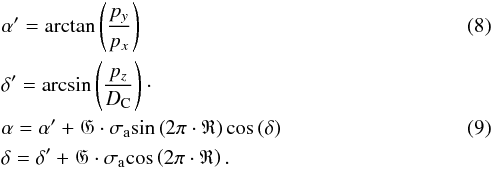 Considering an astrometric uncertainty σa of 0.1 arcsec6, we obtained the observed equatorial coordinates α and δ. The symbol R indicates a uniformly distributed random variable between 0 and 1.
Considering an astrometric uncertainty σa of 0.1 arcsec6, we obtained the observed equatorial coordinates α and δ. The symbol R indicates a uniformly distributed random variable between 0 and 1.
 |
Fig. 3 Redshift dependence of the number densities of the observational data and the mock catalogues. Left panal: 2MRS data; right panel: SDSS data. |
The evolutionary effects on galaxies and their distribution were taken into account by only using the galaxies from the snapshot (see Table 2 for the redshifts of the snapshots) closest to their cosmological redshift zcosmo. This simplification is justified because passive evolution is sufficiently slow for nearby (zcosmo< ~ 0.1) galaxies (Kitzbichler & White 2007).
The Malmquist bias was introduced into our mock catalogues by removing all galaxies with an “observed” (apparent) magnitude mobs fainter than the limiting magnitude of the survey. The limiting magnitude is 17.77 mag (Strauss et al. 2002) in the r band for SDSS and 11.75 mag (Huchra et al. 2012b) in the Ks for 2MRS.
All galaxies with an observed redshift zobs higher than 0.11 are removed from the SDSS mock catalogues.
We restricted our view of “visible galaxies” to the first octant of the coordinate system, which was necessary, because we had shifted the origin by 10 Mpc/h100 inwards earlier to avoid potential problems with the groups of the mock catalogue contributing to the visible distribution being partially cut. We still used the FoF group data from beyond these limits for later calibrations.
The completeness of 2MRS of 97.6% (Huchra et al. 2012b) was taken into account by randomly removing 2.4% of the galaxies from the mock catalogue. The SDSS sample, before considering additional cuts due to fibre collisions (in SDSS only, 2MRS was obtained differently), is more than 99% complete (Blanton et al. 2003), which was implemented in the same way as for 2MRS.
Taking the fibre collision into account correctly is very important, since this is more likely to happen in clusters or dense groups of galaxies, which are essential objects for our group finder. The size of the fibre plugs of SDSS does not allow two spectra to be taken closer than 55 arcsec of one another (Blanton et al. 2003). Consequently if we found any galaxy in our mock catalogue that was closer than this minimal separation to another galaxy we removed one of the two galaxies at random. Foreground stars and background galaxies (at least as long they were in a luminosity range to be considered spectroscopic targets for SDSS) were not considered in our treatment of the fibre collisions, not only because this would be beyond the capabilities of our available simulated data, but also because they should not correlate with the distribution of galaxies in the range of our catalogue. Thanks to the SDSS tiling algorithm (Blanton et al. 2003), some areas are covered more than once. This allows for spectra to be taken from galaxies that were blocked due to fibre collision the first time around. An overall sampling rate of more than 92% was reached. We implemented this by randomly re-including galaxies, which were previously removed due to fibre collision, until this overall sampling rate was reached. Because we selected only SDSS objects, which were spectroscopically classified as galaxies by the automatic pipeline, we randomly exclude a number of galaxies from the mock catalogue corresponding to the number of QSO classifications in the same volume of SDSS (normalized from the spectroscopic sky coverage of SDSS 9376 square degree (Alam et al. 2015) to the coverage of the mock catalogue (one octant = ~5157 square degree).
To complete the construction of our mock catalogues, we applied the same pipeline that we used to process the observational data on the mock catalogue data so far. We ended up with eight mock catalogues for SDSS containing between 209 341 and 234 481 simulated galaxies. These numbers correspond to a relative richness of our mock catalogues compared to SDSS of 94 to 104%. Also eight 2MRS mock catalogues consisting of 5878 to 7386 simulated galaxies (corresponding to a relative richness between 98 to 124% compared to 2MRS) were created. The stronger variations in the number of galaxies per 2MRS mock catalogue is due to the survey’s shallower depth, which makes the mock catalogues more affected by local variations in the matter distribution. As illustrated in Fig. 3, the number densities of the observational data are within the range and scatter of the various mock catalogues for both datasets.
Additionally, we also calculated the distribution of the FoF groups corresponding to the mock catalogues by applying the before-mentioned origin shift and the method, which we used to consider the evolutionary effects on the FoF groups obtained from the Millennium simulation. The masses of the FoF groups were obtained by multiplying the number of particles in them MField..FOF.np with the mass per particle (see Table 1). We produced FoF groups catalogues corresponding to the mock catalogues of simulated galaxies containing between 8 021 151 and 8 022 371 FoF groups. Additonally, unbiased (no Malmquist bias, fibre collision correction, and sampling correction applied) mock catalogues of the simulated galaxies were created (containing between 7 403 914 and 7 407 193 simulated galaxies) for later use in our calibrations of the luminosity function for the Malmquist bias correction.
3.3. Calibrating the group finder
We used a friends-of-friends (FoF) algorithm to detect groups in our data. It recursively found all galaxies, which were separated by less than the linking length blink from any other galaxy and consolidated them in groups.
FoF algorithms are a straightforward procedure, if full 3D information is available (in fact the FoF-groups in the Millennium simulations were obtained that way from the particle distribution). However, data from surveys is strongly affected by observational biases, which have to be considered for the group finder algorithm. Therefore, we required some additional considerations and calibrations before we could get to the group catalogue. We roughly followed Robotham et al. (2011), who created and applied a FoF-group finder algorithm on the GAMA survey (Driver et al. 2011).
We started by calculating a basic values for the linking length blink,0 for our surveys. It was defined as the average distance from one galaxy to the nearest galaxy in the (unbiased) sample. To estimate this distance, we used the present-day snapshot of MM and apply our limits for the absolute magnitudes (brighter than −15 mag in the SDSS r band and −18 mag in 2MASS Ks). We obtained the following values for blink,0: ~ 0.64 Mpc for 2MRS and blink,0 ~ 0.67 Mpc for SDSS (interestingly, very similar to the distance between the Milky Way and M31). This was the baseline for the effective linking length blink, which was used in the group finder and depends on several other parameters.
 |
Fig. 4 Luminosity function for SDSS and 2MRS data are shown in the upper and lower panels correspondingly. Green dashed line: true luminosity function derived using all galaxies from the unbiased mock catalogues. Blue dashed line: corrected (reconstructed) luminosity function from the Malmquist biased mock catalogues. Red solid line: corrected observational data. |
The dominant bias affecting our survey data is the Malmquist bias, which drastically removed the fainter end of the galaxy luminosity function from our sample at larger distances. To this end, we retrieved the luminosity function from the unbiased mock catalogues and compared it to the mock catalogues that consider all the biases (see Fig. 4). With some additional considerations, we proceeded to calcuate a correction that allowed us to retrieve the unbiased luminosity function from observational (biased) data 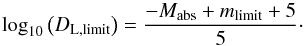 (10)Using the limiting magnitudes mlimit of the surveys, we calculated the limiting luminosity distance DL,limit up to which a galaxy with an absolute magnitude Mabs is still detected
(10)Using the limiting magnitudes mlimit of the surveys, we calculated the limiting luminosity distance DL,limit up to which a galaxy with an absolute magnitude Mabs is still detected 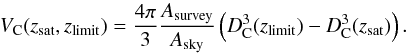 (11)Using the inversion of Eq. (2), we derived the limiting redshift zlimit corresponding to the limiting luminosity distance DL,limit and using Eq. (3) the corresponding co-moving distance DC. The saturation redshift zsat was defined in the same was as the limiting redshift (using Eq. (10), but with the saturation limit of the survey msat instead of the limiting magnitude mlimit). The saturation magnitude of SDSS is 14 mag in r band7 and for 2MRS it does not apply, hence we set the limiting distance/redshift to zero. We thus calculated the co-moving volume VC in which a galaxy with an absolute magnitude Mabs can be detected in a survey covering Asurvey of the total sky area Asky
(11)Using the inversion of Eq. (2), we derived the limiting redshift zlimit corresponding to the limiting luminosity distance DL,limit and using Eq. (3) the corresponding co-moving distance DC. The saturation redshift zsat was defined in the same was as the limiting redshift (using Eq. (10), but with the saturation limit of the survey msat instead of the limiting magnitude mlimit). The saturation magnitude of SDSS is 14 mag in r band7 and for 2MRS it does not apply, hence we set the limiting distance/redshift to zero. We thus calculated the co-moving volume VC in which a galaxy with an absolute magnitude Mabs can be detected in a survey covering Asurvey of the total sky area Asky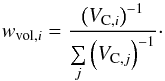 (12)Using the co-moving volumes VC,i within which a galaxy with the index i is detectable, we calculated the volume weights wvol,i. The volume weights allowed us to correct the observed luminosity function (either from observational data or from our mock catalogues) as it is illustrated in Fig. 4. For both, the SDSS and 2MRS mock catalogues, the reconstruction works extremely well, however when comparing these results to the observational data, there are some small deviations, especially for 2MRS. We attributed them to the additional uncertainty introduced into the mock data by using the SDSS-2MRS colour transformation (see Appendix B).
(12)Using the co-moving volumes VC,i within which a galaxy with the index i is detectable, we calculated the volume weights wvol,i. The volume weights allowed us to correct the observed luminosity function (either from observational data or from our mock catalogues) as it is illustrated in Fig. 4. For both, the SDSS and 2MRS mock catalogues, the reconstruction works extremely well, however when comparing these results to the observational data, there are some small deviations, especially for 2MRS. We attributed them to the additional uncertainty introduced into the mock data by using the SDSS-2MRS colour transformation (see Appendix B).
Due to the Malmquist bias, the fainter members of a group are not visible anymore at higher redshifts. With a constant linking length, this would cause groups to fragment at greater distances. To avoid this, we adjusted the linking length of our FoF-group finder accordingly 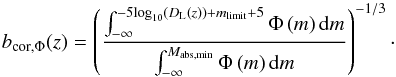 (13)The modification factor bcor,Φ(z) corrects for the Malmquist bias by calculating the fraction of the luminosity function Φ that is visible at a redshift z for a luminosity limited survey with a limiting magnitude mlimit and a minimal absolute magnitude Mabs,min (−15 mag in the r band for SDSS and −18 mag in the Ks band for 2MRS) for galaxies that are still included in dataset. bcor,Φ(z) was used to rescale the basic linking length blink,0.
(13)The modification factor bcor,Φ(z) corrects for the Malmquist bias by calculating the fraction of the luminosity function Φ that is visible at a redshift z for a luminosity limited survey with a limiting magnitude mlimit and a minimal absolute magnitude Mabs,min (−15 mag in the r band for SDSS and −18 mag in the Ks band for 2MRS) for galaxies that are still included in dataset. bcor,Φ(z) was used to rescale the basic linking length blink,0.
In physical space, the linking length is an isotropic quantity, it does not depend on the direction. However, when observing galaxies projected on the sky, one can only directly obtain two coordinates, while the third dimension is derived from the redshift and is affected by so-called redshift-space distortions. This observed redshift cannot be exclusively attributed to the metric expansion of space-time, but also to the peculiar radial velocity of the galaxy. The imprint on the observed redshift from these peculiar motions cannot be distinguished a priori from the cosmological redshift. Hence, when using a redshift–distance relation to convert redshifts into distances, the estimated positions are smeared out in the radial direction with respect to the true positions. In the case of galaxy groups/clusters, this effect is known as the “Fingers of God” effect (Jackson 1972; Arp 1994; Cabré & Gaztañaga 2009).
Although deforming the sphere with the linking length as radius to an ellipsoid appears to be the natural way to incorporate these effects into FoF-group finder algorithms, Eke et al. (2004a) found that cylinders along the line of sight are more efficient. Therefore, instead of one linking length we used two separate linking lengths: an angular linking length αlink and a radial linking length Rlink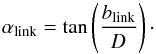 (14)The angular linking length is unaffected by the redshift-space distortion and directly relates to the linking length in real space blink by simple trigonometry. The angular diameter distance DA is defined as:
(14)The angular linking length is unaffected by the redshift-space distortion and directly relates to the linking length in real space blink by simple trigonometry. The angular diameter distance DA is defined as:  (15)The radial linking length is larger than the linking length in real space because of the scatter in the redshift space due to the peculiar motions. We transformed the blink distance into a corresponding redshift difference:
(15)The radial linking length is larger than the linking length in real space because of the scatter in the redshift space due to the peculiar motions. We transformed the blink distance into a corresponding redshift difference: 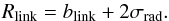 (16)By adding the dispersion of radial peculiar velocities σrad to the linking length in real space, one gets a first estimate of the radial linking length Rlink. In MM, we found a σrad of ~232.3 km s-1 for SDSS and ~233.3 km s-1 for 2MRS, hence about 95% of all possible radial velocity differences were included in an envelope of ±464.7 km s-1, and ±466.6 km s-1 respectively, as illustrated in Fig. 5.
(16)By adding the dispersion of radial peculiar velocities σrad to the linking length in real space, one gets a first estimate of the radial linking length Rlink. In MM, we found a σrad of ~232.3 km s-1 for SDSS and ~233.3 km s-1 for 2MRS, hence about 95% of all possible radial velocity differences were included in an envelope of ±464.7 km s-1, and ±466.6 km s-1 respectively, as illustrated in Fig. 5.
 |
Fig. 5 The red solid line shows the distribution of radial proper motions in MM, which has a roughly Gaussian shape. Black dashed line: zero radial velocity bin. Green dashed lines: dispersion of the radial peculiar velocities σrad, which corresponds to the standard deviation of the plotted distribution. Blue dashed lines: two-σ interval, which is used to stretch the radial linking length. |
We combined all these corrections and modifications to the linking length and obtained one set of equations: 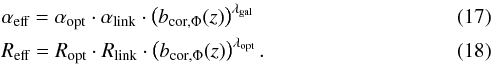 The effective angular linking length αeff and the effective radial linking length Reff define the linking conditions of our group finder. The exponent λopt allows for a completeness correction (see Eq. (13)). The coefficients αopt, Ropt, and λopt allow for fine-tuning of the group finder. This was done using the mock catalogues. For the optimization we followed Robotham et al. (2011), who provided a well-tested method that was successfully applied on GAMA survey data (Driver et al. 2011), and defined a group cost function in the following way:
The effective angular linking length αeff and the effective radial linking length Reff define the linking conditions of our group finder. The exponent λopt allows for a completeness correction (see Eq. (13)). The coefficients αopt, Ropt, and λopt allow for fine-tuning of the group finder. This was done using the mock catalogues. For the optimization we followed Robotham et al. (2011), who provided a well-tested method that was successfully applied on GAMA survey data (Driver et al. 2011), and defined a group cost function in the following way: 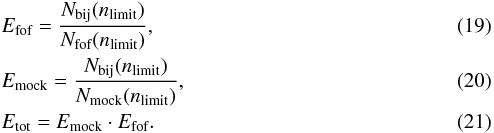 The global halo finding efficiency measurement Etot is defined by the product of the halo finding efficiencies of the mock catalogue Emock and the FoF catalogue Efof. The parameters Nmock(nlimit) and Nfof(nlimit) are the number of groups with at least nlimit members in the mock catalogue and in the results of our FoF-based group finder. Nbij(nlimit) is the number of groups that are found bijectively in both samples (the mock catalogue, which consists of the “true” group information based purely on the simulation, and the FoF catalogue, which consists of the grouping found after applying the group finder on the mock catalogue). This means that at least 50% of the members found in a group in one sample must make up at least 50% of a corresponding group in the other sample as well
The global halo finding efficiency measurement Etot is defined by the product of the halo finding efficiencies of the mock catalogue Emock and the FoF catalogue Efof. The parameters Nmock(nlimit) and Nfof(nlimit) are the number of groups with at least nlimit members in the mock catalogue and in the results of our FoF-based group finder. Nbij(nlimit) is the number of groups that are found bijectively in both samples (the mock catalogue, which consists of the “true” group information based purely on the simulation, and the FoF catalogue, which consists of the grouping found after applying the group finder on the mock catalogue). This means that at least 50% of the members found in a group in one sample must make up at least 50% of a corresponding group in the other sample as well
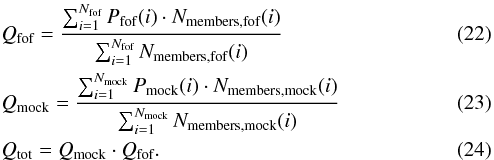 The global grouping purity Qtot is defined using the grouping purity of the mock catalogue Qmock and the grouping purity of the FoF catalogue Qfof. The variables Nmembers,mock(i) and Nmembers,fof(i) are the numbers of galaxies in individual groups i of the mock catalogue and the FoF catalogue respectively. The purity products Pmock(i) and Pfof(i) are defined as the maximal product of the ratio of shared galaxies to all galaxies within a group of one catalogue and the ratio of the same shared galaxies within the other catalogue. An illustrative example was provided in Robotham et al. (2011)
The global grouping purity Qtot is defined using the grouping purity of the mock catalogue Qmock and the grouping purity of the FoF catalogue Qfof. The variables Nmembers,mock(i) and Nmembers,fof(i) are the numbers of galaxies in individual groups i of the mock catalogue and the FoF catalogue respectively. The purity products Pmock(i) and Pfof(i) are defined as the maximal product of the ratio of shared galaxies to all galaxies within a group of one catalogue and the ratio of the same shared galaxies within the other catalogue. An illustrative example was provided in Robotham et al. (2011)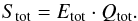 (25)The group cost function Stot is defined by the product of the global halo finding efficiency measurement Etot and the global grouping purity Qtot. Following the definitions, Stot can take values between 0 (total mismatch) and 1 (perfect match).
(25)The group cost function Stot is defined by the product of the global halo finding efficiency measurement Etot and the global grouping purity Qtot. Following the definitions, Stot can take values between 0 (total mismatch) and 1 (perfect match).
Optimal coefficients for the group finders for 2MRS and SDSS.
We started our optimization by performing a coarse parameter scan for the three coefficients αopt, Ropt, and λopt in one of our mock catalogues to get an initial guess for the order of magnitude of optimal coefficients. We then used a Simplex algorithm (Nelder & Mead 1965) to maximise the mean group cost function Stot of all of our 8 mock catalogues. The optimal coefficients for both samples, SDSS and 2MRS, are listed in Table 3. For the calculation of Stot and the optimisation, we used nlimit = 2. We also repeated it with different values for nlimit and found very similar optimal coefficients (a few percent difference).
The coefficients αopt and Ropt are well within an order of magnitude of unity, indicating that our initial definitions of the effective linking lengths are reasonable. The coefficient λopt is clearly below the naive expected value of 1, which shows that it was important to consider this parameter in the optimization. The distribution of the median group cost function depending on the coefficient αopt and Ropt is illustrated in Fig. D.1.
3.4. Obtaining group parameters
After detecting groups using our optimized group finder algorithm, we calculated various parameters for these groups, such as their positions, sizes, masses and luminosities. For most of these parameters, we used methods, which were tested and found to be efficient and robust by Robotham et al. (2011). For some, we had to calibrate them using our own mock catalogues.
3.4.1. Group velocity dispersion
We calculated group velocity dispersions using the gapper estimator of Beers et al. (1990) including the modification of Eke et al. (2004a). Naturally, this could only be done for groups with at least two members. This well-tested method requires the following calculations: 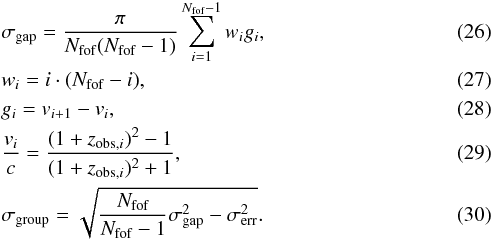 The gapper velocity dispersion σgap of a group with Nfof member was calculated by summing up the product of the weights wi and the radial velocity gaps gi for all all its members. It was essential that the radial velocities vi were ordered for this approach, which we assured by applying a simple sorting algorithm for each group. The radial velocities vi were calculated using the observed redshifts zobs,i. The group velocity dispersion σgroup also took into account the measurement errors of the redshift determination σerr, which were 30 km s-1 for SDSS and ~32 km s-1 for 2MRS. In the case that the obtained group velocity dispersion was lower than the measurement errors of the redshift determination, we set them to σerr.
The gapper velocity dispersion σgap of a group with Nfof member was calculated by summing up the product of the weights wi and the radial velocity gaps gi for all all its members. It was essential that the radial velocities vi were ordered for this approach, which we assured by applying a simple sorting algorithm for each group. The radial velocities vi were calculated using the observed redshifts zobs,i. The group velocity dispersion σgroup also took into account the measurement errors of the redshift determination σerr, which were 30 km s-1 for SDSS and ~32 km s-1 for 2MRS. In the case that the obtained group velocity dispersion was lower than the measurement errors of the redshift determination, we set them to σerr.
3.4.2. Total group luminosity
The observed group luminosity Lobs was calculated by adding up the emitted light, in the SDSS r band or the 2MASS Ks band respectively, of the group members.  The calculation of the luminosity of an individual galaxy Li required the absolute r band/Ks band magnitudes Mabs,i and the solar absolute magnitude Mabs,☉ in the r band of 4.76 mag or in the Ks band of 3.28 mag respectively.
The calculation of the luminosity of an individual galaxy Li required the absolute r band/Ks band magnitudes Mabs,i and the solar absolute magnitude Mabs,☉ in the r band of 4.76 mag or in the Ks band of 3.28 mag respectively. 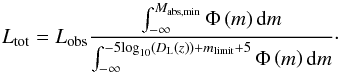 (33)We obtained the total group luminosity Ltot by rescaling the observed group luminosity DL with the fraction of the luminosity function
(33)We obtained the total group luminosity Ltot by rescaling the observed group luminosity DL with the fraction of the luminosity function 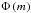 visible at the group’s luminosity distance. mlimit is the limiting magnitude of the survey and the parameter Mabs,min denotes the minimal absolute magnitude to which the luminosity function is still considered in our sample. This method only corrects for the Malmquist bias, but not the saturation bias, because there is no suitable way to predict the group luminosity if the brightest object of the group is missing (or maybe not).
visible at the group’s luminosity distance. mlimit is the limiting magnitude of the survey and the parameter Mabs,min denotes the minimal absolute magnitude to which the luminosity function is still considered in our sample. This method only corrects for the Malmquist bias, but not the saturation bias, because there is no suitable way to predict the group luminosity if the brightest object of the group is missing (or maybe not).
3.4.3. Group centre
The radial and the projected group centre were calculated differently, because the former one was obtained using redshifts, while the latter one from astrometry. Robotham et al. (2011) compared various approaches and we applied those they found to be the most efficient. In the case of the radial group centre, this turned to be simply taking the median of the redshifts of all detected group members. The most efficient method to find the projected group centre was an iterative approach using the centre of light of the group members as explained in Robotham et al. (2011). At first, the coordinates of the centre of light, which is the luminosity-weighted (using Li as weights), were calculated using all group members. Then the group member had the largest angular separation from the centre of light was rejected and the new centre of light was calculated with the remaining members. This process was repeated iteratively until only one galaxy remained and its coordinates were used as the coordinates of the projected group centre.
3.4.4. Group radius
We calculated a characteristic projected radius for groups with two or more members. Again, following Robotham et al. (2011), who tested this method extensively, we define our group radius Rgroup as the radius around the projected group centre in which 50% of the group members are located. To illustrate this simple definition, we provide two examples: for a group with five members the radius corresponds to the distance of the third most distant member from the group centre and for a group with four members, the radius is the mean between the distance from the group centre of the second and third most distant members.
3.4.5. Dynamical mass
Using the previously defined group radii and group velocity dispersions, we calculated approximate dynamical masses Mdyn for our groups using the following equation (Spitzer 1969; Robotham et al. 2011; Chilingarian & Mamon 2008): 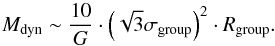 (34)
(34)
3.4.6. Stellar mass
As a part of the 2MRS and SDSS DR12 group catalogues, we provide stellar masses of galaxies included in the two samples. The stellar masses were computed as follows.
For the objects included in the SDSS DR12 sample, we used the RCSED (Chilingarian et al. 2016) in order to obtain stellar population ages and metallicities derived from the full spectrum fitting of SDSS DR7 spectra using the nbursts code (Chilingarian et al. 2007a,b) and a grid of simple stellar population (SSP) models computed with the pegase.hr code (Le Borgne et al. 2004). 371 627 objects from the SDSS DR12 sample matched the RCSED sample. We derived their stellar mass-to-light ratios using the pegase.hr models at the corresponding ages and metallicities, the Kroupa (2002) stellar initial mass function, and then converted them into stellar masses using the K-corrected integrated photometry of all galaxies in the SDSS r and g bands converted into Johnson V. Here we assumed that the SDSS aperture spectra reflected global stellar population properties of galaxies.
 |
Fig. 6 Comparison between stellar masses computed using pegase.hr stellar population models for the V band photometry (converted from SDSS g and r) with those calculated using the near-infrared UKIDSS K band magnitudes and a grid of Maraston (2005) SSP models. RCSED SSP ages in metallicities and the Kroupa IMF were used in both stellar mass estimates. |
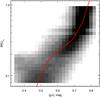 |
Fig. 7 An polynomial approximation of a K band mass-to-light ratio as a function of the optical (g−r) colour shown in red overplotted on a two-dimensional histogram presenting K mass-to-light ratios estimated from the spectroscopic stellar population parameters for a sample of 424 163 galaxies. |
125 383 galaxies of our SDSS DR12 sample possess fully corrected integrated photometry in the near-infrared K band from the UKIDSS survey (Lawrence et al. 2007) available in RCSED, which is known to be a good proxy for a stellar mass. We used the Maraston (2005)K band mass-to-light ratios computed for the Kroupa IMF and SSP ages and metallicities obtained from the full spectrum fitting and computed stellar masses for the subsample of 125,383 SDSS DR12 galaxies. The K band mass-to-light have much weaker dependence on stellar population ages compared to the optical V band mass-to-light ratios, therefore possible stellar population gradients in galaxies should introduce weaker bias in K band stellar masses. The comparison between the optical and K band stellar masses is provided in Fig. 6.
We also see a correlation between the derived K band mass-to-light ratios and the integrated g−r and g−K colours (see Fig. 7). We approximated the K band mass-to-light ratio as a polynomial function of the integrated optical g−r colour. Because the distribution of galaxies in this parameter space is very non-uniform, we used the following procedure to derive the approximation:
-
(i)
We restricted the sample of galaxies to objects at redshifts0.01 <z< 0.15 having Petrosian radii R50< 10 arcsec, good quality of the full spectrum fitting (χ2/ d.o.f.< 0.8), and SSP age uncertainties better than 30% of the age values.
-
(ii)
We selected 20 logarithmically spaced bins in (M/L)K between 0.07 and 1.15 in the solar units, that is ~0.061 in log (M/L)K and computed the median value of the (g−r) colour in every bin.
-
(iii)
We fit log (M/L)K as a third order polynomial function of (g−r)−0.50 in the range 0.47 < (g−r) < 0.79 mag and obtained the following approximation:
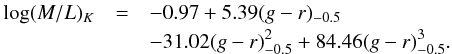 (35)
(35) -
(iv)
For (g−r) < 0.47 mag we used the lower limit (M/L) = 0.07, and for (g−r) > 0.79 mag the upper limit (M/L) = 1.15 which corresponds to the top of red sequence. The uncertainty of the approximation is about 0.2 dex at (g−r) < 0.73 mag and 0.3 dex at the red end, where we see no correlation between the colour and the (M/L)K value. Therefore, we could estimate photometric stellar masses to a factor of 2 provided only broadband optical and K band magnitudes.
7361 galaxies out of 43 425 in the 2MRS sample matched with RCSED objects. For those galaxies we computed stellar masses using the same approach as for SDSS galaxies with available NIR magnitudes but using the 2MASS Ks band photometry instead of UKIDSS.
For the remaining objects, we followed a different strategy. We cross-matched the entire sample of galaxies with the SIMBAD8 database and extract integrated photometry in the B, V, and R bands. In total, we found B−R colours for 11 210 galaxies. We correct the magnitudes for the Galactic extinction, compute and apply K-corrections using the analytical approximations from (Chilingarian et al. 2010), and convert them into the SDSS photometric system using the transformations from Lupton9 as: (g−r) = 0.667(B−Rc)−0.216. Then we estimate the K-band stellar mass-to-light ratios using integrated g−r and the calibration provided above and convert them into stellar masses.
In this fashion, we computed stellar masses for about 400 000 galaxies included into the 2MRS and SDSS DR12 catalogues. We used them to provide an estimate (lower limit) on the stellar masses contained in the galaxy groups of our catalogues.
3.4.7. Group mass
Coefficients of the mass dependence on observed parameters of isolated galaxies.
 |
Fig. 8 Residuals of the fit for the mass determination of groups using 2MRS and SDSS mock data. Top-left panel: residuals of our fit using isolated galaxies (groups with one visible member only) for the 2MRS data. Top-central panel: residuals of groups with two to four members using 2MRS data. Top-right panel: residuals of groups with five or more members using 2MRS data. Bottom-left panel: residuals of our fit using isolated galaxies (groups with one visible member only) for the SDSS data. Bottom-central panel: residuals of groups with two to four members using SDSS data. Bottom-right panel: residuals of groups with five or more members using SDSS data. |
In order to get robust mass estimates for the detected groups, we calibrated a set of mass functions depending on several parameters using our mock catalogues. We split the sample into three sub-samples: isolated galaxies (groups with one visible member only) and all other groups with two to four members, and groups with more than four members. In the case of the isolated galaxies, we had just two quantities at our disposal to derive their masses: luminosity and distance. We fit the following function to these parameters: 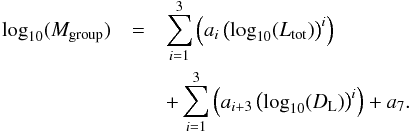 (36)The group mass Mgroup depends on the group luminosity Ltot and the luminosity distance DL. The coefficients a1, a2, a3, a4, a5, a6, and a7 were estimated using a least-square fit to our mock catalogues. The results are listed in Table 4 and the residuals of the fitted group mass ΔM = log 10(Mgroup,fit)−log 10(Mgroup,mock) depending on the true group mass of mock catalogue are illustrated in Fig. 8. Apparently, there is a trend in our fit to underestimate the true masses of groups with just one visible member in the case of high mass groups that is most prominent in the tail of the distribution for SDSS galaxies (see Fig. 8). However, the dependence of the residuals on the fitted parameters (see Fig. 9) does not exhibit any obvious trends, which indicates that considering higher order terms in the fit would not improve our mass function. Not considering the luminosity distance would not visibly change any residuals (in Figs. 8 and 9), but it would increase the root mean square srms of the fit by several percent. Although for Malmquist-bias corrected data the distance should not have a significant impact on the fit, we chose to keep this parameter in, because otherwise it would unnecessarily increase the uncertainty in our mass estimates. We also considered using the colour as an additional parameter, but we found that it did not have any notable impact on the quality of the fit and dropped it for reasons of simplicity and consistency with the other fits. The apparent bi-modality in Fig. 9 is not a consequence of different galaxy populations, but the difference between truly isolated galaxies and groups with just one visible member.
(36)The group mass Mgroup depends on the group luminosity Ltot and the luminosity distance DL. The coefficients a1, a2, a3, a4, a5, a6, and a7 were estimated using a least-square fit to our mock catalogues. The results are listed in Table 4 and the residuals of the fitted group mass ΔM = log 10(Mgroup,fit)−log 10(Mgroup,mock) depending on the true group mass of mock catalogue are illustrated in Fig. 8. Apparently, there is a trend in our fit to underestimate the true masses of groups with just one visible member in the case of high mass groups that is most prominent in the tail of the distribution for SDSS galaxies (see Fig. 8). However, the dependence of the residuals on the fitted parameters (see Fig. 9) does not exhibit any obvious trends, which indicates that considering higher order terms in the fit would not improve our mass function. Not considering the luminosity distance would not visibly change any residuals (in Figs. 8 and 9), but it would increase the root mean square srms of the fit by several percent. Although for Malmquist-bias corrected data the distance should not have a significant impact on the fit, we chose to keep this parameter in, because otherwise it would unnecessarily increase the uncertainty in our mass estimates. We also considered using the colour as an additional parameter, but we found that it did not have any notable impact on the quality of the fit and dropped it for reasons of simplicity and consistency with the other fits. The apparent bi-modality in Fig. 9 is not a consequence of different galaxy populations, but the difference between truly isolated galaxies and groups with just one visible member.
 |
Fig. 9 Residuals of the fit for the mass determination of groups with only one visible member depending on the fitting parameter. Top-left panel: residuals as a function of the total Ks band group luminosity for the 2MRS data. The top-right panel: residuals as a function of the luminosity distance for the 2MRS data. Bottom-left panel: residuals as a function of the total r band group luminosity for the SDSS data. The Bottom-right panel: residuals as a function of the luminosity distance for the SDSS data. |
Coefficients of the mass dependence on observed parameters of groups with two to four members.
For groups with two to four members, we included a dependence on the group velocity dispersion and group radius into the fitting function, which is defined as follows: 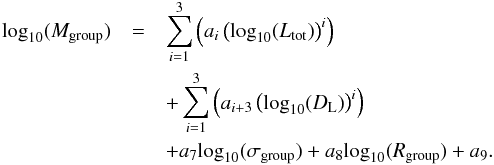 (37)The group velocity dispersion σgroup and the group radius Rgroup were used in addition to the parameters of the fit above in order to obtain the coefficients a1 to a9. We also considered using the dynamical group mass σgroup, which is based on the previous two parameters. However, we found that fitting both parameters separately instead of the dynamical mass improves the quality by up-to one percent. The results of the fit are listed in Table 5, whereas the residuals of these fits depending on the group mass are shown in Fig. 8. The residuals of the fits depending on the fit parameters, which are shown in Fig. 10, do not indicate any strong trends.
(37)The group velocity dispersion σgroup and the group radius Rgroup were used in addition to the parameters of the fit above in order to obtain the coefficients a1 to a9. We also considered using the dynamical group mass σgroup, which is based on the previous two parameters. However, we found that fitting both parameters separately instead of the dynamical mass improves the quality by up-to one percent. The results of the fit are listed in Table 5, whereas the residuals of these fits depending on the group mass are shown in Fig. 8. The residuals of the fits depending on the fit parameters, which are shown in Fig. 10, do not indicate any strong trends.
For the richest groups in our catalogue (with five or more members), we can define the following fitting function: 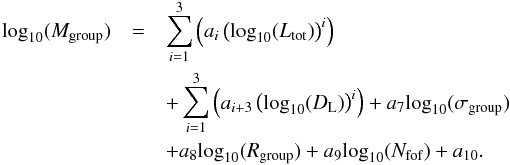 (38)The number of detected galaxies within a group Nfof was used in addition to the parameters of the previous fit to obtain the coefficients a1 to a10. The results of the fit are listed in Table 6, whereas the residuals of these fits depending on the group mass are shown in Fig. 8. The residuals of the fits depending on the fit parameters, which are shown in Fig. 11, do not indicate any strong trends.
(38)The number of detected galaxies within a group Nfof was used in addition to the parameters of the previous fit to obtain the coefficients a1 to a10. The results of the fit are listed in Table 6, whereas the residuals of these fits depending on the group mass are shown in Fig. 8. The residuals of the fits depending on the fit parameters, which are shown in Fig. 11, do not indicate any strong trends.
 |
Fig. 10 Residuals of the fit for the mass determination of groups with two to four members depending on the fitting parameter. Top row: residuals for 2MRS data. Bottom row: residuals for SDSS data. First column: residuals as a function of the luminosity (Ks band for 2MRS, r band for SDSS). Second column: residuals as a function of the luminosity distance. Third column: residuals as a function of the group velocity dispersion. Forth column: residuals as a function of the group radius. |
Coefficients of the mass dependence on observed parameters of groups with more than four members.
 |
Fig. 11 Residuals of the fit for the mass determination of groups with five or more members depending on the fitting parameter. Top row: residuals for 2MRS data. Bottom row: residuals for SDSS data. First column: residuals as a function of the luminosity (Ks band for 2MRS, r band for SDSS). Second column: residuals as a function of the luminosity distance. Third column: residuals as a function of the group velocity dispersion. Forth column: residuals as a function of the group radius. Fifth column: residuals as a function of the number of galaxies detected inside a group. |
The majority of our groups have masses below 1014M⊙ (see Fig. 8). At such low masses, the uncertainty in the mass determination is notoriously high (Old et al. 2015). Therefore, our overall uncertainties for the fits are higher than those of the mass determination methods presented in Old et al. (2015), because they primarily focused on groups more massive than 1014M⊙.
3.5. Calculating the finite infinity regions
In order to derive a catalogue of finite infinity regions (Ellis 1984), which will be used in our upcoming paper (Saulder et al. 2016) to perform a cosmological test that was outlined in Saulder et al. (2012) comparing timescape cosmology (Wiltshire 2007) and Λ-CDM cosmology, we used a simple approximation for the finite infinity regions. They were calculated using spherical regions with an average density that corresponds to the critical density of the timescape cosmology. More complex geometrical shapes would be possible, however with our available computional power as well as the general uncertainties of the mass estimates in mind, we found that this model practical and sufficient for our planned test (Saulder et al. 2016). In the timescape model of Wiltshire (2007), the Universe is approximated by a two-phase model of empty voids and walls with an average density of the true critical density. This renormalized critical density is about 61% of the critical density in the Λ-CDM model according to the best fits for this alternative cosmology (the Hubble parameter10 for the wall environment (inside finite infinity regions) is expected to be 48.2 km s-1Mpc-1 and void environment (outside finite infinity regions) to be 61.7 km s-1Mpc-1 (Wiltshire 2007; Leith et al. 2008) according to the best fit on supernovae Type Ia (Riess et al. 2007), CMB (Bennett et al. 2003; Spergel et al. 2007) and Baryonic acoustic oscillations (Cole et al. 2005; Eisenstein et al. 2005) data within the framework of the simple two phase model presented in Wiltshire (2007). Because our preliminary results (Saulder et al. 2012) had already shown that this basic approximation required all our available computational resources, more complex models for the finite infinity regions are not possible to consider at this time.
In practice, calculating finite infinity regions requires a solid knowledge of the matter distribution. In Table 2, we found that less than half of the simulation’s particles are bound in FoF-groups of 20 or more particles. Because the timescape model that we want to test is a two-phase model and distribution of the matter is very important for it, we used the MM data to locate the missing particles. We calculated the radii Rf of homogeneous spheres around the FoF-groups in MM in the following way: 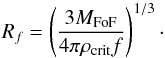 (39)MFoF stands for the mass bound in a FoF-group according to the Millennium simulation. ρcrit is the critical density and f is a factor to modify the critical density. It was set to 0.61 for timescape cosmology.
(39)MFoF stands for the mass bound in a FoF-group according to the Millennium simulation. ρcrit is the critical density and f is a factor to modify the critical density. It was set to 0.61 for timescape cosmology.
We found that about 77 percent of all particles are within R0.61 around the FoF-groups. Expanding the spherical regions iteratively using the masses of the particles, we found that about 82 percent of all particles are located within finite infinity regions, which occupy about 23 percent of the simulations volume, around the FoF-groups. The remaining particles can be assumed to be either uniformly distributed all across the voids or arranged in tendrils (fine filaments in voids using the terminology of Alpaslan et al. 2014) of small halos (less than 20 particles) far outside main clusters and groups.
Coefficients of the mass rescaling for the finite infinity regions and the mass as well as the volume covered by them.
We developed a method to derive the finite infinity regions from observational data. Assuming that the last snapshots of the Millennium simulation provide a reasonable model of the present-day large-scale matter distribution of the Universe, we took the six snapshots of the redshift range of our project from the MM and introduced magnitude limits into them corresponding to the Malmquist bias of SDSS. Because the observational data, which we used in Sect. 4.4 was a combined catalogue of SDSS and 2MRS groups, it compensated for the selection effect due to the SDSS saturation limit. Then we assigned radii using Eq. (39) to every group that has at least one visible/detectable member. We used the total mass of those groups to derive the sizes of these “proto”-finite infinity regions. Afterwards we merged all groups that were fully within the radii of other groups by adding their masses to their host groups and shift their centre of mass accordingly. In the next step, we counted the particles inside the recalculated radii of the remaining groups. To correctly handle the overlapping regions, particles that are located within more than one finite infinity region were assigned weights corresponding to the reciprocal values of the number of finite infinity region they were shared with. Then we adjusted the masses of groups according to the total (weighted) mass of particles inside them. This step was used to calibrate the first (of the two) re-scaling of the masses. 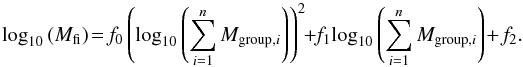 (40)We performed a least square fit to calibrate the mass of the finite infinity region Mfi derived from the particles within it at this step depending on the sum of (original) group masses it is composed of Mgroup. The values of coefficients f0, f1, and f2 are listed in Table 7. We performed this fit for each of the six MM snapshots. The distribution of the parameters and our fit on them is illustrated in Fig. D.2. In the next step, we iteratively merged and expanded (using masses of the particles within the group’s finite infinity radii) the groups in the same way as before until the change of total mass within all finite infinity regions was less than 0.1%11 from one step to the next. Once this was reached, we used the final masses (derived from the particles) of the finite infinity regions to calibrate another re-scaling relation in the same way as before. We fitted the final masses of the finite infinity regions to the sum of the inital masses of the FoF-groups using Eq. (40). The results of the fit for the final rescaling are listed in Table 7 and illustrated in Fig. D.3.
(40)We performed a least square fit to calibrate the mass of the finite infinity region Mfi derived from the particles within it at this step depending on the sum of (original) group masses it is composed of Mgroup. The values of coefficients f0, f1, and f2 are listed in Table 7. We performed this fit for each of the six MM snapshots. The distribution of the parameters and our fit on them is illustrated in Fig. D.2. In the next step, we iteratively merged and expanded (using masses of the particles within the group’s finite infinity radii) the groups in the same way as before until the change of total mass within all finite infinity regions was less than 0.1%11 from one step to the next. Once this was reached, we used the final masses (derived from the particles) of the finite infinity regions to calibrate another re-scaling relation in the same way as before. We fitted the final masses of the finite infinity regions to the sum of the inital masses of the FoF-groups using Eq. (40). The results of the fit for the final rescaling are listed in Table 7 and illustrated in Fig. D.3.
After the calibrations of the rescaling were completed, we applied our method to real data, a combined catalogue of SDSS and 2MRS, in the following way: the masses of groups were obtained using the calibrations described in Sect. 3.4.7. Afterwards we calculated the radii of the proto-finite infinity regions using Eq. (39). In the next step, we iteratively merged all groups that were fully within the radii of other proto-finite infinity regions and shifted the centre of mass of the remaining groups accordingly. Then we applied the first rescaling on the data using the coefficients from Table 7, which belong to the redshift closest to the actual redshift of each group. Afterwards we recalculated the radii using the new masses and repeated the merging procedure from before. Then we applied the final rescaling using the sum of the initial masses of the groups that merged as a basis in the same way as we did for the first rescaling, but with the coefficients of the final rescaling (see Table 7). We used the initial masses for the final rescaling instead of the masses obtained after the first rescaling, because the overall uncertainty was slightly lower this way. The reason to do the first rescaling at all, and not to proceed directly to the final rescaling without it, is that the merging process, which is done after it, slightly shifts the distribution of the mass function and we would introduce an unnecessary source of error by skipping it.
As illustrated in Table 7, the total mass within finite infinity regions decreases at higher redshifts (from ~80% at z = 0 to ~65% at z = 0.116), but not as strikingly as does the number of detectable groups. This means, that although we miss some of the smaller structures, the biggest contributors to the mass are still detected at higher redshifts. Furthermore, many of the smaller masses are close to the bigger ones, hence we still obtained a good representation of the finite infinity regions. Even after the final rescaling there are about 20−30% of the mass missing (over the redshift range of our projects) and not within the defined finite infinity regions. Because the model (Wiltshire 2007), which we intend to test with this data, is only a two-phase model consisting of completely empty voids and finite infinity regions (walls with an average density of the renormalized critical density), we had two options on how to proceed: (i) we could either add the 20−30% missing mass to the detected finite infinity regions and adjust their sizes accordingly; or we could (ii) assume that the 20−30% missing mass is distributed homogeneously throughout the rest of the simulations volume (the voids) and define them as not completely empty. In this paper we provided data for both options. In our follow-up paper (Saulder et al. 2016), we will test them and we will see, which one is the best-suited.
4. Results
We provide four group catalogues, which are made available on VizieR.
4.1. The 2MRS group catalogue
 |
Fig. 12 Distribution of the multiplicity NFoF of the groups detected in 2MRS (green dotted line) and in SDSS (red solid line). |
Our 2MRS based group catalogue is composed of 43 425 galaxies from Huchra et al. (2012b) covering 91% of the sky. Using our group finder with the optimal coefficients from Table 3, we detected 31 506 groups in the 2MRS data. As illustrated in Fig. 12, the majority (25 944 to be precise) of the galaxies can be found in groups with only one visible member. This does not necessarily mean that all of them are isolated objects, but that there is only one galaxy sufficiently bright to be included in the 2MRS. We identify 5452 groups within the multiplicity range from two to ten and only 110 with higher multiplicities (two of them with more than 100 members each). Figure 12 clearly shows that the number of groups rapidly decreases with increasing number of multiplicity.
 |
Fig. 13 Dependence of various group parameters of the 2MRS catalogue on the luminosity distance. First panel upper row: dependence on the total group luminosity Ltot; second panel upper row: dependence on the observed group luminosity Lobs; third panel upper row: dependence on the group velocity dispersion σgroup; fourth panel upper row: dependence on the group radius Rgroup; first panel lower row: dependence on the total group mass Mgroup; second panel lower row: dependence on the stellar mass M∗; third panel lower row: dependence on the dynamical mass Mdyn; fourth panel lower row: dependence on the number of detected galaxies in the group NFoF. |
As illustrated in Fig. 13, the group parameters show different dependences on the luminosity distance. The group luminosity is strongly affected by the Malmquist bias, because fainter groups fall below the detection threshold at larger distances and only the brightest groups are detected. A comparison to the observed luminosity indicates that our corrections might slightly overestimate the total group luminosity at greater distances. The total group mass shows a very similar distribution as does the stellar mass. However, the dynamical mass, as well as the group velocity dispersion and the group radius, show much weaker dependences on the distance. There is an accumulation at the minimum value of the group velocity dispersion, which is due to the way it was calculated (see Sect. 3.4.1). The distribution of group radii shows a step, which corresponds to half of the effective angular linking length. In the case of groups with two members, this is the maximum value of the group radius for which the group is still recognised as bound by the FoF-algorithm. Richer groups containing larger numbers of detected members, become rarer at larger distances, because the fainter group members are not detected in 2MRS any more.
Appendix A contains a detailed description of the catalogue. We identified some of the richest clusters12. A list is provided Appendix A. The fact, that we were able to locate many well known clusters in our catalogue suggests that our group finding algorithm worked as expected.
4.2. The SDSS DR12 group catalogue
Our SDSS based group catalogue is composed of 402 588 galaxies from Alam et al. (2015) covering 9274 square degrees on the sky. Using our group finder with the optimal coefficients from Table 3, we detected 229 893 groups in the SDSS DR12 data up to a redshift of 0.11. As illustrated in Fig. 12, a large fraction (170 983 to be precise) of the galaxies are found in groups with only one visible member. Similar to the results of the 2MRS catalogue, the number of groups rapidly decreases with increasing number of multiplicity, but since the SDSS sample is much deeper, there are more groups with higher multiplicity than for the 2MRS sample. We detected 48 groups with more than 100 visible members each.
 |
Fig. 14 Dependence of various group parameters of the SDSS catalogue on the luminosity distance. Panels: as in Fig. 13. |
As illustrated in Fig. 14, all group parameters show dependences on the luminosity distance to a varying degree. Similar to the 2MRS catalogue, the SDSS group catalogue is also affected by the Malmquist bias, which removes fainter groups from the sample at large distances. However, SDSS is significantly deeper than 2MRS and there are no indications of any over-corrections within the limits of the catalogue. Therefore, the effect of the bias on the dependence of the total group luminosity and the total group mass is not as striking as for 2MRS, but it is still clearly visible in the plots. Despite the impact of the Malmquist bias, the distribution of the stellar mass is nearly constant over the redshift range of our catalogue. The dependence of the dynamical mass, the group velocity dispersion, and the group radius is barely noticeable. Again there is an accumulations at the minimum value of the group velocity dispersion and a step in the distribution of the group radii corresponding to half the effective linking length for the same reasons as for the other group catalogue. The groups with largest numbers of detected members are found at intermediate distances, where the saturation bias effect becomes insignificant, while the Malmquest bias is not dominant yet.
A full description of the catalogue data and a list of prominent clusters can be found in Appendix A. SDSS covers a much smaller area of the sky than 2MRS. Furthermore, due to the saturation limits of SDSS spectroscopy, there is a dearth of galaxies in the SDSS survey at very low redshifts. Hence, we did not detect as many rich nearby groups as in the 2MRS. However, we were able to identify some of the same groups and clusters in both surveys independently.
4.3. The fundamental plane distance group catalogue
 |
Fig. 15 Distribution of the number of early-type galaxies found in our SDSS groups. |
We took advantage of our previous work (Saulder et al. 2013) on the fundamental plane of elliptical galaxies to provide additional information for a subset of groups of our SDSS catalogue. We provide redshift independent fundamental plane distances for all groups that contain at least one early-type galaxy based on our extended and up-dated fundamental plane calibrations in the Appendix of our recent paper (Saulder et al. 2015). We found 49 404 early-type galaxies distributed over 35 849 groups of our SDSS group catalogue. These groups themselves host over 145 000 galaxies of various morphological types. As illustrated in Fig. 15, the majority (30 017 to be exact) of the early-type galaxies are the only detected early-type galaxy in their group. We also found 5832 groups hosting two or more early-type galaxies and 803 of these groups even contain five or more early-type galaxies.
 |
Fig. 16 Difference in the distance measurements for our clusters by comparing the fundamental plane distances with the redshift distances depending on the number of early-type galaxies NETG per group. Black dashed line: average ratio per early-type galaxies multiplicity bin. Red solid line: 1-σ intervals. Green dashed line: expected progression of the 1-σ intervals around one based on the root mean square of our fundamental plane distance error of 0.0920. Magenta dotted line: reference for where both distance measurements yield exactly the same values. |
In Fig. 16, we show that the difference between the co-moving fundamental plane distance and the co-moving redshift distance decreases with the increasing number of elliptical galaxies per group. For higher multiplicities, the statistics is affected by the small number of groups hosting so many detected elliptical galaxies. We compared this to the expected decrease based on the root mean square (of 0.0920 in the z band) of our fundamental plane calibration in our recent paper (Saulder et al. 2015) and found that the measured decrease is comparable to the expected one, although there is a trend for the mean value to rise with higher early-type multiplicity per cluster.
A detailed description of the data included in the catalogue is provided in Appendix A.
4.4. The finite infinity regions catalogues − merging 2MRS and SDSS
While the three previous catalogues were kept relatively general allowing for a wide range of applications, the catalogue of finite infinity regions has been exclusively created as a preparatory work for our next paper (Saulder et al. 2016).
 |
Fig. 17 Distribution of the matter density in dependence of the distance for our catalogues. Dotted black line: expected average value based on the mock catalogue used to calibrate the group masses. Dotted blue line: density distribution of our SDSS catalogue. Dashed green line: density distribution of our 2MRS catalogue. Solid red line: density distribution of our combined dataset, which is a mixture of the SDSS and 2MRS cataloguesbelow the distance at which the SDSS saturation limit becomes negligible. Dashed-dotted cyan line: only the SDSS catalogue is used above this distance. Dotted magenta line: maximum depth of catalogue (z = 0.11). |
 |
Fig. 18 Completeness of our catalogues based on the luminosity function of their galaxies depending on the co-moving distance. Dashed black line: completeness function of the 2MRS catalogue, which is only affected by the Malmquist bias. Solid red line: completeness function of SDSS, which is affected by the Malmquist bias and a saturation limit. Dotted blue line: Malmquist bias for SDSS. Dashed green line: saturation bias for SDSS. Dashed-dotted cyan line denotes the point, when the impact of saturation limit on the completeness function of SDSS becomes negligible (the saturation limit completeness rises about 95%). Dotted magenta line: maximum depth of catalogue (z = 0.11). |
The main reason for using the 2MRS catalogue in addition the SDSS sample is the fact that the SDSS suffers from incompleteness at very low redshifts due to the saturation of their spectroscopic data. The 2MRS catalogue has no saturation limit and allows us to fill in at least some gaps. The merging of the two catalogues is a delicate procedure, which required some deliberations beforehand. When plotting the matter density as a function of distance (see Fig. 17), the density of the 2MRS catalogue fluctuates (due to large local structures) around the average value expected from the mock catalogues in the inner mass shells, but then drops drastically in the outer shells. The density of SDSS catalogue tends to be higher than the density of the 2MRS catalogue in the innermost shells and also exhibits much bigger fluctuations in these shell due to the smaller area of the sky covered by it.
We used a combination of the 2MRS and SDSS catalogue up to a certain distance and beyond that the SDSS catalogue only. We defined this limit as the distance at which the effect of saturation limit on SDSS becomes negligible. We placed it at a co-moving distance of 92.3 Mpc, which corresponds to where 95% of the luminosity function (down to an absolute magnitude of −15 mag in the r band, which was our limit on SDSS data) is unaffected by the saturation limit as illustrated in Fig. 18. This is also where the mass density of 2MRS starts dropping significantly below the expected value (see Fig. 17). The 2MRS catalogue is already strongly effected by the Malmquist bias at this distance. As illustrated in Fig. 18 only the brightest ~15% of the luminosity function (down to an absolute magnitude of −18 mag in the Ks band, which was our limit on 2MRS data) are still visible.
The first step in merging the 2MRS and SDSS catalogue was to remove all 22 190 2MRS groups beyond a co-moving distance of 92.3 Mpc. From this distance outward, only SDSS data were used. In the overlapping area we can encounter three cases, for which the third case required careful assessment:
-
(i)
a group is detected only in SDSS, because its galaxies are toofaint for 2MRS;
-
(ii)
the group is only detected in 2MRS because they are too near and too bright for SDSS or simply because they are outside the area covered by SDSS – in both those cases the group is fully included in the new merged catalogue;
-
(iii)
the same group (or parts of it) is detected in both catalogues. In this case, both detections need to be merged in a meaningful manner.
For this group merging, we took our truncated 2MRS catalogue and verified how many SDSS groups were within one linking length of our 2MRS groups. We use the definition of the linking length of Eqs. (17) and (18) with the optimised parameters for 2MRS from Table 3 but with λopt set to zero, because the corresponding term was calibrated using the galaxy luminosities and not the group luminosities and it was a minor correction at that distance anyway. If one of the linking lengths αeff or Reff was smaller than the group angular radius or the group velocity dispersion respectively, it was scaled up accordingly. We found that 1990 of the 10 085 SDSS groups in the overlapping volume had to be merged with 1654 2MRS groups. There were obviously several cases in which we found more than one SDSS group within a 2MRS group. The parameters of the newly merged groups were the weighted averages of the parameters of their predecessors. One part of the weights was the completeness function: 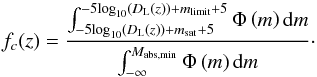 (41)It depends on the luminosity distance DL derived from the redshift z, the saturation limit msat, which is 14 mag in the SDSS r band and none for 2MRS, the limiting magnitude mlimit of the survey, which is 17.77 mag in the r band for SDSS and 11.75 mag in the Ks band for 2MRS. We used the corrected observed luminosity function
(41)It depends on the luminosity distance DL derived from the redshift z, the saturation limit msat, which is 14 mag in the SDSS r band and none for 2MRS, the limiting magnitude mlimit of the survey, which is 17.77 mag in the r band for SDSS and 11.75 mag in the Ks band for 2MRS. We used the corrected observed luminosity function  as illustrated in Fig. 4. The 2MRS and SDSS completeness functions are plotted in Fig. 18. The other part of the weights wmerge = fc·NFoF used for merging the groups is the number of members per group NFoF. This ensured that the masses of galaxy clusters were not biased by a single galaxy from the other survey. In the merging process the centre of mass of the new groups was adjusted according to the weights as well. Our combined catalogue consists of 237 219 groups. They contain in total 39.9% of mass expected for the volume using the Millennium simulation cosmology, which is slightly below the 43.4% of matter in visible groups in the latest snapshot of the millimil simulation.
as illustrated in Fig. 4. The 2MRS and SDSS completeness functions are plotted in Fig. 18. The other part of the weights wmerge = fc·NFoF used for merging the groups is the number of members per group NFoF. This ensured that the masses of galaxy clusters were not biased by a single galaxy from the other survey. In the merging process the centre of mass of the new groups was adjusted according to the weights as well. Our combined catalogue consists of 237 219 groups. They contain in total 39.9% of mass expected for the volume using the Millennium simulation cosmology, which is slightly below the 43.4% of matter in visible groups in the latest snapshot of the millimil simulation.
We applied the method described in Sect. 3.5 to our combined catalogue and obtained the finite infinity regions. We assigned radii for the first estimate of the finite infinity regions based on the masses in the combined catalogue and merged all groups that were fully within these regions of other groups into their hosts. We ended up with 189 712 groups after performing this procedure. The masses of these groups were rescaled using Eq. (40) with the coefficients for the first rescaling from Table 7 of the snapshot nearest in redshift to our groups. We calculated the new finite infinity radii and repeated the merging procedures to find 171 801 groups containing 67.4% of the mass expected for the volume and the cosmology used. The masses of 171 801 groups are rescaled again using the sum of the original masses of member groups as a basis and the coefficients for the final rescaling from Table 7 of the snapshot nearest in redshift to our groups. The total mass of the groups adds up to 70.5% and the finite infinity regions occupy 19.5% of the volume covered by our combined catalogue. These values are within the expected range (see Table 7) for a combined dataset of all snapshots. We note that based on the theory of the two-phase model of Wiltshire (2007), we expect ~25% of the volume to be inside finite infinity regions.
A full description of the format of the catalogue is given in Appendix A. Additionally, we provide another list in the same format, in which the group masses were rescaled so that their sum covers the full mass expected for the catalogue’s volume and the Millennium simulation cosmology. We also applied the merging procedure on the rescaled groups, which left us with 154 903 groups whose finite infinity regions cover 27.1% of the catalogue’s volume.
5. Summary and discussion
In order to provide a robust model of the matter distribution in the local Universe, we used data from the SDSS DR12 (Alam et al. 2015) and the 2MRS (Huchra et al. 2012b). After we preformed some filtering and calibrated the data, we ended up using 43 508 of 44 599 galaxies from the entire 2MRS catalogue and 402 588 of 432 038 galaxies from the SDSS below a redshift of 0.11213. We created several mock catalogues from the Millennium simulation in order to carefully calibrate our techniques.
For the SDSS sample and the 2MRS sample, we provide eight independent mock catalogues each. Every one of them covers one eighth of the sky and the distribution of the luminous matter in them is based on semi-analytic galaxy models from (Guo et al. 2011). The 2MRS mock catalogues consider the Malmquist bias, peculiar motions and all possible measurement uncertainties. The SDSS mock catalogues takes the same effects into account as for the 2MRS mock catalogues, but also includes the saturation limits and fibre collisions bias of SDSS. We also provide a corresponding set of dark catalogues, which were used to optimise the group finder and calibrate the masses derived from the groups. Although our mock catalogues were primarily designed as a calibration tool for our group finder algorithm presented in this paper, they are kept sufficiently general to be used in future work as well.
The core result of our study is the group finder that we developed. It was strongly inspired by the one presented in (Robotham et al. 2011). We considered several effects for our group finder algorithm, which we had to calibrate independently for the 2MRS and the SDSS sample. First, we calculated the basic linking length blink,0, which we defined as the average co-moving distances between the two nearest sufficiently luminous (this requirement excludes (most) dwarf galaxies) neighbour galaxies in our unbiased mock catalogue. The derived parameters provided a first basic estimate of the adaptive linking length used in our algorithm. The linking length was split into a radial and angular (transversal) components and the latter was modified to account for stretching effect in the redshift space due to peculiar motions inside groups (illustrated in Fig. 5). We also considered a correction that rescaled the linking length depending on the fraction of the galaxy luminosity function (see Fig. 4) that is visible at a certain distance. This rescaling effectively corrected for the incompleteness of our data due to the Malmquist bias. The final linking length, which was defined in Eqs. (17) and (18), depends on three free coefficients, that are αopt, Ropt, and λopt. Following Robotham et al. (2011), they were optimized by maximizing the group cost function (see Eqs. (19) to (25)) using a Simplex algorithm (Nelder & Mead 1965). The results of the optimization are provided in Table 3. All coefficients have values between 0.5 and 1. The optimized group finder was applied on our datasets in the next step.
The 2MRS group catalogue includes 31 506 groups, which host a total of 43 425 galaxies. We identified many well-known structures of the local Universe in this catalogue. Aside from basic parameters such as coordinates and redshifts, the most important quantity for our groups are their masses. Therefore, we used our mock catalogues to carefully calibrate the mass function depending on several other parameters of the groups. The advantages of the 2MRS catalogue are its large sky coverage and its high completeness at very low redshifts.
The SDSS group catalogue comprises 229 893 groups, which host 402 588 galaxies. It is restricted to a smaller area of the sky than the 2MRS group catalogue, but it is also deeper providing a clearly more complete sample at higher (up to our limiting redshift of 0.11) redshifts. At very low redshifts the SDSS group catalogue suffers from some additional incompleteness due to the saturation limits of SDSS spectroscopy. This was the main reason why we also provided the 2MRS catalogue to complement the SDSS catalogue a very low redshifts. The two catalogues are not completely disjunct, there is some overlap between them and we were able to identify a few prominent galaxy clusters in both catalogues.
We also studied the dependence of the group parameters on the luminosity distance for the 2MRS and SDSS group catalogues (see Figs. 13 and 14). The total group luminosity and the total group mass strongly depend on the luminosity distance. This is mainly due to the impact of the Malmquist bias. For group catalogues based on volume limited data, all group parameters should be independent of the distance, however 2MRS and SDSS are magnitude limited. Despite some corrections that are applied (for example to compensate the Malmquist bias for the detected groups), the Malmquist bias leaves a distinctive imprint on the distribution of the group parameters, because fainter groups are not detected at larger distances. However, the impact of the bias on parameters such as the group velocity dispersion and the group radius are minimal.
 |
Fig. 19 Dependencies of the difference in the distance measurements for our clusters by comparing the co-moving fundamental plane distances with the co-moving redshift distances on the co-moving redshift distance itself and the number of elliptical galaxies per group. Top-left panel: all groups that contain at least one elliptical galaxy. Top-right panel: all groups containing at least two elliptical galaxies. Bottom-left panel: all groups that host five or more elliptical galaxies. Bottom-right panel: all groups hosting at least 10 elliptical galaxies. The solid red lines indicate fits on the displayed data, which show an increasing dependence of the ratio between the fundamental plane distance and the redshift distance on the redshift distance with an increasing number of elliptical galaxies per group. The dashed black line only provides a reference, if this trend was not detected. |
The fundamental plane distance catalogue was obtained by combining the SDSS group catalogue with our previous work. We provided very detailed calibration of the fundamental plane in Saulder et al. (2013) and listed updated coefficients based on an extended sample from a more recent paper (Saulder et al. 2015). We calibrated the fundamental plane of early-type galaxies fitting the fundamental plane parameters, which are the physical scale radius, the central velocity dispersion, and the surface brightness using a Malmquist-bias corrected modified least-square technique. The physical scale radii were obtained from the angular radii of the galaxies and the redshift distances. We used 119 085 early-type galaxies from SDSS DR10 (Ahn et al. 2014), which were classified using GalaxyZoo (Lintott et al. 2008, 2011) and additional criteria. The aim of the fundamental plane distance catalogue is to provide redshift independent distance measurements for groups hosting elliptical galaxies. As illustrated in Fig. 16, the accuracy of our alternative (to redshift) distance measurements improves for groups with higher elliptical galaxy multiplicities, but there are some residual trends visible. The fundamental plane distances tend to be on average larger than the redshift distances for groups with a higher number of early-type galaxies detected in them.
When we examine our sample closer, we discover a trend in the ratio between the fundamental plane distance and the redshift distance. As illustrated in Fig. 19, there is a trend that the ratio between the co-moving fundamental plane distance and the co-moving redshift distance slightly decreases with a growing co-moving redshift distance. An interesting fact is that this trend becomes steeper for groups hosting more and more elliptical galaxies, as already suggested in Fig. 16. We considered a selection effect on the elliptical galaxies in the nearer groups, a general dependence of elliptical galaxies on their environment, or some selection effect on measurement of the median redshift of the groups. Understanding this systematic trend will be especially relevant for of our planned cosmological test (Saulder et al. 2016). We notice a dearth of early-type galaxies, and consequently groups hosting them, at low distances, which we attribute to the saturation limit of SDSS of 14 mag in the r band. The average absolute r band magnitude of an elliptical galaxy (not counting dwarf galaxies) of roughly −21 mag (Saulder et al. 2013), which means that a significant part of the elliptical galaxies at a luminosity distance of about 100 Mpc is still not included in the sample. A comparison with our mock catalogues allows us to rule out that this selection effect is a major contributor to the observed trend, hence we conclude that it is primarily due to effects of the environment on early type galaxies, which would agree with recent finding on the dependences of fundamental plane residuals by Joachimi et al. (2015).
We provide catalogues of fundamental plane distances for all cluster hosting early-type galaxies for three different cosmological: the Millennium simulation cosmology, the cosmology used in Saulder et al. (2013) and the recent Planck cosmology (Planck Collaboration XVI 2014).
The final catalogue of this paper contains the finite infinity regions, which are a necessary part of the foreground model for our planned cosmological test (Saulder et al. 2012). Although we will be testing the a cosmology that is notably different from the Λ-CDM cosmology used in the Millennium simulation, the assumption that the large-scale matter distribution in the last snapshot of that simulations provides a reasonable model of the matter distribution in the present-day Universe allowed us to use that data. A more detailed discussion of this assumption and its implications will be provided in our recently follow-up paper (Saulder et al. 2016). We found that for the mock catalogues and the Millimil simulation slightly less than half of the simulation’s particles are actually bound to the FoF groups. However, when calculating the finite infinity regions around the groups we saw that up to 80% of the particles of the simulations are within them. We used this to develop and calibrate a rescaling method, which allowed us to calculate the finite infinity regions from the masses of groups as explained in Sect. 3.5. We applied this method on a combined dataset of the 2MRS and SDSS catalogue. The two catalogues were merged using weights based on their completeness function (see Fig. 18) and multiplicities of the groups for the groups, which were in both catalogues. Furthermore, we did not use any 2MRS data beyond 92.3 Mpc. In the end, we provided a catalogue of 171 801 groups and the sizes of the finite infinity regions surrounding them. Since the distribution of the remaining mass influences the cosmological test, we prepared data for two different scenarios. In one, we assumed that the rest is distributed sufficiently homogeneous in the voids between the finite infinity regions. In the other one, we added the missing mass to detected groups and rescaled their masses in a way that their sum accounts for all of the expected mass in the catalogue’s volume, yielding a catalogue of 154 903 finite infinity regions. In our follow-up paper (Saulder et al. 2016), we study in detail which one is a better description of the real data. The finite infinity regions cover approximiately the same fraction of the total volume (~25%, Wiltshire 2007) as expected for timescape cosmology. They also partially overlap. We calculated that there are between 2.1% and 2.7% (depending on the catalogue) of the total volume are within more than one finite infinity region. In our calibrations, we ensured that the masses of these regions were correctly estimated.
Several catalogues with similar premises, but also notable differences, can be found in the literature. The SDSS DR4-based14 (Adelman-McCarthy et al. 2006) catalogue by Yang et al. (2007, 2009) does not contain any galaxies below a redshift of 0.01 in contrast to our SDSS DR12 (Alam et al. 2015), which does contain galaxies below that redshift and even compensates for the saturation bias at low redshifts with the provided 2MRS based catalogue. The catalogue of Nurmi et al. (2013) provides an SDSS DR7 (Abazajian et al. 2009) based sample of groups. However, they use sub-samples of different magnitude range to construct it and they mainly concern themselves with rich groups and clusters and leave isolated galaxies aside. The more recent catalogue by Tempel et al. (2014) is based on SDSS DR10 (Ahn et al. 2014) and supplemented with data from 2dFGRS (Colless et al. 2001, 2003), 2MASS (Skrutskie et al. 2006), 2MRS (Huchra et al. 2012b), and the Third Reference Catalogue of Bright Galaxies (de Vaucouleurs et al. 1991; Corwin et al. 1994). The main difference to our catalogues is that Tempel et al. (2014) created a set of volume limited samples, which is in total less complete than our magnitude limited (up to the selected redshift limit) catalogue. Furthermore, we put a special emphasis on mass completeness, which is essential for the planned cosmological test. The new 2MRS (Huchra et al. 2012b) based group catalogue of Tully (2015) has much in common with our own 2MRS based group catalogue. They used a slightly limited 2MRS sample (clusters between 3000 and 10 000 km s-1 redshift velocity), but investigated their group data into greater detail. For reasons of comparison, we created a sub-sample of our 2MRS group catalogue with the same limits as the catalogue of Tully (2015). We found 25 396 galaxies with our calibrations in that range, while Tully (2015) found 24 044 galaxies. There is a notable difference in the number of group, which we detected in the sample: we identified 17 191 groups compared to 13 607 groups in the Tully catalogue. 3630 of these groups have two or more members in our catalogue and Tully (2015) found a similar number, 3461, for theirs. Furthermore, there are several prominent clusters, which could be identified in both catalogues.
6. Conclusions
We created a set of group catalogues with the intention to use them for a cosmological test in our next paper. In the process, we devised a set of wide-angle mock catalogues for 2MRS and SDSS, which consider all possible biases and uncertainties. We use them to calibrate and optimize our FoF-based group finder algorithm and a mass function. After applying the group finder on 2MRS and SDSS data, we obtain a set of group catalogues, which can be used for various future investigation, even beyond the initial motivation of this paper. As matter of fact, three of the four catalogues, which we create in the process of this paper, are fully independent of the intended cosmological test. The 2MRS and the SDSS group catalogue complement the existing group catalogues based on these surveys, such as Crook et al. (2007), Yang et al. (2007), Nurmi et al. (2013), Tempel et al. (2014), Tully (2015), and others. The advantages of our catalogues are that they consider all groups of all sizes ranging from individual galaxy to massive clusters and that they provide well-calibrated group parameters with a special focus put on total masses and stellar masses. The fundamental plane distance catalogue adds a unique dataset to results of this paper. The final catalogue was obtained by merging or 2MRS and SDSS group catalogue and calculating of the finite infinity regions around the groups. In our upcoming paper (Saulder et al. 2016), we will perform our test of timescape cosmology by using the fundamental distance catalogue and the finite infinity region catalogue.
The survey is sufficiently shallow to only have a handful of galaxies in the overlap, resulting in a nearly empty Fig. 2.
We use the NASA/IPAC Extragalactic Database (http://ned.ipac.caltech.edu/) for a manual search by coordinates to identify this and all other other groups in this section.
With an updated version based on SDSS DR7 (Abazajian et al. 2009).
Acknowledgments
C.S. is grateful to Aaron Robotham for helpful advice and also acknowledges the support from an ESO studentship. I.C. is supported by the Telescope Data Center, Smithsonian Astrophysical Observatory. His activities related to catalogues and databases are supported by the grant MD-7355.2015.2 and Russian Foundation for Basic Research projects 15-52-15050 and 15-32-21062. IC also acknowledges the ESO Visiting Scientist programme. Funding for SDSS-III has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, and the US Department of Energy Office of Science. The SDSS-III web site is http://www.sdss3.org/. SDSS-III is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS-III Collaboration including the University of Arizona, the Brazilian Participation Group, Brookhaven National Laboratory, University of Cambridge, Carnegie Mellon University, University of Florida, the French Participation Group, the German Participation Group, Harvard University, the Instituto de Astrofisica de Canarias, the Michigan State/Notre Dame/JINA Participation Group, Johns Hopkins University, Lawrence Berkeley National Laboratory, Max Planck Institute for Astrophysics, Max Planck Institute for Extraterrestrial Physics, New Mexico State University, New York University, Ohio State University, Pennsylvania State University, University of Portsmouth, Princeton University, the Spanish Participation Group, University of Tokyo, University of Utah, Vanderbilt University, University of Virginia, University of Washington, and Yale University. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation.
References
- Abazajian, K. N., Adelman-McCarthy, J. K., Agüeros, M. A., et al. 2009, ApJS, 182, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Abell, G. O. 1958, ApJS, 3, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Adelman-McCarthy, J. K., Agüeros, M. A., Allam, S. S., et al. 2006, ApJS, 162, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Ahn, C. P., Alexandroff, R., Allen de Prieto, C., et al. 2014, ApJS, 211, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Alam, S., Albareti, F. D., Allen de Prieto, C., et al. 2015, ApJS, 219, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Alpaslan, M., Robotham, A. S. G., Obreschkow, D., et al. 2014, MNRAS, 440, L106 [Google Scholar]
- Arp, H. 1994, ApJ, 430, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Beers, T. C., Flynn, K., & Gebhardt, K. 1990, AJ, 100, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Bennett, C. L., Halpern, M., Hinshaw, G., et al. 2003, ApJS, 148, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Berlind, A. A., Frieman, J., Weinberg, D. H., et al. 2006, ApJS, 167, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bilir, S., Ak, S., Karaali, S., et al. 2008, MNRAS, 384, 1178 [NASA ADS] [CrossRef] [Google Scholar]
- Biviano, A. 2000, in Constructing the Universe with Clusters of Galaxies IAP 2000 meeting, Paris, France, eds. F. Durret, & D. Gerbal [Google Scholar]
- Blanton, M. R., Lin, H., Lupton, R. H., et al. 2003, AJ, 125, 2276 [NASA ADS] [CrossRef] [Google Scholar]
- Brough, S., Forbes, D. A., Kilborn, V. A., & Couch, W. 2006, MNRAS, 370, 1223 [NASA ADS] [CrossRef] [Google Scholar]
- Budzynski, J. M., Koposov, S. E., McCarthy, I. G., & Belokurov, V. 2014, MNRAS, 437, 1362 [NASA ADS] [CrossRef] [Google Scholar]
- Cabré, A., & Gaztañaga, E. 2009, MNRAS, 396, 1119 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., Emsellem, E., Krajnović, D., et al. 2011, MNRAS, 416, 1680 [NASA ADS] [CrossRef] [Google Scholar]
- Chilingarian, I. V., Prugniel, P., Sil’Chenko, O. K., & Afanasiev, V. L. 2007a, MNRAS, 376, 1033 [NASA ADS] [CrossRef] [Google Scholar]
- Chilingarian, I., Prugniel, P., Sil’Chenko, O., & Koleva, M. 2007b, in Stellar Populations as Building Blocks of Galaxies, eds. A. Vazdekis, & R. Peletier, IAU Symp., 241, 175 [Google Scholar]
- Chilingarian, I. V., & Mamon, G. A. 2008, MNRAS, 385, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Chilingarian, I. V., Melchior, A., & Zolotukhin, I. Y. 2010, MNRAS, 405, 1409 [NASA ADS] [CrossRef] [Google Scholar]
- Chilingarian, I. V., & Zolotukhin, I. Y. 2012, MNRAS, 419, 1727 [NASA ADS] [CrossRef] [Google Scholar]
- Chilingarian, I. V., Zolotukhin, I. Y., Katkov, I. Y., Melchior, A.-L., & Rubtsov, E. V. 2016, ApJS, submitted [Google Scholar]
- Cole, S., Percival, W. J., Peacock, J. A., et al. 2005, MNRAS, 362, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Colless, M., Dalton, G., Maddox, S., et al. 2001, MNRAS, 328, 1039 [NASA ADS] [CrossRef] [Google Scholar]
- Colless, M., Peterson, B. A., Jackson, C., et al. 2003, ArXiv e-prints [arXiv:astro-ph/0306581] [Google Scholar]
- Corwin, Jr., H. G., Buta, R. J., & de Vaucouleurs, G. 1994, AJ, 108, 2128 [NASA ADS] [CrossRef] [Google Scholar]
- Crook, A. C., Huchra, J. P., Martimbeau, N., et al. 2007, ApJ, 655, 790 [NASA ADS] [CrossRef] [Google Scholar]
- Croton, D. J., Springel, V., White, S. D. M., et al. 2006, MNRAS, 365, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, M., & Geller, M. J. 1976, ApJ, 208, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, T. M., & Scrimgeour, M. I. 2014, MNRAS, 442, 1117 [NASA ADS] [CrossRef] [Google Scholar]
- De Lucia, G., Springel, V., White, S. D. M., Croton, D., & Kauffmann, G. 2006, MNRAS, 366, 499 [NASA ADS] [CrossRef] [Google Scholar]
- de Vaucouleurs, G., de Vaucouleurs, A., Corwin, Jr., H. G., et al. 1991, Third Reference Catalogue of Bright Galaxies, Vol. I: Explanations and references, Vol. II: Data for galaxies between 0h and 12h, Vol. III: Data for galaxies between 12h and 24h (Springer) [Google Scholar]
- Dressler, A. 1980, ApJ, 236, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A., Oemler, Jr., A., Couch, W. J., et al. 1997, ApJ, 490, 577 [NASA ADS] [CrossRef] [Google Scholar]
- Driver, S. P., Hill, D. T., Kelvin, L. S., et al. 2011, MNRAS, 413, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Duarte, M., & Mamon, G. A. 2014, MNRAS, 440, 1763 [NASA ADS] [CrossRef] [Google Scholar]
- Duarte, M., & Mamon, G. A. 2015, MNRAS, 453, 3848 [NASA ADS] [CrossRef] [Google Scholar]
- Einasto, J., Saar, E., Kaasik, A., & Chernin, A. D. 1974, Nature, 252, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Einasto, M., Lietzen, H., Tempel, E., et al. 2014, A&A, 562, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eisenstein, D. J., Zehavi, I., Hogg, D. W., et al. 2005, ApJ, 633, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Eke, V. R., Baugh, C. M., Cole, S., et al. 2004a, MNRAS, 348, 866 [NASA ADS] [CrossRef] [Google Scholar]
- Eke, V. R., Frenk, C. S., Baugh, C. M., et al. 2004b, MNRAS, 355, 769 [NASA ADS] [CrossRef] [Google Scholar]
- Ellis, G. F. R. 1984, in General Relativity and Gravitation Conference, eds. B. Bertotti, F. de Felice, & A. Pascolini (Cambridge University Press), 215 [Google Scholar]
- Ellis, G. F. R., & Stoeger, W. 1987, Class. Quant. Grav., 4, 1697 [NASA ADS] [CrossRef] [Google Scholar]
- Gal, R. R. 2006, ArXiv e-prints [arXiv:astro-ph/0601195] [Google Scholar]
- Gerke, B. F., Newman, J. A., Davis, M., et al. 2005, ApJ, 625, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Goto, T., Yamauchi, C., Fujita, Y., et al. 2003, MNRAS, 346, 601 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, Q., White, S., Boylan-Kolchin, M., et al. 2011, MNRAS, 413, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, Q., White, S., Angulo, R. E., et al. 2013, MNRAS, 428, 1351 [NASA ADS] [CrossRef] [Google Scholar]
- Hao, J., McKay, T. A., Koester, B. P., et al. 2010, ApJS, 191, 254 [NASA ADS] [CrossRef] [Google Scholar]
- Hearin, A. P., Zentner, A. R., Newman, J. A., & Berlind, A. A. 2013, MNRAS, 430, 1238 [NASA ADS] [CrossRef] [Google Scholar]
- Hinshaw, G., Weiland, J. L., Hill, R. S., et al. 2009, ApJS, 180, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Hogg, D. W. 1999, ArXiv e-prints [arXiv:astro-ph/9905116] [Google Scholar]
- Hou, A., Parker, L. C., Balogh, M. L., et al. 2013, MNRAS, 435, 1715 [NASA ADS] [CrossRef] [Google Scholar]
- Huchra, J. P., & Geller, M. J. 1982, ApJ, 257, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Huchra, J. P., Macri, L. M., Masters, K. L., et al. 2012a, VizieR Online Data Catalog: J/ApJS/119/26 [Google Scholar]
- Huchra, J. P., Macri, L. M., Masters, K. L., et al. 2012b, ApJS, 199, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Huertas-Company, M., Aguerri, J. A. L., Bernardi, M., Mei, S., & Sánchez Almeida, J. 2011, A&A, 525, A157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jackson, J. C. 1972, MNRAS, 156, 1 [Google Scholar]
- Joachimi, B., Singh, S., & Mandelbaum, R. 2015, MNRAS, 454, 478 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, D. H., Saunders, W., Colless, M., et al. 2004, MNRAS, 355, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, D. H., Read, M. A., Saunders, W., et al. 2009, MNRAS, 399, 683 [NASA ADS] [CrossRef] [Google Scholar]
- Kitzbichler, M. G., & White, S. D. M. 2007, MNRAS, 376, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Knebe, A., Knollmann, S. R., Muldrew, S. I., et al. 2011, MNRAS, 415, 2293 [NASA ADS] [CrossRef] [Google Scholar]
- Knobel, C., Lilly, S. J., Iovino, A., et al. 2009, ApJ, 697, 1842 [NASA ADS] [CrossRef] [Google Scholar]
- Koester, B. P., McKay, T. A., Annis, J., et al. 2007, ApJ, 660, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E., Smith, K. M., Dunkley, J., et al. 2011, ApJS, 192, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2002, Science, 295, 82 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lawrence, A., Warren, S. J., Almaini, O., et al. 2007, MNRAS, 379, 1599 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Le Borgne, D., Rocca-Volmerange, B., Prugniel, P., et al. 2004, A&A, 425, 881 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leith, B. M., Ng, S. C. C., & Wiltshire, D. L. 2008, ApJ, 672, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Lintott, C., Schawinski, K., Bamford, S., et al. 2011, MNRAS, 410, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Lintott, C. J., Schawinski, K., Slosar, A., et al. 2008, MNRAS, 389, 1179 [NASA ADS] [CrossRef] [Google Scholar]
- Luparello, H. E., Lares, M., Yaryura, C. Y., et al. 2013, MNRAS, 432, 1367 [NASA ADS] [CrossRef] [Google Scholar]
- Makarov, D., & Karachentsev, I. 2011, MNRAS, 412, 2498 [NASA ADS] [CrossRef] [Google Scholar]
- Maraston, C. 2005, MNRAS, 362, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Moore, B., Frenk, C. S., & White, S. D. M. 1993, MNRAS, 261, 827 [NASA ADS] [Google Scholar]
- Muñoz-Cuartas, J. C., & Müller, V. 2012, MNRAS, 423, 1583 [NASA ADS] [CrossRef] [Google Scholar]
- Nelder, J. A., & Mead, R. 1965, Comput. J., 7, 308 [CrossRef] [Google Scholar]
- Nolthenius, R., & White, S. 1987, in Dark matter in the Universe, eds. J. Kormendy, & G. R. Knapp, IAU Symp., 117, 284 [Google Scholar]
- Nurmi, P., Heinämäki, P., Sepp, T., et al. 2013, MNRAS, 436, 380 [NASA ADS] [CrossRef] [Google Scholar]
- Oemler, Jr., A. 1974, ApJ, 194, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Old, L., Skibba, R. A., Pearce, F. R., et al. 2014, MNRAS, 441, 1513 [NASA ADS] [CrossRef] [Google Scholar]
- Old, L., Wojtak, R., Mamon, G. A., et al. 2015, MNRAS, 449, 1897 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration I. 2014, A&A, 571, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XVI. 2014, A&A, 571, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Postman, M., & Geller, M. J. 1984, ApJ, 281, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., & Davis, M. 1982, ApJ, 259, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical recipes in FORTRAN. The art of scientific computing, 2nd edn. (Cambridge University Press) [Google Scholar]
- Ramella, M., Geller, M. J., & Huchra, J. P. 1989, ApJ, 344, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Strolger, L.-G., Casertano, S., et al. 2007, ApJ, 659, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Robotham, A. S. G., Norberg, P., Driver, S. P., et al. 2011, MNRAS, 416, 2640 [NASA ADS] [CrossRef] [Google Scholar]
- Saulder, C., Mieske, S., & Zeilinger, W. W. 2012, in Dark Side of the Universe, Proc. of VIII Int. Workshop [Google Scholar]
- Saulder, C., Mieske, S., Zeilinger, W. W., & Chilingarian, I. 2013, A&A, 557, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saulder, C., van den Bosch, R. C. E., & Mieske, S. 2015, A&A, 578, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saulder, C., Mieske, S., van Kampen, E., & Zeilinger, W. W. 2016, A&A, submitted [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Spergel, D. N., Bean, R., Doré, O., et al. 2007, ApJS, 170, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Spitzer, Jr., L. 1969, ApJ, 158, L139 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., White, S. D. M., Jenkins, A., et al. 2005, Nature, 435, 629 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Stoughton, C., Lupton, R. H., Bernardi, M., et al. 2002, AJ, 123, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Strauss, M. A., Weinberg, D. H., Lupton, R. H., et al. 2002, AJ, 124, 1810 [NASA ADS] [CrossRef] [Google Scholar]
- Tempel, E., Tago, E., & Liivamägi, L. J. 2012, A&A, 540, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tempel, E., Tamm, A., Gramann, M., et al. 2014, A&A, 566, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tully, R. B. 2015, AJ, 149, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, E. L., & Gott, III, J. R. 1976, ApJS, 32, 409 [NASA ADS] [CrossRef] [Google Scholar]
- van der Wel, A., Bell, E. F., Holden, B. P., Skibba, R. A., & Rix, H.-W. 2010, ApJ, 714, 1779 [NASA ADS] [CrossRef] [Google Scholar]
- Wake, D. A., Whitaker, K. E., Labbé, I., et al. 2011, ApJ, 728, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Wetzel, A. R., Tinker, J. L., Conroy, C., & van den Bosch, F. C. 2013, MNRAS, 432, 336 [NASA ADS] [CrossRef] [Google Scholar]
- Wilman, D. J., Erwin, P., De Lucia, G., Fontanot, F., & Monaco, P. 2011, The Origin of the Morphology-Density Relation (Springer), 215 [Google Scholar]
- Wiltshire, D. L. 2007, New J. Phys., 9, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, X., Mo, H. J., & van den Bosch, F. C. 2009, ApJ, 695, 900 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, X., Mo, H. J., van den Bosch, F. C., et al. 2013, ApJ, 770, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, X., Mo, H. J., van den Bosch, F. C., & Jing, Y. P. 2005, MNRAS, 356, 1293 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, X., Mo, H. J., van den Bosch, F. C., et al. 2007, ApJ, 671, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Zeldovich, I. B., Einasto, J., & Shandarin, S. F. 1982, Nature, 300, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Zwicky, F. 1933, Helvetica Phys. Acta, 6, 110 [Google Scholar]
- Zwicky, F., Herzog, E., Wild, P., Karpowicz, M., & Kowal, C. T. 1961, Catalogue of galaxies and of clusters of galaxies, Vol. I (Pasadena: California Institute of Technology) [Google Scholar]
Appendix A: Catalogue description
In the section, we provide a detailed description of all catalogues presented in this paper and their internal structure.
2MRS group catalogue: we provide a list of all detected groups that includes their 2MRS group ID, the coordinates of the group centre (right ascension and declination are both given in degrees), the median redshifts, the total group luminosity in the Ks band and its uncertainty, the observed group luminosity in the Ks band, the calculated group mass (using the method explained in Sect. 3.4.7) and its uncertainty, the stellar mass using the method of Sect. 3.4.6 and the number of galaxies within that group for which we had stellar masses available15, the dynamical mass of the group, the group velocity dispersion, the physical group (in kpc), the angular group radius (in degrees), the luminosity distance to the group centre (in Mpc), and the number of detected group members. An excerpt of this list is provided in Table A.1. In addition to that list, a list of all the galaxies used is provided in Table A.6, containing the our internal galaxy IDs, the 2MRS group IDs of the group the galaxy belongs to, the 2MASS IDs of the galaxies, as well as its coordinates and redshift.
The cluster with the most detected members and the 2MRS group ID 8 in our catalogue is the well-known Virgo cluster. Furthermore, we identified the following clusters with their parameters listed in Table A.1: the Fornax Cluster with the ID 10, the Centaurus Cluster with the ID 91, the Antlia Cluster with the ID 279, the Norma cluster with the ID 298, the Perseus Cluster with the ID 344, the Hydra Cluster with the ID 354, Abell 194 with the ID 400, the Coma Cluster with the ID 442, Abell 262 with the ID 539, the Leo Cluster with the ID 1007, and the cluster with ID 2246 is associated with the Shapley Supercluster.
SDSS group catalogue: we provide a list of all detected groups containing their SDSS group ID, the coordinates of the group centre (right ascension and declination are both given in degrees), the median redshifts, the total group luminosity in the r band and its uncertainty, the observed group luminosity in the r band, the calculated group mass (using the method explained in Sect. 3.4.7) and its uncertainty, the stellar mass (using the method of Sect. 3.4.6) and the number of galaxies within that group for which we had stellar masses available, the dynamical mass of the group, the group velocity dispersion, the physical group (in kpc), the angular group radius (in degrees), the luminosity distance to the group centre (in Mpc), and the number of detected group members. An excerpt of this list is provided in Table A.2. In addition to that list, a list of all the galaxies used is provided in Table A.7, containing the our internal galaxy IDs, the SDSS group IDs of the group the galaxy belongs to, the SDSS object IDs of the galaxies, as well as its coordinates and redshift.
We identified some of the richest clusters in our catalogue: the Coma Cluster with the ID 153084, the Perseus Cluster with the ID 82182, the Leo Cluster with the ID 176804, Abell 2142 with the ID 112271 and the cluster with the ID 149473 is associated with structures of the Hercules Supercluster. A list of these clusters and others with more than two hundred detected members is provided in Table A.2.
Fundamental plane distance group catalogue: we provide three lists (one of them is shown in Table A.3 as an example) of all our SDSS groups hosting elliptical galaxies for three slightly different sets of cosmological parameters. Naturally, since this paper uses the cosmology of the Millennium simulation (see Table 1 for the parameters), one of our lists is based on it. Another list is based on the cosmological parameters of our previous papers (Saulder et al. 2013, 2015), which are H0 = 70 km s-1 Mpc-1, ΩM = 0.3, and ΩΛ = 0.7, while the last list uses the cosmological parameters of the Planck mission (Planck Collaboration I 2014), H0 = 67.3 km s-1 Mpc-1, ΩM = 0.315, and ΩΛ = 0.685 (Planck Collaboration XVI 2014). The lists contain their SDSS group ID, the coordinates of the group centre (right ascension and declination are both given in degrees), the median redshifts and their uncertainties, the angular, co-moving, and luminosity fundamental plane distances and their respective uncertainties, the angular, co-moving, and luminosity redshift distances and their respective statistical uncertainties, the number of elliptical galaxies hosted in that group andthe total number of detected group members. Additional ~3 Mpc of systematic uncertainties have to be considered for the redshift distances due to peculiar motions (see Fig. 5). As an example of our catalogue, the top ten lines of our catalogue is provided in Table A.3. Additional, we suppliment our catalogue with a list of all 145 359 galaxies within groups that host early-type galaxies for all cosmologies mentioned earlier. As illustrative example we provide that list containing the corresponding IDs, coordinates, and fundamental plane distances in Table A.4. The galaxies used in the fundemtantal plane calibration of Saulder et al. (2015), which lie beyond the limits of our group catalogue, are listed in a seperate table. Table A.5 displays a tiny sample of these almost 70 000 galaxies to illustrate the structure of that list.
Finite infinity region catalogue: we provide a list of all 164,509 remaining groups containing their Cartesian co-moving coordinates cx, cy, and cz, their final masses, and their radii for the finite infinity regions. A sample of the first ten lines of our catalogue is given in Table A.8. Additionally, we provide another list in the same format, in which the masses of the groups have been rescaled so thattheir sum covers the full mass expected for the catalogue’s volume and the Millennium simulation cosmology. We also applied the merging procedure on the rescaled groups, which leaves us with 152 442 groups whose finite infinity regions cover 28.3% of the catalogue’s volume.
Parameters of a selected sample of groups as they appear in our 2MRS group catalogue.
Parameters of a selected sample of groups as they appear in our SDSS group catalogue.
Parameters of a selected sample of groups as they appear in our fundamental plane distance catalogue.
Parameters of the first five galaxies as they appear in our fundamental plane distance catalogue.
Parameters of the first five galaxies as they appear in our fundamental plane distance catalogue.
Identification numbers and parameters of the first five galaxies as they appear in the galaxy list for our 2MRS group catalogue.
Identification numbers and parameters of the first five galaxies as they appear in the galaxy list for our SDSS group catalogue.
Parameters of the first ten groups as they appear in our finite infinity regions catalogue.
Appendix B: SDSS-2MASS transformation
The data from Guo et al. (2011) does not contain any 2MASS magnitudes for the semi-analytic galaxy models in contrast to models in previous runs (De Lucia et al. 2006). Since we want to use the new models from the Millennium simulation for our mock catalogues, we had to extrapolate from the SDSS magnitudes provided in the Guo et al. (2011) data to 2MASS magnitudes. In addition to the data from the Millennium simulation’s first run (Springel et al. 2005) with its semi-analytic galaxy models (De Lucia et al. 2006), we have the full data from the 2MASS Redshift Survey (Huchra et al. 2012b) and all galaxies from the twelfth data release of SDSS (Alam et al. 2015) at hand. We found 8,499 galaxies which are in both datasets (2MRS and SDSS)16 and we therefore have 2MASS and SDSS magnitudes for them. We adopted the functional form of the SDSS-2MASS colour transformation proposed by Bilir et al. (2008):  (B.1)The wild card X stands for any of the 3 2MASS bands (J, H, and Ks). The relation connects the 3 SDSS magnitudes mg, mr, and mi with one 2MASS magnitude mX. We found that the values given for the coefficients dX, eX, and fX in Bilir et al. (2008) were of no good use for galaxies. The coefficients of that paper were derived for a general populations of stars and by applying them on galaxies one gets a clear offset and tilt with respect to the values from observations (see Fig. B.1 top-right panel) as well as to the values from the simulations (see Fig. B.1 bottom-right panel). At first, we tried to obtain the coefficients of the colour transformation by fitting it to the SDSS and 2MASS magnitudes of the semi-analytic galaxy models (De Lucia et al. 2006) from the Millennium simulation. However, we found that the fit derived from the simulated galaxies did not agree with the data from observed galaxies (see Fig. B.1 bottom-left panel). Hence, we finally derived the coefficients of the colour transformation by directly fitting it to the observational data of 8499 galaxies for which we had SDSS and 2MASS magnitudes both. After a 3-σ clipping to remove some clear outliers, 8384 galaxies remained and we obtained the coefficients listed in Table B.1.
(B.1)The wild card X stands for any of the 3 2MASS bands (J, H, and Ks). The relation connects the 3 SDSS magnitudes mg, mr, and mi with one 2MASS magnitude mX. We found that the values given for the coefficients dX, eX, and fX in Bilir et al. (2008) were of no good use for galaxies. The coefficients of that paper were derived for a general populations of stars and by applying them on galaxies one gets a clear offset and tilt with respect to the values from observations (see Fig. B.1 top-right panel) as well as to the values from the simulations (see Fig. B.1 bottom-right panel). At first, we tried to obtain the coefficients of the colour transformation by fitting it to the SDSS and 2MASS magnitudes of the semi-analytic galaxy models (De Lucia et al. 2006) from the Millennium simulation. However, we found that the fit derived from the simulated galaxies did not agree with the data from observed galaxies (see Fig. B.1 bottom-left panel). Hence, we finally derived the coefficients of the colour transformation by directly fitting it to the observational data of 8499 galaxies for which we had SDSS and 2MASS magnitudes both. After a 3-σ clipping to remove some clear outliers, 8384 galaxies remained and we obtained the coefficients listed in Table B.1.
 |
Fig. B.1 Comparison of the correlations between SDSS and 2MASS magnitudes. Top-left panel: our fit on observational data. Top-right panel: correlation from Bilir et al. (2008) as the straight dashed line, which has a clear off-set from our observational data. Bottom-left panel: performance of the relation derived from the one used in the Millennium simulation, which also deviates clearly from our observational data. Bottom-right panel: correlation from Bilir et al. (2008) applied on the Millennium simulation data, which does not fit either. |
Linear correlation coefficients of the fundamental-plane residuals for all possible combinations of the five SDSS filters.
 |
Fig. B.2 Performance of our fit for the SDSS-2MASS transformation. The top panels show an edge-on view on the colour-colour-colour plane for all 2MASS bands (J in the top-left panel, H in the top-middle panel, and Ks in the top-right panel). Our fits are always indicated by the dashed black lines. The bottom panels show the residuals of the fit shown as the difference between the observed magnitude and the magnitude derived from the fit depending on the apparent magnitude in the 3 2MASS bands (J in the bottom-left panel, H in the bottom-middle panel, and Ks in the bottom-right panel). |
The root mean square (rms) increases with longer wavelength which was not surprising, because we performed an extrapolation from the SDSS wavelength range deeper into the infrared and the closer the central wavelength of a filter is located to the SDSS filters, the better is the fit. In Fig. B.2, we show edge-on projections on the fitting plane for all three 2MASS bands and also the residuals, which are displayed for the 2MASS filters themselves and not the colours.
Appendix C: Mock K-correction
When creating a mock catalogue, one cannot simply change the sign of same K-corrections used to corrected the observed data, because the colours before applying the K-correction are, albeit similar, not the same as the colours after applying the K-correction. Although, it is not a huge difference (see Fig. C.1), it is one that can be taken into account with relatively small effort. To this end, we used the K-corrections from Chilingarian et al. (2010) with the updated coefficients for SDSS from Chilingarian & Zolotukhin (2012), Saulder et al. (2013) and the new coefficients for the 2MASS filters taken directly17. To derive the new mock K-correction coefficients  , we fitted a two-dimensional polynomial function:
, we fitted a two-dimensional polynomial function: 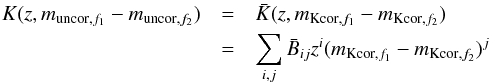 (C.1)which is similar to Eq. (1) to the obtained K-corrections K(z,muncor,f1−muncor,f2), K-corrected colours (mKcor,f1−mKcor,f2) and redshifts z of the galaxies from the SDSS and 2MASS galaxies and a grid of artificial values following the K-correction equation. The wild cards f1 and f2 stand for two different filters. By definition, the real K-corrections K for the uncorrected colours (muncor,f1−muncor,f2) are the same as the mock K-corrections
(C.1)which is similar to Eq. (1) to the obtained K-corrections K(z,muncor,f1−muncor,f2), K-corrected colours (mKcor,f1−mKcor,f2) and redshifts z of the galaxies from the SDSS and 2MASS galaxies and a grid of artificial values following the K-correction equation. The wild cards f1 and f2 stand for two different filters. By definition, the real K-corrections K for the uncorrected colours (muncor,f1−muncor,f2) are the same as the mock K-corrections  for the K-corrected colours (mKcor,f1−mKcor,f2). The coefficients
for the K-corrected colours (mKcor,f1−mKcor,f2). The coefficients  of the mock K-correction are listed in Tables C.1 to C.4 for all colours and filters used in this paper.
of the mock K-correction are listed in Tables C.1 to C.4 for all colours and filters used in this paper.
 |
Fig. C.1 Deviation of the uncorrected colour from the K-corrected colour using the real values for each survey. Top panel: SDSS colours. Bottom panel: 2MASS colours. |
Coefficients for the inverse K-correction in the g band using g−r colours.
Coefficients for the inverse K-correction in the r band using g−r colours.
Coefficients for the inverse K-correction in the J band using J−Ks colours.
Coefficients for the inverse K-correction in the Ks band using J−Ks colours.
Appendix D: Additional figures
 |
Fig. D.1 Distribution of the values of the median group cost function Stot using the 2MRS mock catalogues (in the left panel) and the SDSS mock gatalogues (in the right panel) for different values of αopt and Ropt. High values of Stot are indicated by dark red, while low values are indicated by dark blue. λopt is fixed to its optimal values, which is listed in Table 3. The green × denotes result of the optimal values of αopt and Ropt according to our simplex fit. |
 |
Fig. D.2 Distribution of masses within the finite infinity regions before expanding them iteratively depending on the sum of the masses of the groups they are composed of. The dotted black line indicates our fit on this relation. The panels show the 6 snapshots used from the last one (number 63) in the top left panel to the earliest one (number 58) in the bottom right panel. |
 |
Fig. D.3 Distribution of the final masses of the finite infinity regions depending on the sum of the masses of the groups they are composed of. Symbols and panels: as in Fig. D.2. |
All Tables
Number of galaxies, number of FoF groups, and the percentage of all particles in these groups (with at least 20 particles) by a snapshot used, and corresponding redshifts.
Coefficients of the mass dependence on observed parameters of groups with two to four members.
Coefficients of the mass dependence on observed parameters of groups with more than four members.
Coefficients of the mass rescaling for the finite infinity regions and the mass as well as the volume covered by them.
Parameters of a selected sample of groups as they appear in our 2MRS group catalogue.
Parameters of a selected sample of groups as they appear in our SDSS group catalogue.
Parameters of a selected sample of groups as they appear in our fundamental plane distance catalogue.
Parameters of the first five galaxies as they appear in our fundamental plane distance catalogue.
Parameters of the first five galaxies as they appear in our fundamental plane distance catalogue.
Identification numbers and parameters of the first five galaxies as they appear in the galaxy list for our 2MRS group catalogue.
Identification numbers and parameters of the first five galaxies as they appear in the galaxy list for our SDSS group catalogue.
Parameters of the first ten groups as they appear in our finite infinity regions catalogue.
Linear correlation coefficients of the fundamental-plane residuals for all possible combinations of the five SDSS filters.
All Figures
 |
Fig. 1 Projections of the distribution of galaxies in the SDSS mock catalogues and their overlaps. The fine green and red pixel in every plot show the projected (on the xy-plane) areas, where galaxies from two mock catalogues can be found, which belong to only one of the two catalogues. Yellow pixels indicate galaxies from both catalogues. The tiny blue crosses indicate galaxies that can be found in both catalogues in the same evolutionary stage (from the same redshift snapshot). Left panel: overlap of two mock catalogues whose coordinate origins are located in the neighbouring corners. Central panel: overlap of two mock catalogues whose origins are located in opposite corners, yet in the same plane (side of the cube). Right panel: overlap of two mock catalogues whose origins are located diagonally, opposite across the entire cube. |
| In the text | |
 |
Fig. 2 Projections of the distribution of the galaxies in the 2MRS mock catalogues and their overlaps. Symbols as in Fig. 1. |
| In the text | |
 |
Fig. 3 Redshift dependence of the number densities of the observational data and the mock catalogues. Left panal: 2MRS data; right panel: SDSS data. |
| In the text | |
 |
Fig. 4 Luminosity function for SDSS and 2MRS data are shown in the upper and lower panels correspondingly. Green dashed line: true luminosity function derived using all galaxies from the unbiased mock catalogues. Blue dashed line: corrected (reconstructed) luminosity function from the Malmquist biased mock catalogues. Red solid line: corrected observational data. |
| In the text | |
 |
Fig. 5 The red solid line shows the distribution of radial proper motions in MM, which has a roughly Gaussian shape. Black dashed line: zero radial velocity bin. Green dashed lines: dispersion of the radial peculiar velocities σrad, which corresponds to the standard deviation of the plotted distribution. Blue dashed lines: two-σ interval, which is used to stretch the radial linking length. |
| In the text | |
 |
Fig. 6 Comparison between stellar masses computed using pegase.hr stellar population models for the V band photometry (converted from SDSS g and r) with those calculated using the near-infrared UKIDSS K band magnitudes and a grid of Maraston (2005) SSP models. RCSED SSP ages in metallicities and the Kroupa IMF were used in both stellar mass estimates. |
| In the text | |
 |
Fig. 7 An polynomial approximation of a K band mass-to-light ratio as a function of the optical (g−r) colour shown in red overplotted on a two-dimensional histogram presenting K mass-to-light ratios estimated from the spectroscopic stellar population parameters for a sample of 424 163 galaxies. |
| In the text | |
 |
Fig. 8 Residuals of the fit for the mass determination of groups using 2MRS and SDSS mock data. Top-left panel: residuals of our fit using isolated galaxies (groups with one visible member only) for the 2MRS data. Top-central panel: residuals of groups with two to four members using 2MRS data. Top-right panel: residuals of groups with five or more members using 2MRS data. Bottom-left panel: residuals of our fit using isolated galaxies (groups with one visible member only) for the SDSS data. Bottom-central panel: residuals of groups with two to four members using SDSS data. Bottom-right panel: residuals of groups with five or more members using SDSS data. |
| In the text | |
 |
Fig. 9 Residuals of the fit for the mass determination of groups with only one visible member depending on the fitting parameter. Top-left panel: residuals as a function of the total Ks band group luminosity for the 2MRS data. The top-right panel: residuals as a function of the luminosity distance for the 2MRS data. Bottom-left panel: residuals as a function of the total r band group luminosity for the SDSS data. The Bottom-right panel: residuals as a function of the luminosity distance for the SDSS data. |
| In the text | |
 |
Fig. 10 Residuals of the fit for the mass determination of groups with two to four members depending on the fitting parameter. Top row: residuals for 2MRS data. Bottom row: residuals for SDSS data. First column: residuals as a function of the luminosity (Ks band for 2MRS, r band for SDSS). Second column: residuals as a function of the luminosity distance. Third column: residuals as a function of the group velocity dispersion. Forth column: residuals as a function of the group radius. |
| In the text | |
 |
Fig. 11 Residuals of the fit for the mass determination of groups with five or more members depending on the fitting parameter. Top row: residuals for 2MRS data. Bottom row: residuals for SDSS data. First column: residuals as a function of the luminosity (Ks band for 2MRS, r band for SDSS). Second column: residuals as a function of the luminosity distance. Third column: residuals as a function of the group velocity dispersion. Forth column: residuals as a function of the group radius. Fifth column: residuals as a function of the number of galaxies detected inside a group. |
| In the text | |
 |
Fig. 12 Distribution of the multiplicity NFoF of the groups detected in 2MRS (green dotted line) and in SDSS (red solid line). |
| In the text | |
 |
Fig. 13 Dependence of various group parameters of the 2MRS catalogue on the luminosity distance. First panel upper row: dependence on the total group luminosity Ltot; second panel upper row: dependence on the observed group luminosity Lobs; third panel upper row: dependence on the group velocity dispersion σgroup; fourth panel upper row: dependence on the group radius Rgroup; first panel lower row: dependence on the total group mass Mgroup; second panel lower row: dependence on the stellar mass M∗; third panel lower row: dependence on the dynamical mass Mdyn; fourth panel lower row: dependence on the number of detected galaxies in the group NFoF. |
| In the text | |
 |
Fig. 14 Dependence of various group parameters of the SDSS catalogue on the luminosity distance. Panels: as in Fig. 13. |
| In the text | |
 |
Fig. 15 Distribution of the number of early-type galaxies found in our SDSS groups. |
| In the text | |
 |
Fig. 16 Difference in the distance measurements for our clusters by comparing the fundamental plane distances with the redshift distances depending on the number of early-type galaxies NETG per group. Black dashed line: average ratio per early-type galaxies multiplicity bin. Red solid line: 1-σ intervals. Green dashed line: expected progression of the 1-σ intervals around one based on the root mean square of our fundamental plane distance error of 0.0920. Magenta dotted line: reference for where both distance measurements yield exactly the same values. |
| In the text | |
 |
Fig. 17 Distribution of the matter density in dependence of the distance for our catalogues. Dotted black line: expected average value based on the mock catalogue used to calibrate the group masses. Dotted blue line: density distribution of our SDSS catalogue. Dashed green line: density distribution of our 2MRS catalogue. Solid red line: density distribution of our combined dataset, which is a mixture of the SDSS and 2MRS cataloguesbelow the distance at which the SDSS saturation limit becomes negligible. Dashed-dotted cyan line: only the SDSS catalogue is used above this distance. Dotted magenta line: maximum depth of catalogue (z = 0.11). |
| In the text | |
 |
Fig. 18 Completeness of our catalogues based on the luminosity function of their galaxies depending on the co-moving distance. Dashed black line: completeness function of the 2MRS catalogue, which is only affected by the Malmquist bias. Solid red line: completeness function of SDSS, which is affected by the Malmquist bias and a saturation limit. Dotted blue line: Malmquist bias for SDSS. Dashed green line: saturation bias for SDSS. Dashed-dotted cyan line denotes the point, when the impact of saturation limit on the completeness function of SDSS becomes negligible (the saturation limit completeness rises about 95%). Dotted magenta line: maximum depth of catalogue (z = 0.11). |
| In the text | |
 |
Fig. 19 Dependencies of the difference in the distance measurements for our clusters by comparing the co-moving fundamental plane distances with the co-moving redshift distances on the co-moving redshift distance itself and the number of elliptical galaxies per group. Top-left panel: all groups that contain at least one elliptical galaxy. Top-right panel: all groups containing at least two elliptical galaxies. Bottom-left panel: all groups that host five or more elliptical galaxies. Bottom-right panel: all groups hosting at least 10 elliptical galaxies. The solid red lines indicate fits on the displayed data, which show an increasing dependence of the ratio between the fundamental plane distance and the redshift distance on the redshift distance with an increasing number of elliptical galaxies per group. The dashed black line only provides a reference, if this trend was not detected. |
| In the text | |
 |
Fig. B.1 Comparison of the correlations between SDSS and 2MASS magnitudes. Top-left panel: our fit on observational data. Top-right panel: correlation from Bilir et al. (2008) as the straight dashed line, which has a clear off-set from our observational data. Bottom-left panel: performance of the relation derived from the one used in the Millennium simulation, which also deviates clearly from our observational data. Bottom-right panel: correlation from Bilir et al. (2008) applied on the Millennium simulation data, which does not fit either. |
| In the text | |
 |
Fig. B.2 Performance of our fit for the SDSS-2MASS transformation. The top panels show an edge-on view on the colour-colour-colour plane for all 2MASS bands (J in the top-left panel, H in the top-middle panel, and Ks in the top-right panel). Our fits are always indicated by the dashed black lines. The bottom panels show the residuals of the fit shown as the difference between the observed magnitude and the magnitude derived from the fit depending on the apparent magnitude in the 3 2MASS bands (J in the bottom-left panel, H in the bottom-middle panel, and Ks in the bottom-right panel). |
| In the text | |
 |
Fig. C.1 Deviation of the uncorrected colour from the K-corrected colour using the real values for each survey. Top panel: SDSS colours. Bottom panel: 2MASS colours. |
| In the text | |
 |
Fig. D.1 Distribution of the values of the median group cost function Stot using the 2MRS mock catalogues (in the left panel) and the SDSS mock gatalogues (in the right panel) for different values of αopt and Ropt. High values of Stot are indicated by dark red, while low values are indicated by dark blue. λopt is fixed to its optimal values, which is listed in Table 3. The green × denotes result of the optimal values of αopt and Ropt according to our simplex fit. |
| In the text | |
 |
Fig. D.2 Distribution of masses within the finite infinity regions before expanding them iteratively depending on the sum of the masses of the groups they are composed of. The dotted black line indicates our fit on this relation. The panels show the 6 snapshots used from the last one (number 63) in the top left panel to the earliest one (number 58) in the bottom right panel. |
| In the text | |
 |
Fig. D.3 Distribution of the final masses of the finite infinity regions depending on the sum of the masses of the groups they are composed of. Symbols and panels: as in Fig. D.2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


