| Issue |
A&A
Volume 595, November 2016
|
|
|---|---|---|
| Article Number | A20 | |
| Number of page(s) | 11 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201629290 | |
| Published online | 24 October 2016 | |
Asteroids 87887 – 415992: the youngest known asteroid pair?
1 Institute of Astronomy, Faculty of Mathematics and Physics, Charles University, V Holešovičkách 2, 18000 Prague, Czech Republic
e-mail: jinziz@centrum.cz, vokrouhl@cesnet.cz
2 FMFI, Comenius University, Mlynská dolina F1, 842 48 Bratislava, Slovakia
3 Astronomical Institute, Czech Academy of Sciences, Fričova 298, 25165 Ondřejov, Czech Republic
Received: 11 July 2016
Accepted: 27 August 2016
Context. Pairs of asteroids, that is, couples of single bodies on tightly similar heliocentric orbits, were recently postulated as a new category of objects in the solar system. They are believed to be close twins to binary and multiple systems.
Aims. Ages of the known pairs range from about 15 kyr to nearly a million years. Beyond the upper limit, the pairs disperse in the background population of asteroids and become difficult to detect. Below the lower limit, the pairs should be easily recognizable if they exist and are discovered by surveys. Using the available data, we analyze the possible existence of very young asteroid pairs with clearly proven ages ≤ 10 kyr.
Methods. We searched for candidate very young asteroid pairs in the current catalog of asteroid orbits. After a preliminary analysis, we selected the most promising case of the small asteroids (87887) 2000 SS286 and (415992) 2002 AT49. We collected photometric observations to determine their rotation periods and absolute magnitudes.
Results. The rotation period of (87887) 2000 SS286 is 5.7773 ± 0.0004 h. Analysis of the data for (415992) 2002 AT49 indicates as the most probable period 2.6366 ± 0.0003 h, but other solutions are still possible. The composite light curves of the two asteroids have very low amplitudes, 0.22 and 0.12 mag, suggesting roundish shapes. Our observations also allow us to determine the absolute magnitude in R band HR = 14.99 ± 0.04 and HR = 16.24 ± 0.03 for the primary and secondary components. A transformation to the visible band provides H = 15.44 ± 0.05 and H = 16.69 ± 0.04. These two asteroids experienced a very close encounter, probably a formation event, some 7.4 ± 0.3 kyr ago. The formal extension of our numerical runs backward in time reveal that these close encounters may have continued, starting from ≃ 45 kyr ago. However, based on tests using synthetic fission events, we argue that the older age solutions might be the true solution only at ≃ (10−15)% level, assuming their low initial separation velocity is of between 10−20 cm s-1. This means that 87887–415992 probably is the youngest known asteroid pair in our dataset with a reliable determined age.
Key words: celestial mechanics / minor planets, asteroids: general
© ESO, 2016
1. Introduction
Vokrouhlický & Nesvorný (2008) discovered a population of asteroid pairs that share very similar heliocentric orbits. After they checked that the proximity of the orbits of these pairs was well above a statistical false-positive level, the authors dubbed them asteroid pairs. Noting the anomalously low separation velocities of the two components in the pair at the proposed moment of their origin, Vokrouhlický & Nesvorný (2008) also speculated about the formation mechanisms. They proposed that either (i) the parent body of the pair underwent a rotational fission that directly sent the fragments onto separate heliocentric orbits, or that (ii) a binary or multiple asteroid system became unstable, which caused a satellite to switch from bound to unbound orbit about a primary. Some subsequent studies focused on analysing individual pairs, especially the cases where astronomical observations allowed the best physical characterization. For instance, the very well constrained orbits of (6070) Rheinland and (54827) 2001 NQ8 allowed tracing their mutual configuration back to a near-contact system (e.g., Vokrouhlický & Nesvorný 2009). The conveniently large size of the primary component in this pair allowed obtaining enough photometric observations to solve for the pole orientation of this asteroid (Vokrouhlický et al. 2011); a more detailed analysis of the past convergence conditions of the two asteroids then allowed predicting that the primary and secondary components in this pair had the same rotation sense. Photometric observations of other pairs allowed addressing this problem directly, which proved that in the first case for which complete information is available, (2110) Moore-Sitterly and (44612) 1999 RP27, the pole orientations are indeed similar (Polishook 2014). The relationship of the two components in the asteroid pairs has been confirmed using spectroscopic observations that revealed a close similarity of their color indexes or spectra (e.g., Moskovitz 2012; Polishook et al. 2014a,b; Duddy et al. 2012, 2013; Wolters et al. 2014). Slight differences, in particular redder spectra of the primary component in some pairs, have been interpreted as a possible dust settling on the larger asteroid during the formation of the pair. Finally, the relationship between pairs and binaries received a new twist when it was reported that the primary component in some pairs is a binary, or even multiple, system (e.g., Vokrouhlický 2009; Pravec et al. 2013, 2016).
The most convincing hint about the origin of asteroid pairs was provided by observations of Pravec et al. (2010). These authors analyzed the correlation between the rotation period of the primary (larger) asteroid in the pair and the estimated size ratio of the two asteroids in the pair. They found that the correlation was most easily explained with a model in which the parent body of the pair underwent rotational fission, with prompt ejection of the smaller component onto an unbound orbit.
The next step in unraveling the circumstances of the asteroid pair origin is to determine which process (or processes) caused the fission in the parent object. Vokrouhlický & Nesvorný (2008) speculated that the parent asteroids were spun up by the Yarkovsky-O’Keefe-Radzievski-Paddack (YORP) effect (e.g., Vokrouhlický et al. 2015). This seems to be the only universal process that affects the rotation rate of asteroids smaller than ≲ 20−30 km strongly enough to bring them close to the fission limit within an astronomically relevant timescale. One possibility to confirm the YORP effect as the most likely candidate for the underlying process of asteroid pair formation would be to determine the exact statistics of pair formation in time and compare it with the prediction of the YORP theory. This goal is, however, well beyond the scope of the current paper. Ideally, it would imply selecting a size category of asteroid pairs and determine a complete sample of asteroid pairs that formed in the main belt, for example, within the past one hundred thousand years. However, there are strong selection and observation-incompleteness effects that prevent us from obtaining this information. Deciphering the respective bias correction is a complicated task that is yet to be done. In addition to finding the pairs, we would need to determine when precisely they formed. This is also difficult and uncertain. Previous studies have demonstrated that the uncertainty in the orbit propagation model, which is mainly due to unconstrained thermal accelerations, often results in a wide range of possible age solutions of the given pair. Moreover, in Sect. 4 we describe yet another level of uncertainty in determining the age of a given pair that has to do with the synodic cycles of their mutual heliocentric motion.
A simpler, but still interesting task, is to determine the youngest age of the asteroid pairs that belong to a given size category. This still faces the problem that the asteroid population is observationally not completely known, but at least it is less dependent on our ability of recognizing an asteroid pair among the population of unrelated asteroids (if both components in the pair are currently known in our catalogs). The reason is that when the asteroid pair is formed by a gentle separation that is characterized by a relative velocity of a fraction of a meter per second (see, e.g., Vokrouhlický & Nesvorný 2008, 2009), the heliocentric orbits of the two components are even more similar than is typical of older pairs. We recall that the asteroid pairs have been searched in the five-dimensional space of osculating orbital elements (a,e,I,Ω,ϖ), where a is the semimajor axis, e the eccentricity, I the inclination, Ω the longitude of node, and ϖ the longitude of pericenter (alternatively, the mean orbital elements might be used instead of the osculating ones, e.g., Rożek et al. 2011). For asteroid pairs that are several tens of kyr old, the value of the osculating mean longitude in orbit λ is unrelated because of Keplerian shear and differential Yarkovsky effects in their orbits. In principle, extremely young pairs may also have similar values of λ. A naive calculation shows that simple Keplerian shear would produce | Δλ | ≃ 10°−20° in less than 10 kyr for orbits that have a semimajor axis difference of | Δa | ≃ 10-5 au. This is because the third Kepler law provides a difference Δλ in mean longitudes of two confocal Keplerian orbits with a slightly different values Δa of semimajor axis: | Δλ | /360° ≃ 1.5 ( | Δa | /a) (T/P). Here, P is the orbital period and T is the time elapsed. Plugging in typical values for the orbits in the inner main belt and T = 10 kyr, we obtain the above-mentioned estimate. Even though planetary perturbations make the age determination more complex, numerical tests indicate that this estimate is roughly correct.
However, there is one more fundamental problem that indicates that a similarity of λ values is a necessary, but not sufficient, condition for the young age of the asteroid pair. This problem has been pointed out by Vokrouhlický & Nesvorný (2008), who studied the very close relative configuration of asteroids (1270) Datura and (215619) 2003 SQ168, which currently have | Δλ | ≃ 1.6° and | Δa | ≃ 3 × 10-5 au in osculating elements. Vokrouhlický & Nesvorný (2008; see their Fig. 6) showed that this configuration repeats in time in a cycle of more than 100 kyr. While this pair might be very young, it might also be several hundreds of kyr old. In fact, because it is a member of the Datura family, its age is probably more than 500 kyr (e.g., Nesvorný et al. 2006; Vokrouhlický et al. 2009). This effect has been interpreted in terms of synodic cycles of the relative motion of the pair components about the Sun. At each completion of the synodic cycle, the two asteroids approach each other very closely, mimicking the initial conditions, until orbital perturbations from planets and the Yarkovsky effect do not move the orbits away from each other. Depending on the asteroid pair, this timescale may be longer than one Myr. All of the tightest pairs originally discovered by Vokrouhlický & Nesvorný (2008) belong to this older category, as has been shown in subsequent numerical tests.
With these results, we conclude that the youngest currently known asteroid pairs are ≃ 15 kyr old. This is also the case of the above-mentioned well-studied pair of asteroids (6070) Rheinland and (54827) 2001 NQ8, for which Vokrouhlický et al. (2011) determined an age of 17.0 ± 0.2 kyr (see also Galád 2012, who additionally took into account gravitational effects of the dwarf planet Ceres and the largest asteroids, and obtained slightly younger age for this pair). There are two more cases, mentioned in Table 1 of Pravec et al. (2010), that might be of a comparable age. The question now is whether these are the youngest asteroid pairs among the currently known population. We here examine this question and consider 10 kyr as an order-of-magnitude limit for a young age.
The plan of our paper is as follows. We first sift the data in the current catalog of asteroid orbits and search for very tight asteroid pairs with similar longitudes in orbit (Sect. 2). As explained above, asteroid pairs with potentially youngest ages are expected to be contained in this sample. After eliminating false or very uncertain cases, we select the best candidate containing asteroids (87887) 2000 SS286 and (415992) 2002 AT49. Fortunately, these two objects were included in our observational efforts of determining the physical parameters of the components in asteroid pairs. We therefore report the currently available data and provide an estimate of the rotation periods and absolute magnitudes for the two asteroids in the selected pair (Sect. 3.2). Next, we analyze in detail a suite of numerical integrations of the two orbits backward in time, with the goal of determining the age of the 87887–415992 asteroid pair in Sect. 4. We pay particular attention to discerning the true age from false solutions that tend to repeat with the synodic period of the orbital revolution of these asteroids about the Sun. Implications and conclusions are collected in Sect. 5.
2. Candidate search
We conducted a new search for very close asteroid pairs in the updated catalog of the Minor Planet Center, which contained approximately 713 000 objects as of April 15, 2016. Of these objects some 130 000 resided on single-opposition orbits that we discarded because their elements are typically quite uncertain. As described above, we sought not only for tight pairs in the five-dimensional space of (a,e,I,Ω,ϖ) osculating elements, but we considered the difference in the mean longitude in orbit λ of the two orbits. Based on the discussion at the end of Sect. 1, we selected only the pairs with | Δλ | ≤ 15°. To ensure that we considered potential asteroid pairs, we also required cases with distance d ≤ 15 m s-1, using metrics defined in the space of osculating orbital elements (see Eq. (1) and Figs. 1 and 2 in Vokrouhlický & Nesvorný 2008).
With this procedure we obtained 23 potential candidates for very young pairs. We eliminated situations when the “pair” was a member of a known compact and very young asteroid family, such as (1270) Datura and (215619) 2003 SQ168. These situations arise from the incidental orbital proximity of two fragments that are launched at nearly the same relative velocity with respect to the parent body of the family. After performing this first-level trimming, we were left with 16 candidates that were not in any obvious young asteroid family.
Some of these remaining pairs have been analyzed in previous publications, where we demonstrated their convergence beyond the limit of 10 kyr. This was the case of
-
(21436) Chaoyichi and (334916) 2003 YK39;
-
(23998) 1999 RP29 and (205383) 2001 BV47;
-
(56232) 1999 JM31 and (115978) 2003 WQ56;
-
(63440) 2001 MD and (331933) 2004 TV14; and
-
(76111) 2000 DK106 and (354652) 2005 JY103;
all reported in Pravec et al. (2010). As a consequence, these pairs were eliminated from our further considerations.
We numerically integrated nominal orbits of the remaining candidates and found that some of them did not converge in their formation configuration within the past 10 kyr. This was the case of
-
(70208) 1999 RX33 and2013 GZ99;
-
(74096) 1998 QD15 and (224857) 2006 YE45;
-
(188577) 2005 GM1 and (420756) 2013 EW4;
-
(267333) 2001 UZ193 and 2007 DY95; and
-
(320025) 2007 DT76 and 2007 DP16.
We estimated the greatest Yarkovsky effect in each of these cases and ensured that including this perturbation in our calculation did not change our conclusions.
At this stage, we were left with the following six last cases (sorted here according to increasing difference | Δλ | of the mean longitude in orbit):
-
(229401) 2005 SU152and 2005 UY97(| Δλ | ≃ 1.1°);
-
(17198) Gorjup and (229056) 2004 FC126 (| Δλ | ≃ 1.1°);
-
(355258) 2007 LY4 and (404118) 2013 AF40 (| Δλ | ≃ 4.7°);
-
(87887) 2000 SS286 and (415992) 2002 AT49 (| Δλ | ≃ 5.3°);
-
(356713) 2011 UK160 and 2014 QX220 (| Δλ | ≃ 9.8°); and
-
(99052) 2001 ET15 and (291788) 2006 KM53 (| Δλ | ≃ 10.5°).
Again, some of these cases have been analyzed in the past. For instance, Fig. 4 in the supplementary materials of Pravec et al. (2010) shows the distribution of the past converging solutions for the tightest pair (229401) 2005 SU152 and 2005 UY97. While convergence may have been achieved as early as ≃ 3 kyr ago, many more solutions converge far beyond the 10 kyr limit, some up to 100 kyr ago. This huge spread is mainly caused by the small size of these asteroids and by the still rather poorly constrained orbit of the smaller component 2005 UY97. The former implies that Yarkovsky forces are potentially strong, and different clone variants for the asteroids in this pair therefore have a chance to closely approach at a widely spread time interval in the past. At the moment, we therefore exclude this pair from our analysis. A similar situation occurs for (355258) 2007 LY4 and (404118) 2013 AF40, and (356713) 2011 UK160 and 2014 QX220. In both cases, we have some solutions converging within the past 10 kyr, but most indicate a far older age. In all likelihood, these pairs will be found to be older than 10 kyr when their orbits are improved and physical parameters are determined that allow constraining the thermal accelerations.
Equinoctial orbital elements and their uncertainty as of epoch MJD 57 400.0.
The pairs (17198) Gorjup and (229056) 2004 FC126, and (99052) 2001 ET15 and (291788) 2006 KM53 present a slightly different story. In both cases we performed a detailed backward integration of a large number of clone variants of the two asteroids in the pair (some of which also sampled different possible strengths of the Yarkovsky forces). For the tighter pair (17198) Gorjup and (229056) 2004 FC126 we found that the clone clouds of the two components closely approached some 230 yr ago, but they missed each other at a minimum distance ≃ 50 000 km and at a minimum relative velocity ≃ 3 m s-1. These values exceed our criteria of convergence (e.g., Vokrouhlický & Nesvorný 2008; Pravec et al. 2010), namely an encounter distance of about a Hill radius of the parent body of the pair (some 750 km) and a relative velocity on the order of the escape velocity from the parent body (some 1.5 m s-1). Continuing the integration backward in time, we found that these conditions become eventually satisfied starting from 100 kyr ago. We conclude that this pair is older than 100 kyr and recently repeated their close initial configuration after completing a synodic cycle of their relative motion about the Sun. We found that a similar situation also occurred for the pair (99052) 2001 ET15 and (291788) 2006 KM53. Clone variants of the two asteroids have a chance to encounter some 5 kyr ago at a minimum distance of ≃ 10 000 km and with a minimum relative velocity of ≃ 1.5 m s-1. While the velocity limit barely approaches the required level of the escape velocity from the parent body of the pair, the recorded minimum distance is about 15 times larger than the required threshold. This again indicates that the two asteroids recently completed a synodic cycle of their relative motion, and the true age of this pair is at least 100 kyr.
Finally, our candidate list shrunk to the pair consisting of asteroids (87887) 2000 SS286 and (415992) 2002 AT49. A preliminary orbital integration backward in time indicated a fair possibility of a very close encounter of these bodies some 7 kyr ago that would match our criteria for the common origin of the two bodies in a fission of their parent asteroid. However, we also have to revert the argument: is our finding indicative of a true age of this pair, or are there possible and statistically likely solutions preceding the young one? The analysis of this problem is the core of our paper, and we focus on this in Sect. 4. Before we address these aspects, we recall what is known about these two small main belt asteroids. In particular, we report the photometric observations that allowed us to determine their rotation periods and improve their size estimate.
3. Asteroid pair 87887 – 415992
3.1. What we know so far
The orbital elements and their uncertainty for 87887 and 415992 are listed in the Table 1. We note (i) a similar value of the longitude in orbit λ for the two asteroids (≃ 5.3° difference in this case), and (ii) the associated anomalously small difference in the osculating semimajor axis a value (≃ 1.5 × 10-4 au difference in this case). The typical amplitude of short-period oscillations of the osculating semimajor axis for the orbits of 87887 and 415992 is ≃ 6 × 10-3 au, somewhat enhanced by the resonant effects mentioned below. This is 40 times larger than the current difference of the semimajor axis values of the two asteroids in the pair. This proximity of the a and λ values suggests that this might be a very recently formed pair.
The semimajor axis value ≃ 2.755 au locates the pair in the central part of the belt, just below the major mean motion resonance J5/2 with Jupiter. A closer look at the location of the pair reveals that it belongs to the Gefion family (see Nesvorný et al. 2015, and NASA PDS site Nesvorný asteroid families1). We note that Milani et al. (2014) associated this family with the largest member (93) Minerva. This large asteroid family has formed ≃ 480−490 Myr ago, when a huge number of meteorites rained onto Earth after only a short cosmic travel from their site of origin, as evidenced by data of fossil micrometeorites discovered in Swedish limestone quarries (e.g., Schmitz et al. 1997, 2001; Heck et al. 2004). This also constitutes the suggested link of the Gefion family and the source zone of L chondrite meteorites (Nesvorný et al. 2009). Observations of the WISE spacecraft of numerous larger Gefion members allowed determining the mean geometric albedo pV = 0.27 ± 0.06 for Gefion members (e.g., Masiero et al. 2015). However, we suspect that this result may be overestimated because they used the biased asteroid absolute magnitudes (see Pravec et al. 2012). As a result, we conservatively adopted the mean albedo for the S-type asteroids, pV = 0.20 ± 0.05, in our work. The mean principal components of Sloan Digital Sky Survey (SDSS) spectra for the Gefion-family members read PC1 = 0.10 ± 0.06 and PC2 = −0.02 ± 0.07, and they qualify this family to belong to the complex of S-type families (e.g., Nesvorný et al. 2015; Masiero et al. 2015). SDSS observations allowed determining PC1 = 0.03 ± 0.02 and PC2 = −0.05 ± 0.05 for (87887) 2000 SS286, which are compatible with the Gefion values and confirm its membership in this family.
An instructive exercise is to formally compute the distance vprop of the two asteroids in the 87887–415992 pair in the space of proper orbital elements. Obviously, in usual circumstances we would expect vprop to be very small, perhaps on the order of m s-1. However, using the synthetic proper elements of the two components given by the AstDyS website2, and using standard metric in the proper elements space (e.g., Zappalà et al. 1990), we obtain vprop ≃ 32 m s-1. This is a surprisingly high value. A closer inspection reveals that vprop is dominated (97% of its total value) by a contribution from slightly offset proper eccentricity values of the two asteroids. The difference in nominal proper eccentricity values is ≃ 1.25 × 10-3, but both have an uncertainty ≃ 1.7 × 10-3. A brief numerical integration of the nominal orbits of the two asteroids proved that they are located very close to the three-body (3, −1, −1) mean motion resonance (e.g., Table 1 and Figs. 2 and 4 in Nesvorný & Morbidelli 1998). This produces a slow diffusion in eccentricity that affects the accuracy with which the proper elements could be determined (e.g., Knežević & Milani 2000). However, if the pair 87887–415992 is ≃ 7 kyr young (Sect. 4), then the distance vprop in proper element space is much less relevant and a less useful parameter than in the case of larger and older structures in the main belt. We note that the synthetic proper elements are typically determined by numerical integration and data analysis for a 2 Myr interval of time (e.g., Knežević & Milani 2000; Knežević et al. 2002). This is far longer than the age of this pair.
3.2. Our photometric observations
We conducted photometric observations of the two asteroids with the 1.54 m Danish telescope at La Silla, Chile, on two apparitions each. The individual nightly runs, together with their geometric circumstances, are listed in Tables 2 and 3. They include the mid-time (UTC) of the run rounded to the nearest tenth of a day, the asteroid distances from the Sun r and Earth Δ, the solar phase angle α, and the geocentric ecliptic coordinates of the asteroid (λ, β). All the observations were taken with the Bessell R filter with supplementary observations in the V filter on October 30, 2014 for asteroid 87887. They were calibrated in the Johnson-Cousins photometric system using Landolt (1992) standard stars. The telescope was tracked at half-apparent rate of the asteroid, providing star and asteroid images of the same profile in one frame. The exposure times were 180 s. There occurred several gaps in the coverage on individual nights because we combined the observations with quasi-simultaneous runs on our other asteroid targets, and a few runs were shortened because of less-than-ideal sky conditions on the given nights. We processed and reduced the data with our custom-made aperture photometry software Aphot32.
Aspect data for observations of (87887) 2000 SS286.
Aspect data for observations of (415992) 2002 AT49.
We analyzed the obtained photometric data using the standard Fourier series method (e.g., Harris et al. 1989; Pravec et al. 1996, 2000).
 |
Fig. 1 Composite light curve of asteroid (87887) 2000 SS286 from observations in 2014. |
 |
Fig. 2 Composite light curve of asteroid (87887) 2000 SS286 from observations in 2016. |
3.2.1. (87887) 2000 SS286
The primary rotation period has been uniquely determined as P = 5.7773 ± 0.0004 h. This is the weighted average of our period determinations from the two apparitions in 2014 and 2016. The quoted uncertainty accounts for the transformation between the sidereal and synodic rotation periods. The composite light curves from the two apparitions are shown in Figs. 1 and 2. The mean light-curve amplitude was 0.22 mag, suggesting that the asteroid has an only moderately elongated shape. We determined the color index V−R = 0.45 ± 0.02, which is consistent with an S classification of the asteroid. The mean absolute magnitude in the Cousins R band is HR = 14.99 ± 0.04, converted into the Johnson V band to H = 15.44 ± 0.05. The phase relation slope parameter is G = 0.21 ± 0.05. Assuming the mean geometric albedo for S-type asteroids pV = 0.20 ± 0.05 (Pravec et al. 2012), we obtain a size estimate D1 = 2.43 ± 0.32 km for the primary in our pair.
 |
Fig. 3 Composite light curve of asteroid (415992) 2002 AT49 from observations in 2016. |
We note that the photometric data of (87887) 2000 SS286 do not indicate any obvious signs of tumbling (if any, it should correspond to a small angle between the body axis and the angular rotation vector). The canonical theory for damping of the tumbling state (e.g., Harris 1994), however, would predict a timescale of ≃ 700 kyr, one hundred times longer than the proposed age of the pair. This implies that the pair-formation mechanism in this case should have been rather “gentle”, leaving the primary to rotate about the principal axis of the inertia tensor.
3.2.2. (415992) 2002 AT49
Because of its low light-curve amplitude and the relatively low apparent brightness during our observations, we were unable to determine the rotation period of the secondary member of the asteroid pair uniquely. The formal best-fit solution from the 2016 data provides a period of P = 2.6366 ± 0.0003 h with a light-curve amplitude of 0.12 mag (Fig. 3), but other values are also possible. This is because with such a limited dataset the Fourier fit has a characteristic broad χ2 minimum, punctuated by sharp and separated minima. We report the formally best of them above, but other minima still have statistically admissible χ2 values. We estimate that the realistic range of the synodic rotation periods for this asteroid is ≃ 2.5 h to ≃ 6 h. Clearly, more observations are needed to constrain it better.
Assuming the asteroid has the same G and V−R values as the primary 87887, we obtained HR = 16.24 ± 0.03 and H = 16.69 ± 0.04. The 2014 data, although of a lower quality and even lower light-curve amplitude (≲ 0.1 mag), gave nearly the same HR = 16.25 ± 0.03. Assuming the mean geometric albedo for S-type asteroids pV = 0.20 ± 0.05, we obtain a size estimate D2 = 1.36 ± 0.18 km for the secondary in our pair.
Combining the sizes D1 and D2, we estimate the size of the parent body of this pair to be Dpar ≃ 2.56 ± 0.34 km. Adopting a bulk density between 2 and 2.7 g cm-3, which is appropriate for S-type asteroids (e.g., Carry 2012), we estimate the escape velocity from the parent body of the pair to be ≃ 1.5 ± 0.1 m s-1 (see, e.g., supplementary materials of Pravec et al. 2010). Similarly, we estimate that the characteristic radius of the Hill sphere of the parent body was 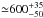 km. For the sake of simplicity we use 1.5 m s-1 and 600 km.
km. For the sake of simplicity we use 1.5 m s-1 and 600 km.
4. Estimated age for the asteroid pair 87887 – 415992
4.1. Clones and backward orbit integration
The recent origin of recognizable asteroid pairs allows estimating their age, that is, the time since their formation, using backward orbit propagation of the two asteroids (e.g., Vokrouhlický & Nesvorný 2008). Here we briefly recall the standard approach. In the next section, we substantiate the traditional methods using a more in-depth analysis, allowing us to eliminate the simulated age solutions related to the near-repetition of the asteroid configuration with the synodic periodicity.
In an ideal world, where (i) the state vectors of the two asteroids in the pair would be known exactly at a given epoch; and (ii) our orbit-propagation model would be complete and absolutely precise, we would propagate nominal asteroid orbits backward in time until they would reach a moment that reflected their separation conditions from the common parent body. Unfortunately, this is not possible and we need to correct for both factors (i) and (ii), at least in approximate way.
For problem (i), the orbit determination procedure incorporates the necessary statistical tools. In particular, for a given initial epoch T0 it provides not only the nominal (best-fit) orbital solution e⋆, but also the covariance matrix Σ, under the assumption of a locally normal distribution of orbital solutions e around e⋆ (e.g., Milani & Gronchi 2010). In our case, we used information provided by the AstDyS website for MJD epoch 57 400.0, and e = (a,k,h,q,p,λ) is a vector of equinoctical orbital elements (see Table 1). An infinitesimal probability dN(e) of finding the correct orbit solution in a volume d 6e around e is therefore given by dN(e) = p(e) d 6e, where the probability density p(e) reads ![\begin{equation} p(\vec{e}) = \frac{1}{(2\pi)^3\tens{\Sigma}^{\frac{1}{2}}}\,\exp\left[-\frac{1}{2} \left(\vec{e} - \vec{e^\star}\right)^\mathrm{T} \tens{\Sigma}^{-1} \left(\vec{e} - \vec{e^\star}\right)\right]\! . \label{nd} \end{equation}](/articles/aa/full_html/2016/11/aa29290-16/aa29290-16-eq145.png) (1)While the nominal solution e⋆ is the most likely representation of the truth, some of the close-by solutions e may also have nearly the same weight. Only those solutions e that deviate too much from e⋆ should be rejected.
(1)While the nominal solution e⋆ is the most likely representation of the truth, some of the close-by solutions e may also have nearly the same weight. Only those solutions e that deviate too much from e⋆ should be rejected.
When searching for the asteroid pair origin by numerical propagation of their orbits backward in time, we therefore need to consider a multitude of possible initial conditions at T0. We use the word “clones” for these different realizations of each of the two asteroids. The clone distribution in the orbital elements space e must be consistent with the distribution in (1). This is achieved by generating the clone elements e using 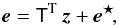 (2)with a six-dimensional vector z whose components are random deviates of the standard normal distribution, and T is a matrix satisfying TT T = Σ. We used a Cholesky decomposition to determine T from Σ (e.g., Gentle 2003; Press et al. 2007).
(2)with a six-dimensional vector z whose components are random deviates of the standard normal distribution, and T is a matrix satisfying TT T = Σ. We used a Cholesky decomposition to determine T from Σ (e.g., Gentle 2003; Press et al. 2007).
For problem (ii), that is, for the accuracy of the orbit propagator, we note that our code takes into account gravitational perturbations from planets and the most massive main belt objects (Ceres, Vesta and Pallas). We considered nominal masses for each of these perturbers, and variations due to their uncertainty were deemed negligible on the required propagation timescale ≲ 1 Myr. Moreover, the motion of both asteroids in the pair is affected by thermal accelerations known as the Yarkovsky effect (e.g., Bottke et al. 2006; Vokrouhlický et al. 2015). The Yarkovsky effect is a subtle non-gravitational acceleration due to recoil of photons that are thermally reradiated by the surface of the asteroid. This effect depends on a number of physical parameters such as the asteroid size, rotation period and pole orientation, surface thermal inertia, and bulk density, to mention only the most important. Unfortunately, except for rotation periods and a rough estimate of the size (Sect. 3.2), we do not have this information for either of the two components in the 87887−415992 pair. In this situation, it would be too difficult to use somewhat sophisticated formulations of the thermal accelerations (see, e.g., Vokrouhlický et al. 2000). We instead simplified the approach and empirically retained only the principal orbital perturbation that is due to the Yarkovsky effect, which is the secular change da/ dt in the semimajor axis (and the related advance in longitude in orbit, as described by Vokrouhlický et al. 2000). This was accomplished by mimicking the Yarkovsky effect with a transverse acceleration described in Farnocchia et al. (2013) (an older implementation of the same idea is provided by Vokrouhlický & Nesvorný 2008). With this approximation we did not include in our computation the off-plane component of the thermal acceleration and the related perturbations or the exact nature of short-period Yarkovsky effects. The magnitude of the empiric transverse acceleration was chosen to (i) have ∝ 1 /r2 heliocentric dependence, and (ii) resulting in the expected da/ dt value (e.g., Farnocchia et al. 2013). At the heliocentric distance of the 87887–415992 pair, the maximum semimajor axis drift value for a kilometer-sized asteroid is approximately (da/ dt)max ≃ 2 × 10-4 au Myr-1 (see, e.g., Fig. 2 in Bottke et al. 2006). Assuming a common value of the surface thermal inertia, the exact semimajor axis drift-rate for either the 87887 or 415992 asteroid reads da/ dt = (da/ dt)max cosγ/D, where γ is the rotation pole obliquity and D is the size in kilometers. For D, we used the values estimated in Sect. 3.2, but γ are not available to us at this moment. In principle, we must assume all admissible values and test the sensitivity of the results on their choice. For simplicity, we assumed an isotropic distribution of the spin axis orientation for both asteroids, which implies that cosγ in the formula for da/ dt is a random quantity with a uniform probability density distribution in the interval (−1,1). Therefore, individual realizations for da/ dt may have equally likely positive or negative values, depending on whether the asteroid rotates in a prograde or retrograde sense.
Combining the two aspects (i) and (ii) from above in this way, we propagated in our model a certain number of clone realizations for each of the asteroids in the pair. Their initial conditions were constructed by Eq. (2), and each of the clones was assumed to have a randomly chosen Yarkovsky value of da/ dt. The initial state vectors of the planets at T0 = 57 400.0 MJD epoch were taken from the JPL ephemerides file, and the state vectors of the three massive main belt objects, Ceres, Vesta, and Pallas, from the AstDyS solution. We used the well-tested computer code swift3, extended by our subroutines to account for the thermal accelerations. We used a three-day propagation time step, and typically let the integration extend to 1−3 Myr maximum backward in time when exploring the origin of the 87887−412992 pair. We complemented the basic version of the swift software with analysis subroutines specific to the asteroid pairs, such as computation of distance and relative velocity for a selected couple of clones. The time step should be short enough to avoid missing the close encounters: anticipating a relative velocity of about ≃ 1 m s-1, the bodies move by ≃ 260 km in one time step. This is less than the estimated Hill radius of the parent body of this pair, and also less than the expected accuracy of our propagation model.
 |
Fig. 4 Repetition of the geometric configuration of the nominal orbits for (87887) 2000 SS286 and (415992) 2002 AT49 (no thermal accelerations included in this run; note the logarithmic scale of the abscissa). The top panel shows the mutual distance of the two asteroids, the bottom panel shows their relative velocity. Both functions have deep minima at conjunctions. The first occurs ~7.42 kyr ago, followed by the second at ≃ 257 kyr after completing one synodic cycle of their relative motion. The gray level line at the top shows a distance of 3 RHill, while that at the bottom shows Vesc of the parent body. |
4.2. Results: clone convergence in the past
To illustrate the effect of near-periodic repetition of close-by configurations of the two asteroids in the pair, we first numerically integrated the nominal orbits of 87887 and 412992 without the thermal accelerations. At every three-day time step, we computed the mutual distance and relative velocities of the two asteroids. Figure 4 shows the result. The first, deep encounter is recorded ≃ 7.42 kyr ago, reaching a minimum mutual distance of ≃ 3900 km and a relative velocity of ≃ 0.14 m s-1. This was the event that classified this pair to be considered as a candidate for a very young pair mentioned in Sect. 2. When the propagation is continued backward in time, the asteroids separate in space for nearly 250 kyr before experiencing another close encounter at ≃ 257 kyr. This time the minimum recorded distance was ≃ 11 000 km and relative velocity ≃ 1.52 m s-1. The situation is then repeated typically four more times in the last 1 Myr.
 |
Fig. 5 Top: minimum distance between clones of (87887) 2000 SS286 and (415992) 2002 AT49 during different synodic cycles in the past (each of the asteroids was represented by 1000 clones, and we considered all possible combinations between them). The first deep encounter is well localized at some 7.4 kyr ago, but the subsequent encounters of different combinations of clones are spread in time starting from ≃ 45 kyr ago. Bottom: relative velocity of the clones at the moment of their nearest encounter from the top panel. Importantly, all possible clone combinations have an extremely low relative velocity (≲ 0.18 m s-1) during their first encounter in the past. The gray solid line at the top shows a distance of 3 RHill, while that at the bottom shows Vesc of the parent body. The gray dashed line at the bottom indicates that the 0.18 m s-1 value is not exceeded by any of the clone pairs during their first encounter. |
The same pattern would obviously be repeated when various clones of the two asteroids were used instead of their nominal realizations (with now the thermal effects included as well). We found that the characteristics of the first deep minimum at ≃ 7.4 kyr remain approximately the same for all possible clone combinations, those of the earlier encounters start to differ significantly. Already the epoch of the second encounter in the past is not always near ≃ 257 kyr, but depending on the strength of the Yarkovsky effect, it could take part any time between ≃ 45 kyr and ≃ 500 kyr. This is illustrated at Fig. 5. In this simulation we considered 1000 clones of each of the asteroids in the pair. The clones sampled the uncertainty hyper-ellipsoid of the initial data e at T0 and each having assigned some random value of the Yarkovsky effect. At every time step, that is, at every three-day interval, we checked the mutual distance of all 106 possible combinations of the clones. We monitored the deep close encounters illustrated in Fig. 4, and for each of them we recorded the relative velocity of the clones.
By focusing on the first deep encounter between the clones, we note that it occurred in a rather short time interval between 7.1 and 7.8 kyr ago. The relative youth of this event implies that all 106 clone combinations have a very similar minimum distance and relative velocity with only a minor spread. All minimum relative velocities are extremely low, with a floor limit of 0.18 m s-1. Some may reach a mm s-1 level. These values are typically an order of magnitude lower than the estimated escape velocity ≃ 1.5 m s-1 from the parent body of the pair. The minimum recorded distances between the clones range from ≃ 900 km to ≃ 4800 km. These values are slightly higher than the estimated radius of the Hill sphere RHill of the parent body, namely ≃ 600 km. However, we should allow some tolerance in missing the ideal convergence. This is because our propagation model is not perfect, and incorrectly modeled effects at the level of ≃ 3 RHill may easily originate from (i) representing the complete model of the Yarkovsky effect with only the transverse acceleration, or (ii) a mismatch in modeling the short-periodic variations using the swift symplectic code that incorporates the Wisdom-Holman mapping algorithm (Wisdom & Holman 1991). Additionally, at such a close distance we need to take the mutual gravitational interaction of the two asteroids in the pair into account, which would help to bring them closer to each other. Empirically, we considered the ≃ 3 RHill level tolerable for the success in convergence of the clones. We thus find that about half of the clone combinations satisfy this liberal condition for the minimum distance.
Examining the second, and further, deep encounters in the past, we note that some may occur as early as ≃ 45 kyr ago. Since this is much earlier than seen for the nominal orbits (Fig. 4), for this to occur we need clones with strong Yarkovsky accelerations, especially for the smaller secondary component. Because we sampled all possible clone combinations, there are many different possibilities and the distance minima occur for basically any epoch beyond the 45 kyr time. However, many are quite distant (≳ 20 000 km) and/or occur very swiftly at relative speed of tens or even hundreds of meters per second. These cases should be considered as false. Nevertheless, close encounters are possible with distances well shorter than RHill, in our simulation some as close as ≃ 50 km that are associated with a relative velocity lower than Vesc. These solutions should be considered as valid. In terms of a fraction of tested clones, there are increasingly fewer of these successful solutions in the past. However, this is mainly an expression of the dilution of the spreading clone clouds by Keplerian shear, gravitational and non-gravitational perturbations. We recall that we used a fixed number of clones.
To conclude, both young (≃ 7.4 kyr) and old (≳ 50 kyr) solutions are possible in principle. Unless we can determine more arguments and tests, we cannot a priori decide which one is correct.
4.3. More results: lessons from integration of synthetic pairs
In an attempt to solve the true-age problem, we conducted the following numerical experiment. In brief, the main and severe constraint we used is the extremely low encounter velocity ≲ 0.18 m s-1 of all possible clone combinations during the first deep encounter ≃ 7.4 kyr ago. As a result, it must have occurred with 100% likelihood. Any solution that would postulate an older age for this pair would need to satisfy the ≃ 7.4 kyr velocity constraint during the subsequent deepest encounter. In what follows, we show that it is very difficult to meet this requirement.
 |
Fig. 6 Results from our numerical experiment with 240 000 synthetic pairs 87887–415992 separated at T0 = 57 400.0 epoch by a low relative velocity vej. We numerically propagate their orbits until their configuration was repeated in a deepest close encounter at time t at which the relative velocity of the two asteroids is venc (we recall that the integration time span was 3 Myr in which the deepest encounter was sought). The top panel shows venc vs. t. The bottom panel shows vej vs. venc. |
To shed a more quantitative light on this problem, we performed a numerical simulation of 240 000 synthetic secondaries ejected from the primary at T0 = 57 400.0 MJD epoch. We assumed that the synthetic secondaries (representing 415 992) were separated from the primary (representing 87 887) in a random direction in space and with a relative velocity vej in some interval of values (0,Vmax). We nominally took Vmax = Vesc, where Vesc ≃ 1.5 m s-1 is the escape velocity from the parent asteroid of the pair, but for the sake for probing our results in more detail, we also considered lower Vmax values. With this procedure we created 240 000 synthetic pairs and additionally gave the primary and secondary components random values of the Yarkovsky drift-rate da/ dt within the respective interval of values. The pairs were numerically propagated to the future for 3 Myr, and we monitored their relative configuration, focusing particularly on minima of distance during the synodic cycles. We recorded the absolute minimum of the relative velocity venc at which the two clones encountered and the time t when it occurred. Most often, this was already during the first encounter, but in some cases it also occurred during the subsequent encounters.
These results allowed us to characterize the probability dP that the two asteroids in the pair will encounter with relative velocity (venc,venc + dvenc) in time (t,t + dt) after their separation with relative velocity (vej,vej + dvej): 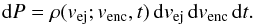 (3)Here ρ(vej;venc,t) is the associated probability density. We imposed the normalization
(3)Here ρ(vej;venc,t) is the associated probability density. We imposed the normalization 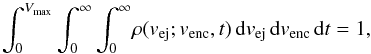 (4)where in practice we replaced infinity in the integral bounds by some high values attained in our simulation. Obviously, we can only approximate the formally infinitesimal quantities with their finite realizations, such as
(4)where in practice we replaced infinity in the integral bounds by some high values attained in our simulation. Obviously, we can only approximate the formally infinitesimal quantities with their finite realizations, such as 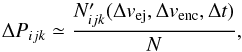 (5)where
(5)where 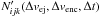 is the number of recorded events in the finite intervals (vej i,vej i + Δvej), (venc j,venc j + Δvenc) and (tk,tk + Δt), and N being number of all events. We had Δvej = Δvenc = 0.04 m s-1 and Δt = 10 kyr. The indexes i, j, and k span positive numbers until the parameter (velocities or time) fills the necessary interval of values with Δ steps.
is the number of recorded events in the finite intervals (vej i,vej i + Δvej), (venc j,venc j + Δvenc) and (tk,tk + Δt), and N being number of all events. We had Δvej = Δvenc = 0.04 m s-1 and Δt = 10 kyr. The indexes i, j, and k span positive numbers until the parameter (velocities or time) fills the necessary interval of values with Δ steps.
Figure 6 shows our raw data: (i) the top panel shows venc as a function of t, and (ii) the bottom panel shows venc as a function of vej. There are two clear trends. First, venc generally increases with t because of the cumulative effect of gravitational and non-gravitational perturbations in the orbits of the two components in the synthetic pairs. Second, venc is nearly always higher than vej, only in very rare cases is the opposite true. This is again an expression of orbital perturbations. We added these data into our procedure to estimate the probability ΔPijk from Eq. (5), and used it to evaluate the following hypothesis: what is the probability that upon separation of the two components with vej in the interval (0,Vmax) they encounter each other at any time in the future with a relative velocity venc in the interval (0,Vcut). We set Vcut = 0.18 m s-1 because this is the hard limit of the encounter velocity of 87887–415912 during their approach ≃ 7.4 kyr ago (see Sect. 4.2). We tested both Vmax = Vesc, for which we have 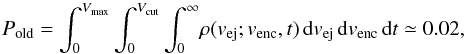 (6)and also strengthened the case Vmax = 0.18 m s-1, for which we have
(6)and also strengthened the case Vmax = 0.18 m s-1, for which we have 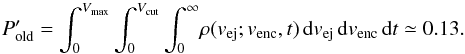 (7)We note that in both cases, we recalculated the proper normalization of the probability density ρ(vej;venc,t) using Eq. (4).
(7)We note that in both cases, we recalculated the proper normalization of the probability density ρ(vej;venc,t) using Eq. (4).
As a sanity check, we now pushed the procedure and determined the Vmax value at which the probability of the old solution Pold from Eq. (6) increases to 50%. We ran this test and found that Vmax would need to be as low as ≃ 0.02 m s-1. While not impossible, this value is about an order of magnitude lower than statistically expected from the separation of the two components in pairs (see, e.g., Jacobson & Scheeres 2011).
Our results in Eqs. (6) and (7) may be expressed in simple words: separating the asteroids by a low relative velocity, orbit perturbations typically act to increase it significantly during the next closest encounter after completing one (or sometimes more) synodic cycle. There is only a ≃ 2% chance of meeting at 0.18 m s-1 when the initial separation extended to Vesc, and this chance increases to only ≃ 13% at 0.18 m s-1 when the initial separation was smaller or equal to this value. Additionally, we note that we did not use the fact that the older age solutions of the 87887–415992 pair preceded the young age by at least 37 kyr (Fig. 5). If this constraint is used, then the probability of the older age would decrease even more.
Therefore, we may conclude that it is very unlikely that the asteroid pair 87887–415992 has an age ≳ 10 kyr and the two components underwent only a close fly-by with an extremely slow relative velocity ≃ 7.4 kyr ago. Instead, this nearest encounter in the past is their true moment of origin.
4.4. More results: analysis of the young-age solution
We now return to our simulations of 87887–415912 past convergence and investigate the encounter conditions at ≃ 7.4 kyr. In particular, we use the information about the given Yarkovsky drift-rate in semimajor axis da/ dt to each of the clones. We recall that da/ dt ∝ cosγ, where γ is the obliquity of the spin axis. Thus the positive or negative sign of da/ dt unambiguously implies either prograde or retrograde sense of rotation of the clone. Therefore, it is interesting to consider the statistics of successfully converging solutions in terms of this parameter because it could tell us about expected rotation state of the asteroid. We note, for instance, that this method has led Vokrouhlický et al. (2011) to predict that the smaller component in the 6070−54827 pair should rotate in a retrograde sense.
Dependence of the age of the (87887) 2000 SS286 and (415992) 2002 AT49 asteroid pair on obliquities γ1 and γ2 of the primary and secondary component.
We note that all 106 clone combinations converged within ≃ 8 RHill ≃ 4800 km distance. Using this largest set of the converging cases, we find no preference between the four combinations of prograde and retrograde modes of the clones of 87887 vs. 415992, however. We only note that solutions for prograde-rotating clones of 415992 occur slightly earlier (by about 0.3 kyr) than those for retrograde-rotating clones of 415992. The results are summarized in Table 4 and Fig. 7.
We also analyzed smaller subsets of the convergence cases that approached to a closer distance. For instance, considering only those that approached at ≃ 3 RHill ≃ 1800 km, little more than one tenth of the cases, or even less, such as ≃ 2 RHill ≃ 1200 km. Unfortunately, no preference in spin axis orientation for the primary or secondary clones was detected. There was always an about equal chance for all four combinations. We assume that this negative result, as compared to that for the 6070−54827 pair, is due to the quite smaller size of the asteroids constituting the pair.
 |
Fig. 7 Statistical distribution of (87887) 2000 SS286 and (415992) 2002 AT49 solutions converging within the past 10 kyr. We select all Ntot = 106 possible clone combinations that approached less than ≃ 8 RHill ≃ 4800 km. The abscissa is the time in kyr, the ordinate gives the number of converging solutions grouped in 20 yr bins. The solutions are grouped into four cases of possible combinations of rotation sense of the clones for each of the components in the pair. The sign of cosγ (γ is the obliquity) serves as a indicator of the rotation sense (see the text). The upper two panels are for secondary clones that rotate in a prograde sense (cosγ2> 0), the lower two panels show the reverse. |
5. Discussion and conclusions
We have shown that determining the age of an asteroid pair might not be as straightforward as it looks and in principle might need detailed considerations. In most of the cases for which our message is irrelevant, the orbit uncertainty of the two components is too large and a continuum of ages from some epoch in the past is possible (see, e.g., the case of asteroids (21436) Chaoyichi and (334916) 2003 YK39 in Fig. 2 of the supplementary materials of Pravec et al. 2010). However, there are cases of more accurate orbits where the age solutions might be localized in time into separate intervals reflecting the synodic cycles of the relative motion of the two asteroids in the pair. These situations require careful analysis to distinguish between the different possibilities. Previously reported age solutions for the pairs did not pay close attention to this aspect, and some of them perhaps need to be verified or reanalyzed (including the most famous case of (6070) Rheinland and (54827) 2001 NQ24).
The second implication of our work is relevant to the general picture of asteroid pair formation. In particular, does the relative rarity of known asteroid pairs with ages younger than 10 kyr fit the general idea of their formation by rotational fission (Pravec et al. 2010)? We addressed this question using approximate arguments in two steps.
First, we checked that a collisional origin is not a likely model for a very recent origin of the 87887−415992 pair. Bottke et al. (2005) developed a model that described the collisional evolution of the asteroid main belt. One of the results that could be inferred from their approach, is a statistically mean timescale Tdisr for a disruption of a body with size D among the current population of asteroids in the belt. As we were interested in the origin of the 87887–415992 pair, we chose D ≃ 2.5 km and found that Tdisr ≃ 15 kyr. We note that the H ≃ 15.3 mag population of asteroids in the inner main belt may be close to completeness, but this is not the case in the outer main belt where the majority of asteroids reside. Therefore we cannot assume that we know all events that have led to the origin of our studied pairs, since a number of them may still have been missed. By comparing the known population of H ≃ 15.3 in the MPC catalog to their expected number by Bottke et al. (2005) (assuming a global mean geometric albedo of ≃ 0.125), we note a factor of ≃ 2 incompleteness. This means that instead of recording every event, we statistically expect detection of every second event, with a frequency of ≃ 30 kyr, for example. Our pair 87887–415992 would have been anomalously young in this model.
We now try to determine how well the formation of the 87887–415992 pair in the last 10 kyr fits within the rotational fission model (Pravec et al. 2010). We should point out that we currently do not have a rigorous procedure or model that would include all participating factors and biases. Our computation should therefore be considered more as an estimate.
We start with the results in Pravec et al. (2008), who analyzed the rotation-rate f distribution N(f) of small asteroids in the main belt and Hungaria regions. They found that N(f) is basically flat, except for an excess of slow rotators with f ≤ 1 cycle per day, where they found about twice as many objects compared to bins corresponding to f ≥ 1 cycle per day frequencies. We estimate that on a timescale over which the YORP effect doubles f, about one-fourth of the population may reach the critical fission limit. However, about half of the asteroids in these bins may decelerate, rather than accelerate their rotation in the model of Pravec et al. (2008). This decreases the fraction to about one-eighth. We should also consider that reaching the estimated fission frequency may not yet be enough, but still a certain time may be needed to mechanically break the body. We do not have a quantitative estimate in this respect, therefore we assume another factor of 2−5 in the population. We thus estimate that about one in 16 to 40 of objects in the asteroid population at small sizes is prone to rotationally fission within the estimated doubling timescale by the YORP effect.
Next, we considered results from Čapek & Vokrouhlický (2004), who computed the strength of the YORP effect for a large sample of asteroids of various shapes. Taking their results for high surface inertia ≃ 130 [SI units], which is appropriate for small asteroids (e.g., Delbò et al. 2007), we concluded that a characteristic doubling timescale for D ≃ 2.5 km asteroids in the main belt is ≃ 20 Myr. Finally, we turned again to the results of Bottke et al. (2005), who showed there are about 120 thousands main belt bodies in their 2.45 km size bin. We found above that about 1/40 to 1/16 of them may be prone to rotationally fission, which is ≃ 3−7.5 thousand. As a result, one such event is statistically expected every ≃ 2.5−6.5 kyr (if evenly distributed). As we expect an observational incompleteness of a factor ≃ 4−9 for these events, however, we estimated that our records should include about one event ≃ (4−9) × (2.5−6.5)/2 ≃ 5−30 kyr old (we note that above we mentioned a population incompleteness of ≃ 2 for 2−2.5 km bodies across the main belt; in pairs, we must find both components, hence the incompleteness factor squares, and the secondary may be slightly smaller than the primary, which leads to a higher incompleteness factor in the population). This is close to the age we determined for the 87887–415992 pair and also because we are currently not aware of more events of that young age. We note that if some of the pairs mentioned in Sect. 2 were to be younger than 10 kyr, which we deem unlikely, the overall conclusions from our study would not be changed. We may therefore conclude that the ≃ 7 kyr age of the youngest known asteroid pair in the belt with a parent body of ≃ 2.5 km size agrees well with the fission model “powered” by the YORP effect.
We finally note that several cases of asteroid activity, such as dust-tail formation or a split into a number of small fragments, were reported over the past decade (e.g., Jewitt et al. 2015, and references therein). It is possible that some of these events were triggered by rotational fission, but by their nature they seem to differ from the generic population of asteroid pairs discussed in this paper. More likely, they correspond to a sudden activation of primitive, cometary-like bodies. In contrast, asteroid pairs are found equally well in all spectral groups of asteroids, and typically produce several near-equal size components.
Acknowledgments
We thank the referee, whose comments helped us to improve the original version of this paper. This work was supported by the Czech Science Foundation (grant P209-12-0229). The work at Modra was supported by the Slovak Grant Agency for Science VEGA (Grant 1/0670/13).
References
- Bottke, W. F., Durda, D. D., Nesvorný, D., et al. 2005, Icarus, 179, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Bottke, W. F., Vokrouhlický, D., Rubincam, D. P., & Nesvorný, D. 2006, Ann. Rev. Earth Planet. Sci., 34, 157 [Google Scholar]
- Čapek, D., & Vokrouhlický, D. 2004, Icarus, 172, 526 [NASA ADS] [CrossRef] [Google Scholar]
- Carry, B. 2012, Planet. Space Sci., 73, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Delbò, M., dell’Oro, A., Harris, A. W., Mottola, S., & Mueller, M. 2007, Icarus, 190, 236 [NASA ADS] [CrossRef] [Google Scholar]
- Duddy, S. R., Lowry, S. C., Wolters, S. D., et al. 2012, A&A, 539, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duddy, S. R., Lowry, S. C., Christou, A., et al. 2013, MNRAS, 429, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Farnocchia, D., Chesley, S. R., Vokrouhlický, D., et al. 2013, Icarus, 224, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Galád, A. 2012, A&A, 548, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gentle, J. E. 2003, Random Number Generation and Monte Carlo Methods (New York: Springer) [Google Scholar]
- Harris, A. W. 1994, Icarus, 107, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, A. W., Young, J. W., Bowell, E., et al. 1989, Icarus, 77, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Heck, P. R., Schmitz, B., Baur, H., Halliday, A. N., & Wieler, R. 2004, Nature, 430, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Jacobson, S. A., & Scheeres, D. J. 2011, Icarus, 214, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Jewitt, D., Hsieh, H., & Agarwal, J. 2015, in Asteroids IV, eds. P. Michel, F. E. DeMeo, & W. F. Bottke, 221 [Google Scholar]
- Knežević, Z., & Milani, A. 2000, Celest. Mech. Dyn. Astron., 78, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Knežević, Z., Lemaître, A., & Milani, A. 2002, in Asteroids III, eds. W. F. Bottke, A. Cellino, P. Paolicchi, & R. P. Binzel, 603 [Google Scholar]
- Landolt, A. U. 1992, AJ, 104, 340 [NASA ADS] [CrossRef] [Google Scholar]
- Masiero, J. R., DeMeo, F. E., Kasuga, T., & Parker, A. H. 2015, in Asteroids IV, eds. P. Michel, F. E. DeMeo, & W. F. Bottke, 323 [Google Scholar]
- Milani, A., & Gronchi, G. F. 2010, Theory of Orbital Determination (Cambridge: Cambridge University Press) [Google Scholar]
- Milani, A., Cellino, A., Knežević, Z., et al. 2014, Icarus, 239, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Moskovitz, N. A. 2012, Icarus, 221, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvorný, D., & Morbidelli, A. 1998, AJ, 116, 3029 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvorný, D., Vokrouhlický, D., & Bottke, W. F. 2006, Science, 312, 1490 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvorný, D., Vokrouhlický, D., Morbidelli, A., & Bottke, W. F. 2009, Icarus, 200, 698 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvorný, D., Brož, M., & Carruba, V. 2015, in Asteroids IV, eds. P. Michel, F. E. DeMeo, & W. F. Bottke, 297 [Google Scholar]
- Polishook, D. 2014, Icarus, 241, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Polishook, D., Moskovitz, N., Binzel, R. P., et al. 2014a, Icarus, 233, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Polishook, D., Moskovitz, N., DeMeo, F. E., & Binzel, R. P. 2014b, Icarus, 243, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Pravec, P., Šarounová, L., & Wolf, M. 1996, Icarus, 124, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Pravec, P., Hergenrother, C., Whiteley, R., et al. 2000, Icarus, 147, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Pravec, P., Harris, A. W., Vokrouhlický, D., et al. 2008, Icarus, 197, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Pravec, P., Vokrouhlický, D., Polishook, D., et al. 2010, Nature, 466, 1085 [NASA ADS] [CrossRef] [Google Scholar]
- Pravec, P., Harris, A. W., Kušnirák, P., Galád, A., & Hornoch, K. 2012, Icarus, 221, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Pravec, P., Kušnirák, P., Hornoch, K., et al. 2013, IAU Circ., 9268 [Google Scholar]
- Pravec, P., Scheirich, P., Kušnirák, P., et al. 2016, Icarus, 267, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 2007, Numerical Recipes: The Art of Scientific Computing (Cambridge: Cambridge University Press) [Google Scholar]
- Rożek, A., Breiter, S., & Jopek, T. J. 2011, MNRAS, 412, 987 [NASA ADS] [Google Scholar]
- Schmitz, B., Peucker-Ehrenbrink, B., Lindström, M., & Tassinari, M. 1997, Science, 278, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Schmitz, B., Tassinari, M., & Peucker-Ehrenbrink, B. 2001, Earth and Planetary Science Letters, 194, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Vokrouhlický, D. 2009, ApJ, 706, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Vokrouhlický, D., & Nesvorný, D. 2008, AJ, 136, 280 [NASA ADS] [CrossRef] [Google Scholar]
- Vokrouhlický, D., & Nesvorný, D. 2009, AJ, 137, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Vokrouhlický, D., Milani, A., & Chesley, S. R. 2000, Icarus, 148, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Vokrouhlický, D., Ďurech, J., Michałowski, T., et al. 2009, A&A, 507, 495 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vokrouhlický, D., Ďurech, J., Polishook, D., et al. 2011, AJ, 142, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Vokrouhlický, D., Bottke, W. F., Chesley, S. R., Scheeres, D. J., & Statler, T. S. 2015, in Asteroids IV, eds. P. Michel, F. E. DeMeo, & W. F. Bottke, 509 [Google Scholar]
- Wisdom, J., & Holman, M. 1991, AJ, 102, 1528 [NASA ADS] [CrossRef] [Google Scholar]
- Wolters, S. D., Weissman, P. R., Christou, A., Duddy, S. R., & Lowry, S. C. 2014, MNRAS, 439, 3085 [NASA ADS] [CrossRef] [Google Scholar]
- Zappalà, V., Cellino, A., Farinella, P., & Knežević, Z. 1990, AJ, 100, 2030 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Dependence of the age of the (87887) 2000 SS286 and (415992) 2002 AT49 asteroid pair on obliquities γ1 and γ2 of the primary and secondary component.
All Figures
 |
Fig. 1 Composite light curve of asteroid (87887) 2000 SS286 from observations in 2014. |
| In the text | |
 |
Fig. 2 Composite light curve of asteroid (87887) 2000 SS286 from observations in 2016. |
| In the text | |
 |
Fig. 3 Composite light curve of asteroid (415992) 2002 AT49 from observations in 2016. |
| In the text | |
 |
Fig. 4 Repetition of the geometric configuration of the nominal orbits for (87887) 2000 SS286 and (415992) 2002 AT49 (no thermal accelerations included in this run; note the logarithmic scale of the abscissa). The top panel shows the mutual distance of the two asteroids, the bottom panel shows their relative velocity. Both functions have deep minima at conjunctions. The first occurs ~7.42 kyr ago, followed by the second at ≃ 257 kyr after completing one synodic cycle of their relative motion. The gray level line at the top shows a distance of 3 RHill, while that at the bottom shows Vesc of the parent body. |
| In the text | |
 |
Fig. 5 Top: minimum distance between clones of (87887) 2000 SS286 and (415992) 2002 AT49 during different synodic cycles in the past (each of the asteroids was represented by 1000 clones, and we considered all possible combinations between them). The first deep encounter is well localized at some 7.4 kyr ago, but the subsequent encounters of different combinations of clones are spread in time starting from ≃ 45 kyr ago. Bottom: relative velocity of the clones at the moment of their nearest encounter from the top panel. Importantly, all possible clone combinations have an extremely low relative velocity (≲ 0.18 m s-1) during their first encounter in the past. The gray solid line at the top shows a distance of 3 RHill, while that at the bottom shows Vesc of the parent body. The gray dashed line at the bottom indicates that the 0.18 m s-1 value is not exceeded by any of the clone pairs during their first encounter. |
| In the text | |
 |
Fig. 6 Results from our numerical experiment with 240 000 synthetic pairs 87887–415992 separated at T0 = 57 400.0 epoch by a low relative velocity vej. We numerically propagate their orbits until their configuration was repeated in a deepest close encounter at time t at which the relative velocity of the two asteroids is venc (we recall that the integration time span was 3 Myr in which the deepest encounter was sought). The top panel shows venc vs. t. The bottom panel shows vej vs. venc. |
| In the text | |
 |
Fig. 7 Statistical distribution of (87887) 2000 SS286 and (415992) 2002 AT49 solutions converging within the past 10 kyr. We select all Ntot = 106 possible clone combinations that approached less than ≃ 8 RHill ≃ 4800 km. The abscissa is the time in kyr, the ordinate gives the number of converging solutions grouped in 20 yr bins. The solutions are grouped into four cases of possible combinations of rotation sense of the clones for each of the components in the pair. The sign of cosγ (γ is the obliquity) serves as a indicator of the rotation sense (see the text). The upper two panels are for secondary clones that rotate in a prograde sense (cosγ2> 0), the lower two panels show the reverse. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


