| Issue |
A&A
Volume 689, September 2024
|
|
|---|---|---|
| Article Number | A291 | |
| Number of page(s) | 11 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202450725 | |
| Published online | 19 September 2024 | |
Asteroid pairs: Survey of the inner main belt
Institute of Astronomy, V. N. Karazin Kharkiv National University,
35 Sumska Str.,
Kharkiv
61022,
Ukraine
Received:
14
May
2024
Accepted:
27
July
2024
Context. An asteroid pair forms when an asteroid splits into two unbound fragments because of collision, rotational fission, or binary system decay. The two components of the asteroid pair share similar physical properties and their orbits converge when integrated into the past. Currently, 268 asteroid pairs are known, and new pairs are discovered alongside the continuous discovery of new asteroids.
Aims. We conducted a survey in the inner asteroid belt to find new asteroid pairs, estimated their age, and classified their physical properties. As presently no M-type asteroid pairs are known, we also conducted a specialized survey of them.
Methods. We preselected asteroid pair candidates based on their distances in the five-dimensional space of osculating orbital elements. We created multiple clones within the uncertainties of their orbital elements and conducted their backtrack integration into the past. We searched for convergence of their clones at close spatial points with small relative velocities, the distribution of which determines the pair formation age.
Results. We find 40 new asteroid pairs, thus increasing the total number of known pairs by 15%. One of the newly discovered pairs, 469759 - 2016 QZ 123, with an age of 2.6−0.2+0.7 kyr is now the third-youngest known asteroid pair. We studied the influence of the mutual gravitation of pair components on the process of their evolution and successfully observed the gravitational catching of the two pair members in the past. As a byproduct of pair search, we find eight asteroids connected in a cluster with an age of 76−25+15 kyr that belongs to the Phocaea family and incorporates one previously known asteroid pair. We confirm the convergence of ten asteroid pairs discovered in our previous research and improve their age estimates. We observed a deficiency of M-type asteroid pairs, and therefore conducted a dedicated search for M-type pairs, but found none.
Key words: celestial mechanics / minor planets, asteroids: general
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
An asteroid pair typically consists of two asteroids with similar heliocentric orbits, often believed to be fragments from a larger parent body that underwent a breakup event, such as binary split (Cuk 2007), asteroid collisions (Vokrouhlický & Nesvorný 2008), or rotational fission (Pravec et al. 2010), the latter likely being the dominant route. While components of a newly formed asteroid pair have very similar heliocentric orbits, they are no longer gravitationally bound, and perturbations from planets and nongravitational forces cause divergence of their orbits. One of the most challenging tasks is to identify asteroids that are members of the same asteroid pair.
In our previous work, Kyrylenko et al. (2021), we adopted an existing approach to identifying and verifying asteroid pairs and successfully tested it on a sample of known pairs. We then applied the same method to search for and identify candidates in the inner part of the main asteroid belt, resulting in the discovery of ten new asteroid pairs.
Since then, further asteroid pairs have been discovered. Most notable is the study by Vokrouhlický et al. (2022) of an extremely young asteroid pair, (458271) 2010 UM26 and 2010 RN221, with an estimated separation time of only 2050 years ago. The study shows that taking into account the mutual gravitational attraction of the components of these pairs is crucial to understanding their evolution and age estimation. A study by Fatka et al. (2023) is dedicated to another very young pair, 2019 PR2-2019 QR6, where the dynamic evolution is also heavily influenced by the mutual gravitational attraction of the components. A work by Vokrouhlický et al. (2024) added new members to known asteroid clusters and young asteroid families.
Despite the rigorous search for asteroid pairs already performed by various authors, the search for new pairs is timely. First, as new asteroids are discovered, there is a chance that they will pair with the known asteroids. Second, as the arc of observation and the precision of the measured positions of known asteroids increase, their improved orbital elements can lead to close encounters, previously overlooked because of their older, more uncertain orbits. This motivates us to continue searching for new asteroid pairs.
We present the results of our new survey of the inner part of the main asteroid belt. Section 2 focuses on our approach to searching for and identifying asteroid pairs and their further verification. Section 3 is dedicated to our results, such as the new asteroid pairs and new asteroid cluster, analysis of their dynamical history, formation age, and physical properties.
2 Methods
2.1 Preselecting candidates
The initial task in searching for asteroid pairs is to select those asteroids from the known asteroid population that can potentially be members of asteroid pairs. For this, the candidate asteroid pairs are preselected in the 5D phase space of Keplerian orbital elements using a metric that is defined by the following formula (Vokrouhlický & Nesvorný 2008):
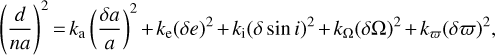 (1)
(1)
where a is the semi-major axis [AU], e is eccentricity, i is inclination [rad], ϖ is longitude of periapsis [rad], Ω is the longitude of the ascending node [rad], n is the mean motion of an asteroid [rad/day], and (δa, δe, δ sin i, δϖ, δΩ) is the separation vector of the neighboring bodies in the phase space. Following Nesvorný & Vokrouhlický (2006), we adopted the following values of the coefficients for our computations: ka = 5/4, ke = ki = 2, and kΩ = kϖ = 10−4.
The resulting value is the phase distance between two asteroids, which indicates their orbit similarity. Using osculating orbital elements ensures we get potentially young asteroid pairs with ages of up to 1 million years (Nesvorný & Vokrouhlický 2006). By this time limit, gravitational shearing and nongravi-tational forces should have mostly erased the similarity between the osculating orbits. In our search, we limited ourselves to a phase distance of d ≤ 25 m/s, resulting in 421 candidates within the 1.9–2.5 au range in the semi-major axis, corresponding to the inner part of the main asteroid belt.
The osculating Keplerian orbital elements of asteroids for our search are provided by the JPL Horizons system1. The values of orbital elements are given for the same epoch. To get information about the existing relationship between asteroids, we used publicly available databases. Data from the Asteroid Families Portal (AFP)2 and AstDyS portal were used to get information on family membership for asteroids, while data from the Johnston database (Johnston 2024) were used to exclude known asteroid pairs.
2.2 Numerical modeling
We then checked the selected candidates in numerical simulations, which allowed us to perform iterative backtrack integration of body dynamics to calculate their state in the past. As the number of selected candidates is large, an efficient approach is required to check them within a reasonable computational time. For this, we adopted the following two-step scheme: first we perform a quick precheck of a candidate pair with a small number of clones to see whether or not it converges in the past and estimate the time of the convergence; we then perform a simulation with a large number of clones and enhanced accuracy to get more accurate results.
To achieve this, a combination of two packages for N-body integration is used: Rebound and Gravitational Encounters with GPU Acceleration (GENGA), both open source. Rebound is a highly modular N-body integrator (Rein & Liu 2012) that uses central processing units (CPUs) to perform integrations, allowing it to quickly perform calculations of systems that contain a relatively small number of bodies. We used this package to perform preliminary simulations for 1 million years into the past with 10 000 pairs of clones for each selected candidate pair. Simulations were performed using the Mercurius integrator, which uses the Wisdom-Holman (Rein & Tamayo 2015) symplectic integrator for stable evolution regimes and switches to the IAS15 (Rein & Spiegel 2015) integrator with an adaptive timestep to resolve close encounters correctly. The preliminary integrations are used to estimate whether or not a selected candidate meets the requirements in terms of relative distance and velocity between its components and to decide whether or not it should be chosen for the next step. It also gives an estimate of the time of the close encounters between the components.
The simulation model includes all the Solar System planets and three of the most massive asteroids in the main asteroid belt: Ceres, Vesta, and Pallas. As shown by Galád (2012), gravitational perturbations from these small planets can significantly influence the dynamics of asteroids. The planets with moons are represented by their barycenters. The model also includes the simplified general relativity corrections for gravitational forces (Tamayo et al. 2020) and the Yarkovsky non-gravitational effect, which are implemented in the Reboundx extension package for Rebound3. The Yarkovsky effect is used in its simplified form (Veras et al. 2019), and calculates the upper bound for the semi-major axis drift for a body with given parameters: bulk density p, body radius Rast, and geometric albedo pv. The resulting values are equally distributed between positive and negative drift of the semi-major axis.
If the pair successfully meets the requirements on the first step, its orbital evolution is simulated using the GENGA package (Grimm & Stadel 2014). GENGA is an N-body integrator written in CUDA-C language and utilizes graphical processing units (GPUs) instead of CPUs. The primary advantage of GPUs is that they allow the efficient integration of systems that contain a large number of massive bodies and/or test particles. In our case, components of an asteroid pair are represented by test particles that are gravitationally influenced by massive bodies and other non-gravitational forces, but do not gravitationally interact with other test particles in the system. Both of the pair components were represented by 1000 clones, which gives 106 potential pairs as a direct product. Every pair was integrated 1 million years into the past, except for the pairs that had encounters close to this time limit, in which case their simulation time was extended to 1.2–1.5 million years.
All pair candidates were integrated with the following parameters: time step of 1–3.65 days, a sixth-order integrator with eight recursion substeps. The model also includes general relativity corrections and the Yarkovsky effect in its full version based on Vokrouhlický et al. (2000) as a velocity kick. For asteroids with unknown rotation periods, we assume a uniform distribution of the rotation period from 2 to 24 hours, as most asteroids in our sample have diameters D ≥ 200 meters. The obliquity is assumed to be uniformly distributed over the sphere for asteroids with unknown pole solutions. The assumed default values of other necessary parameters – if unknown – are as follows: emissivity factor ϵ = 0.9, body density ρ = 2000kg/m3, specific heat capacity C = 500 Jkg−1K−1, albedo pv = 0.15, and asteroid thermal conductivity K = 1 Wm−1K−1
To ensure that close encounters are registered and recorded, simulations were performed using a special mode, in which test particles that represent different components of the pair are divided into separate groups (Grimm et al. 2022). This greatly speeds up integrations, as the encounters between the members of the same group are not considered. The encounters are tracked using built-in GENGA functionality based on the bounding volume hierarchy method and are recorded for subsequent analysis.
To generate clones that represent the asteroid within its orbital uncertainties, we utilize the mechanism proposed by Vokrouhlický et al. (2017). The initial orbital elements of the clones E are determined as
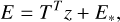 (2)
(2)
where ɀ is the six-dimensional vector, whose components are random deviations from the normal distribution, and E* is the best-fit solution. The covariance matrix T is obtained using the Cholesky decomposition method and satisfies TTT = Σ, where Σ is the normal matrix. The orbital elements, and their uncertainties were taken from the JPL Horizons system.
We are primarily interested in close encounters between the components of the pair. Such encounters can be characterized by relative distances and velocities that can be expressed in terms of the Hill sphere and escape velocity, respectively. The Hill sphere is the radius of the sphere of influence where the body’s gravitational attraction is stronger than that of the Sun, and can be calculated with the following equation:
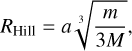 (3)
(3)
where a and m are the semi-axis and mass of the primary body, respectively, and M is the mass of the Sun.
The escape velocity is the lower bound of the speed required to escape the gravitational influence of the given body. The value of the escape velocity can be calculated as
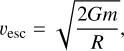 (4)
(4)
where m is the mass of the primary body and R is the radius of the body.
As both Hill sphere and escape velocity calculations require the mass of the body to be a known quantity, we estimate the mass from the radius of the body and its bulk density using the formula
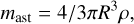 (5)
(5)
where ρ is the bulk density of the body.
If the Horizons system does not have information on the bulk density, and no information on the spectral class is available, bulk density is assumed to be 2 × 103 kg m−3. For asteroids whose radius is unknown, their radius is derived from the absolute magnitude and geometric albedo:
![${R_{{\rm{ast}}}} = {{1329} \over {2\sqrt {{p_\upsilon }} }}{10^{ - 0.2H}}[{\rm{km}}],$](/articles/aa/full_html/2024/09/aa50725-24/aa50725-24-eq8.png) (6)
(6)
where H is the absolute magnitude of the asteroid and pv is the geometric albedo of the asteroid.
Ideally, components of asteroid pairs as nongravitationally bound bodies should converge within 1 RHill, 1 vesc limits: either by having a very close encounter with distances d < 1RHill and relative sufficiently high velocity to escape the sphere of influence (v > 1 vesc), or by having an encounter with a very small relative velocity v < 1 vesc and close to the limit of the Hill sphere. As the orbits of asteroids as well as the forces acting upon the bodies are known with some degree of uncertainty, detecting such exemplary encounters for most pairs is hard to achieve. Thus, we consider a pair to experience a close encounter if d ≤ 5 RHill, v ≤ 2 vesc for the component with the largest mass. In cases where a pair shows a poorer convergence, we extend these conditions to 10 RHill and 4 vesc (Pravec et al. 2019). The time of encounters within these limits determines the time of convergence for the asteroid pair.
For the statistical estimates of pair characteristics, we adopted the approach proposed by Pravec & Vokrouhlický (2009) to estimate the background population density and statistical significance for the pair candidates. The value of P1/2 ≤ 0.05 indicates that the background population density around the pair candidate is not uniform and might contain some larger structures, such as families or clusters. P2/Np estimates the chance that the pair has a purely coincidental nature as a result of a high density of orbits surrounding the components. For values of P2/Np < 0.1, pairs are considered to be statistically significant, whereas for larger values coincidental pairs are possible.
3 Results
3.1 New asteroid pairs
Our survey yielded 40 new asteroid pairs, presented in Table A.14, thus increasing the number of known pairs from 268 Johnston (2024) to 308. For most of the new pairs, the second component is a newly discovered asteroid that was unknown or had a poorly constrained orbit at the time of the previous asteroids pair searches (e.g., Pravec et al. 2019; Kyrylenko et al. 2021).
For a visual representation of the results, we built two histograms for each pair. The first histogram is the time distribution of all detected encounters that satisfy close-encounter conditions. The second histogram is a distribution of close encounters as a function of relative velocity and distance in units of escape velocity and radius of the Hill sphere for the primary component.
We define three limits for the time distribution histograms: 1 RHill and 1 vesc, 5 RHill and 2 vesc, 10 RHill and 4 vesc, and select such a limit for each pair that contains at least 1000 encounters. We still keep 10RHill and 4 vesc constraints if a pair contains fewer than 1000 encounters but not fewer than 100. Pairs with fewer than 100 are considered dubious and are removed from further consideration. From each plot, the median age is determined, as well as the 5th and 95th percentiles, which serve as the error margin. The obtained ages and their errors are listed in Table A.1. The median ages of the discovered pairs range between 2.6 and 858 kyr, with about half of all pair ages being below 200 kyr. The fraction of high ages is relatively small as older pairs tend to show weaker convergence and 1000 kyr was a default limit for our integrations; although we exceeded it for some pairs if we found that the range of the encounter distribution went beyond this limit. Five pair candidates from our survey have P2/Np of between 0.145 and 0.39 but show good convergence in numerical simulations. We can divide the obtained age distributions into three loosely defined classes: unambiguous, well-defined peak (e.g., 44599 – 614882), multiple equivalent peaks (e.g., 211512 - 2014 PG94), and continuous distributions, or distribution with very strong tails stretching far into the past (e.g., 81069 - 2014 WL523). The subvariant of the last case can have a nonmonotonous, picket-fence-like structure (e.g., 111632 - 2018 QX15).
It is also interesting to consider at which distances and velocities each of the pairs converge, and we investigated this in the color maps complementary to each histogram. An ideal convergence below 1 RHill and 1 vesc is rarely achieved. Most structures seem to be stretched in the vertical direction. A possible explanation for this behavior is the fact that the Hill radius for most asteroids represents a smaller fraction of their orbital radius than the escape velocity as a fraction of orbital velocity. An exemplary case of pair convergence inside 1 RHill and 1 vesc is seen on the heat map of 469759 - 2016 QZ123.
Out of 40 pairs, 8 contain one or both of the components that are the members of asteroid families. For those where only one of the components is a member of the family, we expect the second component also to be a new member of the same family. For the pairs, we gathered all the available data on physical parameters presented in Table A.2. Only two of the pairs have spectral classes for both of the components. While available data are scarce, they allow us to make predictions about the physical properties of the components. As at least one of the components has data on the taxonomy class, we estimated diameters for the primary components via Eq. (6) using the median albedo for the corresponding class (Mainzer et al. 2011). In cases where several taxonomic classes are named, the one that stands in first position is used for our estimation.
3.2 Influence of mutual gravitation for 469759 (2005 QM29) -(2016 QZ123)
In our previous study, Kyrylenko et al. (2021), we incorporated the mutual gravitational attraction between pair components without discussing its implications on pair evolution. Subsequent investigations by Fatka et al. (2023) and Vokrouhlický et al. (2022) of the two youngest known asteroid pairs demonstrated that accounting for mutual attraction enables the observation of gravitational capture, providing compelling evidence for their common origin. In the present study, we explored the influence of mutual gravitation on the evolution of the recently discovered pair 2005 QM29 – 2016 QZ123, which currently ranks as the third youngest pair. Our findings reveal that some clones undergo mutual gravitational capture, revolving around their center of mass for 2–3 orbital periods (Fig. 1). We see that when the mutual gravitational attraction is included, the main peak does not change significantly (Fig. 2), but slightly affects the minor encounters in older ages (Fig. 3). A plausible explanation is that mutual perturbations of asteroids during the first close encounter redirect them into orbits that allow more frequent close encounters in older ages, unlike the unperturbed orbits. Although these older peaks are less probable than the most recent peak, they still provide alternative possible routes of pair formation. We advise not to disregard mutual gravity as it can cause unlikely but dramatic errors in the age determination of young pairs with very close encounters.
3.3 Cluster
Already at the stage of pair candidate preselection, we observed that some of the asteroids have more than one close neighbor. Such cases often correlate with nonuniform distribution in the space of orbital elements, which is marked with the letter “c” in Table A.1. In most cases, checking all such connections results in only one confirmed pair, except for one occasion discussed below, where we found a cluster.
At first, we found six asteroids that, pairwise, satisfied our preselection criteria d ≤ 25 m/s, and confirmed their convergence in numerical simulation. We then noticed that one of the asteroids, namely 2005 SA135, belongs to a pair published by Pravec et al. (2019), although the distance to its counterpart 21028 of 39 m/s in osculating elements exceeds our preselection criterion. In an attempt to find more cluster members, we extended our criterion to d ≤ 50 m/s and obtained three additional candidates, including 21028, raising the total number of candidates to nine. One of the new candidates, namely 2017 DC128, did not have any encounters with the other eight asteroids and was excluded from further study. A further eight asteroids listed in Table 1 had encounters that are shown in Figs. 4 and 5.
Figure 4 demonstrates the temporal distribution of pairwise encounters between the cluster members, with different colors corresponding to different pairs, where Fig. 5 serves as a legend explaining the color coding of the encounters. Most of the encounters are grouped around 50-100 kyr. The tails of the distribution are strong, but they include only a few of the supposed cluster members. If we assume that the entire cluster formed in a single disruption event, cluster ages of over 300 kyr or less than 50 kyr seem highly improbable.
Figure 5 shows the relation between asteroids in the cluster. The eight circles represent the members of the cluster. The width of the links between asteroids shows the number of encounters between clones of the corresponding asteroids. Naturally, the best connected is 1989 TO, which is the most massive member of the cluster: it has the largest radius of influence and escape velocity, and thus the convergence conditions with it are the least strict. The median convergence time is marked along each of the lines; the majority of them are clustered around 70–100 kyr with some outliers.
The simultaneous convergence of all the cluster members to close to one point in space with similar velocities would have been an indisputable argument for their common origin, but achieving such convergence at the present level of asteroid orbit uncertainties is highly improbable. The more traditional approach to dating young asteroid clusters is to search for convergence in the nodal longitude of its members. Figure 6 shows the nodal longitudes of all the suspected cluster members with respect to the biggest one, 1989 TO. We see that once again, 2017 DC128 does not converge with other members of the cluster, whereas the rest of the asteroids converge around the same time as previously estimated. We found the time at which the sum of squared differences between cluster members is minimal and repeated it for 1000 clones of cluster members. Thus we obtained the median cluster age of 76 kyr, with a 2σ range of 91 kyr to 51 kyr.
The absolute magnitudes and estimated diameters of cluster members are assembled in Table 1. The albedo is known only for the biggest asteroid, 21028 (1989 TO), but we assume that others have albedos close to it. This assumption allows us to estimate the masses of the asteroids, thus finding that 1989 TO encompasses 98.8% of the cluster mass, whereas all the other known cluster members combined represent only 1.2% of the mass. The main cluster member belongs to the Phocaea family (Pravec et al. 2019). As all the cluster members are very close in terms of their orbital elements, we can assume that the entire cluster is embedded in the Phocaea family. As (25) Phocaea is an S-type asteroid, we can assume the same type for all eight cluster members.
The rotation period of 1989 TO is 3.66 hours (Pravec et al. 2019). It is unlikely to have changed considerably since the formation of the cluster because the YORP timescale for a 6 km main-belt asteroid is about three orders of magnitude longer than the cluster age (Golubov & Scheeres 2019). During the process of cluster formation, the secondary components could not have substantially slowed down the rotation of the primary, as their combined mass is two orders of magnitude smaller than the mass of 1989 TO. Thus at the moment of the cluster formation, the rotation period of the asteroid was still much longer than the critical rotation period for S-type asteroids, which excludes the disruption of a fast rotator as a possible mechanism of cluster formation and leaves us with asteroid collision as the preferred origin of the cluster.
 |
Fig. 1 Example of a close encounter between the clones 469759 (2005 QM29) - (2016 QZ123), where the mutual gravitational attraction influences the dynamics of the pair. The encounter led to gravitational capture, and clones revolved around the center of mass for 2–3 orbital periods. |
 |
Fig. 2 Distribution of encounters during the main convergence for 469759 (2005 QM29) - (2016 QZ123), simulated with (bottom, blue) and without (top, orange) the mutual gravitational interactions between the clones. |
 |
Fig. 3 Density distribution of encounters for 469759 (2005 QM29) - (2016 QZ123), simulated with (blue) and without (orange) the mutual gravitational interactions between the clones. |
Properties of asteroid members of the cluster.
 |
Fig. 4 Time distribution of close encounters for the cluster, where encounters between members are color-coded as in Fig. 5, thus serving as a legend. |
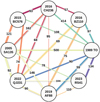 |
Fig. 5 Relation between the asteroids and components of the cluster. The colors of the links correspond to those of the histogram, while the width of connections illustrates the number of encounters between the components. The numbers on the lines represent the median of the encounter time distribution between the components. |
 |
Fig. 6 Nodal longitude difference between the primary body 21028 (1989 TO) and other components of the cluster. |
3.4 Comparison of 2021 with 2024 results
In 2021, we published an article devoted to ten asteroid pairs discovered in the inner part of the main asteroid belt. We decided to revisit those pairs and remodel them with up-to-date modeling capabilities and updated solutions for their orbital parameters. It is particularly interesting to see whether or not the previously estimated ages of asteroid pairs agree with the results based on the newest data.
First, we recalculated the phase distances dphase between the components of our old pairs using their up-to-date orbits obtained from the JPL Horizons SBDB database, which are presented in Table 2. As we can see, some of the pairs moved further, while others got closer. Interestingly, updated distances for some pairs exceed our threshold of dphase ≤ 25 m/s, and would not have been included in our present survey. This once again highlights the incompleteness of all pair searches: due to limited computational resources, only the most promising candidates are selected for further asteroid pair analysis, while many other candidates with larger d have never been rigorously checked.
In a subsequent step, the old pairs were resimulated using the new approach described in Sect. 2. All ten of the old pairs converge well in the new analysis, and most of them retain their estimated age (Fig. 7). Two of the pairs (2006 BJ193 - 2017 FE106) and (1981 VL - 2013 CX44), demonstrate significantly different ages. This difference largely results from the larger statistics available in the new analysis, which allow us to put stricter convergence conditions and retain only the best-converging clones. If the conditions are softened to former values, their distributions better resemble the old ones (pale blue histogram on Fig. 8). These inconsistent ages remind us that the selection of convergence conditions requires further elaboration.
Calculated phase distances for former 2021 orbital elements (dold) and updated orbits (dnew).
 |
Fig. 7 Age comparison between our 2021 and updated 2024 results. The x-axis shows the formation times, and the y-axis shows 2024 results calculated using updated orbital elements and new software. The red lines are the error bars for both cases. The black dashed line represents the case of perfect agreement between the results. |
3.5 Search for M-type asteroid pairs
It is interesting to investigate the taxonomy of asteroid pairs. In Fig. 9 we compare the relative abundance of different asteroid taxonomic complexes among the inner main-belt asteroid pairs with the abundance among all inner main-belt asteroids. The data on taxonomic classes and albedos were taken from Sergeyev & Carry (2021) and Sergeyev et al. (2022), via the rocks library5 (Berthier et al. 2023). Information about asteroid pairs was taken from Johnston (2024) with the addition of 40 asteroid pairs discovered in the present article. We grouped these data into four taxonomic complexes (S complex including also A and L-classes, C complex, X complex, and V class), and plotted the relative abundance of these classes among the asteroid pairs of the inner main belt (ƒpair and among all inner main belt asteroids ƒast). We further single out M-type as a subclass of X-type asteroids with moderate albedos (0.1 ≤ pv ≤ 0.3). As 46 percent of all X-type asteroids have albedos, we divide both ƒast and ƒpair for M-type by 0.46 to correct this bias. We see that for most types and complexes ƒast and ƒpair are commensurable. Still, there are no known M-type asteroids among pairs, while statistically 1–2 M-type asteroids would have been expected (the mathematical expectation is 1.5 asteroids, implying the probability of observing zero M-type asteroids by chance is ∽20%).
The M-type asteroids are thought to have a metal-rich composition and are thus expected to have mechanical and thermal properties different from stony asteroids of other taxonomic classes. The question therefore arises as to whether the absence of the M-type pairs is a pure coincidence or a result of the different physics of their formation. To address this question, we conducted a dedicated search of M-type asteroid pairs.
We started by selecting 19 asteroids in the inner part of the main belt with sufficient information to classify them as M-type. Their semi-major axes range from 2.21 to 2.47 AU and their estimated diameters are from 3.6 to 12 kilometers. For each asteroid, we found the closest neighbors based on the approach described in Sect. 2; these are shown in Table 3. As none of the asteroids had neighbors with phase distance dphase ≤ 20 m/s, we extended our search radius to the closest neighbors, most of which lie around 100 m/s. After that, we numerically backtracked the resulting pairs of asteroids into the past. For some candidates from the sample, namely 9146 - 2010 SM48 and 26526 - 2015 PT362, close encounters within 10 RHill radii were registered but with very high encounter velocities in the range of 45–70 vesc exceeding our constraints (Fig. 10). While there is a possibility that such types of encounters could indicate collisions as a mechanism of separation, at this point it is impossible to distinguish them from random flybys, which can frequently occur between neighboring asteroids. Thus, we conclude that none of the candidates had encounters that satisfied the conditions to consider them to be asteroid pairs.
 |
Fig. 8 Distribution of encounters for the pairs 1981 VL - 2013 CX44 and 2006 BJ193 - 2017 FE106. Histograms colored orange represent previous results, blue ones represent the new results with stricter convergence conditions, and pale blue are distributions of new results with former convergence conditions. |
 |
Fig. 9 Relative fraction of asteroids of different taxonomic types among inner main-belt pairs in comparison with all inner main-belt asteroids. We note that M-type asteroids are presented twice: as a part of the X-complex and as individual asteroids. |
Results on searching for M-type pairs.
 |
Fig. 10 Distribution of close encounters for 9146 - 2018 SM48 M-type pair candidate. |
4 Conclusions and discussion
The present survey of the inner asteroid belt resulted in 40 new asteroid pairs that demonstrate close convergence between pair members in backward integrations of their orbits. This survey is complete up to a distance of d ≤ 25 m/s in 5D space of osculating orbital elements, except for asteroids included in families in the Asteroid Family Portal database. All the detected pairs are relatively young (≤1.5 Myears), which is a natural consequence of their closeness in osculating orbital elements. For most of the new pairs, the secondary components are newly discovered asteroids that until very recently were either unknown or had poorly determined orbits, which explains why these pairs were absent in previous studies.
We were able to gather some information on albedos and spectral classes for some members of newly discovered pairs, although only one of the pairs has physical data for both of the components. We expect the physical affinity of the pair components, and testing this expectation in future research could provide stronger evidence for the evolutionary connection of the pair members than a dynamical study alone. Interestingly, a surprisingly high percentage of the asteroids included in the new pairs were classified as V-type. This could imply an association with the Vesta family, but the significance of this finding is open to interpretation.
In our study Kyrylenko et al. (2021), we first included the mutual gravitational attraction of the pair components without discussing the influence of this factor on the evolution of pairs. The following studies by Fatka et al. (2023) and Vokrouh-lický et al. (2022) of the two youngest known asteroid pairs showed that consideration of the mutual attraction of the components allows observation of their gravitational capture, which serves as a very strong argument for their common origin. In this study, we investigated the influence of mutual gravitation on the evolution of the newly discovered pair 2005 QM29 - 2016 QZ123, which is now the third youngest pair known to date. We find that some of the clones indeed capture each other and revolve around their center of mass for 2-3 orbital periods. Another impact of the mutual gravitation is the appearance of other, older peaks that were absent in the test-particle approach.
We see that when the mutual gravitational attraction is included, minor peaks periodically appear in older ages, which are not registered in the test-particle approach. The most plausible explanation is that mutual perturbations of asteroids during the first close encounter redirected them into orbits that allow older close encounters, unlike the unperturbed orbits. Although these older peaks are less probable than the most recent peak, they still provide alternative possible routes of pair formation. We advise not to disregard mutual gravity as it can cause unlikely but dramatic errors in the age determination of young pairs.
While searching for asteroid pairs, we found a close connection between eight asteroids and serendipitously discovered a cluster. All eight cluster members mutually converge in their state vectors around 50–100 kyr. An independent method of cluster dating via convergence in nodal longitude results in the comparable age of 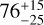 kyr. The cluster belongs to the Phocaea family, and thus is likely of S-type. The biggest cluster member 1989 TO includes about 98.8 percent of the total mass of known cluster members. The relatively slow rotation rate for 1989 TO excludes centrifugal disruption from the possible causes of cluster formation and leaves asteroid collision as the most likely formation mechanism.
kyr. The cluster belongs to the Phocaea family, and thus is likely of S-type. The biggest cluster member 1989 TO includes about 98.8 percent of the total mass of known cluster members. The relatively slow rotation rate for 1989 TO excludes centrifugal disruption from the possible causes of cluster formation and leaves asteroid collision as the most likely formation mechanism.
A dedicated search for M-type asteroid pairs singled out several mediocre pair candidates in terms of their orbital phase distance, and expectedly produced no close encounters with small relative velocities. Still, many encounters at high relative velocities of ~1000 m/s were registered. In principle, these encounters could imply pairs formed from high-speed collisions, but the significance of the obtained results is insufficient to distinguish between high-speed collisions from flybys, which are typical for many main belt asteroids.
We confirm all ten of the pairs discovered in our previous article, Kyrylenko et al. (2021). In the three years that have passed since this latter publication, the accuracy of many orbital elements has improved, as has our capability to simulate more clones. Both these factors result in closer approaches in terms of relative distance and velocity than the one described in our previous article. Still, the new age estimates for all ten pairs fall within or close to the formerly determined margins of error.
Data availability
The individual figures for the pairs (Table A.1) are available at https://zenodo.org/records/13121167
Acknowledgements
The authors thank Alexey Sergeyev for advising on the taxonomy of the asteroids from our sample, and the reviewer David Vokrouhlický for multiple insightful suggestions that significantly improved the quality of the article. This work was partially supported by the National Research Foundation of Ukraine within the framework of the project N2020.02/0371 “Metallic asteroids: search for parent bodies of iron meteorites, sources of extraterrestrial resources”.
Appendix A Additional tables
Data on new asteroid pairs.
Physical properties of the components of new pairs.
References
- Alí-Lagoa, V., & Delbo’, M. 2017, A&A, 603, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berthier, J., Carry, B., Mahlke, M., & Normand, J. 2023, A&A, 671, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cuk, M. 2007, ApJ, 659, L57 [CrossRef] [Google Scholar]
- Fatka, P., Vokrouhlický, D., Moskovitz, N. A., et al. 2023, LPICo, 2851, 2170 [Google Scholar]
- Galád, A. 2012, A&A, 548, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Golubov, O., & Scheeres, D. J. 2019, AJ, 157, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Grimm, S. L., & Stadel, J. G. 2014, ApJ, 796, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Grimm, S. L., Stadel, J. G., Brasser, R., et al. 2022, ApJ, 932, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Johnston, W. R., Asteroid pairs and clusters, last updated 11 January 2020, http://www.johnstonsarchive.net/astro/asteroidpairs.html [Google Scholar]
- Kyrylenko, I., Krugly, Y. N., & Golubov, O. 2021, A&A, 655, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mainzer, A., Grav, T., Masiero, J., et al. 2011, ApJ, 741, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Masiero, J. R., Mainzer, A. K., Grav, T., et al. 2011, ApJ, 741, 68 [Google Scholar]
- Masiero, J. R., Smith, P., Teodoro, L. D., et al. 2020, Planet Sci. J., 1, 9 [Google Scholar]
- Nesvorný, D., & Vokrouhlický, D. 2006, AJ, 132, 1950 [Google Scholar]
- Pravec, P., & Vokrouhlický, D. 2009, Icarus 204, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Pravec, P., Vokrouhlický, D., Polishook, D., et al. 2010, Nature, 466, 1085 [NASA ADS] [CrossRef] [Google Scholar]
- Pravec, P., Fatka, P., Vokrouhlický, D., et al. 2018, Icarus, 304, 110 [Google Scholar]
- Pravec, P., Fatka, P., Vokrouhlický, D., et al. 2019, Icarus 333, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Rein, H., & Liu, S.-F. 2012 A&A 537, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rein, H., & Spiegel, D. S. 2015, MNRAS, 446, 1424 [Google Scholar]
- Rein, H., & Tamayo, D. 2015, MNRAS, 452, 376 [Google Scholar]
- Rein, H., Hernandez, D. M., Tamayo, D., et al. 2019, MNRAS, 485, 5490 [Google Scholar]
- Sergeyev, A. V., & Carry, B. 2021, A&A, 652, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sergeyev, A. V., Carry, B., Onken, C. A., et al. 2022, A&A, 658, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tamayo, D., Rein, H., Shi, P., & Hernandez, D. M. 2020, MNRAS, 491, 2885 [NASA ADS] [CrossRef] [Google Scholar]
- Veras, D., Higuchi, A., & Ida, S. 2019, MNRAS, 485, 708 [NASA ADS] [CrossRef] [Google Scholar]
- Vokrouhlický, D., & Nesvorný, D. 2008, AJ, 136, 280 [Google Scholar]
- Vokrouhlický, D., Milani, A., & Chesley, S. R. 2000, Icarus, 148, 118 [Google Scholar]
- Vokrouhlický, D., Pravec, P., & Durech, J. 2017 AJ, 153, 270 [CrossRef] [Google Scholar]
- Vokrouhlický, D., Fatka P., Micheli, M., Pravec, P., & Christensen, E. J. 2022, A&A, 664, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vokrouhlický, D., Nesvorný, D., Brož, M., & Bottke, W. F. 2024, A&A, 681, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
JPL Small-Body Database, https://ssd.jpl.nasa.gov/sbdb.cgi
Asteroid family portal database, http://asteroids.matf.bg.ac.rs
Reboundx package, https://reboundx.readthedocs.io
The individual figures for the pairs are available at https://zenodo.org/records/13121167
Rocks library, https://github.com/maxmahlke/rocks
All Tables
Calculated phase distances for former 2021 orbital elements (dold) and updated orbits (dnew).
All Figures
 |
Fig. 1 Example of a close encounter between the clones 469759 (2005 QM29) - (2016 QZ123), where the mutual gravitational attraction influences the dynamics of the pair. The encounter led to gravitational capture, and clones revolved around the center of mass for 2–3 orbital periods. |
| In the text | |
 |
Fig. 2 Distribution of encounters during the main convergence for 469759 (2005 QM29) - (2016 QZ123), simulated with (bottom, blue) and without (top, orange) the mutual gravitational interactions between the clones. |
| In the text | |
 |
Fig. 3 Density distribution of encounters for 469759 (2005 QM29) - (2016 QZ123), simulated with (blue) and without (orange) the mutual gravitational interactions between the clones. |
| In the text | |
 |
Fig. 4 Time distribution of close encounters for the cluster, where encounters between members are color-coded as in Fig. 5, thus serving as a legend. |
| In the text | |
 |
Fig. 5 Relation between the asteroids and components of the cluster. The colors of the links correspond to those of the histogram, while the width of connections illustrates the number of encounters between the components. The numbers on the lines represent the median of the encounter time distribution between the components. |
| In the text | |
 |
Fig. 6 Nodal longitude difference between the primary body 21028 (1989 TO) and other components of the cluster. |
| In the text | |
 |
Fig. 7 Age comparison between our 2021 and updated 2024 results. The x-axis shows the formation times, and the y-axis shows 2024 results calculated using updated orbital elements and new software. The red lines are the error bars for both cases. The black dashed line represents the case of perfect agreement between the results. |
| In the text | |
 |
Fig. 8 Distribution of encounters for the pairs 1981 VL - 2013 CX44 and 2006 BJ193 - 2017 FE106. Histograms colored orange represent previous results, blue ones represent the new results with stricter convergence conditions, and pale blue are distributions of new results with former convergence conditions. |
| In the text | |
 |
Fig. 9 Relative fraction of asteroids of different taxonomic types among inner main-belt pairs in comparison with all inner main-belt asteroids. We note that M-type asteroids are presented twice: as a part of the X-complex and as individual asteroids. |
| In the text | |
 |
Fig. 10 Distribution of close encounters for 9146 - 2018 SM48 M-type pair candidate. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


