| Issue |
A&A
Volume 595, November 2016
|
|
|---|---|---|
| Article Number | A14 | |
| Number of page(s) | 4 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201628286 | |
| Published online | 24 October 2016 | |
Research Note
Gravitational light-bending prevents γγ absorption in gravitational lenses
1 Centre for Space Research, North-West University, Potchefstroom 2520, South Africa
e-mail: .Bottcher@nwu.ac.za
2 Astrophysical Institute, Department of Physics and Astronomy, Ohio University, Athens, OH 45701, USA
Received: 10 February 2016
Accepted: 2 September 2016
The magnification effect that is due to gravitational lensing enhances the chances of detecting moderate-redshift (z ~ 1) sources in very high-energy (VHE; E > 100 GeV) γ-rays by ground-based atmospheric Cherenkov telescope facilities. It has been shown in previous work that this prospect is not hampered by potential γ−γ absorption effects by the intervening (lensing) galaxy, nor by any individual star within the intervening galaxy. In this paper, we expand this study to simulate the light-bending effect of a realistic ensemble of stars. We first demonstrate that for realistic parameters of the galaxy’s star field, it is extremely unlikely (probability ≲10-6) that the direct line of sight between the γ-ray source and the observer passes by any star in the field close enough to be subject to significant γγ absorption. Our simulations then focus on the rare cases where γγ absorption by (at least) one individual star might be non-negligible. We show that gravitational light-bending will have the effect of avoiding the γ−γ absorption spheres around massive stars in the intervening galaxy. This confirms previous results and re-inforces arguments in favour of VHE γ-ray observations of lensed moderate-redshift blazars to extend the redshift range of objects detected in VHE γ-rays, and to probe the location of the γ-ray emission region in these blazars.
Key words: gravitational lensing: strong / gravitational lensing: micro / galaxies: active / quasars: general / gamma rays: galaxies
© ESO, 2016
1. Introduction
To date, about 40 blazars (jet-dominated active galactic nuclei whose relativistic jets are oriented at a small angle with respect to the line of sight) have been detected by ground-based atmospheric Cherenkov telescope facilities as sources of very high-energy (VHE; E > 100 GeV) γ-rays1. Their distances span a redshift range 0 < z < 0.944. This range is primarily limited by the γ−γ absorption effect of the extragalactic background light (EBL) on VHE γ-rays from cosmological distances (see e.g. Stecker et al. 1992; De Jager et al. 1994; Dwek & Krennrich 2005; Franceschini et al. 2008; Finke et al. 2010; Dominguez et al. 2013). To expand the γ-ray horizon set by γ−γ absorption, sources at higher redshifts either need to be unusually bright in VHE γ-rays (exhibiting an unusually hard γ-ray spectrum). Alternatively, VHE blazars of known classes can be gravitationally lensed, whereby their observed fluxes are magnified. Two γ-ray blazars detected by the Fermi Large Area Telescope (Fermi-LAT) are known to be gravitationally lensed, namely PKS 1830-211 (Barnacka et al. 2011) and S3 0218+357 (Cheung et al. 2014). The latter has been successfully detected at VHE γ-rays by the Major Atmospheric Cherenkov Telescope (MAGIC, Mirzoyan et al. 2014), thus making it the most distant known VHE γ-ray emitter to date at z = 0.944.
The γ-ray detection of gravitationally lensed blazars not only promises the extension of the VHE blazar catalogue to higher redshifts. Barnacka et al. (2014a, 2015) have shown that the time delay between the two images of a gravitationally lensed blazar depends very sensitively on the exact location of the emission region in the source plane. Thus, differences in the locations of the emission region dominating the variable emission at different frequency ranges (e.g. radio vs. optical vs. γ-rays) may lead to different time delays between the two images in these different frequency bands. Hence, such differences in time delays may be used to probe the location of the γ-ray emission region in blazars, relative to the radio or optical emission region (Barnacka et al. 2014a, 2015). We note that this method may be applied even when the two lensed images are not spatially resolved by searching for repeating variability patterns corresponding to the two lensed images.
An important question concerning the feasibility of such studies is whether the additional IR – optical – UV radiation field provided by the lensing galaxy and its stellar population may provide a significant source of γ−γ opacity, thus effectively preventing the VHE γ-ray detection of lensed blazars in significant numbers. To investigate this, Barnacka et al. (2014b) have calculated the γ−γ opacity of the collective radiation field of a typical L∗ galaxy as well as the opacity provided by an individual star within the lensing galaxy. In both cases, they found that these intervening sources of soft radiation field do not lead to significant γ−γ absorption. Intriguingly, even if the direct line of sight to the background blazar passes very close to a star in the lensing galaxy (i.e. closer than the characteristic radius within which the γ−γ opacity exceeds one), the gravitational-lensing effect naturally bends the light path significantly farther away from the star, thus helping to avoid γ−γ absorption. While this is an exciting result, suggesting that excess γ−γ absorption that is due to the lens is not a hindrance to VHE detections of distant, gravitationally lensed blazars, their study was limited to only one individual star in the lensing galaxy; it is not a priori clear whether this result still holds for the light-bending effect of a realistic ensemble of (typically billions of) stars within the lensing galaxy.
In this paper, we therefore extend the study of Barnacka et al. (2014b) to simulate the paths of γ-rays through a representative star field in an intervening lensing galaxy, finding that even when we consider a realistic stellar population in the galaxy, the light-bending effect still aids VHE γ-rays to avoid the γ−γ absorption spheres of all stars in the field. We describe the general model setup and the numerical method to trace the paths of γ-rays through the lensing galaxy in Sect. 2. Results are presented in Sect. 3, and we summarize in Sect. 4.
2. Numerical setup
To evaluate the effect of gravitational light-bending on the path of a VHE γ-ray (or any other photon) through an intervening galaxy, we performed ray-tracing simulations. The general setup of these simulations is as follows: for a generic case, we assume that the lens is at a distance of 3 Gpc from the observer on Earth, while the background blazar is located a distance of 3 Gpc behind the lens. The average density of stars in the region of the galaxy through which the γ-ray passes is parameterized as n∗ = 10-2n-2 ly-3. For n-2 = 1, this is slightly higher than the density of stars in the solar neighbourhood. An approximately uniform distribution is the first natural follow-up to the study by Barnacka et al. (2014b), therefore we focus on this case here. However, below we also briefly discuss a more realistic scenario, in which a much denser stellar cluster may be located in the γ-ray path.
To assess whether the γ-ray passes through any γ−γ absorption sphere (and, thus, may be subject to significant γ−γ absorption by any of the stellar radiation fields), we estimated the radius rγγ of the γ−γ absorption sphere (where the γ−γ opacity τγγ = 1) using 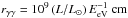 (Barnacka et al. 2014b), where L/L⊙ is the stellar luminosity normalized to the solar luminosity, and EeV is the peak photon energy of the stellar spectrum. The above expression represents the maximum size of the γ−γ absorption sphere for γ-ray photons optimally interacting with the stellar photons, that is,
(Barnacka et al. 2014b), where L/L⊙ is the stellar luminosity normalized to the solar luminosity, and EeV is the peak photon energy of the stellar spectrum. The above expression represents the maximum size of the γ−γ absorption sphere for γ-ray photons optimally interacting with the stellar photons, that is, 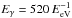 GeV. To express rγγ solely as a function of stellar mass, m ≡ M/M⊙, we used a scaling of the stellar luminosity as L = L⊙m3.5 (which is a convenient interpolation between a slightly shallower mass dependence at low masses and a slightly steeper one at higher masses, e.g. Demircan & Kahraman 1991) and peak photon energy EeV = 0.5 m0.5, yielding finally
GeV. To express rγγ solely as a function of stellar mass, m ≡ M/M⊙, we used a scaling of the stellar luminosity as L = L⊙m3.5 (which is a convenient interpolation between a slightly shallower mass dependence at low masses and a slightly steeper one at higher masses, e.g. Demircan & Kahraman 1991) and peak photon energy EeV = 0.5 m0.5, yielding finally 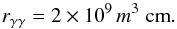 (1)We first estimated the probability of a γ-ray being subject to significant γ−γ absorption in the star field of a galaxy, irrespective of any gravitational light-bending effects. We considered γ−γ absorption to be non-negligible of τγγ ≥ 0.1. Owing to the scaling of τγγ ∝ b-1, with b being the impact parameter (i.e. the distance of closest approach of the direct line of sight of the γ-ray to the star), this means, a star of mass m has an effective cross section of
(1)We first estimated the probability of a γ-ray being subject to significant γ−γ absorption in the star field of a galaxy, irrespective of any gravitational light-bending effects. We considered γ−γ absorption to be non-negligible of τγγ ≥ 0.1. Owing to the scaling of τγγ ∝ b-1, with b being the impact parameter (i.e. the distance of closest approach of the direct line of sight of the γ-ray to the star), this means, a star of mass m has an effective cross section of 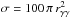 . Assuming an approximately constant stellar density over a scale height h = 1 hkpc kpc of the galaxy, the probability of a γ-ray passing within 10 rγγ of any star, is then
. Assuming an approximately constant stellar density over a scale height h = 1 hkpc kpc of the galaxy, the probability of a γ-ray passing within 10 rγγ of any star, is then 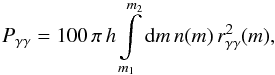 (2)where n(m) is the mass distribution of stars. For the purpose of this simple estimate, we approximated the stellar mass function as a single power-law n(m) = n0m− αm with αm = 2.5 between m1 = 0.08 and m2 = 100. This then yields a probability of Pγγ = 3 × 10-7hkpcn-2. For realistic parameters of the stellar field and the scale height of the galaxy, even without the effects of gravitational light bending, it is therefore extremely unlikely that γγ absorption in the radiation field of any individual star will play a significant role. In the following, we consider the rare case in which one of the stars in the field is, by chance, located close enough to the direct line of sight from the γ-ray source to the observer to cause significant γγ absorption if gravitational light-bending were not taken into account.
(2)where n(m) is the mass distribution of stars. For the purpose of this simple estimate, we approximated the stellar mass function as a single power-law n(m) = n0m− αm with αm = 2.5 between m1 = 0.08 and m2 = 100. This then yields a probability of Pγγ = 3 × 10-7hkpcn-2. For realistic parameters of the stellar field and the scale height of the galaxy, even without the effects of gravitational light bending, it is therefore extremely unlikely that γγ absorption in the radiation field of any individual star will play a significant role. In the following, we consider the rare case in which one of the stars in the field is, by chance, located close enough to the direct line of sight from the γ-ray source to the observer to cause significant γγ absorption if gravitational light-bending were not taken into account.
The deflection angle αdef resulting from the γ-ray passing the star at an impact parameter b, is given by
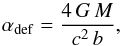 (3)where M is the mass of the star, and is generally αdef ≲ 10-6 for main-sequence stars if b is larger than the stellar radius. Consequently, the total deflection of the γ-ray even when interacting with thousands of stars is very small. We therefore restricted our simulations to a cylinder of radius R = 10 ly and height h = 1 kpc, as a characteristic scale height of the galaxy. Thus, the gravitational influence of stars farther than 5 ly away from the direct line of sight was neglected. Within our simulation volume, we randomly distributed stars with an average number density n∗, except for placing one randomly chosen star deliberately close (at b < rγγ) to the direct line of sight to investigate the rare cases where γγ absorption would be relevant without gravitational light deflection.
(3)where M is the mass of the star, and is generally αdef ≲ 10-6 for main-sequence stars if b is larger than the stellar radius. Consequently, the total deflection of the γ-ray even when interacting with thousands of stars is very small. We therefore restricted our simulations to a cylinder of radius R = 10 ly and height h = 1 kpc, as a characteristic scale height of the galaxy. Thus, the gravitational influence of stars farther than 5 ly away from the direct line of sight was neglected. Within our simulation volume, we randomly distributed stars with an average number density n∗, except for placing one randomly chosen star deliberately close (at b < rγγ) to the direct line of sight to investigate the rare cases where γγ absorption would be relevant without gravitational light deflection.
The masses of the stars were randomly drawn from a Salpeter mass function, N∗(M) ∝ M-2.5. As has been shown in Barnacka et al. (2014b), the luminosity of low-mass stars (lower than a few M⊙) is too low to cause any significant γ−γ absorption. Furhermore, as a result of their low masses, any angular deflection caused by them is also expected to be negligible. In our simulations, we therefore restricted the considered mass range to 1 M⊙ ≤ M ≤ 100 M⊙, neglecting the influence of low-mass stars. This reduced the number density of stars that were considered in the simulations. Specifically, we conservatively included 250 stars in the mass range 1 M⊙ ≤ M ≤ 100 M⊙ within the simulation volume.
 |
Fig. 1 Illustration of a typical example of our γ-ray tracing simulations. Red dots mark the positions of stars; the blue line indicates the path of the γ-ray which continues to propagate towards the observer. The axes are labelled in units of pc. |
Our ray-tracing code then scanned through a fine grid of γ-ray photon arrival directions into the simulation volume to determine the path that ultimately propagates to the observer on Earth (while most photon paths are being deflected in other directions, which will miss the observer). Figure 1 illustrates the observed γ-ray photon path for one of our simulations. The code tracks the distances of closest approach to each star in the simulation volume.
For every star i in the simulation volume, the impact parameter bi was then normalized to 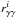 of the star, to check whether the γ-ray photon path traverses or avoids that star’s γ−γ absorption sphere. The simulation was repeated 100 times with different random seeds (to determine the stellar positions and masses) to assess the statistical significance of our results.
of the star, to check whether the γ-ray photon path traverses or avoids that star’s γ−γ absorption sphere. The simulation was repeated 100 times with different random seeds (to determine the stellar positions and masses) to assess the statistical significance of our results.
 |
Fig. 2 Histogram of normalized impact parameters ( |
3. Results
Figure 2 shows a histogram of the impact parameters (normalized to the γ-ray absorption sphere) of the γ-ray photon reaching the observer on Earth for all 250 stars in one of our simulations (blue histogram). It illustrates that the observed γ-ray passes no star in in the simulation at a distance shorter than several hundred times rγγ. This is compared to the result corresponding to a straight photon path along the z axis, that is, what would be expected without gravitational light-bending effects. It is clear that the gravitational light bending systematically shifts the impact parameters to higher values and, in particular, shifts the minimum impact parameter to a value clearly outside the γγ absorption sphere. This suggests that even with a realistic ensemble of stars, the gravitational light bending tends to aid γ-ray photons to avoid the γγ absorption spheres of stars potentially providing a significant γγ opacity.
 |
Fig. 3 Histogram showing the minimum normalized impact parameters (bi/rγγ) for all 100 Monte Carlo realizations of our simulation. |
Clearly, the most important result of our simulations is the minimum normalized impact parameter bi/rγγ, that is, the distance of closest approach, relative to the star’s γ−γ absorption sphere, to any star in the ensemble. Figure 3 shows a histogram of the minimum bi/rγγ for each of the 100 Monte Carlo realizations of our simulations. It illustrates that in no case will any star be passed at a closer range than a few hundred times the γγ absorption sphere radius. Consequently, γ-rays will never be subject to γγ opacities higher than ~10-2. This confirms our conclusion that irrespective of the details of the stellar distribution in the intervening galaxy, even if the direct line of sight were to pass very close (within the γγ absorption sphere) to any star in the galaxy, the light-bending effect will act to help VHE γ-rays avoid the γγ absorption spheres of all stars.
The uniform star distribution used in the above considerations is certainly an over-simplification of the actual distribution of stars in a galaxy. To investigate the effects of a more realistic inhomogeneous star distribution, we also explored situations in which (a) a typical O/B association located within the disk of the galaxy and (b) a globular cluster in the galactic halo are located in the direct line of sight. In both cases, we found results consistent with those displayed in Figs. 2 and 3. For the case of a globular cluster in the line of sight, we note that while the probability of a close encounter of the γ-ray with a star is very high, globular clusters only contain low-mass stars (typically type G and later), which, as a result of their low luminosities, never provide a significant γγ opacity, regardless of the impact parameter (Barnacka et al. 2014b).
4. Summary
We have re-evaluated the result of Barnacka et al. (2014b) that VHE γ-rays from a gravitationally lensed blazar are not expected to be subject to significant γγ absorption by the radiation field of the lens because the gravitational light-bending effect will cause the γ-ray paths to systematically avoid the γγ absorption spheres of lensing systems. Barnacka et al. (2014b) considered only the collective radiation field of an entire galaxy and the radiation fields of one individual star within a lensing galaxy. As this might be over-simplifying the situation for γ-rays passing through the potentially dense star field of a galaxy, we have evaluated the light-bending effect that arises from a realistic stellar population in a lensing galaxy.
We first evaluated the probability of any star to be close enough to the direct line of sight between a background VHE γ-ray source and the observer to cause significant γγ absorption if light bending were not taken into account. We found this probability to be very low, typically ≲10-6. We then concentrated on the few exceptional cases in which a star might be, by chance, located very close to the line of sight. For these cases, we showed that the result of Barnacka et al. (2014b) still holds, namely that the gravitational light-bending effect will deflect the γ-ray path far beyond the γγ absorption sphere of that single star, without causing it to approach any other star close to its γγ absorption sphere.
These results confirm the findings of Barnacka et al. (2014b) and reinforce the prospect of detecting gravitationally lensed γ-ray blazars with ground-based VHE γ-ray observatories, especially the future Cherenkov Telescope Array (CTA). As suggested by Barnacka et al. (2014a, 2015), the measurement of time delays between lensed images (which cannot be directly spatially resolved at γ-ray energies) will then allowus to probe the location of the γ-ray emission region in comparison to the lower-energy emission.
Acknowledgments
We thank the anonymous referee for a constructive and helpful report. M.B. acknowledges support the South African Research Chair Initiative (SARChI) of the Department of Science and Technology and the National Research Foundation2 of South Africa, under SARChI Chair grant No. 64789.
References
- Barnacka, A., Glicenstein, J.-F., & Moudden, Y. 2011, A&A, 528, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barnacka, A., Geller, M. J., Dell’Antonio, I. P., & Benbow, W. 2014a, ApJ, 788, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Barnacka, A., Böttcher, M., & Sushch, Iu. 2014b, ApJ, 790, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Barnacka, A., Geller, M. J., Dell’Antonio, I. P., & Benbow, W. 2015, ApJ, 799, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Cheung, C. C., Larsson, S., Scargle, J. D., et al. 2014, ApJ, 782, L14 [NASA ADS] [CrossRef] [Google Scholar]
- De Jager, O. C., Stecker, F. W., & Salamon, M. H. 1994, Nature, 369, 294 [NASA ADS] [CrossRef] [Google Scholar]
- Demircan, O., & Kahraman, G. 1991, Astrophys. Space Sci., 181, 313 [Google Scholar]
- Dominguez, A., Finke, J. D., Prada, F., et al. 2013, ApJ, 770, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Dwek, E., & Krennrich, F. 2005, ApJ, 618, 657 [NASA ADS] [CrossRef] [Google Scholar]
- Finke, J. D., Razzaque, S., & Dermer, C. D. 2010, ApJ, 712, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Franceschini, A., Rodigheiro, G., & Vaccari, M. 2008, A&A, 487, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mirzoyan, R. 2014, ATel, 6349, 1 [NASA ADS] [Google Scholar]
- Stecker, F. W., de Jager, O. C., & Salamon, M. H. 1992, ApJ, 390, L49 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Illustration of a typical example of our γ-ray tracing simulations. Red dots mark the positions of stars; the blue line indicates the path of the γ-ray which continues to propagate towards the observer. The axes are labelled in units of pc. |
| In the text | |
 |
Fig. 2 Histogram of normalized impact parameters ( |
| In the text | |
 |
Fig. 3 Histogram showing the minimum normalized impact parameters (bi/rγγ) for all 100 Monte Carlo realizations of our simulation. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.