| Issue |
A&A
Volume 594, October 2016
|
|
|---|---|---|
| Article Number | A80 | |
| Number of page(s) | 9 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201629030 | |
| Published online | 14 October 2016 | |
Combined infrared and Raman study of solid CO
1 Dipartimento di Scienze Chimiche, Università degli Studi di Catania, Viale Andrea Doria 6, 95125 Catania, Italy
2 INAF–Osservatorio Astrofisico di Catania, via Santa Sofia 78, 95123 Catania, Italy
e-mail: riccardo.urso@oact.inaf.it; mepalumbo@oact.inaf.it
Received: 31 May 2016
Accepted: 8 July 2016
Context. Knowledge about the composition and structure of interstellar ices is mainly based on the comparison between astronomical and laboratory spectra of astrophysical ice analogues. Carbon monoxide is one of the main components of the icy mantles of dust grains in the interstellar medium. Because of its relevance, several authors have studied the spectral properties of solid CO both pure and in mixtures.
Aims. The aim of this work is to study the profile (shape, width, peak position) of the solid CO band centered at about 2140 cm-1 at low temperature, during warm up, and after ion irradiation to search for a structural variation of the ice sample. We also report on the appearance of the longitudinal optical-transverse optical (LO-TO) splitting in the infrared spectra of CO films to understand if this phenomenon can be related to a phase change.
Methods. We studied the profile of the 2140 cm-1 band of solid CO by means of infrared and Raman spectroscopy. We used a free web interface that we developed that allows us to calculate the refractive index of the sample to measure the thickness of the film.
Results. The profile of the fundamental band of solid CO obtained with infrared and Raman spectroscopy does not show any relevant modification after warm up or ion bombardment in the dose range investigated. We explain that the LO-TO splitting is not connected to a structural variation of the film. Ion irradiation causes the formation of new molecular species. Raman spectroscopy allowed us to detect, among other bands, a band centered at 1817 cm-1 that has been attributed to the infrared inactive species C2 and a band centered at 1767 cm-1 that remains unidentified.
Key words: astrochemistry / methods: laboratory: solid state / ISM: lines and bands / infrared: ISM / techniques: spectroscopic / molecular processes
© ESO, 2016
1. Introduction
After molecular hydrogen, carbon monoxide is the most abundant molecule in space. The first detection of this molecule in the gas phase of the interstellar medium (ISM) was reported by Wilson et al. (1970). Infrared observations have shown the presence of solid CO in quiescent molecular clouds and in both low-mass and high-mass star-forming regions because this molecule, together with water, is one of the main components of the icy mantles of dust grains (e.g., Boogert et al. 2015). Because of the relevance of CO in astrophysics, several laboratories have been involved in the study of this molecule and its spectral properties in astrophysical ices analogues (e.g., Sandford et al. 1988; Tielens et al. 1991; Palumbo & Strazzulla 1993; Quirico & Schmitt 1997; Dartois et al. 2006; Palumbo et al. 2006; Cuppen et al. 2011).
As discussed in detail by Quirico & Schmitt (1997), two main experimental approaches are used: direct deposition on a single window (thin-film technique) and crystal films growth from the liquid phase in a closed cell. The thin-film technique has the advantage that films with good optical quality and well-known thickness can be obtained. On the other hand, only a limited range of temperature can be investigated owing to sample sublimation since it is in direct contact with the chamber vacuum; also a limited range of thicknesses can be investigated (less than few micrometers) making it difficult to study weak absorption features. The closed cell technique allows crystals to be grown from the liquid in a closed cryogenic cell under thermodynamical equilibrium. This allows cm-thick samples to grow with good optical and crystal qualities and it is not possible to form phases outside the thermodynamical equilibrium (e.g., to obtain amorphous solids). Closed cell technique studies have shown that CO has four different phases (namely α-, β-, γ-, and ϵ- CO), a phase transition occurs at 61.6 K between the α- phase (the coldest one) to the β- phase, and that CO melting point is at 68.14 K (e.g., Löwen et al. 1990; Quirico & Schmitt 1997). When deposited following the thin-film technique, CO sublimate at about 30 K (e.g., Collings et al. 2004), which is well below the α- β- phase transition temperature.
The profile of the CO stretching mode in pure ice samples shows two features at about 2138 and 2142 cm-1 known as the transverse optical (TO) and the longitudinal optical (LO) modes (e.g., Chang et al. 1988; Palumbo et al. 2006). Both these features can be observed when IR spectra are taken in reflection-absorption IR spectroscopy (RAIRS ) and oblique transmittance, while only the TO mode is observed in transmittance spectra taken at normal incidence. As discussed by Palumbo et al. (2006) the presence of the LO-TO splitting is not attributable to the presence of crystalline CO.
Recently, an interesting phenomenon has been investigated, which is the appearance of a spontaneous electric field due to dipole orientation within thin films of dipolar molecules. Materials that exhibit this behavior are called spontelectric (from spontaneously electrical). Using RAIRS, Lasne et al. (2015) studied the Stark shift created by the spontelectric field in vibrational frequencies of solid CO. They measured the LO-TO splitting to determine the values of the spontelectric field as a function of film deposition temperature.
In recent decades, several experimental investigations have focused on astrophysical relevant molecules, such as H2O, CO2, CH3OH, CH3CN, and CH3OCHO. Many of these experiments were meant to study the profile (i.e., shape, width, and peak position) of IR bands at different temperatures in pure ices and in mixtures. Laboratory spectra show that during warm up the profile of IR bands change. These changes can be attributed to a transition between a disordered phase to a much ordered one, i.e., an amorphous to crystalline transition. Some examples are reported by Hudgins et al. (1993), Palumbo et al. (1999), Moore et al. (2010), Abdulgalil et al. (2013), and Modica & Palumbo (2010). Bossa et al. (2012) reported about the thermal processing of porous amorphous solid water. They observed that between 20 and 120 K the ice undergoes a thickness decrease that they attribute to a phase transition to a nonporous and more compact structure of the ice.
Other studies have focused on the effects of energetic processing (i.e., ion bombardment and UV photolysis) on the structure and morphology of ices. As an example, on the basis of laboratory experiments, it has been shown that polycrystalline water ice is converted to amorphous ice after energetic processing (e.g., Baratta et al. 1991; Moore & Hudson 1992; Leto & Baratta 2003; Dartois et al. 2015). Furthermore, energetic processing also causes the conversion of porous amorphous water to compact amorphous water (e.g., Palumbo et al. 2006, 2010; Raut et al. 2007; Dartois et al. 2013) at 10–20 K.
Also some attempts have been made to look for a phase change of solid CO, both pure and in solid matrices, by studying its infrared spectrum (Maki 1961; Nealander 1985; Sandford et al. 1988; Loewenschuss et al. 1997). Katz et al. (1984) reported about a Raman scattering experiment of solid CO placed in a diamond cell and subjected to variation in temperature and pressure. Looking at the feature of the CO stretching mode, they identified four structures named α-, β-, γ-, and ϵ- CO, each showing a different profile of the stretching-mode feature.
Fuchs et al. (2006) reported on the change in the heights, widths, and position of the 13CO stretching vibrational band by means of RAIRS spectroscopy during a temperature programmed desorption (TPD) experiment. At low temperatures (18.5 K) these authors observed a single peak at 2096 cm-1 due to amorphous 13CO. Raising the temperature to 27.5 K, a peak centered at 2095.1 cm-1 appears and they attributed it to the α-crystalline LO component. They concluded that these variations are due to a phase change from amorphous to crystalline ice at close to the desorption temperature. Studying the effect of photodesorption in CO ices, Öberg et al. (2009) reported that raising the ice temperature from 15 K to 27 K the CO photodesorption yield decreases. They carried out a RAIRS experiment that shows a change in the CO band profile between 15 K and 27 K. They concluded that because the annealing determines the formation of a more compact ice, its structure, rather than the temperature, affects the photodesorption yield.
Recently, Munõz Caro et al. (2016) reported on some experiments they carried out to evaluate if there is a connection between the structure and photodesorption rate of solid CO by means of IR spectroscopy, vacuum-UV (VUV) spectroscopy, and TPD. They observed that the photodesorption yield linearly decreases with the deposition temperature of CO from 7 to 20 K, but they do not attribute this decrease to a variation in its morphology toward a crystalline solid.
To extend previous work, in this article we present new laboratory experiments on solid CO. Both infrared and Raman spectroscopy are used to analyze the samples. These are two powerful and complementary tools to study the physical and chemical properties of frozen samples. By means of infrared spectroscopy it is possible to identify molecular groups and specific molecules. Raman spectroscopy gives further information on the structural properties of the samples and it is often used to study the effects of ion induced lattice damage in carbonaceous solids (e.g., Elman et al. 1981; Strazzulla & Baratta 1992; Baratta et al. 1996; Kalish et al. 1999; Strazzulla et al. 2001; Costantini et al. 2002). The main purpose of this work is to verify whether it is possible to observe a structural variation in solid CO during warm up and after ion bombardment. The article is organized as follows: the experimental methods are described in Sect. 2, the results are presented in Sect. 3, and a discussion is given is Sect. 4.
2. Experimental methods
Experiments were performed in the Laboratory for Experimental Astrophysics (LASp) at INAF-Osservatorio Astrofisico di Catania (Italy). The solid CO samples were prepared in a stainless steel high vacuum (HV) chamber (pressure <10-7 mbar) in which a crystalline silicon substrate is placed in thermal contact with a cold finger whose temperature can vary between 17 K and 300 K.
 |
Fig. 1 Schematic view of the Raman setup. The Ar laser beam is focused on the sample mounted inside the HV chamber, which is connected to the Ion implanter. |
The samples were analyzed using infrared and Raman spectroscopies. Infrared transmission spectra were taken at oblique incidence (45°) by a Fourier transform infrared (FTIR) spectrometer (Bruker Equinox 55 or Vertex 70). Transmission spectra are obtained through the KBr windows in the chamber and a hole made in the cold finger, which allows the infrared beam to be transmitted through the substrate and the sample. The alignment of the IR beam of the spectrometer through the hole of the cold finger and KBr windows of the chamber is obtained using a moveable optical bench, on which an IR spectrometer is placed that permits fine vertical and horizontal adjustments. A rotatable polarizer placed along the path of the IR beam allows us to take spectra both with the electric vector parallel (p-polarized) and perpendicular (s-polarized) to the plane of incidence. Infrared spectra are taken with a resolution of 1 cm-1.
In situ Raman spectra were acquired using two different setups with visible and near-infrared laser excitation, respectively (Fig.1). In the first setup, a Triplemate spectrometer by SPEX equipped with a Peltier cooled CCD detector is used. A continuous Ar-ion laser beam (λ = 514.5 nm) enters a confocal illuminator by DILOR, perpendicularly to its optical axis, into which it is deflected by a microprism. The confocal optical system is arranged in such a way that any parallel beam incident along the optical axis in the opposite direction of the laser is focused onto the entrance slit of the spectrometer. By means of two flat mirrors, the laser beam is reflected toward the vacuum chamber and focused by an objective lens into a 40 μm spot on the sample. The back-scattered Raman light is collimated by the same objective into a parallel beam that, according to the setup geometry, goes back along the same path of the laser beam and reaches the confocal illuminator where it is focused onto the entrance slit of the spectrometer. Since the incoming laser and the Raman collected light are collimated into parallel beams, this configuration allows us to acquire Raman spectra up to several meters away from the spectrometer with negligible performance loss. The spectral resolution is about 5 cm-1.
The second setup, with near-infrared laser excitation, uses an optical fiber-based compact monocromator HE785 by HORIBA. The spectrometer has a fixed objective grating and is equipped with a Peltier cooled CCD detector. The probe head has a confocal optical configuration and is oriented directly toward the objective lens of the chamber. The optical path of the incoming laser beam that emerges from the head, and the collected Raman beam is analogous to that already described for the visible setup. A solid state continuous wave (CW) 785 nm laser diode is used as exciting source. The near-infrared excitation permits a significant decrease in the strong fluorescence continuum usually observed in carbon containing molecular samples irradiated at low doses, when using visible laser excitation (e.g., Ferini et al. 2004). Although the Raman features are relatively (785 nm/514.5 nm)4 = 5.4 times less intense with respect to the 514.5 nm excitation, this setup is particularly useful when searching for weak features of species formed by ion bombardment. A strong fluorescence continuum can indeed totally mask weak features. The spectral resolution is 10 cm-1.
In the experiments we present here, a needle valve is used to admit gaseous CO (Aldrich, 99.0%) into the vacuum chamber where it freezes on the substrate. The gas inlet is not directed toward the substrate, thus a “background deposition” is obtained. This method ensures a uniform thickness of the film, but has the disadvantage that the gas phase molecules can freeze out onto all of the cold surfaces inside the chamber. To avoid any deposition on the backside of the substrate, this is protected by a 2 cm long copper tube aligned with the IR beam with a central hole of 4.5 mm.
The vacuum chamber is connected to a 200 kV ion implanter by Danfysik. The irradiation experiments were carried out using 200 keV H+. The ion beam is electrostatically swept to ensure a uniform coverage on the target and produces a 2 × 2 cm2 spot on it. To avoid a macroscopic heating of the irradiated sample, we used an ion current density between 100 nA cm-2 and a few μA cm-2. The ion fluence (ions cm-2) was measured by integrating the ion current monitored during irradiation.
The energy deposited by incoming ions to the sample (dose) was obtained by multiplying the fluence and stopping power (i.e., the amount of energy deposited per unit path length; eV cm2/molecule) given by SRIM code (Ziegler et al. 2008). In this work the dose is given in eV/16u, which is a convenient way to characterize chemical changes and to enable a comparison with other experiments with different samples (Strazzulla & Johnson 1991).
2.1. Thickness measurement
We followed the procedure described in Fulvio et al. (2009) and Modica & Palumbo (2010) to measure the thickness of the CO solid film. In the experiments we present here, a He-Ne laser beam (λ = 543.5 nm) is directed toward the sample and reflected at 45° both by the vacuum-ice and ice-substrate interfaces. The reflected laser beam is detected by an external silicon-diode detector. There is a difference in the optical path between the reflected components of the laser beam that varies with the thickness of the film, so that interference is produced. Hence it is possible to follow the accretion of the frozen film by looking at the interference curve (intensity versus time) of the reflected laser beam (see Fig. 2A).
 |
Fig. 2 Panel A): experimental interference curve obtained during the deposition of gaseous CO on a Si cold substrate using an He-Ne laser. Panel B): theoretical interference curve for solid CO film on a Si cold substrate. The comparison between the theoretical and experimental curves allows us to measure the sample thickness using the interference fringe method. Panel C): theoretical interference curves calculated assuming an ice with refractive index equal to 1.26 that is deposited on cold Au substrate for different laser wavelengths. For comparison, the interference curve computed for the same ice deposited on silicon is shown. |
The spikes in the interference curve indicate the time when the infrared spectra are taken. The damping seen in the interference curve is due to scattering loss, either by the bulk or surface of the film, and a loss of coherence of the reflected light at the two, vacuum-film and film-substrate, interfaces. It should be considered that the damping is not usually due to absorption since most of the molecular ices are transparent at visible wavelengths. In general, the reflectance of a thin film deposited over a substrate can be schematically represented by Eq. (1) 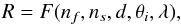 (1)where nf and ns are the complex refractive indexes of the film and substrate respectively, d is the film thickness, θi is the incidence angle and λ is the wavelength. If the incidence angle is not equal to 0, this function also depends on the polarization of the incident electromagnetic field. At fixed wavelength, the reflectance R versus the thickness is, for nonabsorbing materials, a periodic function whose period (distance between two maxima or minima) is given by Eq. (2)
(1)where nf and ns are the complex refractive indexes of the film and substrate respectively, d is the film thickness, θi is the incidence angle and λ is the wavelength. If the incidence angle is not equal to 0, this function also depends on the polarization of the incident electromagnetic field. At fixed wavelength, the reflectance R versus the thickness is, for nonabsorbing materials, a periodic function whose period (distance between two maxima or minima) is given by Eq. (2) 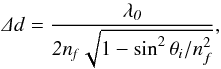 (2)where λ0 is the laser wavelength. From Eq. (2), it is evident that the refractive index of the sample must be known in order to measure the thickness. Nevertheless, the amplitude of the interference curve itself depends on the refractive index, so by measuring this quantity (intensity ratio between maxima and minima) it is possible to derive the refractive index of the sample and then the thickness. In particular in Eq. (1), λ0, θi, and ns are known quantities, hence for a given refractive index of the film (nf), an interference curve (R versus the thickness d) can be computed. In order to derive the refractive index of the film, nf is automatically varied, using a FORTRAN code, until the theoretical amplitude of the interference curve becomes equal to the experimental amplitude. We found nf = 1.30 for frozen CO. As an example, looking at Fig. 2 it is possible to compare the experimental interference curve obtained during the deposition of CO on a silicon cold substrate (A) with the computed theoretical curve (B).
(2)where λ0 is the laser wavelength. From Eq. (2), it is evident that the refractive index of the sample must be known in order to measure the thickness. Nevertheless, the amplitude of the interference curve itself depends on the refractive index, so by measuring this quantity (intensity ratio between maxima and minima) it is possible to derive the refractive index of the sample and then the thickness. In particular in Eq. (1), λ0, θi, and ns are known quantities, hence for a given refractive index of the film (nf), an interference curve (R versus the thickness d) can be computed. In order to derive the refractive index of the film, nf is automatically varied, using a FORTRAN code, until the theoretical amplitude of the interference curve becomes equal to the experimental amplitude. We found nf = 1.30 for frozen CO. As an example, looking at Fig. 2 it is possible to compare the experimental interference curve obtained during the deposition of CO on a silicon cold substrate (A) with the computed theoretical curve (B).
A free web interface to the FORTRAN code used in this work is available at http://www.oact.inaf.it/spess/. This interface calculates the refractive index of the ice sample and gives the theoretical interference curve from the amplitude of the experimental interference curve. The sample thickness can be obtained by comparing the theoretical interference curve with the experimental one. Since the experimental reflectance is usually given in arbitrary units and exhibit a damping due to scattering losses, a direct comparison between the theoretical and experimental curves is not possible. In this work both the experimental and theoretical curves are normalized by placing all the minima at 0 and the maxima at 1 before the comparison. The normalization procedure is straightforward for the theoretical curve since the minima and maxima have the same intensity. In the case of the experimental curve two spline continuum, passing through the minima and maxima, respectively, can be used for normalization. For each chosen point, we read the intensity in the normalized experimental interference curve. Then we identified the point at which the normalized intensity corresponds at the given fringe number in the normalized theoretical curve; the abscissa of the point is the value of the thickness.
This method ensures a measure of the film thickness with an absolute accuracy of about 5%. The main limits are the uncertainties in knowledge of the refractive index of the substrate at low temperature and the error in measuring the incidence angle of the laser. In the present version of the web interface, only some of the more common opaque substrates (silicon, aluminum, gold) are considered. We would like to note that a smaller amplitude of the interference curve increases the uncertainty in the derived refractive index and thickness of the film owing to the experimental noise of the interference curve. In particular in the case of a gold substrate, the use of a laser at violet or UV wavelength is suggested. In fact, as shown in Fig. 2 C, the amplitude of the interference curve is small when laser wavelengths greater than about 500 nm are used. The theoretical optical model for the reflectance does not take into account the reflection at the second substrate interface (the one in contact with the cold finger). Indeed it is not straightforward to consider, in a reliable way, the contribution of the electromagnetic radiation that is transmitted through the substrate and reflected at the second substrate interface. Also, it is not straightforward to take into account the reflected component by mirror-like polished cold finger surface. Hence the procedure can only be used reliably in the case of substrates that are opaque at the laser wavelength.
3. Results
We carried out several experiments to study the profile of the 2140 cm-1 fundamental band of solid CO by infrared transmission spectroscopy and Raman spectroscopy as a function of temperature, irradiation dose and thickness of the CO sample. Throughout the paper IR spectra are plotted in a decreasing wavenumber scale (i.e., increasing wavelength) as this is the common style in the astronomical literature, while Raman spectra are plotted in increasing wavenumber scale. We present our results in the following sections. In Fig. 3 we show the peak position of the CO band at different temperatures (A), irradiation doses (B), and film thicknesses (C). To obtain these values, we fitted each CO band with a polynomial curve and then we reported the position of the maximum of each fit. As said in Sect. 2, the Raman spectral resolution is 5 cm-1, so it is not possible to resolve the LO and TO mode of solid CO.
 |
Fig. 3 Experimental CO peak positions measured in IR and Raman spectra varying the sample temperature (panel A), irradiation dose (panel B), and film thickness (panel C). Red squares: LO band in P polarization; black triangles: TO band in P polarization; green triangles: CO band in S polarization; and blue rhombus: Raman stretching mode band. |
3.1. Temperature experiments
 |
Fig. 4 Experiments performed increasing the sample temperature. Panels A), B): infrared spectra of the fundamental vibrational band of solid CO and panel C): Raman spectra of the stretching mode feature. Black solid line: solid CO film at 17 K; red dashed line: 25 K; and blue dotted line: 32 K. |
 |
Fig. 5 Energetic processing of solid CO film with 200 keV H+. Panel A): IR spectra in P polarization. Panel B): IR spectra in S polarization. CO film as deposited (black solid line); CO film after irradiation dose of 0.5 eV/16u (red dashed line), 5.6 eV/16u (green dotted line), and 18.4 eV/16u (blue dash-dotted line). Panel C): Raman spectra. CO film as deposited (black solid line); CO film after irradiation dose of 1.1 eV/16u (red dashed line), 2.2 eV/16u (green dotted line). |
In this paragraph we show the data collected for a 0.1 μm-thick CO sample increasing its temperature from 17 K to 32 K, the highest temperature at which spectra can be acquired in our experimental condition before which CO starts to sublimate. In Fig. 4A we report the IR spectra in P polarization showing the LO-TO splitting, while in Fig. 4B we show the spectra of the same sample in S polarization. No significant variation of the band profile occurred during the warm up. As is discussed in Sect. 3.3, the relative intensities of TO and LO bands depend on the thickness of the sample. It is possible to notice just a small variation in the intensity of the band. The same experiment has been repeated in the case of Raman analysis and the results are reported in Fig. 4C. It is well known that this technique is particularly sensitive to structural variations, but except for a small increase of the peak intensity, as seen for IR spectra, the band profile does not show any significant change.
In Fig. 3A it is clearly visible that from 17 K to 32 K is not possible to observe any variation of the band peak position either in the IR or in the Raman spectra. The measured values, in fact, differ by less than the uncertainties (0.25 cm-1 in the IR spectra and 1 cm-1 in the Raman spectra). The peak position of the band in the IR spectra, remains nearly constant at about 2138.7 cm-1 for the TO band and 2142.8 cm-1 for the LO band. The Raman peak position also remains almost constant at 2140.0 cm-1.
3.2. Irradiation experiments
In Fig. 5 we show the Raman spectra and IR spectra acquired in P polarization and S polarization of a 0.2 μm-thick solid CO film before and after irradiation with 200 keV H+. In Figs. 5A and B it is possible to see that the band intensity decreases at increasing irradiation doses. The energetic ions (keV-MeV) used to irradiate the sample release their energy to the target along the ion track. As a consequence molecular bonds are broken, and radicals and molecular fragments recombine to form new molecular species not present in the original sample. The irradiation of solid CO causes the synthesis of carbon dioxide and others carbon and oxygen containing molecules, such as carbon chain oxides. This phenomenon is well known and extensive studies have been reported by Trottier & Brooks (2004), Loeffler et al. (2005), Palumbo et al. (2008), and Seperuelo Duarte et al. (2010). In Fig. 5C we report a portion of the Raman spectra showing the solid CO band. As described in Ferini et al. (2004), after ion bombardment, an intense fluorescence continuum appears in all the Raman spectra because of radiative recombination of electron-hole pairs produced by the Raman laser irradiation. For clarity we subtracted this continuum. Because of different selection rules, by using Raman spectroscopy it is possible to observe molecular transitions that are not active in the infrared. In Fig. 6 a different portion of the same spectra shown in Fig. 5C is reported. The contribution due to the fluorescence continuum has also been subtracted in these spectra. We observed a band centered at 1817 cm-1 that is clearly visible at higher irradiation doses and a band centered at 1767 cm-1 since the first irradiation step. The Crovisier database1 reports a vibrational band of gaseous C2 at 1828 cm-1, so we tentatively attribute the 1817 cm-1 band to solid C2. A contribution from C5O, which had been assigned to a feature observed close to this position by Sicilia et al. (2012), could also be present. We were not able to attribute the 1767 cm-1 band to any molecule. Since the feature is not present within the noise level in the IR spectra, this suggests that it could be due to a symmetric vibrational mode in a molecular species without a permanent dipole moment.
In Fig. 3B we report the peak position of the CO band versus the irradiation dose. No significant variation of the CO band peak position is observed during irradiation in the range of doses that we investigated. In fact, the band peak positions remain almost constant at about 2138.4 cm-1 and 2142.6 cm-1 for the TO and LO mode, respectively. The Raman spectra show that the band is centered at about 2139.9 cm-1 and that it remains unaltered, within the noise, throughout the experiment.
In order to decrease the strength of the fluorescence background that adds noise to the Raman spectra, we carried out an experiment using a near-infrared laser excitation wavelength at 785 nm. Nevertheless, in this case there is also no significant variation of the CO profile increasing the irradiation dose, so we do not report the spectra.
 |
Fig. 6 Raman spectra of solid CO irradiated with 200 keV H+. CO film as deposited (black solid line); CO film after irradiation dose of 0.14 eV/16u (red dashed line), 0.37 eV/16u (green dotted line), 0.66 eV/16u (cyan short-dashed line), and 1.01 eV/16u (blue dash-dotted line). Black dotted vertical lines indicate 1767 cm-1 unidentified band and 1817 cm-1 band tentatively attribute to C2. |
3.3. Increasing thickness
 |
Fig. 7 Thickness experiment. Panel A): IR spectra in P polarization; panel B): IR spectra in S polarization. CO film thickness: black solid line: 0.04 μm; red dashed line: 0.3 μm; blue dotted line: 0.6 μm. Panel C): Raman experiment. CO stretching mode band of a 0.2 μm (black solid line) and 0.4 μm (red dashed line) film. |
We carried out some experiments in which the thickness of the solid CO layer has been varied. As shown in Figs. 7A and B, we acquired the IR spectra both in P and S polarization after the deposition of 40 nm (black solid line), 300 nm (red dashed line), and 600 nm (blue dotted line) thick solid CO. Both P and S polarization spectra show an increase in transmittance at about 2133 cm-1. This happens because of the sharp variation in the real part of the refractive index (n) of solid CO at this wavenumber, and also this increase depends on the optical properties of the substrate. This feature is predicted by theory and is well reproduced by theoretical optical models employing experimental optical constants of solid CO (see Fig. 4 in Baratta & Palumbo 1998). In Fig. 3C we observe the band peak position of the TO mode slightly increasing from the 40 nm to the 600 nm thick layer; in particular it varies between 2138.1 and 2138.7 cm-1. The peak position of the LO mode remains almost constant between 2142.6 and 2142.2 cm-1 throughout the experiment.
In Figs. 7 A and B the CO band of the 0.6 μm thick sample is close to reaching saturation. In principle, this could hinder the linear correlation existing between the thickness of the film (related to the amount of CO in the sample) and the area underlying the band. In Fig. 8 black squares represent the values of the CO band area measured at 0.04, 0.3, 0.4, 0.6, 1.3, and 1.9 μm thickness. The graph shows that even if the band is close to saturation at 0.6 μm thickness (see the blue dotted line in Figs. 7A and B), its area still linearly increases with the film thickness, as shown by the linear best fit (red line) in Fig. 8.
Raman spectra are shown in Fig. 7C. They were acquired at 200 nm (black solid line) and 400 nm (red dashed line) thickness. The band shape and peak position do not show any relevant variation.
 |
Fig. 8 Solid CO band area vs. film thickness. Black squares: measured values of the band area; red solid line: linear fit of the measured areas. |
4. Discussion
Comparing our Raman spectra of solid CO with those presented by Katz et al. (1984), we notice that the profile of the CO band is similar to the profile of β-CO, which is a much disordered phase if compared to the ordered α-CO. We explain the formation of a disordered structure in our HV chamber because of the fast cooling of the CO gas when it comes in contact with the cold surface of the substrate on the sample holder.
In the experiments that we carried out at increasing temperatures from 17 K to 32 K (see Fig. 4), we would have expected a relevant variation in the IR and an even more pronounced in the Raman of the CO band profile if a structural change had occurred. But these variations are almost absent. This result is in agreement with Lasne et al. (2015) who studied the LO-TO splitting to calculate the spontelectric field in solid CO. They found that annealing from 18 to 26 K does not produce detectable shifts of the LO and TO bands. A study of the profile of the LO- and TO-components at about 2140 cm-1 of solid CO during warm-up in the temperature range 14–26 K has recently been reported by Munõz Caro et al. (2016). Also, in their experiments, the band profile remained unaltered. Our results are also in agreement with those presented by Löwen et al. (1990). They report that no change of structure and no frequency shifts have been observed in the Raman spectra of solid CO in the temperature range between 4.5 and 30 K. So we conclude that our samples preserve the same structure during warm up. Alternatively, the profile of the CO band does not depend on the structure of the sample.
We have also investigated any possible modification of the CO band profile after ion irradiation (see Fig. 5). As already noticed in the previous section, ion irradiation causes the reduction of the intensity of the CO band in the IR spectra. This is due to the formation of new molecular species in the samples. In Fig. 3B we see that while the peak position of the TO band remains almost constant, the peak position of the LO band slightly shifts to higher wavenumbers between the first and second irradiation step. This small variation is comparable with the shift of the LO peak position observed as a function of film thickness. The Raman spectra do not show any significant variation in the band profile after ion irradiation.
Most of our knowledge about the composition and structure of interstellar and planetary ices is based on the comparison between laboratory and astronomical spectra. When high resolution astronomical spectra are available, it is possible not only to identify a given solid phase species but also, from the band profile, to infer the mixture it is embedded in and the average temperature experienced by the ice in a given environment. As an example, crystalline water ice has been identified toward high-mass young stellar objects based on the profile of the 3 μm water ice band (e.g., Dartois & d’Hendecourt 2001).
Some attempts have been made to infer the structure of solid CO observed toward low-mass young stellar objects. Pontoppidan et al. (2003) reported about the stretching band of solid CO detected toward several young stellar objects by means of the VLT-ISAAC. They found that this band results from the superposition of three components centered at 2143.7 cm-1, 2139.9 cm-1 and 2136.5 cm-1, respectively. They suggested that in the majority of the observed lines of sight, most of the CO is in a nearly pure form. Moreover, they attributed the 2143.7 cm-1 component to the LO mode of the vibrational transition of solid crystalline CO.
To date, the James Webb Space Telescope (JWST) launch is scheduled in October 2018. We expect that the Near Infrared Spectrograph (NIRSpec) and the Mid-Infrared Instrument (MIRI) on board, covering the wavelength range from 0.6 μm to 28 μm, will provide intriguing data that will be largely used to study the chemical composition and physical structure of different objects in space and, among them, of the icy mantles of dust grains in the ISM.
Based on the laboratory results presented in this paper we conclude that the profile of the stretching mode of solid CO obtained following the thin-film technique both in IR and Raman spectra does not provide evidence for any modification after warm up or ion irradiation. As a consequence, the comparison between laboratory and astronomical spectra cannot be used to draw any conclusion on the structure of solid CO in space.
Acknowledgments
The authors thank G. Strazzulla for helpful discussions during the preparation of this manuscript. This work has been supported by the Italian Ministero dell’Istruzione, dell’Università e della Ricerca through the grant Progetti Premiali 2012-iALMA (CUP C52I13000140001).
References
- Abdulgalil, A. G. M., Marchione, D., Thrower, J. D., et al. 2013, Physical and Engineering Sciences, 371 [Google Scholar]
- Baratta, G. A., & Palumbo, M. E. 1998, J. Opt. Soc. Am. A, 15, 307 [Google Scholar]
- Baratta, G. A., Leto, G., Spinella, F., et al. 1991, A&A, 252, 421 [NASA ADS] [Google Scholar]
- Baratta, G. A., Arena, M. M., Strazzulla, G., et al. 1996, Nucl. Instr. Methods B, 116, 195 [Google Scholar]
- Boogert, A. C. A., Gerakines, P. A., & Whittet, D. C. B. 2015, ARA&A, 53, 541 [Google Scholar]
- Bossa, J.-B., Isokoski, K., de Valois, M. S., et al. 2012, A&A, 545, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chang, H. C., Richardson, H. H., & Ewing, G. E. 1988, J. Chem. Phys., 89, 7561 [NASA ADS] [CrossRef] [Google Scholar]
- Collings, M. P., Anderson, M. A., Chen, R., et al. 2004, MNRAS, 354, 1133 [NASA ADS] [CrossRef] [Google Scholar]
- Costantini, J.-M., Couvreur, F., Salvetat, J. P., et al. 2002, Nucl. Instr. Meth. Phys. Res. B, 194, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Cuppen, H. M., Penteado, E. M., Isokoski, K., et al. 2011, MNRAS, 417, 2809 [NASA ADS] [CrossRef] [Google Scholar]
- Dartois, E. 2006, A&A, 445, 959 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dartois, E., & d’Hendecourt, L. 2001, A&A, 365, 144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dartois, E., Ding, J. J., de Barros, A. L. F., et al. 2013, A&A, 557, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dartois, E., Augé, B., Boduch, P., et al. 2015, A&A, 576, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elman, B. S., Dresselhaus, M. S., Dresselhaus, G., et al. 1981, Phys. Rev. B, 24, 1027 [NASA ADS] [CrossRef] [Google Scholar]
- Ferini, G., Baratta, G. A., & Palumbo, M. E. 2004, A&A, 414, 757 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuchs, G. W., Acharyya, K., Bisschop, S. E., et al. 2006, Faraday Discuss., 133, 331 [Google Scholar]
- Fulvio, D., Sivaraman, B., Baratta, G. A., et al. 2009, Spectrochim. Acta A, 72, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Hudgins, D. M., Sandford, S. A., Allamandola, L. J., et al. 1993, ApJS, 86, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Kalish, R., Reznik, A., Nugent, K. W., et al. 1999, Nucl. Instr. Meth. Phys. Res. B, 148, 626 [NASA ADS] [CrossRef] [Google Scholar]
- Katz, A. I., Schiferl, D., & Mills, R. L. 1984, J. Phys. Chem. 88, 3176 [Google Scholar]
- Lasne, J., Rosu-Finsen, Al., Cassidy, A., et al. 2015, Phys. Chem. Chem. Phys., 17, 30177 [CrossRef] [Google Scholar]
- Leto, G., & Baratta, G. A. 2003, A&A, 397, 7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Loeffler, M. J., Baratta, G. A., Palumbo, M. E., et al. 2005, A&A, 435, 587 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Loewenschuss, A., Givan, A., & Nielsen, C. J. 1997, J. Mol. Struct., 408, 533 [NASA ADS] [CrossRef] [Google Scholar]
- Löwen, H. W., Bier, K. D., & Jodl, H. J. 1990, J. Chem. Phys., 93, 8565 [NASA ADS] [CrossRef] [Google Scholar]
- Maki, A. G. 1961, J. Chem. Phys., 35, 931 [NASA ADS] [CrossRef] [Google Scholar]
- Modica, P., & Palumbo, M. E. 2010, A&A, 519, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moore, M. H., & Hudson, R. L. 1992, ApJ, 401, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Moore, M. H., Ferrante, R. F., Moore, W. J., et al. 2010, ApJS, 191, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Munõz Caro, G. M., Chen, Y.-J., Aparicio, S., et al. 2016, A&A, 589, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nealander, B. 1985, J. Phys. Chem, 89, 827 [CrossRef] [Google Scholar]
- Öberg, K. I., van Dishoeck, E. F., & Linnartz, H. 2009, A&A, 496, 281 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Palumbo, M. E., & Strazzulla, G. 1993, A&A, 269, 568 [NASA ADS] [Google Scholar]
- Palumbo, M. E., Castorina, A. C., & Strazzulla, G. 1999, A&A, 342, 551 [NASA ADS] [Google Scholar]
- Palumbo, M. E., Baratta, G. A., Collings, M. P., et al. 2006, Phys. Chem. Chem. Phys., 8, 279 [Google Scholar]
- Palumbo, M. E., Leto, P., Siringo, C., et al. 2008, ApJ, 685, 1033 [NASA ADS] [CrossRef] [Google Scholar]
- Palumbo, M. E., Baratta, G. A., Leto, G., et al. 2010, J. Mol. Struct., 972, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Pontoppidan, K. M., Fraser, H. J., Dartois, E., et al. 2003, A&A, 408, 981 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quirico, E., & Schmitt, B. 1997, Icarus, 127, 354 [NASA ADS] [CrossRef] [Google Scholar]
- Raut, U., Fama, M., Teolis, B. D., et al. 2007, BAAS, 39, 489 [NASA ADS] [Google Scholar]
- Sandford, S. A., Allamandola, L. J., Tielens, A. G. G. M., et al. 1988, ApJ, 329, 498 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Seperuelo Duarte, E., Domaracka, A., Boduch, P., et al. 2010, A&A, 512, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sicilia, D., Ioppolo, S., Vindigni, T., et al. 2012, A&A, 543, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strazzulla, G., & Baratta, G. A. 1992, A&A, 266, 434 [Google Scholar]
- Strazzulla, G., & Johnson, R. E. 1991, in Comets in the post-Halley era, ASSL Series (Dordrecht), 1, 243 [Google Scholar]
- Strazzulla, G., Baratta, G. A., & Palumbo, M. E. 2001, Spectrochim. Acta Part A, 57, 825 [Google Scholar]
- Tielens, A. G. G. M., Tokunaga, A. T., Geballe, T. R., et al. 1991, ApJ, 381, 181 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Trottier, A., & Brooks, R. 2004, ApJ, 612, 1214 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, R. W., Jefferts, K. B., & Penzias, A. A. 1970, ApJ, 161, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Ziegler, J. F., Biersack, J. P., & Ziegler, M. D. 2008, The Stopping and Range of Ions in Solids (New York: Pergamon Press), 321 [Google Scholar]
All Figures
 |
Fig. 1 Schematic view of the Raman setup. The Ar laser beam is focused on the sample mounted inside the HV chamber, which is connected to the Ion implanter. |
| In the text | |
 |
Fig. 2 Panel A): experimental interference curve obtained during the deposition of gaseous CO on a Si cold substrate using an He-Ne laser. Panel B): theoretical interference curve for solid CO film on a Si cold substrate. The comparison between the theoretical and experimental curves allows us to measure the sample thickness using the interference fringe method. Panel C): theoretical interference curves calculated assuming an ice with refractive index equal to 1.26 that is deposited on cold Au substrate for different laser wavelengths. For comparison, the interference curve computed for the same ice deposited on silicon is shown. |
| In the text | |
 |
Fig. 3 Experimental CO peak positions measured in IR and Raman spectra varying the sample temperature (panel A), irradiation dose (panel B), and film thickness (panel C). Red squares: LO band in P polarization; black triangles: TO band in P polarization; green triangles: CO band in S polarization; and blue rhombus: Raman stretching mode band. |
| In the text | |
 |
Fig. 4 Experiments performed increasing the sample temperature. Panels A), B): infrared spectra of the fundamental vibrational band of solid CO and panel C): Raman spectra of the stretching mode feature. Black solid line: solid CO film at 17 K; red dashed line: 25 K; and blue dotted line: 32 K. |
| In the text | |
 |
Fig. 5 Energetic processing of solid CO film with 200 keV H+. Panel A): IR spectra in P polarization. Panel B): IR spectra in S polarization. CO film as deposited (black solid line); CO film after irradiation dose of 0.5 eV/16u (red dashed line), 5.6 eV/16u (green dotted line), and 18.4 eV/16u (blue dash-dotted line). Panel C): Raman spectra. CO film as deposited (black solid line); CO film after irradiation dose of 1.1 eV/16u (red dashed line), 2.2 eV/16u (green dotted line). |
| In the text | |
 |
Fig. 6 Raman spectra of solid CO irradiated with 200 keV H+. CO film as deposited (black solid line); CO film after irradiation dose of 0.14 eV/16u (red dashed line), 0.37 eV/16u (green dotted line), 0.66 eV/16u (cyan short-dashed line), and 1.01 eV/16u (blue dash-dotted line). Black dotted vertical lines indicate 1767 cm-1 unidentified band and 1817 cm-1 band tentatively attribute to C2. |
| In the text | |
 |
Fig. 7 Thickness experiment. Panel A): IR spectra in P polarization; panel B): IR spectra in S polarization. CO film thickness: black solid line: 0.04 μm; red dashed line: 0.3 μm; blue dotted line: 0.6 μm. Panel C): Raman experiment. CO stretching mode band of a 0.2 μm (black solid line) and 0.4 μm (red dashed line) film. |
| In the text | |
 |
Fig. 8 Solid CO band area vs. film thickness. Black squares: measured values of the band area; red solid line: linear fit of the measured areas. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


