| Issue |
A&A
Volume 594, October 2016
|
|
|---|---|---|
| Article Number | A83 | |
| Number of page(s) | 16 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201628431 | |
| Published online | 14 October 2016 | |
Brown dwarf disks with Herschel: Linking far-infrared and (sub)-mm fluxes⋆
1 ETH Zürich, Institut für Astronomie, Wolfgang-Pauli-Strasse 27, 8093 Zürich, Switzerland
e-mail: daemgens@phys.ethz.ch
2 Department of Astronomy & Astrophysics, University of Toronto, 50 St. George Street, Toronto, ON, M5H 3H4, Canada
3 INAF/Osservatorio Astrofisico of Arcetri, Largo E. Fermi, 5, 50125 Firenze, Italy
4 School of Cosmic Physics, Dublin Institute for Advanced Studies, 31 Fitzwilliams Place, Dublin 2, Ireland
5 SUPA School of Physics and Astronomy, University of St. Andrews, North Haugh, St. Andrews, Fife KY16 9SS, UK
6 European Southern Observatory, Karl-Schwarzschildstr. 2, 85748 Garching, Germany
7 Excellence Cluster “Universe”, Boltzmannstr. 2, 85748 Garching bei München, Germany
8 Faculty of Science, York University, 4700 Keele Street, Toronto, ON M3J 1P3, Canada
9 School of Physics & Astronomy, Cardiff University, Queen’s Buildings, Cardiff CF24 3AA, UK
10 Institute for Astronomy, University of Edinburgh, Royal Observatory, Blackford Hill, Edinburgh EH9 3HJ, UK
Received: 4 March 2016
Accepted: 22 July 2016
Brown dwarf disks are excellent laboratories to test our understanding of disk physics in an extreme parameter regime. In this paper we investigate a sample of 29 well-characterized brown dwarfs and very low-mass stars, for which Herschel far-infrared fluxes and (sub)-mm fluxes are available. We measured new Herschel/PACS fluxes for 11 objects and complement these with (sub)-mm data and Herschel fluxes from the literature. We analyze their spectral energy distributions in comparison with results from radiative transfer modeling. Fluxes in the far-infrared are strongly affected by the shape and temperature of the disk (and hence stellar luminosity), whereas the (sub)-mm fluxes mostly depend on disk mass. Nevertheless, there is a clear correlation between far-infrared and (sub)-mm fluxes. We argue that the link results from the combination of the stellar mass-luminosity relation and a scaling between disk mass and stellar mass. We find strong evidence of dust settling to the disk midplane. The spectral slopes between near- and far-infrared are mostly between −0.5 and −1.2 in our sample, which is comparable to more massive T Tauri stars; this may imply that the disk shapes are similar as well, although highly flared disks are rare among brown dwarfs. We find that dust temperatures in the range of 7−15 K, calculated with T ≈ 25 (L/L⊙)0.25 K, are appropriate for deriving disk masses from (sub)-mm fluxes for these low luminosity objects. About half of our sample hosts disks with at least one Jupiter mass, confirming that many brown dwarfs harbor sufficient material for the formation of Earth-mass planets in their midst.
Key words: brown dwarfs / circumstellar matter / stars: pre-main sequence / infrared: stars / submillimeter: stars
© ESO, 2016
1. Introduction
Brown dwarfs (BDs) are a common outcome of star formation and have been found in large numbers in all nearby star-forming regions (see review by Luhman 2012). Just like their more massive stellar siblings, young brown dwarfs are surrounded by dusty disks. Brown dwarfs have masses of 0.01−0.08M⊙ and luminosities several orders of magnitude lower than stars, while their accretion rates and the disk masses are also lower. Their disks represent an interesting laboratory for studying the evolutionary processes in disks, particularly those related to planet formation, and our methods for inferring disk properties, in an extreme parameter range.
Brown dwarf disks, originally found in near- and mid-infrared surveys (Comeron et al. 1998; Muench et al. 2001; Natta & Testi 2001; Natta et al. 2002; Jayawardhana et al. 2003), are now investigated over the infrared, submillimeter, and millimeter spectral range. For the most part, the general evolutionary blueprint adopted for stellar disks applies to brown dwarf disks as well. The disk lifetimes are 5−10 Myr and thus comparable to or slightly longer than in the stellar regime (Dawson et al. 2013; Luhman & Mamajek 2012). At a given age, brown dwarf disks show a range of masses and geometries, including flat and flared disks as well as disks with inner opacity holes (Mohanty et al. 2004). As in stellar disks, evidence for the presence of large, mm-sized dust grains has been found by various methods (e.g., Apai et al. 2005; Scholz et al. 2007), and was recently demonstrated based on the first brown dwarf data from the Atacama Large Millimeter Array (ALMA; Ricci et al. 2012, 2014).
Observations of brown dwarfs in the (sub)-mm and millimeter domain show that disk masses scale with stellar mass, at around 1% of the stellar mass, albeit with large scatter (Scholz et al. 2006; Klein et al. 2003; Mohanty et al. 2013; Andrews et al. 2013). Substellar disk masses rarely exceed 0.001M⊙, thus only the brightest BD disks have been detected at these wavelengths.
Only recently has it been possible to investigate brown dwarfs in the far-infrared between 70 and 160 μm, thanks to the Herschel space observatory. Harvey et al. (2012b,a) carried out a Herschel survey of disks around ~40 very low-mass objects (VLMOs) at 70 and 160 μm. Comparing their data with radiative transfer models, they infer a wide range of disk masses (from <10-6 to 10-3M⊙). While the upper limit agrees with the values inferred from (sub)-mm observations, the minimum values are lower than expected. A few other groups have recently published their analyses of VLMO disks based on Herschel/PACS data (i.e., wavelength of 70−160 μm): Alves de Oliveira et al. (2013, detections for 12 BDs in ρ, Olofsson et al. (2013, detections for a few VLM stars in Chamaeleon), Bulger et al. (2014, detections for 58 VLMOs in Taurus), and Liu et al. (2015b, detections for 5 VLMOs in the TW Hydrae association), most without (sub)-mm detection. One finding of these studies is that the geometrical parameters of the disk, in particular the flaring angle, seem to be similar in VLMOs compared with more massive stars. Finally, Joergens et al. (2013) report a highly flared disk with a mass of 10-4M⊙ for the isolated planetary-mass object OTS44, using a spectral energy distribution (SED) with a detection at 70 μm and an upper limit at 160 μm, but without (sub)-mm data points.
So far, the focus has been on the analysis of VLMO disks in specific wavelength domains (e.g., near-infrared (NIR), far-infrared (FIR), or (sub)-mm), but there is little work on the links between the different parts of the SEDs of these sources. In this paper, we set out to study the FIR and sub-mm to mm fluxes for a sample of well-characterized VLMOs with masses below 0.2 M⊙, for which information is available in both these wavelength domains. This approach allows us to investigate specifically physical properties of the disk that affect the long-wavelength portions of the SED, including the degree of flaring, disk mass, dust temperature, and the interdependence among these parameters.
2. Sample and data
2.1. Observations and literature data
The present study combines our own Herschel observations of VLMOs with previously published Herschel data. We aim to select all VLMOs (defined as spectral type M4 or later) with well-sampled disk SEDs and well-known stellar parameters. More specifically, we focus on objects with a detection in at least one Herschel band and a detection at (sub)-mm wavelengths.
2.1.1. New Herschel observations
Stellar properties.
Observations for our program OT1_ascholz_1 (PI: A. Scholz) were carried out on February 22 and March 12, 2013, in the three PACS (Poglitsch et al. 2010) bands at wavelengths of 70, 100, and 160 μm. Targets were selected to be spectroscopically confirmed low-mass and substellar objects that show strong excess at mid-infrared wavelengths indicating the presence of an inner disk, are bright in the near- to mid-infrared (F(24 μm) > 15 mJy), have been extensively characterized at optical, NIR, and sub-mm wavelengths, and are well-isolated (>1′) from nearest neighbors and strong cloud background at 24 μm. Out of 16 targets selected according to these criteria, 11 were observed, spanning spectral types from M4.75 to M8. Table 1 lists the most important parameters for the central objects and references. Luminosities were inferred from the J-band magnitude and bolometric corrections in Pecaut & Mamajek (2013). Through a comparison with other bolometric correction tables (e.g., Hartigan et al. 1994), we infer a systematic uncertainty on the order of <20%. Stellar masses were derived from effective temperatures, inferred from spectral types using Table 8 in Luhman et al. (2003), and BCAH98 isochrones (Baraffe et al. 1998) assuming an age of 2 Myr based on their membership in the Taurus or ρ-Ophiuchus star-forming regions (Daemgen et al. 2015; Wilking et al. 2005). Inferred masses range from 0.03 M⊙ to 0.2 M⊙.
2.1.2. Literature data
Through an extensive literature search, we found 17 additional objects in the same mass range that have Herschel and (sub)-mm data points. Herschel data for these objects have been published by Bulger et al. (2014), Harvey et al. (2012a), Howard et al. (2013), Olofsson et al. (2013), and Keane et al. (2014). The (sub)-mm data come from a variety of sources. One more object, 2M0444, which ranks among the brightest disks in the VLM domain, has a reliable 70 μm flux from Spitzer/MIPS plus (sub)-mm data, and was also added to the sample. We derive stellar properties in the same way as for our core sample with the exception of the TWA Hydrae sources for which we assume an age of 10 Myr (Bell et al. 2015) to derive their masses. We list all derived values in Table 1. Flux measurements of the core and literature samples are presented in Table 2.
Far-IR and (sub)-mm fluxes or 3σ upper limits.
2.1.3. Sample characteristics
The final sample of 29 objects is a mixed group of VLMOs from different regions, dominated by objects in Taurus, but also including a few in ρ Ophiuchus (3), the TW Hydrae association (3), and Chamaeleon I (1). The sample ranges in mass from 0.03 to 0.2M⊙. Most of the sources are likely to have ages between 1−3 Myr, the exception being the 3 objects in TW Hydrae, which are probably significantly older. Our selection process, as defined above, essentially means that we pick objects with bright disks that have already been targeted by Herschel and by (sub)-mm campaigns, which is obviously not a well-defined category. Therefore, the sample is not complete down to a well-defined mass or luminosity limit.
The same, however, can be said for all brown dwarf samples studied so far in the FIR and (sub)-mm domain. The sample used by Harvey et al. (2012a) includes objects in nine nearby, diverse star-forming regions, with ages from 1 to 10 Myr, handpicked for Herschel observations. The range in spectral types is slightly wider than ours, including objects that are earlier and later than our M4 and M8 limits. The objects analyzed by Liu et al. (2015a) is based on the Harvey sample, plus some more objects observed by Herschel. Their sample is therefore, as the authors state, “biased towards very low-mass substellar objects”. The studies by Alves de Oliveira et al. (2013) and Bulger et al. (2014) cover almost all known disk-bearing brown dwarfs in ρ Ophiuchus and Taurus, respectively, but not all are detected. While these surveys are almost complete for the studied region, they suffer from the fact that the detection limit is not homogeneous. Such selection effects have to be taken into account when comparing results.
Three targets (CFHT-18, FW Tau, TWA 32) have stellar or BD companions that fall within the photometric aperture of our far-IR measurements (Konopacky et al. 2007; Chen et al. 1990; Shkolnik et al. 2011). We keep them in the sample, but caution that binarity can have an effect on the SED and other measured parameters, depending on the brightness and color of the companion. The existence of additional binary companions, including spectroscopic binaries, in the sample cannot be excluded, as no comprehensive binary survey was executed for the sample. Spectroscopic binaries among pre-main-sequence stars are, however, rare (~6% for low-mass stars in Taurus; Nguyen et al. 2012).
2.2. Data reduction and photometry
All Herschel photometry of our core sample of 11 targets rely on the phot project level 3 automatic pipeline results (SPG 11.1.0), obtained using the Herschel Interactive Processing Environment (HIPE; Ott 2010). The pipeline combines all consecutive observations of the same target (usually 2) and performs high-pass filtering with a flux cut at 1.5 times the standard deviation of the flux per pixel and a filter width of 15, 15, and 32 readouts in the 70 μm (blue), 100 μm (green), and 160 μm (red) maps, respectively. The built-in MMT deglitching routine was applied and the output pixel scale was set to 2′′, 3′′, and 4′′ for the blue, green, and red filters, respectively. Smaller pixels scales have been tested for a subset of the reductions and did not lead to significantly different results. Image stamps of the fully reduced Herschel/PACS data are shown in Fig. 1.
 |
Fig. 1 Herschel/PACS observations centered on the individual targets. Postage stamps are 1′× 1′, North is up and east to the left. |
Photometry was performed in IDL using the routine aper.pro to measure sky-subtracted flux values. If possible, our custom procedure recenters on the source and then performs aperture photometry. Aperture radii were set to the values used by Alves de Oliveira et al. (2013), i.e., 5.̋61, 6.̋79, and 11.̋39 in the blue, green, and red filters, respectively. Inner and outer sky radii were set to two and three times this value, respectively. If strong spatially extended emission close to the source was detected by eye (or indications of it in the curve of growth), aperture radii smaller by a factor of 1.5 (2M04152746) or 2 (2M04412534, CFHT-6, GM Tau, ISO32, ISO102, ISO160) were used to exclude as much as possible of the extended emission from leaking into the point-source photometry and to ensure that the sky annuli provide a good estimate of the level of the background at the position of the target. Aperture corrections were applied according to the tabulated values in Balog et al. (2014). Since the detected emission stems from cold dusty material in the circum-substellar disks, color correction factors of −3.4%, 1.8%, and 2.4% in blue, green, and red bands were applied assuming an effective temperature of T = 30 K (Muller et al. 2011). The flux uncertainties introduced through the color correction factor by the − a priory unknown − disk temperatures are smaller than 2%, 5%, and 10% in blue, green, and red for T ≥ 30 K but can be much larger, particularly at 70 μm, for T ≲ 20 K. Flux uncertainties were estimated from the scatter in 15 apertures of the same size as the science aperture, distributed on a circle around the source. Some apertures were excluded from the uncertainty estimate (2σ outlier rejection) to lower the impact of spatial background variability at the position of the noise apertures.
As Popesso et al. (2012) show, the high-pass filter applied by the automatic HIPE/phot project pipeline may compromise flux measurements close to extended emission. To measure the impact on our photometry, we compare our results with two alternative reductions: first, the HIPE pipeline as described above but without high-pass filtering and, second, the scanamorphos pipeline that is designed to conserve large-scale emission (Roussel 2013). We find agreement to within 1σ between our results and those based on both alternative reductions for all targets. It appears, however, that most flux uncertainties in the scanamorphos reduction are larger than their HIPE-reduced counterparts. This is likely because of gradients in the large-scale emission that cause artificially large uncertainties with the applied photometry routine. In the following, we use the fluxes derived from the automatic HIPE/phot project pipeline.
3. Results
3.1. Far-IR photometry and SEDs
We detect all eleven targets at 100 μm. Seven of these were also detected at 160 μm, and we derive 3 sigma upper limits for the rest of the sample at 160 μm. Furthermore, all three attempted 70 μm observations led to detections. In Table 2, we list our results together with complementary literature values at 70 μm (Bulger et al. 2014).
Where available, we compare our far-IR measurements with previous observations of the same targets. Bulger et al. (2014) measure F160 fluxes for all eight Taurus targets of our core sample. Most of our fluxes in Table 2 agree to within 1σ with the Bulger et al. values. Two targets (CIDA-1 and 2M04232801) show deviations of 1.5σ and 2.2σ, respectively. The discrepancy can be explained by source variability, which is an intrinsic feature of young low-mass stars even at far-IR wavelengths (Billot et al. 2012). Despite the fact that we compare optical, far-IR, and sub-mm photometry from different epochs, the observed variability of up to >20% at 70−160 μm does not severely affect our analysis because far-IR fluxes enter our analysis mostly logarithmically (e.g., Eq. (2)), i.e., as an uncertainty of ~0.08 dex. We find agreement for ISO 32 and ISO 160 to within the uncertainties with the values derived by Alves de Oliveira et al. (2013) in all three PACS bands. For ISO 102, Alves de Oliveira et al. (2013) measure F70 = 80.1 ± 5.6 and F100 = 48.4 ± 19.1, which are both significantly smaller than our measurements (2σ and 2.5σ, respectively). Part of the difference can be explained by the different effective temperature assumed for the color correction. The difference between a color correction at Teff = 30 K and the temperature of Teff = 1000 K assumed by Alves de Oliveira et al. (2013) is ~2%, ~5%, and ~10% in the blue, green, and red bands. As Herschel fluxes are dominated by emission from the circumstellar dust at low temperatures, we assume that 30 K is a better representation of the color correction. The remaining discrepancy may be due to systematic biases of the different photometry strategies, which are likely enhanced by the strong nebular background in the surroundings of ISO 102 or by source variability. As the signal-to-noise ratio of our pointed observations is higher than that of the scan maps produced by Alves de Oliveira et al. (2013), we use our photometry in the following.
Using literature data for 18 additional targets, we compiled the largest and mostly complete collection of very low-mass stars and brown dwarfs that were detected at both far-IR and (sub)-mm wavelengths (Table 2). We present a sample of 29 targets that were detected in at least one of the Herschel/PACS bands (28 detections at 70 μm, and 22 at 160 μm). Twenty-eight of these have at least one detection at (sub)-mm wavelengths between 850 μm and 1300 μm. For one target, CFHT-18, only an upper limit at 1300 μm was found in the literature.
We compile SED between optical and millimeter bands from the literature (Appendix A). For easy comparison, all SEDs scaled to their J-band flux are shown in Fig. 2.
 |
Fig. 2 Dereddened SEDs normalized at J band. Red curves show the SEDs of the original sample, and blue lines show the literature SEDs. Targets that were excluded from further discussion (see Sect. 3.1) are shown with dotted lines. For comparison, the expected photospheric emission of an M5 star is shown in dashed gray (Cushing et al. 2005). |
The SEDs of five targets (IRAS 04158+2805, L1521F-IRS, ZZ Tau IRS, 2MASS J04381486+2611399, and TWA 30B, i.e., all targets with a horizontal or positive slope between 10 and 100 μm in Fig. 2), show indications of a dense circumstellar envelope such as that of Class I sources or an edge-on disk. Owing to the different nature and uncertain photometry of these targets, they are excluded from subsequent disk parameter estimates.
For our VLMO sample, we notice a strong correlation between FIR and (sub)-mm fluxes. Figure 3 shows the correlations of F100 and F160 with Fmm (similar for F70).
 |
Fig. 3 F100 and F160 as a function of mm fluxes. Millimeter fluxes are identical to F1300 or were converted from other wavelengths according to Eq. (1). To compare, T Tauri stars in Chamaeleon I and II are shown as plus and cross symbols in the bottom panel (Winston et al. 2012; Spezzi et al. 2013). The dotted lines show linear fits to all points except upper limits and binaries. |
The latter is equal to F1.3 mm, where available, or has been converted from F850 or F890 (see Table 2) according to  (1)This equation has been derived assuming that the (sub)-mm flux is dominated by optically thin emission and can be approximated with the Rayleigh-Jeans law (Fν ∝ ν2). We further use a linear opacity dependence (Fν ∝ κν with κν ∝ νβ for β = 1, see also Sect. 3.3) and scale all measurements to a distance of D = 140 pc.
(1)This equation has been derived assuming that the (sub)-mm flux is dominated by optically thin emission and can be approximated with the Rayleigh-Jeans law (Fν ∝ ν2). We further use a linear opacity dependence (Fν ∝ κν with κν ∝ νβ for β = 1, see also Sect. 3.3) and scale all measurements to a distance of D = 140 pc.
A Spearman’s rank test returns correlation parameters of 0.61, 0.62, and 0.94 for correlations of Fmm with F70, F100, and F160, respectively, taking into account detections in the whole VLM sample and excluding binary stars. The respective significances are 6 × 10-3, 3 × 10-2, and 8 × 10-7, i.e., the measured correlations are significantly different from zero. The measured slopes of best linear fits to the data (in log-log space, considering the same selection as for the correlation coefficients) are m70 = 1.33 ± 0.76, m100 = 1.43 ± 0.63, and m160 = 1.33 ± 0.93. The observed correlations also seem to hold for more massive T Tauri stars, which are shown with black symbols in Fig. 3 (Winston et al. 2012; Spezzi et al. 2013). Their mm fluxes have been derived from F500 using Eq. (1) as well. We discuss the physical reason for the observed correlation in Sect. 5.1.
3.2. Spectral slopes
As a diagnostic for far-infrared fluxes of our young brown dwarf sample, we derive spectral slope indices following (Adams et al. 1987):  (2)Such indices provide model-free estimates of the strength of far-IR dust emission, independent of stellar luminosity. In Table 3, we present the slopes between the J band (λ0 = 1.24 μm), which is dominated by the stellar photosphere, and the Herschel/PACS bands αJ−70, αJ−100 and αJ−160.
(2)Such indices provide model-free estimates of the strength of far-IR dust emission, independent of stellar luminosity. In Table 3, we present the slopes between the J band (λ0 = 1.24 μm), which is dominated by the stellar photosphere, and the Herschel/PACS bands αJ−70, αJ−100 and αJ−160.
Far-IR slopes and disk masses.
A histogram of the slope distribution is shown in Fig. 4.
 |
Fig. 4 Histograms of infrared slopes αJ−70, αJ−100, and αJ−160. At αJ−70 and αJ−160, our brown dwarf samples are compared to T Tauri stars in Chamaeleon I and II (Winston et al. 2012; Spezzi et al. 2013). |
We find that the NIR-FIR slopes of the VLMOs in our samples range mostly between −1.0 and −0.5. The median is −0.72,−0.71, and −0.76 for αJ−70, αJ−100, and αJ−160, respectively, with a 1-sigma spread of ~0.2. For comparison, we calculated the same slopes for a literature sample of T Tauri stars from Winston et al. (2012) and Spezzi et al. (2013), also shown in Fig. 4 as a dash-dotted histogram. The range found for T Tauri stars is very similar to the values quoted for our BD sample, while the medians are marginally smaller (−0.77, −0.79 for αJ−70, αJ−160), but still well within the standard deviation. Thus, BDs and T Tauri stars have similar spectral slopes in the FIR.
We also calculate the same slopes for the Class II Taurus sample by Bulger et al. (2014), which partially overlaps with ours but covers a slightly larger spectral type range. Again the range of the slopes and the peak of the distribution are similar to our results (median −0.71, −0.73 for αJ−70, αJ−160). Since the Bulger et al. sample covers a large percentage of all known low-mass stars in Taurus, the similarity provides reassurance that the spectral slope distribution of our BD sample is not significantly affected by selection biases.
In Fig. 5, we compare αJ−70, αJ−100, and αJ−160 with the mm-flux Fmm (Eq. (1)), which is expected to be proportional to the disk mass (see Sect. 3.3).
 |
Fig. 5 Infrared slope as a function of mm flux. Millimeter fluxes are identical to F1300 or were converted from other wavelengths according to Eq. (1). Binaries are indicated with diamonds. For comparison, data from more massive T Tauri stars in the Chamaeleon star-forming region are shown (Cha I, Winston et al. 2012; Cha II, Spezzi et al. 2013). |
For comparison with higher mass counterparts, we again use the slopes derived from the T Tauri surveys by Winston et al. and Spezzi et al. and mm fluxes converted from F500. The numbers are added to Fig. 5 as black crosses. The bulk of the data points for VLMOs and T Tauri stars occupy the same region in these diagrams, without obvious trends, and a Spearman’s rank test cannot rule out that BD slopes are uncorrelated with mm fluxes (significances of 0.27, 0.65, and 0.25 for αJ−70, αJ−100, and αJ−160, respectively, based on detections in the whole VLM sample exluding binary stars).
3.3. Disk masses
We convert (sub)-mm fluxes to disk masses using 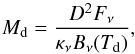 (3)with distance D from Table 1,
(3)with distance D from Table 1, 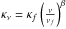 for β = 1 and κf = 230 GHz = 0.02 cm2 g-1, assuming a gas:dust ratio of 100:1. We note that choosing β = 2 instead of β = 1 decreases disk mass estimates of targets observed at F890 by ~0.2 dex. When available, Fν = F1300, otherwise F890 or F850 are used (see Table 2). The dust temperature Td is calculated following the prescription by Andrews et al. (2013)
for β = 1 and κf = 230 GHz = 0.02 cm2 g-1, assuming a gas:dust ratio of 100:1. We note that choosing β = 2 instead of β = 1 decreases disk mass estimates of targets observed at F890 by ~0.2 dex. When available, Fν = F1300, otherwise F890 or F850 are used (see Table 2). The dust temperature Td is calculated following the prescription by Andrews et al. (2013) (4)which yields dust temperatures between ~7 and 20 K. This scaling of the dust temperature with the stellar luminosity appears to be more realistic than using fixed values between 10 and 20 K as in previous brown dwarf disk surveys (e.g., T = 15 K in Scholz et al. 2006, 20 K in Broekhoven-Fiene et al. 2014); see Sect. 5.3 for further justification. In Table 3, we list the derived disk masses according to Eqs. (3), (4). For reference, we also include disk masses with Td = 20 K.
(4)which yields dust temperatures between ~7 and 20 K. This scaling of the dust temperature with the stellar luminosity appears to be more realistic than using fixed values between 10 and 20 K as in previous brown dwarf disk surveys (e.g., T = 15 K in Scholz et al. 2006, 20 K in Broekhoven-Fiene et al. 2014); see Sect. 5.3 for further justification. In Table 3, we list the derived disk masses according to Eqs. (3), (4). For reference, we also include disk masses with Td = 20 K.
Figure 6 shows the distribution of disk masses inferred from (sub)-mm fluxes as a function of stellar host mass.
 |
Fig. 6 Disk mass, derived from (sub)-mm fluxes, in units of solar masses (top panel) and stellar mass (bottom panel) as a function of the mass of the parent body for all targets in this paper. Binaries are highlighted with diamonds. A conservative estimate of disk mass uncertainty arising from unknown individual distances is shown in the bottom left of the top panel, assuming a conservative Δdist = ±10% (cf. Torres et al. 2007, who estimate a “depth” of Taurus of 20 pc). Dotted lines show the typical sensitivity limits derived from Eq. (3) for targets in Taurus (F1300,lim ≈ 1 mJy, dist = 140 pc) and TW Hya (F1300,lim ≈ 0.05 mJy, dist = 50 pc), using BCAH98 isochrones to convert mass to luminosity. |
With disk masses at around 1% of the stellar mass, we see that the current sample shows disk masses mostly at the upper edge of the disk mass distribution in the respective stellar mass range. This is a selection effect because the required detection at (sub)-mm wavelengths prefers targets with the largest reservoirs of circumstellar dust. The figure confirms that relative disk masses for brown dwarfs and stars are in the same range, i.e., the disk mass scales with object mass.
4. Disk models
To investigate the implications of our observational results on the physical properties of VLMO disks, such as flaring and mass, we ran a small grid of disk models. In our models, each disk is characterized by its dust mass, inner and outer radii, and the density distribution of dust in the radial (R) and vertical (z) directions. If Σ is the column density and Hp the pressure scale height at a given R, then the density is given by  (5)where
(5)where  (6)where Σ ∝ R− p and a normalization are defined by the disk mass. The dust pressure scale height Hp has a well-defined physical meaning when the disk is in hydrostatic equilibrium and dust and gas are well mixed. This computation involves an iterative solution of the radiation transfer, as Hp depends on the temperature structure, which, in turn depends on the disk geometry (and thus Hp). Moreover, the dust is likely not well mixed, if significant differential settling occurs. Therefore, in most of the recent papers (e.g., Sicilia-Aguilar et al. 2015; Liu et al. 2015a), Hp is assumed to be a power-law function of R,
(6)where Σ ∝ R− p and a normalization are defined by the disk mass. The dust pressure scale height Hp has a well-defined physical meaning when the disk is in hydrostatic equilibrium and dust and gas are well mixed. This computation involves an iterative solution of the radiation transfer, as Hp depends on the temperature structure, which, in turn depends on the disk geometry (and thus Hp). Moreover, the dust is likely not well mixed, if significant differential settling occurs. Therefore, in most of the recent papers (e.g., Sicilia-Aguilar et al. 2015; Liu et al. 2015a), Hp is assumed to be a power-law function of R,  (7)where Hp(R0) is the pressure scale height at the fiducial radius R0 and ξ is a free parameter, which is often defined in the literature as the flaring index. We note that in fully flared, hydrostatic equilibrium disks ξ ~ 1.3 and in flat disks ξ ~ 1.1. The shape of the disk is defined by the combination of Hp(R0) and ξ, which determine the emission at all wavelengths once all other parameters are fixed (Bulger et al. 2014; Sicilia-Aguilar et al. 2015). In summary, a disk model is defined by six parameters: the disk mass Md, inner and outer radii Ri and Rout, the slope of the surface density profile p, and the two parameters Hp(R0), ξ.
(7)where Hp(R0) is the pressure scale height at the fiducial radius R0 and ξ is a free parameter, which is often defined in the literature as the flaring index. We note that in fully flared, hydrostatic equilibrium disks ξ ~ 1.3 and in flat disks ξ ~ 1.1. The shape of the disk is defined by the combination of Hp(R0) and ξ, which determine the emission at all wavelengths once all other parameters are fixed (Bulger et al. 2014; Sicilia-Aguilar et al. 2015). In summary, a disk model is defined by six parameters: the disk mass Md, inner and outer radii Ri and Rout, the slope of the surface density profile p, and the two parameters Hp(R0), ξ.
In addition, one needs to fix the stellar parameters (mass, luminosity, and radius), and the dust opacity. We adopt a dust model, which is a mixture of 7% (in volume) silicates (amorphous Mg-rich grains with olivine stoichiometry, optical constant from Jaeger et al. 1994), 21% carbonaceous materials (aC_ACH2, optical constants from Zubko et al. 1996), 42% water ice (Warren 1984), and 30% vacuum. For most models, the grain size ranges from a minimum amin = 0.2 μm to amax = 150μm with slope 3.5. The corresponding opacity is 2 cm2 g-1 at 1300 μm, 150 cm2 g-1 at 160 μm, and 700 cm2 g-1 at 1 μm. The opacity at 1.3 mm is the same as the value we used to calculate disk masses in Sect. 3.3. The opacities at 1.3 mm and 890 μm are also simliar to those used by Andrews et al. (2013) and many other studies (e.g., Ricci et al. 2014).
We compute the temperature structure and the emission at selected wavelengths in the FIR and (sub)-mm using the radiation transfer code RADMC-3D1 (version 0.39; C.P. Dullemond). We consider two different central objects; one object, BD in the following, with L⋆ = 0.03 L⊙, M⋆ = 0.05 M⊙, and T⋆ = 2800 K, and a more luminous object, TTS in the following, with L⋆ = 0.15 L⊙, M⋆ = 0.2 M⊙, and T⋆ = 3150 K. All our targets and most of those from the literature have luminosities and effective temperatures roughly within this range. We include in the calculations the heating due to the interstellar radiation field (IRF) as in Draine (2011). As the FIR and (sub)-mm fluxes depend only weakly on the disk inclination as long as i is reasonably small (i ≲ 60−65 deg), we fix i = 0 in all cases.
Table 4 gives the values of the disk parameters for each model.
Model parameters.
In all cases, p = 1 and Ri = 0.1 AU. The values of Hp(R0) and ξ were chosen to encompass a large range of possibilities, from very flat to very flared disks. We note that fully flared disks, when computed using a two-layer disk model as in Chiang & Goldreich (1997), Dullemond et al. (2001) have Hp(10 AU) ~1.5 AU and ~1 AU for the BD and TTS, respectively, with ξ ~ 1.34−1.30. Models with higher values of H0 and/or p are difficult to justify. In Table 4 we give total disk masses, with the usual assumption of a gas-to-dust mass ratio of 100, even if the disk models only depend on the dust mass. For an easier comparison with what is often used by other authors, for each model we give the value of Hp at R = 100 AU in the last column.
As in other studies of disk SEDs for TTS (see, for example, Sicilia-Aguilar et al. 2015), we find that, for fixed stellar poperties, disks are colder when they are less flared or have higher mass. The midplane temperature in the outer disks is rather low, but never smaller than what is expected for the same grains heated only by the IRF (~7.5 K). The (sub)-mm fluxes depend mostly on the disk mass, with a very weak dependence on the other parameters. The dependence on L⋆, in particular, is only weak. On the contrary, the FIR fluxes depend strongly on the temperature and, therefore, on L⋆, the disk shape, and also, although to a lesser degree, on the disk mass, as this also affects the temperature. In our grid, for the adopted opacity, the 100 μm optical depth in the vertical direction is <1 for R> 2 AU only for the lowest disk mass. However, as is always the case, a non-negligible portion of the emission may come from the optically thin, hotter surface layers (see, e.g., Liu et al. 2015a). These trends are summarized in Fig. 7, which plots the 100 μm and 160 μm fluxes as a function of the 1300 μm flux for all the models.
 |
Fig. 7 Model-predicted 100 μm (top panel) and 160 μm fluxes (bottom) vs. 1300 μm flux. Each colored point represents a model. Green symbols indicate the BD models, magenta symbols the TTS models. Different symbols refer to different disk masses: triangles for Md = 3 × 10-5M⊙, squares for Md = 3 × 10-4M⊙, dots for Md= 3 × 10-3M⊙, pentagons for Md= 1.5 × 10-2M⊙. Models for the same Md and different flares are connected by solid lines; flatter disks have lower fluxes at both wavelengths. Models with the same values of Hp(R0) and ξ are connected by dashed lines. Models mod2b, mod2b, small and mod2b,large are all shown with filled squares. Models mod2b1 and mod2b2, characterized by different grain opacity, are shown by empty squares, models with larger grains have larger mm flux and smaller FIR fluxes. For easy comparison, symbols from Fig. 3 are included in gray. |
The figure shows also that both FIR and (sub)-mm fluxes do not depend strongly on Rout nor on reasonable variations of the grain opacity. Another result worth noticing is that changes in the disk shape can more than compensate variations of L⋆, as shown by the fact that flat TTS disks lie in the same region of the diagram than flared BD disks.
5. Discussion
5.1. Correlation between FIR and (sub)-mm fluxes
We have shown in Sect. 3.1 (Fig. 3) that the observed FIR fluxes of our VLMO sample scale positively with the mm fluxes. A similar trend is also seen in Herbig Ae/Be stars (Pascual et al. 2016). How can this be interpreted in the light of our modeling result that FIR fluxes do not scale strongly with disk mass for a star of fixed luminosity?
Radiation transfer models show that the (sub)-mm flux depends primarily on disk mass and only weakly on the other parameters. In contrast, FIR fluxes depend mostly on the temperature distribution, which itself is controlled by the stellar luminosity and disk shape. The dependence of the FIR fluxes on disk mass is weak, becoming only slightly stronger in more flared disks. In particular, the dependence of FIR on disk mass is much weaker than the linear relation between Fmm and Md as given by Eq. (3), which accordingly does not serve to correlate FIR and Fmm disk emission. Self-consistent hydrostatic equilibrium models (e.g., Sicilia-Aguilar et al. 2015) show that, for fixed stellar parameters, disks of increasing mass are more flared and, therefore, have stronger FIR fluxes. However, even for fully flared disks the predicted correlation between the FIR flux and the (sub)-mm flux for a star of fixed luminosity is much weaker than linear.
It is noteworthy that optical depth apparently plays a subordinate role for the FIR−Md relation; despite the fact that the least massive disks are opticaly thin at most radii (>2 AU at 100 μm) and that optically thin layers always contribute to the overall flux, even in regions where the vertical optical depth is >1, our models show no strong correlation of FIR with disk mass. We therefore provide an alternative explanation linking FIR emission directly to the total luminosity of the VLMOs. We suggest that the apparent correlation between FFIR and Fmm is in fact the result of two underlying correlations, namely the mass-luminosity relation for young VLMOs and a correlation of disk mass with stellar mass, paired with the observed strong correlation (Spearman’s rank correlation parameters between 0.5 and 0.8 of all detections excluding binaries) of FFIR and L⋆ (Fig. 8).
 |
Fig. 8 F160 flux as a function of target luminosity. Symbols as in Fig. 3. Best linear fit to all values excluding upper limits and binaries shown as dashed line. Measured slopes mFIR of best linear fits log (FFIR) ∝ mFIRlog (L⋆) in all FIR bands: m70 = 1.30 ± 0.25, m100 = 1.09 ± 0.39, and m160 = 1.14 ± 0.24. |
What is observed in Fig. 3 could then be traced back to a correlation Fmm ↔ Md , according to Eq. (3), a scaling between Md and M⋆ (assumed to be linear, e.g., Andrews et al. 2013), and a M⋆−L⋆ relation (L⋆ ≈ 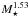 determined for 1 Myr isochrones by Baraffe et al. 2015) (the result is not sensitive to the particular M−L correlation). The predicted slope m of the correlation between Fmm and L⋆ of m = 0.65 [log (mJy)/log (L⊙)] is, however, shallower than what is seen in the observations (m = 1.30 ± 0.27 [log (mJy)/log (L⊙)]). The weak additional dependence between mm fluxes and other parameters (in particular, the temperature) or a stronger dependence between disk mass and stellar mass can make the trend slightly steeper and closer to the observed one. In fact, the most recent study of the Md−M⋆ relation (Ansdell et al. 2016) suggests that the correlation is steeper than linear with a coefficient of 1.7−1.8 (for regions with ages of 1−2 Myr). Their sample extends to masses of about 0.1 M⊙. If this correlation continues into the substellar regime, it would bring our estimate above for the trend between FIR and Fmm in agreement with the observations.
determined for 1 Myr isochrones by Baraffe et al. 2015) (the result is not sensitive to the particular M−L correlation). The predicted slope m of the correlation between Fmm and L⋆ of m = 0.65 [log (mJy)/log (L⊙)] is, however, shallower than what is seen in the observations (m = 1.30 ± 0.27 [log (mJy)/log (L⊙)]). The weak additional dependence between mm fluxes and other parameters (in particular, the temperature) or a stronger dependence between disk mass and stellar mass can make the trend slightly steeper and closer to the observed one. In fact, the most recent study of the Md−M⋆ relation (Ansdell et al. 2016) suggests that the correlation is steeper than linear with a coefficient of 1.7−1.8 (for regions with ages of 1−2 Myr). Their sample extends to masses of about 0.1 M⊙. If this correlation continues into the substellar regime, it would bring our estimate above for the trend between FIR and Fmm in agreement with the observations.
5.2. Spectral slopes in models and observations
In Fig. 9 we compare the spectral slopes derived from the observations (in gray) with the numbers produced by the models.
 |
Fig. 9 Model predictions of infrared slopes as a function of mm flux. Colors and symbols as in Fig. 7. For reference, our measurements from the bottom panel of Fig. 5 were included in gray. |
This is similar to the bottom panel of Fig. 5, but with models overplotted. We show here the J−160 slopes because most literature objects do not have a 100 μm flux. Our results do not depend on that particular choice. As explained in Sect. 4, the shape of the disk is varied in the models by changing the flaring index and the scale height H0, which are both listed in Table 4. The models cover three cases, from fully flared to very flat disk. The spectral slope depends strongly on the disk shape, but little on other parameters and, particularly, not on the disk mass and stellar luminosity.
From Fig. 9 it is clear that the observed slopes are well reproduced by the models for moderately flared and flat disks. The fully flared disks, on the other hand, with a very high flaring index of 1.35 and large H0, predict spectral slopes that are not seen in our sample. Since our sample contains objects that are bright in the FIR (i.e., they are detected with Herschel), it is unlikely that objects with higher spectral slopes exist but are missing. A comparison with literature samples in Sect. 3.2 provides further confirmation. We conclude that the overwhelming majority of disks around very low-mass stars and brown dwarfs shows some flattening of the dust geometry compared to the hydrostatic case.
Our modeling results are in line with the findings of other groups. In Scholz et al. (2006) it was already found that brown dwarf disks do not have the elevated flux levels expected for the hydrostatic case. Papers by Harvey et al. (2012a), Alves de Oliveira et al. (2013), and Liu et al. (2015a) fit SEDs with models calculated with a prescription analogous to ours for samples of mostly brown dwarfs (see Sect. 2.1 for more details on their samples). These authors all find that the flaring index ranges from 1.0 to 1.2 and the scaling factor Hp(100 AU) ranges from a few to 20, which again excludes the fully flared disks. Liu et al. (2015a) also point out that the flaring index ξ might be a function of spectral type (and thus stellar mass) in the brown dwarf regime with lower flaring indices for spectral types later than M8. Our sample does not extend to these late spectral types and therefore we cannot test this particular result.
5.3. Disk masses from mm fluxes
Before Herschel results were available, disk masses for brown dwarfs were mostly derived from single-band measurements at 0.85 or 1.3 mm (e.g., Klein et al. 2003; Scholz et al. 2006; Mohanty et al. 2013), using Eq. (3) with fixed temperature and opacity. At these wavelengths, the disks are optically thin and the emitted flux can be assumed to be proportional to the dust masses. For this calculation, it is assumed that dust grains emit as blackbodies; realistic values for opacity and dust temperature have to be adopted. This is the method we used in Sect. 3.3 to estimate the disk masses in our sample.
With the models presented in Sect. 4 we can check the validity of the assumptions for the blackbody-based disk masses and evaluate uncertainties. In Fig. 10 we show the dust temperature required to reproduce the model disk mass with the blackbody-based prescription used in Sect. 3.3 from the 1300 μm flux (T1300) as function of the slope αJ−160 for the BD and TTS models.
 |
Fig. 10 Values of the temperature needed to recover the model disk mass from the 1300 μm flux T1300 vs. αJ−160 for BD and TTS models. Colors and symbols as in Fig. 7. T1300 increases in more flared disks and decreases with the disk mass. TTS models, which have L⋆ that is five times larger than BD models, have higher T1300 however, there is a large region of overlap. The dashed lines show the values of T1300 according to the Andrews et al. prescription (TA = 25(L⋆/L⊙)1/4 K), green for the BD luminosity and magenta for TTS. |
Very similar results are obtained for the 890 μm flux. The values of T1300 reflect the overall temperature distribution in the disk; they are larger for more flared disks, as shown by the positive correlation of T1300 with αJ−160. The value T1300 is lower for more massive disks because stellar radiation does not penetrate the disk as deeply and the average temperature (at a given distance from the star) remains low. For some models, T1300 is very low, well below 10 K. Only very flared, low-mass BD and TTS disks have T1300 ≳ 20 K. If we consider the observed range of αJ−160, we can conclude that for most disks the appropriate values of T1300 are in the range 10−15 K. Higher values do not seem justified.
In Fig. 10, the horizontal lines indicate the temperatures expected for the BD and TTS luminosity adopted in our models, based on the scaling law derived by Andrews et al. (2013), which we have also used in Sect. 3.3. The values are ~10 and 15 K, respectively. Most models in the observed range of αJ−160 have T1300 within this range and the adoption of their scaling law therefore appears justified. Figure 11 plots, as a function of αJ−160, the difference between the values of Md obtained with TA from the Andrews et al. prescription and the model disk mass.
 |
Fig. 11 Ratio of the disk mass computed from TA over model disk mass as a function of αJ−160. Colors and symbols as in Fig. 7. |
The difference is typically less than a factor two, which is the maximum error that is made by adopting the blackbody assumption with the luminosity-scaled dust temperature.
However, it should be noted that many BD and TTS models have very similar values of T1300, in spite of the factor 5 difference in L⋆. The Andrews et al.T1300 values, which scale only with L⋆, may introduce a spurious trend in the disk mass, especially if extended to very low L⋆, when T1300 may be nominally lower than the value of ~7 K owing to heating by the IRF. A more accurate value of T1300 can be obtained if αJ−160 or any other FIR slope is known. In the case in which only FIR fluxes and no mm fluxes are available one requires an accurate stellar luminosity and a careful assessment of the temperature structure of the disk, since FIR fluxes depend strongly on temperature and disk shape and only weakly on disk mass (see Fig. 7).
Very recently, van der Plas et al. (2016) proposed a new prescription to derive the disk mass from single wavelength (sub)-mm fluxes. They favor a scaling law with L⋆ that is flatter than the Andrews et al. (2013) law, namely Td = 22 K (L⋆/L⊙)0.16, based on a grid of models with fixed shape (H0(100 AU) = 10 AU, ξ = 1.125). The difference between the two laws is larger at lower L⋆, becoming a factor ~1.6 for L⋆ = 0.001 L⊙. The results obtained with the two scaling laws are compared to the disk mass derived by fitting the SED of eight very low luminosity (L⋆ ≲ 0.01 L⊙) objects in the Upper Scorpius star-forming region. Masses derived with the Andrews et al. scaling law are on average 3.5 times larger than the values assumed in their radiative transfer model, a discrepancy that is significantly reduced when using the new scaling law. It is possible that this is due in large part to the fact that disks in Upper Scorpius tend to be more settled and flatter than disks in younger star-forming regions such as Taurus (Scholz et al. 2007, 2012). If so, the van der Plas et al. results confirm our conclusion that the disk shape is an important factor when deciding on the best value of Td to adopt. However, the differences in disk masses are in general not very large.
We conclude that the major drawback in adopting a single scaling law to measure disk masses from (sub)-mm fluxes for a sample of objects is not so much in the error on individual objects but in the trend that this automatically introduces when comparing disks around stars of different luminosity and mass, such as those shown in Fig. 6.
6. Summary
We present far-infrared and (sub)-mm fluxes of 29 very low-mass stars and brown dwarfs with masses ranging from 0.03 to 0.2 solar masses. For 11 objects from this sample, we measured new FIR fluxes from Herschel/PACS images. In addition, we compiled Herschel and (sub)-mm fluxes from the literature and rederived stellar parameters. The objects in this sample have detections in the FIR and in the (sub)-mm as well as well-characterized stellar parameters. To interpret the trends seen in the observations, we model the SED for fiducial brown dwarf/star-disk systems using the radiation transfer code RADMC-3D.
We show that VLMO disk masses can be robustly estimated from single wavelength (sub)-mm fluxes, and assuming blackbody emission, if the adopted dust temperature scales with luminosity as proposed by Andrews et al. (2013, T = 25 K (L⋆/L⊙)1/4. This is the case at least for dust temperatures above ~7 K corresponding to the temperature of large grains in a typical interstellar radiation field. When choosing a temperature in this way, the error in the disk mass caused by assuming emission from a single temperature blackbody is at most a factor of two. The error is only larger for fully flared disks, which seem to be extremely rare. With additional information on the spectral slope in the FIR, these uncertainties can be further reduced. One should keep in mind that major uncertainties in the disk mass are introduced by the poor knowledge of dust opacity and gas-to-dust ratio.
From the (sub)-mm fluxes we estimate disk masses, adopting the aforementioned scaling law between dust temperature and stellar luminosity. The disk masses in our sample range from 10-4 to 10-2 solar masses. More than half of our sample has a disk mass above 10-3 solar masses (corresponding to about 1 Jupiter mass). While our sample is biased toward high disk masses, this shows that a fraction of brown dwarfs has substantial disk masses, as already found by other authors (Scholz et al. 2006; Bouy et al. 2008; Ricci et al. 2014). The disk mass is critical for the outcome of planet-forming processes; simulations by Payne & Lodato (2007) indicate that Jupiter-mass disks around brown dwarfs have the potential to form Earth-mass planets. As found by other authors, the disk masses in our sample are in the range of 1% of the object mass, which is similar to what is found in more massive stars.
A surprising find of our study is that the observed FIR fluxes scale with the (sub)-mm fluxes. This is not expected from disk models because FIR fluxes mostly depend on the temperature structure, whereas (sub)-mm fluxes mostly scale with disk mass. We show that this trend can be qualitatively explained as a result of three interlinked correlations: the strong link between FIR fluxes and stellar luminosity, the stellar mass-luminosity relation, and the scaling of disk mass with stellar mass.
The comparison of the NIR-FIR spectral slopes (αJ−FIR) with the models clearly shows that brown dwarf disks are not fully flared, which is indirect evidence for the settling of large grains to the disk midplane. There is no evidence for a mass-dependence in the NIR-FIR spectral slope, neither in our sample nor when comparing with values measured for more massive T Tauri stars. We note that this does not necessarily mean that the physical processes that determine the disk shape occur in the same way in brown dwarfs and stars (see the discussions in Szücs et al. 2010; Pascucci et al. 2009; Mulders & Dominik 2012).
Acknowledgments
We thank the unknown referee for a thoughtful review. Thanks to Aurora Sicilia-Aguilar and Michael Meyer for instructive comments on the manuscript. A.N. would like to acknowledge funding from Science Foundation Ireland (Grant 13/ERC/I2907). A.S. acknowledges support from STFC grant ST/M001296/1. This work was partly supported by the Italian Ministero dell’Istruzione, Università e Ricerca through the grant Progetti Premiali 2012 – iALMA (CUP C52I13000140001). Our research was also supported by NSERC grants to R.J.. Research visits by S.D. and A.N. to the University of St Andrews and A.S. to the Dublin Institute for Advanced Studies have greatly facilitated the work on this paper. We are grateful for the hospitality and the generous technical/financial support by these two institutions. This research has made use of the SIMBAD database and the VizieR catalog access tool, operated at CDS, Strasbourg, France.
References
- Adams, F. C., Lada, C. J., & Shu, F. H. 1987, ApJ, 312, 788 [NASA ADS] [CrossRef] [Google Scholar]
- Alves de Oliveira, C., Ábrahám, P., Marton, G., et al. 2013, A&A, 559, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andrews, S. M., & Williams, J. P. 2005, ApJ, 631, 1134 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, S. M., Liu, M. C., Williams, J. P., & Allers, K. N. 2008, ApJ, 685, 1039 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, S. M., Rosenfeld, K. A., Kraus, A. L., & Wilner, D. J. 2013, ApJ, 771, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Ansdell, M., Williams, J. P., van der Marel, N., et al. 2016, ApJ, 828, 46 [Google Scholar]
- Apai, D., Pascucci, I., Bouwman, J., et al. 2005, Science, 310, 834 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Balog, Z., Müller, T., Nielbock, M., et al. 2014, Exp. Astron., 37, 129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baraffe, I., Chabrier, G., Allard, F., & Hauschildt, P. H. 1998, A&A, 337, 403 [NASA ADS] [Google Scholar]
- Baraffe, I., Homeier, D., Allard, F., & Chabrier, G. 2015, A&A, 577, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beckwith, S. V. W., Sargent, A. I., Chini, R. S., & Guesten, R. 1990, AJ, 99, 924 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, C. P. M., Mamajek, E. E., & Naylor, T. 2015, MNRAS, 454, 593 [NASA ADS] [CrossRef] [Google Scholar]
- Belloche, A., Schuller, F., Parise, B., et al. 2011, A&A, 527, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Billot, N., Morales-Calderón, M., Stauffer, J. R., Megeath, S. T., & Whitney, B. 2012, ApJ, 753, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Bourke, T. L., Myers, P. C., Evans, II, N. J., et al. 2006, ApJ, 649, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Bouy, H., Huélamo, N., Pinte, C., et al. 2008, A&A, 486, 877 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Broekhoven-Fiene, H., Matthews, B., Duchêne, G., et al. 2014, ApJ, 789, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Bulger, J., Patience, J., Ward-Duong, K., et al. 2014, A&A, 570, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, W. P., Simon, M., Longmore, A. J., Howell, R. R., & Benson, J. A. 1990, ApJ, 357, 224 [NASA ADS] [CrossRef] [Google Scholar]
- Chiang, E. I., & Goldreich, P. 1997, ApJ, 490, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Comeron, F., Rieke, G. H., Claes, P., Torra, J., & Laureijs, R. J. 1998, A&A, 335, 522 [NASA ADS] [Google Scholar]
- Cushing, M. C., Rayner, J. T., & Vacca, W. D. 2005, ApJ, 623, 1115 [NASA ADS] [CrossRef] [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog: II/246 [Google Scholar]
- Daemgen, S., Bonavita, M., Jayawardhana, R., Lafrenière, D., & Janson, M. 2015, ApJ, 799, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Dawson, P., Scholz, A., Ray, T. P., et al. 2013, MNRAS, 429, 903 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2011, Physics of the Interstellar and Intergalactic Medium (Princeton University Press) [Google Scholar]
- Dullemond, C. P., Dominik, C., & Natta, A. 2001, ApJ, 560, 957 [NASA ADS] [CrossRef] [Google Scholar]
- Furlan, E., Luhman, K. L., Espaillat, C., et al. 2011, ApJSS, 195, 3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Geers, V., Scholz, A., Jayawardhana, R., et al. 2011, ApJ, 726, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Guieu, S., Pinte, C., Monin, J.-L., et al. 2007, A&A, 465, 855 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartigan, P., Strom, K. M., & Strom, S. E. 1994, ApJ, 427, 961 [NASA ADS] [CrossRef] [Google Scholar]
- Harvey, P. M., Henning, T., Liu, Y., et al. 2012a, ApJ, 755, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Harvey, P. M., Henning, T., Ménard, F., et al. 2012b, ApJ, 744, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Herczeg, G. J., & Hillenbrand, L. A. 2014, ApJ, 786, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Howard, C. D., Sandell, G., Vacca, W. D., et al. 2013, ApJ, 776, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Jaeger, C., Mutschke, H., Begemann, B., Dorschner, J., & Henning, T. 1994, A&A, 292, 641 [Google Scholar]
- Jayawardhana, R., Ardila, D.R., Stelzer, B., & Haisch, K.E., Jr. 2003, AJ, 126, 1515 [NASA ADS] [CrossRef] [Google Scholar]
- Joergens, V., Bonnefoy, M., Liu, Y., et al. 2013, A&A, 558, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Keane, J. T., Pascucci, I., Espaillat, C., et al. 2014, ApJ, 787, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Klein, R., Apai, D., Pascucci, I., Henning, T., & Waters, L. B. F. M. 2003, ApJ, 593, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Konopacky, Q. M., Ghez, A. M., Rice, E. L., & Duchêne, G. 2007, ApJ, 663, 394 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, Y., Herczeg, G. J., Gong, M., et al. 2015a, A&A, 573, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, Y., Joergens, V., Bayo, A., Nielbock, M., & Wang, H. 2015b, A&A, 582, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Looper, D. L., Bochanski, J. J., Burgasser, A. J., et al. 2010, AJ, 140, 1486 [NASA ADS] [CrossRef] [Google Scholar]
- Luhman, K. L. 2007, ApJSS, 173, 104 [Google Scholar]
- Luhman, K. L. 2012, ARA&A, 50, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Luhman, K. L., & Mamajek, E. E. 2012, ApJ, 758, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Luhman, K. L., Stauffer, J. R., Muench, A. A., et al. 2003, ApJ, 593, 1093 [NASA ADS] [CrossRef] [Google Scholar]
- Luhman, K. L., Mamajek, E. E., Allen, P. R., & Cruz, K. L. 2009, ApJ, 703, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Luhman, K. L., Allen, P. R., Espaillat, C., Hartmann, L., & Calvet, N. 2010, ApJSS, 189, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Mohanty, S., Jayawardhana, R., Natta, A., et al. 2004, ApJ, 609, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Mohanty, S., Greaves, J., Mortlock, D., et al. 2013, ApJ, 773, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Motte, F., & André, P. 2001, A&A, 365, 440 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muench, A. A., Alves, J., Lada, C. J., & Lada, E. A. 2001, ApJ, 558, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Mulders, G. D., & Dominik, C. 2012, A&A, 539, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muller, T., Okumura, K., & Klaas, U. 2011, in PACS calibration and performance, http://herschel.esac.esa.int/twiki/bin/view/Public/PacsCalibrationWeb, PICC-ME-TN8 [Google Scholar]
- Natta, A., & Testi, L. 2001, A&A, 376, L22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Natta, A., Testi, L., Comerón, F., et al. 2002, A&A, 393, 597 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nguyen, D. C., Brandeker, A., van Kerkwijk, M. H., & Jayawardhana, R. 2012, ApJ, 745, 119 [Google Scholar]
- Olofsson, J., Szücs, L., Henning, T., et al. 2013, A&A, 560, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ott, S. 2010, in ASP Conf. Ser., 434, 139 [Google Scholar]
- Pascual, N., Montesinos, B., Meeus, G., et al. 2016, A&A, 586, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pascucci, I., Apai, D., Luhman, K., et al. 2009, ApJ, 696, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Payne, M. J., & Lodato, G. 2007, MNRAS, 381, 1597 [NASA ADS] [CrossRef] [Google Scholar]
- Pecaut, M. J., & Mamajek, E. E. 2013, ApJSS, 208, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Phan-Bao, N., Lee, C.-F., Ho, P. T. P., & Tang, Y.-W. 2011, ApJ, 735, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popesso, P., Magnelli, B., Buttiglione, S., et al. 2012, unpublished [arXiv:1211.4257] [Google Scholar]
- Rayner, J. T., Cushing, M. C., & Vacca, W. D. 2009, ApJSS, 185, 289 [CrossRef] [Google Scholar]
- Ricci, L., Testi, L., Natta, A., Scholz, A., & de Gregorio-Monsalvo, I. 2012, ApJ, 761, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Ricci, L., Testi, L., Natta, A., et al. 2014, ApJ, 791, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Rodriguez, D. R., van der Plas, G., Kastner, J. H., et al. 2015, A&A, 582, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roussel, H. 2013, PASP, 125, 1126 [Google Scholar]
- Scholz, A., Jayawardhana, R., & Wood, K. 2006, ApJ, 645, 1498 [NASA ADS] [CrossRef] [Google Scholar]
- Scholz, A., Jayawardhana, R., Wood, K., et al. 2007, ApJ, 660, 1517 [NASA ADS] [CrossRef] [Google Scholar]
- Scholz, A., Muzic, K., Geers, V., et al. 2012, ApJ, 744, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Shkolnik, E. L., Liu, M. C., Reid, I. N., Dupuy, T., & Weinberger, A. J. 2011, ApJ, 727, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Sicilia-Aguilar, A., Roccatagliata, V., Getman, K., et al. 2015, A&A, 573, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Spezzi, L., Cox, N. L. J., Prusti, T., et al. 2013, A&A, 555, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Szücs, L., Apai, D., Pascucci, I., & Dullemond, C. P. 2010, ApJ, 720, 1668 [NASA ADS] [CrossRef] [Google Scholar]
- Testi, L., Natta, A., Scholz, A., et al. 2016, A&A, 593, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Torres, R. M., Loinard, L., Mioduszewski, A. J., & Rodríguez, L. F. 2007, ApJ, 671, 1813 [NASA ADS] [CrossRef] [Google Scholar]
- van der Plas, G., Ménard, F., Ward-Duong, K., et al. 2016, ApJ, 819, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Warren, S. G. 1984, Appl. Opt., 23, 1206 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Wilking, B. A., Meyer, M. R., Robinson, J. G., & Greene, T. P. 2005, AJ, 130, 1733 [NASA ADS] [CrossRef] [Google Scholar]
- Winston, E., Cox, N. L. J., Prusti, T., et al. 2012, A&A, 545, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zubko, V. G., Mennella, V., Colangeli, L., & Bussoletti, E. 1996, MNRAS, 282, 1321 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Spectral energy distributions
See Figs. A.1 and A.2 for spectral energy distributions of all targets presented in this paper.
 |
Fig. A.1 Dereddened SEDs of our core sample. The filled symbols show data at Herschel wavelengths, the open symbols are literature values at other wavelengths. Upper limits are shown with triangles. A stellar SED (from the IRTF Spectral Library; Cushing et al. 2005; Rayner et al. 2009), normalized at J band, is shown for comparison. |
 |
Fig. A.2 continued. |
All Tables
All Figures
 |
Fig. 1 Herschel/PACS observations centered on the individual targets. Postage stamps are 1′× 1′, North is up and east to the left. |
| In the text | |
 |
Fig. 2 Dereddened SEDs normalized at J band. Red curves show the SEDs of the original sample, and blue lines show the literature SEDs. Targets that were excluded from further discussion (see Sect. 3.1) are shown with dotted lines. For comparison, the expected photospheric emission of an M5 star is shown in dashed gray (Cushing et al. 2005). |
| In the text | |
 |
Fig. 3 F100 and F160 as a function of mm fluxes. Millimeter fluxes are identical to F1300 or were converted from other wavelengths according to Eq. (1). To compare, T Tauri stars in Chamaeleon I and II are shown as plus and cross symbols in the bottom panel (Winston et al. 2012; Spezzi et al. 2013). The dotted lines show linear fits to all points except upper limits and binaries. |
| In the text | |
 |
Fig. 4 Histograms of infrared slopes αJ−70, αJ−100, and αJ−160. At αJ−70 and αJ−160, our brown dwarf samples are compared to T Tauri stars in Chamaeleon I and II (Winston et al. 2012; Spezzi et al. 2013). |
| In the text | |
 |
Fig. 5 Infrared slope as a function of mm flux. Millimeter fluxes are identical to F1300 or were converted from other wavelengths according to Eq. (1). Binaries are indicated with diamonds. For comparison, data from more massive T Tauri stars in the Chamaeleon star-forming region are shown (Cha I, Winston et al. 2012; Cha II, Spezzi et al. 2013). |
| In the text | |
 |
Fig. 6 Disk mass, derived from (sub)-mm fluxes, in units of solar masses (top panel) and stellar mass (bottom panel) as a function of the mass of the parent body for all targets in this paper. Binaries are highlighted with diamonds. A conservative estimate of disk mass uncertainty arising from unknown individual distances is shown in the bottom left of the top panel, assuming a conservative Δdist = ±10% (cf. Torres et al. 2007, who estimate a “depth” of Taurus of 20 pc). Dotted lines show the typical sensitivity limits derived from Eq. (3) for targets in Taurus (F1300,lim ≈ 1 mJy, dist = 140 pc) and TW Hya (F1300,lim ≈ 0.05 mJy, dist = 50 pc), using BCAH98 isochrones to convert mass to luminosity. |
| In the text | |
 |
Fig. 7 Model-predicted 100 μm (top panel) and 160 μm fluxes (bottom) vs. 1300 μm flux. Each colored point represents a model. Green symbols indicate the BD models, magenta symbols the TTS models. Different symbols refer to different disk masses: triangles for Md = 3 × 10-5M⊙, squares for Md = 3 × 10-4M⊙, dots for Md= 3 × 10-3M⊙, pentagons for Md= 1.5 × 10-2M⊙. Models for the same Md and different flares are connected by solid lines; flatter disks have lower fluxes at both wavelengths. Models with the same values of Hp(R0) and ξ are connected by dashed lines. Models mod2b, mod2b, small and mod2b,large are all shown with filled squares. Models mod2b1 and mod2b2, characterized by different grain opacity, are shown by empty squares, models with larger grains have larger mm flux and smaller FIR fluxes. For easy comparison, symbols from Fig. 3 are included in gray. |
| In the text | |
 |
Fig. 8 F160 flux as a function of target luminosity. Symbols as in Fig. 3. Best linear fit to all values excluding upper limits and binaries shown as dashed line. Measured slopes mFIR of best linear fits log (FFIR) ∝ mFIRlog (L⋆) in all FIR bands: m70 = 1.30 ± 0.25, m100 = 1.09 ± 0.39, and m160 = 1.14 ± 0.24. |
| In the text | |
 |
Fig. 9 Model predictions of infrared slopes as a function of mm flux. Colors and symbols as in Fig. 7. For reference, our measurements from the bottom panel of Fig. 5 were included in gray. |
| In the text | |
 |
Fig. 10 Values of the temperature needed to recover the model disk mass from the 1300 μm flux T1300 vs. αJ−160 for BD and TTS models. Colors and symbols as in Fig. 7. T1300 increases in more flared disks and decreases with the disk mass. TTS models, which have L⋆ that is five times larger than BD models, have higher T1300 however, there is a large region of overlap. The dashed lines show the values of T1300 according to the Andrews et al. prescription (TA = 25(L⋆/L⊙)1/4 K), green for the BD luminosity and magenta for TTS. |
| In the text | |
 |
Fig. 11 Ratio of the disk mass computed from TA over model disk mass as a function of αJ−160. Colors and symbols as in Fig. 7. |
| In the text | |
 |
Fig. A.1 Dereddened SEDs of our core sample. The filled symbols show data at Herschel wavelengths, the open symbols are literature values at other wavelengths. Upper limits are shown with triangles. A stellar SED (from the IRTF Spectral Library; Cushing et al. 2005; Rayner et al. 2009), normalized at J band, is shown for comparison. |
| In the text | |
 |
Fig. A.2 SEDs of our literature sample. Symbols and lines as in Fig. A.1. |
| In the text | |
 |
Fig. A.2 continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


