| Issue |
A&A
Volume 593, September 2016
|
|
|---|---|---|
| Article Number | L11 | |
| Number of page(s) | 4 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201629038 | |
| Published online | 13 September 2016 | |
Double resonance rotational spectroscopy of CH2D+
I. Physikalisches Institut, Universität zu Köln, Zülpicher Str. 77, 50937 Köln, Germany
e-mail: asvany@ph1.uni-koeln.de
Received: 1 June 2016
Accepted: 16 August 2016
Context. Deuterated forms of CH3+ are thought to be responsible for deuterium enrichment in lukewarm astronomical environments. There is no unambiguous detection of CH2D+ in space to date.
Aims. Four submillimetre rotational lines of CH2D+ are documented in the literature. Our aim is to present a complete dataset of highly resolved rotational lines, including millimetre (mm) lines needed for a potential detection.
Methods. We used a low-temperature ion trap and applied a novel IR–mm-wave double resonance method to measure the rotational lines of CH2D+.
Results. We measured 21 low-lying (J ≤ 4) rotational transitions of CH2D+ between 23 GHz and 1.1 THz with accuracies close to 2 ppb.
Key words: astrochemistry / line: identification / molecular data / ISM: molecules / radio lines: ISM
© ESO, 2016
1. Introduction
According to current astrochemical models (Roueff et al. 2007; Parise et al. 2009), CH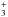 and its deuterated analogues are thought to be responsible for deuteration processes at lukewarm temperatures (~20 K <T<~80 K) following the reaction chain (Smith et al. 1982; Asvany et al. 2004)
and its deuterated analogues are thought to be responsible for deuteration processes at lukewarm temperatures (~20 K <T<~80 K) following the reaction chain (Smith et al. 1982; Asvany et al. 2004)
Unfortunately, this hypothesis rests on weak grounds, as none of the involved cationic species is detected in space, and there are only searches and tentative detections of CH2D+ by Wootten & Turner (2008) and Roueff et al. (2013). Those searches and tentative detections used predicted CH2D+ transition frequencies based on laboratory data available at that time. The first predictions of the rotational transition frequencies were provided by the IR data by Rösslein et al. (1991) and Jagod et al. (1992), and those were later refined by the high-resolution IR work by Gärtner et al. (2010, 2013) and, in particular, by the first four pure rotational lines measured by Amano (2010). More recently, two fundamental rotational transitions were measured in the Cologne laboratories (Brünken et al. 2014b) using a helium attachment technique at 4 K (Brünken et al. 2014a). In the work presented here, a double resonance spectroscopy technique is used to measure 21 rotational transitions of CH2D+ between 23 GHz and 1.1 THz with close to 2 ppb accuracy. With this complete dataset, we hope to trigger a renewed search for CH2D+.
2. Laboratory methods
The experiment was performed in a 4 K 22-pole ion trapping machine, which is described in Asvany et al. (2014); the applied IR-millimetre-wave (mm-wave) double resonance technique was first mentioned in Gärtner et al. (2013) and later documented by Jusko et al. (2014). In brief, CH2D+ ions were produced by ionizing CH3D gas in a storage ion source. The ions were mass selected and a few 10 000 ions were injected into the 22-pole ion trap (Asvany et al. 2010). On entrance, the ion ensemble was cooled down to the ambient trap temperature by a short helium gas pulse. The trap temperature was adjusted between 9 and 25 K, depending on the probed rotational level. During the trapping time of about 700 ms, the ion ensemble was exposed to cold hydrogen gas. The backwards direction of reaction (1) was induced by vibrationally exciting the stored ions, leading to a detectable CH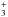 signal. This process is called laser induced reaction (LIR; Schlemmer et al. 1999, 2002). For this vibrational excitation, a cw optical parametric oscillator (OPO) was held in resonance (within ±2 × 10-4 cm-1) on selected transitions of the ν1 or ν4 bands (Jagod et al. 1992; Gärtner et al. 2013). With the IR frequency held on resonance, a cw (sub)mm-wave beam was shone simultaneously onto the trapped ion ensemble. A mirror with a hole was used to superpose the two beams, as shown in Fig. 1 of Jusko et al. (2014). The two coaxial beams then entered the vacuum chamber via a diamond window and reached the 6.6 mm diameter aperture of the 22-pole ion trap. For the generation of long wavelength radiation, synthesizers (Agilent E8257D or Rohde & Schwarz SMF 100A) with suitable horn antennas were used, whereas a modular chain consisting of amplifiers and multipliers (WR9.0M-AMC, Virginia Diodes Inc.) was applied for frequencies beyond 80 GHz. As shown in the inset of Fig. 1, the rotational excitation pumps CH2D+ ions into the state probed by the vibrational transition, increasing the CH
signal. This process is called laser induced reaction (LIR; Schlemmer et al. 1999, 2002). For this vibrational excitation, a cw optical parametric oscillator (OPO) was held in resonance (within ±2 × 10-4 cm-1) on selected transitions of the ν1 or ν4 bands (Jagod et al. 1992; Gärtner et al. 2013). With the IR frequency held on resonance, a cw (sub)mm-wave beam was shone simultaneously onto the trapped ion ensemble. A mirror with a hole was used to superpose the two beams, as shown in Fig. 1 of Jusko et al. (2014). The two coaxial beams then entered the vacuum chamber via a diamond window and reached the 6.6 mm diameter aperture of the 22-pole ion trap. For the generation of long wavelength radiation, synthesizers (Agilent E8257D or Rohde & Schwarz SMF 100A) with suitable horn antennas were used, whereas a modular chain consisting of amplifiers and multipliers (WR9.0M-AMC, Virginia Diodes Inc.) was applied for frequencies beyond 80 GHz. As shown in the inset of Fig. 1, the rotational excitation pumps CH2D+ ions into the state probed by the vibrational transition, increasing the CH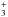 signal count. By scanning the rotational excitation frequency over the resonance (symmetrically up and down), a rotational line can be obtained.
signal count. By scanning the rotational excitation frequency over the resonance (symmetrically up and down), a rotational line can be obtained.
3. Experimental results
 |
Fig. 1 Measurement of the 202 ← 101 rotational ground state transition with the IR-mm-wave double resonance technique at 11 K. The energy level diagram (inset) explains the double resonance method: with the IR light held in resonance (OPO; long green arrow) at 3029.6352 cm-1, more than 5100 CH |
 |
Fig. 2 Transition 220 ← 221 at 23 GHz measured at a nominal trap temperature of 15 K. The broadness of this feature can be recognized by comparison with the narrow Gaussian curve, which is the shape expected for a single line at 40 K. Since pressure or Doppler broadening to this extent can be excluded, unresolved hyperfine structure is the most reasonable explanation for this broadening, whereas some residual power broadening effect cannot be excluded. These hyperfine splittings are dominated by the small electrical quadrupole moment of the deuterium nucleus. To better identify the structure in this feature, the data of 13 single measurements (shown as pale grey dots) have been normalized (to the off-resonant CH |
 |
Fig. 3 Transition 110 ← 111 at 67 GHz measured at a nominal temperature of 9 K. Similar to Fig. 2, the narrow Gaussian is the shape expected for a single line at 40 K. Averaging over several measurements and binning into 4 kHz steps yields the red curve, revealing deviations from a Gaussian shape. |
Owing to the existing predictions, no tedious searches were necessary and the targeted lines were usually found within minutes. A sample measurement of the transition 202 ← 101 is shown in Fig. 1 together with a Gaussian fit and more explanations. To improve the statistics, such measurements were typically repeated five to ten times. In total we detected 21 rotational lines. These are summarized in Table 1 and are compared to the 4 rotational lines measured by Amano (2010), whose conservative error limits are confirmed and improved by at least one order of magnitude in this work. Surprisingly, our measured values also agree extremely well with the very first prediction of rotational transitions of CH2D+ given by Rösslein et al. (1991).
The cold temperatures and good signal-to-noise ratio in this work usually permit us to determine the transitions with uncertainties close to 2 ppb. Transitions with higher uncertainties in the table stem either from weakly populated levels (e.g. 413 ← 414), or are transitions with weak intrinsic transition strength (ΔKa = 2, e.g. 322 ← 302 or 221 ← 202) and/or with limited submm-wave source power (in upper frequency range, e.g. 423 ← 322). We also want to point out the low frequency transitions, for which the unresolved hyperfine splittings, caused mainly by the electrical quadrupole moment of the deuterium nucleus, start broadening and skewing the Doppler line shapes; see Figs. 2 and 3 for the 23 GHz and 67 GHz lines, respectively. For these lines, some residual power broadening effects cannot be excluded. As simple simulations of the hyperfine structure did not fully recover the seen structures, we kept using Gaussian functions, leading to less reliable definitions of the line centres given in Table 1. But because of the large dataset given in Table 1, the line centres and their error limits can be checked by forming combination differences. For instance, the difference between the rotational levels 211 and 313 can be formed in two different ways (see level scheme in Fig. 4 and Table A.1), and shows that our data is reasonable. A full list of 32 such combination differences is given in Table A.1. In this list, the combination differences involving the 67 GHz line show deviations beyond the expected level, the most probable reason being the unresolved hyperfine structure mentioned above. Thus, excluding this line, our data were used as input to an asymmetric rotor model (Western 2016). Transitions from previous publications (Jagod et al. 1992; Amano 2010; Gärtner et al. 2013) were not included here as they did not significantly improve the ground state constants. The obtained rotational constants for the ground state of CH2D+ are summarized in Table 2.
Measurements of low-lying (J ≤ 4) rotational transitions (in MHz) of CH2D+ up to 1.1 THz (for comparison, the hitherto available discharge cell measurements of Amano 2010 are also listed).
Best-fit spectroscopic parameters for the ground state of CH2D+ (in MHz) obtained using 20 rotational lines of this work.
4. Conclusions and outlook
While the IR-mm-wave double resonance technique has been applied before on single fundamental transitions of H2D+ (Gärtner et al. 2013) and OH− (Jusko et al. 2014), its full power is unfolded by measuring the complete set of all low-lying rotational transitions of CH2D+ up to 1.1 THz, thereby leading to highly accurate spectroscopic parameters. A level diagram summarizing the rotational transitions studied in this work is shown in Fig. 4. We hope to trigger renewed searches of CH2D+ in space given the complete set of rotational transitions. As the hyperfine structure might become important for the lower frequency transitions, we also want to encourage high-level ab initio calculations of the hyperfine structure, as carried out previously for H2D+ and D2H+ by Jensen et al. (1991, 1997). A full account of similar rotational experiments for CD2H+ will be given in a later publication.
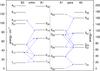 |
Fig. 4 Ground state rotational levels of CH2D+ illustrating the 21 rotational transitions measured in this work. |
Acknowledgments
This work has been financially supported by the Deutsche Forschungsgemeinschaft (DFG) via SFB 956 project B2. P.J. is supported by the Alexander von Humboldt Stiftung. We thank Marius Hermanns and Sven Fanghänel for assistance in the experiment, as well as Sandra Brünken, Holger Müller, Sven Thorwirth, and Jürgen Gauß for valuable discussions.
References
- Amano, T. 2010, A&A, 516, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asvany, O., Schlemmer, S., & Gerlich, D. 2004, ApJ, 617, 658 [Google Scholar]
- Asvany, O., Bielau, F., Moratschke, D., Krause, J., & Schlemmer, S. 2010, Rev. Sci. Instr., 81, 076102 [Google Scholar]
- Asvany, O., Brünken, S., Kluge, L., & Schlemmer, S. 2014, Appl. Phys. B, 114, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Brünken, S., Kluge, L., Stoffels, A., Asvany, O., & Schlemmer, S. 2014a, ApJ, 783, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Brünken, S., Kluge, L., Stoffels, A., & Schlemmer, S. 2014b, unpublished results [Google Scholar]
- Gärtner, S., Krieg, J., Klemann, A., Asvany, O., & Schlemmer, S. 2010, A&A, 516, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gärtner, S., Krieg, J., Klemann, A., et al. 2013, J. Phys. Chem. A, 117, 9975 [CrossRef] [PubMed] [Google Scholar]
- Jagod, M.-F., Rösslein, M., Gabrys, C. M., et al. 1992, J. Chem. Phys., 97, 7111 [NASA ADS] [CrossRef] [Google Scholar]
- Jensen, P., Paidarová, I., Vojtík, J., & Špirko, V. 1991, J. Mol. Spectr., 150, 137 [Google Scholar]
- Jensen, P., Paidarová, I., Špirko, V., & Sauer, S. P. A. 1997, Mol. Phys., 91, 319 [NASA ADS] [Google Scholar]
- Jusko, P., Asvany, O., Wallerstein, A.-C., Brünken, S., & Schlemmer, S. 2014, Phys. Rev. Lett., 112, 253005 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Parise, B., Leurini, S., Schilke, P., et al. 2009, A&A, 508, 737 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rösslein, M., Jagod, M. F., Gabrys, C. M., & Oka, T. 1991, ApJ, 382, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Roueff, E., Parise, B., & Herbst, E. 2007, AA&A, 464, 245 [CrossRef] [EDP Sciences] [Google Scholar]
- Roueff, E., Gerin, M., Lis, D. C., et al. 2013, J. Phys. Chem. A, 117, 9959 [CrossRef] [Google Scholar]
- Schlemmer, S., Kuhn, T., Lescop, E., & Gerlich, D. 1999, Int. J. Mass Spectrom., 185, 589 [NASA ADS] [CrossRef] [Google Scholar]
- Schlemmer, S., Lescop, E. V., Richthofen, J., & Gerlich, D. 2002, J. Chem. Phys., 117, 2068 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, D., Adams, N., & Alge, E. 1982, J. Chem. Phys., 77, 1261 [NASA ADS] [CrossRef] [Google Scholar]
- Western, C. M. 2016, PGOPHER, a Program for Simulating Rotational Structure, C. M. Western, University of Bristol, http://pgopher.chm.bris.ac.uk [Google Scholar]
- Wootten, A., & Turner, B. E. 2008, in Organic Matter in Space, eds. S. Kwok, & S. Sanford, IAU Symp., 251, 334 [Google Scholar]
Appendix A: combination differences
From the 21 rotational lines measured for CH2D+, the 32 combination differences listed in Table A.1 could be obtained by forming sums and differences (see also Fig. 4). The eight combination differences which could be formed in two different ways show that our rotational line centres and their errors are reasonable, except for the 67 GHz line, which exhibits a deviation on the order of 20 kHz. This line is most probably affected by unresolved hyperfine structure (and power broadening effects).
The combination differences (CD) obtained by forming sums or differences of the two rotational transitions T1 and T2 are listed here in ascending order.
All Tables
Measurements of low-lying (J ≤ 4) rotational transitions (in MHz) of CH2D+ up to 1.1 THz (for comparison, the hitherto available discharge cell measurements of Amano 2010 are also listed).
Best-fit spectroscopic parameters for the ground state of CH2D+ (in MHz) obtained using 20 rotational lines of this work.
The combination differences (CD) obtained by forming sums or differences of the two rotational transitions T1 and T2 are listed here in ascending order.
All Figures
 |
Fig. 1 Measurement of the 202 ← 101 rotational ground state transition with the IR-mm-wave double resonance technique at 11 K. The energy level diagram (inset) explains the double resonance method: with the IR light held in resonance (OPO; long green arrow) at 3029.6352 cm-1, more than 5100 CH |
| In the text | |
 |
Fig. 2 Transition 220 ← 221 at 23 GHz measured at a nominal trap temperature of 15 K. The broadness of this feature can be recognized by comparison with the narrow Gaussian curve, which is the shape expected for a single line at 40 K. Since pressure or Doppler broadening to this extent can be excluded, unresolved hyperfine structure is the most reasonable explanation for this broadening, whereas some residual power broadening effect cannot be excluded. These hyperfine splittings are dominated by the small electrical quadrupole moment of the deuterium nucleus. To better identify the structure in this feature, the data of 13 single measurements (shown as pale grey dots) have been normalized (to the off-resonant CH |
| In the text | |
 |
Fig. 3 Transition 110 ← 111 at 67 GHz measured at a nominal temperature of 9 K. Similar to Fig. 2, the narrow Gaussian is the shape expected for a single line at 40 K. Averaging over several measurements and binning into 4 kHz steps yields the red curve, revealing deviations from a Gaussian shape. |
| In the text | |
 |
Fig. 4 Ground state rotational levels of CH2D+ illustrating the 21 rotational transitions measured in this work. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.