| Issue |
A&A
Volume 593, September 2016
|
|
|---|---|---|
| Article Number | A103 | |
| Number of page(s) | 9 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201628991 | |
| Published online | 30 September 2016 | |
The role of medium modifications for neutrino-pair processes from nucleon-nucleon bremsstrahlung
Impact on the protoneutron star deleptonization
Institute for Theoretical Physics, University of Wrocław, plac Maksa Borna 9, 50-204 Wrocław, Poland
e-mail: fischer@ift.uni.wroc.pl
Received: 24 May 2016
Accepted: 16 August 2016
In this article the neutrino-pair production from nucleon-nucleon (NN) bremsstrahlung is explored via medium-modifications of the strong interactions at the level of the one-pion exchange approximation. It governs the bulk part of the NN interaction at low densities relevant for the neutrino physics in core-collapse supernova studies. The resulting medium-modified one-pion exchange rate for the neutrino-pair processes is implemented in simulations of core-collapse supernovae in order to study the impact on the neutrino signal emitted from the deleptonization of the nascent proto-neutron star (PNS). Consequences for the nucleosynthesis of heavy elements of the material ejected from the PNS surface are discussed.
Key words: supernovae: general / neutrinos / dense matter
© ESO, 2016
1. Introduction
The bulk of the trapped neutrinos of a newly born neutron star – known as proto-neutron star (PNS) – is emitted during its early cooling history. PNSs form when the stellar core of an initially imploding massive star bounces back at supersaturation density, due to the repulsive short range nuclear interaction, with the formation of a strong hydrodynamic shock wave (for recent review about supernova theory, see Janka et al. 2007). While the supernova problem is associated with the transport of energy from the PNS interior leading to the ejection of the stellar mantle – a detailed summary about supernova explosion mechanisms can be found in Janka (2012) – the nascent PNS deleptonizes via the emission of neutrinos of all flavors on a timescale on the order of 10–30 s once the supernova explosion has been launched. This has been explored in Fischer et al. (2010) and Hüdepohl et al. (2010) within consistent simulations based on neutrino radiation hydrodynamics with three-flavor Boltzmann neutrino transport. These studies confirmed that the PNS settles into a quasi-stationary state as mass accretion ceases, which approves the description within the hydrostatic treatment of Pons et al. (1999) based on the diffusion approximation for neutrino transport.
In Wu et al. (2015) the “complete” supernova neutrino signal is analyzed for the first time, based on the simulation results of Fischer et al. (2010). They demonstrate that millisecond events can be resolved for the next Galactic supernova explosion, for currently operating and for future generation of neutrino detectors. Therefore, it is of paramount interest to predict neutrino luminosities and spectra from such cosmic events. Particular focus is thereby on the deleptonization of the nascent PNS during which most neutrinos will be detected. From a theoretical point of view, it is important to develop models that are based on accurate neutrino transport considering the relevant weak processes. Following Reddy et al. (1998) the impact of the consistent treatment of nuclear equation of state (EoS) and weak processes has been explored at the mean-field level in Martínez-Pinedo et al. (2012), Roberts et al. (2012) and Horowitz et al. (2012).
Physics beyond the mean-field approach involves nuclear correlations, such as nucleon-nucleon (NN) scattering and pairing. However, NN interactions under supernova conditions – temperatures on the order to tens of MeV and densities slightly above normal nuclear matter density (ρ0) as well as large neutron excess – are highly unknown. This is then reflected in large uncertainties of associated weak processes, for example, NN-bremsstrahlung and the corresponding neutrino-antineutrino pair emission (or absorption) as illustrated in Fig. 1. The different scales for strong and weak interactions involved allow their separation; the latter refers to the emission (and absorption) of 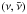 via the coupling to the neutral Z0-boson. Therefore, Friman & Maxwell (1979) derived expressions for the weak rates modeling NN interactions by the one-pion exchange (OPE) approximation, including spin-orbit coupling. Moreover, Hannestad & Raffelt (1998) provided expressions in the long-wavelength limit to the astrophysics community (see also Sigl 1996; Janka et al. 1996, and references therein) which take into account spin fluctuations and their saturation towards high density.
via the coupling to the neutral Z0-boson. Therefore, Friman & Maxwell (1979) derived expressions for the weak rates modeling NN interactions by the one-pion exchange (OPE) approximation, including spin-orbit coupling. Moreover, Hannestad & Raffelt (1998) provided expressions in the long-wavelength limit to the astrophysics community (see also Sigl 1996; Janka et al. 1996, and references therein) which take into account spin fluctuations and their saturation towards high density.
It has long been understood from a series of studies that the free (that is, vacuum) OPE – henceforth denoted as FOPE – underestimates the cooling of neutron stars. Based on FOPE, important medium modifications at ρ ≳ ρ0/ 2 are neglected (this has been discussed in details in Senatorov & Voskresensky 1987; Schaab et al. 1997; Blaschke et al. 1995, 2004, 2012, 2013; Yakovlev et al. 2001, 2005; Hanhart et al. 2001; Page & Reddy 2006; Grigorian & Voskresensky 2005, exploring also the role of medium effects for the charged-current absorption reactions, that is, the modified Urca processes).
Up to ρ0 the framework of chiral effective field theory is the ab-initio approach to the nuclear many-body problem of dilute neutron matter. Hebeler & Schwenk (2010) study the role of three-body forces including 2π-exchange terms (for recent works, see also Tews et al. 2013; Krüger et al. 2013). Based on this approach, recently Bartl et al. (2014) quantified the suppression of the neutrino-pair absorption rate from NN-bremsstrahlung, at conditions relevant for supernovae. The authors found a significant reduction of the neutrino-pair process compared to the FOPE approximation, at an already low density on the order of ρ ≃ 1011–1012 g cm-3.
A more general approach to study medium modifications for weak processes that involve NN interactions is the Fermi-liquid theory of Migdal (1978) and Migdal et al. (1990 see also Voskresensky 2001, and references therein). It assumes that the nucleons are only slightly excited above their Fermi sea such that all the processes occur in a narrow vicinity of the Fermi surface and that the vertices of the processes are dressed by NN correlations. The subsequent medium modification of the OPE includes the “exact” summation of all particle-hole loops and a contribution of the residual s-wave πNN interaction and ππ-scattering, which effectively involves ρ-meson exchange (t-channel) and the σ-meson as correlated ππ (s-wave contribution). Moreover, due to nucleon-hole (and also △-hole) excitations, the subsequent p-wave pion polarization in nuclear matter leads to the softening of the in-medium pion dispersion relation. As explored in Aouissat et al. (1995) and Rapp et al. (1996), it is relevant for the understanding of nuclear saturation (for more details, see Rapp et al. 1997, and references therein).
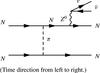 |
Fig. 1 Neutrino pair-emission from NN-bremsstrahlung within the FOPE approximation. |
In this paper, medium modifications to the FOPE approach are studied, that alter FOPE from even low densities (ρ ≪ ρ0) where they start to dress the local πNN-vertex (henceforth denoted as MVOPE – medium-modified-vertex + FOPE). Being mainly interested in the low-density limit and to compare more easily with results based on the chiral perturbation approach, where pion softening is not included, medium effects for the πNN-vertices are incorporated but the FOPE π-propagator is exploited.
Following Senatorov & Voskresensky (1987) and Voskresensky (2001) the current article provides a MVOPE density-dependent parametrization, that is, for the medium modification of the πNN-vertex, for applications in simulations of core-collapse supernovae. It represents the largest modification of the neutrino-pair emission rate from NN-bremsstrahlung at densities relevant for supernova studies, suppressing neutrino-pair emission and absorption compared to the unmodified FOPE approach.
This medium dependence is then implemented into the neutrino transport module of the core-collapse supernova model AGILE-BOLTZTRAN of Liebendörfer et al. (2004) in order to study the impact on the neutrino signal and the evolution during the PNS deleptonization, being able to quantify the general role of NN-bremsstrahlung. The reduction of the neutrino-pair emission and absorption rate obtained towards increasing density reduces the neutrino opacity. This is important for the heavy-lepton flavor neutrino species for which NN-bremsstrahlung is the leading production and absorption process. Unlike for νe which are always dominated by charged-current absorption on neutrons,  are also significantly affected by the high-density suppression of the NN-bremsstrahlung.
are also significantly affected by the high-density suppression of the NN-bremsstrahlung.
The subsequent impact on the neutrino luminosities and average energies has important consequences for the nucleosynthesis relevant conditions, for example, the electron fraction Ye of the neutrino-driven wind, that is, its proton-to-baryon ratio. The latter is a low-mass outflow ejected from the PNS surface via continuous neutrino heating, during the PNS deleptonization over a timescale of about 10–30 s. It has long been studied as a nucleosynthesis site for the production of heavy elements (see Woosley et al. 1994; Otsuki et al. 1999; Wanajo 2006a,b, and references therein).
Note that for ρ ≳ ρ0 also the π-propagator is modified by the nuclear medium, which gives rise to different interaction channels (see the right panel of Fig. 1 in Voskresensky 2001) with neutrino-pair emission from intermediate nucleon-loops. Such additional medium modifications may become relevant during the late-time cooling at the transition from neutrino diffusion to freely streaming, when the PNS core temperature decreases below T ~ 1 MeV such that neutrinos are escaping from densities that are also in excess of ρ0.
This manuscript is organized as follows. In Sect. 2 the supernova model AGILE-BOILTZTRAN is briefly introduced together with the density-dependent parametrization of medium modifications for the neutrino-pair processes from NN-bremsstrahlung. In Sect. 3 simulation results of the PNS deleptonization are analyzed and in Sect. 4 the impact on the nucleosynthesis relevant conditions is discussed. The manuscript closes with the summary in Sect. 5.
Weak processes considered and corresponding references.
2. Supernova input physics
The core-collapse supernova model, AGILE-BOLTZTRAN, is based on spherically symmetric and general relativistic neutrino radiation hydrodynamics with angle- and energy-dependent three-flavor Boltzmann neutrino transport (for details, see Liebendörfer et al. 2001a,b; Liebendoerfer et al. 2002). The implicit method for solving the hydrodynamics equations and the Boltzmann equation on an adaptive Lagrangian mesh has been compared with other methods, for example, in Liebendörfer et al. (2004) with the multi-group flux-limited diffusion approximation and in Liebendoerfer et al. (2005) with the variable Eddington factor technique.
The nuclear EoS employed here from Hempel & Schaffner-Bielich 2010 is based on the relativistic mean-field framework for homogeneous nuclear matter with the parametrization DD2 from Typel et al. (2010), henceforth denoted as HS(DD2). Nuclei are treated within the modified nuclear statistical equilibrium approach for several thousand nuclear species based on tabulated and partly-calculated masses. This EoS is part of the comprehensive CompOSE EoS catalog of Typel et al. (2013). In addition lepton and photon contributions are added following Timmes & Arnett (1999).
2.1. Treatment of weak processes
The set of weak reactions included in the supernova simulations can be found in Table 1, together with the corresponding references. For the weak processes with free nucleons, both charged-current absorption and neutral-current scattering, the elastic approximation is employed. Medium modifications of the charged current absorption processes are taken into account at the mean-field level based in the nuclear EoS HS(DD2). Following Reddy et al. (1998), these enter the elastic expressions via modified Q values, Q = Q0 + △ U, where △ U = Un−Up with nucleon single-particle self energies UN. They also modify the nucleon chemical potentials, μN = ϕN−UN, with free Fermi-gas chemical potentials ϕN, in order to reproduce the low-density limit towards vanishing degeneracy (see Hempel 2015, for details regarding the treatment of effective interactions within relativistic mean-field approach). Note that UN has a strong density dependence, that is related to the nuclear symmetry energy. Even though it was possible to constrain the symmetry energy value and its slope to some extent in Lattimer & Lim (2013), under supernova conditions the symmetry energy is presently rather poorly constrained as discussed in Fischer et al. (2014).
Furthermore, inelastic contributions and weak magnetism corrections are included following Horowitz (2002), for the charged current absorption and neutral current scattering processes. While inelastic contributions are known to reduce the ν rates as much as 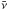 rates towards high density, weak magnetism corrections generally increase differences between neutrinos and antineutrinos. The latter originates from the parity violation of the nucleon weak magnetic moment coupling to its axial current. Both latter effects have been commonly included in core-collapse supernova simulations. Note that contributions due to strange quark contents are not taken into account here.
rates towards high density, weak magnetism corrections generally increase differences between neutrinos and antineutrinos. The latter originates from the parity violation of the nucleon weak magnetic moment coupling to its axial current. Both latter effects have been commonly included in core-collapse supernova simulations. Note that contributions due to strange quark contents are not taken into account here.
In addition to this standard set of weak reactions in Fischer et al. (in prep.) the (inverse) neutron decay is introduced, reaction (3) in Table 1. This channel of opacity was enabled via the medium modifications with Q = −Q0 + △ U, which enters the expression of the elastic approximation. It results in the slight enhancement of the low-energy  -opacity towards increasing density where △ U>Q0, however, with a negligible impact on the overall supernova dynamics and neutrino signal.
-opacity towards increasing density where △ U>Q0, however, with a negligible impact on the overall supernova dynamics and neutrino signal.
2.2. Nucleon-nucleon bremsstrahlung
Neutrino-pair production (p) and absorption (a) were treated via their corresponding reaction kernels 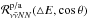 , relating initial as well as final states and depending on the sum of neutrino and antineutrino energies (
, relating initial as well as final states and depending on the sum of neutrino and antineutrino energies (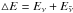 ) as well as on the momentum scattering angle cosθ (see Eq. (5) in Fischer et al. 2012). It depends in turn on the lateral angles (
) as well as on the momentum scattering angle cosθ (see Eq. (5) in Fischer et al. 2012). It depends in turn on the lateral angles (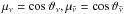 ) and the relative azimuthal angle (φ) between ν and
) and the relative azimuthal angle (φ) between ν and 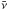 . The corresponding collision term of the Boltzmann transport equation for neutrinos is given in Fischer et al. (2012; assuming here ħ= c = 1),
. The corresponding collision term of the Boltzmann transport equation for neutrinos is given in Fischer et al. (2012; assuming here ħ= c = 1), ![\begin{eqnarray} \label{eq:boltz} \left.\frac{{\rm d}f_\nu(E_\nu,\mu_\nu)}{{\rm d}t}\right\vert_{\nu\bar\nu NN} &=& \left(1-f_\nu(E_\nu,\mu_\nu)\right) \int_0^\infty {\rm d}E_{\bar\nu} E_{\bar\nu}^2 \int_{-1}^{+1} {\rm d}\mu_{\bar\nu} \notag \\[2mm] && \quad \times \int_0^{2\pi} {\rm d}\phi \mathcal{R}_{\nu\bar\nu NN}^\text{p}(-\triangle E,\cos\theta) \left(1 \!- \!f_{\bar\nu}(E_{\bar\nu},\mu_{\bar\nu})\right) \nonumber \\[2mm] && \quad - f_\nu(E_\nu,\mu_\nu) \int_0^\infty {\rm d}E_{\bar\nu} E_{\bar\nu}^2 \int_{-1}^{+1} {\rm d}\mu_{\bar\nu} \notag \\[2mm] && \quad \times \int_0^{2\pi} {\rm d}\phi \,\,\mathcal{R}_{\nu\bar\nu NN}^\text{a}(\triangle E,\cos\theta) f_{\bar\nu}(E_{\bar\nu},\mu_{\bar\nu}), \end{eqnarray}](/articles/aa/full_html/2016/09/aa28991-16/aa28991-16-eq53.png) (1)integrating the antineutrino phase space, including the appropriate (anti)neutrino occupation numbers
(1)integrating the antineutrino phase space, including the appropriate (anti)neutrino occupation numbers 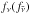 as well as final state blocking for the neutrino-pair production. Note also that the thermal and chemical equilibrium obtained under supernova conditions enables the relation between neutrino-pair emission and absorption kernels in Eq. (1)via detailed balance as follows,
as well as final state blocking for the neutrino-pair production. Note also that the thermal and chemical equilibrium obtained under supernova conditions enables the relation between neutrino-pair emission and absorption kernels in Eq. (1)via detailed balance as follows, 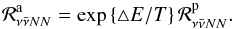 (2)At low densities the NN-interaction is governed by the OPE with the associated matrix element ℳ, for which in turn the relation to the neutrino-pair emission kernel is given in Hannestad & Raffelt (1998),
(2)At low densities the NN-interaction is governed by the OPE with the associated matrix element ℳ, for which in turn the relation to the neutrino-pair emission kernel is given in Hannestad & Raffelt (1998), 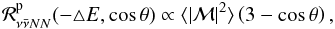 (3)modulo normalization and multiplicative phase-space factors. The momentum integration of the nucleon occupation numbers, including final state Pauli blocking, is included in the matrix element for which the averaging ⟨⟩ is over all spins. Moreover, it has been shown in Friman & Maxwell (1979) that for non-relativistic nucleons, which is typical for temperatures below T ~ 50 MeV, only the axial-vector current contributes to the neutrino-pair processes from NN-bremsstrahlung,
(3)modulo normalization and multiplicative phase-space factors. The momentum integration of the nucleon occupation numbers, including final state Pauli blocking, is included in the matrix element for which the averaging ⟨⟩ is over all spins. Moreover, it has been shown in Friman & Maxwell (1979) that for non-relativistic nucleons, which is typical for temperatures below T ~ 50 MeV, only the axial-vector current contributes to the neutrino-pair processes from NN-bremsstrahlung, 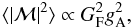 (4)with Fermi constant GF and axial-vector coupling constant gA with vacuum value, gA = 1.27. Analytical expressions for (4)are provided in Hannestad & Raffelt (1998) to the astrophysics community based on the FOPE.
(4)with Fermi constant GF and axial-vector coupling constant gA with vacuum value, gA = 1.27. Analytical expressions for (4)are provided in Hannestad & Raffelt (1998) to the astrophysics community based on the FOPE.
To account for the lowest-order medium dependence within the OPE approach, following Migdal et al. (1990), two modifications can be considered: (a) dressing of the local interaction πNN-vertex (γ), 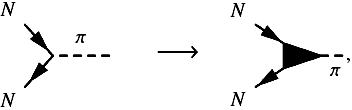 (5)and (b) modifications of the π-propagator (Dπ). Based on the Fermi-liquid model, explicit expressions for (a) and (b) are derived in Voskresensky (2001). The latter article also shows that for the medium modifications of Dπ the most important contribution to the charged current processes (modified Urca) originates from neutrino reactions of intermediate nucleon-loops coupled to the π for ρ ≳ ρ0/ 2. However, these reaction channels are forbidden by symmetry reasons for NN-bremsstrahlung processes on neutral currents.
(5)and (b) modifications of the π-propagator (Dπ). Based on the Fermi-liquid model, explicit expressions for (a) and (b) are derived in Voskresensky (2001). The latter article also shows that for the medium modifications of Dπ the most important contribution to the charged current processes (modified Urca) originates from neutrino reactions of intermediate nucleon-loops coupled to the π for ρ ≳ ρ0/ 2. However, these reaction channels are forbidden by symmetry reasons for NN-bremsstrahlung processes on neutral currents.
The medium modifications denoted via (∗) also alter the OPE matrix element, 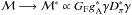 . Furthermore, neglecting contributions from the in-medium pion-propagator, that is, assuming
. Furthermore, neglecting contributions from the in-medium pion-propagator, that is, assuming 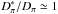 , the ratio of MVOPE-to-FOPE matrix element is given as follows,
, the ratio of MVOPE-to-FOPE matrix element is given as follows, 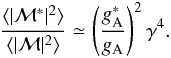 (6)Within the Fermi-liquid approach the πNN-vertex function γ(ω,k,pF) – depending on energy ω, momentum k and Fermi momentum pF – is dressed by the inclusion of the NN correlations according to expression (5)such that,
(6)Within the Fermi-liquid approach the πNN-vertex function γ(ω,k,pF) – depending on energy ω, momentum k and Fermi momentum pF – is dressed by the inclusion of the NN correlations according to expression (5)such that, 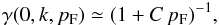 (7)where the constant C is expressed in terms of the appropriate Landau-Migdal parameter. Moreover, Senatorov & Voskresensky (1987) and Voskresensky (2001) provided the following numerical estimate,
(7)where the constant C is expressed in terms of the appropriate Landau-Migdal parameter. Moreover, Senatorov & Voskresensky (1987) and Voskresensky (2001) provided the following numerical estimate, 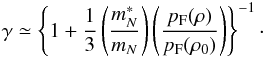 (8)Note that contributions from the effective nucleon mass (
(8)Note that contributions from the effective nucleon mass (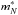 ) can be neglected in expression (8), that is,
) can be neglected in expression (8), that is, 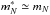 for the densities relevant for neutrino transport and decoupling in core-collapse supernova simulations, ρ< 1014 g cm-3.
for the densities relevant for neutrino transport and decoupling in core-collapse supernova simulations, ρ< 1014 g cm-3.
Moreover, the Goldberger-Treiman relation ensures the partial conservation of axial currents, 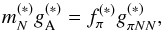 (9)with pion decay constant fπ, pion-nucleon coupling constant gπNN and nucleon mass mN; it connects chiral physics and weak axial-vector currents. Relation (9)holds in vacuum as well as in the nuclear medium, indicated via (∗). Applying the Brown & Rho (1991) scaling,
(9)with pion decay constant fπ, pion-nucleon coupling constant gπNN and nucleon mass mN; it connects chiral physics and weak axial-vector currents. Relation (9)holds in vacuum as well as in the nuclear medium, indicated via (∗). Applying the Brown & Rho (1991) scaling, 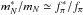 , the ratio of the medium-modified to the vacuum Goldberger-Treiman relation (9)ensures the same scaling for axial-vector and πNN coupling constants; it leads to the following dependence,
, the ratio of the medium-modified to the vacuum Goldberger-Treiman relation (9)ensures the same scaling for axial-vector and πNN coupling constants; it leads to the following dependence, 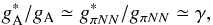 (10)which results in
(10)which results in 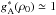 as illustrated in Fig. 2. This medium dependent axial-vector coupling constant is then employed in all other neutrino-matter interaction channels that involve axial-vector interactions.
as illustrated in Fig. 2. This medium dependent axial-vector coupling constant is then employed in all other neutrino-matter interaction channels that involve axial-vector interactions.
Finally, according to the above expressions (3)–(10)the medium dependence of the neutrino-pair emission kernel scales as follows, 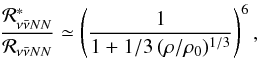 (11)where the Fermi momenta are expressed in terms of the matter density, pF ∝ ρ1 / 3. In the following the medium-modified process according to Eq. (11)is labelled as NN∗, while for the unmodified FOPE rate NN is used. Figure 2 illustrates the density dependence of
(11)where the Fermi momenta are expressed in terms of the matter density, pF ∝ ρ1 / 3. In the following the medium-modified process according to Eq. (11)is labelled as NN∗, while for the unmodified FOPE rate NN is used. Figure 2 illustrates the density dependence of 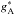 , being in good quantitative agreement with alternative approaches based on the low-density limit of chiral physics (see Friman et al. 1999; Rho 2001; Meißner et al. 2002; Carter & Prakash 2002), together with γ and the ratio (11)labelled as NN∗/NN. The overall onset of reduction of the process starts at densities of about 1012 g cm-3 with a suppression of about a factor of 5 at ρ0, being in quantitative agreement with calculations of Bartl et al. (2014) based on the T-matrix approach as well as chiral effective field theory.
, being in good quantitative agreement with alternative approaches based on the low-density limit of chiral physics (see Friman et al. 1999; Rho 2001; Meißner et al. 2002; Carter & Prakash 2002), together with γ and the ratio (11)labelled as NN∗/NN. The overall onset of reduction of the process starts at densities of about 1012 g cm-3 with a suppression of about a factor of 5 at ρ0, being in quantitative agreement with calculations of Bartl et al. (2014) based on the T-matrix approach as well as chiral effective field theory.
2.3. Neutrino opacity and mean-free path
The neutrino opacity for pair processes, that is, the (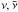 ) absorption rate, is given in Fischer et al. (2012) obtained by integrating the reaction kernel taking into account the initial-state antineutrino phase space as follows,
) absorption rate, is given in Fischer et al. (2012) obtained by integrating the reaction kernel taking into account the initial-state antineutrino phase space as follows, 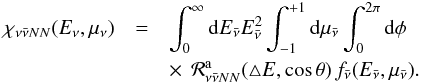 (12)For other weak processes, for example, scattering on nucleons and electrons, a similar expression for the opacity χ as Eq. (12)can be obtained via the integration of the corresponding scattering reaction kernels; they connect initial and final neutrino states similar as for
(12)For other weak processes, for example, scattering on nucleons and electrons, a similar expression for the opacity χ as Eq. (12)can be obtained via the integration of the corresponding scattering reaction kernels; they connect initial and final neutrino states similar as for 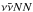 . For scattering the antineutrino occupation number
. For scattering the antineutrino occupation number 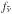 in expression (12)has to be replaced with the final state neutrino occupation number. On the other hand, exceptions are the charged current absorption reactions which depend only on the incoming neutrino energy Eν (within the elastic approximation employed here).
in expression (12)has to be replaced with the final state neutrino occupation number. On the other hand, exceptions are the charged current absorption reactions which depend only on the incoming neutrino energy Eν (within the elastic approximation employed here).
In order to study the medium dependence it is useful to define the inverse mean-free path as spectrum averaged quantity for each neutrino flavour (ν) and weak process separately, based on the corresponding opacity channel χj(Eν,μν). Therefore one has to integrate the remaining neutrino phase space as follows, 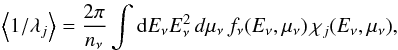 (13)with the local neutrino number density nν and initial state neutrino occupation number fν corresponding to nν. The integration of the neutrino phase space leaves only local dependencies of ⟨ 1 /λ ⟩, for example, in terms of the supernova state of matter given in terms of radial profiles.
(13)with the local neutrino number density nν and initial state neutrino occupation number fν corresponding to nν. The integration of the neutrino phase space leaves only local dependencies of ⟨ 1 /λ ⟩, for example, in terms of the supernova state of matter given in terms of radial profiles.
 |
Fig. 3 Density dependence of the average neutrino opacity (13)for selected weak processes, comparing NN (thin blue lines) and NN∗ (thick brown lines); see text for definitions. The corresponding conditions are shown in Fig. 4. Short vertical black lines at the top of graphs a)–c) mark the locations of the averaged neutrinospheres of last absorption labelled “abs.” (dash-dotted lines) and last elastic scattering labelled “scat.” (solid lines). The grey shaded region in between represents the scattering atmosphere. |
 |
Fig. 4 Profiles of temperature and Ye of the early PNS deleptonization phase at about 3 s post bounce. |
In Fig. 3 the density dependence of the opacity (13)is shown for several weak reaction channels j with the largest contributions to the total opacity – charged current absorptions (dash-dotted lines) – elastic scattering on nucleons (νN, dashed lines) – thermalization via inelastic scattering on electrons and positrons (νe±, dotted lines) – neutrino-pair absorption via NN-bremsstrahlung (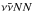 , solid lines). The associated conditions are shown in Fig. 4 corresponding to the early PNS deleptonization phase at about 3 s post bounce. For νe, illustrated in Fig. 3a, the largest opacity is due to νe-absorption on neutrons followed by elastic scattering on neutrons, since the neutrons as targets for these processes are the most abundant nuclear species. The opacity for all other weak processes is strongly suppressed. This also implies that NN-bremsstrahlung plays a negligible role for νe and that medium modifications NN∗ are unlikely to impact the overall νe spectra and fluxes. The situation is different for
, solid lines). The associated conditions are shown in Fig. 4 corresponding to the early PNS deleptonization phase at about 3 s post bounce. For νe, illustrated in Fig. 3a, the largest opacity is due to νe-absorption on neutrons followed by elastic scattering on neutrons, since the neutrons as targets for these processes are the most abundant nuclear species. The opacity for all other weak processes is strongly suppressed. This also implies that NN-bremsstrahlung plays a negligible role for νe and that medium modifications NN∗ are unlikely to impact the overall νe spectra and fluxes. The situation is different for  as shown in Fig. 3b, where the largest contribution to the opacity is due to elastic scattering on neutrons. The absorption of
as shown in Fig. 3b, where the largest contribution to the opacity is due to elastic scattering on neutrons. The absorption of  on protons is heavily suppressed because protons are much less abundant than neutrons by about one order of magnitude and because medium modifications (treated here at the mean level following Martínez-Pinedo et al. 2012) suppress the
on protons is heavily suppressed because protons are much less abundant than neutrons by about one order of magnitude and because medium modifications (treated here at the mean level following Martínez-Pinedo et al. 2012) suppress the  -absorption rate at low energies
-absorption rate at low energies 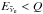 . Note that the latter aspect is compensated by the inverse-neutron decay (reaction (3) in Table 1) for which there is only a finite rate for
. Note that the latter aspect is compensated by the inverse-neutron decay (reaction (3) in Table 1) for which there is only a finite rate for 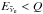 . Concerning the other inelastic channels, the opacity for NN-bremsstrahlung exceeds only slightly the opacity for
. Concerning the other inelastic channels, the opacity for NN-bremsstrahlung exceeds only slightly the opacity for  -absorption on protons based on NN. With the medium dependent suppression NN∗ both opacities become on the same order in the region of neutrino decoupling illustrated through the gray band in Fig. 3b – this will be further discussed below. This shifts back more relevance to the charged-current channel and is expected to modify the
-absorption on protons based on NN. With the medium dependent suppression NN∗ both opacities become on the same order in the region of neutrino decoupling illustrated through the gray band in Fig. 3b – this will be further discussed below. This shifts back more relevance to the charged-current channel and is expected to modify the  properties. Note that for the NN-bremsstrahlung opacity, as well as for inverse mean free path, the neutrino spectra used are those obtained from the supernova simulations based on Boltzmann neutrino transport. The situation for νμ/τ and
properties. Note that for the NN-bremsstrahlung opacity, as well as for inverse mean free path, the neutrino spectra used are those obtained from the supernova simulations based on Boltzmann neutrino transport. The situation for νμ/τ and 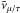 , as illustrated in Fig. 3c, is similar to the one for
, as illustrated in Fig. 3c, is similar to the one for  . Note that, unlike for
. Note that, unlike for  , there is no charged-current absorption reaction for the heavy-lepton flavor neutrinos considered. Also here the largest contribution to the opacity comes from scattering on free neutrons. Inelastic contributions to the opacity are only due to NN-bremsstrahlung and scattering on electrons and positrons, which are strongly suppressed compared to scattering on neutrons. Now with the medium suppression NN∗ the opacity for NN-bremsstrahlung even drops below the one for inelastic scattering on electrons and positrons in the region of neutrino decoupling. Hence, the largest impact from the medium modifications of NN-bremsstrahlung is expected for the spectra of νμ/τ and
, there is no charged-current absorption reaction for the heavy-lepton flavor neutrinos considered. Also here the largest contribution to the opacity comes from scattering on free neutrons. Inelastic contributions to the opacity are only due to NN-bremsstrahlung and scattering on electrons and positrons, which are strongly suppressed compared to scattering on neutrons. Now with the medium suppression NN∗ the opacity for NN-bremsstrahlung even drops below the one for inelastic scattering on electrons and positrons in the region of neutrino decoupling. Hence, the largest impact from the medium modifications of NN-bremsstrahlung is expected for the spectra of νμ/τ and 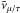 .
.
Note also the small suppression of the other weak processes in Fig. 3, in particular for the charged-current absorption reactions. This is due to the employed medium dependence of 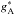 according to expression (10).
according to expression (10).
Figure 3 shows the locations of the averaged neutrinospheres of last absorption and last elastic scattering. For a definition of the neutrinospheres, see Sect. II.B in Fischer et al. (2012). According to Raffelt (2001), the region between “scat.” and “abs.” represents a scattering atmosphere in which neutrinos transfer only momentum before finally reaching the free-streaming condition above “scat.”. Note that unlike for  and νμ/τ, for νe there is no scattering atmosphere because the opacity is dominated by charged-exchange absorption on neutrons by one order of magnitude above scattering on neutrons.
and νμ/τ, for νe there is no scattering atmosphere because the opacity is dominated by charged-exchange absorption on neutrons by one order of magnitude above scattering on neutrons.
3. PNS evolution
In order to study the impact of medium modifications for the neutrino-pair processes from NN-bremsstrahlung in simulations of the PNS deleptonization, the rate according to expression (11)is implemented into the Boltzmann neutrino transport module of AGILE-BOLTZTRAN. The simulations are launched from the 18 M⊙ pre-collapse progenitor of Woosley et al. (2002). In Fischer (2016) it was evolved consistently through all phases prior to the supernova explosion onset. The onset of the neutrino-driven supernova explosion – shock revival during the post-bounce mass accretion phase – is triggered following Fischer et al. (2010) via enhanced νe and  heating in the gain region, that is, where net heating is established. It results in the explosion onset with the continuous shock expansion to increasingly larger radii at about 350 ms post bounce. This scenario for the shock revival is necessary since, in general, neutrino-driven explosions cannot be obtained in spherically symmetric simulations. Exceptions are low-mass stellar progenitors on the order of 8–10 M⊙ (see Kitaura et al. 2006; Melson et al. 2015). Moreover, it is not feasible to simulate the PNS deleptonization up to 10–30 s within multi-dimensional neutrino radiation hydrodynamics simulations. Note further that once the explosion proceeds the standard charged-current rates are switched back on.
heating in the gain region, that is, where net heating is established. It results in the explosion onset with the continuous shock expansion to increasingly larger radii at about 350 ms post bounce. This scenario for the shock revival is necessary since, in general, neutrino-driven explosions cannot be obtained in spherically symmetric simulations. Exceptions are low-mass stellar progenitors on the order of 8–10 M⊙ (see Kitaura et al. 2006; Melson et al. 2015). Moreover, it is not feasible to simulate the PNS deleptonization up to 10–30 s within multi-dimensional neutrino radiation hydrodynamics simulations. Note further that once the explosion proceeds the standard charged-current rates are switched back on.
In the following, two different simulation setups will be discussed; ref. run: unmodified FOPE rate for NN-bremsstrahlung and vacuum gA, compared to NN∗: medium dependent suppression of NN-bremsstrahlung MVOPE and 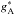 based on Eqs. (10)and (11). Both simulations use the EoS HS(DD2). The PNS deleptonization proceeds qualitatively similar in both simulations; the temperature decreases continuously at the PNS surface in the course of lepton losses and the entire PNS contracts accordingly with continuously increasing central density (for illustration, see Figs. 3 and 7 in Fischer et al. 2012). Note that results of the ref. run have been published in Fischer et al. (2016a).
based on Eqs. (10)and (11). Both simulations use the EoS HS(DD2). The PNS deleptonization proceeds qualitatively similar in both simulations; the temperature decreases continuously at the PNS surface in the course of lepton losses and the entire PNS contracts accordingly with continuously increasing central density (for illustration, see Figs. 3 and 7 in Fischer et al. 2012). Note that results of the ref. run have been published in Fischer et al. (2016a).
Quantitative differences arise in the neutrino signal illustrated in Fig. 5. For the simulation based on NN∗ the average energies of νμ/τ and  are increased up to about 1 MeV, compared to the reference case. For νe the effect is significantly weaker since the neutrino-pair processes act only as perturbation to the total opacity (see Fig. 3). The corresponding enhancement of the neutrino luminosities, in particular for νe and
are increased up to about 1 MeV, compared to the reference case. For νe the effect is significantly weaker since the neutrino-pair processes act only as perturbation to the total opacity (see Fig. 3). The corresponding enhancement of the neutrino luminosities, in particular for νe and  , is partly due to the feedback from νμ/τ via the neutrino-pair process (10) of Table 1.
, is partly due to the feedback from νμ/τ via the neutrino-pair process (10) of Table 1.
This situation continues during the entire PNS deleptonization up to 30 s post bounce, where towards later times the opacity from  -absorption on protons reduces further due to the rising neutron excess and the increasing importance of the medium modifications for this weak process. At even late times, on the order of t> 40 s post bounce, the transition is reached from neutrino opaque to transparent due to the continuously reducing temperatures below T ≃ 1 MeV, associated with neutrino decoupling from all densities including even above ρ0; in order to simulate this transition other weak reaction, such as the (medium) modified Urca processes, drive the further evolution of the PNS towards the final cold neutron star. However, this extends beyond the scopes of the present study.
-absorption on protons reduces further due to the rising neutron excess and the increasing importance of the medium modifications for this weak process. At even late times, on the order of t> 40 s post bounce, the transition is reached from neutrino opaque to transparent due to the continuously reducing temperatures below T ≃ 1 MeV, associated with neutrino decoupling from all densities including even above ρ0; in order to simulate this transition other weak reaction, such as the (medium) modified Urca processes, drive the further evolution of the PNS towards the final cold neutron star. However, this extends beyond the scopes of the present study.
 |
Fig. 5 Evolution of neutrino luminosities and average energies. |
Note that the density-dependent suppression for the neutrino-pair emission and absorption rate from NN-bremsstrahlung obtained here (see Fig. 3) is in quantitative agreement with Bartl et al. (2014), comparing T-matrix approach and chiral effective field theory with FOPE. However, the large enhancement of this rate found also in Bartl et al. (2014) based on the T-matrix approach towards low density – on the order of ρ< 1011 g cm-3 – renders it irrelevant because at such low density (a) the opacity is dominated by other weak processes for all neutrino flavors, as illustrated in Fig. 3, and (b) the neutrinos have already decoupled from matter.
 |
Fig. 6 Evolution of selected tracer mass elements corresponding to dynamically ejected (black lines) material together with the shock expansion (green dash-dotted line) and the neutrino-driven wind (blue lines) ejected from the PNS surface (green sold line). |
4. Nucleosynthesis relevant conditions
The increased spectral difference between  and νe found here for the simulation based on NN∗, compared to the ref. run, has consequences for the nucleosynthesis of heavy elements associated with the low-mass outflow ejected via continuous neutrino heating from the PNS surface (see Fig. 6a) during the deleptonization – known as neutrino-driven wind. This has been studied based on the static wind equations (see Duncan et al. 1986; Hoffman et al. 1997; Thompson et al. 2001) as well as within steady-state models (see Woosley & Baron 1992; Takahashi et al. 1994) while Witti et al. (1994) and Arcones et al. (2007) are based on a hydrodynamics description with parametrized neutrino luminosities. In Fig. 6 the post-bounce evolution of the neutrino-driven wind is illustrated for selected tracer mass elements at the example of the reference case, as well as the material ejected dynamically together with the expanding supernova shock illustrated in graph (a). Differences of the dynamical evolution compared to the simulation based on NN∗ are negligible, continuously decreasing density and temperature as shown in the Figs. 6b and c. The mass ejected in the neutrino-driven wind is on the order of 6 × 10-4M⊙ during the first 10 s. Note that most material is ejected during the early evolution, 5.356 × 10-4M⊙ during the first 2 s. Hence, for the integrated nucleosynthesis analysis the early neutrino-driven wind phase leaves the largest imprint on the yields.
and νe found here for the simulation based on NN∗, compared to the ref. run, has consequences for the nucleosynthesis of heavy elements associated with the low-mass outflow ejected via continuous neutrino heating from the PNS surface (see Fig. 6a) during the deleptonization – known as neutrino-driven wind. This has been studied based on the static wind equations (see Duncan et al. 1986; Hoffman et al. 1997; Thompson et al. 2001) as well as within steady-state models (see Woosley & Baron 1992; Takahashi et al. 1994) while Witti et al. (1994) and Arcones et al. (2007) are based on a hydrodynamics description with parametrized neutrino luminosities. In Fig. 6 the post-bounce evolution of the neutrino-driven wind is illustrated for selected tracer mass elements at the example of the reference case, as well as the material ejected dynamically together with the expanding supernova shock illustrated in graph (a). Differences of the dynamical evolution compared to the simulation based on NN∗ are negligible, continuously decreasing density and temperature as shown in the Figs. 6b and c. The mass ejected in the neutrino-driven wind is on the order of 6 × 10-4M⊙ during the first 10 s. Note that most material is ejected during the early evolution, 5.356 × 10-4M⊙ during the first 2 s. Hence, for the integrated nucleosynthesis analysis the early neutrino-driven wind phase leaves the largest imprint on the yields.
In Qian & Woosley (1996) it has been shown that the nucleosynthesis conditions of the neutrino-driven wind are entirely determined from the neutrino fluxes and energies as well as their evolution. Moreover, in Martínez-Pinedo et al. (2012) it has been found that the consistent treatment of charged current weak processes and nuclear EoS, which increases spectral differences between νe and  , turns material to the neutron rich side with Ye ≃ 0.47–0.49 for the initial neutrino-driven wind. However, with the inclusion of inelastic contributions and in particular weak magnetism corrections – both effects are included here – the neutron excess of the neutrino-driven wind reduces significantly as shown in Fig. 7a for the reference run with minimum Ye ≃ 0.495.
, turns material to the neutron rich side with Ye ≃ 0.47–0.49 for the initial neutrino-driven wind. However, with the inclusion of inelastic contributions and in particular weak magnetism corrections – both effects are included here – the neutron excess of the neutrino-driven wind reduces significantly as shown in Fig. 7a for the reference run with minimum Ye ≃ 0.495.
The inclusion of medium modifications at the level of NN∗, which increases slightly the difference between νe and  (see Fig. 5), turns back slightly the neutron excess during the early neutrino-driven wind with minimum Ye ≃ 0.4895 (see Fig. 7a). Material also stays slightly longer on the neutron rich side for about 1 s, before finally turning to proton-rich conditions, which is due to the continuously reducing spectral differences between νe and
(see Fig. 5), turns back slightly the neutron excess during the early neutrino-driven wind with minimum Ye ≃ 0.4895 (see Fig. 7a). Material also stays slightly longer on the neutron rich side for about 1 s, before finally turning to proton-rich conditions, which is due to the continuously reducing spectral differences between νe and  during the PNS deleptonization (see Fig. 5). The entropy per baryon, as additional nucleosynthesis relevant condition, is on the order of s ≃ 50 kB per baryon during the early evolution, see Fig. 7b, rising only towards later times up to more than s ~ 100 kB per baryon.
during the PNS deleptonization (see Fig. 5). The entropy per baryon, as additional nucleosynthesis relevant condition, is on the order of s ≃ 50 kB per baryon during the early evolution, see Fig. 7b, rising only towards later times up to more than s ~ 100 kB per baryon.
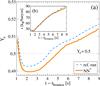 |
Fig. 7 Ye and entropy sampled in the neutrino-driven wind expansion at a radius of 1000 km, corresponding to the freeze-out conditions. |
Note that the entropies here are generally higher than reported previously due to the more massive 18 M⊙ progenitor model explored here, compared to the lighter 11.2 M⊙ progenitor which was explored in Martínez-Pinedo et al. (2014). The current PNS has a baryon mass of MB = 1.65M⊙ compared to the much lighter PNS of MB = 1.19M⊙ of Martínez-Pinedo et al. (2014). The relation between PNS mass and entropy of the neutrino-driven wind is derived in Qian & Woosley (1996).
5. Summary
Neutrino-pair emission and absorption from NN-bremsstrahlung is the relevant source and sink for heavy lepton flavor neutrinos above densities around ρ0/ 10 in core-collapse supernova simulations. This article discusses the impact of medium modification of the vacuum OPE approximation for NN-bremsstrahlung, by means of providing a density-dependent parametrization of the medium-modified πNN-vertex. The latter has been derived within the Fermi-liquid theory framework; details can be found in Migdal (1978), Senatorov & Voskresensky (1987) and Migdal et al. (1990). It effectively suppresses the neutrino-pair emission rate with increasing density. The magnitude of suppression obtained here is in quantitative agreement with recent results of Bartl et al. (2014) based on chiral effective field theory.
The modified neutrino-pair emission rate is then implemented into the Boltzmann neutrino transport module of the core-collapse supernova model AGILE-BOLTZTRAN in order to study the impact in simulations of the PNS deleptonization. Unlike νe, which are dominated by charged-current absorption on neutrons, νμ/τ but also  are affected substantially. In particular, the reduced rate for neutrino-pair processes from NN-bremsstrahlung returns back more relevance to the charged-current
are affected substantially. In particular, the reduced rate for neutrino-pair processes from NN-bremsstrahlung returns back more relevance to the charged-current  -absorption on protons. This shifts the corresponding neutrinospheres for
-absorption on protons. This shifts the corresponding neutrinospheres for  , and also for νμ/τ, to somewhat higher density, which in turn results in enhanced neutrino fluxes and average energies.
, and also for νμ/τ, to somewhat higher density, which in turn results in enhanced neutrino fluxes and average energies.
These findings are in quantitative agreement with the results of Bartl (priv. comm.), which are based on a parametrization of the study of Bartl et al. (2014), and have important consequences for the conditions relevant for the nucleosynthesis in the neutrino-driven wind, ejected from the PNS during the deleptonization. Note that inelastic and weak magnetism contributions reduce the neutron excess, from Ye ≃ 0.48 of Martínez-Pinedo et al. (2014) to Ye ≃ 0.495, due to generally reduced spectral differences between νe and  for the latter. The simulation with the MVOPE approach increases back the spectral differences between νe and
for the latter. The simulation with the MVOPE approach increases back the spectral differences between νe and  , which in turn increases the neutron excess slightly during the early neutrino-driven wind phase. Material also stays longer on the neutron rich side. However, following Hoffman et al. (1997), the overall magnitude of Ye ≃ 0.49 and the generally low entropy per baryon s ≃ 50 kB indicate that the synthesis of heavy elements beyond Mo (with charge number Z = 52) cannot be expected (see also Qian & Wasserburg 2007; Wanajo et al. 2009).
, which in turn increases the neutron excess slightly during the early neutrino-driven wind phase. Material also stays longer on the neutron rich side. However, following Hoffman et al. (1997), the overall magnitude of Ye ≃ 0.49 and the generally low entropy per baryon s ≃ 50 kB indicate that the synthesis of heavy elements beyond Mo (with charge number Z = 52) cannot be expected (see also Qian & Wasserburg 2007; Wanajo et al. 2009).
The medium-modifications for the πNN vertex here explored, and the consequent suppression of the neutrino-pair processes, are likely to also affect the early post-bounce mass-accretion phase of core-collapse supernovae, that is, prior to the possible onset of the supernova explosion which is studied to some extend in Bartl (priv. comm.). In particular the losses associated with heavy-lepton flavor neutrinos may be reduced. Reduced cooling could then in turn lead to more optimistic conditions for the revival of the stalled supernova shock. This remains to be explored in multi-dimensional core-collapse supernova simulations that are based on the sophisticated treatment of neutrino transport including a “complete” set of weak interactions.
The inclusion of inelastic neutrino nucleon-nucleon scattering, νNN ⇆ NNν, in simulations of core-collapse supernovae and for the PNS deleptonization may be complimentary. Even though at finite temperatures on the order of 5–10 MeV the total opacity for all neutrino flavors will always be dominated by reactions with single neutrons as the most abundant nuclear species, this channel may substantially contribute to the energy-transfer for  , νμ/τ and
, νμ/τ and 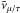 in the region of neutrino decoupling, comparable to the one by neutrino-electron and positron scattering. Expressions for the νNN ⇆ NNν matrix element have been derived in Hannestad & Raffelt (1998) based on the FOPE approach, however, the correct inelastic dependence (momentum transfer) required for the scattering kernels of the collision integrals of the Boltzmann equation still has to be derived. This extends beyond the scope of the present article and remains to be explored in future studies.
in the region of neutrino decoupling, comparable to the one by neutrino-electron and positron scattering. Expressions for the νNN ⇆ NNν matrix element have been derived in Hannestad & Raffelt (1998) based on the FOPE approach, however, the correct inelastic dependence (momentum transfer) required for the scattering kernels of the collision integrals of the Boltzmann equation still has to be derived. This extends beyond the scope of the present article and remains to be explored in future studies.
Note that this may become important towards later times of the PNS deleptonization when the core temperature drops below 1 MeV, entering the transition from neutrino diffuse to freely streaming. At that stage the direct Urca processes (1)–(3) in Table 1 will become suppressed and other weak channels, for example, modified Urca processes will dominate further evolution.
Acknowledgments
Special thanks are due to D. Voskresensky, P. M. Lo and G. Martínez-Pinedo for many discussions and for proofreading the manuscript. I am also grateful for private communications with D. Blaschke, T. Klähn, and C. Sasaki. The author acknowledges support by the Polish National Science Center (NCN) under grant number UMO-2013/11/D/ST2/02645. The supernova simulations were performed at the Center for Scientific Computing (CSC) host at the University of Frankfurt (Germany).
References
- Aouissat, Z., Rapp, R., Chanfray, G., Schuck, P., & Wambach, J. 1995, Nucl. Phys. A, 581, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Arcones, A., Janka, H.-T., & Scheck, L. 2007, A&A, 467, 1227 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bartl, A., Pethick, C. J., & Schwenk, A. 2014, Phys. Rev. Lett., 113, 081101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Blaschke, D., Röpke, G., Schulz, H., Sedrakian, A. D., & Voskresensky, D. N. 1995, MNRAS, 273, 596 [NASA ADS] [CrossRef] [Google Scholar]
- Blaschke, D., Grigorian, H., & Voskresensky, D. N. 2004, A&A., 424, 979 [CrossRef] [EDP Sciences] [Google Scholar]
- Blaschke, D., Grigorian, H., Voskresensky, D. N., & Weber, F. 2012, Phys. Rev. C, 85, 022802 [NASA ADS] [CrossRef] [Google Scholar]
- Blaschke, D., Grigorian, H., & Voskresensky, D. N. 2013, Phys. Rev. C, 88, 065805 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Brown, G. E., & Rho, M. 1991, Phys. Rev. Lett., 66, 2720 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bruenn, S. W. 1985, ApJS, 58, 771 [NASA ADS] [CrossRef] [Google Scholar]
- Buras, R., Janka, H.-T., Keil, M. T., Raffelt, G. G., & Rampp, M. 2003, ApJ, 587, 320 [NASA ADS] [CrossRef] [Google Scholar]
- Carter, G. W., & Prakash, M. 2002, Phys. Lett. B, 525, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Duncan, R. C., Shapiro, S. L., & Wasserman, I. 1986, ApJ, 309, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Fischer, T. 2016, EPJ A, 52, 54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fischer, T., Whitehouse, S. C., Mezzacappa, A., Thielemann, F.-K., & Liebendörfer, M. 2009, A&A, 499, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fischer, T., Whitehouse, S., Mezzacappa, A., Thielemann, F.-K., & Liebendörfer, M. 2010, A&A, 517, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fischer, T., Martínez-Pinedo, G., Hempel, M., & Liebendörfer, M. 2012, Phys. Rev. D, 85, 083003 [NASA ADS] [CrossRef] [Google Scholar]
- Fischer, T., Langanke, K., & Martínez-Pinedo, G. 2013, Phys. Rev. C, 88, 065804 [NASA ADS] [CrossRef] [Google Scholar]
- Fischer, T., Hempel, M., Sagert, I., Suwa, Y., & Schaffner-Bielich, J. 2014, EPJ A, 50, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Fischer, T., Chakraborty, S., Giannotti, M., Mirizzi, A., Payez, A., & Ringwald, A. 2016, Phys. Rev. D, submitted [arXiv:1605.08780] [Google Scholar]
- Friman, B., Rho, M., & Song, C. 1999, Phys. Rev. C, 59, 3357 [NASA ADS] [CrossRef] [Google Scholar]
- Friman, B. L., & Maxwell, O. V. 1979, ApJ, 232, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Fuller, G. M., & Meyer, B. S. 1991, ApJ, 376, 701 [NASA ADS] [CrossRef] [Google Scholar]
- Grigorian, H., & Voskresensky, D. N. 2005, A&A, 444, 913 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hanhart, C., Phillips, D. R., & Reddy, S. 2001, Phys. Lett. B, 499, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Hannestad, S., & Raffelt, G. 1998, ApJ, 507, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Hebeler, K., & Schwenk, A. 2010, Phys. Rev. C, 82, 014314 [NASA ADS] [CrossRef] [Google Scholar]
- Hempel, M. 2015, Phys. Rev. C, 91, 055807 [NASA ADS] [CrossRef] [Google Scholar]
- Hempel, M., & Schaffner-Bielich, J. 2010, Nucl. Phys. A, 837, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Hoffman, R., Woosley, S., & Qian, Y. 1997, ApJ, 482, 951 [NASA ADS] [CrossRef] [Google Scholar]
- Horowitz, C. 2002, Phys. Rev. D, 65, 043001 [NASA ADS] [CrossRef] [Google Scholar]
- Horowitz, C. J., Shen, G., O’Connor, E., & Ott, C. D. 2012, Phys. Rev. C, 86, 065806 [NASA ADS] [CrossRef] [Google Scholar]
- Hüdepohl, L., Müller, B., Janka, H.-T., Marek, A., & Raffelt, G. G. 2010, Phys. Rev. Lett., 104, 251101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Janka, H.-T. 2012, Ann. Rev. Nucl. Part. Sci., 62, 407 [Google Scholar]
- Janka, H.-T., Keil, W., Raffelt, G., & Seckel, D. 1996, Phys. Rev. Lett., 76, 2621 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Janka, H.-T., Langanke, K., Marek, A., Martínez-Pinedo, G., & Müller, B. 2007, Phys. Rep., 442, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Juodagalvis, A., Langanke, K., Hix, W. R., Martínez-Pinedo, G., & Sampaio, J. M. 2010, Nucl. Phys. A, 848, 454 [NASA ADS] [CrossRef] [Google Scholar]
- Kitaura, F., Janka, H.-T., & Hillebrandt, W. 2006, A&A, 450, 345 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krüger, T., Tews, I., Hebeler, K., & Schwenk, A. 2013, Phys. Rev. C, 88, 025802 [NASA ADS] [CrossRef] [Google Scholar]
- Lattimer, J. M., & Lim, Y. 2013, ApJ, 771, 51 [Google Scholar]
- Liebendörfer, M., Mezzacappa, A., & Thielemann, F.-K. 2001a, Phys. Rev. D, 63, 104003 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Liebendörfer, M., Mezzacappa, A., Thielemann, F.-K., et al. 2001b, Phys. Rev. D, 63, 103004 [NASA ADS] [CrossRef] [Google Scholar]
- Liebendörfer, M., Rosswog, S., & Thielemann, F.-K. 2002, ApJS, 141, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Liebendörfer, M., Messer, O., Mezzacappa, A., et al. 2004, ApJS, 150, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Liebendörfer, M., Rampp, M., Janka, H.-T., & Mezzacappa, A. 2005, ApJ, 620, 840 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez-Pinedo, G., Fischer, T., Lohs, A., & Huther, L. 2012, Phys. Rev. Lett., 109, 251104 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Martínez-Pinedo, G., Fischer, T., & Huther, L. 2014, J. Phys. G, 41, 044008 [NASA ADS] [CrossRef] [Google Scholar]
- Meißner, U.-G., Oller, J. A., & Wirzba, A. 2002, Ann. Phys., 297, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Melson, T., Janka, H.-T., & Marek, A. 2015, ApJ, 801, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Mezzacappa, A., & Bruenn, S. W. 1993a, ApJ, 405, 637 [NASA ADS] [CrossRef] [Google Scholar]
- Mezzacappa, A., & Bruenn, S. W. 1993b, ApJ, 410, 740 [NASA ADS] [CrossRef] [Google Scholar]
- Migdal, A. B. 1978, Rev. Mod. Phys., 50, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Migdal, A. B., Saperstein, E. E., Troitsky, M. A., & Voskresensky, D. N. 1990, Phys. Rep., 192, 179 [Google Scholar]
- Otsuki, K., Tagoshi, H., Kajino, T., & Wanajo, S.-Y. 1999, ApJ, 533, 424 [Google Scholar]
- Page, D., & Reddy, S. 2006, Ann. Rev. Nucl. Part. Sci., 56, 327 [Google Scholar]
- Pons, J., Reddy, S., Prakash, M., Lattimer, J., & Miralles, J. 1999, ApJ, 513, 780 [NASA ADS] [CrossRef] [Google Scholar]
- Qian, Y. Z., & Wasserburg, G. J. 2007, Phys. Rep., 442, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Qian, Y. Z., & Woosley, S. 1996, ApJ, 471, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Raffelt, G. G. 2001, ApJ, 561, 890 [NASA ADS] [CrossRef] [Google Scholar]
- Rapp, R., Durso, J. W., & Wambach, J. 1996, Nucl. Phys. A, 596, 436 [NASA ADS] [CrossRef] [Google Scholar]
- Rapp, R., Durso, J. W., & Wambach, J. 1997, Nucl. Phys. A, 615, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, S., Prakash, M., & Lattimer, J. M. 1998, Phys. Rev. D, 58, 013009 [NASA ADS] [CrossRef] [Google Scholar]
- Rho, M. 2001, Phys. Atom. Nucl., 64, 637 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, L. F., Reddy, S., & Shen, G. 2012, Phys. Rev. C, 86, 065803 [NASA ADS] [CrossRef] [Google Scholar]
- Schaab, C., Voskresensky, D., Sedrakian, A. D., Weber, F., & Weigel, M. K. 1997, A&A, 321, 591 [NASA ADS] [Google Scholar]
- Senatorov, A. V., & Voskresensky, D. N. 1987, Phys. Lett. B, 184, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Sigl, G. 1996, Phys. Rev. Lett., 76, 2625 [NASA ADS] [CrossRef] [Google Scholar]
- Takahashi, K., Witti, J., & Janka, H.-Th. 1994, A&A, 286, 857 [Google Scholar]
- Tews, I., Krüger, T., Hebeler, K., & Schwenk, A. 2013, Phys. Rev. Lett., 110, 032504 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Thompson, T. A., Burrows, A., & Meyer, B. S. 2001, ApJ, 562, 887 [NASA ADS] [CrossRef] [Google Scholar]
- Timmes, F. X., & Arnett, D. 1999, ApJS, 125, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Typel, S., Ropke, G., Klahn, T., Blaschke, D., & Wolter, H. 2010, Phys. Rev. C, 81, 015803 [NASA ADS] [CrossRef] [Google Scholar]
- Typel, S., Oertel, M., & Klaehn, T. 2013, ArXiv e-prints [arXiv:1307.5715] [Google Scholar]
- Voskresensky, D. N. 2001, in Physics of Neutron Star Interiors (Berlin: Springer Verlag), eds. D. Blaschke, N. K. Glendenning, & A. Sedrakian, Lect. Notes Phys., 578, 467 [Google Scholar]
- Wanajo, S. 2006a, ApJ, 650, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Wanajo, S. 2006b, ApJ, 647, 1323 [Google Scholar]
- Wanajo, S., Nomoto, K., Janka, H.-Th., Kitaura, F. S., & Müller, B. 2009, ApJ, 695, 208 [NASA ADS] [CrossRef] [Google Scholar]
- Witti, J., Janka, H.-Th., & Takahashi, K. 1994, A&A, 286, 841 [NASA ADS] [Google Scholar]
- Woosley, S. E., & Baron, E. 1992, ApJ, 391, 228 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S., Wilson, J., Mathews, G., Hoffman, R., & Meyer, B. 1994, ApJ, 433, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S., Heger, A., & Weaver, T. 2002, Rev. Mod. Phys., 74, 1015 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, M.-R., Qian, Y.-Z., Martínez-Pinedo, G., Fischer, T., & Huther, L. 2015, Phys. Rev. D, 91, 065016 [NASA ADS] [CrossRef] [Google Scholar]
- Yakovlev, D. G., Kaminker, A. D., Gnedin, O. Y., & Haensel, P. 2001, Phys. Rep., 354, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Yakovlev, D. G., Gnedin, O. Y., Gusakov, M. E., et al. 2005, Nucl. Phys. A, 752, 590 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Neutrino pair-emission from NN-bremsstrahlung within the FOPE approximation. |
| In the text | |
 |
Fig. 2 Medium dependence of the πNN-vertex, axial-vector coupling constant and the ratio Eq. (11). |
| In the text | |
 |
Fig. 3 Density dependence of the average neutrino opacity (13)for selected weak processes, comparing NN (thin blue lines) and NN∗ (thick brown lines); see text for definitions. The corresponding conditions are shown in Fig. 4. Short vertical black lines at the top of graphs a)–c) mark the locations of the averaged neutrinospheres of last absorption labelled “abs.” (dash-dotted lines) and last elastic scattering labelled “scat.” (solid lines). The grey shaded region in between represents the scattering atmosphere. |
| In the text | |
 |
Fig. 4 Profiles of temperature and Ye of the early PNS deleptonization phase at about 3 s post bounce. |
| In the text | |
 |
Fig. 5 Evolution of neutrino luminosities and average energies. |
| In the text | |
 |
Fig. 6 Evolution of selected tracer mass elements corresponding to dynamically ejected (black lines) material together with the shock expansion (green dash-dotted line) and the neutrino-driven wind (blue lines) ejected from the PNS surface (green sold line). |
| In the text | |
 |
Fig. 7 Ye and entropy sampled in the neutrino-driven wind expansion at a radius of 1000 km, corresponding to the freeze-out conditions. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


