| Issue |
A&A
Volume 593, September 2016
|
|
|---|---|---|
| Article Number | A77 | |
| Number of page(s) | 13 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201628843 | |
| Published online | 26 September 2016 | |
Star-forming dwarf galaxies: the correlation between far-infrared and radio fluxes
1 Departamento de Astronomía, Facultad Ciencias Físicas y Matemáticas, Universidad de Concepción, Av. Esteban Iturra s/n, Barrio Universitario, Casilla 160-C, Concepción, Chile.
e-mail: dschleicher@astro-udec.cl
2 Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
e-mail: rbeck@mpifr-bonn.mpg.de
Received: 3 May 2016
Accepted: 30 June 2016
The correlation between far-infrared and radio fluxes connects star formation and magnetic fields in galaxies and has been confirmed over a wide range in luminosities in the far-infrared to radio domain, both in the local Universe and even at redshifts of z ~ 2. Recent investigations have indicated that it may even hold in the regime of local dwarf galaxies, and we therefore explore here the expected behavior in the regime of star formation surface densities below 0.1 M⊙ kpc-2 yr-1. We derive two conditions that can be particularly relevant for inducing a change in the expected correlation: a critical star formation surface density to maintain the correlation between star formation rate and the magnetic field, and a critical star formation surface density below which cosmic-ray diffusion losses dominate their injection through supernova explosions. For rotation periods shorter than 1.5 × 107(H/ kpc)2 yr, with H the scale height of the disk, the first correlation will break down before diffusion losses are relevant because higher star formation rates are required to maintain the correlation between star formation rate and magnetic field strength. For high star formation surface densities ΣSFR, we derive a characteristic scaling of the nonthermal radio to the far-infrared and infrared emission with ΣSFR1/3 , corresponding to a scaling of the nonthermal radio luminosity Ls with the infrared luminosity Lth as Lth4/3 . The latter is expected to change when the above processes are no longer steadily maintained. In the regime of long rotation periods, we expect a transition toward a steeper scaling with ΣSFR2/3, implying Ls ∝ Lth5/3 , while the regime of fast rotation is expected to show a considerably enhanced scatter because a well-defined relation between star formation and magnetic field strength is not maintained. The scaling relations above explain the increasing thermal fraction of the radio emission observed within local dwarfs and can be tested with future observations by LOFAR as well as the Square Kilometer Array (SKA) and its precursor radio telescopes.
Key words: galaxies: magnetic fields / galaxies: dwarf / galaxies: ISM
© ESO, 2016
1. Introduction
Over the past years, magnetic fields have been detected in a significant number of local dwarf galaxies. This includes prominent examples such as the Large Magellanic Cloud (LMC, Gaensler et al. 2005), the Small Magellanic Cloud (SMC, Mao et al. 2008), and many additional examples such as NGC 4449 (Chyży et al. 2000), NGC 1569 (Kepley et al. 2010), NGC 6822 (Chyży et al. 2003), IC 10 (Chyży et al. 2003; Heesen et al. 2011), and NGC 4214 (Kepley et al. 2011). Chyży et al. (2011) pursued a dedicated investigation of radio emission and magnetic fields in an unbiased sample of 12 Local Group (LG) irregular and dwarf irregular galaxies that yielded both detections and upper limits, while Roychowdhury & Chengalur (2012) employed the stacking technique to improve the sensitivity in the radio and to probe average properties of the radio emission for the faintest end of dwarf galaxies. A central result of these two studies is that the magnetic fields in dwarf galaxies are about three times weaker than in normal spirals, with a typical field strength of <4.2 ± 1.8μG as given by Chyży et al. (2011). The detections and upper limits are consistent with the assumption that local dwarf galaxies lie on the far-infrared − radio correlation, with a typical scaling of the magnetic field strength B with the star formation surface density  .
.
The correlation between the far-infrared and radio fluxes was originally observed by van der Kruit (1973a,b,c). Subsequent investigations have been pursued by de Jong et al. (1985) and Helou et al. (1985), while the interpretation in terms of calorimeter models was pursued by Völk (1989). Niklas & Beck (1997) proposed a detailed scenario in which the far-infrared − radio correlation emerges from a relation between the magnetic field strength, the gas surface density, and the star formation rate. In particular, it is well-known that the gas surface density is strongly correlated to star formation activity, as reflected in the Kennicutt-Schmidt relation (Schmidt 1959; Kennicutt 1998; Kennicutt et al. 2008; Walter et al. 2008; Bigiel et al. 2011; Kennicutt & Evans 2012). Massive stars emit UV radiation absorbed by dust grains that is re-emitted in the infrared and far-infrared. In addition, the supernova explosions of massive stars inject cosmic rays and turbulence into the interstellar medium. Such turbulence efficiently amplifies the magnetic field through the small-scale dynamo (Kazantsev 1968; Subramanian 1999; Schekochihin et al. 2002; Schober et al. 2012; Schleicher et al. 2013; Federrath et al. 2011; Grete et al. 2015), and as a result, the feedback from star formation provides the ingredients relevant to driving the radio emission (see, e.g., Groves et al. 2003; Schleicher & Beck 2013).
The potential validity of the far-infrared − radio correlation even in dwarf galaxies has been suggested by Bell (2003), as the dust content in the dwarfs and the efficiency of non-thermal radio emission may decrease in a similar amount toward lower star formation rates. At that time, the correlation had only been observationally established for nearby spiral galaxies, including a sample of 1809 galaxies probed by Yun et al. (2001), for which the correlation has been confirmed over five orders of magnitude in luminosity. More recent work by Lacki et al. (2010) has shown that the escape of UV photons and cosmic rays from the galaxy may be correlated to the characteristic surface densities, and contributes to our overall understanding of the observations. It is worth noting that these correlations do not only hold on a global scale, but have furthermore been confirmed within the galaxies by dedicated investigations (Dumas et al. 2011; Tabatabaei et al. 2013; Heesen et al. 2014). Potential correlations between metallicity, dust content and the far-infrared − radio correlation have been explored by Wu et al. (2008).
Recent studies by Murphy (2009), Ivison et al. (2010), Jarvis et al. (2010), Sargent et al. (2010), and Casey et al. (2012) have provided evidence that the far-infrared − radio correlation holds at least until redshifts of z ~ 2 (see also Schober et al. 2016, for predictions towards higher redshift), and it also holds in the context of galaxy mergers (Drzazga et al. 2011; Rodenbeck & Schleicher 2016). In addition, work by Miettinen et al. (2015) showed that the radio-emitting region is more extended than the infrared-emitting region at least in some cases. The latter is potentially consistent with Taffy-like systems (Condon et al. 2002), mergers (Murphy 2013), or systems undergoing tidal interactions (Donevski & Prodanović 2015), although we suggest that tidal tails as in the Antennae galaxies (Chyży & Beck 2004) may be the more frequent scenario. In the context of mergers, previous studies by Drzazga et al. (2011), for instance, have preferentially considered the effect of magnetic fields, while Lisenfeld & Völk (2010) pointed out the potential importance of particle acceleration. The latter requires rather high Mach numbers, which may not be available in the interstellar medium (Guo et al. 2014a), or the firehose instability, if the acceleration only concerns the electrons (Guo et al. 2014b). In that case, a high plasma beta would be required, while current estimates indicate that it may be rather low (Beck 2015).
The radio-infrared correlation holds for thermal and nonthermal (synchrotron) radio emission, but with different slopes. Thermal radio emission may dominate in dwarf galaxies (Roychowdhury & Chengalur 2012) and hence mask the relation between nonthermal and infrared emission. The interpretation requires a careful separation of the two emission components, for example, with the help of spectral index data, which is nontrivial and often not possible. Alternatively, the thermal radio emission is assumed to be linearly proportional to the infrared emission, although not all infrared emission is directly related to UV radiation from young stars. Only Hα emission can be safely assumed to be proportional to radio thermal emission, if extinction is properly corrected for.
On theoretical grounds, it is expected that magnetic fields can be efficiently amplified even in small systems and at high redshift as a result of the efficient amplification by turbulence (Arshakian et al. 2009; Wang & Abel 2009; Schleicher et al. 2010; de Souza & Opher 2010; Latif et al. 2013; Schober et al. 2013), and it is thus conceivable that the far-infrared − radio correlation is in place early on. As pointed out by Murphy (2009), a potential difficulty is the increasing strength of the cosmic microwave background at high redshift, however, which enhances the inverse Compton emission and provides an additional loss mechanism for the cosmic-ray electrons. It is thus conceivable that the latter may lead to a modification or a breakdown of the correlation at very high redshift owing to differences in the energy-loss mechanisms of cosmic rays (Lacki & Thompson 2010; Schleicher & Beck 2013; Schober et al. 2015).
In this paper, we explore whether a correlation between the far-infrared and radio emission can still be expected in dwarf galaxies, in particular in the limit of star formation surface densities below 0.1 M⊙ kpc-2 yr-1. To do this, we examine several relevant questions. A first concerns the behavior of star formation itself. In the sample explored by Chyży et al. (2011), the Kennicutt-Schmidt relation appeared to hold even in the dwarf galaxy regime, while Roychowdhury et al. (2009) reported potential deviations toward lower star formation rates. Through dedicated spatially resolved investigations of star formation and the HI-dominated gas in nearby spirals and dwarf irregular galaxies using the THINGS (Walter et al. 2008) and FIGGS (Begum et al. 2008) survey, Roychowdhury et al. (2015) have pursued a detailed comparison the Kennicutt-Schmidt relation in the two regimes, finding in particular that there is no dependence on the metallicity of the gas. It is therefore conceivable that this relation will hold in the dwarf galaxy regime, even though the scatter may potentially increase toward lower gas masses.
An important difference compared to spiral galaxies is that the rotation in local dwarfs may be substantially reduced, implying slow or more chaotic rotation with a low differential rotation (Chyży et al. 2003). In the VLA-ANGST survey of 35 nearby dwarf galaxies, the lowest detected rotation velocities have been of the order 20 km s-1. Through the Westerbork HI Survey of Spiral and Irregular Galaxies (WHISP), rotation curves have been measured for a sample of 62 galaxies, finding typical rotational velocities of 20−80 km s-1 on scales of a few disk scale lengths (Swaters et al. 2009). In general, a strong variation is found from dwarf to dwarf, and in some cases such as NGC 4449 (Theis & Kohle 2001) or IC 10 (Ashley et al. 2014), the rotation curves have been explained by tidal interactions of disks with other dwarfs. The implications of the large diversity of dwarf galaxy rotation curves has therefore also been discussed in recent studies (Oman et al. 2015).
In the radio regime, additional differences have been found compared to the typical conditions in local spirals, whose main properties have been described by Condon (1992). In particular, while the fraction of thermal radio emission corresponds to about 8% for local spirals (Murphy et al. 2006), a nonthermal fraction of ~50% has been reported recently by Roychowdhury & Chengalur (2012) in the dwarf galaxy regime. We show here that such a behavior arises rather naturally from the nonlinear nature of the far-infrared − radio correlation.
The structure of this paper is as follows. In Sect. 2 we outline our overall modeling framework, which is employed to derive characteristic timescales for dynamical processes within the dwarfs and for the timescales for thermal and radio emission. These are employed to derive critical star formation surface densities, which are required for these processes to be maintained in a steady fashion. In Sect. 3 these results are employed to distinguish between four characteristic regimes of radio emission in the dwarf galaxies, and we discuss in particular the expected slope and the breakdown of the correlation at very low star formation rates. A discussion with our main conclusions is presented in Sect. 4.
2. Model framework
In the following, we outline our main model framework, starting with the basic assumptions (Sect. 2.1) and including a more detailed framework for the formation of galactic winds (Sect. 2.2). A discussion of relevant timescales for the dynamics and the thermal and radio emission is given in Sect. 2.3 along with a derivation of critical star formation rates, which are presented and compared in Sect. 2.3.4.
2.1. Basic assumptions
We assumed that star formation in dwarf galaxies occurs in a disk of neutral HI gas with surface density Σ, radius Rdisk and height H. We furthermore assumed that the Kennicutt- Schmidt relation provides a valid description of the star formation law, so that the star formation surface density is given as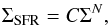 (1)where C is a normalization constant and N ~ 1.5 the slope of the relation. Considering the results by Chyży et al. (2011), we adopted here
(1)where C is a normalization constant and N ~ 1.5 the slope of the relation. Considering the results by Chyży et al. (2011), we adopted here 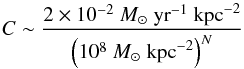 (2)for the normalization. With these quantities, the amount of gas available for star formation is
(2)for the normalization. With these quantities, the amount of gas available for star formation is 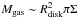 , and the total star formation rate within the galaxy is given as
, and the total star formation rate within the galaxy is given as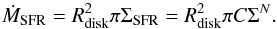 (3)The observed relation between nonthermal radio and infrared emission furthermore suggests a relation between the magnetic field strength B and the star formation surface density ΣSFR of the form
(3)The observed relation between nonthermal radio and infrared emission furthermore suggests a relation between the magnetic field strength B and the star formation surface density ΣSFR of the form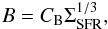 (4)where we determined the normalization constant CB from the investigation of Chyży et al. (2011) as
(4)where we determined the normalization constant CB from the investigation of Chyży et al. (2011) as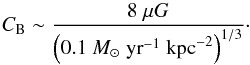 (5)The height of the disk of the warm interstellar medium (ISM) results from the balance between the gravitational force, the turbulent pressure, thermal pressure, magnetic pressure, and cosmic rays. The disk height H is then given as
(5)The height of the disk of the warm interstellar medium (ISM) results from the balance between the gravitational force, the turbulent pressure, thermal pressure, magnetic pressure, and cosmic rays. The disk height H is then given as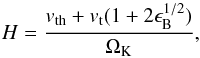 (6)where vth ~ 10 km s-1 corresponds to the thermal velocity of the warm ISM, vt is the turbulent velocity, and ΩK the angular velocity required to balance the gravitational force. In general, we note that the disk height is different depending on the ISM component that is considered because the cold gas may have different turbulent and lower thermal velocities. We assumed here equipartition between the magnetic energy density and cosmic rays, with the magnetic energy density given as a fraction ϵB of the turbulent energy density. Observations have shown that the energy density of turbulence and the magnetic field are essentially comparable, implying ϵB ~ 1 (Beck 2007, 2015). The latter indicates that turbulence may play a central role in amplifying the magnetic field.
(6)where vth ~ 10 km s-1 corresponds to the thermal velocity of the warm ISM, vt is the turbulent velocity, and ΩK the angular velocity required to balance the gravitational force. In general, we note that the disk height is different depending on the ISM component that is considered because the cold gas may have different turbulent and lower thermal velocities. We assumed here equipartition between the magnetic energy density and cosmic rays, with the magnetic energy density given as a fraction ϵB of the turbulent energy density. Observations have shown that the energy density of turbulence and the magnetic field are essentially comparable, implying ϵB ~ 1 (Beck 2007, 2015). The latter indicates that turbulence may play a central role in amplifying the magnetic field.
We also assume in the following approximate equipartition between magnetic and turbulent energy in the warm gas component, that is, in the component that predominantly gives rise to the observed radio emission. We particularly note that we focus here on the disordered component of the magnetic field, which yields the dominant contribution to the radio flux. For comparison, studies by Drzazga et al. (2016) have shown that the ordered component in the outer parts of the galaxy is also affected by tidal interactions. The density of the warm neutral gas can be estimated as Σ / 2H. The typical density ratio between the ionized and neutral warm gas component is denoted as CHII / HI in the following, and we adopt a typical value of CHII / HI ~ 2% following Tielens (2005). The equipartition between turbulent and magnetic energy in the warm ionized gas can then be expressed as 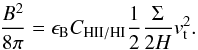 (7)With the order-of-magnitude scaling relation H ~ vt/ ΩK, the above expression can be simplified as
(7)With the order-of-magnitude scaling relation H ~ vt/ ΩK, the above expression can be simplified as 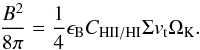 (8)We can therefore solve for the turbulent velocity vt, and insert Eq. (4) as well as the Kennicutt-Schmidt relation (Eq. (1)), yielding
(8)We can therefore solve for the turbulent velocity vt, and insert Eq. (4) as well as the Kennicutt-Schmidt relation (Eq. (1)), yielding 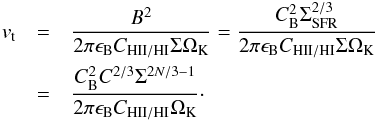 (9)Evaluating the disk height and turbulent velocity in this way, additional properties of the galaxy follow from the more detailed ISM model described in the next subsection. A central parameter is then the amount of rotation ΩK of the dwarf galaxy.
(9)Evaluating the disk height and turbulent velocity in this way, additional properties of the galaxy follow from the more detailed ISM model described in the next subsection. A central parameter is then the amount of rotation ΩK of the dwarf galaxy.
2.2. Wind model
The wind model adopted here is an extension of the framework developed by Shu et al. (2005). They employed the multiphase ISM model for supernova evolution by McKee & Ostriker (1977) and Efstathiou (2000) to construct a model for galactic winds in the context of starburst galaxies. A central assumption in their model is thus that the galactic porosity, that is, the volume filling factor of the hot gas, which is formally defined by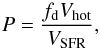 (10)is generally of order 1, with Vhot the volume of the hot gas, VSFR the total volume of the star-forming system and fd ~ 2H/R a correction factor for galactic disks. To generalize this point, we therefore adopted the expression derived by Clarke & Oey (2002) to parametrize the dependence of porosity on galaxy properties, which is given as
(10)is generally of order 1, with Vhot the volume of the hot gas, VSFR the total volume of the star-forming system and fd ~ 2H/R a correction factor for galactic disks. To generalize this point, we therefore adopted the expression derived by Clarke & Oey (2002) to parametrize the dependence of porosity on galaxy properties, which is given as 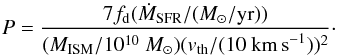 (11)In the above, MISM denotes the mass of the ISM, which we estimated through
(11)In the above, MISM denotes the mass of the ISM, which we estimated through 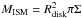 , and ṀSFR denotes the star formation rate in the galaxy. The stellar mass here is not considered, as we only divide by the thermal energy of the warm ISM. The warm gas produced by star formation is compared with the thermal energy of the warm ISM, adopting a thermal velocity of vth ~ 10 km s-1. Unless in the regime of extremely low star formation rates, we generally find P ~ 1, consistent with previous results by Clarke & Oey (2002).
, and ṀSFR denotes the star formation rate in the galaxy. The stellar mass here is not considered, as we only divide by the thermal energy of the warm ISM. The warm gas produced by star formation is compared with the thermal energy of the warm ISM, adopting a thermal velocity of vth ~ 10 km s-1. Unless in the regime of extremely low star formation rates, we generally find P ~ 1, consistent with previous results by Clarke & Oey (2002).
We note that the expressions adopted here assume a Salpeter IMF (Salpeter 1955), consistent with the assumption that about 5% of the stellar mass is in massive stars with more than 8 M⊙. The precise form of the IMF in dwarf galaxies is a matter of ongoing debate, however. For instance, the results by Geha et al. (2013) for ultra-faint dwarf galaxies indicate that the IMF is more shallow than the Salpeter IMF in the mass range between 0.52 M⊙ and 0.77 M⊙. On the other hand, a comparison of Hα and UV data suggests a deficient of high-mass stars below star formation rates of 0.003 M⊙ yr-1 (Lee et al. 2009), in line with expectations of Weidner & Kroupa (2005). For a generalization of the framework adopted here, all star formation rates or surface densities in the following may be considered to be multiplied by a factor ϵhm/ 0.05. We note here in particular that a lower value of ϵhm may imply that some of the relations discussed here could break down even earlier, or, in case of a gradual evolution of this parameter, a steepening of the far-infrared − radio relation would occur. In the absence of more detailed knowledge, we assume in the following that the parameter is constant, however, and explore the corresponding results.
From the star formation surface density ΣSFR in the galaxy, we can estimate the star formation rate per unit volume as 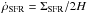 . For the model of Shu et al. (2005), we first need to calculate the supernova rate S-13 in units of 10-13 pc-3 yr-1. The latter is given as
. For the model of Shu et al. (2005), we first need to calculate the supernova rate S-13 in units of 10-13 pc-3 yr-1. The latter is given as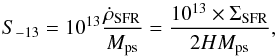 (12)where Mps denotes the required stellar mass to form at least one star massive enough to explode as a supernova. The latter is parametrized by Mps = 8 M⊙/ϵhm, with ϵhm ~ 0.05 the mass fraction of massive stars (Kroupa 2002; Chabrier 2003). From this expression, we can calculate the temperature of the hot gas in cavities as (Efstathiou 2000; Shu et al. 2005)
(12)where Mps denotes the required stellar mass to form at least one star massive enough to explode as a supernova. The latter is parametrized by Mps = 8 M⊙/ϵhm, with ϵhm ~ 0.05 the mass fraction of massive stars (Kroupa 2002; Chabrier 2003). From this expression, we can calculate the temperature of the hot gas in cavities as (Efstathiou 2000; Shu et al. 2005)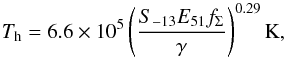 (13)with E51 = 1 the typical energy of supernova explosions in units of 1051 erg and γ = 2.5 the ratio of blast wave velocity to the isothermal sound speed of the hot phase in the case of strong shocks. The quantity fΣ parametrizes the dependence on various properties of the ISM, including conductivity and minimum mass of the clouds. For most of them, we kept the standard parameters employed by Shu et al. (2005), and considered in the following only the effect of the varying the cold gas fraction fc = e− P. The latter yields
(13)with E51 = 1 the typical energy of supernova explosions in units of 1051 erg and γ = 2.5 the ratio of blast wave velocity to the isothermal sound speed of the hot phase in the case of strong shocks. The quantity fΣ parametrizes the dependence on various properties of the ISM, including conductivity and minimum mass of the clouds. For most of them, we kept the standard parameters employed by Shu et al. (2005), and considered in the following only the effect of the varying the cold gas fraction fc = e− P. The latter yields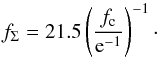 (14)We note here that the final wind velocity scales as
(14)We note here that the final wind velocity scales as 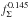 and is therefore highly insensitive to the ISM parameters incorporated into fΣ. In a fully ionized gas, the isothermal sound speed is now given as
and is therefore highly insensitive to the ISM parameters incorporated into fΣ. In a fully ionized gas, the isothermal sound speed is now given as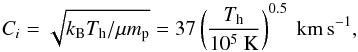 (15)with kB the Boltzmann constant, mp the proton mass and μ the mean molecular weight. In the presence of a pure thermal driving, the wind velocity then follows as
(15)with kB the Boltzmann constant, mp the proton mass and μ the mean molecular weight. In the presence of a pure thermal driving, the wind velocity then follows as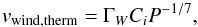 (16)where the factor
(16)where the factor 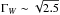 allows for some radiative cooling of the energy injected by the supernova, and the factor P− 1 / 7 provides a correction in the limit of low-porosity parameters developed by Shu et al. (2005).
allows for some radiative cooling of the energy injected by the supernova, and the factor P− 1 / 7 provides a correction in the limit of low-porosity parameters developed by Shu et al. (2005).
Here, we also accounted for the role of magnetic and cosmic-ray pressure in driving these winds. For this purpose, we note that Eq. (16) has been derived from the conservation of the specific enthalpy in the hot gas. We recall that the thermal enthalpy of the hot gas is given as 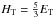 , with ET its thermal energy. The magnetic enthalpy is given as HB = 2EB, with EB the magnetic energy, and the enthalpy of cosmic rays follows as
, with ET its thermal energy. The magnetic enthalpy is given as HB = 2EB, with EB the magnetic energy, and the enthalpy of cosmic rays follows as 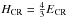 , with ECR the cosmic-ray energy. We assumed here approximate equipartition between the energy in magnetic fields and cosmic rays, and our expression for the total enthalpy is then given as
, with ECR the cosmic-ray energy. We assumed here approximate equipartition between the energy in magnetic fields and cosmic rays, and our expression for the total enthalpy is then given as 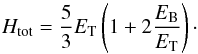 (17)The ratio EB/ET was evaluated using
(17)The ratio EB/ET was evaluated using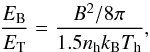 (18)where nh is the number density of the hot gas, which we evaluated as (Efstathiou 2000)
(18)where nh is the number density of the hot gas, which we evaluated as (Efstathiou 2000)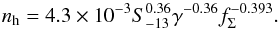 (19)Considering thus the conservation of thermal, magnetic, and cosmic-ray enthalpy, the resulting wind velocity is given as
(19)Considering thus the conservation of thermal, magnetic, and cosmic-ray enthalpy, the resulting wind velocity is given as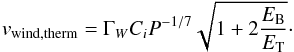 (20)The resulting wind velocities for the full model and the thermally driven wind are illustrated in Fig. 1. To understand the resulting behavior as a function of the star formation surface densitiy, we first note that the porosity P is close to 1 for most of the regime considered here, and we also assumed a constant ratio EB/ET. The main variable through which the star formation surface density enters in the calculation is thus the isothermal sound speed Ci given in Eq. (15), which depends on the temperature of the hot gas in ISM cavities given in Eq. (13). The latter scales with
(20)The resulting wind velocities for the full model and the thermally driven wind are illustrated in Fig. 1. To understand the resulting behavior as a function of the star formation surface densitiy, we first note that the porosity P is close to 1 for most of the regime considered here, and we also assumed a constant ratio EB/ET. The main variable through which the star formation surface density enters in the calculation is thus the isothermal sound speed Ci given in Eq. (15), which depends on the temperature of the hot gas in ISM cavities given in Eq. (13). The latter scales with 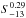 , with S-13 ∝ ΣSFR/H. For a typical case with a Kennicutt-Schmidt index N = 1, we have
, with S-13 ∝ ΣSFR/H. For a typical case with a Kennicutt-Schmidt index N = 1, we have 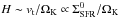 from Eq. (9), where ΩK is independent of the star formation rate. Thus,
from Eq. (9), where ΩK is independent of the star formation rate. Thus, 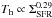 and
and 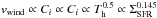 . The latter implies that the wind velocity changes over one order of magnitude when the star formation surface density changes by seven orders of magnitude, consistent with the results in Fig. 1.
. The latter implies that the wind velocity changes over one order of magnitude when the star formation surface density changes by seven orders of magnitude, consistent with the results in Fig. 1.
 |
Fig. 1 Wind velocity as a function of the star formation surface density. Shown are the velocities for a thermally driven wind (Eq. (16)) and our full model including magnetic and cosmic-ray pressure (Eq. (20)). Real dwarf galaxies show a relevant scatter in their typical field strength, therefore we expect realistic cases to lie in between. |
2.3. Characteristic timescales
In this subsection, we evaluate characteristic timescales of the dwarf galaxies and their ISM to assess whether the far-infrared − radio relation can be maintained for low star formation rates. In the following, we distinguish between dynamical timescales, the timescale for the thermal emission, and the timescales for radio emission and cosmic-ray losses.
2.3.1. Dynamical timescales
Assuming that the disk height H corresponds to the size of the largest turbulent eddies, the timescale for the turbulent energy dissipation is given as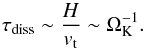 (21)The balance between gravitational force and turbulent pressure within the vertical direction therefore implies that the turbulence dissipation time is comparable to the rotation period of the dwarf galaxy
(21)The balance between gravitational force and turbulent pressure within the vertical direction therefore implies that the turbulence dissipation time is comparable to the rotation period of the dwarf galaxy 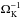 , assuming that the vertical support of the disk is dominated by the turbulent energy, that is, H ~ ΩK/vt. We did not explicitly account here for the potential effects of differential rotation, which may change the rotation period as a function of radius, as we are predominantly interested in an order-of-magnitude estimate. For τdiss, we expect overall a very weak dependence on the star formation surface density, which vanishes under the assumption that H ~ vt/ ΩK. Such a very weak dependence is indeed visible in Fig. 2.
, assuming that the vertical support of the disk is dominated by the turbulent energy, that is, H ~ ΩK/vt. We did not explicitly account here for the potential effects of differential rotation, which may change the rotation period as a function of radius, as we are predominantly interested in an order-of-magnitude estimate. For τdiss, we expect overall a very weak dependence on the star formation surface density, which vanishes under the assumption that H ~ vt/ ΩK. Such a very weak dependence is indeed visible in Fig. 2.
 |
Fig. 2 Turbulence injection timescale (or timescale of massive star formation) compared to turbulence dissipation timescale in dwarf galaxies with rotational velocities of 20 km s-1, 40 km s-1, and 80 km s-1. The timescales are shown as a function of star formation surface density. The critical star formation surface density is found to be ~ 10-5M⊙ kpc-2 yr-1, with only a weak dependence of the rotational velocity. The size of the star-forming region is assumed to be 0.5 kpc. |
The injection of turbulent energy is closely linked to the formation of massive stars with at least 8 M⊙, which have a typical lifetime of about 55 million years. The formation rate of massive stars is given as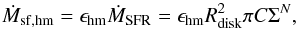 (22)with ϵhm the mass fraction of massive stars introduced above. The characteristic timescale between the formation of two massive stars is then given as
(22)with ϵhm the mass fraction of massive stars introduced above. The characteristic timescale between the formation of two massive stars is then given as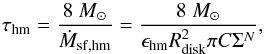 (23)corresponding to the characteristic timescale of turbulent energy injection. The resulting scaling with
(23)corresponding to the characteristic timescale of turbulent energy injection. The resulting scaling with 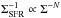 is directly visible in Fig. 2. Now, a sufficient amount of turbulence in the galaxy can be maintained as long as τhm<τdiss, implying that the turbulent energy is efficiently replenished by star formation. In the opposite case with τhm>τdiss, the turbulence in the galaxy will decay before the next injection event. The latter implies the decay of turbulence and the decay of magnetic fields, implying that a relation such as
is directly visible in Fig. 2. Now, a sufficient amount of turbulence in the galaxy can be maintained as long as τhm<τdiss, implying that the turbulent energy is efficiently replenished by star formation. In the opposite case with τhm>τdiss, the turbulence in the galaxy will decay before the next injection event. The latter implies the decay of turbulence and the decay of magnetic fields, implying that a relation such as 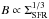 cannot be maintained. In particular, we may expect a significant increase in the scatter depending on the state at which the dwarf galaxy is observed.
cannot be maintained. In particular, we may expect a significant increase in the scatter depending on the state at which the dwarf galaxy is observed.
From this condition, we can derive a critical gas surface density above which the turbulence injection timescale remains sufficiently short: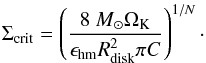 (24)Using the Kennicutt-Schmidt-relation (Eq. (1)), the latter can be translated into a critical star formation surface density, yielding
(24)Using the Kennicutt-Schmidt-relation (Eq. (1)), the latter can be translated into a critical star formation surface density, yielding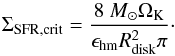 (25)For a prelimary estimate, we adopted here a radius of Rdisk = 0.5 kpc for the size of the star-forming region, and we investigated the turbulence injection and dissipation timescales for dwarf galaxies with rotational velocities of 20 km s-1, 40 km s-1, and 80 km s-1 for the star-forming region. The critical star formation surface density is found to be ~10-5M⊙ kpc-2 yr-1, with only a weak dependence on the rotational velocity. The more detailed results are given in Fig. 2. We also explored the effect of different power-law slopes N in the Kennicutt-Schmidt relation, as shown in Fig. 3, and found only a weak dependence on the form of the relation. The same is true for changes in the normalization of the relation by up to a factor of 10.
(25)For a prelimary estimate, we adopted here a radius of Rdisk = 0.5 kpc for the size of the star-forming region, and we investigated the turbulence injection and dissipation timescales for dwarf galaxies with rotational velocities of 20 km s-1, 40 km s-1, and 80 km s-1 for the star-forming region. The critical star formation surface density is found to be ~10-5M⊙ kpc-2 yr-1, with only a weak dependence on the rotational velocity. The more detailed results are given in Fig. 2. We also explored the effect of different power-law slopes N in the Kennicutt-Schmidt relation, as shown in Fig. 3, and found only a weak dependence on the form of the relation. The same is true for changes in the normalization of the relation by up to a factor of 10.
2.3.2. Timescales for thermal emission
Our considerations so far have predominantly concerned the dynamics in the galaxy and whether they can maintain a power-law relation between star formation and the magnetic field strength. However, to maintain the observed far-infrared − radio correlation, the star formation rate needs to be translated into thermal emission from dust grains, while the radio emission is due to cosmic-ray synchrotron emission in the magnetic field. The infrared emission is due to thermal emission of dust grains, and the corresponding timescale is the cooling time of the dust. It can be shown that the latter is almost independent of the grain-size and mostly depends on the dust temperature (Krügel 2008). Assuming a dust temperature of 10 K, the cooling time corresponds to ~104 yr and is even shorter for higher dust temperatures. The latter implies that the radiation of massive stars deposited onto dust grains is radiated away very quickly. However, the thermal energy of the grains is replenished during the lifetime of the massive stars, which is on the order 50 × 106 yr for a star with eight solar masses.
 |
Fig. 3 Turbulence injection timescale (or timescale of massive star formation) compared to turbulence dissipation timescale in dwarf galaxies for different Kennicutt-Schmidt relations as a function of the star formation surface density. We adopt here a reference case with N = 1.5 as well as two additional cases with N = 1 and N = 2. The size of the star-forming region is assumed to be 0.5 kpc, the rotational velocity 40 km s-1. We find that the critical star formation surface density has no strong dependence on the precise form of the Kennicutt-Schmidt relation. |
Considering Figs. 2 and 3, we find that the timescale for massive star formation becomes longer than the lifetime of a massive star for a star formation surface density of ~3 × 10-5M⊙ kpc-2 yr-1, considering our reference model with Rdisk = 0.5 kpc. We can furthermore generalize this requirement for arbitrary sizes of the star-forming region, yielding a critical star formation surface density for the thermal emission as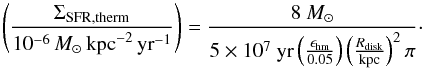 (26)For star formation surface densities lower than 10-6M⊙ kpc−2 yr-1, assuming a star-forming region of 1 kpc and ϵhm ~ 0.05, a constant thermal emission cannot be maintained, leading to strong fluctuations in the far-infrared − radio correlation. A steepening of the IMF at very low star formation rates may somewhat change this transition, and in that case, a breakdown of continuous thermal emission might occur even earlier. Understanding such an effect requires a better understanding of star formation in this regime, however.
(26)For star formation surface densities lower than 10-6M⊙ kpc−2 yr-1, assuming a star-forming region of 1 kpc and ϵhm ~ 0.05, a constant thermal emission cannot be maintained, leading to strong fluctuations in the far-infrared − radio correlation. A steepening of the IMF at very low star formation rates may somewhat change this transition, and in that case, a breakdown of continuous thermal emission might occur even earlier. Understanding such an effect requires a better understanding of star formation in this regime, however.
From a comparison with Eq. (25), we note that the condition becomes relevant for 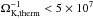 yr because then the continuous thermal emission breaks down while the relation
yr because then the continuous thermal emission breaks down while the relation 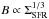 is still maintained. In the opposite case, a breakdown of the relation between B and ΣSFR may occur while still having a steady thermal emission. The rotation rate of the galaxy is thus a key parameter in regulating this transition.
is still maintained. In the opposite case, a breakdown of the relation between B and ΣSFR may occur while still having a steady thermal emission. The rotation rate of the galaxy is thus a key parameter in regulating this transition.
 |
Fig. 4 Characteristic timescales for cosmic-ray loss mechanisms for a reference model with Rdisk = 0.5 kpc and a rotational velocity of 20 km s-1 of the star-forming region. Shown are in particular the injection timescale of the cosmic rays, defined as the timescale for massive star formation, the adiabatic losses for a full and a thermally driven wind model, and the timescale for cosmic-ray diffusion and for synchrotron losses. The dominant loss mechanism in this regime is due to the full wind model, while cosmic-ray diffusion would imply a transition for lower star formation rates. Injection timescales longer than the characteristic timescales for losses may induce significant fluctuations in the nonthermal radio emission. We note that the cosmic-ray diffusion timescale implicitly assumes an observed frequency of 1 GHz, while higher-frequency observations may probe more energetic cosmic rays with shorter diffusion times. |
2.3.3. Timescales for radio emission
In the following, we assess the characteristic timescales for radio emission and cosmic-ray energy losses and their effect on the far-infrared − radio correlation. The timescale for the synchrotron emission can be expressed as (Murphy 2009)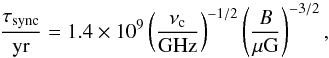 (27)where νc is the characteristic frequency of emission of cosmic rays with an energy E. These quantities are related by (Murphy 2009)
(27)where νc is the characteristic frequency of emission of cosmic rays with an energy E. These quantities are related by (Murphy 2009)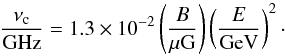 (28)In the following, we consider the synchrotron emission of cosmic rays with a characteristic frequency of 1 GHz, and we evaluate the magnetic field strength assuming the observed relation
(28)In the following, we consider the synchrotron emission of cosmic rays with a characteristic frequency of 1 GHz, and we evaluate the magnetic field strength assuming the observed relation 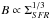 (Eq. (4)). This timescale, along with other characteristic timescales introduced below, is shown in Figs. 4−6 for dwarf galaxies with a star-forming region of Rdisk = 0.5 kpc and rotational velocities of 20 km s-1, 40 km s-1, and 80 km s-1. In particular, the synchrotron timescale does not depend on the amount of rotation, it decreases with ΣSFR and is considerably longer than the other timescales. We can therefore conclude that the cosmic-ray abundance will not be significantly depleted by synchrotron emission.
(Eq. (4)). This timescale, along with other characteristic timescales introduced below, is shown in Figs. 4−6 for dwarf galaxies with a star-forming region of Rdisk = 0.5 kpc and rotational velocities of 20 km s-1, 40 km s-1, and 80 km s-1. In particular, the synchrotron timescale does not depend on the amount of rotation, it decreases with ΣSFR and is considerably longer than the other timescales. We can therefore conclude that the cosmic-ray abundance will not be significantly depleted by synchrotron emission.
An additional effect that can be relevant are the inverse Compton losses of the non-thermal electrons. Considering the inverse Compton scattering due to the cosmic microwave background (CMB), it can be shown that the latter becomes important at a critical field strength (Murphy 2009; Schleicher & Beck 2013) 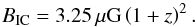 (29)As the magnetic field strength B scales approximately as
(29)As the magnetic field strength B scales approximately as  (cf. Eq. (4)), we expect that inverse Compton losses become relevant in dwarf galaxies. Comparing the Eq. (4) with Eq. (29), these losses are expected to become dominant for star formation surface densities below 0.005 M⊙ kpc-2 yr-1. In this regime, the expected synchrotron flux should thus be corrected by a factor
(cf. Eq. (4)), we expect that inverse Compton losses become relevant in dwarf galaxies. Comparing the Eq. (4) with Eq. (29), these losses are expected to become dominant for star formation surface densities below 0.005 M⊙ kpc-2 yr-1. In this regime, the expected synchrotron flux should thus be corrected by a factor 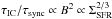 (Murphy 2009), implying a steeper decrease in the nonthermal radio emission at very low star formation rates.
(Murphy 2009), implying a steeper decrease in the nonthermal radio emission at very low star formation rates.
In the presence of additional cosmic-ray loss mechanisms with timescales shorter than the characteristic timescale for the injection, the cosmic rays will be depleted very efficiently, inducing an even steeper scaling relation, along with significant fluctuations in the nonthermal radio emission with peaks occurring at the events of cosmic-ray injection. In particular, the cosmic rays will be depleted through diffusion processes in the interstellar medium. Typical values of the diffusion coefficients range from 3 × 1027 cm2 s-1 (Mulcahy et al. 2014) to 2 × 1029 cm2 s-1 (Heesen et al. 2009) and may depend on the magnetic field strength and the alignment of the magnetic fields. We adopted here a typical diffusion coefficient of DE = 2 × 1028 cm2 s-1, which is characteristic for cosmic-ray energies of 1 GeV and allows us to assess the potential relevance of the diffusion (Murphy 2009). The characteristic diffusion timescale of the cosmic rays is then given as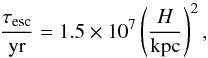 (30)where we assumed that the shortest pathway for the cosmic rays to diffuse out of the galaxy is along the disk height. Assuming observations at a fixed frequency of 1 GHz, the energy of the cosmic rays providing the main contribution to the synchrotron emission is expected to weakly increase with decreasing magnetic field strength, potentially increasing the diffusion coefficient by a factor of 2−3. We neglect this here in the light of the overall uncertainties, however. Another potential uncertainty in this timescale corresponds to the cosmic-ray streaming instability (McKenzie & Webb 1984), as the typical Alfven time
(30)where we assumed that the shortest pathway for the cosmic rays to diffuse out of the galaxy is along the disk height. Assuming observations at a fixed frequency of 1 GHz, the energy of the cosmic rays providing the main contribution to the synchrotron emission is expected to weakly increase with decreasing magnetic field strength, potentially increasing the diffusion coefficient by a factor of 2−3. We neglect this here in the light of the overall uncertainties, however. Another potential uncertainty in this timescale corresponds to the cosmic-ray streaming instability (McKenzie & Webb 1984), as the typical Alfven time 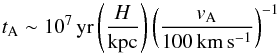 (31)is comparable to the escape time by diffusion. The interaction of these processes thus should be treated in more detail in numerical simulations. With our simplified assumption, the diffusion timescale here depends on the rotational velocity, as the latter influences the scale height of the disk. For a rotational velocity of 20 km s-1, it is evident from Fig. 4 that the diffusion timescale becomes shorter than the injection timescale at a star formation surface density of ~7 × 10-7M⊙ kpc-2 yr-1. In case of a rotational velocity of 40 km s-1, this transition occurs at about 10-5M⊙ kpc-2 yr-1 (Fig. 5), and for a rotational velocity of 80 km s-1 at about 10-4M⊙ kpc-2 yr-1 (Fig. 6). The rotational velocity therefore has a strong effect on the transition, predominantly as it implies a flatter structure that might enhance the escape. We note that the plots showing the diffusion timescale implicitly assume an observed frequency of 1 GHz. Higher-frequency observations could probe more energetic cosmic rays, implying shorter diffusion times.
(31)is comparable to the escape time by diffusion. The interaction of these processes thus should be treated in more detail in numerical simulations. With our simplified assumption, the diffusion timescale here depends on the rotational velocity, as the latter influences the scale height of the disk. For a rotational velocity of 20 km s-1, it is evident from Fig. 4 that the diffusion timescale becomes shorter than the injection timescale at a star formation surface density of ~7 × 10-7M⊙ kpc-2 yr-1. In case of a rotational velocity of 40 km s-1, this transition occurs at about 10-5M⊙ kpc-2 yr-1 (Fig. 5), and for a rotational velocity of 80 km s-1 at about 10-4M⊙ kpc-2 yr-1 (Fig. 6). The rotational velocity therefore has a strong effect on the transition, predominantly as it implies a flatter structure that might enhance the escape. We note that the plots showing the diffusion timescale implicitly assume an observed frequency of 1 GHz. Higher-frequency observations could probe more energetic cosmic rays, implying shorter diffusion times.
From a comparison with Eq. (23), we can derive a critical star formation surface density below which the cosmic-ray diffusion becomes relevant. In this regime, the cosmic rays will be strongly depleted after the ejection event, implying that the radio emission cannot be maintained. The critical rate is given as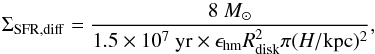 (32)implying an increasing critical star formation rate of larger disk heights. Observationally, the latter may be estimated from a measurement of the turbulent velocity vt and the rotation rate ΩK, thus yielding H ~ vt/ ΩK. We also note that this process depends on the cosmic-ray energy, as more energetic cosmic rays have larger diffusion coefficients and longer diffusion times. We therefore expect that observations at higher frequencies allow us to correct for the effect of cosmic-ray diffusion and probe whether a relation between the star formation rate and the magnetic field is still maintained. From a comparison of Eq. (32) with Eq. (25), a critical point corresponds to the regime where
(32)implying an increasing critical star formation rate of larger disk heights. Observationally, the latter may be estimated from a measurement of the turbulent velocity vt and the rotation rate ΩK, thus yielding H ~ vt/ ΩK. We also note that this process depends on the cosmic-ray energy, as more energetic cosmic rays have larger diffusion coefficients and longer diffusion times. We therefore expect that observations at higher frequencies allow us to correct for the effect of cosmic-ray diffusion and probe whether a relation between the star formation rate and the magnetic field is still maintained. From a comparison of Eq. (32) with Eq. (25), a critical point corresponds to the regime where 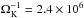 yr (H/ kpc)2. Using H ~ vt/ ΩK, the latter yields a critical transition at
yr (H/ kpc)2. Using H ~ vt/ ΩK, the latter yields a critical transition at 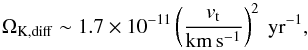 (33)or, focusing on the dependence of the scale height of the disk,
(33)or, focusing on the dependence of the scale height of the disk, 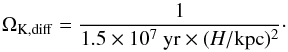 (34)For lower angular velocities, the continuous radio emission may break down as a result of cosmic-ray diffusion even if the correlation between the magnetic field and the star formation rate is still maintained. This behavior can be inverted in the regime of fast rotation, where cosmic-ray diffusion losses are expected to become relevant only after the breakdown of the correlation between the star formation rate and the magnetic field. We may furthermore compare with the expression for the critical star formation rate for thermal emission (Eq. (26)), leading to the critical condition that
(34)For lower angular velocities, the continuous radio emission may break down as a result of cosmic-ray diffusion even if the correlation between the magnetic field and the star formation rate is still maintained. This behavior can be inverted in the regime of fast rotation, where cosmic-ray diffusion losses are expected to become relevant only after the breakdown of the correlation between the star formation rate and the magnetic field. We may furthermore compare with the expression for the critical star formation rate for thermal emission (Eq. (26)), leading to the critical condition that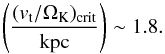 (35)In the regime of large disk heights, the thermal emission thus breaks down before the radio emission, while the inverse behavior is found for very thin disks.
(35)In the regime of large disk heights, the thermal emission thus breaks down before the radio emission, while the inverse behavior is found for very thin disks.
Finally, we considered adiabatic expansion losses through galactic winds. The characteristic timescale can be estimated by (Murphy 2009)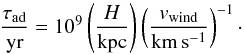 (36)For the latter, we employed the detailed wind model outlined in Sect. 2.2, and we considered the effects of thermally driven winds (Eq. (16)) as well as our full model including magnetic field and cosmic-ray pressure (Eq. (20)). The effect of the wind model again has a strong dependence on the disk height of the galaxy, and thus its rotational velocity. In the reference case with a rotational velocity of 20 km s-1 (Fig. 4), cosmic-ray diffusion is less efficient than the effects of the thermal wind model, although they are comparable within an order of magnitude at the star formation surface density where it becomes comparable to the timescale for injection events. Including magnetic and cosmic-ray pressure enhances the wind and implies a depletion of the cosmic rays already at a star formation rate of ~10-5M⊙ kpc-2 yr-1. For a rotational velocity of 40 km s-1 (Fig. 5), the effects of the thermal wind model and cosmic-ray diffusion are essentially comparable, while magnetically driven winds would be even more efficient. Finally, at rotational velocities of 80 km s-1 (Fig. 6), cosmic-ray diffusion is comparable to the effects of the full wind model.
(36)For the latter, we employed the detailed wind model outlined in Sect. 2.2, and we considered the effects of thermally driven winds (Eq. (16)) as well as our full model including magnetic field and cosmic-ray pressure (Eq. (20)). The effect of the wind model again has a strong dependence on the disk height of the galaxy, and thus its rotational velocity. In the reference case with a rotational velocity of 20 km s-1 (Fig. 4), cosmic-ray diffusion is less efficient than the effects of the thermal wind model, although they are comparable within an order of magnitude at the star formation surface density where it becomes comparable to the timescale for injection events. Including magnetic and cosmic-ray pressure enhances the wind and implies a depletion of the cosmic rays already at a star formation rate of ~10-5M⊙ kpc-2 yr-1. For a rotational velocity of 40 km s-1 (Fig. 5), the effects of the thermal wind model and cosmic-ray diffusion are essentially comparable, while magnetically driven winds would be even more efficient. Finally, at rotational velocities of 80 km s-1 (Fig. 6), cosmic-ray diffusion is comparable to the effects of the full wind model.
Our results thus suggest that adiabatic losses by the wind can be particularly relevant in the regime of low rotation and large disk heights. From these results, it appears that a magnetically driven wind could change the critical star formation rate for cosmic-ray depletion by at most an order of magnitude.
2.3.4. Critical star formation surface densities
From the considerations above, we derived a set of critical star formation surface densities that describe the transition between different physical regimes in the dwarf galaxy and its ISM. Equation (25) describes the condition under which the turbulence injection time remains longer than its decay time, implying that turbulence and turbulent magnetic field structures can be maintained and will be correlated with the star formation rate in the galaxy. This timescale depends in particular on the size of the star-forming region Rdisk and the angular velocity ΩK, which can be expressed as vrot/Rdisk.
Equation (26) denotes the critical star formation rate above which continuous thermal emission can be maintained in the galaxy, as the characteristic timescale for massive star formation is shorter than the typical lifetime of massive stars. This timescale depends essentially on the size of the star-forming region. Finally, Eq. (32) denotes the critical star formation surface density for which the timescale for diffusion losses becomes comparable to the injection timescale of cosmic rays. This condition is therefore important to allow for continuous radio emission. The critical rate depends in particular on the size of the star-forming region and the disk height H.
 |
Fig. 7 Comparison of the critical star formation surface density to maintain the relation between star formation and the magnetic field, given by Eq. (25), with the critical star formation rate to maintain thermal emission, given by Eq. (26). Critical star formation surface densities are given as functions of the size of the star-forming region. Explored are characteristic parameters for the rotational velocity of 20,40,and80 km s-1. For large star-forming regions, the critical star formation rate to maintain thermal emission eventually exceeds the critical star formation rate to maintain the correlation between star formation and the magnetic field. A comparison with Fig. 8 shows, however, that the radio emission will break down even earlier in this regime as a result of cosmic-ray diffusion losses. |
 |
Fig. 8 Comparison of the critical star formation surface density for cosmic-ray diffusion, given by Eq. (32), with the critical star formation rate to maintain the relation between star formation and magnetic field. Critical star formation surface densities are given as functions of the size of the star-forming region. We adopt here a characteristic rotational velocity of 20,40,and80 km s-1, and explore values of the disk scale height of 0.5,1,and2 kpc. The highest critical values can be obtained for more compact star-forming regions. The relative importance of both processes is found to sensitively depend on the two quantities. We note that the critical star formation rate for cosmic-ray diffusion implicitly assumes observations at 1 GHz, while higher-frequency observations will probe more energetic cosmic rays, potentially implying a higher critical star formation rate. |
To assess the relative importance of the different critical star formation surface densities, they are plotted as a function of Rdisk in Figs. 7, 8, considering typical rotational velocities vrot = 20,40,and80 km s-1 and disk scale heights H = 0.5,1,and2 kpc. In particular for large star-forming regions, the dominant mechanism leading to a break-down of the far-infrared − radio correlation is cosmic-ray diffusion, but with critical values of ~10-6M⊙ kpc-2 yr-1, which are difficult to observe. The critical values are significantly enhanced for more compact star-forming regions, scaling approximately as 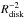 , with characteristic values of about ~10-4M⊙ kpc-2 yr-1 for Rdisk = 0.5 kpc. In this case, the critical values due to cosmic-ray diffusion and to the comparison of turbulence injection and dissipation time are about equally important. The critical star formation rate to maintain thermal emission, on the other hand, never appears to be responsible for a critical transition, as the lifetime of massive stars is still long enough for other processes to become relevant earlier.
, with characteristic values of about ~10-4M⊙ kpc-2 yr-1 for Rdisk = 0.5 kpc. In this case, the critical values due to cosmic-ray diffusion and to the comparison of turbulence injection and dissipation time are about equally important. The critical star formation rate to maintain thermal emission, on the other hand, never appears to be responsible for a critical transition, as the lifetime of massive stars is still long enough for other processes to become relevant earlier.
We note again that the critical star formation surface density for cosmic-ray diffusion implicitly assumes observations at a frequency of 1 GHz. Observations at higher frequencies will probe more energetic cosmic rays and imply shorter timescales for cosmic-ray diffusion, potentially increasing the critical star formation rate to maintain the injection events at a high enough rate.
3. Slope of the far-infrared − radio correlation
The synchrotron emission from an ensemble of relativistic electrons of energy E at a frequency ν is generally given as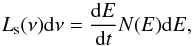 (37)where dE/ dt describes the synchrotron emission of the individual electrons and N(E) denotes the number of electrons at energy E. The losses of the individual electrons are directly proportional to the magnetic energy density UB = B2/ 8π.
(37)where dE/ dt describes the synchrotron emission of the individual electrons and N(E) denotes the number of electrons at energy E. The losses of the individual electrons are directly proportional to the magnetic energy density UB = B2/ 8π.
In spiral galaxies, the injection timescale of cosmic rays is considerably shorter than the timescale for synchrotron losses, cosmic-ray diffusion, losses by winds, or other effects such as inverse Compton scattering (see, e.g., Murphy 2009). In this regime, the amount of cosmic rays that can be maintained in the galaxy corresponds to equipartition with the magnetic field, implying UB = UCR, as for larger amounts of cosmic rays, the cosmic-ray pressure will exceed the pressure from the magnetic field, leading to expansion and an effective loss of the cosmic rays from the galaxy. In this regime, we thus have N(E) ∝ B2/ 8π, and thus 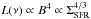 , where we assumed that
, where we assumed that 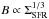 . In the more general case with a synchrotron spectral index α different from 1, we may expect a scaling as B3 + α, while we note that the currently observed value α = 0.7 ± 0.2 is consistent with the above relation in the 2Σ range. The ratio of nonthermal to thermal emission is therefore expected to scale as
. In the more general case with a synchrotron spectral index α different from 1, we may expect a scaling as B3 + α, while we note that the currently observed value α = 0.7 ± 0.2 is consistent with the above relation in the 2Σ range. The ratio of nonthermal to thermal emission is therefore expected to scale as 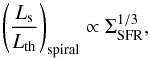 (38)as the thermal emission is expected to be proportional to the star formation rate. In this derivation, we have so far assumed that synchrotron emission is the main loss mechanism for the cosmic rays, and we assumed that galaxies are optically thick to the UV emission of the stars, implying that the energy is trapped and converted into thermal emission of the dust grains. As we have shown in Sect. 2.3.3, inverse Compton losses may start to become relevant at star formation surface densities of ~0.005 M⊙ kpc-2 yr-1, leading to an additional factor
(38)as the thermal emission is expected to be proportional to the star formation rate. In this derivation, we have so far assumed that synchrotron emission is the main loss mechanism for the cosmic rays, and we assumed that galaxies are optically thick to the UV emission of the stars, implying that the energy is trapped and converted into thermal emission of the dust grains. As we have shown in Sect. 2.3.3, inverse Compton losses may start to become relevant at star formation surface densities of ~0.005 M⊙ kpc-2 yr-1, leading to an additional factor 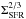 in the scaling of the nonthermal radio emission at very low star formation rates.
in the scaling of the nonthermal radio emission at very low star formation rates.
To take into account the potential effect of optically thin dust opacities for the UV, we adopted here a typical UV dust opacity of κd ~ 300 cm2 g-1 (Tielens 2005). The effects of the optically thin regime thus start to become relevant for surface densities of ~1.5 × 107M⊙ kpc-2. From the Kennicutt-Schmidt relation (Eq. (1)) with N ~ 3 / 2, the latter corresponds to a star formation surface density of ~0.002 M⊙ kpc-2 yr-1. Within the uncertainties present here, this correction thus becomes relevant in the same regime in which the inverse Compton losses also become relevant. To correct for this effect, the thermal emission should be multiplied with a factor proportional to the dust UV opacity 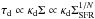 . In the typical case of N = 3 / 2, we thus have a correction factor of
. In the typical case of N = 3 / 2, we thus have a correction factor of 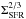 , and the corrections from both effects essentially cancel, so that we expect that Eq. (38) is still valid in this regime. Even for the extreme cases N = 1 or N = 2, we note that the corrections would be small, corresponding to a dependence of the form
, and the corrections from both effects essentially cancel, so that we expect that Eq. (38) is still valid in this regime. Even for the extreme cases N = 1 or N = 2, we note that the corrections would be small, corresponding to a dependence of the form 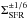 , that is, to a very weak change in the dependence on ΣSFR. We note that this canceling can also be understood in terms of a decreasing efficiency of star formation tracers, as previously described by Bell (2003).
, that is, to a very weak change in the dependence on ΣSFR. We note that this canceling can also be understood in terms of a decreasing efficiency of star formation tracers, as previously described by Bell (2003).
The scaling relation given in Eq. (38) is expected (and observed) for the ratio of nonthermal to thermal radio emission and for the ratio of nonthermal radio emission to thermal emission in the infrared or far-infrared because the thermal component is always proportional to the star formation rate. The latter implies a nonlinear far-infrared − radio correlation with a logarithmic slope of 4 / 3, that is, 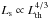 (Niklas & Beck 1997). From the shape of Eq. (38), it is furthermore evident that the ratio of nonthermal to thermal emission decreases with decreasing star formation rates. This is consistent with recent observations by Roychowdhury & Chengalur (2012) of nonthermal radio fractions of up to 50% in dwarf galaxies, in contrast to typical thermal fractions of ~8% in spirals (Niklas 1997; Murphy et al. 2006). Potential deviations from this trend could potentially occur as a result of a steepening in the IMF at very low star formation rates, which would reduce the thermal emission, but also the injection of the cosmic rays. We assumed here, however, that such effects do not yet occur in the regime where equipartition between cosmic rays and magnetic fields can be efficiently maintained.
(Niklas & Beck 1997). From the shape of Eq. (38), it is furthermore evident that the ratio of nonthermal to thermal emission decreases with decreasing star formation rates. This is consistent with recent observations by Roychowdhury & Chengalur (2012) of nonthermal radio fractions of up to 50% in dwarf galaxies, in contrast to typical thermal fractions of ~8% in spirals (Niklas 1997; Murphy et al. 2006). Potential deviations from this trend could potentially occur as a result of a steepening in the IMF at very low star formation rates, which would reduce the thermal emission, but also the injection of the cosmic rays. We assumed here, however, that such effects do not yet occur in the regime where equipartition between cosmic rays and magnetic fields can be efficiently maintained.
While a change in the thermal fraction may already be expected on the grounds given above, we also illustrate below that the slope of the far-infrared − radio correlation, or correspondingly, the slope of the thermal to nonthermal radio emission, will likewise change with decreasing star formation rate. For this purpose, we need to consider the regime where cosmic-ray injection becomes less efficient, so that a state of equipartition with the magnetic field is not reached. In particular, when the timescale for cosmic ray losses through diffusion or galactic winds becomes shorter than the injection timescale, that is, the formation timescale of massive stars, the cosmic-ray abundance in the galaxy will start to decrease. As we have shown in Sect. 2.3.3 that cosmic-ray diffusion and adiabatic losses through winds are yielding roughly similar results, we focus in the following on losses through cosmic-ray diffusion, which are relevant below the critical star formation surface density given in Eq. (32), with a strong dependence on the size of the star-forming region Rdisk and the disk scale height H.
In this regime, the amount of cosmic rays will be dictated by the injection, implying that their number N(E) scales as N(E) ∝ ΣSFR. In this case, the ratio of nonthermal to thermal emission scales as 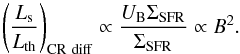 (39)Under these conditions, the magnetic field strength B depends on the rotation rate of the galaxy. As shown in Sect. 2.3.3, there is a critical rotation rate ΩK,diff (Eq. (34)) above which the relation between magnetic field and star formation rate is still maintained, while this relation is no longer valid for lower values of the rotation rate. In terms of the critical star formation rates derived above, we may thus distinguish between the following regimes:
(39)Under these conditions, the magnetic field strength B depends on the rotation rate of the galaxy. As shown in Sect. 2.3.3, there is a critical rotation rate ΩK,diff (Eq. (34)) above which the relation between magnetic field and star formation rate is still maintained, while this relation is no longer valid for lower values of the rotation rate. In terms of the critical star formation rates derived above, we may thus distinguish between the following regimes:
-
high star formation rates with ΣSFR> ΣSFR,crit and ΣSFR> ΣSFR,diff;
-
low star formation rates and low rotation, ΣSFR> ΣSFR,crit but ΣSFR< ΣSFR,diff;
-
low star formation rates and strong rotation, ΣSFR< ΣSFR,crit and ΣSFR> ΣSFR,diff;
-
very low star formation rates with ΣSFR< ΣSFR,crit and ΣSFR< ΣSFR,diff;
-
very low star formation rates with ΣSFR< ΣSFR,therm.
The first case is the regime of spiral galaxies, which we described in Eq. (38). In the regime of low star formation and low rotation, the ratio of nonthermal to thermal emission can be described vby Eq. (39), and a correlation 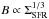 can still be expected. In this case, we have
can still be expected. In this case, we have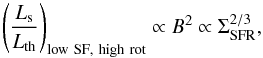 (40)implying a scaling of
(40)implying a scaling of 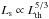 and a change in the slope of the far-infrared − radio correlation by 1 / 3 on a logarithmic scale. In this regime, the ratio thus decreases more steeply with ΣSFR, and the thermal fraction will be additionally enhanced toward low star formation rates. The latter is consistent with the current stacking results by Roychowdhury & Chengalur (2012).
and a change in the slope of the far-infrared − radio correlation by 1 / 3 on a logarithmic scale. In this regime, the ratio thus decreases more steeply with ΣSFR, and the thermal fraction will be additionally enhanced toward low star formation rates. The latter is consistent with the current stacking results by Roychowdhury & Chengalur (2012).
The latter is given in Fig. 9 for a characteristic case with Rdisk = 0.5 kpc and disk scale heights of 0.1,0.25,and0.5 kpc, with a normalization of the relation obtained through NGC 4449, as the latter lies well onto the L2.64 GHz−L60 μm relation given by Chyży et al. (2011). While our results related to cosmic-ray diffusion have been derived assuming a frequency of 1 GHz, we note that the characteristic electron energy scales as 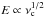 , and the cosmic-ray diffusion coefficient has a weak scaling ∝ E1 / 2. Overall, the difference in frequency thus introduces only a factor of 1.3 difference with respect to cosmic-ray diffusion. We also note that our results have a predominantly illustrative character, and the typical scatter in this relations needs to be taken into account, implying a variation by at least a factor of 3.
, and the cosmic-ray diffusion coefficient has a weak scaling ∝ E1 / 2. Overall, the difference in frequency thus introduces only a factor of 1.3 difference with respect to cosmic-ray diffusion. We also note that our results have a predominantly illustrative character, and the typical scatter in this relations needs to be taken into account, implying a variation by at least a factor of 3.
With the assumptions adopted here, the steepening occurs at a star formation surface density of ~3 × 10-5M⊙ kpc-2 yr-1, with some spread depending on the scale height of the disk. We also show the ratio of the total-to-thermal radio emission in Fig. 10. For normalization purposes, we have adopted a characteristic value of 8% for the ratio of thermal-to-nonthermal radio emission at a star formation surface density of 0.1 M⊙ kpc-2 yr-1 (see Murphy et al. 2006, for the thermal fraction in spiral galaxies). The figure shows a substantial decrease in the total to thermal emission as a function of the star formation rate, with a flattening toward a value of 1 at very low star formation rates. The slope of this ratio changes at the critical star formation rate given in Eq. (34), and the details of the transition depend on the properties of the dwarf galaxy. As the distinction between this and the subsequent regime of low rotation depends on the critical rotation rate, the latter quantity is given in Fig. 11.
We note that the star formation rates for which we expect changes in the slope may also depend on the observed frequency, as cosmic-ray diffusion becomes more efficient at higher observed frequencies, implying shorter diffusion times. High-frequency observations may thus be able to probe this transition already at higher star formation rates. At the same time, we note that the normalization of the thermal-to-nonthermal flux density ratio may be frequency dependent and may require more detailed exploration.
 |
Fig. 9 Ratio of the nonthermal radio (~2.64 GHz) to thermal infrared (~60μm) surface brightness, normalized for NGC 4449 adopting the values of Chyży et al. (2011), as a function of the star formation surface density. We assume a size of the star-forming region of 0.5 kpc, and explore values for the disk height of 0.1,0.25,and0.5 kpc, which influence the critical star formation surface density concerning the relevance of cosmic-ray diffusion losses (Eq. (32)). The transition illustrated here is relevant in the regime of slow rotation defined by Eq. (34), where cosmic-ray diffusion effects become relevant before the relation between magnetic field strengths and star formation surface density breaks down. |
 |
Fig. 10 Total-to-thermal radio flux density ratio as a function of the star formation rate. The evolution of the slope is evaluated from Eqs. (38), (39), assuming a transition at the critical star formation rate given by Eq. (32). We assume a size of the star-forming region of 0.5 kpc, and explore values for the disk height of 0.1,0.25,and0.5 kpc. The normalization of the flux ratios assumes a thermal-to-nonthermal flux ratio of 8% for a star formation rate of 0.1 M⊙ kpc-2 yr-1. The plot assumes a typical radio frequency of ~1 GHz. |
 |
Fig. 11 Critical rotation rate ΩK,diff of the dwarf galaxy as a function of the disk scale height H, as given in Eq. (34), to distinguish between the regime of low star formation and high rotation and the regime of low star formation and low rotation. In the former regime, we still expect a valid but steeper far-infrared − radio correlation, while in the limit of low rotation, the correlation between star formation and the magnetic field will break down before cosmic-ray diffusion becomes relevant. The critical rotation rate adopted here implicitly assumes observations at 1 GHz due to the diffusion timescale of the cosmic rays. Observations at higher frequencies will probe more energetic electrons, implying shorter diffusion times and a higher critical rotation rate. |
In the regime of low star formation rates and high rotation, there is no longer a correlation between star formation rate and magnetic field strength. The ratio of nonthermal to thermal emission can still be described by Eq. (39), but the magnetic field strength may be significantly decreased as a result of turbulent decay. In general, the latter is expected to significantly decrease the radio emission, while in a few cases with very recent injection, the nonthermal emission can be comparable to the case of low star formation and high rotational velocities. Quite generally, we expect here a significant amount of scatter, including many nondetections, and potentially a few detections of nonthermal emission.
For very low star formation rates below ΣSFR,crit and ΣSFR< ΣSFR,diff, the correlation between star formation and magnetic field is broken, and cosmic-ray diffusion is very efficient, rapidly removing any cosmic rays that might be ejected. In this regime, we do not expect a relevant or detectable nonthermal component, and no signs of a far-infrared − radio correlation should be detectable. We expect that the corresponding dwarfs can be detected only through thermal emission. Continuous thermal emission is expected to eventually break down below ΣSFR< ΣSFR,therm.
4. Discussion and conclusions
We have discussed the far-infrared − radio correlation in dwarf galaxies and its potential evolution in the regime of low star formation rates. As a starting point, we assessed under which conditions a correlation between the magnetic field strength and the star formation rate can be maintained through the continuous injection of turbulence, leading to the definition of a critical star formation rate required for the injection of a sufficient amount of turbulent energy (Eq. (25)). The latter will ensure magnetic field amplification through the small-scale dynamo (e.g., Kazantsev 1968; Schekochihin et al. 2002; Schober et al. 2012), which occurs on short timescales and effectively ensures that the magnetic field strength is coupled to the star formation rate. Considering a typical size of the star-forming region of 1 kpc, this relation will break down at critical star formation surface densities of 10-5−10-6M⊙ kpc-2 yr-1 depending on the amount of rotation. We also derived a critical star formation rate to ensure continuous thermal emission in the galaxy, which results from the requirement that the timescale of massive star formation should be shorter than the typical lifetime of massive stars. This criterion was developed in Eq. (26), even though our comparison has shown that it is likely not relevant in practice. Assuming a star-forming region of 1 kpc and a 5% fraction of massive stars, the resulting star formation surface density corresponds to ~10-6M⊙ kpc-2 yr-1.
We furthermore explored the dominant loss mechanisms for cosmic rays in the galaxy, which have a great effect on the nonthermal radio emission and its dependence on the star formation rate. In particular, we derived a critical star formation surface density for the importance of cosmic-ray diffusion losses given by Eq. (32), below which the injection time of cosmic rays becomes longer than the timescale for diffusion losses, thus strongly reducing the amount of cosmic rays in the galaxy. Assuming a star-forming region of 1 kpc, these effects become relevant for star formation surface densities of 10-4−10-6M⊙ kpc-2 yr-1, depending on the scale height of the disk. Overall, the critical star formation surface density for this transition thus appears higher than the corresponding transition for the thermal emission. We compared the cosmic-ray diffusion losses with the losses due to cosmic winds, adopting the thermally driven wind model by Shu et al. (2005) and a generalized model accounting for the effect of cosmic rays and magnetic fields as potential driving agents. Depending on the amount of rotation in the galaxy, we found that the losses from winds can become relevant at somewhat higher or lower star formation rates compared to the cosmic-ray diffusion processes, but they do not change the details of the transition dramatically.
From a comparison of these results, we showed that the critical star formation surface densities for the maintainance of turbulence (Eq. (25)) and for the relevance of cosmic-ray diffusion (Eq. (32)) are most relevant for introducing a potential breakdown in the far-infrared − radio correlation. Which of the transitions occurs first depends on the rotation rate of the dwarf and the scale height of the disk and can be expressed in terms of a critical rotation rate given in Eq. (34), corresponding to rotation period of 1.5 × 107 yr for a galaxy with a scale height of 1 kpc. We note in particular that cosmic-ray diffusion losses become relevant before the breakdown of the magnetic field − star formation surface density relation in the case of low rotation. Whether the rotation period is above or below the critical value thus regulates the subsequent evolution of the far-infrared − radio correlation in the regime of low star formation rates.
We determined four different regimes employing the conditions derived above. In the limit of high star formation rates above the critical star formation surface densities mentioned above, we showed that the ratio of nonthermal radio to far-infrared/infrared luminosity should scale as  , as we expect that the cosmic-ray abundance is limited by the strength of the magnetic field, effectively enforcing equipartition, implying a scaling of the cosmic-ray abundance with B2 and of the overall nonthermal emission as B4 or
, as we expect that the cosmic-ray abundance is limited by the strength of the magnetic field, effectively enforcing equipartition, implying a scaling of the cosmic-ray abundance with B2 and of the overall nonthermal emission as B4 or 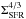 , typically above a star formation surface density of ~10-6M⊙ kpc-2 yr-1 for a star-forming region of 1 kpc.
, typically above a star formation surface density of ~10-6M⊙ kpc-2 yr-1 for a star-forming region of 1 kpc.
For lower star formation rates in the limit of low rotation (below the critical value in Eq. (34)), the correlation between magnetic field strength and star formation will still be in place, but cosmic-ray diffusion losses will start to become efficient. As a result, the cosmic-ray abundance in galaxies will no longer reach equipartition with the magnetic field strength, but is instead expected to be proportional to the injection rate, that is, to the rate of star formation. In this regime, it can then be shown that the ratio of nonthermal radio to far-infrared / infrared luminosity will scale as 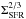 , implying a steeper decrease with decreasing star formation rate. This steepening may be expected below typical star formation surface densities of 3 × 10-5M⊙ kpc-2 yr-1, with some dependence on the size of the star-forming region and the scale height of the disk.
, implying a steeper decrease with decreasing star formation rate. This steepening may be expected below typical star formation surface densities of 3 × 10-5M⊙ kpc-2 yr-1, with some dependence on the size of the star-forming region and the scale height of the disk.
On the other hand, in the regime of low star formation rates and rotation rates above the before-mentioned critical value, the cosmic-ray diffusion losses are not yet significant, but the correlation between the magnetic field strength and the star formation rate is expected to break down because a steady injection of turbulence cannot be maintained, leading to the dissipation of turbulence and the magnetic fields. As a result, we may expect significant nonthermal emission only in those sources with recent injection events, and otherwise no significant emission in the vast majority of sources. Finally, for star formation rates below the critical rates for turbulence driving and cosmic-ray diffusion, it is clear that the correlation is broken down as a result of both mechanisms.
Overall, we therefore expect modifications of the far-infrared − radio correlation in the regime of low star formation rates, which will be particularly relevant for future observations with the Square Kilometre Array (SKA)1 and its Key Science Project on “The Origin and Evolution of Cosmic Magnetism”. Its precursors and pathfinders such as LOFAR2, MeerKAT3 and ASKAP4 are in the process of additional detailed probing of magnetic field structures in local dwarf galaxies, as in the LOFAR Key Science Project on ”Cosmic Magnetism of the Nearby Universe” (Beck et al. 2013). Such dedicated investigations will be particularly valuable to determine the frontiers of cosmic magnetism and the origin of magnetic fields in galaxies.
Website SKA: https://www.skatelescope.org/
Website LOFAR: http://www.lofar.org/
Website MeerKAT: http://www.ska.ac.za/meerkat/
Website ASKAP: http://www.atnf.csiro.au/projects/askap/
Acknowledgments
We thank Chris Chyzy for valuable discussions on the rotation rates in dwarf galaxies and Aritra Basu for valuable comments that helped us to improve our manuscript. R.B. acknowledges support by the DFG Research Unit FOR1254. D.R.G.S. thanks for funding through Fondecyt regular (project code 1161247) and through the “Concurso Proyectos Internacionales de Investigación, Convocatoria 2015” (project code PII20150171).
References
- Arshakian, T. G., Beck, R., Krause, M., & Sokoloff, D. 2009, A&A, 494, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ashley, T., Elmegreen, B. G., Johnson, M., et al. 2014, AJ, 148, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, R. 2007, A&A, 470, 539 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, R. 2015, A&A, 578, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, R., Anderson, J., Heald, G., et al. 2013, Astron. Nachr., 334, 548 [NASA ADS] [CrossRef] [Google Scholar]
- Begum, A., Chengalur, J. N., Karachentsev, I. D., Sharina, M. E., & Kaisin, S. S. 2008, MNRAS, 386, 1667 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, E. F. 2003, ApJ, 586, 794 [Google Scholar]
- Bigiel, F., Leroy, A. K., Walter, F., et al. 2011, ApJ, 730, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Casey, C. M., Berta, S., Béthermin, M., et al. 2012, ApJ, 761, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Chyży, K. T., & Beck, R. 2004, A&A, 417, 541 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chyży, K. T., Beck, R., Kohle, S., Klein, U., & Urbanik, M. 2000, A&A, 355, 128 [NASA ADS] [Google Scholar]
- Chyży, K. T., Knapik, J., Bomans, D. J., et al. 2003, A&A, 405, 513 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chyży, K. T., Weżgowiec, M., Beck, R., & Bomans, D. J. 2011, A&A, 529, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clarke, C., & Oey, M. S. 2002, MNRAS, 337, 1299 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J. 1992, ARA&A, 30, 575 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Condon, J. J., Helou, G., & Jarrett, T. H. 2002, AJ, 123, 1881 [Google Scholar]
- de Jong, T., Klein, U., Wielebinski, R., & Wunderlich, E. 1985, A&A, 147, L6 [NASA ADS] [Google Scholar]
- de Souza, R. S., & Opher, R. 2010, Phys. Rev. D, 81, 067301 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Donevski, D., & Prodanović, T. 2015, MNRAS, 453, 638 [NASA ADS] [CrossRef] [Google Scholar]
- Drzazga, R. T., Chyży, K. T., Jurusik, W., & Wiórkiewicz, K. 2011, A&A, 533, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drzazga, R. T., Chyży, K. T., Heald, G. H., Elstner, D., & Gallagher, J. S. 2016, A&A, 589, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dumas, G., Schinnerer, E., Tabatabaei, F. S., et al. 2011, AJ, 141, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Efstathiou, G. 2000, MNRAS, 317, 697 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., Chabrier, G., Schober, J., et al. 2011, Phys. Rev. Lett., 107, 114504 [NASA ADS] [CrossRef] [Google Scholar]
- Gaensler, B. M., Haverkorn, M., Staveley-Smith, L., et al. 2005, Science, 307, 1610 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Geha, M., Brown, T. M., Tumlinson, J., et al. 2013, ApJ, 771, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Grete, P., Vlaykov, D. G., Schmidt, W., Schleicher, D. R. G., & Federrath, C. 2015, New J. Phys., 17, 023070 [NASA ADS] [CrossRef] [Google Scholar]
- Groves, B. A., Cho, J., Dopita, M., & Lazarian, A. 2003, PASA, 20, 252 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, X., Sironi, L., & Narayan, R. 2014a, ApJ, 794, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, X., Sironi, L., & Narayan, R. 2014b, ApJ, 797, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Heesen, V., Beck, R., Krause, M., & Dettmar, R.-J. 2009, Astron. Nachr., 330, 1028 [NASA ADS] [CrossRef] [Google Scholar]
- Heesen, V., Rau, U., Rupen, M. P., Brinks, E., & Hunter, D. A. 2011, ApJ, 739, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Heesen, V., Brinks, E., Leroy, A. K., et al. 2014, AJ, 147, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Helou, G., Soifer, B. T., & Rowan-Robinson, M. 1985, ApJ, 298, L7 [Google Scholar]
- Ivison, R. J., Magnelli, B., Ibar, E., et al. 2010, A&A, 518, L31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jarvis, M. J., Smith, D. J. B., Bonfield, D. G., et al. 2010, MNRAS, 409, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Kazantsev, A. P. 1968, Sov. Phys. J. Exp. Theor. Phys., 26, 1031 [Google Scholar]
- Kennicutt, Jr., R. C. 1998, ApJ, 498, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., & Evans, N. J. 2012, ARA&A, 50, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, Jr., R. C., Lee, J. C., Funes, J. G. S. J., Sakai, S., & Akiyama, S. 2008, ApJS, 178, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Kepley, A. A., Mühle, S., Everett, J., et al. 2010, ApJ, 712, 536 [NASA ADS] [CrossRef] [Google Scholar]
- Kepley, A. A., Zweibel, E. G., Wilcots, E. M., Johnson, K. E., & Robishaw, T. 2011, ApJ, 736, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2002, Science, 295, 82 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Krügel, E. 2008, An introduction to the physics of interstellar dust, Series in astronomy and astrophysics (New-York: CRC Press, Taylor & Francis Group) [Google Scholar]
- Lacki, B. C., & Thompson, T. A. 2010, ApJ, 717, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Lacki, B. C., Thompson, T. A., & Quataert, E. 2010, ApJ, 717, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Latif, M. A., Schleicher, D. R. G., Schmidt, W., & Niemeyer, J. 2013, MNRAS, 432, 668 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J. C., Gil de Paz, A., Tremonti, C., et al. 2009, ApJ, 706, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Lisenfeld, U., & Völk, H. J. 2010, A&A, 524, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mao, S. A., Gaensler, B. M., Stanimirović, S., et al. 2008, ApJ, 688, 1029 [NASA ADS] [CrossRef] [Google Scholar]
- McKee, C. F., & Ostriker, J. P. 1977, ApJ, 218, 148 [NASA ADS] [CrossRef] [Google Scholar]
- McKenzie, J. F., & Webb, G. M. 1984, Journal of Plasma Physics, 31, 275 [Google Scholar]
- Miettinen, O., Novak, M., Smolčić, V., et al. 2015, A&A, 584, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mulcahy, D. D., Horneffer, A., Beck, R., et al. 2014, A&A, 568, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murphy, E. J. 2009, ApJ, 706, 482 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, E. J. 2013, ApJ, 777, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, E. J., Helou, G., Braun, R., et al. 2006, ApJ, 651, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Niklas, S. 1997, A&A, 322, 29 [NASA ADS] [Google Scholar]
- Niklas, S., & Beck, R. 1997, A&A, 320, 54 [NASA ADS] [Google Scholar]
- Oman, K. A., Navarro, J. F., Fattahi, A., et al. 2015, MNRAS, 452, 3650 [CrossRef] [Google Scholar]
- Rodenbeck, K., & Schleicher, D. R. G. 2016, A&A, in press, DOI: 10.1051/0004-6361/201527393 [Google Scholar]
- Roychowdhury, S., & Chengalur, J. N. 2012, MNRAS, 423, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Roychowdhury, S., Chengalur, J. N., Begum, A., & Karachentsev, I. D. 2009, MNRAS, 397, 1435 [NASA ADS] [CrossRef] [Google Scholar]
- Roychowdhury, S., Huang, M.-L., Kauffmann, G., Wang, J., & Chengalur, J. N. 2015, MNRAS, 449, 3700 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Sargent, M. T., Schinnerer, E., Murphy, E., et al. 2010, ApJ, 714, L190 [NASA ADS] [CrossRef] [Google Scholar]
- Schekochihin, A. A., Cowley, S. C., Hammett, G. W., Maron, J. L., & McWilliams, J. C. 2002, New J. Phys., 4, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Schleicher, D. R. G., & Beck, R. 2013, A&A, 556, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schleicher, D. R. G., Banerjee, R., Sur, S., et al. 2010, A&A, 522, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schleicher, D. R. G., Schober, J., Federrath, C., Bovino, S., & Schmidt, W. 2013, New J. Phys., 15, 023017 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, M. 1959, ApJ, 129, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Schober, J., Schleicher, D., Federrath, C., Klessen, R., & Banerjee, R. 2012, Phys. Rev. E, 85, 026303 [NASA ADS] [CrossRef] [Google Scholar]
- Schober, J., Schleicher, D. R. G., & Klessen, R. S. 2013, A&A, 560, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schober, J., Schleicher, D. R. G., & Klessen, R. S. 2015, MNRAS, 446, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Schober, J., Schleicher, D. R. G., & Klessen, R. S. 2016, ApJ, 827, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, C.-G., Mo, H.-J., & Shu-DeMao. 2005, Chin. Astrophys., 5, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Subramanian, K. 1999, Phys. Rev. Lett., 83, 2957 [NASA ADS] [CrossRef] [Google Scholar]
- Swaters, R. A., Sancisi, R., van Albada, T. S., & van der Hulst, J. M. 2009, A&A, 493, 871 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tabatabaei, F. S., Schinnerer, E., Murphy, E. J., et al. 2013, A&A, 552, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Theis, C., & Kohle, S. 2001, A&A, 370, 365 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tielens, A. G. G. M. 2005, The Physics and Chemistry of the Interstellar Medium (Cambridge, UK: Cambridge University Press) [Google Scholar]
- van der Kruit, P. C. 1973a, A&A, 29, 249 [NASA ADS] [Google Scholar]
- van der Kruit, P. C. 1973b, A&A, 29, 263 [NASA ADS] [Google Scholar]
- van der Kruit, P. C. 1973c, A&A, 29, 231 [NASA ADS] [Google Scholar]
- Völk, H. J. 1989, A&A, 218, 67 [NASA ADS] [Google Scholar]
- Walter, F., Brinks, E., de Blok, W. J. G., et al. 2008, AJ, 136, 2563 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, P., & Abel, T. 2009, ApJ, 696, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Weidner, C., & Kroupa, P. 2005, ApJ, 625, 754 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, Y., Charmandaris, V., Houck, J. R., et al. 2008, ApJ, 676, 970 [Google Scholar]
- Yun, M. S., Reddy, N. A., & Condon, J. J. 2001, ApJ, 554, 803 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Wind velocity as a function of the star formation surface density. Shown are the velocities for a thermally driven wind (Eq. (16)) and our full model including magnetic and cosmic-ray pressure (Eq. (20)). Real dwarf galaxies show a relevant scatter in their typical field strength, therefore we expect realistic cases to lie in between. |
| In the text | |
 |
Fig. 2 Turbulence injection timescale (or timescale of massive star formation) compared to turbulence dissipation timescale in dwarf galaxies with rotational velocities of 20 km s-1, 40 km s-1, and 80 km s-1. The timescales are shown as a function of star formation surface density. The critical star formation surface density is found to be ~ 10-5M⊙ kpc-2 yr-1, with only a weak dependence of the rotational velocity. The size of the star-forming region is assumed to be 0.5 kpc. |
| In the text | |
 |
Fig. 3 Turbulence injection timescale (or timescale of massive star formation) compared to turbulence dissipation timescale in dwarf galaxies for different Kennicutt-Schmidt relations as a function of the star formation surface density. We adopt here a reference case with N = 1.5 as well as two additional cases with N = 1 and N = 2. The size of the star-forming region is assumed to be 0.5 kpc, the rotational velocity 40 km s-1. We find that the critical star formation surface density has no strong dependence on the precise form of the Kennicutt-Schmidt relation. |
| In the text | |
 |
Fig. 4 Characteristic timescales for cosmic-ray loss mechanisms for a reference model with Rdisk = 0.5 kpc and a rotational velocity of 20 km s-1 of the star-forming region. Shown are in particular the injection timescale of the cosmic rays, defined as the timescale for massive star formation, the adiabatic losses for a full and a thermally driven wind model, and the timescale for cosmic-ray diffusion and for synchrotron losses. The dominant loss mechanism in this regime is due to the full wind model, while cosmic-ray diffusion would imply a transition for lower star formation rates. Injection timescales longer than the characteristic timescales for losses may induce significant fluctuations in the nonthermal radio emission. We note that the cosmic-ray diffusion timescale implicitly assumes an observed frequency of 1 GHz, while higher-frequency observations may probe more energetic cosmic rays with shorter diffusion times. |
| In the text | |
 |
Fig. 5 Same as Fig. 4, but with a rotational velocity of 40 km s-1. |
| In the text | |
 |
Fig. 6 Same as Fig. 4, but with a rotational velocity of 80 km s-1. |
| In the text | |
 |
Fig. 7 Comparison of the critical star formation surface density to maintain the relation between star formation and the magnetic field, given by Eq. (25), with the critical star formation rate to maintain thermal emission, given by Eq. (26). Critical star formation surface densities are given as functions of the size of the star-forming region. Explored are characteristic parameters for the rotational velocity of 20,40,and80 km s-1. For large star-forming regions, the critical star formation rate to maintain thermal emission eventually exceeds the critical star formation rate to maintain the correlation between star formation and the magnetic field. A comparison with Fig. 8 shows, however, that the radio emission will break down even earlier in this regime as a result of cosmic-ray diffusion losses. |
| In the text | |
 |
Fig. 8 Comparison of the critical star formation surface density for cosmic-ray diffusion, given by Eq. (32), with the critical star formation rate to maintain the relation between star formation and magnetic field. Critical star formation surface densities are given as functions of the size of the star-forming region. We adopt here a characteristic rotational velocity of 20,40,and80 km s-1, and explore values of the disk scale height of 0.5,1,and2 kpc. The highest critical values can be obtained for more compact star-forming regions. The relative importance of both processes is found to sensitively depend on the two quantities. We note that the critical star formation rate for cosmic-ray diffusion implicitly assumes observations at 1 GHz, while higher-frequency observations will probe more energetic cosmic rays, potentially implying a higher critical star formation rate. |
| In the text | |
 |
Fig. 9 Ratio of the nonthermal radio (~2.64 GHz) to thermal infrared (~60μm) surface brightness, normalized for NGC 4449 adopting the values of Chyży et al. (2011), as a function of the star formation surface density. We assume a size of the star-forming region of 0.5 kpc, and explore values for the disk height of 0.1,0.25,and0.5 kpc, which influence the critical star formation surface density concerning the relevance of cosmic-ray diffusion losses (Eq. (32)). The transition illustrated here is relevant in the regime of slow rotation defined by Eq. (34), where cosmic-ray diffusion effects become relevant before the relation between magnetic field strengths and star formation surface density breaks down. |
| In the text | |
 |
Fig. 10 Total-to-thermal radio flux density ratio as a function of the star formation rate. The evolution of the slope is evaluated from Eqs. (38), (39), assuming a transition at the critical star formation rate given by Eq. (32). We assume a size of the star-forming region of 0.5 kpc, and explore values for the disk height of 0.1,0.25,and0.5 kpc. The normalization of the flux ratios assumes a thermal-to-nonthermal flux ratio of 8% for a star formation rate of 0.1 M⊙ kpc-2 yr-1. The plot assumes a typical radio frequency of ~1 GHz. |
| In the text | |
 |
Fig. 11 Critical rotation rate ΩK,diff of the dwarf galaxy as a function of the disk scale height H, as given in Eq. (34), to distinguish between the regime of low star formation and high rotation and the regime of low star formation and low rotation. In the former regime, we still expect a valid but steeper far-infrared − radio correlation, while in the limit of low rotation, the correlation between star formation and the magnetic field will break down before cosmic-ray diffusion becomes relevant. The critical rotation rate adopted here implicitly assumes observations at 1 GHz due to the diffusion timescale of the cosmic rays. Observations at higher frequencies will probe more energetic electrons, implying shorter diffusion times and a higher critical rotation rate. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


