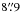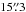EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 593 (September 2016) A&A, 593 (2016) A107 Full HTML
Free Access
Issue
A&A
Volume 593, September 2016
Article Number A107
Number of page(s) 11
Section Catalogs and data
DOI https://doi.org/10.1051/0004-6361/201628731
Published online 30 September 2016

© ESO, 2016

1. Introduction

High angular resolution radio and (sub-)millimeter observations may trace relativistic accretion flows or the footpoint of a jet, which can be found immediately around the Galactic supermassive black hole, Sgr A* (Falcke et al. 2000; Fish et al. 2009; Bower et al. 2014). Modeling frameworks (see Yuan & Narayan 2014 for a review of existing theories) with ray-tracing calculations have suggested that observations of the linear polarization and time variability can constrain the morphology of the emitting gas and thence the origin of the relativistic electrons (Bromley et al. 2001; Brinkerink et al. 2015; Johnson et al. 2015). In addition, the linearly polarized synchrotron emission from the relativistic electrons can be Faraday-rotated by the accreting gas in the foreground, which can be diagnosed by multi-frequency observations of the linear polarization position angles and polarization percentages (Flett et al. 1991; Bower et al. 1999a, 1999c, 2000, 2003, 2005; Aitken et al. 2000; Macquart et al. 2006; Marrone et al. 2006, 2007; Liu et al. 2016). Moreover, a small fraction of the linear polarization may be converted to circular, if the magnetized foreground screen is inhomogeneous and anisotropic, which can be tested by observing circular polarization (Bower et al. 1999b, 2002; Sault & Macquart 1999; Muñoz et al. 2012). The degree of Faraday rotation by the foreground, and its time variability, will provide information about the black hole accretion rate and its time variability, which may (or may not) be related to the flaring activities of the Sgr A* (Zhao et al. 2003, 2004; Marrone et al. 2006; Ponti et al. 2010; Clavel et al. 2013; Bower et al. 2015). Kuo et al. (2014) for the first time derived the accretion rate of the active galactic nucleus of M87, based on the submillimeter array (SMA) observations of rotation measure.

Table 1

ALMA observations.

In this work, we report new constraints on the polarized emission of Sgr A* at ~90–710 GHz, based on Atacama Large Millimeter Array (ALMA) 12 m-Array and Compact Array (ACA) single pointing and mosaic observations. The 90–340 GHz observations we present are the first precisely constrained polarized emission properties within a single night, over such a wide range of observational frequencies. In addition, our ~700 GHz observations represent the highest frequency polarization measurements made by sub-millimeter interferometry so far, which provide valuable information from the optically thinnest part of the spectrum. Details of our observations and data calibrations are provided in Sect. 2. Our direct measurements are provided in Sect. 3. In Sect. 4 we address potential measurement errors. We also compare our observational results with previous observations. A brief conclusion is provided in Sect. 5. We archive the fitting results of polarization percentage and polarization position angles for our calibrator quasars in Appendix A.

Table 2

Angular separation between X polarization and the local vertical (also known as Evector; see Sect. 4.2 of ALMA Cycle 4 Technical Handbook)

2. Observations and data reduction

We analyzed the ALMA observations at band 3 (~3 mm), 6 (~1 mm), 7 (~0.88 mm), 8 (~0.6 mm), and 9 (~0.4 mm). These observations are summarized in Table 1. The receivers have orthogonal linearly polarized feeds. These observations measured the XX and YY linear correlations. Except for band 7, the polarization orientation of the X-dipole is aligned radially in the receiver cryostat, with Y being aligned perpendicular to X. According to ALMA results from tests, the accuracy of this alignment is within 2 degrees. The corresponding angular separations between the X polarization and the local vertical, which is known as Evector, are summarized in Table 2 (see also Sect. 4.2 in the ALMA cycle-4 Technical Handbook). Observations and data reduction for other frequency bands are introduced in the following Sects. 2.1 and 2.2. Our procedures to measure the intensities of the XX and the YY correlations, are introduced in Sect. 2.3.

thumbnail Fig. 1

Mosaic fields of the ALMA 12 m-Array, band 9 observations. The diameter of these circles is .

2.1. ALMA 90-110, 250, 340, and 490 GHz observations (bands 3, 6, 7, and 8)

The ALMA 12 m Array observations of 90–100 GHz (band 3), 250 GHz (band 6), and 340 GHz (band 7), were taken on UTC 2012 May 18 (UTC 03:30:47–10:52:16). There were 19 available antennae for these observations. This is a single-field observations with pointing and phase-referencing centers approximately coincide (~001 offset) with the location of the Sgr A*. The observations switched in between three frequency bands (3, 6, and 7); each frequency band was covered with a ~7.5 GHz simultaneous bandwidth. We referenced to the bright quasars J1924-2914 and J1733–1304 (also known as NRAO530) for passband and gain calibrations. We refer to Brinkerink et al. (2015) for the calibration of the band 3, 6, and 7 observations.

The ALMA 12 m Array and ACA mosaic observations of 490 GHz were taken on UTC 2015 April 30 (UTC 06:48:32–08:04:38). The seven mosaic fields of the 12 m Array observations, which covered the Sgr A*, are used for the analysis of the present paper. There were 39 available antennae in the 12 m Array observations. The simultaneous bandwidth of these observations is ~7.5 GHz. We referenced to J1833-2103/J1517-2422 and J1733-3116 for passband and gain calibrations. We refer the details of the band 8 observations to Liu et al. (2016).

2.2. ALMA 680-710 GHz observations (band 9)

2.2.1. 12 m Array observations

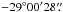The ALMA 12 m Array (consisting of 12 m dishes) mosaic observations of hexagonally packed 23 fields (Fig. 1) were carried out on 2015 May 02 (UTC 06:55:16.7–08:33:28), with 37 antennae. These observations covered an approximately 25′′ × 25′′ rectangular region. The pointing and phase-referencing center of the central field was RA (J2000) =17h45m40036, and Dec (J2000) = 17, which is approximately centered upon Sgr A*. We configured the correlator to provide four 1.875 GHz wide spectral windows (spws), covering the frequency ranges of 687.9–689.7 GHz (spw 0), 689.7–691.6 GHz (spw 1), 691.5–683.4 GHz (spw 2), and 693.3–695.2 GHz (spw 3), respectively. The frequency channel spacing was 3906.25 kHz.

thumbnail Fig. 2

Mosaic fields of the ACA, band 9 observations. The diameter of these circles is .

The projected baseline length sampled by the 12 m-Array observations is 15–347 meter. The system temperature (Tsys) ranged from 600–1100 K. We observed J1733-1304 approximately every 7.5 min for gain calibrations. We observed Titan and J1924-2914 for absolute flux and passband calibrations, respectively.

2.2.2. ACA observations

The Atacama Compact Array (ACA) observations were performed with three different spectral setups:

  • B9-a:

    681.6–683.4 GHz (spw 0),683.4–685.3 GHz (spw 1),685.2–687.1 GHz (spw 2), and687.0–688.9 GHz (spw 3).

  • B9-b:

    705.2–707.0 GHz (spw 0), 707.0–708.8 GHz (spw 1), 708.8–710.6 GHz (spw 2), and 710.6–712.4 GHz (spw 3).

  • B9-c:

    687.9–689.7 GHz (spw 0), 689.7–691.6 GHz (spw 1), 691.5–693.4 GHz (spw 2), and 693.3–695.2 GHz (spw 3).

All spectral setups were configured to provide 1.875 GHz wide spectral windows (spws) and a frequency channel spacing of 3906.25 kHz. The B9-c setup is identical to the spectral setup of the 12 m-Array observations (Sect. 2.2.1).

We used hexagonally packed mosaic of seven fields to cover Sgr A* approximately at the center (Fig. 2). The ACA observations were carried out on 2014 July 26 (UTC 01:51:09.5–03:09:45.9; B9-c setup), 2015 July 25 (UTC 23:02:14.8–July 26 01:01:17.2; B9-b setup), 2015 July 26 (UTC 01:16:20.3–03:08:00.6; B9-a setup), and 2015 July 26 (UTC 21:52:24.0–23:45:45.5; B9-b setup). The ACA at the 2014 epoch consisted of ten dishes, which shared an identical (Mitsubishi, 7 m) design. The ACA at the 2015 epochs additionally included three Mitsubishi 12 m dishes to assist calibrations with the enhanced sensitivities to unresolved sources.

We excluded the ACA B9-c observations in our quantitative analysis, owing to the relatively large amplitude errors. The excluded ACA data were also the observations that were not assisted with the additional 12 m dishes. The Tsys values of the rest of the ACA observations ranged from 500–1500 K. The spatial samplings of the ACA observations (i.e. uv spacing range), and the calibrators that we observed, are listed in Table 1. No available single-dish data are currently available to provide information on the zero-spacing fluxes for these observations. However, the emission source of our interest is spatially very compact (Bower et al. 2014) and, therefore, we do not think missing short-spacing information is a concern for our measurements.

2.2.3. Data calibration

A priori calibrations including the application of Tsys data, the water vapor radiometer (wvr) solution (which is only provided for the 12 m-Array observations), antenna-based passband calibrations, gain amplitude and phase calibrations, and absolute flux scaling, were carried out using the CASA software package (McMullin et al. 2007) version 4.5. To enhance the signal-to-noise ratio, we first solved for and applied phase offsets between the four spectral windows, based on scans on the passband calibrator. We then derived gain calibration solutions. The gain-phase solutions were derived separately for the XX and YY correlations, while the gain-amplitude solutions were derived from the average of XX and YY correlations. We derived gain-phase solutions averaging all spectral windows together. Provided the variations of X and Y gains are dominated by unpolarized effects (e.g. atmosphere), the sum of the two parallel-hand channels is nearly independent of the linear polarization of the gain calibrator, and thus provides a simple calibration route for the parallel hand gains. The absolute flux-scaling was derived incrementally from the gain-amplitude solutions, combining all scans.

We fitted the continuum baselines from line-free channels, using the CASA task uvcontsub. After executing uvcontsub, we generated a continuum dataset for each spectral window, by averaging the line free channels. We then exported the calibrated continuum data and the continuum-subtracted line data in standard FITS format files, using the CASA task exportfits. Finally, we used the Miriad 4.3.8 (Sault et al. 1995) task fits to convert the fits format data into the Miriad data format for further analyses, including imaging.

2.3. Measuring fluxes

We modified the Miriad task uvamp, to permit the fitting of fluxes for a point source as a function of the parallactic angle from the visibility data. We fitted the fluxes of the XX and the YY correlations separately for every 5° bin of parallactic angle. We found that this provides optimized signal-to-noise ratios, but without smearing too much information in the parallactic angle (and time) domain. For the band 3 data, we limited the fittings to data at uv distance >30 kλ (e.g. ~7′′ in terms of angular scale), to avoid the confusion from the bright and extended ionized mini-spiral arms (Lo & Claussen 1983 ; Zhao et al. 2009, 2010). The 12 m antennae were omitted from the ACA before measuring Stokes I fluxes to avoid the potential bias between the absolute flux calibrations of the 7 and 12 m antennae.

For each epoch of observations, we derived the averaged Stokes I flux of Sgr A*. For the band 3, 6, and 7 observations, the uncertainties of the Stokes I fluxes over a particular epoch of observations, were defined by the standard deviations of the Stokes I fluxes from all the 5° bins of parallactic angle. For the band 8 and 9 observations, we assumed a nominal 20% flux error, owing to the relatively uncertain data calibrations.

thumbnail Fig. 3

Stokes I fluxes of the ALMA observations. Note the 3 yr time interval between bands 3, 6, 7 and 8, 9. See Table 1 and Sect. 2. The vertical error bars are explained in Sect. 2.3.

Table 3

Stokes I fluxes of Sgr A*.

3. Results

For the sake of conciseness, XX and YY denote the fluxes (i.e. in Jy units) observed by these two correlations hereafter in this manuscript. The Stokes I flux will simply be denoted by I. The derived Stokes I fluxes are summarized in Sect. 3.1. Results of the Sgr A* polarization are provided in Sect. 3.2.

3.1. Stokes I flux density and spectral indices

Figure 3 shows the observed Stokes I fluxes of the Sgr A*, from individual epochs of ALMA observations, which were also summarized in Table 3.

Observations at <400 GHz, which were taken within a ~7 h period (Brinkerink et al. 2015), show increasing Stokes I fluxes with frequency. However, the Stokes I fluxes at ~250 GHz and ~340 GHz are consistent within 1σ error. The ~690 GHz observations on 2015 May 02 shows lower Stokes I flux than that of the ~490 GHz observations taken on 2015 April 30. If the apparently decreasing flux with observing frequency is not due to flux variability on the daily timescale (e.g. Dexter et al. 2014), then it may indicate that the >500 GHz observations are already in the optically thin regime (see also Falcke et al. 1998). This is also consistent with the data presented in An et al. (2005) and Doi et al. (2011). If this is indeed the case, then the submillimeter very long baseline interferometry (VLBI) observations (e.g. Johnson et al. 2015, and references therein) at these frequencies, may be the key to penetrate to the innermost part of the gas accretion flow surrounding the Sgr A*. However, the 709 GHz Stokes I fluxes obtained from the 2015 July 25–26 observations marginally detected flux variability, although this is also consistent with the calibration error. The future simultaneous, multi-frequency ALMA observations at the >300 GHz bands, are still required to provide better constraints on the instantaneous spectral energy distributions. The detailed analysis the Stokes I flux variability, and the analytical modeling of the spectral energy distribution, are beyond the scope of this paper. They will be elaborated in forthcoming papers.

3.2. Polarization fitting, intrinsic polarization angle, and rotation measure

During the observations, the target source is rotated with respected to the receiver frame, owing to the alt-azimuth mount of the ALMA antennae. If the polarization position angle and the polarization percentage do not vary significantly in a shorter timescale than the durations of our observing tracks (1–2 h, typically), then the polarization percentage and the polarization position angle can be fitted according to the following formula by definition: 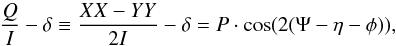(1)where Q denotes the observed Stokes Q flux, δ (Q offset, hereafter) is an assumed constant normalized offset of observed Stokes Q as a result of the amplitude calibration errors or polarization leakage; P is the polarization percentage; Ψ, η, and φ are the polarization position angle in the sky (e.g. right ascension/declination) frame, the parallactic angle, and the Evector (Sect. 2, Table 2), respectively (see also Hildebrand et al. 2000; Li et al. 2005). The application to the interferometric observations of point sources is straightforward since the visibility amplitude does not vary with uv distance. A generalized formulation for extended sources is given in Martí-Vidal et al. (2016).

In practice, we determine our fitting results and errors using an iterative process. First, for each epoch of observations at each frequency, we perform a prior fitting of P, δ and Ψ, based on XX and YY observed at various η. From all data points, we then derive the standard deviation (σQ) of the difference between the observed (XX − YY)/2I − δ and the priori fit. Finally, we disturb each data point of (XX − YY)/2I with a Gaussian random number of which the standard deviation is σQ, and then re-fit P, Ψ, and δ. In the end, P, Ψ, and δ and their errors are determined by mean and standard deviations of fittings to 1000 independent realizations of the perturbed (XX − YY)/2I. We checked that those means converged to the values close to a priori fittings. We reject records which present poor signal-to-noise ratios with the measurements of Stokes I fluxes, which could be observations at low elevation, or with poor weather conditions, or are observations of mosaic fields of which the pointing centers are far away from Sgr A* (e.g. outside of the central seven fields, see Figs. 1, 2).

Table 4

Polarization properties of Sgr A*.

We note that the extended emission surrounding Sgr A* is dominated by the unpolarized, free-free emission of the ionized mini-spiral arms (e.g. Zhao et al. 2009, 2010). Without considering the effect of polarization leakage, the contribution of this extended component should be canceled out in the measurement of (XX − YY) /I. This extended component is largely filtered out owing to our uv sampling range; its contribution is further suppressed by the fitting of a point source component in the uv domain (Sect. 2.3).

For more details of the observational results of band 8 (on UTC 2015 April 30), see Liu et al. (2016). Other observational results are introduced in the following sections. Our fitting results are summarized in Table 4.

thumbnail Fig. 4

Fittings of the (XX − YY)/I intensity ratio, to determine polarization percentages and polarization position angles. Data presented in this figure are self-calibrated ALMA band 3 (bottom 4 panels, from each of the four spectral windows of band 3), 6 (top right), 7 (top left) observations of the Sgr A* on UTC 2012 May 18. XX and YY are intensities of the two orthogonal polarizations in the receiver frame. Only the uv-sampling range of >30 kλ was fitted for the band 3 (93–107 GHz) data. The best fits of polarization percentage (P), polarization position angle (in the receiver frame, i.e. Ψ − φ; PA), and a constant normalized Stokes Q offsets (Q offset), are provided in the upper left of each panel, which are represented by a black curve. For each observed frequency, errors of fitted quantities were determined by one standard deviation of fittings of 1000 random realizations of noisy data (details are in Sect. 3.2). Gray lines in each panel plot every 100 of the random realizations.

thumbnail Fig. 5

Fittings of the (XX − YY)/I intensity ratio, to determine polarization percentages and polarization position angles. Data presented in this figure are self-calibrated ALMA observations of the Sgr A* at band 9. XX and YY are intensities of the two orthogonal polarizations in the receiver frame. Top left: ALMA 12 m-Array observations at passband setup-c (Table 1). Top right: ACA observations at passband setup B9-a. Bottom left: ACA observations at passband setup B9-b on UTC 2015 July 25/26. Bottom right: ACA observations at passband setup B9-b on UTC 2015 July 26. The best fits of polarization percentage (P), polarization position angle (in the receiver frame, i.e. Ψ − φ; PA), and a constant normalized Stokes Q offsets (Q offset), are provided in the upper left of each panel, which are represented by a black curve. For each observed frequency, errors of fitted quantities were determined by one standard deviation of fittings of 1000 random realizations of noisy data (details are in Sect. 3.2). Gray lines in each panel plot every 100 of the random realizations. The ACA observations at setup B9-b only covered a small parallactic range, and therefore cannot provide independent constraints on P, PA, and Q offset. Nevertheless, the observing UTC time and observing frequency of the two epochs of setup B9-b observations, are close to those of the setup B9-a observations, so may serve as consistency checks. We overplot in blue the best fit of the setup B9-a observations of ACA, to the panel which presents the setup B9-b data (bottom left and right panels).

3.2.1. Band 3 (90–110 GHz), 6 (250 GHz) and 7 (340 GHz) observations on UTC 2012 May 18

We fitted P, Ψ, and δ for the four spectral windows taken with band 6 and band 7 together, given that the frequency separations of these spectral windows are small, compared with the observing frequencies of these two bands. The four spectral windows of band 3 were fitted separately. The (XX − YY) /I values of the passband averaged band 6 and band 7 data, and those of the four spectral windows of the band 3 data are plotted in Fig. 4. We additionally provide fittings to the calibrator observations in Appendix A.

We found that the observed (XX − YY) /I at each frequency can be approximated by assuming constant P, Ψ, and δ. However, as compared with the much nicer fits to the calibrators J1924-2914 and NRAO530 (see Appendix), the data of the Sgr A* appear more scattered from the sinusoidal fits, which may be due to a small time variation in the polarization position angle and polarization percentage. There is a monotonic increase of the polarization percentage from low to high frequency. In particular, we found that the two >100 GHz spectral windows of band 3 present ~3 times higher polarization percentages than those two <100 GHz spectral windows. Since data from the four spectral windows of band 3 were taken simultaneously, and were calibrated uniformly, their differences in polarization percentages are unlikely to be due to calibration defects. The polarized signal is only marginally detected at the two <100 GHz spectral windows of band 3, and therefore fittings were subject to large uncertainties.

3.2.2. Band 9 (680-710 GHz) observations in 2015

We fitted P, Ψ, and δ for the band 9, 12 m-Array observations taken on 2015 May 02, and the ACA observations taken on 2015 July 25/26. The four spectral windows of these band 9 observations were fitted together, to enhance the signal-to noise-ratio. We have checked and confirmed that the (XX − YY) /I values measured from the four spectral windows are consistent, which can be expected by the observed rotation measure of the Sgr A* (see Sect. 4 for more discussion).

The (XX − YY) /I values of the passband averaged band 9 data are plotted in Fig. 5. We found that the observed (XX − YY) /I of the band 9, 12 m-Array observations, and the ACA observations of setup B9-a, can be approximated by assuming constant P, Ψ, and δ. The good data in both epochs of ACA observations of setup B9-b only covered small parallactic angle ranges, and therefore do not independently provide constraints on P and Ψ. Nevertheless, overplotting the fitting results for the observations of setup B9-a (Fig. 5, top right) on the B9-b measurements (Fig. 5, bottom row) indicate that the P, Ψ, and δ during the time period for the B9-b observations, are consistent with those during the time period of for the B9-a observations. Fitting together all B9-a and B9-b observations (Fig. 6) may therefore provide a better constraint on P and Ψ.

In spite of the ~3 months of time separations of the band 9 12 m-Array and the ACA B9-a observations, and their largely different δ, they present consistent (within 1σ) polarization position angle Ψ. The measured P from those band 9 observations are different by a factor of ~1.6. However, the parallactic angle range covered by these observations (Fig. 5) may not permit the polarization percentage P to be precisely constrained, which may tend to be slightly overestimated. A better constraint on P requires future observations that incorporate polarization calibration, or cover sufficiently large parallactic angle ranges. Presently, the P and Ψ constrained by the combined ACA B9-a and B9-b data seem to show deviation of Ψ from the band 9 12 m-Array observations (Fig. 7), but show consistent (within 1σ) P (Fig. 8). These observed values of P at band 9 (~700 GHz) are comparable or lower than the value of P observed at band 8 (~500 GHz). More discussion of these observations are discussed in Sect. 4.

thumbnail Fig. 6

Fittings of the (XX − YY)/I intensity ratio of the ACA setups B9-a and B9-b observations together. Symbols, lines, and labels are similar to those in Fig. 5. The frequency listed in the upper right is the mean of the observing frequencies of the B9-a and the B9-b setups.

thumbnail Fig. 7

Observed polarization position angle at ALMA band 3, 6, 7, 8, and 9 is compared with prior data from Aitken et al. (2000), Bower et al. (2003; 2005), the mean of Macquart et al. (2006), and Marrone et al. (2006; 2007). The polarization position angles of the Macquart et al. (2006) data were unwrapped by −180°. Vertical error bars are ±1σ uncertainties, which were determined using the procedure introduced in Sect. 3.2. We overplot the mean fitted intrinsic polarization position angle the and rotation measure by Marrone et al. (2007), and the updated fit based only on ALMA band 3, 6, 7 data. Gray curves show 50 independent random realizations which characterize our fitting errors.

4. Discussion

Figures 7 and 8 summarize the measured polarization position angles and polarization percentages from our ALMA observations, and provide a comparison with the earlier observations of Aitken et al. (2000), Bower et al. (2003; 2005), Macquart et al. (2006), and Marrone et al. (2006; 2007). The polarization position angles presented in Fig. 7 have taken the polarization feed alignments (i.e. Table 2) into considerations. Our observations cannot distinguish the 180° ambiguity of the polarization position angle. The presented polarization position angles in Fig. 7 were ±180° unwrapped to the nearest possible values to the previous observations.

Least square fittings of the band 3, 6, and 7 observations on 2012 May 18 yield χ0 = 138° ± 6°, and RM of (−4.7 ± 0.2) × 105 rad m-2, where χ0 and RM are the assumed constant intrinsic polarization position angle and rotation measure (e.g. Marrone et al. 2006). The RM measured from 2012 May 18 is very close to the previously measured RM = (−5.6 ± 0.7) × 105 rad m-2 reported by Marrone et al. (2007), and RM = (−4.4 ± 0.3) × 105 rad m-2 reported by Macquart et al. (2006). However, Marrone et al. (2007) and Macquart et al. (2006) both reported a derived intrinsic polarization position angle of χ0 ~ 167 ± 7°. The fitted χ0 from the 2012 May 18 observations deviates significantly from those of earlier observations. Benefiting from the good signal-to-noise ratios provided by the ALMA observations, and the coverage of a large frequency range of the 2012 May 18 observations, we clearly demonstrate that the scattering of the polarization position angles at ~230 GHz and ~345 GHz from the existing measurements (Fig. 7) is at least partially (if not fully) attributed to the time variation of polarization properties, instead of merely calibration errors. The expected polarization position angle at 492 GHz from extrapolating fitting of the 2012 May 18 observations, is also not consistent with the direct measurement made on 2015 April 30. The polarization position angle measured from the band 9, 12 m-Array observations (UTC 2015 May 02) is very close to (~1σ) the fitting of the band 3, 6, and 7 observations on 2012 May 18 (Fig. 7), however, deviates significantly from the fitting of earlier data (e.g. Marrone et al. 2007). The intrinsic polarization position angle of Sgr A* may vary/oscillate with time, which needs to be confirmed with observations that are more precise. The polarization position angle measured from the band 9, ACA B9-a observations on 2015 July 26 is consistent with the fitting of earlier data. The combined ACA B9-a and B9-b observations on 2015 July 25–26 also shows consistent Ψ with the fittings of earlier data (e.g. Marrone et al. 2007). We note that our analysis here does not consider the effect that the observations at different frequencies may trace different photospheres. A better analytic modeling of the polarized emission (e.g. Huang et al. 2009) is still required to fully understand the data presented in this manuscript.

The deviations in Stokes I fluxes (Fig. 3) and polarization position angles (Fig. 7) of the Band 9 12 m-Array observations, from those measured by the ACA B9-a/b observations, are indicative. However, with two epochs of observations only, our information about whether or not, or how the values of I, Ψ and P at ~700 GHz are correlated, remains limited. In the case that the polarization percentage indeed remains the same when the total flux increases, then this suggests that the polarized emission may be associated with the flare. If the polarization position angle remains constant during the flare, then this suggests that there may be a stable underlying magnetic field which is not perturbed by the energy of the flare. A time-varying polarization position angle during the flare may, on the other hand, suggest the growing and collapsing of magnetic loops which have relatively low magnetic field strength. If future observations show a smooth evolution of polarization position angle, then propagation of radiating particles around a stable B field geometry is an interesting possibility. There are more complicated radiative transfer effects which need to be quantified in the ray-tracing calculations. For example, changes in the Stokes I flux will also result in changes in the source opacity, which could lead to variations in both polarization position angle and polarization percentage owing to depolarization and Faraday rotation within the emission source. These are beyond the scope of the present paper, which focuses on measurements.

thumbnail Fig. 8

Observed polarization percentage at ALMA band 3, 6, 7, 8, and 9 is plotted with prior data from Aitken et al. (2000), Bower et al. (2003; 2005), the mean of Macquart et al. (2006), and Marrone et al. (2006; 2007). Vertical error bars are ±1σ uncertainties, which were determined using the procedure introduced in Sect. 3.2.

We note that the derived P from the band 9 12 m-Array observations, and from the combined band 9 ACA B9-a and B9-b observations, appear lower than the derived P from the band 8 observations (Fig. 8). The 12 m-Array observations of band 8 and 9 were close in time. The consistent P derived from the band 9 12 m-Array observations with the derivation from the combined ACA B9-a and B9-b observations may suggest that P at ~700 GHz does not vary significantly on daily or monthly timescales. P and Ψ cannot significantly vary on the hourly (and shorter) timescales, otherwise will prohibit our fittings of polarization using the procedure outlined in the beginning of Sect. 3.2. Although our sampling in the time domain remains sparse at the observing frequency of band 9, we consider it is less likely that the lower P at band 9 (~700 GHz) than that at band 8 (~500 GHz) is merely due to time variation (Fig. 8). It is more likely related to the polarization properties of the photospheres probed at these observing frequencies (e.g. Liu et al. 2007).

Finally, the presented new measurements do not yet detect the 90° flip in the polarization position angle around the transitional observing frequency from the optically thick to the optically thick regimes, which is expected by theories (Bromley et al. 2001; Liu et al. 2007; Huang et al. 2009). This may require higher (>1 THz) frequency observations.

5. Conclusion

We present new measurements of the Stokes I intensity, the polarization position angle, and the polarization percentages for the Galactic supermassive black hole Sgr A*, at frequencies ~100, ~230, ~345, ~500, and ~700 GHz. We found that the Stokes I intensity at ~700 GHz may be lower than that at ~500 GHz, which suggests that the observations at ≳500 GHz may be well into the submillimeter-hump where the emission becomes optically thin. At ~700 GHz, both the Stokes I intensity and the polarization position angle may vary with time, while the observed polarization percentage is consistent with no obvious variations. After comparing with the previous and the newly reported observations at lower frequency (90–490 GHz), we found that the intrinsic polarization position angle of Sgr A* may vary with time as well. Below 500 GHz, we see a monotonic increase of polarization percentage with frequency. Our observations indicate that the polarization percentage at ~700 GHz may be lower than that at ~500 GHz, which remains to be confirmed with simultaneous measurements at these two frequency bands.

Acknowledgments

This paper makes use of the following ALMA data: ADS/JAO.ALMA 2013.1.00071.S (PI: Hauyu Baobab Liu), 2013.1.00126.S (PI: Paul T. P. Ho), and 2011.0.00887.S (PI: Heino Falcke). ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada) and NSC and ASIAA (Taiwan), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ. We thank Shin’ichiro Asayama, Ted Huang, Hiroshi Nagai and Charles Hull for providing clarification on the ALMA feed orientation.

References

  1. Aitken, D. K., Greaves, J., Chrysostomou, A., et al. 2000, ApJ, 534, L173 [NASA ADS] [CrossRef] [Google Scholar]
  2. An, T., Goss, W. M., Zhao, J.-H., et al. 2005, ApJ, 634, L49 [NASA ADS] [CrossRef] [Google Scholar]
  3. Bower, G. C., Backer, D. C., Zhao, J.-H., Goss, M., & Falcke, H. 1999a, ApJ, 521, 582 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bower, G. C., Falcke, H., & Backer, D. C. 1999b, ApJ, 523, L29 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bower, G. C., Wright, M. C. H., Backer, D. C., & Falcke, H. 1999c, ApJ, 527, 851 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bower, G. C., Falcke, H., Sault, R. J., & Backer, D. C. 2002, ApJ, 571, 843 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bower, G. C., Wright, M. C. H., Falcke, H., & Backer, D. C. 2003, ApJ, 588, 331 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bower, G. C., Falcke, H., Wright, M. C., & Backer, D. C. 2005, ApJ, 618, L29 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bower, G. C., Markoff, S., Brunthaler, A., et al. 2014, ApJ, 790, 1 [NASA ADS] [CrossRef] [Google Scholar]
  10. Bower, G. C., Markoff, S., Dexter, J., et al. 2015, ApJ, 802, 69 [NASA ADS] [CrossRef] [Google Scholar]
  11. Brinkerink, C. D., Falcke, H., Law, C. J., et al. 2015, A&A, 576, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Bromley, B. C., Melia, F., & Liu, S. 2001, ApJ, 555, L83 [NASA ADS] [CrossRef] [Google Scholar]
  13. Dexter, J., Kelly, B., Bower, G. C., et al. 2014, MNRAS, 442, 2797 [NASA ADS] [CrossRef] [Google Scholar]
  14. Doi, A., Nakanishi, K., Nagai, H., Kohno, K., & Kameno, S. 2011, AJ, 142, 167 [NASA ADS] [CrossRef] [Google Scholar]
  15. Falcke, H., & Markoff, S. 2000, A&A, 362, 113 [NASA ADS] [Google Scholar]
  16. Falcke, H., Goss, W. M., Matsuo, H., et al. 1998, ApJ, 499, 731 [NASA ADS] [CrossRef] [Google Scholar]
  17. Fish, V. L., Doeleman, S. S., Broderick, A. E., Loeb, A., & Rogers, A. E. E. 2009, ApJ, 706, 1353 [NASA ADS] [CrossRef] [Google Scholar]
  18. Flett, A. M., & Murray, A. G. 1991, MNRAS, 249, 4 [Google Scholar]
  19. Hildebrand, R. H., Davidson, J. A., Dotson, J. L., et al. 2000, PASP, 112, 1215 [NASA ADS] [CrossRef] [Google Scholar]
  20. Huang, L., Liu, S., Shen, Z.-Q., et al. 2009, ApJ, 703, 557 [NASA ADS] [CrossRef] [Google Scholar]
  21. Johnson, M. D., Fish, V. L., Doeleman, S. S., et al. 2015, Science, 350, 1242 [NASA ADS] [CrossRef] [Google Scholar]
  22. Kuo, C. Y., Asada, K., Rao, R., et al. 2014, ApJ, 783, L33 [NASA ADS] [CrossRef] [Google Scholar]
  23. Li, H., Griffin, G. S., Krejny, M., et al. 2005, Astronomical Polarimetry: Current Status and Future Directions, ASP Conf. Ser., 343, 43 [NASA ADS] [Google Scholar]
  24. Liu, S., Qian, L., Wu, X.-B., Fryer, C. L., & Li, H. 2007, ApJ, 668, L127 [NASA ADS] [CrossRef] [Google Scholar]
  25. Liu, H. B., Wright, M. C. H., Zhao, J.-H., et al. 2016, A&A, 593, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Lo, K. Y., & Claussen, M. J. 1983, Nature, 306, 647 [NASA ADS] [CrossRef] [Google Scholar]
  27. Macquart, J.-P., Bower, G. C., Wright, M. C. H., Backer, D. C., & Falcke, H. 2006, ApJ, 646, L111 [NASA ADS] [CrossRef] [Google Scholar]
  28. Marrone, D. P., Moran, J. M., Zhao, J.-H., & Rao, R. 2006, ApJ, 640, 308 [NASA ADS] [CrossRef] [Google Scholar]
  29. Marrone, D. P., Moran, J. M., Zhao, J.-H., & Rao, R. 2007, ApJ, 654, L57 [NASA ADS] [CrossRef] [Google Scholar]
  30. Martí-Vidal, I., Muller, S., Vlemmings, W., Horellou, C., & Aalto, S. 2015, Science, 348, 311 [NASA ADS] [CrossRef] [Google Scholar]
  31. Marti-Vidal, I., Vlemmings, W. H. T., & Muller, S. 2016, A&A, 593, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. McMullin, J. P., Waters, B., Schiebel, D., Young, W., & Golap, K. 2007, Astronomical Data Analysis Software and Systems XVI, 376, 127 [NASA ADS] [Google Scholar]
  33. Muñoz, D. J., Marrone, D. P., Moran, J. M., & Rao, R. 2012, ApJ, 745, 115 [NASA ADS] [CrossRef] [Google Scholar]
  34. Sault, R. J., & Macquart, J.-P. 1999, ApJ, 526, L85 [NASA ADS] [CrossRef] [Google Scholar]
  35. Sault, R. J., Teuben, P. J., & Wright, M. C. H. 1995, Astronomical Data Analysis Software and Systems IV, 77, 433 [Google Scholar]
  36. Yuan, F., & Narayan, R. 2014, ARA&A, 52, 529 [NASA ADS] [CrossRef] [Google Scholar]
  37. Zhao, J.-H., Young, K. H., Herrnstein, R. M., et al. 2003, ApJ, 586, L29 [NASA ADS] [CrossRef] [Google Scholar]
  38. Zhao, J.-H., Herrnstein, R. M., Bower, G. C., Goss, W. M., & Liu, S. M. 2004, ApJ, 603, L85 [NASA ADS] [CrossRef] [Google Scholar]
  39. Zhao, J.-H., Morris, M. R., Goss, W. M., & An, T. 2009, ApJ, 699, 186 [NASA ADS] [CrossRef] [Google Scholar]
  40. Zhao, J.-H., Blundell, R., Moran, J. M., et al. 2010, ApJ, 723, 1097 [Google Scholar]

Appendix A: Polarization of calibrator data

In this section, we report fitting results of polarization properties for calibrators observed on UTC 2012 May 18 by the 12 m-Array observations (Figs. A.1, A.2). Polarization of J1924-2914 has been discovered and mentioned in Brinkerink et al. (2015). The newly reported band 9 observations in this manuscript covered parallactic angle ranges that were too small. In combination with the effects of the potentially relatively large

leakages, the band 9 observations cannot provide good fits. This paper focuses on fitting polarization properties of point sources. We refer to Martí-Vidal et al. (2015) for a method of constraining polarization properties of spatially resolved sources. Martí-Vidal et al. (2016) formulate the problem of the extraction of polarimetry information from dual-polarization observations in detail. These authors also discuss the importance of several instrumental effects (like polarization leakage or beam squint) in the special case of the ALMA antennae.

thumbnail Fig. A.1

Fittings of the (XX − YY) /I intensity ratio, to determine polarization percentages and polarization position angles. Data presented in this figure are self-calibrated ALMA band 3, 6, 7 observations of J1924-2914 on UTC 2012 May 18. The best fits of polarization percentage (P), polarization position angle (in the receiver frame, i.e. Ψ − φ; PA), and a constant normalized Stokes Q offsets (Q offset), are provided in the upper left of each panel, which are represented by a black curve. For each observed frequency, errors of fitted quantities were determined by one standard deviation of fittings of 1000 random realizations of noisy data (details are in Sect. 3.2). Gray lines in each panel plot every 100 of the random realizations.

thumbnail Fig. A.2

Fittings of the (XX − YY) /I intensity ratio, to determine polarization percentages and polarization position angles. Data presented in this figure are self-calibrated ALMA band 3, 6, 7 observations of NRAO530 on UTC 2012 May 18. We fitted the four spectral windows of the band 3 observations together to enhance the signal to noise ratio. The best fits of polarization percentage (P), polarization position angle (in the receiver frame, i.e. Ψ − φ; PA), and a constant normalized Stokes Q offsets (Q offset), are provided in the upper left of each panel, which are represented by a black curve. For each observed frequency, errors of fitted quantities were determined by one standard deviation of fittings of 1000 random realizations of noisy data (details are in Sect. 3.2). Gray lines in each panel plot every 100 of the random realizations.

All Tables

Table 1

ALMA observations.

In the text
Table 2

Angular separation between X polarization and the local vertical (also known as Evector; see Sect. 4.2 of ALMA Cycle 4 Technical Handbook)

In the text
Table 3

Stokes I fluxes of Sgr A*.

In the text
Table 4

Polarization properties of Sgr A*.

In the text

All Figures

thumbnail Fig. 1

Mosaic fields of the ALMA 12 m-Array, band 9 observations. The diameter of these circles is .
In the text
thumbnail Fig. 2

Mosaic fields of the ACA, band 9 observations. The diameter of these circles is .
In the text
thumbnail Fig. 3

Stokes I fluxes of the ALMA observations. Note the 3 yr time interval between bands 3, 6, 7 and 8, 9. See Table 1 and Sect. 2. The vertical error bars are explained in Sect. 2.3.
In the text
thumbnail Fig. 4

Fittings of the (XX − YY)/I intensity ratio, to determine polarization percentages and polarization position angles. Data presented in this figure are self-calibrated ALMA band 3 (bottom 4 panels, from each of the four spectral windows of band 3), 6 (top right), 7 (top left) observations of the Sgr A* on UTC 2012 May 18. XX and YY are intensities of the two orthogonal polarizations in the receiver frame. Only the uv-sampling range of >30 kλ was fitted for the band 3 (93–107 GHz) data. The best fits of polarization percentage (P), polarization position angle (in the receiver frame, i.e. Ψ − φ; PA), and a constant normalized Stokes Q offsets (Q offset), are provided in the upper left of each panel, which are represented by a black curve. For each observed frequency, errors of fitted quantities were determined by one standard deviation of fittings of 1000 random realizations of noisy data (details are in Sect. 3.2). Gray lines in each panel plot every 100 of the random realizations.
In the text
thumbnail Fig. 5

Fittings of the (XX − YY)/I intensity ratio, to determine polarization percentages and polarization position angles. Data presented in this figure are self-calibrated ALMA observations of the Sgr A* at band 9. XX and YY are intensities of the two orthogonal polarizations in the receiver frame. Top left: ALMA 12 m-Array observations at passband setup-c (Table 1). Top right: ACA observations at passband setup B9-a. Bottom left: ACA observations at passband setup B9-b on UTC 2015 July 25/26. Bottom right: ACA observations at passband setup B9-b on UTC 2015 July 26. The best fits of polarization percentage (P), polarization position angle (in the receiver frame, i.e. Ψ − φ; PA), and a constant normalized Stokes Q offsets (Q offset), are provided in the upper left of each panel, which are represented by a black curve. For each observed frequency, errors of fitted quantities were determined by one standard deviation of fittings of 1000 random realizations of noisy data (details are in Sect. 3.2). Gray lines in each panel plot every 100 of the random realizations. The ACA observations at setup B9-b only covered a small parallactic range, and therefore cannot provide independent constraints on P, PA, and Q offset. Nevertheless, the observing UTC time and observing frequency of the two epochs of setup B9-b observations, are close to those of the setup B9-a observations, so may serve as consistency checks. We overplot in blue the best fit of the setup B9-a observations of ACA, to the panel which presents the setup B9-b data (bottom left and right panels).
In the text
thumbnail Fig. 6

Fittings of the (XX − YY)/I intensity ratio of the ACA setups B9-a and B9-b observations together. Symbols, lines, and labels are similar to those in Fig. 5. The frequency listed in the upper right is the mean of the observing frequencies of the B9-a and the B9-b setups.
In the text
thumbnail Fig. 7

Observed polarization position angle at ALMA band 3, 6, 7, 8, and 9 is compared with prior data from Aitken et al. (2000), Bower et al. (2003; 2005), the mean of Macquart et al. (2006), and Marrone et al. (2006; 2007). The polarization position angles of the Macquart et al. (2006) data were unwrapped by −180°. Vertical error bars are ±1σ uncertainties, which were determined using the procedure introduced in Sect. 3.2. We overplot the mean fitted intrinsic polarization position angle the and rotation measure by Marrone et al. (2007), and the updated fit based only on ALMA band 3, 6, 7 data. Gray curves show 50 independent random realizations which characterize our fitting errors.
In the text
thumbnail Fig. 8

Observed polarization percentage at ALMA band 3, 6, 7, 8, and 9 is plotted with prior data from Aitken et al. (2000), Bower et al. (2003; 2005), the mean of Macquart et al. (2006), and Marrone et al. (2006; 2007). Vertical error bars are ±1σ uncertainties, which were determined using the procedure introduced in Sect. 3.2.
In the text
thumbnail Fig. A.1

Fittings of the (XX − YY) /I intensity ratio, to determine polarization percentages and polarization position angles. Data presented in this figure are self-calibrated ALMA band 3, 6, 7 observations of J1924-2914 on UTC 2012 May 18. The best fits of polarization percentage (P), polarization position angle (in the receiver frame, i.e. Ψ − φ; PA), and a constant normalized Stokes Q offsets (Q offset), are provided in the upper left of each panel, which are represented by a black curve. For each observed frequency, errors of fitted quantities were determined by one standard deviation of fittings of 1000 random realizations of noisy data (details are in Sect. 3.2). Gray lines in each panel plot every 100 of the random realizations.
In the text
thumbnail Fig. A.2

Fittings of the (XX − YY) /I intensity ratio, to determine polarization percentages and polarization position angles. Data presented in this figure are self-calibrated ALMA band 3, 6, 7 observations of NRAO530 on UTC 2012 May 18. We fitted the four spectral windows of the band 3 observations together to enhance the signal to noise ratio. The best fits of polarization percentage (P), polarization position angle (in the receiver frame, i.e. Ψ − φ; PA), and a constant normalized Stokes Q offsets (Q offset), are provided in the upper left of each panel, which are represented by a black curve. For each observed frequency, errors of fitted quantities were determined by one standard deviation of fittings of 1000 random realizations of noisy data (details are in Sect. 3.2). Gray lines in each panel plot every 100 of the random realizations.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.