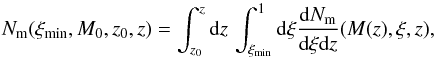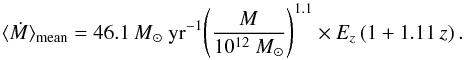| Issue |
A&A
Volume 593, September 2016
|
|
|---|---|---|
| Article Number | A81 | |
| Number of page(s) | 11 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201628414 | |
| Published online | 26 September 2016 | |
Can giant radio halos probe the merging rate of galaxy clusters?
1 INAF-Istituto di Radioastronomia,
Bologna, via P.Gobetti, 101, 40129
Bologna,
Italy
e-mail: rcassano@ira.inaf.it
2 Aix Marseille Université, CNRS, LAM
(Laboratoire d’Astrophysique de Marseille) UMR 7326, 13388
Marseille,
France
3 INAF/Osservatorio Astronomico di
Bologna, via Ranzani 1, 40127
Bologna,
Italy
4 INFN, Sezione di Bologna, viale Berti
Pichat 6/2, 40127
Bologna,
Italy
Received:
1
March
2016
Accepted:
13
June
2016
Observations of galaxy clusters both in the radio and X-ray bands probe a direct link
between cluster mergers and giant radio halos, suggesting that these sources can be used
as probes of the cluster merging rate with cosmic time. While all giant radio halos are
found in merging clusters, not every merging cluster hosts a giant radio halo. In this
paper we carry out an explorative study that combines the observed fractions of merging
clusters and radio halos with the merging rate predicted by cosmological simulations, and
we attempt to infer constraints on merger properties of clusters that appear disturbed in
X-rays and clusters that host radio halos. We used classical morphological parameters to
identify merging systems and analysed the largest current (mass-selected M500 ≳ 6 ×
1014M⊙ and 0.2 ≤ z ≤ 0.33) sample of
galaxy clusters with radio and X-ray data; we extracted this sample from the
Planck Sunyaev-Zeldovich cluster catalogue. We found that the fraction
of merging clusters in this sample is fm ~ 62−67%, while that of clusters
with radio halos is fRH ~ 44−51%. We assume that the
morphological disturbance measured in the X-rays is driven by the merger with the largest
mass ratio, ξ
(ξ =
Mi/M1<
1, where Mi and
M1 are the progenitor masses), which is
still ongoing in the cluster at the epoch of observation. Results from theoretical studies
allow us to derive the fraction of mergers with mass ratio above a minimum threshold
(those with 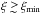 ) in our sample, under the assumption of a timescale
τm for the duration of merger-induced
disturbance. The comparison of the theoretical merger fraction with the observed merger
fraction allows us to constrain a region in the (ξmin,
τm) plane. We find that under the
assumption of τm
~ 2−3 Gy, as constrained by simulations, the observed merger
fraction matches the theoretical value for ξmin ~ 0.1−0.18. This is consistent
with optical and near-infrared (IR) observations of galaxy clusters in the sample that
constrain ξmin ≃
0.14−0.16 through weak lensing analysis or study of the velocity
distribution of galaxies in the clusters. The fact that radio halos are only found in a
fraction of merging galaxy clusters may suggest that merger events generating radio halos
are characterized by larger mass ratios; this seems to be supported by optical/near-IR
observations of radio halo clusters in the sample that indeed allow us to constrain
ξmin ~
0.2−0.25. Alternatively, radio halos may be generated in all mergers
but their lifetime is shorter (by ~fRH/fm) than
the timescale of the merger-induced disturbance. We stress that this is an explorative
study, however it suggests that follow-up studies using the forthcoming radio surveys and
adequate numerical simulations have the potential to derive quantitative constraints on
the link between cluster merging rate and radio halos at different cosmic epochs and for
different cluster masses.
) in our sample, under the assumption of a timescale
τm for the duration of merger-induced
disturbance. The comparison of the theoretical merger fraction with the observed merger
fraction allows us to constrain a region in the (ξmin,
τm) plane. We find that under the
assumption of τm
~ 2−3 Gy, as constrained by simulations, the observed merger
fraction matches the theoretical value for ξmin ~ 0.1−0.18. This is consistent
with optical and near-infrared (IR) observations of galaxy clusters in the sample that
constrain ξmin ≃
0.14−0.16 through weak lensing analysis or study of the velocity
distribution of galaxies in the clusters. The fact that radio halos are only found in a
fraction of merging galaxy clusters may suggest that merger events generating radio halos
are characterized by larger mass ratios; this seems to be supported by optical/near-IR
observations of radio halo clusters in the sample that indeed allow us to constrain
ξmin ~
0.2−0.25. Alternatively, radio halos may be generated in all mergers
but their lifetime is shorter (by ~fRH/fm) than
the timescale of the merger-induced disturbance. We stress that this is an explorative
study, however it suggests that follow-up studies using the forthcoming radio surveys and
adequate numerical simulations have the potential to derive quantitative constraints on
the link between cluster merging rate and radio halos at different cosmic epochs and for
different cluster masses.
Key words: galaxies: clusters: intracluster medium / cosmology: theory / radio continuum: general / X-rays: galaxies: clusters
© ESO, 2016
1. Introduction
In the paradigm of the hierarchical structure formation scenario, galaxy clusters, the largest and more recently assembled structures in the Universe, form via mergers of smaller halos and continuous accretion of unbound matter. The process of mass accretion of dark matter halos is a clear outcome of the cosmological model. This process can be statistically investigated with N-body simulations and semi-analytical models through the identification of merger trees of dark matter halos, which lead to the derivation of the mass accretion history and merging rate as a function of redshift, halo mass, and mass ratio of the progenitors (e.g. van den Bosh 2002; Giocoli et al. 2007; Moreno et al. 2007; 2008; Fakhouri & Ma 2008; McBride et al. 2009; Fakhouri et al. 2010; Giocoli et al. 2012).
Observationally, the exploration of the merging rate of dark matter halos has only been attempted on the scales of galaxies using two main methods for tracing the merging history in the observations: morphological identification techniques (Conselice et al. 2003; Lotz et al. 2004) and the close galaxy pair method (e.g. Patton et al. 2000; De Propris et al. 2005). These methods are then combined with the merger timescale derived from N-body simulations to obtain the merging rate (e.g. Lotz et al. 2011; Jian et al. 2012; Conselice 2014). Current results are inconclusive, however, because the merger rate of dark matter halos and the merger rate of galaxies do not necessary coincide. This is because they are related by dissipative processes, such as dynamical friction, tidal interaction, and stellar feedback, that are difficult to model (Fakhouri & Ma 2008; Guo & White 2008; Lotz et al. 2011; Hopkins et al. 2013). Dissipative processes are instead less relevant during the mass accretion of galaxy clusters. Nevertheless only recently a method based on the possibility to measure the cluster mass in a thin spherical shell surrounding the cluster beyond R200 (with the caustic technique) and by estimating its infalling time (e.g. Diaferio 2015; De Boni et al. 2016), has been proposed to measure the mass accretion rate of galaxy clusters. Yet, in general, the growth of structures on the scale of galaxy clusters remains poorly explored from an observational prospective (e.g. Lemze et al. 2013).
Mergers between clusters are the most energetic phenomena since the Big Bang with a release of a gravitational potential energy of ~1063−1064 erg during one cluster crossing time (~1 Gyr). During such events, shock waves and random vortical flows, if not turbulence, are produced in the intracluster medium (ICM; e.g. Kulsrud et al. 1997; Norman & Bryan 1999; Ricker & Sarazin 2001). These motions originate as a result of vorticity generation in oblique accretion shocks and instabilities during the cluster formation, and in the wake of the smaller subclusters (e.g. Subramanian et al. 2006; Brunetti & Jones 2014; Brüggen &Vazza 2015). The bulk of the gravitational energy associated with the collision is released as thermal energy in the final system (e.g. Kravtsov & Borgani 2012), while another fraction can be channelled into non-thermal plasma components, i.e. relativistic particles and magnetic fields in the ICM (e.g. Brunetti & Jones 2014). The existence of cosmic ray electrons and magnetic fields in the ICM is in fact demonstrated by radio observations. Cluster-scale (~Mpc-scale) diffuse synchrotron emission is frequently found in merging galaxy clusters in the form of so-called giant radio halos (hereafter RHs or RH), apparently unpolarized synchrotron emission associated with the cluster X-ray emitting regions, and giant radio relics, elongated and often highly polarized synchrotron sources typically seen in the clusters outskirts (e.g. Feretti et al. 2012, for an observational review). The properties of radio relics suggest a connection with large-scale shocks that cross the ICM during mergers and may accelerate locally injected electrons or reaccelerate pre-existing energetic electrons, while RHs likely trace gigantic turbulent regions in the ICM, where relativistic electrons can be reaccelerated through scattering with magnetohydrodynamic (MHD) turbulence (e.g. Brunetti & Lazarian 2007; Brüggen et al. 2012).
In recent decades, radio observations of statistical samples of galaxy clusters have shown that RHs are not ubiquitous; only ~20−30% of the X-ray luminous (LX(0.1−2.4 keV) ≥ 5 × 1044 erg/s) clusters host a RH (e.g. Venturi et al. 2008; Kale et al. 2015), while the fraction of clusters with RHs becomes larger in Sunyaev Zeldovich (SZ)-selected clusters (e.g. Basu 2012; Cassano et al. 2013; Sommer & Basu 2014; Cuciti et al. 2015; Bernardi et al. 2016). Most importantly, it was found that RH and non-RH clusters are clearly separated in the P1.4−LX and P1.4−M500 (Y500) diagrams according to the cluster dynamical status, where RHs are always associated with dynamically disturbed clusters and clusters without RHs are statistically more relaxed (e.g. Brunetti et al. 2007, 2009; Cassano et al. 2010, 2013). The connection between RHs and merging clusters has been further supported by a number of independent studies (e.g. Rossetti et al. 2011; Wen & Han 2013; Parekh et al. 2015; Mantz et al. 2015; Yuan et al. 2015; Kale & Parekh 2016). The RH-cluster merger connection suggests that RHs can be used as signposts of cluster mergers and supports the idea that RHs are transient phenomena tracing turbulent regions in the ICM during the process of cluster formation. Not all merging clusters host a giant RH (see Cassano et al. 2013 and ref. therein), however, and this poses fundamental questions about the conditions that are necessary to generate cluster-scale synchrotron diffuse emission.
The connection between mergers and non-thermal phenomena also opens to the possibility of inferring constraints on the cluster merging rate from radio observations. In this paper we start exploring this possibility. In particular we attempt to combine the observed fraction of merging clusters and the observed fraction of RHs in clusters with the merging rate predicted by cosmological simulations to infer constraints on the properties of the mergers that induce disturbances observed in X-rays and those responsible for RHs.
We stress that this is an explorative study whose the main aim is to start to investigate the possibility to use diffuse radio emission in galaxy clusters as tracer of the cluster dynamical status. In particular, we stress that current statistical information is still limited to very massive (M500>~ 6 × 1014M⊙) and relatively nearby systems (z ≃ 0.2−0.33), while we anticipate that better constraints can be obtained using less massive systems or clusters at higher redshifts.
In Sect. 2 we present the cluster sample and derive the fractions of merging clusters and those of clusters with RHs; in Sect. 3 we describe the formalism by Fakhouri et al. (2010) to derive the merging rate in simulations and derive the expected merger fraction. In Sect. 4 we compare the observed merger fraction and RH fraction with expectations from simulations, and we attempt to constrain the properties that cluster mergers should have to explain the observed fraction of clusters with X-ray disturbances and that of clusters with RHs. Finally, in Sect. 5 we summarize the main results and discuss the main implications for the origin of giant RHs in galaxy clusters.
A Lambda cold dark matter (ΛCDM) cosmology (H0 = 70 km s-1 Mpc-1, Ωm = 0.3, ΩΛ = 0.7) is adopted.
2. Data and sample selection
We used the Planck SZ cluster catalogue (PSZ; Planck Collaboration XXIX 2014) to select 54 clusters with M500 ≳ 6 × 1014M⊙1, redshift 0.2 ≤ z ≤ 0.33 and δ> −30° and | b | ≥ ± 20°, where b is the galactic latitude (Table A.1). With such a selection the sample has a mass completeness of ~80%2.
This selection has been thought to optimize the available information in the radio band; indeed 37 out of 54 clusters belong to the Giant Metrewave Radio Telescope (GMRT) RH Survey and its extension (EGRHS; Venturi et al. 2007, 2008; Kale et al. 2013, 2015) and for 39 out of 54 clusters (~72% of the sample) information about the presence/absence of diffuse radio emission is available. In particular, 17 clusters host giant RHs, while 3 clusters host candidate RHs (see Table A.1). The fraction of RHs, defined as fRH = NH/Ntot, where NH is the number of RHs and Ntot the total number of clusters, is thus ~44% and can reach ~51% if we include the 3 uncertain cases.
Fifty-one out of 54 clusters (~94% of the sample, including all the 39 clusters with available radio information) have X-ray data (Chandra and/or XMM-Newton) that can be used to derive information about the cluster dynamical status. In particular, 41 of these clusters have Chandra data for which morphological indicators, such as the power ratio P3/P0 (e.g. Buote & Tsai 1995), the emission centroid shift w (e.g. Mohr et al. 1993), and the surface brightness concentration parameter c (e.g. Santos et al. 2008), can be homogeneously derived to quantitatively establish the cluster dynamical status. Following Cassano et al. (2010, 2013), we adopted an algorithm for an automatic detection of the point sources, which are then removed from the images. We study the cluster substructures on a typical RH scale by analysing the surface brightness inside an aperture radius of 500 kpc, since we are interested in the cluster dynamics on the scales where the energy is most likely dissipated to generate radio emission. The power ratio is a multipole decomposition of the two-dimensional projected mass distribution within a given aperture, and P3/P0 is the lowest power ratio moment providing a clear substructure measure (Böhringer et al. 2010). The centroid shift w is defined as the standard deviation of the projected separation between the peak and centroid of the cluster X-ray brightness distribution in unit of the aperture radius. The concentration parameter c is defined as the ratio of the peak (within 100 kpc) over the ambient (within 500 kpc) X-ray surface brightness. Following previous papers (Cassano et al. 2010, 2013; Cuciti et al. 2015), we adopt the following threshold values to classify clusters as mergers: P3/P0>~1.2 × 10-7, w>~0.012 and c<~0.2. Morphological parameters are already published in Cassano et al. (2010, 2013) and Cuciti et al. (2015) for 32 clusters with Chandra data; here we derive the morphological quantities for additional 9 clusters following the approach outlined above (and described in previous works; see e.g. Sect. 3 of Cassano et al. 2010, for details). The resulting dynamical status of the clusters, “merger” versus “relaxed”, is reported in Table A.1 (Col. 6); the values of the morphological parameters for the 41 clusters with Chandra data are reported in Table A.2.
Ten more clusters with available XMM-Newton observations can be added to this sample and after a visual inspection of their images we can assess (even if with less confidence) their dynamical status (also reported in Table A.1, Col. 6).
In deriving the merger fraction3 we assume that the disturbance we measure in the X-rays is mainly due to the merger with the largest mass ratio that is ongoing in the system at the epoch of the observation, i.e. a binary merger approximation. Under this assumption the merger fraction is equivalent to the fraction of clusters that is actually in phase of merger (where we consider clusters as the final product of the merger). Considering the sample of 39 clusters with available radio information, we found that the fraction of dynamically disturbed systems, or the merger fraction, which is defined as fm = Nm/Ntot with Nm being the number of merging clusters, is ~62−67% (including the uncertainty on the classification of two clusters; see Table A.1). If we extend this analysis to the sample of 51 clusters with X-ray data, we found fm ~ 65−69%. We can only speculate on the fraction of RHs in this sample of 51 clusters, for instance, by assuming that the fraction of merging clusters with RHs in these additional 12 clusters is the same as we measure in the sample of 39 clusters (that is ~70%); we obtain fH ~ 45−51%. The derived fractions are summarized in Table 1.
Cluster fractions.
Calculations in the paper are based on the fractions extracted from the sample of 39 clusters (for which both radio and X-ray data4 are available), although these fractions are not expected to change significantly in the extended sample (under reliable assumptions, see Table 1).
3. Merging rate of halos from simulations
In the ΛCDM scenario dark matter halos grow in mass and size primarily through mergers with other halos: merger with comparable mass halos (“major mergers”) and merger with smaller satellite halos (“minor mergers”). To derive the merging rate of halos we use the result derived from the combined Millennium (Springel et al. 2005) and Millennium-II (Boylan-Kolchin et al. 2009) simulations (Fakhouri et al. 2010; FMB10 hereafter). FMB10 used merger trees of dark matter halos to extract a catalogue of mergers containing for each descendent halo at redshift zd ≥ 0 with mass M the Np (Np ≥ 1) progenitors at zp = zd + Δz, with masses M1 ≥ M2 ≥ ...MNp.These authors include all the progenitors (above a given mass threshold) to derive the merging rate, and since they do not have information about the order the progenitors merge, they assume that each progenitor Mi with i ≥ 2 mergers with the most massive progenitor M1 at a given point between zp and zd. Thus a descendent halo with Np progenitors is assumed to be the result of Np − 1 binary merger events with mass ratio ξ = Mi/M1 ≤ 1 (i = 2,...,Np). The progenitor mass ratio, ξ, is defined so that, for instance, ξ = 0.3 indicates major mergers with mass ratio 1:3, while ξ = 0.1 indicates mergers with mass ratio 1:10. The derived mean merging rate per halo, dNm/ dξ/ dz, which gives the mean number of mergers per unit halo per unit z per unit ξ, can be well described by the following formula (FMB10):
were the best-fit parameters are: α = 0.133, β = −1.995, γ = 0.263, η = 0.0993, and A = 0.0104, 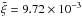 . This formula has a negligible dependence on the redshift and it is also nearly independent of the mass. The main dependence is on the mass ratio ξ, so that the number of mergers per halo is larger for smaller mass ratio. For example, the number of mergers (per halo) with ξ = 0.01 is about 90 times larger than the number of mergers with ξ = 0.1 (see Fig. 1, right panel, in FMB10).
. This formula has a negligible dependence on the redshift and it is also nearly independent of the mass. The main dependence is on the mass ratio ξ, so that the number of mergers per halo is larger for smaller mass ratio. For example, the number of mergers (per halo) with ξ = 0.01 is about 90 times larger than the number of mergers with ξ = 0.1 (see Fig. 1, right panel, in FMB10).
Integrating Eq. (1) for ξ ≥ ξmin and between z0 and z, one obtains the cumulative number of mergers, Nm(ξmin,M0,z0,z). That is the total number of mergers with ξ ≥ ξmin that a halo of mass M0 at redshift z0 has encountered between z0 and an earlier z during the halo’s history,
where M(z) is the mass accretion history and can be obtained integrating the fitting formula for the mass accretion rate, Ṁ = (M0 − M1)/Δt ,where M0 is the descendent mass at time t and M1 is the mass of its most massive progenitor at time t − Δt, that is given by (FMB10)
The quantity we derived observationally is the merger fraction, which is the fraction of clusters with significant dynamical disturbance in X-rays (see Sect. 2). To compare this quantity with expectations given by Eqs. (1)−(3), we need to assume a merger timescale, τm, associated with the duration of the morphological disturbance that we infer from X-ray images. This is a free parameter in our calculations that however can be constrained through numerical simulations (see Sect. 4). We derive the average fraction of mergers with ξ ≥ ξmin expected in our sample by integrating Eq. (2) for each cluster of the sample with mass M0 and redshift z0 up to the redshift z corresponding to the lookback time τm and then computing ∑ iNm(ξmin,M0,i,z0,i,zi) /Ntot, where the sum is on the Ntot number of clusters in the sample. The derived average merger fraction is reported in Fig. 1 as a function of ξmin for three values of τm (τm = 1,2,3 Gyr) and is compared with the observed merger fraction and observed fraction of clusters with RH (shadowed regions).
The predicted merger fraction decreases for larger mass ratios simply because major mergers are less common than minor mergers and it obviously increases by assuming larger timescales.
 |
Fig. 1 Predicted average merger fraction for clusters in the sample as a function of ξmin, assuming three different values for the merger timescale τm = 1,2,3 Gyr (from bottom to top). The observed merger fraction and RH fraction are also reported (shadowed regions). |
4. Comparison with theory
The comparison between the observed and theoretical merging fractions allows us to derive constraints on relevant parameters, such as τm and ξmin. Before proceeding in this direction, we need to discuss some caveats in our procedures. In principle, the comparison between the “observed” and “theoretical” merging fractions allows us to derive constraints on relevant parameters, such as τm and ξmin.
4.1. Caveats
The observed merger fraction is derived by measuring the fraction of clusters with significant X-ray disturbances. This means that our method is limited to events with significant mass accretion, otherwise it would be difficult to classify these events as “mergers” based on the morphological parameters. The dynamical parameters are derived within a region of radius 500 kpc. On the other hand, in FMB10 the merger fraction is derived from the merging rate that considers all the infalling halos within the virial radius of the main cluster (that for our clusters is ~2−3 Mpc). Since we are considering a “rate”, or number of infalling halos per unit time, it is important that the halos crossing the virial radius of the main cluster cross, at a given time, the radius of 500 kpc reaching the central regions. According to cosmological simulations, halos with a mass ratio ξ>~0.1 reach their pericentric distance, that is ~0.2−0.3 Rv, within a timescale of ~0.9 Gyr from the virial crossing (e.g. Tormen et al. 2004).
The other assumption is that of binary mergers, i.e. we assume that the disturbance we measure in the X-rays is mainly caused by a binary merger event between the two main progenitors. Consequently, we derive the expected average merger fraction from the fitting formulae by FMB10 assuming that in a merger timescale there is a main binary merger event with 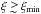 that influences the observed dynamical status. However, in a merger timescale, especially for a long timescale, clusters might experience multiple merger episodes characterized by lower mass ratio (ξ<ξmin). If the number of mergers with a mass ratio that is slightly lower than ξmin is significant, our assumption would be no longer valid since the interplay of these mergers would also contribute to the morphological disturbance.
that influences the observed dynamical status. However, in a merger timescale, especially for a long timescale, clusters might experience multiple merger episodes characterized by lower mass ratio (ξ<ξmin). If the number of mergers with a mass ratio that is slightly lower than ξmin is significant, our assumption would be no longer valid since the interplay of these mergers would also contribute to the morphological disturbance.
 |
Fig. 2 Allowed regions of parameters (ξmin, τm) constrained by requiring that the observed merger fraction (black region) and RH fraction (red regions) match those predicted by theory (these regions account for the uncertainty in the observed fraction). For each ξmin the maximum allowed value of τm, τm,max (blue region with arrows; see Sect. 4.2) and a lower limit to τm (horizontal blue dashed line, see Sect. 4.2) are also shown. The merger timescale constrained by cosmological simulation is also reported (green line; Tormen et al. 2004). Ranges of ξmin constrained through optical/near-IR observations of galaxy clusters in the sample (see Sect.4.4) are shown for merging clusters (black rectangular region ) and for clusters with RHs (red rectangular region). These values of ξmin both constrain τm ~ τRH ~ 2.5−3 Gyr; this is also show in the figure. |
4.2. Mergers and observed X-ray morphology
Given these premises, we proceed with the comparison between the observed merger fraction and the results by FMB10. From Fig. 1 it is clear that we can find combinations (τm, ξmin) for which the expected merger fraction can match that observed in our sample. Figure 2 (black region) shows the allowed regions of (τm, ξmin) that is derived by matching theory and observations. As expected, there is a clear degeneracy between τm and ξmin.
We first identify forbidden regions in the τm-ξmin diagram. A lower limit on τm can be obtained by assuming that the merger-driven perturbations within a region of diameter 1 Mpc cannot last for a timescale shorter than the sound crossing time of that region, which for a galaxy cluster with T ~ 108 K is τsound ≃ 1 Gyr. The values of τm constrained by the observations are always larger than τsound (at least for ξmin ≥ 0.05). An upper bound to τm can be derived by considering the fact that extremely large duration of mergers would make dynamically disturbed all the clusters that are observed at a given cosmic epoch. Specifically, for each cluster of the sample with mass M0 at redshift z0 we derive the values of τm,max, as a function of the progenitor mass ratio ξmin, corresponding to the redshift z for which Eq. (2) gives Nm = 1. This means that a merger event with ξ ≥ ξmin is still producing a disturbance in all clusters of our sample at the epoch of observation. The derived distribution of τm,max, for each value of ξmin, and its mean value are reported in Fig. 2 (blue region and line, respectively); the values of τm constrained by the observations are always smaller than τm,max.
 |
Fig. 3 Ratio between the number of mergers with ηξmin<ξ<ξmin and that with ξ ≥ ξmin for η = 1/2 (bottom black dots) and η = 1/3 (upper red dots). The shadowed region indicates the range of ξmin = 0.1−0.18 constrained by the merger timescale derived from numerical simulations (Tormen et al. 2004). |
Owing to the degeneracy between τm and ξmin in principle large merger timescales can be admitted to explain the observed merger fraction. As already anticipated, however, under this condition our hypothesis of binary mergers can be no longer valid since multiple merger events with mass ratio slightly smaller than ξmin can contribute to the disturbance. To check this, hydrodynamical simulations are necessary to unambiguously relate the merger mass ratio to the cluster morphological parameters, but this is beyond the scope of the paper and deserves future ad hoc simulations. Here we limit ourselves to the following test. In Fig. 3 we use the values (τm, ξmin) constrained in Fig. 2 and show the ratio between the number of mergers with mass ratio in the range ηξmin − ξmin and that of mergers with ξ ≥ ξmin; η = 1/2 and 1/3 are considered. We conclude that the binary approach adopted in our paper is appropriate for merger timescale as large as 3−4 Gyr (those corresponding to ξmin ~ 0.2−0.3).
A possibility to break the degeneracy between τm and ξmin is to adopt values of τm inferred from numerical simulations. A reference timescale is the time necessary for a subcluster to complete an orbit around the centre of mass of the main cluster. Following Tormen et al. (2004) this time can be estimated as 2 × (τa − τp), where τa = τa(ξ) = 1.6(ξ + 0.02)-0.17 Gyr and τp = 0.9 Gyr are the apocentric and pericentric timescale, respectively. This timescale is reported in Fig. 2 (green line) as a function of ξmin. It intercepts the region constrained by the observations for τm ≃ 2.5 Gyr implying ξmin ≃ 0.14. In Tormen et al. (2004), τa and τp are derived from analytic fits to the results of numerical simulations, however the dispersion around the median value is ~0.5 Gyr. As a consequence the merger timescale is constrained as τm ~ 2−3 Gyr, implying ξmin ~ 0.1−0.18. Coming back to Fig. 3, we note that for ξmin ≃ 0.1−0.18 (shadowed region) the number of mergers with mass ratio 1/3 ξmin<ξ<ξmin is about the same as that of mergers with ξ ≥ ξmin and that the number of mergers with 1/2 ξmin<ξ<ξmin is about half of that of mergers with ξ ≥ ξmin. As these mergers are characterized by relatively small mass ratio (ξ ~ 0.03−0.09) and are not numerous, they should have a negligible influence on the cluster morphological parameters, and thus our assumption of binary mergers is reasonably correct.
4.3. Mergers and radio halos
Radio halos are always observed in dynamically disturbed systems, however they are found only in a fraction of the clusters that are classified as merging systems. In this section we follow the approach already adopted in Sect. 4.2 and attempt to constrain the properties that cluster mergers should have to explain the observed fraction of clusters with RHs. In Fig. 2 we report on the region (τm, ξmin) constrained by requiring that the predicted merger fraction matches the observed fraction of clusters with RHs (red shadowed region). At this point we can adopt two main scenarios:
-
(i)
We can assume that the lifetime of a RH is equivalent to thelifetime of the merger-induced disturbances identified byX-ray parameters. Under this hypothesis and since RHsare found in disturbed systems, we can assume that RHsare generated in those systems that have larger mass ratiosamong merging clusters in our sample. In this case we deriveξmin ~ 0.18−0.25 for τm = 2−3 Gyr as constrained in Sect. 4.3.
-
(ii)
We can assume that RHs are statistically generated in all mergers identified in our sample, but they are short-lived compared to the timescale of the merger-induced disturbance. Under this assumption, the lifetime of a RH is simply τRH ~ τm × (fRH/fm) ~ (0.7−0.8)τm, i.e. τRH ~ 1.4−2.4 Gyr for τm = 2−3 Gyr.
4.4. Constraints on ξmin from observations
The mass ratio ξmin is a simple outcome of our procedure that is appropriate for binary mergers, however, this value can be constrained independently by observations of clusters in our sample. Observations of single clusters may be used to derive independent constraints on ξ. We collected information in the literature about the mass ratio of the merging clusters of our sample. These mass ratio are derived from optical or near-IR observations of galaxy clusters through weak lensing analysis or through the study of the galaxy velocity distributions in the clusters (see Table A.1). We found information for seven clusters with RH and for Z5247, which hosts a candidate RH (see Table A.1). For five merging clusters without RH, we looked at the reconstructed convergence maps from weak gravitational lensing (see Table A.1). For these clusters we estimated the mass ratio of the different merging components adopting circular filters on the reconstructed convergence maps with a typical scale that allows us to isolate the different correlated peaks. Owing to the restricted number density of sources beyond the clusters from which the weak lensing signal is measured and and also to the limited resolution of the recovered convergence maps (around the arcmin scale), we stress that in these cases the quoted values represent an upper limit for the mass ratio.
The minimum values of ξ we found for merging clusters in our sample is ~0.14−0.16. If we use these values, ξmin ~ 0.14−0.16 (black rectangular region in Fig. 2), we can derive τm ≃ 2.5−3 Gyr, which is consistent with the reference values of merging timescales derived from results of cosmological simulations (see Fig. 2).
We found some evidence (the information is available only for half of the merging clusters in the sample) that merging clusters with RH are in general characterized by mergers with larger mass ratio than merging clusters without RH: ξ ranges from ξ ~ 0.2−0.25 up to ξ ~1. If we assume ξmin ~ 0.2−0.25 for merging clusters with RH (red rectangular region in Fig. 2), we constrain τRH ~ τm ~ 2.5−3 Gyr, thus in this case the RH lifetime would be comparable with the merger timescale, potentially supporting the scenario (i) in Sect. 4.3.
5. Summary and discussion
Observations establish a clear connection between RHs and mergers (e.g. Cassano et al. 2010), suggesting that RHs can be used as probes of the cluster merging rate with cosmic time. Based on this possibility, in this paper we carry out an exploratory study. By combining the observed fraction of merging clusters and the observed fraction of RH in clusters with the merging rate predicted by fitting formulae based on cosmological simulations, we attempt to infer constraints on merger properties of clusters that appear disturbed in X-rays and of clusters that host RHs.
We use the Planck SZ cluster catalogue (PSZ; Planck Collaboration XXIX 2014) and select a sample of 54 clusters with mass M500 ≳ 6 × 1014M⊙ and redshift 0.2 ≤ z ≤ 0.33. 39 of these clusters have both X-ray and radio information and represent a subsample that can be used to measure the fraction of RHs and that of merging clusters. Mergers in the sample are identified by means of X-ray morphological parameters. We find that all RHs are in merging clusters whereas not all merging clusters host a RH; specifically ~44−51% of the clusters in the sample have a RH, while (using Chandra and XMM-Newton X-ray data) the total fraction of merging clusters is ~62−67%.
We convert the theoretical merging rate per halo (FMB10), which mainly depends on the mass ratio of the two progenitors, ξ = Mi/M1< 1, into merger fraction by adopting a merger timescale τm as a free parameter. The predicted fraction of merging clusters has a strong dependence on ξmin, i.e. the minimum mass ratio of the mergers (larger is ξmin smaller is the number of mergers; Fig. 1) and on τm (larger is τm larger is the expected fraction of merging clusters; Fig. 1). The comparison between the observed and predicted merger fraction allows us to constrain an allowed region in the diagram (ξmin, τm) where there is degeneracy between these two parameters (Fig. 2).
We attempt to break the degeneracy between ξmin and τm:
-
a)
by assuming the merger timescale thatis derived by cosmological simulations(e.g. Tormen et al. 2004),τm ~ 2−3 Gyr, we find that a value ξmin ~ 0.1−0.18 explains the observed merger fraction;
-
b)
by assuming values of ξmin derived through the analysis of optical or near-IR observations of merging clusters in the sample ξmin ~ 0.14−0.16, we find that a merger timescale τm ≃ 2.5−3 Gyr explains the observed merger fraction.
Interestingly, values of the parameters that are obtained independently in a) and b) are consistent.
We find that all clusters with RH in our sample are merging systems but that not all merging clusters host a RH. There are two main possibility to interpret this difference:
-
Scenario 1) RHs have lifetimes similar to the lifetimes ofmerger-driven disturbances in the X-rays, but they are generatedin the merging events with larger mass ratios. Values of massratios derived from optical or near-IR observations of galaxyclusters in the sample (through weak lensing analysis or throughthe study of the velocity distribution of galaxies in the clusters)may support this possibility. Indeed we find thatξ ranges between ~0.2−0.25 and ~1 for RH clusters, whereas values of ξ ~ 0.14−0.16 up to ξ ~ 0.25−0.3 are found for merging clusters without RH. If we assume ξmin ~ 0.2−0.25, we find that τRH ~ τm ≃ 2−2.5 Gyr should be adopted to explain the observed RH fraction.
-
Scenario 2) the lifetime of RHs (τRH) is shorter than the timescale of merger-induced disturbance in the X-rays with τRH ~ τm × (fRH/fm) ~ (0.7−0.8)τm. In this case assuming no difference between the mass ratio of clusters with and without RH, we find τRH ~ 1.4−2.4 Gyr.
In general, we note that both different timescales (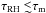 ; i.e. Scenario 2) and mass ratios (i.e. Scenario 1) are likely to govern the statistics of giant RHs.
; i.e. Scenario 2) and mass ratios (i.e. Scenario 1) are likely to govern the statistics of giant RHs.
This study deals with several limitations and is based on simplified assumptions:
-
(i)
The observed fraction of merging clusters is derived bymeasuring the fraction of clusters with significant X-raydisturbance, this means that we are sensitive only to mergerepisodes with relevant mass accretion.
-
(ii)
While observationally, the fraction of merging clusters is derived by measuring the morphological disturbances of clusters in the sample on a circular region of ~1 Mpc (diameter), the theoretical merging rate (FBMI10) and hence the merger fraction is derived by considering all the infalling halos within the virial radius (~2−3 Mpc) of the main clusters. However, it should be mentioned that numerical simulations allow us to argue that for ξ>~0.1 the two rates should be comparable (see Sect. 4 and Tormen et al. 2004, for more details).
-
(iii)
We assume that the X-ray disturbance that we measure in the X-rays is mainly caused by a binary merger event, specifically by that with larger mass ratio. Thus in deriving the expected merger fraction from theoretical fitting formulae, we attempt to select the values of ξmin that matches the merger fraction assuming that mergers with smaller mass ratio do not play a role. In principle, however, in the timescale of the merger-induced disturbance, τm, clusters might experience multiple merger episodes with slightly lower mass ratio that can contribute to the morphological disturbance. We show that for typical merger timescale, constrained by simulations and the observed values of ξmin, the contribution of these slightly minor mergers is not expected to be relevant. Clearly, ad hoc simulations and follow-up studies are necessary to establish a more solid connection between mergers and X-ray disturbances.
It is currently thought that giant RHs are generated as a consequence of the acceleration of relativistic electrons by the MHD turbulence stirred up in the ICM by cluster-cluster mergers (e.g. Brunetti & Jones 2014). In this framework scenario 1) discussed above implies that the timescale of the X-ray merger-induced disturbances and that of the turbulent stirring of the ICM by cluster mergers in the central 1 Mpc (diameter) region are similar. These timescales are shorter than the dynamical timescale of the merger, which is defined as the time interval between the moment when the centre of the less massive cluster first crosses the virial radius of the main one and the moment when the final system reaches a relaxed state. As a consequence, in this scenario RHs are not switched on at the beginning of the merger but after a time period that is necessary for the infalling subcluster to generate ICM turbulence in the central Mpc region (~0.9 Gyr; see Sect. 4.1). Since gravity drives mergers between galaxy clusters, it is expected that the turbulent energy budget should scale with the cluster thermal energy. As a consequence, very massive and merging systems should be the natural host of Mpc-scale RHs (e.g. Cassano & Brunetti 2005; Vazza et al. 2006, 2011; Paul et al. 2011). In line with these expectations, we find fRH ≃ 44−51% for clusters with M500>~6 × 1014M⊙ at 0.2<~z<~0.33 (see also Sommer & Basu 2014; Cuciti et al. 2015). Also the mass-ratio may play a role because major mergers are more powerful events and have the potential to generate more turbulence in larger volumes. For instance, using a semi-analytic approach, Cassano & Brunetti (2005) showed that, for a given cluster mass, the ratio between the turbulent energy and cluster thermal energy increases with increasing ξ, becoming smaller than 5% for ξ< 0.2 (see also Fig. 3 in Cassano & Brunetti 2005). This can explain the absence of RHs in clusters undergoing merger events with mass ratio ξ< 0.2.
On the other hand, scenario 2) would imply that mergers drive turbulent re-acceleration of relativistic particles in the ICM on a timescale that is ~0.7−0.8 shorter than the timescale duration of the morphological disturbances in the X-rays. Lagrangian (SPH) simulations of two colliding idealized clusters have been used to study the time evolution of the RH emission during mergers (Donnert et al. 2013). These simulations predict shortly living RHs that are generated after the first core passage and fade within ≲1 Gyr timescale. In fact, this timescale is shorter than that constrained assuming the scenario 2), however this can be due to the idealized set-up of the model and it is very likely that the lifetime of a RH is significantly larger in a cosmological contest. High resolution cosmological simulations also show an increase of the turbulence (both compressible and incompressible) and of the acceleration rate during major mergers (Miniati 2015). These simulations add also important information as they allow us to evaluate the ratio τRH/τm under different assumptions about the ICM microphysics. This is an important point as it implies that statistical studies of the connection between RHs and merging rates combined with numerical simulations also have the potential to put fundamental constraints on the ICM microphysics and acceleration mechanisms (Miniati 2015; Brunetti 2016).
To conclude, while it is clear that massive and merging clusters are the natural hosts of giant RHs, the presence of merging clusters without RHs pose fundamental questions: is there a role of the merger mass ratio in the formation of a giant RH? What is the lifetime of a RH with respect to the merger timescale? Is the RH lifetime tied by the microphysics of the ICM?
Our exploratory study has shown that meaningful values of the merger parameters can be derived combining the observed fraction of RHs and the theoretical merging rate in the ΛCDM model. More specifically our results seem to suggest that the mass-ratio may play a role in the generation of RHs, however this result is not conclusive and we cannot conclude whether scenario 1) is favored with respect to scenario 2), or whether mass ratios and different timescales both play a role. An important step forwards to address the lifetime of RHs and the connection with mergers can be achieved by increasing the statistics of merging clusters without RHs. Our study is limited by current data that allow us to infer these constraints only in very massive clusters at relatively low redshifts. In fact in our study we use the currently most complete mass-selected sample of galaxy clusters with radio and X-ray information that, however, is limited to very massive (M500>~6 × 1014M⊙) and relatively nearby systems (z ≃ 0.2−0.33). Based on energy arguments the occurrence of “radio quiet” merging clusters should increase at smaller masses (or at higher redshifts or small mass-ratio mergers; e.g. Cassano et al. 2006). Thus extending the samples of clusters at smaller masses (or at higher redshift) is necessary to obtain stronger constraints on the physical conditions necessary to generate RHs. This will be possible with the upcoming new generation of radio facilities, such as LOFAR, ASKAP, and MeerKAT up to SKA1 (e.g. Cassano et al. 2015). Future surveys also offer the possibility of exploring the frequency dependence of the occurrence of RHs in galaxy clusters. Current models predict the presence of RHs with ultra-steep radio spectra (USSRHs) especially in low massive (or high-z) galaxy clusters (e.g. Cassano et al. 2006; Brunetti et al. 2008). As a consequence, it is possible that some of the merging clusters without RHs actually host USSRHs and observations with LOFAR (and SKA1-LOW in the future) will be crucial to check this possibility.
The values of M500 in the PSZ catalogue are obtained from Y500 as described in Sect. 7.2.2 in Planck Collaboration XXIX (2014).
To compare the observed merger fraction with theoretical expectations, we convert the M500 to virial masses, Mvir, by assuming a NFW profile (e.g. Navarro et al. 1997) for the dark matter halos and the concentration-mass relation in Duffy et al. (2008); see Appendix A in Ettori et al. (2010). Both values of M500 and Mvir are reported in Table A.1.
Acknowledgments
We thank the anonymous referee for his/her valuable report. S.E. acknowledges support from ASI-INAF No. I/009/10/0 and NuSTAR-ASI/INAF No. I/037/12/0. G.B. and R.C. acknowledge partial support from PRIN-INAF 2014. G.B. acknowledges support from the Alexander von Humboldt Foundation. We thank K. Dolag for useful discussion and V. Cuciti for providing the morphological parameters of five clusters (denoted with ∗∗∗ in Table A.1).
References
- Bacchi, M., Feretti, L., Giovannini, G., & Govoni, F. 2003, A&A, 400, 465 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bardeau, S., Soucail, G., Kneib, J.-P., et al. 2007a, A&A, 470, 449 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barrena, R., Boschin, W., Girardi, M., & Spolaor, M. 2007b, A&A, 467, 37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barrena, R., Girardi, M., Boschin, W., De Grandi, S., & Rossetti, M. 2014, MNRAS, 442, 2216 [NASA ADS] [CrossRef] [Google Scholar]
- Bernardi, G., Venturi, T., Cassano, R., et al. 2016, MNRAS, 456, 1259 [NASA ADS] [CrossRef] [Google Scholar]
- Basu, K. 2012, MNRAS, 421, 112 [Google Scholar]
- Böhringer, H., Pratt, G. W., Arnaud, M., et al. 2010, A&A, 514, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonafede, A., Intema, H., Brüggen, M., et al. 2015, MNRAS, 454, 3391 [NASA ADS] [CrossRef] [Google Scholar]
- Boschin, W., Girardi, M., Spolaor, M., & Barrena, R. 2006, A&A, 449, 461 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boylan-Kolchin, M., Springel, V., White, S. D. M., Jenkins, A., & Lemson, G. 2009, MNRAS, 398, 1150 [NASA ADS] [CrossRef] [Google Scholar]
- Brüggen, M., Bykov, A., Ryu, D., & Röttgering, H. 2012, Space Sci. Rev., 166, 187 [Google Scholar]
- Brüggen, M., & Vazza, F. 2015, in Magnetic Fields in Diffuse Media (Berlin: Springer-Verlag), 407, 599 [Google Scholar]
- Brunetti, G. 2016, Plasma Physics and Controlled Fusion, 58, 014011 [Google Scholar]
- Brunetti, G., & Jones, T. W. 2014, Int. J. Mod. Phys. D, 23, 1430007 [Google Scholar]
- Brunetti, G., & Lazarian, A. 2007, MNRAS, 378, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Brunetti G., Venturi, T., Dallacasa, D., et al. 2007, ApJ , 670, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Brunetti, G., Giacintucci, S., Cassano, R., et al. 2008, Nature, 455, 944 [NASA ADS] [CrossRef] [Google Scholar]
- Brunetti G., Cassano, R. Dolag, K., & Setti, G. 2009, A&A, 507, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buote, D. A., & Tsai, J. C. 1995, ApJ, 452, 522 [NASA ADS] [CrossRef] [Google Scholar]
- Cassano, R., & Brunetti, G. 2005, MNRAS, 357, 1313 [NASA ADS] [CrossRef] [Google Scholar]
- Cassano, R., Brunetti, G., & Setti, G. 2006, MNRAS, 369, 1577 [NASA ADS] [CrossRef] [Google Scholar]
- Cassano, R., Ettori, S., Giacintucci, S., et al. 2010, ApJ, 721, L82 [NASA ADS] [CrossRef] [Google Scholar]
- Cassano, R., Ettori, S., Brunetti, G., et al. 2013, ApJ, 777, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Cassano, R., Bernardi, G., Brunetti, G., et al. 2015, Proc. of Conf. on Advancing Astrophysics with the Square Kilometre Array (AASKA14), 73 [Google Scholar]
- Conselice, C. J. 2014, ARA&A, 52, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Conselice, C. J., Bershady, M. A., Dickinson, M., & Papovich, C. 2003, AJ, 126, 1183 [NASA ADS] [CrossRef] [Google Scholar]
- Cuciti, V., Cassano, R., Brunetti, G., et al. 2015, A&A, 580, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dahle, H., Kaiser, N., Irgens, R. J., Lilje, P. B., & Maddox, S. J. 2002, ApJS, 139, 313 [NASA ADS] [CrossRef] [Google Scholar]
- De Boni, C., Serra, A. L., Diaferio, A., Giocoli, C., & Baldi, M. 2016, ApJ, 818, 188 [NASA ADS] [CrossRef] [Google Scholar]
- De Propris, R., Liske, J., Driver, S. P., Allen, P. D., & Cross, N. J. G. 2005, AJ, 130, 1516 [NASA ADS] [CrossRef] [Google Scholar]
- Diaferio, A. 2015 ArXiv e-print [arXiv:1502.01195] [Google Scholar]
- Donnert, J., Dolag, K., Brunetti, G., & Cassano, R. 2013, MNRAS, 429, 3564 [NASA ADS] [CrossRef] [Google Scholar]
- Duffy, A. R., Schaye, J., Kay, S. T., & Dal la Vecchia, C. 2008, MNRAS, 390, L64 [NASA ADS] [CrossRef] [Google Scholar]
- Ettori, S., Gastaldello, F., Leccardi, A., et al. 2010, A&A, 524, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fakhouri, O., & Ma, C.-P. 2008,MNRAS, 386, 577 [Google Scholar]
- Fakhouri, O., Ma, C.-P., & Boylan-Kolchin, M. 2010, MNRAS, 406, 2267 [NASA ADS] [CrossRef] [Google Scholar]
- Feretti, L., Fusco-Femiano, R., Giovannini, G., & Govoni, F. 2001, A&A, 373, 106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feretti, L., Giovannini, G., Govoni, F., & Murgia, M. 2012, A&ARv, 20, 54 [Google Scholar]
- Giacintucci, S., Venturi, T., Cassano, R., Dallacasa, D., & Brunetti, G. 2009, ApJ, 704, L54 [NASA ADS] [CrossRef] [Google Scholar]
- Giacintucci, S., Dallacasa, D., Venturi, T., et al. 2011, A&A, 534, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giacintucci, S., Kale, R., Wik, D. R., Venturi, T., & Markevitch, M. 2013, ApJ, 766, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Giovannini, G., Feretti, L., Govoni, F., Murgia, M., & Pizzo, R. 2006, Astron. Nachr., 327, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Giocoli, C., Moreno, J., Sheth, R. K., & Tormen, G. 2007, MNRAS, 376, 977 [NASA ADS] [CrossRef] [Google Scholar]
- Giocoli, C., Tormen, G., & Sheth, R. K. 2012, MNRAS, 422, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Govoni, F., Enßlin, T. A., Feretti, L., & Giovannini, G. 2001, A&A, 369, 441 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Govoni, F., Murgia, M., Giovannini, G., Vacca, V., & Bonafede, A. 2011, A&A, 529, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guo, Q., & White, S. D. M. 2008, MNRAS, 384, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Cox, T. J., Hernquist, L., et al. 2013, MNRAS, 430, 1901 [NASA ADS] [CrossRef] [Google Scholar]
- Jian, H.-Y., Lin, L., & Chiueh, T. 2012, ApJ, 754, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Kale, R., & Parekh, V. 2016, MNRAS, 459, 2940 [NASA ADS] [CrossRef] [Google Scholar]
- Kale, R., Venturi, T., Giacintucci, S., et al. 2013, A&A, 557, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kale, R., Venturi, T., Giacintucci, S., et al. 2015, A&A, 579, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kravtsov, A. V., & Borgani, S. 2012, ARA&A, 50, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Kulsrud, R. M., Cen, R., Ostriker, J. P., & Ryu, D. 1997, ApJ, 480, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Landry, D., Bonamente, M., Giles, P., et al. 2013, MNRAS, 433, 2790 [NASA ADS] [CrossRef] [Google Scholar]
- Lemze, D., Postman, M., Genel, S., et al. 2013, ApJ, 776, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Lotz, J. M., Primack, J., & Madau, P. 2004, AJ, 128, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Lotz, J. M., Jonsson, P., Cox, T. J., et al. 2011, ApJ, 742, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Mahdavi, A., Hoekstra, H., Babul, A., Balam, D. D., & Capak, P. L. 2007, ApJ, 668, 806 [NASA ADS] [CrossRef] [Google Scholar]
- Mantz, A. B., Allen, S. W., Morris, R. G., et al. 2015, MNRAS, 449, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Miniati, F. 2015, ApJ, 800, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Mohr, J. J., Fabricant, D. G., & Geller, M. J. 1993, ApJ, 413, 492 [NASA ADS] [CrossRef] [Google Scholar]
- McBride, J., Fakhouri, O., & Ma, C.-P. 2009, MNRAS, 398, 1858 [NASA ADS] [CrossRef] [Google Scholar]
- Moreno, J., Giocoli, C., & Sheth, R. K. 2008, MNRAS, 391, 1729 [NASA ADS] [CrossRef] [Google Scholar]
- Murgia, M., Govoni, F., Markevitch, M., et al. 2009, A&A, 499, 679 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Norman, M. L., & Bryan, G. L. 1999, The Radio Galaxy Messier 87, 530, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Okabe, N., & Umetsu, K. 2008, PASJ, 60, 345 [NASA ADS] [Google Scholar]
- Okabe, N., Takada, M., Umetsu, K., Futamase, T., & Smith, G. P. 2010, PASJ, 62, 811 [NASA ADS] [Google Scholar]
- Parekh, V., van der Heyden, K., Ferrari, C., Angus, G., & Holwerda, B. 2015, A&A, 575, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Patton, D. R., Carlberg, R. G., Marzke, R. O., et al. 2000, ApJ, 536, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Paul, S., Iapichino, L., Miniati, F., Bagchi, J., & Mannheim, K. 2011, ApJ, 726, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XX. 2014, A&A, 571, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXIX. 2014, A&A, 571, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poole, G. B., Fardal, M. A., Babul, A., et al. 2006, MNRAS, 373, 881 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, A. D., Hunstead, R. W., Lemonon, L., & Pierre, M. M. 1999, MNRAS, 302, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Ricker, P. M., & Sarazin, C. L. 2001, ApJ, 561, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Rossetti, M., Eckert, D., Cavalleri, B. M., et al. 2011, A&A, 532, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, J.S., Rosati, P., Tozzi, P., Böhringer, H., Ettori, S., & Bignamini, A. 2008, A&A, 483, 35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sommer, M. W., & Basu, K. 2014, MNRAS, 437, 2163 [NASA ADS] [CrossRef] [Google Scholar]
- Soucail, G. 2012, A&A, 540, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Springel, V., White, S. D. M., Jenkins, A., et al. 2005, Nature, 435, 629 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Subramanian, K., Shukurov, A., & Haugen, N. E. L. 2006, MNRAS, 366, 1437 [NASA ADS] [CrossRef] [Google Scholar]
- Tormen, G., Moscardini, L., & Yoshida, N. 2004, MNRAS, 350, 1397 [NASA ADS] [CrossRef] [Google Scholar]
- Vazza, F., Tormen, G., Cassano, R., Brunetti, G., & Dolag, K. 2006, MNRAS, 369, L14 [NASA ADS] [Google Scholar]
- Vazza, F., Brunetti, G., Gheller, C., Brunino, R., & Brüggen, M. 2011, A&A, 529, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Venturi, T., Giacintucci, S., Brunetti, G., et al. 2007, A&A, 463, 937 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Venturi, T., Giacintucci, S., Dallacasa, D., et al. 2008, A&A, 484, 327 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Venturi, T., Giacintucci, G., Dallacasa, D., et al. 2011, MNRAS, 414, L65 [NASA ADS] [CrossRef] [Google Scholar]
- van den Bosch, F. C. 2002, MNRAS, 331, 98 [Google Scholar]
- Wen, Z. L., & Han, J. L. 2013, MNRAS, 436, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, Z. S., Han, J. L., & Wen, Z. L. 2015, ApJ, 813, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Wittman, D., Dawson, W., & Benson, B. 2014, MNRAS, 437, 3578 [NASA ADS] [CrossRef] [Google Scholar]
- Ziparo, F., Braglia, F. G., Pierini, D., et al. 2012, MNRAS, 420, 2480 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Additional tables
Cluster properties.
Cluster morphological parameters.
In Table A.1 we report the main properties of the 54 clusters belonging to our sample, specifically: Col. (1) cluster name; Col. (2) cluster redshift; Col. (3) M500 from Planck Collaboration XXIX (2014); Col. (4) virial mass, Mvir (see Sect. 2); Col. (5) information about the presence of diffuse radio emission; Col. (6) cluster dynamical status; Col. (7) mass ratio, when available.
The first two panels contain the 39 clusters with both radio and X-ray information (clusters with RHs are in the second panel); the third panel contains clusters with X-ray information; the three clusters in the forth panel are those without radio and X-ray information. In Table A.2 we report the morphological parameters derived for the 41 clusters with Chandra X-ray data (see Sect. 2): P3/P0, w and c, with their inferior and superior values ([P3/P0 − 1σ, P3/P0 + 1σ], and so on for the others).
All Tables
All Figures
 |
Fig. 1 Predicted average merger fraction for clusters in the sample as a function of ξmin, assuming three different values for the merger timescale τm = 1,2,3 Gyr (from bottom to top). The observed merger fraction and RH fraction are also reported (shadowed regions). |
| In the text | |
 |
Fig. 2 Allowed regions of parameters (ξmin, τm) constrained by requiring that the observed merger fraction (black region) and RH fraction (red regions) match those predicted by theory (these regions account for the uncertainty in the observed fraction). For each ξmin the maximum allowed value of τm, τm,max (blue region with arrows; see Sect. 4.2) and a lower limit to τm (horizontal blue dashed line, see Sect. 4.2) are also shown. The merger timescale constrained by cosmological simulation is also reported (green line; Tormen et al. 2004). Ranges of ξmin constrained through optical/near-IR observations of galaxy clusters in the sample (see Sect.4.4) are shown for merging clusters (black rectangular region ) and for clusters with RHs (red rectangular region). These values of ξmin both constrain τm ~ τRH ~ 2.5−3 Gyr; this is also show in the figure. |
| In the text | |
 |
Fig. 3 Ratio between the number of mergers with ηξmin<ξ<ξmin and that with ξ ≥ ξmin for η = 1/2 (bottom black dots) and η = 1/3 (upper red dots). The shadowed region indicates the range of ξmin = 0.1−0.18 constrained by the merger timescale derived from numerical simulations (Tormen et al. 2004). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{equation} \label{Eq.MR} \frac{{\rm d}N_{\rm m}}{{\rm d}\xi {\rm d}z} (M,\xi,z)=A\,\left(\frac{M}{10^{12}~M_{\odot}}\right)^{\alpha}\,\xi^{\beta}\exp\left[\left(\frac{\xi}{\tilde{\xi}}\right)^\gamma \right]\,(1+z)^\eta \,, \end{equation}](/articles/aa/full_html/2016/09/aa28414-16/aa28414-16-eq81.png)