| Issue |
A&A
Volume 593, September 2016
|
|
|---|---|---|
| Article Number | A36 | |
| Number of page(s) | 13 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201628083 | |
| Published online | 06 September 2016 | |
Constraints on CEMP-no progenitors from nuclear astrophysics
1 Geneva Observatory, University of
Geneva, Maillettes
51, 1290 Sauverny, Switzerland
e-mail: arthur.choplin@unige.ch
2 Leibniz-Institut für Astrophysik
Potsdam, An der Sternwarte
16, 14482
Potsdam,
Germany
Received:
6
January
2016
Accepted:
7
June
2016
Context. The CEMP-no stars are long-lived small mass stars presenting a very low iron content and overabundances of carbon with no sign or only very weak signs of s- or r-elements. Although the origin of this abundance pattern is still a matter of debate, it was very likely inherited from a previous massive star, which we call the source star.
Aims. We rely on a recent classification of CEMP-no stars arguing that some of them are made of a material processed by hydrogen burning that was enriched in products of helium burning during the nuclear life of the source star. We examine the possibility of forming CEMP-no stars with this material.
Methods. We study the nucleosynthesis of the CNO cycle and the Ne-Na Mg-Al chains in a hydrogen burning single zone while injecting the helium burning products 12C, 16O, 22Ne, and 26Mg. We investigate the impact of changing density, temperature and the injection rate. The nuclear reaction rates involving the creation and destruction of 27Al are also examined.
Results. 14N, 23Na, 24Mg, and 27Al are formed when injecting 12C, 16O, 22Ne, and 26Mg in the hydrogen burning zone. The 12C/13C ratio is constant under various conditions in the hydrogen burning zone. The predicted [Al/Fe] ratio varies up to ~ 2 dex depending on the prescription used for the reaction rates involving 27Al.
Conclusions. The experiments we carried out support the view that some CEMP-no stars are made of a material processed by hydrogen burning that comes from a massive star experiencing mild to strong rotational mixing. During its burning, this material was likely enriched in helium burning products. No material coming from the carbon-oxygen rich core of the source star should be added to form the daughter star, otherwise the 12C/13C ratio would be largely above the observed range of values.
Key words: nuclear reactions, nucleosynthesis, abundances / stars: chemically peculiar / stars: abundances
© ESO, 2016
1. Introduction
The content of iron at the surface of a star is often used as an indication of the chemical enrichment of its environment. A very small amount of iron relative to the sun indicates a region similar to the early universe where only few nucleosynthetic events occurred. A way to obtain new clues on stars in the early universe is then to examine the most iron deficient objects. Carbon-enhanced metal-poor stars (CEMP) are a subclass of iron deficient stars that have an excess of carbon relative to the sun and also an excess of oxygen and nitrogen in general. Although it can vary a bit from one author to another, the two common criteria defining a CEMP are1 [Fe/H] <−1.0 and [C/Fe] >0.7 (Aoki et al. 2007). The range of [C/Fe] covers ~3.5 dex, from [C/Fe] =0.7 to [C/Fe] =4.26 for HE1327-2326 (Norris et al. 2013; Allen et al. 2012). The frequency of CEMP seems to rise toward lower [Fe/H] (Lee et al. 2013), but also with increasing distance from the Galactic plane (Frebel et al. 2006) or moving from inner to outer halo (Carollo et al. 2012). The so-called CEMP-no subclass is characterized by its low content in s- or r-elements, contrary to the other sublasses of CEMP stars: CEMP-s, CEMP-r, and CEMP-r/s (Beers & Christlieb 2005). CEMP-no stars are of particular interest since they dominate at [Fe/H] ≲−3 (Aoki 2010; Norris et al. 2013).
Among the scenarios explored to explain CEMP-no stars, we note the “spinstar” scenario (Meynet et al. 2006, 2010; Hirschi 2007; Chiappini 2013; Maeder et al. 2015) and the “mixing and fallback” scenario (Umeda & Nomoto 2002, 2005; Tominaga et al. 2014). The latter explains CEMP-no with a model of faint supernovae from Pop III stars with mixing and fallback. The mixing considered in these models occurs just before or during the explosion. The zone of mixing and the mass cut2 are free parameters of the models adjusted differently in each star to reproduce observed abundance patterns of CEMP-no stars.
According to the spinstar scenario, CEMP-no form in a region previously enriched by material that comes from low metallicity, rotating massive stars. During their nuclear lifetimes, spinstars experience mass loss and strong mixing triggered by rotation. As developed in Maeder et al. (2015), although they are different, these two models appear more complementary than contradictory. Processes like strong internal mixing in the source star, winds, or faint supernova may all have happened. Recently, Takahashi et al. (2014) has presented results based on rotating models with strong fallback (but no mixing in the sense of the works by Umeda & Nomoto) and tried to deduce the initial rotation of the source stars from comparisons with observed abundance patterns from three CEMP-no stars.
 |
Fig. 1 Schematic view of the “back and forth” process at work in the spinstar. It occurs during the core helium burning phase and it is an exchange of chemical species between the helium burning core and the hydrogen burning shell. |
Maeder et al. (2015) proposed the idea that the variety of observed ratios is likely due to material being processed back and forth by hydrogen and helium burning regions in the spinstar. In other words, these two burning regions are exchanging material between them. These exchanges are triggered by the rotational mixing. In a first step, the helium burning products diffuse into the hydrogen burning shell. More specifically, 12C and 16O synthesized in the helium core diffuse in the hydrogen burning shell, boosting the CNO cycle and creating primary 14N and 13C (see left panel of Fig. 1). In turn, the products of the hydrogen burning shell (among them 14N) diffuse back into the helium core. The isotope 22Ne is synthesized through the nuclear chain 14N(α,γ)18F(,e+νe)18O(α,γ)22Ne. The isotope 26Mg can also be synthesized thanks to the reaction 22Ne(α,γ)26Mg (middle panel of Fig. 1). Some 25Mg can also be created through the reaction 22Ne(α,n)25Mg. Neon and magnesium can enter the hydrogen burning shell again, boosting the Ne-Na and Mg-Al chains and therefore creating sodium and aluminium (right panel of Fig. 1). Through these back and forth exchanges between the hydrogen and helium burning regions, a series of isotopes can be formed. The abundances can vary a lot depending on the strength and number of these exchanges and thus such models can easily account for the variety of the abundance ratios observed at the surface of CEMP-no stars. For a given initial mass and rotation rate, the rotational mixing responsible for the exchanges described above is stronger at low metallicity. This effect is mainly due to the higher compactness of low metallicity stars (Maeder & Meynet 2001).
Type (MS if Teff ≥ 5500 K and log g ≥ 3.25, RGB otherwise), class, and abundance data for the CEMP-no stars considered in this work.
Putting aside the complexity of stellar models, we realize in this work simple nuclear experiments in order to illustrate the idea of Maeder et al. (2015) and to constrain the conditions needed in the source stars that would lead to the appropriate nucleosynthesis required to form CEMP-no stars. We study the impact of injecting 12C, 16O, 22Ne, and 26Mg in a hydrogen burning single zone at typical temperatures and densities of the hydrogen burning shell of a 20−60M⊙ source star model at very low metallicity (Z = 10-5). Different sets of nuclear rates are tested for the three main reactions involving 27Al. We compare our results with a subsample of five CEMP-no stars which have a similar metallicity to that considered in our models and which are, according to Maeder & Meynet (2015), made of a material processed by hydrogen burning coming from the source star. We note that the active hydrogen burning shell in the source star can be enriched in products of helium burning, as explained previously. Although limited, these numerical experiments, by focusing mainly on the nucleosynthesis of the problem, allow us to explore just what nuclear physics can do and how the results are sensitive to only some nuclear aspects of the problem. As we shall see, even these very simple numerical experiments allow us to obtain very interesting constraints on the sources of CEMP-no stars, constraints that are particularly strong since they are based on the most simple numerical experiments that we can imagine doing.
In Sect. 2, we recall briefly the classification of CEMP-no stars made by Maeder & Meynet (2015) and select the subsample of CEMP-no stars used in this work. The experiments we carried out are described in Sect. 3 and the results obtained in Sect. 4. Sections 5 and 6 are dedicated to a discussion about the 12C/13C ratio, the lithium and aluminium abundances. In Sect. 7, we discuss the possible astronomical origin of the CEMP-no stars considered. Conclusions are given in Sect. 8.
2. CEMP-no stars in classes 2 and 4
Maeder & Meynet (2015) provided a method for classifying the abundance patterns observed at the surface of CEMP-no stars based on two main ideas: the first is that some material can be exchanged between the hydrogen and helium burning regions inside the star. As noted in the previous section, the hydrogen burning reactions can transform the material enriched in helium burning products. This will boost the abundance of some isotopes, for instance 14N. This 14N can in turn diffuse into the helium burning region where it is transformed into 22Ne, and 22Ne can migrate into the hydrogen burning region, being transformed (at least in part) into 23Na. Focusing on hydrogen burning regions, we speak of secular mixing of first order when the CNO cycle processes material enriched by the normal products of helium burning (typically C and O), and of second order when the nuclear reactions process material enriched in helium burning products resulting from material that was enriched in hydrogen burning products (typically 22Ne, resulting from α-captures on 14N). Similar definitions can be made for the helium burning region. Different families of abundance patterns resulting from hydrogen and helium burning and secular mixing of various orders can result from these back and forth exchanges.
The second idea is that a second type of mixing can be envisaged; this one occurs between the stellar ejecta when the nuclear reactions have stopped. We call this type stellar ejecta mixing. Typically, some CEMP-no stars show signs of being made of material processed by hydrogen and helium burning and then mixed once ejected into the ISM. The material processed by hydrogen burning can result from secular mixing of various orders.
Using these lines of reasoning, Maeder & Meynet (2015) divided the CEMP-no class in five subclasses.
-
Class 0: the CEMP-no is made of a material processed byhydrogen burning, but not enriched in helium burning products(no secular mixing, no mixing of the ejecta).
-
Class 1: the CEMP-no is made of a material processed by helium burning, but not enriched in hydrogen burning products (no secular mixing, no mixing of the ejecta).
-
Class 2: the CEMP-no is made of a material processed by hydrogen burning enriched in the normal products of helium burning (secular mixing of first order, no mixing of the ejecta).
-
Class 3: the CEMP-no is made of a mixture of ejecta involving material processed by both hydrogen and helium burning. The material processed by hydrogen burning results from a secular mixing of first order, and the material processed by helium burning results from a secular mixing of second order (which means that the material processed by helium burning has been enriched by hydrogen burning products that have transformed helium burning products). For instance, large amounts of 14N and 13C coming from the transformation of 12C and 16O, enter the helium core by mixing. Then, successive α-captures on 14N create some 22Ne and 25,26Mg.
-
Class 4: the CEMP-no is made of a material processed by hydrogen burning (no mixing of the ejecta) resulting from secular mixing of second order. This means that the hydrogen burning transforms material that was processed two times by helium burning. Typically, neon and magnesium enter the hydrogen shell again, boosting the Ne-Na and Mg-Al chains.
In each of the classes, refinements are made depending on how advanced the nuclear burning is. For instance, the Mg-Al chain may have acted to a greater or lesser degree in the source star so that more or less aluminium has been be created. A “+” after the class number indicates a material that is more processed. A material that is even more processed is indicated with “++” after the class number. We see that classes 1 and 3 are, at least partly, made of helium burning products while classes 0, 2, and 4 are made of hydrogen burning products. Maeder & Meynet (2015) attributed a class to 30 out of 46 CEMP-no stars: 4 belonging to class 2, 17 to class 3, and 9 to class 4.
In the present work, we focus on CEMP-no stars in classes 0, 2, and 4, i.e. made of a material processed by hydrogen burning that was eventually enriched in helium burning products. A characteristic shared by both stars in classes 2 and 4 (to date there are no observed CEMP-no in class 0) is a relatively low 12C/13C ratio, between 2 and 12 with a mean of 5.1. This value is characteristic of the CNO processing. The other CEMP-no stars generally have a higher 12C/13C (up to 50). Part of the helium burning region (12C-rich and 13C-poor) expelled by the source star is used to form classes 1 and 3, which explains the higher 12C/13C ratios for class 3 CEMP-no stars (there are no observed CEMP-no in class 1).
Our subsample is finally made of 13 CEMP-no stars in classes 2 and 4 with a mean [Fe/H] of −3.9. Table 1 gives the type, the class, and the abundance data for the sample of CEMP-no stars considered in this work. We note the class 2+Na for HE 0057-5959; “Na” stands because of the high [Na/Fe] ratio. The interpretation is the following: owing to a sufficiently high temperature, a significant amount of 20Ne was synthesized in the helium burning core of the source star. Some of it diffused in the hydrogen burning shell, boosting the Ne-Na chain and therefore creating some 23Na.
We note that among those 13 CEMP-no stars, 5 are dwarfs (MS, cf. Table 1) and 8 are giants (RGB, cf. Table 1) according to the following criteria: the stars with Teff ≥ 5500 K and log g≥ 3.25 are dwarfs, the others are giants. The RGB CEMP may have undergone a dredge-up event, modifying their surface abundances. Such a dredge-up decreases the 12C surface abundances and increases the 13C and 14N surface abundance. The abundances of O, Ne, Na, Mg, and Al elements will not change since the temperature inside the hydrogen burning shell of such a low mass star is likely too low to activate the ON, Ne-Na, and Mg-Al cycles. If we look at the plots [C/Fe] and [N/Fe] versus log g for the observed CEMP-no stars (cf. Choplin et al. 2016, Fig. 1) we see that the dispersion of the carbon and nitrogen abundances with respect to iron are quite similar for MS and RGB stars. This means that the effect of the first dredge-up does not change the abundance of carbon and nitrogen significantly with respect to the changes related to the dispersion of the initial abundances (about 4 dex). Based on stellar evolution models, Placco et al. (2014) have determined a correction ![\begin{equation} \Delta \rm [C/Fe] = [C/Fe]_{\rm ini} - [C/Fe]_{\mathrm{after \, 1DUp}} \end{equation}](/articles/aa/full_html/2016/09/aa28083-16/aa28083-16-eq37.png) (1)to apply to the [C/Fe] ratio of 505 metal-poor stars in order to recover their initial [C/Fe]. This correction corresponds to the effect of the first dredge-up (if any). Any dredge-up would decrease [C/Fe] so that Δ[C/Fe] ≥0. We note that Δ[C/Fe] =0 for MS CEMP since they likely did not experience the first dredge-up. Five out of the eight RGB CEMP considered here belong to this sample; three have Δ[C/Fe] <0.1, one Δ[C/Fe] =0.31 (CS 29498-043), and one Δ[C/Fe] =0.74 (CS 22949-037). These corrections are small compared to the observed range of [C/Fe] ratios.
(1)to apply to the [C/Fe] ratio of 505 metal-poor stars in order to recover their initial [C/Fe]. This correction corresponds to the effect of the first dredge-up (if any). Any dredge-up would decrease [C/Fe] so that Δ[C/Fe] ≥0. We note that Δ[C/Fe] =0 for MS CEMP since they likely did not experience the first dredge-up. Five out of the eight RGB CEMP considered here belong to this sample; three have Δ[C/Fe] <0.1, one Δ[C/Fe] =0.31 (CS 29498-043), and one Δ[C/Fe] =0.74 (CS 22949-037). These corrections are small compared to the observed range of [C/Fe] ratios.
In addition, because the CNO equilibrium value of 12C/13C is obtained at the surface of the MS stars, this implies that such low values, at least in these stars, cannot be due to a dredge-up event. Moreover, the highest 12C/13C belong to HE 1419-1324, a RGB CEMP, showing that the RGB feature is not necessarily associated with a low 12C/13C ratio, as expected by the effect of the dredge-up. Correcting the CNO abundances of the evolved CEMP-no stars is of course important in general, but in the framework of the present work we focus on the range of observed abundances rather than of individual stars, and hence these small corrections have no impact on our conclusions.
3. Presentation of the experiment
The conducted experiment consists in injecting products synthesized in the helium burning core of massive stars like 12C, 16O, 22Ne, or 26Mg in a hydrogen burning single zone of 1 M⊙ (hereafter H-box) with a constant temperature T and density ρ. The H-box schematically reproduces the convective hydrogen burning shell during the core helium burning phase of the source star.
To set the initial conditions in the H-box, we rely on a rotating 60 M⊙ model computed with the Geneva code. The initial metallicity is Z = 10-5. It corresponds to [Fe/H] =−3.8 for the initial mixture we considered (α-enhanced). The initial abundances in the H-box are taken from the hydrogen burning shell of this model, at the beginning of the core helium burning phase, when the mass fraction of 4He in the core Xc(4He) = 0.98. Figure 2 shows the temperature and density profiles of this model during the core helium burning phase. The variable Mr is the mass coordinate and Xc(4He) the central mass fraction of 4He. We see from this figure that T and ρ in the convective hydrogen burning shell take values of 30−80 MK and 1−5 g cm-3, respectively. For a 20 M⊙ model, the ranges of T and ρ are 30−60 MK and 1−10 g cm-3. As a first step, we fix T = 50 MK and ρ = 1 g cm-3 in the H-box. Different temperatures and densities in the H-box are discussed later. The simulation is stopped either when the hydrogen in the box is exhausted (when the mass fraction of hydrogen in the H-box X(1H) < 10-8) or when the time t exceeds 10 Myr. We note that depending on the stellar model chosen for setting the initial abundances in the H-box, we can have a slightly different initial chemical composition in the H-box. This will depend on the chemical composition of the model in its hydrogen burning shell, at the core helium burning ignition (Xc(4He) = 0.98). The CNO abundances in the hydrogen burning shell at the core helium burning ignition do not change significantly from a 20 M⊙ to a 60 M⊙ model. The abundances of neon, sodium, magnesium, and aluminium do vary a bit more owing to the difference in temperature that implies a slightly different nucleosynthesis in the hydrogen burning shell at the very beginning of the core helium burning phase.
 |
Fig. 2 Mr as a function of Xc(4He), the central mass fraction of 4He for a rotating 60 M⊙ model at a metallicity Z = 10-5 (similar to a Kippenhahn diagram). Shown in color is the temperature T6 in MK (upper panel) and the density ρ in g cm-3 (lower panel) in the convective hydrogen burning shell during the core helium burning phase from Xc(4He) = 0.98 to Xc(4He) = 0. |
 |
Fig. 3 Abundances in the H-box as a function of the logarithm of X0(H) − X(H). The four panels (from left to right) correspond to the four considered cases: when no injection is made; when 12C and 16O are injected; when 12C, 16O, and 22Ne are injected; and when 12C, 16O, 22Ne, and 26Mg are injected. Density and temperature in the box are ρ = 1 g cm-3 and T6 = 50 MK. |
Regarding the nuclear reaction rates, we took the ones used in the Geneva code (see Ekström et al. 2012). These rates are mainly from Angulo et al. (1999) for the CNO cycle, but almost all rates for Ne-Na Mg-Al chains are from Hale et al. (2002). Only 20Ne(p,γ)21Na and 21Ne(p,γ)22Na are taken from Angulo et al. (1999) and Iliadis et al. (2001), respectively. We note that the final abundance of 26Al in the H-box is added to the one of 26Mg since 26Al is a radioactive isotope (t1/2 = 7.17 × 105 yrs) decaying into 26Mg.
In order to reproduce schematically the diffusion of 12C, 16O, 22Ne, and 26Mg from the helium core to the hydrogen shell, we inject a constant mass per year into the H-box, which comes from a reservoir composed only of the considered species (12C, 16O, 22Ne, or 26Mg). We consider injection rates of 10-10, 10-8, and 10-6M⊙ yr-1 for 12C and 16O and 10-12, 10-10, and 10-8M⊙ yr-1 for 22Ne and 26Mg. More details about the method for injecting the species and the justification of the adopted injection rates are given in the Appendix. Four cases are tested in the present experiment:
-
no injection is made in the H-box;
-
12C and 16O are injected;
-
12C, 16O, and 22Ne are injected;
-
12C, 16O, 22Ne, and 26Mg are injected.
We note that in a real star, the mass is conserved and thus any injection into the hydrogen burning shell implies that some matter has to diffuse away from that region. In complete stellar models, the elements that are more abundant in the hydrogen burning shell than in one of the two adjacent regions will diffuse into the region(s) where this element is less abundant. However to keep the model as simple as possible we do not consider that complication here. The present work can be seen as a numerical experiment and not as an attempt to model all the details of what happens in stars. Indeed, the most important gradients of abundances are those from the difference in the abundances between the helium core and the hydrogen burning shell. Diffusion from the helium core to the hydrogen burning shell is therefore clearly the dominant feature, blurring all the other diffusion processes. In complete stellar models, injection of nitrogen into the helium core occurs dominantly by convection when the helium core slightly grows in regions left over by the hydrogen burning shell, not by diffusion from the hydrogen to the helium burning region. Also, as we show, the results obtained from complete stellar models (that follow in a consistent way the mixing of the elements) are well reproduced by our simple box model. Thus we are quite confident that our simple approach grasps the essentials of the process.
We also note that the origin of the iron is not investigated in the present work. By choosing a non-zero metallicity, we assume that the small iron content observed at the surface of the CEMP-no stars is already present in the source star (and in the H-box). Our sample of class 2 and 4 CEMP-no stars is expected to be made of a material processed by hydrogen burning that comes from the source star, i.e. from the outer layers of this star. The iron abundance in those outer layers is likely not affected by the nucleosynthesis and remains equal to its initial value. As a consequence, a comparison of the models with the observed ratios like [C/Fe] or [N/Fe] can be made, provided that the iron content in the models (the [Fe/H] ratio) is similar to the iron content of the CEMP-no stars. In our models, [Fe/H] =−3.8 so that the observed CEMP-no stars around this value can be consistently compared with the models.
 |
Fig. 4 [X/Fe] ratios in the H-box for the four considered cases (from left to right). The [12C/13C] ratio is also shown (i.e. 12C/13C ratio relative to the sun, in logarithm). The red points show the CEMP-no stars of Table 1 with [Fe/H] =−3.8 ± 0.3. The abundance patterns in the box at t = 0 are represented by black lines with squares and the patterns at the end of the simulation by black lines with triangles. The lower and upper black dotted lines represent the final composition in the H-box when the rates of injection are divided and multiplied by 102, respectively. The green pattern on the second (third) panel shows the composition in the hydrogen burning shell at the end of the core helium burning phase of a complete 20 M⊙ stellar model at 30% (70%) of the critical velocity on the ZAMS. Density and temperature in the box are ρ = 1 g cm-3 and T6 = 50 MK. |
4. Results of the experiment
Figure 3 shows the mass fraction of elements as a function of log (X0(H) − X(H)) (i.e. the logarithm of the initial mass fraction of hydrogen minus the current hydrogen mass fraction in the H-box) for the four cases presented in Sect. 3. The initial mass fraction of 1H in the box is equal to 0.33, the temperature and density are set to T = 50 MK and ρ = 1 g cm-3, and the injection rates are 10-8M⊙ yr-1 for 12C and 16O and 10-10M⊙ yr-1 for 22Ne and 26Mg. We describe now the four panels in Fig. 3, from left to right:
-
When no injection is made only 4.28 × 10-2 of hydrogen (in mass fraction) is consumed at the end of the limited time, which we fixed at 10 Myr. No transient regime is seen for the CNO elements since the CNO cycle is already at equilibrium at t = 0. The initial increase of X(23Na), the mass fraction of sodium, is due to the effect of the Ne-Na chain. It finally drops, like X(20Ne), in favour of X(24Mg) owing to the reaction 23Na(p,γ)24Mg. At T6 = 50, since the 24Mg(p,γ)25Al reaction is weak, it does not transform efficiently the 24Mg synthesized so that the 24Mg abundance increases. A small amount of 27Al is destroyed when little 1H remains in the shell and is transformed either into 28Si through 27Al(p,γ)28Si, or into 24Mg through 27Al(p,α)24Mg, both channels being almost equal at this temperature.
-
When 12C and 16O are injected, the CNO cycle is boosted and primary 14N and 13C are created. The CNO elements are more and more abundant so that more and more hydrogen is burnt. It is finally exhausted after ~0.8 Myr. The reactions in the CN cycle are fast so that an equilibrium is almost instantaneously reached for 12C, 13C, and 14N. Since the reaction 16O(p,γ)17F is much slower, the injected 16O accumulates before being transformed into 17F. These two regimes can be seen in the second panel of Fig. 3: the curve showing 16O first increases until log (X0(H) − X(H)) ~ −3 (accumulation) and then becomes flatter for −3 < log (X0(H) − X(H)) < −1 (16O destruction becomes important). No permanent regime is attained for 16O. At the end 12C and 16O rise dramatically because the hydrogen is almost exhausted: the CNO cycle works less and less, implying an accumulation of the injected 12C and 16O. Regarding the other elements, we see that 22Ne decreases in favour of 23Na, but the duration of the simulation is too short in this case for the Ne-Na and Mg-Al chains to operate significantly.
-
When the same experiment is performed and some 22Ne is also injected, 23Na and 24Mg are synthesized through the reactions 22Ne(p,γ)23Na and 23Na(p,γ)24Mg. Some 20Ne is also created when the reaction 23Na(p,α)20Ne occurs. At this temperature and for the selected rates, the (p,α) channel is 1.6 higher than the (p,γ) channel so that 23Na is almost equally destroyed in 20Ne and 24Mg. The reaction 24Mg(p,α)25Al is too slow to activate the Mg-Al chain. Since neon, sodium, and magnesium are much less abundant than the CNO elements, the hydrogen is not burnt significantly quicker than in case 2 when only 12C and 16O are injected.
-
When injecting 26Mg as well there is a ~2 dex increase in 27Al due to the direct transformation of 26Mg into 27Al thanks to a proton capture. For the temperature, density, and time of simulation considered, the 27Al destruction through either the (p,α) or (p,γ) channels is not significant.
Figure 4 shows the [X/Fe] ratios for the four cases presented in Fig. 3. The initial abundance pattern in the H-box (lines with squares) and the final pattern (lines with triangles) are plotted. The grey area corresponds to the range of values covered during the simulation. The dotted lines correspond to the final patterns in the H-box when the rates of injection are divided and multiplied by 100. The red points represent the observed ratios in CEMP-no stars of similar metallicities ([Fe/H] =−3.8 ± 0.3) to the metallicity considered in our numerical experiment ([Fe/H] =−3.8). As mentioned in Sect. 3, it is important to focus on the CEMP-no stars that have similar metallicities to the one in the models since the iron abundance in our model is an initial condition that is not modified by the nuclear reactions occurring in the H-box. Any change in the initial iron abundance in the models will produce a shift of the [X/Fe] ratios predicted by the models.
 |
Fig. 5 Left: same as Fig. 4 but for three different temperatures in the H-box. The [Si/Fe] ratio is also shown. Only the final abundance patterns in the box are plotted. The injected species are 12C, 16O, 22Ne, and 26Mg. Density is unchanged (1 g cm-3) and the injection rate is 10-8M⊙ yr-1 for 12C and 16O and 10-10M⊙ yr-1 for 22Ne and 26Mg). Right: same as the left panel but for three different densities in the H-box. The temperature is set to 50 MK. |
Without injection, the abundance pattern in the H-box does not change very much and all the [X/Fe] ratios (except [N/Fe] and [Al/Fe]) stay below the observed values. This is not surprising since the observed values correspond to classes 2 and 4, while the present experiment (no injection) would instead correspond to the CEMP-no stars in class 0. This class is made of a material processed only by hydrogen burning and where no mixing occurred between the hydrogen and helium burning regions. Injecting some 12C and 16O enhances the corresponding [X/Fe] ratios and the [N/Fe] (Fig. 4, second panel). Increasing or decreasing the rate of injection by a factor of 100 (dotted lines) changes the final pattern in the box, but not dramatically: from the lower to the upper dotted line, the rate of injection is multiplied by 4 dex while the difference in [X/Fe] values does not exceed 2 dex (for C, N, and O) because when injecting more 12C and 16O in the H-box, the hydrogen is burnt more rapidly and hydrogen exhaustion occurs earlier. We have here a negative feedback process: increasing the rate of injection increases the amount of injected species, but at the same time reduces the available time for injecting those new chemical species in the H-box. This explains qualitatively why injecting 12C and 16O at a rate 104 higher does not lead to an increase of 4 dex in the final [C/Fe], [N/Fe], and [O/Fe] ratios. The third case shows enhancements of [Ne/Fe], [Na/Fe], and [Mg/Fe] ratios: protons captured on the injected 22Ne create 23Na and then 24Mg. The final patterns of the fourth case present enhancements of [Mg/Fe] and [Al/Fe] ratios compared to case 3: owing to the injection of 26Mg, the Mg-Al chain is boosted, hence creating some 27Al.
Changing the temperature and the density in the H-box leads to the results presented in Fig. 5. We tested temperatures of T6= 50, 60, and 80 MK at a constant density ρ= 1 g cm-3 (left panel) and densities of ρ= 1, 10, and 100 g cm-3 at a constant temperature T6 = 50 MK (right panel). For both cases, the injected species are 12C, 16O, 22Ne, and 26Mg and the injection rates are 10-8M⊙ yr-1 for 12C and 16O and 10-10M⊙ yr-1 for 22Ne and 26Mg. In addition to the other [X/Fe] ratios, [Si/Fe] is also shown. Increasing either the temperature or the density leads to lower [X/Fe] ratios at hydrogen exhaustion (except for the [Si/Fe] ratio at T6 = 80 MK). When raising the density for instance, the rates of the nuclear reactions increase allowing a quicker synthesis of the chemical species than at lower densities. At the same time, the hydrogen is burnt more rapidly so that hydrogen exhaustion occurs earlier, leaving less time to inject new species. Summing those two opposite effects finally leads to lower [X/Fe] ratios at hydrogen exhaustion. For the same reasons, similar results are found when varying the temperature, although the dependance of the nuclear rates on temperature is much stronger than the dependance on the density. This is the reason why the various temperatures spanning a relatively small range of values (see Fig. 5) change the [X/Fe] ratios much more significantly than the various densities, even though they cover a much larger range of values.
The initial [Si/Fe] ratio in the box is about 1 and it is little affected by changes in temperature and density. However, increasing the temperature to T6 = 80 MK leads to about 0.5 dex more silicon at the end. The first reason is that the nuclear rates associated with Mg, Al, and Si are generally 3−4 dex higher at T6 = 80 MK than at T6 = 50 MK, allowing the synthesis of some 28Si. The second reason is that the 27Al is destroyed either to form 28Si thanks to the 27Al(p,γ)28Si reaction or to form 24Mg owing to the reaction 27Al(p,α)24Mg. When 27Al transforms into 24Mg, the Mg-Al chain operates and synthesizes 27Al again. Instead, 27Al is definitely destroyed when it is transformed into 28Si. At T6 = 50 and 60 MK, both channels are roughly equal. At T6 = 80 MK, the (p,γ) channel is ~40 times higher than the (p,α) channel. This tends to reduce Mg and Al and to increase Si.
Also shown in Figs. 4 and 5 is the [12C/13C] ratio, i.e. log (12C/13C) – log (12C/13C)⊙. The isotopic ratio in the Sun is taken from Lodders (2003). In all cases, the [12C/13C] ratio does not vary more than 0.5 dex, always staying around −1.5 because the equilibrium value is quickly reached when the CNO cycle operates. After each injection of 12C, the equilibrium ratio is reached again almost instantaneously compared to the current timestep. In particular, [12C/13C] reaches similar final values under all the explored temperatures and densities. When the CNO cycle operates, the [12C/13C] equilibrium ratio is indeed almost temperature and density independent.
We see that the observed [X/Fe] ratios are best covered when injecting 12C, 16O, and 22Ne (see the grey area in the third panel of Fig. 4). We note, however, that the models always give values that are too high for the [Al/Fe] ratios (see Sect. 6). For all the other ratios, our very simple numerical experiment confirms the need for some mixing between the helium and hydrogen burning zones in the source star to explain the general pattern observed in CEMP-no stars in classes 2 and 4. The injection of 22Ne seems to be needed, which supports the view that a strong mixing might be at work in the source star: 22Ne can enter the hydrogen burning shell if 12C and 16O have first diffused in the hydrogen burning shell, but also if the created 14N have entered in turn in the helium burning core. For most of the ratios, however, we note that the grey region is wider than the ranges covered by the observations. We do not think this is a very serious problem when considering that CEMP-no stars are not made of pure hydrogen shell material. To be used to form new stars, this matter needs to be ejected either by winds or at the time of the supernova. In this process, the region where the CNO cycle is active (hydrogen shell) is mixed with other layers of the star and eventually with some interstellar medium. For instance, any mixing with the outer layers of the star where the iron has the same abundance as in the hydrogen shell – but where the CNO abundances are smaller and close to their initial values (~10-5 for a model with Z = 10-5) – will shift the nitrogen abundance downward. Therefore, in order to obtain the observed nitrogen abundances in CEMP-no stars, it is likely needed that much higher abundances are reached in the hydrogen burning shell. While our box experiments provide some interesting constraints on the nuclear processes that might be needed to reproduce the peculiar abundance patterns of CEMP-no stars, only the computation of complete stellar models that take into account the ejection mechanism (both through winds and through the supernova explosion) and some possible mixing with the circumstellar material can provide abundances ratios that might be compared with the observed ratios in CEMP-no stars. This has to be kept in mind when interpreting the comparison shown in Fig. 4.
We note also that injecting some 26Mg raises the [Al/Fe] ratio far above the observed range. In stellar models, 26Mg comes from the transformation of 22Ne which occurs at the very end of the core helium burning phase. Thus, 26Mg could be injected (if at all) only at the very end or after the core helium burning phase, leaving little time for nuclear burning to transform this 26Mg into 27Al in the hydrogen burning shell. In this respect, the present numerical experiments injecting 26Mg regularly all along the burning of the hydrogen shell clearly overestimates what occurs in real stars. Thus, the hypothesis without 26Mg injection is by far the most probable.
It is interesting to note that detailed stellar models are qualitatively well enough reproduced by this simple one-zone model. The two green patterns in Fig. 4 show the [X/Fe] ratio in the hydrogen burning shell of a complete stellar model at the end of the core helium burning phase. The abundances are taken in the hydrogen shell where the energy released by hydrogen burning is the highest. The two stellar models are 20 M⊙, Z = 10-5 stars computed at 30% (second panel) and 70% (third panel) of the critical velocity on the ZAMS, which correspond to an initial equatorial velocity of 280 and 610 km s-1, respectively. Increasing the initial velocity can be modelled in the single-zone model by increasing the injection rate and injecting some 22Ne in addition to the 12C and 16O. By comparing the two green patterns, it is also interesting to see the strong impact of the initial rotation on the [X/Fe] ratios in the hydrogen burning shell at core helium exhaustion. This shows that the stellar rotation at low metallicity is likely a non-negligible process.
One point that deserves more discussion is the constant value found for the 12C/13C ratio under various conditions. What can be learnt from this ratio? How can it be used in stellar evolution models? The lithium content at the surface of the CEMP-no stars can give interesting constraints as well. A deeper investigation into the [Al/Fe] ratio also seems worthwhile because of the discrepancy we found between models and observations. Which conditions or assumptions will favour a lower [Al/Fe] ratio, closer to the observed values?
5. Dilution with material processed by helium burning and with initial ISM
In the previous section we investigate the secular mixing between the hydrogen and helium burning regions during the nuclear life of the source star. We now discuss the mixing events that can happen outside the star when the nuclear reactions are no longer active. Different kinds of materials can be ejected by the source star into the ISM. We consider two of them here: (i) the material processed by hydrogen burning and (ii) the material processed by helium burning. Outside the star, these materials can be mixed together and/or with the ISM. We distinguish two kinds of dilutions:
-
the dilution between the material processed by hydrogenburning and the material processed by helium burning. Thiscorresponds to a mixing between different parts of the star. Bymixing we mean mixing of the ejecta (or stellar ejecta mixing, asdefined in Sect. 2), hence outside of the star andwithout nuclear reactions.
-
the dilution between all the material ejected by the source star (processed by either hydrogen or helium burning) and the initial ISM, in which the source star formed. This is a mixing of the stellar ejecta with the initial ISM.
Based on considerations of the 12C/13C ratio and the lithium abundance, we investigate the possibility of constraining these two kinds of mixing events.
5.1. Using the 12C/13C ratio to constrain the amount of ejecta processed by helium burning
The 12C/13C ratio of the selected CEMP-no stars gives a strong constraint on the kind of material needed to form these stars. As we see in Fig. 4, this ratio is very close to the value found in a CNO processed material. We see from Figs. 4 and 5 that injecting some 12C into a hydrogen burning region does not change the 12C/13C ratio under various densities, temperatures, and rates of injection. However, when the nuclear reactions are switched off (which is what happens when the material is ejected from the source star) and the CNO processed material is mixed with part of the region processed by helium burning, this ratio will no longer stay around the observed values.
This point can be illustrated with a simple experiment. It is possible to mix the two kinds of material ejected by the source star, the ejecta processed by hydrogen burning and by helium burning (hereafter H-ejecta and He-ejecta). It is interesting to follow the evolution of the [12C/13C] ratio as adding more and more He-ejecta to the H-ejecta. The left panel of Fig. 6 shows [12C/13C] as a function of fmix defined as the fraction of He-ejecta added to the H-ejecta. For instance, fmix = 10-2 means 1% of He-ejecta with 99% of H-ejecta. We tested two compositions for the H-ejecta. The first has mass fraction of 12C and 13C equal to 1.11 × 10-7 and 3.10 × 10-8. It is called C-poor H-ejecta. These mass fractions are the ones in the H-box at t = 0. The second mixture has a 12C mass fraction of 2.01 × 10-4 and a 13C mass fraction of 5.45 × 10-5. We call it C-rich H-ejecta. These values correspond to the mass fractions of 12C and 13C in the H-box, a short time before hydrogen exhaustion when 12C is injected.
-
The C-poor H-ejecta corresponds to the low rotational mixingcase. A small amount of 12C has diffused from the helium core to the hydrogen shell so that the mass fractions of 12C and 13C in the hydrogen burning shell stay around their initial value, i.e. around 10-7. When this part of the star is expelled, we get ejecta that is poor in carbon.
-
The C-rich H-ejecta corresponds to the strong rotational mixing case. A lot of 12C has diffused into the hydrogen burning shell, raising its abundance and that of 13C far above their initial values. At the time of the ejection, this material is more enriched in carbon than in the previous case.
For the carbon abundances in the He-ejecta, we took the characteristic values in the helium burning core. We set XHeb(12C) = 0.1 and XHeb(13C) = 0 as a correct approximation.
 |
Fig. 6 Left: [12C/13C] ratio as a function of the mixing factor fmix, which represents the fraction of material processed by helium burning mixed with the material processed by hydrogen burning. Two compositions are tested for the material processed by hydrogen burning: a C-rich composition (red line) and a C-poor composition (black line). Right: green histogram showing the distribution of the CEMP-no stars used in this work. They belong to class 2 or 4. The grey histogram shows all known CEMP-no stars with a measured 12C/13C ratio. |
We see in the left panel of Fig. 6 that mixing 1% (i.e. fmix = 10-2) of the He-ejecta with 99% of a C-rich H-ejecta leads to a [12C/13C] of −0.6, which lies above the range of observed values for the CEMP-no stars in classes 2 and 4 (see green histogram in left panel of Fig. 6 and Table 1). If no rotational mixing has occurred between the helium burning core and hydrogen burning shell of the source star, the H-ejecta is C-poor. In this case, mixing the same amount of He-ejecta as before with the H-ejecta material leads to a [12C/13C] ratio of 2.6, far above the observed range. It seems that whatever the C-richness of the H-ejecta, hence whatever the amount of helium products that enter the hydrogen burning shell during the life of the source star, the final contribution of the material processed by helium burning coming from the source star should be null to form the CEMP-no stars in classes 2 and 4. This strongly supports the idea that the CEMP-no stars in classes 2 and 4 are only made of the hydrogen envelope of the source star. More generally, since 12C/13C is highly sensitive to the burning region considered (it is low for a hydrogen burning region and high for helium burning), this ratio could be used to constrain the mass cut of spinstar models at the time of the supernova: the mass cut could be chosen in order to reproduce the observed 12C/13C ratio of the considered CEMP-no star.
The grey histogram in the right panel of Fig. 6 shows the distribution of all observed [12C/13C] ratios at the surface of CEMP-no stars. It contains the 12 CEMP-no stars from Table 1 with a measured [12C/13C] ratio plus 15 other CEMP-no stars. Some CEMP-no stars have higher [12C/13C] ratios, suggesting the need for a small amount of material processed by helium burning to form them. We see, however, that the amount of material processed by helium burning needed should remain small in any case (fmix ≲ 0.05): mainly the hydrogen envelope of the progenitor should be used to form the CEMP-no stars. Nevertheless, we note that some CEMP-no stars only have a lower limit for the [12C/13C] ratio (3 out of 12 in our subsample). An accurate determination of this ratio for those stars would be interesting in order to validate the previous statement regarding these stars.
5.2. A(Li) to constrain the dilution with the initial ISM
In the previous section, we discussed the mixing of the stellar ejecta: the regions processed by hydrogen and helium burning ejected by the source star can be mixed together when the nuclear burning has stopped. The following discussion is related to the mixing (or the dilution) of the whole stellar ejecta with the initial ISM in which the source star formed.
Lithium is an interesting element that can be used to obtain information on the amount of ISM that should be mixed with the source star ejecta to form the CEMP-no stars. The abundance of lithium A(Li) in the pristine ISM is equal to 2.72 according to Cyburt et al. (2008). It is totally destroyed in massive stars. As a consequence, as soon as the ejecta of the massive source star is mixed with the ISM, the abundance of lithium is raised (in the mixture made of initial ISM and source star ejecta). If we assume that the lithium content at the surface of the CEMP-no star reflects the lithium content in the cloud where it formed, then the higher the lithium content at the surface of the CEMP-no star, the more the source star ejecta was diluted with the ISM. The dilution factor for mixing the progenitor ejecta with the ISM can be chosen in order to obtain the observed A(Li) value of the considered CEMP-no star.
One difficulty is that the lithium at the surface of the CEMP-no star can be depleted by internal mixing processes in the CEMP-no star itself. However, such processes might not be able to explain the low content of lithium observed at the surface of some CEMP-no stars. Meynet et al. (2010) pointed out that the maximal depletion predicted by the models of Korn et al. (2009) (1.2 dex) is unable to account for the A(Li) value observed at the surface of HE 1327-2326 (A(Li) < 0.62, see Table 1). According to the models of Korn et al. (2009), we would indeed expect a minimum observed value of A(Li) = 2.72−1.2 = 1.52 i.e. the WMAP content minus the maximum predicted depletion factor. We see that the depletion mechanism cannot easily account for the lowest observed A(Li) values. The alternative for HE 1327-2326 is that it formed from Li-poor material.
The A(Li) values (or upper limits) for nine of the considered CEMP-no stars are shown in Table 1. The lower panel of Fig. 3 in Meynet et al. (2010) shows the dilution factor MISM/Meje vs. A(Li). According to this figure and if we consider that the lithium was not depleted by the CEMP-no stars themselves, the dilution factor should be less than ~0.1 for the stars considered in this work. The highest dilution factor being for CS 22945-017, which has A(Li) < 1.51. The final mass fraction of 12C, 14N, and 16O in the H-box when injecting 12C and 16O is at least 10-3 (see Fig. 3). The mass fraction of the CNO elements in a Z = 10-5 ISM is about 10-6. Using 90% of 10-3 with 10% of 10-6 gives ~10-3; the dilution does not play a significant role in this case.
We now suppose that the lithium was depleted by the CEMP-no stars. We take the maximum depletion factor (1.2 dex) from Korn et al. (2009) and we add it to the observed A(Li) in order to get the initial A(Li) value before the depletion process. The two highest A(Li) belong to CS 22945-017 (<2.71) and CS 22958-042 (<2.53). Because A(Li) is close to the WMAP value for CS 22945-017, it would imply a high dilution factor. However, for CS 22958-042 and all the other considered CEMP-no stars, the dilution factor should be less than ~2. There is still not enough ISM for the dilution to have a significant effect, except for CS 22945-017. Caution is needed when considering these simple statements about the dilution between ejecta and ISM, but in the framework of our simple model we see that the dilution with the initial ISM might only play a limited role because the metal abundances in the region processed by hydrogen burning are much higher than the values in the initial ISM and because the dilution factors derived from the lithium abundance are small in most of the cases.
 |
Fig. 7 [Al/Fe] ratios in the H-box as a function of |
6. Al and Si abundances
The experiments presented in Sect. 4 show that the [Al/Fe] ratio in the H-box at hydrogen exhaustion always lies above the observed range of values. Even the initial [Al/Fe] – taken from the hydrogen burning shell of a 60 M⊙ model at the beginning of the core helium burning phase – is just above the observed range (see lines with squares in Fig. 4). We investigate now three effects on the aluminium abundance: the injection (species and rate), the temperature, and the nuclear reaction rates.
6.1. Impact of injection on Al: species and rate
First of all, a lower final [Al/Fe] ratio is expected if no 26Mg is injected. If it is injected, some 27Al is created through the reaction 26Mg(p,γ)27Al. This is illustrated in the third and fourth panels of Fig. 4. We see indeed that injecting 26Mg leads to a higher final [Al/Fe] than if no 26Mg is injected.
Figure 7 shows [Al/Fe] as a function of  : the rate of injection of 22Ne at T6 = 50 MK (left panel) and T6 = 80 MK (right panel). The injected species are 12C, 16O, and 22Ne. The blue, black, and green lines are associated with three sets of nuclear reactions rates that we tested and that will be discussed in Sect. 6.3. We focus on case 2 (black lines), which corresponds to the nuclear rates used here so far. The horizontal black line shows the initial [Al/Fe] ratio in the H-box and the black line with triangles shows the final values. We see that the final [Al/Fe] ratio at T6 = 80 MK (right panel of Fig. 7) is lower when less 22Ne is injected. When the injection rate is low enough, overall there is more 27Al destroyed than created. We see that some aluminium is created at the end if
: the rate of injection of 22Ne at T6 = 50 MK (left panel) and T6 = 80 MK (right panel). The injected species are 12C, 16O, and 22Ne. The blue, black, and green lines are associated with three sets of nuclear reactions rates that we tested and that will be discussed in Sect. 6.3. We focus on case 2 (black lines), which corresponds to the nuclear rates used here so far. The horizontal black line shows the initial [Al/Fe] ratio in the H-box and the black line with triangles shows the final values. We see that the final [Al/Fe] ratio at T6 = 80 MK (right panel of Fig. 7) is lower when less 22Ne is injected. When the injection rate is low enough, overall there is more 27Al destroyed than created. We see that some aluminium is created at the end if  > 3 × 10-11M⊙ yr-1 for the considered case. This aluminium comes mainly from the injected 22Ne thanks to successive proton captures.
> 3 × 10-11M⊙ yr-1 for the considered case. This aluminium comes mainly from the injected 22Ne thanks to successive proton captures.
These two arguments suggest that a moderate amount of 22Ne coming from the helium burning core to the hydrogen burning shell together with no 26Mg would probably play in favour of a lower final [Al/Fe] ratio.
6.2. Impact of temperature on Al
The final abundance of aluminium depends on the strength of the nuclear reactions rates that create and destroy it. The nuclear rates for the Ne-Na and Mg-Al cycles are generally 3−4 dex higher at T6 = 80 MK than at T6 = 50 MK so that the synthesis of aluminium is slower at T6 = 50 MK. Figure 7 shows that indeed the final [Al/Fe] ratios deviate very little from their initial values at T6 = 50 MK (left panel), while the difference is much more significant at T6 = 80 MK (right panel). We note however that the case 3 pattern at T6 = 50 MK lies largely below its initial value (horizontal green line), but this is due to the 26Al that has decayed into 26Mg at the end of the simulation (this reduces [Al/Fe] by about 1 dex). The green triangle at the abscissa 10-12M⊙ yr-1 also deviates from the others. The considered nuclear rates in this case disfavour the synthesis of 27Al (see discussion in Sect. 6.3). This, together with the low injection rate that implies a longer time before hydrogen exhaustion, allows a larger depletion of 27Al than at higher injection rates.
In addition, we saw in Sect. 4 (see also Fig. 5, left panel) that increasing the temperature leads to a lower final [Al/Fe] ratio (and a higher [Si/Fe]). This remains true as long as some 26Mg is injected: if 22Ne is injected but not 26Mg (as in Fig. 7), [Al/Fe] can be higher when increasing the temperature. This can be seen by comparing the left and right panels of Fig. 7 at the abscissa 10-9M⊙ yr-1 for instance. In this case, no 26Mg is injected so that 27Al comes mainly from the successive protons captured on the injected 22Ne. The chain leading to 27Al is longer when starting from 22Ne than from 26Mg. In that chain, the rate of 24Mg(p,γ)25Al at T6 = 50 MK is very low compared to the other reaction rates. This reaction tends to stop the chain at T6 = 50 MK so that the final content in 27Al is generally close to the initial one, even with high injection rates of 22Ne. Injecting some 26Mg is a way to avoid this bottleneck reaction and synthesize some aluminium, even at T6 = 50 MK (see the fourth panel of Fig. 4). The rate of 24Mg(p,γ)25Al strongly increases from T6 = 50 to 80 MK (by about 7 dex) so that the chain leading to 27Al (and 28Si) is no longer blocked at T6 = 80 MK.
A moderate temperature in the hydrogen shell (~50 MK) is likely more compatible with a lower [Al/Fe] under various amounts of 22Ne coming from the helium core to the hydrogen shell. In the strong mixing case (high  ) and at high temperatures, this could lead to a very high [Al/Fe] ratio (Fig. 7, right panel).
) and at high temperatures, this could lead to a very high [Al/Fe] ratio (Fig. 7, right panel).
6.3. Impact of changing the nuclear rates on Al
A point that deserves to be investigated is the uncertainties of the nuclear rates. In a hydrogen burning region, the two reactions destroying 27Al are 27Al(p,γ)28Si and 27Al(p,α)24Mg. The reaction which creates 27Al is 26Mg(p,γ)27Al. The three nuclear rates associated with these reactions are very uncertain at the considered temperatures. To illustrate this point, we compared three sets of nuclear rates for the three reactions involving 27Al. We used rates provided by the JINA REACLIB database (Cyburt et al. 2010).
-
Case 1: the best scenario for the 27Al synthesis. We took the maximum rate (at T6 = 80) for 26Mg(p,γ)27Al (Cyburt et al. 2010). The minimum rate was taken for both 27Al(p,γ)28Si and 27Al(p,α)24Mg (van Wormer et al. 1994).
-
Case 2: we used the rates taken from this work (see Sect. 3).
-
Case 3: the best scenario for 27Al destruction. The minimum rate for 26Mg(p,γ)27Al is from Angulo et al. (1999) and the maximum rates for 27Al(p,γ)28Si and 27Al(p,α)24Mg are from Cyburt et al. (2010).
To be consistent, we computed two other complete stellar models from the ZAMS to core helium burning ignition with the two new sets of nuclear rates (cases 1 and 3). Depending on the set of nuclear rates chosen, the initial abundances in the H-box are taken from the hydrogen burning shell of the corresponding stellar model. The three initial [Al/Fe] ratios taken in the H-box are shown by the blue (case 1), black (case 2), and green (case 3) horizontal lines. We see that the scatter is significant. This occurs because the Mg-Al cycle is already operating in the core of the complete stellar model during the main sequence so that the aluminium abundance is affected if the nuclear rates are changed. Depending on the set of nuclear rates, it finally leads to a different aluminium content in the hydrogen shell at core helium burning ignition, hence in the H-box.
The lines with triangles correspond to the final [Al/Fe] ratios in the H-box for the three cases. We verify that the rates considered in this work (case 2) lead to a final [Al/Fe] ratios that is between the two extreme cases. Whatever the injection rate, at least 1.5 dex separates the blue pattern from the green; the green pattern gives lower [Al/Fe] since this is the case where 27Al is the most destroyed and the least synthesized. A word of caution: for case 3, the abundance of 26Al is higher than that of 27Al during the burning, so that [Al/Fe] is significantly affected when 26Al decays into 26Mg. For cases 1 and 2, 27Al is more abundant so that decaying 26Al at the end reduces [Al/Fe] only a little.
Four out of five CEMP-no stars with [Fe/H] =−3.8 ± 0.3 have an observed [Al/Fe]. These ratios are represented by the red dashed lines in Fig. 7. The scatter of the observed [Al/Fe] ratios is covered well enough by case 3 (green pattern) when relying on different values of 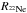 , the injection rate of 22Ne. If we select that set of rates, our model indicates that (i) the CEMP-no stars with [Al/Fe] ≳0 could be made of a material processed by hydrogen burning at relatively high temperatures (about 80 MK) because T~50 MK would not lead to a high enough aluminium content (see left panel of Fig. 7) and (ii) only a high enough injection rate of 22Ne can account for Al-enhanced CEMP-no stars. The four stars considered here do not show such a high [Al/Fe] ratio (except a modest enhancement in CS 29498-043). This might tend to disfavour the progenitors where the mixing is very strong (very high initial velocity) and with a high temperature in the hydrogen shell (≳ 60M⊙ stars). The two remaining possibilities are either a high temperature (~80 MK) in the hydrogen shell but a weak mixing (a low
, the injection rate of 22Ne. If we select that set of rates, our model indicates that (i) the CEMP-no stars with [Al/Fe] ≳0 could be made of a material processed by hydrogen burning at relatively high temperatures (about 80 MK) because T~50 MK would not lead to a high enough aluminium content (see left panel of Fig. 7) and (ii) only a high enough injection rate of 22Ne can account for Al-enhanced CEMP-no stars. The four stars considered here do not show such a high [Al/Fe] ratio (except a modest enhancement in CS 29498-043). This might tend to disfavour the progenitors where the mixing is very strong (very high initial velocity) and with a high temperature in the hydrogen shell (≳ 60M⊙ stars). The two remaining possibilities are either a high temperature (~80 MK) in the hydrogen shell but a weak mixing (a low 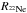 ), or a moderate temperature in the hydrogen shell (~50 MK) with a weak to strong mixing. A moderate temperature in the hydrogen shell is more likely achieved in ~20 M⊙ progenitors (30−60 MK) rather than in ~60 M⊙ ones (30−80 MK, see Fig. 2).
), or a moderate temperature in the hydrogen shell (~50 MK) with a weak to strong mixing. A moderate temperature in the hydrogen shell is more likely achieved in ~20 M⊙ progenitors (30−60 MK) rather than in ~60 M⊙ ones (30−80 MK, see Fig. 2).
6.4. Sensitivity of the Si abundance
The silicon abundance is also affected when changing the injection, temperature, or nuclear reaction rates. In the explored range of parameters (temperature, injection rate, and nuclear reaction rates; see Fig. 7) and for the injected species considered (12C, 16O, and 22Ne), the final [Si/Fe] ranges from 1 to 1.8.
At T6 = 50 MK, the final [Si/Fe] ratio depends very weakly on the injection rate because the Ne-Si chain is stopped by the 24Mg(p,γ)25Al reaction (see Sect. 6.2). In this case, the final [Si/Fe] ratio is almost equal to the initial value, which ranges from 1 (case 1, lowest rate for 27Al(p,γ)28Si) to 1.2 (case 3, highest rate for 27Al(p,γ)28Si).
At T6 = 80 MK, the final abundance of silicon is always enhanced compared to the initial level. The 24Mg(p,γ)25Al reaction no longer blocks the Ne-Si chain so that the injected 22Ne synthesizes some 28Si. The final [Si/Fe] ratios range between 1.2 and 1.8.
Three CEMP-no stars with [Fe/H] =−3.8 ± 0.3 have a measured [Si/Fe]. The values are 0.77, 0.82, and 0.87. These values are closer to the results given by the model at T6 = 50 MK (1 < [Si/Fe] < 1.2), which might indicate a moderate temperature in hydrogen shell of the progenitor (T6 ≃ 50 MK), consistent with the discussion in Sect. 6.3.
7. Possible astronomical sources of classes 2 and 4 CEMP-no stars
Through the present work, we suggest that the high observed abundances of C together with that of N, O, Na, and Mg at the surface of the CEMP-no stars are the signatures of a mixing between the helium and hydrogen burning regions of the source star during its nuclear life. What objects are able to experience such a mixing process? In the framework of our results, but also in a more global context, we speculate on the possible progenitors of classes 2 and 4 CEMP-no stars.
7.1. AGB stars
AGB stars are known contributors to s-process elements. They are generally believed to be responsible for the enrichment, by mass transfer, in s-elements observed at the surface of the CEMP-s stars. In addition to the abundances, the models have to reproduce the period of the binary system for instance, which can give tight contraints but also increase the difficulty of finding models matching the observations (see e.g. Abate et al. 2015).
In AGB stars, there is a mixing between the two shells. It could also, in principle, be enhanced by rotation or, at the very least, rotation may change the chemical structure of the star at the beginning of the AGB phase (see e.g. the 7 M⊙ model in Meynet et al. 2010).
It seems however that there are at least two difficulties in this scenario to explain the CEMP-no stars. First, the AGB stars are experiencing the s-process and by definition, the CEMP-no class is not enriched in s-elements (or is weakly enriched). This feature would be difficult to explain relying on AGB stars. Second, it seems difficult to account for the CEMP-no stars having [Fe/H] ≲−4 with the AGB stars: such a low iron content likely indicates that only the most massive objects, more massive than the AGB stars, have contributed.
7.2. Faint supernovae, mixing and fallback
Tominaga et al. (2014) discussed the scenario of faint supernovae from Pop III stars with mixing and fallback. In these models, only the outer layers are ejected from the progenitor. It is indeed needed to explain the observed CNO abundance patterns, as well as the low 12C/13C ratios. This is in line with the discussion about the mixing of the ejecta; we see in Sect. 5 that little or no material processed by helium burning coming from the source star should be mixed into the hydrogen rich envelope when the nuclear life of the star is finished. In other words, mainly the hydrogen rich envelope of the progenitor would be needed to form the future CEMP-no star.
On the other hand, these models are generally non-rotating, leading to some difficulties in explaining the high nitrogen abundance observed in some CEMP-no stars without invoking an extra mixing process in the progenitor. Rotating models were however considered in Takahashi et al. (2014), predicting higher N/Fe ratios in the ejecta, almost in line with the observed values at the surface of two out of the three CEMP-no stars they considered (HE 0107-5240 and HE 1327-2326).
7.3. Contribution of more than one source
Limongi et al. (2003) proposed a two-step scenario: a normal supernova from a ~15 M⊙ progenitor responsible for the iron-peak elements, followed by a fainter one experiencing strong fallback coming from a ~35 M⊙ progenitor. The second more massive progenitor enriches the ISM in light elements: C, N, Na, and Mg. These elements are produced thanks to a partial mixing between hydrogen and helium burning shells that can occur in Z = 0 models, even in non-rotating models.
What seems to not match with the CEMP-no stars in classes 2 and 4 is the predicted 12C/13C ratio of 240 for this two-step model. The corresponding [12C/13C] ratio is 0.4 and this is not compatible with the values of the CEMP-no stars considered here (see Fig. 6, right panel). We note, however, that 3 out of 12 have only a lower limit for the 12C/13C ratio (see Table 1) so that such a high predicted 12C/13C could be consistent with these CEMP-no stars.
7.4. Spinstars
Several signatures of fast rotation at low metallicity have been found over the past years. One strong signature is that the high nitrogen abundances and the low 12C/13C ratios observed in normal very metal-poor (VMP) stars are much better reproduced by low metallicity chemical evolution models when including fast rotators, also called spinstars (Chiappini et al. 2006, 2008). Because of the high rotation, the injection process we investigate here operates in the spinstar and it could be a way to obtain material enriched in C, N, O, Na, and Mg, together with a low 12C/13C, that will ultimately form a CEMP-no star in class 2 or 4.
The spinstars and more generally the objects experiencing mixing between hydrogen and helium burning regions appear to be interesting progenitor candidates for class 2 and 4 CEMP-no stars.
8. Conclusions
We studied the possibility of forming CEMP-no stars with a material processed by hydrogen burning coming from the source star. We carried out nuclear experiments where the convective hydrogen burning shell of the source star was modelled by a hydrogen burning single zone (H-box). The mixing between the helium burning core and the hydrogen burning shell was mimicked by injecting the products of helium burning 12C, 16O, 22Ne, and 26Mg in the H-box. When injecting these species in the hydrogen burning zone 14N, 23Na, 24Mg, and 27Al are synthesized. The 12C/13C ratio is constant under various densities, temperatures in the H-box, and also under various injection rates. The [Al/Fe] ratio in the hydrogen burning zone lies generally above the observations. Using different nuclear reaction rates found in the literature for the reactions involving 27Al leads to a better coverage of the observed [Al/Fe] scatter. The high observed [Al/Fe] ratios are reproduced at sufficiently high hydrogen burning temperature (80 MK) and if the injection rate of 22Ne is high enough. This might point toward a massive (high temperature) and fast rotating (high injection rate) progenitor.
Throughout this work, we suggest that the high observed abundances of light elements at the surface of the CEMP-no stars are the signatures of a mixing between the helium and hydrogen burning regions of the progenitor during its nuclear life. It supports the CEMP-no star formation scenario of Maeder & Meynet (2015) for classes 2 and 4. This scenario states that these stars are made of a material processed by hydrogen burning only, but were products of helium burning coming from the helium core of the source star diffused into the hydrogen burning shell thanks to the rotational mixing. This arrival of new elements boosts the nucleosynthesis in the hydrogen burning shell. Considerations on the 12C/13C ratio confirmed that the CEMP-no stars in classes 2 and 4 are made of a material that was only processed by hydrogen burning in the source star. This corroborates the assumption that the CEMP-no stars formed mainly with the hydrogen-rich envelope of the source star. The 12C/13C ratio is highly sensitive to the burning region considered in the source star (hydrogen or helium burning region). It could be used to constrain the part expelled from the source star at the time of the supernova in order to reproduce the observed 12C/13C ratio at the surface of the CEMP-no stars.
The spinstars are interesting candidates for being the class 2 and 4 CEMP-no progenitors because of their rotation which induces exchanges of material between the hydrogen and helium burning regions. This gives some support to the idea that the rotation played an important role in the early chemical evolution of galaxies.
Acknowledgments
The authors thank the anonymous referee who helped to improve this paper through very constructive remarks. This work was supported by the Swiss National Science Foundation (project number 200020-160119).
References
- Abate, C., Pols, O. R., Karakas, A. I., & Izzard, R. G. 2015, A&A, 576, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allen, D. M., Ryan, S. G., Rossi, S., Beers, T. C., & Tsangarides, S. A. 2012, A&A, 548, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nucl. Phys. A, 656, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Aoki, W. 2010, in IAU Symp. 265, eds. K. Cunha, M. Spite, & B. Barbuy, 111 [Google Scholar]
- Aoki, W., Beers, T. C., Christlieb, N., et al. 2007, ApJ, 655, 492 [NASA ADS] [CrossRef] [Google Scholar]
- Beers, T. C., & Christlieb, N. 2005, ARA&A, 43, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Carollo, D., Beers, T. C., Bovy, J., et al. 2012, ApJ, 744, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Chiappini, C. 2013, Astron. Nachr., 334, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Chiappini, C., Hirschi, R., Meynet, G., et al. 2006, A&A, 449, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiappini, C., Ekström, S., Meynet, G., et al. 2008, A&A, 479, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Choplin, A., Meynet, G., Maeder, A., Hirschi, R., & Chiappini, C. 2016, ArXiv e-prints [arXiv:1602.04122] [Google Scholar]
- Cyburt, R. H., Fields, B. D., & Olive, K. A. 2008, J. Cosmol. Astropart. Phys., 11, 012 [Google Scholar]
- Cyburt, R. H., Amthor, A. M., Ferguson, R., et al. 2010, ApJS, 189, 240 [NASA ADS] [CrossRef] [Google Scholar]
- Ekström, S., Georgy, C., Eggenberger, P., et al. 2012, A&A, 537, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frebel, A., Christlieb, N., Norris, J. E., et al. 2006, ApJ, 652, 1585 [NASA ADS] [CrossRef] [Google Scholar]
- Frebel, A., Norris, J. E., Aoki, W., et al. 2007, ApJ, 658, 534 [NASA ADS] [CrossRef] [Google Scholar]
- Frebel, A., Collet, R., Eriksson, K., Christlieb, N., & Aoki, W. 2008, ApJ, 684, 588 [NASA ADS] [CrossRef] [Google Scholar]
- Hale, S. E., Champagne, A. E., Iliadis, C., et al. 2002, Phys. Rev. C, 65, 015801 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Hansen, T., Hansen, C. J., Christlieb, N., et al. 2014, ApJ, 787, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, T., Hansen, C. J., Christlieb, N., et al. 2015, ApJ, 807, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Hirschi, R. 2007, A&A, 461, 571 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iliadis, C., D’Auria, J. M., Starrfield, S., Thompson, W. J., & Wiescher, M. 2001, ApJS, 134, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Keller, S. C., Bessell, M. S., Frebel, A., et al. 2014, Nature, 506, 463 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Korn, A. J., Richard, O., Mashonkina, L., et al. 2009, ApJ, 698, 410 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, Y. S., Beers, T. C., Masseron, T., et al. 2013, AJ, 146, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Limongi, M., Chieffi, A., & Bonifacio, P. 2003, ApJ, 594, L123 [CrossRef] [Google Scholar]
- Lodders, K. 2003, ApJ, 591, 1220 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A., & Meynet, G. 2001, A&A, 373, 555 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maeder, A., & Meynet, G. 2015, A&A, 580, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maeder, A., Meynet, G., & Chiappini, C. 2015, A&A, 576, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masseron, T., van Eck, S., Famaey, B., et al. 2006, A&A, 455, 1059 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masseron, T., Johnson, J. A., Plez, B., et al. 2010, A&A, 509, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masseron, T., Johnson, J. A., Lucatello, S., et al. 2012, ApJ, 751, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Meynet, G., Ekström, S., & Maeder, A. 2006, A&A, 447, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meynet, G., Hirschi, R., Ekstrom, S., et al. 2010, A&A, 521, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Norris, J. E., Yong, D., Bessell, M. S., et al. 2013, ApJ, 762, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Placco, V. M., Frebel, A., Beers, T. C., & Stancliffe, R. J. 2014, ApJ, 797, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Roederer, I. U., Preston, G. W., Thompson, I. B., et al. 2014, AJ, 147, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Takahashi, K., Umeda, H., & Yoshida, T. 2014, ApJ, 794, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Tominaga, N., Iwamoto, N., & Nomoto, K. 2014, ApJ, 785, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Umeda, H., & Nomoto, K. 2002, ApJ, 565, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Umeda, H., & Nomoto, K. 2005, ApJ, 619, 427 [NASA ADS] [CrossRef] [Google Scholar]
- van Wormer, L., Görres, J., Iliadis, C., Wiescher, M., & Thielemann, F.-K. 1994, ApJ, 432, 326 [NASA ADS] [CrossRef] [Google Scholar]
Appendix
Let us consider a box of initial mass m= 1 M⊙, where Xi denotes the mass fraction of the element i. We also consider a reservoir composed only of the element e, so that its mass fraction 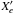 in the reservoir is 1. During a time Δt, we inject a mass
in the reservoir is 1. During a time Δt, we inject a mass 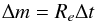 (A.1)from the reservoir into the box. Re is the injection rate of the element e expressed in M⊙ yr-1. After the injection, the new mass fraction
(A.1)from the reservoir into the box. Re is the injection rate of the element e expressed in M⊙ yr-1. After the injection, the new mass fraction 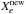 of the injected element in the box is
of the injected element in the box is 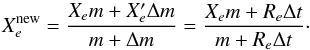 (A.2)The new mass fraction of the other elements in the box can be expressed as
(A.2)The new mass fraction of the other elements in the box can be expressed as 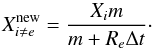 (A.3)We note that the H-box that was initially 1 M⊙ grows in mass as a result of the injection. Its final mass is generally similar to the initial one and never exceeds ~1.3M⊙ for the presented results, which stays relatively close to 1 M⊙.
(A.3)We note that the H-box that was initially 1 M⊙ grows in mass as a result of the injection. Its final mass is generally similar to the initial one and never exceeds ~1.3M⊙ for the presented results, which stays relatively close to 1 M⊙.
The point is now to estimate Re the injection rate. Let us consider the example of the carbon. In stellar models, the primary 14N is synthesized through the diffusion of 12C and 16O from the helium core to the hydrogen burning shell. The secondary 14N is formed with the initial CNO elements in the star. It is possible to roughly quantify 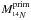 the mass fraction of primary 14N formed during the core helium burning phase as
the mass fraction of primary 14N formed during the core helium burning phase as 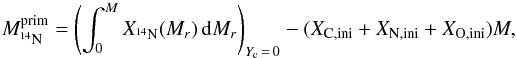 (A.4)
(A.4)
where Yc is the central 4He mass fraction; X14N(Mr) the mass fraction of 14N at coordinate Mr; XC,ini, XN,ini, XO,ini the mass fractions of the CNO elements at the ZAMS; and M the total mass of the star at the end of the core helium burning phase. 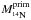 is defined as the total amount of 14N in the star at core helium exhaustion minus the amount of 14N that can be formed with the initial CNO content (secondary 14N). We suppose that all the 12C and 16O diffusing from the helium core to the hydrogen shell are transformed into 14N. In this case, to get a mass
is defined as the total amount of 14N in the star at core helium exhaustion minus the amount of 14N that can be formed with the initial CNO content (secondary 14N). We suppose that all the 12C and 16O diffusing from the helium core to the hydrogen shell are transformed into 14N. In this case, to get a mass 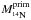 of primary nitrogen in the star at the end of core helium burning, an average injection rate of (12C + 16O) is needed in the hydrogen shell of
of primary nitrogen in the star at the end of core helium burning, an average injection rate of (12C + 16O) is needed in the hydrogen shell of 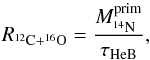 (A.5)where τHeB is the duration of the core helium burning phase. For a 60 M⊙ model at Z = 10-5 and at 70% of the critical velocity at the ZAMS, we find R12C + 16O = 5×10-8M⊙ yr-1.
(A.5)where τHeB is the duration of the core helium burning phase. For a 60 M⊙ model at Z = 10-5 and at 70% of the critical velocity at the ZAMS, we find R12C + 16O = 5×10-8M⊙ yr-1.
The amount of primary nitrogen synthesized (hence the value of 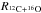 ) can change significantly depending on the rotation, the mass of the model, or the prescription for the rotational mixing for instance. In the present work we consider 10-10<R12C< 10-6M⊙ yr-1 (the chosen values are 10-10, 10-8, and 10-6M⊙ yr-1). In addition, we set R12C = R16O and R22Ne = R26Mg = R12C/ 100. The factor 100 between the two rates accounts at first order for the fact that 22Ne and 26Mg are ~100 times less abundant than 12C and 16O in the helium burning core of a low metallicity massive stellar model, so that ~100 times less 22Ne and 26Mg will enter by rotational mixing into the hydrogen burning shell.
) can change significantly depending on the rotation, the mass of the model, or the prescription for the rotational mixing for instance. In the present work we consider 10-10<R12C< 10-6M⊙ yr-1 (the chosen values are 10-10, 10-8, and 10-6M⊙ yr-1). In addition, we set R12C = R16O and R22Ne = R26Mg = R12C/ 100. The factor 100 between the two rates accounts at first order for the fact that 22Ne and 26Mg are ~100 times less abundant than 12C and 16O in the helium burning core of a low metallicity massive stellar model, so that ~100 times less 22Ne and 26Mg will enter by rotational mixing into the hydrogen burning shell.
All Tables
Type (MS if Teff ≥ 5500 K and log g ≥ 3.25, RGB otherwise), class, and abundance data for the CEMP-no stars considered in this work.
All Figures
 |
Fig. 1 Schematic view of the “back and forth” process at work in the spinstar. It occurs during the core helium burning phase and it is an exchange of chemical species between the helium burning core and the hydrogen burning shell. |
| In the text | |
 |
Fig. 2 Mr as a function of Xc(4He), the central mass fraction of 4He for a rotating 60 M⊙ model at a metallicity Z = 10-5 (similar to a Kippenhahn diagram). Shown in color is the temperature T6 in MK (upper panel) and the density ρ in g cm-3 (lower panel) in the convective hydrogen burning shell during the core helium burning phase from Xc(4He) = 0.98 to Xc(4He) = 0. |
| In the text | |
 |
Fig. 3 Abundances in the H-box as a function of the logarithm of X0(H) − X(H). The four panels (from left to right) correspond to the four considered cases: when no injection is made; when 12C and 16O are injected; when 12C, 16O, and 22Ne are injected; and when 12C, 16O, 22Ne, and 26Mg are injected. Density and temperature in the box are ρ = 1 g cm-3 and T6 = 50 MK. |
| In the text | |
 |
Fig. 4 [X/Fe] ratios in the H-box for the four considered cases (from left to right). The [12C/13C] ratio is also shown (i.e. 12C/13C ratio relative to the sun, in logarithm). The red points show the CEMP-no stars of Table 1 with [Fe/H] =−3.8 ± 0.3. The abundance patterns in the box at t = 0 are represented by black lines with squares and the patterns at the end of the simulation by black lines with triangles. The lower and upper black dotted lines represent the final composition in the H-box when the rates of injection are divided and multiplied by 102, respectively. The green pattern on the second (third) panel shows the composition in the hydrogen burning shell at the end of the core helium burning phase of a complete 20 M⊙ stellar model at 30% (70%) of the critical velocity on the ZAMS. Density and temperature in the box are ρ = 1 g cm-3 and T6 = 50 MK. |
| In the text | |
 |
Fig. 5 Left: same as Fig. 4 but for three different temperatures in the H-box. The [Si/Fe] ratio is also shown. Only the final abundance patterns in the box are plotted. The injected species are 12C, 16O, 22Ne, and 26Mg. Density is unchanged (1 g cm-3) and the injection rate is 10-8M⊙ yr-1 for 12C and 16O and 10-10M⊙ yr-1 for 22Ne and 26Mg). Right: same as the left panel but for three different densities in the H-box. The temperature is set to 50 MK. |
| In the text | |
 |
Fig. 6 Left: [12C/13C] ratio as a function of the mixing factor fmix, which represents the fraction of material processed by helium burning mixed with the material processed by hydrogen burning. Two compositions are tested for the material processed by hydrogen burning: a C-rich composition (red line) and a C-poor composition (black line). Right: green histogram showing the distribution of the CEMP-no stars used in this work. They belong to class 2 or 4. The grey histogram shows all known CEMP-no stars with a measured 12C/13C ratio. |
| In the text | |
 |
Fig. 7 [Al/Fe] ratios in the H-box as a function of |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


