| Issue |
A&A
Volume 593, September 2016
|
|
|---|---|---|
| Article Number | A8 | |
| Number of page(s) | 9 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201527549 | |
| Published online | 29 August 2016 | |
Particle acceleration in the vacuum gaps in black hole magnetospheres
1 ISDC, Astronomy Department,
University of Geneva, Ch. d’Ecogia
16, 1290
Versoix,
Switzerland
e-mail: ptitsyna.k@gmail.com
2 Institute for Nuclear Research of the
Russian Academy of Sciences, 60th
October Anniversary Prospect 7a, 117312
Moscow,
Russia
3 Physics Department, M.V. Lomonosov
Moscow State University, 119991
Moscow,
Russia
Received:
13
October
2015
Accepted:
2
February
2016
Aims. We consider particle acceleration in the vacuum gaps in magnetospheres of black holes powered by the Blandford-Znajek mechanism and embedded in the radiatively-inefficient accretion flow (RIAF) environment. In this situation, the gap height is limited by the onset of gamma-gamma pair production on the infrared photons originating in the RIAF.
Methods. We numerically calculated the acceleration and propagation of charged particles by taking the detailed structure of the electric and magnetic fields in the gap and in the entire black hole magnetosphere into account, as well as the radiative energy losses and interactions of γ-rays produced by the propagated charged particles with the background radiation field of the RIAF.
Results. We show that the presence of the vacuum gap has clear observational signatures. The spectra of emission from gaps embedded in a relatively high-luminosity RIAF are dominated by the inverse Compton emission with a sharp, super-exponential cut-off in the very-high-energy gamma-ray band. The cut-off energy is determined by the properties of the RIAF and is largely independent of the structure of magnetosphere and geometry of the gap. The spectra of the gap residing in low-luminosity RIAFs are dominated by synchrotron or curvature emission with the spectra extending into 1−100 GeV energy range. We also consider the effect of possible acceleration of protons in the gap and find that proton energies could reach the ultra-high-energy cosmic ray (UHECR) range only in extremely low-luminosity RIAFs.
Key words: galaxies: active / gamma rays: galaxies / acceleration of particles / black hole physics
© ESO, 2016
1. Introduction
Observations of fast variability of high-energy and very-high-energy γ-ray emission from blazars and radio galaxies (Aharonian 2007, 2006; Abramowski 2012; Aleksić 2014; Vovk & Neronov 2013; Foschini et al. 2013) indicate that the region of particle acceleration and of the associated high-energy γ-ray emission is situated in the vicinity of the supermassive black hole powering these sources. This indirect evidence is supported by the direct measurement of the size of the γ-ray emission region using the effect of gravitational microlensing (Neronov et al. 2015; Vovk & Neronov 2016).
Most of the fast variable sources with compact high-energy γ-ray emission regions belong to either the Fanaroff-Riley type-I (FR I) radio galaxies or BL Lac type object classes. These two source types are different versions of one and the same class of low-luminosity radio galaxies with jets misaligned (for the FR I) or aligned (for BL Lacs) along the line of sight (Urry & Padovani 1995). In these sources the central engine of the active galactic nucleus (AGN) is probably to be embedded in a radiatively inefficient accretion flow (RIAF) that is characterised by moderate matter density and luminosity (Narayan et al. 1998; Chiaberge et al. 1999).
Several possible mechanisms of particle acceleration in the compact region near the black hole could be considered. High-energy particle acceleration in the astrophysical environments is conventionally attributed to the shock acceleration mechanism (Krymskii 1977; Bell 1978; Drury 1983). In the case of radio galaxies, relativistic shocks form in the relativistic jet ejected by the black hole Bridle & Perley (1984). A shock at the base of the jet close to the black hole could be the source of high-energy particles Marscher et al. (2008). Otherwise, the jet and the RIAF typically generate strong magnetic fields with the energy density reaching the equipartition with the kinetic or gravitational potential energy of the accretion flow. Reconnection of magnetic field lines in the innermost part of the RIAF could lead to the generation of transient electric field accelerating high-energy particles (Romanova & Lovelace 1992; Yuan et al. 2003; Yuan & Narayan 2014). Finally, if the black hole is rotating, it works as a unipolar inductor generating large scale electric field in the presence of external magnetic field (Wald 1974). Such an electric field could also accelerate particles that could produce fast variable γ-ray emission (Boldt & Ghosh 1999; Levinson 2000; Neronov et al. 2005, 2009; Neronov & Aharonian 2007; Krawczynski 2007.
A rotating black hole could also be the source of the energy for the source activity. Power could be extracted from the black hole rotation such as via the Blandford-Znajek process (Blandford & Znajek 1977). The Blandford-Znajek process operates in the force-free black hole magnetosphere filled with plasma. However, the plasma is continuously “washed out” from the magnetosphere and needs to be replenished through in situ generation of free charges. On one hand, this leads to possible generation of the regions with a charge deficit, namely the “gaps”, where the force-free condition is broken and large scale electric field accelerates particles. On the other hand, it is in these gaps where the charge could be generated. The accelerated particles induce pair production cascades that supply the force-free part of the magnetosphere with charges (Blandford & Znajek 1977). This mechanism is identical to that operating in the pulsar magnetospheres (Goldreich & Julian 1969; Sturrock 1971; Cheng et al. 1986.
The possibility of there being charge-starved regions in black hole magnetosphere was discussed by Blandford & Znajek (1977), Beskin et al. (1992), Levinson (2000) and Levinson & Rieger (2011). Beskin et al. (1992), Hirotani & Okamoto (1998) have shown that the gaps could be considered as the analogues of the outer gaps in pulsar magnetospheres, lying near the surfaces that separate areas with opposite space charge densities. Krawczynski (2007), Vincent & Lebohec (2010) made the first attempts to calculate both the spectrum of synchrotron and inverse Compton emission from electrons accelerated in the vacuum gap and details of development of the pair cascade induced by the gamma-gamma pair production. The analysis of the gap properties in particular cases was done by Levinson & Rieger (2011), Broderick & Tchekhovskoy (2015).
In what follows we study observational signatures of operation of vacuum gaps in the magnetospheres of black holes powered by the Blandford-Znajek process. We argue that these observational signatures could be searched for in the signal of radio galaxies and BL Lacs. In Sect. 2 we discuss the properties of the gaps in black hole magnetospheres using analytical estimates. In Sect. 3 we verify the analytical estimates with numerical simulations and compute the spectra of electromagnetic emission from the gaps. Section 4 presents the results of numerical modelling and links them with the observations.
2. Qualitative estimates of parameters of the vacuum gaps
2.1. Gap location in the magnetosphere
The electric charge volume density in stationary axisymmetric force-free magnetosphere is given by the Goldreich-Julian density (Beskin et al. 1992) 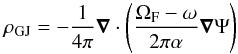 (1)where Ψ = Ψ(r,θ) is a magnetic flux within the axisymmetric “magnetic tube”, formed by the rotation of the magnetic field line, passing through the (r,θ) point, ΩF = ΩF(Ψ) is an “angular velocity” of the magnetic line, constant on the magnetic flux tubes. (r,θ,φ) is the spherical coordinate system in the Kerr space time described by the metric
(1)where Ψ = Ψ(r,θ) is a magnetic flux within the axisymmetric “magnetic tube”, formed by the rotation of the magnetic field line, passing through the (r,θ) point, ΩF = ΩF(Ψ) is an “angular velocity” of the magnetic line, constant on the magnetic flux tubes. (r,θ,φ) is the spherical coordinate system in the Kerr space time described by the metric 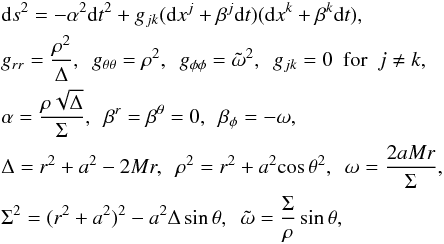 (2)where M and a = J/M are the mass and specific angular momentum of a rotating black hole. In the following we always assume that the particle velocities, charge and current densities, and the fields components are those measured in the locally non-rotating frames, LNRF (Bardeen et al. 1972). We use the system of units in which the gravitational constant and the speed of light are unities: GN = 1;c = 1.
(2)where M and a = J/M are the mass and specific angular momentum of a rotating black hole. In the following we always assume that the particle velocities, charge and current densities, and the fields components are those measured in the locally non-rotating frames, LNRF (Bardeen et al. 1972). We use the system of units in which the gravitational constant and the speed of light are unities: GN = 1;c = 1.
 |
Fig. 1 Goldreich-Julian charge density in the split-monopole force-free black hole magnetosphere. The black hole rotation moment is a = 0.1M. The horizon is the boundary of the blue circle in the bottom left corner of the map. The black area is the region with negative charge density. The colour scale shows the region of positive values of ρ(r,θ) with the colour scaling logarithmically with ρGJ. The green curve shows the location of the gap at the surface ρGJ = 0. |
Figure 1 shows the Goldreigh-Julian density map for the black hole force-free magnetosphere with the split-monopole global geometry (Blandford & Znajek 1977). Numerical simulations show that split monopole field, the simplest analytical model for the global magnetic field configuration in the magnetosphere, naturally forms in the vicinity of the black hole horizon of a black hole embedded into uniform magnetic field (Komissarov 2004a,b, 2005). In locations where the charge density is exactly equal to the Goldreigh-Julian density, the electromagnetic field satisfies the ideal magnetohydrodynamics condition ![\begin{equation} \vec E+\left[\vec v\times \vec B\right]=0 \end{equation}](/articles/aa/full_html/2016/09/aa27549-15/aa27549-15-eq16.png) (3)where v is the bulk velocity of the plasma filling the magnetosphere, and E and B are the electric and magnetic fields.
(3)where v is the bulk velocity of the plasma filling the magnetosphere, and E and B are the electric and magnetic fields.
The force-free condition could be violated at locations where the peculiarities of the plasma flow do not allow adjusting the charge balance to provide the Goldreich-Julian charge density. In this case a gap in the force-free magnetosphere could be formed. Such a gap forms first of all around the surfaces ρGJ = 0 (Beskin et al. 1992). We call these GJ surfaces. Indeed, inside and outside the GJ surface, there are two surfaces through which charges, both negative and positive, could flow in only one direction: outwards through the light cylinder and inwards through the horizon. In the absence of a continuous injection of particles, the part of the magnetosphere between these two one-way surfaces gets “charge starved”. Since this washing out does not depend on the charge’s sign, the charge deficit occurs at the first place with the lowest charge density, i.e. on the GJ surface.
Following Beskin et al. (1992), we use an analytical approximation for the electric field in the gap 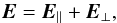 (4)where E⊥ is the poloidal force-free electric field component, perpendicular to the magnetic field, and E is the component parallel to the magnetic field, which satisfies the equation
(4)where E⊥ is the poloidal force-free electric field component, perpendicular to the magnetic field, and E is the component parallel to the magnetic field, which satisfies the equation 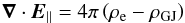 (5)with ρe being the total charge density. Choosing the x axis along B field away from the black hole with x = 0 on the GJ surface, one can an approximate solution to the above equation
(5)with ρe being the total charge density. Choosing the x axis along B field away from the black hole with x = 0 on the GJ surface, one can an approximate solution to the above equation 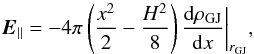 (6)which satisfies the boundary condition E∥ = 0 at the boundaries of the gap of the height x = ± H/ 2, where H is the gap height.
(6)which satisfies the boundary condition E∥ = 0 at the boundaries of the gap of the height x = ± H/ 2, where H is the gap height.
2.2. Particle acceleration in the gap
An order-of-magnitude estimate of the energies of particles accelerated in the gap could be found in the following way. Adopting an estimate ρGJ ~ (1/8π2)(B/r)(a/M) and 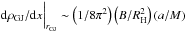 , where
, where 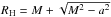 is the horizon radius, we find the mean parallel electric field in the gap
is the horizon radius, we find the mean parallel electric field in the gap 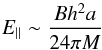 (7)where h = H/RH. The mean acceleration rate dℰ+/ dt is
(7)where h = H/RH. The mean acceleration rate dℰ+/ dt is 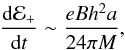 (8)where e is the particle charge.
(8)where e is the particle charge.
If the rate of energy losses due to the synchrotron/curvature and inverse Compton emission is much lower than the acceleration rate Eq. (8), particles are accelerated in the gap to the maximum energy: ![\begin{equation} {\cal{E}}\sim \frac{eBR_{\rm H}h^3a}{24\pi M}\sim 2\times 10^{12}\left[\frac{h}{0.01}\right]^3\left[\frac{B}{10^4\mbox{ G}}\right]\left[\frac{M}{10^9~M_\odot}\right]\mbox{ eV} , \end{equation}](/articles/aa/full_html/2016/09/aa27549-15/aa27549-15-eq40.png) (9)here and after in this section we assume a = 0.1M in the second part of the equation. This is nearly always the case for protons. In contrast, electrons suffer from much stronger energy losses. Their maximum energies are determined by the balance of the energy gain rate Eq. (8) and the energy loss. The loss rate is dominated by the synchrotron/curvature radiation loss for the low-luminosity RIAF:
(9)here and after in this section we assume a = 0.1M in the second part of the equation. This is nearly always the case for protons. In contrast, electrons suffer from much stronger energy losses. Their maximum energies are determined by the balance of the energy gain rate Eq. (8) and the energy loss. The loss rate is dominated by the synchrotron/curvature radiation loss for the low-luminosity RIAF: 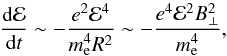 (10)with R ranging between R ~ RH for the curvature radiation and R = ℰ /eB⊥ for the synchrotron radiation in magnetic field with the component B⊥ normal to the particle velocity. The maximum energies attainable by electrons are then
(10)with R ranging between R ~ RH for the curvature radiation and R = ℰ /eB⊥ for the synchrotron radiation in magnetic field with the component B⊥ normal to the particle velocity. The maximum energies attainable by electrons are then ![\begin{eqnarray} {\cal E}&\sim& \frac{h^{1/2}B^{1/4}R_{\rm H}^{1/2}a^{1/4}}{\left(24\pi\right)^{1/4}e^{1/4}M^{1/4}}m_{\rm e}\\ & \sim& 3\times 10^{14}\left[\frac{h}{0.01}\right]^{1/2}\left[\frac{B}{10^4\mbox{ G}}\right]^{1/4}\left[\frac{M}{10^9~M_\odot}\right]^{1/2}\mbox{eV}\nonumber \end{eqnarray}](/articles/aa/full_html/2016/09/aa27549-15/aa27549-15-eq46.png) (11)for the curvature radiation and
(11)for the curvature radiation and ![\begin{eqnarray} {\cal E}&\sim& \frac{hm_{\rm e}^2B^{1/2}a^{1/2}}{(24\pi)^{1/2}e^{3/2}B_{\bot}M^{1/2}} \\ & \sim&4\times 10^{13}\left[\frac{h}{0.01}\right]\left[\frac{B}{10^4\mbox{ G}}\right]^{1/2}\left[\frac{B_\bot}{1\mbox{ G}}\right]^{-1}\mbox{eV}\nonumber \end{eqnarray}](/articles/aa/full_html/2016/09/aa27549-15/aa27549-15-eq47.png) (12)for the dominant synchrotron radiation loss (where we have assumed B⊥ ~ E∥ for the numerical estimate).
(12)for the dominant synchrotron radiation loss (where we have assumed B⊥ ~ E∥ for the numerical estimate).
High-luminosity RIAF leads to the dominance of the inverse Compton energy loss, which scales as 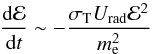 (13)in the Thomson regime. This loss limits electron energies to
(13)in the Thomson regime. This loss limits electron energies to ![\begin{eqnarray} {\cal E}&\sim& \frac{(4\pi)^{1/2}e^{1/2}B^{1/2}hm_{\rm e}R_{\rm ir}a^{1/2}}{(24\pi)^{1/2}\sigma_{\rm T}^{1/2}L^{1/2}M^{1/2}}\nonumber \\ &\sim&2\times 10^{12}\left[\frac{h}{0.01}\right]\left[\frac{B}{10^4\mbox{ G}}\right]^{1/2}\left[\frac{M}{10^9~M_\odot}\right]\left[\frac{L}{10^{42}\mbox{ erg/s}}\right]^{-1/2}\mbox{eV,}\nonumber \end{eqnarray}](/articles/aa/full_html/2016/09/aa27549-15/aa27549-15-eq50.png) where Rir ~ 10RH is the characteristic size of the infrared source in RIAF.
where Rir ~ 10RH is the characteristic size of the infrared source in RIAF.
The number of electrons in the gap Ne is limited by the Goldreich-Julian density ρGJ. The gap volume is estimated as 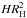 , and we have
, and we have 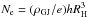 . Thus the maximum total luminosity of the gap Lgap due to the electrons synchrotron/curvature or inverse Compton radiation in the energy gain - energy loss balanced regime is given by
. Thus the maximum total luminosity of the gap Lgap due to the electrons synchrotron/curvature or inverse Compton radiation in the energy gain - energy loss balanced regime is given by ![\begin{eqnarray} \label{fL} L_{\rm gap}&\sim& N_{\rm e}({\rm d}{\cal{E}}/{\rm d}t) \\ &\sim&3\times10^{40}\left[\frac{h}{0.1}\right]^3\left[\frac{B}{10^3~\mbox{G}}\right]^2\left[\frac{M}{10^9~M_{\odot}}\right]^2 \mbox{erg/s.}\nonumber \end{eqnarray}](/articles/aa/full_html/2016/09/aa27549-15/aa27549-15-eq56.png) (14)
(14)
2.3. Gamma-gamma pair production in the gap
The height of the gap is limited by the onset of the electron-positron pair production in interactions of the inverse Compton/curvature/synchrotron photons with the infrared radiation from the RIAF. The threshold γ-ray energy for the pair production on the infrared photons of the energy ϵir is ![\begin{equation} E_{\gamma,{\rm thr}}=\frac{m_{\rm e}^2}{\epsilon_{\rm ir}}\simeq 3\left[\frac{\epsilon_{\rm ir}}{0.1\mbox{ eV}}\right]^{-1}\mbox{ TeV} . \end{equation}](/articles/aa/full_html/2016/09/aa27549-15/aa27549-15-eq58.png) (15)The energy of the curvature
(15)The energy of the curvature ![\begin{equation} E_\gamma=\frac{{\cal E}^3}{m_{\rm e}^3R}\sim 10^9\left[\frac{\cal E}{10^{15}\mbox{ eV}}\right]^3 \left[\frac{M}{10^9~M_\odot}\right]^{-1}\mbox{ eV} \end{equation}](/articles/aa/full_html/2016/09/aa27549-15/aa27549-15-eq59.png) (16)and synchrotron
(16)and synchrotron ![\begin{equation} E_\gamma=\frac{eB_\bot{\cal E}^2}{m_{\rm e}^3}\sim 10^7\left[\frac{B_\bot}{1\mbox{ G}}\right]\left[\frac{\cal E}{10^{13}\mbox{ eV}}\right]^2\mbox{ eV}, \end{equation}](/articles/aa/full_html/2016/09/aa27549-15/aa27549-15-eq60.png) (17)photons typically does not reach the pair production threshold. In contrast, the energy of the inverse Compton photons is
(17)photons typically does not reach the pair production threshold. In contrast, the energy of the inverse Compton photons is 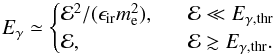 (18)The pair production process can limit the height of the gap only if the potential difference in the gap is sufficient for accelerating electrons to the energy at which the inverse Compton γ-rays start to produce pairs:
(18)The pair production process can limit the height of the gap only if the potential difference in the gap is sufficient for accelerating electrons to the energy at which the inverse Compton γ-rays start to produce pairs: ![\begin{eqnarray} \label{f4} h\ga h_{*,{\rm acc}} &\sim& \left(\frac{24\pi m_{\rm e}^2 M}{e\epsilon_{\rm ir}BR_{\rm H} a}\right)^{1/3} \\ &\sim &10^{-2}\left[\frac{\epsilon_{\rm ir}}{0.1\mbox{ eV}}\right]^{-1/3}\left[\frac{B}{10^{4}\mbox{ G}}\right]^{-1/3}\left[\frac{M}{10^{9}~M_\odot}\right]^{-1/3}\nonumber. \end{eqnarray}](/articles/aa/full_html/2016/09/aa27549-15/aa27549-15-eq62.png) (19)If the energies of electrons are limited by the balance between the acceleration rate and inverse Compton loss rate, the minimum gap height necessary for the onset of the pair production is
(19)If the energies of electrons are limited by the balance between the acceleration rate and inverse Compton loss rate, the minimum gap height necessary for the onset of the pair production is ![\begin{eqnarray} h\ga \ &h_{*,{\rm ic}}&\sim\left(\frac{6\sigma_{\rm T}Lm_{\rm e}^2M}{4\pi e\epsilon_{\rm ir}^2BR_{\rm ir}^2a}\right)^{1/2}\simeq 10^{-2}\\ & \times &\left[\frac{L}{10^{42}\mbox{ erg/s}}\right]^{1/2}\left[\frac{B}{10^4\mbox{ G}}\right]^{-1/2}\left[\frac{M}{10^9~M_\odot}\right]^{-1}\left[\frac{\epsilon_{\rm ir}}{0.1\mbox{ eV}}\right]^{-1}\nonumber\cdot \end{eqnarray}](/articles/aa/full_html/2016/09/aa27549-15/aa27549-15-eq63.png) (20)The pair production occurs on a distance scale that is close to the γ-ray mean free path of γ-rays
(20)The pair production occurs on a distance scale that is close to the γ-ray mean free path of γ-rays ![\begin{eqnarray} \lambda_{\gamma\gamma}&=&\frac{1}{\sigma_{\gamma\gamma}n_{\rm ph}}=\frac{4\pi R_{\rm ir}^2\epsilon_{\rm ir}}{\sigma_{\gamma\gamma}L} \\ &\simeq& 2\times 10^{-2}R_{\rm H}\left[\frac{L}{10^{42}\mbox{ erg/s}}\right]^{-1}\left[\frac{M}{10^9~M_\odot}\right]\left[\frac{\epsilon_{\rm ir}}{0.1\mbox{ eV}}\right]\nonumber, \end{eqnarray}](/articles/aa/full_html/2016/09/aa27549-15/aa27549-15-eq64.png) (21)which could become comparable to the distance on which electrons acquire enough energy for the pair production, h∗ ,accRH,h∗ ,icRH, if the luminosity of RIAF is low. In general, the gap height could be estimated as
(21)which could become comparable to the distance on which electrons acquire enough energy for the pair production, h∗ ,accRH,h∗ ,icRH, if the luminosity of RIAF is low. In general, the gap height could be estimated as 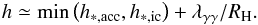 (22)The gap height is determined mostly by h∗ ,ic in the high-luminosity RIAF regime. In this situation the constant gap height lines in the parameter space L,B are the lines L ∝ B, shown in Fig. 2. If the inverse Compton energy loss is negligible, the gap height h∗ ,acc is determined by the minimal necessary potential difference in the gap needed for the onset of the gamma-gamma pair production. Here, h∗ ,acc does not depend on L. This regime is reached at the tip of the “wedge” regions in Fig. 2. In the regime of small L, the mean free path of photons increases. This influences the gap height in a magnetic-field-independent way. For each pre-defined gap height, there is a minimal “threshold” luminosity scale at which the photon mean free path becomes much larger than the height. This threshold value is shown as a set of vertical lines in Fig. 2.
(22)The gap height is determined mostly by h∗ ,ic in the high-luminosity RIAF regime. In this situation the constant gap height lines in the parameter space L,B are the lines L ∝ B, shown in Fig. 2. If the inverse Compton energy loss is negligible, the gap height h∗ ,acc is determined by the minimal necessary potential difference in the gap needed for the onset of the gamma-gamma pair production. Here, h∗ ,acc does not depend on L. This regime is reached at the tip of the “wedge” regions in Fig. 2. In the regime of small L, the mean free path of photons increases. This influences the gap height in a magnetic-field-independent way. For each pre-defined gap height, there is a minimal “threshold” luminosity scale at which the photon mean free path becomes much larger than the height. This threshold value is shown as a set of vertical lines in Fig. 2.
 |
Fig. 2 Height of the gap as a function of L,B for a range of black hole masses (from left to right): M = 3 × 105M⊙ (green) M = 3 × 107M⊙ (yellow) and M = 3 × 109M⊙ (red). Gap height h and mean free path λ are in the units of RH. |
Overall, the qualitative considerations presented above show that the constant gap height curves form a set of “wedges” in the L,B parameter space. For a given magnetic field strength, the gap “opens” (becomes large) either when the luminosity of RIAF is too low or it is too high. The infrared photon density in the low-luminosity RIAF is not sufficient for the interception of the high-energy γ-rays, which could produce electron-positron pairs. Strong inverse Compton energy loss in the high-luminosity RIAF precludes particle acceleration to the energies they are capable of to produce γ-rays that could produce pairs in interactions with the infrared photons.
2.4. Gap stability
Pair production process leads to the deposition of the plasma around the gap location. The initial assumption that was used to calculate the profile of the parallel electric field strength in the gap (6) is that the charge density reaches the Goldreigh-Julian value exactly at the boundary of the gap.
This assumption could be verified with a more detailed understanding of the process of particle acceleration followed by the pair production. The gamma-gamma pair production homogeneously deposits electron-positron pairs on the distance scale λγγ. This indicates that the characteristic distance scale on which the charge density and the parallel component of the electric field in the gap vary is λγγ. It is this distance scale that should be identified with H, as considered in Sect. 2.1. This identification could clearly be done in the situation when h∗ ,acc,h∗ ,ic ≪ λγγ/RH.
In the regime of high luminosity, the mean free path of the γ-rays that are able to produce pairs in interactions with the bulk of the infrared photons of RIAF is much shorter than the distance on which electrons are able to gain the energy sufficient for the production of such γ-rays. If such γ-rays were the only γ-rays capable of pair production, the configuration would be unstable. Indeed, the gap that initially opens up to the height h∗ ,ic would shrink immediately after opening down the h ~ λγγ ≪ h∗ ,ic, thus shutting down the pair production process. This instability is, however, naturally avoided because of the presence of the broad energy distribution of the RIAF’s photons.
Still, in this situation the gap height, which is about the electron acceleration length, is also about the γ-ray mean free path. If the spectrum of synchrotron infrared emission from the RIAF emits mostly in the energy band ϵir, there are still infrared photons of higher energies, even if the spectrum has an exponential higher energy cut-off. The presence of these higher energy photons provides a possibility for the γ-rays with energies somewhat lower than Eγ,thr to interact via the pair production. Much lower density of the higher energy infrared photons leads to a larger mean free path for the lower energy γ-rays. There exists an energy at which the mean free path of the γ-rays is comparable to the height scale h∗ ,ic. Electron acceleration to this energy (i.e. somewhat lower than ℰ = Eγ,thr) provides the stable gap configuration in which the charge density in the gap varies on the distance scale h ~ h∗ ,ic ~ λγγ/RH.
A realistic RIAF spectrum consists of three components: synchrotron, inverse Compton, and Bremsstrahlung emission from electrons in the accretion flow (Narayan et al. 1998; Yuan & Narayan 2014. Close to the black hole horizon, where heating electrons by protons is most efficient, the energies of electrons reach 10−100 MeV, and the synchrotron emission from such electrons is in the infrared range. The inverse Compton scattering of the synchrotron photons boosts the photon energies into the X-ray range. The high-energy γ-rays could produce pairs in interactions not only with the exponentially suppressed high-energy tail of the synchrotron spectrum of the RIAF, but also with the inverse Compton photons. We leave the detailed modelling of the imprint of the RIAF spectrum and spatial properties for future work.
2.5. Proton acceleration in the gap
Contrary to electrons, protons accelerated in the gap do not suffer from the severe energy losses that limit their energy. They could be accelerated to much higher energies than electrons. An estimate of the energies of protons is given by the total potential difference between the gap boundaries, ℰp ~ eBRHh3.
In the low-luminosity RIAF regime the gap height is determined by the mean free path of γ-rays that produce pairs in interactions with the bulk of the infrared emission from RIAF, h ~ λγγ/RH. In this case the maximum proton energies reach ![\begin{eqnarray} {\cal E}_{\rm p}&\sim& \frac{8\pi^2eBR_{\rm ir}^6\epsilon_{\rm ir}^3a}{3\sigma_{\gamma\gamma}^3L^3R_{\rm H}^2M}\simeq 7\times 10^{}\\ &&\quad \times \left[\frac{L}{10^{40}\mbox{ erg/s}}\right]^{-3}\left[\frac{B}{10^{4}\mbox{ G}}\right]\left[\frac{\epsilon_{\rm ir}}{0.1\mbox{ eV}}\right]^3\left[\frac{M}{10^9~M_\odot}\right]^4\mbox{eV.}\nonumber \end{eqnarray}](/articles/aa/full_html/2016/09/aa27549-15/aa27549-15-eq87.png) (23)One can see that in this regime proton energies typically do not reach the UHECR range unless the luminosity of RIAF is very low, L ≲ 1040 erg/s.
(23)One can see that in this regime proton energies typically do not reach the UHECR range unless the luminosity of RIAF is very low, L ≲ 1040 erg/s.
In the high-luminosity regime, the gap height is estimated as h ~ h∗ ,ic, and the maximum energies of protons are ![\begin{eqnarray} {\cal E}_{\rm p}&\sim& \frac{eBR_{\rm H}a}{24\pi M}\left(\frac{6\sigma_{\rm T}Lm_{\rm e}^2M}{4\pi e \epsilon_{\rm ir}^2BR_{\rm ir}^2a}\right)^{3/2} \simeq 2\times 10^{15}\\ &&\quad\times \left[\frac{L}{10^{44}\mbox{ erg/s}}\right]^{3/2}\left[\frac{B}{10^4\mbox{ G}}\right]^{-1/2}\left[\frac{M}{10^9~M_\odot}\right]^{-2}\left[\frac{\epsilon_{\rm ir}}{0.1\mbox{ eV}}\right]^{-3}\mbox{ eV.}\nonumber \end{eqnarray}](/articles/aa/full_html/2016/09/aa27549-15/aa27549-15-eq90.png) (24)Such gaps could not work as UHECR accelerators. The lines of the constant proton energy, passing the whole potential difference in the gap, in the (L,B) parameter space are shown in Fig. 3.
(24)Such gaps could not work as UHECR accelerators. The lines of the constant proton energy, passing the whole potential difference in the gap, in the (L,B) parameter space are shown in Fig. 3.
 |
Fig. 3 Proton energy, passing the whole potential difference in the gap, shown as a colour map and its levels in the (L,B) parameter space on logarithmic scale for the black hole mass M = 3 × 109M⊙. The dark diagonal valley corresponds to the minimal energy ~1013eV of the protons able to pass the gap’s full potential. This minimal energy does not depend on the black hole mass. The energies of about ≥ 1019eV are only reachable for the “big” opened gaps with a height of about H> 0.1RH. |
3. Numerical modelling
To verify the qualitative arguments presented in the previous sections, we perform Monte Carlo simulations of propagation of electrons and protons in the split monopole magnetospheres of black holes powered through the Blandford-Znajek process (Blandford & Znajek 1977). We only consider slowly rotating black holes with a = 0.1M.
Charged particles (electrons or protons) are injected at different locations in the vacuum gap. Particle trajectories inside and outside the gap are calculated by solving the equations of motion in the background magnetic and gravitational fields, following the methodology of Ref.(Neronov et al. 2009). Particles propagating in the force-free part of the magnetosphere and in the gap emit curvature and inverse Compton radiation. The power of this radiation is taken into account to calculate the synchrotron/curvature and inverse Compton energy losses that contribute to the radiative friction force. The inverse Compton energy loss in the Thomson and Klein-Nishina regimes is calculated based on a realistic emission spectrum of the synchrotron component of RIAF 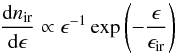 (25)with a high-energy cut-off at ϵ = ϵir. The overall normalisation of the synchrotron spectrum is determined by the assumed luminosity of RIAF, L. The size of the synchrotron emission region is assumed to be Rir = 10RH. Calculating the spectra of radiation from the propagated charged particles take the Doppler and gravitational redshift effects into account.
(25)with a high-energy cut-off at ϵ = ϵir. The overall normalisation of the synchrotron spectrum is determined by the assumed luminosity of RIAF, L. The size of the synchrotron emission region is assumed to be Rir = 10RH. Calculating the spectra of radiation from the propagated charged particles take the Doppler and gravitational redshift effects into account.
 |
Fig. 4 Mean free path of γ-rays of energy Eγ propagating through the photon background of the RIAFs of different luminosities with a model spectrum (25). Black hole mass M = 3 × 109M⊙. |
The gap height is calculated in a self-consistent way as a boundary of the pair production region. For each photon emitted by the propagated charged particle, we calculate its mean free path in the background radiation field 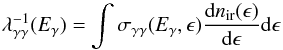 (26)(see Fig. 4) and check that the photon is absorbed within the calculation region. For the photons that are absorbed via pair production, the distances of the pair production points are recorded. The gap height is determined by the locations of the pair production points by the highest energy photons with the shortest mean free path. The height of the gap determined in this way is a function of the latitude θ.
(26)(see Fig. 4) and check that the photon is absorbed within the calculation region. For the photons that are absorbed via pair production, the distances of the pair production points are recorded. The gap height is determined by the locations of the pair production points by the highest energy photons with the shortest mean free path. The height of the gap determined in this way is a function of the latitude θ.
 |
Fig. 5 Height of the gap (thick solid curves), proton (thin solid curves), and mean electron (dashed curves) energies in the gap as a function of the latitude θ for a black hole of the mass M = 3 × 109M⊙, embedded in RIAF with “low” luminosity L = 8 × 1040 erg/s, magnetic field B = 103 G (red curves), and “high” luminosity L = 5 × 1043 erg/s, B = 102 G (blue curves). Electron and proton energies are almost independent of the latitude θ. |
Figure 5 shows the dependence of the height of the gap on the lattitude coordinate θ. One can see that the height is almost θ-independent. One could use the height measurement at a reference latitude, e.g. θ = 45°, to characterise the height dependence on other parameters of the system.
Figure 6 shows the gap height at θ = 45° as a function of the RIAF luminosity L and magnetic field B for several black hole masses. One can see that the numerically calculated curves generally agree with the qualitative curves of Fig. 2. The main difference is the absence of the sharp edge-like feature at h∗ ,acc = λγγ, which is replaced by a smooth turnover that interpolates between the low-luminosity and high-luminosity asymptotes. The gap height gets smaller with increasing magnetic field and luminosity. The gap completely opens below a certain threshold luminosity, which depends on the black hole mass. The calculations shown in Fig. 6 extend up to 0.01 Eddington luminosity LEdd = 1047[M/ 109M⊙]erg/s. This might be somewhat higher than the range of luminosities at which the RIAF model of accretion flow is valid.
 |
Fig. 6 Gap height as a function of RIAF luminosity L and magnetic field B for a range of black hole masses (from left to right): M = 3 × 105M⊙ (green), M = 3 × 107M⊙ (yellow) and M = 3 × 109M⊙ (red). |
We find that the observational appearance of the gap depends on the level of the luminosity of the accretion flow. Taking this into account, we divide the luminosity range onto “low”, “intermediate”, and “high”, depending on the part of the Fig. 6 curve at which the system parameters fit. The low-luminosity regime corresponds to the sharply rising (near vertical) part of the constant gap height curves, the “intermediate” regime is in the horizontal plateau range, and the “high-luminosity” regime corresponds to the rising part of the curves at high L values.
The maximal energies of electrons in the gap are shown as a function of L and B in Fig. 7. The energies increase with the decrease of the luminosity and increase of the magnetic field, as expected from the qualitative arguments presented above.
 |
Fig. 7 Maximum energies of electrons accelerated in the gap as a function of L,B. The black hole mass is M = 3 × 109M⊙. |
Higher energies of electrons lead to the higher energies of the synchrotron/curvature photons from these electrons. This is shown in Fig. 8. One can notice that the energy of the synchrotron/curvature emission varies in a very broad range from the ultraviolet and soft X-ray up to the TeV γ-ray band. The highest energies of synchrotron/curvature photons violate the so-called self-regulated cut-off of the synchrotron spectrum, Es ≲ me/α, where α is the fine structure constant (Aharonian 2004). This is because the acceleration proceeds in a large scale electric field aligned with the particle velocity. In this situation, the acceleration rate is higher than the ~eB⊥ assumed for calculating the self-regulated cut-off.
 |
Fig. 8 Maximum energies of synchrotron/curvature radiation photons produced by electrons in the gap, as a function of L and B. The black hole mass is M = 3 × 109M⊙. |
Pair production process limits the energy of inverse Compton photons to Eic ~ Eγ,thr independently of the parameters of the system. This is clear from Figs. 9−11, which show the spectra of emission from electrons in the low-, intermediate-, and high-luminosity systems. In all the spectra, the maximum energies of γ-rays escaping to infinity are E ~ 1012 eV, which corresponds to the redshifted energies of photons with energies comparable to the pair production threshold.
 |
Fig. 9 Spectra of emission from electrons in the gap in the split monopole magnetosphere in a low-luminosity RIAF with L = 8 × 1040 erg/s around a black hole of the mass M = 3 × 109M⊙ and magnetic field B = 103 G (top) and B = 104 G (bottom). Red shows the synchrotron/curvature emission, blue and green show the inverse Compton emission, green corresponds to the photons that escape from the source, and blue shows the photons absorbed via pair production. A red arrow shows the normalisation uncertainty. |
The spectra of emission from the low-, intermediate-, and high-luminosity RIAFs have a qualitatively different appearance. The low-luminosity RIAF spectra shown in Fig. 9, the dominant flux contribution is from the synchrotron/curvature component that is sharply peaked in the 1−100 GeV range. The inverse Compton emission is largely subdominant and is perhaps barely detectable, provided that its flux is some three orders of magnitude below the GeV component flux. The GeV bump in the spectrum of the synchrotron/curvature emission is rather broad, spanning several decades in energy. The normalisation of the gap spectra is defined by the maximum (Goldreich-Julian) density of the radiating electrons in the gap, though the gap luminosity is uncertain and varies with the changes of parameters (14).
One of the examples of the low-luminosity RIAF (L ~ 1040−1041erg/s) is M87 (Neronov & Aharonian 2007; Broderick & Tchekhovskoy 2015). The characteristic size of the infrared source is estimated as ~10 RH. The direct mid-infrared observations of M87 (Perlman et al. 2007; Whysong & Antonucci 2004) resolves the central source within ~10 pc ~ 104RH. On the other hand, millimetre wavelength observations (Doeleman et al. 2012) limit its size within horizon scale RH.We compare the calculated spectra with M87 high-energy observations (Fig. 9) (Abdo et al. 2009; Aharonian 2006; Acciari et al. 2008; Aleksić et al. 2012).
 |
Fig. 10 Same as in Fig. 9 but for the intermediate luminosity RIAF L = 5 × 1041 erg/s around the M = 3 × 109M⊙ black hole in magnetic field B = 103 G (top) and B = 104 G (bottom). |
In the higher luminosity RIAFs, the synchrotron/curvature component becomes sub-dominant. Its spectrum shifts to lower energies and becomes more peaked towards the higher energy. Overall, the synchrotron/curvature emission could appear as a narrow feature in the observed spectra of X-ray/soft γ-ray emission from intermediate RIAF luminosity sources (see Fig. 10). In contrast, the dominant very-high-energy inverse-Compton emission in these sources has a very characteristic observational appearance: it is a relatively hard spectrum with the slope dN/ dE ∝ E− Γ with Γ ~ 1.5 and an abrupt (“super-exponential”) cut-off at the energy of the threshold of the pair production. In a realistic situation, the cut-offf could be sharper or smoother depending on the details of the RIAF spectrum in the source, but the strong imprint of the pair production on the spectrum of emission from the vacuum gap is a generic feature of the VHE spectrum.
 |
Fig. 11 Same as in Fig. 9 but for the high-luminosity RIAFs L = 1044 erg/s and magnetic field B = 100 G (top) and L = 1043 erg/s and magnetic field B = 102 G (bottom). The black hole mass is M = 3 × 109M⊙. |
Spectra of the high-luminosity RIAF also have a strong imprint of the pair production, see Fig. 11. In these spectra, the synchrotron/curvature component might be not detectable at all, until the magnetic field is extremely high. Besides this, strong radiation drag on the accelerated electrons produces a soft low-energy tail in the spectrum of the inverse-Compton emission component.
 |
Fig. 12 Maximum energies of protons ejected from the gap. Black hole mass is M = 3 × 109M⊙. |
The maximum achievable energy protons, passing through the full available potential difference in the gap, do not depend strongly on the coordinate θ. We can use the energy at the reference latitude θ = π/ 4 as the characteristic value. The dependence of the proton maximal energies on L and B is shown in Fig. 12. In accordance with the analytical estimates, the maximum protons energies are not lower than 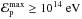 , where 1014 eV is an energy that corresponds to the line h∗ ,acc = λγγ. This minimal energy is reached exactly on this line in the L,B diagram.
, where 1014 eV is an energy that corresponds to the line h∗ ,acc = λγγ. This minimal energy is reached exactly on this line in the L,B diagram.
In accordance with analytical estimates, in our numerical calculations, we find that only energies of about ℰp ~ 1017−1018 are reachable in the gap in the magnetosphere of black holes with masses in the range M = 105−109M⊙ with magnetic field up to B ~ 104 G in low-luminosity RIAFs. This maximum energy is reached in the widest possible gaps and highest possible magnetic fields in the low-luminosity RIAF regime. Our calculations do not extend to the situations in which UHECR production in black hole magnetospheres is possible. This would require still lower luminosity RIAFs where the gap height could become comparable to the size of the black hole (in other words, where the force-free magnetosphere does not form at all).
4. Discussion and conclusions
In a realistic situation, the spectrum of electromagnetic emission from the vacuum gap is superimposed on the spectrum of emission from the inner part of the FR I/BL Lac jet. The jet spectrum is typically represented by the broad synchrotron and inverse-Compton components, which could be modelled as log parabolas or cut-off power laws. Taking the similar appearance of the gap and jet emission spectra into account, it might be challenging to prove or falsify the existence of the gap contribution to the overall spectra of the nuclear emission of the FR I galaxies and of the BL Lacs. In this respect, it is important to identify the distinguishing feature of the gap emission spectrum. This could be done for the low-, intermediate-, and high-luminosity RIAF cases based on Figs. 9−11.
The high- and intermediate-luminosity RIAF cases are characterised by the strong inverse Compton component reaching the TeV band and having a sharp cut-off at the energy of the threshold of the pair production on the RIAF synchrotron photons. The presence of the shape cut-off is understood wellqualitatively and appears to be the distinguishing feature of emission from the gap. The details of the spectral shape of the cut-off is determined by the details of the spectrum of the synchrotron component of RIAF. If this component is observed in the infrared band, the shape of the cut-off of the inverse Compton emission from the gap could be predicted. Observations of the FR I galaxies with identifiable synchrotron component of the RIAF and with the spectra extending into the very-high-energy (VHE) range would provide a crucial test for the gap emission model. The test will be the detection/non-detection of a VHE spectral component component with the sharp cut-off with the shape determined by the shape of the RIAF spectral component.
The sharply cut-off inverse Compton component in the intermediate-luminosity RIAF case also has a hard spectrum below the cut-off. The slope of the spectrum could be harder than the conventional slope Γ ≃ 1.5 expected from the E-2 type distribution of electrons in the Thomson regime. The presence of the gap emission could then potentially provide an explanation for the hard spectra of VHE γ-ray emission from BL Lacs, such as the flaring spectrum of Mrk 501 in 2009 Neronov et al. (2012). Actually, the hard slope of the spectrum, combined with the sharp high-energy cut-off could make the gap emission appear as a sharp, almost line-like (within the energy resolution of the γ-ray telescope) feature on top of a broad spectrum of inverse-Compton emission from the jet.
The sharp VHE γ-ray band spectral feature is accompanied by a comparably sharp (or even sharper) feature at the lower energies (soft γ-ray band) produced by the synchrotron/curvature emission from electrons accelerated in the gap. This feature is also potentially detectable with the telescope sensitive in the MeV−GeV band (see Fig. 10).
This sharp spectral feature in the VHE part of the spectrum is perhaps not detectable in the case of the emission from the gap embedded into low-luminosity RIAF. In this case only synchrotron/curvature emission is detectable. It appears as a hard-spectrum or high-energy cut-off feature in the 1−100 GeV band, and it could also be easily distinguished from the broad inverse Compton emission from the jet, which usually dominates the spectrum of FR I galaxies and BL Lacs in this energy range (see Fig. 9).
Overall, the observational appearance of the gaps in low-, intermediate-, and high-luminosity RIAFs is always in the form
of the sharp spectral features appearing on top of the broader or smoother jet spectra. Improving quality of the γ-ray data expected with CTA should allow identification of these sharp features in the high-statistics spectral measurements of the spectra of BL Lacs and FR I galaxies. The data of the Fermi/LAT telescope could be mined for the search of possibly transient narrow spectral components in the spectra of the LAT-detected sources from these source classes.
Acknowledgments
We thank V. S. Beskin and D. Malyshev for the discussions. The work of K.P. was supported by the Russian Science Foundation grant 14-12-01340. K.P. acknowledges the Swiss Government Scholarship.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009, ApJ, 707, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Abramowski, A., Acero, F., Aharonian, F., et al. 2012, ApJ, 746, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Acciari, V. A., Beilicke, M., Blaylock, G., et al. 2008, ApJ, 679, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F. A. 2004, Very high energy cosmic gamma radiation : a crucial window on the extreme Universe (World Scientific Publ.) [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2006, Science, 314, 1424 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2007, ApJ, 664, L71 [Google Scholar]
- Aleksić, J., Alvarez, E. A., Antonelli, L. A., et al. 2012, A&A, 544, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aleksić, J., Ansoldi, S., Antonelli, L. A., et al. 2014, Science, 346, 1080 [NASA ADS] [CrossRef] [Google Scholar]
- Bardeen, J. M., Press, W. H., & Teukolsky, S. A. 1972, ApJ, 178, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, A. R. 1978, MNRAS, 182, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Beskin, V. S., Istomin, Y. N., & Parev, V. I. 1992, Sov. Astron. Lett., 36, 642 [Google Scholar]
- Blandford, R. D., & Znajek, R. L. 1977, MNRAS, 179, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Boldt, E., & Ghosh, P. 1999, MNRAS, 307, 491 [NASA ADS] [CrossRef] [Google Scholar]
- Bridle, A. H., & Perley, R. A. 1984, ARA&A, 22, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Broderick, A. E., & Tchekhovskoy, A. 2015, ApJ, 809, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Cheng, K. S., Ho, C., & Ruderman, M. 1986, ApJ, 300, 500 [NASA ADS] [CrossRef] [Google Scholar]
- Chiaberge, M., Capetti, A., & Celotti, A. 1999, A&A, 349, 77 [NASA ADS] [Google Scholar]
- Doeleman, S. S., Fish, V. L., Schenck, D. E., et al. 2012, Science, 338, 355 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Drury, L. O. 1983, Rep. Prog. Phys., 46, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Foschini, L., Bonnoli, G., Ghisellini, G., et al. 2013, A&A, 555, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldreich, P., & Julian, W. H. 1969, ApJ, 157, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Hirotani, K., & Okamoto, I. 1998, ApJ, 497, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Komissarov, S. S. 2004a, MNRAS, 350, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Komissarov, S. S. 2004b, MNRAS, 350, 1431 [NASA ADS] [CrossRef] [Google Scholar]
- Komissarov, S. S. 2005, MNRAS, 359, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Krawczynski, H. 2007, ApJ, 659, 1063 [NASA ADS] [CrossRef] [Google Scholar]
- Krymskii, G. F. 1977, Akademiia Nauk SSSR Doklady, 234, 1306 [NASA ADS] [Google Scholar]
- Levinson, A. 2000, Phys. Rev. Lett., 85, 912 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Levinson, A., & Rieger, F. 2011, ApJ, 730, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Marscher, A. P., Jorstad, S. G., D’Arcangelo, F. D., et al. 2008, Nature, 452, 966 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Narayan, R., Mahadevan, R., & Quataert, E. 1998, in Theory of Black Hole Accretion Disks, eds. M. A. Abramowicz, G. Björnsson, & J. E. Pringle (Cambridge University Press), 148 [Google Scholar]
- Neronov, A., & Aharonian, F. A. 2007, ApJ, 671, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Neronov, A., Tinyakov, P., & Tkachev, I. 2005, Sov. J. Exp. Theor. Phys., 100, 656 [NASA ADS] [CrossRef] [Google Scholar]
- Neronov, A. Y., Semikoz, D. V., & Tkachev, I. I. 2009, New J. Phys., 11, 065015 [NASA ADS] [CrossRef] [Google Scholar]
- Neronov, A., Semikoz, D., & Taylor, A. M. 2012, A&A, 541, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neronov, A., Vovk, I., & Malyshev, D. 2015, Nat. Phys., 11, 664 [NASA ADS] [CrossRef] [Google Scholar]
- Perlman, E. S., Mason, R. E., Packham, C., et al. 2007, ApJ, 663, 808 [NASA ADS] [CrossRef] [Google Scholar]
- Romanova, M. M., & Lovelace, R. V. E. 1992, A&A, 262, 26 [NASA ADS] [Google Scholar]
- Sturrock, P. A. 1971, ApJ, 164, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Vincent, S., & Lebohec, S. 2010, MNRAS, 409, 1183 [NASA ADS] [CrossRef] [Google Scholar]
- Vovk, I., & Neronov, A. 2013, ApJ, 767, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Vovk, I., & Neronov, A. 2016, A&A, 586, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wald, R. M. 1974, Phys. Rev. D, 10, 1680 [NASA ADS] [CrossRef] [Google Scholar]
- Whysong, D., & Antonucci, R. 2004, ApJ, 602, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, F., & Narayan, R. 2014, ARA&A, 52, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, F., Quataert, E., & Narayan, R. 2003, ApJ, 598, 301 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Goldreich-Julian charge density in the split-monopole force-free black hole magnetosphere. The black hole rotation moment is a = 0.1M. The horizon is the boundary of the blue circle in the bottom left corner of the map. The black area is the region with negative charge density. The colour scale shows the region of positive values of ρ(r,θ) with the colour scaling logarithmically with ρGJ. The green curve shows the location of the gap at the surface ρGJ = 0. |
| In the text | |
 |
Fig. 2 Height of the gap as a function of L,B for a range of black hole masses (from left to right): M = 3 × 105M⊙ (green) M = 3 × 107M⊙ (yellow) and M = 3 × 109M⊙ (red). Gap height h and mean free path λ are in the units of RH. |
| In the text | |
 |
Fig. 3 Proton energy, passing the whole potential difference in the gap, shown as a colour map and its levels in the (L,B) parameter space on logarithmic scale for the black hole mass M = 3 × 109M⊙. The dark diagonal valley corresponds to the minimal energy ~1013eV of the protons able to pass the gap’s full potential. This minimal energy does not depend on the black hole mass. The energies of about ≥ 1019eV are only reachable for the “big” opened gaps with a height of about H> 0.1RH. |
| In the text | |
 |
Fig. 4 Mean free path of γ-rays of energy Eγ propagating through the photon background of the RIAFs of different luminosities with a model spectrum (25). Black hole mass M = 3 × 109M⊙. |
| In the text | |
 |
Fig. 5 Height of the gap (thick solid curves), proton (thin solid curves), and mean electron (dashed curves) energies in the gap as a function of the latitude θ for a black hole of the mass M = 3 × 109M⊙, embedded in RIAF with “low” luminosity L = 8 × 1040 erg/s, magnetic field B = 103 G (red curves), and “high” luminosity L = 5 × 1043 erg/s, B = 102 G (blue curves). Electron and proton energies are almost independent of the latitude θ. |
| In the text | |
 |
Fig. 6 Gap height as a function of RIAF luminosity L and magnetic field B for a range of black hole masses (from left to right): M = 3 × 105M⊙ (green), M = 3 × 107M⊙ (yellow) and M = 3 × 109M⊙ (red). |
| In the text | |
 |
Fig. 7 Maximum energies of electrons accelerated in the gap as a function of L,B. The black hole mass is M = 3 × 109M⊙. |
| In the text | |
 |
Fig. 8 Maximum energies of synchrotron/curvature radiation photons produced by electrons in the gap, as a function of L and B. The black hole mass is M = 3 × 109M⊙. |
| In the text | |
 |
Fig. 9 Spectra of emission from electrons in the gap in the split monopole magnetosphere in a low-luminosity RIAF with L = 8 × 1040 erg/s around a black hole of the mass M = 3 × 109M⊙ and magnetic field B = 103 G (top) and B = 104 G (bottom). Red shows the synchrotron/curvature emission, blue and green show the inverse Compton emission, green corresponds to the photons that escape from the source, and blue shows the photons absorbed via pair production. A red arrow shows the normalisation uncertainty. |
| In the text | |
 |
Fig. 10 Same as in Fig. 9 but for the intermediate luminosity RIAF L = 5 × 1041 erg/s around the M = 3 × 109M⊙ black hole in magnetic field B = 103 G (top) and B = 104 G (bottom). |
| In the text | |
 |
Fig. 11 Same as in Fig. 9 but for the high-luminosity RIAFs L = 1044 erg/s and magnetic field B = 100 G (top) and L = 1043 erg/s and magnetic field B = 102 G (bottom). The black hole mass is M = 3 × 109M⊙. |
| In the text | |
 |
Fig. 12 Maximum energies of protons ejected from the gap. Black hole mass is M = 3 × 109M⊙. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


