| Issue |
A&A
Volume 592, August 2016
|
|
|---|---|---|
| Article Number | A25 | |
| Number of page(s) | 18 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201628142 | |
| Published online | 06 July 2016 | |
Towards automatic classification of all WISE sources
1 Astronomical Observatory of the Jagiellonian University, ul.Orla 171, 30-244 Cracow, Poland
e-mail: kurcz.agnieszka@gmail.com
2 Janusz Gil Institute of Astronomy, University of Zielona Góra, ul. Szafrana 2, 65-516 Zielona Góra, Poland
3 Leiden Observatory, Leiden University, Niels Bohrweg 2, 2333 CA Leiden, The Netherlands
4 Astrophysics, Cosmology and Gravity Centre, Department of Astronomy, University of Cape Town, Rondebosch, South Africa
5 National Centre for Nuclear Research, ul.Hoża 69, 00-681 Warszawa, Poland
Received: 15 January 2016
Accepted: 11 April 2016
Context. The Wide-field Infrared Survey Explorer (WISE) has detected hundreds of millions of sources over the entire sky. Classifying them reliably is, however, a challenging task owing to degeneracies in WISE multicolour space and low levels of detection in its two longest-wavelength bandpasses. Simple colour cuts are often not sufficient; for satisfactory levels of completeness and purity, more sophisticated classification methods are needed.
Aims. Here we aim to obtain comprehensive and reliable star, galaxy, and quasar catalogues based on automatic source classification in full-sky WISE data. This means that the final classification will employ only parameters available from WISE itself, in particular those which are reliably measured for the majority of sources.
Methods. For the automatic classification we applied a supervised machine learning algorithm, support vector machines (SVM). It requires a training sample with relevant classes already identified, and we chose to use the SDSS spectroscopic dataset (DR10) for that purpose. We tested the performance of two kernels used by the classifier, and determined the minimum number of sources in the training set required to achieve stable classification, as well as the minimum dimension of the parameter space. We also tested SVM classification accuracy as a function of extinction and apparent magnitude. Thus, the calibrated classifier was finally applied to all-sky WISE data, flux-limited to 16 mag (Vega) in the 3.4 μm channel.
Results. By calibrating on the test data drawn from SDSS, we first established that a polynomial kernel is preferred over a radial one for this particular dataset. Next, using three classification parameters (W1 magnitude, W1−W2 colour, and a differential aperture magnitude) we obtained very good classification efficiency in all the tests. At the bright end, the completeness for stars and galaxies reaches ~95%, deteriorating to ~80% at W1 = 16 mag, while for quasars it stays at a level of ~95% independently of magnitude. Similar numbers are obtained for purity. Application of the classifier to full-sky WISE data and appropriate a posteriori cleaning allowed us to obtain catalogues of star and galaxy candidates that appear reliable. However, the sources flagged by the classifier as “quasars” are in fact dominated by dusty galaxies; they also exhibit contamination from sources located mainly at low ecliptic latitudes, consistent with solar system objects.
Key words: methods: data analysis / methods: statistical / astronomical databases: miscellaneous / catalogs / infrared: general / surveys
© ESO, 2016
1. Introduction
The Wide-field Infrared Survey Explorer (WISE, Wright et al. 2010) is a space-borne telescope that has scanned the entire sky in four infrared (IR) bands (3.4–23 μm) and has delivered one of the largest catalogues of astronomical objects to date. It has detected almost 750 million sources, which are compiled in the publicly released AllWISE Source Catalogue (Cutri et al. 2013). WISE provides at present the most comprehensive census of the entire sky in the IR, and offers large advancement in comparison to earlier all-sky IR surveys, such as IRAS (Neugebauer et al. 1984), 2MASS (Skrutskie et al. 2006), or AKARI (Murakami et al. 2007).
Such a vast amount of data, which gives access to all-sky information in unprecedented volumes, has found multiple astronomical applications starting from our closest neighbourhood (near-Earth objects, nearby stars, and brown dwarfs), through the galaxies in the local volume, and up to the largest possible distances of high-redshift quasars (Wright et al. 2010). All these types of sources are present in the WISE database (within its sensitivity limits), but reliably extracting them in large numbers is challenging. Briefly, the WISE data release does not provide separate catalogues of different objects. What is more, at present there is no separate point- and extended-source catalogues extracted from this survey, although efforts towards the latter are underway (Cluver et al. 2014).
There are several reasons for the lack of comprehensive object identification in WISE. Firstly, this survey is mostly a near-IR selected one. Practically all the sources listed in the WISE catalogue have S/N> 2 detections in the W1 band (3.4 μm), and 83% of them have W2 (4.6 μm) measured with this accuracy; the detection rates in W3 (12 μm) and W4 (23 μm) are much lower1. The light emitted at 3.4 and 4.6 μm comes mainly from the photospheres of evolved stars. This means that in the low-redshift Universe, where a large part of the extragalactic WISE sources are located, the W1−W2 colour of galaxies will be very similar to that of Galactic stars and cannot in general provide a comprehensive criterion for distinguishing one from the other. This is readily seen in WISE colour–colour diagrams such as those provided by Jarrett et al. (2011). These diagrams also show that even adding the W3 band, which traces dust such as silicates and PAHs, is not sufficient to unambiguously distinguish stars from elliptical galaxies. Last but not least, such colour-colour plots assume negligible photometric errors, while in reality significant scatter will occur, as is the case for the W3 and W4 bands, for which most of the WISE sources have only upper limits or are not even detected.
Another way to separate galaxies from stars in WISE could be identifying extended sources in the sample. Similarly to the case of the 2MASS Extended Source Catalogue (XSC, Jarrett et al. 2000), such sources in WISE are expected to be mainly extragalactic, especially at sufficiently high Galactic latitudes. However, despite much better sensitivity of WISE with respect to 2MASS (e.g. 0.054 mJy in W1 vs. 2.7 mJy in Ks) and the lack of atmospheric nuisances in the former, lower angular resolution of WISE and higher background levels mean that the eventual all-sky WISE XSC is expected to contain a similar number of sources to the 2MASS catalogue (~30 per square degree; Jarrett et al. 2016). This will be a very small percentage of all WISE galaxies: Cluver et al. (2014) showed that only 3–4% of WISE sources matched with the Galaxy And Mass Assembly (GAMA, Driver et al. 2011) survey are resolved in W1, while the WISE×GAMA sample itself is already much shallower than expected from the full WISE galaxy catalogue (Bilicki et al. 2016; Jarrett et al. 2016). One possible avenue leading to a WISE-based all-sky catalogue of galaxies of a similar depth to those in GAMA is to cross-match WISE sources with SuperCOSMOS data (Hambly et al. 2001), as was first discussed by Bilicki et al. (2014). Such a catalogue has been recently compiled (Bilicki et al. 2016; Krakowski et al., in prep.), but it includes only a part of the WISE galaxies owing to limitations of the SuperCOSMOS scans of photographic plates (both in depth and in the colour space).
Until now, most of the studies dealing with WISE source classification were based on cross-matching this catalogue with other samples and using multiband magnitudes and colours as discriminants. Stern et al. (2012), who paired up WISE with COSMOS, have proposed using W1−W2 ≥ 0.8 mag (Vega) to identify WISE active galactic nuclei (AGNs). Assef et al. (2013) have extended this work to a larger and deeper NOAO Deep Wide-Field Survey Boötes field and showed that this criterion is no longer optimal at fainter magnitudes. A more comprehensive effort has been undertaken by Yan et al. (2013), where WISE sources were cross-matched with SDSS to derive colour cuts for object selection. The Stern et al. (2012) AGN identification has been confirmed and WISE colours (especially W1−W2 vs. W2−W3) have been shown to be sufficient to separate star-forming galaxies from AGNs and stars from some galaxies, although this was not the case for early-type, low-redshift galaxies, which occupy practically the same region in the W1–W2–W3 colour-colour space as stars. More recently, Ferraro et al. (2015) have defined their own colour cuts to identify galaxies and quasars from the WISE database; however, this left position-dependent contamination visible in all-sky maps. Nikutta et al. (2014) have explored WISE colours of Galactic and other nearby sources, while Mateos et al. (2012) have used the XMM-Newton survey to define a WISE colour-based selection of luminous AGN. The latter criterion has recently been applied to the all-sky WISE data by Secrest et al. (2015) to select a sample of 1.4 million AGN candidates. We note, however, that their criterion of w1,2,3snr ≥ 5 (signal-to-noise ratios in W1, W2 and W3) eliminates about 95% of AllWISE sources from the parent catalogue, mostly owing to a very low level of WISE detection in the W3 channel. Last but not least, Jarrett et al. (2016) have identified various source types in the G12 equatorial field by calibrating WISE magnitude and colour cuts on GAMA and SDSS spectroscopic data.
Some other WISE source classification studies where additional colours from external surveys were used include Edelson & Malkan (2012) and Wu et al. (2012) for QSOs/ AGNs, Tu & Wang (2013) for asymptotic giant branch stars, and Kovács & Szapudi (2015) for general star-galaxy separation in a WISE – 2MASS PSC cross-match. Finally, Anderson et al. (2014) compiled a catalogue of Galactic H II regions from WISE, based on their mid-IR morphology.
In the present paper, we go beyond simple colour and magnitude cuts and explore a more sophisticated classification of WISE sources. Our approach is based on automatised procedures of machine learning, and we use a specific algorithm – the support vector machines (SVM) – which has proven its aptitude for similar tasks within AKARI (Solarz et al. 2012) and VIPERS (Małek et al. 2013) surveys. A similar idea was explored in the independent study by Kovács & Szapudi (2015) where multiband photometry of those WISE sources that had cross-matches with the 2MASS Point Source Catalogue (PSC) was used for SVM-based source classification. Our analysis is more general, as we do not limit the final source selection to a cross-match with an external catalogue. In addition, for the classification we use only the two shortest WISE bands in order to retain the highest all-sky completeness possible. By training the classifier on WISE data cross-matched with the tenth spectroscopic release of the Sloan Digital Sky Survey (SDSS, Ahn et al. 2014), we make the first step towards building reliable and comprehensive WISE catalogues of stars, galaxies, and AGNs/QSOs. At present, this classification is limited by the spectroscopic data that we used for training, but the methodology can be extended with forthcoming data from different star, galaxy, and quasar catalogues. Solar system bodies should probably be included, as we find hints of them contaminating especially our final quasar candidate dataset.
The paper is organised as follows. Section 2 describes the data used in our analysis: the photometric sample extracted from WISE (Sect. 2.1) and the spectroscopic sample from SDSS (Sect. 2.2) used by the classification algorithm. In Sect. 3, we present the support vector machines classifier and how to apply it to imbalanced datasets (Sect. 3.1) such as ours. Various tests of the SVM method on WISE data are shown in Sect. 4. Section 5 presents the application of the SVM classifier to a full-sky sample drawn from WISE data. We summarise our work in Sect. 6.
All the WISE magnitudes in this paper will be given in the Vega system. For transformation to AB see Jarrett et al. (2011).
2. Data selection
2.1. WISE
The WISE is a Medium Class Explorer mission funded by NASA and launched in December 2009. With the use of a 40 cm space-based telescope, WISE has mapped the whole sky (with a total 47 × 47 arcmin field of view) in four infrared bands W1−W4, centred respectively at 3.4, 4.6, 12, and 23 μm2, with an angular resolution of 6.1′′, 6.4′′, 6.5′′, and 12.0′′, respectively. Its 5σ point source sensitivities exceeded 0.054, 0.071, 0.73, and 5 mJy in the four respective bands; in the W3 channel, for instance, this is more than a hundred times better than that of IRAS at similar wavelengths. The publicly available AllWISE catalogue contains positional, photometric, quality, and reliability information and motion fit parameters for over 747 million sources (Cutri et al. 2013).
The goal of the present study is to obtain a comprehensive source classification for as many WISE objects as possible, and so for object selection we decided to rely uniquely on the parameters provided in the WISE database as there is no other all-sky survey of comparable depth currently available. The basic dataset we employ is the “AllWISE” data release3 (Cutri et al. 2013), which was made publicly available in 2013 and combines data from the WISE cryogenic and NEOWISE (Mainzer et al. 2014) post-cryogenic survey stages. This dataset offers enhanced photometry and astrometry in comparison to the earlier WISE “All-Sky” release and includes estimates of source apparent motions.
We wanted to have the greatest sky coverage and depth possible, and we thus chose to be flexible in the preliminary source selection for our catalogue. Regarding the photometry, we use only the two shortest WISE bands, W1 and W2, and we employ additional quality parameters to ensure reliability of the sources. Our catalogue includes the sources that match the following criteria in the WISE database: w1snr≥ 5; w2snr≥ 2; w?sat ≤ 0.1 (no more than 10% of saturated pixels in the respective bands, where ? stands for 1 or 2); cc_flags[?] ≠ ‘DPHO’ (no severe artefacts). These criteria ensure that the sources are detected in the two bands with reliable photometry (most of the objects have S/N much higher than the limits used for the preselection; see below). There are over 606 million such sources in WISE; however, a large number of these are concentrated in the Galactic Plane, where the WISE data suffer from severe blending and saturation due to the enhanced source density. Our ability to classify data at low Galactic latitudes is thus very much compromised, and practically impossible within the Galactic Plane and Bulge.
An important caveat here is that the AllWISE catalogue is not complete at the very bright end (W1 < 8 mag and W2 < 7 mag) owing to the saturation of such sources and also in two strips at ecliptic longitudes of 45° < λ < 55° and 231° <λ < 239°. Both these issues are related to instrumental limitations4, while the survey strategy causes additional patterns related to Moon avoidance manoeuvres5. This will be reflected in the all-sky maps that we are producing.
Here we are not able to comprehensively classify all the WISE sources preselected as discussed above owing to the limitations brought about by the training set from the spectroscopic SDSS DR10 that we use. Namely, that dataset cross-matched with WISE practically does not provide galaxies fainter than Vega W1 < 16 mag6. This is one magnitude brighter than the average all-sky photometric completeness of WISE, so the present analysis will need to be extended once deeper training data become available. This should be possible in the coming years thanks to the plethora of spectroscopic surveys currently underway. The all-sky sample of preselected W1 < 16 mag AllWISE sources includes 314 million sources and is illustrated in the Aitoff projection in Fig. 1. We note the logarithmic scaling of the counts and one order of magnitude larger source density in the Galactic Plane than at high latitudes. We also note that at this flux limit most of our sources have very reliable photometry, especially in the W1 channel. The median signal-to-noise ratios in W1 and W2 are respectively 31.3 and 16, and more than 99% of the sources have magnitude errors smaller than 0.08 mag for W1 and 0.28 mag for W2.
 |
Fig. 1 Aitoff projection in Galactic coordinates of 314 million sources in the AllWISE catalogue, flux-limited to W1 < 16 mag. |
In the machine learning procedure of source classification described later in the text we use the following parameters provided by WISE:
-
1.
magnitude w1mpro measured with profile-fitting photometry in the W1 band (hereafter W1);
-
2.
colour W1−W2 defined as the difference in the w1mpro and w2mpro (hereafter W2) profile-fitting magnitudes;
-
3.
a concentration parameter defined as the difference of two circular aperture magnitudes in the W1 channel, w1mag_1−w1mag_3, measured respectively in radii 5.5” and 11” centred on the source; we note that these apertures were fixed, independent of the actual size or shape of the sources, and were not corrected for contamination or bad pixels, thus they cannot be used on their own as reliable measurements of fluxes for resolved sources.
As already mentioned, measurements in the W1 band in our flux-limited sample have typically very high signal-to-noise ratios; the other two parameters used for the classification are somewhat noisier. The error in the W1−W2 colour is mostly driven by the less accurate W2 channel, and respectively 90% (99%) of the sources have δ(W1−W2) < 0.16 mag (<0.29 mag). For the concentration parameter, the same percentiles are δ(w1mag_1−w1mag_3) < 0.17 mag (<0.41 mag).
We also tested the usefulness of apparent motions for source classification. These motions, as provided in the AllWISE database (pmra and pmdec), are composed of source proper motions and those due to the parallax, and are expected to be different for various source types. We note, however, different caveats related to their measurements by WISE, discussed by Kirkpatrick et al. (2014) and in the data description7. The accuracy and signal-to-noise of AllWISE proper motions are strongly correlated with the source’s flux, which means they cannot be reliably used for the whole catalogue (about 2% of WISE objects have no motion measurements at all). We consider using them as a proof of concept for future datasets and surveys that will bring much more precise and comprehensive motion measurements, such as the MaxWISE proposal (Faherty et al. 2015), Gaia (Perryman et al. 2001) or LSST (Ivezić et al. 2008). The fourth parameter used in such a case was
-
4.
apparent motion defined as pm= (pmra2 + pmdec2)1/2, where pmra and pmdec are the apparent motion in right ascension and declination, respectively.
All the tests involving the apparent motions were carried out with the imposed condition on their signal-to-noise being larger than 1: pm>sigpm, where sigpm= (sigpmra2 + sigpmdec2)1/2 is the motion accuracy as provided in the database. This condition introduces a selection effect as it removes mostly faint, point-like sources. This constraint is avoided in the final classification procedure when proper motions are not used.
One can further increase the number of parameters used for machine learning classification; however, it should first be noted that every new parameter considerably extends computation time. In addition, many of the WISE database parameters are available or are sufficiently reliable only for a subset of all the sources. For instance, the two longer WISE bands, W3 and W4, which are often also used for source classification (Ferraro et al. 2015; Kovács & Szapudi 2015), have much worse sensitivity than W1 and W2. Most of the WISE sources are not detected at the longer wavelengths or have only upper limits of S/N< 2. In view of classifying a considerable number of WISE objects (selected as discussed above), we have thus decided to limit ourselves to the basic information from the W1 and W2 bands. A possible extension employing more WISE parameters would first require determining which of them are optimal, for instance thorough a principal component analysis (Soumagnac et al. 2015). In addition, similarly to other applications of SVM in astronomy, our study does not take the observational errors explicitly into account. For the present sample this should be a good approximation, as the noise level of the parameters we use for classification is relatively low (or even very low for the W1 magnitude). In Sect. 6 we discuss how this issue can be dealt with in future work by using what is known as fuzzy logic.
2.2. Training sample: WISE × SDSS DR10
Machine learning methods for source classification, like the one we employ here, rely on the availability of a training sample that has relevant classes already identified. Ideally, this dataset should be as typical of the whole sample as possible. At present, however, such samples drawn from WISE are not available, and the only solution is to cross-match the WISE data with an external dataset that has relevant source types listed. Such an auxiliary dataset is provided by the Sloan Digital Sky Survey (SDSS, York et al. 2000), which in its third phase (SDSS III, Eisenstein et al. 2011) comprises several dedicated star, galaxy, and quasar surveys; however, these three classes are available only for the spectroscopic part of the SDSS (the photometric classes are “stars”, i.e. point-like, and “galaxies”, i.e. resolved). For this reason we chose to use only those SDSS sources that have spectra (Bolton et al. 2012). Here we use the spectroscopic sample in the SDSS Data Release 10 (DR10, Ahn et al. 2014), which includes almost 3.4 million sources, 26% of which are classified by the SDSS pipeline as stars, 59% are galaxies, and the remaining 15% are quasars/AGNs (class “QSO” in SDSS). We have cross-matched this sample with the WISE catalogue selected as described above, using a 1′′ matching radius, which gave us 2.1 million sources (18% stars, 72% galaxies, and 10% QSOs). However, not all of them had SDSS spectra of sufficient quality, so in order to maintain the reliability of the training sample, we filtered the sources according to redshift (velocity) quality, keeping only those with zWarning= 0. Additional visual inspection of redshift and error distributions of WISE × SDSS sources led us to eliminate the following outliers: zErr> 0.001 for stars, zErr> 0.001 or zErr/ z> 0.1 for galaxies, and zErr> 0.01 for QSOs. This filtering left us with about 390 000 stars, 1.5 million galaxies, and 190 000 quasars in our training sample (i.e. present both in SDSS and in WISE), which reduces further to 120 000 stars, 620 000 galaxies, and 55 000 QSOs if the condition on the apparent motions to have S/N> 1 is applied (Sect. 2.1).
 |
Fig. 2 Distributions of the observed W1−W2 colour for stars, galaxies, and quasars in the cross-matched WISE × SDSS DR10 sample. |
Figure 2 presents the W1−W2 colour histogram of our training sources (as observed, i.e. without extinction- or k-corrections applied). It clearly shows that while a simple selection in this colour may allow a large fraction of WISE quasars to be identified (although the W1−W2 > 0.8 mag cut proposed by Stern et al. 2012 will miss some of them), it is not sufficient to reliably separate stars from galaxies. For instance, a constant W1−W2 colour cut will not produce samples that are both complete and pure at the same time. Maps presented in Ferraro et al. (2015) also indicate that applying fixed colour cuts to WISE data may leave position-dependent contamination. In the WISE × SuperCOSMOS dataset (Bilicki et al. 2016) this issue was partly alleviated by varying the star-galaxy colour separation as a function of distance from the Galactic Centre. Here we move beyond this simple methodology.
 |
Fig. 3 Normalised apparent W1 magnitude counts for galaxies, quasars, and stars in the WISE × SDSS DR10 sample. |
As already mentioned in Sect. 2.1, using the SDSS as the training sample imposes restrictions on the depth up to which we can classify WISE sources in the present application. As shown in Fig. 3, presenting normalised W1 counts for the three source types in the WISE × SDSS cross-match, there are hardly any galaxies fainter than W1 = 16 mag, so we are not able to create reliable training samples beyond this magnitude, although both stars and galaxies are present in the WISE × SDSS sample at considerably fainter fluxes. The histogram for galaxies also displays two clear peaks. This shape for the galaxy counts can be attributed to the combination of two effects: one results from the heterogeneity of the SDSS dataset itself (due to preselections of the Main, CMASS, and BOSS samples) and the other is related to the selection of the WISE × SDSS catalogue, which is also based on the detections in the W1 filter. First, as demonstrated in Figs. 4 and 5, the SDSS-based galaxy selection does not sample all the regions of the redshift-magnitude space equally. In particular, as illustrated in the left panel of Fig. 4 which shows the redshift-magnitude diagram for the z band (the longest wavelength measured by SDSS), in the pure SDSS data we observe a clear depletion of faint red galaxies at z ≤ 0.3 in comparison to higher redshifts. This effect persists after adding the W1-based selection of the WISE × SDSS sample, as shown in the right panel of Fig. 4. The enhancement of this effect can be attributed to the properties of the W1 filter, which at low redshifts probes the part of the galaxy spectrum where strong PAH features are very prominent. Second, in Fig. 6 the convolution of the W1 filter with a spectrum of a typical spiral galaxy at various redshifts (taken from the Brown et al. 2014b library) demonstrates that observing in W1 we can expect a selection function which does not change monotonically with redshift. In particular, it has a minimum at z ~ 0.15, and then rises again until z ~ 0.28. The combination of these effects results in a relatively complex sampling of galaxies in the redshift – W1 magnitude space in the WISE × SDSS data, as demonstrated in Fig. 5.
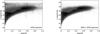 |
Fig. 4 Redshift – apparent magnitude diagrams for the SDSS z band: SDSS-only galaxies (left panel) and galaxies from the WISE × SDSS cross-match (right panel). |
Finally, we cannot hope for reliable classification also at the very bright end. The WISE W1 < 8 mag or W2 < 7 mag sources are saturated; in addition, the WISE × SDSS sample does not include galaxies or quasars brighter than W1 ~ 9.5 mag. These brightest objects are thus removed from our final samples, which has a minor influence on the results because the W1 < 9.5 mag WISE sources are concentrated mostly in the Galactic Bulge (i.e. they are stars and blends thereof).
We are aware of all these biases, and we would like to note that introducing them is a trade-off if we want to use the training sample providing star, galaxy, and quasar spectral classifications. At the depths we are interested in, these spectral classifications are currently available only from the SDSS. As a final caveat, the training sample applied in this study does not include solar system bodies; however, they are present in the WISE database. Our final classification thus ignores this contamination, which affects mostly the sources flagged as quasars by our classifier.
3. Classification method: support vector machines
In general, classification is a process that uses pattern recognition. A classifier is a function that maps a feature vector of a given object’s characteristics into a discriminant vector containing likelihoods that the objects belong to the different considered classes. Classification schemes rely on choosing a feature space where different classes occupy different volumes with minimal overlapping. This approach has been used to develop machine learning algorithms – statistical methods which constitute a branch of artificial intelligence and are based on creating and exploiting systems which learn from data.
In this work for the task of identifying object types we adopt the support vector machines (SVM) algorithm. This supervised method based on kernel algorithms (Shawe-Taylor & Cristianini 2004) was designed to extract structures from data, and thanks to its excellent ability to deal with multidimensional samples combined with its high accuracy, it has been extensively applied to many diverse astronomical problems. To name a few, SVMs have been used to solve problems like classifying different structures in the interstellar medium (Beaumont et al. 2011), pinpointing active galactic nucleus (AGN) candidates (Cavuoti et al. 2014), or distinguishing different subclasses of specific spectral type stars (Bu et al. 2014). Last but not least, and of particular relevance here, SVM has been proven efficient in classifying different objects, such as stars, quasars, and galaxies (e.g. Saglia et al. 2012; Solarz et al. 2012; Małek et al. 2013; Kovács & Szapudi 2015).
In what follows, we draw the general outline of the nature of the algorithm; for an in-depth discussion we refer the reader to Vapnik (1999), Cristianini & Shawe-Taylor (2000), Hsu et al. (2003).
Each training object can be described by a number of quantities, N, which determine its discriminating properties. The SVM regards the values of the quantities as a position of a given object in an N-dimensional parameter space; in other words, the algorithm maps the feature vector from the input space X to a feature space H using a non-linear function φ:X → H. In the feature space H, the discriminant function, which will determine the boundary, takes the form of  (1)Here k(x,x′) represents the kernel function, which returns the inner product of the mapped vectors; αi is a linear coefficient; and b is a perpendicular distance called bias, which translates the discriminant function into a given direction.
(1)Here k(x,x′) represents the kernel function, which returns the inner product of the mapped vectors; αi is a linear coefficient; and b is a perpendicular distance called bias, which translates the discriminant function into a given direction.
With a substantial amount of feature vectors representing different classes of objects, the algorithm searches for boundaries segregating those classes with the biggest possible distance from each data point (a margin). The objects lying closest to the boundary are called support vectors. In other words, the SVM algorithm searches for a decision boundary B that will maximise a fitness function F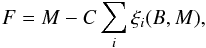 (2)where M denotes the margin of the boundary. The number of training examples violating this criterion is given by ξi(B,M). If a position of a point i is found within a distance higher than M from B, then ξi = 0. In the opposite case, ξi will be equal to the distance that point i should be shifted so that the condition is satisfied. To set a trade-off between the large margins M and misclassifications ξi, an adjustable cost parameter is used (more details in Beaumont et al. 2011).
(2)where M denotes the margin of the boundary. The number of training examples violating this criterion is given by ξi(B,M). If a position of a point i is found within a distance higher than M from B, then ξi = 0. In the opposite case, ξi will be equal to the distance that point i should be shifted so that the condition is satisfied. To set a trade-off between the large margins M and misclassifications ξi, an adjustable cost parameter is used (more details in Beaumont et al. 2011).
 |
Fig. 5 Redshift – apparent magnitude diagram for the WISE W1 band for the galaxies from the WISE × SDSS cross-match. |
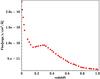 |
Fig. 6 Convolution of the W1 filter with a template spectrum of a typical spiral galaxy as a function of redshift. |
Using kernel functions allows a shift into a higher dimensional parameter space, where the data are usually much more simply separated than in lower dimensional space. There are many possible kernel functions that can be used (such as polynomials, exponential radial basis functions, or multilayer perceptrons; Cristianini & Shawe-Taylor 2000). The choice of the proper kernel suitable for a given problem is crucial; the usual procedure is to try several, beginning from the simplest cases (to avoid overfitting and to save on parameter tuning time) and then to move towards more complex ones in order to gain accuracy. For this particular dataset we tested two kernel functions to obtain the most reliable classification outcome: the Gaussian radial basis function (GRB) and the polynomial function. The GRB is given by 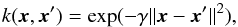 (3)where x and x′ represent feature vectors in the input space, ||·|| denotes the Euclidean distance, and γ is the adjustable kernel width parameter, which is responsible for the curvature of the decision surface. The polynomial kernel is defined as
(3)where x and x′ represent feature vectors in the input space, ||·|| denotes the Euclidean distance, and γ is the adjustable kernel width parameter, which is responsible for the curvature of the decision surface. The polynomial kernel is defined as 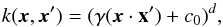 (4)where x and x’ represent feature vectors in the input space, x·x′ is their inner product, d stands for the degree of the polynomial function, and c0 is a constant coefficient.
(4)where x and x’ represent feature vectors in the input space, x·x′ is their inner product, d stands for the degree of the polynomial function, and c0 is a constant coefficient.
Therefore, for the GRB kernel there are two adjustable parameters, γ and C, which will determine the separation boundary and complete the training of the SVM classifier. In the case of the polynomial kernel, the number of adjustable parameters increases to four: in addition to γ and C, the degree d and the coefficient c0 have to be known. Then, after the most efficient kernel function is chosen, a classification of the new data points depends on their position relative to the boundary: SVM will assign a type to unknown objects based on which side of the separation hyperplane they fall.
Numbers of objects before and after oversampling in the bins for which oversampling was applied.
Furthermore, instead of assigning discrete class labels, it is possible to determine the class probability for a given object. In the case of binary SVM this can be done by implementing Platt’s a posteriori probabilities (Platt 1999; Lin et al. 2007): once the decision values f of the SVM classifiers are computed, a sigmoid function 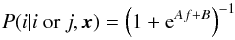 (5)is fitted (where i and j represent two classes). Then, A and B are estimated by minimising the negative log-likelihood function. In order to extend the probabilities of classes to a three-class problem, all class probabilities from output of binary classifiers are combined (Fan Wu et al. 2003). The probabilities calculated this way are used in the final classification to eliminate sources that have low probabilities of belonging to any class (meaning that each class has p< 0.5, and in some cases the three probabilities are p ~ 0.33).
(5)is fitted (where i and j represent two classes). Then, A and B are estimated by minimising the negative log-likelihood function. In order to extend the probabilities of classes to a three-class problem, all class probabilities from output of binary classifiers are combined (Fan Wu et al. 2003). The probabilities calculated this way are used in the final classification to eliminate sources that have low probabilities of belonging to any class (meaning that each class has p< 0.5, and in some cases the three probabilities are p ~ 0.33).
Support vector machines are currently available in a variety of software packages; the most widely used is libsvm (Chang & Lin 2011)8, which provides robust implementation of SVM for both classification and regression. In this work we use the R (R Development Core Team 2005)9 implementation of SVM included in the e1071 package (Dimitriadou et al. 2005), which provides an interface to libsvm.
3.1. SVM on imbalanced datasets: oversampling
Our training dataset is characterised by low numbers of bright objects in the QSO sample. It was then necessary to address the problem of the accuracy decreasing as a result of this imbalance. This feature is common in many classification schemes, especially those which aim for the maximisation of accuracy, like SVMs (Akbani et al. 2004). If not accounted for properly, this can result in making a simple decision that is the basis of the maintenance of the highest success rate: assigning the most common class to the test objects. There are two ways of addressing this problem: it can be solved eiher through rebalancing the dataset or by altering the algorithm itself. The first solution works at the level of manipulating the data, where the under-represented population(s) can be oversampled, or the dominant class can be undersampled. In the latter case, when reducing the number of objects contained within the majority class, distributional assumptions on the data must be made: some crucial information may be lost or additional noise may be introduced. On the other hand, changing the algorithm mainly relies on cost-sensitive learning where a higher penalty is assigned to the misclassifications, resulting in a shift of the classifiers towards the minority class, which improves the detection accuracy.
Since SVM decision making relies solely on the support vectors, it works well against any noise in the data and any light imbalance. Therefore, if the distribution of the training sets is very skewed, the number of support vectors in the majority class overweighs the ones from the minority class. In the case of the WISE data we decided to perform oversampling of the under-represented class of QSO, i.e. additional artificial objects were created. The number of missing objects (Xmissing) needed to be added to QSO training samples was calculated using the equation (Małek et al. 2013) 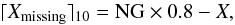 (6)where ⌈ ⌉ 10 stands for rounding the value up to the nearest ten, X corresponds to the number of original QSOs in the sample, and NG is the number of galaxies. This strategy provides fully balanced training samples, which are essential for building an effective classifier.
(6)where ⌈ ⌉ 10 stands for rounding the value up to the nearest ten, X corresponds to the number of original QSOs in the sample, and NG is the number of galaxies. This strategy provides fully balanced training samples, which are essential for building an effective classifier.
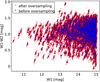 |
Fig. 7 Representative colour–magnitude diagram before and after oversampling for quasars. |
We created mock samples of missing objects by slight changes in the real parameters. In the first step a real QSO was randomly chosen, and then its parameters were reassigned by shifting the real ones by an amount drawn from a Gaussian distribution with specific standard deviations σ. Different values of σ were used, depending on the type of parameter: σpm for proper motions and σW for magnitudes. They were calculated as the median values of the proper motion and magnitude uncertainties, respectively. These values are given in Table 1, which lists the cases in which the oversampling was applied, providing numbers of objects before and after the oversampling (see Sect. 4 for details on the magnitude and extinction divisions). Figure 7 presents an example of a colour-magnitude diagram for quasars before and after oversampling. The distribution of objects after the oversampling closely mimics the real one, as designed.
4. Calibrating the SVM classifier for the WISE data
In this section we present various tests of the SVM algorithm performed on the WISE × SDSS training data to verify and optimise the performance of the classifier. In particular, we tested the algorithm’s efficiency as a function of the following: i) choice of the kernel; ii) number of sources in the training samples; iii) number of parameters used for the classification; iv) Galactic extinction; v) limiting magnitude of the sample; and vi) use of source apparent motions. This information allowed us to prepare the SVM for the application to the all-sky WISE dataset (Sect. 5).
Comparison of SVM performances for two kernels, polynomial and radial, for the self-check and cross-test.
In each of the tests, we used a ten-fold cross-validation technique: we divided the training set into ten subsets of equal size, selected nine of the subsets to train the classification model, and then tested it on the remaining subset; this was repeated ten times, leaving out a different subset each time. We then counted the training objects whose nature was correctly identified by SVM: TS (true star), TG (true galaxy), TQ (true QSO), and those misclassified by the algorithm: FG (false galaxy), FS (false star), and FQ (false QSO).
Then we define completeness c, contamination f, and purity p for the three classes of objects (e.g. Soumagnac et al. 2015). For galaxies we have 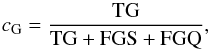 (7)
(7)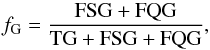 (8)
(8)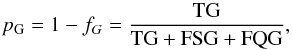 (9)where TG, FGS, and FGQ stand for galaxies classified respectively as galaxies, stars, and quasars, and FSG (FQG) define stars (quasars) misclassified as galaxies. Analogous definitions are used for completeness, contamination, and purityof stellar (cS, fS, pS) and quasar (cQ, fQ, pQ) samples.
(9)where TG, FGS, and FGQ stand for galaxies classified respectively as galaxies, stars, and quasars, and FSG (FQG) define stars (quasars) misclassified as galaxies. Analogous definitions are used for completeness, contamination, and purityof stellar (cS, fS, pS) and quasar (cQ, fQ, pQ) samples.
In each case we measure completeness, purity, and contamination for two variants: a self-check and a cross-test. For the self-check we classified the same objects used in the given training sample. In the cross-test we classified objects from the subsamples that were not in the current training set.
The tests described below were performed for different combinations of magnitude limits and Galactic extinction levels. Three flux limits were adopted: W1 < 14 mag, W1 < 15 mag, and W1 < 16 mag. In each data were also binned according to the measured Galactic dust emission. Here we chose the 100-micron intensity (I100) sky map made from a combination of COBE/DIRBE and IRAS 100 μm measurements (Schlegel et al. 1998). We preferred the I100 parameter over the commonly applied E(B−V) because the former was directly measured from data, while the latter was derived. We adopted four extinction bins: I100< 1, 1 ≤ I100< 2, 2 ≤ I100< 3, and 3 ≤ I100< 10 [MJy/sr]. Above I100 = 10 MJy/sr, which constitutes about 1% of the WISE × SDSS catalogue, there are practically no galaxies or quasars in the training set. In general, the I100 ≥ 10 MJy/sr areas cover about 17% of the full sky, practically only in the Galactic Plane and regions of high dust obscuration where our classification is not expected to be reliable.
In some cases, the above splitting of the full sample left us with very small numbers of quasars in the relevant training sets, and the oversampling methodology had to be applied (see Sect. 3.1).
4.1. Kernel performance comparison
The first test served to determine the optimal kernel for our application. We compared the performance of the two kernel functions described in Sect. 3, polynomial and radial (see Table 2), and analysed the so-called univariate histograms of projections from the self-check and cross-test of the known data. A univariate histogram of projections is a graphical representation of the training data for a given binary classification (in the case of a three-class classifier we have three two-class classifiers) and the decision boundary SVM provides given the data. To obtain the best efficiency of the classification, it is standard practice to divide the training set into two subsets: one is used for actual training and the other is a validation subset used as a verification of the accuracy of the created hyperplane against other known objects, even if not used for training. In this test, the training set contains 99% of the total number of sources with known classification, while the validation test is composed of the remaining 1% of known objects.
 |
Fig. 8 Comparison of the histograms of projection values of the training data samples onto the normal direction of the SVM decision boundary for a radial (left column) and polynomial kernel (right column). The top row represents the division between galaxies and stars (red and blue, respectively), the middle row between galaxies and quasars (red and green), the bottom row between stars and quasars. Vertical lines represent the boundaries of the decision hyperplane margins for the two classes (+1 and −1), and 0 marks the position of the hyperplane itself. |
For non-linear SVM kernels, projected values f(x) (Eq. (1)) are obtained though the kernel representation in a dual space. This means that there are three support vector machines (in the case of WISE × SDSS data), each of which has its own decision function. Projection of an object xk from a training set onto the normal direction of a non-linear SVM boundary can be written as 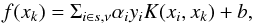 (10)where xi denotes a support vector, and classification of each example is determined by the sign of this function. The soft margin of a classifier can be written as
(10)where xi denotes a support vector, and classification of each example is determined by the sign of this function. The soft margin of a classifier can be written as 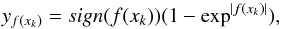 (11)and the boundaries of the soft margin are then yf(xk) ∈ [−1;1]. Then, yf(xk) describes two aspects of each example. The first comes from the sign: it encodes a “hard” decision whether the example xk belongs to a given class or not. The second comes from its absolute value: it represents how strong the decision is. This means that the farther a given example xk falls from the decision boundary, the more certain the decision is.
(11)and the boundaries of the soft margin are then yf(xk) ∈ [−1;1]. Then, yf(xk) describes two aspects of each example. The first comes from the sign: it encodes a “hard” decision whether the example xk belongs to a given class or not. The second comes from its absolute value: it represents how strong the decision is. This means that the farther a given example xk falls from the decision boundary, the more certain the decision is.
As can be seen from Table 2, the differences between completeness and purity of the training samples and validation datasets are small for the two kernels considered. However, when we compare the histograms of projections of each point with respect to the boundary we see clear differences (Figs. 8 and 9). For the radial kernel we observe an effect of data piling on the margins, which is typical for high-dimensional data (Cherkassky & Mulier 2006). Separability of the set on which the classifier was trained does not imply that the validation or test sets will be equally well separated (see Figs. 8 and 9, left columns). As the SVM optimisation aims at high separability of the training data, it penalises the data that fall into the soft margin of the separation boundary. However, the aim is also to have a good separation of the validation set (which in turn should improve the separability of the test sample), which is why the preferred model should allow data points to fall into the soft margin. Moreover, it is desirable to have as decision values that are as strong as possible; therefore, the data piling effect should be avoided, which is why the kernel that displays a clearer division of validation – the polynomial kernel in this case – is preferable, as is shown in Fig. 9.
4.2. Optimal number of objects in the training samples
 |
Fig. 10 Dependence of the completeness (upper panels) and purity (lower panels) on the number of objects in the training set of a W1 < 14 mag flux-limited sample, for the self-check (left panels) and the cross-test (right panels) cases. Relevant contamination levels are 100%−Purity. |
As our WISE × SDSS training set is much larger than in earlier SVM classification applications (e.g. in AKARI by Solarz et al. 2012 or in VIPERS by Małek et al. 2013), in the first step, after deciding which kernel function to use, we performed a series of tests to check whether we were able to calibrate our SVM method on smaller subsamples without deteriorating the results. We conducted four tests for each of the three flux-limited samples (in this case there was no extra division according to the extinction), where we randomly chose 100, 1000, 3000, and 5000 objects for each class (i.e. 100 galaxies, 100 stars, 100 quasars, etc.), and we used these training sets to compute relevant statistics as defined above. Each test was repeated ten times, and in all the cases the error bars provided represent the standard deviation from the mean of the ten tests.
Figure 10 shows, as an example, the dependence of the completeness and purity on the number of training objects for a bin W1 < 14 mag for the self-check and cross-test. The results for other flux limits are similar. As seen in this figure, our results stabilise for subsamples with 3000 randomly chosen objects from each class. Based on these results, the following tests were applied for these numbers of objects. This allowed us to significantly save on computation time in the tests, as it scales highly non-linearly with the size of the training set.
 |
Fig. 11 Dependence of the completeness (upper panels) and purity (lower panels) on the number of parameters used for SVM training of a sample with W1 < 14 mag and I100< 1 [MJy/sr], for the self-check (left panels) and the cross-test (right panels) cases. The specific classification parameters for the training were W1 (1st), W1−W2 (2nd), w1mag_1−w1mag_3 (3rd), and apparent motions (4th). See text for details. Relevant contamination levels are 100%−Purity. |
4.3. Parameter space for classification
After establishing the optimal size of the training samples, we performed a series of tests to determine the minimum number of parameters sufficient for optimal classification. Each additional parameter significantly extends computation time, while it does not necessarily improve overall accuracy, for instance in cases when it is noise-dominated and/or not related to the source type. We thus started by using just two, the W1 magnitude and the W1−W2 colour, and then extended the parameter space by first adding the differential aperture magnitude w1mag_1−w1mag_3, and then the apparent motions pm (cf. Sect. 2.1 for parameter descriptions). For a proper comparison, these tests were applied on sources with “detected” proper motions, i.e. pm>sigpm. In addition, they were employed in various combinations of magnitude cuts and extinction bins, as described earlier.
Figure 11 shows how completeness and purity change when the number of implemented parameters increases. This particular example is for W1 < 14 mag and I100< 1 [MJy/sr] , but the results were qualitatively the same for each of the magnitude cut – extinction combinations. While quasars were already very accurately classified for the two parameters used (W1 and W1−W2), for stars and galaxies both completeness and purity significantly increased after the differential aperture magnitude was used as the third parameter. On the other hand, the proper motions did not bring any improvement, and sometimes even a slight deterioration in accuracy was observed once they were applied. This is hardly surprising given all the caveats associated with WISE apparent motion measurements (Kirkpatrick et al. 2014): they are not accurate enough for our type of analysis, and from now on we will thus focus on tests not using proper motions. We can expect, however, that longer time baselines and/or better photometric accuracy possible with the NEOWISE data (Mainzer et al. 2014), once combined into the MaxWISE data product (Faherty et al. 2015)10, and with future surveys (such as the LSST) should allow proper motions to become a useful parameter for the classification of sources, including extragalactic ones. This would also identify a fourth type of source, one that we have not considered here as we do not have them in the training samples, although they are certainly present in the WISE database, namely minor bodies of the solar system. As is shown in Sect. 5, they most likely contaminate the quasar candidate sample in the final all-sky classification.
4.4. Dependence of classification accuracy on extinction and limiting magnitude
Two final tests of the SVM algorithm applied to WISE × SDSS data were to check its performance against varying extinction levels and increased magnitude cut. Figures 12 and 13 summarise the results, and show how completeness and purity change with varying magnitude for four I100 bins, for the three classes of sources. Here we used smaller increments (0.5 mag) than in the other tests where it was 1 mag.
At the bright end, both completeness and purity retain very high levels of greater than 90% irrespective of extinction. These numbers for stars and galaxies gradually deteriorate for fainter sources, and some dependence on the extinction starts to appear as larger magnitudes are reached. The statistics are relatively stable and are at very good levels for quasars (where a slight increase in purity is actually observed at the faint end). We note however that even for fainter sources, star and galaxy samples exhibit completeness of over ~80% and purity of over 77%. Detailed results regarding completeness, purity, and contamination for all magnitude-extinction bins for the self-check and cross-test in the three dimensional parameter-space are presented in Tables A.1 and A.2 in the Appendix.
 |
Fig. 12 Dependence of the completeness on the magnitude for four I100 bins when using three classification parameters (W1, W1−W2 and w1mag_1−w1mag_3) for galaxies (upper panel), stars (middle panel) and quasars (lower panel) from the WISE × SDSS sample. These results are for the cross-test. |
 |
Fig. 13 Dependence of the purity on the magnitude for four I100 bins when using three classification parameters (W1, W1−W2, and w1mag_1−w1mag_3) for galaxies (upper panel), stars (middle panel), and quasars (lower panel) from the WISE × SDSS sample. These results are for the cross-test. |
We note, however, that such statistics may be partly misleading as they refer to the test sample, which is statistically consistent with the training set. The full-sky catalogue will differ, and in particular may (and does) contain sources not represented in the training, such as asteroids. The classifier tuned to the training set will underperform in such cases, which in particular will be reflected in low probabilities of such objects belonging to any of the three classes used in the analysis. We discuss this further in the following section.
5. Application of the SVM classifier to all-sky WISE
Having verified in various ways the performance of our classifier, we finally applied it to the all-sky WISE data limited to W1 < 16 mag. In this case, to tune the classifier we used the most comprehensive and general training data; we randomly selected 104 galaxies, 104 stars, and 104 quasars from the cross-matched WISE × SDSS dataset with W1 < 16 mag. Thus, the trained classifier flagged 70%/27%/3% of our WISE sources respectively as stars/galaxies/QSOs on the full sky. These numbers are consistent with the fact that stars dominate the source counts at the bright end of WISE (Jarrett et al. 2011, 2016); however, they should not be taken at face value. At low Galactic latitudes and in other highly crowded areas (Magellanic Clouds, Galactic extended sources such as dust clouds) the classification is highly unreliable. In addition, these numbers refer to the sources for which the probability of being of a given type was higher than that of the other two (e.g. p(star) >p(galaxy) & p(star) >p(QSO) for stars). However, for a considerable number of objects, especially in the galaxy and QSO classes, the three probabilities were comparable, which means a very low level of confidence for a class assignment. Thus, to obtain galaxy and quasar candidate catalogues based on our data, the masking of problematic areas was necessary, as was additional cleanup of low-probability sources. In the case of stars this was not needed, first, because we do expect them to be present in the highly crowded areas and second, their class assignment was the most robust: 99.4% of the sources classified as stars had p(star) > 0.5. A map of the 220 million star candidates is shown in Fig. 14. A decrease in counts at b ~ 0° is caused by saturation and blending.
 |
Fig. 14 All-sky map of 220 million star candidates identified by our classifier in AllWISE W1 < 16 mag data, in Aitoff projection in Galactic coordinates. We note the logarithmic scaling of the count colour bar. |
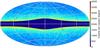 |
Fig. 15 All-sky map of 45 million galaxy candidates identified by our classifier in AllWISE W1 < 16 mag data, in Aitoff projection in Galactic coordinates. This plot shows sources over the probability threshold of p(gal) > 0.6 after appropriate cleanup and masking (see text for details). |
The catalogue of candidate galaxies, unlike stars, needed considerable purification. First of all, we had to cut out the most confused areas of the Galactic Plane and Bulge, using a longitude-dependent masking of the | b | < 6.5° sources at ℓ = 180° up to | b | < 20° near the Galactic Centre. This removed almost 30 million objects out of the 84.5 × 106 pre-assigned to the galaxy class all-sky. As seen in Fig. 15, this mask could have been wider, but we leave it in this form to emphasise classification issues at low Galactic latitudes where blends become a significant problem for star/galaxy separation in WISE. In addition to the bright-end cut already mentioned in Sect. 2.2 (due to saturation and lack of bright sources in the training set), which affected a very small number of the objects, we also eliminated over 400 000 outliers at the faint end in the W2 band, W2 > 16.1 mag. These were located mostly near the Ecliptic Poles where WISE coverage was the highest owing to the scanning strategy. This cutout also automatically removed the sources with W1−W2 < −0.1 mag which are most certainly stellar (Wright et al. 2010). In the final stage of the galaxy catalogue cleanup, we used the probabilities assigned by SVM as described in Sect. 3, and examined the sky and colour distribution of the galaxy candidates after applying different thresholds in p(gal). More aggressive cuts in this probability lead to a more uniform distribution of the sources as a function of latitude. However, even for p(gal) > 0.7 or more, differences of over 50% in the source density remain between the Galatic Caps and | b | ~ 20°. As the W1−W2 colours of the objects with high galaxy probability were consistent with those of genuine galaxies, the effect of gradually increasing number counts from high to low Galactic latitudes must be related to both the stellar contamination (blending) and galaxy incompleteness going up with decreasing | b |.
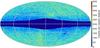 |
Fig. 16 Sources flagged by our classifier as quasar candidates in the WISE W1 < 16 mag catalogue. This sample shows 6 million objects with an SVM probability p(QSO) > 0.5 after appropriate cleanup and masking (see text for details). |
Figure 15 shows an example of all-sky source distribution of galaxy candidates. Included are 45 million sources obtained after the masking, bright- and faint-magnitude cutouts, and placement of a threshold of p(gal) > 0.6. There is clear contamination at low Galactic latitudes, but the classifier seems to be working well at least for half of the sky down to | b | = 30°. The missing data in stripes on the left above the Plane and just below it on the right are due to AllWISE instrumental artefacts (saturation at the beginning of the post-cryogenic phase) as already discussed in Sect. 2.1.
The quasar candidates underwent similar purification to the galaxy candidates. The same cutout of the Galactic plane was first applied, which removed almost 30% of the 9.4 million all-sky sources flagged by SVM as QSO. In addition, more aggressive bright-end cuts than in the galaxy case were necessary to avoid dangerous extrapolation from the training sample. We removed quasar candidates with W1 < 10.4 mag or W2 < 10.1 mag, as such bright QSOs are practically non-existent in WISE × SDSS. In the SVM output, they were mostly misclassified stars or blends of stars, localised chiefly at low Galactic latitudes and in the Magellanic Clouds. A further cleanup to keep only the p(QSO) > 0.5 sources resulted in 6 million objects as pictured in Fig. 16. This number is most certainly an overestimate for the true WISE quasar population at W1 < 16 mag. In addition to the saturation-related artefacts, we note some interesting features in the map which are not seen for the galaxy candidates. First, there is a lack of sources at low Galactic latitudes, qualitatively similar to the WISE AGN distribution presented in Ferraro et al. (2015), where sources were classified based on colour cuts. Second, various WISE scanning issues are imprinted here, the most important being overdensity stripes perpendicular to the ecliptic, resulting from Moon avoidance manoeuvres (cf. the mask applied in Ferraro et al. 2015). There is, however, additional spurious overdensity which seems to roughly follow the ecliptic, visible at the top right of the map and below the Bulge, to the left. This suggests some very local contamination, such as from asteroids or maybe zodiacal light, and most likely reflects the presence of a fourth type of source in addition to the three types in the training set from SDSS.
Unlike in the test phase described in Sect. 4, here we do not know the “truth” to which we could compare the classifier’s performance; however, some indirect a posteriori tests are possible. The first is the all-sky distribution, which for stars and galaxy candidates (at high latitudes) is consistent with expectations, but much less for the quasars. The second test is to verify source properties, such as colours. For identified galaxies, the W1−W2 colour is very consistent with the colour found in the WISE × SDSS training set (cf. Fig. 2) when the higher p(gal) cut is applied. For quasar candidates the situation is different. Even for very high thresholds of p(QSO), the peak in this colour is at W1−W2 ~ 0.6 mag rather than ~ 1 mag as in the training set (Fig. 17). In fact, the sources of expected quasar nature with W1−W2 > 0.8 mag (Stern et al. 2012) are only 1/5 of our QSO candidate sample. As already seen from their all-sky map, some of the contamination may come from solar system objects. As an additional verification, we checked the location of the SVM QSO in the W2−W3 vs. W1−W2 diagram for those sources that had a W3 detection. The bulk of the QSO candidates are located at 3 <W2−W3 < 4 [mag] and 0.4 <W1−W2 < 0.7 [mag], which does not give a clear characterisation of their nature. Indeed, following Wright et al. (2010), this is where various galaxy types overlap in this parameter space (“normal” spirals, Seyferts, strabursts, LIRGs, etc.). This also indicates that even if we had used the W3 parameter (which, as we emphasise, is robustly measured only for a small subset of our sources), this degeneracy between quasars and non-AGN galaxies would most likely remain.
 |
Fig. 17 Distribution of the W1−W2 colour for WISE × SDSS quasars (grey bars) and for SVM quasar candidates identified in all-sky WISE data, with no threshold on the SVM QSO probability (red), and for p(QSO) > 0.5 and >0.75 (blue and black, respectively). |
6. Summary and future prospects
In this paper we presented an application of a machine learning algorithm – the support vector machines – to classify sources in an all-sky catalogue drawn from WISE. The algorithm was trained and tested on a sample of WISE objects cross-matched with SDSS spectroscopic data, where three main types of astrophysical sources – stars, galaxies and quasars – had been independently identified. To optimise the performance of SVM, we first determined that a polynomial kernel of the third degree is preferred over the traditionally used radial one. We next verified that a training sample of less than 10 000 randomly chosen sources was sufficient to obtain stable results; in addition, the algorithm had already performed satisfactorily for a three-dimensional parameter space (W1 magnitude; W1−W2 colour; differential aperture mag in the W1 channel).
Having established the optimal set-up of the SVM method for our purposes, we performed several tests of its performance on WISE data. Here we focused on completeness and purity as a function of the limiting magnitude of the test sample, and on their dependence on Galactic extinction. For stars and galaxies both these statistics deteriorate for increasing magnitudes, but even at the faint end they rarely fall below ~80%. On the other hand, no obvious dependence of the SVM performance on magnitude is observed for quasars. Finally, Galactic extinction does not seem to have influence on the results, although we note that the tests were limited to regions of EBV ≲ 0.3, outside of which there is practically no calibration data.
We finally applied the SVM algorithm, trained on the WISE × SDSS sample, to the full-sky WISE data flux-limited to W1 < 16 mag. About 220 million sources preselected in this way were flagged by SVM as star candidates; the remaining objects required significant cleanup to obtain galaxy-candidate and QSO-candidate samples. This cleanup consisted in removing the brightest sources, as well as those located in the Galactic Plane and Bulge areas, for which the classification is not expected to be reliable. We also used source type probabilities provided by SVM to remove the objects of insecure classification. As a result, we obtained catalogues of 45 million galaxy candidates, as well as of 6 million QSOs. In the latter case, however, we observe significant contamination by sources consistent with dusty (non-AGN) galaxies and by probable solar system objects.
These shortcomings of our classification are related to the limitations of the training sample and to the lack of additional classification parameters that could be reliably used for the full sample together with the three basic ones employed here. It is possible to mitigate the former drawback thanks to forthcoming spectroscopic data, for example from SDSS-IV; however, it is not clear how much it is possible to improve the latter if only WISE data are to be used for the classification on the full sky while keeping a deep and uniform sample. Measurements in WISE W3 (12 μm) and W4 (23 μm) channels would certainly help to break degeneracies that result in unreliable identification of quasars in the present approach; however, these two bands offer much shallower and very inhomogeneous coverage compared to W1 and W2. Some improvement in classification could also be expected if there were reliable proper motions for a much larger sample of WISE sources than presently available, as these data would help identify at least some of the minor bodies of the solar system which most likely contaminate our current QSO sample.
In general, a natural next step in the process of classification of WISE sources is to expand the current scheme to a larger number of object classes, which will allow the creation of more robust catalogues or at least the purification of the current ones. For this to be accomplished, more classification parameters, and more comprehensive training sets will be necessary. We plan to explore this in forthcoming studies (Wypych et al., in prep.). Last but not least, it is possible to work on improving the training scheme itself by implementing the so-called fuzzy logic (e.g. Klir & Yuan 1995) into the SVM algorithm. While in the classical SVM approach all training examples are treated equally, the fuzzy logic procedure handles the uncertainties of the classification data by weighting the training examples (e.g. Abe & Inoue 2002; Tsujinishi & Abe 2003). Each training point may belong to no more then one class, but by weighting the training points Fuzzy-SVM (FSVM) can ensure that the meaningful data points will be classified correctly, while the noisier ones will have more freedom to be misclassified in order to ensure the maximum margin benefit. This in turn expands the classification regions in the parameter space. However, this approach heavily extends the computational time owing to the introduction of the additional free parameter, which, like other SVM parameters (e.g. misclassification parameter C or kernel parameters), must be tuned for best performance. While this method could help to improve the current classification, the uncertainties of the measurements of the objects considered in this work are relatively small. In view of the largely extended computational time, the FSVM was not favourable for the purpose of the current analysis, but it will be considered in our future studies of classification in noisier WISE or other data.
Recalibration of the W4 effective wavelength from 22 μm was carried out by Brown et al. (2014a).
Available from the NASA/IPAC Infrared Science Archive at http://irsa.ipac.caltech.edu/.
The situation has not improved in the final SDSS-III Data Release 12 (Alam et al. 2015).
Acknowledgments
We thank the referee for the helpful review. Special thanks to Mark Taylor for the TOPCAT (Taylor 2005) and STILTS (Taylor 2006) software11. Some of the results in this paper have been derived using the HEALPix package (Górski et al. 2005)12. This work was supported by the Polish National Science Center under contracts # UMO-2012/07/D/ST9/02785. M.B. was supported by the Netherlands Organization for Scientific Research, NWO, through grant No. 614.001.451, by the European Research Council through FP7 grant No. 279396 and by the South African National Research Foundation (NRF). A.P. was partially supported by the Polish-Swiss Astro Project, co-financed by a grant from Switzerland, through the Swiss Contribution to the enlarged European Union. This publication makes use of data products from the Wide-field Infrared Survey Explorer, which is a joint project of the University of California, Los Angeles, and the Jet Propulsion Laboratory/California Institute of Technology, funded by the National Aeronautics and Space Administration. Funding for SDSS-III has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, and the US Department of Energy Office of Science. The SDSS-III web site is http://www.sdss3.org/. SDSS-III is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS-III Collaboration including the University of Arizona, the Brazilian Participation Group, Brookhaven National Laboratory, Carnegie Mellon University, University of Florida, the French Participation Group, the German Participation Group, Harvard University, the Instituto de Astrofisica de Canarias, the Michigan State/Notre Dame/JINA Participation Group, Johns Hopkins University, Lawrence Berkeley National Laboratory, Max Planck Institute for Astrophysics, Max Planck Institute for Extraterrestrial Physics, New Mexico State University, New York University, Ohio State University, Pennsylvania State University, University of Portsmouth, Princeton University, the Spanish Participation Group, University of Tokyo, University of Utah, Vanderbilt University, University of Virginia, University of Washington, and Yale University.
References
- Abe, S., & Inoue, T. 2002, in European Symposium on Artificial Neural Networks, 113 [Google Scholar]
- Ahn, C. P., Alexandroff, R., Allen de Prieto, C., et al. 2014, ApJS, 211, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Akbani, R., Kwek, S., & Japkowicz, N. 2004, in Proc. of the 15th European Conference on Machine Learning (ECML), 39 [Google Scholar]
- Alam, S., Albareti, F. D., Allen de Prieto, C., et al. 2015, ApJS, 219, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, L. D., Bania, T. M., Balser, D. S., et al. 2014, ApJS, 212, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Assef, R. J., Stern, D., Kochanek, C. S., et al. 2013, ApJ, 772, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Beaumont, C. N., Williams, J. P., & Goodman, A. A. 2011, ApJ, 741, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Bilicki, M., Jarrett, T. H., Peacock, J. A., Cluver, M. E., & Steward, L. 2014, ApJS, 210, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Bilicki, M., Peacock, J. A., Jarrett, T. H., et al. 2016, ApJS, in press [Google Scholar]
- Bolton, A. S., Schlegel, D. J., Aubourg, É., et al. 2012, AJ, 144, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, M. J. I., Jarrett, T. H., & Cluver, M. E. 2014a, PASA, 31, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, M. J. I., Moustakas, J., Smith, J.-D. T., et al. 2014b, ApJS, 212, 18 [Google Scholar]
- Bu, Y., Chen, F., & Pan, J. 2014, New A, 28, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Cavuoti, S., Brescia, M., D’Abrusco, R., Longo, G., & Paolillo, M. 2014, MNRAS, 437, 968 [Google Scholar]
- Chang, C.-C., & Lin, C.-J. 2011, ACM Trans. Intell. Syst. Technol., 2, 27:1 [Google Scholar]
- Cherkassky, V., & Mulier, F. 2006, Learning from Data: Concepts, Theory, and Methods, Second Edition (Wiley Online Library) [Google Scholar]
- Cluver, M. E., Jarrett, T. H., Hopkins, A. M., et al. 2014, ApJ, 782, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Cristianini, N., & Shawe-Taylor, J. 2000, An introduction to Support Vector Machines (Cambridge University Press) [Google Scholar]
- Cutri, R. M., Wright, E. L., Conrow, T., et al. 2013, Explanatory Supplement to the AllWISE Data Release Products, Tech. rep. [Google Scholar]
- Dimitriadou, E., Hornik, K., Leisch, F., Meyer, D., & Weingessel, A. 2005, e1071: Misc Functions of the Department of Statistics (e1071), TU Wien, Version 1.5-11 [Google Scholar]
- Driver, S. P., Hill, D. T., Kelvin, L. S., et al. 2011, MNRAS, 413, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Edelson, R., & Malkan, M. 2012, ApJ, 751, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenstein, D. J., Weinberg, D. H., Agol, E., et al. 2011, AJ, 142, 72 [Google Scholar]
- Faherty, J. K., Alatalo, K., Anderson, L. D., et al. 2015, ArXiv e-prints [arXiv:1505.01923] [Google Scholar]
- Fan Wu, T., Lin, C.-J., & Weng, R. C. 2003, J. Machine Learning Research, 5, 975 [Google Scholar]
- Ferraro, S., Sherwin, B. D., & Spergel, D. N. 2015, Phys. Rev. D, 91, 083533 [NASA ADS] [CrossRef] [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Hambly, N. C., MacGillivray, H. T., Read, M. A., et al. 2001, MNRAS, 326, 1279 [NASA ADS] [CrossRef] [Google Scholar]
- Hsu, C.-W., Chang, C.-C., & Lin, C.-J. 2003, Bioinformatics, 1, 1 [Google Scholar]
- Ivezić, Ž., Monet, D. G., Bond, N., et al. 2008, in IAU Symp. 248, eds. W. J. Jin, I. Platais, & M. A. C. Perryman, 537 [Google Scholar]
- Jarrett, T. H., Chester, T., Cutri, R., et al. 2000, AJ, 119, 2498 [NASA ADS] [CrossRef] [Google Scholar]
- Jarrett, T. H., Cohen, M., Masci, F., et al. 2011, ApJ, 735, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Jarrett, T. H., Cluver, M. E., Magoulas, C., et al. 2016, ApJ, submitted [Google Scholar]
- Kirkpatrick, J. D., Schneider, A., Fajardo-Acosta, S., et al. 2014, ApJ, 783, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Klir, G. J., & Yuan, B. 1995, Fuzzy Sets and Fuzzy Logic: Theory and Applications (Upper Saddle River, NJ, USA: Prentice-Hall, Inc.) [Google Scholar]
- Kovács, A., & Szapudi, I. 2015, MNRAS, 448, 1305 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, H.-T., Lin, C.-J., & Weng, R. C. 2007, Mach. Learn., 68, 267 [Google Scholar]
- Mainzer, A., Bauer, J., Cutri, R. M., et al. 2014, ApJ, 792, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Małek, K., Solarz, A., Pollo, A., et al. 2013, A&A, 557, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mateos, S., Alonso-Herrero, A., Carrera, F. J., et al. 2012, MNRAS, 426, 3271 [NASA ADS] [CrossRef] [Google Scholar]
- Murakami, H., Baba, H., Barthel, P., et al. 2007, PASJ, 59, 369 [Google Scholar]
- Neugebauer, G., Habing, H. J., van Duinen, R., et al. 1984, ApJ, 278, L1 [Google Scholar]
- Nikutta, R., Hunt-Walker, N., Nenkova, M., Ivezić, Ž., & Elitzur, M. 2014, MNRAS, 442, 3361 [NASA ADS] [CrossRef] [Google Scholar]
- Perryman, M. A. C., de Boer, K. S., Gilmore, G., et al. 2001, A&A, 369, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Platt, J. C. 1999, in Advances in large Margin Classifiers (MIT Press), 61 [Google Scholar]
- R Development Core Team 2005, R: A Language and Environment for Statistical Computing, R Foundation for Statistical Computing, Vienna, Austria [Google Scholar]
- Saglia, R. P., Tonry, J. L., Bender, R., et al. 2012, ApJ, 746, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Secrest, N. J., Dudik, R. P., Dorland, B. N., et al. 2015, ApJS, 221, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Shawe-Taylor, S., & Cristianini, N. 2004, Kernel Methods for Pattern Analysis (Cambridge, UK: Cambridge, UP) [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Solarz, A., Pollo, A., Takeuchi, T. T., et al. 2012, A&A, 541, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soumagnac, M. T., Abdalla, F. B., Lahav, O., et al. 2015, MNRAS, 450, 666 [NASA ADS] [CrossRef] [Google Scholar]
- Stern, D., Assef, R. J., Benford, D. J., et al. 2012, ApJ, 753, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, M. B. 2005, in Astronomical Data Analysis Software and Systems XIV, eds. P. Shopbell, M. Britton, & R. Ebert, ASP Conf. Ser., 347, 29 [Google Scholar]
- Taylor, M. B. 2006, in Astronomical Data Analysis Software and Systems XV, eds. C. Gabriel, C. Arviset, D. Ponz, & S. Enrique, ASP Conf. Ser., 351, 666 [Google Scholar]
- Tsujinishi, D., & Abe, S. 2003, Neural Networks, 16, 785 [CrossRef] [Google Scholar]
- Tu, X., & Wang, Z.-X. 2013, RA&A, 13, 323 [Google Scholar]
- Vapnik, V. 1999, IEEE Transactions on Neural Networks, 10, 988 [Google Scholar]
- Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, X.-B., Hao, G., Jia, Z., Zhang, Y., & Peng, N. 2012, AJ, 144, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Yan, L., Donoso, E., Tsai, C.-W., et al. 2013, AJ, 145, 55 [NASA ADS] [CrossRef] [Google Scholar]
- York, D. G., Adelman, J., Anderson, Jr., J. E., et al. 2000, AJ, 120, 1579 [Google Scholar]
Appendix A: Tables with detailed results of the tests
In this appendix we provide tables with detailed results of the tests described in Sect. 4. Tables A.1 and A.2 summarise the statistics of the completeness, purity, and contamination for various combinations of extinction bins and flux limits in the test sets, for the self-check and cross-test cases.
Overall classification statistics (in %) for various combinations of extinction bins and flux limits for the self-check case (classified objects were the same as in the training sample).
Overall classification statistics (in %) for various combinations of extinction bins and flux limits for the cross-test case (classified objects were different from those in the training sample).
All Tables
Numbers of objects before and after oversampling in the bins for which oversampling was applied.
Comparison of SVM performances for two kernels, polynomial and radial, for the self-check and cross-test.
Overall classification statistics (in %) for various combinations of extinction bins and flux limits for the self-check case (classified objects were the same as in the training sample).
Overall classification statistics (in %) for various combinations of extinction bins and flux limits for the cross-test case (classified objects were different from those in the training sample).
All Figures
 |
Fig. 1 Aitoff projection in Galactic coordinates of 314 million sources in the AllWISE catalogue, flux-limited to W1 < 16 mag. |
| In the text | |
 |
Fig. 2 Distributions of the observed W1−W2 colour for stars, galaxies, and quasars in the cross-matched WISE × SDSS DR10 sample. |
| In the text | |
 |
Fig. 3 Normalised apparent W1 magnitude counts for galaxies, quasars, and stars in the WISE × SDSS DR10 sample. |
| In the text | |
 |
Fig. 4 Redshift – apparent magnitude diagrams for the SDSS z band: SDSS-only galaxies (left panel) and galaxies from the WISE × SDSS cross-match (right panel). |
| In the text | |
 |
Fig. 5 Redshift – apparent magnitude diagram for the WISE W1 band for the galaxies from the WISE × SDSS cross-match. |
| In the text | |
 |
Fig. 6 Convolution of the W1 filter with a template spectrum of a typical spiral galaxy as a function of redshift. |
| In the text | |
 |
Fig. 7 Representative colour–magnitude diagram before and after oversampling for quasars. |
| In the text | |
 |
Fig. 8 Comparison of the histograms of projection values of the training data samples onto the normal direction of the SVM decision boundary for a radial (left column) and polynomial kernel (right column). The top row represents the division between galaxies and stars (red and blue, respectively), the middle row between galaxies and quasars (red and green), the bottom row between stars and quasars. Vertical lines represent the boundaries of the decision hyperplane margins for the two classes (+1 and −1), and 0 marks the position of the hyperplane itself. |
| In the text | |
 |
Fig. 9 Same as Fig. 8, but for the validation dataset. |
| In the text | |
 |
Fig. 10 Dependence of the completeness (upper panels) and purity (lower panels) on the number of objects in the training set of a W1 < 14 mag flux-limited sample, for the self-check (left panels) and the cross-test (right panels) cases. Relevant contamination levels are 100%−Purity. |
| In the text | |
 |
Fig. 11 Dependence of the completeness (upper panels) and purity (lower panels) on the number of parameters used for SVM training of a sample with W1 < 14 mag and I100< 1 [MJy/sr], for the self-check (left panels) and the cross-test (right panels) cases. The specific classification parameters for the training were W1 (1st), W1−W2 (2nd), w1mag_1−w1mag_3 (3rd), and apparent motions (4th). See text for details. Relevant contamination levels are 100%−Purity. |
| In the text | |
 |
Fig. 12 Dependence of the completeness on the magnitude for four I100 bins when using three classification parameters (W1, W1−W2 and w1mag_1−w1mag_3) for galaxies (upper panel), stars (middle panel) and quasars (lower panel) from the WISE × SDSS sample. These results are for the cross-test. |
| In the text | |
 |
Fig. 13 Dependence of the purity on the magnitude for four I100 bins when using three classification parameters (W1, W1−W2, and w1mag_1−w1mag_3) for galaxies (upper panel), stars (middle panel), and quasars (lower panel) from the WISE × SDSS sample. These results are for the cross-test. |
| In the text | |
 |
Fig. 14 All-sky map of 220 million star candidates identified by our classifier in AllWISE W1 < 16 mag data, in Aitoff projection in Galactic coordinates. We note the logarithmic scaling of the count colour bar. |
| In the text | |
 |
Fig. 15 All-sky map of 45 million galaxy candidates identified by our classifier in AllWISE W1 < 16 mag data, in Aitoff projection in Galactic coordinates. This plot shows sources over the probability threshold of p(gal) > 0.6 after appropriate cleanup and masking (see text for details). |
| In the text | |
 |
Fig. 16 Sources flagged by our classifier as quasar candidates in the WISE W1 < 16 mag catalogue. This sample shows 6 million objects with an SVM probability p(QSO) > 0.5 after appropriate cleanup and masking (see text for details). |
| In the text | |
 |
Fig. 17 Distribution of the W1−W2 colour for WISE × SDSS quasars (grey bars) and for SVM quasar candidates identified in all-sky WISE data, with no threshold on the SVM QSO probability (red), and for p(QSO) > 0.5 and >0.75 (blue and black, respectively). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


