| Issue |
A&A
Volume 592, August 2016
|
|
|---|---|---|
| Article Number | A82 | |
| Number of page(s) | 10 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201527712 | |
| Published online | 02 August 2016 | |
Tiling strategies for optical follow-up of gravitational-wave triggers by telescopes with a wide field of view
1 Department of Astrophysics, IMAPP, Radboud University, 6500 GL, Nijmegen, The Netherlands
e-mail: shaon@astro.ru.nl
2 LIGO Laboratory, California Institute of Technology, Pasadena, CA 91125, USA
3 Nikhef − National Institute for Subatomic Physics, Science Park 105, 1098 XG Amsterdam, The Netherlands
4 Institute of Astronomy, KU Leuven, Belgium
Received: 7 November 2015
Accepted: 23 May 2016
Aims. Binary neutron stars are among the most promising candidates for joint gravitational-wave and electromagnetic astronomy. The goal of this work is to investigate various observing strategies that telescopes with wide field of view might incorporate while searching for electromagnetic counterparts of gravitational-wave triggers.
Methods. We examined various strategies of scanning the gravitational-wave sky localizations on the mock 2015−16 gravitational-wave events. First, we studied the performance of the sky coverage using a naive tiling system that completely covers a given confidence interval contour using a fixed grid. Then we propose the ranked-tiling strategy where we sample the localization in discrete two-dimensional intervals that are equivalent to the telescope’s field of view and rank them based on their sample localizations. We then introduce an optimization of the grid by iterative sliding of the tiles. Next, we conducted tests for all the methods on a large sample of sky localizations that are expected in the first two years of operation of the Laser interferometer Gravitational-wave Observatory (LIGO) and Virgo detectors. We investigated the performance of the ranked-tiling strategy for telescope arrays and compared their performance against monolithic telescopes with a giant field of view. Finally, we studied the ability of optical counterpart detection by various types of telescopes.
Results. Our analysis reveals that the ranked-tiling strategy improves the localization coverage over the contour-covering method. The improvement is more significant for telescopes with larger fields of view. We also find that while optimizing the position of the tiles significantly improves the coverage compared to contour-covering tiles. For ranked-tiles the same procedure leads to negligible improvement in the coverage of the sky localizations. We observed that distributing the field of view of the telescopes into arrays of multiple telescopes significantly improves the coverage efficiency, by as much as 50% over a single telescope with a large field of view in 2016 localizations while scanning ~100 deg2. Finally, through analyzing a range telescopes with wide field of view, we discovered that counterpart detection can be improved by sacrificing coverage of localization in order to achieve a greater observation depth for telescopes with very large field of view and small aperture, especially if the intrinsic brightness of the optical counterparts is weak.
Key words: gravitational waves / telescopes / methods: data analysis
© ESO, 2016
1. Introduction
The discovery of the gravitational-waves (GW) event GW150914 from a coalescence of a binary stellar-mass black hole system by the Laser Interferometer Gravitational-wave Observatory (LIGO) has established our ability to detect and measure with ground-based detectors perturbations of spacetime due to events of astrophysical origin. (Abbott et al. 2016a). Future upgrades of the LIGO (Aasi et al. 2015) will improve its sensitivity by a factor of a few resulting in an increase in the detection volume. The advanced Virgo (Acernese et al. 2015), which is scheduled to come online later this year will add a third kilometer-scale detector to the network that would improve the sky localization of sources. As a consequence of these two developments, we will be able to conduct gravitational-wave astronomy for the first time. The estimated rates of double neutron star binary mergers from theoretical estimates as well as from extrapolations based on the known sample of binary radio pulsars suggest a detection rate of several tens per year for the final advanced LIGO-Virgo network at their design sensitivity (Abadie et al. 2010). The detection rate of neutron star – black hole mergers is based solely on theoretical estimates and might well be similar, in part because of a larger detection horizon at a given detector sensitivity.
Compact binary coalescences (CBC) are extremely energetic events that may also provide an electromagnetic (EM) counterpart when one of the binary components is a neutron star (Eichler et al. 1989; Narayan et al. 1992; Li & Paczyński 1998). When EM as well as GW data are available, the scientific yield of the detection will be significantly enhanced: the EM counterpart will provide a very accurate position and possibly redshift, for instance. Additional information on the type of object may also be obtained, for example, EM signals can help us distinguish between neutron star − black hole binaries with a massive neutron star from binary black hole systems. We also expect to be able to understand the physics of the merger better as it is encoded in the properties of the ejecta and an estimate of the orbital inclination can be constrained more accurately (Rhoads 1997). The accurate position can be used not only to aid the GW data analysis, but also for a detailed study of the merger environment, which in turn could provide crucial information about the pre-merger evolution of the system (circumstellar material, host galaxy information, position in or outside galaxy, etc.).
One of the most promising candidates for joint observation of EM counterpart of a GW signal is a kilonova (Li & Paczyński 1998; Kulkarni 2005; Metzger et al. 2010; Barnes & Kasen 2013; Rosswog et al. 2014). A kilonova is an optical/infrared signal generated from the radioactive decay of small amounts (~0.01 M⊙) of high angular momentum neutron star material that is ejected from the merger of a binary neutron star or a neutron star black hole binary. Kilonovae are expected to be emitted isotropically, although a slight polar dependence may be present and might be used to constrain the orbital inclination (Kasen et al. 2015; Grossman et al. 2014). Current models indicate that the expected luminosity of kilonovae is weaker than that of supernovae. Assuming heavy-element r-process nucleosynthesis, the peak bolometric luminosity for these events is ~1040.5−1041.5 erg/s. This corresponds to an absolute magnitude of −12 to −15 in the optical Sloan i band (Tanaka & Hotokezaka 2013; Barnes & Kasen 2013; Grossman et al. 2014). Currently the best hope to observe kilonovae is to receive external triggers from other observatories and conduct a targeted search around the triggered sky position. This is precisely the method that led to the discovery of the first kilonova by the Hubble Space Telescope (Tanvir et al. 2013; Berger et al. 2013), which was triggered by GRB 130603B. The constrained beaming angles of GRBs imply that most of these triggers for kilonovae are located at very large distances. That is why the apparent magnitude of this event in the near-infrared and optical was ~25−28. This means that detecting kilonova events at their typical GRB triggered distances will be a challenge for most telescopes. However, as a result of the isotropic nature of GW emission, we expect to receive triggers for kilonova events associated with binary neutron star coalescences at closer distances than what has been observed for the short GRB triggered kilonova. A kilonova with absolute magnitudes in the aforementioned range, within a typical LIGO-Virgo BNS detectable distance of ~200 Mpc, will have an apparent i-band magnitude of ~21.5−24.5. Furthermore, the longer duration of these events (~days) provides us the opportunity for detailed follow-up with photometric and possibly, spectroscopic tools. These properties, namely temporal coincidence with the coalescence, isotropy of emission, and long-duration make kilonovae ideal candidates for EM follow-up of GW events.
These are three main challenges of EM follow-up of GW triggers:
-
1.
rapid detection and sky localization based on the GW data;
-
2.
an operational set-up in which EM facilities with sufficiently large field of view (FOV) and sensitivity can react quickly to survey the GW sky-localizations; and
-
3.
an efficient selection scheme in which the (candidate) counterparts can be identified in a potential sea of false positives.
The key element in EM follow-up of gravitational wave triggers is that we are able to detect the gravitational wave events in real time. If the gravitational wave events have associated optical counterparts, then these could last for hours to days (Li & Paczyński 1998; Berger 2011; Tanvir et al. 2013; Berger et al. 2013). During the first few hours to about a day we expect the optical/infrared luminosity from these sources to be at their highest. The time and sky localization of a GW candidate are known within a minute or two after the merger signal has passed the detectors (Singer et al. 2014; Berry et al. 2015). The GW sky localizations will typically be as large as hundreds of square degrees (Abbott et al. 2016b; Singer et al. 2014). Following-up such wide sky-localization patches within this time window − as deep as 22nd-23rd magnitude in at least two bands is a challenging task.
When the GW sky-localization is known the task for the optical telescopes is to observe that area with the minimum number of telescope pointings. Since a telescope pointing would cover a tile in the sky commensurate to its FOV, the observation of any desired confidence interval of the sky localizations requires generating a set of tiles that most efficiently captures the confidence interval. This act of capturing the confidence interval with the telescope tiles is termed coverage in this study (Sect. 2). In this paper we discuss and compare for the first time the various strategies (Sect. 2) that can be implemented to generate the sky-tiles necessary for observing the GW sky localizations using telescopes with wide FOV. Based on the analysis conducted on the sky localizations simulated by Singer et al. (2014), we recommend a best-suitable tiling strategy that takes key aspects into account, such as the number of telescope pointings (Sect. 3.1), issues of image subtraction (Sect. 3.3) and false-positive probabilities (Sect. 3.2).
We then use this tiling strategy to investigate how the coverage of the sky-localization regions can be optimized for a given observation area (total sky-area covered by the tiles) (Sect. 4). Here the notion of a distributed FOV array is introduced, and we compare the performance in covering a population of simulated GW sky-localizations with that of traditional monolithic FOV telescopes. A distributed FOV array could simply be a group of telescopes with smaller FOV operating in a coordinated fashion from different geographical location. Finally, using the tiling strategy developed, we study the observing strategy for EM counterparts of GW events (Sect. 5). Here we analyze how the depth of the observation can be optimized, tuning it against the coverage of the GW localization.
2. Sky-tiling for gravitational wave localization
The rapid gravitational wave sky-localization algorithm, BAYESTAR (Singer et al. 2014; Singer 2015) pixelates the sky using the Hierarchical Equal Area isoLatitude Pixelization (HEALPix) projection, computes the sky-localization probability distribution function (p.d.f) of the GW event at every pixel, and then outputs this information in FITS file format. We define this p.d.f as a function L(α,δ), where α and δ are the sky coordinates. We define S95 as the surface on the sky with the smallest possible area that contains 95% of the total localization p.d.f (Sidery et al. 2014). The 95% localization probability is chosen as an example for the purpose of illustration. 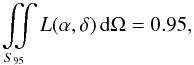 (1)where dΩ is the solid angle subtended by an infinitesimal surface element on the celestial sphere at the center of the Earth. Any telescope observing this confidence interval of GW sky localization can choose the minimum number of telescope pointings required to enclose S95. For every such area S95 there exists (at least) an area τ95( ≥S95) that is constructed out of the tiles needed for covering it. The tiles enclosing S95 forms a subset of the tiles that cover the full sky defining a sky-grid. The NCC tiles constituting this area, τ95, are the required sky-tiles that enclose the 95% confidence interval, and we call them contour-covering tiles or CC tiles. This is the most straightforward and simple tiling strategy.
(1)where dΩ is the solid angle subtended by an infinitesimal surface element on the celestial sphere at the center of the Earth. Any telescope observing this confidence interval of GW sky localization can choose the minimum number of telescope pointings required to enclose S95. For every such area S95 there exists (at least) an area τ95( ≥S95) that is constructed out of the tiles needed for covering it. The tiles enclosing S95 forms a subset of the tiles that cover the full sky defining a sky-grid. The NCC tiles constituting this area, τ95, are the required sky-tiles that enclose the 95% confidence interval, and we call them contour-covering tiles or CC tiles. This is the most straightforward and simple tiling strategy.
If the coordinates of the sky-grid are not fixed on the plane of the sky (we call this the free-grid), then the area τ95 can be obtained by optimizing the grid location in the sky. On the other hand, if the grid is fixed on the sky (which we call fixed-grid), then τ95 is uniquely defined. Many optical surveys, including the currently active PTF (Rau et al. 2009; Law et al. 2009) and Skymapper projects (Keller et al. 2007) and the future BlackGEM1 and ZTF facilities (Kulkarni 2012; Bellm 2014; Smith et al. 2014), use a fixed-grid on the sky. This grid is predefined and covers the whole sky that is visible from the observatory location. Although a more flexible grid will in general lead to more efficient contour coverage, a fixed-grid has advantages. First, the search for optical transients is typically performed by subtracting a reference image taken at an earlier epoch, and searching the residual image to find new sources. Distortions caused by optical elements in the telescope and the camera vary with the position in the FOV of the telescope. Looking at the same part of the sky on roughly the same position in the FOV all the time limits the complexity of image resampling. The more complex this process, the more artifacts are present in the residuals, which can be picked up as false-positive detections. Finally, a fixed-grid simplifies the data flow, storage, and access because the images taken at a certain sky coordinate of interest can easily be retrieved based on the ID of the field that contains the coordinate.
The area S95 defined in Eq. (1) is unique for a given event. The τ95 is more important for an EM observer, however, and not the S95. Minimizing the τ95 will result in the most effective tiling strategy. Instead of choosing the minimum number of tiles required to enclose the smallest confidence interval contour, we can sample the entire sky-localization map with discrete 2D intervals equal to the FOV of the telescope and select the smallest number of these sampled intervals that constitutes 95% localization posterior probability.
Let us consider a telescope with a FOV of ΔαΔδ for which we would wish to construct the sky-tiles required for observation. We can construct an equal-area grid on the sky with grid spacing Δα and Δδ along the right ascension and declination respectively, to cover the entire sky with an integral number of tiles. The probability of localization at an arbitrary sample on the grid would thus be given by 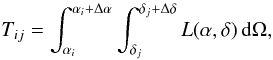 (2)where (i,j) are the coordinates of the sample in the sky-localization map. After ranking based on the value of the integral in Eq. (2), we can select from the top of the list of these samples until we have reached a cumulative probability ≥95%. We call these sampled intervals of sky localizations the ranked tiles (RT). It is straightforward to show that this strategy is guaranteed to give us a number of tiles NRT that is smaller than or equal to NCC (Appendix A).
(2)where (i,j) are the coordinates of the sample in the sky-localization map. After ranking based on the value of the integral in Eq. (2), we can select from the top of the list of these samples until we have reached a cumulative probability ≥95%. We call these sampled intervals of sky localizations the ranked tiles (RT). It is straightforward to show that this strategy is guaranteed to give us a number of tiles NRT that is smaller than or equal to NCC (Appendix A).
In Fig. 1 we show the CC tiles and the ranked tiles for a gravitational-wave sky localization observed by a telescope with a FOV = 2.7 deg2. The ranked tiles are shown by blue solid tiles and the CC tiles are all the tiles including the blue solid tiles and the dashed open tiles. The S95 surface is enclosed by the red contour. In this case, the ranked tiles are a subset of the 42 CC-tiles, reducing the number of tiles by 14.
 |
Fig. 1 Comparison between tiling generated for a three-detector network for the two tiling strategies. The contour shows the smallest 95% credible area on the sky as obtained from BAYESTAR. The dashed and solid squares constitute the tiles required to cover this contour (CC tiles). This set of tiles contains 96.5% localization likelihood. Shaded tiles are obtained from the ranked-tiling strategy. We note that fewer ranked tiles are required to cover the 95% localization than would be required if we were to cover the contour. |
3. Sky tiling in the first two years LIGO − Virgo observation scenarios
An astrophysically motivated simulation of low-latency detection and rapid sky localization for the first two years of LIGO and Virgo operation was presented in Singer et al. (2014). About a hundred thousand binary neutron star sources with different intrinsic parameters were injected in simulated 2015 and 2016 detector noise power spectral density (PSD). Out of these Singer et al. detected around 1000 injections using the low-latency detection pipeline (Cannon et al. 2010). They localized all the detected sources using BAYESTAR. For a thorough understanding of the observing scenarios during the first two years using optical telescopes we generated tiles for localizations employing the two methods discussed above. First, we present the results of the comparison between the two methods. Then we relax the fixed-grid constraint and investigate the coverage resulting from the optimization.
3.1. Comparison of the ranked-tiling method and the 95% confidence interval tiling in the first two years
We show the percentage reduction in the number of tiles required from using the ranked-tiling strategy instead of the CC-tiling strategy in Fig. 2. Once again we covered the 95% localization as an example with a 2.7 deg2 FOV telescope. The tile reduction percentage is 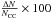 , where ΔN = NCC−NRT. The positive values of the reduction for all the GW events from the first two years clearly show that the ranked-tiling method minimizes the number of tiles required to observe a given confidence interval of GW sky localization. It is not immediately evident from Fig. 2 whether this reduction in the number of tiles occurs because ranked tiles are a subset of CC tiles (as we observed in Fig. 1).
, where ΔN = NCC−NRT. The positive values of the reduction for all the GW events from the first two years clearly show that the ranked-tiling method minimizes the number of tiles required to observe a given confidence interval of GW sky localization. It is not immediately evident from Fig. 2 whether this reduction in the number of tiles occurs because ranked tiles are a subset of CC tiles (as we observed in Fig. 1).
 |
Fig. 2 Fractional reduction (%) in the number of tiles required to cover 95% GW sky localization in 2015 and 2016 due to implementation of the ranked-tiling strategy. Note the trend of lower reduction for larger sky localization. (The apparent bimodality in the tile reduction is accidental and disappears for other confidence intervals and FOVs.) |
For any given GW event the sky-localization distribution is such that the lowest-probability tiles are at the periphery of the set of CC tiles. The localization area scales as N, the number of tiles. If the ranked-tiles are just a subset of the CC tiles, and are obtained by dropping the least probable CC tiles then we would expect that the tile reduction must scale as 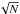 since the circumference scales with
since the circumference scales with 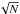 . Hence, the tile reduction percentage over the CC tiles should scale as 1/
. Hence, the tile reduction percentage over the CC tiles should scale as 1/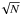 . In Fig. 3 we plot the bin-wise median percentage reduction as a function of the number of tiles. It shows the decreasing trend of the tile reduction percentage with the total number of tiles, but much less steeply than 1/
. In Fig. 3 we plot the bin-wise median percentage reduction as a function of the number of tiles. It shows the decreasing trend of the tile reduction percentage with the total number of tiles, but much less steeply than 1/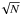 (shown as the dashed line), or, in other words, there is considerably greater gain from using ranked tiles for larger sky localization than expected if ranked tiles were a subset of CC tiles.
(shown as the dashed line), or, in other words, there is considerably greater gain from using ranked tiles for larger sky localization than expected if ranked tiles were a subset of CC tiles.
 |
Fig. 3 Median reduction in the number of tiles in the various tile bins illustrating the lowering of the reduction as a function of the GW sky-localization size in 2015 and 2016. The shaded regions represent the root mean square variation of the percentage reduction of tiles in the bins. The dip near the 250 tiles is an artifact of the discrete FOV. The dashed lines represents tile reduction if ranked tiles are obtained by dropping less probable peripheral CC-tiles. |
We found that when we consider the same number of ranked and CC tiles, in 92% of all the GW triggers the ranked tiles enclose more localization probabilities than CC tiles.
We repeated this exercise for telescopes with different FOVs and found that telescopes with smaller FOV are more likely to have such cases where localization probability contained within ranked tiles is greater than that contained within the same number of CC tiles. Furthermore, we also found that in a fair number of cases there are ranked tiles that fall completely outside the contour that encloses the smallest 95% localization. Once again this occurs more frequently for telescopes smaller FOV. For example, our analysis has shown that out of the 475 GW sky localizations in the 2016 era simulation, there is at least one ranked tile in 65 cases that has fallen outside the smallest 95% GW localization contour for a 2.7 deg2 telescope. For a 1.0 deg2 telescope this number is 283 out of 475, while for a 43.2 deg2 telescope it drops to just 2. These number are far greater if we target smaller confidence intervals. Thus, we have 156, 338, and 5 ranked tiles falling completely outside the smallest 50% confidence contour for the 2.7, 1.0 and 43.2 deg2 FOV telescopes respectively. In Fig. 4 we show the reduction in the required area of coverage that results from adopting the ranked-tiling strategy for six different FOVs (1.0, 2.7, 5.4, 10.8, 21.6 and 43.2 deg2) and six different localization confidence intervals (50%,60%,70%,80%,90%, and 95%). We find that the reduction in required sky-area is greatest for telescopes with the largest FOV and for the smallest localization confidence regions. The reduction of the sky area has implication on the false positive probability of the search, which we discuss next.
 |
Fig. 4 The median reduction in sky-area required to be observed for various telescope FOVs and confidence intervals using ranked-tiles. CC-tiles are more numerous than ranked-tiles to cover the same localization likelihood. Note that since the false positive probability scales with the amount of sky-area observed, this can be interpreted as a false probability reduction as well. The reduction is greater for smaller confidence intervals and larger FOVs. |
Comparison between tiling before and after optimization for a random selection of events from Singer et al. (2014).
3.2. False positives
One of the main challenges of optical follow-up of GW triggers is that the optical-sky will have more transients than in any other wavelengths, which can serve as false positives. Extragalactic transients such as supernovae are distributed uniformly across the sky. Galactic interlopers such as M-dwarf flares, binaries that were in eclipse when the reference catalog was made, outbursting CVs (novae and dwarf novae) follow the distribution of stars in the Milky Way, which means higher rate of false positives closer to the Galactic Plane. However, both contour covering and ranked-tiling methods cover similar parts of the sky, and on an event-by-event basis, both methods therefore probe the same population of interlopers. Thus, a false-positive probability comparison between the methods can be made assuming that the number of false positives per square degree of sky area is constant within the error box, and hence the number of false positives is proportional to the observed area. In the preceding sections we have established that the ranked-tiling strategy allows us to reduce the number of tiles required to capture the sky-localization region of any given confidence level. Thus, the percentage decrease in false positives upon employing ranked tiles as the observing strategy instead of the CC tiles can be written as 100 × (NCC−NRT) /NCC. Therefore, the color coding in Fig. 4 can be interpreted as a reduction in the false-positive rate. Of course, if we were to only analyze an area containing a fixed localization percentage (e.g., 95%) that is enclosed within the tile set, the CC method would by definition cover the smallest area, (S95) that contains that percentage and thus have the smallest number of false positives. But in practice observers will be analyzing the whole area observed by the telescope and any transient candidate found outside the S95− but within the area defined by NCC tiles will also be analyzed.
3.3. Optimization in free-grid
In Sect. 3.1 we presented the results of the two strategies to cover the GW sky localizations using the FOV of telescopes when the sky-grid is pre-defined. It is expected that additional minimizations of tiles can be achieved if this constraint is lifted and we are allowed to move coordinates of the tiles in the grid. The covering of the GW localizations, which are essentially irregular polygons, with the least number of square tiles is a member of a class of problems called NP-complete problems (NP stands for nondeterministic polynomial time). Any known solution of this class of problems can be verified within polynomial time (i.e., solvable in Nk steps, where N is the complexity of the problem and k is a non-negative integer). However, there is no known method of finding the solution from first principles. In the absence of a general recipe of finding the solution we resorted to an iterative optimization, where we iteratively shifted the tiles in the grid covering the GW sky localization to determine the configuration that yields the best result. This is done in the following two steps:
-
1.
Create the initial grid to cover the GW sky-localization: forevery sky-localization we find the smallest size of the grid that isrequired to cover it. The right ascension (RA) and declination(Dec) values at the center of the grid lie at the mean RA and Decvalue of the localization’s credible region.
-
2.
Optimize rows of tiles at constant declination angle: once the initial grid is laid, every row in the grid is slid in the horizontal direction (along the right ascension angle) by steps of 0.1° to look for the configuration that requires the lowest number of tiles in that particular row. Continuing the same process for all the rows we optimize the tiling.
Owing to the periodic nature of the initial grid, the shifting of the rows needs to be done for one tile length. We then conducted this exercise for ranked tiles:
-
1.
Once again we started from a primary sky-grid. We created aranked list of Tij values for all the samples in this grid. This gives us theranked-tiles for this instance of sky-grid.
-
2.
Then we slide the first row of the grid in steps of 0.1°, record the Tij values of all the tiles and create the ranked-tiles for each of these instances of the sky-grid. Note that unlike in the case of the CC-tiles, here there is no a priori way of optimizing each row of ranked-tiles but must optimize the entire grid after every iteration.
-
3.
Conducting this exercise for all the rows we collect the ranked-tiles for all the instances and choose the minimum of these which should be the optimal solution.
In Table 1 we show the results of the optimization carried out on ten randomly selected sky localizations from the first two years of simulation. We note that reasonable reduction in the required number of tiles is achieved by optimizing the CC-tiles. However, a similar reduction was not observed for ranked tiling. This indicates that the ranked-tiling strategy gives us a solution that is already close to the optimal solution. The ranked tiles are therefore an excellent approximation of the continuum sky localization and with virtually no need for optimization. This is an important point since it liberates the observation efficiency from the choice of the sky-grid. As we argued that many telescopes with wide FOV will be using a fixed-grid to simplify image subtraction, the independence of the ranked-tiling strategy of the choice of the grid is a major advantage.
4. Optimization of observation area − monolithic vs. distributed FOV
To scan the GW sky localizations spanning over hundreds of square degrees with a reasonable chance of detecting an optical counterpart we need telescopes with wide FOV. Other telescopes may only be successful in this endeavor if they incorporate additional information such as galaxy catalogs and distance localization (Singer, in prep.; Gehrels et al. 2016). These telescopes would target galaxies within the sky-localization region to search for the counterpart and are unlikely to base their search on any sky-tiling strategy, hence we exclude them here. A list of currently operating telescopes with wide FOV that participated in the first observing run of LIGO is reported in Abbott et al. (2016c). In addition, new facilities that might participate in the electromagnetic follow-up of GW triggers in the near future can be found in Nissanke et al. (2013), Kasliwal & Nissanke (2014) and Chu et al. (2016).
Of course, the larger the FOV of a telescope, the greater is its capability of scanning any given sky localization. Although the observing area scales linearly with the FOV, the coverage of the sky localization might scale less strongly because above a certain size, wider-angle telescopes will end up covering a greater area extraneous to the confidence region contour than telescopes with smaller FOV. Since smaller FOV telescopes can tile the localization contour more efficiently, we can imagine the possibility of incorporating multiple such telescopes in the form of a distributed FOV array of telescopes with a combined FOV equal to that of a large FOV telescope and expect to cover the credible region more efficiently. We performed the following analysis to test the implementation of distributed FOV arrays for ranked tiles. We assume a telescope with large FOV with which we would like to scan the sky to detect the optical counterpart corresponding to the mock GW triggers from 2015 and 2016 eras. In our studies we used the telescope with the largest FOV from the previous analysis, namely, 43.2 deg2. For each GW event we counted the number of ranked tiles that we need to observe until we reach the location of the simulated GW source. As we go down the list of the ranked tiles and observe a larger fraction of the sky, more event locations are covered. This is shown by the blue curves of Fig. 5, where we can see that with the increase of the total observing area the fraction of source locations that were covered also increases.
 |
Fig. 5 Comparison between detection fraction as a function of sky coverage for different FOV optical observing facilities in 2015 (top) and 2016 (bottom). Here we have selected six different arrays that have the same total observing area. Arrays with a smaller FOV in the individual telescopes are more efficient in covering the gravitational-wave sky localization. |
Next we distributed the 43.2 deg2 FOV into two telescopes with equal observing area of 21.6 deg2 FOV each. Figure 5 shows that this results in a greater fraction of coverage. Two telescopes of half the observing area are able to use their FOVs more efficiently to cover the highest localization regions, thereby converging on the source location faster than the original telescope with twice the FOV. Continuing this distribution of FOV further, we note that the increase in detection fraction steadily increases, underscoring the benefit of using a distributed FOV array over a monolithic FOV telescope in scanning the GW sky localizations.
In the upper plot of Fig. 5 we see that in the synthetic 2015 sky localization, while scanning the top 100 deg2 of the ranked tiles of the sky localizations, the gain in the coverage of the triggers would have been ~100% for an array consisting of forty-three 1.0 deg2 or sixteen 2.7 deg2 FOV telescopes compared to a monolithic 43.2 deg2 FOV telescope. The presence of the third detector in 2016 greatly improves the GW sky localizations, making the sky localizations smaller and less elongated in general. For such localizations the coverage is less sensitive to the distribution of the FOV of the telescope. This is the reason why the improvement in the 2016 era is more modest than in 2015 (see lower plot of Fig. 5). Nevertheless we found a ~50% gain when we scanned the top 100 deg2 of the ranked tiles using the telescope arrays with smaller FOV (1.0 deg2 and 2.7 deg2 FOV) instead of a single telescope with a FOV of 43.2 deg2. It is important to emphasize here that even though Virgo is expected to join the second observing run (O2), a significant fraction of the detections would be Hanford-Livingston double-coincident events because of the combined effect of finite-duty cycles and the lower Virgo sensitivity (Abbott et al. 2016c). Thus, the information from the localizations of the 2015 era is pertinent to the 2016 era and hence was included in the results of this work. We note that in 2016 the sensitivity of the LIGO detectors will also increase. The same event from 2015 will be better localized in 2016, but the increased sensitivity also means that the detectors will be able to detect weaker sources that were undetectable in 2015. Thus, as a fraction of the population, the localizations of the sources do not improve through better sensitivity of 2016.
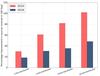 |
Fig. 6 Improvement(%) in the number of sources covered from using distributed FOV arrays instead of a single monolithic telescope in the highest likelihood 100 deg2 sky-area. Note that in 2016 the coverage improves by as much as 50% if we use a 16-fold distributed array instead of a single large FOV telescope. In 2015 this improvement would have been even larger (as much as 100%). This implies that the coverage improvement from using distributed FOV is even greater for double-coincident events (see discussion in Sect. 4). |
Note that the gain in coverage diminishes rapidly below 2.7 deg2 FOV telescopes for the 2015−16 sky-localizations as is evident from the lack of any significant gain in detection upon distributing the FOV further from an array of 2.7 deg2 to an array of 1.0 deg2 FOV. Figure 5 also shows that the differences between the distributed FOV arrays and the monolithic FOV telescope are minimal for very large observed areas, which is to be expected since if we were to observe a very large area in the sky, we expect to cover most of the event locations regardless of the tiling strategies or whether we use a monolithic FOV telescope or a distributed FOV array. However, we will be able to observe such large areas only for very slowly varying light curves. The most interesting and meaningful part of the plots in Fig. 5 is around ~100 square degrees where distributed FOV arrays improves the coverage. This is shown in Fig. 6 where we show, for the highest likelihood 100 deg2, the improvement (in %) of the sources covered over the single monolithic FOV telescope for the various arrays. The coverage of the source location improves by as much as 50% if the observers uses distributed FOV arrays instead of a single monolithic FOV telescopes. The improvement is expected to be even better for cases where the GW events were observed by only two detectors.
5. Depth and coverage
Until now, we discussed the tiling strategies in the context of efficient covering of the GW localization regions. However, the detection of the optical counterpart will depend on the depth of the observation and not just on the mere coverage of the localization area. The depth of observation by a particular telescopes depends on various factors, including the optical seeing quality of the site, the phase of the moon on the night of observation, the air mass of the observation, etc. However, the most important quantity is the integration time of the observation and the mirror size. We therefore here assume for simplicity that all the other factors are held constant at their optimum values at a typical site (seeing = 1.0, airmass = 1.0, moon phase = 0 (new moon)). We present studies for three different apertures sizes, 0.6, 0.9 and 4.0 m. The limiting magnitude as a function of the integration time is shown in Fig. 7. We used the exposure time calculator from NOAO (2016) to obtain the limiting magnitudes for the 0.9 and 4.0 meter class telescopes and scaling them we derived the same for the 0.6 meter class telescope.
 |
Fig. 7 Variation of the limiting magnitude for observations with integration times for telescopes with three different apertures. |
To make our study more general, we did not assume any geographical location of the observer. During actual observations, the GW localizations are not always visible from the any given location. For this general study we assume that all sky locations are entirely visible all the time.
5.1. Expected number of accessible sources
Increasing the integration time allows us to see deeper into the Universe. If we can see deeper by a factor of f, then, assuming a uniform density of GW sources (which is true for non-cosmological distances), we have a factor of f3 increase in the number of sources that are observable. However, longer integration times also mean that in the same total observation time we are able to observe a smaller fraction of the GW localization. Thus, the increase in depth comes at the expense of coverage. Here we present a study in which we investigate how the number of observable sources varies with the changing integration time and coverage for a uniform-volume distribution of sources and a total of two hours of observation time. Identification of the optical counterpart would require more than a single epoch of observation of the candidates, preferably in multiple filters to obtain photometric and light-curve information. Thus two hours of observation per epoch is a reasonable choice. We assumed that integrating for tA seconds allows us to observe at a limiting magnitude of mA = m(tA), where m(tA) is obtained from Fig. 7. Similarly, integrating for tB seconds we reach a magnitude of of mB = m(tB). If M is the absolute magnitude of the source, then the ratio of the accessible distances (disregarding extinction) for the two integration times 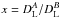 is given by,
is given by, ![\begin{equation} x = \frac{D_{\rm L}^A}{D_{\rm L}^B} = 10^{\frac{1}{5}[m(t_A) - m(t_B)]} , \label{Eq:magnitudeExpression} \end{equation}](/articles/aa/full_html/2016/08/aa27712-15/aa27712-15-eq60.png) (3)where
(3)where 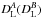 is the limiting accessible distance for observations conducted with integration times of tA(tB) seconds. Furthermore, let the total GW localization probability that the observer is able to cover if each pointing requires tA(tB) seconds of integration be PA(PB). Therefore, the ratio of the expected number of accessible sources for the two observations is:
is the limiting accessible distance for observations conducted with integration times of tA(tB) seconds. Furthermore, let the total GW localization probability that the observer is able to cover if each pointing requires tA(tB) seconds of integration be PA(PB). Therefore, the ratio of the expected number of accessible sources for the two observations is: 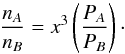 (4)We present a comparative study between different depths of observation where, as a reference, we used the 95% localizations region tiling. For an event the number of ranked tiles required to cover a particular confidence interval gives us the integration time for each pointing. Using this time and Fig. 7, we computed the value of x. Thus, the integration time on an event-by-event basis is not the same, but the covered GW localization likelihood is constant.
(4)We present a comparative study between different depths of observation where, as a reference, we used the 95% localizations region tiling. For an event the number of ranked tiles required to cover a particular confidence interval gives us the integration time for each pointing. Using this time and Fig. 7, we computed the value of x. Thus, the integration time on an event-by-event basis is not the same, but the covered GW localization likelihood is constant.
 |
Fig. 8 Median of the ratio of accessible source population for various confidence intervals w.r.t accessible source population for 95% confidence interval. The expected number of detections for uniform-volume distribution of sources peaks at an intermediate localization confidence interval. This shows that the likelihood of the detection of the optical counterparts is higher if the observer goes deeper at the expense of coverage of the localization. |
We note from Fig. 8 that the competing effects of longer integration time and reduced coverage result in a maximum in the expected number of accessible sources at localizations likelihood ~50%. Observing deeper gives access to a greater number of sources than covering larger localization regions.
5.2. Number of detectable optical counterparts of binary neutron star coalescences
There is one caveat to this geometrical argument given above, however, namely here we have assumed a uniform-volume distribution of sources. While this is a reasonable assumption for all sources in the Universe, the distribution of the number of binary neutron stars from which gravitational waves are detectable by LIGO and Virgo are not uniform in volume. The strength of the gravitational-wave signal strongly depends on the inclination angle of the binary, with face-on systems being stronger emitters than edge-on systems. This introduces a bias in our detectability, namely we are more likely to detect face-on system at larger distances (Nissanke et al. 2013). Thus, the distribution of the detectable sources by LIGO and Virgo will not scale as r3. This is evident from Fig. 9, where we show the histogram of the detected events from the 2016 scenario study.
 |
Fig. 9 Simulation of the distance distribution of the detected events from 2016. |
 |
Fig. 10 Detection fraction as a function of sky area covered and the distance reached in two hours is shown for nine different types of telescopes. Owing to the uncertainty in kilonova light-curve models we show the detection percentage for four kilonova absolute magnitude cases, M = −12, −13,−14, and −15. In the M = −14 and −15 cases for the 4.0 meter class telescope all sources are detectable, hence not shown. |
This implies that the apparent benefit that we saw in Fig. 8 from observing deeper at the cost of covering less of the localization region would be less profound (if any). To check this we conducted the following study. For the nine different telescopes with FOVs = 2.7,10.8, and 43.2 deg2 and apertures = 0.6,0.9, and 4.0 meters we determine the distance that can be reached as a function of the sky area covered if we have two hours of observation time at our disposal. The detectability of the source depends on the intrinsic brightness of the sources just as they depend on the telescope FOV and aperture size. However, currently the kilonova light-curve models are not very well constrained. Therefore, we conducted this analysis for four models with absolute magnitudes M = −12,−13,−14, and −15 (Roberts et al. 2011; Tanaka & Hotokezaka 2013). These values are believed to capture the range of kilonova brightness within reasonable accuracy. In Fig. 10 we show the result of this analysis. The fraction of the optical counterpart that can be detected from the 2016 scenario is shown in the color scale. First, we note that there is no detectability maximum in the observed sky area (on any slice along the x-axis). This is contrary to what we observed for the case of uniform distribution of sources. Second, it is obvious from Fig. 10 that for a smaller observed sky area (≲150 deg2) there is virtually no benefit from increasing the depth of the observation beyond ~150 Mpc. An observer will be constrained by time and will not be able cover an arbitrarily large sky-localization area to an arbitrarily high depth. Thus, an observer would typically be constrained on the curves like the ones shown in blue solid, red dotted and black dashed lines in Fig. 10 for the 0.6 m, 0.9 m and 4.0 m class telescopes respectively. When an observer wishes to cover greater fraction of the localization region, then the observation must be carried out towards the right end of these curves, while when the observer intends to observe at greater depth then the observation should be conducted at the left end of the curves. The background color gives us the corresponding detection probability. The location of the star on the lines indicates the depth and coverage at which maximum detectability of optical counterparts is achieved. The top panel shows that for the telescopes with smaller FOV it is almost never productive to cover smaller area in favor of observing deeper unless kilonovae are intrinsically very faint. For a telescope with intermediate FOV (middle panel), the benefits of observing deeper at the expense of coverage is absent for very large aperture telescopes. For smaller aperture telescopes there is some benefit in observing deeper especially if kilonovae are intrinsically faint. For telescopes with very large FOV (bottom panel), it appears that it is almost always beneficial to observe deeper at the expense of coverage, which is understandable since they can cover most of the source locations within few pointings. The observed variation in the detection probability as a function of sky coverage and depth of the search is in qualitative agreement with what was found by Nissanke et al. (2013) for the advanced LIGO-Virgo design sensitivity.
6. Conclusion
The discovery of gravitational wave (GW150914) from the binary black hole has opened a new window in transient astronomy. We expect to detect GW from compact binary systems involving neutron star(s) in the coming years as the LIGO detectors improve their sensitivity and new detectors come online worldwide. A scenario study for the 2015−16 era performed for the binary neutron star systems showed what we can expect during the initial years in GW localization. This work used the results of that study to investigate how well we would be able to cover these localizations on the sky using optical telescopes with wide FOV. We examined the performance of the coverage for various different types of telescopes with square FOVs. We compared two different ways to tile up the sky to facilitate the observation of the GW sky localization. The most obvious and straightforward approach would be to determine the smallest area of a given confidence interval (90%, 95% etc.) on the sky and cover this with the telescopes. We showed in our work that due to the discreteness of the FOV of the optical telescopes, a ranked-tile strategy leads to a better performance as far as the number of tiles required is concerned. In this method, we first generated a grid that covered the entire sky. Each grid element (which we called a tile) in this grid is of the size of the FOV of the telescope. Next, instead of finding the GW localization contour we, computed the localization probability in each tile. We ranked these tiles based on their localization probability values and selected the top tiles (ranked tiles) that cumulatively constituted the required confidence interval. We found in our study that ranked tiling makes the optimization of the location of the tiles irrelevant. It ensures that the observer can use a fixed grid of tiles, making it more suitable for image subtraction. We compared the performance of the two methods of tiling up the sky for observations for various FOVs and different confidence intervals. Telescopes with larger FOV and observations conducted over smaller confidence interval regions showed greater benefits from using the ranked tiles. The reduced search sky-area required to reach any confidence interval also implies a reduction in the number of false positives. The fact that for an equal number of tiles the ranked tiles accommodated a greater localization percentage indicates that in an actual search for optical counterpart of GW events, where (in most cases) observers will be constrained by the number of telescope pointings, adopting the ranked-tiling strategy will give the observers a better chance of covering the true sky-position of the event.
We investigated the performance of distributed FOV arrays of telescopes with wide field of view (≥1.0 deg2) with that of the traditional monolithic FOV telescopes in scanning of the simulated gravitational wave sky-localization regions. Our studies showed the clear benefit from using such arrays with the strongest effect observed at search areas ~100 deg2. The distributed FOV arrays need not be a single facility containing an array of identical telescopes. They might very well be multiple optical telescopes with wide FOV around the world with diverse FOVs operating in a joint fashion. Non local telescopes in such arrays will have greater sky coverage, which might be extremely beneficial in the initial years given the size and structures of the expected GW sky localizations.
Finally, we studied the effects of the observation depth. Here we analyzed the detectability of the sources using nine different types of telescopes of various FOVs and aperture sizes, each for four different kilonova brightnesses. Our investigation shows that for telescopes with smaller FOV there is no advantage in sacrificing coverage of the sky-localization area to observe deeper unless kilonovae are intrinsically extremely faint. Telescopes with larger FOV (>10 deg2) can afford to observe deeper by increasing their integration time.
Acknowledgments
The authors would like to thank Leo Singer for his meticulous review and suggestions for the work and the contents of the paper. S.B. and S.G. were supported by the research programme of the Foundation for Fundamental Research on Matter (FOM), which is partially supported by the Netherlands Organisation for Scientific Research (NWO). S.B. and P.J.G. acknowledge the Aspen Center for Physics, which is supported by National Science Foundation grant PHY-1066293, where part of this work was performed.
References
- Aasi, J., Abbott, B. P., Abbott, R., et al. 2015, Class. Quant. Grav., 32, 074001 [CrossRef] [Google Scholar]
- Abadie, J., et al. 2010, Class. Quant. Grav., 27, 173001 [NASA ADS] [CrossRef] [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2016a, Phys. Rev. Lett., 116, 061102 [Google Scholar]
- Abbott, B. P., Collaboration, L. S., & Collaboration, V. 2016b, Liv. Rev. Relat., 19 [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2016c, ApJ, 826, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Acernese, F., Agathos, M., Agatsuma, K., et al. 2015, Class. Quant. Grav., 32, 024001 [Google Scholar]
- Barnes, J., & Kasen, D. 2013, ApJ, 775, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Bellm, E. C. 2014, ArXiv e-prints [arXiv:1410.8185] [Google Scholar]
- Berger, E. 2011, New Astron. Rev., 55, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, E., Fong, W., & Chornock, R. 2013, ApJ, 774, L23 [Google Scholar]
- Berry, C. P. L., Mandel, I., Middleton, H., et al. 2015, ApJ, 804, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Cannon, K., Chapman, A., Hanna, C., et al. 2010, Phys. Rev. D, 82, 044025 [NASA ADS] [CrossRef] [Google Scholar]
- Chu, Q., Howell, E. J., Rowlinson, A., et al. 2016, MNRAS, 459, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Eichler, D., Livio, M., Piran, T., & Schramm, D. N. 1989, Nature, 340, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N., Cannizzo, J. K., Kanner, J., et al. 2016, ApJ, 820, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Grossman, D., Korobkin, O., Rosswog, S., & Piran, T. 2014, MNRAS, 439, 757 [NASA ADS] [CrossRef] [Google Scholar]
- Kasen, D., Fernández, R., & Metzger, B. D. 2015, MNRAS, 450, 1777 [NASA ADS] [CrossRef] [Google Scholar]
- Kasliwal, M. M., & Nissanke, S. 2014, ApJ, 789, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Keller, S. C., Schmidt, B. P., Bessell, M. S., et al. 2007, PASA, 24, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Kulkarni, S. 2005, [arXiv:astro-ph/0510256] [Google Scholar]
- Kulkarni, S. R. 2012, in IAU Symp. 285, eds. E. Griffin, R. Hanisch, & R. Seaman, 55 [Google Scholar]
- Law, N. M., Kulkarni, S. R., Dekany, R. G., et al. 2009, PASP, 121, 1395 [NASA ADS] [CrossRef] [Google Scholar]
- Li, L.-X., & Paczyński, B. 1998, ApJ, 507, L59 [Google Scholar]
- Metzger, B. D., Martínez-Pinedo, G., Darbha, S., et al. 2010, MNRAS, 406, 2650 [NASA ADS] [CrossRef] [Google Scholar]
- Narayan, R., Paczynski, B., & Piran, T. 1992, ApJ, 395, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Nissanke, S., Kasliwal, M., & Georgieva, A. 2013, ApJ, 767, 124 [NASA ADS] [CrossRef] [Google Scholar]
- NOAO 2016, Computing Exposure Times with the IRAF Task CCDTIME, http://www.noao.edu/scope/ccdtime/ [Google Scholar]
- Rau, A., Kulkarni, S. R., Law, N. M., et al. 2009, PASP, 121, 1334 [NASA ADS] [CrossRef] [Google Scholar]
- Rhoads, J. E. 1997, ApJ, 487, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, L. F., Kasen, D., Lee, W. H., & Ramirez-Ruiz, E. 2011, ApJ, 736, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Rosswog, S., Korobkin, O., Arcones, A., Thielemann, F.-K., & Piran, T. 2014, MNRAS, 439, 744 [NASA ADS] [CrossRef] [Google Scholar]
- Sidery, T., Aylott, B., Christensen, N., et al. 2014, Phys. Rev. D, 89, 084060 [NASA ADS] [CrossRef] [Google Scholar]
- Singer, L. P. 2015, Ph.D. Thesis, California Institute of Technology [arXiv:1501.03765] [Google Scholar]
- Singer, L. P., Price, L. R., Farr, B., et al. 2014, ApJ, 795, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. M., Dekany, R. G., Bebek, C., et al. 2014, in SPIE Conf. Ser., 9147, 79 [Google Scholar]
- Tanaka, M., & Hotokezaka, K. 2013, ApJ, 775, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Tanvir, N. R., Levan, A. J., Fruchter, A. S., et al. 2013, Nature, 500, 547 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Appendix A: Ranked tiling requires fewer tiles
We denote the set of all tiles in the grid sorted in descending order as { Θ:Θi> Θi + 1 ∀ i }, where Θi is the ith tile of the sorted grid. The set of all tiles that are required to cover the A95 region (T) is a subset of Θ. We define the elements of T as 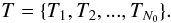 (A.1)Thus we can write
(A.1)Thus we can write 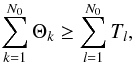 (A.2)where the subscript k indexes the set of tiles denoted by Θ and l indexes set of tiles denoted by T. The equal sign is for the trivial (and extreme) case that the set T happens to be the highest N0 elements of Θ. If we denote the quantity in the left-hand side of the inequality as
(A.2)where the subscript k indexes the set of tiles denoted by Θ and l indexes set of tiles denoted by T. The equal sign is for the trivial (and extreme) case that the set T happens to be the highest N0 elements of Θ. If we denote the quantity in the left-hand side of the inequality as 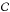 , and the one in the right as C then
, and the one in the right as C then ![\hbox{$\exists \,c \in [C, \mathcal{C}]$}](/articles/aa/full_html/2016/08/aa27712-15/aa27712-15-eq89.png) that satisfies
that satisfies 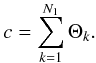 (A.3)If the lowest value of c that satisfies this happens to be
(A.3)If the lowest value of c that satisfies this happens to be 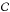 then N1 = N0 for any other values of
then N1 = N0 for any other values of 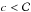 , we obtain N1<N0, i.e, the number of ranked tiles needed to reach a required localization probability, N1, is fewer than the number of tiles required to cover a given smallest confidence contour.
, we obtain N1<N0, i.e, the number of ranked tiles needed to reach a required localization probability, N1, is fewer than the number of tiles required to cover a given smallest confidence contour.
All Tables
Comparison between tiling before and after optimization for a random selection of events from Singer et al. (2014).
All Figures
 |
Fig. 1 Comparison between tiling generated for a three-detector network for the two tiling strategies. The contour shows the smallest 95% credible area on the sky as obtained from BAYESTAR. The dashed and solid squares constitute the tiles required to cover this contour (CC tiles). This set of tiles contains 96.5% localization likelihood. Shaded tiles are obtained from the ranked-tiling strategy. We note that fewer ranked tiles are required to cover the 95% localization than would be required if we were to cover the contour. |
| In the text | |
 |
Fig. 2 Fractional reduction (%) in the number of tiles required to cover 95% GW sky localization in 2015 and 2016 due to implementation of the ranked-tiling strategy. Note the trend of lower reduction for larger sky localization. (The apparent bimodality in the tile reduction is accidental and disappears for other confidence intervals and FOVs.) |
| In the text | |
 |
Fig. 3 Median reduction in the number of tiles in the various tile bins illustrating the lowering of the reduction as a function of the GW sky-localization size in 2015 and 2016. The shaded regions represent the root mean square variation of the percentage reduction of tiles in the bins. The dip near the 250 tiles is an artifact of the discrete FOV. The dashed lines represents tile reduction if ranked tiles are obtained by dropping less probable peripheral CC-tiles. |
| In the text | |
 |
Fig. 4 The median reduction in sky-area required to be observed for various telescope FOVs and confidence intervals using ranked-tiles. CC-tiles are more numerous than ranked-tiles to cover the same localization likelihood. Note that since the false positive probability scales with the amount of sky-area observed, this can be interpreted as a false probability reduction as well. The reduction is greater for smaller confidence intervals and larger FOVs. |
| In the text | |
 |
Fig. 5 Comparison between detection fraction as a function of sky coverage for different FOV optical observing facilities in 2015 (top) and 2016 (bottom). Here we have selected six different arrays that have the same total observing area. Arrays with a smaller FOV in the individual telescopes are more efficient in covering the gravitational-wave sky localization. |
| In the text | |
 |
Fig. 6 Improvement(%) in the number of sources covered from using distributed FOV arrays instead of a single monolithic telescope in the highest likelihood 100 deg2 sky-area. Note that in 2016 the coverage improves by as much as 50% if we use a 16-fold distributed array instead of a single large FOV telescope. In 2015 this improvement would have been even larger (as much as 100%). This implies that the coverage improvement from using distributed FOV is even greater for double-coincident events (see discussion in Sect. 4). |
| In the text | |
 |
Fig. 7 Variation of the limiting magnitude for observations with integration times for telescopes with three different apertures. |
| In the text | |
 |
Fig. 8 Median of the ratio of accessible source population for various confidence intervals w.r.t accessible source population for 95% confidence interval. The expected number of detections for uniform-volume distribution of sources peaks at an intermediate localization confidence interval. This shows that the likelihood of the detection of the optical counterparts is higher if the observer goes deeper at the expense of coverage of the localization. |
| In the text | |
 |
Fig. 9 Simulation of the distance distribution of the detected events from 2016. |
| In the text | |
 |
Fig. 10 Detection fraction as a function of sky area covered and the distance reached in two hours is shown for nine different types of telescopes. Owing to the uncertainty in kilonova light-curve models we show the detection percentage for four kilonova absolute magnitude cases, M = −12, −13,−14, and −15. In the M = −14 and −15 cases for the 4.0 meter class telescope all sources are detectable, hence not shown. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


