| Issue |
A&A
Volume 592, August 2016
|
|
|---|---|---|
| Article Number | A121 | |
| Number of page(s) | 18 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201527377 | |
| Published online | 09 August 2016 | |
SDSS-IV eBOSS emission-line galaxy pilot survey⋆
1 Instituto de Fisica Teorica UAM/CSIC, Universidad Autónoma de
Madrid, Cantoblanco, 28049 Madrid, Spain
e-mail: j.comparat@csic.es
2 Departamento de Fisica Teorica,
Universidad Autónoma de Madrid, Cantoblanco, 28049
Madrid,
Spain
3 Laboratoire d’Astrophysique, École
Polytechnique Fédérale de Lausanne (EPFL), Observatoire de Sauverny,
1290
Versoix,
Switzerland
4 Department of Physics and Astronomy,
University College London, Gower
Street, London WC1E6 BT, UK
5 CEA, Centre de Saclay, IRFU/SPP, 91191
Gif-sur-Yvette,
France
6 Aix Marseille Université, CNRS, LAM
(Laboratoire d’Astrophysique de Marseille) UMR 7326, 13388
Marseille,
France
7 Department of Physics &
Electronics, Rhodes University, 6140
Grahamstown, South
Africa
8 Institute of Cosmology and
Gravitation, University of Portsmouth, Portsmouth, PO1 3FX, UK
9 Department of Physics &
Astronomy, Johns Hopkins University, 3400 N. Charles Street, Baltimore, MD
21218,
USA
10 Instituto de Astrofísica de
Andalucía (CSIC), Glorieta de la
Astronomía, 18080
Granada,
Spain
11 Lawrence Berkeley National
Laboratory, 1 Cyclotron
Road, Berkeley,
CA
94720,
USA
12 Key Laboratory of Optical
Astronomy, National Astronomical Observatories, Chinese Academy of Sciences,
100012
Beijing, PR
China
13 Department of Physics and
Astronomy, University of Utah, 115
S 1400 E, Salt Lake
City, UT
84112,
USA
14 Apache Point Observatory and New
Mexico State University, PO Box
59, Sunspot,
NM, 88349-0059,
USA
15 Sternberg Astronomical Institute, Moscow State University,
Moscow
16 CPPM, Aix-Marseille Université,
CNRS/IN2P3, 13388
Marseille,
France
17 Department of Physics and Astronomy
and PITT PACC, University of Pittsburgh, Pittsburgh, PA
15260,
USA
18 Department of Astronomy and
Astrophysics, The Pennsylvania State University, University Park, PA
16802,
USA
19 Institute for Gravitation and the
Cosmos, The Pennsylvania State University, University Park, PA
16802,
USA
20 Cerro Tololo Inter-American
Observatory, National Optical Astronomy Observatory, Casilla 603, La Serena, Chile
21 Fermi National Accelerator
Laboratory, PO Box
500, Batavia,
IL
60510,
USA
22 Institute of Astronomy, University
of Cambridge, Madingley
Road, Cambridge
CB3 0HA,
UK
23 Kavli Institute for Cosmology,
University of Cambridge, Madingley
Road, Cambridge
CB3 0HA,
UK
24 CNRS, UMR 7095, Institut
d’Astrophysique de Paris, 75014
Paris,
France
25 Sorbonne Universités, UPMC Univ
Paris 06, UMR 7095, Institut d’Astrophysique de Paris, 75014
Paris,
France
26 Laboratório Interinstitucional de e-Astronomia
− LIneA, Rua Gal. José
Cristino 77, Rio de Janeiro, RJ − 20921-400, Brazil
27 Observatório Nacional,
Rua Gal. José Cristino 77, Rio de Janeiro, RJ -
20921-400,
Brazil
28 Department of Astronomy, University
of Illinois, 1002 W. Green
Street, Urbana,
IL
61801,
USA
29 National Center for Supercomputing
Applications, 1205 West Clark St., Urbana, IL
61801,
USA
30 Institut de Ciències de l’Espai,
IEEC-CSIC, Campus UAB, Carrer de
Can Magrans, s/n, 08193 Bellaterra, Barcelona, Spain
31 Institut de Física d’Altes
Energies, Universitat Autònoma de Barcelona, 08193 Bellaterra, Barcelona,
Spain
32 Kavli Institute for Particle
Astrophysics & Cosmology, PO Box 2450, Stanford University,
Stanford,
CA
94305,
USA
33 Excellence Cluster Universe,
Boltzmannstr. 2,
85748
Garching,
Germany
34 Faculty of Physics,
Ludwig-Maximilians University, Scheinerstr. 1, 81679
Munich,
Germany
35 Department of Physics and
Astronomy, University of Pennsylvania, Philadelphia, PA
19104,
USA
36 Jet Propulsion Laboratory,
California Institute of Technology, 4800 Oak Grove Dr., Pasadena, CA
91109,
USA
37 Kavli Institute for Cosmological
Physics, University of Chicago, Chicago, IL
60637,
USA
38 Department of Physics, University
of Michigan, Ann
Arbor, MI
48109,
USA
39 Max Planck Institute for
Extraterrestrial Physics, Giessenbachstrasse, 85748
Garching,
Germany
40 Universitäts-Sternwarte, Fakultät
für Physik, Ludwig-Maximilians Universität München, Scheinerstr. 1, 81679
München,
Germany
41 Center for Cosmology and
Astro-Particle Physics, The Ohio State University, Columbus, OH
43210,
USA
42 Department of Physics, The Ohio
State University, Columbus, OH
43210,
USA
43 Australian Astronomical
Observatory, North
Ryde, NSW
2113,
Australia
44 Departamento de Física Matemática,
Instituto de Física, Universidade de São Paulo, CP66318, CEP 05314-970, São
Paulo, SP,
Brazil
45 George P. and Cynthia Woods
Mitchell Institute for Fundamental Physics and Astronomy, and Department of Physics
and Astronomy, Texas A&M University, College Station, TX
77843,
USA
46 Institució Catalana de Recerca i
Estudis Avançats, 08010
Barcelona,
Spain
47 SLAC National Accelerator
Laboratory, Menlo
Park, CA
94025,
USA
48 Department of Physics and
Astronomy, Pevensey Building, University of Sussex, Brighton, BN1 9QH, UK
49 Centro de Investigaciones
Energéticas, Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
50 Department of Physics, University
of Illinois, 1110 W. Green
St., Urbana,
IL
61801,
USA
Received:
16
September
2015
Accepted:
13
June
2016
The Sloan Digital Sky Survey IV extended Baryonic Oscillation Spectroscopic Survey (SDSS-IV/eBOSS) will observe 195 000 emission-line galaxies (ELGs) to measure the baryonic acoustic oscillation (BAO) standard ruler at redshift 0.9. To test different ELG selection algorithms, 9000 spectra were observed with the SDSS spectrograph as a pilot survey based on data from several imaging surveys. First, using visual inspection and redshift quality flags, we show that the automated spectroscopic redshifts assigned by the pipeline meet the quality requirements for a reliable BAO measurement. We also show the correlations between sky emission, signal-to-noise ratio in the emission lines, and redshift error. Then we provide a detailed description of each target selection algorithm we tested and compare them with the requirements of the eBOSS experiment. As a result, we provide reliable redshift distributions for the different target selection schemes we tested. Finally, we determine an target selection algorithms that is best suited to be applied on DECam photometry because they fulfill the eBOSS survey efficiency requirements.
Key words: large-scale structure of Universe / galaxies: general / methods: observational
The catalog is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/592/A121
© ESO, 2016
1. Introduction
Galaxy surveys permit studying the cosmological structures formed by the network of galaxies and the evolution of galaxies. The recent increase in the number of multiplexing of spectrographs (Le Fèvre et al. 2003; Sharp et al. 2006; Smee et al. 2013; Flaugher & Bebek 2014) and in the field of view of photometric cameras (Gunn et al. 1998; Boulade et al. 2003; Flaugher et al. 2015) allows galaxy surveys to cover larger areas of the sky and to measure large numbers of accurate redshifts. The precision of a cosmological statement based on a galaxy survey is directly related to the volume sampled by the survey: the larger, the better. To extract cosmological information from a magnitude-limited galaxy survey, we therefore construct the largest possible volume-limited sample (Martinez & Saar 2002). To enhance the covered volume and increase survey efficiency, galaxy surveys push the high-redshift limit as far as possible and pre-select galaxies by discarding low-redshift faint galaxies to obtain an observed sample as close as possible to the desired volume-limited sample.
Three recent surveys successfully applied a color selection to a magnitude-limited sample to map a given redshift range more efficiently and to extract cosmological information. The Baryonic Oscillation Spectroscopic Survey (BOSS; Dawson et al. 2013; Eisenstein et al. 2011) observed a specific part of the galaxy population, the most massive ellipticals at redshift 0.57, by selecting in the color−color diagram g − r, r − i (Maraston et al. 2013). BOSS is the first to measure the baryonic acoustic oscillation (BAO) standard ruler at the percent level (Seo & Eisenstein 2003), which directly constrains the cosmological model (Anderson et al. 2014). The WiggleZ survey targeted star-forming galaxies at redshift 0.6 (Drinkwater et al. 2010) and measured the BAO standard ruler at the 5% level (Kazin et al. 2014). Finally, the VIMOS Public Extragalactic Redshift Survey (VIPERS, Guzzo et al. 2014) observed galaxies at redshift 0.8 and measured the growth rate of structure at the 17% level (de la Torre et al. 2013).
Measuring standard rulers and the growth rate of structure is key to understand the cosmological model (Weinberg et al. 2013), but this does not require the galaxy sample to be volume limited. As illustrated by the measurement of the BAO feature using samples that are not volume limited, such as the Lyα forest of quasars (QSOs; Delubac et al. 2015) or the WiggleZ survey, the BAO feature is an intrinsic property of the matter field and does not require a volume-limited sample. However, it is mandatory to understand in depth how the selected tracers are related to the dark matter field (Bautista et al. 2015; Poole et al. 2015; Favole et al. 2016; Rodríguez-Torres et al. 2016). Furthermore, Angulo et al. (2014) found that galaxy formation effects, such as the selection function or bias models, can bias the BAO scale measurement at the 0.2% level, which is well below the expected precision by eBOSS. Therefore, we can spectroscopically observe any tracer of the matter field. In particular, we can choose any type of galaxy that is believed to be a Poisson sampling of the underlying density field, provided its density is sufficient to overcome the shot noise and that accurate redshifts can be obtained in a short time, so that a large (>h-3Gpc3) volume can be covered within a few years of observations.
The extended Baryonic Oscillation Spectroscopic Survey (eBOSS, Dawson et al. 2016) uses color selection to identify three types of galaxies: luminous red galaxies (LRGs, Prakash et al. 2016), emission-line galaxies (ELGs), and QSOs (Myers et al. 2015). The ELG and QSO samples will not provide volume-limited samples. eBOSS will measure the angle-averaged BAO distance ladder with point-like tracers to the 1% precision at redshift 0.7 using LRGs , 2.2% at redshift 0.87 using ELGs (or dA(z) to an accuracy of 3.1% and H(z) to 4.7%), and 1.6% at redshift 1.37 using QSOs (Dawson et al. 2016; Zhao et al. 2016). We expect to reach this measurement by acquiring 195,000 emission line galaxy redshifts at an effective redshift of z = 0.87 using 300 dedicated plates. The efficiency of the targeting algorithm needs to be higher than N(0.6 <zreliable< 1) /Ntargets> 74.5% or N(0.7 <zreliable< 1.1) /Ntargets> 74.5% to obtain the correct amount of reliable redshifts in the range of interest. Additionally, the fraction of catastrophic redshifts in the range 0.6 <z< 1 or 0.7 <z< 1.1 must be below 1%.
The target selection of the ELG for BAO surveys is driven by the requirement to acquire as many spectra as possible in the smallest amount of observing time to maximize the volume covered by the survey. The resulting precision on the measurement of the BAO scale is directly related to the effective volume sample, that is, the volume where the density of tracers is above shot noise. For a constant density as a function of redshift, increasing the area is the only handle to increase the effective volume. For a peaked redshift distribution, increasing the density also increases the effective volume by overcoming shot noise at the tails of the redshift distribution. The trade-off of density vs. area was studied, and we found that targeting 340 ELG deg-2 on 750 deg2 or 170 ELG deg-2 on 1500 deg2 would provide the same effective volume and therefore the same BAO measurement (Dawson et al. 2016). We present here the pilot data that were observed to investigate the possible target selection algorithms using photometric data sets that are available on an area at least larger than 750 deg2 and that can provide a density of targets, denoted ρ, such as 170 <ρ< 340 deg-2. These target selection algorithms must fulfill the redshift efficiency requirement mentioned above.
For both ELGs and QSOs, schemes that select targets for spectroscopy exist using either color selection (Comparat et al. 2013b; Schneider et al. 2010) or higher dimensional algorithms (Raichoor et al. 2016; Bovy et al. 2012). To assess algorithms, eBOSS tested them on a 10 deg2 sky patch covered by many photometric surveys around α ~ 36° and δ ~ −4.5°. This region was indeed observed by the following surveys SDSS, CFHT-LS Wide, DES, SCUSS, and WISE (Ahn et al. 2012; Gwyn 2012; Banerji et al. 2015; Zou et al. 2015a; Wright et al. 2010, respectively).
In addition to finding the right algorithm, we face another challenge: we need to develop the best targeting algorithm implementable with existing photometry to construct a homogeneous ELG sample.
This paper is included in a series of eBOSS papers. Dawson et al. (2016) gave an overview of the eBOSS survey. Zhao et al. (2016) provided the Fisher matrix forecast on the accuracy of the BAO and RSD measurements expected. This paper presents the results of the ELG pilot survey that enables a complete study of the ELG target selection algorithm. We mitigated the risk by investigating TS algorithms using existing well-known photometry (SDSS and WISE) and more recent deeper ones (DES and SCUSS). Raichoor et al. (2016) described in depth the optimization of the SDSS+WISE+SCUSS algorithms using the Fisher technique, while the further optimization of algorithms using DES photometry is described in this paper. The clustering properties and the homogeneity of targeting catalogs on large areas are discussed in Jouvel et al. (2015) for the DES-based TS and in Delubac et al. (in prep) for the SDSS+WISE -based TS.
In this paper, we analyze the pilot survey observations from eBOSS ELG carried out at the SDSS telescope (Gunn et al. 2006). In Sect. 2 we describe the photometric catalog from which the targets were drawn and how the spectroscopy of the ELG was performed. Section 3 describes how the redshifts are automatically measured. Section 4 details the exact selection algorithms applied and the corresponding galaxy population observed. In Sect. 4.4 we introduce an optimized selection scheme based on DECAM imaging that is suited for the eBOSS ELG observations.
Throughout the paper, we quote magnitudes in the AB system (Oke & Gunn 1983) and provide the measurements in a flat ΛCDM cosmology h = 0.7, Ωm = 0.3.
2. Data
2.1. Photometry
To select targets, we used photometry from the following surveys.
SDSS, WISE, and SCUSS
The SDSS photometry (Alam et al. 2015)1 is constituted of the five broadbands u, g, r, i, z (Fukugita et al. 1996) and covers about 14 000 deg2.
We computed so-called forced photometry on the SDSS r-band detected objects, which is 75% complete at 22.5 (Ahn et al. 2012; Lang et al. 2014). It uses measured SDSS source positions, star-galaxy separation, and galaxy profiles to define the sources whose fluxes are to be measured in the WISE images (Wright et al. 2010). The WISE imaging has a 6.1 arc seconds seeing in the band W1 at 3.4 μm.
We used data from the SCUSS survey, which is a u-band survey with a magnitude limit of 23.2 with a seeing of ~2 arc seconds (Zou et al. 2015a). We also apply the SDSS-based forced photometry model to these data (Zou et al. 2015b). It constructs 2D models (de Vaucouleurs and exponential) based on SDSS r-band galaxy profiles and star-galaxy separation, and estimates object fluxes through comparing the models with the object images of SCUSS. The modelMag magnitudes in SCUSS are derived from the object flux with higher likelihood in the de Vaucouleurs and exponential model fitting.
Problems related to colors computed with magnitudes measured through different surveys are significantly mitigated for our SDSS-SCUSS-WISE colors because our SCUSS and WISE photometry is acquired consistently with the SDSS (forced photometry on SDSS objects, using SDSS structural information: Lang et al. 2014; Zou et al. 2015b).
We created a multiband catalog of detections. The SDSS-SCUSS-WISE catalog extends the full South Galactic Cap; see Raichoor et al. (2016) and Delubac et al. (in prep.) for the complete description of the catalog.
DES and DECaLS
The Dark Energy Camera (DECam Flaugher et al. 2015) was mounted, installed, and commissioned in 2012 on the Blanco four-meter telescope at Cerro Tololo Inter-American Observatory in Chile (Doel et al. 2012).
The Dark Energy Survey (DES) is an imaging survey of the grizY photometric bands (Flaugher & DES Collaboration 2013; Diehl et al. 2014) that will cover 5000 deg2 to an unprecedented 5σ depth of iAB< 24 (Flaugher 2012) using DECam. A Science Verification (SV) period followed, and data were acquired between end of 2012 through February 2013. As the data were taken shortly after DECam commissioning and were used to test survey operations and assess data quality, the DES-SV data quality is not as good as the full survey data is expected to be, but it was deep enough for our purpose. The SV fields were chosen to cover sky areas observed by spectroscopic galaxy surveys such as DEEP2 (Newman et al. 2013) and VVDS (Le Fèvre et al. 2013). To test the target selections, we used the DES-SV around the CFHTLS-W1 field.
The DECaLS photometry is part of the Legacy Survey2, which is producing an inference model catalog of the sky from a set of optical and infrared imaging data, comprising 14 000 deg2 of extragalactic sky visible from the northern hemisphere in three optical bands (g,r,z) and four infrared bands (w1, w2, w3, w4 from WISE). The sky coverage that will eventually be surveyed by DECam is approximately bounded by −18°<δ< + 30° in celestial coordinates and | b | > 18° in Galactic coordinates. This survey should provide a sufficient area to target ELGs from in a zone accessible to the SDSS telescope.
The DES and DECaLS photometries are about ten times deeper than the SDSS photometry and therefore allow a narrower and more efficient redshift selection; see the discussion in Comparat et al. (2013b). For instance, because the scatter in the magnitude−color or color−color diagrams is smaller, it permits cleaner selections. Given that the area available to target from DECam-based imaging is smaller, we tried denser selections that extend to higher redshifts.
Finally, we created a matched detection catalog from the SDSS, CFHT-LS Wide, DES, SCUSS, and WISE photometric surveys. In the match all entries from the different catalogs are kept, even when they did not have a match in the other catalogs.
2.2. Spectroscopy
 |
Fig. 1 Top panel: ELG spectra represented in the observed frame sorted by redshift. Each horizontal line corresponds to one spectrum. Vertical patterns correspond to the residuals of the sky subtraction. Diagonal patterns are the emission and absorption lines seen in the galaxy spectra. As redshift increases, the [Oii] , Hβ, [Oiii] , and Hαemission lines become redshifted. Starting at redshift 0.5, UV absorption lines enter the spectrograph window. Bottom panel: ELG spectra stacked by 50, ordered as a function of redshift represented in the rest-frame. The spectral features align vertically and are detected with higher signal-to-noise-ratio, in particular the absorption lines in the UV. Extended details about the UV absorption and emission systems are given in Zhu et al. (2015). |
The SDSS-BOSS spectrograph is an optical multifiber spectrograph mounted on the 2.5 m f/5 modified Ritchey-Chretien altitude-azimuth telescope located at the Apache Point Observatory, (APO Gunn et al. 2006; Smee et al. 2013). SDSS spectra cover the wavelength range 3600 <λ< 10 400 Å at an average resolution of 2000. The wavelength λ is calibrated to vacuum wavelengths. The BOSS spectrophotometric calibration is accurate at the <5% level in the r band and <10% in the other bands (Shen et al. 2015).
2.3. Previous ELG observations with the SDSS spectrograph
During the SDSS-III BOSS survey, 11,883 ELG were observed and visually inspected (see Comparat et al. 2013b, 2015; Alam et al. 2015). We added this sample to the eBOSS pilot survey to study the reliability of automated redshift assignment. The plates that contain ELGs are 4386-4389, 4391, 4392, 4394, 4395, 4397, and 4399 with a sparse ELG sampling and 5017, 5018, 6931-6933, 7239-7243, and 7245-7247 that are dedicated plates. The redshifts are estimated with the pipeline described in Bolton et al. (2012).
2.4. ELG pilot observations for SDSS-IV/eBOSS
At the APO facility, 9000 fibers, or ten plates, were dedicated to the eBOSS ELG pilot survey. The exposure time was 4 × 15 min for each plate. The test extended over ~10 deg2 and was located around α(J2000) ~36° and δ(J2000) ~−4.5°. They were labeled as “chunks” – SDSS jargon for an observational run – “eboss6” (plates 8123 to 8130) and “eboss7” (plates 8355 and 8356). The spectra were reduced with the current SDSS pipeline (Bolton et al. 2012). They showed strong emission lines and weak absorption lines; see Fig. 1. These clear features enabled clean redshift identification for about 75% of the targets.
2.5. VIPERS data, a parent sample
To understand the completeness properties of the ELG selection function, we use VIPERS, which has a >90% redshift determination rate for magnitudes brighter than i< 22.5 and at redshift higher than z> 0.6. We use its first data release, containing 57 204 slit-extracted 1 d spectra and their measured and visually inspected redshifts (Garilli et al. 2014) from 45-min-long exposures. The VIPERS data cover the fields W1 and W4 of the CFHT-LS. The eBOSS ELG pilot survey footprint and the VIPERS W1 field overlap slightly. These spectra were observed by the ESO Very Large Telescope (VLT) and VIMOS, which is a visible (360 to 1000 nm) wide-field imager and multi-object spectrograph mounted on the Nasmyth focus B of UT3 Melipal (Le Fèvre et al. 2003). It was used in a mode with a resolution of 230 and a wavelength coverage of 550 nm−950 nm.
3. Redshift determination
The SDSS/BOSS pipeline (Bolton et al. 2012) fits the redshifts of the observed spectra. In this section, we investigate the precision obtained on the estimation of the redshifts and the rate of catastrophic errors. To measure the two-point correlation function in redshift space for BAO in the redshift range 0.6 to 1.1, we require a redshift precision better than 300 km s-1 and a share of redshifts with an error larger than 1000 km s-1 to be smaller than 1% (the so-called catastrophic redshifts). Because eBOSS is required to observe very many spectra, it is necessary to have reliable redshifts estimated automatically.
This pipeline has not yet been thoroughly tested in its ability to automatically determine ELG redshifts at z ~ 0.8. This is therefore important to properly evaluate the efficiency of ELG selection functions.
Visual inspection
To assess the fit redshifts, we inspect them visually to infirm or confirm the results. In total, we visually inspected 13 450 of the 21 500 spectra reduced by the same pipeline to assess the plausibility of the redshift assignment. We did not inspect all of them because this is a highly time-consuming task. In this task, we profit from the previous ELG observations by BOSS that have been visually inspected (11 650 spectra), and in addition, we inspected two of the pilot survey plates (8123 and 8130, i.e.. 1800 spectra). Each plate was assigned two inspectors. Using the same software, inspectors produced a file that contained for each spectrum the category of the object (star, galaxy, QSO, unknown) and a confidence level (from 0, or low confidence, to 5, or high confidence) and the redshift. Any disagreements between inspectors were discussed between them and a truth table was constructed based on the inspection result for each plate. For confidence levels >3 the inspectors always agreed. Disagreements were rare and occurred when the signal-to-noise ratios (S/Ns) in the emission lines were very low. In most of these cases, these objects were categorized as unknown to combine inspections into the truth table. We note that when an object was classified as unknown, zinspection was set to −1. This classification follows conventions used by spectroscopic surveys such as VVDS, DEEP2, or zCOSMOS (Le Fèvre et al. 2013; Newman et al. 2013; Lilly et al. 2009) with a slightly higher degree of detail and without comparison to photometric redshifts.
Redshift fits from the pipeline
The pipeline fits templates (stars, galaxies, and QSOs) to the observations and outputs the most likely redshift, Z, an estimate of the error associated with the redshift, ZERR, and warning flags ZWARNING3 (Bolton et al. 2012). The best-fit template gives the object its class: star, galaxy, or QSO. The ZWARNING values of interest are 0, meaning that there was no problem during the fit, and 4, meaning that there is a small difference in χ2 between the first and the second best fit. The other values of ZWARNING enable tracking issues, but mean that we the redshift output should not be considered.
A posteriori redshift flags, zQ, and zCont
The reliability of the redshift of an emission-line galaxy is mainly correlated with the S/N of the detection of the line(s): 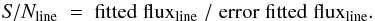 (1)In some cases, it can also be correlated to the detection of a small 4000 Å break.
(1)In some cases, it can also be correlated to the detection of a small 4000 Å break.
We use the redshift fit by the pipeline to classify the spectra according to the strength of their emission lines, using a flag zQ (where Q stands for quality), and to the features seen in the continuum, using a flag zCont. We define the flags in Table 1. In this classification, we consider a line with 3 ≤ S/N< 5 as a low S/N detection and a line with S/N ≥ 5 as a high S/N detection. To give an order of magnitude, the S/N value in the fitted line flux correspond roughly to the S/N value in the pixel that contains the maximum of the line.
In the following we mean the a posteriori redshift flags and not those from the inspection when we refer to redshift flags.
Redshift flags.
Classification of 13,450 visually inspected redshifts per category of redshift flag.
3.1. Redshift reliability
In this section we compare the inspections, the outputs of the pipeline, and the flags zQ and zCont. We determine a scheme that makes more inspections redundant and provides reliable redshifts to the collaboration.
To gather the three sources of information into a single table, we convert the results from the inspections into a single decision: the inspector agrees or disagrees with the redshift proposed by the pipeline: | zinspection − zpipeline | / (1 + zpipeline) ≤ 0.005. Table 2 presents the results. The higher the flag value, the higher the agreement rate, thus the flags are a good estimator of the redshift quality. Based on Table 2, we can create a criterion to select the largest number of redshifts for the highest tolerated error rate, that is, we investigate the trade-off between the total amount of redshift considered and the fraction of redshifts that are catastrophic.
For the purpose of eBOSS clustering analysis, we select galaxies with a pipeline redshift in the range 0.7 <z< 1.1 that are brighter than g< 22.8 (using DES or CFHT photometry, in total, we have 2660 such galaxies to study this trade-off).
We find that the following criterion fulfills the eBOSS/ELG redshift quality requirement: 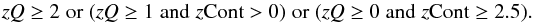 (2)The criterion excludes 278 objects and keeps 2382 objects. Of the 2382, the inspection disagrees with 22 redshifts, which corresponds to a 1% share. Of the 278 excluded objects, the inspection agrees with 147 redshifts, which is a 52% share. Future pipeline improvement could therefore lead to an improvement of 5.5% in efficiency at most. For a clustering analysis, we were unable to consider all the redshifts provided by the pipeline because it produces a fraction of incorrect redshifts of about 6%. In other words, we need to discard redshifts of lower quality to obtain a purer sample. With the current observations, we cannot determine the effect of this poor-redshift exclusion on the redshift distribution and on the clustering measurement.
(2)The criterion excludes 278 objects and keeps 2382 objects. Of the 2382, the inspection disagrees with 22 redshifts, which corresponds to a 1% share. Of the 278 excluded objects, the inspection agrees with 147 redshifts, which is a 52% share. Future pipeline improvement could therefore lead to an improvement of 5.5% in efficiency at most. For a clustering analysis, we were unable to consider all the redshifts provided by the pipeline because it produces a fraction of incorrect redshifts of about 6%. In other words, we need to discard redshifts of lower quality to obtain a purer sample. With the current observations, we cannot determine the effect of this poor-redshift exclusion on the redshift distribution and on the clustering measurement.
3.1.1. Comparison with VIPERS redshifts
In the eBOSS ELG test plates, 383 match redshifts in the VIPERS DR1 field W1. We find 370 (97.6%) redshifts in agreement (with dz/ (1 + z) ≤ 0.005) and 13 redshifts in disagreement (with dz/ (1 + z) > 0.005). Ten out of the 13 galaxies have a low-quality flag in VIPERS and a high-quality flag in eBOSS. A second visual inspection of these ten eBOSS redshifts indicates that they are correct. Three out of 13 have a low-quality flag in both VIPERS and eBOSS: both redshifts may not be reliable. The last category is 3 / 383 = 0.78% of the total.
3.1.2. Redshift efficiency and fiber number
As shown in Fig. 9 of Bolton et al. (2012), the redshift efficiency decreases for the fiber numbers around 0, 500, and 1000 because they are the most off-center with respect to the spectrograph camera optics. The ELGs demonstrate the same trends.
3.2. Line confusion
If the continuum is not detected (zCont = 0), then the redshifts in classes zQ = 1, 2, and 3.5 only rely on the detection of a single emission line (SEL hereafter). The BOSS spectrograph covers 3600 Åto 10 400 Å, and prominent lines with similar strengths are
-
Hα(λ6564) detectable at
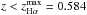 ;
; -
[Oiii] (λ5007) detectable at
![\hbox{$\rm {\it z<z}^{max}_{[{\sc O_{III}}]}=1.077$}](/articles/aa/full_html/2016/08/aa27377-15/aa27377-15-eq86.png) ;
; -
Hβ(λ4862) detectable at
![\hbox{$\rm {\it z<z}^{max}_{[{\sc H\beta}]}=1.139$}](/articles/aa/full_html/2016/08/aa27377-15/aa27377-15-eq87.png) ;
; -
[Oii] (λλ3727,3729) detectable at
![\hbox{$\rm {\it z<z}^{max}_{[{\sc O_{II}}]}=1.790$}](/articles/aa/full_html/2016/08/aa27377-15/aa27377-15-eq89.png) .
.
At redshift 1.8, the Lyman α line is at λ = 3400 Å and cannot be detected. The eBOSS survey will first observe quasar targets with a similar limiting magnitude as ELGs. The quasar sampling is quite complete in particular for bright Lyman α QSOs (Myers et al. 2015; Palanque-Delabrouille et al. 2016). The remaining quasar contamination of the ELG sample will be very small (<0.5%) and cannot be quantified with current data. We therefore examine the following possible confusions: ![\begin{eqnarray} \rm \lambda^{detection}_{line}\! \!&=&\! \!(1+{\it z}_{\rm H\alpha})\lambda_{\rm H\alpha} =(1+{\it z}_{\rm H\beta})\lambda_{\rm H\beta} \notag\\&=&\rm (1+{\it z}_{[{\sc O_{III}}]})\lambda_{[{\sc O_{III}}]} = (1+{\it z}_{[{\sc O_{II}}]}) \lambda_{[{\sc O_{II}}]} . \end{eqnarray}](/articles/aa/full_html/2016/08/aa27377-15/aa27377-15-eq92.png) (3)We set aside the case zQ = 3.5 and zCont = 0 because the [Oii] doublet is sometimes seen as a blended doublet and therefore provides more information than a single line detection.
(3)We set aside the case zQ = 3.5 and zCont = 0 because the [Oii] doublet is sometimes seen as a blended doublet and therefore provides more information than a single line detection.
The set of observed SEL redshifts as a function of the emission line and S/N is detailed in Table 3. At S/N ≥ 5, all SEL redshifts are primarily based on prominent lines (6 exceptions out of 3329), whereas for the 3 ≤ S/N< 5 SEL redshifts, we encounter a variety of line detections (284 exceptions out of 855).
We re-inspected the low and high S/N line detections that are not in the set of prominent lines. We found that these lines are fit on residuals of the sky subtraction. The low and high S/N line detections found to be prominent lines are not convincing either, and line confusion is possible. For this reason, we exclude the classes (zQ = 1 or 2) and zCont = 0 from the pool of reliable redshifts in the reliable redshift selection criterion.
There are 3225 S/N5 [Oii] detection cases with zQ = 3.5 and zCont = 0. For the [Oii] line, we fit the share of the flux in each component of the line: 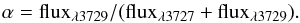 (4)We define X = α/αerr and show in Fig. 2 a few [Oii] lines measurements and fits that span the range of X values. We find that X is correlated to the S/N detection of the line. On average, if the doublet is detected at S/N 7, then the double Gaussian model is significantly more accurate than a simple Gaussian model. We note that at redshift 0.8, the typical velocity dispersion in the ELG is around 70 km s-1, so that the line width of each component in the fits is dominated by the instrumental resolution (Comparat et al. 2013a).
(4)We define X = α/αerr and show in Fig. 2 a few [Oii] lines measurements and fits that span the range of X values. We find that X is correlated to the S/N detection of the line. On average, if the doublet is detected at S/N 7, then the double Gaussian model is significantly more accurate than a simple Gaussian model. We note that at redshift 0.8, the typical velocity dispersion in the ELG is around 70 km s-1, so that the line width of each component in the fits is dominated by the instrumental resolution (Comparat et al. 2013a).
 |
Fig. 2 Example of fits of the [Oii] doublets by a double Gaussian on some spectra from plate 8130. Each spectrum (blue error bars) is labeled by its fiber number and the fits (black solid) are characterized by the χ2/d.o.f. given above each panel. We show the two individual Gaussians as red dashes. The vertical magenta dashed lines are at (1 + z)λ[OII]. The panels are ordered by increasing value of X. Around a value of X = 7, the blended doublet starts to be a better model than a single Gaussian. The last panel shows the [Oii] S/N vs. X with horizontal and vertical solid lines at a value of 7. X is the S/N with which the two components of the doublets are detected. |
3.3. Pipeline redshift error
The previous subsection demonstrated that the redshift failures are correlated with the S/N in the lines. We now quantify this statement using the pipeline redshift errors.
We consider all the redshifts (with zQ ≥ −1) and the correlation between the detection S/N of the line, the redshift, and redshift error. Figure 3 shows the redshift error as a function of redshift coded with the emission line S/N for the lines HαHβ, [Oii] , and [Oiii] 5007. Regardless of redshift, the S/N of the line S/N is highly anticorrelated with the redshift error: the higher the S/N, the lower the error. The effect of the sky brightness on the redshift error is also evident: for a fixed S/N in a line, the redshift error increases and decreases as the sky brightness. A S/N = 3 in the [Oii] line corresponds to an average error of zerr ~ (1 + z) × 10-4, suggesting that the pipeline redshift errors are within the requirements. To conclude, the stronger the emission lines, the more accurate the centroid of the redshift.
 |
Fig. 3 Redshift uncertainty vs. redshift for the ELGs for the Hα, [Oiii] , Hβ, and [Oii] emission lines detected coded as a function of the log of the detection S/N. The sky emission line is imprinted on the variation in S/N with redshift. The last row presents the correlation between redshift error and line S/N detection. The redshift error is anticorrelated with the line S/N. |
4. ELG selection algorithms
 |
Fig. 4 Summary of eBOSS ELG pilot observations. RA vs. Dec colored with Galactic extinction (top left). The area covered has a low Galactic extinction. Number of ELGs as a function of redshift and [Oiii] , Hβ, and [Oii] line flux when measured with a signal-to-noise ratio higher than 5. [Oii] is the strongest emission line and is seen throughout the redshift range. |
 |
Fig. 5 Redshift distribution obtained for each selection. The DES-based selections have a higher density and a higher mean redshift. The identification rates (galaxies with redshifts) are des-b: 76%, des-f: 71%, gri-uri: 68%, fisher griw: 72%, and fisher ugrizw: 76%. |
Using the photometric catalogs described previously and the target selection algorithms described in this section, we targeted 9000 ELGs (chunks eboss 6 and 7). The positions of the observed targets on the sky and the measured line flux as a function of redshift for the main emission lines [Oii] , Hβ, and [Oiii] are presented in Fig. 4. The position of the observations on the sky are shown in the first panel, coded by the level of Galactic extinction (Schlegel et al. 1998): we observed a region with low extinction. The other three panels show that most lines have a flux greater than log (flux / erg s-1 cm-2) >−16.5. In this section, we detail how each selection was designed and describe their efficiency in targeting ELGs in the redshift range 0.6 to 1.1. We use the criterion to automatically select reliable redshifts given in Eq. (2).
4.1. Observational strategy
For this test, we designed seven different selection schemes. Two of them are based on the DES photometry, the others on the SDSS-WISE-SCUSS photometry. We gave first priority to the selections based on the SDSS-WISE-SCUSS photometry because they have lower surface densities and are limited by brighter magnitude cuts. We gave second priority to the fainter and denser DES-based selections. Table 4 summarizes all the selections probed, their density, and the observed fraction. As a result, the first-priority selections had more than 90% of their targets assigned fibers and the second-priority selections had between 60 and 70% of their targets observed.
For the first-priority objects, the targets are drawn randomly and the obtained sample is a fair subsample of the parent sample. For the second-priority objects, we apply conditional weights to the second-priority objects to compute moments of its distribution or to produce histograms because there are some common targets in the second- and first-priority selections.
The observations were designed with large overlaps between the plates to neglect fiber collision in the central area 34 < RA < 38° and −6 < Dec < −3.8 where Jouvel et al. (2015) computed the clustering of the observed ELGs.
We designed a broad selection to then re-cut the final selection for eBOSS inside these observations. This is important to have some data around the fiducial selection to understand the effects of each cut on the observed galaxy population. These observations constitute a super-set of the actual eBOSS ELG sample in color-magnitude redshift space.
4.2. ELG selection with SDSS-WISE-SCUSS
Using the photometry from SDSS-WISE-SCUSS, we tested two approaches, a color selection and a Fisher linear discriminant (Fisher 1936) selection, attempting to maximize both the share of ELGs in the redshift range of interest and the mean redshift of the sample with a lowest density of 180 ELG per deg2. Selecting ELGs at this redshift with such a photometry slightly pushes the limits. There is only little wiggle room for the magnitude limit, which drags the density of tracers to the lower limit.
The priority scheme did not influence the completeness from one sample to another, and the observed samples are fair subsamples of the complete selections.
4.2.1. Color selection
The color selection uses two color spaces U − r − i and g − r − i (see Fukugita et al. 1996, who defined the filters). We call this selection the gri-Uri selection. This is a further optimization of the color selections observed in Comparat et al. (2013b). It selects a mean of 197 targets per deg2 (averaged over ~50 deg2) by applying the following selections on the photometric catalog.
-
RESOLVE_STATUS in the SDSS photometry has SURVEY_PRIMARY on
-
gmodel,rmodel,imodel> 0 and
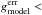 0.6 and
0.6 and 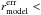 1 and
1 and  0.4
0.4 -
and [(a) OR (b)] where
-
(a)
21 ≤ gmodel < 22.5 and rmodel < 22.5 and imodel < 21.65 and gmodel − rmodel < 0.8 and rmodel − imodel > 0.8
-
(b)
20< gmodel < 23 and rmodel < 22.5 and imodel < 21.6 and 21 <UmodelAdd < 22.5 and rmodel − imodel > 0.7 and rmodel − UmodelAdd > 0.7−3.5 ∗ (rmodel − imodel),
-
(a)
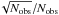 . We securely measured the redshifts of 68±2% of the targets as galaxies or QSOs; see Table A.1. This sample has a mean redshift of 0.734. The percentage of detections classified as stars is 7.7%, which leaves a 25% fraction of unknown objects.
. We securely measured the redshifts of 68±2% of the targets as galaxies or QSOs; see Table A.1. This sample has a mean redshift of 0.734. The percentage of detections classified as stars is 7.7%, which leaves a 25% fraction of unknown objects.
4.2.2. Fisher selections
The Fisher selection algorithm allows us to make additionally optimized color-selections in a greater number of dimensions, which slightly improves the selection efficiency. For a thorough description of the Fisher selection method, see Raichoor et al. (2016). We constituted a training spectroscopic data sample using the SDSS, BOSS ELG, VIPERS, DEEP2, zCOSMOS, and VVDS surveys (Alam et al. 2015; Comparat et al. 2015; Guzzo et al. 2014; Newman et al. 2013; Lilly et al. 2009; Le Fèvre et al. 2013, respectively) to derive the best possible selection with a Fisher discriminant. We test this selection function in the chunk eboss7, that is, a sub-region of the eboss6 chunk. We consider two types of selection, first using the combination of SDSS and WISE, designated griW, and second, using the combination of SCUSS, SDSS, and WISE, named UgrizW. We emphasize that the selections published in Raichoor et al. (2016) are slightly different from those tested in eboss7 because the selection function was further optimized based on the eboss6-7 tests. The redshift distributions obtained using the Fisher approach are given in Table A.2.
We use the first two filters of the WISE photometry W1 and W2 to construct a composite extinction-corrected AB magnitude, Wmodel, which takes advantage of the two measurements (see Myers et al. 2015, for the details about the WISE composite magnitude). First, we convert W1 and W2 magnitudes to the AB magnitude system (AB = Vega + dm, with dm(W1) = 2.699 and dm(W2) = 3.339). We then define W as follows:
-
W = W1, if no W2 measurement
-
W = W2, if no W1 measurement
-
else: flux(W) = (flux(W1) + 0.5*flux(W2))/1.5 when both W1 and W2 measurements are present.
For the uncertainty, we construct 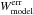 from W1_MAGERR and W2_MAGERR using the propagation of uncertainties in quadrature. For the extinction, we consider extinction_W = extinction_W1 because abs(extinction_W1-extinction_W2) < 5e-3 in the test region). Finally, we use Wmodel = W − extinction_W1.
from W1_MAGERR and W2_MAGERR using the propagation of uncertainties in quadrature. For the extinction, we consider extinction_W = extinction_W1 because abs(extinction_W1-extinction_W2) < 5e-3 in the test region). Finally, we use Wmodel = W − extinction_W1.
Fisher UgrizW
The Fisher UgrizW selection selection was adopted as a first priority and contains
-
RESOLVE_STATUS in the SDSS photometry has SURVEY_PRIMARY on
-
OBJC_TYPE = 3 or rmodel> 22
-
20.0 <gmodel< 22.7 and
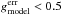 and 19.0 <rmodel< 22.5 and
and 19.0 <rmodel< 22.5 and 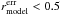 and 19.0 <imodel< 21.5 and
and 19.0 <imodel< 21.5 and 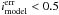 and 17.0 <Wmodel< 21.0 and
and 17.0 <Wmodel< 21.0 and  and UmodelAdd> 0
and UmodelAdd> 0 -
1.23 < FisherUgrizW< 5.0,
with FisherUgrizW = −0.390197(umodelAdd − rmodel) − 0.497885(gmodel − rmodel) + 0.0734933(rmodel − imodel) + 0.480957(rmodel − Wmodel) + 0.152151(rmodel − zmodel) + 0.847598. It has a target density of 199 per square degree. A total of 76% are identified as galaxies or QSOs with a mean redshift at 0.788. The detections classified as stars are 1.7%, and 22% remain unknown.
Fisher UgrizW bright
The Fisher selection UgrizW bright selection was chosen as a second priority; the overlap with the first selection is broad.
-
Same as the Fisher UgrizW selection points 1 to 3 (not 4)
-
gmodel< 22.5 and 1.13 < FisherUgrizW< 1.23.
It has a target density of 43 per square degree; 71% are identified as galaxies or QSOs with a mean redshift at 0.724. The detections classified as stars are 0.34%, and 28% remain unknown. It seems less efficient, but the uncertainty on the efficiency is 9% because there are only a few targets.
Fisher UgrizW bright all
The Fisher selection UgrizW bright all is the same as the UgrizW bright, but without the FisherUgrizW < 1.23 selection. It has a target density of 196 per square degree; 78% are identified as galaxies or QSOs with a mean redshift at 0.778. The detections classified as stars are 1.47%, and 20% remain unknown.
Fisher griW
The Fisher selection griW was selected as a third priority and does not use the SCUSS U band or the SDSS z band, which are quite shallow.
-
RESOLVE_STATUS in the SDSS photometry has SURVEY_PRIMARY on
-
OBJC_TYPE = 3 or rmodel> 22
-
20.0 <gmodel< 22.5 and
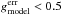 and 19.0 <rmodel< 22.5 and
and 19.0 <rmodel< 22.5 and 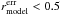 and 19.0 <imodel< 21.5 and
and 19.0 <imodel< 21.5 and 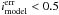 and 17.0 <Wmodel< 21.0 and
and 17.0 <Wmodel< 21.0 and 
-
0.61 < FishergriW< 5.00,
with FishergriW = −0.50972(gmodel − rmodel) + 0.304366(rmodel − imodel) + 0.353073(rmodel − Wmodel) + 0.0306172. This selection has a target density of 196 per square degree; 72% are identified as galaxies or QSOs with a mean redshift at 0.788. The detections classified as stars are 2.61%, and 25% remain unknown.
Table A.2 gives the detailed density of galaxies observed as a function of redshift using the Fisher approach.
4.2.3. Results with the SDSS-WISE-SCUSS selections
For the same target density, the Fisher selections improve the identification rate by up to 10%, increase the mean redshift, and diminish the contamination by lower redshift galaxies and stars compared to the color selection. The first decile of the redshift distribution is higher than 0.6 compared to 0.43 for the gri-Uri selection, see Table 6.
The Fisher selection was further optimized by Raichoor et al. (2016), and it meets the requirement.
ELG selection target surface densities (after applying the bright star mask) and observed surface densities.
4.3. ELG selection with DECam − DES photometry
We performed two tests selecting either brighter and redder galaxies (DES bright) or fainter and bluer galaxies (DES faint). These objects are targeted as last-priority objects after the gri-Uri targets in eboss6 and after the Fisher targets in eboss7.
4.3.1. DES, bright selection
The bright selection is defined by
-
20.5 <gmodel< 22.8,
-
and −0.7 <gmodel − rmodel< 0.9, and 0 <rmodel − zmodel< 2 and rmodel − zmodel> 0.4 ∗ (gmodel − rmodel) + 0.4
-
g2′′ − gmodel< 2 and r2′′ − rmodel< 2 and z2′′ − zmodel< 2: it rejects false detections near bright stars or saturated bright stars,
where magmodel is the model magnitude (MAG_DETMODEL) and mag2′′ is the 2′′ diameter aperture magnitude (MAG_APER_4) reported by the DES pipeline. We designate this selection by des bright. It has a target density of 615 per square degree; 76% are identified as galaxies with a mean redshift at 0.843. The detections classified as stars are 7.7%, and 16% remain unknown.
4.3.2. DES, faint selection
The faint selection is defined by
-
gmodel> 20.45 and rmodel< 22.79
-
0.285 <rmodel − zmodel< 1.585 and gmodel − rmodel< 1.1458 (rmodel − zmodel) − 0.209 and gmodel − rmodel< 1.4551−1.1458 (rmodel − zmodel)
-
g2” − gmodel< 2 and r2” − rmodel< 2 and z2” − zmodel< 2.
It has a target density of 650 per square degree. Seventy-one percent are identified as galaxies with a mean redshift at 0.9. The detections classified as stars are 6.3% and 23% remain unknown. The observed redshift distribution is given in Table A.3. We designate this selection by des faint.
4.3.3. Results with DECam − DES photometry
The DES-based selections were observed at a lower completeness level (60%−70%) and the average redshift is higher than with the SDSS-based selections. We weight the observations accordingly to recover the correct redshift distribution. The redshift distributions are too extended for the purpose of eBOSS.
4.4. Optimized selection using DECam imaging
Using the eboss6 and 7 observations, we further optimize the DECam-based target selection to increase its efficiency for the purpose of eBOSS ELG selection. The further optimization of the Fisher algorithms is presented in Raichoor et al. (2016). The eBOSS ELG program will target 255 000 ELGs. We will draw targets from 1500 deg2 of imaging observed by DES or DECaLS. The target density of fibers assigned to ELGs is therefore 170 deg-2. Given a 95% fiber assignment efficiency, we need to provide 180 deg-2.
We found a further optimization of the DES-based ELG algorithms that satisfies the eBOSS requirements. We name this algorithm decam 180. It has the same bright-star-contamination exclusion scheme: g2′′ − gmodel< 2 and r2′′ − rmodel< 2 and z2′′ − zmodel< 2. Then, the ELG selection is
-
22.1 <gmodel< 22.8
-
0.3 <gmodel − rmodel< 0.7 and 0.25 <rmodel − zmodel< 1.4
-
0.5(gmodel − rmodel) + 0.4 <rmodel − zmodel< 0.5(gmodel − rmodel) + 0.8.
Figure 6 shows the selection box in the g − r, r − z plane.
It selects 182 ± 3 targets per deg2 and outputs N(0.7 <zgood< 1.1) = 75.8 ± 0.4% with a mean redshift at 0.864. The redshift quality flags discard 4% of the total amount of redshifts in the range 0.7 <z< 1.1. These are detections with low S/N, and one half of the redshift are incorrect and one half is correct, which means that future pipeline improvement could increase the efficiency by 2% at most. The redshift identification rate is 87± 0.5%. The contaminants are low-redshift galaxies (2.3%), higher redshift galaxies (7.7%), and unknown redshifts (14%). The median [Oii] ([Oiii] ) flux observed is 7(6) × 10-17erg s-1 cm-2. These numbers are based on the observation of 2604 (decam 180) targets in eboss6 and eboss7. For the decam 180 selection, fewer than 0.5% of the targets fall in the category SEL.
Summary of the selections ordered by median redshift.
The redshift distribution is given in Tables 6 and A.4. It has a narrow redshift range and is mainly contaminated by low-quality redshifts and higher redshift, z> 1.1, galaxies. An independent study of this selection on the COSMOS [Oii] catalog (Comparat et al. 2015) and its corresponding DECam photometry4 provides the same redshift distributions and success rates.
The selection scheme presented was chosen from a handful of other selections producing similar efficiencies and densities. To do so, we sorted all possible selection schemes with the mean [Oii] emission line flux so that this scheme guarantee strong lines.
Using the current spectroscopic data (eboss6-7) and applying the same method as described in Jouvel et al. (2015), we measure the monopole clustering and deduce the galaxy bias for both samples: b = 1.7 ± 0.1. The further optimization of the selection increased the efficiency without changing the clustering amplitude.
 |
Fig. 6 Color (g − r) −color (r − z) diagram showing the optimized DECam-based ELG selection algorithms. We show all the good spectroscopic redshifts observed by eboss6 and 7. The mean error on the DES colors is shown with the red cross in the top left corner. |
5. Pilot observations, results
We compare the target density and redshift distribution of the observed and optimized selection algorithms in Tables 5 and 6. It is difficult to target ELGs beyond redshift one using the SDSS-WISE-SCUSS selections photometry, but it is feasible with the DES photometry. Beyond redshift 1.1, the [Oii] doublet is not systematically split, and the efficiency in assigning correct redshift therefore diminishes. Sky lines also become stronger. The optimized decam algorithm meets the requirements set by eBOSS (we note that the observed selections do not meet the requirements). In addition, the optimized Fisher is at the limit of meeting the requirements with a 71% efficiency.
Moments of the eBOSS ELG redshift distribution: first decile D10, first, second (median), and third quartiles Q25, Q50, Q75, and last decile D90.
Using shallower photometry to reach the density of galaxies required by eBOSS, we are forced to target near the limit of the photometry. In this regime, the Malmquist bias becomes non-negligible and the actual mean magnitude of the selection is fainter than the magnitude selection imposed on the data, so that the sample becomes dominated by fainter galaxies and the redshift identification rate decreases.
Result of the inspection of two plates from eboss6.
5.1. Insights on the object classification of plates 8123 and 8130
We use the class information from the inspection made on the two eboss6 plates 8123 and 8130 to determine stellar contamination; see Table 7. The selection algorithms gri-Uri, des bright, and des faint mostly target galaxies. The contamination by QSOs or stars is small. The main contamination is due to spectra with a low S/N where the redshift cannot be securely determined; these are probably faint galaxies. The current automated classification that identifies the type of object (star, galaxy, or quasar) is only reliable for high S/N spectra and not for the low S/N spectra where the class assignments should not be trusted.
6. Summary
In this article, we demonstrated that the automated redshift estimation for ELGs at redshift 0.8 is reliable, in particular, we confined the possible line confusion rate to a sub-percent level. We also documented the eBOSS ELG pilot survey: 9000 new spectra targeted from different photometric surveys. We provided reliable redshift distributions for each selection scheme. We additionally optimized and finalized one of the possible eBOSS ELG selections using DECam-based imaging. This selection has a density of 180 for a galaxy bias of 1.7 ± 0.1 and an efficiency of nearly 76 percent. This selection is best suited for a wide-angle survey to precisely measure the BAO in the two-point correlation function at redshift 0.85.
Future plans
The ELG samples under construction will be extremely useful for investigating the galaxy population that forms stars most efficiently.
The spectroscopic signature of ELGs is quite specific and mixes light emitted by the stellar population (which is a combination of recently formed and older stars and light reprocessed by the interstellar medium) and by the circumgalactic medium. To provide a global panchromatic view of these galaxies, we will study the infrared light emitted by their dust component in a future publication.
By combining N-body simulations with semi-analytical models that reproduce observations, we aim to develop the analysis reported in Favole et al. (2016) to provide a more complete description of ELG properties, clarify their nature, and maximize their potential for constraining cosmological models.
Acknowledgments
J.C .and F.P. acknowledge support from the Spanish MICINNs Consolider-Ingenio 2010 Programme under grant MultiDark CSD2009-00064, MINECO Centro de Excelencia Severo Ochoa Programme under the grants SEV-2012-0249, FPA2012-34694, and the projects AYA2014-60641-C2-1-P and AYA2012-31101. We also thank the Lawrence Berkeley National Laboratory for its hospitality. F.P. acknowledges the spanish MEC Salvador de Madariaga program, Ref. PRX14/00444. T.D. and J.P.K. acknowledge support from the LIDA ERC advanced grant. AR acknowledges funding from the P2IO LabEx (ANR-10-LABX-0038) in the framework Investissements d’Avenir (ANR- 11-IDEX-0003-01) managed by the French National Research Agency (ANR). E.J. acknowledges the support of CNRS and the Labex OCEVU. This paper represents an effort by the SDSS-III, SDSS-IV and DES collaborations. Funding for SDSS-III was provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, and the US Department of Energy Office of Science. The SDSS web site is http://www.sdss.org. SDSS-IV acknowledges support and resources from the Center for High-Performance Computing at the University of Utah. SDSS-IV is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS Collaboration including the Brazilian Participation Group, the Carnegie Institution for Science, Carnegie Mellon University, the Chilean Participation Group, the French Participation Group, Harvard-Smithsonian Center for Astrophysics, Instituto de Astrofísica de Canarias, The Johns Hopkins University, Kavli Institute for the Physics and Mathematics of the Universe (IPMU)/University of Tokyo, Lawrence Berkeley National Laboratory, Leibniz Institut für Astrophysik Potsdam (AIP), Max-Planck-Institut für Astronomie (MPIA Heidelberg), Max-Planck-Institut für Astrophysik (MPA Garching), Max-Planck-Institut für Extraterrestrische Physik (MPE), National Astronomical Observatory of China, New Mexico State University, New York University, University of Notre Dame, Observatário Nacional/MCTI, The Ohio State University, Pennsylvania State University, Shanghai Astronomical Observatory, United Kingdom Participation Group, Universidad Nacional Autónoma de México, University of Arizona, University of Colorado Boulder, University of Portsmouth, University of Utah, University of Virginia, University of Washington, University of Wisconsin, Vanderbilt University, Yale University and the french participation group. Funding for the DES Projects has been provided by the US Department of Energy, the U.S. National Science Foundation, the Ministry of Science and Education of Spain, the Science and Technology Facilities Council of the United Kingdom, the Higher Education Funding Council for England, the National Center for Supercomputing Applications at the University of Illinois at Urbana-Champaign, the Kavli Institute of Cosmological Physics at the University of Chicago, the Center for Cosmology and Astro-Particle Physics at the Ohio State University, the Mitchell Institute for Fundamental Physics and Astronomy at Texas A&M University, Financiadora de Estudos e Projetos, Fundação Carlos Chagas Filho de Amparo à Pesquisa do Estado do Rio de Janeiro, Conselho Nacional de Desenvolvimento Científico e Tecnológico and the Ministério da Ciência, Tecnologia e Inovação, the Deutsche Forschungsgemeinschaft and the Collaborating Institutions in the Dark Energy Survey. The Collaborating Institutions are Argonne National Laboratory, the University of California at Santa Cruz, the University of Cambridge, Centro de Investigaciones Energéticas, Medioambientales y Tecnológicas-Madrid, the University of Chicago, University College London, the DES-Brazil Consortium, the University of Edinburgh, the Eidgenössische Technische Hochschule (ETH) Zürich, Fermi National Accelerator Laboratory, the University of Illinois at Urbana-Champaign, the Institut de Ciències de l’Espai (IEEC/CSIC), the Institut de Física d’Altes Energies, Lawrence Berkeley National Laboratory, the Ludwig-Maximilians Universität München and the associated Excellence Cluster Universe, the University of Michigan, the National Optical AstronomyObservatory, the University of Nottingham, The Ohio State University, the University of Pennsylvania, the University of Portsmouth, SLAC National Accelerator Laboratory, Stanford University, the University of Sussex, and Texas A&M University. The DES data management system is supported by the National Science Foundation under Grant Number AST-1138766. The DES participants from Spanish institutions are partially supported by MINECO under grants AYA2012-39559, ESP2013-48274, FPA2013-47986, and Centro de Excelencia Severo Ochoa SEV-2012-0234. Research leading to these results has received funding from the European Research Council under the European Union’s Seventh Framework Programme (FP7/2007−2013) including ERC grant agreements 240672, 291329, and 306478. We are grateful for the extraordinary contributions of our CTIO colleagues and the DECam Construction, Commissioning and Science Verification teams in achieving the excellent instrument and telescope conditions that have made this work possible. The success of this project also relies critically on the expertise and dedication of the DES Data Management group. This paper includes targets derived from the images of the Wide-Field Infrared Survey Explorer, which is a joint project of the University of California, Los Angeles, and the Jet Propulsion Laboratory/California Institute of Technology, funded by the National Aeronautics and Space Administration. This paper has gone through internal review by the DES collaboration.
References
- Ahn, C. P., Alexandroff, R., Allen de Prieto, C., et al. 2012, ApJS, 203, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Alam, S., Albareti, F. D., Allen de Prieto, C., et al. 2015, ApJS, 219, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, L., Aubourg, É., Bailey, S., et al. 2014, MNRAS, 441, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Angulo, R. E., White, S. D. M., Springel, V., & Henriques, B. 2014, MNRAS, 442, 2131 [NASA ADS] [CrossRef] [Google Scholar]
- Banerji, M., Jouvel, S., Lin, H., et al. 2015, MNRAS, 446, 2523 [NASA ADS] [CrossRef] [Google Scholar]
- Bautista, J. E., Bailey, S., Font-Ribera, A., et al. 2015, J. Cosmol. Astropart. Phys., 5, 60 [Google Scholar]
- Bolton, A. S., Schlegel, D. J., Aubourg, É., et al. 2012, AJ, 144, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Boulade, O., Charlot, X., Abbon, P., et al. 2003, in Instrument Design and Performance for Optical/Infrared Ground-based Telescopes, eds. M. Iye, & A. F. M. Moorwood, SPIE Conf. Ser., 4841, 72 [Google Scholar]
- Bovy, J., Myers, A. D., Hennawi, J. F., et al. 2012, ApJ, 749, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Comparat, J., Kneib, J.-P., Bacon, R., et al. 2013a, A&A, 559, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Comparat, J., Kneib, J.-P., Escoffier, S., et al. 2013b, MNRAS, 428, 1498 [NASA ADS] [CrossRef] [Google Scholar]
- Comparat, J., Richard, J., Kneib, J.-P., et al. 2015, A&A, 575, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dawson, K. S., Schlegel, D. J., Ahn, C. P., et al. 2013, AJ, 145, 10 [Google Scholar]
- Dawson, K. S., Kneib, J.-P., Percival, W. J., et al. 2016, AJ, 151, 44 [NASA ADS] [CrossRef] [Google Scholar]
- de la Torre, S., Guzzo, L., Peacock, J. A., et al. 2013, A&A, 557, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delubac, T., Bautista, J. E., Busca, N. G., et al. 2015, A&A, 574, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Diehl, H. T., Abbott, T. M. C., Annis, J., et al. 2014, in SPIE Conf. Ser., 9149, 0V [Google Scholar]
- Doel, P., Brooks, D., Antonik, M. L., et al. 2012, in SPIE Conf. Ser., 8446, 6F [Google Scholar]
- Drinkwater, M. J., Jurek, R. J., Blake, C., et al. 2010, MNRAS, 401, 1429 [Google Scholar]
- Eisenstein, D. J., Weinberg, D. H., Agol, E., et al. 2011, AJ, 142, 72 [Google Scholar]
- Favole, G., Comparat, J., Prada, F., et al. 2016, MNRAS, 461, 3421 [NASA ADS] [CrossRef] [Google Scholar]
- Fisher, R. A. 1936, Annals of Eugenics, 7, 179 [CrossRef] [Google Scholar]
- Flaugher, B. 2012, in APS April Meeting Abstracts, 7007 [Google Scholar]
- Flaugher, B., & Bebek, C. 2014, in SPIE Conf. Ser., 9147, 0S [Google Scholar]
- Flaugher, B., & DES Collaboration. 2013, in Am Astron. Soc. Meet. Abstr., 221, #335.02 [Google Scholar]
- Flaugher, B., Diehl, H. T., Honscheid, K., et al. 2015, AJ, 150, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Fukugita, M., Ichikawa, T., Gunn, J. E., et al. 1996, AJ, 111, 1748 [NASA ADS] [CrossRef] [Google Scholar]
- Garilli, B., Guzzo, L., Scodeggio, M., et al. 2014, A&A, 562, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gunn, J. E., Carr, M., Rockosi, C., et al. 1998, AJ, 116, 3040 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E., Siegmund, W. A., Mannery, E. J., et al. 2006, AJ, 131, 2332 [NASA ADS] [CrossRef] [Google Scholar]
- Guzzo, L., Scodeggio, M., Garilli, B., et al. 2014, A&A, 566, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gwyn, S. D. J. 2012, AJ, 143, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Jouvel, S., Delubac, T., Comparat, J., et al. 2015, ArXiv e-prints [arXiv:1509.07121] [Google Scholar]
- Kazin, E. A., Koda, J., Blake, C., et al. 2014, MNRAS, 441, 3524 [NASA ADS] [CrossRef] [Google Scholar]
- Lang, D., Hogg, D. W., & Schlegel, D. J. 2014, ArXiv e-prints [arXiv:1410.7397] [Google Scholar]
- Le Fèvre, O., Saisse, M., Mancini, D., et al. 2003, in Instrument Design and Performance for Optical/Infrared Ground-based Telescopes, eds. M. Iye, & A. F. M. Moorwood, SPIE Conf. Ser., 4841, 1670 [Google Scholar]
- Le Fèvre, O., Cassata, P., Cucciati, O., et al. 2013, A&A, 559, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lilly, S. J., Le Brun, V., Maier, C., et al. 2009, ApJS, 184, 218 [Google Scholar]
- Maraston, C., Pforr, J., Henriques, B. M., et al. 2013, MNRAS, 435, 2764 [NASA ADS] [CrossRef] [Google Scholar]
- Martinez, V., & Saar, E. 2002, in Astronomical Data Analysis II, eds. J.-L. Starck, & F. D. Murtagh, SPIE Conf. Ser., 4847, 86 [Google Scholar]
- Myers, A. D., Palanque-Delabrouille, N., Prakash, A., et al. 2015, ApJS, 221, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Newman, J. A., Cooper, M. C., Davis, M., et al. 2013, ApJS, 208, 5 [Google Scholar]
- Oke, J. B., & Gunn, J. E. 1983, ApJ, 266, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Palanque-Delabrouille, N., Magneville, C., Yèche, C., et al. 2016, A&A, 587, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poole, G. B., Blake, C., Marín, F. A., et al. 2015, MNRAS, 449, 1454 [NASA ADS] [CrossRef] [Google Scholar]
- Prakash, A., Licquia, T. C., Newman, J. A., et al. 2016, ApJS, 224, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Raichoor, A., Comparat, J., Delubac, T., et al. 2016, A&A, 585, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rodríguez-Torres, S. A., Prada, F., Chuang, C.-H., et al. 2016, MNRAS, 460, 1173 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, D. P., Richards, G. T., Hall, P. B., et al. 2010, AJ, 139, 2360 [NASA ADS] [CrossRef] [Google Scholar]
- Seo, H.-J., & Eisenstein, D. J. 2003, ApJ, 598, 720 [NASA ADS] [CrossRef] [Google Scholar]
- Sharp, R., Saunders, W., Smith, G., et al. 2006, in SPIE Conf. Ser., 6269, 0G [Google Scholar]
- Shen, Y., Brandt, W. N., Dawson, K. S., et al. 2015, ApJS, 216, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Smee, S. A., Gunn, J. E., Uomoto, A., et al. 2013, AJ, 146, 32 [Google Scholar]
- Weinberg, D. H., Mortonson, M. J., Eisenstein, D. J., et al. 2013, Phys. Rep., 530, 87 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, G.-B., Wang, Y., Ross, A. J., et al. 2016, MNRAS, 457, 2377 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, G. B., Comparat, J., Kneib, J.-P., et al. 2015, ApJ, 815, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Zou, H., Jiang, Z., Zhou, X., et al. 2015a, AJ, 150, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Zou, H., Wu, X.-b., Zhou, X., et al. 2015b, PASP, 127, 94 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Redshift distributions
Redshift distribution for reliably identified redshifts per square degree during eboss6 observations N = Nobs(zmin<z ≤ zmax) / TSR /area.
Redshift distribution for the DECam-optimized algorithm selecting ~182 ELG per deg2.
All Tables
Classification of 13,450 visually inspected redshifts per category of redshift flag.
ELG selection target surface densities (after applying the bright star mask) and observed surface densities.
Moments of the eBOSS ELG redshift distribution: first decile D10, first, second (median), and third quartiles Q25, Q50, Q75, and last decile D90.
Redshift distribution for reliably identified redshifts per square degree during eboss6 observations N = Nobs(zmin<z ≤ zmax) / TSR /area.
Redshift distribution for the DECam-optimized algorithm selecting ~182 ELG per deg2.
All Figures
 |
Fig. 1 Top panel: ELG spectra represented in the observed frame sorted by redshift. Each horizontal line corresponds to one spectrum. Vertical patterns correspond to the residuals of the sky subtraction. Diagonal patterns are the emission and absorption lines seen in the galaxy spectra. As redshift increases, the [Oii] , Hβ, [Oiii] , and Hαemission lines become redshifted. Starting at redshift 0.5, UV absorption lines enter the spectrograph window. Bottom panel: ELG spectra stacked by 50, ordered as a function of redshift represented in the rest-frame. The spectral features align vertically and are detected with higher signal-to-noise-ratio, in particular the absorption lines in the UV. Extended details about the UV absorption and emission systems are given in Zhu et al. (2015). |
| In the text | |
 |
Fig. 2 Example of fits of the [Oii] doublets by a double Gaussian on some spectra from plate 8130. Each spectrum (blue error bars) is labeled by its fiber number and the fits (black solid) are characterized by the χ2/d.o.f. given above each panel. We show the two individual Gaussians as red dashes. The vertical magenta dashed lines are at (1 + z)λ[OII]. The panels are ordered by increasing value of X. Around a value of X = 7, the blended doublet starts to be a better model than a single Gaussian. The last panel shows the [Oii] S/N vs. X with horizontal and vertical solid lines at a value of 7. X is the S/N with which the two components of the doublets are detected. |
| In the text | |
 |
Fig. 3 Redshift uncertainty vs. redshift for the ELGs for the Hα, [Oiii] , Hβ, and [Oii] emission lines detected coded as a function of the log of the detection S/N. The sky emission line is imprinted on the variation in S/N with redshift. The last row presents the correlation between redshift error and line S/N detection. The redshift error is anticorrelated with the line S/N. |
| In the text | |
 |
Fig. 4 Summary of eBOSS ELG pilot observations. RA vs. Dec colored with Galactic extinction (top left). The area covered has a low Galactic extinction. Number of ELGs as a function of redshift and [Oiii] , Hβ, and [Oii] line flux when measured with a signal-to-noise ratio higher than 5. [Oii] is the strongest emission line and is seen throughout the redshift range. |
| In the text | |
 |
Fig. 5 Redshift distribution obtained for each selection. The DES-based selections have a higher density and a higher mean redshift. The identification rates (galaxies with redshifts) are des-b: 76%, des-f: 71%, gri-uri: 68%, fisher griw: 72%, and fisher ugrizw: 76%. |
| In the text | |
 |
Fig. 6 Color (g − r) −color (r − z) diagram showing the optimized DECam-based ELG selection algorithms. We show all the good spectroscopic redshifts observed by eboss6 and 7. The mean error on the DES colors is shown with the red cross in the top left corner. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


