| Issue |
A&A
Volume 590, June 2016
|
|
|---|---|---|
| Article Number | L2 | |
| Number of page(s) | 5 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201628638 | |
| Published online | 12 May 2016 | |
Orbital clustering of distant Kuiper belt objects by hypothetical Planet 9. Secular or resonant?
1
Université Grenoble Alpes, IPAG,
CS 40700,
38058
Grenoble Cedex 9,
France
e-mail:
Herve.Beust@univ-grenoble-alpes.fr
2
CNRS, IPAG, CS
40700, 38058
Grenoble Cedex 9,
France
Received: 4 April 2016
Accepted: 1 May 2016
Context. Statistical analysis of the orbits of distant Kuiper belt objects (KBOs) has led to the suggestion that an additional planet should reside in the solar system. According to recent models, the secular action of this body should cause orbital alignment of the KBOs.
Aims. It was recently claimed that the KBOs affected by these dynamics are presumably trapped in mean-motion resonances with the suspected planet. I reinvestigate here the secular model underlying this idea.
Methods. The original analysis was carried out by expanding and truncating the secular Hamiltonian. I show that this is inappropriate, as the series expansion is not convergent. I present a study based on numerical computation of the Hamiltonian with no expansion.
Results. I show in phase-space diagrams the existence of apsidally anti-aligned, high eccentricity libration islands that were not present in the original modelling, but match numerical simulations. These island were claimed to correspond to bodies trapped in mean-motion resonances with the hypothetical planet and match the characteristics of the distant KBOs observed.
Conclusions. My main result is that regular secular dynamics can account for the anti-aligned particles itself as well as mean-motion resonances. I also perform a semi-analytical study of resonant motion and show that some resonance are actually capable of producing the same libration islands. I then discuss the relative importance of both mechanisms.
Key words: celestial mechanics / Kuiper belt: general / planets and satellites: dynamical evolution and stability
© ESO, 2016
1. Introduction
The growing statistics about distant Kuiper belt objects (KBOs) recently revived interest in the possible presence of an additional distant planet (hereafter termed Planet 9 or P9) in the solar system. This came out after the discovery of 2012 VP113, a large KBO with orbital parameters similar to those of Sedna (Trujillo & Sheppard 2014). As noted by de la Fuente Marcos & de la Fuente Marcos (2014), all such objects with large perihelia and eccentricities have arguments of perihelia ω concentrating around 0. Even if the statistics is poor, such a distribution is unlikely, as orbital precession induced by the giant planets is expected to quickly randomize ω values. This led de la Fuente Marcos & de la Fuente Marcos (2014) and Trujillo & Sheppard (2014) to suggest that the perturbing action of a distant super-Earth sized planet could help maintain this apsidal clustering.
This issue was recently investigated in more detail by Batygin & Brown (2016, hereafter B16). They first note that the distant KBOs not only gather around ω = 318° ± 8°, but that the same applies to their longitudes of ascending nodes Ω, which satisfy Ω = 113° ± 13°. As a consequence the orbits of all bodies concerned are roughly aligned physically. Based on the idea that this orbital confinement is due to the secular action of the suspected P9, they develop a secular dynamical model to constrain its parameters. They come to the conclusion that the planet that best reproduces the observational data has mass m′ = 10 M⊕, semi-major axis a′ = 700 au, and eccentricity e′ = 0.6.
Further constraints on this planet are hard to derive. Based on the analysis of residuals in the orbital motion of Saturn recorded by the Cassini spacecraft in the last decade, Fienga et al. (2016) recently showed that the residuals are better explained by P9 if we give it a current true anomaly around ~120°. This can indicate a preferred region to try to detect this planet. Cowan et al. (2016) claim that if it is large enough, P9 could be detected as a 30 mJy at 1 mm wavelength by existing cosmology experiments.
The purpose of this paper is to reinvestigate secular model and conclusions of B16. More specifically, B16 first develop a semi-analytical dynamical model of distant particles as secularly perturbed by the giant planets and hypothetical P9, and show that if it is eccentric enough P9 can actually confine the orbits in an apsidally aligned configuration with respect to itself. Then they move to numerical simulations. They recover the apsidally resonant islands noted in their semi-analytical study, but note that the particles trapped there do not have high enough eccentricities to account for the population of distant KBOs under consideration. Conversely, they notice the presence of new, high eccentricity and anti-aligned libration islands in their numerical work that did not appear in the semi-analytical work. They claim that these anti-aligned particles are presumably trapped in mean-motion resonances (MMRs) with P9, as resonant dynamics is not taken into account in secular theory. They show that some particles in their numerical study exhibit resonant trapping.
This issue was further investigated by who found that the orbital periods of the main distant KBOs present commensurabilities that could indicate resonant configurations with P9. According to Malhotra et al. (2016), Sedna is putatively trapped in 3:2 MMR with P9.
I reinvestigate here the latter hypothesis. I show that the semi-analytical analysis of B16 is inappropriate to the present case. This is because of the assumed expansion of the secular Hamiltonian that is not convergent. I thus perform a full numerical computation of the secular Hamiltonian and show that anti-aligned, high eccentricity libration islands that were not present in the simplified analysis appear in the non-resonant phase-space maps. Hence invoking resonant trapping might not be necessary. I subsequently investigate the resonant dynamics in a similar semi-analytical manner and show that various MMRs can actually also generate high eccentricity, anti-aligned librating particles as well, as suggested by B16. I discuss and compare the relevance of both mechanisms.
2. Non-resonant secular dynamics
 |
Fig. 1 Phase portraits of untruncated, secular averaged Hamiltonian (1) in (Δϖ,e) space, computed in the same conditions as B16, i.e. assuming parameters m′ = 10 M⊕, a′ = 700 au and e′ = 0.6 for P9. Plots are drawn for various semi-major axis values listed on top of the panels. On each plot, the red curve separates regions where both orbits cross from regions where they do not. In the a = 50 au case, the orbits never cross; for a = 150 au and a = 250 au, the orbits cross in the regions located above the red curves around Δϖ = 180°; for a = 350 au, a = 450 au and a = 550 au, the orbits cross in most configurations, except above the red curves centred around Δϖ = 0° where both orbits remain nested. |
Consider a massless particle test orbiting the Sun, perturbed by Planet 9. In the following, all applications are carried out with the following parameters for P9: m′ = 10 M⊕, a′ = 700 au and e′ = 0.6, as this appears to be the best model quoted by B16. As long as MMRs are not concerned, the long-term behaviour of the orbit of the particle is well described with the secular Hamiltonian, which is obtained by taking the time average of the instantaneous interaction Hamiltonian over both orbits independently, 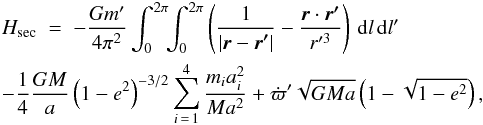 (1)
(1)
where M is the mass of the Sun; r and r′ are the instantaneous heliocentric radius vectors of the particle and of P9, respectively; l and l′ are their mean anomalies; a is the semi-major axis of the particle and e its eccentricity. See Appendix A for the derivation of this expression. The last two terms account for the perturbing action of the known giant planets on the particle and on P9. In the second term, the sum extends over the four giant planets, each of which have mass mi and semi-major axis ai; 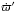 is the precession rate of perihelion of P9 caused by the same planets.
is the precession rate of perihelion of P9 caused by the same planets.
This Hamiltonian cannot be expressed in closed form though. However, taking advantage of the fact that the orbit of the particle lies inside the orbit of P9, the disturbing function can be expanded in ascending powers of a/a′. The integral appearing in Eq. (1) can be written as 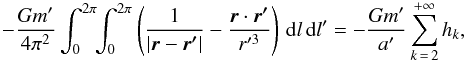 (2)
(2)
where the hks are dimensionless coefficients that can be expressed in closed form (Laskar & Boué 2010). Each hk is proportional to (a/a′)k. For coplanar orbits, they are also functions of e, e′, and of Δϖ = ϖ′ − ϖ only, where ϖ and ϖ′ are the longitudes of periastron of the particle and of P9, respectively. Whenever a<a′, the hks are generally assumed to decrease with increasing order k, so that the expansion can be truncated to some finite order n. The Hamiltonian given in Eq. (4) of B16 corresponds to a truncation at n = 3 order (octupole approximation).
Two potential problems may arise with this approach if one wants the truncated Hsec to accurately represent the actual dynamics of the particle. First, to ensure the validity of the secular model, the particle must not be trapped in any MMR and must remain protected from close encounters. Beust et al. (2014) showed however that even in the case of crossing orbits, secular theory provides a relevant description of the dynamics as long as a close encounter does not occur. Second, one must ensure that the series expansion of the secular Hamiltonian is convergent and that the truncation order is large enough to allow the truncation to accurately approximate to the full sum.
Numerical values of hks for various values of orbital parameters corresponding to configurations tested by B16.
Convergence of the series expansion is usually ensured for small enough a/a′ ratio. In the configurations described in B16 with orbits that sometimes cross, this is far from obvious. Table 1 lists various numerical values of hks computed for different configurations of the orbit of the particle. For configurations with a = 150 au, the orbit of the particle lies well inside that of the planet, whilst when a = 450 au, both orbits clearly cross. In the former case, the hks rapidly decrease, ensuring convergence of the expansion, but in the latter case it is obviously divergent.
An alternate way to avoid the expansion is to compute numerically the double integral appearing in Eq. (1). The integral is computed using Gauss-Legendre numerical quadrature with 70 × 70 points and taking special care of the regions where the orbits cross. This technique was already applied to the semi-analytic study of Fomalhaut b dynamics in Beust et al. (2014). The result is shown in Fig. 1. This figure was built assuming the same input conditions as Fig. 3 from B16, except that the latter was computed assuming octupolar approximation. On each plot, the red curve indicates the separation between regions where both orbits actually cross and regions where they do not.
Although the general shape of the various phase portraits agree in both cases, there are nevertheless striking differences. In all situations, libration islands around Δϖ = 0° (i.e. apsidal alignment) appear, but for large a, they are systematically narrower and centred around a secular equilibrium located at lower eccentricity than in the octupolar approximation. Moreover, for a ≥ 250 au, new libration islands appear around Δϖ = 180° (i.e. anti-alignment) at high eccentricity. These are not present in Fig. 3 from B16.
My phase portraits appear to match the results of the numerical exploration of B16 (their Fig. 4) much more closely than their original maps. The apsidally aligned libration islands now appear at the right eccentricity with corresponding widths. Moreover, the anti-aligned libration islands reported by B16 in their numerical exploration exactly match those I obtain in my phase portaits. These anti-aligned librating particles are of prime importance in the discussion by B16, as they suggest that the apsidally confined distant KBOs could be trapped in this dynamical state.
The authors of B16 claimed that the particles exhibiting this behaviour in their numerical exploration were actually trapped in a MMR with the perturbing planet. Resonant dynamics in indeed not described by the secular theory, irrespective of whether the Hamiltonian is truncated or not. Indeed, in their simulations, B16 show some particles that appear to be trapped in MMRs, at least temporarily. Whilst there is no doubt about the reality of resonant behaviours, I claim here that secular dynamics is able to generate the anti-aligned, high eccentricity librating particles that B16 find in their numerical exploration as well.
3. Resonant dynamics
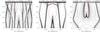 |
Fig. 2 Phase portraits of resonant Hamiltonian (3) in (Δϖ,e) space after averaging over the orbital motion of P9, for particles with zero resonant amplitude libration (see text), with the same input parameters in Fig. 1. Each map corresponds to a specific MMR that is specified on top of the plot together with the corresponding semi-major axis value. The red curve has the same meaning as in Fig. 1. |
In this section, I explore, in a similar semi-analytic way, the dynamics of particles trapped in (p + q : p) MMR with P9 (p and q are integers) and perturbed by the giant planets, as detailed above. Appendix B describes the way the secular resonant Hamiltonian is obtained. This derivation proceeds through the introduction of the critical argument of the resonance σ = ((p + q) /p) λ′ − (p/q) λ − ϖ, where λ and λ′ are the mean longitudes of the particle and of P9, respectively. As before, I treat the interaction with the known planet in a secular way. After some algebra (see Appendix B), the instantaneous resonant Hamiltonian can be written as 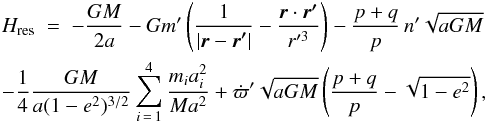 (3)
(3)
where n′ = dλ′/ dt is the mean angular velocity of P9. As a result of the resonant configuration, the Hamiltonian cannot be averaged over both orbital motions independently, but the critial angle σ is a slow varying variable. Hres can then be averaged for fixed σ over the orbital motion of P9. This leaves an autonomous two degrees of freedom Hamiltonian describing the resonant motion.
When e′ = 0, the resulting Hamiltonian does not depend on Δϖ. In that case, the conjugate action to Δϖ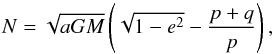 (4)
(4)
is a constant of motion and the planar problem becomes integrable (Moons & Morbidelli 1995). The resonant motion is characterized by libration of σ around a secular equilibrium, combined with eccentricity and semi-major axis oscillations, but the orbit of P9 is eccentric. It can nevertheless be shown (Morbidelli & Moons 1993) that the motion is still characterized by coupled libations of σ, a, and e. The action N is no longer a constant and its value is subject to changes on a longer timescale. This slower drift of N can drive the particle towards high eccentricity regime.
The slower drift of N is characterized by the preservation of a new action J (Morbidelli & Moons 1993; Henrard 1990) that is related to the amplitude of the σ libration. A good way to investigate the dynamics is then to consider negligible libration amplitude orbits. The preservation of J ensures that an orbit with small initial libration amplitude maintains this amplitude during the N-drift process. For such orbits, the semi-major axis remains unchanged. After averaging, the resonant Hamiltonian (3) reduces thus to one degree of freedom so that phase portraits can be drawn. This technique was first used by Yoshikawa (1989) to explore the dynamics of inner resonances with Jupiter and, furthermore, by Beust & Morbidelli (1996) to study dynamical routes that may generate star-grazing comets in the βPictoris system.
I present in Fig. 2 phase portraits for a selection of MMRs, which are all computed still assuming the same parameters for P9, except that I have set the semi-major axis of P9 to 665 au instead of 700 au. This makes the 3:2 MMR fall at a = 507 au, the semi-major axis value quoted by Malhotra et al. (2016) for Sedna, who suggest indeed that Sedna could be trapped in that MMR with P9. I have tested many more MMRs. Those presented here were selected because they fall in the suitable range of semi-major axis, and because they present anti-aligned libration islands at high eccentricity. Some other resonances, such as 9:5, 8:5, and 7:5 also present similar libration islands. Particles trapped in these MMRs evolving in the quoted anti-aligned islands could well match the particles depicted by B16 in their simulations.
4. Discussion
The high eccentricity, anti-aligned librating particles quoted by B16 as representative for the distant KBOs in relationship with the hypothetical P9 could well correspond to bodies trapped in some of the MMRs listed above. They could also be non-resonant particles, however, subject to regular secular dynamics as shown in Fig. 1. It is difficult to state which process is dominant. Contrary to resonances, non-resonant configurations have the advantage that they are not confined to specific semi-major axis locations with respect to P9. They may therefore concern many more particles. However, the particles in the anti-aligned libration islands move on orbits that cross that of P9. They are thus subject to possible ejection via close encounters, but this may occur after a long time. Numerical simulations by Beust et al. (2014) applied to the case of Fomalhaut showed that particles moving on orbits that cross that of an eccentric ~10 M⊕ planet may survive hundreds of Myrs before they are ejected. The planet considered in the Fomalhaut simulations had an orbital period of 1000 yr. With a′ = 700 au, the hypothetical P9 has a similar mass, but a period of 15 000 yr. The survival time of any particle crossing its orbit should thus scale similarly and could be comparable to the age of the solar system.
Figure 1 also shows aligned libration islands (Δϖ = 0) next to anti-aligned libration islands. Bodies trapped in these islands are potentially longer-lived than anti-aligned bodies, as they move in non-crossing regions of phase-space (see the red curves in Fig. 1). However, as pointed out by B16, these islands are located too low in eccentricity to match the observed distant KBOs. Nonetheless, if P9 is real, numerous bodies should be present in these islands, but these are beyond observing capabilities.
Conversely, as suggested by B16, the survival of resonant particles despite crossing orbits is facilitated by the phase protection mechanism. More specifically, the confinement of the critical angle σ around an equibrium position prevents the particle from encountering the planet at the time it crosses its orbit (Morbidelli & Moons 1993; Moons & Morbidelli 1995). In some cases, however, this situation may not last forever. Owing to perturbations by other planets, particles can have large libration amplitudes and be extracted from resonances. Indeed, B16 note this in their simulations particles exhibiting temporary resonant trapping.
It turns out that any of the two mechanisms outlined here has its own advantages and disadvantages. It is difficult to state which of these is dominant because it should depend on the specific configuration. The constraints on the hypothetical P9 are still too weak to conclude, but I stress here that the anti-aligned librating particles quoted by B16 are not necessarily resonant, but could reside there thanks to regular secular dynamics as well. Hopefully, a better statistics on distant KBOs will help refine this analysis in the next future.
References
- Batygin, K., & Brown, M. E. 2016, ApJ, 151, 22 (B16) [Google Scholar]
- Beust, H., & Morbidelli, A. 1996, Icarus, 120, 358 [NASA ADS] [CrossRef] [Google Scholar]
- Beust, H., Augereau, J.-C., Bonsor, A., et al. 2014, A&A, 561, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cowan, N. B., Holder, G., & Kaib, N. A. 2016, ApJ, 822, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Fienga, A., Laskar, J., Manche, H., & Gastineau, M. 2016, A&A, 587, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de la Fuente Marcos, C., & de la FuenteMarcos, R. 2014, MNRAS, 443, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Henrard, J. 1990, Celest. Mech., 49, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Laskar, J., & Boué, G. 2010, A&A, 522, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Malhotra, M., Volk, K., & Wang, X. 2016, ArXiv e-print [arXiv:1603.02196v2] [Google Scholar]
- Moons, M., & Morbidelli, A. 1995, Icarus, 114, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Morbidelli, A., & Moons, M. 1993, Icarus, 102, 316 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo, C. A., & Sheppard, S. S. 2014, Nature, 507, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Yoshikawa, M. 1989, A&A, 213, 436 [NASA ADS] [Google Scholar]
Appendix A: The non-resonant secular Hamiltonian
I describe here the averaging and expansion process of the non-resonant secular
Hamiltonian. In the framework of the restricted three-body problem, the instantaneous
interaction Hamiltonian between the particle and P9 reads
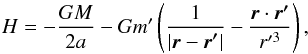 (A.1)where M is the mass of the Sun,
a is the
semi-major axis of the particle, and r and r′ are the
heliocentric radius vectors of the particle and of P9, respectively. The secular
Hamiltonian is obtained taking the time average of H over both orbits
independently. This reads
(A.1)where M is the mass of the Sun,
a is the
semi-major axis of the particle, and r and r′ are the
heliocentric radius vectors of the particle and of P9, respectively. The secular
Hamiltonian is obtained taking the time average of H over both orbits
independently. This reads 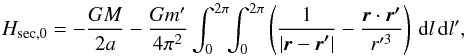 (A.2)where
l and
l′ are the
mean anomalies of the particle and P9, respectively. I note that a is now a secular
invariant. This a consequence of the averaging process, as the secular Hamiltonian does
not depend of the mean longitudes.
(A.2)where
l and
l′ are the
mean anomalies of the particle and P9, respectively. I note that a is now a secular
invariant. This a consequence of the averaging process, as the secular Hamiltonian does
not depend of the mean longitudes.
Then, as explained by B16, terms must be added to Hsec,0 to
account for the perturbing action of the giant planets. I first add the direct term, so
that we have now 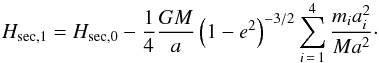 (A.3)This Hamiltonian is
implicitly expressed as a function of the canonically conjugate planar Delaunay orbital
elements of the particle, namely
(A.3)This Hamiltonian is
implicitly expressed as a function of the canonically conjugate planar Delaunay orbital
elements of the particle, namely 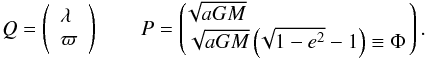 (A.4)As the semi-major axis is
a secular invariant, Hsec,1 reduces to one degree of freedom
with (ϖ,Φ) as
conjugate variable. The constant Keplerian term − GM/ 2a can also be removed from
it. Nevertheless, Hsec,1 is time dependent as
ϖ′ is not
constant. I thus perform a canonical transformation, changing ϖ to Δϖ. To do this, I use the
generating function S = −
Φϖ =−Φ(Δϖ + ϖ′).
The new momentum conjugate to Δϖ is still Φ, and the new autonomous Hamiltonian reads
(A.4)As the semi-major axis is
a secular invariant, Hsec,1 reduces to one degree of freedom
with (ϖ,Φ) as
conjugate variable. The constant Keplerian term − GM/ 2a can also be removed from
it. Nevertheless, Hsec,1 is time dependent as
ϖ′ is not
constant. I thus perform a canonical transformation, changing ϖ to Δϖ. To do this, I use the
generating function S = −
Φϖ =−Φ(Δϖ + ϖ′).
The new momentum conjugate to Δϖ is still Φ, and the new autonomous Hamiltonian reads
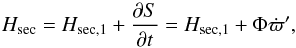 (A.5)which is Eq. (1) from the text.
(A.5)which is Eq. (1) from the text.
Unfortunately, the above expression cannot be computed in closed form, so that to get a
closed form expression, expansion of the disturbing function is required before averaging.
If the orbit of the particle lies inside the orbit of P9 (which is the situation supposed
here), then the instantaneous Hamiltonian can be expanded using Legendre polynomials
Pk (k ≥ 0), 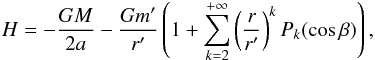 (A.6)where
β is the
angle between radius vectors r and r′. Each term of
the sum can then be averaged over both orbital motions independently. The result reads
(A.6)where
β is the
angle between radius vectors r and r′. Each term of
the sum can then be averaged over both orbital motions independently. The result reads
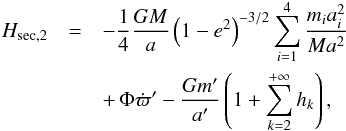 (A.7)where
(A.7)where
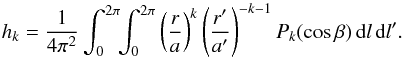 (A.8)Each hk is proportional to
(a/a′)k
and can be expressed in closed form as a function of the orbital elements of both orbits
with growing complexity, making use of so-called Hansen coefficients. Details about this
process are given in Laskar & Boué (2010)
with explicit expressions of the hks up to
k = 10. In
the case of coplanar orbits, apart from being proportional to (a/a′)k,
the hks are function of
e,
e′, and of
Δϖ = ϖ′ −
ϖ only, where ϖ and ϖ′ are the longitudes of
periastron of the particle and of P9, respectively. As an example, the first
hks read
(A.8)Each hk is proportional to
(a/a′)k
and can be expressed in closed form as a function of the orbital elements of both orbits
with growing complexity, making use of so-called Hansen coefficients. Details about this
process are given in Laskar & Boué (2010)
with explicit expressions of the hks up to
k = 10. In
the case of coplanar orbits, apart from being proportional to (a/a′)k,
the hks are function of
e,
e′, and of
Δϖ = ϖ′ −
ϖ only, where ϖ and ϖ′ are the longitudes of
periastron of the particle and of P9, respectively. As an example, the first
hks read
![\appendix \setcounter{section}{1} \begin{eqnarray} h_2 & = & \frac{1}{4}\left(\frac{a}{a'}\right)^2\frac{(3/2)e^2+1}{(1-e'^2)^{3/2}},\\ h_3 & = & -\frac{3}{16}\left(\frac{a}{a'}\right)^3e\,e'\frac{(15/4)e^2+5}{ (1-e'^2)^{5/2}}\,\cos\left(\Delta\varpi\right),\\ h_4 & = & \left(\frac{a}{a'}\right)^4\frac{1}{(1-e'^2)^{7/2}}\left[ \frac{15}{256}\left(\frac{21}{2}e^2+1\right)e^2\,e'^2\,\cos\left(2\Delta\varpi\right) \right.\nonumber\\ &&\left. +\,\frac{9}{64}\left(\frac{15}{8}e^4+5e^2+1\right)\left(1+\frac{3}{2}e'^2\right)\right]. \end{eqnarray}](/articles/aa/full_html/2016/06/aa28638-16/aa28638-16-eq122.png)
Appendix B: The resonant secular Hamiltonian
I consider now a situation where the particle is trapped in (p + q :
p) MMR with P9 and perturbed by the giant planets. As
above I treat the interaction with the giant planet in a secular way, so that my starting
instantaneous Hamiltonian reads ![\appendix \setcounter{section}{2} \begin{eqnarray} H_\mathrm{res,0} & = & -\frac{1}{4}\frac{GM}{a}\left(1-e^2\right)^{-3/2}\sum_{i=1}^4 \frac{m_ia_i^2}{Ma^2}\nonumber\\[-1mm] &&-\,\frac{GM}{2a}-Gm'\left(\frac{1}{|\vec{r}-\vec{r'}|}-\frac{\vec{r}\cdot \vec{r'}}{r'^3}\right), \end{eqnarray}](/articles/aa/full_html/2016/06/aa28638-16/aa28638-16-eq123.png) (B.1)This
Hamiltonian is still implicitly expressed as a function of the Delaunay elements (A.4), but now it does not immediately reduce to
one degree of freedom. Owing to the resonance, the semi-major axis can indeed have secular
variations. Hres,0 cannot thus be averaged over both
orbits independently. I introduce now the critical argument of the resonance
(B.1)This
Hamiltonian is still implicitly expressed as a function of the Delaunay elements (A.4), but now it does not immediately reduce to
one degree of freedom. Owing to the resonance, the semi-major axis can indeed have secular
variations. Hres,0 cannot thus be averaged over both
orbits independently. I introduce now the critical argument of the resonance
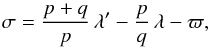 (B.2)and the new
coordinate vector Q1 =
(σ,Δϖ). I have Q1 =
AQ +
B(t), where
(B.2)and the new
coordinate vector Q1 =
(σ,Δϖ). I have Q1 =
AQ +
B(t), where
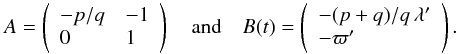 (B.3)Considering now the
generating function S(P,Q1) =
− tPQ = −tPA-1(Q1
− B(t)), I perform a canonical
transformation with Q1 as new coordinate
vector, and
(B.3)Considering now the
generating function S(P,Q1) =
− tPQ = −tPA-1(Q1
− B(t)), I perform a canonical
transformation with Q1 as new coordinate
vector, and 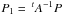 as new momenta vector,
as new momenta vector,
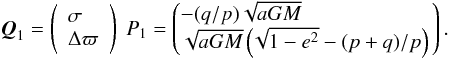 (B.4)The new Hamiltonian then
reads
(B.4)The new Hamiltonian then
reads
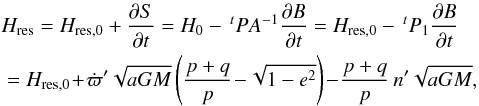 (B.5)where
n′ = dλ′/
dt is the mean angular velocity of the perturbing
planet. This corresponds to Eq. (3) from
the text.
(B.5)where
n′ = dλ′/
dt is the mean angular velocity of the perturbing
planet. This corresponds to Eq. (3) from
the text.
All Tables
Numerical values of hks for various values of orbital parameters corresponding to configurations tested by B16.
All Figures
 |
Fig. 1 Phase portraits of untruncated, secular averaged Hamiltonian (1) in (Δϖ,e) space, computed in the same conditions as B16, i.e. assuming parameters m′ = 10 M⊕, a′ = 700 au and e′ = 0.6 for P9. Plots are drawn for various semi-major axis values listed on top of the panels. On each plot, the red curve separates regions where both orbits cross from regions where they do not. In the a = 50 au case, the orbits never cross; for a = 150 au and a = 250 au, the orbits cross in the regions located above the red curves around Δϖ = 180°; for a = 350 au, a = 450 au and a = 550 au, the orbits cross in most configurations, except above the red curves centred around Δϖ = 0° where both orbits remain nested. |
| In the text | |
 |
Fig. 2 Phase portraits of resonant Hamiltonian (3) in (Δϖ,e) space after averaging over the orbital motion of P9, for particles with zero resonant amplitude libration (see text), with the same input parameters in Fig. 1. Each map corresponds to a specific MMR that is specified on top of the plot together with the corresponding semi-major axis value. The red curve has the same meaning as in Fig. 1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


