Timing calibration and spectral cleaning of LOFAR time series data

A. Corstanje; S. Buitink; J. E. Enriquez; H. Falcke; J. R. Hörandel; M. Krause; A. Nelles; J. P. Rachen; P. Schellart; O. Scholten; S. ter Veen; S. Thoudam; T. N. G. Trinh

doi:10.1051/0004-6361/201527809

Home

All issues

Volume 590 (June 2016)

A&A, 590 (2016) A41

Full HTML

Free Access

Issue		A&A Volume 590, June 2016


Article Number		A41
Number of page(s)		9
Section		Astronomical instrumentation
DOI		https://doi.org/10.1051/0004-6361/201527809
Published online		04 May 2016

A&A 590, A41 (2016)

Timing calibration and spectral cleaning of LOFAR time series data

A. Corstanje¹, S. Buitink⁶, J. E. Enriquez¹, H. Falcke¹^,2^,3^,4, J. R. Hörandel¹^,2, M. Krause⁸, A. Nelles¹^,7, J. P. Rachen¹, P. Schellart¹, O. Scholten⁵^,9, S. ter Veen¹, S. Thoudam¹ and T. N. G. Trinh⁵

¹ Department of Astrophysics/IMAPP, Radboud University Nijmegen, PO Box 9010, 6500 GL Nijmegen, The Netherlands
² Nikhef, Science Park Amsterdam, 1098 XG Amsterdam, The Netherlands
³ Netherlands Institute for Radio Astronomy (ASTRON), Postbus 2, 7990 AA Dwingeloo, The Netherlands
⁴ Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
⁵ KVI-CART, University Groningen, PO Box 72, 9700 AB Groningen, The Netherlands
⁶ Astrophysical Institute, Vrije Universiteit Brussel, Pleinlaan 2, 1050 Brussels, Belgium
⁷ Department of Physics and Astronomy, University of California Irvine, Irvine, CA 92697-4575, USA
⁸ Deutsches Elektronen-Synchrotron (DESY), Platanenallee 6, 15738 Zeuthen, Germany
⁹ Interuniversity Institute for High-Energy, Vrije Universiteit Brussel, Pleinlaan 2, 1050 Brussels, Belgium

Received: 23 November 2015
Accepted: 25 March 2016

Abstract

We describe a method for spectral cleaning and timing calibration of short time series data of the voltage in individual radio interferometer receivers. It makes use of phase differences in fast Fourier transform (FFT) spectra across antenna pairs. For strong, localized terrestrial sources these are stable over time, while being approximately uniform-random for a sum over many sources or for noise. Using only milliseconds-long datasets, the method finds the strongest interfering transmitters, a first-order solution for relative timing calibrations, and faulty data channels. No knowledge of gain response or quiescent noise levels of the receivers is required. With relatively small data volumes, this approach is suitable for use in an online system monitoring setup for interferometric arrays. We have applied the method to our cosmic-ray data collection, a collection of measurements of short pulses from extensive air showers, recorded by the LOFAR radio telescope. Per air shower, we have collected 2 ms of raw time series data for each receiver. The spectral cleaning has a calculated optimal sensitivity corresponding to a power signal-to-noise ratio of 0.08 (or −11 dB) in a spectral window of 25 kHz, for 2 ms of data in 48 antennas. This is well sufficient for our application. Timing calibration across individual antenna pairs has been performed at 0.4 ns precision; for calibration of signal clocks across stations of 48 antennas the precision is 0.1 ns. Monitoring differences in timing calibration per antenna pair over the course of the period 2011 to 2015 shows a precision of 0.08 ns, which is useful for monitoring and correcting drifts in signal path synchronizations. A cross-check method for timing calibration is presented, using a pulse transmitter carried by a drone flying over the array. Timing precision is similar, 0.3 ns, but is limited by transmitter position measurements, while requiring dedicated flights.

Key words: instrumentation: interferometers / techniques: interferometric / site testing

© ESO, 2016

1. Introduction

An interferometric radio telescope relies on an accurate timing calibration of the signals of all its constituent receivers, in order to be able to combine signals with a time or phase shift corresponding to the direction of a given source in the sky. Furthermore, spurious narrowband transmitter signals, which are present even in relatively radio-quiet regions, will also show up in the processed signals. These signals have to be identified and removed, preferably early in the analysis process.

This paper is organized as follows: below we briefly review some methods that are used for detection and removal of radio-frequency interference (RFI), as well as methods for timing and phase calibration. After this, we introduce our methods. Section 2 describes the methods in detail, and in Sect. 3, their application to data taken with the LOFAR radio telescope is discussed.

Most of the RFI present at radio telescope sites consists of either narrowband signals from radio transmitters, or short pulses in the time domain (Offringa et al. 2013). For both cases, there are several methods being used to identify interference, either before or after signal correlation. Before correlation in the interferometer, these algorithms typically involve detecting threshold crossings of amplitudes in the time or frequency domain, where the threshold is adapted based on signal properties (Offringa et al. 2010). For instance, a threshold can be calculated by using a median filter, such as that used in the Auger Engineering Radio Array (AERA) for radio detection of cosmic rays (Schmidt et al. 2011). It replaces a sample in time or frequency domain by the median of a number of its neighbours in order to set a threshold. More elaborate techniques, also exploiting correlations of multiple samples crossing the threshold, are found e.g. in Offringa et al. (2010). After correlation, adaptive thresholds can also be used on correlated visibility amplitudes instead of data streams from single receivers.

Another approach that has been considered for use in the AERA experiment is described in Szadkowski et al. (2013). It uses linear prediction, implemented as a finite impulse response (time domain) filter in FPGAs. This approach operates online on single receivers and adapts to changes in the interference environment.

Another method is fringe fitting, which makes use of the fact that most RFI sources are at a fixed position, and therefore produce sinusoidal fringes in visibility data of a fringe-stopping interferometer (Athreya 2009). These sinusoids are then fitted and removed. This latter method is somewhat similar to the method we present below, which operates on short time series.

Timing and phase calibration in interferometric radio telescopes is typically done based on the principle of self-calibration (Pearson & Readhead 1984; Taylor et al. 1999), where redundant information in the interferometric data is used; for instance, there are N_ant(N_ant−1) / 2 baselines giving correlated signals, while having only N_ant antennas to calibrate. For this method, suitable calibrator sources for which the structure is known, e.g. point sources, are used as a model for optimizing the calibration. The calibration solution can be obtained as a function of frequency, providing a phase calibration for every frequency in the spectrum. The phase calibration at a given frequency equals a timing calibration at the same frequency, taken modulo the wave period.

Moreover, there are methods that also take into account directional dependencies of the calibration. As antennas have a complex gain that has directional dependence, the calibration in general depends on this as well, especially considering differences in gain between antennas. One of these methods, which is used at LOFAR, is SAGECal (Kazemi et al. 2011). A review of similar calibration methods is given in e.g. Wijnholds et al. (2010).

Alternative approaches involve calibrating on a fixed custom transmitter, as is done by the LOPES cosmic-ray detection experiment (Schroeder et al. 2010), which yields a timing calibration per antenna for a single, or a few frequencies. In our approach, as described below, we use the spectral cleaning method to identify a suitable public transmitter, and also make use of the position of the most useful transmitter in order to obtain a calibration solution. This is sufficient for a precise (subnanosecond) timing analysis of cosmic ray pulses (Corstanje et al. 2015). It can also serve as a starting point and cross-check for dedicated phase calibrations as used in radio astronomy.

Instead of a fixed transmitter, satellites or drones flying overhead can be used, which makes amplitude calibration possible as well. This is similar to the amplitude calibration from a fixed transmitter as has been performed at LOFAR (Nelles et al. 2015).

Calibration on pulses from the far field, e.g. emitted by airplanes passing overhead, has also been considered (Pierre Auger Collaboration 2016). However, this relies on randomly occurring pulses that need to be detected in real-time in order to record them.

Here, we describe a method of spectral cleaning of time series data that we use to remove narrowband radio-frequency (RF) transmitter signals from our data. At the same time it allows a calibration of clock differences to be obtained across the array. The method applies only to narrowband signals, which are present continuously for about 0.2 to 2 ms, where shorter signals need to be stronger to be detected. Signals with somewhat larger bandwidth are treated as a set of narrowband signals. Broadband pulses are not removed.

Using the phase component of the Fourier transform of each channel, we take into account that strong, localized transmitters produce approximately constant phase differences across the array. Astronomical signals are typically broadband, and arrive at the antennas as a sum over many sources on the sky, and therefore produce random phase differences over time. This difference allows for an accurate identification (and removal) of disturbing signals. Using the identified constant phases of a public radio transmitter signal, we can also calibrate signal timing offsets in each antenna pair. If the geometric delay from the signal path lengths of the radio signal to each antenna is known, this leads to a known difference in phase of the (continuous-wave) signal as it is measured at each antenna. Comparing the actually measured phases with the expected phases gives a calibration correction. It has been suggested as a promising improvement in Offringa et al. (2010) to add the use of phase information to existing amplitude-based RFI cleaning methods. The method presented here uses only the phase component.

We apply this method to data taken with the Low Frequency Array (LOFAR; van Haarlem et al. 2013) radio telescope. The antennas of LOFAR are distributed over northern Europe, with the densest concentration in the north of the Netherlands. The antennas are organized into stations, each consisting of 96 low-band antennas (LBA, 10−90 MHz), and 48 high-band antennas (HBA, 110−240 MHz). Within the core region of about 6 km², 24 of these stations have been distributed.

For the cosmic-ray data collection, we record radio emission from extensive air showers, which reaches the ground as a short pulse, on the order of 10 to 100 ns long (Schellart et al. 2013). We use the Transient Buffer Boards installed in the data channel of every LOFAR antenna to record these pulses and other fast radio transients. Each recording is 2 to 5 ms long and consists of the raw voltage time series from every data channel. The buffer is capable of storing signals up to 5 s in length.

These datasets need spectral cleaning in order to measure the pulses accurately. The relative timings of the pulses contain information about the air shower process. For instance, by measuring pulse arrival times, we have evaluated the shape of the radio wavefront as it arrives at the antenna array (Corstanje et al. 2015).

As our datasets are much shorter than typical astronomical observations (a few milliseconds, instead of hours), and are stored as unprocessed voltage time series per receiver, a dedicated spectral cleaning method is required. Still, our method can be easily adapted for other purposes and instruments as long as raw time series are available.

We tested our timing calibration using a pulse transmitter carried by an octocopter drone flying above the array. The precision of the pulse arrival time measurements is similar to the phase measurements.

2. Method

In this section we explain in detail the method and performance of our RFI identification algorithm, and show how the phases of the strong transmitters identified in this way can be used for timing calibration.

2.1. Radio frequency interference identification

In order to identify frequencies that are contaminated by human-made interference, a typical approach is to search for strong signals above the noise level in an amplitude or power spectrum. However, this requires knowledge of the noise power spectra in the absence of RFI transmitters, or an adaptive or iterative technique to estimate them, as mentioned in the Introduction.

Therefore, we use the relative phases between pairs of antennas. At the frequency used by a transmitter, the phase difference across an antenna pair is stable over time because the signals are typically transmitted from a fixed location. In contrast, at frequencies where no terrestrial transmitter is present, we measure emission from the Milky Way as well as electronic noise. The Galactic emission is a sum of many sources, assuming the antennas are omnidirectional or have a substantial field of view. Therefore, the detected phases can be treated as random on millisecond integration timescales.

In situations where one localized source in the sky fully dominates the signal, for example during strong solar bursts, this assumption is not valid. However, this only happens for a small fraction of the time.

We take phase measurements from a fast Fourier transform (FFT) of consecutive data blocks for every antenna. One antenna is taken as reference; for every frequency channel, its phase is subtracted to measure only relative phases.

It is also possible to consider the phase differences across all antenna pairs (baselines), instead of selecting a single antenna as reference. This is more sensitive (see Sect. 2.2), but also requires more computation time, and hence can be omitted if the single-reference approach meets the requirements for spectral cleaning.

For every frequency channel we calculate the average and variance of the phase over all data blocks. The phase average across antenna indices j and k for frequency ω is defined as follows (denoting relative phases as Φ and the data block number as superscript l),

$\begin{matrix} Φ_{j,k}^{l} (ω) = φ_{j}^{l} (ω) - φ_{k}^{l} (ω), \\ Φ̅ j,k (ω) = \arg (\sum_{l = 0}^{N_{blk} - 1} \exp (i Φ_{j,k}^{l} (ω))), \end{matrix}$ $\begin{eqnarray} &&\Phi_{j,k}^l(\omega) = \phi_j^l(\omega) - \phi_k^l(\omega), \\[2mm] \label{eq:phaseaverage} &&\bar{\Phi}_{j,k}(\omega) = \arg\left(\sum_{l=0}^{N_{\rm blk}-1} \exp({\rm i}\, \Phi_{j,k}^l(\omega))\right), \end{eqnarray}$

and the phase variance as $s_{j,k} (ω) = 1 - \frac{1}{N_{blk}} | \sum_{l = 0}^{N_{blk} - 1} \exp (i Φ^{l} (ω)) |,$ $\begin{equation} \label{eq:phasevariance} s_{j,k}(\omega) = 1 - \frac{1}{N_{\rm blk}}\left|\sum_{l=0}^{N_{\rm blk}-1} \exp({\rm i}\, \Phi^l(\omega))\right|, \end{equation}$ (3)where Φ^l(ω) is the relative phase measured in data block l at frequency ω and N_blk is the number of data blocks. The phase variance s_j,k(ω) is close to unity for completely random phases and is zero for completely aligned phases.

If the phases follow a narrow, peaked distribution around the average with variance σ², then the phase variance is $s_{j,k} = \frac{σ^{2}}{2} + 𝒪 (σ^{4})$ $\hbox{$s_{j,k} = \frac{\sigma^2}{2} + \mathcal{O}(\sigma^4)$}$ . Hence, this quantity is then indeed proportional to the variance. For wider distributions, the 2π-periodicity of phases becomes important, and the phase variance has a maximum value of unity for a uniform distribution, in the large-N limit.

For random phases, N_blk(1−s_j,k) describes the traveled distance in a two-dimensional random walk as the right-hand part of Eq. (3) represents the length of the sum-vector of N_blk unit vectors, each of which has a random direction in the complex plane.

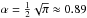For large N_blk, this distance follows a Rayleigh distribution with scale parameter $s = \sqrt{N_{blk} / 2}$ $\hbox{$s=\sqrt{N_{\rm blk}/2}$}$ (Rayleigh 1905) and has an expected value of $α \sqrt{N_{blk}}$ $\hbox{$\alpha\,\sqrt{N_{\rm blk}}$}$ , with $α = \frac{1}{2} \sqrt{π} \approx 0.89$ $\hbox{$\alpha = \frac{1}{2}\sqrt{\pi}\approx0.89$}$ . It has a standard deviation of $β \sqrt{N_{blk}}$ $\hbox{$\beta\, \sqrt{N_{\rm blk}}$}$ , with $β = \sqrt{1 - \frac{π}{4}} \approx 0.46$ $\hbox{$\beta=\sqrt{1-\frac{\pi}{4}}\approx0.46$}$ . In practice, the large-N approximation is already accurate for N_blk ≳ 10.

Therefore, we have $s_{j,k} (ω) \approx 1 - \frac{α}{\sqrt{N_{blk}}} \cdot$ $\begin{equation} \label{eq:phase_noiselevel} s_{j,k}(\omega) \approx 1 - \frac{\alpha}{\sqrt{N_{\rm blk}}}\cdot \end{equation}$ (4)It is clear that for a coherent, narrowband signal seen at all antennas, the variance should be rather small.

In order to determine a threshold for significantly detecting a transmitter, we take the average of the phase variances over all antennas or all baselines. This leaves one averaged phase-variance spectrum, i.e. one phase variance per frequency channel. To take the average is a simple, generic choice; when partial detections are expected, e.g. in a more sparse array or for very nearby RFI, it is possible to consider the full distribution of the phase variance over the antennas and test for deviations of random behavior. This is, however, not pursued here.

We sort the values of the phase variance over all frequencies, and estimate its standard deviation by taking the 95th percentile value minus the median, which is about 1.65 σ for Gaussian noise. This has the advantage of considering only the upper half of the sample which is assumed to follow the random-walk characteristics. It selects out all transmitter signals as they only lower the variance below the median. This naturally assumes that less than half of the frequency channels contain an interfering transmitter signal, which is reasonable for astronomical observations in general. Should this not be the case for the particular site, a higher percentile value can be taken instead of the median. Alternatively, it is possible to follow the random-walk statistics directly for mean and standard deviation, to compare them with the data afterwards. The threshold is set to the median value minus a multiple of the standard deviation, which is tunable, for example, to trade a lower false-positive probability for a lower sensitivity.

For the run-time complexity, we note that the algorithm requires N_blkN_ant FFTs of a fixed length, set by the desired spectral resolution. Moreover, when treating all baselines, it requires $𝒪 (N_{ant}^{2})$ $\hbox{$\mathcal{O}(N_{\rm ant}^2)$}$ phase spectrum comparisons. When instead using a single antenna as reference (or a fixed number of them), only $\hbox{$\mathcal{O}(N_{\rm ant})$}$ comparisons are done, and the FFTs always dominate.

2.2. Sensitivity of RFI detection

The sensitivity of RFI detection can be analyzed by noting the correspondence of the detection of an RFI transmitter to the detection of bias, i.e. a preference towards a certain direction, in a set of identically distributed random walks. The full analysis is deferred to the Appendix.

We start by assuming that a signal is present in the noisy time series of each receiver, with power signal-to-noise ratio S² defined by the absolute-square of the FFT in one frequency channel, for the signal and the noise, respectively.

With this definition, the sensitivity becomes (asymptotic approximation, see Appendix A) $S^{2} > 3.8 \sqrt{k / 6} N_{blk}^{- 1 / 2} N_{ant}^{- 1 / 2},$ $\begin{equation} \label{eq:sensitivity} S^2 > 3.8 \;\sqrt{k/6}\; N_{\rm blk}^{-1/2}\; N_{\rm ant}^{-1/2}, \end{equation}$ (5)aimed at a six-sigma (k = 6) detection threshold as used in the LOFAR cosmic-ray analysis (Schellart et al. 2013). Typical numbers for this analysis are N_blk = 50 and N_ant = 48, leading to a threshold of S² = 0.08, or -11 dB, which is easily sufficient for the purpose of analyzing pulses from air showers. With a specific bandwidth fraction in mind, e.g. for wideband radio signals, this sensitivity can be used to give an upper bound to residual RFI levels.

To put this result into perspective, we consider a straightforward, simplified method that detects excess power in a power spectrum, averaged over all antennas and data blocks. The noise power in a given FFT channel has an exponential distribution (Papoulis & Pillai 2002) with mean and standard deviation equal to the mean noise power per channel. The signal power is uncorrelated to the noise, and hence the total power is the sum of signal and noise power. Summing spectra of N_ant antennas each having N_blk blocks then yields a threshold $S^{2} = 6 (k / 6) N_{blk}^{- 1 / 2} N_{ant}^{- 1 / 2},$ $\begin{equation} \label{eq:asympt_powerexcess} S^2 = 6\;(k/6)\; N_{\rm blk}^{-1/2}\; N_{\rm ant}^{-1/2}, \end{equation}$ (6)plus the uncertainty in determining the average quiescent noise spectrum, which is not flat in general. The asymptotic behavior is therefore the same as in Eq. (5). It is assumed that estimating a single, flat noise level as for the phase variance (Eq. (4)) has a lower uncertainty than estimating a spectrum curve.

We note that, since both methods use averaging over many blocks, or many phase variance values, by the Central Limit Theorem these averages can be regarded as estimating the mean of a Gaussian distribution. Hence, in both cases the k-sigma thresholds refer to exceeding probabilities, and corresponding false alarm rates, of a Gaussian distribution.

Our method based on phases has a somewhat favorable detection threshold, the difference with respect to Eq. (6) being at least 2.0 dB. Moreover, it does not require an estimate of the noise spectrum in the absence of transmitters. This has made it easier for us to implement in practice where background levels are variable. However, this does not imply that this comparison holds when looking at more elaborate, amplitude-based cleaning methods.

We note that when, instead of power excess, the amplitude excess would be used in an absolute spectrum rather than absolute-squared, the asymptotics of S are the same, i.e. given by Eq. (6). In the weak-field and large-N limit, the difference is at most 7 % in the constant factor in favor of the absolute spectrum.

2.3. Timing calibration

Observations using an interferometric telescope require precise timing and phase calibration of each receiver in order to have precise pointings and to perform imaging with optimal signal quality. The timing precision should be about an order of magnitude below the sampling period.

For timing calibration we use one or multiple narrowband transmitters as a beacon, producing fixed relative phases between antennas at the transmitting frequency. This is similar to the procedure followed in Schroeder et al. (2010); we extend this by a more precise phase measurement, and by using the geometric delays from the transmitter location to find the calibration delays per antenna pair.

We measure relative phases per antenna pair in the same way as in Sect. 2.1, taking Fourier transforms of consecutive data blocks for all antennas and averaging phases using Eq. (2). This also allows frequencies suitable for timing calibration to be identified from the values of the phase variance, Eq. (3), where lower values are better.

The geometric delays from the transmitter to each antenna are needed to determine the calibration delays between antennas. Therefore, a transmitter at a known location must be used with a frequency above about 30 MHz. At lower frequencies, i.e. the HF-band (High Frequency), signals may reflect off the ionosphere and propagation characteristics may vary from time to time; see e.g. Gilliland et al. (1938).

The signals propagate with the light speed in air, which is c/n. The index of refraction n is on average 1.00031; we note that variations of ± 4 × 10^-5 are possible with temperature and humidity (Grabner & Kvicera 2011). Omitting the refractive index would therefore introduce a timing mismatch of 1.0 ns between two antennas separated by 1 km, along the line of sight to the transmitter. This value is therefore significant at intermediate and longer baselines.

The phase difference across a given antenna pair, after accounting for geometric delays from the transmitter, corresponds to a time difference (calibration mismatch) $Δ t = \frac{Δ φ}{2 πf} (\mod \frac{1}{f}) \cdot$ $\begin{equation} \label{eq:time_phase} \Delta t = \frac{\Delta \phi}{2\pi f}\;\;\left({\rm mod}\;\frac{1}{f}\right)\cdot \end{equation}$ (7)Thus, the calibration solution obtained by using one transmitter is only determined up to a multiple of the signal period 1 /f. This can be improved by combining results from multiple transmitters. However, in order to obtain the correct solution it is then required that the different transmitters have larger differences in period than the phase or timing noise. Moreover, in general the correct calibration phase depends on frequency, i.e. the optimal phase calibration may have deviations from the group delay, as a function of frequency. When using a custom beacon for calibration measurements as described here, it is preferred therefore to choose frequencies that are far apart.

Once antenna timings have been calibrated, the relative phases can be monitored over time without reference to the transmitter location and geometric delays.

Fig. 1

Example power spectrum from 2 ms of LOFAR data, averaged over 48 LBA antenna dipoles. Crosses indicate channels with detected transmitters.

3. Application to LOFAR data

In this section, we describe how the RFI identification and timing calibration methods are used for the analysis of air shower datasets with LOFAR.

3.1. Identification of radio-frequency interference

The LOFAR radio telescope, located in the north of the Netherlands, is in a relatively radio-quiet region. Nevertheless, in all observations there are several signals present that come from narrowband transmitters. Therefore, spectral cleaning methods are required to remove them from astronomical observation data.

Fig. 2

Example power spectrum from 2 ms of LOFAR time series data (lower curve). The phase variance is shown in the upper data points (red). It consistently becomes lower whenever a narrowband transmitter is seen in the power spectrum.

We have used the core stations of LOFAR. For all but a few very bright air showers, our data contain antenna baselines up to about 1 km, and most of the antennas with signal are in the central ring that is 320 m in diameter. An example power spectrum is shown in Fig. 1. For demonstration purposes, the dataset of this example has particularly bad RFI as there are several flagged frequencies in the 30 to 80 MHz-band. However, this case is still not too extreme, and spectral cleaning is indeed necessary in similar instances. The power spectrum is averaged over the 48 antennas in one LOFAR station, and averaged over 2 ms, which is the length of a typical cosmic-ray dataset. We treat each of the two instrumental polarizations separately as RFI signals may be detectable in only one of the two polarizations. It is a spectrum of the LBA antennas ranging from 10 to 90 MHz. In what follows we focus only on the low-band spectra as these are best used for air shower measurements; the methods work identically for the high-band antenna data. For the detection of the transmitter frequencies, we use FFTs with a block size of 8000 samples, which amounts to a spectral resolution of 25 kHz. There are then 50 blocks in a time series of 2 ms, which are used to calculate the phase variance over the entire 2 ms of data as in Eq. (3). The result is shown in Fig. 2. The phase variance, taken as the median value of the 48 antennas, is shown as the upper signal. It has random noise due to the finite number of data blocks; at frequencies where a narrowband transmitter is present in the power spectrum (lower curve), the variance is significantly lower. The random noise has a median value of 0.879, consistent with the expected value from Eq. (4) of 0.875 for 50 data blocks. This is a basic test of our randomness assumption for the phases.

The phase variance threshold is then set to a value of nearly six sigma. The standard deviation is estimated by the 95th percentile value minus the median, which is about 1.65 σ for Gaussian noise. Every frequency channel with lower phase variance is flagged.

When frequency resolution (set by the chosen FFT block size) is high enough to resolve the transmitters’ frequency responses, it can also be necessary to flag a number of adjacent frequency channels as the edges of resolved transmitter spectra may not meet the threshold criterium for flagging. This is especially important when a large block size is taken, e.g. to comply with FFT resolution used in later analysis. The number of adjacent channels to flag is currently set as a manually tunable parameter, scaling with frequency resolution.

Fig. 3

Close-up of the power spectrum in a frequency range with several RFI sources. Flagged frequencies are shown as red dashed lines. The lower panel shows the phase variance, where the black horizontal line indicates the threshold for flagging. Although the RFI-quiet noise level would follow a smooth curve, fitting the curve and RFI flagging using the excess power are interdependent.

In Fig. 3, a close-up of the power spectrum and the phase variance are shown.

3.2. Timing calibration: results for the LOFAR core

For calibration of short time series, i.e. 2 to 5 ms in length, we use one or multiple narrowband transmitters as a beacon, producing fixed relative phases between antennas at the transmitting frequency. The signals at the high end of the spectrum (>87 MHz) are from public radio transmitters which are always present. They are clearly detectable even though they are outside the passband of the filters, which ends at 80 MHz. Moreover, the phase variance we measure in the spectral cleaning algorithm, and the corresponding timing precision, is found to be best for these frequencies. Therefore, we work with the high-frequency transmitters, especially the strongest one at 88.0 MHz. The radio signals at frequencies 88.0, 88.6, 90.8, and 94.8 MHz are transmitted from a 300-m radio tower located in Smilde¹ at 31.8 km from the LOFAR core. For 88.0 MHz, the signal period is 11.3 ns, which is still much larger than the desired (and attainable) subnanosecond calibration precision.

The timing calibration signal follows from the relative phases after accounting for the geometric delays between transmitter and antennas, according to Eq. (7). The relative phases are once again obtained from the FFT of 50 consecutive data blocks, taking average phases as from Eq. (2). As was done for the RFI detection method, we treat the two polarizations of the LOFAR LBA antennas separately. We thereby make use of the identical design and orientation of the LOFAR antennas. If antenna orientations and/or the design of their polarizations are different, this could lead to larger timing errors in this procedure, when using transmitters with polarized signals. Monitoring of a cross-calibration over time would still be accurate (see Sect. 3.3 below).

The geometric delays are calculated using the International Terrestrial Reference Frame (ITRF) coordinates (Altamimi et al. 2002) of each antenna, and the GPS (WGS-84) (Defense Mapping Agency 1987) ellipsoid coordinates of the Smilde tower converted to ITRF. This is a cartesian coordinate system, allowing for an easy calculation of straight-line distance between two points. For the effective height of the emission we consider half the height of the tower; the uncertainty in relative timings per 100 m of height is less than 0.05 ns across LOFAR core stations and below 0.005 ns within one station, and therefore negligible for our purposes.

As a starting point we take an existing LOFAR timing calibration per antenna, which is performed using astronomical phase-calibration a few times a year (van Haarlem et al. 2013). We compare measured relative phases with those from the straight-line propagation, in the LOFAR core area, consisting of a circular area 320 m in diameter, plus some additional stations up to about 1 km away. There are many more stations, but our air shower measurements are limited to this area.

Fig. 4

Difference between measured and expected phases per antenna, converted to time in nanoseconds. Red solid bars represent the median time delay per LOFAR station (48 antennas); the stations are separated by the vertical grid lines. The range of the y-axis corresponds to the signal period at 88 MHz.

The phases correspond to a timing correction per antenna as shown in Fig. 4. The values depicted in this plot consist of both calibration errors and possible systematic effects from our measurement. The latter may include differences in filter characteristics at 88.0 MHz, i.e. the delays obtained from phases at this frequency may deviate from the full group delay. Wave propagation effects may vary slightly over antennas, e.g. owing to the presence of other LOFAR antenna(s) along the line of sight to the transmitter.

We can assume that any calibration mismatch with respect to the earlier LOFAR calibration is independent of these systematic effects. Dedicated calibration observations use astronomical sources instead of a terrestrial transmitter and span the entire frequency band. It is important to note, therefore, that the timing correction signal we find here provides an upper limit on both calibration errors and systematic effects.

The standard deviation of the timing correction signal is 0.44 ns. Per station, the standard deviation varies from 0.36 to 0.40 ns.

Our measurements and data collection started in June 2011, which was within the commissioning period of LOFAR; the “cycle 0” observations started in December 2012. This means that some technical timing issues (which were resolved later) were still present during the early observations. Using this method, these problems were detected in the same datasets that contain our cosmic-ray measurements and have since been corrected. Hence, our older data can also be fully used.

As LOFAR is divided into separate stations, timing calibration across stations is also required. Especially before October 2012, only the six innermost stations had a common clock, but all other core stations had their own clock synchronized by GPS. This caused clock drifting across stations on the order of 10 ns, which is much longer than interferometric accuracy requirements.

Therefore, we calculated the inter-station clock offsets by taking the median of the time delays per antenna in each station. Using the median instead of the mean is more robust against calibration errors or malfunctioning of a small fraction of antennas. On the other hand, the median has a higher uncertainty for estimating the mean than taking the average. Still, taking the median is useful when batch-processing thousands of datasets.

When inter-station clock offsets vary by more than the signal period of 11.3 ns, they are still known accurately up to a multiple of this period. For the cosmic-ray pulse timing measurements as performed in Corstanje et al. (2015), the actual solution can be identified by using fits of the incoming direction of the radio pulse of the air shower. These fits are done on single-station level and hence are not influenced by the inter-station offsets.

The standard error of the median over one station amounts to 0.08 ns, and is a factor of $\sqrt{π / 2} \approx 1.25$ $\hbox{$\sqrt{\pi / 2} \approx 1.25$}$ higher than the standard error of the mean. Therefore, the inter-station clock offsets can be determined to about 0.1 ns precision, assuming that the systematic effects average out over the antennas of each station.

3.2.1. Multiple transmitters for calibration

The calibration solution obtained from using one transmitter is only given up to a multiple of the signal period. This can be improved by combining results from multiple transmitters. However, to obtain the correct solution, it is required that the different transmitters have larger differences in period compared to the phase or timing noise. For the LOFAR environment, the difference in period between 88.0 and 90.8 MHz is only 0.35 ns, which is not always above the timing noise. The transmitter at 94.8 MHz is not as reliable because its signal is rather weak. Moreover, in general the correct calibration phase depends on frequency, i.e. the optimal phase calibration may have deviations from the group delay as a function of frequency. This leads to an additional source of uncertainty when combining multiple frequencies.

When instead using a custom beacon for calibration measurements, in the way we described here for the public radio signals, it would be better to choose frequencies that are farther apart. Differences in phase delay versus group delay may also show up in this case. Another option is to use a beacon sending short pulses or bursts, as we show in the next section. These pulses are not affected by periodicity.

3.2.2. Pulse arrival times from an octocopter drone

As a cross-check, we performed a pulse arrival time measurement in the LOFAR inner core region using a pulse transmitter mounted below an octocopter drone. The octocopter flies along a pre-programmed flight path using GPS coordinates. We set it to fly above the central antenna of the six innermost stations of LOFAR. A pulse of approximately 250 V is then transmitted every 8 μs from a height of about 50 m. The incoming signal is recorded using the Transient Buffer Boards. The individual pulses are timed by interpolating the time series using up-sampling, and taking the time of the first positive maximum after the signal exceeds a given threshold, set as a fraction of its amplitude. This method was found suitable for timing relatively long pulses with a broad maximum. The rise time of the pulses was on the order of 50 ns, corresponding to about 3 periods at the resonance frequency of the LBA antennas, near 58 MHz. The pulses showed a strong signal-to-noise ratio in all the antennas we used, hence it was possible to identify the correct maximum for timing.

Geometric delays follow from a straight-line path from the pulse transmitter to each antenna; the calibration signal for each antenna pair is the remaining time delay after accounting for the geometric delays.

The actual position of the octocopter can vary depending on wind and flight control uncertainties. In order to determine the transmitter location more precisely at the time of the measurement, an optimization procedure was performed. The calibration signals have been minimized with respect to a given calibration of LOFAR, which for the majority of the antennas has an uncertainty of at most σ = 0.4 ns as shown in Sect. 3.2. The position shifts by the optimization procedure were found to be about 1 to 1.5 m, which is significant for timing purposes when calibrating from scratch. The fit uncertainty then depends nontrivially on the calibration delays themselves.

Comparing pulse arrival times at each antenna with the expected geometric delay of the signal path from transmitter to receiver, we obtain the calibration signal shown in Fig. 5. The calibration signal is an average over 10 pulses.

The standard deviation of the timing calibration signal amounts to 0.26 ns. This is comparable to the result of 0.44 ns obtained using continuous-wave radio transmitters. Nevertheless, there is still some structure visible in the arrival times for one of the stations, labeled CS003. This may point to a non-optimal fit for the transmitter position.

Fig. 5

Arrival times of pulses from the octocopter drone. The points show the difference between measured and expected pulse arrival time per antenna for four of the innermost LOFAR stations indicated by the labeled arrows at the bottom.

3.3. System monitoring

We have monitored the relative delays between antennas over the course of nearly four years, comparing the results of the given procedure for all datasets in our collection. With at least one calibration at a given date, for which we also know the relative phases, the time variations can be monitored without reference to the transmitter location, wave propagation etc. Only the measured relative phases need to be compared.

A typical time variation plot is given in Fig. 6. Timing corrections have been binned, using one bin per day. The given uncertainties are the standard deviations over one day. The median value of this uncertainty is 0.08 ns, taken only from those days where at least five measurements were taken. This median uncertainty is also assigned to data points from days with less than five measurements. The relative timing between these two antennas is mostly stable over time at the 0.5 ns level, except for the first month of measurements which was within the commissioning time of LOFAR. After this, there were only three days when no stable solution for the timing was found; they are shown as large uncertainties in Figs. 6 and 7.

Figure 7 shows a close-up of the same plot. It shows slow clock drifting, and demonstrates that signal path synchronization at the level of 0.1 ns can indeed be followed and corrected.

Fig. 6

Time variation of the relative delay between two antennas within one LOFAR station over the course of our nearly four-year data collection. Residual delay values are binned per day, showing average and standard deviation within one bin.

Fig. 7

A close-up of the time variation of the relative delay for the same antenna pair, showing the precision of the delay monitoring as well as some clock drifting.

4. Conclusion and outlook

We have developed a spectral cleaning method and a timing calibration method for interferometric radio antenna arrays. These were designed to operate on milliseconds-long time series datasets for individual receivers. The methods were used for our analysis of cosmic-ray datasets, to calibrate and clean voltage time series data. Using phases from an FFT for spectral cleaning was shown to be simpler to use than a straightforward threshold in an averaged power spectrum as no a priori knowledge of the antenna gain curve or noise spectrum is required. Moreover, when compared to this average spectrum threshold, the method has a slightly favorable detection power threshold that is at least 2.0 dB lower. In our application, the threshold of the method is at a power signal-to-noise ratio of -11 dB in a 25 kHz spectral window.

Timing calibration using the phases of public radio transmitter signals was performed to a precision of 0.4 ns for each antenna, at a sampling period of 5 ns (or 200 MHz sampling rate). Monitoring a given calibration over time has a precision of 0.08 ns for each antenna pair in a LOFAR station. Obtaining a timing calibration from a pulse transmitter aboard a drone flying over the array is possible to a similar precision of 0.3 ns, mainly limited by the accuracy of the position measurement of the transmitter.

As the methods described here only require datasets with lengths of 2 to 5 ms, they would be well suited for system monitoring and (pre-)calibration purposes of interferometric radio arrays in general. In addition to detecting interference and timing calibration, malfunctioning receiver data channels can also be identified. Examples include zero or unusual signal power, unstable timing calibrations, polarization errors, and outlying receiver gain curves. Detecting these issues at an early stage prevents the propagation of faulty signals into the correlation and imaging process, where they are more difficult to remove.

It is expected that future low-frequency radio telescopes such as the SKA-Low (low-frequency part of the Square Kilometre Array) will also comprise many individual antenna elements laid out in a relatively dense pattern on the ground. In Dewdney (2015) it has been shown that the majority of antennas will be located at a distance of up to 10 km from a central core. These would be in the line of sight of a single transmitting beacon, either custom or RFI. Ideally a custom beacon would be used and turned on only a few parts per million of the time, for calibration.

Timing and phase calibration of all signal paths is a similar to the challenge in LOFAR, only on a much larger scale. Even with the use of one common clock signal, the entire signal path to the analog-digital conversion unit can exhibit nontrivial variations over time, e.g. along the analog signal transport to the central processing facility. This is already seen in Fig. 7, where the given antenna pair was located inside one LOFAR station, sharing the same clock signal. The techniques presented here, when merged with more elaborate existing methods, could prove useful for this.

¹

GPS coordinates: 6.403565 ° east, 52.902671 ° north.

Acknowledgments

The LOFAR Key Science Project Cosmic Rays gratefully acknowledges the scientific and technical support from ASTRON. The authors thank K. Weidenhaupt, R. Krause, and M. Erdmann for providing and operating the octocopter drone. We also thank the anonymous referee for useful comments. The project acknowledges funding from an Advanced Grant of the European Research Council (FP/2007−2013)/ERC Grant Agreement No. 227610. The project has also received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 640130). We furthermore acknowledge financial support from FOM, (FOM-project 12PR304) and NWO (VENI grant 639-041-130). A.N. is supported by the DFG (research fellowship NE 2031/1-1). LOFAR, the Low Frequency Array designed and constructed by ASTRON, has facilities in several countries, that are owned by various parties (each with their own funding sources), and that are collectively operated by the International LOFAR Telescope (ILT) foundation under a joint scientific policy.

References

Altamimi, Z., Sillard, P., & Boucher, C. 2002, J. Geophys. Res., 107, 2214 [NASA ADS] [CrossRef] [Google Scholar]
Athreya, R. 2009, ApJ, 696, 885 [NASA ADS] [CrossRef] [Google Scholar]
Corstanje, A., Schellart, P., Nelles, A., et al. 2015, Astropart. Phys., 61, 22 [Google Scholar]
Defense Mapping Agency 1987, DMA, TR 8350.2-B [Google Scholar]
Dewdney, P. 2015, SKA1 System Baseline Description v2, https://www.skatelescope.org/wp-content/uploads/2014/03/SKA-TEL-SKO-0000308_SKA1_System_Baseline_v2_DescriptionRev01-part-1-signed.pdf [Google Scholar]
Gilliland, T., Kirby, S. S., Smith, N., & Reymer, S. E. 1938, J. Res. Nat. Bureau Standards, 20, 627 [CrossRef] [Google Scholar]
Grabner, M., & Kvicera, V. 2011, Atmospheric Refraction and Propagation in Lower Troposphere, ed. V. Zhurbenko (In Tech) [Google Scholar]
Kazemi, S., Yatawatta, S., Zaroubi, S., et al. 2011, MNRAS, 414, 1656 [NASA ADS] [CrossRef] [Google Scholar]
Nelles, A., Hörandel, J. R., Karskens, T., et al. 2015, J. Instr., 10, 11005 [Google Scholar]
Offringa, A. R., de Bruyn, A. G., Biehl, M., et al. 2010, MNRAS, 405, 155 [NASA ADS] [Google Scholar]
Offringa, A. R., de Bruyn, A. G., Zaroubi, S., et al. 2013, A&A, 549, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Papoulis, A., & Pillai, S. 2002, Probability, Random Variables and Stochastic Processes, 4th edn. (McGraw-Hill) [Google Scholar]
Pearson, T. J., & Readhead, A. C. S. 1984, ARA&A, 22, 97 [NASA ADS] [CrossRef] [Google Scholar]
Pierre Auger Collaboration. 2016, J. Instr., 11, P01018 [Google Scholar]
Rayleigh, L.. 1905, Nature, 72, 318 [NASA ADS] [CrossRef] [Google Scholar]
Schellart, P., Nelles, A., Buitink, S., et al. 2013, A&A, 560, A98 [Google Scholar]
Schmidt, A., Gemmeke, H., Haungs, A., et al. 2011, IEEE on Trans. Nucl. Sci., 58, 1621 [NASA ADS] [CrossRef] [Google Scholar]
Schroeder, F., Asch, T., Bähren, L., et al. 2010, Nucl. Instr. Meth. Phys. Res. Sect. A: Accelerators, Spectrometers, Detectors and Associated Equipment, 615, 277 [Google Scholar]
Szadkowski, Z., Fraenkel, E., & van den Berg, A. 2013, IEEE on Trans. Nucl. Sci., 60, 3483 [Google Scholar]
Taylor, G. B., Carilli, C. L., & Perley, R. A. 1999, Synthesis Imaging in Radio Astronomy II, 180 [Google Scholar]
van Haarlem, M. P., Wise, M. W., Gunst, A. W., et al. 2013, A&A, 556, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Wijnholds, S., van der Tol, S., Nijboer, R., & van der Veen, A.-J. 2010, IEEE Signal Processing Magazine, 27, 30 [NASA ADS] [CrossRef] [Google Scholar]

Appendix

Here we describe the details of the sensitivity analysis for the spectral cleaning method described in Sect. 2.1.

The problem of finding the threshold for detecting a transmitter can be reduced to a problem of determining whether a given random walk (or ensemble of random walks) is biased or not. The sum of a sequence of phase vectors e^{i φ_j} forms a random walk in the complex plane, with unit step size. The random walk is biased if it has a preference towards a certain direction; on average this gives a longer distance for the random walk.

Assume a transmitter signal measured in one frequency channel of the FFT of a noisy time series, with amplitude a at each receiver. Let the mean noise power in this channel be σ², so the power signal-to-noise ratio is defined as S² ≡ a²/σ². For this calculation, the receivers are assumed to have equal gain, which may not be the case in practice.

The noise in each frequency channel of an FFT is then Rayleigh-distributed in amplitude, with scale parameter $σ / \sqrt{2}$ $\hbox{$\sigma /\! \sqrt{2}$}$ , and uniformly distributed in phase (Papoulis & Pillai 2002). Therefore, denoting the random variable for the noise amplitude as b, the complex amplitude measured at two antennas can be written as $\begin{matrix} z_{1} & = & a + b e^{i φ_{1}} \\ z_{2} & = & a e^{i θ} + c e^{i φ_{2}}, \end{matrix}$ $\appendix \setcounter{section}{1} \begin{eqnarray} z_1 & = & a + b\; \e^{{\rm i}\, \phi_1} \\ z_2 & = & a\; \e^{{\rm i}\, \theta} + c\; \e^{{\rm i}\, \phi_2}, \end{eqnarray}$ where S² = a²/ E(b²). Here, E(·) denotes expected value, and θ is the phase difference of the transmitter signal across the two antennas. As the noise phases are uniform-random and the following analysis is circular-symmetric, the transmitter signal phase difference θ can be omitted. For this analysis, the preferential direction of the random walk is then along the real axis.

Accumulating the phase variance s_1,2 for antenna indices 1 and 2 as in Eq. (3) corresponds to taking an average of the signal over all data blocks as follows: 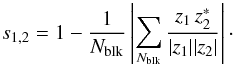$s_{1, 2} = 1 - \frac{1}{N_{blk}} | \sum_{N_{blk}} \frac{z_{1} z_{2}^{*}}{| z_{1} | | z_{2} |} | \cdot$ $\appendix \setcounter{section}{1} \begin{equation} \label{eq:phasevariance_complex} s_{1,2} = 1 - \frac{1}{N_{\rm blk}} \left| \sum_{N_{\rm blk}} \frac{z_1\, z_2^*}{|z_1| |z_2|} \right|\cdot \end{equation}$ (A.3)As a first step, we calculate the expected value of the bias in the random walk. This follows from the expected value of the real part of the fraction in Eq. (A.3). As b and c are independent and identically Rayleigh-distributed, this expected value is given by $\begin{matrix} \frac{1}{(2 π)^{2}} \int_{- π}^{π} d φ_{1} d φ_{2} \int_{0}^{\infty} d b d c \frac{2 b}{σ^{2}} e^{- b^{2} / σ^{2}} \frac{2 c}{σ^{2}} e^{- c^{2} / σ^{2}} \\ \times \frac{Re (a^{2} + a c e^{- i φ_{2}} + a b e^{i φ_{1}} + b c e^{i (φ_{1} - φ_{2})})}{\sqrt{a^{2} + b^{2} + 2 a b \cos (φ_{1})} \sqrt{a^{2} + c^{2} + 2 a c \cos (φ_{2})}} \cdot \end{matrix}$ $\appendix \setcounter{section}{1} \begin{eqnarray} \frac{1}{(2 \pi)^2} \int_{-\pi}^{\pi} {\rm d}\phi_1 {\rm d}\phi_2 \int_0^\infty {\rm d}b\,{\rm d}c \frac{2\,b}{\sigma^2}\e^{-b^2/\sigma^2}\, \frac{2\,c}{\sigma^2} \e^{-c^2 / \sigma^2}\nonumber \\ \times \frac{{\mathrm{Re}} \left(a^2 + a\,c\,\e^{-{\rm i}\,\phi_2} + a\,b\,\e^{{\rm i} \phi_1} + b\,c\,\e^{{\rm i}(\phi_1 - \phi_2)}\right)}{\sqrt{a^2 + b^2 + 2\,a\,b \cos(\phi_1)}\; \sqrt{a^2 + c^2 + 2\,a\,c \cos(\phi_2)}}\cdot \end{eqnarray}$ (A.4)As we are dealing with low-amplitude thresholds well below the noise level (i.e. S ≪ 1), an asymptotic lowest-order expansion in a/b is used in order to make the integral more tractable.

After collecting the lowest-order terms, the integral evaluates to $E (\frac{Re (z_{1} z_{2}^{*})}{| z_{1} | | z_{2} |}) = \frac{π}{4} S^{2} + 𝒪 (S^{4}) .$ $\appendix \setcounter{section}{1} \begin{equation} E \left({\frac{{\rm Re}\,(z_1 z_2^*)}{|z_1||z_2|}}\right) = \frac{\pi}{4}\, S^2 + \mathcal{O}(S^4). \end{equation}$ (A.5)The bias B in a random walk of N_blk steps is therefore expected to be $B = \frac{π}{4} S^{2} N_{blk},$ $\appendix \setcounter{section}{1} \begin{equation} \label{eq:bias} B = \frac{\pi}{4} S^2 N_{\rm blk}, \end{equation}$ (A.6)and the random walk effectively reduces, again to lowest order in S, to an unbiased random walk with respect to a point at distance B from the origin. Using the Rayleigh distribution for the unbiased random-walk distance to the origin, and displacing it by the bias, we obtain for the expected distance $\begin{matrix} E (d) = \frac{1}{2 π} \int_{- π}^{π} d φ \int_{0}^{\infty} d R \frac{R}{τ^{2}} e^{- R^{2} / (2 τ^{2})} \\ \times \sqrt{R^{2} + B^{2} + 2 R B \cos (φ)}, \end{matrix}$ $\appendix \setcounter{section}{1} \begin{eqnarray} E(d) = \frac{1}{2\pi}\int_{-\pi}^{\pi}{\rm d}\phi \int_0^{\infty}{\rm d}R \;\frac{R}{\tau^2} \;\e^{-R^2/(2\tau^2)} \nonumber\\ \times \sqrt{R^2 + B^2 + 2\,R\,B\, \cos(\phi)}, \end{eqnarray}$ (A.7)with scale parameter $τ = \sqrt{N_{blk} / 2}$ $\hbox{$\tau=\sqrt{N_{\rm blk}/2}$}$ . To lowest order in B this yields $E (d) ~ E (d)_{unbiased} + \frac{1}{4} B^{2} \sqrt{\frac{π}{N_{blk}}} \cdot$ $\appendix \setcounter{section}{1} \begin{equation} \label{eq:excessdistance} E(d) \sim E(d)_{\rm unbiased} + \frac{1}{4} \,B^2 \,\sqrt{\frac{\pi}{N_{\rm blk}}}\cdot \end{equation}$ (A.8)The excess distance needs to be above a chosen factor k times the standard error of the unbiased random walk distance (see discussion of Eq. (4)), using the ensemble having one random walk for each of the N_ant(N_ant−1) / 2 antenna pairs. Hence we have a condition $\frac{1}{4} B^{2} \sqrt{\frac{π}{N_{blk}}} > k β \sqrt{2} N_{blk}^{1 / 2} N_{ant}^{-1},$ $\appendix \setcounter{section}{1} \begin{equation} \frac{1}{4} \,B^2 \,\sqrt{\frac{\pi}{N_{\rm blk}}} > k\,\beta\, \sqrt{2}\;N_{\rm blk}^{1/2}\; N_{\rm ant}^{-1}, \end{equation}$ (A.9)where the right-hand side is k times the standard error for large N_ant, approximating the number of antenna pairs by $N_{ant}^{2} / 2$ $\hbox{$N_{\rm ant}^2 / 2$}$ .

Comparing these using Eq. (A.6) gives as a threshold for large N_ant $S^{2} > \frac{8}{π} {(\frac{2}{π} - \frac{1}{2})}^{1 / 4} \sqrt{k} N_{blk}^{- 1 / 2} N_{ant}^{- 1 / 2},$ $\appendix \setcounter{section}{1} \begin{equation} S^2 > \frac{8}{\pi} \,\left(\frac{2}{\pi} - \frac{1}{2}\right)^{1/4}\,\sqrt{k}\;N_{\rm blk}^{-1/2}\;N_{\rm ant}^{-1/2}, \end{equation}$ (A.10)reducing to $S^{2} > 3.8 \sqrt{k / 6} N_{blk}^{- 1 / 2} N_{ant}^{- 1 / 2},$ $\appendix \setcounter{section}{1} \begin{equation} S^2 > 3.8\;\sqrt{k/6}\;N_{\rm blk}^{-1/2}\;N_{\rm ant}^{-1/2}, \end{equation}$ (A.11)aimed at a six-sigma detection threshold (k = 6).

All Figures

	Fig. 1 Example power spectrum from 2 ms of LOFAR data, averaged over 48 LBA antenna dipoles. Crosses indicate channels with detected transmitters.
In the text

	Fig. 2 Example power spectrum from 2 ms of LOFAR time series data (lower curve). The phase variance is shown in the upper data points (red). It consistently becomes lower whenever a narrowband transmitter is seen in the power spectrum.
In the text

	Fig. 3 Close-up of the power spectrum in a frequency range with several RFI sources. Flagged frequencies are shown as red dashed lines. The lower panel shows the phase variance, where the black horizontal line indicates the threshold for flagging. Although the RFI-quiet noise level would follow a smooth curve, fitting the curve and RFI flagging using the excess power are interdependent.
In the text

	Fig. 4 Difference between measured and expected phases per antenna, converted to time in nanoseconds. Red solid bars represent the median time delay per LOFAR station (48 antennas); the stations are separated by the vertical grid lines. The range of the y-axis corresponds to the signal period at 88 MHz.
In the text

	Fig. 5 Arrival times of pulses from the octocopter drone. The points show the difference between measured and expected pulse arrival time per antenna for four of the innermost LOFAR stations indicated by the labeled arrows at the bottom.
In the text

	Fig. 6 Time variation of the relative delay between two antennas within one LOFAR station over the course of our nearly four-year data collection. Residual delay values are binned per day, showing average and standard deviation within one bin.
In the text

	Fig. 7 A close-up of the time variation of the relative delay for the same antenna pair, showing the precision of the delay monitoring as well as some clock drifting.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

[1] Altamimi, Z., Sillard, P., & Boucher, C. 2002, J. Geophys. Res., 107, 2214 [NASA ADS] [CrossRef] [Google Scholar]

[2] Athreya, R. 2009, ApJ, 696, 885 [NASA ADS] [CrossRef] [Google Scholar]

[3] Corstanje, A., Schellart, P., Nelles, A., et al. 2015, Astropart. Phys., 61, 22 [Google Scholar]

[4] Defense Mapping Agency 1987, DMA, TR 8350.2-B [Google Scholar]

[5] Dewdney, P. 2015, SKA1 System Baseline Description v2, https://www.skatelescope.org/wp-content/uploads/2014/03/SKA-TEL-SKO-0000308_SKA1_System_Baseline_v2_DescriptionRev01-part-1-signed.pdf [Google Scholar]

[6] Gilliland, T., Kirby, S. S., Smith, N., & Reymer, S. E. 1938, J. Res. Nat. Bureau Standards, 20, 627 [CrossRef] [Google Scholar]

[7] Grabner, M., & Kvicera, V. 2011, Atmospheric Refraction and Propagation in Lower Troposphere, ed. V. Zhurbenko (In Tech) [Google Scholar]

[8] Kazemi, S., Yatawatta, S., Zaroubi, S., et al. 2011, MNRAS, 414, 1656 [NASA ADS] [CrossRef] [Google Scholar]

[9] Nelles, A., Hörandel, J. R., Karskens, T., et al. 2015, J. Instr., 10, 11005 [Google Scholar]

[10] Offringa, A. R., de Bruyn, A. G., Biehl, M., et al. 2010, MNRAS, 405, 155 [NASA ADS] [Google Scholar]

[11] Offringa, A. R., de Bruyn, A. G., Zaroubi, S., et al. 2013, A&A, 549, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[12] Papoulis, A., & Pillai, S. 2002, Probability, Random Variables and Stochastic Processes, 4th edn. (McGraw-Hill) [Google Scholar]

[13] Pearson, T. J., & Readhead, A. C. S. 1984, ARA&A, 22, 97 [NASA ADS] [CrossRef] [Google Scholar]

[14] Pierre Auger Collaboration. 2016, J. Instr., 11, P01018 [Google Scholar]

[15] Rayleigh, L.. 1905, Nature, 72, 318 [NASA ADS] [CrossRef] [Google Scholar]

[16] Schellart, P., Nelles, A., Buitink, S., et al. 2013, A&A, 560, A98 [Google Scholar]

[17] Schmidt, A., Gemmeke, H., Haungs, A., et al. 2011, IEEE on Trans. Nucl. Sci., 58, 1621 [NASA ADS] [CrossRef] [Google Scholar]

[18] Schroeder, F., Asch, T., Bähren, L., et al. 2010, Nucl. Instr. Meth. Phys. Res. Sect. A: Accelerators, Spectrometers, Detectors and Associated Equipment, 615, 277 [Google Scholar]

[19] Szadkowski, Z., Fraenkel, E., & van den Berg, A. 2013, IEEE on Trans. Nucl. Sci., 60, 3483 [Google Scholar]

[20] Taylor, G. B., Carilli, C. L., & Perley, R. A. 1999, Synthesis Imaging in Radio Astronomy II, 180 [Google Scholar]

[21] van Haarlem, M. P., Wise, M. W., Gunst, A. W., et al. 2013, A&A, 556, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[22] Wijnholds, S., van der Tol, S., Nijboer, R., & van der Veen, A.-J. 2010, IEEE Signal Processing Magazine, 27, 30 [NASA ADS] [CrossRef] [Google Scholar]