| Issue |
A&A
Volume 590, June 2016
|
|
|---|---|---|
| Article Number | A65 | |
| Number of page(s) | 20 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201527350 | |
| Published online | 12 May 2016 | |
Dust destruction by the reverse shock in the Cassiopeia A supernova remnant
1 Institut d’Astrophysique Spatiale, UMR 8617, Université Paris-Sud, 91405 Orsay, France
2 Observational Cosmology Lab, Code 665, NASA Goddard Space Flight Center, Greenbelt, MD 20771, USA
e-mail: elisabetta.micelotta@helsinki.fi
3 Harvard-Smithsonian Center for Astrophysics, 60 Garden Street, Cambridge, MA 02138, USA
Received: 12 September 2015
Accepted: 6 February 2016
Context. Core collapse supernovae (CCSNe) are important sources of interstellar dust, which are potentially capable of producing 1 M⊙ of dust in their explosively expelled ejecta. However, unlike other dust sources, the dust has to survive the passage of the reverse shock, generated by the interaction of the supernova blast wave with its surrounding medium. Knowledge of the net amount of dust produced by CCSNe is crucial for understanding the origin and evolution of dust in the local and high-redshift Universe.
Aims. We identify the dust destruction mechanisms in the ejecta and derive the net amount of dust that survives the passage of the reverse shock.
Methods. We use analytical models for the evolution of a supernova blast wave and of the reverse shock with special application to the clumpy ejecta of the remnant of Cassiopeia A (Cas A). We assume that the dust resides in cool oxygen-rich clumps, which are uniformly distributed within the remnant and surrounded by a hot X-ray emitting plasma (smooth ejecta), and that the dust consists of silicates (MgSiO3) and amorphous carbon grains. The passage of the reverse shock through the clumps gives rise to a relative gas-grain motion and also destroys the clumps. While residing in the ejecta clouds, dust is processed via kinetic sputtering, which is terminated either when the grains escape the clumps or when the clumps are destroyed by the reverse shock. In either case, grain destruction proceeds thereafter by thermal sputtering in the hot shocked smooth ejecta.
Results. We find that 11.8 and 15.9 percent of silicate and carbon dust, respectively, survive the passage of the reverse shock by the time the shock has reached the centre of the remnant. These fractions depend on the morphology of the ejecta and the medium into which the remnant is expanding, as well as the composition and size distribution of the grains that formed in the ejecta. Results will therefore differ for different types of supernovae.
Key words: dust, extinction / ISM: supernova remnants / shock waves / supernovae: general / supernovae: individual: Cassiopeia A
© ESO, 2016
1. Introduction
Core collapse supernovae (CCSNe) are major producers of heavy elements and drive the chemical enrichment in galaxies. The high densities and preponderance of refractory elements in their ejecta provide the necessary conditions for the formation and growth of dust. Dust of supernova (SN) origin was found in meteorites (see reviews in Clayton & Nittler 2004; Zinner 2008), and its presence was also inferred from their infrared (IR) and sub-millimeter emission in young SNe, such as SN 1987A (Moseley et al. 1989; Dwek et al. 1992; Wooden 1997; Bouchet et al. 2004; Indebetouw et al. 2014; Matsuura et al. 2015, and references therein), and in young unmixed supernova remnants (SNRs) such as Cassiopeia A (Cas A; Lagage et al. 1996; Rho et al. 2008; Dunne et al. 2009; Barlow et al. 2010; Arendt et al. 2014) or the Crab Nebula (Hester 2008; Gomez et al. 2012; Temim & Dwek 2013). The observations of SNRs suggest that the typical yield of dust is about 0.1 M⊙, with the largest inferred dust mass of ~0.5 M⊙ in SN 1987A (Matsuura et al. 2015). Theoretical models suggest that refractory elements precipitate very efficiently from the gas phase, giving a dust yield of 0.1−0.5 M⊙ for a typical 25 M⊙ progenitor star (Todini & Ferrara 2001; Schneider et al. 2004; Cherchneff & Dwek 2010; Nozawa et al. 2010). A review of the production of dust in galaxies was presented by Gall et al. (2011c).
Supernovae also destroy dust during the remnant phase of their evolution. Most recent calculations show that in the local solar neighbourhood SNRs destroy more dust than is produced by SNe and asymptotic giant branch (AGB) stars combined (Bocchio et al. 2014; Slavin et al. 2015, and references therein). Similar conclusions were reached for the Magellanic Clouds (Temim et al. 2015). This imbalance between the production and destruction rate also prevails in local and high-redshift galaxies; this suggests that dust may need to reconstitute by accretion in the dense phases of the interstellar medium (ISM; Dwek & Scalo 1980; Valiante et al. 2011; Dwek et al. 2011; Gall et al. 2011a,b). The problem becomes more acute in the very high redshift Universe (z ≳ 6) where large amounts of dust have been detected (≳107M⊙ – Bertoldi et al. 2003; Watson et al. 2015), but AGB stars have not yet evolved to form dust. If they are to be the sole source of dust in the early Universe Dwek & Cherchneff (2011), SNe must then produce ~1 M⊙ of dust. Supernovae are net producers of interstellar dust in galaxies with metallicities below ~0.002 only, and SNe are capable of producing a significant amount of dust with a dust yield of ~0.1 M⊙/SN without resorting to the need of grain growth in the ISM (Dwek et al. 2014).
Calculated dust yields, and dust yields that are observationally inferred for very young SNe, do not reflect the net amount of dust that is ultimately injected by SNe into the ISM. The pressure of the ISM gas that is shocked by the expanding SN blast wave generates a reverse shock that propagates through the expanding ejecta (McKee 1974; Truelove & McKee 1999), partially destroying the newly formed dust by sputtering (Dwek 2005; Bianchi & Schneider 2007; Nath et al. 2008; Nozawa et al. 2007; Silvia et al. 2010, 2012; Micelotta & Dwek 2013; Biscaro & Cherchneff 2014, 2016). However, because of the complexity of the problem, the total amount of mass destroyed is still unclear.
In this paper we calculate the mass of dust destroyed in the most extensively studied SNR, Cas A. We illustrate the relative importance of the many physical processes in the shocked ejecta by generalizing the analytical model of Truelove & McKee (1999, hereafter TM99) to describe the evolution of the forward and reverse shock in the remnant. We adopt a set of parameters that reproduce the dynamics and the density and temperature profile of the Cas A ejecta. The reverse shock has partially propagated through its ejecta (Gotthelf et al. 2001) heating the SN-condensed dust, which gives rise to observed mid- to far-IR emission from the remnant (Ennis et al. 2006; Rho et al. 2008; Arendt et al. 2014). The mass of dust inferred from these observations is about 0.1 M⊙ (Arendt et al. 2014). We assume that all the dust is initially in the clumps, and that there is no dust in the interclump region. The mass, composition, and size distribution of the dust that survives the passage of the reverse shock and is injected into the ISM is the subject of this publication.
The paper is organized as follows. We first present our generalization of the analytical model of TM99 to the case of non-uniform ejecta expanding into a non-uniform ambient medium (Sect. 2), and in Sect. 3 we provide the specific results of this model for Cas A. We assume that the dynamics of the reverse shock is unaffected by the presence of clumps (clouds) in the ejecta, and adopt the parameters of Sutherland & Dopita (1995) to describe their density. The density contrast between the clumps and the smooth ejecta determines the velocity of the reverse shock that propagates into the clumps.
The reverse shock propagating through the clumps has low velocity compared to that of the reverse shock propagating through the smooth ejecta. The passage of the reverse shock causes a relative dust-gas motion and subjects the dust to kinetic sputtering. The amount of grain destruction depends on the initial velocity of the grains, and the mass column density they traverse through the clump, which in turn depends on both the size of the grains and their position in the cloud. In Sect. 4 we present the formalism that we use to investigate the effect of kinetic sputtering inside the clumps.
Kinetic sputtering is terminated either when the grains escape the clump, or when the clump is destroyed by crushing and evaporation. At the end of the kinetic sputtering process, the grains are injected into the ambient hot gas. The average thermal kinetic energy of the gas exceeds the kinetic energy of the grains, and grain destruction proceeds predominantly by thermal sputtering. In Sect. 5 we study the time it takes the dust to travel through the cloud, and compare this to the cloud crushing and evaporation timescales.
Any dust escaping the clumps is subjected to thermal sputtering in the hot SN cavity. Conditions in the cavity evolve with time as the density and temperature of the X-ray emitting gas decrease by expansion and radiative cooling. The destruction of dust in this evolving environment is presented in Sect. 6. We adopt silicates in the form of MgSiO3 and amorphous carbon as the main dust components in the ejecta, and assume that their initial size distribution is characterized by a power law in grain radii. Section 7 presents our Monte Carlo approach to evaluate kinetic and thermal sputtering, together with our results in terms of the net amount and mass distribution as a function of grain size of the surviving dust in Cas A. A discussion of the astrophysical significance of our findings is presented in Sect. 8, and our results are summarized in Sect. 9.
2. Dynamics
Cas A is a young SNR (~333 yr in 2004) currently in an intermediate stage between the two non-radiative phases of supernova remnants evolution (Laming & Hwang 2003): the ejecta-dominated phase (ED), when the mass of the ejecta is dominant with respect to the swept-up circumstellar material, and the Sedov-Taylor phase (ST), which starts as the remnant has swept-up an amount of circumstellar material comparable with the mass of the stellar ejecta.
To describe the dynamical evolution of the SNR through the ED and ST stages, we refer to the analytical treatment of TM99. This seminal work focused on the evolution of supernova ejecta expanding into an uniform density ambient medium, emphasising the dependence of the ED stage on the ejecta parameters and providing analytical expressions that smoothly merge the blast-wave and reverse shock solutions between the ED and ST stages. We generalize their treatment to general power-law ambient media (described by an index s: ρ(r) = ρsr− s), following the indications provided in their Appendix A. Then, referring to the work of Laming & Hwang (2003), we consider the specific case of s = 2 appropriate for Cas A, i.e. ejecta expanding into a pre-supernova steady stellar wind (van den Bergh 1971; Chevalier & Fransson 1994; Laming & Hwang 2003, and references therein).
2.1. Characteristic scales
As shown by TM99, in the problem considered here the initial conditions introduce three independent dimensional parameters: the ejecta energy, E, ejecta mass, Mej and normalization parameter for the ambient density, ρs. These three dimensional parameters can be combined in a unique way to define characteristic scales of length, time, and mass as follows: 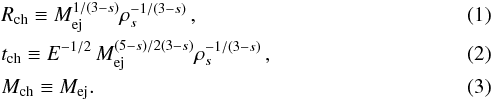 Additional scales can be derived from the following base set:
Additional scales can be derived from the following base set: 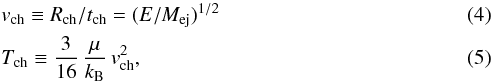 where μ is the mean mass per particle and kB is the Boltzmann constant.
where μ is the mean mass per particle and kB is the Boltzmann constant.
We adopt s = 2, which corresponds to ejecta expanding into a pre-supernova steady stellar wind. In this case, 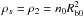 , where Rb0 is the blast-wave radius at a given time and n0 is the circumstellar density at Rb0. We can write
, where Rb0 is the blast-wave radius at a given time and n0 is the circumstellar density at Rb0. We can write 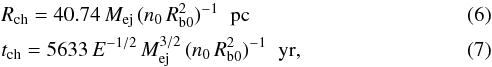 with Mej in solar masses, E in units of 1051 erg, n0 in H atoms per cubic centimeter, and Rb0 in parsecs.
with Mej in solar masses, E in units of 1051 erg, n0 in H atoms per cubic centimeter, and Rb0 in parsecs.
Following TM99, we perform our calculations using the dimensionless starred variables defined as R∗ ≡ R/Rch, t∗ ≡ t/tch, v∗ ≡ v/vch, etc. The results are presented in usual units for clarity.
2.2. Initial conditions
We assume that the SN ejecta initially expands homologously with a maximum ejecta velocity vej, and velocity profile v(r) ~ r/t for r<Rej, where Rej ≡ vejt is the free-expansion radius of the outer layer of the ejecta if no ambient medium is present. The density is given by the following expression (Eq. (A.1) in TM99): 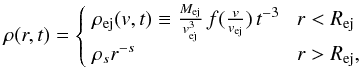 (8)where ρs is a normalization constant and the condition s< 3 is required to ensure a finite ambient mass. In the initial ejecta density distribution, the term t-3 accounts for the free expansion of the ejecta before encountering the circumstellar medium, while the time-independent shape of the density distribution is described by the structure function f(v/vej). We consider a power-law structure function expressed as
(8)where ρs is a normalization constant and the condition s< 3 is required to ensure a finite ambient mass. In the initial ejecta density distribution, the term t-3 accounts for the free expansion of the ejecta before encountering the circumstellar medium, while the time-independent shape of the density distribution is described by the structure function f(v/vej). We consider a power-law structure function expressed as  (9)where w ≡ v/vej, wcore = vcore/vej and vcore is the velocity of the ejecta at the boundary between an inner uniform core region and an external power-law envelope region characterized by the index n. Following Chevalier & Oishi (2003) and Laming & Hwang (2003), we adopt for Cas A the value n = 9, which provides: i) the correct ratio between the forward and reverse shock radii; ii) the correct relationship between the forward shock and free-expansion rates; and iii) a more plausible ejecta mass of 2 M⊙. As discussed by TM99, a power-law ejecta envelope with index n> 5 requires the presence of a core in order for Mej to be finite.
(9)where w ≡ v/vej, wcore = vcore/vej and vcore is the velocity of the ejecta at the boundary between an inner uniform core region and an external power-law envelope region characterized by the index n. Following Chevalier & Oishi (2003) and Laming & Hwang (2003), we adopt for Cas A the value n = 9, which provides: i) the correct ratio between the forward and reverse shock radii; ii) the correct relationship between the forward shock and free-expansion rates; and iii) a more plausible ejecta mass of 2 M⊙. As discussed by TM99, a power-law ejecta envelope with index n> 5 requires the presence of a core in order for Mej to be finite.
The parameter f0 can be determined imposing the continuity of f(w) in wcore, i.e. 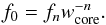 (10)The value of fn results from the condition that the integral of the mass must equal Mej, i.e.
(10)The value of fn results from the condition that the integral of the mass must equal Mej, i.e. ![\begin{equation} \label{f_n} f_n = \frac{3}{4\pi}\,\left[\frac{1-n/3}{1-(n/3)\,w^{3-n}_{\rm core}}\right]\cdot \end{equation}](/articles/aa/full_html/2016/06/aa27350-15/aa27350-15-eq47.png) (11)We can introduce the following dimensionless ratio:
(11)We can introduce the following dimensionless ratio: 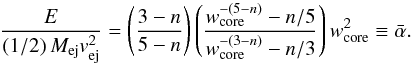 (12)If n> 5, in the limit wcore → 0, from Eq. (8) we obtain
(12)If n> 5, in the limit wcore → 0, from Eq. (8) we obtain 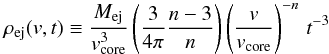 (13)while Eq. (12) becomes
(13)while Eq. (12) becomes 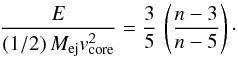 (14)From this, we can derive the expression for vcore as follows:
(14)From this, we can derive the expression for vcore as follows: 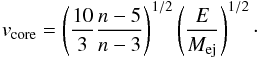 (15)Remembering that vch = (E/Mej)1/2 and that v∗ ≡ v/vch we then obtain
(15)Remembering that vch = (E/Mej)1/2 and that v∗ ≡ v/vch we then obtain 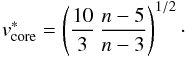 (16)For the density profile of the ejecta core, Eqs. (8) and (9) yield
(16)For the density profile of the ejecta core, Eqs. (8) and (9) yield 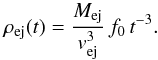 (17)To derive f0, we impose the continuity between Eqs. (17) and (13), which is valid for the ejecta envelope, at the boundary between the inner uniform core and the external power-law envelope, where v = vcore. For vcore, we use Eq. (15). Following this procedure we obtain
(17)To derive f0, we impose the continuity between Eqs. (17) and (13), which is valid for the ejecta envelope, at the boundary between the inner uniform core and the external power-law envelope, where v = vcore. For vcore, we use Eq. (15). Following this procedure we obtain 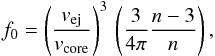 (18)which substituted in Eq. (17) provides the following expression for the density profile of the ejecta core:
(18)which substituted in Eq. (17) provides the following expression for the density profile of the ejecta core: 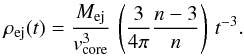 (19)It is convenient to characterize the layers of the ejecta by a dimensionless parameter α, defined by v(0) ≡ αvej (α ≤ 1), where v(0) is the initial velocity of the layer with respect to the unperturbed ISM. The outer layer of the ejecta expands at velocity vej and is therefore characterized by α = 1, whereas the innermost layer has a value of α = 0. A layer α encounters the reverse shock at time tr when its radius is equal to the position of the reverse shock, i.e. when αvejtr = Rr(tr). From this, we obtain
(19)It is convenient to characterize the layers of the ejecta by a dimensionless parameter α, defined by v(0) ≡ αvej (α ≤ 1), where v(0) is the initial velocity of the layer with respect to the unperturbed ISM. The outer layer of the ejecta expands at velocity vej and is therefore characterized by α = 1, whereas the innermost layer has a value of α = 0. A layer α encounters the reverse shock at time tr when its radius is equal to the position of the reverse shock, i.e. when αvejtr = Rr(tr). From this, we obtain 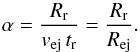 (20)The relation between tr and the parameter α is shown in Fig. 1, while the ejecta density from Eqs. (13) and (19), but expressed as a function of α, is reported in Fig. 2. The mass density of the Cas A ejecta in 2004 (α = 0.33) is indicated by the horizontal line and corresponds to a number density of 0.23 cm-3. This value is consistent with the average density of ~0.25 cm-3 estimated by Morse et al. (2004) for the smooth X-ray emitting ejecta in Cas A.
(20)The relation between tr and the parameter α is shown in Fig. 1, while the ejecta density from Eqs. (13) and (19), but expressed as a function of α, is reported in Fig. 2. The mass density of the Cas A ejecta in 2004 (α = 0.33) is indicated by the horizontal line and corresponds to a number density of 0.23 cm-3. This value is consistent with the average density of ~0.25 cm-3 estimated by Morse et al. (2004) for the smooth X-ray emitting ejecta in Cas A.
 |
Fig. 1 Time, tr, after the explosion at which an ejecta layer characterized by the parameter α encounters the reverse shock. The outer layer has the value α = 1, while the inner one has α = 0. The vertical line indicates the value α = 0.33, corresponding to the ejecta layer which encounters the reverse shock in 2004, and of course intersects the red solid curve at the time corresponding to the age of Cas A in 2004, i.e. tr = 333 yr (indicated by the horizontal line). |
2.3. Final equations for the supernova shocks
To derive the equations describing the evolution of the blast wave and of the reverse shock, we use the treatment from Laming & Hwang (2003) as a starting point. However, to develop our calculations we fully evaluated the implications of the assumption that wcore → 0 (instead of adopting wcore → 1 as by Laming & Hwang 2003).
In this section, we report the final expressions that we use in the rest of our study. For more details about the derivation of these equations, see Appendix A.
We introduce the quantity φ, defined as the ratio of the pressures behind the reverse and blastwave shocks (McKee 1974). The lead factor ℓ is defined as the ratio of the radii of the forward shock to the reverse shock: 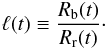 (21)Following TM99, we make the approximations φ(t) ≅ φ(0) ≡ φED and ℓ(t) ≅ ℓ(0) ≡ ℓED. The subscript “ED” refers to the ejecta-dominated phase of the evolution of the supernova remnant. With these approximations, from Eq. (21) we obtain Rr = Rb/ℓED. The quantities φED and ℓED are well fitted by the following expressions (Hwang & Laming 2011): During the ejecta-dominated phase, the reverse shock propagates through the ejecta envelope before reaching the ejecta core. The blast-wave radius during the initial envelope phase is given by the following expression:
(21)Following TM99, we make the approximations φ(t) ≅ φ(0) ≡ φED and ℓ(t) ≅ ℓ(0) ≡ ℓED. The subscript “ED” refers to the ejecta-dominated phase of the evolution of the supernova remnant. With these approximations, from Eq. (21) we obtain Rr = Rb/ℓED. The quantities φED and ℓED are well fitted by the following expressions (Hwang & Laming 2011): During the ejecta-dominated phase, the reverse shock propagates through the ejecta envelope before reaching the ejecta core. The blast-wave radius during the initial envelope phase is given by the following expression: 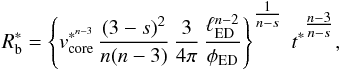 (22)while the velocity of the forward shock is written as
(22)while the velocity of the forward shock is written as 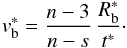 (23)This comes directly from Eq. (22) using the definition of velocity,
(23)This comes directly from Eq. (22) using the definition of velocity, 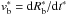 .
.
 |
Fig. 2 Density structure of the ejecta calculated from Eq. (13) but expressed as a function of the parameter α. Vertical line as in Fig. 1. The horizontal line indicates the mass density of the Cas A smooth ejecta in 2004 and the label indicates the corresponding number density. |
 |
Fig. 3 Left: blast-wave and reverse shock radii as a function of the time elapsed since explosion. Right: zoom of left panel for t ≤ 1000 yr. |
During the core phase, when the reverse shock propagates through the ejecta core, the blast-wave radius is given by ![\begin{eqnarray} \label{blast_radius_core_eq} R^{*}_{\rm b} & = & \Bigg \{\left[\left(\frac{(3-s)^2}{n(n-3)}\,\frac{3}{4\pi}\,\frac{l_{\rm ED}^{n-2}} {\phi_{\rm ED}}\right)\left(v^{*}_{\rm core}\,t^{*}_{\rm conn}\right)^{n-3}\right]^{\tfrac{5-s}{2(n-s)}} \nonumber \\ && \quad +\,\xi_s^{1/2}\left(t^{*} - t^{*}_{\rm conn}\right)\Bigg \}^{\tfrac{2}{5-s}} \end{eqnarray}](/articles/aa/full_html/2016/06/aa27350-15/aa27350-15-eq86.png) (24)and the blast-wave velocity is written as
(24)and the blast-wave velocity is written as 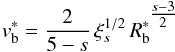 (25)with
(25)with 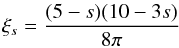 (26)and
(26)and 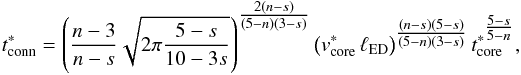 (27)where
(27)where 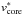 comes from Eq. (16) and
comes from Eq. (16) and 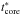 is the time at which the reverse shock hits the ejecta core, i.e.
is the time at which the reverse shock hits the ejecta core, i.e. ![\begin{equation} \label{t_core_star} t^{*}_{\rm core} = \left[\frac{\ell_{\rm ED}^{s-2}}{\phi_{\rm ED}} \frac{3}{4\pi}\frac{(3-s)^2}{n(n-3)}\right]^{1/(3-s)}\frac{1}{v^{*}_{\rm core}}\cdot \end{equation}](/articles/aa/full_html/2016/06/aa27350-15/aa27350-15-eq92.png) (28)Equations (22) and (23) are valid for
(28)Equations (22) and (23) are valid for 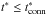 , while Eqs. (24) and (25) are valid for
, while Eqs. (24) and (25) are valid for 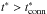 . The reason for the introduction of the time
. The reason for the introduction of the time 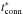 , its definition and derivation can be found in Appendix A.
, its definition and derivation can be found in Appendix A.
The equations for the reverse shock are the following. During the envelope phase, i.e. for 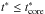 , the reverse shock radius is written as
, the reverse shock radius is written as 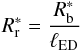 (29)and the reverse shock velocity (in the frame of the unshocked ejecta) is written as
(29)and the reverse shock velocity (in the frame of the unshocked ejecta) is written as 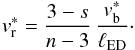 (30)During the core phase, i.e. for
(30)During the core phase, i.e. for 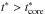 , we have for the reverse shock radius the following expression:
, we have for the reverse shock radius the following expression: ![\begin{eqnarray} \label{reverse_radius_core_eq} R_{\rm r}^{*} = \left[\frac{R_{\rm b}^{*}(t^{*} = t^{*}_{\rm core})}{\ell_{\rm ED}\,t^{*}_{\rm core}} - \frac{3-s}{n-3}\,\frac{v_{\rm b}^{*}(t^{*} = t^{*}_{\rm core})}{\ell_{\rm ED}} \ln{\frac{ t^{*}}{t^{*}_{\rm core}}}\right]\,t^{*}, \end{eqnarray}](/articles/aa/full_html/2016/06/aa27350-15/aa27350-15-eq100.png) (31)and the reverse shock velocity is given by
(31)and the reverse shock velocity is given by 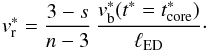 (32)We assume that inside the core the reverse shock velocity remains constant and equal to the value for
(32)We assume that inside the core the reverse shock velocity remains constant and equal to the value for 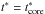 .
.
The radius of the blast-wave shock (Eqs. (22) and (24)) and of the reverse shock (Eqs. (29) and (31)) as a function of the time elapsed since the progenitor of Cas A exploded as a supernova are shown in Fig. 3. The velocity of the blast-wave shock (Eqs. (23) and (25)) and of the reverse shock (Eqs. (30) and (32)) as a function of the parameter α are shown in Fig. 4.
 |
Fig. 4 Blast-wave and reverse shock velocities (vb and vr, respectively) as a function of the parameter α. The reverse shock velocity (right y-axis, in units of 103 km s-1) is calculated in the frame of the unshocked ejecta ahead of it. We assume that after the reverse shock has entered the ejecta core (α< 0.75), its velocity remains constant and equal to the value for |
Physical properties of Cas A.
3. Application to Cas A
3.1. Ejecta geometry and physical properties
The Cas A supernova remnant is the result of the explosion of a Type IIb supernova (Krause et al. 2008) with a progenitor mass estimated between 15 and 25 M⊙ (Young et al. 2006; Vink et al. 1996). The remnant is located at a distance of 3.4 kpc (Reed et al. 1995) and its age was ~333 yr in 2004 (date of the Chandra observations which have been used to determine some of the parameters of Cas A used in this work). From our calculations (Sect. 2.3) we obtain the following values for the radius and velocity of the forward and reverse shock of Cas A in 2004: Rb = 2.5 pc, vb = 5226 km s-1, Rr = 1.71 pc and vr = 1586 km s-1. Our numbers are consistent with the values derived from observations: Rb = 2.32−2.72 pc, vb = 4000−6000 km s-1, Rr = 1.52−2.01 pc, vr = 1000−2000 km s-1 (see Table 1 for the corresponding references).
We obtained this nice match adopting the ejecta mass Mej = 2 M⊙ (consistent with the value of 2.2 M⊙ inferred by Willingale et al. 2002, 2003), and the explosion energy E = 2.2 × 1051 erg, in agreement with the amount of energy expected from a core-collapse SN (Laming & Hwang 2003), and the circumstellar (preshock) density n0 = 2.07 H atom cm-3, which is compatible with the value of 1.99 cm-3 from Willingale et al. (2003).
The density distribution of the supernova ejecta is described in a more realistic and observationally motivated way by a series of overdense clouds embedded into a smooth and tenuous medium (e.g. Peimbert & van den Bergh 1971; Kamper & van den Bergh 1976; Chevalier & Kirshner 1978, 1979; Fesen et al. 2001; Rho et al. 2009, 2012; Wallström et al. 2013). For the ejecta clouds, we assume a pre-shock density ncloud = 100 cm-3 with a density contrast with respect to the smooth component χ = ncloud/nsmooth = 100. These values allow to reproduce the optical spectra of the fast moving knots (FMKs) in Cas A in a fairly accurate way (Sutherland & Dopita 1995). For the smooth ejecta, therefore, we obtain the pre-shock density nsmooth = ncloud/χ = 1.0 cm-3, which is consistent with the ambient density of 0.1−10 cm-3 (average ~0.25 cm-3) estimated for the X-ray emitting gas on the bases of ram pressure arguments (Morse et al. 2004). This value for the smooth ejecta density should be considered as indicative. To evaluate the effect of dust sputtering we use the density structure shown in Fig. 2, which has been calculated with our model for the evolution of the Cas A ejecta. Our model predicts for 2004 a number density of 0.23 cm-3, which is very close to the average value estimated by Morse et al. (2004).
The most recent determinations of the amounts of dust produced in Cas A were carried out by Barlow et al. (2010) and Arendt et al. (2014). The warm dust emission at 5−35 μm observed by Spitzer is mostly generated by ~0.04 M⊙ of mainly silicate dust. Most of the dust mass is associated with a colder dust component that dominates the broadband emission at wavelengths ≳60 μm and is associated with the Si II] 34.82 μm line emission. Because of the lack of any distinguishing dust emission features at these wavelengths, its composition could not be uniquely determined and its mass was estimated to be <0.1M⊙. This cold dust component has probably not yet encountered the reverse shock. Its distribution is very different from the warm dust that is spatially coincident with reverse shock features. We assume that the dust, initially present solely in the clumps, does not make the clumps affect the dynamics of the reverse shock.
The ejecta clouds become visible due to reverse shock heating and they constitute the bright main shell of the remnant. Optical maps show that the diameter of the ejecta clumps, D = 2Rcloud, is in the range 0.2−1.0″ (Fesen et al. 2011), which corresponds to (1−5) × 1016 cm at a distance of 3.4 kpc1. These clumps are bigger than the knots located outside the main shell of the remnant, at or ahead of the forward shock front (Fesen et al. 2006; Hammell & Fesen 2008), whose size is typically lower than ~1015 cm (Fesen et al. 2011). Kamper & van den Bergh (1976) and van den Bergh & Kamper (1985) found that optical clumps brighten up and gradually fade with time, and the number of clouds visible at any time is described well by an exponential decay that has an e-folding time of around 25 yr (Kamper & van den Bergh 1976). We adopt as a representative cloud size the intermediate value 2Rcloud = 1.5 × 1016 cm ≃ 0.005 pc, which provides a cloud lifetime (see below) that is consistent with the aforementioned determination from Kamper & van den Bergh (1976).
When the reverse shock encounters an ejecta cloud, it generates a cloud shock which propagates into the cloud with velocity 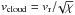 . The clumps heated up by the shock become visible before fading gradually away. The timescale for this process is correlated to the time required by the cloud shock to reach the opposite side of the clump. This latter time is given by twice the cloud crushing time, tcc ≡ Rcloud/vcloud (Klein et al. 1994), which in addition provides an indication of the dynamical timescale for shock-induced cloud fragmentation.
. The clumps heated up by the shock become visible before fading gradually away. The timescale for this process is correlated to the time required by the cloud shock to reach the opposite side of the clump. This latter time is given by twice the cloud crushing time, tcc ≡ Rcloud/vcloud (Klein et al. 1994), which in addition provides an indication of the dynamical timescale for shock-induced cloud fragmentation.
From our calculated value vr ~ 1600 km s-1, we obtain vcloud = 160 km s-1, which gives 2tcc = 2Rcloud/vcloud = 30 yr, in agreement with the lifetime of the Cas A FMKs as deduced from optical observations (Kamper & van den Bergh 1976, see above). The physical properties of Cas A are summarized in Table 1. Figure 5 shows a schematic illustration of the propagation of the reverse shock into the smooth ejecta and through an ejecta clump.
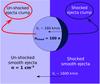 |
Fig. 5 Schematic illustration of the propagation of the reverse shock (velocity vr ~ 1600 km s-1) into the smooth ejecta and through an ejecta clump. The reverse shock hitting the clump generates a cloud shock that propagates with velocity |
The ejecta clouds contain 80%–90% of oxygen, with a small contribution from Ne, Si, S, Ar, and negligible abundances of hydrogen and helium (Docenko & Sunyaev 2010). Optical observations have revealed some knots made of almost pure oxygen, dubbed [O iii] filaments (Chevalier & Kirshner 1979). This justifies our simplifying assumption of ejecta clouds with a composition of 100% oxygen.
We assume that all the dust resides in the oxygen rich clumps and that it is composed of silicates (MgSiO3) and amorphous carbon. Because the initial dust grain size distribution of the newly formed dust is not determined well, as a test case we adopt the classical MRN power-law expression (Mathis et al. 1977): g(a) ~ a-3.5 and amin<a<amax, with amin = 50 Å and amax = 2500 Å. The quantity g(a) represents the number of grains with radius a in the interval da.
For the smooth (X-ray emitting) ejecta, we assume a composition of O, Ne, Mg, Si, S, Ar, and Fe as determined by Hwang & Laming (2012) and reported in their Table 2. This work provides the elemental masses with respect to oxygen, Mi/MO. To convert them to Mi/MH, elemental masses with respect to hydrogen, we use the equation Mi/MH = (Mi/MO)(MO/MH), where the protosolar MO/MH = 8.59 × 10-3 is given by Table 1.4 in Draine (2011) and based on Asplund et al. (2009). The values of all masses are reported in Table 2.
Elemental masses in the smooth ejecta of Cas A.
3.2. Temperature evolution of the ejecta
When a shock propagates through a gas, it heats the gas located right beyond the shock front up to a temperature T given by the following expression: 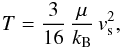 (33)where μ is the mean molecular mass per particle and vs is the velocity of the shock. For a mixture of neutral elements, μ is written as
(33)where μ is the mean molecular mass per particle and vs is the velocity of the shock. For a mixture of neutral elements, μ is written as 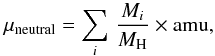 (34)where amu is the atomic mass unit. For a mixture of ionized elements in different ionization states j, we have
(34)where amu is the atomic mass unit. For a mixture of ionized elements in different ionization states j, we have 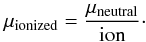 (35)The quantity ion represents the total number of particles (nuclei plus electrons) per hydrogen atom and can be calculated from the following relation:
(35)The quantity ion represents the total number of particles (nuclei plus electrons) per hydrogen atom and can be calculated from the following relation: ![\begin{equation} \label{ion_eq} {\rm ion} = \sum_i\, \frac{{N}_i}{N_{\rm H}}\, \left[\sum_j\, f_{ij} \left(1+N_{\rm e}^{ij} \right) \right] . \end{equation}](/articles/aa/full_html/2016/06/aa27350-15/aa27350-15-eq181.png) (36)The index i runs over the elemental species and the index j runs over the ionization states. For each species i, the quantity Ni/NH = (Mi/MH)/(⟨ mi ⟩/amu) represents the number of atoms per H atom, where ⟨ mi ⟩/amu is the mean mass in atomic units. The number of electrons ejected per atom i in the ionization state j is given by
(36)The index i runs over the elemental species and the index j runs over the ionization states. For each species i, the quantity Ni/NH = (Mi/MH)/(⟨ mi ⟩/amu) represents the number of atoms per H atom, where ⟨ mi ⟩/amu is the mean mass in atomic units. The number of electrons ejected per atom i in the ionization state j is given by 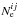 and the fraction of such atoms by fij.
and the fraction of such atoms by fij.
In the ejecta clouds, the rise of temperature is due to the cloud shock, which has velocity vcloud = 160 km s-1. As mentioned above we assume a composition of pure oxygen, and an ionization state of +2. This implies that ion = 1 + 2 = 3 and μ = 5.34 × amu = 8.9 × 10-24 g. Using the above equations, we obtain the cloud temperature Tcloud ~ 3 × 106 K. This is consistent with the results from Sutherland & Dopita (1995) and Borkowski & Shull (1990), who obtained temperatures of 2.75 × 106 K and 3.46 × 106 K for cloud shock velocities of 150 km s-1 and 170 km s-1, respectively.
Equation (33) assumes equilibration between the ion and electron temperatures. The work of Itoh (1981) on the emission from oxygen-rich supernova ejecta (the case of Cas A) shows that in the immediate post-shock region the electron temperature, Te, is much lower than the ion temperature, Tion. Figure 2 however indicates that Te and Tion equilibrate over a scale length of ~4 × 1013 cm, which corresponds to only ~0.27% of the diameter of our clumps. This is confirmed by recent shock calculations performed for cases comparable to those studied here, which show that both the equilibration and the cooling length scales are very short, ~2 × 1013 cm at most even for the case of Te/Tion = 0.01 at the shock front (J. Raymond, priv. comm.). Such results imply that temperature equilibration occurs quickly; these results are in agreement with van Adelsberg et al. (2008) and Ghavamian et al. (2007), who both find that full equilibration occurs in non-radiative shocks (not necessarily strongly cooling) for shock velocities below ~400 km s-1. The assumption of temperature equilibration appears therefore justified in the present case.
The shock propagating into the smooth ejecta is the reverse shock with velocity vr = 1600 km s-1. To calculate the resulting temperature of the shocked smooth ejecta, we would need the ionization state of the pre-shock gas, which is pre-ionized by the incoming reverse shock. Unfortunately, there are no determinations of such an ionization state. To make an estimate, we use the results from the photo-ionization and shock modelling code Mappings III (Allen et al. 2008). For the elemental composition given by Hwang & Laming (2012), we adopt for each element the ionization state calculated by Mappings III for a gas of solar abundances, with number density n = 1 cm-3, pre-ionized by a shock with velocity of 1000 km s-1 (Model M). We adopt a transverse magnetic field B = 1 μG, to be consistent with the model of Sutherland & Dopita (1995) who assumed this value for the ejecta clumps; we make the assumption that the pre-shock magnetic field is the same in both the clumps and smooth ejecta. Such a magnetic field does not affect the temperature or dynamics, but it would imply betatron acceleration of the charged grains, which would affect the cloud shock. In a following study, we will investigate the modifications of the velocity profiles of the grains induced by betatron acceleration and their impact on the dust sputtering process.
The set of parameters described above is the closest match to Cas A among those available from the code. The resulting ionization states are the following: O6+, Ne5+, Mg7+, Si8+, S8+, Ar6+, Fe7+. Because the maximum shock velocity considered by Mappings III is lower than the velocity of the reverse shock in Cas A (vr = 1600 km s-1), we expect that the resulting ionization states are underestimated. With these parameters, the temperature of the shocked smooth ejecta from Eq. (33) is Tsmooth = 1.38 × 108 K. Even if we consider the extreme (and unrealistic) case of complete pre-ionization of the pre-shock gas, the temperature is only reduced to 1.02 × 108 K.
It should be noted that in the smooth ejecta the hypothesis of equal ion and electron temperatures may not be fully justified. Yamaguchi et al. (2014) show that in the reverse shock of Tycho there is some electron heating via ion-electron Coulomb collisions, but that it is weak. The results from van Adelsberg et al. (2008) would indicate that the electron-to-ion temperature ratio, β ≡ Te/Tion, has a value of ~3−8% for a shock speed of 1600 km s-1. In Cas A the electron temperature derived from X-ray observations is ~1.7 × 107 K (kBT = 1−2 eV; Hwang & Laming 2009). This number combined with the values of β reported above gives Tion = (2−5.7) × 108 K, which is higher than the temperature derived from Eq. (33). The implications of this situation will be evaluated in a follow-up work, while for the present study we maintain the hypothesis of ion-electron temperature equilibration in the smooth ejecta.
The temperature of the gas in which the dust is embedded determines the type and level of processing of the grains. It is therefore important to evaluate the cooling of both the cloud and smooth ejecta. To determine the cooling time as a function of temperature, τcool(T), we adopt the formalism from Sutherland & Dopita (1993). For a gas composed of only one elemental species in a single ionization state, this gives 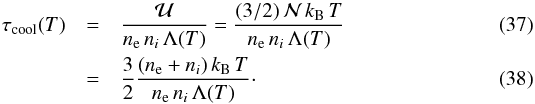 In this set of equations,
In this set of equations, 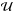 is the internal energy, Λ(T) the cooling function and
is the internal energy, Λ(T) the cooling function and 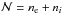 , where ne and ni are the number density of electrons and ions, respectively. Because ne = Ani, where A is the number of electrons ejected from each atom (i.e. its ionization state), Eq. (40) can be rewritten in a more general form as
, where ne and ni are the number density of electrons and ions, respectively. Because ne = Ani, where A is the number of electrons ejected from each atom (i.e. its ionization state), Eq. (40) can be rewritten in a more general form as 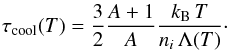 (39)We have assumed a composition of pure oxygen for the ejecta clumps, which implies that ni = nO = ncloud. For the cooling function of the shocked ejecta clouds, we use the values computed by Sutherland & Dopita (1995, see their Fig. 2) for vcloud = 150 km s-1, which is very close to our own value of 160 km s-1. To our knowledge, this study provides the only available estimate of the cooling function of an oxygen-rich shocked gas. To determine ne, we would need the oxygen ionization structure for a 160 km s-1 cloud shock, which is not available. Instead, we use the ionization structure of the 200 km s-1 shock model from Sutherland & Dopita (1995) shown in their Fig. 3 (lower panel), which gives O5+ as the dominant ionization state. This results in A = 5, ne = 5ni and
(39)We have assumed a composition of pure oxygen for the ejecta clumps, which implies that ni = nO = ncloud. For the cooling function of the shocked ejecta clouds, we use the values computed by Sutherland & Dopita (1995, see their Fig. 2) for vcloud = 150 km s-1, which is very close to our own value of 160 km s-1. To our knowledge, this study provides the only available estimate of the cooling function of an oxygen-rich shocked gas. To determine ne, we would need the oxygen ionization structure for a 160 km s-1 cloud shock, which is not available. Instead, we use the ionization structure of the 200 km s-1 shock model from Sutherland & Dopita (1995) shown in their Fig. 3 (lower panel), which gives O5+ as the dominant ionization state. This results in A = 5, ne = 5ni and 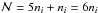 . Docenko & Sunyaev (2010) performed their own calculation of the post-shock oxygen ion distribution for a 200 km s-1 cloud shock obtaining results similar to Sutherland & Dopita (1995), but only if the spectroscopic symbols in the original figure are increased by unity. Docenko & Sunyaev (2010) assumed a misprint. In this case, the dominant ionization state would be O6+, which leads to A = 6, ne = 6ni, and
. Docenko & Sunyaev (2010) performed their own calculation of the post-shock oxygen ion distribution for a 200 km s-1 cloud shock obtaining results similar to Sutherland & Dopita (1995), but only if the spectroscopic symbols in the original figure are increased by unity. Docenko & Sunyaev (2010) assumed a misprint. In this case, the dominant ionization state would be O6+, which leads to A = 6, ne = 6ni, and 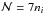 .
.
 |
Fig. 6 Cooling time as a function of temperature for a shocked O-rich ejecta cloud in Cas A, calculated from Eq. (40). |
For our shocked ejecta cloud, the number density to include in Eq. (39) is that in the immediate post-shock gas, which is increased by a factor of 4 with respect to the unshocked gas. As a result, for the number density of the shocked cloud we have 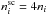 . The cooling time of a shocked ejecta cloud is then given by Eq. (39) modified as follows
. The cooling time of a shocked ejecta cloud is then given by Eq. (39) modified as follows 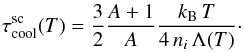 (40)The cooling time
(40)The cooling time 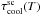 from Eq. (40) is shown in Fig. 6 assuming O5+ as the dominant ionization state. If in the plot showing the oxygen ionization structure for the 200 km s-1 cloud shock model (Fig. 3, lower panel in Sutherland & Dopita 1995) there is indeed the misprint indicated by Docenko & Sunyaev (2010), the dominant ionization state for oxygen would be O6+. In this case, the cooling time for the shocked cloud is given again by Eq. (40) with the same cooling function Λ(T), but adopting A = 6. The curves for O5+ and O6+ are indistinguishable (the ratio between the two is 3%), so we consider negligible the variation induced by an eventual misprint and follow Sutherland & Dopita (1995) adopting O5+ as the dominant ionization state produced by a 200 km s-1 shock propagating into an oxygen-rich cloud. To determine the temporal evolution of the gas temperature in the shocked cloud, we have to solve the following differential equation:
from Eq. (40) is shown in Fig. 6 assuming O5+ as the dominant ionization state. If in the plot showing the oxygen ionization structure for the 200 km s-1 cloud shock model (Fig. 3, lower panel in Sutherland & Dopita 1995) there is indeed the misprint indicated by Docenko & Sunyaev (2010), the dominant ionization state for oxygen would be O6+. In this case, the cooling time for the shocked cloud is given again by Eq. (40) with the same cooling function Λ(T), but adopting A = 6. The curves for O5+ and O6+ are indistinguishable (the ratio between the two is 3%), so we consider negligible the variation induced by an eventual misprint and follow Sutherland & Dopita (1995) adopting O5+ as the dominant ionization state produced by a 200 km s-1 shock propagating into an oxygen-rich cloud. To determine the temporal evolution of the gas temperature in the shocked cloud, we have to solve the following differential equation: 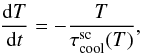 (41)with
(41)with 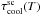 from Eq. (40). The solution of the equation is shown in Fig. 7. Because of the extreme metallicity, it takes only six months for the temperature of the ejecta in the clouds to go from ~3 × 106 K to 300 K. While the cloud shock progresses through the clump, the layer beyond the shock front with a temperature close to ~105 K, i. e. high enough for thermal sputtering to be effective, has a thickness of ~2 × 1014 cm; this layer is only 1.4% of the diameter of the clump. The small amount of dust in such a thin layer allows us to neglect thermal sputtering and to assume that, while residing in the ejecta clumps, the dust is affected only by inertial (kinetic) sputtering (see Sect. 4).
from Eq. (40). The solution of the equation is shown in Fig. 7. Because of the extreme metallicity, it takes only six months for the temperature of the ejecta in the clouds to go from ~3 × 106 K to 300 K. While the cloud shock progresses through the clump, the layer beyond the shock front with a temperature close to ~105 K, i. e. high enough for thermal sputtering to be effective, has a thickness of ~2 × 1014 cm; this layer is only 1.4% of the diameter of the clump. The small amount of dust in such a thin layer allows us to neglect thermal sputtering and to assume that, while residing in the ejecta clumps, the dust is affected only by inertial (kinetic) sputtering (see Sect. 4).
To estimate the temperature evolution of the shocked smooth ejecta, we used Mappings III with appropriate modifications of the input parameters, to obtain the closest match with the observed properties of Cas A. The calculations are performed under non-equilibrium ionization (NEI) conditions. We adopted the elemental composition determined by Hwang & Laming (2012) for the smooth ejecta in Cas A and run the code for a shock with the velocity of the reverse shock, vr = 1600 km s-1. This value is above the nominal limit of the code (1000 km s-1) and is expected to increase the pre-ionization state of the pre-shock gas. However, we have shown early on in this section that even a complete pre-ionization does not significantly modify the resulting post-shock temperature. We consider therefore that the calculation could provide a reasonable estimate of the temperature evolution for the faster shock as well. The result is shown in Fig. 8 and is consistent with our previous calculation. With the same ejecta composition but a shock velocity of 1000 km s-1, we obtain a post-shock temperature of the order of 107 K, which is consistent with the value of the electron temperature derived from X-ray observations (Hwang & Laming 2009). The same calculations performed using the updated code Mappings IV2, give very similar results. As can be seen in Fig. 8, in both cases, after a phase of rapid cooling (~10 yr) the temperature remains fairly constant at ~108 K and ~107 K for more than 104 yr before dropping abruptly.
 |
Fig. 7 Temperature evolution as a function of time for a shocked O-rich ejecta cloud in Cas A, calculated from Eq. (41) using the cooling time from Eq. (40). |
 |
Fig. 8 Temperature evolution as a function of time in the shocked smooth ejecta, calculated for two shock velocities under non-equilibrium ionization (NEI) conditions, using the Mappings III code. |
4. Grain destruction by the reverse shock: Kinetic sputtering
The rate at which a dust grain is sputtered as a result of its relative motion through a gas, a process also known as kinetic or inertial sputtering, is given by the sum over colliding gas species i (e.g. Dwek & Arendt 1992), i.e. 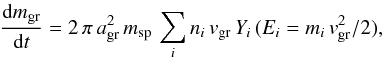 (42)where agr is the grain radius; msp is the average mass of the atom/molecule sputtered from the grain, vgr the grain velocity relative to the ambient gas, which is equivalent to the velocity of the incident projectile seen by a target grain considered stationary; ni is the number density of the different gas species; mi is their atomic mass; and Yi, the sputtering yield, is the number of atoms/molecules ejected from the grain per incident projectile of composition i (Tielens et al. 1994; Nozawa et al. 2006). The factor of 2 in Eq. (42) corrects the yield, which is measured for normally incident projectiles on a target material for a distribution of incident angles.
(42)where agr is the grain radius; msp is the average mass of the atom/molecule sputtered from the grain, vgr the grain velocity relative to the ambient gas, which is equivalent to the velocity of the incident projectile seen by a target grain considered stationary; ni is the number density of the different gas species; mi is their atomic mass; and Yi, the sputtering yield, is the number of atoms/molecules ejected from the grain per incident projectile of composition i (Tielens et al. 1994; Nozawa et al. 2006). The factor of 2 in Eq. (42) corrects the yield, which is measured for normally incident projectiles on a target material for a distribution of incident angles.
 |
Fig. 9 Sputtering yields of silicate (left column) and amorphous carbon grains as a function of the relative grain-gas velocity (top row) and corresponding kinetic energy for the incident projectiles: oxygen, present in the ejecta clouds, helium, and hydrogen. The sputtering yields were calculated using Eq. (11) in Nozawa et al. (2006). |
For the sputtering yield Yi we adopt the expression given by Eq. (11) in Nozawa et al. (2006). This is the same provided by Tielens et al. (1994) except for the different formula used for the function αi, which appears in the yield and allows for a better agreement with sputtering data (for details see Nozawa et al. 2006; Tielens et al. 1994, and references therein).
For simplicity, we assume that all the grains in the SN ejecta are made of silicates (in the form of MgSiO3) and amorphous carbon (see Sect. 3.1). For these two kinds of grains, we adopt the sputtering parameters summarized in Table 3. The quantities M and Z are the atomic mass and atomic number of the target material, respectively, U0 is the surface binding energy, defined as the minimum energy which is necessary to transfer into the target to remove an atom from the top surface layer. The constant K enters in one of the terms of the expression for the sputtering yield Yi(E) and has been determined via a comparison with laboratory experiments. Following Tielens et al. (1994) and Nozawa et al. (2006), for MgSiO3 we adopt the sputtering parameters of SiO2, which can be considered a good representative of silicates and for which experimental sputtering data are available. The mass of the ejected species is given by the average value msp = 23 amu. For carbonaceous grains, we assume a composition of pure carbon, thus there is no hydrogenation following collisions because oxygen is the only projectile present in the clouds. As a consequence, the only sputtered atoms are carbon atoms, therefore, msp = 12 amu.
Figure 9 presents the sputtering yield of amorphous carbon (Am C) and silicate (MgSiO3) grains as a function of the velocity and kinetic energy of the incident projectiles, calculated using Eq. (11) in Nozawa et al. (2006).
Dust grain properties for sputtering calculations.
Equation (42) assumes that the thermal velocities of the colliding atoms are negligible compared to the grain’s velocity. The rate at which a grain slows down as a result of collisional drag forces is given by (dvgr/ dt) = Fdrag/mgr. For grains moving through a cold gas (2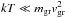 ), the plasma correction to the drag force (Baines et al. 1965, Sect. 6) can be neglected and Fdrag is expressed as
), the plasma correction to the drag force (Baines et al. 1965, Sect. 6) can be neglected and Fdrag is expressed as 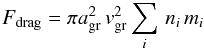 (43)so that
(43)so that 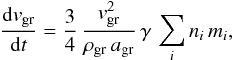 (44)where ρgr is the mass density of the grain.
(44)where ρgr is the mass density of the grain.
Combining Eqs. (42) and (44) we can write the erosion rate of the dust mass as it slows down through the gas as 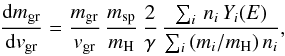 (45)which can readily be solved for the grain mass mgr(vgr), i.e.
(45)which can readily be solved for the grain mass mgr(vgr), i.e. ![\begin{equation} \label{eq:m_m} \frac{m_{\rm gr}(v_{\rm gr})}{m_{\rm gr}(0)} = \exp\left[\frac{2}{\gamma}\, \frac{m_{\rm sp}}{m_{\rm H}}\, \int_{v_{\rm gr}(0)}^{v_{\rm gr}(t)}\, \frac{\sum_i n_i\, Y(E)}{\sum_i \, (m_i/m_{\rm H})\, n_i}\, \frac{{\rm d}v_{\rm gr}}{v_{\rm gr}}\right], \end{equation}](/articles/aa/full_html/2016/06/aa27350-15/aa27350-15-eq266.png) (46)where mgr(0) and vgr(0) are the initial grain mass and velocity, respectively, and mgr(vgr) is the grain’s mass at velocity vgr(t).
(46)where mgr(0) and vgr(0) are the initial grain mass and velocity, respectively, and mgr(vgr) is the grain’s mass at velocity vgr(t).
The column density of gas traversed by a grain is 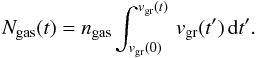 (47)Using Eq. (44), we obtain that
(47)Using Eq. (44), we obtain that ![\begin{eqnarray} \label{eq:dng_dv1} \frac{{\rm d}N_{\rm gas}(v_{\rm gr})}{{\rm d}v_{\rm gr}} & = & \left[\frac{{\rm d}N_{\rm gas}(v_{\rm gr})}{{\rm d}t}\right]\, \left[\frac{{\rm d}(v_{\rm gr})}{{\rm d}t}\right]^{-1} ,\\ \nonumber & = & (n_{\rm gas}\, v_{\rm gr})\, \frac{4}{3 \gamma}\, \frac{a_{\rm gr}(t)}{v_{\rm gr}^2}\, \frac{\rho_{\rm gr}}{\sum_i \rho_i} \end{eqnarray}](/articles/aa/full_html/2016/06/aa27350-15/aa27350-15-eq271.png) (48)where ρi ≡ nimi. Defining a characteristic slowing down time, τsd as
(48)where ρi ≡ nimi. Defining a characteristic slowing down time, τsd as ![\begin{equation} \label{eq:taud} \tau_{\rm sd} \equiv \frac{4}{3}\, \left[\frac{a_{\rm gr}(0)}{v_{\rm gr}(0)}\right]\, \left(\frac{\rho_{\rm gr}}{\sum_i \rho_i}\right), \end{equation}](/articles/aa/full_html/2016/06/aa27350-15/aa27350-15-eq274.png) (49)we obtain that
(49)we obtain that ![\begin{equation} \label{eq:dng_dv2} \frac{{\rm d}N_{\rm gas}(v_{\rm gr})}{{\rm d}v_{\rm gr}} = \frac{1}{\gamma}\left[\frac{a_{\rm gr}(t)}{a_{\rm gr}(0)}\right]\, \left[\frac{v_{\rm gr}(0)}{v_{\rm gr}(t)}\right]\, \tau_{\rm sd}\, \sum_i n_i , \end{equation}](/articles/aa/full_html/2016/06/aa27350-15/aa27350-15-eq275.png) (50)where ngas ≡ ∑ ini. Since [ agr(t) /agr(0) ] = [ mgr(t) /mgr(0) ] 1/3, Eq. (50) can be integrated to give
(50)where ngas ≡ ∑ ini. Since [ agr(t) /agr(0) ] = [ mgr(t) /mgr(0) ] 1/3, Eq. (50) can be integrated to give 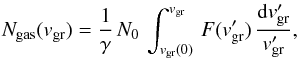 (51)where
(51)where ![\begin{equation} \label{fv} F(v_{\rm gr}') = \exp\left[\frac{2}{3\gamma}\, \frac{m_{\rm sp}}{m_{\rm H}}\, \int_{v_{\rm gr}(0)}^{v_{\rm gr}'}\,\frac{\sum_j n_j\, Y(E)}{\sum_i (m_i/m_{\rm H})\, n_i}\, \frac{{\rm d}v}{v}\right] \end{equation}](/articles/aa/full_html/2016/06/aa27350-15/aa27350-15-eq279.png) (52)and where N0 is the column density, defined as
(52)and where N0 is the column density, defined as 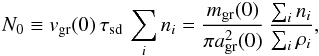 (53)so that the mass of gas contained within the volume swept up by the grain is equal to the initial mass of the grain if it was not eroded by the gas.
(53)so that the mass of gas contained within the volume swept up by the grain is equal to the initial mass of the grain if it was not eroded by the gas.
Figure 10 shows which fraction of the initial mass of a dust grain survives the effect of kinetic sputtering. The mass fraction, represented as a function of the initial velocity of the grain vgr(0), has been calculated after the grain has slowed down to zero, assuming ngas = ncloud = 100 cm-3. The mass fraction does not depend on the initial grain size, since the same atoms that slow the grain down are also eroding it by sputtering.
 |
Fig. 10 Mass fraction of a carbon (top panel) and MgSiO3 (bottom panel) dust grain surviving the erosion by kinetic sputtering as a function of its initial velocity vgr(0), as it traverses a gas of pure H, He, and O composition with density ngas = ncloud = 100 cm-3. The vertical line indicates the initial grain velocity for Cas A, vgr(0) = vcloud = 160 km s-1. |
 |
Fig. 11 Contour plot showing the time tesc required by a dust grain with initial velocity vgr(0) = 160 km s-1 to traverse a column density of gas Ngas, as a function of the grain radius agr. |
To calculate the time tesc required by a dust grain to traverse a column density of gas Ngas, we use the expression dNgas = ngasvgr(N) dt, from which we derive 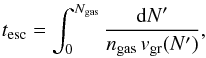 (54)where we obtained vgr(N′) numerically from Eq. (51). Figure 11 is a contour diagram depicting tesc as a function of the dust grains radius and column density of gas traversed. We calculated the curves for the initial velocity vgr(0) = vcloud = 160 km s-1. This is appropriate for Cas A, where the cloud shock is highly radiative, therefore the post-shock gas is compressed by a factor ≫4 and the relative gas-grain velocity is close to vcloud (in an adiabatic shock the relative velocity would be (3/4) vcloud).
(54)where we obtained vgr(N′) numerically from Eq. (51). Figure 11 is a contour diagram depicting tesc as a function of the dust grains radius and column density of gas traversed. We calculated the curves for the initial velocity vgr(0) = vcloud = 160 km s-1. This is appropriate for Cas A, where the cloud shock is highly radiative, therefore the post-shock gas is compressed by a factor ≫4 and the relative gas-grain velocity is close to vcloud (in an adiabatic shock the relative velocity would be (3/4) vcloud).
Given an initial dust grain velocity, vgr(0), the amount of destruction taking place in a clump depends on the column density traversed by the grains after the passage of the shock, which in turns depends on the size of the grains and their location in the cloud. The grains, because of their large inertia, move ballistically through the shock, slipping through the gas at a relative velocity close to vcloud. We assume that the shock is planar, so that all the shocked dust grains move perpendicular to the shock front. Big grains sitting close to the edge of the clumps are able to escape without experiencing substantial sputtering, while smaller grains located deeper inside the cloud are eroded and/or stopped before reaching the surface.
In Appendix B we report an estimate of the amount of kinetic sputtering occurring in the clumps based on a statistical approach. However, this approach is only valid for the largest grain sizes. A Monte Carlo approach is required to properly evaluate the effect of inertial sputtering in the ejecta clouds, which takes all grains sizes and positions inside the clumps into account. Methods and results of our simulation are discussed in Sect. 7.
5. Clump survival: Instabilities and evaporation
Inertial sputtering occurs in the ejecta clouds and the corresponding amount of destruction depends on how long the grains stay inside the clouds. In the present case, we assume that the residence time depends on three phenomena. The first is the capability of the grains to escape from the cloud owing to their ballistic velocities; we discussed this in Sect. 4. The two other phenomena that we consider are the dynamical fragmentation of the clouds and the thermal evaporation of the clouds, which we discuss below.
The cloud crushing time, tcc ≡ Rcloud/vcloud (Klein et al. 1994), provides an indication of the dynamical time required for the cloud shock to fragment the cloud. For Rcloud = 7.5 × 1015 cm and vcloud = 160 km s-1, we obtain tcc = 15 yr. For the destruction time, tdest, we adopt the value of 3.5tcc found by Klein et al. (1994) for density contrasts between 10 and 100 (we have 100). This destruction time is defined as the time at which the mass of the core of the cloud has been reduced to a fraction 1/e of the initial cloud mass; it is assumed that the cloud develops a core-plume structure following the passage of the shock. We assume that after tdest = 3.5tcc the ejecta cloud is destroyed and dispersed. At that moment, the fresh dust still residing in the cloud will have been released into the smooth ejecta.
 |
Fig. 12 Comparison between timescales relevant for the processing of carbon (left panel) and silicate (right panel) dust grains in an ejecta cloud: cloud destruction time tdest, cloud evaporation time tsat, calculated for two temperatures of the gas surrounding the clouds, and dust escape time tesc, calculated for two grain sizes. Both tesc and tdest has been calculated assuming vgr(0) = vcloud = 160 km s-1. All timescales are represented as a function of the diameter of the clump. The vertical line indicates the diameter adopted for the ejecta clouds in Cas A. See text for details. |
A competing process for the disruption of the clumps is thermal evaporation. Thermal evaporation occurs because electron thermal conduction transfers heat from the hot smooth ejecta to the outer layers of the colder clouds. The heated material has an excess of pressure, which then drives an outflow. Cowie & McKee (1977) examined the steady evaporation of spherical clouds including the effects of saturation of the conductive heat flux. Saturation of the heat flux occurs when the heat flux predicted based on the Spitzer conductivity and the temperature gradient exceeds that which can be carried by the electrons given their density and thermal speed. Dalton & Balbus (1993) found an analytical solution for cloud evaporation that includes cases of highly saturated conduction which applies for the Cas A knots. Dalton & Balbus (1993) ignore radiative cooling, which may be important at the high densities and enormous cooling coefficients in the Cas A clouds. However, the contribution of radiative processes decreases progressively with increasing saturation. For the present work, we decided to focus on the effects of saturation and we will include radiative evaporation in a follow-up paper. Using the results from Dalton & Balbus (1993) for the relation between the saturation parameter, σ0, and mass loss rate, Ṁ and taking the highly saturated limit we find 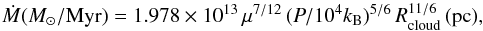 (55)where P is the pressure in the hot medium, Rcloud is the cloud radius (in pc), and μ is the mean mass per particle in g. There is no explicit dependence on temperature, although there is a dependence on pressure, which depends on the temperature if density is held constant as it is in Fig. 11. For a cloud of pure O5+, μ = 4.45 × 10-24 g. We take as the evaporation timescale the quantity tsat = Mcloud/Ṁ, which is then written as
(55)where P is the pressure in the hot medium, Rcloud is the cloud radius (in pc), and μ is the mean mass per particle in g. There is no explicit dependence on temperature, although there is a dependence on pressure, which depends on the temperature if density is held constant as it is in Fig. 11. For a cloud of pure O5+, μ = 4.45 × 10-24 g. We take as the evaporation timescale the quantity tsat = Mcloud/Ṁ, which is then written as 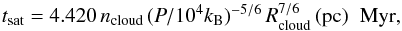 (56)where ncloud is the cloud space density (in cm-3). The high pressure in the remnant reduces the evaporation timescale well below typical ISM values, but it is still generally larger than the cloud crushing time in this context. Thus the cloud is torn apart before it can evaporate, although evaporation could play a role in destroying some cloud fragments.
(56)where ncloud is the cloud space density (in cm-3). The high pressure in the remnant reduces the evaporation timescale well below typical ISM values, but it is still generally larger than the cloud crushing time in this context. Thus the cloud is torn apart before it can evaporate, although evaporation could play a role in destroying some cloud fragments.
The timescales discussed above are shown in Fig. 12 as a function of the diameter of the clouds, for carbon and silicate grains. We calculated the evaporation time tsat for the two temperatures T = 107 K and T = 108 K. For the escape time tesc, the two curves correspond to two grain sizes: 2500 Å (the upper limit of our grain size distribution, see Sect. 7) and 1000 Å, an intermediate value. For each cloud diameter, the value of tesc in the figure represents the time required to cross that diameter, which is the maximum path that a grain has to traverse to escape the cloud. Therefore, tesc is the maximum escape time. We calculated both tesc and tdest assuming vgr(0) = vcloud = 160 km s-1, where vgr(0) is the initial velocity of the grains. The value 160 km s-1 is the cloud shock velocity corresponding to the constant reverse shock velocity in the ejecta core, which is also the lowest velocity reached by the reverse shock in Cas A (see Fig. 4). From the definition of tdest = 3.5tcc = Rcloud/vcloud and tesc (Eq. (54)) it follows, therefore, that for each cloud size, the values of tdest and tesc shown in Fig. 12 are upper limits.
From Fig. 12 and from the considerations above it follows that, for Cas A, the trade is between the escape time and the destruction time. For both carbon and silicate dust, grains that are sufficiently big are able to escape before the cloud is disrupted, even if they are located far from the surface. These fugitive grains experience thermal sputtering in the hot phase of the ejecta before their counterparts ejected at time tdest. The injection of dust in the hot medium is a continuous process depending on the grain size and position inside the clouds. To properly investigate such a process, an analytical approach is not applicable, therefore we decided to perform a Monte Carlo simulation; this is described in Sect. 7.
6. Grain destruction by the reverse shock: Thermal sputtering
After a dust grain is ejected from a cloud, because of its ballistic velocity or because of the destruction of the cloud, it will find itself in the smooth hot ejecta. Here the temperature is much higher than in the clouds, therefore the dominant erosion mechanism is thermal sputtering, where the velocity of the ions is determined by the temperature of the shocked gas (thermal motion). The effect of thermal sputtering has been calculated for two temperatures of the smooth ejecta: T ~ 108 K (from Eq. (33)) and T ~ 107 K (for comparison).
The variation of the grain radius, agr, due to thermal sputtering is given by Eq. (4.20) in Tielens et al. (1994), 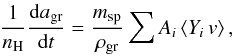 (57)where ⟨ Yiv ⟩ is the sputtering yield of ion i averaged over the Maxwellian distribution (Yi as in Sect. 4), v is the velocity of the ions, nH is the hydrogen number density of the smooth ejecta, and Ai is the abundance of ion i with respect to hydrogen. As discussed in Sect. 3.2, we assume for the smooth ejecta a mixture of O, Ne, Mg, Si, S, Ar, and Fe as determined by Hwang & Laming (2012). Because of the compression due to the shock, the density of the smooth ejecta must be increased by a factor of four with respect of its pre-shock value. The Monte Carlo approach used to evaluate thermal sputtering across the remnant is described in Sect. 7.
(57)where ⟨ Yiv ⟩ is the sputtering yield of ion i averaged over the Maxwellian distribution (Yi as in Sect. 4), v is the velocity of the ions, nH is the hydrogen number density of the smooth ejecta, and Ai is the abundance of ion i with respect to hydrogen. As discussed in Sect. 3.2, we assume for the smooth ejecta a mixture of O, Ne, Mg, Si, S, Ar, and Fe as determined by Hwang & Laming (2012). Because of the compression due to the shock, the density of the smooth ejecta must be increased by a factor of four with respect of its pre-shock value. The Monte Carlo approach used to evaluate thermal sputtering across the remnant is described in Sect. 7.
7. A Monte Carlo approach to evaluate kinetic and thermal sputtering: Methods and results
For each ejecta cloud, we consider a population of 3 × 106 particles of each dust grain type (carbon and silicate) with a given size distribution and homogeneously distributed over the entire volume of the cloud. We follow the journey of each particle to determine its final size (and consequently mass) as a result of kinetic sputtering (in the ejecta clumps) and thermal sputtering (in the smooth ejecta). As described in Sect. 3, we adopt the classical MRN expression for the dust grain size distribution (Mathis et al. 1977).
Following the encounter with the reverse shock, the dust grains inside the cloud acquire a relative velocity with respect to gas. This velocity decreases asymptotically to zero because of gas-grain collisions, which at the same time are responsible for the progressive erosion of the grains (kinetic sputtering). Depending on their initial size and position inside the cloud, some of the grains are able to escape into the smooth ejecta before the cloud gets disrupted. These fugitive grains therefore experience thermal sputtering for a longer time than their counterparts trapped inside the cloud.
The basic equation governing our Monte Carlo simulation, which allows us to calculate the final radius afinal of a dust grain that experienced the processing previously described, is the following: ![\begin{equation} \label{eq:a_final} a_{\rm final}(t) = K_{\rm s}(t)\,a_{\rm initial} - T_{\rm s} \times \left[\frac{1}{(t_{\rm r} + t_{\rm inj})^2} - \frac{1}{t^2}\right]\cdot \end{equation}](/articles/aa/full_html/2016/06/aa27350-15/aa27350-15-eq321.png) (58)The simulation starts when the reverse shock touches the outer layer of ejecta (α = 1, ~0.9 years after explosion, see Fig. 1), and stops when the reverse shock reaches the centre of the remnant (α = 0, ~8000 years after explosion). In Eq. (58), ainitial is the size of the grain before processing; tr is the time when the reverse shock hits an ejecta cloud located in a layer α (see Sect. 2.2); and tinj is the time interval (starting from tr) after which the grains are expelled from the clouds and injected into the smooth ejecta and is given by the relation tinj = Min(tesc, tdest). For each layer, we computed α, tesc and tdest using the value for vgr(0) = vcloud corresponding to that layer and derived from vr (see Fig. 4), and we appropriately calculated tesc from Eq. (54) for each grain size and position inside the cloud (Sect. 4).
(58)The simulation starts when the reverse shock touches the outer layer of ejecta (α = 1, ~0.9 years after explosion, see Fig. 1), and stops when the reverse shock reaches the centre of the remnant (α = 0, ~8000 years after explosion). In Eq. (58), ainitial is the size of the grain before processing; tr is the time when the reverse shock hits an ejecta cloud located in a layer α (see Sect. 2.2); and tinj is the time interval (starting from tr) after which the grains are expelled from the clouds and injected into the smooth ejecta and is given by the relation tinj = Min(tesc, tdest). For each layer, we computed α, tesc and tdest using the value for vgr(0) = vcloud corresponding to that layer and derived from vr (see Fig. 4), and we appropriately calculated tesc from Eq. (54) for each grain size and position inside the cloud (Sect. 4).
 |
Fig. 13 Density structure of the smooth ejecta as a function of the parameter α. Solid red line: density at the time tr when the layer α encounters the reverse shock (same as Fig. 2); dashed blue line: density at the time tr + 3.5tcc, when the ejecta cloud is dispersed and the dust still in there is injected into the smooth phase.Vertical line as in Fig. 1. |
The term Ks(t) is the reduction factor of the grain radius due to kinetic sputtering. We derived this term from Eq. (46) (to the power 1/3 to convert from mass to radius), where we derived the final velocity of the grain at time t, vgr(t), inverting Eq. (51), and the column density Ngr comes from inversion of Eq. (54). It is useful to remember here that the effect of kinetic sputtering is of reducing the mass of each dust grain by the same factor, regardless of its initial size (Eq. (46)). Because of the relationship between grain mass and grain radius, the same statement holds true for the grain radius as well, therefore afinal(t) /ainitial is independent from ainitial. Kinetic sputtering is switched OFF for t>tinj, when the grains leave the clouds.
The term Ts × [ ... ] accounts for the effect of thermal sputtering; this process removes a layer of equal thickness from each grain, regardless of its size. This implies of course that the smaller grains are more affected than the bigger grains. We obtain 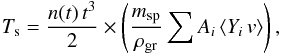 (59)where the term in parenthesis comes from Eq. (57) and the density of the expanding smooth ejecta, n(t) has been calculated from Eqs. (13) and (19). Because of the expansion of the supernova remnant, the density of the smooth ejecta changes while inertial sputtering is occurring inside the clouds. Therefore, the dust is progressively injected into a medium whose density changes continuously. Figure 13 illustrates this phenomenon. The solid red line represents the density of the smooth ejecta at the time tr when each layer α encounters the reverse shock (same curve as in Fig. 2). The dashed blue line shows the density of the same layer α but at the time tr + 3.5tcc, when the clumps in that layer are destroyed and the dust still residing in them is released into the smooth phase of the ejecta. In the outer layers (α close to one) the difference is very pronounced, and decreases progressively towards the inner layers (α close to zero). This has to be taken into account to properly evaluate the effect of thermal sputtering, which strongly depends on the density of the medium.
(59)where the term in parenthesis comes from Eq. (57) and the density of the expanding smooth ejecta, n(t) has been calculated from Eqs. (13) and (19). Because of the expansion of the supernova remnant, the density of the smooth ejecta changes while inertial sputtering is occurring inside the clouds. Therefore, the dust is progressively injected into a medium whose density changes continuously. Figure 13 illustrates this phenomenon. The solid red line represents the density of the smooth ejecta at the time tr when each layer α encounters the reverse shock (same curve as in Fig. 2). The dashed blue line shows the density of the same layer α but at the time tr + 3.5tcc, when the clumps in that layer are destroyed and the dust still residing in them is released into the smooth phase of the ejecta. In the outer layers (α close to one) the difference is very pronounced, and decreases progressively towards the inner layers (α close to zero). This has to be taken into account to properly evaluate the effect of thermal sputtering, which strongly depends on the density of the medium.
Using Eq. (58) we have evaluated the fraction of dust which is expected to survive processing while the reverse shock progresses towards the centre of the remnant, expressed in terms of the parameter α. We assume a homogeneous distribution of ejecta clouds in each layer. The fraction of surviving dust is calculated for the entire remnant, i.e. this calculation includes not only the amount of dust remaining after processing down to (but excluding) layer α, but also the unprocessed dust located inside and inwards of layer α. Because we stopped our simulation at α = 0, we did not consider further processing of the dust due to the secondary blast-wave shock which generates when the reverse shock bounces at the centre of the remnant (Truelove & McKee 1999).
 |
Fig. 14 Fraction of surviving carbon (left panel) and silicate dust (right panel) over the entire Cas A remnant as a function of α. For each value of α the curve provides the fraction of remaining dust, which is given by the grains able to survive processing located in the outer layers down to α plus the unprocessed dust residing in the inner layers. The three curves show the effect of kinetic sputtering only and of kinetic+thermal, the latter evaluated for two temperatures of the smooth ejecta: T = 107 K and T = 108 K. |
 |
Fig. 15 Surviving mass distribution as a function of the grain radius from Eq. (60), for carbon (left panel) and silicate dust (right panel), evaluated for temperatures of the smooth ejecta between 107 K and 108 K. The distributions were normalized to the total surviving dust mass (with M(α) ≡ Mresidual) so that the area under each curve equals 1. |
Our results are shown in Fig. 14, depicting the evolution of the fraction of surviving dust, Mresidual/Minit as a function of α for Am C and MgSiO3 grains. In each panel, the top curve illustrates the effect of kinetic sputtering only; this sputtering occurs inside the clumps. The two other curves refer to the combined effect of kinetic and thermal sputtering, and this latter is evaluated for two temperatures of the smooth ejecta: 107 K and 108 K. We notice that the effect of sputtering is important over the entire remnant. At the end of the processing (α = 0), kinetic sputtering has contributed significantly to particle erosion, removing 20% of the mass of carbon grains and 40% of the mass of silicate grains (note that the plots are in semi-logarithmic scale). Thermal sputtering reduces the final amount of surviving dust even more dramatically.
Silicate grains appear more fragile than carbonaceous grains. This behaviour results from the combination of different factors: their slightly higher sputtering yield; the average mass of the sputtered particles, almost twice that for Am C (23 amu versus 12 amu); and the tendency of a larger fraction of silicate grains to escape the ejecta cloud before disruption, which exposes them to thermal sputtering for a longer time.
To provide a feeling for the preferred grain sizes of the surviving dust, in Fig. 15 we plot the dust mass distribution as a function of the grain radius, which is normalized to the total surviving mass for different values of α, i.e. 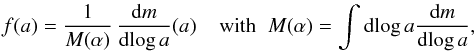 (60)where M(α) ≡ Mresidual (Fig. 14). The initial mass distribution of carbon and silicate dust (α = 1, no processed layers) is modified into the final mass distribution (α = 0, all layers processed). We evaluated the mass distribution for two temperatures of the smooth ejecta, T = 107 K and T = 108 K, and the resulting curves are almost indistinguishable. We decided to show the evolution corresponding to T = 108 K, but the curves are indeed representative of the temperature range 107–108 K. Both dust types show a progressive modification towards their final distributions, which are very similar and cover the original size range (50–2500 Å) with a small leakage down to 30 Å. The differences reflect the tendency of MgSiO3 grains to dissociate more easily than carbonaceous grains.
(60)where M(α) ≡ Mresidual (Fig. 14). The initial mass distribution of carbon and silicate dust (α = 1, no processed layers) is modified into the final mass distribution (α = 0, all layers processed). We evaluated the mass distribution for two temperatures of the smooth ejecta, T = 107 K and T = 108 K, and the resulting curves are almost indistinguishable. We decided to show the evolution corresponding to T = 108 K, but the curves are indeed representative of the temperature range 107–108 K. Both dust types show a progressive modification towards their final distributions, which are very similar and cover the original size range (50–2500 Å) with a small leakage down to 30 Å. The differences reflect the tendency of MgSiO3 grains to dissociate more easily than carbonaceous grains.
8. Discussion and conclusions
In Table 4 we report the percentage of surviving dust mass for Am C and MgSiO3 grains evaluated at two specific times during the evolution of the remnant: in 2004 (α = 0.33), when some of the astronomical observations used in this work were carried out, and after the reverse shock reached the centre of the remnant (α = 0).
In 2004, the amounts of surviving dust are of the same order of magnitude, but we can notice the difference between the two type of grains and the increased destructive effect of the higher temperature (see Fig. 14). Arendt et al. (2014) estimated the amount of dust that should be currently present in Cas A: ≲0.1 M⊙ (cold unshocked ejecta) +~0.04 M⊙ (shocked circumstellar/interstellar and ejecta regions). If we assume that this amount of dust represents the percentage of surviving mass that we calculate, we can derive the corresponding amount of dust that Cas A should have produced. Taking a representative value of 13.5%, to average over dust type and gas temperature, we obtain an initial mass of dust of about 1 M⊙, which reduces to ~0.8 M⊙ if only silicates are considered. These values are larger than the current estimate of 0.1–0.5 M⊙ (Todini & Ferrara 2001; Schneider et al. 2004; Cherchneff & Dwek 2010; Nozawa et al. 2010). The situation is similar after the reverse shock has swept the entire cavity of the SNR, reaching the centre (α = 0). This is not surprising because, after 2004, the fraction of surviving dust mass tends to reach a plateau, as shown in Fig. 14.
We compared our findings with the results from Bianchi & Schneider (2007), calculated for homogeneous (smooth) ejecta with a post-shock temperature of the order of 107–108 K expanding in a homogeneous medium, for a progenitor star of 15–25 M⊙ and a density of the surrounding ISM of 10-24 g cm-3. These values are the closest to the parameters that we adopt for Cas A: same mass range for the progenitor star and a circumstellar medium with density n0 = 2.071 H atom cm-3, corresponding to ρ0 = 3.6 × 10-24 g cm-3. We evaluated the effect of the two temperature values separately. We assume that the amount of surviving dust calculated by Bianchi & Schneider (2007), shown in their Fig. 5, refers to a mixture of amorphous carbon and Fe3O4, whose pre- and post-shock size distributions are reported in their Fig. 4.
Percentage of dust mass, Mresidual/Minit, surviving the passage of the reverse shock in Cas A, evaluated in two different stages of supernova evolution identified by the corresponding values of α.
From Fig. 5 in Bianchi & Schneider (2007) we derive that the amount of dust surviving the passage of the reverse shock is around 7.5%. This is around a factor of (1.2–2.1) lower than our findings. Some considerations have to be made when comparing these results. Bianchi & Schneider (2007) adopted for Cas A homogenous smooth ejecta only (no clumps), expanding into a uniform medium. This choice has two implications. The first is a different velocity profile for the reverse shock than the more realistic case of inhomogeneous smooth ejecta (uniform core + power-law envelope) expanding into a power-law ambient medium, which we considered in this work. The second is that the absence of oxygen-rich, fast-cooling ejecta clumps means that the dust spends all its life in the highly destructive hot smooth ejecta. In our case the grains reside for some time in the protective environment represented by the cold clumps, where they are processed by kinetic sputtering, which is less efficient in destroying the dust.
A comparison of our results with previous work is complicated by a number of factors: the different approaches (numerical or analytical) and descriptions of the supernova ejecta and ambient environment adopted in the various studies, and the different choices for the grain destruction processes, grain composition and size distribution. Following the quantitative description of Dwek (2005), Nozawa et al. (2007) calculated the dust survival in the SN ejecta, exploring various explosion energies, ambient media densities, and grain sizes and composition. Using numerical models, they find that the fraction of the dust mass destroyed ranges from 0.2 to 1.0, depending on model parameters. Using the analytical model of Truelove & McKee (1999) and the SN dust composition and size distribution of Todini & Ferrara (2001), Bianchi & Schneider (2007) found that only between 2 and 20% of the dust mass survives the passage of the reverse shock depending on the parameters adopted. Exploring a wide range of dust parameters and ambient gas density profiles, Nath et al. (2008) found that the fractional mass of grains destroyed is ≲20%, and they provide a detailed discussion of why their results are significantly lower than those found by Nozawa et al. (2007) or Bianchi & Schneider (2007). Recently, Biscaro & Cherchneff (2016) derived a dust mass survival fraction between 6 and 11%, using the analytical model of Truelove & McKee (1999) and the SN dust composition and size distribution of Biscaro & Cherchneff (2014).
All models discussed above (except Biscaro & Cherchneff 2016) assumed that the dust grains are embedded in homogeneous ejecta. Silvia et al. (2010, 2012) performed 3D numerical simulations of the interaction of planar shocks with dense spherical clumps for a range of shock velocities, clump-ejecta density contrasts, and clump metallicities. Taking the effects of cloud crushing into account, they calculated the amount of grain destruction as a function of their parameter grid using a SN dust compositions with the size distribution calculated by Nozawa et al. (2003). Silvia et al. find a dust mass survival fraction between 7 and 99% depending on the parameters of the simulation and the dust composition. These results however are not included in an evolutionary model of the reverse shock. Our surviving fractions are significantly below those of Silvia et al. (2010), although the differences in approaches prevent direct comparison.
Our estimate of the surviving dust mass fraction has to be considered a lower limit because we focused on the phenomena able to destroy the dust. We did not consider conditions which could help the dust to survive, for instance we set to zero the differential velocities that grains of different size retain once they have leaved the ejecta clouds. These velocities could allow the dust to escape the shell of shocked ejecta before suffering excessive thermal sputtering. Our present work does not include betatron acceleration of the charged grains induced by the magnetic field nor radiative evaporation of the ejecta clumps. The impact of all these phenomena on the survival of the dust will be evaluated in a follow-up paper.
An interesting fact to point out is that if most of the C and Si in the FMKs is in dust, and if the dust destruction in such clumps is mainly due to kinetic sputtering at low temperatures induced by the cloud shock, then there would be little emission in lines such as the UV lines of C iii], C iv, Si iii] and Si iv or the [Fe ii] lines even if the abundances of those elements are substantial. The UV is, of course, not observable in Cas A because of the heavy galactic reddening, but spectra of the SNRs N132D (in the LMC) and 1E0102.2-7219 (in the SMC) are available (Blair et al. 2000). These spectra show some carbon, a little silicon, and some magnesium, providing indicative lower limits to the carbon grain destruction or gas phase abundance.
9. Summary
In this work, we approach the still-open question of the survival of freshly formed dust against processing by the reverse shock inside the cavity of supernova remnants, where the dust is actually formed. We have developed analytical or semi-analytical expressions for the relevant quantities, which we implemented into a Monte Carlo simulation. We focus on the specific case of the well-studied supernova remnant Cas A. Our main findings are summarized below.
-
Following the seminal work of Truelove & McKee (1999) further developed by Laming & Hwang (2003), we derived analytical expressions to describe the evolution of the forward and reverse shock in Cas A, considering inhomogeneous ejecta (uniform core+power-law envelop) expanding into a non-uniform (power-law) ambient medium. This configuration is a closer match to the physical situation of the remnant.
-
We adopted a set of parameters that allows us to reproduce the dynamics, and the density and temperature profile of the Cas A ejecta, as deduced by recent observations. In particular, we assume that the dust forms in dense clumps immersed in smooth and tenuous ejecta.
-
The ejecta in the clumps are heated up by the cloud shock generated by the impact between the clumps and the reverse shock. Because of their high oxygen content, the ejecta cool down quickly to temperatures below 1000 K. Under these conditions, kinetic sputtering is at work.
-
For the smooth ejecta, we consider two temperatures: ~108 K (from our calculations) and ~107 K (average value from observations). Once the dust grains are injected into the smooth hot ejecta (because of their ballistic velocities or due to cloud destruction), they are processed by thermal sputtering. For the destruction of the clouds, we compared the effects of dynamical instabilities and thermal evaporation.
-
We adopted a Monte Carlo approach to derive the mass and size distribution of the processed dust during the progression of the reverse shock inside the remnant. The sputtering of dust is calculated across the remnant and during its evolution, making use of the appropriate profiles that we have derived for relevant quantities, such as the velocity of the reverse shock and the ejecta density.
-
Our simulation starts when the reverse shock touches the outer layer of ejecta (α = 1, ~0.9 yr after explosion), and stops when the reverse shock reaches the centre of the remnant (α = 0, ~8000 yr after explosion).
-
The fraction of surviving dust mass decreases while the reverse shocks proceeds towards the centre of the remnant and more ejecta are processed. Silicate grains (MgSiO3) are more prone to erosion than amorphous carbon (Am C) grains.
-
The effect of rising the temperature of the smooth ejecta from 107 K to 108 K becomes noticeable in the inner layers of the ejecta (decreasing values of α): α ≲ 0.55 for both carbon and silicate dust.
-
For 2004 (α = 0.33), we calculate a survival fraction of 16.9% and 13.3% for Am C, and of 13.4% and 10.4% for MgSiO3, when the grains are immersed in a gas with a temperature of 107 K and 108 K respectively. About 0.1 M⊙ of dust is currently observed in Cas A. If all this dust represents the surviving fraction, then about 0.8–1 M⊙ of dust must have formed in the ejecta. This suggests that almost all refractory elements condensed onto dust, implying a condensation efficiency that is somewhat higher than in models that predict the formation of 0.1–0.5 M⊙ of dust in CCSNe ejecta.
-
After the reverse shock has reached the centre of the remnant (α = 0), we obtain the following survival fraction: 15.9% for Am C and 11.8% for MgSiO3 for a gas temperature of 107 K, 12.3% for Am C and 8.7% for MgSiO3 when the gas temperature is 108 K. Kinetic sputtering destroys by itself 20% of the carbon and 40% of the silicate grains.
The surviving mass fractions depend on the morphology of the ejecta and medium the remnant is expanding into, as well as the composition and size distribution of the grains that formed in the ejecta. Results, therefore, differ for different types of supernova. The framework that we have developed to study dust processing and survival in Cas A can be adapted to other supernova remnants, both young (SN 1985A, the Crab Nebula, Kepler and Tycho) and more evolved (Cygnus Loop).
Acknowledgments
We are grateful to our anonymous referee for the careful reading and valuable suggestions and we would like to thank Martin Laming, Richard Arendt, Mordecai-Mark Mac Low, and Alex Hill for useful and stimulating discussions. E.R.M. wishes to acknowledge the support from a Marie Curie Intra-European Fellowship within the 7th European Community Framework Programme under project number PIEF-GA-2012-328902 NANOCOSMOS. E.D. acknowledges the support of NASA’s 13-ADAP13-0094.
References
- Allen, M. G., Groves, B. A., Dopita, M. A., Sutherland, R. S., & Kewley, L. J. 2008, ApJS, 178, 20 [Google Scholar]
- Arendt, R. G., Dwek, E., Kober, G., Rho, J., & Hwang, U. 2014, ApJ, 786, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Baines, M. J., Williams, I. P., & Asebiomo, A. S. 1965, MNRAS, 130, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Barlow, M. J., Krause, O., Swinyard, B. M., et al. 2010, A&A, 518, L138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertoldi, F., Carilli, C. L., Cox, P., et al. 2003, A&A, 406, L55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bianchi, S., & Schneider, R. 2007, MNRAS, 378, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Biscaro, C., & Cherchneff, I. 2014, A&A, 564, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Biscaro, C., & Cherchneff, I. 2016, A&A, 589, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blair, W. P., Morse, J. A., Raymond, J. C., et al. 2000, ApJ, 537, 667 [NASA ADS] [CrossRef] [Google Scholar]
- Bocchio, M., Jones, A. P., & Slavin, J. D. 2014, A&A, 570, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borkowski, K. J., & Shull, J. M. 1990, ApJ, 348, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Bouchet, P., De Buizer, J. M., Suntzeff, N. B., et al. 2004, ApJ, 611, 394 [NASA ADS] [CrossRef] [Google Scholar]
- Cherchneff, I., & Dwek, E. 2010, ApJ, 713, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Chevalier, R. A., & Fransson, C. 1994, ApJ, 420, 268 [NASA ADS] [CrossRef] [Google Scholar]
- Chevalier, R. A., & Kirshner, R. P. 1978, ApJ, 219, 931 [NASA ADS] [CrossRef] [Google Scholar]
- Chevalier, R. A., & Kirshner, R. P. 1979, ApJ, 233, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Chevalier, R. A., & Oishi, J. 2003, ApJ, 593, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Clayton, D. D., & Nittler, L. R. 2004, ARA&A, 42, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Cowie, L. L., & McKee, C. F. 1977, ApJ, 211, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Dalton, W. W., & Balbus, S. A. 1993, ApJ, 404, 625 [NASA ADS] [CrossRef] [Google Scholar]
- DeLaney, T., & Rudnick, L. 2003, ApJ, 589, 818 [NASA ADS] [CrossRef] [Google Scholar]
- Docenko, D., & Sunyaev, R. A. 2010, A&A, 509, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Draine, B. T. 2011, Physics of the Interstellar and Intergalactic Medium (Princeton University Press) [Google Scholar]
- Dunne, L., Maddox, S. J., Ivison, R. J., et al. 2009, MNRAS, 394, 1307 [NASA ADS] [CrossRef] [Google Scholar]
- Dwek, E. 2005, in The Spectral Energy Distributions of Gas-Rich Galaxies: Confronting Models with Data, eds. C. C. Popescu, & R. J. Tuffs, AIP Conf. Ser., 761, 103 [Google Scholar]
- Dwek, E., & Arendt, R. G. 1992, ARA&A, 30, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Dwek, E., & Cherchneff, I. 2011, ApJ, 727, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Dwek, E., & Scalo, J. M. 1980, ApJ, 239, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Dwek, E., Moseley, S. H., Glaccum, W., et al. 1992, ApJ, 389, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Dwek, E., Staguhn, J. G., Arendt, R. G., et al. 2011, ApJ, 738, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Dwek, E., Staguhn, J., Arendt, R. G., et al. 2014, ApJ, 788, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Ennis, J. A., Rudnick, L., Reach, W. T., et al. 2006, ApJ, 652, 376 [NASA ADS] [CrossRef] [Google Scholar]
- Fesen, R. A., Morse, J. A., Chevalier, R. A., et al. 2001, AJ, 122, 2644 [Google Scholar]
- Fesen, R. A., Hammell, M. C., Morse, J., et al. 2006, ApJ, 636, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Fesen, R. A., Zastrow, J. A., Hammell, M. C., Shull, J. M., & Silvia, D. W. 2011, ApJ, 736, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Gall, C., Andersen, A. C., & Hjorth, J. 2011a, A&A, 528, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gall, C., Andersen, A. C., & Hjorth, J. 2011b, A&A, 528, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gall, C., Hjorth, J., & Andersen, A. C. 2011c, A&ARv, 19, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Ghavamian, P., Laming, J. M., & Rakowski, C. E. 2007, ApJ, 654, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Gomez, H. L., Krause, O., Barlow, M. J., et al. 2012, ApJ, 760, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Gotthelf, E. V., Koralesky, B., Rudnick, L., et al. 2001, ApJ, 552, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Hammell, M. C., & Fesen, R. A. 2008, ApJS, 179, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Helder, E. A., & Vink, J. 2008, ApJ, 686, 1094 [NASA ADS] [CrossRef] [Google Scholar]
- Hester, J. J. 2008, ARA&A, 46, 127 [Google Scholar]
- Hwang, U., & Laming, J. M. 2009, ApJ, 703, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Hwang, U., & Laming, J. M. 2012, ApJ, 746, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Indebetouw, R., Matsuura, M., Dwek, E., et al. 2014, ApJ, 782, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Itoh, H. 1981, PASJ, 33, 521 [Google Scholar]
- Kamper, K., & van den Bergh, S. 1976, ApJS, 32, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Klein, R. I., McKee, C. F., & Colella, P. 1994, ApJ, 420, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Krause, O., Birkmann, S. M., Usuda, T., et al. 2008, Science, 320, 1195 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lagage, P. O., Claret, A., Ballet, J., et al. 1996, A&A, 315, L273 [NASA ADS] [Google Scholar]
- Laming, J. M., & Hwang, U. 2003, ApJ, 597, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Matsuura, M., Dwek, E., Barlow, M. J., et al. 2015, ApJ, 800, 50 [NASA ADS] [CrossRef] [Google Scholar]
- McKee, C. F. 1974, ApJ, 188, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Micelotta, E. 2013, Oral presentation at the conference: The Life Cycle of Dust in the Universe: Observations, Theory, and Laboratory Experiments (LCDU2013), 18−22 November, Taipei, Taiwan, http://eventz.asiaa.sinica.edu.tw/meeting/20131118/talk/2013112211_Talk_ElisabettaMicelotta.pdf [Google Scholar]
- Micelotta, E., & Dwek, E. 2013, in Proc. Life Cycle of Dust in the Universe: Observations, Theory, and Laboratory Experiments (LCDU2013), 18–22 November, Taipei, Taiwan, eds. A. Andersen, M. Baes, H. Gomez, C. Kemper, & D. Watson [Google Scholar]
- Morse, J. A., Fesen, R. A., Chevalier, R. A., et al. 2004, ApJ, 614, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Moseley, S. H., Dwek, E., Glaccum, W., Graham, J. R., & Loewenstein, R. F. 1989, Nature, 340, 697 [NASA ADS] [CrossRef] [Google Scholar]
- Nath, B. B., Laskar, T., & Shull, J. M. 2008, ApJ, 682, 1055 [NASA ADS] [CrossRef] [Google Scholar]
- Nozawa, T., Kozasa, T., Umeda, H., Maeda, K., & Nomoto, K. 2003, ApJ, 598, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Nozawa, T., Kozasa, T., & Habe, A. 2006, ApJ, 648, 435 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Nozawa, T., Kozasa, T., Habe, A., et al. 2007, ApJ, 666, 955 [NASA ADS] [CrossRef] [Google Scholar]
- Nozawa, T., Kozasa, T., Tominaga, N., et al. 2010, ApJ, 713, 356 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Peimbert, M., & van den Bergh, S. 1971, ApJ, 167, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Reed, J. E., Hester, J. J., Fabian, A. C., & Winkler, P. F. 1995, ApJ, 440, 706 [NASA ADS] [CrossRef] [Google Scholar]
- Rho, J., Kozasa, T., Reach, W. T., et al. 2008, ApJ, 673, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Rho, J., Jarrett, T. H., Reach, W. T., Gomez, H., & Andersen, M. 2009, ApJ, 693, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Rho, J., Onaka, T., Cami, J., & Reach, W. T. 2012, ApJ, 747, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, R., Ferrara, A., & Salvaterra, R. 2004, MNRAS, 351, 1379 [NASA ADS] [CrossRef] [Google Scholar]
- Silvia, D. W., Smith, B. D., & Shull, J. M. 2010, ApJ, 715, 1575 [NASA ADS] [CrossRef] [Google Scholar]
- Silvia, D. W., Smith, B. D., & Shull, J. M. 2012, ApJ, 748, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Slavin, J. D., Dwek, E., & Jones, A. P. 2015, ApJ, 803, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Sutherland, R. S., & Dopita, M. A. 1993, ApJS, 88, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Sutherland, R. S., & Dopita, M. A. 1995, ApJ, 439, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Temim, T., & Dwek, E. 2013, ApJ, 774, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Temim, T., Dwek, E., Tchernyshyov, K., et al. 2015, ApJ, 799, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Thorstensen, J. R., Fesen, R. A., & van den Bergh, S. 2001, AJ, 122, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Tielens, A. G. G. M., McKee, C. F., Seab, C. G., & Hollenbach, D. J. 1994, ApJ, 431, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Todini, P., & Ferrara, A. 2001, MNRAS, 325, 726 [NASA ADS] [CrossRef] [Google Scholar]
- Truelove, J. K., & McKee, C. F. 1999, ApJS, 120, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Valiante, R., Schneider, R., Salvadori, S., & Bianchi, S. 2011, MNRAS, 416, 1916 [NASA ADS] [CrossRef] [Google Scholar]
- van Adelsberg, M., Heng, K., McCray, R., & Raymond, J. C. 2008, ApJ, 689, 1089 [CrossRef] [Google Scholar]
- van den Bergh, S. 1971, ApJ, 165, 457 [NASA ADS] [CrossRef] [Google Scholar]
- van den Bergh, S., & Kamper, K. 1985, ApJ, 293, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Vink, J., Kaastra, J. S., & Bleeker, J. A. M. 1996, A&A, 307, L41 [NASA ADS] [Google Scholar]
- Wallström, S. H. J., Biscaro, C., Salgado, F., et al. 2013, A&A, 558, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Watson, D., Christensen, L., Knudsen, K. K., et al. 2015, Nature, 519, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Willingale, R., Bleeker, J. A. M., van der Heyden, K. J., Kaastra, J. S., & Vink, J. 2002, A&A, 381, 1039 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Willingale, R., Bleeker, J. A. M., van der Heyden, K. J., & Kaastra, J. S. 2003, A&A, 398, 1021 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wooden, D. H. 1997, in AIP Conf. Ser. 402, eds. E. K. Zinner, & T. J. Bernatowicz, 317 [Google Scholar]
- Yamaguchi, H., Eriksen, K. A., Badenes, C., et al. 2014, ApJ, 780, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Young, P. A., Fryer, C. L., Hungerford, A., et al. 2006, ApJ, 640, 891 [NASA ADS] [CrossRef] [Google Scholar]
- Zinner, E. 2008, PASA, 25, 7 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Derivation of the equations for the forward and reverse shocks
The starting point to derive the equation for the blast-wave radius during the initial envelope phase (Eq. (22)) is the first line of Eq. (A.7) in TM99, which we report here for clarity, i.e. ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{blast_radius_appendix} R^{*(3-s)/2}_{\rm b} & = & (3-s)\,\left(\frac{\ell_{\rm ED}}{\phi_{\rm ED}}\right)^{1/2} \\ \nonumber & & \times \; \frac{f_n^{1/2}}{3-n}\,\left[ 1-\left(\frac{w_{\rm b}}{\ell_{\rm ED}}\right)^{(3-n)/2}\right] \;\;\;\;\;\; w_{\rm core} \le \left(\frac{w_{\rm b}}{\ell_{\rm ED}}\right) \le 1, \end{eqnarray}](/articles/aa/full_html/2016/06/aa27350-15/aa27350-15-eq354.png) (A.1)where wb ≡ [ Rb(t) /t ] /vej and the term in squared brackets represents the velocity of the free expanding ejecta at a radius equal to Rb. Using Eqs. (4) and (12) we can rewrite wb in terms of starred variables as follows:
(A.1)where wb ≡ [ Rb(t) /t ] /vej and the term in squared brackets represents the velocity of the free expanding ejecta at a radius equal to Rb. Using Eqs. (4) and (12) we can rewrite wb in terms of starred variables as follows: 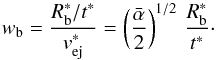 (A.2)Substituting Eq. (A.2) in Eq. (A.1) we can derive Eq. (A.8) in TM99, which expresses t∗ as a function of
(A.2)Substituting Eq. (A.2) in Eq. (A.1) we can derive Eq. (A.8) in TM99, which expresses t∗ as a function of 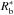 (below),
(below), ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{t_star} t^*(R^*_{\rm b}) & = & \left(\frac{\bar \alpha}{2}\right)^{1/2} \frac{R^*_{\rm b}}{\ell_{\rm ED}} \\ \nonumber & & \times \left[1-\left(\frac{3-n}{3-s}\right) \left(\frac{\phi_{\rm ED}}{\ell_{\rm ED}\,f_n}\right)^{1/2} R^{*(3-s)/2}_{\rm b}\right]^{-2/(3-n)}. \end{eqnarray}](/articles/aa/full_html/2016/06/aa27350-15/aa27350-15-eq360.png) (A.3)To derive Eq. (22), we consider the case when wcore → 0. This implies fn → 0 (see Eq. (11)) and allows us to neglect the term “1” within square brackets in Eq. (A.3). For wcore → 0, Eqs. (11) and (12) lead to
(A.3)To derive Eq. (22), we consider the case when wcore → 0. This implies fn → 0 (see Eq. (11)) and allows us to neglect the term “1” within square brackets in Eq. (A.3). For wcore → 0, Eqs. (11) and (12) lead to 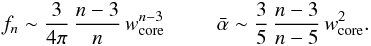 (A.4)Substituting the above expressions and Eq. (16) in the modified Eq. (A.3), we derive
(A.4)Substituting the above expressions and Eq. (16) in the modified Eq. (A.3), we derive  during the envelope phase (Eq. (22)).
during the envelope phase (Eq. (22)).
To derive the time 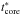 at which the reverse shock hits the ejecta core, we used the fact that
at which the reverse shock hits the ejecta core, we used the fact that 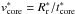 and
and 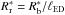 . This leads to
. This leads to 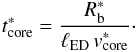 (A.5)Substituting
(A.5)Substituting 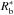 with the envelope solution at
with the envelope solution at 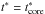 we obtained Eq. (28) for
we obtained Eq. (28) for 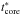 .
.
The radius of the blast wave during the core phase is given, in implicit form, by the second line of equation A7 in TM99, which is written as ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{blast_radius_appendix_core} R^{*(3-s)/2}_{\rm b} & = & (3-s)\,\left(\frac{\ell_{\rm ED}}{\phi_{\rm ED}}\right)^{1/2} \, \frac{f_0^{1/2}}{3}\,\left[ w^{3/2}_{\rm core} -\left(\frac{w_{\rm b}}{\ell_{\rm ED}}\right)^{3/2}\right] \\ \nonumber & & + \; \frac{f_n^{1/2}}{3-n}\left(1- w^{(3-n)/2}_{\rm core}\right) \;\;\;\;\;\;\;\;\;\;\;\;\, 0 \le \left(\frac{w_{\rm b}}{\ell_{\rm ED}}\right) \le w_{\rm core}. \end{eqnarray}](/articles/aa/full_html/2016/06/aa27350-15/aa27350-15-eq368.png) (A.6)For s ≥ 2, the derivation of
(A.6)For s ≥ 2, the derivation of 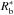 from Eq. (A.6) is extremely complicated, thus we decided to adopt the same approach as Laming & Hwang (2003). This procedure extends the blast-wave solution for the envelope phase into the core phase, matching it to the solution that is appropriate in the Sedov-Taylor (ST) limit. During the ST phase, the mass of the swept-up material exceeds Mej and the remnant expands following a self-similar motion. The appropriate solution in the ST limit is the offset power-law given in Eq. (A.12) from TM99, i.e.
from Eq. (A.6) is extremely complicated, thus we decided to adopt the same approach as Laming & Hwang (2003). This procedure extends the blast-wave solution for the envelope phase into the core phase, matching it to the solution that is appropriate in the Sedov-Taylor (ST) limit. During the ST phase, the mass of the swept-up material exceeds Mej and the remnant expands following a self-similar motion. The appropriate solution in the ST limit is the offset power-law given in Eq. (A.12) from TM99, i.e. ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{radius_ST_offset_eq} R^*_{\rm b}(t^*) & = & \left[R^{*(5-s)/2}_{\rm ST} + \xi^{1/2}_s \left(t^*-t^*_{\rm ST}\right)\right]^{2/(5-s)}\;\; {\rm with} \\ \nonumber \xi_s & = & \frac{(5-s)(10-3s)}{8\pi}, \end{eqnarray}](/articles/aa/full_html/2016/06/aa27350-15/aa27350-15-eq370.png) (A.7)which is obtained integrating the classical ST solution from a characteristic radius
(A.7)which is obtained integrating the classical ST solution from a characteristic radius 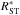 and time
and time 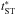 to the current radius and time,
to the current radius and time, 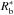 and t∗, respectively. The blast-wave velocity (Eq. (25)) comes directly from Eq. (A.7). To derive the time,
and t∗, respectively. The blast-wave velocity (Eq. (25)) comes directly from Eq. (A.7). To derive the time, 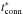 at which the envelope solution and the ST offset power-law solution connect, we equated Eqs. (23) and (25) to derive an expression for t∗ as a function of
at which the envelope solution and the ST offset power-law solution connect, we equated Eqs. (23) and (25) to derive an expression for t∗ as a function of 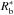 . Then, we substituted in this expression the envelope solution for
. Then, we substituted in this expression the envelope solution for 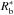 (Eq. (22)) obtaining Eq. (27) for
(Eq. (22)) obtaining Eq. (27) for 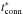 . The final expression for the blast-wave radius valid for
. The final expression for the blast-wave radius valid for 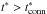 (Eq. (24)), is derived from ST offset power-law solution (Eq. (A.7)) imposing the conditions
(Eq. (24)), is derived from ST offset power-law solution (Eq. (A.7)) imposing the conditions 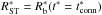 (where
(where 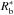 is the envelope solution) and
is the envelope solution) and 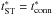 , and using for
, and using for 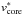 the expression from Eq. (16).
the expression from Eq. (16).
To calculate the velocity of the reverse shock in the frame of the unshocked ejecta during the envelope phase (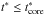 ), we start from the following equation:
), we start from the following equation: 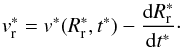 (A.8)The first term on the right side of the equation represents the velocity of the freely expanding ejecta when they encounter the reverse shock and equals
(A.8)The first term on the right side of the equation represents the velocity of the freely expanding ejecta when they encounter the reverse shock and equals 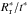 , while the second term is the velocity of the reverse shock in the rest frame. Using Eqs. (23) and (29), with few manipulations we obtain Eq. (30) for the reverse shock velocity.
, while the second term is the velocity of the reverse shock in the rest frame. Using Eqs. (23) and (29), with few manipulations we obtain Eq. (30) for the reverse shock velocity.
Following Laming & Hwang (2003), we assume that during the core phase (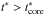 ) the reverse shock velocity remains constant at the value given by Eq. (30) evaluated for
) the reverse shock velocity remains constant at the value given by Eq. (30) evaluated for 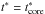 . This leads immediately to Eq. (32).
. This leads immediately to Eq. (32).
To derive the radius of the reverse shock during the core phase, we rewrite Eq. (A.8) as follows: 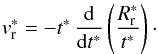 (A.9)The solution of the above equation evaluated between
(A.9)The solution of the above equation evaluated between 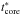 and t∗ provides the expression for the reverse shock radius
and t∗ provides the expression for the reverse shock radius 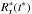 (Eq. (31)), where Eq. (24) has to be used for
(Eq. (31)), where Eq. (24) has to be used for 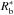 .
.
Appendix B: A statistical approach to calculate the fraction of dust surviving kinetic sputtering
We report here an analytical calculation to estimate, for a given grain size, the fraction of dust able to survive kinetic sputtering in the ejecta clouds. This statistical approach considers a normalized distribution of purely geometrical column densities, while the velocity dependency, which is related to the particle size, is given by Eq. (46).
Figure B.1 is a cross section of a sphere of radius R representing an ejecta cloud of Cas A. The shock impinges on the cloud from the right. The grey region in the figure is the locus of all the dust grains that are at a distance b from the cloud’s surface. The volume occupied by all the grains at a vertical distance y from the x-axis and a distance between b−db/ 2 and b + db/ 2 from the surface is given by the projected volume of 2 πy dy db, where ym, the maximum value of y for a given b is equal to ![\hbox{$\overline{OG} = [R^2-(b/2)^2]^{1/2}$}](/articles/aa/full_html/2016/06/aa27350-15/aa27350-15-eq389.png) . The differential volume dV(b) is then
. The differential volume dV(b) is then ![\appendix \setcounter{section}{2} \begin{equation} \label{vol} {\rm d}V(b) ={\rm d}b\, \int_0^{y_{\rm m}}\, 2\pi y\, {\rm d}y = \pi\, [R^2-(b/2)^2] . \end{equation}](/articles/aa/full_html/2016/06/aa27350-15/aa27350-15-eq391.png) (B.1)The distribution of distances, normalized to the volume of the cloud is then given by
(B.1)The distribution of distances, normalized to the volume of the cloud is then given by 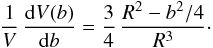 (B.2)The average column density ⟨b⟩ is
(B.2)The average column density ⟨b⟩ is 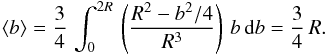 (B.3)The column density, N, traversed by a dust grain until it reaches the clouds’s surface is given by N = ngasb, where ngas is the gas density. So the normalized distribution of column densities is given by
(B.3)The column density, N, traversed by a dust grain until it reaches the clouds’s surface is given by N = ngasb, where ngas is the gas density. So the normalized distribution of column densities is given by 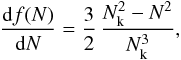 (B.4)where Nk = 2ngasR is the column density through the centre of the cloud.
(B.4)where Nk = 2ngasR is the column density through the centre of the cloud.
We let fM(vgr(0),N) ≡ mgr(t) /mgr(0) be the fraction of surviving dust, with an initial velocity vgr(0) after it traversed a columnn density N. The mass fraction of the dust in a cloud that survives the passage of the reverse shock, ξ [ vcloud(α) ] is given by the integral ![\appendix \setcounter{section}{2} \begin{equation} \label{fracM} \xi[v_{\rm cloud}(\alpha)] = \int_0^{N_{\rm k}}\ f_{\rm M}(v_{\rm cloud}(\alpha),N)\, \frac{{\rm d}f(N)}{{\rm d}N}, \end{equation}](/articles/aa/full_html/2016/06/aa27350-15/aa27350-15-eq401.png) (B.5)\newpage
(B.5)\newpage
where vcloud(α) is the velocity of the cloud shock through a clump located in the ejecta layer α, and where we assumed that because of the strong compression, the reverse shock gives all grains an initial velocity vcloud(α), relative to the gas.
The statistical approach described above is only applicable for the largest grain sizes, for which the maximum column density through the clump, 2ngasR is smaller than that required to slow them down to the kinetic sputtering threshold. For smaller grain sizes, a Monte Carlo approach, as described in Sect. 7, is needed to determine the actual amount of kinetic sputtering before the grain exits the clump, or before the clump is destroyed by the reverse shock.
 |
Fig. B.1 Cross section of a spherical ejecta cloud of radius R in Cas A. The grey area is the locus of all points in the cloud that are at the same distance b (represented by the red lines) from the surface of the cloud. |
All Tables
Percentage of dust mass, Mresidual/Minit, surviving the passage of the reverse shock in Cas A, evaluated in two different stages of supernova evolution identified by the corresponding values of α.
All Figures
 |
Fig. 1 Time, tr, after the explosion at which an ejecta layer characterized by the parameter α encounters the reverse shock. The outer layer has the value α = 1, while the inner one has α = 0. The vertical line indicates the value α = 0.33, corresponding to the ejecta layer which encounters the reverse shock in 2004, and of course intersects the red solid curve at the time corresponding to the age of Cas A in 2004, i.e. tr = 333 yr (indicated by the horizontal line). |
| In the text | |
 |
Fig. 2 Density structure of the ejecta calculated from Eq. (13) but expressed as a function of the parameter α. Vertical line as in Fig. 1. The horizontal line indicates the mass density of the Cas A smooth ejecta in 2004 and the label indicates the corresponding number density. |
| In the text | |
 |
Fig. 3 Left: blast-wave and reverse shock radii as a function of the time elapsed since explosion. Right: zoom of left panel for t ≤ 1000 yr. |
| In the text | |
 |
Fig. 4 Blast-wave and reverse shock velocities (vb and vr, respectively) as a function of the parameter α. The reverse shock velocity (right y-axis, in units of 103 km s-1) is calculated in the frame of the unshocked ejecta ahead of it. We assume that after the reverse shock has entered the ejecta core (α< 0.75), its velocity remains constant and equal to the value for |
| In the text | |
 |
Fig. 5 Schematic illustration of the propagation of the reverse shock (velocity vr ~ 1600 km s-1) into the smooth ejecta and through an ejecta clump. The reverse shock hitting the clump generates a cloud shock that propagates with velocity |
| In the text | |
 |
Fig. 6 Cooling time as a function of temperature for a shocked O-rich ejecta cloud in Cas A, calculated from Eq. (40). |
| In the text | |
 |
Fig. 7 Temperature evolution as a function of time for a shocked O-rich ejecta cloud in Cas A, calculated from Eq. (41) using the cooling time from Eq. (40). |
| In the text | |
 |
Fig. 8 Temperature evolution as a function of time in the shocked smooth ejecta, calculated for two shock velocities under non-equilibrium ionization (NEI) conditions, using the Mappings III code. |
| In the text | |
 |
Fig. 9 Sputtering yields of silicate (left column) and amorphous carbon grains as a function of the relative grain-gas velocity (top row) and corresponding kinetic energy for the incident projectiles: oxygen, present in the ejecta clouds, helium, and hydrogen. The sputtering yields were calculated using Eq. (11) in Nozawa et al. (2006). |
| In the text | |
 |
Fig. 10 Mass fraction of a carbon (top panel) and MgSiO3 (bottom panel) dust grain surviving the erosion by kinetic sputtering as a function of its initial velocity vgr(0), as it traverses a gas of pure H, He, and O composition with density ngas = ncloud = 100 cm-3. The vertical line indicates the initial grain velocity for Cas A, vgr(0) = vcloud = 160 km s-1. |
| In the text | |
 |
Fig. 11 Contour plot showing the time tesc required by a dust grain with initial velocity vgr(0) = 160 km s-1 to traverse a column density of gas Ngas, as a function of the grain radius agr. |
| In the text | |
 |
Fig. 12 Comparison between timescales relevant for the processing of carbon (left panel) and silicate (right panel) dust grains in an ejecta cloud: cloud destruction time tdest, cloud evaporation time tsat, calculated for two temperatures of the gas surrounding the clouds, and dust escape time tesc, calculated for two grain sizes. Both tesc and tdest has been calculated assuming vgr(0) = vcloud = 160 km s-1. All timescales are represented as a function of the diameter of the clump. The vertical line indicates the diameter adopted for the ejecta clouds in Cas A. See text for details. |
| In the text | |
 |
Fig. 13 Density structure of the smooth ejecta as a function of the parameter α. Solid red line: density at the time tr when the layer α encounters the reverse shock (same as Fig. 2); dashed blue line: density at the time tr + 3.5tcc, when the ejecta cloud is dispersed and the dust still in there is injected into the smooth phase.Vertical line as in Fig. 1. |
| In the text | |
 |
Fig. 14 Fraction of surviving carbon (left panel) and silicate dust (right panel) over the entire Cas A remnant as a function of α. For each value of α the curve provides the fraction of remaining dust, which is given by the grains able to survive processing located in the outer layers down to α plus the unprocessed dust residing in the inner layers. The three curves show the effect of kinetic sputtering only and of kinetic+thermal, the latter evaluated for two temperatures of the smooth ejecta: T = 107 K and T = 108 K. |
| In the text | |
 |
Fig. 15 Surviving mass distribution as a function of the grain radius from Eq. (60), for carbon (left panel) and silicate dust (right panel), evaluated for temperatures of the smooth ejecta between 107 K and 108 K. The distributions were normalized to the total surviving dust mass (with M(α) ≡ Mresidual) so that the area under each curve equals 1. |
| In the text | |
 |
Fig. B.1 Cross section of a spherical ejecta cloud of radius R in Cas A. The grey area is the locus of all points in the cloud that are at the same distance b (represented by the red lines) from the surface of the cloud. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



