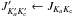| Issue |
A&A
Volume 589, May 2016
|
|
|---|---|---|
| Article Number | A127 | |
| Number of page(s) | 13 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201628074 | |
| Published online | 25 April 2016 | |
Laboratory microwave, millimeter wave and far-infrared spectra of dimethyl sulfide⋆
1 Laboratoire Interuniversitaire des Systèmes Atmosphériques (LISA), UMR 7583 (CNRS)/IPSL, Université Paris-Est Créteil, Université Paris Diderot, 61 av. du Général de Gaulle, 94010 Créteil Cedex, France
e-mail: Atef.jabri@lisa.u-pec.fr
2 Institute of Physical Chemistry, RWTH Aachen University, Landoltweg 2, 52074 Aachen, Germany
3 Synchrotron SOLEIL, Ligne AILES, L’Orme des Merisiers, 91192 Gif-sur-Yvette, France
4 MONARIS, CNRS UMR 8233, 4 place Jussieu, 75252 Paris Cedex, France
Received: 4 January 2016
Accepted: 23 February 2016
Context. Dimethyl sulfide, CH3SCH3 (DMS), is a nonrigid, sulfur-containing molecule whose astronomical detection is considered to be possible in the interstellar medium. Very accurate spectroscopic constants were obtained by a laboratory analysis of rotational microwave and millimeter wave spectra, as well as rotation-torsional far-infrared (FIR) spectra, which can be used to predict transition frequencies for a detection in interstellar sources.
Aims. This work aims at the experimental study and theoretical analysis of the ground torsional state and ground torsional band ν15 of DMS in a large spectral range for astrophysical use.
Methods. The microwave spectrum was measured in the frequency range 2−40 GHz using two Molecular Beam Fourier Transform MicroWave (MB-FTMW) spectrometers in Aachen, Germany. The millimeter spectrum was recorded in the 50−110 GHz range. The FIR spectrum was measured for the first time at high resolution using the FT spectrometer and the newly built cryogenic cell at the French synchrotron SOLEIL.
Results. DMS has two equivalent methyl internal rotors with a barrier height of about 730 cm-1. We performed a fit, using the XIAM and BELGI-Cs-2Tops codes, that contained the new measurements and previous transitions reported in the literature for the ground torsional state νt = 0 (including the four torsional species AA, AE, EA and EE) and for the ground torsional band ν15 = 1 ← 0 (including only the AA species). In the microwave region, we analyzed 584 transitions with J ≤ 30 of the ground torsional state νt = 0 and 18 transitions with J ≤ 5 of the first excited torsional state νt = 1. In the FIR range, 578 transitions belonging to the torsional band ν15 = 1 ← 0 with J ≤ 27 were assigned. Totally, 1180 transitions were included in a global fit with 21 accurately determined parameters. These parameters can be used to produce a reliable line-list for an astrophysical detection of DMS.
Key words: astrochemistry / line: identification / ISM: molecules
Full Tables B.1 and C.1, and Table E.1 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/589/A127
© ESO, 2016
1. Introduction
In recent years, substantial progress in astrophysical observation has permitted the detection of many, and more complex, molecules in the interstellar medium (ISM) and in circumstellar envelopes. According to the Cologne Database for Molecular Spectroscopy (CDMS; Müller et al. 2001, 2005), 188 different molecules have been detected and almost a third of these contain more than six atoms (Herbst & Van Dishoeck 2009). Today, the new observatories such as Atacama Large Millimeter Array (ALMA) and Stratospheric Observatory for Infrared Astrononomy (SOFIA) are becoming operational. Besides the isotopologues of already detected molecules, one can expect the detection of even more complex substances in the future.
The detection of molecular species in space by microwave, millimeter wave and sub-millimeter wave telescopes would have been impossible without dedicated studies in the laboratory addressing the high resolution rotational and rovibrational spectroscopy, both in theory and experiment, of the relevant species. These investigations produce reliable data that is indispensable for an astrochemical interpretation of interstellar surveys. Precise knowledge of the rotational spectra was the key point for the detections of many complex molecules compiled and updated in the existing international databases. These databases include: CDMS (Müller et al. 2001, 2005); SPLATALOG (2010); JPL CATALOG (Pickett et al. 1998); NIST Recommended Rest Frequencies for Observed Interstellar Molecular Microwave Transitions 2009 (NIST 2009); Toyama Microwave Atlas for spectroscopists and astronomers (Toyama 2008). One of the most efficient strategies to gain this knowledge is a combination of experimental microwave, millimeter wave and sub-millimeter wave spectroscopy, followed by the spectral analysis using appropriate effective Hamiltonians and ab initio calculations.
In recent decades, several molecules exhibiting internal rotations of the methyl group have been detected in the interstellar and circumstellar media, e.g. methanol (CH3OH; Ball et al. 1970; Gottlieb et al. 1979), methyl formate (HCOOCH3; Churchwell & Winnewisser 1975; Favre et al. 2014), acetaldehyde (CH3CHO; Fourikis et al. 1974; Matthews et al. 1985), acetic acid (CH3COOH; Mehringer et al. 1997; Remijan et al. 2003) and acetamide (CH3CONH2; Hollis et al. 2006; Halfen et al. 2011). On the other hand, fewer molecules containing two methyl groups such as acetone (CH3)2CO; Combes et al. 1987; Friedel et al. 2005), dimethyl ether and its isotopologues (CH3OCH3, (13CH3)2O; Snyder et al. 1974; Lovas et al. 1979; Bisschop et al. 2013; Koerber et al. 2013) and methyl acetate (CH3(CO)OCH3; Tercero et al. 2013) have been studied in the laboratory and detected in ISM.
Sulfur-containing molecules can be important in the chemical evolution of hot cores. Their molecular ratios have been previously used as chemical clocks to obtain information about the age of those hot cores (Charnley 1997; Wakelam et al. 2004). However the chemistry of interstellar sulfur is still undetermined. Much less sulfur is found in dense regions of ISM than in diffuse regions (Anderson et al. 2013). Therefore, there is some mystery about this missing sulfur and what might be its reservoir. About 20 sulfur-containing molecules have been identified in space so far, but only one of them, methyl mercaptan (CH3SH), exhibits observable internal rotation splittings (called A-E splittings) because of the internal rotation of the methyl group (Linke et al. 1979; Müller et al. 2016). Ethyl mercaptan (CH3CH2SH) has been recently detected in the Orion Cloud (Kolesniková et al. 2014), but no A-E splittings could be observed owing to the high barrier to internal rotation.
Dimethyl sulfide (DMS) is the sulfure analog of dimethyl ether, a relatively abundant molecule in ISM (Snyder et al. 1974; Lovas et al. 1979; Bisschop et al. 2013; Koerber et al. 2013). It is thus considered as a potentially detectable species, since the detection of sulfur-containing molecules often follows the detection of the corresponding oxygen-analogs (Cernicharo et al. 1987). Considering the astrophysical interest of DMS, it is surprising that the microwave data for this molecule is rather sparse in the literature and consists of mainly transitions in the ground torsional state νt = 0. The first measurements were carried out by Rudolph et al. (1960). Afterward, Pierce & Hayashi (1961) measured the spectrum between 10 and 25 GHz and improved the accuracy of the rotational constants and the potential barrier hindering the two equivalent methyl internal rotors. In 1973, the excited torsional states of DMS were studied by Trinkaus et al. (1973) using perturbation theory.
The next decade, the νt = 0 measurements were extended by Vacherand et al. (1987) with 98 transitions with 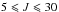 in the millimeter wave range 140−300 GHz. These authors combined their measurements with 85 transitions in the 12−64 GHz region reported in Dreizler & Rudolph (1965) and Demaison et al. (1980). However, the measurement resolution often prevented the observation of all four torsional components, called AA, AE, EA and EE using the symmetry species of the C
in the millimeter wave range 140−300 GHz. These authors combined their measurements with 85 transitions in the 12−64 GHz region reported in Dreizler & Rudolph (1965) and Demaison et al. (1980). However, the measurement resolution often prevented the observation of all four torsional components, called AA, AE, EA and EE using the symmetry species of the C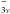 ⊗ C
⊗ C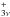 direct product of the C3ν point group (Myers & Wilson Jr. 1960). In 2004, Niide and Hayashi assigned 66 rotational transitions with
direct product of the C3ν point group (Myers & Wilson Jr. 1960). In 2004, Niide and Hayashi assigned 66 rotational transitions with 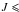 5 in the 12−35 GHz spectral range, which belong to the first torsional excited states ν11 = 1 and ν15 = 1 (Niide & Hayashi 2004). In most of these previous studies, internal rotation analyses were carried out using the XIAM code or other prior codes (Vacherand et al. 1987), providing rotational and torsional parameters for each torsional state. However, several problems occur in these previous works: (i) Certain residuals between calculated and observed line frequencies are as large as 10 MHz in Vacherand et al. (1987); (ii) separate fits were performed for each νt torsional state (Niide & Hayashi 2004), and thus no interactions between different torsional states were taken into account and (iii) the torsional excited state transitions were so weak that only transitions with
5 in the 12−35 GHz spectral range, which belong to the first torsional excited states ν11 = 1 and ν15 = 1 (Niide & Hayashi 2004). In most of these previous studies, internal rotation analyses were carried out using the XIAM code or other prior codes (Vacherand et al. 1987), providing rotational and torsional parameters for each torsional state. However, several problems occur in these previous works: (i) Certain residuals between calculated and observed line frequencies are as large as 10 MHz in Vacherand et al. (1987); (ii) separate fits were performed for each νt torsional state (Niide & Hayashi 2004), and thus no interactions between different torsional states were taken into account and (iii) the torsional excited state transitions were so weak that only transitions with 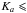 1 could be unambiguously assigned (Niide & Hayashi 2004).
1 could be unambiguously assigned (Niide & Hayashi 2004).
In the far-infrared (FIR) or Raman spectral range, only low resolution data has been published. The Raman spectra was recorded between 50 and 3500 cm-1 by Durig & Griffin (1977), the FIR spectra were first measured by Fateley & Miller (1962) in the spectral range 80−500 cm-1, then by Smith et al. (1966) between 10 and 240 cm-1. These authors used the position of the fundamental torsional band νt = 1 ← 0 to determine a value for the barrier heights hindering the internal rotations.
DMS was also the subject of several ab initio studies that employed the Møller-Plesset theory to explore the potential energy surface (PES) (Senent et al. 1995). Recently, Senent et al. (2014) performed highly correlated ab initio methods combined with large basis sets. This work presented a complete characterization of the rotational parameters at equilibrium and in the ground and excited vibrational states. The barrier height, energy levels and splittings were calculated using a variational procedure, which also allows calculating values for the PES developed in Fourier series containing the potential barrier height and the interaction terms of the two tops. Finally, all the torsional levels and transitions (with J = 0) up to the 4th quanta of the torsional modes were predicted. The nondegenerate components of the two torsional levels (ν11, ν15 = 1, 0) and (ν11, ν15 = 0, 1) were calculated to be 176.516 cm-1 (ν11) and 182.289 cm-1 (ν15), respectively. Finally, using state-of-the-art computational methodologies, Puzzarini et al. (2014) also predict a set of reliable rotational and torsional parameters for the monosubstituted isotopologues of DMS as well as ethyl mercaptan.
The present paper aims at completing the microwave, millimeter wave and FIR dataset of DMS to produce a reliable line-list for astronomical purposes. We present a global fit for the four symmetry species AA, AE, EA and EE in the ground torsional state and for the AA species in the excited torsional state. The microwave dataset was measured between 2 and 40 GHz using two Molecular Beam Fourier Transform MicroWave (MB-FTMW) spectrometers in Aachen. With an accuracy of 2 kHz, it was possible to resolve even small splittings arising from internal rotations of the methyl groups. In addition, room temperature measurements in the millimeter wave region were performed between 50 and 110 GHz, which completed the coverage of the J values. Finally, we also measured the FIR spectrum from 50 to 300 cm-1 at high resolution corresponding to the fundamental band νt = ν15 = 1 ← 0 using the French synchrotron beamline combined with a FT spectrometer and a cryogenic cell. It should be noted that only the ν15 band is infrared active and can be observed in this spectrum.
Section 2 presents the experimental details; Sect. 3 is dedicated to a short presentation of the theoretical model and to the assignments and fits of the spectral data. The intensity calculation and the line-lists for astronomical purposes are given in Sect. 4. The discussion of our results can be found in Sect. 5.
2. Experiments
DMS was purchased from Alfa Aesar GmbH & Co KG, Karlsruhe, Germany and used without further purification.
Firstly, the rotational spectrum of DMS was measured in the microwave region with two MB-FTMW spectrometers operating in the 2−26.5 GHz and 26.5−40 GHz frequency ranges, respectively (Andresen et al. 1990; Grabow et al. 1996; Merke et al. 1994). A mixture of 20 mbar of DMS in helium, used as the carrier gas, at a total pressure of 2 bar was expanded into a vacuum chamber containing a Fabry-Pérot resonator. The spectrometers operate in two different modes: the high resolution mode and scan mode. Since the rotational constants reported in Vacherand et al. (1987) possess sufficient accuracy, all spectra could be measured directly in the high resolution mode. All lines are split into doublets due to the Doppler effect; the molecular transition frequency is the center frequency. The accuracy for an isolated line is 2 kHz, but since a number of lines are blended, we safely weighted all microwave lines 5 kHz in the fit.
The millimeter wave spectrum was recorded between 50 and 110 GHz using a source modulated millimeter wave spectrometer in Aachen to improve and complete available data in the ground torsional state. The experimental accuracy is about 40 kHz for most lines.
The FIR spectrum between 50 and 340 cm-1 was recorded at high resolution using the Bruker IFS125HR FT spectrometer on the AILES Beamline coupled to the synchrotron light (Roy et al. 2008; Brubach et al. 2010) and the newly built cryogenic cell at the French synchrotron SOLEIL (Tchana et al. 2013). The instrument was equipped with a Mylar/Si beamsplitter and evacuated at about 5 × 10-3 Pa in order to minimize H2O and CO2 absorptions. The synchrotron source was operated with 430 mA ring current and a liquid-helium cooled Si/bolometer detector with a 380 cm-1 cold cutoff filter and operated without entrance aperture at the full spectral resolution (0.00102 cm-1) given by the 882 cm maximum optical path difference (MOPD) with the Res = 0.9/MOPD Bruker criterion and no apodization. In total, 304 interferograms were recorded and averaged. We took the ratio of the spectra against a single channel background spectrum of the empty cell which was recorded at a resolution of 0.048 cm-1 to ensure the best possible signal to noise ratio in the transmission spectrum. For the FT, a Mertz-phase correction, 4 cm-1 phase resolution, a zero-filling factor of 2 and a boxcar apodization function were applied to the averaged interferograms. The spectra were calibrated with residual CO2 and H2O lines observed in the spectra with their wavenumbers taken from HITRAN (Rothman et al. 2013). The resulting precision is about ±0.0005 cm-1 for well-isolated lines. For this experiment, the spectrum was recorded at a regulated temperature of 203 ± 2 K, along the entire optical path, with 0.42 ± 0.01 mbar DMS sample pressure. To limit acoustic noise during data acquisition, only totally vibration-free ionic and cryogenic pumps are in operation.
3. Analysis of the DMS spectra
3.1. Theoretical models
As mentioned in the introduction, DMS contains two equivalent methyl internal rotors. Therefore, the spectral analysis requires suitable theoretical models and Hamiltonians to treat the internal rotation splittings.
Two different codes have been used for this purpose. At the beginning, the XIAM code (Hartwig & Dreizler 1996) was applied, which uses the Combined Axis Method (CAM). This method sets up the rotation-torsion Hamiltonian in the rho axis system for each top, and then converts the rho axis wave functions into the principal axis system. The XIAM code has shown its efficiency for treating internal rotation problems with high potential barriers for molecules with two internal rotors as well (Nguyen et al. 2014).
The second code is a slightly modified version of the BELGI-Cs-2Tops code, which has been applied so far for molecules with two nonequivalent internal rotors (Tudorie et al. 2011). One of the differences with XIAM is the choice of the axis system. The BELGI-Cs-2Tops code uses the so-called “quasi principal-axis-method” (Tudorie et al. 2011), instead of the rho axis method (Hougen et al. 1994), which requires placing the z axis nearly parallel to the top axis. The quasi PAM takes its name from the fact that the coefficients of the three quadratic rotational operators (JxJy + JyJx), (JyJz + JzJy) and (JzJx + JxJz) are kept fixed to zero in the fits. Following the procedure described in Ohashi et al. (2004), the Hamiltonian is given by Eq. (6) of this reference for the lowest order terms. For nonequivalent two-top molecules, relations between the kinetic energy parameters appearing in the quasi PAM system of Eq. (6) and those appearing in the PAM system of Eq. (7) of (Ohashi et al. 2004) can be obtained after performing a rotation through an angle θ about the y axis, which relates the a, b, c principal axes in Eq. (7) to the x, y, z axes in Eq. (6). Another important difference is that BELGI-Cs-2Tops includes the interactions between different torsional states, whereas XIAM treats each rotation-torsion νt level as an isolated level with its own set of parameters.
In the BELGI-Cs-2Tops code, the two-step diagonalization procedure adopted is similar to that initially used by Herbst et al. (1984), and later on in the BELGI-Cs code for one top (Hougen et al. 1994). In the first diagonalization step, only the lowest order, pure torsional operators of the Hamiltonian are considered (Eq. (3) of Tudorie et al. (2011) and Eq. (6) of Ohashi et al. (2004)). They can be written as ![\begin{eqnarray} \label{eq:equation1} &&H_{\rm torsion} = \left[{f _{1} p _{\alpha_{1}} ^{2} } + \left(\frac{1}{2}\right) {V_{31}}(1-\cos3\alpha_{1}) + {f_{2} p_{\alpha_{2}}^{2}}\right. \\[3mm] && \quad\left. + \left(\frac{1}{2}\right) {V_{32}}(1-\cos3\alpha_{2})\right]+ {f_{12} p_{\alpha_{1}} p_{\alpha_{2}}}+ {V_{12S} \sin3\alpha_{1} \sin3\alpha_{2}}\nonumber \\[3mm] && \quad + {V_{12C}}(1-\cos3\alpha_{1})(1-\cos3\alpha_{2}). \nonumber \end{eqnarray}](/articles/aa/full_html/2016/05/aa28074-16/aa28074-16-eq37.png) (1)Here, the subscripts 1 and 2 indicate the two nonequivalent tops, respectively. In Eq. (1), the f1 and f2 parameters are the internal rotation constants. They multiply the angular momentum in the kinetic energy
(1)Here, the subscripts 1 and 2 indicate the two nonequivalent tops, respectively. In Eq. (1), the f1 and f2 parameters are the internal rotation constants. They multiply the angular momentum in the kinetic energy 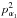 and
and 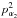 relative to each top, respectively. The f1 parameter is the prefactor of the top-top kinetic energy interaction operators pα1pα2. The parameters V31 and V32 are the torsional potential for each top; V12S and V12C are the parameters multiplying the sin3α1sin3α2 and (1−cos3α1)(1−cos3α2) terms describing the interaction between the two tops, respectively.
relative to each top, respectively. The f1 parameter is the prefactor of the top-top kinetic energy interaction operators pα1pα2. The parameters V31 and V32 are the torsional potential for each top; V12S and V12C are the parameters multiplying the sin3α1sin3α2 and (1−cos3α1)(1−cos3α2) terms describing the interaction between the two tops, respectively.
The basis set for our first diagonalization step consists of the products of exponentials with the form ![\hbox{$\frac{1}{2\pi}\exp[({\rm 3k_{1}+\sigma_{1}}){i\alpha_{1}}]\exp[({3k_{2}+\sigma_{2}}){i\alpha_{2}}]$}](/articles/aa/full_html/2016/05/aa28074-16/aa28074-16-eq50.png) , where the integers |k1| and |k2| are both less than a basis set cutoff parameter ktronc. In the present calculation, we set ktronc = 10 as in the case of methyl acetate (Tudorie et al. 2011), e.g. 441 torsional basis functions are used in this first step. Following this diagonalization, we kept the lowest (2ktronc + 1) × 2 = 42 torsional energy levels and wave functions for the second step. This corresponds (for similar torsional ladders in the two tops) to somewhat more than the first six torsional levels for each top, together with all their combination levels.
, where the integers |k1| and |k2| are both less than a basis set cutoff parameter ktronc. In the present calculation, we set ktronc = 10 as in the case of methyl acetate (Tudorie et al. 2011), e.g. 441 torsional basis functions are used in this first step. Following this diagonalization, we kept the lowest (2ktronc + 1) × 2 = 42 torsional energy levels and wave functions for the second step. This corresponds (for similar torsional ladders in the two tops) to somewhat more than the first six torsional levels for each top, together with all their combination levels.
The second step of the procedure consists of diagonalizing the rest of the torsion-rotation matrix, i.e. Hrot + Htorsion−rot described in Eq. (6) of Ohashi et al. (2004). As explained in (Tudorie et al. 2011), terms in this Hamiltonian can be constructed by taking symmetry-allowed and Hermitian products of a rotational factor (chosen from operators of the form 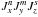 , where m, n and s are integer exponents) and a torsional factor for each top i = 1, 2 (constructed from products of operators of the form
, where m, n and s are integer exponents) and a torsional factor for each top i = 1, 2 (constructed from products of operators of the form 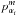 , cos3nαi, sin3sαi, where m, n and s again represent integers).
, cos3nαi, sin3sαi, where m, n and s again represent integers).
The BELGI-Cs-2Tops program has been applied for fitting high resolution torsion-rotational spectra of molecules with: (i) two nonequivalent methyl rotors; (ii) two different three-fold barriers and (iii) a plane of symmetry at equilibrium, e.g. methyl acetate (Tudorie et al. 2011), methyl propionate (Nguyen et al. 2012), three isomers of dimethyl benzaldehyde (Tudorie et al. 2013) and ethyl methyl ketone (Nguyen et al. 2014). In the case of DMS, we modified the code slightly so that all internal rotor parameters corresponding to one methyl group, referred as top 1, possess the same magnitudes as those of the other methyl top, referred as top 2. In the present study, the following parameters have the same values and signs: 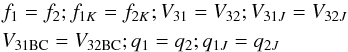 (2)whereas the following parameters were set to the same values but opposite signs:
(2)whereas the following parameters were set to the same values but opposite signs: 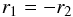 (3)(see Appendix A for the definitions of those parameters). The signs of q1, q2, r1 and r2 can be derived from Eq. (11) of (Ohashi et al. 2004). It should be noted that the angle θ about the y axis relating the principal axes a, b, c to the x, y, z axes is zero in the case of two equivalent tops. In Eq. (2), f1, f2, V31 and V32 are defined as in Eq. (1). The parameters V31J, V32J, V31BC, V32BC, V31AB and V32AB represent the rotational dependences of the potential barrier. In Eqs. (2) and (3), the constants q1 and r1 are related to Jzpα1 and Jxpα1, respectively (see Appendix A). They are essentially equal to −2f1ρ1a and −2f1ρ1b (Tudorie et al. 2011). Similar definitions hold for top 2. The parameters f1K, f2K, q1J and q2J are higher-order terms.
(3)(see Appendix A for the definitions of those parameters). The signs of q1, q2, r1 and r2 can be derived from Eq. (11) of (Ohashi et al. 2004). It should be noted that the angle θ about the y axis relating the principal axes a, b, c to the x, y, z axes is zero in the case of two equivalent tops. In Eq. (2), f1, f2, V31 and V32 are defined as in Eq. (1). The parameters V31J, V32J, V31BC, V32BC, V31AB and V32AB represent the rotational dependences of the potential barrier. In Eqs. (2) and (3), the constants q1 and r1 are related to Jzpα1 and Jxpα1, respectively (see Appendix A). They are essentially equal to −2f1ρ1a and −2f1ρ1b (Tudorie et al. 2011). Similar definitions hold for top 2. The parameters f1K, f2K, q1J and q2J are higher-order terms.
Energy levels obtained using the BELGI-Cs-2Tops code, which has been originally written for nonequivalent rotors, belong to the permutation-inversion group G18. The symmetries are labeled as A1 or A2, E1, E2, E3 and E4 using the irreducible representations of this group. When the torsional parameters corresponding to top 1 are set to the same values as for top 2, energy values of the E1 species are equal to those of the E2 species, i.e. a quartet is observed for each rotational transition instead of a quintet as for the case of two nonequivalent rotors. The labeling A1 or A2, E1, E2, E3 and E4 is thus confusing since the correct permutation-inversion group for DMS should be G36 as for acetone (Ilyushin & Hougen 2013). Therefore, we decided to keep a notation that reflects the Hamiltonian block-diagonalization performed in our code. The energy levels are labeled as AA, AE, EA and EE in (Vacherand et al. 1987) and (Niide & Hayashi 2004). The spin-weight statistics AA: EE: AE: EA depend on the parity of KaKc, i.e. 6:16:4:2 for KaKc: ee-oo and 10:16:4:6 for KaKc: eo-oe (Vacherand et al. 1987). The zero point energies calculated by our model are 187.6294 cm-1, 187.6299 cm-1 and 187.6303 cm-1 for the AA, EE and EA/AE species, respectively.
Molecular parameters for dimethyl sufide in the principal axis system derived from the least-squares fitted parameters in Appendix A (fit BELGI-Cs-2Tops) compared with some parameters from a XIAM fit (Fit XIAM), ab initio (Calc.) and previous works (Fit (00), Fit (10) and Fit (01)).
 |
Fig. 1 Spectrum of the 110← 101 transition of dimethyl sulfide measured using a MB-FTMW spectrometer in Aachen. All four torsional species AA, EE, EA and AE are present. The brackets indicate the Doppler doublets. For this spectrum, 98 decays were coadded. |
 |
Fig. 2 a) Section of the FIR spectrum of dimethyl sulfide from 150 to 220 cm-1. b) An enlargement from 183.0 to 183.7 cm-1 showing the structure of an rQ0-branch (in symmetric top notation) of the ν15 torsion band. Some transitions |
3.2. Assignments and fits
3.2.1. XIAM fits of the ground torsional state
The XIAM code was first used because of its efficiency to treat molecules containing methyl rotors hindered by relatively high potential barriers. We started with a fit including the millimeter wave transitions from Vacherand et al. (1987) to optimize the overall rotational and torsional parameters. This fit enables a prediction of the microwave spectrum with sufficient accuracy to measure new lines with low J values using the two MB-FTMW spectrometers in Aachen. After including these lines in the fit, a new prediction with higher predictive power is provided and further transitions with 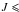 8 and
8 and 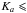 4 could be measured. As a result of the very low rotational temperature of about 2 K in the molecular beam, no transitions with higher J and Ka values were observed.
4 could be measured. As a result of the very low rotational temperature of about 2 K in the molecular beam, no transitions with higher J and Ka values were observed.
In total, 99 lines were measured and assigned in the 2−40 GHz spectral range. About half of these lines, with 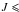 7 and
7 and 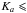 2 were already measured by Hayashi et al. (1989) but our goal was (i) to improve the accuracy of the line positions and (ii) to be able to distinguish lines that are very close to each other since the occurring splittings in the ground torsional state of DMS are small and sometimes could not be resolved in previous experiments. Figure 1 exhibits an example of such transitions. In Vacherand et al. (1987), the AE and EA components could not be distinguished. The above mentioned 99 microwave lines were fitted by the XIAM code with a root-mean-square (rms) deviation of 9.3 kHz which is almost twice the measurement accuracy. However, only a limited number of parameters were used; these are the rotational constants A, B, C, the centrifugal distortion constants ΔJ, ΔK, ΔJK, δj, δk and the barriers to internal rotation V31 = V32. This fit is given as Fit XIAM in Table 1.
2 were already measured by Hayashi et al. (1989) but our goal was (i) to improve the accuracy of the line positions and (ii) to be able to distinguish lines that are very close to each other since the occurring splittings in the ground torsional state of DMS are small and sometimes could not be resolved in previous experiments. Figure 1 exhibits an example of such transitions. In Vacherand et al. (1987), the AE and EA components could not be distinguished. The above mentioned 99 microwave lines were fitted by the XIAM code with a root-mean-square (rms) deviation of 9.3 kHz which is almost twice the measurement accuracy. However, only a limited number of parameters were used; these are the rotational constants A, B, C, the centrifugal distortion constants ΔJ, ΔK, ΔJK, δj, δk and the barriers to internal rotation V31 = V32. This fit is given as Fit XIAM in Table 1.
Using these parameters, we predicted the frequencies of the transitions in the millimeter wave region between 50 GHz and 110 GHz. In this spectral region, only 45 transitions were reported in previous works. We decided to complete the measurements in order to determine more accurately the molecular parameters. In total, 305 lines (which include 260 newly measured lines) in the ground torsional state with 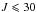 and
and 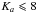 were measured and fitted with the XIAM code to a rms deviation of 37.8 kHz. Additionally, 98 transitions between 140−300 GHz reported in (Vacherand et al. 1987) were fitted with the XIAM code. However, three lines at 214 565.74 MHz, 282 636.26 MHz and 288 879.54 MHz show very large observed minus calculated values up to 1.6 MHz and were excluded from the fit. The rms deviation for these data combined with 85 transitions from (Dreizler & Rudolph 1965) and (Demaison et al. 1980) is 69.2 kHz.
were measured and fitted with the XIAM code to a rms deviation of 37.8 kHz. Additionally, 98 transitions between 140−300 GHz reported in (Vacherand et al. 1987) were fitted with the XIAM code. However, three lines at 214 565.74 MHz, 282 636.26 MHz and 288 879.54 MHz show very large observed minus calculated values up to 1.6 MHz and were excluded from the fit. The rms deviation for these data combined with 85 transitions from (Dreizler & Rudolph 1965) and (Demaison et al. 1980) is 69.2 kHz.
3.2.2. BELGI-Cs-2Tops global fit of the ground and excited states
The BELGI-Cs-2Tops code uses a global approach taking the interactions between the rotation-torsional levels into account. All measurements can be fitted with the corresponding weights, equal to the inverse of the square of the measurement accuracy estimated to be 5 kHz, 40 kHz and 100 kHz for 99 transitions in FTMW, 305 transitions in Fit mm1, and 180 transitions in Fit mm2, respectively (see Table 2).
Overview of the measurements and fit quality using the BELGI-Cs-2Tops code.
In total, 584 rotational transitions in the ground torsional state νt = 0, including the four torsional species AA, AE, EA and EE were fitted with a unitless standard deviation of 0.99. Nevertheless, since the barriers to internal rotation are high (V31 = V32 ≈ 730 cm-1) which result in rather small splittings in the ground torsional state (on the order of 2 MHz at J = 10), the torsion-rotation spectroscopic parameters such as V31, f1, f12, V12S, q1 and r1 are highly correlated. To decrease these correlations, we measured the FIR spectra of DMS between 50 and 340 cm-1 at high resolution. Figure 2 shows an overview of the spectrum between 150 and 220 cm-1 and a zoom-in over the band center at 183.5711 cm-1.
The assignment of rotational lines for the torsional band, which is referred as (ν11,ν15) ← (ν11,ν15) = (01) ← (00) in (Senent et al. 2014), was firstly carried out using the Loomis-Wood program package. This software has been shown to be very useful for analyzing the vibration-rotational spectra of rigid molecules (Łodyga et al. 2007) and also molecules exhibiting large amplitude motion (Loomis-Wood 2006). In the FIR spectrum of DMS, the torsional splittings are very small for the νt = 1 ← 0 torsional band (about 10-3 cm-1 at J = 15). The coupling terms between the overall and internal rotation are also small, as indicated by the parameters ρ1 = ρ2 ≈ 0.095. Therefore, our analysis only takes the AA component into account. So, we used the Loomis-Wood version for an asymmetric top (Łodyga et al. 2007). The preliminary assignment of the AA species for the torsional band νt = 1 ← 0 was straightforward, especially for two branches with 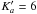 and 7, in which the K doublet components are degenerate and the line intensities are strong. In total, 578 FIR AA species lines with Ka ≤ 10 and J ≤ 28 were assigned and fitted. Using the BELGI-Cs-2Tops code, rotational transitions belonging to these two branches were combined with transitions of the ground state mentioned in Sect. 3.2.1. In addition, 18 AA species microwave lines of two first excited states reported in (Niide & Hayashi 2004) were also included in the fit with a weight of 50 kHz. These two states are noted as (10)p and (10)m in (Niide & Hayashi 2004) and correspond to the (ν11, ν15) = (1, 0) and (ν11, ν15) = (0, 1) states, respectively.
and 7, in which the K doublet components are degenerate and the line intensities are strong. In total, 578 FIR AA species lines with Ka ≤ 10 and J ≤ 28 were assigned and fitted. Using the BELGI-Cs-2Tops code, rotational transitions belonging to these two branches were combined with transitions of the ground state mentioned in Sect. 3.2.1. In addition, 18 AA species microwave lines of two first excited states reported in (Niide & Hayashi 2004) were also included in the fit with a weight of 50 kHz. These two states are noted as (10)p and (10)m in (Niide & Hayashi 2004) and correspond to the (ν11, ν15) = (1, 0) and (ν11, ν15) = (0, 1) states, respectively.
Finally, a global fit with 1180 transitions was performed including 584 transitions in the ground state (νt = 0 ), 18 transitions in the first torsional excited state (νt = 1) and 578 transitions of the torsional band νt = 1 ← 0. This fit is given as Fit BELGI-Cs-2Tops in Table 1. Each group of transitions with their weights are presented in Table 2 along with their rms deviations, number of lines and maximum values of J and Ka.
Twenty-one parameters were determined: three rotational constants A’, B’, C’, six centrifugal distortion constants DJ, DK, δJ, δK, HJ, HK, the barrier heights V31 = V32, the J(J+1) dependence terms V31J = V32J, as well as the rotation-torsion coupling terms q2 = q1 and r1 = −r2 (Eqs. (2) and (3)). The parameter DJK could not be determined and was fixed to zero. The torsional dependence parameters of the barrier height, V31AB = −V32AB, multiplying the term (1−cos3α1) { Jx,Jz } could not be determined well either and was set to zero. On the other hand, the internal rotation constants f1 = f2 and higher order constants f1K = f2K as well as the parameter f12 = 0.490(12) cm-1 (Eq. (1)) were determined well. The top-top interaction constant in the potential energy V12S was fitted to be −32.86(44) cm-1, but the other term V12C could not be floated and was fixed to zero. The set of parameters of our final fit is shown in Appendix A.
4. Intensity calculation
To calculate the line strengths, we use the same method as described for methyl acetate (Tercero et al. 2013). The calculations used the energy parameters determined in Sect. 3 by the BELGI-Cs-2Tops code. The dipole moment μb was fixed to 1.5 Debye (Pierce & Hayashi 1961). For all the transitions, observed frequencies, calculated frequencies from our parameters, difference between observed and calculated values, line strengths, upper and lower state energies for the microwave and millimeter wave lines and for FIR lines are given in Appendix B and Appendix C respectively.
The partition function was calculated in Appendix D using the approximation obtained from the simple asymmetric top expression (Townes & Schawlow 1975) multiplied by the total spin weight (2I + 1)6 = 64 (where I is the nuclear spin of Hydrogen, 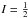 ) and divided by the overall symmetry number, which is equal to 2, for the C2v point group (Groner et al. 2002). Appendix D also gives the vibrational partition function. Also, a detailed discussion of Groner et al. (2002) follows Eq. (3). We note that our line strengths already contain the square of the b-component of the electric dipole moment μb (Pierce & Hayashi 1961) but to obtain the proper intensities they must be multiplied by the appropriate spin weights (see end of Sect. 3.1).
) and divided by the overall symmetry number, which is equal to 2, for the C2v point group (Groner et al. 2002). Appendix D also gives the vibrational partition function. Also, a detailed discussion of Groner et al. (2002) follows Eq. (3). We note that our line strengths already contain the square of the b-component of the electric dipole moment μb (Pierce & Hayashi 1961) but to obtain the proper intensities they must be multiplied by the appropriate spin weights (see end of Sect. 3.1).
Finally in Appendix E, which is available at the CDS, we provide a complete line-list containing the line assignments, line frequencies and line strengths as well as upper state and lower state energies in the spectral range from 0 to 300 GHz. As our experimental data and fit covers up to J = 30 and Ka = 10, we do not expect our spectroscopic parameters to be very reliable for quantum numbers above those values.
5. Discussion
A global fit consisting of pure rotational transitions and rotation-torsional transitions of DMS using the BELGI-Cs-2Tops code for a molecule with two equivalent rotors was carried out. This fit allows us to reproduce the microwave, millimeter wave and FIR data up to J = 30. In the microwave and millimeter wave range, the rms deviations are very close to the experimental accuracies for 584 transitions in the ground state νt = 0 ← 0 (including the four AA, EE, AE and EA species) and for 18 transitions in the first excited states (ν11, ν15 = 1, 0) and (ν11, ν15 = 0, 1) (including only the AA species). In the FIR range, the deviation for 578 AA species lines is 0.00085 cm-1, about twice the estimated experimental accuracy for isolated lines. However, isolated lines are rare in our spectrum. Most of the lines are blended, probably due to unresolved internal rotation splittings. In fact, the torsional splittings are very small for the νt = 1 ← 0 torsional band (about 10-3 cm-1 at J = 15), therefore, AA-EE splitting (and any of the AA-EA or AA-AE splittings) cannot be clearly resolved in most cases.
The comparison of the molecular constants with those deduced from previous studies is not straightforward because of the differences both in the theoretical methods and in the datasets (see Table 1). To compare the BELGI-Cs-2Tops rotational constants A′ and B′ in the quasi PAM system with the rotational constants A and B in the principal axis system, A′ and B′ need to be transformed using Eq. (11) of Ohashi et al. (2004). The results of this transformation are given in Fit BELGI-Cs-2Tops of Table 1. It should be noted that the uncertainty of the A rotational constant is quite high (0.1% of the transformed value). This observation is relatively common in cases of molecules possessing high barriers to internal rotation and small values of the coefficient ρ which describes coupling between overall rotation and internal rotation (Tudorie et al. 2011).
Furthermore, the rotational constants A, B and C reported by Niide & Hayashi (2004) for the ground torsional state (Fit (00) in Table 1) differ by about 0.17%, 0.6% and 0.12%, respectively, from the values determined for the excited torsional state (ν11, ν15 = 0, 1) (Fit (01) in Table 1). These differences are very similar to those obtained by comparing the values in Fit (00) with the values for the excited torsional state (ν11, ν15 = 1, 0) (Fit (10) in Table 1) and the values in Fit BELGI-Cs-2Tops which come from a unique set of parameters determined for all the torsional states. For the same reason, a direct comparison with the ab initio ground state values in (Senent et al. 2014) is also not possible.
On the other hand, the barrier height of 735.784(44) cm-1 determined by BELGI-Cs-2Tops differs by 2% from the ground state value of 752.04(84) cm-1 in (Niide & Hayashi 2004). This parameter increases to 848.44(21) cm-1 (almost 13%) for the excited state (ν11, ν15 = 0,1) (see Fit (01) in Table 1). The calculated barrier height of 706.7 cm-1 (Senent et al. 2014) is 4% lower than our fitted value. On the other hand, the angles between the methyl groups and the principal axes from the BELGI-Cs-2Tops fit are in satisfactory agreement with the values in (Niide & Hayashi 2004) and (Senent et al. 2014).
The top-top interaction constant V12S, which multiplies the sin3α1sin3α2 terms, is −32.86(44) cm-1 which is close to the value of −30.0(51) cm-1, 36.0(90) cm-1 and 24.8 cm-1 found in (Niide & Hayashi 2004), (Trinkaus et al. 1973) and (Durig & Griffin 1977), respectively. The sign difference between our value and the values of those two last references is due to the different sign convention for α1 and α2. The V12C term, which multiplies (1−cos3α1)(1−cos3α2), could not be determined and was thus fixed to zero (see Sect. 3.2.2). The values of these interaction terms are comparable to those found for methyl acetate (34 cm-1 for V12S and −3.5 cm-1 for V12C; Tudorie et al. 2011). For DMS, the effective two-dimensional PES derived by Senent et al. (2014) at the CCSD(T)-F12/VTZ-F12 level shows only a very small dependence of the torsional modes on the other small amplitude vibrations, after the authors verified the validity of such a 2D Hamiltonian with a full dimensional anharmonic analysis. The effective PES is given by 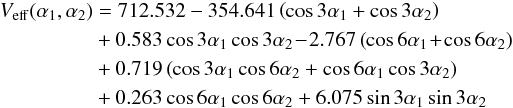 which can be partly compared to the results in our fit
which can be partly compared to the results in our fit 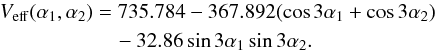 (4)As stated in Senent et al. (2014), the long distance between the two methyl groups in DMS makes the coupling effects associated with this top-top torsional mode near the equilibrium configuration rather small in comparison with its oxygen analog dimethyl ether. As shown in Eq. (5) of Tudorie et al. (2011), V12S corresponds to an off-diagonal quadratic force constant, which couples the torsional modes of the two tops and classifies the geared and anti-geared character of the torsional normal modes. The term sin3α1sin3α2 distinguishes the in-phase (α1α2> 0) and out-of-phase (α1α2< 0) methyl-top oscillations when both tops are near their equilibrium configurations, i.e. where α1 and α2 are small.
(4)As stated in Senent et al. (2014), the long distance between the two methyl groups in DMS makes the coupling effects associated with this top-top torsional mode near the equilibrium configuration rather small in comparison with its oxygen analog dimethyl ether. As shown in Eq. (5) of Tudorie et al. (2011), V12S corresponds to an off-diagonal quadratic force constant, which couples the torsional modes of the two tops and classifies the geared and anti-geared character of the torsional normal modes. The term sin3α1sin3α2 distinguishes the in-phase (α1α2> 0) and out-of-phase (α1α2< 0) methyl-top oscillations when both tops are near their equilibrium configurations, i.e. where α1 and α2 are small.
The kinetic energy term f12pα1pα2 in our theoretical model also distinguishes the in-phase and out-of-phase methyl-top oscillations. A good agreement was obtained between f1 and f12 from our fit and those from ab initio calculations (see Table 1). The value of f12 is about 9% of f1, showing a relatively small coupling of the top-top torsional modes arising from kinetic effects. It should be mentioned that the values of V12S and f12 describe the magnitude of the splittings between the two torsional states ν11 and ν15.
In the future, we will also extend the investigations of the excited torsional states (ν11,ν15 = 1, 0) and (ν11,ν15 = 0, 1).
6. Conclusion
We measured and modeled the microwave and millimeter wave spectrum of DMS in the ground torsional state νt = 0 including the four species AA, AE, EA and EE for 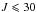 and
and 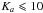 . The high resolution far-infrared spectrum was also recorded for the νt = 1 ← 0 torsional fundamental band ν15 and 584 transitions belonging to the AA species for
. The high resolution far-infrared spectrum was also recorded for the νt = 1 ← 0 torsional fundamental band ν15 and 584 transitions belonging to the AA species for 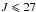 and
and 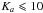 were analyzed. A global fit using the BELGI-Cs-2Tops, which was slightly modified to treat the internal rotations of two equivalent tops, was performed with 21 floated parameters. The root-mean-square deviations are within the experimental accuracies for the pure rotational transitions in the microwave and millimeter wave range. The rotation-torsional νt = 1 ← 0 transitions only fit to twice the experimental accuracy because of numerous blended lines.
were analyzed. A global fit using the BELGI-Cs-2Tops, which was slightly modified to treat the internal rotations of two equivalent tops, was performed with 21 floated parameters. The root-mean-square deviations are within the experimental accuracies for the pure rotational transitions in the microwave and millimeter wave range. The rotation-torsional νt = 1 ← 0 transitions only fit to twice the experimental accuracy because of numerous blended lines.
The set of spectroscopic parameters determined in this work allows us to provide a line-list of rotational transitions in the ground torsional state with line frequencies and line strengths for an astrophysical search of DMS.
Acknowledgments
We thank Dr. O. Pirali and S. Gruet for helpful discussions and advices in the far-infrared analysis using the Loomis-Wood program. I.K. and A.J. are indebted to Dr. V.V. Ilyushin for helpful discussions and careful reading of the manuscript. A.J. and I.K. thank the Groupe de Recherche International GDRI HighRes (especially Dr. A. Perrin) and the Programme Chimie Milieu Interstellaire PCMI for travel funding. V. V. thanks the Fonds der Chemischen Industrie (FCI) for a Ph.D. fellowship.
References
- Andresen, U., Dreizler, H., Grabow, J.-U., & Stahl, W. 1990, Rev. Sci. Instrum., 61, 3694 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, D. E., Bergin, E. A., Maret, S., & Wakelam, V. 2013, ApJ, 779, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Ball, J. A., Gottlieb, C. A., Lilley, A. E., & Radford, H. E. 1970, ApJ, 162, L203 [NASA ADS] [CrossRef] [Google Scholar]
- Bisschop, S. E., Schilke, P., Wyrowski, F., et al. 2013, A&A, 552, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brubach, J., Manceron, L., Rouzières, M., et al. 2010, AIP Conf. Proc., 81, 1214 [Google Scholar]
- Cernicharo, J., Kahane, C., Guelin, M., & Hein, H. 1987, A&A, 181, L9 [NASA ADS] [Google Scholar]
- Charnley, S. B. 1997, ApJ, 481, 396 [NASA ADS] [CrossRef] [Google Scholar]
- Churchwell, E., & Winnewisser, G. 1975, A&A, 45, 229 [NASA ADS] [Google Scholar]
- Combes, F., Gerin, M., Wootten, A., et al. 1987, A&A, 180, L13 [NASA ADS] [Google Scholar]
- Demaison, J., Schwoch, D., Tan, B. T., & Rudolph, H. D. 1980, J. Mol. Spectr., 83, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Dreizler, H., & Rudolph, H. D. 1965, Z. Naturforsch., A, Phys. Sci., 20, 749 [Google Scholar]
- Durig, J. R., & Griffin, M. G. 1977, J. Chem. Phys., 67, 2220 [NASA ADS] [CrossRef] [Google Scholar]
- Fateley, W. G., & Miller, F. A. 1962, Spectrochim. Acta, 18, 977 [NASA ADS] [Google Scholar]
- Favre, C., Carvajal, M., Field, D., et al. 2014, ApJS, 215, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Fourikis, N., Sinclair, M. W., Robinson, B. J., Godfrey, P. D., & Brown, R. D. 1974, Aust. J. Phys., 27, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Friedel, D. N., Snyder, L. E., Remijan, A. J., & Turner, B. E. 2005, ApJ, 632, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Gottlieb, C. A., Ball, J. A., Gottlieb, E. W., & Dickinson, D. F. 1979, ApJ, 227, 422 [NASA ADS] [CrossRef] [Google Scholar]
- Grabow, J.-U., Stahl, W., & Dreizler, H. 1996, Rev. Sci. Instrum., 67, 4072 [NASA ADS] [CrossRef] [Google Scholar]
- Groner, P., Albert, S., Herbst, E., et al. 2002, ApJSS, 142, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Halfen, D. T., Ilyushin, V., & Ziurys, L. M. 2011, ApJ, 743, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Hartwig, H., & Dreizler, H. 1996, Z. Naturforsch., A, Phys. Sci., 51, 923 [Google Scholar]
- Hayashi, M., Nakata, N., & Miyazaki, S. 1989, J. Mol. Spectr., 135, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Herbst, E., & Van Dishoeck, E. F. 2009, ARA&A, 47, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Herbst, E., Messer, J. K., De Lucia, F. C., & Helminger, P. 1984, J. Mol. Spectr., 108, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Hollis, J. M., Lovas, F. J., Remijan, A. J., et al. 2006, ApJ, 643, L25 [Google Scholar]
- Hougen, J. T., Kleiner, I., & Godefroid, M. 1994, J. Mol. Spectr., 163, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Ilyushin, V. V., & Hougen, J. T. 2013, J. Mol. Spectr., 289, 41 [Google Scholar]
- Koerber, M., Bisschop, S. E., Endres, C. P., et al. 2013, A&A, 558, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kolesniková, L., Tercero, B., Cernicharo, J., et al. 2014, ApJ, 784, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Linke, R. A., Frerking, M. A., & Thaddeus, P. 1979, ApJ, 234, L139 [NASA ADS] [CrossRef] [Google Scholar]
- Łodyga, W., Kręglewski, M., Pracna, P., & Urban, Š. 2007, J. Mol. Spectr., 243, 182 [NASA ADS] [CrossRef] [Google Scholar]
- Loomis-Wood. 2006, The Loomis-Wood Software home page, last update: 2015, http://www.lww.amu.edu.pl/welcome.html [Google Scholar]
- Lovas, F. J., Lutz, H., & Dreizler, H. 1979, J. Phys. Chem. Ref. Data, 8, 1051 [NASA ADS] [CrossRef] [Google Scholar]
- Matthews, H. E., Friberg, P., & Irvine, W. M. 1985, ApJ, 290, 609 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Mehringer, D. M., Snyder, L. E., Miao, Y., & Lovas, F. J. 1997, ApJ, 480, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Merke, I., Stahl, W., & Dreizler, H. 1994, Z. Naturforsch., A, Phys. Sci., 49, 490 [Google Scholar]
- Müller, H. S. P., Thorwirth, S., Roth, D. A., & Winnewisser, G. 2001, A&A, 370, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, H. S. P., Belloche, A., Xu, L.-H., et al. 2016, A&A, 587, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Myers, R. J., & Wilson, Jr., E. B. 1960, J. Chem. Phys., 33, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Nguyen, H. V. L., Stahl, W., & Kleiner, I. 2012, Mol. Phys., 110, 2035 [NASA ADS] [CrossRef] [Google Scholar]
- Nguyen, H. V. L., Van, V., Stahl, W., & Kleiner, I. 2014, J. Chem. Phys., 140, 214303 [NASA ADS] [CrossRef] [Google Scholar]
- Niide, Y., & Hayashi, M. 2004, J. Mol. Spectr., 223, 152 [NASA ADS] [CrossRef] [Google Scholar]
- NIST. 2009, NIST Recommended Rest Frequencies for Observed Interstellar Molecular Microwave Transitions by F. J. Lovas, Revision, http://www.nist.gov/pml/data/micro/index.cfm/ [Google Scholar]
- Ohashi, N., Hougen, J. T., Suenram, R. D., et al. 2004, J. Mol. Spectr., 227, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Pickett, H. M., Poynter, R. L., Cohen, E. A., et al. 1998, J. Quant. Spectr. Rad. Transf., 60, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Pierce, L., & Hayashi, M. 1961, J. Chem. Phys., 35, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Puzzarini, C., Senent, M. L., Domínguez-Gómez, R., et al. 2014, ApJ, 796, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Remijan, A., Snyder, L. E., Friedel, D. N., Liu, S.-Y., & Shah, R. Y. 2003, ApJ, 590, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Rothman, L. S., Gordon, I. E., Babikov, Y., et al. 2013, J. Quant. Spectr. Rad. Transf., 130, 4 [Google Scholar]
- Roy, P., Brubach, J.-B., Rouzières, M., et al. 2008, Rev. Electricité et Electronique, 2, 23 [Google Scholar]
- Rudolph, H. D., Dreizler, H., & Maier, W. 1960, Z. Naturforsch. A, 15, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Senent, M. L., Moule, D. C., & Smeyers, Y. G. 1995, J. Phys. Chem., 99, 7970 [CrossRef] [Google Scholar]
- Senent, M. L., Puzzarini, C., Domínguez-Gómez, R., Carvajal, M., & Hochlaf, M. 2014, J. Chem. Phys., 140, 124302 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, D. R., McKenna, B. K., & Möller, K. D. 1966, J. Chem. Phys., 45, 1904 [NASA ADS] [CrossRef] [Google Scholar]
- Snyder, L. E., Buhl, D., Schwartz, P. R., et al. 1974, ApJ, 191, L79 [NASA ADS] [CrossRef] [Google Scholar]
- SPLATALOG. 2010, Splatalogue database for astronomical spectroscopy, http://www.cv.nrao.edu/php/splat/advanced.php [Google Scholar]
- Tchana, F. K., Willaert, F., Landsheere, X., et al. 2013, Rev. Sci. Instrum., 84, 093101 [NASA ADS] [CrossRef] [Google Scholar]
- Tercero, B., Kleiner, I., Cernicharo, J., et al. 2013, ApJ, 770, L13 [Google Scholar]
- Townes, C. H., & Schawlow, A. L. 1975, Microwave Sptctroscopy, (New York: McGraw-Hill) [Google Scholar]
- Toyama. 2008, Toyama Microwave Atlas for spectroscopists and astronomers, Last update: May 2014, http://www.sci.u-toyama.ac.jp/phys/4ken/atlas/ [Google Scholar]
- Trinkaus, A., Dreizler, H., & Rudolph, H. D. 1973, Z. Naturforsch. A., 28, 750 [NASA ADS] [Google Scholar]
- Tudorie, M., Kleiner, I., Hougen, J. T., et al. 2011, J. Mol. Spectr., 269, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Tudorie, M., Kleiner, I., Jahn, M., et al. 2013, J. Phys. Chem. A, 117, 13636 [CrossRef] [Google Scholar]
- Vacherand, J. M., Wlodarczak, G., Dubrulle, A., & Demaison, J. 1987, Can. J. Phys., 65, 1159 [NASA ADS] [CrossRef] [Google Scholar]
- Wakelam, V., Caselli, P., Ceccarelli, C., Herbst, E., & Castets, A. 2004, A&A, 422, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix
Spectroscopic constants of dimethyl sulfide in the quasi principal axis system obtained with the program BELGI-Cs-2Tops
Appendix
Excerpt the line-list for DMS in the microwave and millimeter wave range.
Appendix C: Appendix C
Small part of the line-list for DMS in the Far-Infrared Range.
Appendix D: Appendix D
Partition function for dimethyl sulfide.
All Tables
Molecular parameters for dimethyl sufide in the principal axis system derived from the least-squares fitted parameters in Appendix A (fit BELGI-Cs-2Tops) compared with some parameters from a XIAM fit (Fit XIAM), ab initio (Calc.) and previous works (Fit (00), Fit (10) and Fit (01)).
Spectroscopic constants of dimethyl sulfide in the quasi principal axis system obtained with the program BELGI-Cs-2Tops
All Figures
 |
Fig. 1 Spectrum of the 110← 101 transition of dimethyl sulfide measured using a MB-FTMW spectrometer in Aachen. All four torsional species AA, EE, EA and AE are present. The brackets indicate the Doppler doublets. For this spectrum, 98 decays were coadded. |
| In the text | |
 |
Fig. 2 a) Section of the FIR spectrum of dimethyl sulfide from 150 to 220 cm-1. b) An enlargement from 183.0 to 183.7 cm-1 showing the structure of an rQ0-branch (in symmetric top notation) of the ν15 torsion band. Some transitions |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.