| Issue |
A&A
Volume 589, May 2016
|
|
|---|---|---|
| Article Number | A8 | |
| Number of page(s) | 12 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201527628 | |
| Published online | 04 April 2016 | |
Long-term activity and outburst of comet C/2013 A1 (Siding Spring) from narrow-band photometry and long-slit spectroscopy⋆
1
Institut d’Astrophysique et Géophysique, Université de Liège,
allée du 6 Août 17,
4000
Liège, Belgium
e-mail: cyrielle.opitom@ulg.ac.be
2
CNRS – UTINAM UMR 6213, Avenue de l’Observatoire, 25000
Besançon,
France
3
Department of Physics and Astronomy, University College
London, London
NW1 2PS,
UK
4
European Space Agency – ESTEC Kerplerlaan 1,
2201 AZ
Noordwijk, The
Netherlands
Received: 23 October 2015
Accepted: 17 January 2016
We present a unique data set of more than one year’s worth of regular observations of comet C/2013 A1(Siding Spring) taken with TRAPPIST, along with low-resolution spectra obtained with the ESO/VLT FORS 2 instrument. The comet made a close approach to Mars on October 19, 2014, and was then observed by many space-borne and ground-based telescopes. We followed the evolution of the OH, NH, CN, C3, and C2 production rates as well as the Afρ parameter, a proxy for the dust production. We detected an outburst two weeks after perihelion, with gas and dust production rates increased by a factor of five within a few days. By modelling the shape of the CN and C2 radial profiles, we determined that the outburst happened on November 10 around 15:30 UT (±5 h) and measured a gas expansion velocity of 1.1 ± 0.2 km s-1. We used a thermal evolution model to reproduce the activity pattern and outburst. Our results are consistent with the progressive formation of a dust mantle explaining the shallow dependence of gas production rates, which may be partially blown off during the outburst. We studied the evolution of gas composition, using various ratios such as CN/OH, C2/OH, or C3/OH, which showed little or no variation with heliocentric distance, including at the time of the outburst. This indicates a relative level of homogeneity of the nucleus composition.
Key words: comets: general / comets: individual: C/2013 A1 (Siding Spring) / techniques: spectroscopic / techniques: photometric
© ESO, 2016
1. Introduction
Nearly isotropic comets (NIC) are believed to have formed in the giant planets region, before being scattered onto their current orbits by planetary perturbations (Dones et al. 2004). The emplacement efficiency in the Oort Cloud is approximately 1−10%, which means that most objects were lost to the interstellar medium in the early phases of the solar system evolution. Once a cometary nucleus has been placed in the Oort Cloud, it can return in the inner solar system as a result of gravitational perturbations from a passing star, molecular cloud or galactic tide. Since these comets have spent the last 3.5 to 4.5 Gyr at the edge of the solar system, barely bound to the Sun, in a collisionless environment, and at an equilibrium temperature of 10−20 K, they are possibly among the best preserved objects in the solar system. However, because they are rare and fast moving, they present very little opportunity to be thoroughly studied and are very difficult to investigate. In particular, we cannot expect to achieve the level of understanding we get for Jupiter Family comets (like comet 67P/Churyumov-Gerasimenko), which can be studied by in situ space missions.
Comet C/2013 A1 (Siding Spring) is a new NIC, discovered in January 2013 (McNaught et al. 2013) while at 7.2 au from the Sun. Early orbit determinations suggested a very close encounter with the planet Mars on October 19, 2014. This close encounter occurred at 134 000 km from the centre of Mars, at a relative speed of 56 km s-1 (Kelley et al. 2014). This close approach represented both a threat for orbiters around Mars and a tremendous opportunity to observe this comet from both ground- and Mars-based facilities. In particular, it allowed the study of the deposition of cometary dust into the Mars atmosphere and to potentially study the dust composition. The SHARAD radar aboard Mars Reconnaissance Orbiter (MRO) recorded high values of its total electron content on the nightside (Restano et al. 2015), while the MARSIS radar aboard Mars Express (MEX) detected a strong ionospheric layer just below 100 km of altitude, consistent with a meteor shower produced by cometary dust particles (Gurnett et al. 2015). These observations were complemented by the MAVEN data, in which metallic ions – Na, Mg, Al, K, Ti, Cr, Mn, Fe, Co, Ni, Cu, and Zn, and possibly Si and Ca – were identified from ion mass and ultraviolet spectrometry (Benna et al. 2015; Schneider et al. 2015).
In this paper, we present observations of comet Siding Spring obtained over more than a year with the 60 cm TRAPPIST telescope, along with low-resolution spectra obtained by the ESO/VLT at 6 epochs between July 27 and September 28, 2014. These observations allow us to study the evolution of this comet activity from ~5 au pre-perihelion to ~1.4 au post-perihelion, and to detect an outburst shortly after perihelion, which we try to characterize by modelling the comet thermal evolution. Sections 2.1 and 2.2 present the observations and data reduction, while Sect. 2.3 presents the simultaneous analysis of both TRAPPIST narrow-band images and VLT/FORS 2 low-resolution spectra. We present the evolution of the comet’s dust activity as it approached perihelion and shortly after in Sect. 3.1. We study the gas coma evolution and composition in Sect. 3.2, and look for morphological features that could provide information about the position and number of active areas on the nucleus in Sect. 3.3. Finally, Sect. 4 describes the characterization of the outburst.
2. Observations, data reduction and analysis
2.1. TRAPPIST
TRAPPIST (TRAnsiting Planets and Planetesimals Small Telescope) is a 60 cm robotic telescope installed in 2010 at La Silla observatory (Jehin et al. 2011). The telescope is equipped with a 2K×2K thermoelectrically cooled FLI Proline CCD camera with a field of view of 22′ × 22′. We binned the pixels 2 by 2 and obtained a resulting plate scale of 1.302′′/pixel. The telescope is equipped with a set of narrow-band filters designed for the observing campaign of comet Hale-Bopp (Farnham et al. 2000). These filters isolate the emission of OH (309.7 nm), NH (336.1 nm), CN (386.9 nm), C3 (406.3 nm), and C2 (513.5 nm), and emission free continuum regions at four wavelengths (UC at 344.9 nm, BC at 445.3 nm, GC at 525.9 nm, and RC at 713.3 nm). A set of B,V,Rc, and Ic Johnson-Cousin filters is also permanently mounted.
OH, NH, CN, C3, and C2 production rates and Afρ of comet C/2013 A1 (Siding Spring) from TRAPPIST observations.
 |
Fig. 1 CN (top) and C2 (bottom) brightness profiles from Jul. 25 and Sep. 19, 2014. TRAPPIST data are represented with red circles and the closest VLT data is overplotted. Data extracted from both sides of the nucleus in the spectra are represented respectively with green triangles and blue squares. |
CN and C2 production rates of C/2013 A1 (Siding Spring) from VLT/FORS 2 observations.
We started to observe the comet on September 20, 2013, when it was 4.95 au from the Sun. At this time, it was too faint for gases to be detected with TRAPPIST, so we mainly observed with broad-band B,V,Rc, and Ic filters. We also performed a few observations with the narrow-band continuum filters. Observations were performed once or twice a week, until the comet was lost owing to the solar conjunction on April 7, 2014. We recovered the comet on May 21, 2014, and started to observe with broad-band and narrow-band filters. We followed the comet until November 15, 2014, a few weeks after its perihelion passage. Exposure times range from 60 s to 240 s for the broad-band filters, and from 300 s to 900 s for the narrow-band filters.
Calibration followed standard procedures using frequently updated master bias, flat and dark frames. The removal of the sky contamination and the flux calibration were performed as described in Opitom et al. (2015). Median radial profiles were extracted from each image and dust contamination was removed from gas radial profiles. The fluxes of OH, NH, CN, C3, and C2 were converted into column densities and we adjusted a Haser model (Haser 1957) on the profiles to derive the production rates. The model adjustment was performed around a physical distance of 10 000 km from the nucleus to avoid PSF and seeing effects around the optocentre and low signal-to-noise ratio (S/N) at larger nucleocentric distances. The Haser model is not physically realistic as it assumes the single step photodissociation of parent species into daughter species in a spherically symmetric coma. However, it is widely used to compute gas production rates from optical comet observations, allows observations made by different observers to be compared, and also allows comets to be compared to each others. We used scalelengths from A’Hearn et al. (1995) scaled as r2, r being the heliocentric distance. We chose to use these scalelengths to allow an easy comparison with different data sets, especially the large data set from A’Hearn et al. (1995). We used the observations with the narrow-band BC,GC, and RC filters and with the broad-band Rc filter to estimate the dust production. From the dust profiles, we derived the Afρ parameter, as first introduced by A’Hearn et al. (1984). All Afρ values were corrected from the phase angle according to the phase function described by Schleicher1, which is a composite of two different phase functions from Schleicher et al. (1998) and Marcus (2007). The observational circumstances and production rates for each night are given in Table 1.
2.2. VLT/FORS 2
Low-resolution spectra were acquired with the FORS 2 instrument (Appenzeller et al. 1998) installed at UT1 of the Very Large Telescope of the European Southern Observatory. We obtained spectra of comet Siding Spring on six dates between July and September 2014 (Table 2). All observations were made using the grism 150I covering the 330−600 nm range. We chose a 6.8′ – long and 1.3′′ – wide slit. The FORS 2 detector is composed of two 2k × 4k MIT CCDs (15 μm pixel size) separated by a 480 μm gap. The pixel scale is 0.25′′/pixel in the spatial direction and 6.9 Å/pixel in the spectral direction. For each observation, two or three short exposures (from 30 to 180 s depending on the comet brightness and geocentric distance) ensured non-saturated observations of the nucleus and one long exposure (1500 s) allowed to get good S/N ratio for the gas at larger nucleocentric distances. Except for the first observations, the slit was oriented perpendicular to the tail of the comet. Since the coma filled the whole slit, we took exposures with a large offset every night to account for the sky background. We noticed a strong contamination from unknown origin in all September 28 spectra. This contamination was mostly located in the blue part of the spectra and prevented us from deriving reliable production rates. We thus discarded these observations from the data set presented here.
We removed the bias, and then flat fielded and wavelength calibrated the spectra. The absolute flux calibration was made from spectroscopic standard stars observed the same night as the comet. The sky background was calibrated the same way as the scientific images. We measured the emission in the strongest sky lines from the background and comet images in order to properly scale the background and subtract it from the scientific images. This was done separately for each image and for each chip. The best way to account for the sky background would have been to alternate comet and background expositions, but there was not enough observing time available to apply this strategy. After the background subtraction, we binned the pixels by 10 in the spatial direction to increase the S/N. Each bin was then extracted separately. Observations of solar analogues (made with the same grism and slit width as the comet observations) were used to subtract the continuum from each 1D spectrum across the spatial direction. Spatial profiles of CN and C2 were obtained by summing every 1D spectra over the 383−390.5 nm and 486−521 nm wavelength ranges. We obtained two CN and C2 radial profiles (one on each side of the nucleus) for each exposure. We discarded the first point of each profile, containing the nucleus, to avoid PSF and seeing effects and also strong dust contribution difficult to remove close to the nucleus. The Haser model was adjusted on the profiles to derive CN and C2 production rates. The derived production rates and observational circumstances are given in Table 2. The values in this table are the mean values for each night, and the error bars are computed from the dispersion of the production rates from a single night.
2.3. Comparative analysis of TRAPPIST and FORS 2 data
We start our analysis by comparing the radial profiles and production rates obtained from TRAPPIST and FORS 2 data to ensure that they are consistent with each other. It is usually difficult to compare data obtained with different instruments, and even more difficult to compare data obtained with different techniques. We only have almost simultaneous observations with FORS 2 and TRAPPIST for two dates, so we use these observations to assess the agreement between the two data sets. Figure 1 shows CN and C2 radial brightness profiles for FORS 2 and the closest TRAPPIST observations. We first notice that the data dispersion is usually smaller in TRAPPIST profiles, especially at large nucleocentric distances, even though we binned the FORS 2 data by 10 pixels in the spatial direction to increase the S/N. The reason is that TRAPPIST profiles result from a median of the flux over the whole coma while FORS 2 profiles are only extracted over a 1.3′′-wide slit.
In the case of CN, TRAPPIST radial brightness profiles are in good agreement with the FORS 2 profiles (Fig. 1). The two FORS 2 profiles match each other, indicating that the coma is symmetric along the slit axis. The comparison of production rates derived from both telescopes (see Tables 1 and 2) shows that, within the error bars, production rates derived from FORS 2 observations fit within the trend of TRAPPIST production rates. Comparison of C2 fluxes between narrow-band images and low-resolution spectroscopy is more difficult than for the CN fluxes because of the extent of the band and the higher dust contamination. Nevertheless, our measurements of C2 radial profiles and production rates are also in good agreement with each other. Given that the TRAPPIST and FORS 2 radial profiles are a good match for two dates two months apart and that production rates seem consistent with each other, we conclude that these observations can be merged into a single data set. We then analysed this entire data set while studying the evolution of the comet activity and coma composition. The results presented in the next sections thus rely on both FORS 2 and TRAPPIST observations.
3. Evolution of activity and coma
3.1. Dust
We observed comet Siding Spring almost uninterruptedly over more than a year. Figure 2 shows the evolution of the A(0)fρ corrected from phase angle effects, from almost 5 au pre-perihelion to more than two weeks after perihelion passage. The long-term trend observed is the same for all continuum filters. The major features are the following:
-
The comet activity slowly rises as it approaches the Sun.
-
At approximately 4.3 au, the activity starts to decrease at a regular pace until the comet reaches 3 au. Because of the solar conjunction that prevented us from observing between Apr. 7 and May 21, 2014, it is difficult to determine when the activity decrease stopped.
-
From late May 2013 (r = 2.5 au) to mid July (r = 2.0 au) the dust activity rises again, then goes through a standstill or a slow decrease period until the comet reaches perihelion.
-
After the perihelion passage on October 25 (r = 1.4 au), the comet activity rises regularly.
-
Between November 7 and November 11 (r = 1.4 au), the data show a sudden rise in activity, consistent with a cometary outburst: both gas and dust production rates increase by a factor of 5 within a few days. Dust production peaks on Nov. 12, then decreases regularly.This outburst was also observed from total visual magnitudes measurements by amateur astronomers (see e.g. Seiichi Yoshida’s web page2).
Li et al. (2014) reported measurements of comet Siding Spring Afρ from observations performed with the Hubble Space Telescope. They measured a value of 2520 cm, 2120 cm, and 1720 cm at heliocentric distances of 5.58, 3.77, and 3.28 au respectively. These measurements are corrected from the phase angle effect using the same function that we used in this paper. From the closest TRAPPIST observations in the broad-band Rc filter, we measured Afρ values of 2230 ± 30, 1870 ± 24, and 1540 ± 22 cm at respectively 4.61, 3.73, and 3.33 au from the Sun. Our measurements are lower than those reported by Li et al. (2014); however, the Afρ values we report here are measured at a cometocentric distance of 10 000 km instead of 5000 km for the Li et al. (2014) values. We observed a decrease in Afρ with cometocentric distance, and measured values around 5000 km of 2360 ± 32, 2060 ± 26, and 1720 ± 25 cm at respectively 4.61, 3.73, and 3.33 au from the Sun, consistent with Li et al. (2014). Other Afρ values have been published by Stevenson et al. (2015) from NEOWISE infrared observation, but any comparison between infrared and visible measurements is made difficult by colour effects and the different size of the field of view.
 |
Fig. 2 Logarithm of the A(0)fρ corrected from phase angle effect as a function of the heliocentric distance r. The A(0)fρ was measured from Rc broad-band filter and from narrow-band BC,GC, and RC filters when the comet was bright. The vertical line indicates perihelion. The inset shows zoomed image of post-perihelion data. |
 |
Fig. 3 Evolution of the dust colour as a function of the heliocentric distance. Pre-perihelion values are represented with full circles and post-perihelion values with open circles. |
Taking advantage of our regular observations of the dust continuum through RC and BC
narrow-band filters during the same night, we are able to study the dust colour and its
evolution with heliocentric distance. The dust colour is usually computed as the
normalized gradient of A(θ)fρ from two
continuum filters: ![\begin{equation} \text{colour} [\lambda _{1},\lambda _{2}]=\frac{Af\rho _{1}-Af\rho _{2}}{\lambda _{1}-\lambda _{2}}\frac{2000}{Af\rho _{1}+Af\rho _{2}}\cdot \end{equation}](/articles/aa/full_html/2016/05/aa27628-15/aa27628-15-eq179.png) (1)The normalized reflectivity gradient is
expressed as the percentage of reddening per 1000 Å. Figure 3 shows the evolution of the dust colour as a function of heliocentric distance.
Because of the large dispersion, it is impossible to draw a clear trend with the
heliocentric distance. Our values are higher than those published by (Li et al. 2014) at about the same heliocentric distance
(6%/1000 Å at 3.8 au), but consistent if we consider the large dispersion in the data.
Li et al. reported a reddening of the dust
between 4.6 and 3.3 au, which they attributed to icy grains sublimating in the coma. We
only have a few colour measurements after perihelion, so it is difficult to assess the
effect of the outburst on the dust colour, even though we may be seeing a bluer dust
colour at that time.
(1)The normalized reflectivity gradient is
expressed as the percentage of reddening per 1000 Å. Figure 3 shows the evolution of the dust colour as a function of heliocentric distance.
Because of the large dispersion, it is impossible to draw a clear trend with the
heliocentric distance. Our values are higher than those published by (Li et al. 2014) at about the same heliocentric distance
(6%/1000 Å at 3.8 au), but consistent if we consider the large dispersion in the data.
Li et al. reported a reddening of the dust
between 4.6 and 3.3 au, which they attributed to icy grains sublimating in the coma. We
only have a few colour measurements after perihelion, so it is difficult to assess the
effect of the outburst on the dust colour, even though we may be seeing a bluer dust
colour at that time.
 |
Fig. 4 OH, NH, CN, C3, and C2 production rates and A(0)fρ as a function of the heliocentric distance (r). Pre-perihelion data are represented with filled symbols and post-perihelion data with open symbols. The inset shows zoomed image of post-perihelion data. For CN and C2, spectroscopic determination from FORS 2 have been added. |
3.2. Gas composition
Figure 4 shows the evolution of the gas production rates and A(0)fρ with the heliocentric distance from 2.43 au pre-perihelion until after perihelion. Figure 4 and Table 1 reveal there is no clear increase in most gas production rates while the comet approaches the Sun. They vary only slightly between 2.43 au and perihelion, which may seem surprising. The NH production rates are the only values that increase significantly while the comet approaches the Sun. However, the uncertainties of the NH production rates are larger given the low S/N. The rise of the activity after perihelion followed by the outburst is also clearly visible in Fig. 4. Gas production rates are multiplied by a factor of approximately 5 between November 7 and November 11, 2014. They peak on November 11 and decrease during the following days. This outburst is further analysed in Sect. 4.
Water production rates were reported by Bodewits et al. (2015) from observations with the UltraViolet-Optical Telescope on board Swift between November 2013 and October 2014. They measured H2O production rates of (11.1 ± 1.0) × 1027, (12.1 ± 0.27) × 1027, (13.0 ± 0.45) × 1027, (12.5 ± 0.62) × 1027, and (17.2 ± 0.5) × 1027 mol/s on July 09, August 19, September 18, October 13, and October 23, 2014, respectively. They could not detect water until the comet reached 2.46 au pre-perihelion. Then they observed an increase in water production rates and active area between 2.46 and 2.0 au, followed by a plateau of water production rate along with a decrease in active area between 2 au and perihelion. The closest TRAPPIST observations allowed us to derive equivalent water production rates (Q(H2O) = 1.361r-0.5Q(OH), Cochran & Schleicher 1993) of (8.3 ± 1.3) × 1027, (8.5 ± 1.5) × 1027, (8.75 ± 1.2) × 1027, (11.9 ± 1.6) × 1027, and (9.6 ± 1.6) × 1027 mol/s for observations made respectively on July 10, August 20, September 19, October 13, and October 20, 2014. Most of these observations are consistent within the error bars with values reported by Bodewits et al. (2015). The only large discrepancy is between the H2O production rates measured by Bodewits et al. (2015) on October 23 and our observations performed on October 20. The origin of this discrepancy is not clear, even though the production rate we report for October 20 is lower than the contemporary observation in Table 1. Measurements of OH production rates have also been reported by Crovisier et al. (2014) from observations with the Nancay radio telescope. They measured production rates of (1.3 ± 0.3) × 1028 mol/s between October 5 and 8, 2014, and of (3.3 ± 0.4) × 1028 mol/s between October 11 and 13, 2014. The first measurement is in agreement within the error bars with the value we report for October 6 (Table 1). The second is larger than the OH production we measured on October 13, but Crovisier et al. (2014) mention that their value might be overestimated owing to uncertain Galactic background. Finally, OH, CN, and C2 production rates have also been reported by Schleicher et al. (2014) from observations at the Lowell Observatory on October 12 and 20, 2014, and are mostly in good agreement with the values we report in Table 1.
We computed several production rate ratios in order to characterize the coma composition. Comet Siding Spring is a typical comet in terms of C2/CN and C3/CN ratios, as defined by A’Hearn et al. (1995). The evolution of NH, CN, C3, C2 production rates, and the A(0)fρ relative to OH, are represented in Fig. 5. A linear fit is adopted for each ratio in order to assess the evolution of the coma composition more easily. The C2/OH, C3/OH and CN/OH ratios do not significantly vary with heliocentric distance. On the contrary, the NH/OH ratio increases with decreasing heliocentric distance. However, NH scalelengths and their dependence with heliocentric distance are poorly known, which makes it difficult to interpret the trend in the evolution of the NH/OH ratio. The bottom part of Fig. 5 shows the evolution of the dust-to-gas ratio. The slope of the linear fit is significantly larger than zero, meaning that the coma becomes less dusty as it approaches the Sun. Although we only have a few measurements of these ratios during the outburst, no significant variation of the coma composition at that particular time can be pointed out.
 |
Fig. 5 Ratio of NH, CN, C3, and C2 production rates and the A(0)fρ to OH production rate as a function of the heliocentric distance. Pre-perihelion values are represented with filled symbols and post-perihelion values with open red symbols. Full lines represent linear fits of the ratio variations with the heliocentric distance pre-perihelion. |
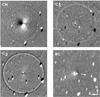 |
Fig. 6 C/2013 A1 (Siding Spring) CN, C3, C2, and dust from BC filter images from November 11 and 12 processed by subtracting an azimuthal median profile. All images are oriented with north up and east left. The field of view is 4.3′ × 4.3′. The arrow indicates the direction of the Sun. The circles in the images are artefacts due to a bright star in the field of view. |
3.3. Morphology
In this section, we discuss the morphology of the coma and its evolution during our observations. We subtracted an azimuthal median profile from every image in order to enhance the contrast between the average coma and the morphological features. Except for CN, we only detect weak or no features. We show an example of CN, C3, C2, and dust from BC filter images in Fig. 6. These images were taken one day after the outburst on November 11, 2014 (but on November 12 for C3). The features visible in Fig. 6 were already there in the August and September images, but they were not as bright and contrasted. We do not observe any particular change of the coma morphology during the observations, or at the time of the outburst, except for a change in the position of the features caused by a variation of the viewing geometry.
The BC enhanced image shows two small jets in opposite directions, different from the tail direction. Some of the BC images (not shown here) also display an enhancement of the coma in the tail direction, which is barely visible in Fig. 6. The position of the dust jets is difficult to determine precisely, given their small spatial extension. The C3 and C2 enhanced images are very similar to each other. They both display two short jets in opposite directions. Even though it is difficult to determine their precise position, they appear close to the dust jets we identified before. However, they are weaker than the dust jets, and are not detected in every image before the outburst. Finally, the CN morphology is completely different: two broader and more extended fans can be observed around PA 185° and PA 330°.
4. Outburst
4.1. Observational characterization
In Sect. 3.2, we inferred that Siding Spring underwent an outburst approximately two weeks after its perihelion passage. From our data set, we can indeed observe an increase in both gas and dust productions consistent with an outburst occurring between November 7.02 and November 11.02, 2014. The CN and C2 radial profiles observed on November 11 diverge from stationary profiles. Figure 7 shows CN and C2 radial profiles from November 11 (i.e. our first observation after the outburst), November 12, and November 13. The most prominent feature visible on the November 11 CN profile is a bump with a rather well-defined edge at around 60 000 km from the nucleus, in addition to the usual stationary radial profile which is still visible at large nucleocentric distance (after 125 000 km). In the following two profiles, this feature is moving away from the nucleus as it propagates into the coma. The same feature is also visible in the C2 profiles. We believe that this is the signature of the outburst. A large amount of gas is released at the time of the outburst, and then expands through the coma. Measuring the position of this shell of material from day to day could in theory allow us to derive the expansion speed of the gas in the coma. However, as can be seen in Fig. 7, its edge is not sharp enough to unambiguously determine the position of the gas shell in each profile. On November 14 and 15, the shape of the CN profile gradually comes back to its pre-outburst shape.
 |
Fig. 7 CN (top) and C2 (bottom) brightness profiles from November 11, 12, and 13, 2014 (r = 1.4 au). The observed profiles are represented with red dots, the Haser model is represented by the dashed line and the outburst model is represented by the black line. |
We attempted to reproduce the shape of the radial profiles observed in Fig. 7 in order to constrain the expansion velocity of the gas during the outburst, and the time at which it occurred. For each profile in Fig. 7, the dashed line represents the Haser model adjusted on the data. As expected, the Haser model fails to reproduce the shape of these radial profiles observed shortly after the outburst. This also means that the production rates we derived in Sect. 3.2 are not representative of the real gas production at the time of the outburst. From the profile shape, we estimate that a two-components model could reproduce the observations. We thus considered a constant underlying gas emission Qb in stationary state and described by the Haser model, to which we added the brief emission of a large amount of gas that expands at a given velocity vo into the coma.
The true physical meaning of this velocity vo is somewhat difficult to interpret. As has already been mentioned, the Haser model is not physically realistic (Combi et al. 2004). It assumes that both parent and daughter species follow purely radial motion. However, as a result of the photodissociation of the parent species, the daughter species have an additional velocity component distributed isotropically in the reference frame of the parent species, which is not accounted for in the Haser model. This problem has been addressed using more complicated models, such as the Vectorial Model (Festou 1981), or using Monte Carlo techniques (Combi & Delsemme 1980). In this paper, we use the velocity vo to describe the expansion of a shell of material (in our case CN or C2) observed in the coma of comet Siding Spring following its outburst. We thus refer to this as the gas expansion velocity, but it is important to keep in mind that it probably does not represent the velocity of the gas directly ejected from the nucleus at the time of the outburst.
We used two exponentials to describe the gas release during the outburst: an increasing
exponential with a characteristic timescale τ1 of typically a few hours to describe
the onset of outburst activity, and a decreasing exponential with a characteristic
timescale τ2 of typically a few days to describe the
slow decrease in the gas emission following the outburst. We consider the start of the
outburst to as the time at which the peak gas
emission Qo occurs. As for the Haser model, we
assumed spherical symmetry for the gas emission, a constant radial velocity
vo, and a single-step photodissociation of
parent molecules into daughter molecules. We used the same scalelengths as for the rest of
our analysis. In our model, the radial density distribution of daughter molecules
n(r) is thus described by:
![\begin{equation} n(r) = \frac{Q}{4\pi r^{2}}\left[\frac{\beta_{0}}{\beta_{1}-\beta_{0}} \right] \left[\mathrm{exp}(-\beta_{0}r) - \mathrm{exp}(-\beta_{1}r) \right] \end{equation}](/articles/aa/full_html/2016/05/aa27628-15/aa27628-15-eq203.png) (2)with
(2)with 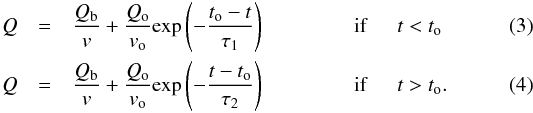 In these equations r is the radial distance in
the coma, v
is the velocity of the gas in stationary equilibrium fixed to 1 km s-1 as in Sect. 3.2, and β0 and β1 are
respectively the parent and daughter scalelengths. First, we tried to model the outburst
using only one exponential to simulate the decrease in the gas emission directly following
the outburst. However, the transition between stationary equilibrium and the outburst was
too sharp compared to the profiles shown in Fig. 7,
and so we added a second exponential to simulate the onset of the activity. We also tried
to use simpler functions as slopes, but they could not reproduce the shape of the profiles
observed at the time of the outburst as did exponentials.
In these equations r is the radial distance in
the coma, v
is the velocity of the gas in stationary equilibrium fixed to 1 km s-1 as in Sect. 3.2, and β0 and β1 are
respectively the parent and daughter scalelengths. First, we tried to model the outburst
using only one exponential to simulate the decrease in the gas emission directly following
the outburst. However, the transition between stationary equilibrium and the outburst was
too sharp compared to the profiles shown in Fig. 7,
and so we added a second exponential to simulate the onset of the activity. We also tried
to use simpler functions as slopes, but they could not reproduce the shape of the profiles
observed at the time of the outburst as did exponentials.
For CN we determined the constant gas emission Qb by adjusting the Haser model on the November 11 observations. We made the adjustment between cometocentric distances of 100 000 km and 160 000 km, since the gas released during the outburst could not have had the time to reach this part of the coma yet. We obtained Qb(CN) = 4.2 × 1025 mol/s. This production rate is close to the one measured four days earlier, on November 7 (see Table 1). As explained before, we used a constant value of Qb for all outburst profiles. Even if the gas production rates vary from day to day, as can be seen from Table 1, this variation is small compared to the amount of gas released at the time of the outburst. Furthermore, in the November 12 and 13 profiles, the influence of the gas released during the outburst extends so far into the coma that it is impossible to independently adjust the value of Qb as was done for the November 11 profile. We then tried to constrain the values of Qo, vo, to, τ1, and τ2 that match simultaneously the observed profiles on Nov. 11, 12, and 13. From the CN profiles, we obtained Qo(CN) = (2.7 ± 0.5) × 1026 mol/s, vo = 1.1 ± 0.2 km s-1, τ1 = 0.3 ± 0.1 j, τ2 = 1.6 ± 0.2 j, and to = Nov. 10.6±0.2. This set of models is overplotted on the observed CN profiles in the upper part of Fig. 7 using a black line. For the three dates, the observed CN profile is much better represented by our model (black curve) than by the Haser model (black dashed line). This model is able to reproduce the bump observed in the radial profile, and its propagation through the coma during the days following the outburst. Larger discrepancies between the observed and modelled profiles only appear at large nucleocentric distances, however. This is mainly caused by the uncertainties in the measurements due to the high airmass of these observations and the faint signal at these distances.
We repeated the same process for the C2 profiles. We measured Qb(C2) = 6.55 × 1025 mol/s. Once again, this value is close to the one measured on November 7. We then attempted to find the best set of parameters to simultaneously reproduce the three C2 profiles. We obtained Qo(C2) = (3.9 ± 0.5) × 1026 mol/s, vo = 1.1 ± 0.2 km s-1, τ1 = 0.4 ± 0.1 j, τ2 = 1.8 ± 0.2 j and to = Nov. 10.7±0.2. This set of models is overplotted on the observed C2 profiles in the lower part of Fig. 7. For the November 11 profile, our model is a much better representation of the data than the Haser model. For the other two profiles, the agreement is not as good as for CN, especially at large nucleocentric distances, but still better than with the Haser model. We were not able to apply our model on the OH data because the S/N of these profiles was too poor. We do not have any NH observations at the time of the outburst, nor do we have C3 observations the day after the outburst to perform the same analysis. We note that it is usual for a cometary outburst’s typical time to reach the peak emission to be shorter than the recovery time, even though the characteristic times for an outburst vary from one comet to another (see Schleicher & Osip 2002; Li et al. 2011; Manfroid et al. 2007). The C2/CN ratio produced during the outburst is 1.46. Within the error bars, this is consistent with the ratios measured before the outburst, indicating that no obvious change of the coma gas composition occurred during the outburst.
Our model provides a satisfactory representation of the shape of the radial brightness profile of the coma of comet Siding Spring for the three days following the outburst using one single set of parameters for each species. Parameters derived from the C2 profiles and from the CN profiles agree with each other within the error bars. We can determine that the outburst most probably occurred on November 10 around 15:30 UT (±5 h). The expansion velocity of the gas after the outburst was vo = 1.1 ± 0.2 km s-1. This velocity is consistent with the gas outflow velocity of 1 km s-1 that we assumed in the Haser model. Only a few measurements of gas velocity during an outburst have been made, but our value is close to the CN radial expansion velocity of 0.85 ± 0.04 km s-1 measured by Schulz et al. (2000) during the activity outburst of comet C/1995 O1 (Hale-Bopp). Manfroid et al. (2007) measured gas velocities of 0.4−0.6 km s-1 in the coma of comet 9P/Tempel 1 after the Deep Impact event. This is lower than the velocity we measured here, but the outburst of comet Tempel 1 was caused by the impact of a 362 kg mass on the nucleus and the outburst mechanism is thus different from the one observed here. Finally, the velocity we measure here is also in agreement with OH expansion velocities in the coma of quiescent comets at the same heliocentric distance (e.g. Bockelee-Morvan et al. 1990; Tseng et al. 2007).
Unfortunately, we were only able to determine an upper limit for the velocity of the dust ejected during the outburst. We attempted to measure the position of the dust shell ejected during the outburst in successive BC images taken on the days after the outburst. However, the S/N in the images is low, making the determination of the dust shell position difficult. The S/N was higher in RC filter but we do not have regular observations in this filter around the time of the outburst. We could only determine an upper limit of 100 m/s. This seems low compared to the dust velocities usually measured during cometary outbursts. Indeed, Hsieh et al. (2010) and Lin et al. (2009) measured velocities around 550 m/s for the outburst of comet 17P/Holmes, while Schulz et al. (2000) measured a velocity of 200 m/s for the outburst of comet C/1995 O1 (Hale-Bopp). Lara et al. (2007) measured velocities ranging from 150 to 230 m/s in the coma of comet 9P/Tempel 1 after the Deep Impact event. Such a low dust velocity could indicate that the outburst mostly released large grains.
4.2. Modelling the outburst and activity pattern
Based on the gas production rates determined in the previous sections, our goal is to
estimate the thickness of dust that would be required at the surface to reproduce the
pre-perihelion production rates and the outburst observed in our dataset, using a
technique similar to the one described in Guilbert-Lepoutre et al. (2014). We based our calculation on the measurement of
the CN production rates. CN is the daughter molecule of HCN, which if present in the
nucleus under a dusty crust, may not sublimate freely. If buried under a dusty crust, it
would follow a diffusion regime, with a mass loss rate written as (assuming an ideal gas
law, Fanale & Salvail 1984; Schorghofer 2008; Gundlach et al. 2011; Guilbert-Lepoutre et al.
2014) 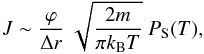 (5)where J is the ice loss rate from
a subsurface layer buried under the crust, ϕ the permeability of the crust, Δr [m] its thickness,
m [kg] the
molecular weight, kB [JK-1] the Boltzmann constant,
T [K] the
temperature, and PS(T) [Pa] the
saturation vapour pressure given by the Clausius-Clapeyron equation
(5)where J is the ice loss rate from
a subsurface layer buried under the crust, ϕ the permeability of the crust, Δr [m] its thickness,
m [kg] the
molecular weight, kB [JK-1] the Boltzmann constant,
T [K] the
temperature, and PS(T) [Pa] the
saturation vapour pressure given by the Clausius-Clapeyron equation
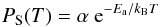 (6)with α = 3.86 × 1010
Pa and −Ea/kB =
4023.66 K for HCN. In our calculations, the temperature distribution at
the surface and in the nucleus of the comet is determined using a numerical model of
three-dimensional heat transport (Guilbert-Lepoutre et al.
2011). The model solves the heat equation taking into account conduction via
contacts between grains, radiation within pores, insolation, and thermal emission at the
surface. This distribution is computed as a function of time and orbital position of the
comet. Since Siding Spring is a dynamically new comet with no previously known perihelion
passage, we start our simulation at 100 au with a temperature of 20 K. We assume that the
upper layer is made of porous dust, with 85% porosity and thermal inertia of 15 J
m-2
K-1
s−1/2, which is
consistent with the measurements of low thermal inertias for comets in general and
67P/Churyumov-Gerasimenko, which is being thoroughly studied by the ESA/Rosetta mission
(Lowry et al. 2012; Gulkis et al. 2015). We then estimate the thickness Δr of the dusty crust by
inverting Eq. (5) for each orbital position
of the comet where we have a measurement of CN production rate.
(6)with α = 3.86 × 1010
Pa and −Ea/kB =
4023.66 K for HCN. In our calculations, the temperature distribution at
the surface and in the nucleus of the comet is determined using a numerical model of
three-dimensional heat transport (Guilbert-Lepoutre et al.
2011). The model solves the heat equation taking into account conduction via
contacts between grains, radiation within pores, insolation, and thermal emission at the
surface. This distribution is computed as a function of time and orbital position of the
comet. Since Siding Spring is a dynamically new comet with no previously known perihelion
passage, we start our simulation at 100 au with a temperature of 20 K. We assume that the
upper layer is made of porous dust, with 85% porosity and thermal inertia of 15 J
m-2
K-1
s−1/2, which is
consistent with the measurements of low thermal inertias for comets in general and
67P/Churyumov-Gerasimenko, which is being thoroughly studied by the ESA/Rosetta mission
(Lowry et al. 2012; Gulkis et al. 2015). We then estimate the thickness Δr of the dusty crust by
inverting Eq. (5) for each orbital position
of the comet where we have a measurement of CN production rate.
Given that our study of the coma morphology has shown that Siding Spring presents jets, it is unlikely that the entire surface of its nucleus is active: we expect that this would lead to local variations in the crust thickness. We must therefore keep in mind that our modelling is aimed at providing order of magnitude results, in order to understand the general behaviour of Siding Spring’s activity. Before the outburst, our calculations show that CN production rates can be reproduced if we assume that the thickness of the dusty crust at the surface of Siding Spring (assuming that the overall surface is active) is steadily increasing, from 3.5 cm on June 03, when at 2.42 au, to ~8 cm on October 29, when at 1.4 au. This is consistent with the expected progressive formation of a dust mantle at the surface of an active comet, and also consistent with our inference of a coma becoming less dusty when the comet approaches the Sun. Eventually, the porosity of the dust mantle may become too small to allow any particle to be released, thus forming a stable crust, with a cohesive strength greater than the vapour pressure building up below it. However, with insolation becoming more efficient in sublimating subsurface ice when the comet reaches perihelion, the gas pressure below the crust would increase, and the dust mantle could be totally or partially blown off. This process can be invoked to explain the outburst of comet Siding Spring. From November 7, our calculations show that the crust thickness required to reproduce the CN production rates decreases with a minimal thickness of 4.5 cm achieved on November 11. Afterwards, the crust thickness increases again. It is unclear from the available data whether the whole dust mantle was blown off, or only part of it. Although many parameters involved in these calculations are unknown or poorly constrained, we can estimate that 50 to 120 × 106 kg of dust were released during the outburst. These numbers are in fact consistent with the dust production we measured, and the low velocity of dust particles at the time of the outburst, which indicates that large grains were emitted. The dust particles forming a dust mantle are expected to be the heaviest relative to their cross section to be entrained by the outgassing. Therefore, by basing our calculations on the CN production rates measured before and during the outburst, we can reproduce the activity pattern and dust properties observed for comet Siding Spring in a self-consistent way. This may indicate that the mechanism at the origin of Siding Spring’s outburst is related to dust mantle formation and destruction.
5. Conclusion
In this paper, we have presented a unique data set consisting of more than a year of regular observations of comet C/2013 A1 (Siding Spring) with the TRAPPIST telescope in Chile, along with low-resolution spectra obtained with the ESO/VLT FORS 2 instrument. We first demonstrated that simultaneous measurements of gas radial profiles and production rates from narrow-band photometry with TRAPPIST and low-resolution spectroscopy with FORS 2 were in good agreement and could be used to complement each other in the future. We then studied the evolution of the comet activity, along with its gas and dust composition, using various ratios such as CN/OH, C2/OH, or C3/OH, which showed little or no variation with heliocentric distance. Only the NH/OH ratio increased while the comet approached the Sun, but this could just be the effect of poorly known NH scalelengths. Enhancement techniques applied to all images allowed us to detect morphological features in the coma. Except for the dust and CN, these features were weak and could not be detected in all images. The orientation of C3 and C2 features is difficult to determine owing to their small spatial extension. CN and dust features both have an hourglass shape, but are not oriented in the same direction. This indicates that they probably do not originate from the same source region(s). This monitoring allowed us to detect an outburst of activity, which we have characterized and modelled. The CN and C2 production rates were measured at the peak of the outburst. The C2/CN ratio measured at that time is consistent within the error bars with the ratios measured before the outburst, while the production rates were multiplied by about a factor of 5. Overall, we could not detect any significant change in the coma composition or dust-to-gas ratio after perihelion, nor at the time of the outburst, which may indicate a certain level of homogeneity of the nucleus composition.
The gas radial profiles observed shortly after the outburst were different from those usually observed for this comet. We provided a simple model for representing them. This model represents the outburst as a sudden emission of a large quantity of gas that expands in the coma at a given velocity. The outburst is added to the equilibrium gas emission described by the Haser model. We considered an exponential rise in the gas emission with a characteristic timescale τ1 to reach a maximum production rate, then an exponential decrease with a characteristic timescale τ2. For consistency, we used the same hypothesis as in the Haser model, as well as the same scalelengths. We found a set of modelling parameters that simultaneously provided a good representation of the radial profiles for the three days following the outburst. In addition, the parameters determined from CN and C2 profiles agree within the error bars. We used a thermal evolution model to reproduce the activity pattern and outburst, by constraining the thickness of a dusty crust present at the surface of the comet. Our results are consistent with the progressive formation of a dust mantle, which may be partially blown off during the outburst. Overall, our observations and modelling results, i.e. the shallow dependence of pre-perihelion gas production rates, consistent with the progressive formation of a dust mantle, are in fact quite typical for dynamically new comets as concluded by A’Hearn et al. (1995). Comet Siding Spring is therefore behaving like a typical dynamically new comet.
For example, the evolution of Siding Spring’s activity between 2.5 au and perihelion is relatively similar to that of comet C/2009 P1 (Garradd) (Combi et al. 2013; Bodewits et al. 2014) at around the same pre-perihelion heliocentric distance. The behaviour of comet Garradd’s activity was attributed to the presence of an extended source of water. According to Bodewits et al. (2015), CO2 sublimation from a constant area on the nucleus may have dominated the activity of comet Siding Spring at heliocentric distances larger than 2.5 au. At this distance, the sublimation of icy grains, in addition to ice sublimating from the nucleus itself, may explain the increase in the water production, as was the case for comet Garradd. Icy grains in the coma of this comet have also been invoked by Li et al. (2014) to explain the dust colour trend in the coma and its temporal evolution. The scenario suggested by Bodewits et al. (2015) thus seems consistent with our results.
Even though outbursts may seem to be a rather common phenomenon among comets, their origin is still not well understood. The amplitude of the brightness increases and the frequency varies from comet to comet. Some comet nuclei may be splitting: such an event would expose a large amount a fresh ice that would explain the sudden increase in gas and dust production. We carefully searched the enhanced images of the comet for five days after the outburst and could not detect any sign of nucleus fragmentation such as a blob of material in the coma, or the so-called coma wings (Boehnhardt 2000). A nucleus splitting being the origin of the outburst thus seems unlikely. Outbursts can also be caused by a collision with another body. However, these collisions are extremely rare and no evidence in our observations points to an external source as the origin of this outburst. Cavities under the surface of the nucleus containing gas under high pressure have already been invoked to explain cometary outbursts (Ipatov & A’Hearn 2011). This process is similar to the one we have inferred in our model, where a dusty crust may be totally or partially blown away by an increase of the gas pressure underneath. Although this scenario may adequately reproduce both gas and dust production evolution before and during the outburst, we cannot exclude other mechanisms. In particular, by studying the coma morphology, Li et al. (2014) determined two pole solutions for comet Siding Spring resulting in different seasonal effect on the nucleus. For their second solution (rotational pole: Right Ascension = 190 ± 10° and Declination = 50 ± 5°), they predicted that the Sun would illuminate a new area just after perihelion. The onset of sublimation on this fresh newly active area of the nucleus just after perihelion may thus also explain the outburst we observed on November 10.
Acknowledgments
TRAPPIST is a project funded by the Belgian Fund for Scientific Research (Fond National de la Recherche Scientifique, F.R.S.-FNRS) under grant FRFC 2.5.594.09.F, with the participation of the Swiss National Science Fundation (SNF). C. Opitom acknowledges the support of the FNRS. E. Jehin and M. Gillon are FNRS Research Associates, D. Hutsemékers is FNRS Senior Research Associate and Jean Manfroid is Research Director of the FNRS. We are grateful to David Schleicher and the Lowell Observatory for the loan of a set of NASA HB comet filters.
References
- A’Hearn, M. F., Schleicher, D. G., Millis, R. L., Feldman, P. D., & Thompson, D. T. 1984, AJ, 89, 579 [NASA ADS] [CrossRef] [Google Scholar]
- A’Hearn, M. F., Millis, R. C., Schleicher, D. O., Osip, D. J., & Birch, P. V. 1995, Icarus, 118, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Appenzeller, I., Fricke, K., Fürtig, W., et al. 1998, The Messenger, 94, 1 [NASA ADS] [Google Scholar]
- Benna, M., Mahaffy, P. R., Grebowsky, J. M., et al. 2015, Geophys. Res. Lett., 42, 4670 [NASA ADS] [CrossRef] [Google Scholar]
- Bockelee-Morvan, D., Crovisier, J., & Gerard, E. 1990, A&A, 238, 382 [NASA ADS] [Google Scholar]
- Bodewits, D., Farnham, T. L., A’Hearn, M. F., et al. 2014, ApJ, 786, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Bodewits, D., Kelley, M. S. P., Li, J.-Y., Farnham, T. L., & A’Hearn, M. F. 2015, ApJ, 802, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Boehnhardt, H. 2000, Earth Moon Planets, 89, 91 [Google Scholar]
- Cochran, A. L., & Schleicher, D. G. 1993, Icarus, 105, 235 [Google Scholar]
- Combi, M. R., & Delsemme, A. H. 1980, ApJ, 237, 633 [NASA ADS] [CrossRef] [Google Scholar]
- Combi, M. R., Harris, W. M., & Smyth, W. H. 2004, Gas dynamics and kinetics in the cometary coma: theory and observations, ed. G. W. Kronk, 523 [Google Scholar]
- Combi, M. R., Mäkinen, J. T. T., Bertaux, J.-L., et al. 2013, Icarus, 225, 740 [NASA ADS] [CrossRef] [Google Scholar]
- Crovisier, J., Colom, P., Biver, N., et al. 2014, Central Bureau Electronic Telegrams, 4001, 1 [NASA ADS] [Google Scholar]
- Dones, L., Weissman, P. R., Levison, H. F., & Duncan, M. J. 2004, Oort cloud formation and dynamics, eds. M. C. Festou, H. U. Keller, & H. A. Weaver (Tucson: Univ. og Arizona), 153 [Google Scholar]
- Fanale, F. P., & Salvail, J. R. 1984, Icarus, 60, 476 [NASA ADS] [CrossRef] [Google Scholar]
- Farnham, T., Schleicher, D., & A’Hearn, M. 2000, Icarus, 147, 180 [NASA ADS] [CrossRef] [Google Scholar]
- Festou, M. C. 1981, A&A, 95, 69 [NASA ADS] [Google Scholar]
- Guilbert-Lepoutre, A., Lasue, J., Federico, C., et al. 2011, A&A, 529, A71 [Google Scholar]
- Guilbert-Lepoutre, A., Schulz, R., Rożek, A., et al. 2014, A&A, 567, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gulkis, S., Allen, M., von Allmen, P., et al. 2015, Science, 347, 0709 [Google Scholar]
- Gundlach, B., Kilias, S., Beitz, E., & Blum, J. 2011, Icarus, 214, 717 [NASA ADS] [CrossRef] [Google Scholar]
- Gurnett, D. A., Morgan, D. D., Persoon, A. M., et al. 2015, Geophys. Res. Lett., 42, 4745 [NASA ADS] [CrossRef] [Google Scholar]
- Haser, L. 1957, Bulletin de l’Académie Royal des Sciences de Belgique, 63, 739 [Google Scholar]
- Hsieh, H. H., Fitzsimmons, A., Joshi, Y., Christian, D., & Pollacco, D. L. 2010, MNRAS, 407, 1784 [NASA ADS] [CrossRef] [Google Scholar]
- Ipatov, S. I., & A’Hearn, M. F. 2011, MNRAS, 414, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Jehin, E., Gillon, M., Queloz, D., et al. 2011, The Messenger, 145, 2 [NASA ADS] [Google Scholar]
- Kelley, M. S. P., Farnham, T. L., Bodewits, D., Tricarico, P., & Farnocchia, D. 2014, ApJ, 792, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Lara, L. M., Boehnhardt, H., Gredel, R., et al. 2007, A&A, 465, 1061 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, J., Jewitt, D., Clover, J. M., & Jackson, B. V. 2011, ApJ, 728, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Li, J.-Y., Samarasinha, N. H., Kelley, M. S. P., et al. 2014, ApJ, 797, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, Z.-Y., Lin, C.-S., Ip, W.-H., & Lara, L. M. 2009, AJ, 138, 625 [NASA ADS] [CrossRef] [Google Scholar]
- Lowry, S., Duddy, S. R., Rozitis, B., et al. 2012, A&A, 548, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Manfroid, J., Hutsemékers, D., Jehin, E., et al. 2007, Icarus, 187, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Marcus, J. N. 2007, International Comet Quarterly, 29, 39 [NASA ADS] [Google Scholar]
- McNaught, R. H., Sato, H., & Williams, G. V. 2013, Central Bureau Electronic Telegrams, 3368, 1 [NASA ADS] [Google Scholar]
- Opitom, C., Jehin, E., Manfroid, J., et al. 2015, A&A, 574, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Restano, M., Plaut, J. J., Campbell, B. A., et al. 2015, Geophys. Res. Lett., 42, 4663 [NASA ADS] [CrossRef] [Google Scholar]
- Schleicher, D. G., & Osip, D. J. 2002, Icarus, 159, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Schleicher, D. G., Millis, R. L., & Birch, P. V. 1998, Icarus, 132, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Schleicher, D., Knight, M., & Skiff, B. 2014, Central Bureau Electronic Telegrams, 4004, 1 [NASA ADS] [Google Scholar]
- Schneider, N. M., Stewart, A. I. F., McClintock, W. E., et al. 2015, in Lunar and Planetary Science Conference, 46, 2804 [Google Scholar]
- Schorghofer, N. 2008, ApJ, 682, 697 [NASA ADS] [CrossRef] [Google Scholar]
- Schulz, R., Stüwe, J. A., Tozzi, G. P., & Owens, A. 2000, A&A, 361, 359 [NASA ADS] [Google Scholar]
- Stevenson, R., Bauer, J. M., Cutri, R. M., Mainzer, A. K., & Masci, F. J. 2015, ApJ, 798, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Tseng, W.-L., Bockelée-Morvan, D., Crovisier, J., Colom, P., & Ip, W.-H. 2007, A&A, 467, 729 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
OH, NH, CN, C3, and C2 production rates and Afρ of comet C/2013 A1 (Siding Spring) from TRAPPIST observations.
CN and C2 production rates of C/2013 A1 (Siding Spring) from VLT/FORS 2 observations.
All Figures
 |
Fig. 1 CN (top) and C2 (bottom) brightness profiles from Jul. 25 and Sep. 19, 2014. TRAPPIST data are represented with red circles and the closest VLT data is overplotted. Data extracted from both sides of the nucleus in the spectra are represented respectively with green triangles and blue squares. |
| In the text | |
 |
Fig. 2 Logarithm of the A(0)fρ corrected from phase angle effect as a function of the heliocentric distance r. The A(0)fρ was measured from Rc broad-band filter and from narrow-band BC,GC, and RC filters when the comet was bright. The vertical line indicates perihelion. The inset shows zoomed image of post-perihelion data. |
| In the text | |
 |
Fig. 3 Evolution of the dust colour as a function of the heliocentric distance. Pre-perihelion values are represented with full circles and post-perihelion values with open circles. |
| In the text | |
 |
Fig. 4 OH, NH, CN, C3, and C2 production rates and A(0)fρ as a function of the heliocentric distance (r). Pre-perihelion data are represented with filled symbols and post-perihelion data with open symbols. The inset shows zoomed image of post-perihelion data. For CN and C2, spectroscopic determination from FORS 2 have been added. |
| In the text | |
 |
Fig. 5 Ratio of NH, CN, C3, and C2 production rates and the A(0)fρ to OH production rate as a function of the heliocentric distance. Pre-perihelion values are represented with filled symbols and post-perihelion values with open red symbols. Full lines represent linear fits of the ratio variations with the heliocentric distance pre-perihelion. |
| In the text | |
 |
Fig. 6 C/2013 A1 (Siding Spring) CN, C3, C2, and dust from BC filter images from November 11 and 12 processed by subtracting an azimuthal median profile. All images are oriented with north up and east left. The field of view is 4.3′ × 4.3′. The arrow indicates the direction of the Sun. The circles in the images are artefacts due to a bright star in the field of view. |
| In the text | |
 |
Fig. 7 CN (top) and C2 (bottom) brightness profiles from November 11, 12, and 13, 2014 (r = 1.4 au). The observed profiles are represented with red dots, the Haser model is represented by the dashed line and the outburst model is represented by the black line. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


