| Issue |
A&A
Volume 589, May 2016
|
|
|---|---|---|
| Article Number | A112 | |
| Number of page(s) | 9 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201527484 | |
| Published online | 20 April 2016 | |
Pseudomagnitudes and differential surface brightness: Application to the apparent diameter of stars
1 Laboratoire Lagrange, Université Côte d’Azur, Observatoire de la Côte d’Azur, CNRS, Bd de l’Observatoire, 06304 Nice, France
e-mail: Alain.Chelli@oca.eu
2 Univ. Grenoble Alpes, IPAG, 38000 Grenoble, France
3 CNRS, IPAG, 38000 Grenoble, France
Received: 30 September 2015
Accepted: 28 January 2016
The diameter of a star is a major observable that serves to test the validity of stellar structure theories. It is also a difficult observable that is mostly obtained with indirect methods since the stars are so remote. Today only ~600 apparent star diameters have been measured by direct methods: optical interferometry and lunar occultations. Accurate star diameters are now required in the new field of exoplanet studies, since they condition the planets’ sizes in transit observations, and recent publications illustrate a visible renewal of interest in this topic. Our analysis is based on the modeling of the relationship between measured angular diameters and photometries. It makes use of two new reddening-free concepts: a distance indicator called pseudomagnitude, and a quasi-experimental observable that is independent of distance and specific to each star, called the differential surface brightness (DSB). The use of all the published measurements of apparent diameters that have been collected so far, and a careful modeling of the DSB allow us to estimate star diameters with a median statistical error of 1.1%, knowing their spectral type and, in the present case, the VJHKs photometries. We introduce two catalogs, the JMMC Measured Diameters Catalog (JMDC), containing measured star diameters, and the second version of the JMMC Stellar Diameter Catalog (JSDC), augmented to about 453 000 star diameters. Finally, we provide simple formulas and a table of coefficients to quickly estimate stellar angular diameters and associated errors from (V, Ks) magnitudes and spectral types.
Key words: stars: fundamental parameters / methods: data analysis / astronomical databases: miscellaneous / catalogs / techniques: interferometric
© ESO, 2016
1. Introduction
Most of our knowledge of the Universe still comes from, either directly or indirectly, an analysis of starlight. Stellar physics is used, implicitly or explicitly, in every astrophysical research field, and must be continually tested against observations. One of the most fundamental and dimensioning parameters of the physics of a star is its size, measured through its distance and its apparent angular size. The original interest in measuring stellar angular sizes was to get precise estimates of the stellar effective temperature, Teff, which is pivotal to, for example, determining ages and metallicities. But there is renewed interest, such as the precise stellar radii now needed to measure transiting exoplanets’ sizes and densities, which can eventually fall into the host star’s so-called habitable zone (von Braun et al. 2014).
Primary distance measurements are the realm of the space missions Hipparcos (ESA 1997) and Gaia (de Bruijne 2012). The most straightforward method to measure the angular sizes of stars is interferometry (Michelson & Pease 1921; Hanbury Brown & Twiss 1958; Labeyrie 1975), and in a less measure, more historically, lunar occultations (Cousins & Guelke 1950). Modern interferometric techniques – combining adaptive optics, mononode fibers, cophasing, fast and low noise near-infrared cameras – are today able to measure stellar diameters with a precision better than 1% (Cruzalèbes et al. 2013; Boyajian et al. 2012a,b). However the ultimate precision is often dominated by the calibration process. To reach very high precision, it is mandatory to know and to observe with the state of the art procedures, together with the object of interest, a star called calibrator. In other words, a single star, as close as possible to the object, with similar magnitude, with a known angular diameter and associated error, that is used to measure the transmission of the observing system. This underlines the importance of angular diameter predictions for calibration purposes. The angular diameter predictions are based on two kind of methods: the first are based on a polynomial fit of measured angular diameters as a function of colors, from Wesselink (1969) to Boyajian et al. (2013, 2014); the second, like the Infrared Flux Method (Blackwell et al. 1979; Casagrande et al. 2010), are based on a subtle mix of experimental data and modeling. Other methods, like Asteroseismology (Brown & Gilliland 1994; Chaplin & Miglio 2013), provide linear diameters that must be converted to angular diameters using a distance estimate.
Our initial motivation for this work was to optimize the calibrator-finding utility SearchCal1 (Bonneau et al. 2006, 2011), an angular diameter estimator of the first kind described above, with a rigorous treatment of error propagation. The aim was to produce a more robust version of the catalog of ~40 000 star diameters, the JMMC Stellar Diameter Catalog (JSDC; Lafrasse et al. 2010). This led us to reconsider the general problem of deriving the polynomial coefficients that are used in such estimators, which usually come from star magnitudes that need to be de-reddened before use. We solved the visual extinction problem by introducing two new concepts: a distance indicator called pseudomagnitude, and the differential surface brightness (DSB), both reddening-free. The DSB is an observable specific to each star, independent of distance, which depends only on measured quantities: the stellar diameter and the observed magnitudes.
Our approach to predict stellar diameters, definitely experimental, consists of a polynomial fit of the DSB as a function of the spectral type number for a database of stars with known diameters. It allows us to by-pass the knowledge of visual extinction and that of intrinsic colors. The polynomial coefficients are then applicable to any star with a known spectral type and magnitudes to provide an apparent diameter value. As an illustration of our method, we compiled a catalog of ~600 measured star diameters and photometries that we used to compute the DSB polynomial fit. Using these polynomials and all the stars in the ASCC catalog (Kharchenko 2001) that have an associated spectral type, we are able to give the apparent diameter of ~453 000 stars with a median diameter precision of 1.1%, as well as possible astrophysical biases up to 2% (due to luminosity classes, DSB fine structures, metallicity, and so on), that is in agreement with the limiting precisions discussed in Casagrande et al. (2014).
Section 2 introduces the new formalism, especially the concepts of pseudomagnitudes and differential surface brightness. Section 3 describes the least squares fit approach. Section 4 describes how we built the database of measured diameters from the literature, discusses their validity, and how we tried to avoid any systematics. The results are presented and discussed in Sect. 5.
2. Pseudomagnitudes and differential surface brightness
In this section, we introduce the concept of pseudomagnitudes and a new experimental observable: the differential surface brightness (DSB). Our starting point is the expression of the surface brightness Si of a star (Wesselink 1969), see Eq. (9) of Barnes & Evans (1976): 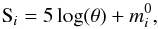 (1)where θ is the angular diameter of the star and
(1)where θ is the angular diameter of the star and 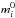 the unreddened magnitude in the photometric band i.
the unreddened magnitude in the photometric band i. 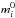 can be written as:
can be written as: 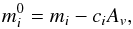 (2)where mi is the observed magnitude, ci is the ratio between the extinction coefficients Ri and Rv in the i and visible bands, respectively. Given two photometric bands i and j, the interstellar extinction can be writtten as
(2)where mi is the observed magnitude, ci is the ratio between the extinction coefficients Ri and Rv in the i and visible bands, respectively. Given two photometric bands i and j, the interstellar extinction can be writtten as 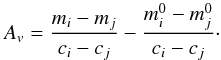 (3)Combining the three previous equations, the surface brightness may be expressed as a function of the angular diameter, the measured magnitudes, and the intrinsic color of the star,
(3)Combining the three previous equations, the surface brightness may be expressed as a function of the angular diameter, the measured magnitudes, and the intrinsic color of the star, 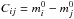 . That is to say
. That is to say 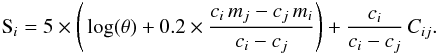 (4)At this point, it is useful to introduce a new stellar observable that we call pseudomagnitude, defined by
(4)At this point, it is useful to introduce a new stellar observable that we call pseudomagnitude, defined by 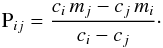 (5)The pseudomagnitudes have remarkable properties and applications that will be discussed in a forthcoming paper. Basically, they are reddening free distance indicators:
(5)The pseudomagnitudes have remarkable properties and applications that will be discussed in a forthcoming paper. Basically, they are reddening free distance indicators: 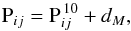 (6)where
(6)where 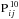 is the absolute pseudomagnitude, i.e., the pseudomagnitude at 10 pc distance, dM = 5log (d)−5 is the distance modulus and d the distance in parsecs. We note that if one of the coefficients ci or cj tends to zero, then the pseudomagnitude tends to the magnitude mi or mj. Hence, the absolute pseudomagnitude is, in some way, related to the stellar luminosity.
is the absolute pseudomagnitude, i.e., the pseudomagnitude at 10 pc distance, dM = 5log (d)−5 is the distance modulus and d the distance in parsecs. We note that if one of the coefficients ci or cj tends to zero, then the pseudomagnitude tends to the magnitude mi or mj. Hence, the absolute pseudomagnitude is, in some way, related to the stellar luminosity.
The surface brightness may simply be rewritten as follows: 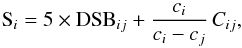 (7)where DSBij is the DSB between the photometric bands i and j, defined as
(7)where DSBij is the DSB between the photometric bands i and j, defined as 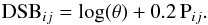 (8)DSBij is a self-calibrated observable specific to each star. It is reddening-free, independent of the distance, and can be measured via photometry and interferometry. The only a priori is the diameter limb-darkening correction, which induces a diameter error that is generally less than 1%, smaller than the errors managed in this work.
(8)DSBij is a self-calibrated observable specific to each star. It is reddening-free, independent of the distance, and can be measured via photometry and interferometry. The only a priori is the diameter limb-darkening correction, which induces a diameter error that is generally less than 1%, smaller than the errors managed in this work.
The knowledge of the DSB, as a function of the spectral type, the luminosity class, the metallicity, and so on, is sufficient to predict the angular diameter of a star, given its observed magnitudes. Unfortunately, we do not possess this level of detailed information because of the poor spectral type-sampling owing to the small number of useable measured diameters (~600) available today. To compensate our lack of knowledge, we fit the DSB as a function of the spectral type number ns (varying from 0 to 69 for spectral types between O0 to M9) with simple polynomial laws. Within the present framework, if the determination of spectral type is robust to reddening (e.g., is not derived from colors), then the intrinsic color, replaced by the spectral type number, is no longer a variable of the diameter prediction problem and our approach is fully reddening-free.
3. Algorithmic approach
This is a two-step process: 1) polynomial estimate based on the DSBs derived from database values; 2) diameter calculations from polynoms and pseudomagnitudes.
3.1. Polynomial
A data point consists in a limb-darkened diameter θ and NB photometric bands, which provides NB−1 linearly independent (but statistically dependent) equations. We can build many sets of NB−1 linearly independent equations, but each set provides the same polynomial solution. We then have to characterize, NB−1 polynomials of degree m, each associated with a pair of photometric bands. This corresponds to (m + 1) × (NB−1) unknowns, that we evaluate simultaneously via a simple linear least squares fit (see Appendix A.1).
Wherever possible, we used the mean interstellar extinction coefficients of Fitzpatrick (1999) that give: (cV,cJ,cH,cKs) = (1.0,0.28,0.17,0.12). Strictly speaking, the coefficients ci depend on the spectral type (McCall 2004). In principle, one can consider variable coefficients, but for the present analysis we restrict ourselves to constant values, since the influence of these variations, with respect to diameter calculation, is smaller than the errors and the biases reported here.
Also, it may be necessary to reject anomalous data points. For example, in the production of the star diameter catalog described in Sect. 5, we use the database described in Sect. 4. From the found polynomial solution, for each entry of our database we can estimate NB−1 single diameters and a mean diameter. It sometimes occurs that one or various single diameters deviate from the mean diameter by more than 5 times the error on the difference. This may be due to observational biases in the diameter measurements, or that the star is not single, etc. In this case, we excluded the entry from the database that was used. Table 2 lists all the stars and references retained for fitting the polynomials, as discussed in Sect. 5.
3.2. Diameters
A polynomial, together with two magnitudes (pseudomagnitude), provides an estimate of the diameter. Several pairs of magnitudes gives several estimates of the same diameter. These are not statistically independent and we show in Appendix A.2 how to rigorously combine them in a single diameter value and its associated error. Beyond the error improvement, which is generally modest, the main interest of using more than two photometric bands is to produce various diameter estimates that can be recombined and, above all, compared through a quality factor, see Sect. 5.
4. The database of measured angular diameters
4.1. Building the database
The empirical approach used in this paper relies on the knowledge of a statistically significant number of accurately measured angular diameters, ideally obtained with different techniques, such as avoiding as much as possible any technique-related bias. The angular diameters must be prime results, i.e., not the result of a modeling of the observations. Ideally, they should be equally distributed, both in space and in spectral type.
Several star diameter compilations exist that contain a fair amount of published angular diameters values. The CADARS (Pasinetti Fracassini et al. 2001) has entries for 6888 stars and is complete up to 1997. CHARM2 (Richichi et al. 2005) lists 8231 measurements of 3243 stars, up to 2005. However these catalogs mix results from very direct methods, such as intensity interferometry with indirect methods, or spectrophotometric estimates of various kind (always including some model of the star), or linear diameters from eclipsing binaries (1600 entries in CADARS), which need some modelling of the two stars, as well as a good estimate of the distance to be converted into an angular diameter.
Another difficulty is that, the published angular diameters have been obtained at various wavelengths and may include, or not, a compensation for the limb-darkening effect. As a result, we initiated a new compilation of measured stellar diameters that would suit our needs. This database, called JMDC2, only uses direct methods, merges multiwavelength measurements into one value of limb-darkened diameter (LDD), and aims to be complete up to the most recent publications by being updated on a regular basis through a peer-reviewed submission process.
The JMDC used in this paper gathers 1072 apparent diameter values that have been published since the first experiments by Michelson. Prior to 1997, our bibliography relies only on the reference list of Pasinetti Fracassini et al. (2001). After this date we used NASA’s ADS hosted at CDS. We retained only the measurements obtained from visible/IR interferometry, intensity interferometry and lunar occultation in the database. We always retrieved the values in the original text3 and used SIMBAD to properly and uniquely identify the stars.
The three techniques retained share the same method of converting the measurements (squared visibilities for optical interferometry, correlation of photon-counts for intensity interferometry, fast photometry for lunar occultations) into an angular diameter: fitting a geometrical function into the values, in many cases a uniform disk, which provides a uniform disk diameter (UDD) value. This UDD is wavelength-dependent owing to the limb-darkening effect of the upper layers of a star’s photosphere, and JMDC retains the wavelength or photometric band at which the observation was made.
To measure a star’s apparent diameter consistently, i.e., with the same meaning as our Sun’s well-resolved apparent diameter, it was necessary for the authors of these measurements to take into account the star’s limb-darkening, for which only theoretical estimates exist as yet. They chose one of the various limb-darkening parameters available in the literature (see Claret 2000, for a discussion on the classical limb-darkening functions used), either by multiplying the UDD by a coefficient function of the wavelength and the star’s adopted effective temperature, or directly fitting a limb-darkened disk model in the data. Of course this adds some amount of theoretical bias in the published measurements, which however diminishes as the wavelength increases. An additional difficulty for the lunar occultations is that the result depends on the exact geometry of the occulting portion of the lunar limb, which can, more or less, be correctly estimated.
To deal with the limb-darkening problem as efficiently as possible, in the publications where reported diameters are measured in several optical/IR bands, we retained the measurement with the best accuracy and favored the measurement at the longest wavelength to minimize the effect of limb-darkening correction. Furthermore, we further used the published UDD measurement, or retrieved the original, unpublished UDD measurement from the LDD value and the limb-darkening coefficient used by the authors, and uniformly converted these UDD values into limb-darkened angular diameters using the most recent correction factors published (Neilson & Lester 2013a,b), when possible. This, in our opinion, works towards minimizing the biases of the database, which will be confirmed afterwards by the statistical analysis of our results.
We did not keep any other information from the original references. Instead, we retrieved all the ancillary information such as photometries, parallaxes, spectral types etc, at once by using our GetStar service, a specially crafted version of our SearchCal server4 that fetches all relevant information from a dozen CDS-based catalogs (VizieR, Simbad for object and spectral types). This ensures that there is no difference in the origin, thus no added bias, between the database we use to derive our polynomials (see below) and those that will be used in the reverse process, for any object known by Simbad at CDS.
4.2. Database properties
As of today, the database retains 1072 different measurements on 627 stars from 169 publications. Of them, 204 stars have multiple entries, from 2 (205 stars) to 18 (α Tau). In addition, 1041 measurements have an UDD value, 565 reported an LDD value. After an eventual LDD to UDD conversion and use of the above-mentioned conversion factors (for compatible spectral types), we are left with 853 entries with useable LDD measurements.
With regard to the techniques, data is issued from long-baseline optical/IR interferometry (68%), then lunar occultations (26%), and finally intensity interferometry (6%). Of the measurements retained, 36% are in the K band (around 2200 nm), the rest being equally distributed between the B, V, R, I, and H bands.
4.3. Database final filtering
For the purposes of this work (single stars of classical spectral types), we remove the known multiples or strongly variable stars (cepheids, miras, close doubles5, spectroscopic binaries, elliptical variables etc) to obtain a set of (apparently) standard stars. In addition, we consider only stars with the following complete information: VJHKs magnitudes and errors6; SIMBAD spectral types within half a subclass precision; LDD diameters and their errors. Finally, keeping only measurements with an S/N above five for LDDs, we are left with 573 measurements of 404 distinct stars.
The spectral types of the 573 selected measurements range from O5 to M7 in five luminosity classes: 124 dwarves (V), 42 subgiants (IV), 297 giants (III), 38 subsupergiants (II), 56 supergiants (I), and 16 without luminosity class (in the SIMBAD database). The diameter measurements range over more than two decades, from 0.23 to 44 mas.
5. Results and discussion
To derive the polynomial coefficients and their errors, we used the 573 selected measurements of our database (see Sect. 4.3), and simultaneously fitted the DSB of the photometric pairs (V, J), (V, H), and (V, Ks).
The quality of the polynomial fit is evaluated by the associated chi-square, 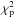 (see Appendix A.1), and that of the reconstructed diameters by the mean diameter chi-square
(see Appendix A.1), and that of the reconstructed diameters by the mean diameter chi-square 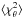 , (see Appendix A.2).
, (see Appendix A.2).
5.1. Influence of luminosity class
To test the influence of the luminosity class (LC), we first computed three sets of polynomials of degree 6 separately, from: 1) LC I, II and III (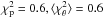 ); 2) LC IV and V (
); 2) LC IV and V (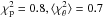 ); and 3) all, including unknown LC (
); and 3) all, including unknown LC (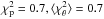 ). Then in each case, we computed the angular diameters of all stars of the Hipparcos (ESA 1997) catalog with known spectral types and magnitudes (93 142 stars). Within an rms bias of 2%, we found no difference between cases 1) and 3), and cases 2) and 3). As a consequence, we decided to use all the selected measurements of our database, irrespective of their luminosity class (or absence thereof), to derive a single set of polynomials that is applicable to all stars.
). Then in each case, we computed the angular diameters of all stars of the Hipparcos (ESA 1997) catalog with known spectral types and magnitudes (93 142 stars). Within an rms bias of 2%, we found no difference between cases 1) and 3), and cases 2) and 3). As a consequence, we decided to use all the selected measurements of our database, irrespective of their luminosity class (or absence thereof), to derive a single set of polynomials that is applicable to all stars.
 |
Fig. 1 Histogram of retained stellar diameter measurements for the DSB polynomial fit. Top: note the overabundance of luminosity classes I–III (363 entries), around K and M spectral types and the poor sampling for earlier ones. Bottom: spectral distribution for luminosity classes IV and V (150 entries). |
5.2. Selected database measurements and their DSB
From the initial 573 entries, 526 (92%) filled the fitting condition (see end of Sect. 3.1) and were retained for polynomial calculations (363 entries with LC I, II, and III, 150 with LC IV and V, and 13 with unknown LC). The spectral type distribution for luminosities classes I–III is shown in Fig. 1 (top). There is an overabundance of measurements around K and M spectral types and a poor sampling for earlier ones. Instead, for luminosity classes IV and V (Fig. 1, bottom) the spectral types are quite well distributed between B and M types. Also note that 100% (31 entries) of interferometry intensity data, 92% (407 entries) of classical interferometry data and 87% (88 entries) of lunar occultation data, have been retained.
Figure 2 shows the DSB in the three selected photometric pairs as a function of the spectral type, together with the polynomial fit. The entries were binned, with an interval of one subspectral type, separately for LC I, II and III (filled circles) and LC IV and V (open circles), to understand their similarity. Figure 3 shows the same DSB with all entries binned with an interval of 2.5 subspectral type. It is clear that the spectral metric is not smooth, especially for the (V, J) pair. It presents a period of about one spectral type plus some possible fine structures. In fact no polynomial of reasonable degree is able to reproduce the exact structure of the DSB and we must always keep in mind the 2% rms bias on the diameter.
 |
Fig. 2 DSB values in the three selected photometric pairs, together with polynomial fits of degree 6 (dotted lines), as a function of the spectral type. The entries were binned separately, with an interval of one subspectral type, for LC I, II, and III (filled circles) and LC IV and V (open circles), to understand their similarity. |
 |
Fig. 3 Differential surface brightness for (from top to bottom) the (V, J), (V, H) and (V, Ks), photometric pairs versus spectral type. The (V, J) and (V, Ks) curves have been shifted by ± 0.2 for clarity. The entries were binned, with an interval of 2.5 subspectral type. The dotted lines represent the best fit with polynomials of degree 6. Note that the spectral metric is not smooth (see text). |
 |
Fig. 4 Computed diameters as a function of measured diameters, for eight stars recently observed with interferometry and not used for the polynomial fit. Stars with increasing diameter, HD numbers: 209458 (G0V), 189733 (K1.5V), 69830 (G8), 185351 (G9III), 190658 (M2.5III), 183589 (K5I), 95687 (M3I), 97671 (M3I), (Johnson et al. 2014; Boffin et al. 2014; Tanner et al. 2015; Boyajian et al. 2015; Arroyo-Torres et al. 2015). The agreement is excellent, with a mean-squared difference between measured and computed diameters expressed in noise units of 0.5. The straight dotted line corresponds to x = y. |
Differential surface brightness polynomial values p and associated errors σp for stars measured in the (V, Ks) photometric pair.
5.3. Comparison of diameter predictions with recent measurements
To test the diameter predictions of our model, we computed the diameter of eight stars, which had recently been measured by interferometry and not used for the polynomial fit. Figure 4 shows the computed diameters as a function of the measured ones. The agreement is excellent, with a mean-squared difference between measured and computed diameters that is expressed in noise units of about 0.5.
List of stars and associated references of angular diameter measurements that have been retained to calibrate the DSB in this work.
5.4. The JMMC stellar diameter catalogue
We used the present formalism to compute the angular diameters of stars in the Tycho2 catalog7 (Høg et al. 2000) with known spectral type. The resulting median diameter error is 1.1%. About 453 000 stars have an associated internal diameter 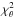 less than 5, and 393 000 less than 2.
less than 5, and 393 000 less than 2.
5.5. Simplified formula
For a star which could be absent in the JMMC catalog and for which two tycho-like magnitudes and a spectral type are known, it is easy to derive a diameter estimate using the formula below.
Knowing the DSB polynomial values p and their errors σp, the stellar diameter (mas) and its relative error may quickly be computed using the following formulas: 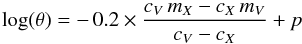 (9)and
(9)and 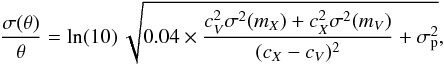 (10)with X = J, H or Ks. Table 1 provides the pair (p, σp) for the (V, Ks) photometries and stars of spectral type O5 to M6.
(10)with X = J, H or Ks. Table 1 provides the pair (p, σp) for the (V, Ks) photometries and stars of spectral type O5 to M6.
It is also possible to estimate angular diameters without a precise knowledge of the spectral type, but with a degraded precision. For a star whose spectral type is known within some range, it suffices to replace in Eqs. (9) and (10), the pair (p, σp) by the pair (a,σa), where a is the mean value of p, and σa its dispersion over the spectral range. If the spectral type is in the range O5–M6, then for any X, (a,σa) = (0.56, 0.12), for the range A0–M6, (a,σa) = (0.62, 0.05), which respectively provides 28% and 12% diameter error.
6. Conclusion
Our approach to predict stellar angular diameters is based on the modeling of the relationship between angular diameters and photometries. We developed a new methodology that is based on two reddening-free observables: 1) a distance indicator called pseudomagnitude and 2) the differential surface brightness, a handy quasi-experimental observable, that is independent of distance and specific to each star. This, together with our new database of measured angular diameters, allows us to provide estimates of star diameters with statistical errors of ~1.1%, plus possible biases of ~2%. It permits us to upgrade the JSDC catalog of stellar diameters to about 453 000 stars, a tenfold improvement in number of stars and diameter precision.
The polynomial method developed in this work may be used with any photometric system, selecting optical bands that best represent the stellar continuum. However, the exercise has severe limits because the DSB is not smooth. The only way to reduce the biases and to go beyond 1% error is to measure its structure for all spectral types and luminosity classes. This emphasises this importance to get precise photometry with biases smaller than 1% and above all the importance of optical interferometry to get precise and numerous angular diameters.
JMMC Measured stellar Diameters Catalog, available at http://www.jmmc.fr/jmdc
Our GetStar service is used to retrieve Johnson V magnitudes from the ASCC (Kharchenko 2001) and Hipparcos (ESA 1997) catalogs, and JHKs from 2MASS (Skrutskie et al. 2006). GetStar makes a careful cross-match on the stellar properties reported in these catalogs, comparing them with Simbad values, and takes into account proper motions in its cross-matching.
See the JSDC catalog at http://www.jmmc.fr/jsdc. The Tycho2 catalog is used here as a list of star positions and photometries are retrieved through GetStar, as described in Sect. 4.3.
Available at http://www.starlink.ac.uk/topcat/
Acknowledgments
This research has made use of NASA’s Astrophysics Data System. This research has made use of the SIMBAD database (Wenger et al. 2000), and of the VizieR catalog access tool (Ochsenbein et al. 2000), CDS, Strasbourg, France. The TOPCAT tool8 (Taylor 2005) was pivotal in the analysis and filtering of our databases. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation.
References
- Africano, J. L., Evans, D. S., Fekel, F. C., & Ferland, G. J. 1976, AJ, 81, 650 [NASA ADS] [CrossRef] [Google Scholar]
- Africano, J. L., Evans, D. S., Fekel, F. C., & Montemayor, T. 1977, AJ, 82, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Africano, J. L., Evans, D. S., Fekel, F. C., Smith, B. W., & Morgan, C. A. 1978, AJ, 83, 1100 [NASA ADS] [CrossRef] [Google Scholar]
- Arroyo-Torres, B., Martí-Vidal, I., Marcaide, J. M., et al. 2014, A&A, 566, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arroyo-Torres, B., Wittkowski, M., Chiavassa, A., et al. 2015, A&A, 575, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baines, E. K., McAlister, H. A., ten Brummelaar, T. A., et al. 2008, ApJ, 680, 728 [NASA ADS] [CrossRef] [Google Scholar]
- Baines, E. K., McAlister, H. A., ten Brummelaar, T. A., et al. 2009, ApJ, 701, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Baines, E. K., Döllinger, M. P., Cusano, F., et al. 2010, ApJ, 710, 1365 [NASA ADS] [CrossRef] [Google Scholar]
- Baines, E. K., Armstrong, J. T., Schmitt, H. R., et al. 2014, in Optical and Infrared Interferometry IV, SPIE Conf. Ser., 9146 [Google Scholar]
- Barnes, T. G., & Evans, D. S. 1976, MNRAS, 174, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Beavers, W. I., & Eitter, J. 1979, ApJ, 228, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Beavers, W. I., Eitter, J. J., Dunham, D. W., & Stein, W. L. 1980, AJ, 85, 1505 [NASA ADS] [CrossRef] [Google Scholar]
- Beavers, W. I., Eitter, J. J., & Cadmus, Jr., R. R. 1981, AJ, 86, 1404 [NASA ADS] [CrossRef] [Google Scholar]
- Beavers, W. I., Cadmus, R. R., & Eitter, J. J. 1982, AJ, 87, 818 [NASA ADS] [CrossRef] [Google Scholar]
- Blackwell, D. E., Shallis, M. J., & Selby, M. J. 1979, MNRAS, 188, 847 [NASA ADS] [CrossRef] [Google Scholar]
- Boehme, D. 1978, Astron. Nachr., 299, 243 [Google Scholar]
- Boffin, H. M. J., Hillen, M., Berger, J. P., et al. 2014, A&A, 564, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonneau, D., Koechlin, L., Oneto, J. L., & Vakili, F. 1981, A&A, 103, 28 [NASA ADS] [Google Scholar]
- Bonneau, D., Clausse, J.-M., Delfosse, X., et al. 2006, A&A, 456, 789 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonneau, D., Delfosse, X., Mourard, D., et al. 2011, A&A, 535, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boyajian, T. S., McAlister, H. A., Baines, E. K., et al. 2008, ApJ, 683, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Boyajian, T. S., McAlister, H. A., van Belle, G., et al. 2012a, ApJ, 746, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Boyajian, T. S., von Braun, K., van Belle, G., et al. 2012b, ApJ, 757, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Boyajian, T. S., von Braun, K., van Belle, G., et al. 2013, ApJ, 771, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Boyajian, T. S., van Belle, G., & von Braun, K. 2014, AJ, 147, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Boyajian, T., von Braun, K., Feiden, G. A., et al. 2015, MNRAS, 447, 846 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, T. M., & Gilliland, R. L. 1994, ARA&A, 32, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, A., Bunclark, P. S., Stapleton, J. R., & Stewart, G. C. 1979, MNRAS, 187, 753 [NASA ADS] [CrossRef] [Google Scholar]
- Casagrande, L., Ramírez, I., Meléndez, J., Bessell, M., & Asplund, M. 2010, A&A, 512, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casagrande, L., Portinari, L., Glass, I. S., et al. 2014, MNRAS, 439, 2060 [Google Scholar]
- Challouf, M., Nardetto, N., Mourard, D., et al. 2014, A&A, 570, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chaplin, W. J., & Miglio, A. 2013, ARA&A, 51, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Claret, A. 2000, A&A, 363, 1081 [NASA ADS] [Google Scholar]
- Cousins, A. W. J., & Guelke, G. 1950, Mon. Notes Astron. Soc. S. Afr., 9, 36 [NASA ADS] [Google Scholar]
- Cruzalèbes, P., Jorissen, A., Rabbia, Y., et al. 2013, MNRAS, 434, 437 [NASA ADS] [CrossRef] [Google Scholar]
- Currie, D. G., Knapp, S. L., & Liewer, K. M. 1974, ApJ, 187, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Cusano, F., Paladini, C., Richichi, A., et al. 2012, A&A, 539, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Davis, J., Morton, D. C., Allen, L. R., & Hanbury Brown, R. 1970, MNRAS, 150, 45 [NASA ADS] [CrossRef] [Google Scholar]
- de Bruijne, J. H. J. 2012, Ap&SS, 341, 31 [NASA ADS] [CrossRef] [Google Scholar]
- de Vegt, C. 1976, A&A, 47, 457 [NASA ADS] [Google Scholar]
- di Benedetto, G. P., & Conti, G. 1983, ApJ, 268, 309 [NASA ADS] [CrossRef] [Google Scholar]
- di Benedetto, G. P., & Rabbia, Y. 1987, A&A, 188, 114 [NASA ADS] [Google Scholar]
- Di Folco, E., Thévenin, F., Kervella, P., et al. 2004, A&A, 426, 601 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dunham, D. W., Evans, D. S., Silverberg, E. C., & Wiant, J. R. 1973, AJ, 78, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Dunham, D. W., Evans, D. S., & Sandmann, W. H. 1974, AJ, 79, 483 [NASA ADS] [CrossRef] [Google Scholar]
- Dunham, D. W., Evans, D. S., & Vogt, S. S. 1975, AJ, 80, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Dyck, H. M., Benson, J. A., Carleton, N. P., et al. 1995, AJ, 109, 378 [NASA ADS] [CrossRef] [Google Scholar]
- ESA 1997, The Hipparcos and Tycho Catalogues, Vol. 1, ESA SP-1200 [Google Scholar]
- Evans, D. S., & Edwards, D. A. 1981, AJ, 86, 1277 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, D. S., Edwards, D. A., Pettersen, B. R., et al. 1980, AJ, 85, 1262 [NASA ADS] [CrossRef] [Google Scholar]
- Faucherre, M., Bonneau, D., Koechlin, L., & Vakili, F. 1983, A&A, 120, 263 [NASA ADS] [Google Scholar]
- Fitzpatrick, E. L. 1999, PASP, 111, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Fors, O., Richichi, A., Núñez, J., & Prades, A. 2004, A&A, 419, 285 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Glass, I. S., & Morrison, L. V. 1976, MNRAS, 175, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Hanbury Brown, R., & Twiss, R. Q. 1958, Roy. Soc. London Proc. Ser. A, 248, 222 [Google Scholar]
- Hanbury Brown, R., Davis, J., Allen, L. R., & Rome, J. M. 1967, MNRAS, 137, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Hanbury Brown, R., Davis, J., & Allen, L. R. 1974, MNRAS, 167, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Harwood, J. M., Nather, R. E., Walker, A. R., Warner, B., & Wild, P. A. T. 1975, MNRAS, 170, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Høg, E., Fabricius, C., Makarov, V. V., et al. 2000, A&A, 355, L27 [NASA ADS] [Google Scholar]
- Hutter, D. J., Johnston, K. J., Mozurkewich, D., et al. 1989, ApJ, 340, 1103 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. A., Huber, D., Boyajian, T., et al. 2014, ApJ, 794, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Kervella, P., Thévenin, F., Morel, P., Bordé, P., & Di Folco, E. 2003a, A&A, 408, 681 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., Thévenin, F., Ségransan, D., et al. 2003b, A&A, 404, 1087 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., Thévenin, F., Di Folco, E., & Ségransan, D. 2004, A&A, 426, 297 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., Mérand, A., Pichon, B., et al. 2008, A&A, 488, 667 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kharchenko, N. V. 2001, Kinematika i Fizika Nebesnykh Tel, 17, 409 [NASA ADS] [Google Scholar]
- Labeyrie, A. 1975, ApJ, 196, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Lafrasse, S., Mella, G., Bonneau, D., et al. 2010, in Optical and Infrared Interferometry II, SPIE Conf. Ser., 7734 [Google Scholar]
- Lane, B. F., Boden, A. F., & Kulkarni, S. R. 2001, ApJ, 551, L81 [Google Scholar]
- Maestro, V., Che, X., Huber, D., et al. 2013, MNRAS, 434, 1321 [NASA ADS] [CrossRef] [Google Scholar]
- McCall, M. L. 2004, AJ, 128, 2144 [NASA ADS] [CrossRef] [Google Scholar]
- Michelson, A. A., & Pease, F. G. 1921, ApJ, 53, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Mourard, D., Bonneau, D., Koechlin, L., et al. 1997, A&A, 317, 789 [Google Scholar]
- Mozurkewich, D., Johnston, K. J., Simon, R. S., et al. 1991, AJ, 101, 2207 [NASA ADS] [CrossRef] [Google Scholar]
- Mozurkewich, D., Armstrong, J. T., Hindsley, R. B., et al. 2003, AJ, 126, 2502 [NASA ADS] [CrossRef] [Google Scholar]
- Nather, R. E., McCants, M. M., & Evans, D. S. 1970, ApJ, 160, L181 [NASA ADS] [CrossRef] [Google Scholar]
- Neilson, H. R., & Lester, J. B. 2013a, A&A, 554, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neilson, H. R., & Lester, J. B. 2013b, A&A, 556, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nelson, M. R. 1975, ApJ, 198, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Nordgren, T. E., Germain, M. E., Benson, J. A., et al. 1999, AJ, 118, 3032 [NASA ADS] [CrossRef] [Google Scholar]
- Nordgren, T. E., Sudol, J. J., & Mozurkewich, D. 2001, AJ, 122, 2707 [NASA ADS] [CrossRef] [Google Scholar]
- Ochsenbein, F., Bauer, P., & Marcout, J. 2000, A&AS, 143, 23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Panek, R. J., & Leap, J. L. 1980, AJ, 85, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Pasinetti Fracassini, L. E., Pastori, L., Covino, S., & Pozzi, A. 2001, A&A, 367, 521 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quirrenbach, A., Mozurkewich, D., Armstrong, J. T., Buscher, D. F., & Hummel, C. A. 1993, ApJ, 406, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Radick, R. R., & Africano, J. L. 1981, AJ, 86, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Ragland, S., Chandrasekhar, T., & Ashok, N. M. 1997, MNRAS, 287, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Richichi, A., & Calamai, G. 2003, A&A, 399, 275 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Richichi, A., & Lisi, F. 1990, A&A, 230, 355 [NASA ADS] [Google Scholar]
- Richichi, A., di Giacomo, A., Lisi, F., & Calamai, G. 1992a, A&A, 265, 535 [NASA ADS] [Google Scholar]
- Richichi, A., Lisi, F., & di Giacomo, A. 1992b, A&A, 254, 149 [NASA ADS] [Google Scholar]
- Richichi, A., Ragland, S., & Fabbroni, L. 1998, A&A, 330, 578 [NASA ADS] [Google Scholar]
- Richichi, A., Percheron, I., & Khristoforova, M. 2005, A&A, 431, 773 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ridgway, S. T., Wells, D. C., & Carbon, D. F. 1974, AJ, 79, 1079 [NASA ADS] [CrossRef] [Google Scholar]
- Ridgway, S. T., Wells, D. C., & Joyce, R. R. 1977, AJ, 82, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Ridgway, S. T., Wells, D. C., Joyce, R. R., & Allen, R. G. 1979, AJ, 84, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Ridgway, S. T., Jacoby, G. H., Joyce, R. R., & Wells, D. C. 1980, AJ, 85, 1496 [NASA ADS] [CrossRef] [Google Scholar]
- Ridgway, S. T., Jacoby, G. H., Joyce, R. R., Siegel, M. J., & Wells, D. C. 1982a, AJ, 87, 808 [NASA ADS] [CrossRef] [Google Scholar]
- Ridgway, S. T., Jacoby, G. H., Joyce, R. R., Siegel, M. J., & Wells, D. C. 1982b, AJ, 87, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidtke, P. C., Africano, J. L., Jacoby, G. H., Joyce, R. R., & Ridgway, S. T. 1986, AJ, 91, 961 [NASA ADS] [CrossRef] [Google Scholar]
- Ségransan, D., Kervella, P., Forveille, T., & Queloz, D. 2003, A&A, 397, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Stecklum, B. 1987, AJ, 94, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Tanner, A., Boyajian, T. S., von Braun, K., et al. 2015, ApJ, 800, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, M. B. 2005, in Astronomical Data Analysis Software and Systems XIV, eds. P. Shopbell, M. Britton, & R. Ebert, ASP Conf. Ser., 347, 29 [Google Scholar]
- Thévenin, F., Kervella, P., Pichon, B., et al. 2005, A&A, 436, 253 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vilas, F., & Lasker, B. M. 1977, PASP, 89, 95 [NASA ADS] [CrossRef] [Google Scholar]
- von Braun, K., Boyajian, T. S., van Belle, G. T., et al. 2014, MNRAS, 438, 2413 [NASA ADS] [CrossRef] [Google Scholar]
- Wenger, M., Ochsenbein, F., Egret, D., et al. 2000, A&AS, 143, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wesselink, A. J. 1969, MNRAS, 144, 297 [NASA ADS] [CrossRef] [Google Scholar]
- White, N. M. 1974, AJ, 79, 1076 [NASA ADS] [CrossRef] [Google Scholar]
- White, N. M. 1978a, in The HR Diagram – The 100th Anniversary of Henry Norris Russell, eds. A. G. D. Philip, & D. S. Hayes, IAU Symp., 80, 447 [Google Scholar]
- White, N. M. 1978b, AJ, 83, 1639 [NASA ADS] [CrossRef] [Google Scholar]
- White, N. M. 1979, AJ, 84, 872 [NASA ADS] [CrossRef] [Google Scholar]
- White, N. M. 1980, ApJ, 242, 646 [NASA ADS] [CrossRef] [Google Scholar]
- White, N. M., & Kreidl, T. J. 1984, AJ, 89, 424 [NASA ADS] [CrossRef] [Google Scholar]
- White, N. M., Kreidl, T. J., & Goldberg, L. 1982, ApJ, 254, 670 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Linear least squares fit
The data consist of a set of NS stars that are characterized by their measured diameter θ (corrected for limb-darkening) and NB observed magnitudes. Each star provides NB−1 linearly independent pseudomagnitude, which combined with the diameter θ, give NB−1 correlated measurements (differential surface brightness) per star. Each measurement is fitted as a function of the stellar spectral type number (from 0 to 69 for O0 to M9) with a polynomial of degree m. The problem is then to evaluate (m + 1) × (NB−1) polynomial coefficients, which we do via a simple linear least squares fit, described below.
Appendix A.1: Polynomials calculation
We align the (NB−1) × NS measurements in a vector M, and we define the transition matrix T of dimensions (NB−1).NS × (m + 1).(NB−1) as the derivative of M with respect to the unknowns. For simplicity, we assume that the NS stars are distinct, implying no correlations between the measurements of different stars. This allows us to define NS independent covariance matrices Ci,i = 0,1,...,NS−1, of dimension (NB−1) × (NB−1). Given the photometric pairs that were selected in this work (V, J), (V, H), (V, Ks), the generic expression of the covariance matrix is ![\appendix \setcounter{section}{1} \begin{eqnarray} \mathbf{C} &\!\!=\!\!& \frac{\sigma_\theta^2}{\theta^2 \ln(10)^2} + 0.04 \\ && \times \left[\begin{array}{ccc} \frac{c_J^2\sigma_V^2+c_V^2\sigma_J^2}{(c_V-c_J)^2} & \frac{c_Jc_H\sigma_V^2}{(c_V-c_J)\times(c_V-c_H)} & \frac{c_Jc_{K{\rm s}}\sigma_V^2}{(c_V-c_J)\times(c_V-c_{K{\rm s}})}\\[2mm] \frac{c_J\,c_H\sigma_V^2}{(c_V-c_J)\times(c_V-c_H)} & \frac{c_H^2\sigma_V^2+c_V^2\sigma_H^2}{(c_V-c_H)^2} & \frac{c_Hc_{K{\rm s}}\sigma_V^2}{(c_V-c_H)\times(c_V-c_{K{\rm s}})}\\[2mm] \frac{c_Jc_{K{\rm s}}\sigma_V^2}{(c_V-c_J)\times(c_V-c_{K{\rm s}})} & \frac{c_Hc_{K{\rm s}}\sigma_V^2}{(c_V-c_H)\times(c_V-c_{K{\rm s}})} & \frac{c_{K{\rm s}}^2\sigma_V^2+c_V^2\sigma_{K{\rm s}}^2}{(c_V-c_{K{\rm s}})^2} \\ \nonumber \end{array} \right], \end{eqnarray}](/articles/aa/full_html/2016/05/aa27484-15/aa27484-15-eq114.png) (A.1)where θ is the measured diameter and σθ its error, (σV,σJ,σH,σKs), and (cV,cJ,cH,cKs) are the magnitude errors and the interstellar extinction coefficients in the corresponding bands. Next we place the inverse of the covariance matrices
(A.1)where θ is the measured diameter and σθ its error, (σV,σJ,σH,σKs), and (cV,cJ,cH,cKs) are the magnitude errors and the interstellar extinction coefficients in the corresponding bands. Next we place the inverse of the covariance matrices 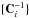 along the diagonal of a matrix D of dimensions (NB−1).NS × (NB−1).NS. The solution for the polynomial coefficients is contained in a vector A of dimensions (m + 1) × (NB−1), given by
along the diagonal of a matrix D of dimensions (NB−1).NS × (NB−1).NS. The solution for the polynomial coefficients is contained in a vector A of dimensions (m + 1) × (NB−1), given by ![\appendix \setcounter{section}{1} \begin{equation} \label{eq:polynom_coefficients} \vec{A}=\Big [^t\mathbf{T} \times \mathbf{D} \times \mathbf{T} \Big]^{-1} \times ^t\mathbf{T} \times \mathbf{D} \times \mathbf{V} . \end{equation}](/articles/aa/full_html/2016/05/aa27484-15/aa27484-15-eq122.png) (A.2)The covariance matrix Ca of the solution A is
(A.2)The covariance matrix Ca of the solution A is ![\appendix \setcounter{section}{1} \begin{equation} \mathbf{C}_a=\Big [^t\mathbf{T} \times \mathbf{D} \times \mathbf{T} \Big]^{-1} . \end{equation}](/articles/aa/full_html/2016/05/aa27484-15/aa27484-15-eq124.png) (A.3)
(A.3)
The reconstructed measurement vector writes: Mr = T × A, and the reduced 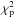 of the fitting process is
of the fitting process is 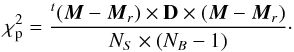 (A.4)
(A.4)
Appendix A.2: Diameter calculation
For a given star with a spectral type number ns and an associated pseudomagnitude vector P of dimension NB−1, the reconstructed iest (i = 0,...NB−1) diameter θi is given by ![\appendix \setcounter{section}{1} \begin{equation} \log(\theta_i) = \sum_{k\,=\,0}^{k\,=\,m} \mathbf{A}\big [\vec{k}+i\times (m+1) \big] \times n_{\rm s}^k-0.2\times \mathbf{P}(i) . \end{equation}](/articles/aa/full_html/2016/05/aa27484-15/aa27484-15-eq130.png) (A.5)The covariance matrix Cd between log diameter estimates writes
(A.5)The covariance matrix Cd between log diameter estimates writes
![\appendix \setcounter{section}{1} \begin{eqnarray} &&\mathbf{C}_{\rm d}\big[\log(\theta_i),\log(\theta_j)\big] = 0.04 \,\mathrm {cov}\big [\mathbf{P}(i),\mathbf{P}(j) \big]\nonumber \\ &&\qquad +\sum_{k\,=\,0}^{k\,=\,m}\sum_{l\,=\,0}^{l\,=\,m} \mathbf{C}_a\big[k+i\times (m+1),l+j\times (m+1) \big]\times n_{\rm s}^{k+l}. \end{eqnarray}](/articles/aa/full_html/2016/05/aa27484-15/aa27484-15-eq132.png) (A.6)Let us range the NB−1 log diameter estimates within a vector R. The mean log diameter
(A.6)Let us range the NB−1 log diameter estimates within a vector R. The mean log diameter 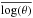 and the associated error are
and the associated error are ![\appendix \setcounter{section}{1} \begin{eqnarray} &&{\overline {\log (\theta)}} = \frac {\sum \mathbf{C}_{\rm d}^{-1} \times \vec{R}}{\sum \mathbf{C}_{\rm d}^{-1}} \\ &&\sigma \big[\overline {\log (\theta)}\big] = \Big [\sum \mathbf{C}_{\rm d}^{-1} \Big]^{-0.5} , \end{eqnarray}](/articles/aa/full_html/2016/05/aa27484-15/aa27484-15-eq135.png) where ∑ stands for the sum of all the matrix elements. The mean diameter
where ∑ stands for the sum of all the matrix elements. The mean diameter 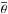 and its error are computed as follows:
and its error are computed as follows: ![\appendix \setcounter{section}{1} \begin{eqnarray} &&\overline{\theta} = 10^{\overline {\log (\theta)}} \\ &&\sigma(\overline{\theta})= \ln (10) \, \sigma \big[\overline {\log (\theta)}\big]\times \overline{\theta} . \end{eqnarray}](/articles/aa/full_html/2016/05/aa27484-15/aa27484-15-eq138.png) At last, we define the chi-square
At last, we define the chi-square 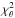 associated with the reconstructed log diameter (from the database) by
associated with the reconstructed log diameter (from the database) by ![\appendix \setcounter{section}{1} \begin{equation} \chi^2_\theta = \frac{^t\vec{B}\times[\mathbf{C}_{\rm d}+\sigma_\theta^2]^{-1}\times \vec{B}}{N_B-1} , \end{equation}](/articles/aa/full_html/2016/05/aa27484-15/aa27484-15-eq140.png) (A.11)where B is the vector of the difference between the log of the diameter estimates (R) and that of the measured diameter, and σθ is the error of the measured log diameter. In the case of a catalog of stars with no measured diameter, we can define an internal
(A.11)where B is the vector of the difference between the log of the diameter estimates (R) and that of the measured diameter, and σθ is the error of the measured log diameter. In the case of a catalog of stars with no measured diameter, we can define an internal 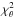 , replacing the measured diameter and its error with the mean computed diameter and its error.
, replacing the measured diameter and its error with the mean computed diameter and its error.
All Tables
Differential surface brightness polynomial values p and associated errors σp for stars measured in the (V, Ks) photometric pair.
List of stars and associated references of angular diameter measurements that have been retained to calibrate the DSB in this work.
All Figures
 |
Fig. 1 Histogram of retained stellar diameter measurements for the DSB polynomial fit. Top: note the overabundance of luminosity classes I–III (363 entries), around K and M spectral types and the poor sampling for earlier ones. Bottom: spectral distribution for luminosity classes IV and V (150 entries). |
| In the text | |
 |
Fig. 2 DSB values in the three selected photometric pairs, together with polynomial fits of degree 6 (dotted lines), as a function of the spectral type. The entries were binned separately, with an interval of one subspectral type, for LC I, II, and III (filled circles) and LC IV and V (open circles), to understand their similarity. |
| In the text | |
 |
Fig. 3 Differential surface brightness for (from top to bottom) the (V, J), (V, H) and (V, Ks), photometric pairs versus spectral type. The (V, J) and (V, Ks) curves have been shifted by ± 0.2 for clarity. The entries were binned, with an interval of 2.5 subspectral type. The dotted lines represent the best fit with polynomials of degree 6. Note that the spectral metric is not smooth (see text). |
| In the text | |
 |
Fig. 4 Computed diameters as a function of measured diameters, for eight stars recently observed with interferometry and not used for the polynomial fit. Stars with increasing diameter, HD numbers: 209458 (G0V), 189733 (K1.5V), 69830 (G8), 185351 (G9III), 190658 (M2.5III), 183589 (K5I), 95687 (M3I), 97671 (M3I), (Johnson et al. 2014; Boffin et al. 2014; Tanner et al. 2015; Boyajian et al. 2015; Arroyo-Torres et al. 2015). The agreement is excellent, with a mean-squared difference between measured and computed diameters expressed in noise units of 0.5. The straight dotted line corresponds to x = y. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


