| Issue |
A&A
Volume 589, May 2016
|
|
|---|---|---|
| Article Number | A96 | |
| Number of page(s) | 20 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201424738 | |
| Published online | 20 April 2016 | |
Shaping the GeV-spectra of bright blazars
1
Institut für Astro- und Teilchenphysik, Leopold-Franzens-Universität
Innsbruck, 6020
Innsbruck, Austria
e-mail: lars.hunger@brainlinks-braintools.uni-freiburg.de
2
Institut für Theoretische Physik, Leopold-Franzens-Universität
Innsbruck, 6020
Innsbruck,
Austria
3
Brainlinks-Braintools, University of Freiburg,
79104
Freiburg im Breißgau,
Germany
Received: 3 August 2014
Accepted: 15 February 2016
Aims. The non-thermal spectra of jetted active galactic nuclei (AGN) show a variety of shapes and degrees of curvature in their low- and high energy components. From some of the brightest Fermi-LAT blazars, prominent spectral breaks at a few GeV have been regularly detected, which is inconsistent with conventional cooling effects. We study the effects of continuous time-dependent injection of electrons into the jet with differing rates, durations, locations, and power-law spectral indices, and evaluate its impact on the ambient emitting particle spectrum that is observed at a given snapshot time in the framework of a leptonic blazar emission model. With this study, we provide a basis for analyzing ambient electron spectra in terms of injection requirements, with implications for particle acceleration modes.
Methods. The emitting electron spectrum is calculated by Compton cooling the continuously injected electrons, where target photons are assumed to be provided by the accretion disk and broad line region (BLR). From this setup, we calculate the non-thermal photon spectra produced by inverse Compton scattering of these external target radiation fields using the full Compton cross-section in the head-on approximation.
Results. By means of a comprehensive parameter study we present the resulting ambient electron and photon spectra, and discuss the influence of each injection parameter individually. We found that varying the injection parameters has a notable influence on the spectral shapes, which in turn can be used to set interesting constraints on the particle injection scenarios. By applying our model to the flare state spectral energy distribution (SED) of 3C 454.3, we confirm a previous suggestion that explained the observed spectral changes at a few GeV by a combination of the Compton-scattered disk and BLR radiation. We determine the required injection parameters for this scenario. We also show that this spectral turn-over can also be understood as Compton-scattered BLR radiation only, and provide the corresponding injection parameters. Here the spectral turn-over is explained by a corresponding break in the ambient electron spectrum. In a similar way, we also applied our model to the FSRQ PKS 1510-089, and present two possible model fits. Here, the GeV-spectrum is either dominated by Compton-scattered accretion disk radiation or is a combination of Compton-scattered disk and BLR radiation. We provide the required injection parameters for these fits. In all four scenarios, we found that impulsive particle injection is disfavored.
Conclusions. The presented injection model that is embedded in a leptonic blazar emission model for external Compton-loss dominated jets of AGN aims towards bridging jet emission with acceleration models using a phenomenological approach. Blazar spectral data can be analyzed with this model to constrain injection parameters, in addition to the conventional parameter values of steady-state emission models, if sufficient broad multifrequency coverage is provided.
Key words: galaxies: jets / galaxies: active / gamma rays: galaxies / radiation mechanisms: non-thermal
© ESO, 2016
1. Introduction
Jetted active galactic nuclei (AGN) comprise the most numerous variable source population in the γ-ray sky (e.g., Ackermann et al. 2013). Their jets are considered as the site of intense broadband emission, with apparently random flaring events, shich cover the electromagnetic band from the radio up to GeV, or TeV energies. Variability timescales for this continuum emission range from months (radio) down to few minutes (TeV). Their broadband spectral energy distribution (SED) can be described as having two broad components, with the lower energy component usually attributed to synchrotron radiation from a population of relativistic electrons in the magnetized emission region. The origin of the photons of the higher energy component is still under debate, and strongly depends on the relativistic particle content of the jet (e.g., Reimer & Böttcher 2013). In many cases, it is only by considering leptonic processes together with external target photon fields that can lead to snapshot or time-averaged SEDs that are in agreement with the corresponding multifrequency observations (e.g., Böttcher et al. 2013). An often used approach for calculating these SEDs is based on an ad hoc assumption of the emitting electron spectrum as having log-parabolic shapes, (broken) power laws with possible exponential cutoffs, and with the minimum and maximum electron energies, energy of possible breaks and power law indices or curvature of this spectrum as free parameters (e.g., Dermer et al. 2009; Finke & Dermer 2010; Dermer et al. 2014).
The observation of spectral breaks in the high energy photon spectra of bright flat spectrum radio quasars (FSRQ) was among the first findings of the Fermi-LAT in the extragalactic γ-ray sky (Abdo et al. 2009, 2010d, and confirmed subsequently in Ackermann et al. 2011). Typically, bright FSRQs (and also some low frequency peaked-BL Lacs (LBLs) and intermediate frequency peaked-BL Lacs (IBLs)) show γ-ray spectra that can be described phenomenologically either by broken power laws or log-parabolas with strong concave curvature (Harris et al. 2014) between 1 and 10 GeV, which is too low to be caused by absorption in the extragalactic background light (e.g., Abdo et al. 2010c), and with a power-law index change much larger than expected from cooling (ΔΓ = 0.5). For example, the turn-over in the GeV spectra of FSRQ 3C 454.3 is located at ~2.5 GeV with a power law index change of about ΔΓ = 1.1 ± 0.1. The break energy does not seem to be correlated with the γ-ray luminosity. Several scenarios have been proposed to explain these breaks. These range from photon pair production in the broad-line region of the source (BLR; Poutanen & Stern 2010), to a two-component γ-ray spectrum (Finke & Dermer 2010), or GeV breaks in the photon spectra owing to corresponding breaks in the electron spectra (Abdo et al. 2010d).
Some recent studies, however, have cast doubt on the internal absorption scenario, which would predict well-defined break energies in the AGN’s source frame. Harris et al. (2012) did not find such universal values of the break energies. Kohler & Nalewajko (2015) described the occurence of spectral breaks, which were investigated from a set of 40 bright LAT-blazars as “random”. In fact they report a tendency for short duration flares to possess stronger curvature than those hat are integrated over a longer timescale. The other two non-absorption scenarios mentioned above invoke ad hoc broken power-law particle spectra. Ghisellini & Tavecchio (2009) show that Klein-Nishina or simple cooling effects cannot explain the strength and shape of the observed peaks (see however, Cerruti et al. 2013 who propose a high-energy cutoff at GeV energies from Klein-Nishina effects in scattering Lyα photons).
Using the ambient particle spectrum as an input parameter, however, broadly ignores the build-up of this emitting particle spectrum that is impacted by the various particle energy losses, and gains through particle energization mechanisms which, in general, requires a time-dependent treatment of the problem. As a consequence one can not gain much information on the particle acceleration mechanisms at work in these environments from modeling broadband SEDs this way.
In the present work we attempt to improve on this situation by studying the impact of various injection scenarios of relativistic particles on the resulting emitting particle and photon spectrum. Specifically, we calculate the ambient particle spectrum that results from injection during a finite time range in the past, and viewed at a given (snapshot) time. Comparing to the broken power-law, emitting-particle spectra, which are required in broadband modeling of blazar snapshot SEDs, will then help us draw inferences on the required particle acceleration mechanisms.
In this sense, our approach differs from works which directly implement a specific acceleration mechanism into an emission code (e.g., Diltz & Böttcher 2014).
We restrict ourselves to leptonic emission processes in blazar jets here where external photon fields, such as accretion disk radiation and radiation partly re-scattered at the BLR, present the dominant target for particle-photon interactions. This setup is expected to be suitable for application to those radio-loud jetted AGN, which show a strong accretion disk radiation field, such as FSRQs and LBLs. The analog procedure, including hadronic interactions as well, is more complex and will be postponed to a subsequent paper.
We aim to explain the observed breaking spectra at GeV-energies, and hence focus here on steep spectrum LAT-AGN. This is unlike Pacciani et al. (2014), whose study on spectral shapes is based on a data set in which those periods are exclusively considered where the sources emitted significant >10 GeV photons and are therefore associated with hard γ-ray spectrum-flaring events. Diltz & Böttcher (2014) complemented their time-dependent leptonic blazar emission code with an implementation of a Fermi-II acceleration scenario, in addition to time-dependent particle “pick-up”, with the goal of identifying observational signatures for the origin of flares. Hence they studied the effect of a perturbation of various input parameters that could potentially be associated with causing outbursts on top of a steady-state situation. They explored observational signatures such as correlations between lightcurves at different frequencies, possible time lags, etc. Our present work attempts to explore the impact of a specific injection history on the resulting high-energy spectrum thereby offering an alternative explanation for the often observed strong breaks in bright FSRQ spectra at GeV-energies.
Section 2 of this paper describes the emission model used here (an external inverse Compton emission model that broadly follows Dermer & Schlickeiser 1993; Dermer et al. 2009), and the calculation of the emitting electron spectrum, which is the result of radiative losses that impact upon an electron population that has been continuously injected while propagating along the jet. Such continuously injected electron spectra, like the one we use in this work, were first proposed by Mücke & Pohl (2000). We present a detailed parameter study in Sect. 3, and summarize and discuss the results of our work in Sect. 4.
2. Model
2.1. Basic model
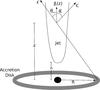 |
Fig. 1 Geometry of the blazar jet model considered in this work (figure adapted from Dermer & Schlickeiser 1993). |
We consider the AGN to be powered by accretion onto a supermassive Schwarzschild black
hole of mass MBH. The central black hole is surrounded
by a Shakura-Sunyaev accretion disk (Shakura & Sunyaev
1973). Accretion disk photons, with energy ε∗, enter the
jet under the angle 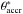 . These photons are scattered into the
angle
. These photons are scattered into the
angle 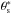 with scattered photon energy
with scattered photon energy
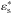 , by the jet electrons. The plasma outflow
of the jet starts at a distance z0 from the central black hole and flows
along the symmetry axis of the system with bulk Lorentz factor Γ and the velocity βΓc, where
, by the jet electrons. The plasma outflow
of the jet starts at a distance z0 from the central black hole and flows
along the symmetry axis of the system with bulk Lorentz factor Γ and the velocity βΓc, where
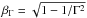 . Figure 1 illustrates the basic model used in this work. Other than in the model of
Dermer & Schlickeiser (1993), electrons are
injected continuously along the jet axis between heights za and zb with a
time-dependent injection rate ∝z(t)−
α, with α being a free parameter.
We consider cooling of the injected electrons as being dominantly the result of inverse
Compton losses on external target radiation fields. Two target photon fields are
considered here: the aforementioned accretion disk radiation, which generally enters the
jet under small angles
. Figure 1 illustrates the basic model used in this work. Other than in the model of
Dermer & Schlickeiser (1993), electrons are
injected continuously along the jet axis between heights za and zb with a
time-dependent injection rate ∝z(t)−
α, with α being a free parameter.
We consider cooling of the injected electrons as being dominantly the result of inverse
Compton losses on external target radiation fields. Two target photon fields are
considered here: the aforementioned accretion disk radiation, which generally enters the
jet under small angles 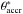 , and the accretion disk radiation that has
been backscattered by the BLR. Most of this backscattered radiation enters the jet under
angles θ∗>
90°, which leads to a different scattering behavior. Because the two
target photon fields have different angular distributions in the jet frame, the inverse
Compton scattered photon distributions that are produced by each of the target photon
fields shows correspondingly different spectral shapes. The BLR model used here largely
follows Dermer et al. (2009) and is described in
Sect. 2.2.1.
, and the accretion disk radiation that has
been backscattered by the BLR. Most of this backscattered radiation enters the jet under
angles θ∗>
90°, which leads to a different scattering behavior. Because the two
target photon fields have different angular distributions in the jet frame, the inverse
Compton scattered photon distributions that are produced by each of the target photon
fields shows correspondingly different spectral shapes. The BLR model used here largely
follows Dermer et al. (2009) and is described in
Sect. 2.2.1.
In the following, quantities with asterisks are in the rest frame of the accretion disk. All energies are in units of the electron rest mass mec2.
2.2. Compton cooling rates
We consider Compton cooling of electrons in the comoving frame of the jet. This radiative
cooling rate is dependent on the differential Compton photon production rate,
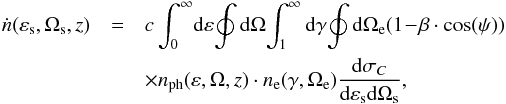 (1)which is dependent on
(1)which is dependent on
-
nph(ε,Ω,z), the photon density of the target photon field at solid angle (Ω), energy (ε) and position (z) along the jet axis;
-
ne(γ,Ωe), the electron density at electron Lorentz factor γ and the solid angle (Ωe);
-
the differential Compton scattering cross section
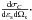
Here, 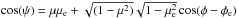 describes the three-dimensional collision
angle.
describes the three-dimensional collision
angle.
We assume that the electron density is isotropic in the comoving frame of the jet,
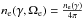 . To calculate the energy loss rate, we set
. To calculate the energy loss rate, we set
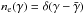 ,
where δ()
denotes the Delta distribution. By only considering relativistic electrons, the assumption
γ ≫ 1 is
justified. Furthermore, we use the Thomson approximation for the differential
cross-section with the δ-approximation in the head-on case:
,
where δ()
denotes the Delta distribution. By only considering relativistic electrons, the assumption
γ ≫ 1 is
justified. Furthermore, we use the Thomson approximation for the differential
cross-section with the δ-approximation in the head-on case: ![\begin{eqnarray} \frac{{\rm d}\sigma}{{\rm d}\varepsilon_{\rm s} {\rm d}\Omega_{\rm s}}=\sigma_{\rm T} \delta\left[\varepsilon_{\rm s}-\gamma^2\varepsilon(1-\beta \cos (\psi))\right]\delta(\Omega_{\rm s}-\Omega_{\rm e}) \label{Thomsoncross} \end{eqnarray}](/articles/aa/full_html/2016/05/aa24738-14/aa24738-14-eq37.png) (2)where σT denotes the
Thomson cross-section. This is valid as long as ε′ ≡ γε(1−cos(ψ)) ≤
1. For ε′> 1 (Klein-Nishina regime) we assume that the
cross-section is zero when calculating the cooling rates, since the Klein-Nishina
cross-section declines rapidly at high energies.
(2)where σT denotes the
Thomson cross-section. This is valid as long as ε′ ≡ γε(1−cos(ψ)) ≤
1. For ε′> 1 (Klein-Nishina regime) we assume that the
cross-section is zero when calculating the cooling rates, since the Klein-Nishina
cross-section declines rapidly at high energies.
With these approximations, the integrations over Ωe and ε are trivial. To achieve further simplification, we average the azimuthally symmetric problem over φ implying ⟨ cos(ψ) ⟩ = μμs.
The integrations then lead to 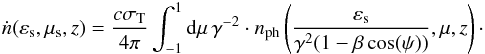 (3)To make progress in calculating the scattered
differential photon production rate the two differential target photon densities
nph (in the comoving frame) are required.
Their calculations are shown in the following two sections.
(3)To make progress in calculating the scattered
differential photon production rate the two differential target photon densities
nph (in the comoving frame) are required.
Their calculations are shown in the following two sections.
2.2.1. BLR target photon density
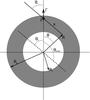 |
Fig. 2 Our BLR model, which consists of a spherically symmetric shell of gas between Ri and Ro and a density gradient ζ with ne(R) ∝ Rζ (figure adapted from Dermer et al. 2009). |
Figure 2 sketches the BLR model used here, mainly following Dermer et al. (2009), where the BLR target photon field is the result of reprocessing the accretion disk radiation and with any direct BLR line emissivity being neglected. For the purpose of calculating the target photon field re-scattered at the BLR (BLR target photon field), we consider the central source as an isotropically emitting point source.
An anisotropic central source would slightly increase the energy density caused by the BLR in the jet-frame with distance from the illuminating disk (Ghisellini & Madau 1996).
The central source radiation is isotropically Thomson-scattered by material of the BLR, back to a distance z (above the black hole) on the jet axis. We consider a spherically symmetric shell of thin gas for the scattering BLR material with a density gradient inside this shell (see Fig. 2). Taking into account a clumpy BLR, instead, would require the introduction of further free parameters (cloud radius distribution) while the expected impact on the distribution of the reprocessed radiation likely stays small for not too large cloud sizes: one would expect additional inhomogenities to some extent on top of an R-dependence from the BLR density gradient.
The calculations here are all carried out in the rest frame of the BLR.
The Thomson-scattered photon density is obtained by 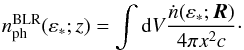 (4)Here x2 =
R2 +
z2−2zRcos(θ),
and ṅ(ε∗;R),
the differential BLR-scattered photon density rate, is given by
(4)Here x2 =
R2 +
z2−2zRcos(θ),
and ṅ(ε∗;R),
the differential BLR-scattered photon density rate, is given by 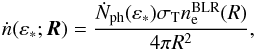 (5)where
(5)where
-
Ṅph(ε∗) is the central source photon production rate;
-
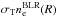 gives the fraction of the incoming
flux that is scattered;
gives the fraction of the incoming
flux that is scattered; -
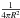 is the geometric dilution from an
isotropic source.
is the geometric dilution from an
isotropic source.
With spherical coordinates and Eq. (5),
Eq. (4) we find: 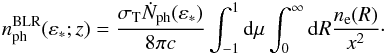 (6)Since inverse Compton scattering is angle
dependent, we need the angle-dependent target photon spectrum. With
(6)Since inverse Compton scattering is angle
dependent, we need the angle-dependent target photon spectrum. With
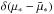 ,
μ∗ = cos
θ∗ and by changing the variables to
g =
R/z we get
,
μ∗ = cos
θ∗ and by changing the variables to
g =
R/z we get ![\begin{eqnarray} n^{\rm{BLR}}_{\rm{ph}}(\varepsilon_*;z) & = & \frac{\sigma_{\rm T} \dot{N}_{\rm{ph}}(\varepsilon_*)}{8\pi c z} \\\nonumber && \times \int_{-\mu^*}^1 {\rm d}\mu \int_0^{\infty} {\rm d}g \frac{n_{\rm e}(gz) \delta[\mu_*-\bar{\mu}_*(\mu,g)]}{g^2+1-2g\mu}\cdot \label{BLRtarphotdelta} \end{eqnarray}](/articles/aa/full_html/2016/05/aa24738-14/aa24738-14-eq61.png) (7)We use the law of sines
(7)We use the law of sines
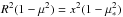 to calculate the angle μ∗ under which
the scattered photons reach the point z:
to calculate the angle μ∗ under which
the scattered photons reach the point z: 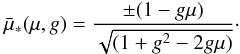 (8)
(8)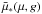 defines a line. If the scattering process takes place on that line, a photon emitted
into the angle μ arrives with angle μ∗ at point
z.
Formally, there are two solutions with the positive one being the physically relevant
one for the already φ-integrated quantity
defines a line. If the scattering process takes place on that line, a photon emitted
into the angle μ arrives with angle μ∗ at point
z.
Formally, there are two solutions with the positive one being the physically relevant
one for the already φ-integrated quantity
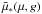 .
.
Carrying out the integration we find: 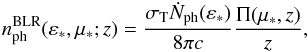 (9)where
(9)where 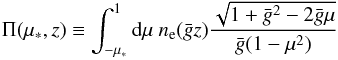 and
and 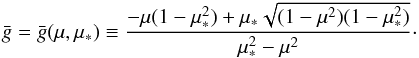 Here
Here
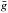 describes the radius R at which the photons, emitted into the angle
μ, have
to be scattered to end up in μ∗.
describes the radius R at which the photons, emitted into the angle
μ, have
to be scattered to end up in μ∗.
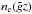 is the electron density at the scattering point. This means Π(μ∗,z) gives a measure
for the total number of photons that end up in the angle element μ∗ at point
z along
the jet axis.
is the electron density at the scattering point. This means Π(μ∗,z) gives a measure
for the total number of photons that end up in the angle element μ∗ at point
z along
the jet axis.
Π cannot be solved analytically, but numerically. The results of these calculations, which we find in agreement with Dermer et al. (2009), are shown in Fig. 3. The figure shows the angular distribution of the BLR photons for different positions z. For z ≥ Ro there are no incoming photons from the front (μ∗< 0) since there is no scattering BLR material in front of z.
 |
Fig. 3 Angle dependence of |
The central source photon-production rate Ṅph(ε∗) is
calculated by assuming that this photon source emits a monochromatic spectrum with
luminosity L0: 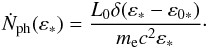 (10)Here L0 =
Leddledd,
with Ledd the Eddington luminosity of the
black hole. Tavecchio & Ghisellini (2008)
have shown that the BLR radiation, simulated with the photoionization code CLOUDY, as
the target field for inverse Compton scattering can be adequately approximated by a
blackbody with a peak at 1.5 times the Lyα-frequency, when considering the IC
spectrum above a few keV. Afterwards, we approximate this blackbody with a monochromatic
spectrum.
(10)Here L0 =
Leddledd,
with Ledd the Eddington luminosity of the
black hole. Tavecchio & Ghisellini (2008)
have shown that the BLR radiation, simulated with the photoionization code CLOUDY, as
the target field for inverse Compton scattering can be adequately approximated by a
blackbody with a peak at 1.5 times the Lyα-frequency, when considering the IC
spectrum above a few keV. Afterwards, we approximate this blackbody with a monochromatic
spectrum.
 |
Fig. 4 Comparison of radiative electron energy-loss rates. Here we choose BLR1 at z = 100 as an example, while noting that the qualitative picture, with the negligible BLR losses, is the same in all the cases we considered in our study. We compare with synchrotron loss rates for a B = 4.5 G magnetic field. a) Radiative electron energy loss rates for varying z for electron energy γ = 500 and BLR1 with τBLR = 0.01. b) Radiative electron energy loss rates for varying γ at z = 100 and BLR1 with τBLR = 0.01. BLR shows the BLR energy loss used in our calculations, here we set the energy loss in the Klein-Nishina regime to 0. |
The resulting BLR target photon density is 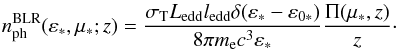 (11)To transform this into the comoving frame
we use ε∗ =
Γε(1 +
βΓμ) and
(11)To transform this into the comoving frame
we use ε∗ =
Γε(1 +
βΓμ) and
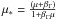 , to get
, to get 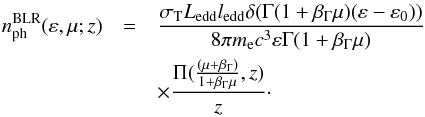 (12)
(12)
2.2.2. Accretion disk target photon density
To calculate the accretion disk photon density in the comoving jet-frame, we follow the
procedure outlined in Dermer & Schlickeiser
(1993). The accretion disk target photon density at the point z is given by
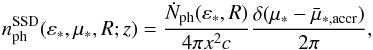 (13)with
(13)with 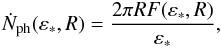 (14)and the surface energy flux for a
Shakura-Sunyaev disk is
(14)and the surface energy flux for a
Shakura-Sunyaev disk is 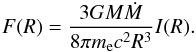 (15)Here
(15)Here
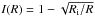 , Ṁ is the mass accretion
rate and Ri =
6Rg for a Schwarzschild black hole with
Rg =
GM/c2 the
gravitational radius. In gravitational units,
, Ṁ is the mass accretion
rate and Ri =
6Rg for a Schwarzschild black hole with
Rg =
GM/c2 the
gravitational radius. In gravitational units, 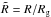 , Eq. (15) becomes
, Eq. (15) becomes 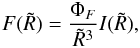 (16)with ΦF = 8.43 × 1024Ψ
cm-2 s-1 and Ψ =
ledd/ϵfM8
where M8 is the black hole mass in
108 solar
masses.
(16)with ΦF = 8.43 × 1024Ψ
cm-2 s-1 and Ψ =
ledd/ϵfM8
where M8 is the black hole mass in
108 solar
masses.
We use a monochromatic approximation for the blackbody radiation that is emitted
locally at a specific radius 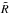 of the accretion disk. The mean photon
energy emitted at a radius
of the accretion disk. The mean photon
energy emitted at a radius 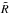 is then given by
is then given by 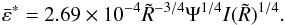 (17)By combining Eqs. (14), (16) and, (17) we get
(17)By combining Eqs. (14), (16) and, (17) we get
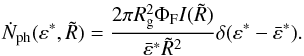 (18)After substituting Ṅph in Eq.
(13) with Eq. (18) and transforming the result into the
comoving frame we find
(18)After substituting Ṅph in Eq.
(13) with Eq. (18) and transforming the result into the
comoving frame we find 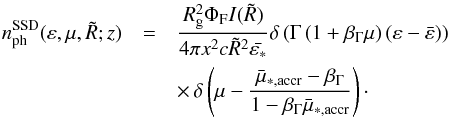 (19)
(19)
2.3. Energy loss and equation of motion
2.3.1. Energy loss in the BLR radiation field
With the differential target photon density, we now calculate the scattered photon
density. We use Eq. (12) together with
Eq. (3) to calculate ṅBLR(εs,μs,z).
By integrating over all scattering angles μs, and all scattering energies
εs, we get the energy-loss rate of a
single electron of given γ: 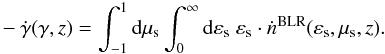 (20)After integrating over εs we get:
(20)After integrating over εs we get:
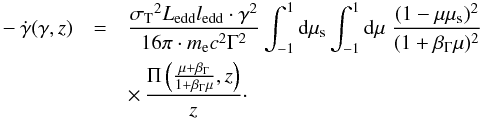 (21)Because the electron energy loss rate
depends on (1 −
μμs)2/ (1 +
βΓμ)2
photons with incident angles μ< 0 contribute more strongly to the electron
energy loss rate than photons with incident angles μ> 0. The small number
of reprocessed BLR photons causes the energy loss due to the BLR to be negligible for
the cases that we considered here (see Fig. 4).
(21)Because the electron energy loss rate
depends on (1 −
μμs)2/ (1 +
βΓμ)2
photons with incident angles μ< 0 contribute more strongly to the electron
energy loss rate than photons with incident angles μ> 0. The small number
of reprocessed BLR photons causes the energy loss due to the BLR to be negligible for
the cases that we considered here (see Fig. 4).
2.3.2. Energy loss in the accretion disk photon field
The procedure is analogous to the BLR case: we use Eq. (3) to calculate the differential photon production rate for one
electron: 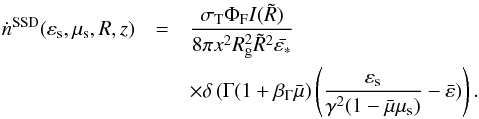 (22)This leads to the energy-loss rate induced
by the accretion disk target photons of
(22)This leads to the energy-loss rate induced
by the accretion disk target photons of 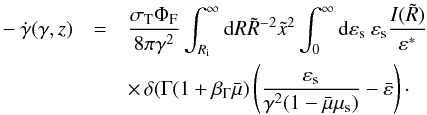 (23)The very good approximation for the
solution of Eq. (23) in the near-field
regime (z<
0.1Γ4(1 + βΓ)4)
is given by Dermer & Schlickeiser (1993),
which we use in the following.
(23)The very good approximation for the
solution of Eq. (23) in the near-field
regime (z<
0.1Γ4(1 + βΓ)4)
is given by Dermer & Schlickeiser (1993),
which we use in the following.
2.3.3. Thomson scattering criterion
The energy loss rates are calculated in the Thomson regime, and are therefore only
valid for ε′ ≡
γε(1−cos(ψ)) ≤ 1 while, in the
Klein-Nishina regime, the cross section is set to zero. After transforming the target
photon energy ε into the rest frame of the BLR, we obtain the
Thomson limit criterion: 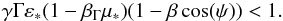 (24)Again, we use the monochromatic
approximation for both external target photon fields to confine the range of
γ, where
both energy loss rates are in the Thomson regime. Since 1 −
βcos(ψ) can never be larger than 2,
the scattering will always be in the Thomson regime if the following relation is
fulfilled:
(24)Again, we use the monochromatic
approximation for both external target photon fields to confine the range of
γ, where
both energy loss rates are in the Thomson regime. Since 1 −
βcos(ψ) can never be larger than 2,
the scattering will always be in the Thomson regime if the following relation is
fulfilled: 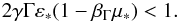 (25)The accretion disk photons will mainly
enter the jet from behind, i.e. μ∗ ≈ 1. In this case, the Thomson
criterion for scattering the accretion disk target photons is:
(25)The accretion disk photons will mainly
enter the jet from behind, i.e. μ∗ ≈ 1. In this case, the Thomson
criterion for scattering the accretion disk target photons is:
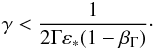 (26)The BLR photons that are most important for
the problem will enter the jet from the front, μ∗ ≈ −1. In
this case the Thomson criterion changes to:
(26)The BLR photons that are most important for
the problem will enter the jet from the front, μ∗ ≈ −1. In
this case the Thomson criterion changes to:
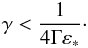 (27)For larger γ, the rate of inverse
Compton scattering in the BLR reduces to the Klein-Nishina regime, which we neglect in
the following. We can neglect the energy loss in the Klein-Nishina regime for the BLR
target photons. This neglect is justified since the energy loss owing to the BLR is
negligible with respect to the energy loss caused by the accretion disk target photons
in the cases that are considered in this work (see Fig. 4). In the cases we studied, the accretion disk photons are usually scattered
in the Thomson regime.
(27)For larger γ, the rate of inverse
Compton scattering in the BLR reduces to the Klein-Nishina regime, which we neglect in
the following. We can neglect the energy loss in the Klein-Nishina regime for the BLR
target photons. This neglect is justified since the energy loss owing to the BLR is
negligible with respect to the energy loss caused by the accretion disk target photons
in the cases that are considered in this work (see Fig. 4). In the cases we studied, the accretion disk photons are usually scattered
in the Thomson regime.
2.3.4. Omission criterium for synchrotron energy losses
In particular, this work targets accretion radiation-strong blazars such as FSRQs. Here
synchrotron energy losses of the charged particles are typically weak when compared to
Compton losses (see also Fig. 4). In the Thomson
limit, synchrotron losses can therefore be neglected when, in the jet-frame, the
magnetic field energy density 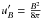 is much lower than the sum of all target
photon fields, i.e.:
is much lower than the sum of all target
photon fields, i.e.: 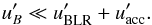 (28)The jet-frame accretion disk energy density
in the near field regime for a Schwarzschild black hole reads
(28)The jet-frame accretion disk energy density
in the near field regime for a Schwarzschild black hole reads
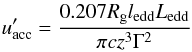 (see Dermer
& Menon 2009), while the jet-frame BLR radiation field is given by
(see Dermer
& Menon 2009), while the jet-frame BLR radiation field is given by
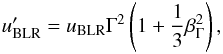 where the galaxy-frame BLR energy density
uBLR can be evaluated following Finke & Dermer (2010). In the case of negligible
BLR Compton energy losses, Eq. (28) reduces to:
where the galaxy-frame BLR energy density
uBLR can be evaluated following Finke & Dermer (2010). In the case of negligible
BLR Compton energy losses, Eq. (28) reduces to: ![\begin{eqnarray*} z \ll 380R_{\rm g} \left[\frac{1+\beta_{\Gamma})\Gamma}{B_G}\right]^{2/3} \left(\frac{l_{\rm edd}}{\epsilon_{\rm f} M_8}\right)^{1/3} \end{eqnarray*}](/articles/aa/full_html/2016/05/aa24738-14/aa24738-14-eq135.png) where leddLedd =
ϵfṀc2
(see Dermer & Schlickeiser 1993).
where leddLedd =
ϵfṀc2
(see Dermer & Schlickeiser 1993).
2.4. The emitting electron spectrum
The equation of motion of the relativistically outflowing jet with constant velocity
βΓc is 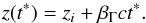 (29)The time interval in the rest frame of the
disk is related to the comoving frame by δt∗ =
Γδt. By combining Eq. (29) with Eq. (21) and
using the solution of Eq. (23) in the
near-field regime we get
(29)The time interval in the rest frame of the
disk is related to the comoving frame by δt∗ =
Γδt. By combining Eq. (29) with Eq. (21) and
using the solution of Eq. (23) in the
near-field regime we get 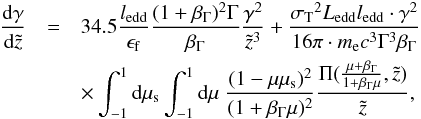 (30)which describes the change of electron energy
over a distance dz. We note that, while in the model of Dermer & Schlickeiser (1993) only Compton energy
losses in the disk radiation field are discussed, here we also take energy losses from
Compton scattering in the BLR radiation field into account. The initial value problem for
calculating the electron spectrum consists of Eq. (30), the point z, the injection point zi, and the Lorentz
factor γ that
the electrons possess, after having propagated from zi to z. This can only be solved
numerically. For all
(30)which describes the change of electron energy
over a distance dz. We note that, while in the model of Dermer & Schlickeiser (1993) only Compton energy
losses in the disk radiation field are discussed, here we also take energy losses from
Compton scattering in the BLR radiation field into account. The initial value problem for
calculating the electron spectrum consists of Eq. (30), the point z, the injection point zi, and the Lorentz
factor γ that
the electrons possess, after having propagated from zi to z. This can only be solved
numerically. For all 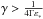 , the BLR component does not play a role.
In this case Eq. (30) simplifies to
, the BLR component does not play a role.
In this case Eq. (30) simplifies to
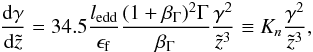 (31)which has an analytic solution:
(31)which has an analytic solution: 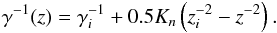 (32)We consider the continuous injection of an
electron power-law spectrum, with spectral index s, into a moving plasma
blob along the jet at an injection rate that depends on the height above the disk and with
an injection index α. The electron spectrum injected at height
zi can be described by
(32)We consider the continuous injection of an
electron power-law spectrum, with spectral index s, into a moving plasma
blob along the jet at an injection rate that depends on the height above the disk and with
an injection index α. The electron spectrum injected at height
zi can be described by
![\hbox{$N_{\rm e}(\gamma_i)=Q_0 \gamma_i^{-s}H[\gamma_i - \gamma_1] H[\gamma_2-\gamma_i]$}](/articles/aa/full_html/2016/05/aa24738-14/aa24738-14-eq145.png) , with Q0 the
normalization parameter. Using Eq. 32, the
cooled injected electron spectrum then has the form
, with Q0 the
normalization parameter. Using Eq. 32, the
cooled injected electron spectrum then has the form ![\begin{eqnarray} N_{\rm e}(\gamma,z,z_i)=Q_0 \cdot \gamma^{-2} \left[\gamma^{-1}-0.5K_n(z_i^{-2}-z^{-2})\right]^{s-2} \label{cooled_inj_espec} \end{eqnarray}](/articles/aa/full_html/2016/05/aa24738-14/aa24738-14-eq147.png) (33)(see also Dermer & Schlickeiser 1993).
(33)(see also Dermer & Schlickeiser 1993).
When continuously injecting power-law electron spectra into the moving plasma blob with a
given injection rate ∝ , the resulting emitting electron spectrum
Ne(γ,z) is a
superposition of the cooling electron spectra that have been injected and weighted by the
corresponding injection rate. This is described by
, the resulting emitting electron spectrum
Ne(γ,z) is a
superposition of the cooling electron spectra that have been injected and weighted by the
corresponding injection rate. This is described by ![\begin{eqnarray} N_{\rm e}(\gamma,z)=\int_{z_a}^{z_{\rm b}} {\rm d} z_i {z_i}^{-\alpha} N_{\rm e}(\gamma,z,z_i) H[\gamma - \tilde{\gamma}_1(z)] H[\tilde{\gamma}_2(z)-\gamma], \label{espec} \end{eqnarray}](/articles/aa/full_html/2016/05/aa24738-14/aa24738-14-eq150.png) (34)where
(34)where 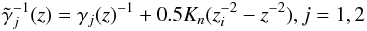 (35)describe the limits of the cooling electron
spectrum (see also Mücke & Pohl 2000).
(35)describe the limits of the cooling electron
spectrum (see also Mücke & Pohl 2000).
An electron that was injected with an initial energy γi cooled down to
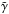 after having propagated a distance
ztravel =
z − zi.
Accordingly,
after having propagated a distance
ztravel =
z − zi.
Accordingly, 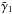 corresponds to the energy that an electron
injected at point zi with the energy
γ1 possesses after having propagated from
zi to z. The two Heaviside
functions
corresponds to the energy that an electron
injected at point zi with the energy
γ1 possesses after having propagated from
zi to z. The two Heaviside
functions ![\hbox{$H[\gamma - \tilde{\gamma}_1(z)]$}](/articles/aa/full_html/2016/05/aa24738-14/aa24738-14-eq157.png) and
and
![\hbox{$H[\tilde{\gamma}_2(z)-\gamma]$}](/articles/aa/full_html/2016/05/aa24738-14/aa24738-14-eq158.png) prevent all electrons that are injected
outside of the contributing energy range from adding to Ne(γ,z).
prevent all electrons that are injected
outside of the contributing energy range from adding to Ne(γ,z).
2.5. Calculating the photon spectrum
Having determined the emitting electron spectrum, we now proceed to calculate the
scattered photon spectrum of both the accretion disk target photon field and the BLR
target photon field. For this purpose, we follow Dermer et
al. (2009). The νFν
spectrum is given by 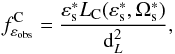 where dL is the
distance to the source.
where dL is the
distance to the source.
Here 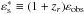 with zr the redshift of the
photons that are emitted by the source. The νLν
spectrum is related to the photon production rate via
with zr the redshift of the
photons that are emitted by the source. The νLν
spectrum is related to the photon production rate via 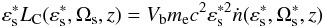 (36)where
(36)where 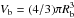 is the (observer frame) volume of the
emitting plasma blob with a radius Rb. We now calculate the photon
scattering in the rest frame of the accretion disk. Equation (1) in the rest frame of the accretion disk
reads
is the (observer frame) volume of the
emitting plasma blob with a radius Rb. We now calculate the photon
scattering in the rest frame of the accretion disk. Equation (1) in the rest frame of the accretion disk
reads 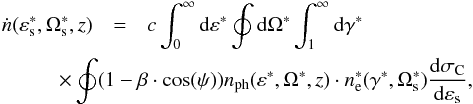 (37)where, again, the head-on approximation has
been used, which implies Ωe =
Ωs.
(37)where, again, the head-on approximation has
been used, which implies Ωe =
Ωs.
To calculate the scattered photon spectrum, we use the full Compton cross-section with
the scattering treated in the head-on approximation: 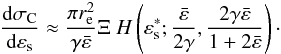 (38)
(38)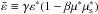 is the invariant collision energy after
having averaged over φ and
is the invariant collision energy after
having averaged over φ and 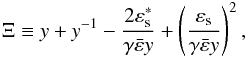 (39)with
(39)with 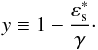 The Heaviside function gives the integration
limits:
The Heaviside function gives the integration
limits: 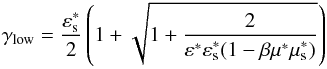 (40)is the lowest γ value at which an
electron can still transfer enough energy to a photon so that it reaches the energy
(40)is the lowest γ value at which an
electron can still transfer enough energy to a photon so that it reaches the energy
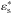 after the scattering.
after the scattering. 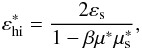 (41)is the highest photon energy, so that the
smallest energy transfer still yields a scattered photon with
(41)is the highest photon energy, so that the
smallest energy transfer still yields a scattered photon with
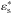 .
.
After transforming the emitting electron spectrum (calculated in the comoving frame) into
the rest frame of the accretion disk by 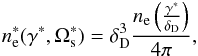 (42)we combine Eq. (36) with Eqs. (37)–(39) and (42) to arrive at
(42)we combine Eq. (36) with Eqs. (37)–(39) and (42) to arrive at 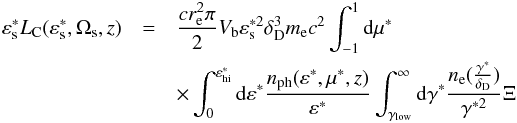 (43)for the νLν
spectrum.
(43)for the νLν
spectrum.
The final photon spectrum that is due to the BLR target photons is calculated by using Eq. (11) in conjunction with Eq. (43).
To calculate the target photon density nph(ε∗,μ∗)
that is produced by the accretion disk photons, we integrate over the whole disk first. We
substitute Ṅph in Eq. (13) with Eq. (18) and
get 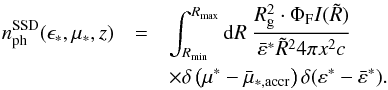 (44)From
(44)From 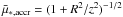 we introduce
we introduce 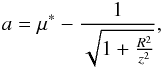 with
with 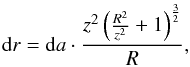 and
and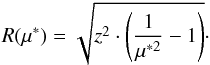 Scaling the length scales
Scaling the length scales
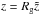 and
and
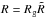 in terms of the gravitational radius
Rg we obtain
in terms of the gravitational radius
Rg we obtain
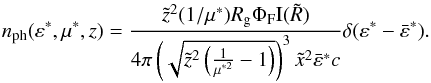 (45)This can be used in conjunction with Eq.
(43) to find the scattered photon
spectrum that is produced by the accretion disk target photon field. The total photon
spectrum produced is the sum of the photon spectra from both target photon fields.
(45)This can be used in conjunction with Eq.
(43) to find the scattered photon
spectrum that is produced by the accretion disk target photon field. The total photon
spectrum produced is the sum of the photon spectra from both target photon fields.
We note that a further leptonic high-energy radiation process which contributes to the broadband blazar SED is synchrotron-self Compton (SSC) scattering. In the case of quasars with strong accretion disks, as considered in this work, the radiative output from this process has been found to typically dominate in a rather small energy range at X-rays (see e.g., Böttcher 2000; Dermer et al. 2009). Hence its contribution to the overall shape of the SED is markedly limited. We therefore do not include this process in our model, noting that our studies and the predictions given in the following should be considered with care at X-ray energies.
3. Results
We present the electron and photon spectra following the calculations outlined in Sects.
2.2 and 2.5.
For our calculations we set the black hole mass to 108M⊙
(noting that the spectral shape only depends weakly on the black hole mass), the bulk
Lorentz factor to Γ = 25, a
fraction of ledd =
0.1 of the Eddington luminosity for the central source and use a value of
ϵ∗ 0 =
25(mec2)-1
eV as the characteristic photon energy of the BLR (monochromatic) spectrum. Here,
synchrotron energy losses can be neglected for field values smaller than ~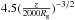 G.
G.
In the following, we focus on photon spectra up to ~10 GeV. Hence, γ-ray absorption during propagation through the diffuse extragalactic background light can be neglected here (e.g., Abdo et al. 2010c). We also neglect internal γ-ray absorption in the external radiation fields, which could potentially affect the spectral shape beyond ~50 GeV for typical bright Fermi-LAT FSRQs (see Sect. 4), and focus our spectral considerations below this energy. We also note that most Fermi-LAT FSRQs were not detected beyond such energies owing to their typically strong spectral decline at a few GeV (e.g., Ackermann et al. 2011), although few notable exceptions (e.g., 3C 279 (MAGIC Collaboration 2008), 4C +21.35 (Aleksić et al. 2011), PKS 1510-089 H.E.S.S. Collaboration et al. 2013) exist.
Below, the photon spectra are shown in the observer frame using a source redshift of zr = 1. All distances are given in terms of the gravitational radius Rg.
In our parameter study, we discuss the impact of varying selected parameters, with respect to a reference model, on the resulting particle and photon spectra. The varied parameters are:
-
the height z above the disk where the emission region is located at observing time tobs;
-
the injection-rate index α at the position z;
-
the starting and end points za<z and zb>za of the particle injection; we set z = zb unless specified otherwise;
-
the spectral index s and the high (low) energy cutoff, γ2 (γ1), of the injected power-law electron spectrum
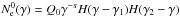 ;
; -
the geometry of the BLR:
-
Ri, Ro, inner and outer border of the BLR;
-
ζ describes the density decline inside the BLR,
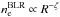 ;
; -
the BLR optical depth
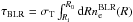 ;
;
-
The
free parameters of the BLR are combined to result in four different BLR configurations
BLR1-BLR4 (see Table 1) that are used to explore
their effect on the emitting electron and photon spectrum. For the reference model, we use
the following parameters: s =
3,α = 2,za =
200,z = zb =
2000,γ1 = 1000,γ2 = 5 ×
105,τBLR = 0.01, and BLR1 as the
BLR geometry. We use a dimensionless injection energy parameter
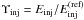 to provide the total injected particle
energy Einj in each model in terms of the total
injected particle energy of the reference model,
to provide the total injected particle
energy Einj in each model in terms of the total
injected particle energy of the reference model, 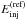 .
.
3.1. The BLR geometry
 |
Fig. 5 IC photon spectra (and ambient electron spectrum as an inlay in panel b for the reference model) for different BLR geometries used. a) Composite IC photon spectrum for the case of BLR1. b) Resulting IC photon spectra when varying the BLR geometries. The inlay shows the underlying ambient electron spectrum. |
List of BLR geometries used.
We first study the influence of different BLR geometries (as listed in Table 1) upon the inverse Compton (IC) photon spectrum. Geometries BLR1 and BLR2 follow a ζ = −2 density distribution of the BLR gas. Here most of its density is located close to the inner BLR boundary. BLR3 and BLR4 follow a constant density distribution between the inner and the outer radius of the BLR. The BLR geometry has no significant influence on the shape of the electron spectrum, a consequence of the electron energy-loss rates in the BLR being rather low in general (see Sect. 2.2.1).
Figure 5a shows the total IC photon spectrum being composed of two components: the lower energy one is produced by IC scattering the accretion disk target photons, the second component, with a peak at around 3 GeVs, is produced by scattering the BLR target photons. Using different BLR configurations with respect to the emission region leads to quite different IC spectra, as we present in Fig. 5b.
The BLR3 gas is distributed in a rather thin shell. With the emitting region located at z = 2000 at the time of observation, i.e., beyond the outer boundary of the BLR3, the BLR photons enter the blob from behind with a collision angle similar to the accretion disk photons. The BLR3 contribution is drowned out by the much more numerous accretion disk photons. Hence, Fig. 5b shows that the total IC spectrum for the BLR3 case is nearly indistinguishable from the dominating accretion disk IC component (Fig. 5a).
In the BLR1 configuration the emission region is located within the BLR with parts of the BLR1 gas being in front of this region. Target photons from this front part experience a higher energy transfer than the photons from the accretion disk, therefore they are scattered to higher energies. Hence at high energies, the BLR IC component starts to poke through the accretion disk IC component (Fig. 5b). This behaviour becomes most prominent in the BLR2 configuration, where an even larger fraction of the BLR gas lies in front of the blob. Here again, the high energy BLR peak is produced by target photons that are backscattered by the BLR gas in front of the emission region.
The resulting IC spectrum from the BLR4 configuration, also shown in Fig. 5b, displays a shifted BLR peak position with respect to BLR1 and BLR2. In the BLR4 configuration, the emission region is located on the outer edge of the BLR. No target photons enter the blob from the front, but a large number of target photons enter from the sides. The maximum energy transfer for these photons is smaller than for photons that enter the blob from the front, thereby shifting the peak position of the IC component to smaller energies.
In summary, if the ambient electron spectrum is unambiguously determined, the relative position of the emission region with respect to the BLR geometry influences the relative strength of BLR and accretion disk component, and may shift the peak energy of the BLR IC component.
3.2. The luminosity of the accretion disk
The accretion disk luminosity, here measured in terms of a fraction ledd of the Eddington luminosity, directly influences the density of the target radiation field along the jet. Higher accretion disk luminosities lead to increased particle cooling; the ambient electron spectrum reaches to lower minimum electron energies (see Fig. 6a). Consequently, the corresponding IC scattered photon spectra also reach lower energies as shown in Fig. 6b, as do the corresponding synchrotron radiation spectra.
3.3. The injected particle spectrum
The injected electron spectrum, a simple power law with spectral index s, is bracketed by the low-energy and high-energy cutoff particle Lorentz factors γ1 and γ2. The effects of varying γ1, γ2 and s with respect to the reference model are explored below.
 |
Fig. 6 Emitting electron (left) and resulting photon spectra (right) for various ledd. Where ledd = 0.01 we also show the photon components produced by both target photon fields separately. |
 |
Fig. 7 Emitting electron (left) spectra and corresponding photon spectra (right) for γ1 that varies with respect to the reference model. The total injected particle energies are strongly determined by γ1. For γ1 = (100,500,1000,1500), we find Υinj = (10.1,2.0,1,0.7). |
 |
Fig. 8 Emitting electron (left) and corresponding photon spectra (right) for spectral injection indices s, varying with respect to the reference model. The total injected electron energies for s = (2,3,4) are Υinj = (4.7 × 103,1,5.1 × 10-4). In the case of s = 4, the photon components produced by both target photon fields are shown separately as well. |
In Fig. 7a we show the resulting electron spectra when γ1 is varied, while leaving all the other parameters unchanged. Clearly, at γ = γ1 a break in the emitting electron spectrum generally occurs unless the injection rate is very steep (see Sect. 3.4). The amount of the spectral index change at the break energy can be understood as follows: For energies larger than γ1, electrons are continuously injected and cooled at the same time. Hence, the produced power-law spectrum in this regime depends on the injected electron spectral index s. At electron energies smaller than γ1, only cooled particles accumulate. Thus the spectral shape depends on the injection rate index α (see Sect. 3.4). The combination of s and α thus influences the broadness of the break in the emitting particle spectrum. In particular, breaks that are larger than typical cooling breaks, as implied, e.g., from observed GeV spectra of bright LAT FSRQs, become possible here.
The corresponding photon spectra are shown in Fig. 7b. The peak of the emitting electron spectrum translates into peaks in the corresponding components of the photon spectra. The different incident angles of the BLR target photon component, as compared to the accretion disk component, lead to a larger range of electron energies that can scatter photons up to the same energy. The geometric area from which the target photons can contribute to a certain scattered photon energy slowly decreases, leading to a more gradual decrease, rather than a sharp cut-off towards high energies. The BLR peak is shifted to higher energies with respect to the accretion disk peak, again the reason is the different incident angle distribution of the BLR target photons. In the BLR component, head-on scattering with a higher energy transfer to the photon is common. Thus electrons with the same energy lead to higher energetic scattered photons for the BLR target photons than for the accretion disk photons. In Fig. 7b, we also note the decreasing contribution of the Compton scattered BLR radiation to the total photon spectrum with increasing γ1, a consequence of scattering in the Klein-Nishina regime of the cross-section with increasing energy.
As mentioned above, a change of the spectral injection index s impacts the energy range above γ1 in the emitting particle spectrum, becoming softer for softer injection spectra, and behaving as ne(γ) ∝ γ− s−1. Hence for a given injection rate index α, the spectral break in the emitting particle spectrum becomes broader for harder injection spectra (see Fig. 8a). For sufficient broad ambient electron spectra, the corresponding photon spectra from IC scattering the accretion disk and BLR radiation tend to merge into one component as is shown in Fig. 8b. Again, we also note the impact of the IC scattering in the Klein-Nishina regime, which leads, for the same ambient electron spectrum, to softer photon spectra of the BLR-scattered component, as compared to the accretion disk scattered IC component beyond the respective peak energy.
 |
Fig. 9 Emitting electron spectra (left) and corresponding photon spectra (right) for γ2 that vary with respect to the reference model. The total injected electron energy is rather insensitive to γ2. For γ2 = (3000,5000,8000,10 000) we find Υinj = (0.7,0.8,0.9,0.9). In the case of γ2 = 3000, we show the photon components produced by both target photon fields. |
Very high energy electrons cool efficiently in the dense target radiation fields. Hence the particle spectrum above γ1 quickly re-arranges to a state where injection rates balance the loss rates. For a sufficiently large high-energy cutoff of the injected electron spectrum, γ2, where the radiative loss timescales at γ2 are much smaller than the injection timescale, any variation of this parameter therefore only marginally impacts on the resulting emitting electron and photon spectrum: the ambient particle spectra become very similar after only a short time owing to severe Compton losses.
For cases where the injected electron spectrum is bounded to an energy range where injection rates reach at least the radiative loss rates, a variation of γ2 results in a corresponding cut-off of the ambient particle and photon spectra, as shown in Fig. 9. The values used in Fig. 9 for γ2 within the reference model lead to a turn-over of the photon spectrum in the tens of MeV energy range when accretion disk photons are scattered, and in the GeV energy range when BLR target photons are scattered. The two photon components are visibly seperated only for sufficiently low γ2.
3.4. The particle injection mode
The effects of different particle injection scenarios on the resulting emitting electron
and photon spectra are explored in this section. Particle injection starts within the jet
at height za above the
accretion disk and continues with a rate ∝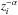 (where α is the injection rate
index) up to a height zb.
(where α is the injection rate
index) up to a height zb.
 |
Fig. 10 Ambient electron (left) and photon spectra (right) with different injection rate parameters α, with respect to the reference model. The total injected electron energies for α = (0,1,2,3,4) are calculated to Υinj = (4 × 105,512,1,0.3,9 × 10-6). In the case of α = 4, we also show the IC components produced by both target photon fields separately. |
The injection rate index α controls the spectral shape of the ambient particle
spectrum below γ1 and (together with s) the spectral index
change of the break. Figure 10 shows that harder
pre-break spectral shapes develop for steeper injection rate distributions (large
α). This
can be understood as follows: particles in the pre-break regime γ<γ1 are cooled
electrons, which have suffered energy losses while propagating at least a distance that
corresponds to 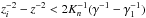 , where zi was the injection
point. This implies a direct relation between γ and zi. Hence those
particles injected at point zi contribute to the
ambient spectrum at γ<γ1. Since cooling
rates are highest where the injection starts (at za), the number of
particles injected there contribute to the lowest energies γ ≪
γ1 in the ambient spectrum. As a
consequence, for very steep injection rate distributions, rather soft ambient spectra
develop while, for shallow injection distributions, hard emitting particle spectra build
up at γ<γ1 (see Fig. 10). Specifically, for constant injection rates
(α = 0), we
find an approximately ∝γ−
1/2 behaviour at γ<γ1. For
α = 3,
injection rates decrease with distance z at the same rate as the cooling decreases. The
ambient electron spectrum becomes independent of the blob location, and the well-known
ne ∝
γ-2 emitting electron spectrum develops
for γ<γ1. For
well-developed electron distributions, α does not impact the spectral shape at
γ>γ1.
, where zi was the injection
point. This implies a direct relation between γ and zi. Hence those
particles injected at point zi contribute to the
ambient spectrum at γ<γ1. Since cooling
rates are highest where the injection starts (at za), the number of
particles injected there contribute to the lowest energies γ ≪
γ1 in the ambient spectrum. As a
consequence, for very steep injection rate distributions, rather soft ambient spectra
develop while, for shallow injection distributions, hard emitting particle spectra build
up at γ<γ1 (see Fig. 10). Specifically, for constant injection rates
(α = 0), we
find an approximately ∝γ−
1/2 behaviour at γ<γ1. For
α = 3,
injection rates decrease with distance z at the same rate as the cooling decreases. The
ambient electron spectrum becomes independent of the blob location, and the well-known
ne ∝
γ-2 emitting electron spectrum develops
for γ<γ1. For
well-developed electron distributions, α does not impact the spectral shape at
γ>γ1.
Particle injection starts within the jet at height za above the accretion disk. Figure 11 shows the resulting electron and photon spectra for different values of za, all other injection parameters are kept constant.
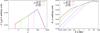 |
Fig. 11 Ambient electron (left) and photon spectra (right) when varying za (in Rg) with respect to the reference model. The injected total electron energies for za = (100,200,500,1000) are Υinj = (2.1,1,0.33,0.1). The total injected energy decreases with rising za. |
A higher cooling rate in the accretion disk radiation field, as well as a longer total cooling time (due to larger z − za distance), leads to lower electron energies with decreasing za (see Fig. 11a). Hence, the corresponding photon spectrum below γ1 (Fig. 11b) softens and extends to very low energies depending on za.
 |
Fig. 12 Ambient electron (left) and photon spectra (right) when varying the distances between the points z and zb (in Rg), with respect to the reference model. The total injected electron energy is Υinj = 1 in all cases. For z = 2100, we also show the IC photon components produced by the two target photon fields considered separately. |
Next, we explore the situation of a finite particle injection duration (corresponding to a distance zb − za in the jet) where the resulting spectra are observed at a given time after the last particle injection has occured. This time corresponds to a distance z − zb in the jet. Figure 12 shows the resulting electron and photon spectrum for various z with fixed points za and zb. Because of the strong energy dependence of the electron cooling (with higher energy electrons cooling faster than lower energy electrons; see Sect. 3.3) we observe the exponential high energy cut-off in the electron spectrum moving to lower energies while, below γ1, the electron spectrum does not change significantly.
The influence of the electron cut-off is reflected in the corresponding photon spectrum. Although the electron injection spectral index s is constant, the post-break photon spectrum becomes softer, owing to the lower energies of the electron energy cut-off. In Fig. 12b, we also show the total photon spectrum decomposed into the IC-scattered accretion disk and BLR photon spectrum. We note that the turn-over in the photon spectrum at a few GeV has its origin in the break of the underlying electron spectrum.
 |
Fig. 13 ambient electron (left) and photon spectra (right) for various zb (in Rg) with respect to the reference model. The total injected electron energies for zb = (1000,2000,3000,4000) are Υinj = (0.9,1,1.04,1.06). For zb = 1000, the IC photon components produced by the two target photon fields are also shown separately. |
We now explore the impact of a changing injection duration upon the resulting spectra. For this purpose, we vary zb while keeping za fixed, and analyse the resulting particle and photon spectra at z = zb. The longer the injection at a given rate, the higher the total injected particle energy. At the same time, the particles cool, at a, generally, decreasing rate with increasing distance from the black hole. Hence, we find a strong dependence of the resulting spectral shapes upon the interplay between the injection and energy-loss rates. Therefore, we also present our results for various injection rate indices α.
For a sufficiently shallow decrease of the injection rate, a pile-up forms in the emitting particle spectrum at γ = γ1, with the spectral index below γ1 becoming harder. This is a result of the cooling rate of particles at low energies not being sufficiently large to be able to fully balance the injection rate at these energies. Long injection times at sufficiently large z ensure an accumulation of particles at low energies, with reduced cooling rates leading to the pile-ups becoming more prominent with increasing zb. This is demonstrated in Figs. 13a and b, where the spectra are shown for α = 2 and various zb.
Electrons pile up at a given particle energy γ in a spectrum when, in momentum space, the net change of the number of electrons entering this γ-bin (either from injection or from cooling down from a higher energy bin γ + dγ) and leaving this bin to γ − dγ, due to cooling, is positive. For an increasing cooling rate with energy, this occurs at the low-energy end of the injected spectrum, i.e., at γ = γ1. For broad injection distributions α< 3 particle injection at large z, where cooling rates are diminished, is still significant. This facilitates accumulating particles within an energy bin. A pile-up forms. As noted above, for α = 3, the emitting electron spectrum becomes independent of the blob location, and hence also of zb. Thus, in this case, a pile-up does not form (see Fig. 14a). For α> 3, the effects discussed above reverse and the spectral index becomes softer after the break γ = γ1. In Fig. 14c we present the case of α = 7. Here the injection scenario becomes more “instantaneous-like”, and we follow the evolution of the injected spectrum for a time that corresponds to (zb − za) /βΓc. For increasing zb, the emitting electron spectrum steepens while extending to low energies γ<γ1 owing to cooling. In the limit of large zb, all electrons have cooled and the injected power law is mapped into the γ<γ1 energy regime. The overall peak of the emitting electron spectrum for an instantaneous-like injection is therefore found at the low-energy end. Here, the emitting electrons correspond to the cooled particles that were injected at γ1. Their energy depends on the cooling rate, which is highest at the injection point za.
The corresponding photon spectra (see Figs. 13b, 14b and d) reflect the shapes of the respective ambient electron spectra, with some impact of the relative position of the emitting region with respect to the BLR (the latter has been discussed in more detail in Sect. 3.1). We note the shift of the IC peaks in Fig. 14d to lower energies which is due to the corresponding emitting electron spectra peaking in these cases at the very low-energy end.
 |
Fig. 14 Photon and ambient electron spectra for zb (in Rg) and α with respect to the reference model. The total injected electron energies for α = 3 and zb = (1000,2000,3000,4000) are Υinj = (2.7,2.75,2.8,2.8) × 10-3 while, for α = 7, the total injected electron energies for zb = (1000,2000,3000,4000) are Υinj = (5.8,5.8,5.8,5.8) × 10-13. For α = 3 and α = 7 with zb = 1000, we also show the IC photon components produced by the two target photon fields separately. a) Normalized electron spectra for various zb (in Rg) and α = 3. b) Corresponding photon spectra for various zb (in Rg) and α = 3. c) Normalized electron spectra for various zb (in Rg) and α = 7. d) Corresponding photon spectra for various zb (in Rg) and α = 7. |
4. Modeling the 3C 454.3 and PKS 1510-089 multifrequency SEDs
To show the viability of our model, we apply it to quasi-simultaneous broadband data that was collected during the November 2010 outburst of 3C 454.3 (Abdo et al. 2011; Wehrle et al. 2012), with a particular focus on the Fermi-LAT spectrum that shows a distinct spectral decline at a few GeV. Additionally, we use our model to also fit the quasi-simultaneous broadband SED of PKS 1510-089, as reported in Abdo et al. 2010b. The low-energy photon data provides additional valuable constraints on the emitting electron distributions. Within our model, we calculate the synchrotron radiation from the ambient electron distribution following Dermer et al. (2009), assuming a tangled magnetic field of strength B, and including synchrotron-self absorption.
4.1. Modeling the 3C 454.3 multifrequency SED
 |
Fig. 15 Two-component IC model fit to multifrequency data of 3C 454.3. The model is shown in red with the data points shown in blue. The model parameter values are listed in Table 2. a) Emitting electronspectrum. b) Synchroton spectrum with Swift, Herschel and Submillimeter Array data taken during the November 2010 flare (Wehrle et al. 2012). c) Gamma-ray spectrum with Fermi-LAT data taken during the November 2010 flare (Abdo et al. 2011). d) Zooming into the γ-ray spectrum with Fermi-LAT data taken during the November 2010 flare (Abdo et al. 2011). |
 |
Fig. 16 Dominant-BLR IC model fit with multifrequency data of 3C 454.3. The model is shown in red with the data points shown in blue. The model parameter values are listed in Table 2. a) Emitting electron spectrum. b) Synchroton spectrum with Swift, Herschel and Submillimeter Array data taken during the November 2010 flare (Wehrle et al. 2012). c) Gamma-ray spectrum with Fermi-LAT data taken during the November 2010 flare (Abdo et al. 2011). d) Zooming into the γ-ray spectrum with Fermi-LAT data taken during the November 2010 flare (Abdo et al. 2011). |
In the following, we discuss two possible model fits to the data. The parameter values used for these fits are listed in Table 2, including the required particle power Ppar of the complete injection event, which was calculated by assuming that the total power in particles (electrons and cold protons) is tenfold the power in nonthermal electrons, the magnetic field power PB, and the equipartition field Beq.
In Fig. 15 we present a model representation of the broadband data with parameter values similar to those used in Finke & Dermer (2010). The size of the BLR used in our model agrees well with Bonnoli et al. 2011, but is different from the one used in Finke & Dermer (2010). Other slight differences in the fit parameter values are due to the different data set we used. We note that the (observer frame) sizes of the emitting region, which are used in the model fits we present, are roughly around the size limits inferred by Sbarrato et al. (2011). Here, we searched for particle injection parameter values that lead, in the framework of our model, to an ambient snapshot electron spectrum similar to the ad hoc ambient electron spectrum used in the aforementioned paper. We find that continuous electron injection is indeed able to generate a broken power-law emitting electron spectrum that is similar to the one assumed in Finke & Dermer (2010). For this model fit, the γ-ray photon spectrum is explained by the combination of a BLR and an accretion disk target photon component in the same way as in Finke & Dermer (2010). We found reasonable fits for a range of particle injection parameter values. The injection spectral index s of the electron spectrum is required to lie within the range of 2 and 3. The model fit is somewhat insensitive to changes in α, the injection rate index, providing α ≤ 4. For α> 4, the ambient electron spectrum would become too soft to be able to fit the low energy part (<1 eV) of the optically thin synchrotron radiation component. The parameter γ1 controls the position of the break in the emitting electron spectrum. Hence the model fit is quite sensitive to changes in this parameter. We found reasonable fits with γ1 between 800 and 1300. Furthermore, sensible fits were found when z = zb was between 1500 and 3000. For γ2> 20 000 the post-break (>3 GeV) spectral index does not adequately represent the data. For γ2< 10 000 the GeV-spectrum becomes two-peak shaped, which does not fit the data well. The first injection point za is not well constrained here by the data since it merely influences the pre-break photon spectrum. Reasonable fits can be achieved for values between za = 100 and 800.
In the previous section, we demonstrated that broken power-law ambient electron spectra with changes in the spectral index, which are greater than the cooling break, can develop as a result of the continuously varying injection of non-thermal particles along the jet. We apply this property to the broadband data of 3C 454.3 to demonstrate that the observed decline of the GeV-spectrum in bright FSRQs can be consistently modeled by this kind of scenario. Unlike in the previous fit, where two IC components are required, this scenario requires only one, but dominating IC component. In Fig. 16, we show a model fit to the data with a higher optical thickness (τBLR = 0.05) of the BLR. As a consequence, the BLR IC component dominates at γ-ray energies >10 MeV. The GeV spectral turn-over here is due to a corresponding break in the emitting electron spectrum, i.e., not the result of a combination of the accretion disk and BLR IC component. This different behavior also leads to differences with respect to the sensitivity of the model parameter values. The parameter value of za here is more constrained, since the pre-break emission of the BLR IC component dominates in the sub-GeV energy range (around 100 MeV). We require za< 200 to adequately fit the data. Similarly, changes in the last injection point zb also impact the shape of the resulting ambient spectrum in the pre- as well as post-break regime. Choosing zb between 2000 and 3000 leads to reasonable model fits. The injection rate index α influences the pre-break spectrum, and is therefore rather tightly constrained, as well, to values between α = 4 and 4.5, with electron injection spectral indices lying in the range s = 1.5–2.5. This choice also leads to a satisfying model representation of the observed synchrotron spectrum. The parameter values for γ1 and γ2 are similarly constrained, as in the previous model fit.
In summary, both model fits to the flare 3C 454.3 data set point towards gradually decreasing injection rates that start close to the inner boundary of the BLR but do not extend beyond the outer boundary of the BLR at the time of observations. Nalewajko et al. (2014) explored the efficiency of several constraints for the location of the blazar zone, such as the collimation, SSC, cooling and internal γ-ray opacity constraints. Although, in our modeling, we adopted a somewhat weaker accretion disk and BLR luminosity than Nalewajko et al. (2014) for the November 2010 flare of 3C 454.3, we find that the blazar zone location in our model fits is in agreement with Nalewajko et al. (2014).
The injection spectrum is found to be surprisingly narrow, between γ ~ 103−104. The Thomson optical thickness τBLR of the diffuse BLR gas influences the relative importance of the BLR and accretion disk IC components. Accordingly, for a very low τBLR, the spectral decline observed at a few GeV from 3C 454.3 can be explained by the combination of both IC components while, for sufficiently larger τBLR, the GeV-break in the photon spectrum is due to an intrinsic break in the emitting electron spectrum where the injection properties play a decisive role. The break energy is determined by the low-energy cut-off γ1 of the injected electron spectrum. The observed, approximately constant, break energies that are independent of flux state (e.g., Abdo et al. 2011) imply a correspondingly constant γ1 for a constant Doppler factor, if there is no rapid change from a continuous to impulsive-like injection mode (or vice versa). The energy density of the magnetic field for these model fits is found below the jet-frame disk energy density up to distances ~2000–3000 Rg above the black hole, and therefore justifies the neglect of synchrotron losses up to these distances.
Potentially, γ-ray absorption, followed by pair production in the BLR radiation field, may impact the emerging photon spectrum (e.g., Donea & Protheroe 2003). Here, not only absolute luminosities of the BLR are important, but also its geometrical structure. For example, for a flat BLR geometry in blazars with typical BLR parameters, Lei & Wang (2014) demonstrate that high energy photons up to tens of GeV can escape this region.
We therefore investigate the importance of this process for the above parameter values.
For a smooth broadband target spectrum, most of the photon-photon interactions take place
in a small energy interval that is centered on 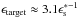 (e.g., Reimer 2007) in the galaxy frame owing to the strongly peaked cross-section near
the threshold. Gamma-gamma absorption in the BLR radiation field therefore modifies the
observed γ-ray spectrum beyond ϵ ≈ 3.1(ϵ0 ∗(1 +
zr))-1, which
is above the highest photon energy detected from this source for our parameter choice of
ϵ0 ∗ =
10(mec2)-1
eV.
(e.g., Reimer 2007) in the galaxy frame owing to the strongly peaked cross-section near
the threshold. Gamma-gamma absorption in the BLR radiation field therefore modifies the
observed γ-ray spectrum beyond ϵ ≈ 3.1(ϵ0 ∗(1 +
zr))-1, which
is above the highest photon energy detected from this source for our parameter choice of
ϵ0 ∗ =
10(mec2)-1
eV.
During the April and September 2013 outbursts of this source, Pacciani et al. (2014) noted a very different flaring behavior: hard LAT-flares with exceptional hard power-law spectra, as opposed to the soft flaring events from 3C 454.3 that are considered in this work, which typically show strong declines or even cut-offs in the GeV range. From γγ-pair production arguments and the non-detection of any KN-curvature during these hard flare events, Pacciani et al. (2014) argue that the emission region must be beyond or at the outer rim of the BLR, where the bulk of the gamma-rays are produced by Comptonization of photons from the IR torus.
Model parameters fitting the November 2010 flare state SED of 3C 454.3.
4.2. Modeling the PKS 1510-089 multifrequency SED
The FSRQ PKS 1510-089 at redshift ~0.361 is among the best observed γ-ray blazars with a well-constrained SED from radio to γ rays. We apply our model to the quasi-simultanuous broadband data from the January 2009 flare, as published in Abdo et al. (2010b), the first flare in a series of outbursts from this source in early 2009. These observations indicate variability on timescales of a day down to a few hours (e.g., Abdo et al. 2010a). Though PKS 1510-089 is a known VHE FSRQ (Wagner et al. 2010), it has not been detected at VHEs during the considered outburst. Apart from γ-ray observations, this source has also been monitored during the 2009 activity at radio, optical (including polarization measurements) and X-rays (Marscher et al. 2010). The appearance of two new knots on VLBA 43 GHz radio maps around August 2008 and April 2009, which move with superluminal speeds of ~24c and ~22c along the jet, seem to indicate a relation between these flaring events and their appearance (Marscher et al. 2010). The optical polarization vector started rotating by ~720° just after the flare that we consider here. The Fermi-LAT spectrum, during the January 2009 flare, indicates a pronounced steep decline at a few GeV, which has been observationally described by a log-parabolic shaped spectrum (Abdo et al. 2010a).
Model parameters fitting the SED of PKS 1510-089.
We present two sets of parameter values (see Table 3) that have been found to represent the data from the January 2009 flare well. Here again, the listed particle power Ppar (including electrons and cold protons) is given as tenfold the total injected power of the nonthermal electrons. To quantify the black hole mass and accretion disk luminosity, we use M8 = 5 and ledd = 0.16, which agrees well with data presented in Pucella et al. (2008).
In Fig. 17, we show a model fit where the joint Compton-scattered disk and BLR radiation explains the observed LAT-spectrum. In this fit, we keep the BLR geometry unchanged with respect to the 3C 454.3 fits, and use a (observer-frame) size of the emitting region of Rb = 1 × 1015 cm, in agreement with Abdo et al. (2010a) and the inferred limits of Sbarrato et al. (2011). We now discuss the robustness of the parameter values used for our model fit. As in the fit to 3C 454.3, the model is quite sensitive to changes in γ1 since it controls the position of the breaks in the electron spectrum and, in turn, also controls the position of the respective breaks in the photon spectra. The injection spectral index s for this fit is required to lie between 1.5 and 2.5 for a reasonable fit. The model fit is again rather insensitive to changes in the injection parameter α since changes in this parameter mostly influence the spectral index before the break in the respective photon spectra. We get the best fit for z = zb = 3000Rg, but values from 2000Rg to 4000Rg also lead to reasonable fits. For γ2, we can achieve reasonable fits up to a value of 2 × 104, otherwise the model does not describe the high energy part (>1 GeV) of the data adequately. As in the 3C 454.3 case, the first injection point za is not well constrained. Values between za = 200Rg and za = 800Rg lead to reasonable fits. We note that the parameter values for this fit are quite similar to the ones used for the 3C 454.3 data set.
In Fig. 18 we present a model that is able to explain the γ-ray data with Compton-scattered accretion disk radiation only. Here, the break in the GeV-spectrum is generated by the break in the corresponding emitting electron spectrum. By reducing the geometric thickness of the BLR and keeping a realistic BLR optical depth, the importance of the BLR as a target photon field is diminished for the emitting region, since it is located at snapshot time just beyond the BLR border. Particle injection started when the emission region was inside the BLR and stopped just beyond the border of the BLR. We found that the accretion disk radiation dominated the target photon field energy density in this case. Other than the change of the BLR geometry, the fit parameter values are similar to the ones fitting the two-component model with only slight changes in γ1 and the bulk Doppler factor. Our fit is found to be sensitive again to changes in γ1 since it controls the position of the break. The injected electron spectrum is as narrow as in the 3C 454.3 fit, extending from γ ~ 103−104. For the other parameters, we reached reasonable fits at roughly the same parameter ranges that we used for the two-component fit.
 |
Fig. 17 Two-component IC model fit to multifrequency data of PKS 1510-089. The model is shown in red with the data points shown in blue. The model parameter values are listed in Table 3. a) Emitting electron spectrum. b) Synchroton spectrum fit to data from Abdo et al. (2010b). c) Gamma-ray spectrum with Fermi-LAT data Abdo et al. (2010b). d) Zooming into the γ-ray spectrum with Fermi-LAT data (Abdo et al. 2010b). |
 |
Fig. 18 Dominant accretion-disk IC model fit with multifrequency data of PKS 1510-089. The model is shown in red with the data points shown in blue. The model parameter values are listed in Table 3. a) Emitting electron spectrum. b) Synchroton spectrum fit to data from Abdo et al. (2010b). c) Gamma-ray spectrum with Fermi-LAT data (Abdo et al. 2010b)). d) Zooming into the γ-ray spectrum with Fermi-LAT data (Abdo et al. 2010b). |
Both model fits to the PKS 1510-089 data require a continuous injection scenario with gradually decreasing injection rates. Thus, impulsive injection scenarios (i.e., α> 5) are again disfavored. In both of our model representations of the PKS 1510-089 data set, the accretion disk IC component is more prominent than in the 3C 454.3 fits. The energy density of the magnetic field for these model fits is found below the jet-frame disk energy density up to distances ~2000–3000Rg above the black hole, and therefore justifies the neglect of synchrotron losses up to these distances.
Abdo et al. (2010a) modelled this flare by also using a stationary leptonic blazar model, however, they were using parameter values that put more emphasis on the (assumed non-stratified) BLR and less on the accretion disk radiation field than our model parameter set values (and also the modeling of Böttcher et al. (2013) of this source). As a consequence the LAT-data are explained rather by dominantly Compton-scattered BLR-photons from lower energetic electrons than our model envisions. The corresponding SSC component is found to be negligible.
Interestingly, our spectral modeling of this flaring event being due to the Compton scattered accretion disk and BLR photons from a ~1 G magnetized jet emission region, is in qualitative agreement with the scenario Marscher et al. (2010) proposed for this activity period.
Nalewajko et al. (2014) place the emission region of the April 2009 flare of this source outside the BLR, while no constraints were put on the January 2009 outburst. Our model fit parameters for this January 2009 flare point towards an emission region that is located inside the BLR at the time of this flare. If the series of flares in 2009 of PKS 1510-089 were causally connected, possibly originating from the same so-called blob that was moving along the jet, then the location of this blob that caused the January 2009 flare would be well outside the BLR at the time of the April 2009 flare, assuming no strong blob-braking. This would be compatible with the results of Nalewajko et al. (2014).
We note that the Herschel PACS & SPIRE data from observations of this source in late 2011 (Nalewajko et al. 2012) lie above our model curves. Hence, if this IR flux were comparable during the here considered 2009 event, these IR photons would have to be produced by a further region within the jet with possibly some notable contribution from the dusty torus.
Similar to 3C 454.3 (see Sect. 4.1), we find γγ-pair production being negligible for the parameter set used for the above model fits and below the last LAT data point (Barnacka 2013).
Chen et al. (2012) modelled the last flare in the extended early 2009 flaring episode of this source by using a time-dependent Monte Carlo Fokker-Planck code, where the emission region is treated as an extended cylindrical volume within the jet. In addition to a particle “pick-up” term in the Fokker-Planck equation, they also included a stochastic acceleration term and took into account all external and internal target photon fields. Although, in their modeling, they did not discuss pronounced GeV spectral turn-over, but rather focused on spectral variability, they note the impact of not only internal but also external light-travel time effects causing complex spectral shapes and variations in this March 2009 flaring event. In our approach to explain complex high-energy spectral shapes, we found that the injection history already has a strong impact, and is able to reproduce the typically observed pronounced turn-overs at GeV energies.
5. Summary and conclusion
Within the framework of a leptonic emission model for blazars, where inverse Compton scattering on external radiation fields dominates, we considered the case of continuous particle injection of a given simple power law along the jet with various injection rates, durations, and locations of the emission region within the jet. We calculated the emitting particle spectrum that results from this kind of setup at a snapshot time tobs, taking into account radiative cooling (in the Thomson regime) in the accretion disk and BLR radiation field during injection self-consistently. This prescription offers the possibility to explain a broad range of ambient electron spectral shapes, including spectral breaks that are significantly larger than simple cooling breaks. The injection properties may provide valuable information on the acceleration mode at work. Hence, our simple phenomenological prescription has the potential to find interesting clues in this aspect by rigorously analyzing the ambient electron spectrum that is required for the broadband fit of a given quasi-simultaneous multifrequency data set, in conjunction with constraints that are inferred from correlated variability studies and γ-ray opacity arguments.
For example, the peak of the emitting electron spectrum can, in general, be linked to the minimum injection energy γ1mec2 if the injection rate distribution is not too steep. For impulsive-like injections (i.e., large α within our model) the peak in the ambient particle spectrum is, instead, associated with the smallest cooled electron energy. The peak in the electron spectrum results in corresponding spectral turn-overs in the Compton-scattered photon components. Thus γ1 is a parameter that may influence the γ-ray break energy.
Our model has the potential to describe broad high-energy components, as well as double-peaked ones (with one peak corresponding to Compton-scattered accretion disk photons, and the second one from IC-scattered BLR radiation field). The former case arises for not too steep injection spectra, while very steep ones, or injections where γ2 is suitably small, can give SEDs with double-peaked γ-ray spectra. In general the injection spectral index s, together with γ2 and the time since last injection (given the accretion disk luminosity), mostly determine the post-break shape of the spectrum. For example, fitting the flare state SEDs of 3C 454.3 and PKS 1510-089 required rather conservative injection indices (s = 2–3), as expected from, for example, Fermi acceleration.
The injection rate index α strongly influences the ambient electron spectrum ahead of the peak. Observationally, this may be visible below the photon turnover frequency in case of one Compton-scattered component that dominates the high-energy regime, or in the synchrotron component in the optically thin pre-break energy range. The accretion disk IC component would mask the low-energy part of the BLR IC component in a two-component IC scenario. Accordingly, the rate of injection might be directly reflected in the pre-break shape of the GeV-spectrum in the former case.
Limits in the initial injection point za of the flare can be derived if the smallest particle energy in the cooled electron spectrum can be estimated, given the accretion disk luminosity.
In summary, if the ambient electron spectrum is unambiguously determined (e.g., from the optically thin synchrotron spectrum), it is possible to set limits on the injection rate index α. Together with analyzing the high energy component with sufficient broadband coverage and a fair knowledge of the accretion disk radiation, the remaining particle injection properties can be constrained.
We have demonstrated this for the SEDs of two FSRQs, 3C 454.3 and PKS 1510-089 where the flare state broadband SEDs have been analyzed to derive information on the required injection scenario. Two principally different scenarios per source were found to be viable: a one-component IC model, where either the Compton-scattered BLR or accretion disk radiation field dominates, and a two-component model as proposed in Finke & Dermer (2010) for 3C 454.3. Accordingly, the origin of the observed spectral turn-over at a few GeV is either found in the corresponding break in the ambient electron spectrum, or is due to the combination of Compton-scattered accretion disk and BLR radiation field.
The observed turnover energy in the GeV range is, in both scenarios, approximately
determined by ∝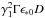 .
.
A constant GeV break energy that is independent of flux state has been reported for 3C 454.3 (Abdo et al. 2011), which implies that γ1 is broadly independent of the flux level for not significantly changing beaming parameters during flux variations. The required injection parameters for both cases of the two sources studied disfavor impulsive-like/instantaneous electron injection, but point towards rather narrow particle spectra injected continuously with a gradually decreasing rate into the moving plasma blob. For all of our model fits, the emitting region is either inside or just beyond the BLR, which is compatible with the results of Nalewajko et al. (2014), thus making the BLR an integral part of the model. In this context, we also note that the BLR geometry impacts the resulting γ-ray spectra. A good knowledge of the BLR structure therefore improves accurate and unambiguous modeling of the γ-ray spectrum. In all scenarios, a further spectral break would be expected at a few tens of MeV. In the one-component IC scenario for 3C 454.3, this break arises from the combination of IC-scattered accretion disk and BLR photons. The break energy is determined by the smallest energy in the ambient electron spectrum, which in turn is influenced by the initial injection point za. In the two-component IC scenario, this energy corresponds to the IC scattered (in the accretion disk) ambient particle break energy or the smallest energy of this spectrum. Potentially, these scenarios could, observationally, be distinguished by an improved coverage of the 0.1–1 eV (12.4–1.3 μm) energy range of the optically thin jet emission quasi-simultaneously to the γ-ray observations, and/or precision measurements at MeV energies, in conjunction with GeV observations, which might become possible with future projects like AstroMeV1 or the proposed GAMMA-LIGHT (Morselli et al. 2013) instrument. Extending the GeV energy range of the Fermi-LAT instrument down to few tens of MeV and using the LAT Pass 8 event-level analysis (Atwood et al. 2013) may already provide a possibility of distinguishing between models that show notably different spectral signatures in that energy range, as is the case, of the presented 3C 454.3 models.
Acknowledgments
We thank Benoît Lott for valuable discussions and providing tables of the 3C 454.3 data. We also acknowledge particularly valuable discussions with Chuck Dermer and Ann Wehrle on this work. This project was funded by the FWF Doctoral School CIM Computational Interdisciplinary Modelling under contract W 1227-N16 (DK-plus CIM), and by a Marie Curie International Reintegration Grant (grant 24803) within the 7th European Community Framework Programme. The publication is supported by the Austrian Science Fund (FWF). This work was performed on the computational resource bwUniCluster funded by the Ministry of Science, Research and the Arts Baden-Württemberg and the Universities of the State of Baden-Württemberg, Germany, within the framework program bwHPC.
References
- Abdo, A. A., Ackermann, M., Agudo, I., et al. 2009, ApJ, 699, 817 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Agudo, I., et al. 2010a, ApJ, 721, 1425 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Agudo, I., et al. 2010b, ApJ, 716, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Agudo, I., et al. 2010c, ApJ, 723, 1082 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Agudo, I., et al. 2010d, ApJ, 710, 1271 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Agudo, I., et al. 2011, ApJ, 733, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Albert, A., et al. 2011, ApJ, 743, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Albert, A., et al. 2013, ApJ, 771, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Aleksić, J., Antonelli, L. A., Antoranz, P., et al. 2011, ApJ, 730, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Atwood, W., Albert, A., Baldini, L., et al. 2013, Fermi Symp. Proc. – eConf C121028 [arXiv:1303.3514] [Google Scholar]
- Barnacka, A. 2013, Ph.D. Thesis, Nicolaus Copernicus Astronomical Center, Université Paris-Sud [arXiv:1307.4050] [Google Scholar]
- Bonnoli, G., Ghisellini, G., Foschini, L., Tavecchio, F., & Ghirlanda, G. 2011, MNRAS, 410, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Böttcher, M. 2000, in AIP Conf. Ser. 515, eds. B. L. Dingus, M. H. Salamon, & D. B. Kieda, 31 [Google Scholar]
- Böttcher, M., Reimer, A., Sweeney, K., & Prakash, A. 2013, ApJ, 768, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Cerruti, M., Dermer, C. D., Lott, B., Boisson, C., & Zech, A. 2013, ApJ, 771, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, X., Fossati, G., Böttcher, M., & Liang, E. 2012, MNRAS, 424, 789 [NASA ADS] [CrossRef] [Google Scholar]
- Dermer, C. D., & Menon, G. 2009, High Energy Radiation from Black Holes: Gamma Rays, Cosmic Rays, and Neutrinos (Princeton University Press) [Google Scholar]
- Dermer, C. D., & Schlickeiser, R. 1993, ApJ, 416, 458 [NASA ADS] [CrossRef] [Google Scholar]
- Dermer, C. D., Finke, J. D., Krug, H., & Böttcher, M. 2009, ApJ, 692, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Dermer, C. D., Cerruti, M., Lott, B., Boisson, C., & Zech, A. 2014, ApJ, 782, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Diltz, C., & Böttcher, M. 2014, J. High Energy Astrophysics, 1, 63 [Google Scholar]
- Donea, A.-C., & Protheroe, R. J. 2003, Astropart. Phys., 18, 377 [Google Scholar]
- Finke, J. D., & Dermer, C. D. 2010, ApJ, 714, L303 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., & Madau, P. 1996, MNRAS, 280, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., & Tavecchio, F. 2009, MNRAS, 397, 985 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, J., Daniel, M. K., & Chadwick, P. M. 2012, ApJ, 761, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, J., Chadwick, P. M., & Daniel, M. K. 2014, MNRAS, 441, 3591 [NASA ADS] [CrossRef] [Google Scholar]
- H.E.S.S. Collaboration et al. 2013, A&A, 554, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kohler, S., & Nalewajko, K. 2015, MNRAS, 449, 2901 [NASA ADS] [CrossRef] [Google Scholar]
- Lei, M., & Wang, J. 2014, PASJ, 66, 92 [NASA ADS] [Google Scholar]
- MAGIC Collaboration, Albert, J., Aliu, E., & Anderhub, H. 2008, Science, 320, 1752 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Marscher, A. P., Jorstad, S. G., Larionov, V. M., et al. 2010, ApJ, 710, L126 [NASA ADS] [CrossRef] [Google Scholar]
- Morselli, A., Argan, A., Barbiellini, G., et al. 2013, Nucl. Phys. B Proc. Suppl., 239, 193 [Google Scholar]
- Mücke, A., & Pohl, M. 2000, MNRAS, 312, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Nalewajko, K., Sikora, M., Madejski, G. M., et al. 2012, ApJ, 760, 69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nalewajko, K., Begelman, M. C., & Sikora, M. 2014, ApJ, 789, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Pacciani, L., Tavecchio, F., Donnarumma, I., et al. 2014, ApJ, 790, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Poutanen, J., & Stern, B. 2010, ApJ, 717, L118 [Google Scholar]
- Pucella, G., Vittorini, V., D’Ammando, F., et al. 2008, A&A, 491, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reimer, A. 2007, ApJ, 665, 1023 [NASA ADS] [CrossRef] [Google Scholar]
- Reimer, A., & Böttcher, M. 2013, Astropart. Phys., 43, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Sbarrato, T., Foschini, L., Ghisellini, G., & Tavecchio, F. 2011, Adv. Space Res., 48, 998 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Tavecchio, F., & Ghisellini, G. 2008, MNRAS, 386, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Wagner, S. J., Behera, B., & H.E.S.S. Collaboration. 2010, in BAAS, 42, 660 [Google Scholar]
- Wehrle, A. E., Marscher, A. P., Jorstad, S. G., et al. 2012, ApJ, 758, 72 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Geometry of the blazar jet model considered in this work (figure adapted from Dermer & Schlickeiser 1993). |
| In the text | |
 |
Fig. 2 Our BLR model, which consists of a spherically symmetric shell of gas between Ri and Ro and a density gradient ζ with ne(R) ∝ Rζ (figure adapted from Dermer et al. 2009). |
| In the text | |
 |
Fig. 3 Angle dependence of |
| In the text | |
 |
Fig. 4 Comparison of radiative electron energy-loss rates. Here we choose BLR1 at z = 100 as an example, while noting that the qualitative picture, with the negligible BLR losses, is the same in all the cases we considered in our study. We compare with synchrotron loss rates for a B = 4.5 G magnetic field. a) Radiative electron energy loss rates for varying z for electron energy γ = 500 and BLR1 with τBLR = 0.01. b) Radiative electron energy loss rates for varying γ at z = 100 and BLR1 with τBLR = 0.01. BLR shows the BLR energy loss used in our calculations, here we set the energy loss in the Klein-Nishina regime to 0. |
| In the text | |
 |
Fig. 5 IC photon spectra (and ambient electron spectrum as an inlay in panel b for the reference model) for different BLR geometries used. a) Composite IC photon spectrum for the case of BLR1. b) Resulting IC photon spectra when varying the BLR geometries. The inlay shows the underlying ambient electron spectrum. |
| In the text | |
 |
Fig. 6 Emitting electron (left) and resulting photon spectra (right) for various ledd. Where ledd = 0.01 we also show the photon components produced by both target photon fields separately. |
| In the text | |
 |
Fig. 7 Emitting electron (left) spectra and corresponding photon spectra (right) for γ1 that varies with respect to the reference model. The total injected particle energies are strongly determined by γ1. For γ1 = (100,500,1000,1500), we find Υinj = (10.1,2.0,1,0.7). |
| In the text | |
 |
Fig. 8 Emitting electron (left) and corresponding photon spectra (right) for spectral injection indices s, varying with respect to the reference model. The total injected electron energies for s = (2,3,4) are Υinj = (4.7 × 103,1,5.1 × 10-4). In the case of s = 4, the photon components produced by both target photon fields are shown separately as well. |
| In the text | |
 |
Fig. 9 Emitting electron spectra (left) and corresponding photon spectra (right) for γ2 that vary with respect to the reference model. The total injected electron energy is rather insensitive to γ2. For γ2 = (3000,5000,8000,10 000) we find Υinj = (0.7,0.8,0.9,0.9). In the case of γ2 = 3000, we show the photon components produced by both target photon fields. |
| In the text | |
 |
Fig. 10 Ambient electron (left) and photon spectra (right) with different injection rate parameters α, with respect to the reference model. The total injected electron energies for α = (0,1,2,3,4) are calculated to Υinj = (4 × 105,512,1,0.3,9 × 10-6). In the case of α = 4, we also show the IC components produced by both target photon fields separately. |
| In the text | |
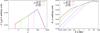 |
Fig. 11 Ambient electron (left) and photon spectra (right) when varying za (in Rg) with respect to the reference model. The injected total electron energies for za = (100,200,500,1000) are Υinj = (2.1,1,0.33,0.1). The total injected energy decreases with rising za. |
| In the text | |
 |
Fig. 12 Ambient electron (left) and photon spectra (right) when varying the distances between the points z and zb (in Rg), with respect to the reference model. The total injected electron energy is Υinj = 1 in all cases. For z = 2100, we also show the IC photon components produced by the two target photon fields considered separately. |
| In the text | |
 |
Fig. 13 ambient electron (left) and photon spectra (right) for various zb (in Rg) with respect to the reference model. The total injected electron energies for zb = (1000,2000,3000,4000) are Υinj = (0.9,1,1.04,1.06). For zb = 1000, the IC photon components produced by the two target photon fields are also shown separately. |
| In the text | |
 |
Fig. 14 Photon and ambient electron spectra for zb (in Rg) and α with respect to the reference model. The total injected electron energies for α = 3 and zb = (1000,2000,3000,4000) are Υinj = (2.7,2.75,2.8,2.8) × 10-3 while, for α = 7, the total injected electron energies for zb = (1000,2000,3000,4000) are Υinj = (5.8,5.8,5.8,5.8) × 10-13. For α = 3 and α = 7 with zb = 1000, we also show the IC photon components produced by the two target photon fields separately. a) Normalized electron spectra for various zb (in Rg) and α = 3. b) Corresponding photon spectra for various zb (in Rg) and α = 3. c) Normalized electron spectra for various zb (in Rg) and α = 7. d) Corresponding photon spectra for various zb (in Rg) and α = 7. |
| In the text | |
 |
Fig. 15 Two-component IC model fit to multifrequency data of 3C 454.3. The model is shown in red with the data points shown in blue. The model parameter values are listed in Table 2. a) Emitting electronspectrum. b) Synchroton spectrum with Swift, Herschel and Submillimeter Array data taken during the November 2010 flare (Wehrle et al. 2012). c) Gamma-ray spectrum with Fermi-LAT data taken during the November 2010 flare (Abdo et al. 2011). d) Zooming into the γ-ray spectrum with Fermi-LAT data taken during the November 2010 flare (Abdo et al. 2011). |
| In the text | |
 |
Fig. 16 Dominant-BLR IC model fit with multifrequency data of 3C 454.3. The model is shown in red with the data points shown in blue. The model parameter values are listed in Table 2. a) Emitting electron spectrum. b) Synchroton spectrum with Swift, Herschel and Submillimeter Array data taken during the November 2010 flare (Wehrle et al. 2012). c) Gamma-ray spectrum with Fermi-LAT data taken during the November 2010 flare (Abdo et al. 2011). d) Zooming into the γ-ray spectrum with Fermi-LAT data taken during the November 2010 flare (Abdo et al. 2011). |
| In the text | |
 |
Fig. 17 Two-component IC model fit to multifrequency data of PKS 1510-089. The model is shown in red with the data points shown in blue. The model parameter values are listed in Table 3. a) Emitting electron spectrum. b) Synchroton spectrum fit to data from Abdo et al. (2010b). c) Gamma-ray spectrum with Fermi-LAT data Abdo et al. (2010b). d) Zooming into the γ-ray spectrum with Fermi-LAT data (Abdo et al. 2010b). |
| In the text | |
 |
Fig. 18 Dominant accretion-disk IC model fit with multifrequency data of PKS 1510-089. The model is shown in red with the data points shown in blue. The model parameter values are listed in Table 3. a) Emitting electron spectrum. b) Synchroton spectrum fit to data from Abdo et al. (2010b). c) Gamma-ray spectrum with Fermi-LAT data (Abdo et al. 2010b)). d) Zooming into the γ-ray spectrum with Fermi-LAT data (Abdo et al. 2010b). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.