| Issue |
A&A
Volume 588, April 2016
|
|
|---|---|---|
| Article Number | L6 | |
| Number of page(s) | 6 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201628312 | |
| Published online | 16 March 2016 | |
Departure from the constant-period ephemeris for the transiting exoplanet WASP-12 b⋆,⋆⋆
1 Centre for Astronomy, Faculty of Physics, Astronomy and Informatics, Nicolaus Copernicus University, Grudziadzka 5, 87-100 Torun, Poland
e-mail: gmac@umk.pl
2 Institute of Astronomy, Bulgarian Academy of Sciences, 72 Tsarigradsko Chausse Blvd., 1784 Sofia, Bulgaria
3 Instituto de Astrofísica de Andalucía (IAA-CSIC), Glorieta de la Astronomía 3, 18008 Granada, Spain
4 Instituto de Astrofísica de Canarias, C/ vía Láctea, s/n, 38205 La Laguna, Tenerife, Spain
5 Departamento de Astrofísica, Universidad de La Laguna, Av. Astrofísico Francisco Sánchez, s/n, 38206 La Laguna, Tenerife, Spain
6 Michael Adrian Observatorium, Astronomie Stiftung Trebur, 65428 Trebur, Germany
7 University of Applied Sciences, Technische Hochschule Mittelhessen, 61169 Friedberg, Germany
8 Korea Astronomy & Space Science Institute (KASI), 305-348 Daejeon, Republic of Korea
9 Stellar Astrophysics Centre, Institut for Fysik og Astronomi, Åarhus Universitet, Ny Munkegade 120, 8000 Åarhus C, Denmark
10 Department of Physics, Shumen University, 9700 Shumen, Bulgaria
Received: 15 February 2016
Accepted: 27 February 2016
Aims. Most hot Jupiters are expected to spiral in toward their host stars because the angular momentum of the orbital motion is transferred to the stellar spin. Their orbits can also precess as a result of planet-star interactions. Calculations show that both effects might be detected for the very-hot exoplanet WASP-12 b using the method of precise transit-timing over a time span of about 10 yr.
Methods. We acquired new precise light curves for 29 transits of WASP-12 b, spannning four observing seasons from November 2012 to February 2016. New mid-transit times, together with those from the literature, were used to refine the transit ephemeris and analyze the timing residuals.
Results. We find that the transit times of WASP-12 b do not follow a linear ephemeris with a 5σ confidence level. They may be approximated with a quadratic ephemeris that gives a change rate in the orbital period of (−2.56 ± 0.40) × 10-2 s yr-1. The tidal quality parameter of the host star was found to be equal to 2.5 × 105, which is similar to theoretical predictions for Sun-like stars. We also considered a model in which the observed timing residuals are interpreted as a result of the apsidal precession. We find, however, that this model is statistically less probable than the orbital decay.
Key words: stars: individual: WASP-12 / planets and satellites: individual: WASP-12 b / planet-star interactions
Partly based on (1) data collected with the Nordic Optical Telescope, operated on the island of La Palma jointly by Denmark, Finland, Iceland, Norway, and Sweden, in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias, (2) observations made at the Centro Astronómico Hispano Alemán (CAHA), operated jointly by the Max-Planck Institut für Astronomie and the Instituto de Astrofísica de Andalucía (CSIC), and (3) data collected with telescopes at the Rozhen National Astronomical Observatory.
The light curves are available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/588/L6
© ESO, 2016
1. Introduction
With its orbital period of about 26 hours, the transiting planet WASP-12 b (Hebb et al. 2009) belongs to a group of hot Jupiters on the tightest orbits. It has a mass of Mb = 1.39 ± 0.19MJup (Knutson et al. 2014) and a radius Rb = 1.90 ± 0.09RJup (Maciejewski et al. 2013), which results in a mean density of only 20% that of Jupiter. The planet is inflated; it fills ~60% of its Roche lobe (Li et al. 2010; Budaj 2011).
The planet shape departs from spherical symmetry, and the two bodies in the system – the planet and the host star – raise mutual tides. The nonspherical mass component of the gravitational field results in precession of the orbit (e.g., Ragozzine & Wolf 2009). This apsidal rotation might be observed through precise timing of transits for non-zero orbital eccentricities. The total apsidal precession is the sum of components such as tidal bulges, rotation bulges, and relativistic effects. With a precession period of 18 yr, WASP-12 b was found to be a promising candidate for detecting apsidal precession, mainly produced by tides risen on the planet (Ragozzine & Wolf 2009; Damiani & Lanza 2011). The precession rate may be used to determine the second-order Love number, which is related to the planet’s internal density profile.
Planets on short-period orbits are expected to be unstable to tidal dissipation and finally spiral in toward the host star because they transfer the angular momentum of the orbital motion through tidal dissipation inside the star (e.g., Levrard et al. 2009; Essick & Weinberg 2016). The rate of this orbital decay can help determine the efficiency of the tide dissipation. The decaying orbital period is expected to be observed through transit timing. For some planets, the cumulative shift in transit times may be about 102 s after ten years (Birkby et al. 2014). Tentative detections of the orbital decay were reported for the systems OGLE-TR-113 and WASP-43 (Adams et al. 2010; Blecic et al. 2014), but have not been confirmed by further observations (Hoyer et al. 2016; Jiang et al. 2016).
In this study, we analyze new light curves for the transits of WASP-12 b and reanalyze some literature light curves to detect any longtime variations in the orbital period that may be attributed to one of the two mechanisms mentioned above.
2. Observations and data processing
We acquired 31 complete light curves for 29 transits between November 2012 and February 2016 using seven telescopes:
-
the 2.56 m Nordic Optical Telescope (NOT) at the Observatoriodel Roque de los Muchachos, La Palma (Spain) with theALFOSC instrument in spectroscopic mode;
-
the 2.2 m reflector (CA) at the Calar Alto Astronomical Observatory (Spain) with CAFOS in imaging mode;
-
the 2.0 m Ritchey-Chrétien-Coudé telescope (ROZ) at the National Astronomical Observatory Rozhen (Bulgaria), equipped with a Roper Scientific VersArray 1300B CCD camera;
-
the 1.8 m Bohyunsan optical telescope (BOAO) at the Bohyunsan Optical Astronomy Observatory (South Korea), equipped with a 4k CCD imaging instrument;
-
the 1.5 m Ritchey-Chrétien telescope (OSN) at the Sierra Nevada Observatory (Spain) with a Roper Scientific VersArray 2048B CCD camera;
-
the 1.2 m Trebur one-meter telescope (TRE) at the Michael Adrian Observatory in Trebur (Germany), equipped with an SBIG STL-6303 CCD camera;
-
the 0.6 m Cassegrain telescope (PIW) at the Center for Astronomy of the Nicolaus Copernicus University in Piwnice (Poland), equipped with an SBIG STL-1001 CCD camera.
One transit was observed simultaneously with two telescopes and the other with a single telescope in two bands. Most of the data were acquired through R-band filters. To achieve a higher transit timing precision, some data were acquired without any filter. The list of observing runs is presented in Table A.1.
The data reduction was performed with the AstroImageJ package1 (AIJ, Collins et al. 2016) following a standard procedure including de-biasing (or dark current removal) and flat-fielding. Photometric time series were obtained with differential aperture photometry. The aperture radius was allowed to vary to compensate for variable seeing. A set of comparison stars was optimized to achieve the lowest photometric scatter and to minimize trends caused by the differential atmospheric extinction. The light curves were examined for linear trends against airmass, position on the matrix, time, and seeing. The fluxes were normalized to unity for out-of-transit brightness. Time stamps were converted to barycentric Julian dates in barycentric dynamical time (BJDTDB).
The same procedure was applied to re-reduce data acquired with the 2.2 m telescope at Calar Alto, with the 2.0 m telescope at Rozhen, with the 1.8 m BOAO, and with the 1.2 m telescope in Trebur. These data were published in Maciejewski et al. (2011) and Maciejewski et al. (2013). The re-reduction improved the photometric quality of the light curves by up to 15%.
The light curves from the NOT/ALFOSC were generated from series of low-resolution spectra obtained with a custom-built slit with a width of 40′′. We bias- and flat-field corrected the data and extracted spectra and corresponding calibration arcs. The wavelength calibration was based on He and Ne lamps using an IRAF script dedicated to NOT/ALFOSC long-slit data. On 2014 Jan. 31, grism 10, which covers the spectral range 3300–10 550 Å, was used and the light curve was constructed from the whole spectral range. On 2015 Jan. 22 and 24, we used grism 4, which covers the spectral range 3200–9100 Å. The light curves were constructed from the 4950–6050 Å spectral range, which corresponds to a photometric V-band filter.
The set of new light curves was enhanced with photometric time series that are available in the literature. To limit the sample to the most reliable data, we considered only complete transit light curves that were acquired with telescopes with mirrors greater than 1 m. In addition to data from Maciejewski et al. (2011) and Maciejewski et al. (2013), we used photometric time series from Copperwheat et al. (2013), Chan et al. (2011), Cowan et al. (2012), and Stevenson et al. (2014).
The Transit Analysis Package (Gazak et al. 2012) was employed to determine mid-transit times and their uncertainties for individual epochs. The transit parameters such as the orbital inclination, scaled semi-major axis, ratio of planetary to stellar radii, and coefficients of the quadratic limb-darkening (LD) law for R-band data were taken from Maciejewski et al. (2013). For the remaining bands, the LD coefficients were linearly interpolated from tables of Claret & Bloemen (2011). During the fitting procedure, the parameters were allowed to vary under Gaussian penalty determined by their uncertainties. The mid-transit time, airmass slope, and flux offsets were the free parameters. The median values of marginalized posteriori probability distributions of the ten Markov chain Monte Carlo values with 105 steps each and the 15.9 and 85.1 percentile values of these distributions were taken as the best-fit parameters and upper and lower 1σ errors, respectively.
The mid-transit times for the new light curves, which are shown in Fig. 1, are given in Table A.2, those that we redetermined from literature data are presented in Table A.3. To extend the time covered by the observations, we also used the mid-transit time for epoch 0 from Hebb et al. (2009). It was obtained from a global fit and therefore represents an averaged value for the early epochs.
3. Results
 |
Fig. 1 Left: new transit light curves for WASP-12 b, sorted by observation date. Right: the residuals from the transit model adopted from Maciejewski et al. (2013). |
 |
Fig. 2 Transit timing residuals from the linear ephemeris. The black open and filled circles denote literature and new data, respectively. Each point represents a half-season average of individual observations, which are marked with gray dots. The continuous line sketches the quadratic ephemeris discussed in Sect. 3. The dashed line illustrates the periodic signal discussed in Sect. 4. The gray area shows the next observing season, in which new data are expected from which we hope to be able to distinguish between both models. |
The transit times were used to refine the transit ephemeris, and the timing residuals were examined for any long-term variations. Individual timing residuals were binned into half-season bins. Since complete transits of WASP-12 b are observable from the ground from October to March, the first bin of each observing season included data acquired between October and December, the second observations acquired between January and March. Uncertainties of individual mid-transit times were taken as weights, and the weighted standard deviations were calculated as errors. A fit of a linear ephemeris was found to be unsatisfying with the reduced χ-squared (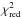 ) equal to 4.02. This value corresponds to a p-value of 5.3 × 10-7 , which allows us to reject the null hypothesis with a 5σ (99.9999%) conficence level. A Lomb-Scargle periodogram of the timing residuals reveals a long-term (~3300 d) signal that is similar to the time span covered by the observations. A quadratic ephemeris in the form of
) equal to 4.02. This value corresponds to a p-value of 5.3 × 10-7 , which allows us to reject the null hypothesis with a 5σ (99.9999%) conficence level. A Lomb-Scargle periodogram of the timing residuals reveals a long-term (~3300 d) signal that is similar to the time span covered by the observations. A quadratic ephemeris in the form of 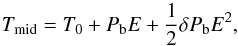 (1)where E is the transit number from the cycle-zero epoch T0 and δPb is the change in the orbital period between succeeding transits, yields a much better fit with
(1)where E is the transit number from the cycle-zero epoch T0 and δPb is the change in the orbital period between succeeding transits, yields a much better fit with 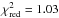 . We obtained T0 = 2 454 508.97696 ± 0.00016 BJDTDB, Pb = 1.09142162 ± 0.00000021 d, and δPb = (−8.9 ± 1.4) × 10-10 days epoch-2. The latter quantity translates into the short-term change rate in the orbital period Ṗb = δPb/Pb = (−2.56 ± 0.40) × 10-2 s yr-1. The timing residuals from the linear ephemeris together with the quadratic model are plotted in Fig. 2.
. We obtained T0 = 2 454 508.97696 ± 0.00016 BJDTDB, Pb = 1.09142162 ± 0.00000021 d, and δPb = (−8.9 ± 1.4) × 10-10 days epoch-2. The latter quantity translates into the short-term change rate in the orbital period Ṗb = δPb/Pb = (−2.56 ± 0.40) × 10-2 s yr-1. The timing residuals from the linear ephemeris together with the quadratic model are plotted in Fig. 2.
4. Discussion
The negative value of δPb may be interpreted as evidence of an orbital decay that is driven by tidal dissipation in the host star. For a star-planet system in which the total angular momentum Ltot is conserved, but energy is dissipated by tides, no equilibrium state exists if Ltot is smaller than the critical angular momentum Lcrit (see Eq. (2) in Levrard et al. 2009), which is required for the star-planet system to reach a state of dual synchronization. The spin of the star may be a significant, if not dominant, component of Ltot. It depends on the rotational velocity of the star ω∗, which remains roughly constrained for the WASP-12 star by spectral observations (Albrecht et al. 2012). For the WASP-12 system, we obtained Ltot/Lcrit = 0.4−0.7, depending on the rotation period of the star. Since this ratio is obviously lower than 1, the planet will unavoidable spiral inward2. Following Eq. (5) in Levrard et al. (2009), we find a relatively short in-spiral time of about 106 yr, which is very short compared to the age of the system of ~2 × 109 yr (Hebb et al. 2009).
The observed rate of the orbital decay may be used to determine the stellar tidal quality parameter 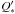 . This quantity is the ratio of the stellar tidal quality factor Q, which characterizes a body’s response to tides, to the second-order stellar tidal Love number k2. Following Blecic et al. (2014), we adopted Eq. (3) of Levrard et al. (2009) for synchronous planetary rotation and negligible eccentricity and obliquity
. This quantity is the ratio of the stellar tidal quality factor Q, which characterizes a body’s response to tides, to the second-order stellar tidal Love number k2. Following Blecic et al. (2014), we adopted Eq. (3) of Levrard et al. (2009) for synchronous planetary rotation and negligible eccentricity and obliquity 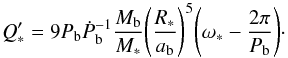 (2)We obtained
(2)We obtained 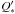 of about 2.5 × 105, which is on the same order as
of about 2.5 × 105, which is on the same order as 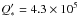 calculated from models of Essick & Weinberg (2016) for solar-type host stars.
calculated from models of Essick & Weinberg (2016) for solar-type host stars.
Alternatively, the observed departure from the linear ephemeris may be a part of the 3300 d periodic signal induced by star-planet tidal interactions. Using Eq. (86) of Migaszewski (2012), we found the timescale of the rotation of the pericenter caused by tides that have risen in the planet as a response to stellar gravity to be of about 101 yr. This value might correspond to the observed signal3. To explore this possibility, we employed the Systemic software (version 2.182, Meschiari et al. 2009). We used the transit-timing dataset enhanced with occultation times from Campo et al. (2011), Croll et al. (2011, 2015), Crossfield et al. (2012). We also included a homogenous set of precise radial velocity (RV) measurements from Knutson et al. (2014). This Doppler time series, free of any year-to-year instrumental trends, was acquired with the Keck/HIRES instrument between December 2009 and December 2013. The orbital period, planetary mass, mean anomaly for a given epoch, eccentricity eb, longitude of periastron for a given epoch, and periastron precession rate 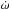 were allowed to be fitted. The Levenberg-Marquardt algorithm was used to find the best-fit model with a Keplerian approach. The parameter uncertainties were estimated as median absolute deviations from a bootstrap run of 105 trails. We obtained eb = 0.00110 ± 0.00036 and
were allowed to be fitted. The Levenberg-Marquardt algorithm was used to find the best-fit model with a Keplerian approach. The parameter uncertainties were estimated as median absolute deviations from a bootstrap run of 105 trails. We obtained eb = 0.00110 ± 0.00036 and 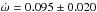 deg per day, which corresponds to a period of the periastron precession τω = 10.4 ± 2.2 yr.
deg per day, which corresponds to a period of the periastron precession τω = 10.4 ± 2.2 yr.
The periastron precession with the very low value of eb would have a marginal effect on transit parameters that are directly determined from light curves. In particular, the range of variations in transit duration is expected to be 2.7 s, much smaller than typical transit duration uncertainties of 1–3 min.
In Fig. 2 we also show the best-fit sinusoidal signal with a period equal to τω. With 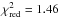 , the goodness of fit is noticeably poorer than for the quadratic model. The Bayesian information criterion (BIC, Schwarz 1978)
, the goodness of fit is noticeably poorer than for the quadratic model. The Bayesian information criterion (BIC, Schwarz 1978) 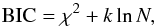 (3)where k is the number of fit parameters and N is the number of data points, also favors the quadratic model with BIC = 21.8 over the periodic model with BIC = 28.6 with a probability ratio of eΔBIC/2 = 29. We note that observations in the upcoming season 2016/2017, which is represented by the gray area in Fig. 2, are expected to let us clearly distinguish between both models.
(3)where k is the number of fit parameters and N is the number of data points, also favors the quadratic model with BIC = 21.8 over the periodic model with BIC = 28.6 with a probability ratio of eΔBIC/2 = 29. We note that observations in the upcoming season 2016/2017, which is represented by the gray area in Fig. 2, are expected to let us clearly distinguish between both models.
5. Conclusions
Our new precise observations, spread over four years, show that mid-transit times of the WASP-12 b planet do not follow a linear ephemeris. This phenomenon may be interpreted as the result of orbital decay, periastron precession due to planetary tides, or a combination of these two effects. The statistics formally favors the orbital decay scenario. The tidal quality parameter for the host star 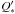 was found to be slightly lower than the theoretical predictions. In turn, the periastron precession model is consistent with theoretical predictions and places tight constraints on the orbital eccentricity of the planet. It may be used to precisely determine the Love number of the planet, which is related to its internal structure. Future precise timing observations are expected to provide evidence in favor of one of the two scenarios. This will lead to a better understanding of the properties of the host star or the planet.
was found to be slightly lower than the theoretical predictions. In turn, the periastron precession model is consistent with theoretical predictions and places tight constraints on the orbital eccentricity of the planet. It may be used to precisely determine the Love number of the planet, which is related to its internal structure. Future precise timing observations are expected to provide evidence in favor of one of the two scenarios. This will lead to a better understanding of the properties of the host star or the planet.
In calculations we used a normalized moment of inertia (NMoI) equal to 0.04 for the star. The quantity was interpolated from tables of Claret & Gimenez (1989). For the planet, we used Jupiter’s NMoI of 0.26 from Helled et al. (2011).
Acknowledgments
We would like to thank the NOT and Calar Alto staff for their help during observing runs. We are grateful to Chris Copperwheat and Nick Cowan for making the light curves available to us. G.M. acknowledges funding from the European Community’s Seventh Framework Programme (FP7/2007-2013) under grant agreement number RG226604 (OPTICON). G.M. and G.N. acknowledge the financial support from the Polish Ministry of Science and Higher Education through the Iuventus Plus grant and IP2011 031971. MF was supported by the Spanish grant AYA2014-54348-C3-1-R. T.C.H., J.W.L. & C.U.L. acknowledge travel support from KASI grant number 2013-9-400-00 and astronomical observations were carried out during a KRCF Young Scientist Research Fellowship Program. D.K. acknowledges the financial support from Shumen University, project RD 08-81. A part of this paper is the result of the exchange and joint research project Spectral and photometric studies of variable stars between the Polish and Bulgarian Academies of Sciences. The data presented here were obtained in part with ALFOSC, which is provided by the Instituto de Astrofísica de Andalucía (IAA) under a joint agreement with the University of Copenhagen and NOTSA.
References
- Adams, E. R., López-Morales, M., Elliot, J. L., Seager, S., & Osip, D. J. 2010, ApJ, 721, 1829 [NASA ADS] [CrossRef] [Google Scholar]
- Albrecht, S., Winn, J. N., Johnson, J. A., et al. 2012, ApJ, 757, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Birkby, J. L., Cappetta, M., Cruz, P., et al. 2014, MNRAS, 440, 1470 [NASA ADS] [CrossRef] [Google Scholar]
- Blecic, J., Harrington, J., Madhusudhan, N., et al. 2014, ApJ, 781, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Budaj, J. 2011, AJ, 141, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Campo, C. J., Harrington, J., Hardy, R. A., et al. 2011, ApJ, 727, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Chan, T., Ingemyr, M., Winn, J. N., et al. 2011, AJ, 141, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Claret, A., & Bloemen, S. 2011, A&A, 529, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A., & Gimenez, A. 1989, A&AS, 81, 37 [NASA ADS] [Google Scholar]
- Collins, K. A., Kielkopf, J. F., & Stassun, K. G. 2016, AJ, submitted [arXiv:1601.02622] [Google Scholar]
- Copperwheat, C. M., Wheatley, P. J., Southworth, J., et al. 2013, MNRAS, 434, 661 [NASA ADS] [CrossRef] [Google Scholar]
- Cowan, N. B., Machalek, P., Croll, B., et al. 2012, ApJ, 747, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Croll, B., Lafreniere, D., Albert, L., et al. 2011, AJ, 141, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Croll, B., Albert, L., Jayawardhana, R., et al. 2015, ApJ, 802, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Crossfield, I. J. M., Barman, T., Hansen, B. M. S., Tanaka, I., & Kodama, T. 2012, ApJ, 760, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Damiani, C., & Lanza, A. F. 2011, A&A, 535, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Essick, R., & Weinberg, N. N. 2016, ApJ, 816, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Fulton, B. J., Shporer, A., Winn, J. N., et al. 2011, AJ, 142, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Gazak, J. Z., Johnson, J. A., Tonry, J., et al. 2012, Adv. Astron., 2012, 30 [Google Scholar]
- Hebb, L., Collier-Cameron, A., Loeillet, B., et al. 2009, ApJ, 693, 1920 [NASA ADS] [CrossRef] [Google Scholar]
- Helled, R., Anderson, J. D., Schubert, G., & Stevenson, D. J. 2011, Icarus, 216, 440 [NASA ADS] [CrossRef] [Google Scholar]
- Hoyer, S., López-Morales, M., Rojo, P., Minniti, D., & Adams, E. R. 2016, MNRAS, 455, 1334 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, I.-G., Lai, C.-Y., Savushkin, A., et al. 2016, AJ, 151, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Knutson, H. A., Fulton, B. J., Montet, B. T., et al. 2014, ApJ, 785, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Levrard, B., Winisdoerffer, C., & Chabrier, G. 2009, ApJ, 692, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Li, S.-L., Miller, N., Lin, D. N. C., & Fortney, J. J. 2010, Nature, 463, 1054 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Maciejewski, G., Errmann, R., Raetz, S., et al. 2011, A&A, 528, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maciejewski, G., Dimitrov, D., Seeliger, M., et al. 2013, A&A, 551, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meschiari, S., Wolf, A. S., Rivera, E., et al. 2009, PASP, 121, 1016 [NASA ADS] [CrossRef] [Google Scholar]
- Migaszewski, C. 2012, Celest. Mech. Dyn. Astron., 113, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Ragozzine, D., & Wolf, A. S. 2009, ApJ, 698, 1778 [NASA ADS] [CrossRef] [Google Scholar]
- Schwarz, G. 1978, Ann. Statist., 6, 461 [Google Scholar]
- Stevenson, K. B., Bean, J. L., Madhusudhan, N., & Harrington, J. 2014, ApJ, 791, 36 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Supplementary materials
Table A.1 presents details of new light curves acquired for the transits of WASP-12 b. Table A.2 lists the mid-transit times for the new light curves. Table A.3 shows the mid-transit times based on the literature data that were used in our study.
Details on new light curves obtained by us.
New mid-transit times for individual epochs.
Mid-transit times based on literature data.
All Tables
All Figures
 |
Fig. 1 Left: new transit light curves for WASP-12 b, sorted by observation date. Right: the residuals from the transit model adopted from Maciejewski et al. (2013). |
| In the text | |
 |
Fig. 2 Transit timing residuals from the linear ephemeris. The black open and filled circles denote literature and new data, respectively. Each point represents a half-season average of individual observations, which are marked with gray dots. The continuous line sketches the quadratic ephemeris discussed in Sect. 3. The dashed line illustrates the periodic signal discussed in Sect. 4. The gray area shows the next observing season, in which new data are expected from which we hope to be able to distinguish between both models. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


