| Issue |
A&A
Volume 588, April 2016
|
|
|---|---|---|
| Article Number | A121 | |
| Number of page(s) | 4 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201628153 | |
| Published online | 30 March 2016 | |
Updated study of the quintuple system V994 Herculis
1 Astronomical Institute, Charles University in Prague, Faculty of Mathematics and Physics, 180 00 Praha 8, V Holešovičkách 2, Czech Republic
e-mail: zasche@sirrah.troja.mff.cuni.cz
2 Private Observatory, Pohoří 71, 254 01 Jílové u Prahy, Czech Republic
Received: 18 January 2016
Accepted: 27 February 2016
Aims. We present a new updated study of the unique quintuple system of two eclipsing binaries, V994 Her.
Methods. Based on new obtained photometric observations, we analysed the period variations of the two eclipsing pairs of V994 Her.
Results. We found that the orbital period of the two eclipsing binaries around a common barycenter is about 2.9 yrs instead of the original period, which was reported as 6.3 yrs. Moreover, the system now seems to be close to coplanar (i ≈ 84°), and we also revised the individual masses of all four eclipsing components. The two eclipsing pairs show slow apsidal motion with periods of about 116 and 111 yrs, respectively. Pairs A and B are distant by about 17 mas on the sky, which is encouraging for observers because an interferometric detection may be possible in the next years.
Conclusions. All of these results are based on the photometric observations of V994 Her and its detailed analysis of the period changes of the two eclipsing binaries.
Key words: binaries: eclipsing / binaries: visual / stars: fundamental parameters / stars: individual: V994 Her
© ESO, 2016
1. Introduction
The eclipsing system V994 Her was classified as an eclipsing binary of Algol type by Kazarovets et al. (1999), who also published a short remark about a possible variability of the secondary component. Even though the system was observed by the Hipparcos satellite (Perryman et al. 1997), its true nature was not discovered until the detailed study of V994 Her by Lee et al. (2008). Its quadruple nature of two eclipsing binaries was recognized, which was the first discovery of such a system in the whole sky. The system still remains interesting today because the two eclipsing pairs are being monitored for more than 20 yrs now, and the orbital evolution of both binaries can be studied.
Quadruple (or even higher-order multiple) systems like V994 Her can teach us to better understand the formation and evolution of stars and stellar systems. They may answer questions like how such complex structures were formed (Tohline 2002), how they evolve into their current state (Tokovinin 2008), what the preferred initial configuration of the system parameters is, and whether we can trace it somehow from the current configuration (Goodwin & Kroupa 2005), or we may find out the multiplicity fraction of these stars (Duchêne & Kraus 2013). All of these interesting questions can partly be answered through a detailed study of eclipsing binaries as parts of complex multiple systems. Following the theoretical modelling, for example, indicates that the so-called Heggie-Hills law plays a role (Heggie 1975) for a tight close binary and a distant companion, but also for a configuration where the mass ratio of the close pair tends to be closer to unity (see e.g. Goodwin et al. 2007). These two aspects can clearly be seen in the system V994 Her. Even the existence of planets in such a system cannot be easily ruled out. We know of several planetary systems that orbit eclipsing binaries, for instance, Kepler 47 (Orosz et al. 2012).
About three years ago, we published the first study of the orbital motion of the system V994 Her based on new eclipse-timing observations (Zasche & Uhlař 2013). We found that the system is the only one known complex system of two eclipsing binaries orbiting a common barycenter on a rather eccentric orbit (e = 0.747) and with the orbital period of about 6.3 yrs. Despite its rather poor coverage in the O–C diagrams, we were able to identify the (rather sharp) period changes of the two pairs around a periastron. From this solution it followed that the two pairs orbit each other on a slightly inclined orbit with an inclination of about 37°.
2. Inconsistency of our original solution for V994 Her
New heliocentric minima of V994 Her used for the analysis.
The double eclipsing system V994 Her was first correctly separated into two independent periods in 2008 by Lee et al. (2008). The authors found that the orbital periods of the two pairs are of about PA = 2.08 days, and PB = 1.42 days. Using detailed spectroscopic observations, they were also able to derive the individual masses of the eclipsing components and their spectral types: pair A (B8V + A0V) and pair B (A2V + A4V). All four components are apparently clearly detached and are still placed on the main sequence. Another more distant (about 1′′) component was discovered and is listed in the Washington Double Star Catalog (Mason et al. 2001), which means that this is a quintuple stellar system. At the time of Lee et al. publication, it was the only known such system with two eclipsing binaries located on the sky. The number of such systems has increased today, mainly as a result of the OGLE detections of the Magellanic Cloud eclipsing binaries. For example, Pawlak et al. (2013) listed 15 new potential double eclipsing systems in the SMC. In addition, Cagaš & Pejcha (2012) and Lohr et al. (2013) announced the discovery of new interesting double eclipsing systems. However, a similar study of the period changes for their new discovered systems is still difficult because we lack data spanning a longer time interval.
However, our previous result on the system published in Zasche & Uhlař (2013) seems to be incorrect. The inclination of the eclipsing orbits and their mutual orbit of about 37° is an improbable geometrical configuration and not very stable on longer periods of time. Because of the Kozai cycles (see e.g. Eggleton & Kisseleva-Eggleton 2006), the two orbits should tend to be coplanar or to have a different inclination. And finally, the new minima time observations also significantly deviated from the published predicted fit of V994 Her (for both pairs).
From these reasons we decided to continue monitoring this interesting eclipsing system in the years after our study in 2013 was published. Since then, 36 new observations of minima (of both pairs A and B) were obtained by the authors in seasons 2013, 2014, and 2015 during more than 980 days. The data used for the analysis are presented in Table 1. From studying these new data points, we found that our original hypothesis was incorrect because we had insufficient data. This is well visible in the plot in Fig. 1, where we plot O–C diagrams for pairs A and B according to our original solution together with the grey area that represents the time epoch without observations. Unfortunately, this epoch of lacking data is placed exactly in between the two periastron passages in 2006 and 2012. Hence, this paper should not be considered as an erratum, but rather as a reanalysis of the system with new data (new times of minima), as well as a reanalysis of the older radial velocities by Lee et al. (2008). We finally introduce the correct hypothesis of the true system configuration.
 |
Fig. 1 O–C diagrams of the two pairs A and B. The dots stand for the primary, while the open circles for the secondary minima, the bigger the symbol, the higher the weight. The red dash-dotted lines indicate the LTTE fit, while the black and blue curves represent the final fit (LTTE plus the apsidal motion). This solution is taken from our original study in 2013; the grey area indicates where observations are missing exactly in between the two periastron passages. |
3. Updated analysis
The star with the new data was analysed using the same approach as in our previous study. This means that the times of minima were fitted using all 16 parameters for the orbits of the two binaries (the two ephemerides, two apsidal motion hypotheses, and the period changes that are due to the orbit around a common barycenter). The well-known light-travel time effect (LTTE) hypothesis (Irwin 1959) was used to describe the variation in the O–C diagrams.
In Fig. 2 we plot the updated O–C diagrams for the two A and B pairs, showing their period changes (the y-axis) with respect to time (the x-axis). Our current hypothesis describes the observed data much better (the χ2 resulted in a value about five times lower). The parameters describing the LTTE fit are given below in Table 2. The orbital period of the two pairs resulted in about half the value presented in our previous study (Zasche & Uhlař 2013), which is also due to the missing data near the periastron passage in 2009. With the new data the sharp curvatures near the periastron passages are clearly visible and well covered with the observations.
 |
Fig. 2 Updated plot of the O–C diagrams of the two pairs A and B (see Fig. 1 for description). The missed periastron passage in 2009 is clearly seen in the grey area. |
Updated orbital parameters for V994 Her.
Our hypothesis based on the much shorter orbital period of the two pairs is also able to solve the problem of radial velocities published in Lee et al. (2008). The radial velocities they reported are somewhat distorted. Especially theose of pair B were unusual because some jumps between the individual datasets near the quadrature are visible. Using our approach, we are also able to compute the radial velocities on the mutual orbit and subtract this contribution from the radial velocities. This is shown in Fig. 3, where the calculated radial velocities are shown exactly in the time epochs when the data by Lee et al. (2008) were obtained. The difference between the first and the last data point of about 10 km s-1 for pair A and of about 16 km s-1 for pair B is significant enough for such a shift. Hence, we applied this correction to the radial velocities by Lee et al. (2008) and reanalysed their data. We found the mass ratios to be only slightly different (the change is below 0.05). We discuss the masses in the next section.
4. Results
Our hypothesis led to several important results, which are completely different from the findings published in the previous analysis. At first, the orbital motion has a period of only about 2.9 yrs. The other parameters also slightly changed, but the amplitudes and relatively high eccentricity of the mutual orbit remained almost unchanged. However, the apsidal motion of the two pairs resulted in (116 ± 50) yrs for pair A and (111 ± 40) for pair B. But the most significant change is the resulting geometry of the whole system, which now seems to be close to coplanar (i.e. the orbits of the two eclipsing pairs and their mutual orbit seem to lie very close to one plane, see below). And moreover, if we adopt the Hipparcos (Perryman et al. 1997) value of the parallax as correct (πHIP = (3.90 ± 0.74) mas), the predicted angular separation of the components is about Δα12 = (16.7 ± 5.6) mas (instead of the original Δα12 = (27.6 ± 6.8) mas). This value is still rather high and should encourage a prospective interferometric direct detection of the two pairs in the sky. However, the attempt of detection should be made in specific phases on the 2.9 yr orbit to be successful.
 |
Fig. 3 Radial velocities of V994 Her as re-interpreted from the original paper by Lee et al. (2008). Top: radial velocity corrections of the two A and B pairs as these pairs revolve on the orbit around the common barycenter. Middle: radial velocities of pair A (before (plus and cross signs) and after (dot signs) the correction). Bottom: radial velocities of pair B (the same notation). |
V994 Her: updated component masses.
 |
Fig. 4 Masses (total mass of the pair A and B) as derived from the analysis of period changes with respect to the inclination of the 2.9 yr orbit. The red solid lines represent the masses reported by Lee et al. (2008), the blue lines stand for the masses from our analysis (with the grey area showing the uncertainties). The black line represents the different masses with respect to the inclination between the orbits. |
As a byproduct of our analysis, we also found that the masses of all components as derived by Lee et al. (2008) need to be reconsidered. The masses of the two pairs were calculated using the fact that a so-called mass function of the third body (see e.g. Mayer 1990) can be computed from the orbital parameters, and the inclinations of the two orbits are also close to 90°, that is,
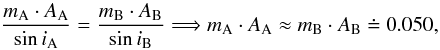 where the masses of pairs are denoted as mA, and mB (in solar masses), respectively, and the amplitudes of the period variations in the O–C diagrams for the two pairs are labelled AA and AB (in days). The correct mass values are slightly higher for pair A but remained similar for pair B, see Table 3 for a comparison of Lee et al. (2008) and our results. The plot with the resulting masses for the A and B binaries with respect to the inclination is plotted in Fig. 4. The derived mass of pair A is significantly higher than the value published by Lee et al. (2008). Moreover, the plot shows that the inclination of the wide orbit is probably close to 90°, hence the system is close to coplanar. This means that the mutual inclination angle is i ≈ (84 ± 10)° for pair A and i ≈ (85 ± 12)° for pair B.
where the masses of pairs are denoted as mA, and mB (in solar masses), respectively, and the amplitudes of the period variations in the O–C diagrams for the two pairs are labelled AA and AB (in days). The correct mass values are slightly higher for pair A but remained similar for pair B, see Table 3 for a comparison of Lee et al. (2008) and our results. The plot with the resulting masses for the A and B binaries with respect to the inclination is plotted in Fig. 4. The derived mass of pair A is significantly higher than the value published by Lee et al. (2008). Moreover, the plot shows that the inclination of the wide orbit is probably close to 90°, hence the system is close to coplanar. This means that the mutual inclination angle is i ≈ (84 ± 10)° for pair A and i ≈ (85 ± 12)° for pair B.
The question also arises whether it is possible to detect some orbital precession when the two orbits are close to coplanar, and whether we can see some mutual eclipses of all components in the future. Only a dedicated spectroscopic, photometric, and interferometric monitoring is able to answer this question.
5. Conclusion
The system V994 Her was reanalysed with new photometric observations. Our solution yielded a very different geometrical configuration than originally assumed. In this 2+2 quadruple system with coplanar orbits, the precession of all orbits is only very slow and hard to detect. This system structure is much more probable and seems to be adequately stable for a long period of time. There still remain some open questions, such as the other parameters of the 2.9 yr orbit, and the confirmation that the distant component also belongs to the system (which would make this a quintuplet). However, the most promising way to proceed today seems to be an interferometric detection of the two components because they should have a semi-major axis of about 17 mas and a magnitude difference between the components of about 1.4 mag. This is well within the limits for modern stellar interferometers.
The main advantage of the system V994 Her is that it is bright enough for photometric monitoring by only small telescopes (all of our new data were obtained with telescopes with apertures of 20 cm or smaller). It is also quite promising that the periods are relatively short, which means that this is an ideal laboratory of celestial mechanics.
Acknowledgments
We would like to thank David Vokrouhlický for a useful discussion and valuable comments. We also thank the anonymous referee for helpful and critical suggestions. This work was supported by the Czech Science Foundation grants No. P209/10/0715 and GA15-02112S. This research has made use of the Washington Double Star Catalog maintained at the US Naval Observatory, the SIMBAD database, operated at CDS, Strasbourg, France, and of NASA’s Astrophysics Data System Bibliographic Services.
References
- Cagaš, P., & Pejcha, O. 2012, A&A, 544, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duchêne, G., & Kraus, A. 2013, ARA&A, 51, 269 [Google Scholar]
- Eggleton, P. P., & Kisseleva-Eggleton, L. 2006, Ap&SS, 304, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Goodwin, S. P., & Kroupa, P. 2005, A&A, 439, 565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goodwin, S. P., Kroupa, P., Goodman, A., & Burkert, A. 2007, Protostars and Planets V, 133 [Google Scholar]
- Heggie, D. C. 1975, MNRAS, 173, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, J. B. 1959, AJ, 64, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Kazarovets, E. V., Samus, N. N., Durlevich, O. V., et al. 1999, IBVS, 4659, 1 [Google Scholar]
- Lee, C.-U., Kim, S.-L., Lee, J. W., et al. 2008, MNRAS, 389, 1630 [NASA ADS] [CrossRef] [Google Scholar]
- Lohr, M. E., Norton, A. J., Kolb, U. C., et al. 2013, A&A, 549, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mason, B. D., Wycoff, G. L., Hartkopf, W. I., Douglass, G. G., & Worley, C. E. 2001, AJ, 122, 3466 [Google Scholar]
- Mayer, P. 1990, Bull. Astr. Inst. Czechosl., 41, 231 [Google Scholar]
- Orosz, J. A., Welsh, W. F., Carter, J. A., et al. 2012, Science, 337, 1511 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Pawlak, M., Graczyk, D., Soszyński, I., et al. 2013, Acta Astron., 63, 323 [NASA ADS] [Google Scholar]
- Perryman, M. A. C., Lindegren, L., Kovalevsky, J., et al. 1997, A&A, 323, L49 [NASA ADS] [Google Scholar]
- Tohline, J. E. 2002, ARA&A, 40, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Tokovinin, A. 2008, MNRAS, 389, 925 [NASA ADS] [CrossRef] [Google Scholar]
- Zasche, P., & Uhlař, R. 2013, MNRAS, 429, 3472 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 O–C diagrams of the two pairs A and B. The dots stand for the primary, while the open circles for the secondary minima, the bigger the symbol, the higher the weight. The red dash-dotted lines indicate the LTTE fit, while the black and blue curves represent the final fit (LTTE plus the apsidal motion). This solution is taken from our original study in 2013; the grey area indicates where observations are missing exactly in between the two periastron passages. |
| In the text | |
 |
Fig. 2 Updated plot of the O–C diagrams of the two pairs A and B (see Fig. 1 for description). The missed periastron passage in 2009 is clearly seen in the grey area. |
| In the text | |
 |
Fig. 3 Radial velocities of V994 Her as re-interpreted from the original paper by Lee et al. (2008). Top: radial velocity corrections of the two A and B pairs as these pairs revolve on the orbit around the common barycenter. Middle: radial velocities of pair A (before (plus and cross signs) and after (dot signs) the correction). Bottom: radial velocities of pair B (the same notation). |
| In the text | |
 |
Fig. 4 Masses (total mass of the pair A and B) as derived from the analysis of period changes with respect to the inclination of the 2.9 yr orbit. The red solid lines represent the masses reported by Lee et al. (2008), the blue lines stand for the masses from our analysis (with the grey area showing the uncertainties). The black line represents the different masses with respect to the inclination between the orbits. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


