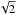| Issue |
A&A
Volume 588, April 2016
|
|
|---|---|---|
| Article Number | A57 | |
| Number of page(s) | 13 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201527599 | |
| Published online | 17 March 2016 | |
Probing spacetime around Sagittarius A* using modeled VLBI closure phases
1 Department of Astrophysics/IMAPP, Radboud University, PO Box 9010 6500 GL Nijmegen, The Netherlands
e-mail: r.fraga@astro.ru.nl
2 ASTRON, Oude Hoogeveensedijk 4, 7991 PD Dwingeloo, The Netherlands
Received: 19 October 2015
Accepted: 27 December 2015
Context. The emission region and black hole shadow of Sagittarius A*, the supermassive black hole at the Galactic Center, can be probed with millimeter Very Long Baseline Interferometry.
Aims. Our goal is to probe the geometry of the emitting plasma around Sgr A* by using modeled mm-VLBI closure phase calculations at 1.3 mm and to constrain the observer’s inclination angle and position angle of the black hole spin axis.
Methods. We have simulated images for three different models of the emission of Sgr A*: an orbiting spot, a disk model, and a jet model. The orbiting spot model was used as a test case scenario, while the disk and jet models are physically driven scenarios based on standard three-dimensional general relativistic magnetohydrodynamic simulations of hot accretion flows. Our results are compared to currently available closure phase observational limits.
Results. Our results indicate that more models with closer to edge-on viewing angles are consistent with observational limits. In general, jet and disk geometries can reproduce similar closure phases for different sets of viewing and position angles. Consequently, the favored black hole spin orientation and its magnitude are strongly model dependent.
Conclusions. We find that both the jet and the disk models can explain current VLBI limits. We conclude that new observations at 1.3 mm and possibly at longer wavelengths including other triangles of VLBI baselines are necessary to interpret Sgr A* emission and the putative black hole spin parameters.
Key words: Galaxy: center / galaxies: individual: Sagittarius / accretion, accretion disks / techniques: interferometric / submillimeter: general
© ESO, 2016
1. Introduction
The compact radio source at the center of the Milky Way, Sagittarius A* (Sgr A*), is the strongest candidate for a supermassive black hole (SMBH; Ghez et al. 2000; Genzel et al. 2010; Falcke & Markoff 2013). Stellar orbits indicate a central object mass of about four million solar masses concentrated in a very small volume (Eisenhauer et al. 2005; Ghez et al. 2008; Gillessen et al. 2009). Sgr A* is the closest known SMBH to us, and it is an excellent candidate for imaging the shadow of an event horizon (Falcke et al. 2000) and for testing general relativity (Broderick et al. 2014; Ricarte & Dexter 2015). Its angular diameter on the sky is approximately 50 μas, which can be resolved by the currently constructed Event Horizon Telescope (EHT; Doeleman et al. 2009a).
The EHT is a global Very Long Baseline Interferometry (VLBI) experiment aimed at imaging Sgr A* (and the core of M87) at λ = 1.3 mm and 0.87 mm (230 GHz and 345 GHz, respectively). Here, the positive spectral index at the lower frequencies changes to a negative spectral index at higher frequencies, which is suggestive of the plasma becoming optically thin (Bower et al. 2015) and is crucial to take an unobscured picture of the SMBH shadow and plasma around it. Additionally, at millimeter wavelengths the interstellar medium scattering screen smearing effects become negligible and so the EHT promises to take sharp images of Sgr A*. Various theoretical models have been developed and used to construct the expected source appearance at EHT wavelengths (e.g., Broderick & Loeb 2006; Doeleman et al. 2009b; Mościbrodzka et al. 2009; Dexter et al. 2010; Dexter & Fragile 2011; Mościbrodzka et al. 2012; Dolence et al. 2012; Shcherbakov et al. 2012; Kamruddin & Dexter 2013; Mościbrodzka et al. 2014, and references therein).
In addition to image reconstruction, the geometry of Sgr A* can be constrained by using closure phases. This method is particularly useful if a small number of VLBI stations is available (as is the case at present) and the uv-coverage in the Fourier domain is too sparse to directly and accurately reconstruct the image from the VLBI visibilities.
The goal of this work is to investigate the geometry of the plasma near the SMBH using non-imaging VLBI techniques. Based on various theoretical models of plasma near the SMBH, we here present the expected closure phase variations for the current triangles of EHT stations and compare them with observational limits. The closure phases are predicted for 1.3 mm VLBI observations for the triangle formed by baselines including existing EHT stations (CARMA, Hawaii, SMTO) at which Sgr A* has already been detected and observational constraints exist. For one of the models, which is used as a simple test case, we also present closure phases for triangles including European (IRAM PV, IRAM PdB) and American stations (CARMA, SMTO, LMT, Hawaii, Chile). Information on all of the stations is summarized in Table 1.
Determining the intrinsic size and shape of Sgr A* are challenging problems. Measurements of the source morphology are highly affected by calibration uncertainties. These uncertainties arise from the variability of antenna gains and the atmospheric opacity that is due to the low antenna elevations that are needed to observe Sgr A* from the Northern hemisphere. Because closure quantities such as closure amplitude and closure phase are independent of antenna-based amplitude errors and phase shifts due to atmospheric turbulence, they are extremely handy non-imaging tools used to determine the structure of a source (Rogers et al. 1974; Cotton 1979; Bower et al. 2004).
These closure quantities have previously been used to constrain the structure of Sgr A* at mm wavelengths. VLBI observations at 3.5 mm resulted in some estimates for the size of Sgr A*; the data were modeled assuming a circular Gaussian brightness distribution. The data were also consistent with an elliptical Gaussian structure (with an elongation in the north-south direction) due to interstellar scattering of a point source (Doeleman et al. 2001). Additional VLBI observations at 3.5 mm using the array formed by the Effelsberg telescope, the IRAM Pico Veleta telescope, and the IRAM Plateau de Bure interferometer yielded a closure phase measurement of 0° ± 10° (Krichbaum et al. 2006).
Simulated images of jets at 7 mm (43 GHz) based on models consistent with the spectrum of Sgr A* have also been constructed and compared to 7 mm VLBI observations through closure quantities (Markoff et al. 2007). These jet models with a bipolar structure, high-inclination with respect to the line of sight of 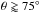 , and position angle in the sky of 105° east of north produced results that are comparable to Gaussian models from previously done work. Furthermore, by using 7 mm VLBI observations and closure quantities, limits have been placed on the size versus wavelength relation (Bower et al. 2004, 2006), where the intrinsic size of Sgr A* decreases with observing wavelength following a power law with index of ~1.6. The implications are that the source is optically thick and presents a photosphere that changes in size depending on the observing wavelength.
, and position angle in the sky of 105° east of north produced results that are comparable to Gaussian models from previously done work. Furthermore, by using 7 mm VLBI observations and closure quantities, limits have been placed on the size versus wavelength relation (Bower et al. 2004, 2006), where the intrinsic size of Sgr A* decreases with observing wavelength following a power law with index of ~1.6. The implications are that the source is optically thick and presents a photosphere that changes in size depending on the observing wavelength.
Estimated system equivalent flux densities (SEFD) at 1.3 mm.
1.3 mm VLBI closure phases have also been used to constrain the structure of the accretion flow of Sgr A*. Radiatively inefficient accretion flow models (RIAFs, as described in Broderick et al. 2011b) consistent with observed 1.3 mm VLBI visibility amplitudes produced closure phases of 0° ± 30° with a predicted most probable value of 0° ± 13° (Broderick et al. 2011a) on the triangle of baselines formed by CARMA-SMTO-JCMT. VLBI observations at 1.3 mm on the same triangle of stations reported, for the first time at this wavelength, a closure phase measurement of 0° ± 40° (Fish et al. 2011). An increase in the flux density during one of the nights was detected, which is an indicator of time-variability of Sgr A* at Schwarzschild radius scales.
Since the structure of Sgr A* still remains elusive, the work in this paper explores three different emission models for Sgr A* at 1.3 mm: an orbiting hot spot, a disk, and a jet model. The hot spot model is presented as a test case to compare our results with the work done by Doeleman et al. (2009b), where a hot spot embedded in an accretion disk could be a plausible explanation for the flares observed in Sgr A* in the NIR (Genzel et al. 2003; Bélanger et al. 2006; Ghez et al. 2004) and in the X-ray band (Baganoff et al. 2001). For the disk and jet models, the three-dimensional general relativistic magnetohydrodynamic (3D GRMHD) simulations are used to model the emission of magnetized plasma accreting onto a spinning SMBH (Mościbrodzka & Falcke 2013; Mościbrodzka et al. 2014 and references therein). These 3D GRMHD models are investigated because they can provide a more physically accurate description of the accretion flow than an orbiting hot spot model (Broderick & Loeb 2006) or an adiabatically expanding blob model (Yusef-Zadeh et al. 2009). These relativistic magnetohydrodynamic (MHD) models are well suited for modeling millimeter emission that comes from the areas closest to the black hole, and therefore regions where relativistic effects are strong. In previous work, time-dependent images of millimeter synchrotron emission from a 3D GRMHD accretion disk model were fitted to mm-VLBI data (Dexter et al. 2009). The models of the accretion flow were explored to estimate values for the inclination of the accretion disk with respect to the observer, position angle in the sky, accretion rate, and electron temperature of the accretion flow (Dexter et al. 2010). In the work presented here, we introduce for the first time in addition to a relativistic disk model a jet model based on 3D GRMHD simulations. Our goal is to use the modeled and observed visibility closure phases to place constraints on the possible structures of Sgr A* and putative black hole spin orientation in space.
The paper is organized as follows. In Sect. 2 we recall basic definitions and properties of VLBI visibility amplitudes, visibility phases, and closure phases. In Sect. 3 we present theoretical, general relativistic models of Sgr A*. In Sect. 4 we describe the method for simulating the closure phase observations and the parameters we used to reconstruct the observational noise. We present the model appearances and the resulting closure phase evolution for selected VLBI triangles in Sect. 5. We discuss the results in Sect. 6 and conclude in Sect. 7.
2. Closure phases
2.1. Closure phase calculation
The visibility function is a Fourier transform of the intensity distribution on the sky and is given by 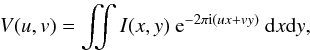 (1)where I(x,y) is the intensity distribution at a given set of coordinates x,y on the sky (the x,y angular coordinates are left-handed, i.e., x and y are positive in east and north directions on the sky, respectively), and u,v are the projected (also left-handed) baseline lengths. The V(u,v) is by definition a complex function, so it has an amplitude, A, and a phase, φ,
(1)where I(x,y) is the intensity distribution at a given set of coordinates x,y on the sky (the x,y angular coordinates are left-handed, i.e., x and y are positive in east and north directions on the sky, respectively), and u,v are the projected (also left-handed) baseline lengths. The V(u,v) is by definition a complex function, so it has an amplitude, A, and a phase, φ, 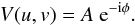 (2)The sum of visibility phases around a closed loop is known as the closure phase, first introduced by Jennison (1958). The closure phase of a triangle formed by the baselines between stations i, j, and k is the sum of the visibility phases on each baseline:
(2)The sum of visibility phases around a closed loop is known as the closure phase, first introduced by Jennison (1958). The closure phase of a triangle formed by the baselines between stations i, j, and k is the sum of the visibility phases on each baseline: 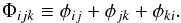 (3)Hence, the closure phase is the sum of the arguments of the complex visibilities on the baselines forming a triangle of stations:
(3)Hence, the closure phase is the sum of the arguments of the complex visibilities on the baselines forming a triangle of stations: ![\begin{eqnarray} \label{eq:closure_phase} \Phi_{ijk}=\arg[V(u_{ij},v_{ij})]+\arg[V(u_{jk},v_{jk})]+\arg[V(u_{ki},v_{ki})]. \end{eqnarray}](/articles/aa/full_html/2016/04/aa27599-15/aa27599-15-eq22.png) (4)The closure phase is a good observable because it is unaffected by phase errors introduced by individual stations due to atmospheric turbulence or instrumental instabilities. Consider three stations i,j,k. A blob of air with high moisture content over station j will introduce a phase delay above this station, so that the fringes detected by the baselines formed by i and j will be shifted in phase. However, because there will also be an equal but opposite phase shift in the fringes detected by stations j and k, then the overall sum of phases over the triangle of stations will be insensitive to the phase delay introduced by station j. For point sources, Gaussian distributions (symmetric and elliptical), and annular distributions the closure phase is always equal to 0° or 180°. Non-zero (non-180°) values of closure phase indicate asymmetries or skewness in the source structure (Monnier 2007). For Sgr A*, on the triangle formed by the CARMA-SMTO-JCMT baselines, a closure phase of 0° ± 40° has been measured at 1.3 mm (Fish et al. 2011).
(4)The closure phase is a good observable because it is unaffected by phase errors introduced by individual stations due to atmospheric turbulence or instrumental instabilities. Consider three stations i,j,k. A blob of air with high moisture content over station j will introduce a phase delay above this station, so that the fringes detected by the baselines formed by i and j will be shifted in phase. However, because there will also be an equal but opposite phase shift in the fringes detected by stations j and k, then the overall sum of phases over the triangle of stations will be insensitive to the phase delay introduced by station j. For point sources, Gaussian distributions (symmetric and elliptical), and annular distributions the closure phase is always equal to 0° or 180°. Non-zero (non-180°) values of closure phase indicate asymmetries or skewness in the source structure (Monnier 2007). For Sgr A*, on the triangle formed by the CARMA-SMTO-JCMT baselines, a closure phase of 0° ± 40° has been measured at 1.3 mm (Fish et al. 2011).
2.2. Closure phase errors
The errors on the closure phases are dependent on the signal-to-noise-ratio (S/N, sij) of the complex visibilities on individual baselines (Broderick et al. 2011a),  (5)where | Vij | is the complex visibility amplitude, B is the bandwidth, τ is the coherence time of the atmosphere, and SEFDi is the system equivalent flux density for a given station. Values for the coherence time, which depends on the observing wavelength, at these sites can range from a few seconds to τ ~ 20 s under good weather conditions (Doeleman et al. 2002). For our work, we chose a value of τ = 20 s. Since, as we previously mentioned, the closure phases are independent of phase delays introduced by atmospheric instabilities, they can be averaged over timescales longer than τ. Nevertheless, we have to take into account some limiting factors such as the timescales on which the structure of Sgr A* and the orientation of the baselines do not change significantly. When Sgr A* is not in a quiescent state, that is, flaring, these timescales could be shorter. The bandwidth is chosen to be one of the observing bandwidths for the EHT with B = 4 GHz of total on-sky bandwidth with 2 GHz per polarization. The values for the SEFD of given observatories adopted from Doeleman et al. (2009b) are listed in Table 1.
(5)where | Vij | is the complex visibility amplitude, B is the bandwidth, τ is the coherence time of the atmosphere, and SEFDi is the system equivalent flux density for a given station. Values for the coherence time, which depends on the observing wavelength, at these sites can range from a few seconds to τ ~ 20 s under good weather conditions (Doeleman et al. 2002). For our work, we chose a value of τ = 20 s. Since, as we previously mentioned, the closure phases are independent of phase delays introduced by atmospheric instabilities, they can be averaged over timescales longer than τ. Nevertheless, we have to take into account some limiting factors such as the timescales on which the structure of Sgr A* and the orientation of the baselines do not change significantly. When Sgr A* is not in a quiescent state, that is, flaring, these timescales could be shorter. The bandwidth is chosen to be one of the observing bandwidths for the EHT with B = 4 GHz of total on-sky bandwidth with 2 GHz per polarization. The values for the SEFD of given observatories adopted from Doeleman et al. (2009b) are listed in Table 1.
Summary of parameters for four orbiting spot models (A, B, C, and D).
The noise estimates can be calculated as shown in Rogers et al. (1995): ![\begin{eqnarray} \label{eq:closure_phase_error} \sigma_{\Phi_{ijk}} = \frac{\sqrt{4+s_{ij}^2 s_{jk}^2+s_{ij}^2 s_{ki}^2+s_{jk}^2 s_{ki}^2+2(s_{ij}^2+s_{jk}^2+s_{ki}^2)}}{(s_{ij} s_{jk} s_{ki})(T/\tau)^{1/2}} \, {\rm [rad]}, \end{eqnarray}](/articles/aa/full_html/2016/04/aa27599-15/aa27599-15-eq55.png) (6)where T is the integration time. It is important to note that σΦijk is model dependent because its value depends on the S/N of the complex visibilities on individual baselines. Equation (6) for high S/N (sij,sjk,ski ≫ 1) converges to Eq. (11) in Broderick et al. (2011a)1.
(6)where T is the integration time. It is important to note that σΦijk is model dependent because its value depends on the S/N of the complex visibilities on individual baselines. Equation (6) for high S/N (sij,sjk,ski ≫ 1) converges to Eq. (11) in Broderick et al. (2011a)1.
3. Theoretical emission models
The theoretical emission images are produced using the general relativistic ray-tracing method used in Mościbrodzka et al. (2009, 2014). These numerical ray-tracing calculations simulate the radiative transfer equations for synchrotron radiation from a thermal distribution of electrons near a black hole.
To simulate the effects of source smearing by free electrons in the Galaxy, we convolved all the theoretical images of the source with the elliptical scattering Gaussian function. The Gaussian parameters were adopted from radio observations of the source at long wavelengths at which the source is completely dominated by the scattering (Bower et al. 2004, 2006). We note that the adopted scattering screen is described by a function for which the complex visibility only has a non-zero real part.
For each model (described in detail in the next subsections), we created frames showing the observed image of the model every 10 s over the 12 h observation interval (the source is visible at various VLBI stations at different times). For each model, we created frames with a resolution of 128 × 128 pixels of the Milky Way central 40 × 40Rg. The Rg = GM/c2 is the gravitational radius of the SMBH and for Sgr A* Rg = 6.6 × 1011 cm. Therefore our modeled field of view is about 200 × 200μas on the sky. The visibility amplitude and phase at each moment in time were computed from the complex visibility function produced by a 2D Fourier transformation of the corresponding theoretical image (Eq. (1)).
We considered three emission models. The first, an orbiting spot model, is a simplified model of a quiescent accretion flow with a variable component to simulate a flaring event, and the computations were carried out for reference only. The other two, the disk and jet models, are realistic models of emission from an accreting black hole derived from 3D GRMHD simulations (Mościbrodzka & Falcke 2013; Mościbrodzka et al. 2014, and references therein).
3.1. Images of the orbiting spot
Our orbiting spot model is similar to the spot model studied in (Doeleman et al. 2009b, and references therein). In this model, the background radiation (or a “quiescent”, stationary emission) is produced by a RIAF (see, e.g., Broderick et al. 2011b) onto a spinning black hole (hereafter a∗ is the dimensionless spin of the SMBH). In our RIAF model, the plasma number density, the electron temperature (always defined in electron rest mass units, i.e., Θe = kTe/mec2), and the magnetic field strength are constant in time and have the following radial distributions: 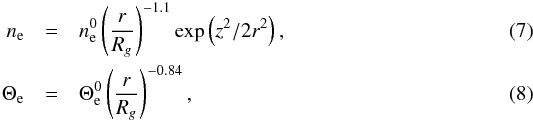 and
and 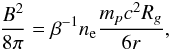 (9)where
(9)where 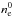 ,
, 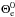 , and β (a parameter describing the ratio of gas to magnetic field pressure, β = Pgas/Pmag) are the model free parameters. The RIAF rotates around the central object with a Keplerian angular velocity:
, and β (a parameter describing the ratio of gas to magnetic field pressure, β = Pgas/Pmag) are the model free parameters. The RIAF rotates around the central object with a Keplerian angular velocity: 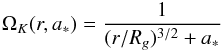 (10)and has a zero radial velocity. The model variable component, the orbiting spot, as in Doeleman et al. (2009b), is described by a Gaussian shape of size Rspot = 0.75Rs and it is orbiting at a Keplerian orbit at the equatorial plane of the BH at a radius rspot (model parameter). The density inside of a spot is enhanced:
(10)and has a zero radial velocity. The model variable component, the orbiting spot, as in Doeleman et al. (2009b), is described by a Gaussian shape of size Rspot = 0.75Rs and it is orbiting at a Keplerian orbit at the equatorial plane of the BH at a radius rspot (model parameter). The density inside of a spot is enhanced: 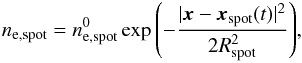 (11)where | x−xspot(t) | is the varying distance between the photon geodesics and the spot center to account for a delay between the observer time and the current coordinate time at the position of the spot (for more details on the spot model see, e.g., Schnittman 2006).
(11)where | x−xspot(t) | is the varying distance between the photon geodesics and the spot center to account for a delay between the observer time and the current coordinate time at the position of the spot (for more details on the spot model see, e.g., Schnittman 2006).
To check the consistency of our computations with the results presented in Doeleman et al. (2009b), we adopted free parameters of the model to reconstruct models similar to runs A230, B230, C230, and D230 shown in their work. Our model parameters are summarized in Table 2.
3.2. Images of disk and jet based on GRMHD simulations
The theoretical images of a disk and a jet were constructed by combining the ray-tracing radiative transfer model with a 3D GRMHD simulation of magnetized, turbulent plasma accreting onto a spinning SMBH (a∗ ≈ 0.94). In the 3D GRMHD simulations, the magnetized jet is naturally produced by preexisting, poloidal magnetic fields and the spinning black hole. The plasma density and the magnetic field strength used in the radiative transfer models are taken directly from the simulations. The synchrotron emission that we observe is most probably produced by electrons. The electron temperature, Te, is not explicitly computed in the current GRMHD simulations and so it has to be parameterized. In this work, we used the following prescription for electron temperatures: 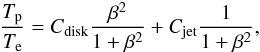 (12)where Tp is the temperature of protons (provided by the GRMHD simulations), and Tp/Te is the unknown proton-to-electron temperature ratio. We assumed that Tp/Te is a function of the β plasma parameter. The coupling constants Cdisk and Cjet describe the proton-to-electron coupling in the weakly and strongly magnetized plasma, respectively. In the case of a weakly magnetized plasma β ≫ 1 (e.g., inside of a turbulent accretion disk), Tp/Te → Cdisk. For a strongly magnetized plasma, β ≪ 1 (e.g., along the jet) Tp/Te → Cjet.
(12)where Tp is the temperature of protons (provided by the GRMHD simulations), and Tp/Te is the unknown proton-to-electron temperature ratio. We assumed that Tp/Te is a function of the β plasma parameter. The coupling constants Cdisk and Cjet describe the proton-to-electron coupling in the weakly and strongly magnetized plasma, respectively. In the case of a weakly magnetized plasma β ≫ 1 (e.g., inside of a turbulent accretion disk), Tp/Te → Cdisk. For a strongly magnetized plasma, β ≪ 1 (e.g., along the jet) Tp/Te → Cjet.
In particular, we assumed in our disk model that electrons are strongly coupled to protons both in the disk and in the jet (Cdisk = 1, Cjet = 1). Since the plasma density is the highest in the equatorial plane of the accretion disk, Cdisk = 1 will lead to an image with a bright disk.
In the jet model, the electrons are weakly coupled to protons in the accretion disk (Cdisk = 20), but remain strongly coupled to protons in the jet (Cjet = 1); and synchrotron emission from the jet will overcome the disk emission. It is worth mentioning that jets produced in the GRMHD simulations have two components: a jet spine and a jet sheath. The spine of the jet is strongly magnetized and has a low matter component, and therefore it does not produce any detectable electromagnetic signal. The jet sheath is a thin layer of outflowing gas surrounding the empty spine, it moves away from the BH relatively slowly at the considered distances and is made of baryonic plasma that originates from the inner parts of the accretion disk. As a result of the much higher matter content of the jet sheath in comparison to the spine, any synchrotron emission produced by the jet will be dominated by the sheath component.
Both models, disk and jet, were normalized to produce a similar total flux of approximately 2 Jansky at λ = 1.3 mm, in accordance with observations (Doeleman et al. 2008). The renormalization was made by changing the mass accretion rate Ṁ (i.e., multiplying the matter densities in the entire model by a constant scaling density factor).
As shown in Mościbrodzka & Falcke (2013) and in Mościbrodzka et al. (2014), the different electron temperature prescriptions in regions around the SMBH defined as the disk and jet significantly change a single GRMHD model appearance and the shape of its observed spectral energy distribution. Our current prescription that defines electron temperatures in the jet and disk has been slightly modified compared to that used in Mościbrodzka et al. (2014). This was done to obtain smoother images, that is, avoid sharp boundaries between the disk and jet zones (see, e.g., Mościbrodzka et al. 2016).
 |
Fig. 1 Model B at λ = 1.3 mm (here PA = 0°). Rows show orbital phases of the spot at t = 0, 0.2, 0.4, 0.6, and 0.8 from top to bottom. Left to right panels show an image of the model, that image convolved with the scattering screen, the visibility amplitude, and the visibility phase of the scatter-broadened images. The color intensity for the panels in the first two columns indicates the intensity of radiation, which has been normalized to unity. The visibility amplitude is in units of Jansky, and eighth contours are spaced by a factor of |
Since our electron temperature prescriptions in the disk and jet models are still robust, we time-averaged the images produced by time-dependent simulations over the duration of a few hours. Hence, any closure phase variations, based on the time-averaged disk and jet images, will be due to the VLBI baselines rotation due to Earth’s rotation and probing different uv-values in the Fourier space. This is not the case for the orbiting spot model, which is fully time-dependent.
4. Simulated data
The closure phase observations were simulated using the images of the orbiting spot model, the time-averaged disk model, and the time-averaged jet model. For a given T = 10-s scan, the Fourier transform of the brightness distribution was computed using Eq. (1), and the components of the complex visibility function (amplitude and phase) were obtained for each baseline. The S/N for individual baselines was calculated using Eq. (5) with a coherence time for the atmosphere of τ = 20 s and the appropriate system equivalent flux densities given in Table 1. Values for the closure phase and its errors were calculated using Eqs. (4) and (6), respectively.
5. Results
5.1. Theoretical closure phase evolution for the orbiting spot model
As a test case, we studied the radiation and VLBI observables produced by the orbiting spot model. Figure 1 shows the orbiting spot model B (see Table 2) at various moments in time. The panels from left to right show the image of the model, the same image convolved with the scattering screen, the visibility amplitude map with contours, and lastly the phase of the visibility function. The rows represent different orbital phases ranging from 0 to 0.8 from top to bottom.
The emission from RIAF that we see in the images of the model, where the peak brightness has been scaled to 1, has the shape of a crescent. The crescent is formed by light-bending effects because the strong gravity dominates the SMBH surroundings as well as relativistic Doppler beaming effects due to the Keplerian orbital motion of the gas. Relativistic Doppler beaming of the approaching plasma causes the prograde orbiting spot to become brighter only when moving toward the observer (i.e., see the second panel in the first column), while the spot becomes dimmer as it recedes from the observer (i.e., last two panels in the first column). In addition, the spot intensity is not exactly Gaussian due to relativistic effects (time delays) of ray tracing. All the panels in the second column show a much broader and brighter image of the crescent shape because of the convolution with the scattering screen and because of the different amplitude scaling. Changes in the phase of the visibility function are shown in the last column.
Figure 2 shows the predicted closure phase evolution (solid red line) for the four orbiting spot models summarized in Table 2. Each row from top to bottom shows models from A to D, and each column shows a given model for the following set of triangles of VLBI stations, from left to right: Hawaii-SMTO-CARMA, Hawaii-CARMA-LMT, Hawaii-CARMA-Chile, and IRAM PV-IRAM PdB-Chile. These models and specific triangles of baselines were chosen to compare our results with those presented in Fig. 5 by Doeleman et al. (2009b).
All the models display periodicity on the closure phases due to the short (27 min) orbital period of the spot around the SMBH. However, we also observe a secular trend in the closure phase evolution due to the Earth’s rotation. At first glance, the most noticeable feature of the panels in Fig. 2 is that the closure phase prediction depends strongly on the parameters chosen for a given model. Small triangles of baselines are expected to yield lower values of the closure phase than large triangles of baselines. This is simply a consequence of the scale of the features in the brightness distribution on the sky and the angular resolution that goes with the projected baseline length. Since interpreting closure phases is highly non-trivial, we can only safely conclude at this point that closure phases can be used to distinguish between models with different position and inclination angles.
The observational noise is plotted in Fig. 2 as black points. Here we assume B = 4 GHz, T = 10 s, and τ = 20 s to calculate σΦijk and generate Gaussian random noise. The closure phases that include the Chile station assume the SEFD of APEX, hence the noise is slightly higher than in other triangles.
Our results (curve shape, phase signs, and evolution of the closure phases), although not identical, are roughly consistent with those presented in Fig. 5 in Doeleman et al. (2009b). We conclude that our tools for calculating visibilities and closure phases are hereby found to be valid, and therefore we proceed to explore the brightness distribution functions that are produced by more physically driven scenarios.
 |
Fig. 2 Closure phases at λ = 1.3 mm on various triangles of VLBI stations. Different models of the orbiting spot are presented (from top to bottom) with parameters given in Table 2. Each point represents an integration time of 10 s, and the same 2 h period is shown except for the triangle including the European stations. The solid red line shows the closure phase without noise. Chile refers to the APEX telescope and Hawaii refers to 3 Hawaiian facilities phased together as described in Table 1. |
5.2. Theoretical closure phase evolution for the disk and jet models
Our disk model is shown in Fig. 4. The panels, from left to right, show the intrinsic image of the disk model, its convolution with the scattering screen, the amplitude of the visibility function (overplotted with contours), and lastly the phase of the visibility function. From top to bottom, the inclinations of the disk range from i = 30° to i = 150°, while the BH spin position angle (PA) is kept at 0° (BH spin is pointing north). In our models, i is the angle between the observer’s line of sight and the BH spin axis, with i = 0° being face-on and i = 90° being edge-on. PA is the position angle of the BH spin axis on the sky, where PA is positive in the direction west of north (see Fig. 3).
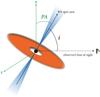 |
Fig. 3 Geometry of our models in terms of observer’s inclination angle (i) and BH spin axis position angle (PA). |
In Fig. 4 the disk model emission is more extended than in the RIAF images shown in Fig. 1. The disk appearance is dominated by the gravitational lensing and relativistic Doppler effects. The ring shape is evident in the top and bottom panels with inclinations that are more face-on (i = 30° and 150°). However, at i = 90° the disk appears as a Gaussian-like spot rather than a crescent. Another important feature to note is that the emission is dominated by the left side of the disk. This is because the orbiting plasma in the disk becomes Doppler boosted as it approaches the observer. The panels depicting the visibility function, third column, indicate that the black hole shadow is only clearly discernible as two minima in cases when the disk is observed face-on. The last column represents the phase of the complex visibility for the different inclinations.
 |
Fig. 4 Disk model at λ = 1.3 mm (here BH spin PA = 0°). Rows show inclinations of 30°, 60°, 90°, 120°, and 150°from top to bottom. Left to right panels show an image of the disk model, that image convolved with the scattering screen, the visibility amplitude, and the visibility phase of the scatter-broadened images. The color intensity for the panels in the first two columns indicates the intensity of radiation, which has been normalized to unity. In the third column the color intensity indicates the amplitude of the visibility in Jy and contours are spaced by a factor of |
The jet model is shown in Fig. 5 (panels are the same as in Fig. 4). Compared to the disk model, the image of a jet near the SMBH horizon is not well represented by a Gaussian or by a crescent, it has a more complicated structure. In the jet images, most of the emission is produced by the jet component. The disk component is weaker, but still visible as a ring (at i = 30° and i = 150°), or as a ring plus a tongue-like feature that sweeps across the near side of the black hole (i = 60°–120°). The jet component is best visible at i = 90° as two spots separated by a dimmer disk tongue-like feature. These two spots are the footprints of the large-scale jet.
In general, both the intrinsic and the scatter-broadened images of the jet model are more extended compared to the disk images. One contributing factor is that the accretion rate value for the jet model is approximately Ṁ ≈ a few × 10-8M⊙/yr, whereas for the disk model is around Ṁ ≈ 10-9M⊙/yr. These values are used for the normalization of the flux at 1.3 mm. Consequently, in our jet scenario the black hole shadow is clearly visible at all viewing angles. In the visibility amplitude panels the two minima denoting the shadow are detectable regardless of the inclination angle. Again, the last column represents changes in the phase of the visibility function with inclination. For i = 60°–120°, the jet model phase maps are significantly different from the corresponding maps computed based on the disk images.
 |
Fig. 5 Jet model at λ = 1.3 mm (here BH spin PA = 0°). Rows show inclinations of 30°, 60°, 90°, 120°, and 150°from top to bottom. Left to right panels show an image of the jet model, that image convolved with the scattering screen, the visibility amplitude, and the visibility phase of the scatter-broadened images. The color intensity for the panels in the first two columns indicates the intensity of radiation, which has been normalized to unity. In the third column the color intensity indicates the amplitude of the visibility in Jy and contours are spaced by a factor of |
 |
Fig. 6 Closure phase values at λ = 1.3 mm for the disk model and jet model for the triangle formed by the CARMA-Hawaii-SMTO baselines. Rows show inclination angles between the observer’s line of sight and the BH spin axis with values of i = 30°, 60°, 90°, 120°, and 150° (from top to bottom) with the left column displaying the disk model and the right column the jet model. Solid colored lines represent the simulated measurements at different BH spin position angles of PA = 0°, 30°, 60°, 90°, 120°, 150°, and 180° west of north (the images shown in the second column of Figs. 4 and 5 are rotated in the clock-wise direction). The horizontal dotted lines represent values of ±40° closure phase as measured by Fish et al. (2011) over a 3.5 h interval. The gap between UT = 0–5 h is due to the lack of baselines visible from Sgr A* during this period of time for this triangle. |
The closure phases at 1.3 mm for the CARMA-Hawaii-SMTO triangle are shown in Fig. 6 for both the disk and jet models. This is the main new result delivered by this work. In Fig. 6 the colored lines represent the predicted closure phases for different BH spin position angles (PA is positive in the direction west of north, i.e., we rotated the images shown in the second column of Figs. 4 and 5 in the clock-wise direction, which is opposite of the normal convention) and the panels from top to bottom show different inclinations. We present closure phases for PAs ranging from 0° to 180°. Position angles offset by 180° yield mirror results. We plot a T = 5 min average of the closure phase (average of thirty 10 s scans) with the corresponding error bars, spanning a measurement period of about seven hours. In Fig. 6 we have included dotted lines to indicate a closure phase value of ±40° as was measured over a 3.5 h interval by Fish et al. (2011).
 |
Fig. 7 Same as Fig. 6, but zooming-in into the area of interest. The y-axis range has been set to ±13°, this limit represents the most likely values for closure phase as shown in the models by Broderick et al. (2011a). Solid lines are closure phases without noise, shaded areas represent the noise for the corresponding curve. |
First, for both models the closure phases are the largest at face-on viewing angles, as expected for the ring-like structures. Second, the most obvious difference between the closure phases of the disk model and the jet model is that for the jet model they tend to have higher values at viewing angles i = 60–120°. This is expected since closure phases give us information about the amount of asymmetric flux the source has, and we can see in the images of the jet model (see Fig. 5) that their structure is more asymmetric than that of the disk model.
Based on the ±40° closure phase measurements by Fish et al. (2011; dotted lines in Fig. 6), models can already be constrained. For example, the disk model, at inclinations of i = 60° to 120° cannot be ruled out for any PAs since all have closure phase values that are close to zero. For more face-on inclinations (30° and 150°), a disk model with BH spin axis position angle of PA = 60°, 90°, or 120° can be discarded since the predicted closure phases fall outside the measured values. For all inclinations of the jet model, position angles of PA = 60°, 90°, and 120° are clearly inconsistent with the preliminary observations. Other orientations require further inspection.
Figure 7 depicts the same jet and disk models, but zooming-in into the area of interest (±13° limits from Broderick et al. (2011a) are the most likely limits based on accretion flow models consistent with measured visibility amplitudes). The difference in the predicted values of closure phases based on the studied models can also be examined. Jet and disk geometries can reproduce similar closure phases for different sets of i and PA. Consequently, the black hole spin orientation (and possibly the spin value) will be strongly model dependent. We conclude that new observations at 1.3 mm (and possibly simultaneous observations at longer wavelengths) including other triangles of baselines are necessary to constrain the source geometry and the orientation of the black hole spin, for instance.
6. Discussion
We have constructed a number of images of the SMBH shadow for various surrounding plasma configurations and have predicted the observed 1.3 mm VLBI closure phases.
Previous work on RIAF models has resulted in most probable values for the BH spin of a∗ ≈ 0, inclination of i ≈ 68° and position angles of PA ≈−52° or +128° east of north (Broderick et al. 2011b). Their values of PA ≈−52° or +128° would be consistent with our disk models with inclinations ranging from 60° to 120°, but our jet model at corresponding i = 60° and PA = 60° west of north is inconsistent with the observational limits. In previous 3D GRMHD models of a disk, although quite dynamically different from the RIAF models, similar favored values of i ≈ 50° and PA ≈ −23° east of north have been reported for instance by Dexter et al. (2010) based on visibility amplitude analyses.
As is evident from the jet models (Figs. 6 and 7), the closure phases show more variability and higher values at close to edge-on inclinations than for the disk models, and more possibilities for orientations are discarded if we follow the constraint of a modeled closure phase of ±13° compared to a measured closure phase of ±40°. Nevertheless, we should not be too quick to discard the possibility that Sgr A* has a mildly relativistic jet. Observational signatures such as a flat-to-inverted radio spectrum resembling that of an AGN, changes in source size depending on the observing frequency (Bower et al. 2004), time lags between flares at 43 GHz and 22 GHz indicating the presence of relativistic outflows (Yusef-Zadeh et al. 2006), and Chandra X-ray observations suggesting an outflow from the accretion flow (Wang et al. 2013) are all clues indicating the presence of a jet.
In our jet models the preferred orientations that fall within observational and modeled closure phase limits are PA = 0°, 30°, 150°, and 180°, and preferred inclinations are more edge-on, so the jet would seem to be pointing close to the plane of the sky. In terms of the inclination angle, but not necessarily position angle, our results seem to agree with previous analyses of 7 mm data that favored a highly inclined jet (Markoff et al. 2007). Regarding the systematic uncertainties in this work, it is important mention that we sample the parameter space sparsely in our models, both the inclination and position angle change in increments of 30°. As a result, we do not cover the whole parameter space. Therefore, it would be possible to have models that are not represented here and are still consistent with the closure phase limits described.
Furthermore, all the models investigated here have the axis of the BH angular momentum aligned with the accretion disk axis. Past work has posed the idea that the accretion disk and the black hole angular momentum axes do not necessarily have to be aligned (tilt of 15°), and that it is possible to reproduce the observed time-variable mm and NIR emission and the crescent shape of Sgr A* with a tilted model (Dexter & Fragile 2013). Because we have not yet investigated the dependence of closure phase on BH spin, magnetic field strength (free parameters), and disk and black hole spin axes alignment, the conclusions presented here might change in the future if a more comprehensive study of magnetized models and spin models is carried out.
Finally, it is important to note that we have examined emission models based on standard GR, but other studies have been conducted using a quasi-Kerr metric to predict the image of the accretion flow (Johannsen & Psaltis 2010; Broderick et al. 2014).
7. Conclusions
Disk and jet models of Sgr A* have been investigated to try to constrain the intrinsic geometry of the source by using closure phase values. We showed that a significant fraction of the disk and jet models can be excluded for a certain combination of the parameters observer’s inclination angle and BH spin axis position angle. However, we cannot yet distinguish between disk and jet models given the range of allowed parameters for both models. Similar analyses of observations and simulations need to be conducted at wavelengths of 0.8 mm, 3.5 mm, and 7 mm to further constrain the emission models for Sgr A*. At these wavelengths the emission regions probed will be very different to those presented here. At VLBI wavelengths longer than 1.3 mm interstellar scattering broadens the images of Sgr A*, which tends to dilute the structural information. At VLBI wavelengths much shorter than 1.3 mm observations are not possible because the atmosphere becomes optically thick. Although the disk and jet models have a different appearance because the geometry and emission mechanism are intrinsic properties of Sgr A*, consistent values for the observer’s inclination angle and BH spin position angle are expected for the aforementioned wavelengths. Hence, analyses of closure phases at 0.8 mm, 3.5 mm, and 7 mm will help to distinguish among the types of emission models. Additional measurements of closure phases in more baseline triangles will help us to distinguish even better among the possible model solutions because this work was mainly focused on the CARMA-Hawaii-SMTO triangle of stations.
Note the typo in power in Eq. (11) in Broderick et al. (2011a).
Acknowledgments
This work is partially supported by the NWO Spinoza Prize awarded to Heino Falcke and by the ERC Synergy Grant “BlackHoleCam: Imaging the Event Horizon of Black Holes” awarded to Heino Falcke, Michael Kramer and Luciano Rezzolla.
References
- Baganoff, F. K., Bautz, M. W., Brandt, W. N., et al. 2001, Nature, 413, 45 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bélanger, G., Terrier, R., de Jager, O. C., Goldwurm, A., & Melia, F. 2006, J. Phys. Conf. Ser., 54, 420 [NASA ADS] [CrossRef] [Google Scholar]
- Bower, G. C., Falcke, H., Herrnstein, R. M., et al. 2004, Science, 304, 704 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bower, G. C., Goss, W. M., Falcke, H., Backer, D. C., & Lithwick, Y. 2006, ApJ, 648, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Bower, G. C., Markoff, S., Dexter, J., et al. 2015, ApJ, 802, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Broderick, A. E., & Loeb, A. 2006, MNRAS, 367, 905 [NASA ADS] [CrossRef] [Google Scholar]
- Broderick, A. E., Fish, V. L., Doeleman, S. S., & Loeb, A. 2011a, ApJ, 738, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Broderick, A. E., Fish, V. L., Doeleman, S. S., & Loeb, A. 2011b, ApJ, 735, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Broderick, A. E., Johannsen, T., Loeb, A., & Psaltis, D. 2014, ApJ, 784, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Cotton, W. D. 1979, AJ, 84, 1122 [NASA ADS] [CrossRef] [Google Scholar]
- Dexter, J., & Fragile, P. C. 2011, ApJ, 730, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Dexter, J., & Fragile, P. C. 2013, MNRAS, 432, 2252 [NASA ADS] [CrossRef] [Google Scholar]
- Dexter, J., Agol, E., & Fragile, P. C. 2009, ApJ, 703, L142 [NASA ADS] [CrossRef] [Google Scholar]
- Dexter, J., Agol, E., Fragile, P. C., & McKinney, J. C. 2010, ApJ, 717, 1092 [NASA ADS] [CrossRef] [Google Scholar]
- Doeleman, S. S., Shen, Z.-Q., Rogers, A. E. E., et al. 2001, AJ, 121, 2610 [NASA ADS] [CrossRef] [Google Scholar]
- Doeleman, S. S., Phillips, R. B., Rogers, A. E. E., et al. 2002, in Proc. 6th EVN Symp., eds. E. Ros, R. W. Porcas, A. P. Lobanov, & J. A. Zensus, 223 [Google Scholar]
- Doeleman, S. S., Weintroub, J., Rogers, A. E. E., et al. 2008, Nature, 455, 78 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Doeleman, S., Agol, E., Backer, D., et al. 2009a, in Astronomy, The Astronomy and Astrophysics Decadal Survey, 2010, 68 [NASA ADS] [Google Scholar]
- Doeleman, S. S., Fish, V. L., Broderick, A. E., Loeb, A., & Rogers, A. E. E. 2009b, ApJ, 695, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Dolence, J. C., Gammie, C. F., Shiokawa, H., & Noble, S. C. 2012, ApJ, 746, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenhauer, F., Genzel, R., Alexander, T., et al. 2005, ApJ, 628, 246 [NASA ADS] [CrossRef] [Google Scholar]
- Falcke, H., & Markoff, S. B. 2013, Class. Quant. Grav., 30, 244003 [Google Scholar]
- Falcke, H., Melia, F., & Agol, E. 2000, ApJ, 528, L13 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Fish, V. L., Doeleman, S. S., Beaudoin, C., et al. 2011, ApJ, 727, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Genzel, R., Schödel, R., Ott, T., et al. 2003, Nature, 425, 934 [CrossRef] [PubMed] [Google Scholar]
- Genzel, R., Eisenhauer, F., & Gillessen, S. 2010, Rev. Mod. Phys., 82, 3121 [NASA ADS] [CrossRef] [Google Scholar]
- Ghez, A. M., Morris, M., Becklin, E. E., Tanner, A., & Kremenek, T. 2000, Nature, 407, 349 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ghez, A. M., Wright, S. A., Matthews, K., et al. 2004, ApJ, 601, L159 [CrossRef] [Google Scholar]
- Ghez, A. M., Salim, S., Weinberg, N. N., et al. 2008, ApJ, 689, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- Gillessen, S., Eisenhauer, F., Trippe, S., et al. 2009, ApJ, 692, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Jennison, R. C. 1958, MNRAS, 118, 276 [NASA ADS] [CrossRef] [Google Scholar]
- Johannsen, T., & Psaltis, D. 2010, ApJ, 718, 446 [NASA ADS] [CrossRef] [Google Scholar]
- Kamruddin, A. B., & Dexter, J. 2013, MNRAS, 434, 765 [NASA ADS] [CrossRef] [Google Scholar]
- Krichbaum, T. P., Graham, D. A., Bremer, M., et al. 2006, J. Phys. Conf. Ser., 54, 328 [NASA ADS] [CrossRef] [Google Scholar]
- Markoff, S., Bower, G. C., & Falcke, H. 2007, MNRAS, 379, 1519 [NASA ADS] [CrossRef] [Google Scholar]
- Monnier, J. D. 2007, New A Rev., 51, 604 [Google Scholar]
- Mościbrodzka, M., & Falcke, H. 2013, A&A, 559, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mościbrodzka, M., Gammie, C. F., Dolence, J. C., Shiokawa, H., & Leung, P. K. 2009, ApJ, 706, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Mościbrodzka, M., Shiokawa, H., Gammie, C. F., & Dolence, J. C. 2012, ApJ, 752, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Mościbrodzka, M., Falcke, H., Shiokawa, H., & Gammie, C. F. 2014, A&A, 570, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mościbrodzka, M., Falcke, H., & Shiokawa, H. 2016, A&A, 586, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ricarte, A., & Dexter, J. 2015, MNRAS, 446, 1973 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, A. E. E., Hinteregger, H. F., Whitney, A. R., et al. 1974, ApJ, 193, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, A. E. E., Doeleman, S. S., & Moran, J. M. 1995, AJ, 109, 1391 [NASA ADS] [CrossRef] [Google Scholar]
- Schnittman, J. D. 2006, Ph.D. Thesis, 212 [Google Scholar]
- Shcherbakov, R. V., Penna, R. F., & McKinney, J. C. 2012, ApJ, 755, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Q. D., Nowak, M. A., Markoff, S. B., et al. 2013, Science, 341, 981 [NASA ADS] [CrossRef] [Google Scholar]
- Yusef-Zadeh, F., Roberts, D., Wardle, M., Heinke, C. O., & Bower, G. C. 2006, ApJ, 650, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Yusef-Zadeh, F., Bushouse, H., Wardle, M., et al. 2009, ApJ, 706, 348 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Model B at λ = 1.3 mm (here PA = 0°). Rows show orbital phases of the spot at t = 0, 0.2, 0.4, 0.6, and 0.8 from top to bottom. Left to right panels show an image of the model, that image convolved with the scattering screen, the visibility amplitude, and the visibility phase of the scatter-broadened images. The color intensity for the panels in the first two columns indicates the intensity of radiation, which has been normalized to unity. The visibility amplitude is in units of Jansky, and eighth contours are spaced by a factor of |
| In the text | |
 |
Fig. 2 Closure phases at λ = 1.3 mm on various triangles of VLBI stations. Different models of the orbiting spot are presented (from top to bottom) with parameters given in Table 2. Each point represents an integration time of 10 s, and the same 2 h period is shown except for the triangle including the European stations. The solid red line shows the closure phase without noise. Chile refers to the APEX telescope and Hawaii refers to 3 Hawaiian facilities phased together as described in Table 1. |
| In the text | |
 |
Fig. 3 Geometry of our models in terms of observer’s inclination angle (i) and BH spin axis position angle (PA). |
| In the text | |
 |
Fig. 4 Disk model at λ = 1.3 mm (here BH spin PA = 0°). Rows show inclinations of 30°, 60°, 90°, 120°, and 150°from top to bottom. Left to right panels show an image of the disk model, that image convolved with the scattering screen, the visibility amplitude, and the visibility phase of the scatter-broadened images. The color intensity for the panels in the first two columns indicates the intensity of radiation, which has been normalized to unity. In the third column the color intensity indicates the amplitude of the visibility in Jy and contours are spaced by a factor of |
| In the text | |
 |
Fig. 5 Jet model at λ = 1.3 mm (here BH spin PA = 0°). Rows show inclinations of 30°, 60°, 90°, 120°, and 150°from top to bottom. Left to right panels show an image of the jet model, that image convolved with the scattering screen, the visibility amplitude, and the visibility phase of the scatter-broadened images. The color intensity for the panels in the first two columns indicates the intensity of radiation, which has been normalized to unity. In the third column the color intensity indicates the amplitude of the visibility in Jy and contours are spaced by a factor of |
| In the text | |
 |
Fig. 6 Closure phase values at λ = 1.3 mm for the disk model and jet model for the triangle formed by the CARMA-Hawaii-SMTO baselines. Rows show inclination angles between the observer’s line of sight and the BH spin axis with values of i = 30°, 60°, 90°, 120°, and 150° (from top to bottom) with the left column displaying the disk model and the right column the jet model. Solid colored lines represent the simulated measurements at different BH spin position angles of PA = 0°, 30°, 60°, 90°, 120°, 150°, and 180° west of north (the images shown in the second column of Figs. 4 and 5 are rotated in the clock-wise direction). The horizontal dotted lines represent values of ±40° closure phase as measured by Fish et al. (2011) over a 3.5 h interval. The gap between UT = 0–5 h is due to the lack of baselines visible from Sgr A* during this period of time for this triangle. |
| In the text | |
 |
Fig. 7 Same as Fig. 6, but zooming-in into the area of interest. The y-axis range has been set to ±13°, this limit represents the most likely values for closure phase as shown in the models by Broderick et al. (2011a). Solid lines are closure phases without noise, shaded areas represent the noise for the corresponding curve. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.