| Issue |
A&A
Volume 588, April 2016
|
|
|---|---|---|
| Article Number | A88 | |
| Number of page(s) | 12 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201526077 | |
| Published online | 23 March 2016 | |
The X-ray/radio and UV luminosity expected from symbiotic systems as the progenitor of SNe Ia
1
Yunnan Observatories, Chinese Academy of Sciences,
650216
Kunming,
PR China
e-mail: xiangcunmeng@ynao.ac.cn; zhanwenhan@ynao.ac.cn
2
Key Laboratory for the Structure and Evolution of Celestial
Objects, Chinese Academy of Sciences, 650216
Kunming, PR
China
Received: 12 March 2015
Accepted: 25 January 2016
Context. Symbiotic systems (i.e. a white dwarf + red giant star, WD + RG), which experience mass loss and form circumstellar material (CSM), have been suggested as being a possible progenitor system of type Ia supernovae (SNe Ia). After a supernova explosion, the supernova ejecta may interact with the CSM or the RG secondary. X-ray/radio emission (excess UV photons) is expected from the interaction between supernova ejecta and the CSM (RG secondary). However, no X-ray or radio emission that has originated from this type of system has been observationally detected, and only four SNe Ia have shown any possible signal of excess UV emission. These observational discrepancies need to be interpreted.
Aims. We seek to determine the luminosity of these emissions, using detailed binary evolution algorithms to obtain the parameters of binary systems at the moment of the supernova explosion.
Methods. We carried out a series of binary stellar evolution calculations, in which the effect of tidally enhanced wind on the evolution of WD + RG systems is incorporated. The WDs increase their mass to the Chandrasekhar mass limit, and then explode as SNe Ia. Based on the binary evolution results, we estimated the X-ray/radio (the excess UV) luminosity from the interactions between supernova ejecta and the CSM (the secondary) using a variety of published standard models.
Results. We found that the X-ray flux may be high enough to be detected for a nearby SN Ia from a symbiotic system, while the radio flux is more likely to de detected when the companion is an asymptotic giant branch (AGB) star, and for a first giant branch (FGB) companion, the radio flux is generally lower than the detection limit. For two well observed SNe Ia, 2011fe and 2014J, almost all symbiotic systems are excluded by X-ray observations, but WD + FGB systems may not be ruled out by radio observations. The excess UV luminosity that results from the collision of supernova ejecta with the RG secondary may be high enough to be detected if the secondary fills its Roche lobe at the moment of a supernova explosion.
Conclusions. The X-ray/radio emissions are more prevalent in SNe Ia from WD + AGB systems, although SNe Ia from such systems are rare. The UV luminosity from the collision of supernova ejecta to RG secondary is high enough, but only one in every few hundred SNe Ia manifests the signal from the collision.
Key words: binaries: symbiotic / stars: evolution / supernovae: general / white dwarfs
© ESO, 2016
1. Introduction
Type Ia supernovae (SNe Ia) play an important role in many astrophysical fields, especially in cosmology. SNe Ia appear to be good cosmological distance indicators and have been successfully applied in determining cosmological parameters (e.g., Ω and Λ), which resulted in the discovery of the accelerating expansion of the universe (Riess et al. 1998; Schmidt et al. 1998; Perlmutter et al. 1999). SNe Ia are also proposed as cosmological probes to test the evolution of the dark energy equation of state with time (Howell et al. 2009; Meng et al. 2015). However, the progenitor systems of SNe Ia have not yet been confidently identified (Hillebrandt & Niemeyer 2000; Leibundgut 2000; Wang & Han 2012; Maoz et al. 2014), although the identification of the progenitor is crucial in many astrophysical fields, e.g., in determining cosmological parameters, studying galaxy chemical evolution, understanding the explosion mechanism of an SN Ia, and constraining the theory of binary stellar evolution (see the review by Livio 1999).
It is widely believed that an SN Ia results from the explosion of a carbon-oxygen white dwarf (CO WD) in a binary system (Hoyle & Fowler 1960). The CO WD may increase its mass by accreting from its companion to a maximum stable mass, and then explode as a thermonuclear runaway. A large amount of radioactive nickel-56 (56Ni) is produced in the explosion (Branch 2004), and the amount of 56Ni determines the maximum luminosity of the SN Ia (Arnett 1982). Based on the nature of the companion of the mass accreting WD, two basic progenitor models for SN Ia have been discussed over the last three decades. One is the single degenerate (SD) model (Whelan & Iben 1973; Nomoto et al. 1984), in which a CO WD accretes hydrogen- or helium-rich materials from its companion to increase its mass, and finally explodes if its mass approaches the Chandrasekhar mass limit. The companion may be either a main-sequence (MS), a slightly evolved star (WD+MS) or a red giant star (WD+RG), or a helium star (WD + He star; Yungelson et al. 1995; Li & van den Heuvel 1997; Hachisu et al. 1999a,b; Nomoto et al. 1999; 2003; Langer et al. 2000; Han & Podsiadlowski 2004; 2006; Chen & Li 2007; 2009; Meng et al. 2009; Lü et al. 2009; Wang et al. 2009a,b). An alternative is the double degenerate (DD) model (Iben & Tutukov 1984; Webbink 1984; Han 1998; Chen et al. 2012), in which a system that consists of two CO WDs loses orbital angular momentum by gravitational wave radiation and ultimately merges. The merger may explode if the total mass of the system exceeds the Chandrasekhar mass limit (see the reviews by Hillebrandt & Niemeyer 2000 and Maoz et al. 2014). Apart from these two basic scenarios, several other models have also been frequently discussed by many groups, such as the core-degenerate model (Kashi & Soker 2011; Ilkov & Soker 2012), the WD−WD collision model (Raskin et al. 2009; Kushnir et al. 2013) and the double-detonation scenarios (Woosley & Weaver 1994; Livne & Arnett 1995; Ruiter et al. 2011), and one may refer to Tsebrenko & Soker (2015) for further information. At present, it is premature to exclude any of these channels.
The symbiotic channel (WD + RG), where the CO WD mainly increases its mass by wind accretion, is believed to be a possible channel for producing SNe Ia (Branch et al. 1995; Hachisu et al. 1999b), but some observations seem to disfavour this channel, e.g., no radio emission, which is expected from the interaction between supernova ejecta and lost material from the binary system, was detected, although other observations exist that uphold the channel. (Please see Sect. 2 for observations.) In this paper, we try to interpret observations that disfavor the WD + RG channel, and demonstrate that these observational results are expected to occur naturally as a consequence of this channel.
In Sect. 2, we summarize various observational facts. In Sect. 3, we describe our model and present the calculation results in Sect. 4. We provide discussions in Sect. 5 and draw our conclusions in Sect. 6.
2. Observations and models
2.1. Observations
There are at least four recurrent symbiotic novae, such as RS Oph and T CrB, whose WD masses are very massive (Mikolajewska 2010; 2012). The massive WDs may increase their mass by wind accretion, from which SNe Ia can arise (Hachisu & Kato 2001; Sokoloski et al. 2006; Podsiadlowski 2008). If some symbiotic novae are reliable progenitor systems for SNe Ia, we can expect certain special observational properties in SNe Ia to be as follows:
-
1)
Prior to the supernova explosion, the systems must lose a large amount of material to form circumsteller material (CSM). Although the expected UV flux is, in general, expected to be low, there may be enough flux from the photosphere to ionize atoms in the CSM with low ionization potential. If the SN ejecta were to interact with the CSM, or impact an RG, the amount of UV flux may be disputable (Kasen 2010; Lundqvist et al. 2013), and a large fraction of the CSM will be ionized. As the number of UV photons varies with time, we can expect to see variable circumstellar absorption lines in the spectra of SNe Ia. Variable circumstellar Na I absorption lines were first observed in the spectra of SN 2006X (Patat et al. 2007). The distance from the explosion center to the absorbing material was estimated as being less than 1017 cm (Patat et al. 2007; Simon et al. 2009). The variable circumstellar absorption lines have also been observed in RS Oph (Patat et al. 2011), which linked the symbiotic system to SNe Ia. Judging by the expansion velocity of the CSM, Patat et al. (2007) suggested that the progenitor of SN 2006X is a WD + RG system, although the possibility of a WD + MS system cannot be excluded completely (Hachisu et al. 2008a). Subsequently, two twins of SN 2006X have also been reported (Blondin et al. 2009; Simon et al. 2009). Recently, Graham et al. (2015) have found that several spectra with variable K I absorption lines and they argue that the most plausible explanation for this is the photoionization of CSM, but the origin of the CSM is controversial (Soker 2015; Maeda et al. 2016). In addition, owing to the existence of the CSM, the possibility of significant blueshifts for some absorption lines can be expected in the spectra of some SNe Ia, even though the true nature of the blueshift is not fully understood (Sternberg et al. 2014). Sternberg et al. (2011) checked the absorption properties of 35 SNe Ia and found that the velocity structure of absorbing material along the line of sight for more than 50% of Ia supernovae tends to be blueshifted. These structures are likely to be the signatures of gas outflows from the SD systems, although it is possible for some DD systems to show signs of CSM as well, e.g., Shen et al. (2013). Furthermore, Foley et al. (2012a) even find that SNe Ia with blueshifted circumstellar/interstellar absorption systematically have higher ejecta velocities, which could mean that the SNe Ia comes from a variety of progenitor systems and that SNe Ia from systems with possible winds tends to have more kinetic energy per unit mass than those from systems with weak or no winds. Maguire et al. (2013) also noticed that SNe Ia that display blue-shifted absorption features are skewed towards later-type galaxies and have broader light curves, compared to those without absorption features.
-
2)
The wind from symbiotic systems may interact with interstellar material and this kind of interaction may reveal itself during the remnant stage. Chiotellis et al. (2012) present a model about the remnant of Kepler’s supernova and find that the main features of the remnant can be explained by a symbiotic binary, which consists of a white dwarf and an asymptotic giant branch (AGB) donor star with an initial mass of 4–5 M⊙. In their model, the interaction between the stellar wind and the interstellar material plays a very important role in explaining the X-ray properties of Kepler’s supernova remnant (see also Patnaude et al. 2012; Burkey et al. 2013). Recently, on the basis of a Spitzer 24μ image, Williams et al. (2014) have linked the SNR 0509-68.7 in the Large Magellanic Cloud (LMC) to pre-supernova mass loss from a possible SD system, where the companion may have been a relatively unevolved star at the time of the explosion owing to a lack of N-enhancement.
-
3)
After the supernova explosion, the explosion ejecta runs into the CSMs and interacts with them. The interacting materials may emit at radio band and X-ray (Chevalier 1990). Therefore, radio and X-ray observation may help to discriminate between different progenitor models by shedding light on the properties of the environment that was shaped by the evolution of the progenitor system since these forms of radiation are generally not expected from the DD model (Boffi & Branch 1995; Eck et al. 1995). However, see Shen et al. (2013) for a different view. Motivated by this, several dozen SNe Ia have been observed in radio (Panagia et al. 2006; Hancock et al. 2011) and in X-rays (Hughes et al. 2007; Immler et al. 2006; Russell & Immler 2012; Margutti et al. 2012). No SN Ia has been ever detected in radio and in X-rays, except perhaps for a possible detection of SN 2005ke (Immler et al. 2006, which was disputed by Hughes et al. 2007), and which seems to exclude evolved stars as the companion objects in the progenitor systems of SNe Ia, such as symbiotic systems. The progenitor model of an SNe Ia should try to explain these observations, especially for the wind accretion model from WD + RG systems.
-
4)
After the supernova explosion, the supernova ejecta may collide into the RG companion whereby the interaction may produce an excess of UV radiation (Kasen 2010). This kind of UV excess was expected in early UV observations. In any case, reporting the detection of UV excess is usually negative (Hayden et al. 2010; Tucker 2011; Bianco et al. 2011; Brown et al. 2012b; Olling et al. 2015), which seems to exclude a red supergiant companion, at least in the case of a Roche-lobe overflow. However, Ganeshalingam et al. (2011) find that there is a substantial degree of degeneracy between the adopted power-law index of the SN light-curve template, the rise time, and the amount of shock emission required to match the data, and that a conclusive result is difficult to obtain. Recently, there have been four positive reports for this kind of UV excess detection, which supports the WD + RG systems (2009ig, Foley et al. 2012b; 2011de, Brown 2014; iPTF14atg, Cao et al. 2015) and systems with massive MS companions (SN 2012cg, Marion et al. 2015) as possible progenitor systems. In addition, the early tail of the light curves of 35 high-z SNe Ia, which was found by the Supernova Cosmology Project in Goldhaber et al. (2001) definitely looks different from the lack-of-companion prediction, although the RG companions does not seem to be favored by these data (see the review by Ruiz-Lapuente 2014). However, these observations raise a question, i.e. why do so few SNe Ia definitely show signs of UV excess among the hundreds of SNe Ia? In addition to the direct impact, surely evaporated material from the RG/MS star would be heated and excited by the radioactive input from the supernova, and show up after about one year in the form of emission lines with a width of ~103 km s-1 (Marietta et al. 2000; Meng et al. 2007; Pan et al. 2012). So far, no such lines have been detected for the seven SNe Ia discussed in the literature (Mattila et al. 2005; Leonard 2007; Lundqvist et al. 2013; 2015). Based on modeling, none of these SNe seem to have been the result of a WD + RG system (see Lundqvist et al. 2015). This agrees with few cases of observed UV excess among SNe Ia.
In the above observations, Observations (1) and (2) favor WD + RG, while observation (3) disfavors them. Observation (4) brings out an interesting question which needs to be addressed by the SD model. We show in theory that actually, observations (3) and (4) are natural results in both physics and statistics.
2.2. Previous binary evolution model
Although there are some symbiotic systems with large massive WDs, it is difficult for these systems to produce SNe Ia by standard binary evolution because the mass transfer would be dynamically unstable when the RG companions fill their Roche lobe. To overcome this problem, some mechanisms were suggested. By a simple analytical method to treat binary interactions, Hachisu et al. (1999b) studied the binary evolution of WD + MS and WD + RG systems. In their study, a mass-stripping effect from an optically thick wind (OTW) was introduced. The effect may attenuate the mass-transfer rate from the companion to the WD, and was adopted by way of explaining some quasi-regular SSSs (Hachisu & Kato 2003a,b). According to these studies, Hachisu (2008b) produced a power-law DTD that follows on the Eq. (1) of Iben & Tutukov (1984), i.e. 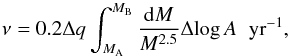 (1)where Δq, Δlog A, MA, and MB are the appropriate ranges of the initial mass ratio and separation, and the lower and upper limits of the primary mass for producing SNe Ia in units of solar masses, respectively. However, the birth rate from this equation is probably overestimated since some parameter spaces, which are considered as producing SNe Ia from this equation, may not contribute to SNe Ia. Instead of the mass-stripping effect, Chen et al. (2011) constructed a tidally-enhanced wind (TEW) model, which may effectively avoid the dynamically instable mass transfer between the WD and its RG companion, and produce SNe Ia with a very long delay time. In this paper, our method for binary evolution is similar to that in Chen et al. (2011; see also Meng & Podsiadlowski 2013).
(1)where Δq, Δlog A, MA, and MB are the appropriate ranges of the initial mass ratio and separation, and the lower and upper limits of the primary mass for producing SNe Ia in units of solar masses, respectively. However, the birth rate from this equation is probably overestimated since some parameter spaces, which are considered as producing SNe Ia from this equation, may not contribute to SNe Ia. Instead of the mass-stripping effect, Chen et al. (2011) constructed a tidally-enhanced wind (TEW) model, which may effectively avoid the dynamically instable mass transfer between the WD and its RG companion, and produce SNe Ia with a very long delay time. In this paper, our method for binary evolution is similar to that in Chen et al. (2011; see also Meng & Podsiadlowski 2013).
3. Model and method
3.1. Physical input
We use the stellar evolution code of Eggleton (1971; 1972; 1973) to calculate the binary evolutions of SD systems. The code has been updated with the latest input physics from over the last four decades (Han et al. 1994; Pols et al. 1995; 1998). Roche-lobe overflow (RLOF) is treated within the code described by Han et al. (2000). We set the ratio of mixing length to local pressure scale height, α = l/Hp, to 2.0, and set the convective overshooting parameter, δOV, to 0.12 (Pols et al. 1997; Schröder et al. 1997), which roughly corresponds to an overshooting length of 0.25HP. The solar metallicity is adopted here (Z = 0.02). The opacity table for the metallicity is compiled by Chen & Tout (2007) from Iglesias & Rogers (1996) and Alexander & Ferguson (1994).
3.2. Wind accretion
If the WD companion is a main-sequence (MS) star, the velocity of the outflow from the binary system is usually very high, in which case it would be very difficult to detect the CSM. Therefore, we only consider the case of the red-giant (RG) companion in this paper. The method that calculates binary evolution here is similar to that in Chen et al. (2011) and Meng & Podsiadlowski (2013).
We assume that the stellar wind mass-loss rate of a secondary in a binary system is increased by the presence of the WD companion star, i.e. the tidal enhancement of the mass-loss rate from the secondary which is modelled by Reimers’ (1975) formula with the extra tidal term included by Tout & Eggleton (1988) so that ![\begin{equation} \begin{array}{lc} \dot{M}_{\rm 2w}=-\,4\times 10^{\rm -13}\frac{\eta(L/L_{\odot})(R/R_{\odot})}{(M_{\rm 2}/M_{\odot})}\\ \hspace{1.05cm}\times\left[1+B_{\rm W}\min\left(\frac{1}{2},\frac{R}{R_{L}}\right)^{\rm 6}\right] M_{\odot}~{\rm yr}^{\rm -1}, \end{array} \end{equation}](/articles/aa/full_html/2016/04/aa26077-15/aa26077-15-eq21.png) (2)where L and R are the luminosity and radius of the giant secondary, RL is its Roche-lobe radius, and η is the Reimers wind coefficient, which is set at 0.25. The wind enhancement factor BW is still uncertain, where it is more than 3000 in Tout & Eggleton (1988), and is 10 000 in the wind-driven mass transfer theory of Tout & Hall (1991). Chen et al. (2011) have shown that the parameter space leading to SNe Ia increases with BW, i.e. the birth rate of SNe Ia from the WD + RG channel increases with BW. However, BW does not affect other properties of the WD + RG systems that lead to SNe Ia at the moment of supernova explosion, such as the mass-loss rate (Meng & Podsiadlowski 2013). Here, we set BW = 10 000, which means that the parameter space for SNe Ia here is an upper limit, i.e. the results here include all possibilities resulting from the uncertainties of BW, and that the mass-loss rate from the secondary could be 150 times as large as the Reimers rate, when the star nearly fills its Roche lobe.
(2)where L and R are the luminosity and radius of the giant secondary, RL is its Roche-lobe radius, and η is the Reimers wind coefficient, which is set at 0.25. The wind enhancement factor BW is still uncertain, where it is more than 3000 in Tout & Eggleton (1988), and is 10 000 in the wind-driven mass transfer theory of Tout & Hall (1991). Chen et al. (2011) have shown that the parameter space leading to SNe Ia increases with BW, i.e. the birth rate of SNe Ia from the WD + RG channel increases with BW. However, BW does not affect other properties of the WD + RG systems that lead to SNe Ia at the moment of supernova explosion, such as the mass-loss rate (Meng & Podsiadlowski 2013). Here, we set BW = 10 000, which means that the parameter space for SNe Ia here is an upper limit, i.e. the results here include all possibilities resulting from the uncertainties of BW, and that the mass-loss rate from the secondary could be 150 times as large as the Reimers rate, when the star nearly fills its Roche lobe.
Some of the material lost in the form of stellar wind from the secondary may be accreted by the WD and the mass accretion rate is expressed by Boffin & Jorissen (1988) as 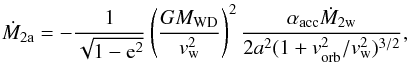 (3)where
(3)where 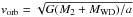 is the orbital velocity, G is Newton’s gravitational constant, a is the semi-major axis of the orbit, and e is its eccentricity. In this paper, we take e = 0. The accretion efficiency αacc is set to be 1.5. For simplicity, the wind velocity is set to be a constant (500 kms-1 in MS stage and 5kms-1 in RGB stage). Wind velocity may significantly affect the accretion rate of the WDs as well as the parameter space that leads to the SNe Ia or the birth rate of SNe Ia from the WD + RG channel. Broadly speaking, the parameter space for SNe Ia sharply decreases with the wind velocity. Here, 5kms-1 is a lower limit for the wind velocity, which means an upper limit of the parameter space that leads to SNe Ia, i.e. the results here include all possibilities resulting from the uncertainties of vw. Actually, both BW and vw are poorly known and we will discuss their effects on the results in Sect. 5.3. In Eq. (3), if a is small enough, the right-hand side could be larger than −Ṁ2w, and then we limit that Ṁ2a ≤ −Ṁ2w as did by Chen et al. (2011).
is the orbital velocity, G is Newton’s gravitational constant, a is the semi-major axis of the orbit, and e is its eccentricity. In this paper, we take e = 0. The accretion efficiency αacc is set to be 1.5. For simplicity, the wind velocity is set to be a constant (500 kms-1 in MS stage and 5kms-1 in RGB stage). Wind velocity may significantly affect the accretion rate of the WDs as well as the parameter space that leads to the SNe Ia or the birth rate of SNe Ia from the WD + RG channel. Broadly speaking, the parameter space for SNe Ia sharply decreases with the wind velocity. Here, 5kms-1 is a lower limit for the wind velocity, which means an upper limit of the parameter space that leads to SNe Ia, i.e. the results here include all possibilities resulting from the uncertainties of vw. Actually, both BW and vw are poorly known and we will discuss their effects on the results in Sect. 5.3. In Eq. (3), if a is small enough, the right-hand side could be larger than −Ṁ2w, and then we limit that Ṁ2a ≤ −Ṁ2w as did by Chen et al. (2011).
Wind accretion is the only way to transfer material from the RG secondary to the WD before Roche-lobe overflow (RLOF) begins, in which case the mass-transfer rate is Ṁtr = Ṁ2a. After RLOF occurs, the material is transferred by both a stream and by wind so that Ṁtr = Ṁ2a + | Ṁ2RLOF |, where Ṁ2RLOF is the mass-transfer rate by RLOF.
3.3. WD mass growth
We adopt the prescription of Hachisu et al. (1999a) and Hachisu et al. (2008a) on WDs accreting hydrogen-rich material from their companions (see also Han & Podsiadlowski 2004 and Meng et al. 2009). The following is a brief introduction of this prescription. If the WD accretion rate, Ṁtr, exceeds a critical value, Ṁc, we assume that a part of the accreted hydrogen burns steadily on the surface of the WD and is converted into helium at the rate of Ṁc. The unprocessed matter is assumed to be lost from the system as an optically thick wind at a rate of Ṁwind = Ṁtr − Ṁc (Hachisu et al. 1996). The critical accretion rate is 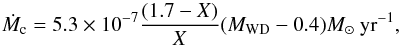 (4)where X is hydrogen mass fraction and MWD is the mass of the accreting WD (mass is in M⊙ and mass-accretion rate is in M⊙ yr-1, Hachisu et al. 1999a).
(4)where X is hydrogen mass fraction and MWD is the mass of the accreting WD (mass is in M⊙ and mass-accretion rate is in M⊙ yr-1, Hachisu et al. 1999a).
We adopt the following assumptions when Ṁtr is smaller than Ṁc. (1) When Ṁtr is higher than 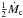 , the hydrogen-shell burning is steady and no mass is lost from the system. At this stage, the system may appear to be a supersoft X-ray source (SSS) (2) When Ṁtr is lower than
, the hydrogen-shell burning is steady and no mass is lost from the system. At this stage, the system may appear to be a supersoft X-ray source (SSS) (2) When Ṁtr is lower than 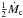 but higher than
but higher than 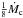 , a very weak shell flash is triggered but no mass is lost from the system. At this stage, the system may be a recurrent nova (RN) (3) When Ṁtr is lower than
, a very weak shell flash is triggered but no mass is lost from the system. At this stage, the system may be a recurrent nova (RN) (3) When Ṁtr is lower than 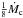 , the hydrogen-shell flash is so strong that no material is accumulated on to the surface of the CO WD. We define the growth rate of the mass of the helium layer under the hydrogen-burning shell as
, the hydrogen-shell flash is so strong that no material is accumulated on to the surface of the CO WD. We define the growth rate of the mass of the helium layer under the hydrogen-burning shell as 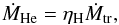 (5)where ηH is the mass-accumulation efficiency for hydrogen burning. According to the assumptions above, the values of ηH are:
(5)where ηH is the mass-accumulation efficiency for hydrogen burning. According to the assumptions above, the values of ηH are: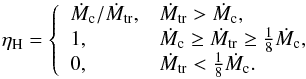 (6)Therefore, based on the prescription above, the system may experience one, two, or three of the OTW, SSSs, and RNe stages. In other words, the supernova may explode in the OTW, SSSs, or RNe stage.
(6)Therefore, based on the prescription above, the system may experience one, two, or three of the OTW, SSSs, and RNe stages. In other words, the supernova may explode in the OTW, SSSs, or RNe stage.
Helium is ignited when a certain amount of helium is accumulated. If an He flash occurs, some of the helium is blown off from the surface of the CO WD. Then, the mass growth rate of the CO WD, ṀWD, is 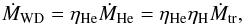 (7)where ηHe is the mass-accumulation efficiency for helium-shell flashes, and its value is taken from Kato & Hachisu (2004).
(7)where ηHe is the mass-accumulation efficiency for helium-shell flashes, and its value is taken from Kato & Hachisu (2004).
We incorporated all the above prescriptions into Eggleton’s stellar evolution code and followed the evolutions of both the mass donor and the accreting CO WD. The material that is lost as optically thick wind is assumed to take away the specific orbital angular momentum of the accreting WD, while the wind material that is not accreted by the WD is assumed to take away the specific orbital angular momentum of the donor star. For simplicity, we chosen 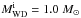 and 1.1 M⊙,
and 1.1 M⊙, 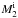 ranging from 0.8 M⊙ to 5.6 M⊙ step by 0.2 M⊙ and initial orbital period from log (Pi/ day) = 1.5 to 3.5 step by 0.1, i.e. the initial separation is from 55 R⊙ to 1100 R⊙. Generally, the parameter space leading to SNe Ia deceases with the initial WDs. Considering the maximum CO WD mass is about 1.10 M⊙ (Umeda et al. 1999; Meng et al. 2008), the possible parameter space leading to SNe Ia here is an upper limit. In addition, the aim of choosing two different initial WD masses is to show the potential dependence of the final results on the initial WD mass.
ranging from 0.8 M⊙ to 5.6 M⊙ step by 0.2 M⊙ and initial orbital period from log (Pi/ day) = 1.5 to 3.5 step by 0.1, i.e. the initial separation is from 55 R⊙ to 1100 R⊙. Generally, the parameter space leading to SNe Ia deceases with the initial WDs. Considering the maximum CO WD mass is about 1.10 M⊙ (Umeda et al. 1999; Meng et al. 2008), the possible parameter space leading to SNe Ia here is an upper limit. In addition, the aim of choosing two different initial WD masses is to show the potential dependence of the final results on the initial WD mass.
In the calculations, we assume that the WD explodes as an SN Ia when its mass reaches a value close to the Chandrasekhar mass limit, i.e., 1.378 M⊙ (Nomoto et al. 1984). According to the mass-transfer rate at that moment, the supernovae may explode in the OTW stage, or after the wind phase, where hydrogen-shell burning is stable (SSSs) or the mildly unstable stage (RNe). At the moment of supernova explosion, the companions climb along the first-giant branch (FGB)1 or the asymptotic giant branch (see Fig. 1). In Fig. 1, we show the distribution of the final state of the symbiotic systems leading to SNe Ia in a (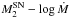 ) plane. From this figure, we can see that the distribution of the final state of the systems is clearly divided into two groups, i.e. the top one is the AGB group and the bottom one is the FGB one. Interestingly, only when the initial WD is massive enough, i.e., 1.10 M⊙, do the companions of the systems that produce SNe Ia be AGB stars, as suggested by the X-ray observation of Kepler’s supernova remnant (Chiotellis et al. 2012; see also Chen et al. 2011). In addition, the mass-loss rate from the system with the AGB companion is generally between 10-7M⊙ yr-1 and 10-6M⊙ yr-1, while it is between lower than 10-8M⊙yr-1 and 10-5M⊙yr-1 for systems with FGB companions.
) plane. From this figure, we can see that the distribution of the final state of the systems is clearly divided into two groups, i.e. the top one is the AGB group and the bottom one is the FGB one. Interestingly, only when the initial WD is massive enough, i.e., 1.10 M⊙, do the companions of the systems that produce SNe Ia be AGB stars, as suggested by the X-ray observation of Kepler’s supernova remnant (Chiotellis et al. 2012; see also Chen et al. 2011). In addition, the mass-loss rate from the system with the AGB companion is generally between 10-7M⊙ yr-1 and 10-6M⊙ yr-1, while it is between lower than 10-8M⊙yr-1 and 10-5M⊙yr-1 for systems with FGB companions.
At the moment of a supernova explosion, we record the status of the binary system, e.g. the secondary mass, 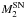 , the orbital separation, a, and the mass-loss rate from the system, and so on. In the following sections, we show how we estimate the luminosity of the X-Ray/radio (UV excess) from the interaction between supernova ejecta and CSM (companion).
, the orbital separation, a, and the mass-loss rate from the system, and so on. In the following sections, we show how we estimate the luminosity of the X-Ray/radio (UV excess) from the interaction between supernova ejecta and CSM (companion).
 |
Fig. 1 Final companion mass and mass-loss rate from the system at the moment of supernova explosion. The red and black points are from the cases of |
3.4. The method to estimate the X-Ray flux from the interaction between supernova ejecta and CSM
In our model, a large amount of material is lost from the system by the optically thick wind or the tidally enhanced wind so that CSM forms. Supernova ejecta interact with the CSM, and then X-ray emission is expected. There are two models to estimate X-ray luminosity. One is the thermal bremsstrahlung (TB) model, in which X-ray emission is expected from the heated plasma (Immler et al. 2006), the other is the inverse Compton (IC) model, in which the X-ray emission from an SNe is dominated by the scattering of photospheric optical photons from relativistic electrons that were accelerated by the SN shock on a timescale of weeks to a month after the explosion (Chevalier & Fransson 2006). Generally, the IC mechanism dominates the X-ray flux from an SN Ia exploding in a low-CSM density environment and the X-ray flux from this mechanism is very sensitive to the observed bolometric light curve of an SN Ia (see Margutti et al. 2012, in their Appendix A). The X-ray luminosity from the TB model in Immler et al. (2006) is generally consistent with that from the numerical simulation in Dimitriadis et al. (2014), i.e., from around maximum light to 150 day later after an SNe Ia explosion, although the model is very simple and some input parameters may be over- or underestimated (see Dimitriadis et al. 2014, in details). This consistency is mainly because both Immler et al. (2006) and Dimitriadis et al. (2014) only assumed emission from the reverse shock, as did also by Hughes et al. (2007). The estimated X-ray luminosity from both models with a high given mass-loss rate may be comparable with each other, but for a low mass-loss rate, the IC mechanism dominates the X-ray emission. In addition, the X-ray luminosity from the IC model decreases in much more quickly than in the TB model (see the following text and Liu et al. 2015). To account for both cases, we calculated the X-ray luminosity for both models, respectively. It should be noted here that we extrapolated the IC model in Margutti et al. (2012) to higher mass-loss rates, since Margutti et al. (2012) only dealt with single-scattering Compton events, and did not consider inverse Compton scattering on thermal electrons (see also Lundqvist & Fransson 1988), thereby limiting their analysis to low mass-loss rates.
Regardless of the mechanism that produces X-ray emission, the X-ray luminosity depends on a mass-loss rate. The measurement of the X-ray emission may be helpful in constraining the mass-loss rate, as well as the progenitor model since the CSM is generally expected from the SD model. As indicated in Sect. 2, no conclusive X-ray detections are reported, which may only provide an upper limit for mass-loss rate and seems not to uphold the symbiotic systems as one progenitor channel of SNe Ia. Based on the calculations from the TEW model here, we record the mass-loss rate at the moment of supernova explosion and use the equation from Immler et al. (2006) and Margutti et al. (2012) to calculate the X-ray luminosity. For the TB model, the X-ray luminosity is derived from 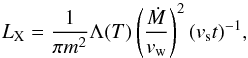 (8)where LX is the X-ray luminosity, m is the mean mass per particle of 2.1 × 10-24g for an H+He plasma with solar composition, t is the time after outburst, vs is the shock speed, which depends on the CSM density, and the density slope of supernova ejecta (Chevalier 1982a; Chomiuk et al. 2012; Pérez-Torres et al. 2014). But here for simplicity, we set it as 10 000 km s-1, with the caveat that this velocity can be much higher for a low density CSM. In addition, vw is the wind speed and Λ(T) is the cooling function:
(8)where LX is the X-ray luminosity, m is the mean mass per particle of 2.1 × 10-24g for an H+He plasma with solar composition, t is the time after outburst, vs is the shock speed, which depends on the CSM density, and the density slope of supernova ejecta (Chevalier 1982a; Chomiuk et al. 2012; Pérez-Torres et al. 2014). But here for simplicity, we set it as 10 000 km s-1, with the caveat that this velocity can be much higher for a low density CSM. In addition, vw is the wind speed and Λ(T) is the cooling function: 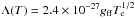 , where
, where 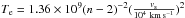 K is the electron temperature, and gff is the free-free Gaunt factor. In this scenario, n is the power index of the outer density of supernova ejecta and is set to 10 (Chevalier & Fransson 2006), and then, Te = 2.13 × 107 K. Here, we assume that the reverse shock dominates the X-ray flux as did in Immler et al. (2006), i.e., the X-ray luminosity from the reverse shock is 30 times higher than that from the forward shock, and then the total X-ray luminosity is the sum of the luminosity from both forward and reverse shocks. Here, we assume the free-free Gaunt factor to be 1 (Sutherland 1998).
K is the electron temperature, and gff is the free-free Gaunt factor. In this scenario, n is the power index of the outer density of supernova ejecta and is set to 10 (Chevalier & Fransson 2006), and then, Te = 2.13 × 107 K. Here, we assume that the reverse shock dominates the X-ray flux as did in Immler et al. (2006), i.e., the X-ray luminosity from the reverse shock is 30 times higher than that from the forward shock, and then the total X-ray luminosity is the sum of the luminosity from both forward and reverse shocks. Here, we assume the free-free Gaunt factor to be 1 (Sutherland 1998).
For the IC model, with a wind-like CSM structure, the X-ray luminosity is derived from ![\begin{equation} \begin{array}{lc} \displaystyle \frac{{\rm d}L_{\rm x}}{{\rm d}\nu}\approx2.1\times10^{\rm -4}\left(\frac{\epsilon_{\rm e}}{0.1}\right)^{\rm 2}\left(\frac{M_{\rm ej}}{1.4~M_{\odot}}\right)^{\rm -0.93}\left(\frac{A}{{\rm g}\hspace{0.05cm}{\rm cm}^{\rm -1}}\right)^{\rm 0.64}\\[2mm] \displaystyle \hspace{1cm}\times\left(\frac{E}{10^{\rm 51}~{\rm erg}}\right)^{\rm 1.29}\left(\frac{t}{\rm s}\right)^{\rm -1.36}\left(\frac{L_{\rm bol}}{{\rm erg}\hspace{0.05cm}{\rm s}^{\rm -1}}\right)\nu^{\rm -1},\label{eq:lxic} \end{array} \end{equation}](/articles/aa/full_html/2016/04/aa26077-15/aa26077-15-eq88.png) (9)where the equation is obtained by assuming that electrons are accelerated on the basis of a power-law distribution n(γ) ∝ γ− p with p = 3 (Margutti et al. 2014), and ϵe = 0.1 is the fraction of thermal energy in the shock that is used to accelerate the electrons (Chevalier & Fransson 2006), and A = Ṁ/ 4πvw. For simplicity, we set E = 1051erg and Mej = 1.4 M⊙, which are typical values for a normal SN Ia, and Lbol is set to be 1043ergs-1, a typical value at the maximum brightness epoch of a SN Ia.
(9)where the equation is obtained by assuming that electrons are accelerated on the basis of a power-law distribution n(γ) ∝ γ− p with p = 3 (Margutti et al. 2014), and ϵe = 0.1 is the fraction of thermal energy in the shock that is used to accelerate the electrons (Chevalier & Fransson 2006), and A = Ṁ/ 4πvw. For simplicity, we set E = 1051erg and Mej = 1.4 M⊙, which are typical values for a normal SN Ia, and Lbol is set to be 1043ergs-1, a typical value at the maximum brightness epoch of a SN Ia.
Compared to Eqs. (8) and (9), we can see that the TB mechanism is more sensitive to the mass-loss rate and the wind velocity, while being less sensitive to an explosion epoch than the IC model. For both models, t is set at 20 days, i.e., X-ray observations for these emissions are carried on around maximum light. We assume a spherically symmetric mass loss, which means that the lost material excavates a wind bubble around the binary system. The CSM consists of two components. One is the mass loss for the optically thick wind or helium flash from the surface of the CO WD, where the wind velocity is ~1000 kms-1 (Hachisu et al. 1996), the other is the tidally enhanced wind from the secondary surface, where the wind velocity is set as ~5 kms-1. We calculate the X-ray luminosity from these two components according to Eqs. (8) and (9), respectively, and the sum of the luminosity from the two components is taken as the final X-ray luminosity.
However, please note that there are two connotative assumptions in the above method: one is that the SNe Ia explode immediately when the MWD= 1.378M⊙, i.e., we do not consider the possible delay time of the explosion owing to the rotation of the WD. The other is that the ejecta velocity is much higher than the wind velocity. The second assumption usually holds, while the first one may significantly affect the final results and we will discuss it in Sects. 5.2 and 5.3.
3.5. The method to estimate the radio flux from the interaction between supernova ejecta and CSM
Radio radiation is also expected from the interaction between supernova ejecta and the CSM. When a shockwave plows into the CSM, it accelerates particles and amplifies the magnetic field, which produces synchrotron emission that peaks in the cm band (Chevalier 1982a; 1982b). The early synchrotron signal traces the CSM particle density, nCSM, on a radial scale of ≤1 pc, in which the region is shaped by the final stage of progenitor evolution, i.e., the final mass loss from the binary system. So, the radio luminosity is mainly determined by the mass-loss rate from the progenitor system. As a result, a measurement about the radio radiation may obtain the information about the mass-loss rate as well as the progenitor system. However, the VLA observations on some archival SNe Ia may only provide an upper limit on the radio emission as well as on the mass-loss rate (Panagia et al. 2006; Hancock et al. 2011). According to the TEW model here, we may obtain the mass-loss rate at the moment of a supernova explosion. For simplicity, we adopt the parameterized model in Panagia et al. (2006) and calculate the radio luminosity based on the equation as followings: 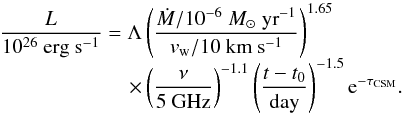 (10)Here, we set Λ = 1285 and ν = 5 GHz. t − t0 is set to be a typical value of 20 days, i.e., around maximum light (Panagia et al. 2006). Equation (10) is for the forward shock, and generally, the radio emission from the reverse shock is most likely significantly lower than that from the forward shock. We then omit the radio emission from the reverse shock and only take into account that from the forward shock, which we proceed to calculate using Eq. (10), where the forward shocked materials are from two wind components, i.e., OTW and TEW. We still assume a spherically symmetric mass loss, where the velocity of TEW, lost from the surface of the WDs, is 1000 kms-1 and the TEW velocity is 5 kms-1. We calculate the radio luminosity from these two wind components according to Eq. (10), respectively, and the sum of the luminosity from the two wind components is taken as the final radio luminosity. The external absorption depth, τCSM, depends on the shock radius and the wind temperature (Weiler 1986; Lundqvist & Fransson 1988). For simplicity, rather arbitrarily we assume that τCSM = 0, which means that the results here are the conservative upper limits (please see Eq. (10)). The connotative assumptions in Sect. 3.4 may also exist, but we do not repeat them again here.
(10)Here, we set Λ = 1285 and ν = 5 GHz. t − t0 is set to be a typical value of 20 days, i.e., around maximum light (Panagia et al. 2006). Equation (10) is for the forward shock, and generally, the radio emission from the reverse shock is most likely significantly lower than that from the forward shock. We then omit the radio emission from the reverse shock and only take into account that from the forward shock, which we proceed to calculate using Eq. (10), where the forward shocked materials are from two wind components, i.e., OTW and TEW. We still assume a spherically symmetric mass loss, where the velocity of TEW, lost from the surface of the WDs, is 1000 kms-1 and the TEW velocity is 5 kms-1. We calculate the radio luminosity from these two wind components according to Eq. (10), respectively, and the sum of the luminosity from the two wind components is taken as the final radio luminosity. The external absorption depth, τCSM, depends on the shock radius and the wind temperature (Weiler 1986; Lundqvist & Fransson 1988). For simplicity, rather arbitrarily we assume that τCSM = 0, which means that the results here are the conservative upper limits (please see Eq. (10)). The connotative assumptions in Sect. 3.4 may also exist, but we do not repeat them again here.
3.6. The method to estimate the optical/UV flux from the interaction of supernova ejecta and companion
If SNe Ia are from the SD system, then after the explosion, a large amount of material is ejected as a series of expanding shells, which impact on the surface of the companion. The leading edge of these expanding shells collides into the envelope of the companion with a velocity of VSN at t0 = a/VSN, where a is the orbital separation of the binary system at the moment of the supernova explosion. These collisions may produce an excess of optical/UV emission. The optical/UV emission may exceed the radioactively powered luminosity of the supernova for the first few days after the explosion and may reveal itself by about 10% of time (Kasen 2010). However, the detection of this kind of signature is usually negative, which constrains the companion in the SD model to be a MS star of less than 6 M⊙, and seems to disfavor an RG star undergoing RLOF (Hayden et al. 2010; Tucker 2011; Bianco et al. 2011; Brown et al. 2012b). Even taking the dependence of the luminosity on a viewing angle into consideration, Brown et al. (2012b) may only rule out the RG companion. Actually, the companion is usually less massive than 2 M⊙ (Han 2008; Hachisu et al. 2008a; Meng & Yang 2010b) at the moment of a supernova explosion. Therefore, it should be very difficult to detect the UV excess from the WD + MS channel except that the companion is as massive as 6 M⊙ (Marion et al. 2015). The most strict observational constraint is from SN 2011fe (Brown et al. 2012a), where the companion should be less massive than 1 M⊙ assuming that the companion fills its Roche lobe. Here, we use the Eq. (22)2 in Kasen (2010) to calculate the collision luminosity at three days after an explosion as followings: 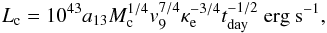 (11)where tday is the time since the explosion measured in days, and is set to be three days, which means the measurement of the UV flux began 14–17 days before the maximum luminosity of SNe Ia. κe = 0.2 cm2 g-1 and v9 = 1 is a transition velocity in units of 109 cm s-1 between inner and outer regions of supernova ejecta. Here, a13 is the orbital separation in units of 1013 cm and Mc is the mass injected into the companion in units of the Chandrasekhar mass. We set
(11)where tday is the time since the explosion measured in days, and is set to be three days, which means the measurement of the UV flux began 14–17 days before the maximum luminosity of SNe Ia. κe = 0.2 cm2 g-1 and v9 = 1 is a transition velocity in units of 109 cm s-1 between inner and outer regions of supernova ejecta. Here, a13 is the orbital separation in units of 1013 cm and Mc is the mass injected into the companion in units of the Chandrasekhar mass. We set 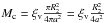 , where R2 is the secondary radius and ξv is a correction factor that depends on the ejecta velocity V and orbital separation a,
, where R2 is the secondary radius and ξv is a correction factor that depends on the ejecta velocity V and orbital separation a, 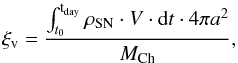 (12)where V = a/t. VSN is set to be 10 000 kms-1, which approximately corresponds to a total ejecta kinetic energy of 1 × 1051 erg s-1. Here, ρSN is the ejecta density at a distance a from the explosion center and is scaled as (Chugai 1986; Meng et al. 2007)
(12)where V = a/t. VSN is set to be 10 000 kms-1, which approximately corresponds to a total ejecta kinetic energy of 1 × 1051 erg s-1. Here, ρSN is the ejecta density at a distance a from the explosion center and is scaled as (Chugai 1986; Meng et al. 2007) 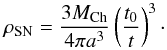 (13)Then,
(13)Then,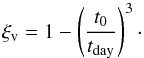 (14)Based on Eq. (14), during the first or second day after the supernova explosion, there may be no UV excess from the interaction between supernova ejecta and companion if the orbital separation is large enough. Here, we set tday = 3 days, which means that even for the largest orbital separation of a WD + RG system leading to SN Ia, the supernova ejecta may collide into the companion envelope at this time.
(14)Based on Eq. (14), during the first or second day after the supernova explosion, there may be no UV excess from the interaction between supernova ejecta and companion if the orbital separation is large enough. Here, we set tday = 3 days, which means that even for the largest orbital separation of a WD + RG system leading to SN Ia, the supernova ejecta may collide into the companion envelope at this time.
4. Results
 |
Fig. 2 X-ray luminosity on the basis of the different X-ray emission mechanisms from the interaction between supernova ejecta and CSM, as well as the total mass-loss rate from symbiotic systems at 20 days after supernova explosion. The black dotted lines are the observational constraints from Russell & Immler (2012), while the green ones are for SNe 2011fe and 2014J in Margutti et al. (2012; 2014). The green filled star and circle show the upper limit of the progenitor mass-loss rate for SNe 2011fe and 2014J, respectively, assuming a wind velocity of 1000 km s-1 and the inverse Compton mechanism dominating the X-ray flux based on the results in Margutti et al. (2012; 2014). The X-ray luminosity here is clearly divided into two sequences. The top sequence indicates that the tidally enhanced wind (TEW) dominates the mass loss, while the bottom one means that mass loss from the surface of WDs as the optically thick wind (OTW) is dominant. The red and black points are from the cases of |
4.1. X-ray emission from the interaction between supernova ejecta and CSM
The X-ray luminosity estimated from the assumptions in Sect. 3.4 is shown in Fig. 2, as well as the total mass-loss rate from the binary systems. We also plot the observational constraint from Russell & Immler (2012) and two well observed SNe Ia, 2011fe and 2014J (Margutti et al. 2012; 2014). From the figure, we can see that the maximum mass-loss rate at the moment of supernova explosion is ~10-5M⊙ yr-1, where the SNe Ia explode in the OTW stage, and the minimum mass-loss rate is even lower than ~10-8M⊙ yr-1, where the SNe Ia probably explode in the RN stage. In the figure, the X-ray luminosity is clearly divided into two sequences, no matter what the emission mechanism is. The top one indicates that the TEW dominates the mass loss, while the bottom one indicates that mass loss from the surface of WDs is dominant.
From Fig. 2, we can see that, for the TB model, the maximum X-ray luminosity may be higher than 1038 erg s-1, even higher than the upper limit from Russell & Immler (2012), while the minimum value is ~1029 erg s-1, which is much lower than those from any detection, i.e., for the TB model, almost all the SNe Ia from the WD + RG systems fulfill the conservational constraint from Russell & Immler (2012). However, for the IC model, the maximum X-ray luminosity is close to 1040 erg s-1, and the luminosity for almost all the systems is higher than 1037 erg s-1. Especially, the X-ray luminosity from all the WD + AGB models is higher than the upper limit from Russell & Immler (2012), but a large amount of WD + FGB models still fulfill this constraint. Compared with TB and IC models, for a lower mass-loss rate, the X-ray luminosity from the IC model is higher than that from the TB model by a factor of ~107, but for a higher mass-loss rate, the X-ray luminosity from the IC model is higher than that from the TB model by only a factor of dozens, i.e., the difference between the two models decreases. However, for a high mass-loss rate, the X-ray luminosity from these two models would very likely be comparable, especially regarding the material from the TEW. Therefore, the significant difference for high mass-loss rates between the two models shown in Fig. 2 implies that the IC model proposed in Margutti et al. (2012) is not suitable for direct extrapolation to high-mass loss rate, since multiple scattering and inverse Compton scattering on thermal electrons were not accounted for in the model (Lundqvist & Fransson 1988).
For the strict constraints from two well observed SNe Ia, 2011fe and 2014J, the WD + AGB systems are very likely excluded, whatever the emission mechanism is. However, for the TB model, the X-ray luminosity from many WD + FGB models fulfill the observational limit of Chandra (3.8 × 1036 erg s-1, Margutti et al. 2012), while for the IC model, the X-ray observations of 2011fe and 2014J almost ruled out all the WD + FGB models. As a result, we confirm that SN 2011fe and 2014J are unlikely to come from the WD + AGB system on the basis of their low progenitor mass-loss rate.
So, at present, it seems that the X-ray observation has the ability to rule out the WD + AGB systems as the progenitor of SNe Ia if the tidally-enhanced wind velocity is not much higher than 5 km s-1, as adopted here, and the IC mechanism dominates the X-ray emission from low-density CSM. On the other hand, the WD + FGB systems cannot be excluded completely, and a definite conclusion very much depends on the X-ray emission mechanism and on the distance of the SNe Ia. The wind velocity from MS stars is much higher than that from RG ones, which makes it difficult to detect X-ray from an SN Ia arising from the WD + MS channel. Generally, there is no CSM around a DD system before a supernova explosion, and therefore, the X-ray observation may give a meaningful constraint to the WD + RG channel if the SNe Ia are as near as SNe 2011fe and 2014J. In any case, X-ray flux is more likely to be detected from the WD + AGB system, rather than the WD + FGB system, based on the results shown in Figs. 1 and 2, since the material is more likely to be lost as the tidally enhanced wind with a low velocity for the WD + AGB system. We note that only when the initial WD mass is high enough, i.e. 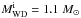 , may the WD + AGB systems be the progenitors of SNe Ia.
, may the WD + AGB systems be the progenitors of SNe Ia.
 |
Fig. 3 Radio luminosity of 5 GHz from the interaction between supernova ejecta and CSM, as well as the total mass-loss rate from the symbiotic system, 20 days after a supernova explosion. The black dotted lines are the observational constraints from Hancock et al. (2011), while the green dotted lines are for SNe 2011fe and 2014J. The data for 2011fe is the stacked EVLA radio luminosity on an averaged date of 9.1 days after explosion and an average baseband of 5.9 GHz (Chomiuk et al. 2012). The data for 2014J is from the observation of 5.5 GHz, 8.2 days after the explosion, which is the most stringent constraint among the observations in Pérez-Torres et al. (2014). The green-filled star and circle show the upper limit of the progenitor mass-loss rate for SNe 2011fe and 2014J, respectively, assuming a wind velocity of 1000 km s-1. The radio luminosity here is clearly divided into two sequences. The top sequence indicates that the tidally enhanced wind dominates the mass loss, while the bottom one means that mass loss from the surface of WDs is dominant. The red and black points are from the cases of |
4.2. Radio emission from the interaction between supernova ejecta and CSM
Figure 3 shows the radio luminosity that is estimated from the assumptions in Sect. 3.5, as well as the total mass-loss rate from the binary systems. The observational constraints from Hancock et al. (2011) and two well-observed SNe Ia, 2011fe, and 2014J (Chomiuk et al. 2012; Pérez-Torres et al. 2014) are also plotted in the figure. The results here are similar to those in Sect. 4.1. The radio luminosity is also divided into two sequences. The top one is derived from the tidally enhanced mass loss from the secondary, and the bottom one is derived from the mass loss from the surface of the CO WD by the optically thick wind or helium flash. In addition, the maximum radio luminosity is less than 1028 erg s-1 Hz-1, which is higher than the upper limit obtained from VLA observations (1.2 × 1025 erg s-1 Hz-1, Hancock et al. 2011). But almost all of them, whose radio luminosity is higher than the observational limit, are from the WD + AGB systems. Such WD + AGB systems are relatively rare according to the initial mass function, which is consistent with the non-detection results in Panagia et al. (2006) and Hancock et al. (2011). However, there is still a large parameter space fulfilling the constraint from the radio observations, which are from the WD + FGB systems. The WD + FGB systems are the dominant channel to produce SNe Ia via the symbiotic channel (see also Fig. 2 in Chen et al. 2011). Even for SN 2011fe, which is believed to be exploding in a very clean environment (Patat et al. 2013), many models still fulfill the EVLA constraints (3.2 × 1023 erg s-1 Hz-1). Although the origin of the CSM of SN 2014J is controversial (Graham et al. 2015; Soker 2015; Maeda et al. 2016), many models here also fulfill its radio constraint. So, it seems impossible for radio research to rule our WD + FGB systems as the progenitor of SNe Ia, even for SNe Ia as near as SN 2011fe and 2014J, but the radio flux may be detected by present observation apparatus if the SNe Ia are derived from the WD + AGB systems and the tidly-enhanced wind velocity is not much higher than that 5 km s-1 that is adopted here. As a result, we confirm that it it is unlikely that SNe 2011fe and 2014J are from the WD + AGB systems owing to their low radio luminosity.
 |
Fig. 4 Collision luminosity at tday = 3 days after supernova explosion from the interaction between supernova ejecta and companion, as well as the orbital separation in unit of 1013 cm. The red and black points are from the cases of |
4.3. The optical/UV flux from the interaction of supernova ejecta and companion
Following on from the descriptions in Sect. 3.6, we obtain the collision luminosity shown in Fig. 4. For most cases in the symbiotic systems considered here, the excess UV luminosity is between 1043ergs-1 and 1044ergs-1, similar to luminosity of Kasen (2010). We note, however, that we have not considered the effect of the view angle, i.e. the luminosity that results from the collision is obtained for the viewing angles looking down on the collision region (θ = 0°). However, if the companion of a SN Ia is a RG star which fills its Roche lobe, a very early observation for the SN Ia could detect the UV excess flux if the SN Ia is viewed along the collision region. In addition, the UV excess flux is not sensitive to the initial WD mass and to whether the companion is an AGB star or a FGB. So, compared with the X-ray and radio observations, the probability of detecting the UV excess flux is relatively high, which is consistent with the results that there are a few positive reports for the UV excess flux-detection while there are negative reports for the X-ray/radio detection.
5. Discussions
5.1. X-ray/radio emission
As discussed in Sects. 2, 4.1, and 4.2, the X-ray and radio observations may provide meaningful constraints on the mass-loss rate from progenitor systems, but only have an ability to rule out WD + AGB systems as the progenitor of SNe Ia for the present observation apparatus. For the SNe Ia from the WD + FGB systems, X-ray flux is generally expected if the SNe Ia are as near as SN 2011fe and 2014J, while radio emission may be difficult to detect, even if the SNe Ia are as near as SN 2011fe and 2014J.
In fact, the real physics for X-ray and radio emission may be more complex than the simple methods adopted here, such as the radio emission, as well as the X-ray emission, is sensitive to varying microphysics parameters and at which epoch a supernova is observed (Pérez-Torres et al. 2014; Margutti et al. 2012). For the simple analytic methods adopted here, two key factors mainly determine the fluxes of X-ray and radio emission. One is the mass-loss rate. For the symbiotic channel considered here, a large amount of materials are lost from the secondary before the supernova explosion, and then the mass-loss rate at the moment of a supernova explosion may not be as high as that expected from a single RG star. The other is the wind velocity. For WD + MS systems, the optically thick wind dominates the mass loss (Han & Podsiadlowski 2004; Hachisu et al. 2008a; Meng et al. 2009; Meng & Yang 2010a). The wind velocity for the optically thick wind may be as high as ~1000 km s-1, which makes it very difficult to detect the interaction between the supernova ejecta and the CSM from the optically thick wind by the radio observation. In addition, for the SD model, the WD + MS channel is the main contributor to SNe Ia, and even if the material is lost from the surface of the MS companions, instead of the surface of the WDs, the lost materials are still difficult to detect by radio observation owing to their relatively high wind velocity. Fortunately, X-ray observation could provide a powerful tool to detect such low-density CSM if the SNe Ia are near enough. For the material lost from the RG star, we note that the tidally-enhanced wind velocity adopted here is a lower limit, which could be much lower than a real value. So, the maximum luminosity of X-ray and radio emission here would represent an upper limit.
Statistically, the progenitor systems leading to SNe Ia are more likely to be RNe at the moment of supernova explosion (Meng & Yang 2011), in which the CSM structure may be shaped by a series of nova explosions. The X-ray luminosity from the interaction between the supernova ejecta and the shaped CSM is at least one order of magnitude less than that of an SN evolving in a wind bubble (Dimitriadis et al. 2014). Therefore, the X-ray luminosity from most SNe Ia could be much smaller than that shown in Russell & Immler (2012), if only the thermal X-ray emission is considered. For low CSM densities, however, this reduction could be easily offset by inverse Compton scattering.
In particular, radio emission from SN 2002ic was not detected by the VLA (Berger et al. 2003; Stockdale et al. 2003). SN 2002ic is the first SN Ia to definitely show a CSM signal (Hamuy et al. 2003), where the amount of CSM is very massive, i.e. 0.5 M⊙ ~ 6 M⊙ (Wang et al. 2004; Chugai & Yungelson 2004a; Uenishi et al. 2004; Kotak et al. 2004). Moreover, the radio emission from another twin of SN 2002ic (SN 2005gj, Aldering et al. 2006) was also not detected by the VLA (Soderberg & Frail 2005). Although the non-detection of radio flux was not completely unexpected from SN 2002ic (Chugai et al. 2004b), non-detection results from both SNe 2002ic and 2005gj could indicate that the mechanism that was successfully used for SNe Ib/c might not work for SNe Ia.
In Sects. 4.1 and 4.2, we assume that the mass loss is spherically symmetric. The real structure may be more complex than this simple structure. For example, the tidally enhanced wind concentrates near the orbital plane, while the wind from the surface of the WDs is mainly along the direction that is perpendicular to the orbital plane. As an example, three-dimensional modelling of RS Oph has shown that the CSM is expected to be concentrated in the binary orbital plane, which suggests that the probability of detecting CSM is also strongly dependent on the viewing angle (Mohamed et al. 2013). However, the complex structure may only change the X-ray/radio luminosity estimated here by a factor of 2, and the effect of the asymmetry may be partly counteracted by a relatively high shock velocity that was adopted in this paper. Therefore, the discussions here still hold, at least to first order.
In addition, based on the results in this paper and the present detection limit, the expected X-ray/radio flux detection is more likely from the WD + AGB systems, in which the initial WD mass must be massive, i.e. 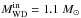 . But, compared with the WD + FGB systems, these systems are relatively rare owing to the initial mass function, which increases the difficulty to detect the X-ray/radio flux predicted from the symbiotic systems. Even for WD + FGB systems, their contribution to all SNe Ia may only be several per cent (Han & podsiadlowski 2004; Ruiter et al. 2009). Furthermore, we have not considered the possible delay time between the moment of MWD = 1.378M⊙ and supernova explosion for the rapid rotation of the accreting WDs (Justham 2011; Di Stefano et al. 2011), which may significantly clean the environment of a part of the SNe Ia.
. But, compared with the WD + FGB systems, these systems are relatively rare owing to the initial mass function, which increases the difficulty to detect the X-ray/radio flux predicted from the symbiotic systems. Even for WD + FGB systems, their contribution to all SNe Ia may only be several per cent (Han & podsiadlowski 2004; Ruiter et al. 2009). Furthermore, we have not considered the possible delay time between the moment of MWD = 1.378M⊙ and supernova explosion for the rapid rotation of the accreting WDs (Justham 2011; Di Stefano et al. 2011), which may significantly clean the environment of a part of the SNe Ia.
5.2. Optical/UV flux
As shown in Sect. 4.3, the optical/UV flux from the impact between supernova ejecta and its RG companion is very high, even higher than the radioactively powered luminosity of the supernova. Therefore, the optical/UV emission should be detected. However, the report of the detection of the UV excess was usually negative, except for SN 2009ig, 2011de, 2012cg, and iPTF14atg (Foley et al. 2012b; Brown 2014; Marion et al. 2015; Cao et al. 2015). This could be a natural result in statistics. Kasen (2010) predicted that about 10% of all SN Ia have a favourable viewing angle with strong detectable emission in the ultraviolet and B optical bands, but this does not mean that we can detect the UV excess in the light curve of about 10% of all SN Ia. In observations, the UV luminosity cannot be detected for a MS star with a mass smaller than 6 M⊙ (in which case SN 2012cg may be a wonderful candidate, Marion et al. 2015). Actually, the companion is usually less massive than 2 M⊙ at the moment of a supernova explosion (Han 2008; Hachisu et al. 2008a; Meng & Yang 2010b). The UV excess from the WD + MS channel is therefore almost undetected. For the SNe Ia from the WD + RG channel in which the RG is experiencing RLOF, even if the birth rate is very uncertain, their contribution to all SNe Ia must be lower than 1% ~ 10% (Branch et al. 1995; Meng & Yang 2010a; Wang et al. 2010). Although the parameter space for SNe Ia is enlarged for the tidally enhanced stellar wind (Chen et al. 2011), the contribution of the SNe Ia from the wind accretion symbiotic systems is still in a magnitude of a few percent (see discussion in Han & Podsiadlowski 2004). So, the 10% predicted by Kasen (2010) should be multiplied by a factor of 0.01 ~ 0.1 for SNe Ia from WD + RG channel, in which case, in about 100 ~ 1000 SNe Ia, we may have an opportunity to see the UV excess from 1 SNe Ia. Bearing in mind that, for most SNe Ia from the symbiotic systems, the luminosity obtained here could be overestimated since Eq. (11) is deduced from a RLOF assumption. As such, the number 1 in 100 ~ 1000 SNe Ia is a conservative upper limit, which is consistent with a number of detections within several hundred SNe Ia.
In addition, Justham (2011) and Di Stefano et al. (2011) have suggested that the radius of the donor star in the SD model may shrink remarkably prior to a supernova explosion for the exhaustion of its hydrogen-rich envelope owing to a long spin-down time of the rapidly rotating WD. Therefore, the cross-section of supernova ejecta would become smaller and the optical/UV luminosity could be much smaller than that from the Roche lobe model considered in Kasen (2010; see also in Hachisu et al. 2012). For example, Justham (2011) have shown that the companion radius may shrink from about 100 R⊙ to a value lower than 1 R⊙. Assuming that the angle of the oblique shock front relative to the flow direction also decreases by factor of 100, then the UV flux presented in Fig. 4 is overestimated by at least five orders of magnitude, which is much lower than that from the radioactively powered luminosity of the supernovae. However, it must be mentioned that the spin-down timescale of the WDs is quite uncertain (see discussions in Meng & Podsiadlowski 2013) and, based on the discussion in Cao et al. (2015), the radius of the companion of iPTF14atg seems not to shrink significantly, as suggested in Justham (2011). Furthermore, Ganeshalingam (2011) noticed that a substantial degree of degeneracy exists between the adopted power-law index of the SN light-curve template, the rise time, and the amount of shock emission required to match the data, which makes it very difficult to distinguish the UV excess from the UV flux of SNe Ia. The discovery of Ganeshalingam (2011) could indicate that it is very difficult to detect this type of UV flux, except that the UV excess is very significant, such as that from WD + RG systems. Moreover, Kutsuna & Shigeyama (2015) recently found that the UV flux could not be detected from the binary systems with a separation less than 2 × 1013 cm. As shown in Fig. 4, a lot of systems that lead to SNe Ia have a separation that is less than this separation limit. However, for a very large separation, the supernova ejecta may not collide into the companion within one or two days after the supernova explosion (see Eq. (14)), which is the best time to detect the UV excess (e.g. Fig. 2 in Kasen 2010). This situation reduces the opportunity to detect the UV excess further. For the discussion above, the rare report of the UV excess from the interaction between supernova ejecta and companion is a natural result in both physics and statistics, and we can expect one in several hundred SNe Ia to show this kind of UV excess in their early light curves.
 |
Fig. 5 Similar to the upper panel in Fig. 2 but for various BW and vW as shown in this figure, where |
5.3. Uncertainties
In this paper, we assume that when MWD = 1.378 M⊙, the WD explodes as an SNe Ia, and then we recorded the parameters to estimate the X-ray/radio/optical/UV flux at the moment of MWD = 1.378 M⊙. If the rapid rotation of the WD is considered, the WD may increase its mass to 2.0 M⊙ (Yoon & Langer 2004; 2005; Justham 2011; Hachisu et al. 2012) and the parameters, e.g. mass-loss rate and the companion radius, could be smaller than the value used here. Meng & Podsiadlowski (2013) estimate that the delay time from the moment of MWD = 1.378 M⊙ to the supernova explosion is less than a few 107 yr. If the delay time is as long as 107 yr, all FGB companions may have enough time to become He WDs or horizontal branch stars, and most of the AGB companions to become CO WDs. Therefore, the estimated X-ray/radio/optical/UV flux here should be taken as an upper limit.
Actually, the WD + RG channel discussed in this paper is strongly dependent on two poorly known parameters, i.e. BW and vW, which may significantly change the parameter space leading to SNe Ia (Chen et al. 2011). Here, we choose two values, e.g. BW = 1000 and vW = 10km s-1 to test their effect on the results in this paper. We only show the effect on X-ray emission based on the TB model and the discussions here are also applicable to radio/UV emissions and X-ray emission from the IC mechanism, since these discussions are not specific to the emission mechanism involved.
In Fig. 5, we show the X-ray luminosity from the TB mechanism and the total mass-loss rate from the symbiotic system for different BW and vW, where 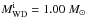 . A clear trend in the figure is that the number of models leading to SNe Ia decreases with decreasing BW and increasing vW, which is consistent with the discovery in Chen et al. (2011). It is clearly shown in the figure that the basic results here still hold no matter what BW and vW are. In addition, the maximum X-ray luminosity becomes lower for a low initial WD mass (see Fig. 2 and Panel 1 in Fig. 5). Generally, the
. A clear trend in the figure is that the number of models leading to SNe Ia decreases with decreasing BW and increasing vW, which is consistent with the discovery in Chen et al. (2011). It is clearly shown in the figure that the basic results here still hold no matter what BW and vW are. In addition, the maximum X-ray luminosity becomes lower for a low initial WD mass (see Fig. 2 and Panel 1 in Fig. 5). Generally, the 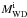 is more likely to be around 0.8 M⊙ owing to the effect of the initial mass function, although the parameter space that leads to SNe Ia for
is more likely to be around 0.8 M⊙ owing to the effect of the initial mass function, although the parameter space that leads to SNe Ia for 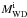 = 0.8M⊙ is much smaller than that for
= 0.8M⊙ is much smaller than that for 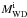 = 1.1M⊙ (Meng et al. 2009; Meng & Yang 2010a; Chen et al. 2011). As a result, for most SNe Ia, the real X-ray flux would be lower than the maximum value estimated here.
= 1.1M⊙ (Meng et al. 2009; Meng & Yang 2010a; Chen et al. 2011). As a result, for most SNe Ia, the real X-ray flux would be lower than the maximum value estimated here.
For this study, we did not carry out a binary population synthesis (BPS) study but just show a possible range for the luminosity of the X-ray/radio/UV emission from the interaction between supernova ejecta and the CSM/secondary. Since the initial mass of the CO WDs is generally less massive than 1.1 M⊙ (Umeda et al. 1999; Meng et al. 2008), e.g., generally the initial WD mass is mainly between 0.8 M⊙ and 1.0 M⊙ (Chen et al. 2011), and considering that the maximum luminosity of the X-ray/radio/optical/UV emission decreases with a reduction in the initial mass as presented in Fig. 2 and Panel 1 in Fig. 5, the luminosity range shown here is a conservative upper limit and thus the basic results obtained in this paper are reasonable.
However, we emphasise that the emission mechanisms for X-ray/radio are very complex and that the analytic methods adopted here are very simple. In fact, for IC and radio emission, there are several significant uncertainties, e.g. the ϵ parameters in Margutti et al. (2012) and Pérez-Torres et al. (2014), which may change the X-ray/radio luminosity by as much as a factor of ~10, none of which have been accounted for in our study. For example, ϵe = 0.3 in Eq. (9) is possible (Chevalier & Fransson 2006), in which case the X-ray luminosity from the TB mechanism would become comparable to that from the IC mechanism at a high Ṁ/vw value. In any case, the IC mechanism dominates the X-ray emission for low wind densities, and the X-ray luminosity will be significantly underestimated at low Ṁ/vw values when only the TB mechanism is considered. However, the IC model adopted here does not take the effects of multiple scattering and inverse Compton scattering on thermal electrons into consideration, which will become important at high Ṁ/vw. Although the ratio of thermal to non-thermal inverse Compton scattering is complicated to estimate, the situation in which the inverse Compton scattering on the thermal electrons becomes significant may be similar to that for the core-collapse SN 1993J, with only a somewhat larger contribution from the inverse Compton scattering, compared to that of thermal emission (Fransson et al. 1996). Therefore, regarding the X-ray luminosities obtained in this paper, those from the TB mechanism at the high Ṁ/vw end and those from the IC mechanism at the low Ṁ/vw end can better approximate actual observations, such as those discussed in Chevalier et al. (2006; see also Immler et al. 2007).
6. Conclusions
In summary, incorporating the effect of tidally enhanced wind on the evolution of WD binaries into Eggleton’s stellar evolution code, and also including the prescription of Hachisu et al. (1999a) for mass-accretion of CO WD, we performed a series of binary evolution calculations for WD + RG systems. Assuming that an SN Ia occurs when MWD = 1.378 M⊙, we found that the mass-loss rate at the moment of a supernova explosion is generally from a value lower than 10-8M⊙ yr-1 to 10-5M⊙ yr-1. For an SN Ia from a WD + AGB system, the mass loss is dominated by TEW, while dominated by OTW for an SN from a WD + FGB system. Based on the calculations here, we estimated the X-ray/radio (UV excess) luminosity from the interaction between supernova ejecta and CSM (secondary) using some standard published models. We found that if an SN Ia is derived from a WD + AGB system and the wind velocity is not much higher than the 5 km s-1 adopted in this paper, it may be detected by both X-ray and radio observations. For an SN Ia from a WD + FGB system, it is generally difficult to detect radio emission from the supernova since the materials lost from the system as the OTW usually move at high velocity, even for SNe Ia as near as SN 2011fe and 2014J, but X-ray observation may provide a meaningful constraint, i.e., the X-ray emission may be detected from an SNe Ia that is derived from a symbiotic system if it is near enough, in which the inverse Compton scattering dominates the X-ray emission. For the two well observed SNe Ia, 2011fe and 2014J, almost all the symbiotic systems are excluded by X-ray observations, while WD + FGB systems may not be excluded completely through radio observation. As a result, we confirm that SNe 2011fe and 2014J very unlikely arise from WD + AGB systems. The UV excess luminosity from the interaction between supernova ejecta and RG secondaries is usually comparable to the radioactively powered luminosity of the supernova for the first few days after a supernova explosion if the companion fills its Roche lobe, no matter whether the companion is an AGB star or an FGB star. However, we can only expect one among hundreds of SNe Ia to show the excess UV emission. So, the rare reporting of UV excess that is derived from the interaction between SN ejecta and companion is a natural result in both physics and statistics.
Please keep in mind that the Eq. (22) in Kasen (2010) was obtained by assuming a RLOF. The secondaries in the symbiotic systems considered here may not fill their Roche lobe and then the collision luminosity based on the Eq. (22) in Kasen (2010) could be overestimated in this paper. See discussion in Sect. 5.2.
Acknowledgments
We are very grateful to the anonymous referee for his/her constructive suggestions that greatly improved this manuscript. This work was partly supported by NSFC (11473063,11522327, 11390374, 11521303), CAS “Light of West China” Program, CAS (No. KJZD-EW-M06-01) and Key Laboratory for the Structure and Evolution of Celestial Objects, Chinese Academy of Sciences. Z.H. thanks the support by the Strategic Priority Research Program “The Emergence of Cosmological Structures” of the Chinese Academy of Sciences, Grant No. XDB09010202, and Science and Technology Innovation Talent Programme of the Yunnan Province (Grant No. 2013HA005).
References
- Aldering, G., Antilogus, P., Bailey, S., et al. 2006, ApJ, 650, 510 [NASA ADS] [CrossRef] [Google Scholar]
- Alexander, D. R., & Ferguson, J. W. 1994, ApJ, 437, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Arnett, W. D. 1982, ApJ, 253, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, E., Soderberg, A. M., & Frail, D. A. 2003, IAU Circ., 8157, 2 [NASA ADS] [Google Scholar]
- Blondin, S., Prieto, J. L., Patat, F., et al. 2009, ApJ, 693, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Bianco, F. B., Howell, D. A., Sullivan, M., et al. 2011, ApJ, 741, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Boffi, F. R., & Branch, D. 1995, PASP, 107, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Boffin, H. M. J., & Jorissen, A. 1988, A&A, 205, 155 [NASA ADS] [Google Scholar]
- Branch, D. 2004, Nature, 431, 1044 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Branch, D., Livio, M., Yungelson, L. R., et al. 1995, PASP, 107, 1019 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, P. J. 2014, ApJ, 796, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, P. J., Dawson, K. S., de Pasquale, M., et al. 2012a, ApJ, 753, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, P. J., Dawson, K. S., Harris, D. W., et al. 2012b, ApJ, 749, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Burkey, M. T., Reynolds, S. P., Borkowski, K. J., & Blondin, J. M. 2013, ApJ, 764, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Cao, Y., Kulkarni, S. R., Howell, D. A., et al. 2015, Nature, 521, 328 [NASA ADS] [CrossRef] [Google Scholar]
- Chevalier, R. A. 1982a, ApJ, 258, 790 [NASA ADS] [CrossRef] [Google Scholar]
- Chevalier, R. A. 1982b, ApJ, 259, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Chevalier, R. A. 1990, in Supernovae, ed. A. G. Petschek (New York: Springer-Verlag), 91 [Google Scholar]
- Chevalier, R. A., & Fransson, C. 2006, ApJ, 651, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Chevalier, R. A., Fransson, C. & Nymark, T. K. 2006, ApJ, 641, 1029 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, X., & Tout, C. A. 2007, ChJAA, 7, 2, 245 [Google Scholar]
- Chen, W., & Li, X. 2007, ApJ, 658, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, W., & Li, X. 2009, ApJ, 702, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, X., Han, Z., & Tout, C. A. 2011, ApJ, 735, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, X., Jeffery, C. S., Zhang, X., & Han, Z. 2012, ApJ, 775, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Chiotellis, A., Schure, K. M., & Vink, J. 2012, A&A, 537, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chomiuk, L., Soderberg, A., Moe, M., et al. 2012, ApJ, 750, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Chugai, N. N. 1986, Sov. Astron., 30, 563 [NASA ADS] [Google Scholar]
- Chugai, N. N., & Yungelson, L. R. 2004a, Astron. Lett., 30, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Chugai, N. N., Chevalier, R. A., & Lundqvist, P. 2004b, MNRAS, 355, 627 [NASA ADS] [CrossRef] [Google Scholar]
- Dimitriadis, G., Chiotellis, A., & Vink, J. 2014, MNRAS, 443, 1370 [NASA ADS] [CrossRef] [Google Scholar]
- Di Stefano, R., Voss, R., & Claeys, J. S. W. 2011, ApJ, 738, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Eck, C. R., Cowan, J. J., Roberts, D. A., et al. 1995, ApJ, 451, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Eggleton, P. P. 1971, MNRAS, 151, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Eggleton, P. P. 1972, MNRAS, 156, 361 [NASA ADS] [Google Scholar]
- Eggleton, P. P. 1973, MNRAS, 163, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Foley, R. J., Simon, J. D., Burns, C. R., et al. 2012a, ApJ, 752, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Foley, R. J., Challis, P. J., Filippenko, A. V., et al. 2012b, ApJ, 744, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Fransson, C., Lundqvist, P., & Chevalier, R. A. 1996, ApJ, 461, 993 [NASA ADS] [CrossRef] [Google Scholar]
- Ganeshalingam, M., Li, W., & Filippenko, A. V. 2011, MNRAS, 416, 2607 [NASA ADS] [CrossRef] [Google Scholar]
- Goldhaber, G., Groom, D. E., Kim, A., et al. 2001, ApJ, 558, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Graham, M. L., Valenti, S., Fulton, B. J., et al. 2015, ApJ, 801, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Hachisu, I., & Kato, M. 2001, ApJ, 558, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Hachisu, I., & Kato, M. 2003a, ApJ, 588, 1003 [NASA ADS] [CrossRef] [Google Scholar]
- Hachisu, I., & Kato, M. 2003b, ApJ, 590, 445 [NASA ADS] [CrossRef] [Google Scholar]
- Hachisu, I., Kato, M., & Nomoto, K. 1996, ApJ, 470, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Hachisu, I., Kato, M., Nomoto, K., & Umeda, H. 1999a, ApJ, 519, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Hachisu, I., Kato, M., & Nomoto, K. 1999b, ApJ, 522, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Hachisu, I., Kato, M., & Nomoto, K. 2008a, ApJ, 679, 1390 [Google Scholar]
- Hachisu, I., Kato, M., & Nomoto, K. 2008b, ApJ, 683, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Hachisu, I., Kato, M., Saio, H., & Nomoto, K. 2012, ApJ, 744, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Hamuy, M., Phillips, M. M., Suntzeff, N. B., et al. 2003, Nature, 424, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z. 1998, MNRAS, 296, 1019 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z. 2008, ApJ, 677, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z., & Podsiadlowski, Ph. 2004, MNRAS, 350, 1301 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z., & Podsiadlowski, Ph. 2006, MNRAS, 368, 1095 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z., Podsiadlowski, P., & Eggleton, P. P. 1994, MNRAS, 270, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z., Tout, C. A., & Eggleton, P. P. 2000, MNRAS, 319, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Hancock, P. P., Gaensler, B. M., & Murphy, T. 2011, ApJ, 735, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Hayden, B. T., Garnavich, P. M., Kasen, D., et al. 2010, ApJ, 722, 1691 [NASA ADS] [CrossRef] [Google Scholar]
- Hillebrandt, W., & Niemeyer, J. C. 2000, ARA&A, 38, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Howell, D. A., Conley, A., Della Valle, M., et al. 2009, ArXiv e-prints [arXiv:0903.1086] [Google Scholar]
- Hoyle, F., & Fowler, W. A. 1960, ApJ, 132, 565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hughes, J. P., Chugai, N., Chevalier, R., et al. 2007, ApJ, 670, 1260 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, I., & Tutukov, A. V. 1984, ApJS, 54, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Ilkov, M., & Soker, N. 2012, MNRAS, 419, 1695 [NASA ADS] [CrossRef] [Google Scholar]
- Immler, S., Brown, P. J., Milne, P., et al. 2006, ApJ, 648, L119 [NASA ADS] [CrossRef] [Google Scholar]
- Immler, S., Brown, P. J., Milne, P., et al. 2007, ApJ, 664, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Justham, S. 2011, ApJ, 730, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Kasen, D. 2010, ApJ, 708, 1025 [NASA ADS] [CrossRef] [Google Scholar]
- Kashi, A., & Soker, N. 2011, MNRAS, 417, 1466 [NASA ADS] [CrossRef] [Google Scholar]
- Kato, M., & Hachisu, I. 2004, ApJ, 613, L129 [NASA ADS] [CrossRef] [Google Scholar]
- Kotak, R., Meikle, W. P. S., Adamson, S., et al. 2004, MNRAS, 354, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kutsuna, M., & Shigeyama, T. 2015, PASJ, 67, 54 [NASA ADS] [Google Scholar]
- Kushnir, D., Katz, B., Dong, S., et al. 2013, ApJ, 778, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, N., Deutschmann, A., Wellstein, S., et al. 2000, A&A, 362, 1046 [NASA ADS] [Google Scholar]
- Leibundgut, B. 2000, A&ARv, 10, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Leonard, D. C. 2007, ApJ, 670, 1275 [NASA ADS] [CrossRef] [Google Scholar]
- Li, X. D., & van den Heuvel, E. P. J. 1997, A&A, 322, L9 [NASA ADS] [Google Scholar]
- Liu, Z., Moriya, T. J., Stancliffe, R. J., & Wang, B. 2015, A&A, 574, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Livio, M. 1999, in Type Ia Suppernova: Theory and Cosmology, eds. J. Truran, & T. Niemeyer (New York: Cambridge Univ. Press), 33 [Google Scholar]
- Livne, E., & Arnett, D. 1995, ApJ, 452, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Lü, G., Zhu, C., Wang, Z., & Wang, N. 2009, MNRAS, 396, 1086 [NASA ADS] [CrossRef] [Google Scholar]
- Lundqvist, P., & Fransson, C. 1988, A&A, 192, 221 [NASA ADS] [Google Scholar]
- Lundqvist, P., Mattila, S., Sollerman, J., et al. 2013, MNRAS, 435, 329 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lundqvist, P., Nyholm, A., Taddia, F., et al. 2015, A&A, 577, A39 [Google Scholar]
- Maeda, K., Tajitsu, A., Kawabata, K. S., et al. 2016, ApJ, 816, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Maguire, K., Sullivan, M., Patat, F., et al. 2013, MNRAS, 436, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Maoz, D., Mannucci, F., & Nelemans, G. 2014, ARA&A, 52, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Marietta, E., Burrows, A., & Fryxell, B. 2000, ApJS, 128, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Marion, G. H., Brown, P. J., Vinkó, J., et al. 2015, ApJ, submitted [arXiv:1507.7261] [Google Scholar]
- Margutti, R., Soderberg, A. M., Chomiuk, L., et al. 2012, ApJ, 751, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Margutti, R., Parrent, J., Kamble, A., et al. 2014, ApJ, 790, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Mattila, S., Lundqvist, P., Sollerman, J., et al. 2005, A&A, 443, 649 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meng, X., & Podsiadlowski, Ph. 2013, ApJ, 778, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Meng, X., & Yang, W. 2010a, ApJ, 710, 1310 [NASA ADS] [CrossRef] [Google Scholar]
- Meng, X., & Yang, W. 2010b, MNRAS, 401, 1118 [NASA ADS] [CrossRef] [Google Scholar]
- Meng, X., & Yang, W. 2011, Res. Astron. Astrophys., 11, 965 [NASA ADS] [CrossRef] [Google Scholar]
- Meng, X., Chen, X., & Han, Z. 2007, PASJ, 59, 835 [NASA ADS] [Google Scholar]
- Meng, X., Chen, X., & Han, Z. 2008, A&A, 487, 625 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meng, X., Chen, X., & Han, Z. 2009, MNRAS, 395, 2103 [NASA ADS] [CrossRef] [Google Scholar]
- Meng, X., Gao, Y., & Han, Z. 2015, Int. J. Mod. Phys. D, 24, 1530029 [Google Scholar]
- Mikolajewska, J. 2010, ArXiv e-prints [arXiv:1011.5657] [Google Scholar]
- Mikolajewska, J. 2012, Balt. Astron., 21, 5 [NASA ADS] [Google Scholar]
- Mohamed, S., Booth, R., & Podsiadlowski, P. 2013, in Binary Paths to Type Ia Supernovae Explosions, eds. R. Di Stefano, M. Orio, & M. Moe (Cambridge: Cambridge Univ. Press), Proc. IAU Symp., 281, 195 [Google Scholar]
- Nomoto, K., Thielemann, F.-K., & Yokoi, K. 1984, ApJ, 286, 644 [Google Scholar]
- Nomoto, K., Umeda, H., Hachisu, I., et al. 1999, in Type Ia Suppernova: Theory and Cosmology, eds. J. Truran, & T. Niemeyer (New York: Cambridge Univ. Press), 63 [Google Scholar]
- Nomoto, K., Uenishi, T., Kobayashi, C., et al. 2003, in From Twilight to Highlight: The Physics of supernova, ESO/Springer serious ESO Astrophysics Symp., eds. W. Hillebrandt, & B. Leibundgut (Berlin: Springer), 115 [Google Scholar]
- Olling, R. P., Mushotzky, R., Shaya, E. J., et al. 2015, Nature, 521, 332 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Pan, K., Ricker, P., & Taam, R. 2012, ApJ, 750, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Panagia, N., Van Dyk, S. D., Weiler, K. W., et al. 2006, ApJ, 646, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Patat, F., Chandra, P., Chevalier, R., et al. 2007, Science, 317, 924 [NASA ADS] [CrossRef] [EDP Sciences] [PubMed] [Google Scholar]
- Patat, F., Chugai, N. N., Podsiadlowski, Ph., et al. 2011, A&A, 530, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Patat, F., Cordiner, M. A., Cox, N. L. J., et al. 2013, A&A, 549, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Patnaude, D. J., Badenes, C., Park, S., & Laming, J. M. 2012, ApJ, 756, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Podsiadlowski, P. 2008, ASP Conf. Ser., 401, 63 [NASA ADS] [Google Scholar]
- Perlmutter, S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez-Torres, M., Lundqvist, P., Beswick, R., et al. 2014, ApJ, 792, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Pols, O. R., Tout, C. A., Eggleton, P. P., et al. 1995, MNRAS, 274, 964 [NASA ADS] [CrossRef] [Google Scholar]
- Pols, O. R., Tout, C. A., Schröder, K. P., et al. 1997, MNRAS, 289, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Pols, O. R., Schröder, K. P., Hurly, J. R., et al. 1998, MNRAS, 298, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Raskin, C., Timmes, F. X., Scannapieco, E., et al. 2009, MNRAS, 399, L156 [NASA ADS] [CrossRef] [Google Scholar]
- Reimers, D. 1975, Mem. Soc. Roy. Sci. Liège, 8, 369 [Google Scholar]
- Riess, A., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Ruiter, A. J., Belczynski, K., & Fryer, C. 2009, ApJ, 699, 2026 [NASA ADS] [CrossRef] [Google Scholar]
- Ruiter, A. J., Belczynski, K., Sim, S. A., et al. 2011, MNRAS, 417, 408 [NASA ADS] [CrossRef] [Google Scholar]
- Ruiz-Lapuente, P. 2014, New Astron. Rev., 62, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Russell, B. R., & Immler, S. 2012, ApJ, 748, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Schröder, K. P., Pols, O. R., & Eggleton, P. P. 1997, MNRAS, 285, 696 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, B. P., Suntzeff, N. B., Phillips, M. M., et al. 1998, ApJ, 507, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, K. J., Guillochon, J., & Foley, R. J. 2013, ApJ, 770, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, J. D., Gal-Yam, A., Gnat, O., et al. 2009, ApJ, 702, 1157 [NASA ADS] [CrossRef] [Google Scholar]
- Soderberg, A. M., & Frail, D. A. 2005, ATel, 663, 1 [NASA ADS] [Google Scholar]
- Soker, N. 2015, MNRAS, 450, 1333 [NASA ADS] [CrossRef] [Google Scholar]
- Sokoloski, J. L., Luna, G. J. M., Mukai, K., et al. 2006, Nature, 442, 276 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Stockdale, C. J., Sramek, R. A., Weiler, K. W., et al. 2003, IAU Circ., 8157, 3 [NASA ADS] [Google Scholar]
- Sternberg, A., Gal-Yam, A., Simon, J. D., et al. 2011, Science, 333, 856 [NASA ADS] [CrossRef] [Google Scholar]
- Sternberg, A., Gal-Yam, A., Simon, J. D., et al. 2014, MNRAS, 443, 1849 [NASA ADS] [CrossRef] [Google Scholar]
- Sutherland, R. S. 1998, MNRAS, 300, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Tout, C. A., & Eggleton, P. P. 1988, ApJ, 334, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Tout, C. A., & Hall, D. S. 1991, MNRAS, 253, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Tsebrenko, D., & Soker, N. 2015, MNRAS, 447, 2568 [NASA ADS] [CrossRef] [Google Scholar]
- Tucker, B. E. 2011, Ap&SS, 335, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Uenishi, T., Suzuki, T., Nomoto, K., & Hachisu, I. 2004, Rev. Mex. Astron. Astrofis., 20, 219 [Google Scholar]
- Umeda, H., Nomoto, K., Yamaoka, H., et al. 1999, ApJ, 513, 861 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, B., & Han, Z. 2012, New Astron. Rev., 56, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, L., Baade, D., Höflich, P., et al. 2004, ApJ, 604, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, B., Meng, X., Chen, X., & Han, Z. 2009a, MNRAS, 395, 847 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, B., Chen, X., Meng, X., & Han, Z. 2009b, ApJ, 701, 1540 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, B., Li, X., & Han, Z. 2010, MNRAS, 401, 2729 [NASA ADS] [CrossRef] [Google Scholar]
- Webbink, R. F. 1984, ApJ, 277, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Weiler, K. W., Sramek, R. A., Panagia, N., et al. 1986, ApJ, 301, 790 [NASA ADS] [CrossRef] [Google Scholar]
- Whelan, J., & Iben, I. 1973, ApJ, 186, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, B. J., Borkowski, K. J., Reynolds, S. P., et al. 2014, ApJ, 790, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., & Weaver, T. A. 1994, ApJ, 423, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Yoon, S.-C., & Langer, N. 2004, A&A, 419, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yoon, S.-C., & Langer, N. 2005, A&A, 435, 967 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yungelson, L., Livio, M., Tutukou, A., & Kenyon, S. J. 1995, ApJ, 447, 656 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Final companion mass and mass-loss rate from the system at the moment of supernova explosion. The red and black points are from the cases of |
| In the text | |
 |
Fig. 2 X-ray luminosity on the basis of the different X-ray emission mechanisms from the interaction between supernova ejecta and CSM, as well as the total mass-loss rate from symbiotic systems at 20 days after supernova explosion. The black dotted lines are the observational constraints from Russell & Immler (2012), while the green ones are for SNe 2011fe and 2014J in Margutti et al. (2012; 2014). The green filled star and circle show the upper limit of the progenitor mass-loss rate for SNe 2011fe and 2014J, respectively, assuming a wind velocity of 1000 km s-1 and the inverse Compton mechanism dominating the X-ray flux based on the results in Margutti et al. (2012; 2014). The X-ray luminosity here is clearly divided into two sequences. The top sequence indicates that the tidally enhanced wind (TEW) dominates the mass loss, while the bottom one means that mass loss from the surface of WDs as the optically thick wind (OTW) is dominant. The red and black points are from the cases of |
| In the text | |
 |
Fig. 3 Radio luminosity of 5 GHz from the interaction between supernova ejecta and CSM, as well as the total mass-loss rate from the symbiotic system, 20 days after a supernova explosion. The black dotted lines are the observational constraints from Hancock et al. (2011), while the green dotted lines are for SNe 2011fe and 2014J. The data for 2011fe is the stacked EVLA radio luminosity on an averaged date of 9.1 days after explosion and an average baseband of 5.9 GHz (Chomiuk et al. 2012). The data for 2014J is from the observation of 5.5 GHz, 8.2 days after the explosion, which is the most stringent constraint among the observations in Pérez-Torres et al. (2014). The green-filled star and circle show the upper limit of the progenitor mass-loss rate for SNe 2011fe and 2014J, respectively, assuming a wind velocity of 1000 km s-1. The radio luminosity here is clearly divided into two sequences. The top sequence indicates that the tidally enhanced wind dominates the mass loss, while the bottom one means that mass loss from the surface of WDs is dominant. The red and black points are from the cases of |
| In the text | |
 |
Fig. 4 Collision luminosity at tday = 3 days after supernova explosion from the interaction between supernova ejecta and companion, as well as the orbital separation in unit of 1013 cm. The red and black points are from the cases of |
| In the text | |
 |
Fig. 5 Similar to the upper panel in Fig. 2 but for various BW and vW as shown in this figure, where |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



