| Issue |
A&A
Volume 587, March 2016
|
|
|---|---|---|
| Article Number | A52 | |
| Number of page(s) | 6 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201527791 | |
| Published online | 16 February 2016 | |
Detection of multiple velocity components in partially overlapping emitting regions
1
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69,
53121
Bonn,
Germany
e-mail:
florent.mertens@gmail.com
2
Institut für Experimentalphysik, Universität
Hamburg, Luruper Chaussee
149, 22761
Hamburg,
Germany
Received: 19 November 2015
Accepted: 18 January 2016
Context. Velocity measurements made from multiple-epoch astronomical images of evolving objects with optically thin continuum emission (e.g. as relativistic jets or expanding supernova shells) may be confused as a result of the overlap of semi-transparent features moving at different speeds.
Aims. Multi-scale wavelet decomposition can be effectively applied to identify and track such overlapping features, provided that their respective structural responses can be separated over the spatial scales used for the decomposition.
Methods. We developed a new method that combines the stacked cross-correlation with the wavelet-based image segmentation and evaluation (WISE) technique of decomposition of two-dimensional structures, to separate and track dominant spatial responses of overlapping evolving features.
Results. The method is tested on a set of simulated images of a stratified relativistic jet, demonstrating the robust detection of both the faster spine and the slower sheath speeds. The method is applied to mutliple-epoch images from the MOJAVE survey, revealing two different superluminal streams inside the jet in 3C 273 and the acceleration of the flow in 3C 120.
Conclusions. The method can be applied to densely monitored objects with composite structural evolution such as the parsec-scale jet in M 87 or heavily resolved expanding supernova shells.
Key words: methods: data analysis / galaxies: jets / galaxies: individual: 3C 120 / galaxies: individual: 3C 273
© ESO, 2016
1. Introduction
Images of various astronomical objects, such as relativistic jets or supernova shells, display dynamically evolving, optically thin continuum emission, which is likely to feature partially overlapping semi-transparent emitting regions with different kinematic and structural properties. In this situation, analysis of structural evolution of the emitting material often becomes difficult and inconclusive. The ensuing ambiguity of interpretation of the structural changes can be resolved in some cases with the help of spectroscopic measurements (e.g. Guillard et al. 2012).
However, the application of spectroscopy is limited to objects with substantial line emission that can be kinematically associated with the same material that emits the continuum emission. No such association can be made in objects dominated by the continuum: for instance in objects in which the continuum is generated in a relativistic plasma. Radio emission from extragalactic jets presents a strong example of such a setting. Optically thin synchrotron emission and prominent transverse stratification of the flow are expected to be found in jets as a direct consequence of the jet formation mechanism (Sol et al. 1989; Gracia et al. 2005; Komissarov et al. 2007) or as a result of shocks (Lobanov & Zensus 1999; Lobanov et al. 2006) and instability development (Lobanov et al. 1998; Lobanov & Zensus 2001; Perucho et al. 2006; Perucho & Lobanov 2007; Perucho et al. 2012). Observational measurements of the flow stratification in relativistic jets are critically needed to understand the physical processes governing the dynamics of the emitting plasma (cf. Lobanov et al. 2003; Hardee et al. 2005; Walker et al. 2008; Mertens & Lobanov 2014).
Wavelet decomposition has been applied in a number of works to analyse the structure of extended objects in astronomical images (cf. Starck & Murtagh 2006). The wavelet-based image segmentation and evaluation (WISE) algorithm developed for determining two-dimensional velocity fields (Mertens & Lobanov 2015) can also be used to differentiate between structural components dominating at different spatial scales. The principal feasibility for WISE to detect multiple velocity components has already been demonstrated (Mertens & Lobanov 2015). In this paper, we extend this capability to partially overlapping optically thin regions, by combining the WISE approach with stacked-cross-correlation (SCC; cf. Fuhrmann et al. 2014).
The basic approach for applying SCC to the detection of multiple velocity components is introduced in Sect. 2 and tested on simulated images containing two overlapping optically thin streams. In Sect. 3, the SCC method is applied to MOJAVE data on the jets in 3C 120 and 3C 273, revealing the complexity of the kinematic parameters of these outflows. Further potential applications of the method are discussed in Sect. 4.
Throughout this paper, we adopt a cosmology of H0 = 71 km s-1 Mpc-1, ΩM = 0.27 and ΩΛ = 0.73 (Lister et al. 2013).
2. Stacked cross-correlation for detection of multiple velocity components
The WISE algorithm combines segmented wavelet decomposition (SWD) and multi-scale cross-correlation (MCC) to provide robust identification and tracking of structural patterns in astronomical images. The SWD algorithm provides a structural representation of astronomical images with exceptional sensitivity for identifying compact and marginally resolved features as well as large scale structural patterns. The SWD decomposition delivers a set of two-dimensional significant structural patterns (SSP), which are identified at each scale of the wavelet decomposition. Tracking of these SSP detected in multiple-epoch images is performed with a MCC algorithm. It combines structural information on different scales of the wavelet decomposition and provides a robust and reliable cross-identification of related SSP. Mertens & Lobanov (2015) provide a full description of the method.
Initial results of application of WISE have indicated that the method can discriminate overlapping features with different velocities (Mertens & Lobanov 2015). The successful detection of multiple velocity components has however remained challenging and prone to an increasing failure rate at low signal-to-noise ratios. This deficiency can be alleviated with the use of stacked cross-correlation.
The displacement of a single SSP can be inferred from the location of the maximum of the cross-correlation obtained for this SSP between two given epochs. In optically thin objects with complex and stratified three-dimensional structures, the resulting cross-correlation map may contain several peaks corresponding to several potential displacements. The MCC procedure resolves the potential ambiguity of interpretation of these peaks by combining the displacements found at different scales of the wavelet decomposition and determining the group motion of causally connected SSP.
A different approach can be adopted if the stratification is homogeneous over an extended region (e.g. one is dealing with two large-scale flows with different but constant velocities) and/or if several observations of the same steady stratified flow are available. In this case, it is possible to detect two or more main velocity components, corresponding to different layers of the flow consistently over an extended region and across several scales of the SWD, and the cross-correlation response of several SSP may be joined or stacked. The basic outline of the resulting stacking cross-correlation algorithm is illustrated in Fig. 1.
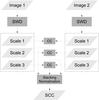 |
Fig. 1 Simplified scheme of the stacked cross-correlation (SCC) algorithm for determining multiple velocity components. The SCC combines the SSP identified at different scales of the SWD and (in case of more than two images analysed) different pairs of epochs. |
The SWD provides scale-dependent models (SDM) of the target image by identifying SSP at each wavelet scale. The SCC algorithm combines the information contained in the scale-dependent models of two images (reference and target image) in the following way:
-
1.
The SWD is used to identify sets of SSP in both images at different scales of the wavelet decomposition.
-
2.
The SSPs of the reference image are cross-correlated with the target image.
-
3.
The cross-correlation results for all SSP, all scales, and (in case of more than two images analysed) different pairs of epochs are stacked together and normalized.
This procedure yields a two-dimensional distribution of the cumulative correlation coefficients, with peaks corresponding to different velocity components. The significance and uncertainty of each of these peaks can be evaluated using Monte Carlo simulations.
2.1. Segmented wavelet decomposition
The SWD used at the first step of the SCC algorithm comprises the following steps to describe an image structure with a set of SSP (Mertens & Lobanov 2015):
-
1.
A wavelet transform is performed on an image I by decomposing the image into a set of J sub-bands (scales), wj, and estimating the residual image noise (variable across the image).
-
2.
At each sub-band, statistically significant wavelet coefficients are extracted from the decomposition by thresholding them against the image noise.
-
3.
The significant coefficients are examined for local maxima, and a subset of the local maxima satisfying composite detection criteria is identified. This subset defines the locations of SSP in the image.
-
4.
Two-dimensional boundaries of the SSP are defined by the watershed segmentation using the feature locations as initial markers.
The resulting SDM representation of an image at the scale j is derived as a group of SSP as 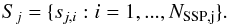 (1)The combination of all SDMs provides a structure representation that is sensitive to compact and marginally resolved features and to structural patterns that are much larger than the full width at half maximum (FWHM) of the instrumental point spread function (PSF) in the image.
(1)The combination of all SDMs provides a structure representation that is sensitive to compact and marginally resolved features and to structural patterns that are much larger than the full width at half maximum (FWHM) of the instrumental point spread function (PSF) in the image.
A well approximated estimate of the uncertainty on the SSP position can be derived following Fomalont (1999): 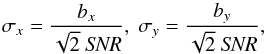 (2)where bx and by are the beam size along the x and y coordinate, respectively, assuming an elliptical PSF, which is approximately the case for application to VLBA maps, and SNR is the signal-to-noise ratio of the SSP.
(2)where bx and by are the beam size along the x and y coordinate, respectively, assuming an elliptical PSF, which is approximately the case for application to VLBA maps, and SNR is the signal-to-noise ratio of the SSP.
2.2. Stacked cross-correlation
To detect structural changes between the reference and target images, each single SSP sj,i identified on a scale j of the reference image is cross-correlated with the target image. For this purpose, a zero-mean cross-correlation, insensitive to both the image intensity offset and scale change, is used and is defined as follows (Giachetti 2000; Mertens & Lobanov 2015): 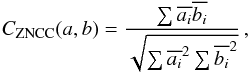 (3)where a and b the two images to cross-correlate.
(3)where a and b the two images to cross-correlate.
The cross-correlation γi,j,t between an SSP i detected at scale j of reference epoch t, and target epoch t + 1 is then written as 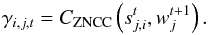 (4)In order to reduce the adverse impact of the image noise on the calculation, we consider here only prominent peaks p above a certain threshold κ (typically, 0.6−0.8) and model them as two-dimensional Gaussian shapes g(p,σ) with the width σ corresponding to the error of the displacement (typically a fraction of the beam size). Additionally, if the total set of analysed images consists of multiple epochs with inhomogeneous time intervals between the successive epochs, an additional linear transformation Vt that converts displacement to velocity needs to be applied so that all cross-correlation results can be stacked together. The resulting modified cross-correlation coefficient is then defined as
(4)In order to reduce the adverse impact of the image noise on the calculation, we consider here only prominent peaks p above a certain threshold κ (typically, 0.6−0.8) and model them as two-dimensional Gaussian shapes g(p,σ) with the width σ corresponding to the error of the displacement (typically a fraction of the beam size). Additionally, if the total set of analysed images consists of multiple epochs with inhomogeneous time intervals between the successive epochs, an additional linear transformation Vt that converts displacement to velocity needs to be applied so that all cross-correlation results can be stacked together. The resulting modified cross-correlation coefficient is then defined as 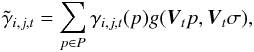 (5)where P = { p } is the group of local maxima of γi,j,t, which are above threshold κ.
(5)where P = { p } is the group of local maxima of γi,j,t, which are above threshold κ.
Finally, combining all the SSP identified at different scales of the SWD and across different epochs, we define the stack cross-correlation as 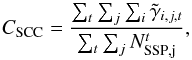 (6)where
(6)where 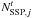 are the number of SSP identified at scale j of the SWD in the image of epoch t. The complete procedure yields a two-dimensional representation of the global correlation between all images analysed with peaks corresponding to the main displacement/velocity components.
are the number of SSP identified at scale j of the SWD in the image of epoch t. The complete procedure yields a two-dimensional representation of the global correlation between all images analysed with peaks corresponding to the main displacement/velocity components.
2.3. Significance of detected velocity components
To ensure robust identification of different velocity components, we need to determine the significance of individual maxima found using the stacked cross-correlation. If the cross-correlation is obtained from multiple epoch data, bootstrapping can be applied to determine the probability for a given correlation coefficient to result from an inadequate sampling. The bootstrapping consists of computing test SCCs for a large number of trials (typically 1000) in which the individual epochs are randomly shuffled. The confidence interval (CI) for each velocity components can then be calculated from the mean and standard deviation of the test SCCs. For the velocities corresponding to small displacements (typically, below 1/2 the beam size), the mean coefficient of the shuffled sets are overestimated and corrected CI have to be computed in this case by adding a small shift (1/5 the beam size) to the images.
2.4. Uncertainty on the velocity components
 |
Fig. 2 Stacked cross-correlation analysis of simulated images of a spine-sheath (“two-fluid”) jet with two constant velocity components (left) and a jet with random velocity field (right). For each test, a total of ten epochs are simulated. The resulting cross-correlation map is shown in greyscale in the respective top panel. The bottom panels shows the derived significance of the velocity components obtained. The significance is measured along the slice corresponding to the zero transverse speed. For the stratified spine-sheath flow on the left, the SCC successfully identifies the velocities of the two layers with a significance of ≥5σ. For the jet on the right with the random velocity field, no peak with a significance greater than 2 σ is found. |
An estimate of the uncertainty of a significant velocity component can be obtained from Monte Carlo simulations. A large number of test SCCs are again computed, this time with all the SSP randomly shifted by an amount derived from a normal distribution with a standard deviation set by the uncertainty on the SSP location (see Sect. 2.1). It should be noted that for this measure to be valid, the distribution of shifts must be Gaussian with the mean corresponding to the velocity component identified with the SCC.
2.5. Testing the SCC method
To test the performance of the SCC method, two sets of simulated images of a compact jet are prepared, following the prescription developed for testing the WISE method (Mertens & Lobanov 2015). The first set features a “two-fluid” jet with a faster inner spine and a slower outer sheath. In the second set, random velocity distribution is simulated. Images at multiple epochs are generated for each set with structural displacements introduced accordingly. The SCC is then computed for all consecutive image pairs. Examples of the resulting cross-correlation map is shown in the top panels of Fig. 2. Peaks in the map are then located by searching for local maxima. A 2D Gaussian is fitted to a small box with dimensions equal to the beam size around each local maximum found to obtain sub-pixel precision on the peak location. The significance of each peak and its associated velocity error are determined following the procedures introduced in Sects. 2.3 and 2.4.
For the two-fluid scenario, the jet is simulated with one group of features propagating with Δx1 = 5 px, Δy1 = 0 px between each pair of images, and a second group of features evolving with Δx2 = 20 px, Δy2 = 0 px between each pair of images (with x and y describing the longitudinal and transverse dimensions, respectively). Noise is added to the simulated displacements with σx = σy = 2 px or 1/5 of the beam size, which is set to 10 px in all simulated images. Thus the faster jet component moves by twice the beam size and the slower jet component moves by half the beam size between each two consecutive epochs.
A total of ten epochs is generated and SCC is computed in a region that extends over 10 beam sizes longitudinally. The SCC includes the scales 1, 2, and 3 of the SWD decomposition, producing a total of 264 SSP identified in the jet over all epochs. Results of this test are shown in the left panels of Fig. 2. The SCC velocity map obtained in simulation shows two prominent peaks at velocities corresponding to the two simulated displacements. No other peaks are found. For the first peak, a displacement of Δx1 = 4.5 ± 0.4 px and a significance of 11.4 σ is found. For the second peak, we measure Δx1 = 20.5 ± 0.8 px with a significance of 6.7 σ. As a cross check, we confirm that for both peaks the distribution of displacements found in the test SCC used to measure the uncertainties is Gaussian with mean value corresponding to the formal displacements. These results are in excellent agreement with the simulated displacements. The uncertainties of the displacement detection are improved by a factor of 3 to 4 in comparison with a similar test performed using the WISE analysis (Sect. 5.3.2 in Mertens & Lobanov 2015).
In the second simulated set, jet images are produced without any significant regular velocity component. To achieve this, we simulate a single group of features with random displacements drawn from a uniform distribution 0 px ≤ Δx ≤ 40 px and −5 px ≤ Δy ≤ 5 px between each pair of images. A similar procedure as described for the first test is then applied to determine the locations and the significance of the correlation peaks. The results are shown in the right panels of Fig. 2. No peaks are found with significance exceeding 2σ, which is compatible with the simulated random displacements. These tests demonstrate the robustness of the SCC method for identifying multiple velocity components manifested by partially overlapping regions of the flow.
3. Applications to astronomical images
After testing the SCC on simulated data, we have applied it to several image sequences obtained as part of the MOJAVE1 long-term monitoring program of extragalactic jets with Very Large Baseline Interferometry (VLBI) observations (Lister et al. 2013, and references therein). The particular focus of this analysis was made on prominent radio jets in the quasar 3C 273 and the radio galaxy 3C 120.
3.1. Stratification in the jet of 3C 273
The jet in 3C 273 is transversely resolved in the MOJAVE images. Stratification of the flow has been previously suggested for this jet (Lobanov & Zensus 2001; Perucho et al. 2006) and a large range of apparent speeds has been reported at similar core separation based on the analysis of the MOJAVE data (Lister et al. 2013; Savolainen et al. 2006).
The SCC has been performed on the entire MOJAVE data for 3C 273 comprising 69 images obtained in the 1996–2010 period. The average beam (PSF) is 0.5 mas × 1.0 mas in these images. The WISE decomposition was performed using four wavelet scales with the finest scale of 0.2 mas (scale 1, corresponding to one fifth of the beam).
The SCC results are shown in Fig. 3, indicating a systematically higher speed of βapp ~ 9 c, detected at the two larger scales (scale 3 and 4) compared to the slower apparent speed of βapp ~ 7.5 c measured at the smaller scales (scale 1 and 2). The position angle distribution of the SSP identified at the larger and smaller scales (Fig. 4) indicates that the faster moving SSP are concentrated towards the central spine of the flow, while the slower moving SSP tend to be found in the outer layers of the flow. This may be indicative of jet stratification, which results from either true transverse velocity distribution in the flow or produced by fast shocks or disturbances traveling through a slower underlying flow.
We note that the average apparent velocity of all components identified by the MOJAVE team in this source is βapp ~ 8 c (with a standard deviation of ~3 c), which is similar to the average of the large- and small-scale velocity obtained from the SCC analysis. The SCC was thus able to single out in this source the two major superluminal streams responsible for the large velocity discrepancy found by the MOJAVE team and to assign them to structure of different scales.
 |
Fig. 3 SCC analysis of the jet in 3C 273. The analysis is performed in three different regions in the jet: between 1 and 6 mas, 6 and 11 mas, 11 and 16 mas. The SSP detected at larger scales (scales 3 and 4, corresponding to 0.8 and 1.6 mas) of the SWD decomposition are found to be on average faster than SSP detected at smaller scale (scales 1 and 2, corresponding to 0.2 and 0.4 mas). |
 |
Fig. 4 Analysis of the position angle of the SSP detected in the inner 6 mas region of the jet in 3C 273 on small scales (scales 1 and 2) compared to that detected at larger scales (scales 3 and 4). The comparison indicates that the slower SSP detected on scales 1 and 2 are predominantly located in the outer part of the jet, while the faster SSP detected on scales 3 and 4 are concentrated towards the centre of the flow. |
3.2. Acceleration in the jet of 3C 120
The analysis of the jet in 3C 120 comprises the total of 87 MOJAVE images covering the period of 1996–2010. The average beam of the MOJAVE images is 0.5 mas × 1.2 mas. The SWD decomposition was performed using four wavelet scales ranging between 0.2 mas (scale 1) and 1.6 mas (scale 4). The SCC result does not reveal any statistically different velocity components, nor does comparing SCC results individually on small- and large-scale structure. Contrary to 3C 273, the jet in 3C 120 is not transversally resolved in the MOJAVE images, which limit the possibility of detecting the flow stratification. However, the high precision of the SCC measurement can be used in this case to track the evolution of the flow speed with distance from the core.
 |
Fig. 5 SCC analysis of the jet in 3C 120. The lack of transverse resolution in the MOJAVE images only warrants probing the longitudinal velocity distribution. Significant acceleration is detected up to a distance from the core of 7 mas, which is comparable to the acceleration detected from WISE analysis of the source. |
We computed the SCC individually for ten regions of the jet between a distance from the core from 0.5 mas to 10.5 mas with a bin size of 1 mas. The result of this analysis (Fig. 5) reveals a significant flow acceleration from βapp = 4.0 c ± 0.2 c at zobs = 1 mas to βapp = 6.0 c ± 0.4 c at zobs = 7 mas, followed by an apparent deceleration of the flow.
A similar analysis can be achieved using the results from the WISE analysis of the source performed in Mertens & Lobanov (2015). Apparent velocities of each component detected in this study is obtained at several distances from the core (DFC), between 1 mas and 10 mas with a step of 1 mas, via linear fitting of the component separation with time taking into account only the features 2 mas before and 2 mas after the DFC. An average apparent velocity is then obtained for each DFC. The result is over-plotted in Fig. 5 in orange, and we found it to be comparable to the result obtained from the SCC analysis, proving the robustness of this last method.
The observed apparent acceleration can be intrinsic flow acceleration or the geometrical effect of a decreasing viewing angle due for example to the jet bending. We estimate that for a Lorentz factor of 6, a decrease in viewing angle of ~15° would be required to increase the apparent speed from 4 c to 6 c. While the jet in 3C 120 is known to display a significant bending at large scales (Benson et al. 1984), only a slight jet direction changes is observed at the scale of our analysis, and we can thus discard apparent acceleration due to geometrical effects. There is also strong evidence that flow acceleration can extend to a distance of few parsec from the core (Homan et al. 2015).
Using a viewing angle of 15° (Agudo et al. 2012; Hardee et al. 2005), the evolution of the Lorentz factor with distance from the core can be described by a power-law function γ = azk with k ~ 0.3. Magnetic jet acceleration (Vlahakis 2015) or thermal/pressure induced acceleration (Georganopoulos & Marscher 1998) would require an initial linear acceleration phase with γ ∝ z for a conical jet like that in 3C 120. The acceleration profile that we observe is hence more likely the manifestation of a late-phase, slower, magnetic acceleration at which stage the Poynting flux conversion starts to saturate (Lyubarsky 2009).
4. Discussion
Stacked cross-correlation (SCC) introduced in this paper can be applied to recover multiple velocity components from partially overlapping emitting regions. The SCC extends and expands the multi-scale cross-correlation (MCC) approach originally introduced for the WISE analysis of astronomical images (Mertens & Lobanov 2015). While the MCC can partially recover overlapping displacements in different SSP identified by WISE, the SCC provides a fully statistical approach for robust identification of multiple velocity components, which also includes evaluation of statistical significance and estimation of uncertainty for each velocity component.
The SCC analysis of the transversely resolved jet in 3C 273 reveals two statistically significant velocity components corresponding to jet plasma propagating at apparent superluminal speeds of ~7.5 c and ~9 c. These two speeds may reflect the transverse stratification of the flow. They may also be explained in a framework of faster shock or plasma disturbances traveling through a slower underlying flow.
In 3C 120, the lack of transverse resolution in the MOJAVE data has limited the SCC analysis to the longitudinal dimension of the flow. In this setting, the SCC results have been found to be consistent with the kinematic properties of the flow recovered previously using the WISE analysis of the same data.
The method that we introduce can be applied to sources with composite structural evolution for which we have sufficient epochs of observation, and the criteria is the ability to obtain velocity components with statistically significant SCC coefficients. An ideal candidate for this analysis would be the sub-parsec scale of the jet in M87 for which flow stratification has already been suggested (Mertens & Lobanov 2014).
Acknowledgments
This research has made use of data from the MOJAVE database that is maintained by the MOJAVE team (Lister et al. 2009). FM was supported for this research through a stipend from the International Max Planck Research School (IMPRS) for Astronomy and Astrophysics at the Universities of Bonn and Cologne.
References
- Agudo, I., Gómez, J. L., Casadio, C., Cawthorne, T. V., & Roca-Sogorb, M. 2012, ApJ, 752, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Benson, J. M., Walker, R. C., Seielstad, G. A., & Unwin, S. C. 1984, in VLBI and Compact Radio Sources, eds. R. Fanti, K. I. Kellermann, & G. Setti, IAU Symp., 110, 125 [Google Scholar]
- Fomalont, E. B. 1999, in Synthesis Imaging in Radio Astronomy II, eds. G. B. Taylor, C. L. Carilli, & R. A. Perley, ASP Conf. Ser., 180, 301 [Google Scholar]
- Fuhrmann, L., Larsson, S., Chiang, J., et al. 2014, MNRAS, 441, 1899 [NASA ADS] [CrossRef] [Google Scholar]
- Georganopoulos, M., & Marscher, A. P. 1998, ApJ, 506, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Giachetti, A. 2000, Image and Vision Computing, 18, 247 [Google Scholar]
- Gracia, J., Tsinganos, K., & Bogovalov, S. V. 2005, A&A, 442, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guillard, P., Boulanger, F., Pineau des Forêts, G., et al. 2012, ApJ, 749, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Hardee, P. E., Walker, R. C., & Gómez, J. L. 2005, ApJ, 620, 646 [NASA ADS] [CrossRef] [Google Scholar]
- Homan, D. C., Lister, M. L., Kovalev, Y. Y., et al. 2015, ApJ, 798, 134 [Google Scholar]
- Komissarov, S. S., Barkov, M. V., Vlahakis, N., & Königl, A. 2007, MNRAS, 380, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Lister, M. L., Cohen, M. H., Homan, D. C., et al. 2009, AJ, 138, 1874 [NASA ADS] [CrossRef] [Google Scholar]
- Lister, M. L., Aller, M. F., Aller, H. D., et al. 2013, AJ, 146, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Lobanov, A. P., & Zensus, J. A. 1999, ApJ, 521, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Lobanov, A. P., & Zensus, J. A. 2001, Science, 294, 128 [Google Scholar]
- Lobanov, A. P., Krichbaum, T. P., Witzel, A., et al. 1998, A&A, 340, L60 [NASA ADS] [Google Scholar]
- Lobanov, A., Hardee, P., & Eilek, J. 2003, New A Rev., 47, 629 [Google Scholar]
- Lobanov, A. P., Krichbaum, T. P., Witzel, A., & Zensus, J. A. 2006, PASJ, 58, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Lyubarsky, Y. 2009, ApJ, 698, 1570 [NASA ADS] [CrossRef] [Google Scholar]
- Mertens, F., & Lobanov, A. 2014, in Proc. 12th European VLBI Network Symposium and Users Meeting (EVN 2014), 26 [Google Scholar]
- Mertens, F., & Lobanov, A. 2015, A&A, 574, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perucho, M., & Lobanov, A. P. 2007, A&A, 469, L23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perucho, M., Lobanov, A. P., Martí, J.-M., & Hardee, P. E. 2006, A&A, 456, 493 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perucho, M., Martí-Vidal, I., Lobanov, A. P., & Hardee, P. E. 2012, A&A, 545, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Savolainen, T., Wiik, K., Valtaoja, E., & Tornikoski, M. 2006, A&A, 446, 71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sol, H., Pelletier, G., & Asseo, E. 1989, MNRAS, 237, 411 [NASA ADS] [Google Scholar]
- Starck, J.-L., & Murtagh, F. 2006, Astronomical image and data analysis (Springer) [Google Scholar]
- Vlahakis, N. 2015, in The Formation and Disruption of Black Hole Jets, eds. I. Contopoulos, D. Gabuzda, & N. Kylafis (Springer International Publishing), Astrophys. Space Sci. Lib., 414, 177 [Google Scholar]
- Walker, R. C., Ly, C., Junor, W., & Hardee, P. J. 2008, J. Phys.: Conf. Ser., 131, 012053 [Google Scholar]
All Figures
 |
Fig. 1 Simplified scheme of the stacked cross-correlation (SCC) algorithm for determining multiple velocity components. The SCC combines the SSP identified at different scales of the SWD and (in case of more than two images analysed) different pairs of epochs. |
| In the text | |
 |
Fig. 2 Stacked cross-correlation analysis of simulated images of a spine-sheath (“two-fluid”) jet with two constant velocity components (left) and a jet with random velocity field (right). For each test, a total of ten epochs are simulated. The resulting cross-correlation map is shown in greyscale in the respective top panel. The bottom panels shows the derived significance of the velocity components obtained. The significance is measured along the slice corresponding to the zero transverse speed. For the stratified spine-sheath flow on the left, the SCC successfully identifies the velocities of the two layers with a significance of ≥5σ. For the jet on the right with the random velocity field, no peak with a significance greater than 2 σ is found. |
| In the text | |
 |
Fig. 3 SCC analysis of the jet in 3C 273. The analysis is performed in three different regions in the jet: between 1 and 6 mas, 6 and 11 mas, 11 and 16 mas. The SSP detected at larger scales (scales 3 and 4, corresponding to 0.8 and 1.6 mas) of the SWD decomposition are found to be on average faster than SSP detected at smaller scale (scales 1 and 2, corresponding to 0.2 and 0.4 mas). |
| In the text | |
 |
Fig. 4 Analysis of the position angle of the SSP detected in the inner 6 mas region of the jet in 3C 273 on small scales (scales 1 and 2) compared to that detected at larger scales (scales 3 and 4). The comparison indicates that the slower SSP detected on scales 1 and 2 are predominantly located in the outer part of the jet, while the faster SSP detected on scales 3 and 4 are concentrated towards the centre of the flow. |
| In the text | |
 |
Fig. 5 SCC analysis of the jet in 3C 120. The lack of transverse resolution in the MOJAVE images only warrants probing the longitudinal velocity distribution. Significant acceleration is detected up to a distance from the core of 7 mas, which is comparable to the acceleration detected from WISE analysis of the source. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


