| Issue |
A&A
Volume 587, March 2016
|
|
|---|---|---|
| Article Number | A13 | |
| Number of page(s) | 8 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201527636 | |
| Published online | 11 February 2016 | |
The slimming effect of advection on black-hole accretion flows
1
Institut d’Astrophysique de Paris, CNRS et Sorbonne Universités, UPMC Paris
06, UMR 7095,
98bis Bd Arago,
75014
Paris,
France
e-mail:
lasota@iap.fr
2
Nicolaus Copernicus Astronomical Center, Bartycka
18, 00-716
Warsaw,
Poland
3
Instituto de Astronomia, Geofísica e Ciências Atmosféricas,
Universidade de São Paulo, 05508-090
São Paulo, SP, Brazil
4
MIT Kavli Institute for Astrophysics and Space
Research, 77 Massachusetts
Ave, Cambridge,
MA
02139,
USA
5
Harvard-Smithsonian Center for Astrophysics, 60 Garden
St., Cambridge,
MA
02138,
USA
6
Physics Department, Gothenburg University,
412-96
Göteborg,
Sweden
Received: 24 October 2015
Accepted: 23 December 2015
Context. At super-Eddington rates accretion flows onto black holes have been described as slim (aspect ratio H/R ≲ 1) or thick (H/R> 1) discs, also known as tori or (Polish) doughnuts. The relation between the two descriptions has never been established, but it was commonly believed that at sufficiently high accretion rates slim discs inflate, becoming thick.
Aims. We wish to establish under what conditions slim accretion flows become thick.
Methods. We use analytical equations, numerical 1 + 1 schemes, and numerical radiative MHD codes to describe and compare various accretion flow models at very high accretion rates.
Results. We find that the dominant effect of advection at high accretion rates precludes slim discs becoming thick.
Conclusions. At super-Eddington rates accretion flows around black holes can always be considered slim rather than thick.
Key words: accretion, accretion disks / black hole physics
© ESO, 2016
1. Introduction
At high accretion rates discs around compact bodies cease to be thin1. When radiation provides the dominant pressure and opacities are mainly due to electron scattering, the thin-disc equations imply that the disc thickness increases linearly with the accretion rate H(R) ∝ Ṁ (Shakura & Sunyaev 1973; Frank et al. 2002), where H(R) is the disc semi-thickness at the distance R from the centre. Hence the general belief that with increasing accretion rates discs become very thick: they are tori rather than discs. Such accretion flows are supposed to be described adequately only by 2D or 3D structures, contrary to thin discs whose properties (including the observed ones) are depicted very well by a (1 + 1)D formalism.
However, this conclusion might be not self-consistent because it follows from the thin-disc equations in which H/R ≪ 1 is assumed and 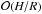 terms omitted. In particular the (proportional to the radial velocity) terms corresponding to advection are neglected. Taking these terms into account, as required for consistency, modifies the conclusions about the disc thickness at high accretion rates. This can be clearly seen in the case of advection-dominated accretion flows, known as slim discs in the optically thick case, and as ADAFs when accretion flows are optically thin.
terms omitted. In particular the (proportional to the radial velocity) terms corresponding to advection are neglected. Taking these terms into account, as required for consistency, modifies the conclusions about the disc thickness at high accretion rates. This can be clearly seen in the case of advection-dominated accretion flows, known as slim discs in the optically thick case, and as ADAFs when accretion flows are optically thin.
The disc thickness depends mainly on temperature through the speed of sound cs, since H/R ≈ cs/vK, where vK is the Keplerian velocity. Therefore the disc thickness is determined by the efficiency of the cooling mechanism. Efficiently cooled optically thick discs are geometrically thin, but for both low and high accretion rates radiative cooling might not be efficient enough to ensure the geometrical thinness of the accretion flow. At low accretion rates, optically thin, gas-pressure dominated flows cannot be assumed to be geometrically thin; the same is true of high-luminosity (close to Eddington luminosity LE = 4πGMc/κes, where M is the mass of the accreting object and κes the electron-scattering opacity coefficient), radiation-pressure dominated accretion configurations when opacity is mainly due to electron scattering. In such cases H/R ≪ 1 is no longer satisfied and the 1+1 scheme not strictly valid. One can, however, still try to use such a scheme to describe accretion flows as long as H/R ≲ 1. In this case one should take into account the 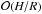 terms that are dropped in the thin-disc approximation. This means taking advection of energy and the advective terms in the momentum conservation equation into account (which in the thin-disc approximation reduces to Ω = ΩK, where Ω is the angular velocity and ΩK its Keplerian form). Begelman (1979) found that photon-trapping, related to (but not identical to) advection plays an important role in the super-Eddington regime and allows (contrary to a wide-spread prejudice) for limitless rates of accretion onto a black hole.
terms that are dropped in the thin-disc approximation. This means taking advection of energy and the advective terms in the momentum conservation equation into account (which in the thin-disc approximation reduces to Ω = ΩK, where Ω is the angular velocity and ΩK its Keplerian form). Begelman (1979) found that photon-trapping, related to (but not identical to) advection plays an important role in the super-Eddington regime and allows (contrary to a wide-spread prejudice) for limitless rates of accretion onto a black hole.
Using a non-α viscosity prescription, Ichimaru (1977) was the first to study optically thin advection-dominated accretion flows (ADAFs) which, in the framework of the α-prescription, have been investigated in Narayan & Yi (1994, 1995) and Abramowicz et al. (1995). In the case of optically thick discs, Paczyński & Bisnovatyi-Kogan (1981) were the first to solve accretion disc equations including advective terms, but they restricted themselves to the H/R ≪ 1 case. The slim (H/R ≲ 1) disc case has been addressed and solved by Abramowicz et al. (1988). In all these models a 1+1 scheme was used; only in Sa¸dowski et al. (2011), Sa¸dowski (2011), Dotan & Shaviv (2011) the vertical and radial slim-disc structures have been coupled in a “pseudo-2D” approximation (see also Abolmasov & Chashkina 2015, for a “complementary” approach).
On the other hand there exists a class of accretion flow solutions for which H/R> 1. Various versions of these models are known as accretion tori, Polish doughnuts or fat discs (see Abramowicz 2005, and references therein). Such structures are supposed to correspond to super-Eddington luminosities. Indeed, for non-selfgravitating accretion discs the effective (tidal) gravitational force at the surface must be larger than the radiative force (Abramowicz 2005): 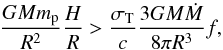 (1)where mp is the proton mass, σT the Thomson scattering cross-section, and the inner-boundary condition factor f = 1−ℓin/ℓ, where ℓ and ℓin are respectively the specific angular momentum and its value at the inner boundary. From Eq. (1) it is easy to obtain
(1)where mp is the proton mass, σT the Thomson scattering cross-section, and the inner-boundary condition factor f = 1−ℓin/ℓ, where ℓ and ℓin are respectively the specific angular momentum and its value at the inner boundary. From Eq. (1) it is easy to obtain 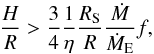 (2)where η ~ 0.1 is the gravitational efficiency, ṀE = 4πGM/ηcκes the Eddington accretion rate, κes the electron-scattering opacity, and RS = 2GM/c2 the Schwarzschild radius. Clearly, Eq. (2) implies that for super-Eddington accretion rates Ṁ>ṀE accretion flows must be “fat”, at least close to the black hole2. However, this is true only if the flow is radiatively efficient because in writing the right hand side of Eq. (1) one assumes that viscous heating is equal to radiative cooling. In advection-dominated flows this is not the case and the rhs of Eq. (1) should be multiplied by the radiative efficiency which, in the case of slim discs or ADAFs, can be much lower than one. Since at high accretion rates advection is important, this leaves open the question of how thick realistic accretion flows can be or, in other words: can one transform a slim disc into a thick disc by increasing the accretion rate?
(2)where η ~ 0.1 is the gravitational efficiency, ṀE = 4πGM/ηcκes the Eddington accretion rate, κes the electron-scattering opacity, and RS = 2GM/c2 the Schwarzschild radius. Clearly, Eq. (2) implies that for super-Eddington accretion rates Ṁ>ṀE accretion flows must be “fat”, at least close to the black hole2. However, this is true only if the flow is radiatively efficient because in writing the right hand side of Eq. (1) one assumes that viscous heating is equal to radiative cooling. In advection-dominated flows this is not the case and the rhs of Eq. (1) should be multiplied by the radiative efficiency which, in the case of slim discs or ADAFs, can be much lower than one. Since at high accretion rates advection is important, this leaves open the question of how thick realistic accretion flows can be or, in other words: can one transform a slim disc into a thick disc by increasing the accretion rate?
The aim of the present article is to answer this question by investigating how well various approximate schemes describe an accretion flow whose geometrical thinness is not a priori assumed. In Sect. 2 we use a simple analytical model to show that in (totally) advection-dominated flows the disc height is independent of the accretion rate. The same is true of ADAFs. It is different from the case of the radiation-pressure, electron-scattering dominated Shakura-Sunyaev solution in which H ~ Ṁ. In Sect. 3 we show that also for numerical slim-disc solutions with coupled vertical and radial structures, H is independent of the accretion rate. We show in Sect. 4 that the recently obtained axisymmetric global general relativistic radiation magnetohydrodynamical (GRRMHD) solutions (Sa¸dowski et al. 2015), for which no assumption about the value of H/R is made, are also radiatively inefficient at very high accretion rates and can be considered to be slim (H/R ≲ 1) discs. In Sect. 5 we discuss the relations between fat discs (Polish doughnuts) and advection dominated flows. Section 6 contains a discussion of the implications of our results and Sect. 7 our conclusions.
2. In advection-dominated accretion flows H/R is constant
It is rather straightforward to show (in the 1+1 framework) that in advection-dominated accretion flows (ADAFs and slim discs) the aspect ratio H/R at a given distance R must be constant, independent of the accretion rate. For simplicity but without loss of generality we assume that the black hole is non-rotating and use the “pseudo-Newtonian” approximation of Paczyński & Wiita (1980).
In the case of a non-rotating black hole, the vertically integrated hydrostatic equation leads to (Abramowicz et al. 1995; Lasota 2015) 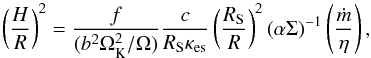 (3)where ṁ = Ṁ/ṀE, η = 1/16 is the pseudo-Newtonian efficiency of accretion. We assume a polytropic relation between the vertical profiles of p and ρ. The disc semi-thickness z = H corresponds to the location of ρ = p = 0 and b is a constant defined through
(3)where ṁ = Ṁ/ṀE, η = 1/16 is the pseudo-Newtonian efficiency of accretion. We assume a polytropic relation between the vertical profiles of p and ρ. The disc semi-thickness z = H corresponds to the location of ρ = p = 0 and b is a constant defined through 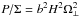 , where P is the vertically integrated pressure, Σ is the surface density, Ω⊥ is the vertical epicyclic frequency (see Eqs. (15) and (16)). For a polytropic index N = 3 one has b = 1/3. Hence hρ = bH, where
, where P is the vertically integrated pressure, Σ is the surface density, Ω⊥ is the vertical epicyclic frequency (see Eqs. (15) and (16)). For a polytropic index N = 3 one has b = 1/3. Hence hρ = bH, where 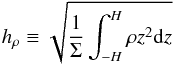 (4)is the density scale height3.
The properties of the disc thickness are then determined by the function ṁ(Σ) which, when plotted on the Σ−ṁ – plane, forms S-shaped curves representing disc thermal equilibria.
(4)is the density scale height3.
The properties of the disc thickness are then determined by the function ṁ(Σ) which, when plotted on the Σ−ṁ – plane, forms S-shaped curves representing disc thermal equilibria.
Let us assume first that the accretion flow is radiation-pressure dominated and that the opacity is solely due to electron scattering. This regime corresponds to high-rate accretion onto black holes (Shakura & Sunyaev 1973). Using the Paczyński & Wiita (1980) pseudo-Newtonian potential and the vertically integrated formalism of Sa¸dowski et al. (2011), the energy conservation equation can be written as 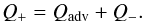 (5)In this equation
(5)In this equation 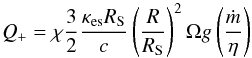 (6)is the viscous heating term (per unit surface), with χ = (cRS/Rκes)2fΩ, and g = −2/3(dlnΩ/dlnR).
(6)is the viscous heating term (per unit surface), with χ = (cRS/Rκes)2fΩ, and g = −2/3(dlnΩ/dlnR).
The first rhs term 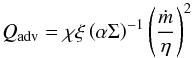 (7)represents advective “cooling”. The parameter ξ is defined through:
(7)represents advective “cooling”. The parameter ξ is defined through: 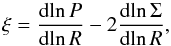 (8)where P = Pr is the vertically integrated total pressure (in our case equal to the integrated radiative pressure Pr).
(8)where P = Pr is the vertically integrated total pressure (in our case equal to the integrated radiative pressure Pr).
Q− corresponds to radiative cooling. The form of this term depends on the disc plasma microphysics. For an electron-scatterring-opacity dominated, “optically thick”4 disc it can be written as5. 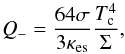 (9)(Sa¸dowski 2011, where Tc is the mid-plane temperature) which, in the radiation-pressure dominated case, becomes
(9)(Sa¸dowski 2011, where Tc is the mid-plane temperature) which, in the radiation-pressure dominated case, becomes 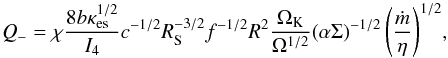 (10)where I4 = 128/315 (Sa¸dowski 2011). The energy equation takes then the form
(10)where I4 = 128/315 (Sa¸dowski 2011). The energy equation takes then the form 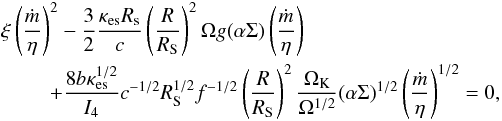 (11)which is a third order equation for ṁ1/2 in terms of Σ.
(11)which is a third order equation for ṁ1/2 in terms of Σ.
In the case of one-temperature, bremsstrahlung cooled ADAFs the analogous equation (differing only in the cooling term) is quadratic in ṁ (Eq. (5) in Abramowicz et al. 1995). (For a simple version of Eqs. (11) and the corresponding ADAF equations see Lasota 2015.)
High and low ṁ solutions of Eq. (11) correspond to advection-dominated flows:
-
slim discs at high column densities (high optical depths);
-
ADAFs at low column densities (low optical depths).
In the case of ADAFs there exists a maximum allowed rate ṁ ~ α2 above which no optically thin solution exists. On the other hand there is minimum accretion rate for the slim disc solutions (see e.g. Chen et al. 1995) below which the last two terms of Eq. (11) dominate and one obtains the (“inner-region”) Shakura-Sunyaev solution. For this solution ṁ ~ Σ-1 hence the disc thickness, H ~ ṁ, increases with accretion rate.
In advection-dominated solutions ṁ ~ Σ so from Eq. (3) H/R = const., independent of the accretion rate. Since cs ~ H this is also true for the speed of sound. (In the self-similar solutions of Narayan & Yi 1995, this corresponds to the constant 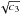 .) Therefore once they become advection-dominated, accretion flows stop inflating with increasing accretion rate.
.) Therefore once they become advection-dominated, accretion flows stop inflating with increasing accretion rate.
The black solid line in Fig. 1 shows the relative density scale height hρ/R for Keplerian discs in the Paczyński & Wiita (1980) potential, for R = 30 M (in what follows distances are expressed in geometrical units, i.e., with G = c = 1). The solution has ξ = 1, α = 0.01 and M = 10 M⊙. At the lowest accretion rates the aspect ratio hρ/R grows slowly (to the power 1/5) with ṁ: this corresponds to the lower, gas-pressure dominated Shakura-Sunyaev solutions. Then hρ/R grows almost linearly with ṁ for the (unstable) radiation-pressure dominated solutions and hρ/R ~ 0.8 on the slim-disc branch, quickly reaching a saturation value for high ṁ. This behavior does not depend on the particular radius chosen (or on the mass of the central object).
In Fig. 2 the continuous black line represents the solutions of Eq. (5) for accretion discs in which opacity is dominated by electron scattering. The two upper branches correspond to the solutions of the Eq. (11), the uppermost one corresponding to slim-disc solutions. The lowest branch is gas-pressure dominated and is not described by (11) but represents the middle-region solution of Shakura & Sunyaev. The lines represent thermal equilibria calculated using the Paczyński-Wiita potential, assuming a Keplerian flow, ξ = 1. The black hole mass is M = 10 M⊙.
 |
Fig. 1 Aspect ratio hρ/R as a function of accretion rate ṁ. Solid black line: calculated at R = 30 M for the analytical model described in Sect. 2 assuming M = 10 M⊙, ξ = 1 and α = 0.01. Markers: the corresponding aspect ratio for numerical slim disc solutions (blue diamonds, Sect. 3) and GRRMHD simulations (orange circles, Sect. 4). |
Since hρ/R depends on ξ and Ω/ΩK, models assuming them to be equal to one could be excessively simple, since e.g. as ṁ increases and advection starts to dominate (the slim-disc branch) the flow becomes sub- or super Keplerian depending on the value of α and radius. However, using numerical simulations (see below), we checked that these effects do not make much difference and the idealized model gives a pretty accurate description of the S-curves (see Fig. 2).
One can conclude therefore that a slim, advection-dominated flow never becomes thick or fat, whatever the accretion rate. The same is true of ADAFs. This is the simple consequence of the fact that since, in this approximation, all the energy gets advected, not only nothing is left to be radiated away, but also nothing is left to inflate the disc. The question is how “realistic” are such “totally advection-dominated flows” (TADAF). We study this problem in the following sections.
3. Slim discs
 |
Fig. 2 Thermal equilibrium (ṁ–Σ) diagram for slim-disc solutions at R = 30 M. Red dots: Numerical solutions from the slim-disc code (Sa¸dowski 2011). Black line: analytical S-curve, obtained from the Paczyński-Wiita potential. Both sets have M = 10 M⊙ and α = 0.01. The analytical S-curve has also ξ = 1, Ω/ΩK = 1. Green crosses: obtained from the Paczyński-Wiita potential but with the same ξ, Ω/ΩK values as the corresponding slim-disc simulations. Although the black line does deviate from the red points, we see that when the above corrections are taken into account, the analytical pseudo-Newtonian slim discs agree with the stationary, general relativistic, “1+1” simulations with great precision. |
The numerical solutions of stationary (optically thick) slim discs that we use in this work were developed in Sa¸dowski (2009, 2011) as a “1+1” approach to solve the conservation laws equations in general relativity. An a priori vertical distribution of density and pressure was assumed in order to vertically integrate the disc quantities; the resulting ordinary differential equations were then solved numerically in order to obtain the radial dependency of the physical parameters of the disc.
Details of the general relativistic model, as well as of numerical techniques, are presented in Sa¸dowski (2009, 2011). Here we present only the results for a non-rotating BH which are needed for our discussion.
The disc’s vertical structure is assumed to obey a relation p = Kρ1 + 1 /N, where p is the disc pressure, ρ is its rest-mass density, and N = 3. The vertical equilibrium equation is then written as 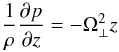 (12)and gives
(12)and gives 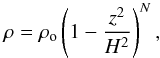 (13)where z = H determines the location of disc surface, and Ω⊥ is the vertical epicyclic frequency of geodesic motion (for zero BH spin, Ω⊥ = ΩK). The temperature profile is assumed to follow (Sa¸dowski 2011)
(13)where z = H determines the location of disc surface, and Ω⊥ is the vertical epicyclic frequency of geodesic motion (for zero BH spin, Ω⊥ = ΩK). The temperature profile is assumed to follow (Sa¸dowski 2011) 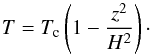 (14)The assumed polytropic “equation of state” for the vertical structure implies that the disc has a well-defined “edge” at z = H. At this height (which depends on radius), ρ = p = T = 0.
(14)The assumed polytropic “equation of state” for the vertical structure implies that the disc has a well-defined “edge” at z = H. At this height (which depends on radius), ρ = p = T = 0.
Having the vertical profiles, the slim-disc model uses vertically integrated quantities such as 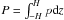 ,
, 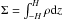 which satisfy mass, momentum, angular momentum and energy conservation laws. Vertical integration of Eq. (12) implies that P and Σ obey the vertical hydrostatic equilibrium equation
which satisfy mass, momentum, angular momentum and energy conservation laws. Vertical integration of Eq. (12) implies that P and Σ obey the vertical hydrostatic equilibrium equation 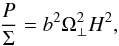 (15)with b2 = 1/(2N + 3) (Sa¸dowski 2011).
(15)with b2 = 1/(2N + 3) (Sa¸dowski 2011).
The scale height of the disc is, of course, smaller than H. A good definition of a scale height, taking into account the vertical distribution of matter and/or pressure, should give a reasonable measure of the disc thickness. We consider the density scale height hρ (Eq. (4)) as a good estimate of the scale height, since it takes into account the variance of the density distribution. It can be shown that, for the above vertical profiles, hρ = bH (independent of N), and then 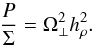 (16)
(16)
The general form of the conservation laws (in Kerr geometry) is described in Sa¸dowski (2011). For a Schwarzschild black hole we find, as expected, that local properties are well described by the Paczyński-Wiita potential in regions not too close to the black hole. In particular, the ṁ–Σ relation was recovered for different values of the radial coordinate. Figure 2 shows one of these S-curves, for a Schwarzschild black hole of mass M = 10 M⊙ and for a radius R = 30 M. The red dots correspond to numerical slim-disc solutions constructed for α = 0.01 and clearly form an S-curve, ranging from the lower (stable) gas-pressure dominated Shakura-Sunyaev branch to the (middle) Shakura-Sunyaev radiation-pressure dominated solutions and the upper slim-disc branch. Comparison with analytical Keplerian pseudo-Newtonian S-curves (with ξ = 1, black line in Fig. 2) shows reasonable agreement.
If one takes into account the non-Keplerianity of orbits and the correct values of ξ given by the simulations, calculated via 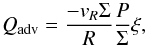 (17)one obtains solutions represented by green crosses in Fig. 2. The agreement is then almost perfect. Therefore the differences between the two approaches are not due directly to relativistic corrections, but result from the non-Keplerian character of the flow and the different values of ξ for each solution. Similar results were obtained for R = 100 M.
(17)one obtains solutions represented by green crosses in Fig. 2. The agreement is then almost perfect. Therefore the differences between the two approaches are not due directly to relativistic corrections, but result from the non-Keplerian character of the flow and the different values of ξ for each solution. Similar results were obtained for R = 100 M.
As in the case of analytical solutions the slim-disc numerical model (Abramowicz et al. 1988) predicts that the value of the relative disc scale-height hρ/R will eventually saturate with increasing ṁ. Moreover, in the pseudo-Newtonian approximation, the behavior of hρ/R as a function of R is predicted to follow 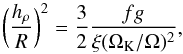 (18)obtained from Eqs. (3) and (5) in the advection-dominated branch. This expression would be exactly constant for ξ = 1 and Ω = ΩK. Figure 1 shows the behavior of hρ/R in numerical solutions of slim discs, for different values of ṁ. As expected, the disc aspect ratio saturates for the highest accretion rates. For the chosen value of α = 0.01, this plateau has hρ/R ≈ 0.7, thus characterizing a slim disc. The 1+1 numerical scheme preserves the “no inflation with accretion rate property” of slim discs.
(18)obtained from Eqs. (3) and (5) in the advection-dominated branch. This expression would be exactly constant for ξ = 1 and Ω = ΩK. Figure 1 shows the behavior of hρ/R in numerical solutions of slim discs, for different values of ṁ. As expected, the disc aspect ratio saturates for the highest accretion rates. For the chosen value of α = 0.01, this plateau has hρ/R ≈ 0.7, thus characterizing a slim disc. The 1+1 numerical scheme preserves the “no inflation with accretion rate property” of slim discs.
Since we use the density scale height to determine the disc thickness, one should be sure that the vertical hydrostatic equilibrium equation used, is an adequate representation of the action of the relativistic tidal “force” on the disc’s gas.
Gu & Lu (2007) raised doubts about the validity of the vertical equilibrium equation used in the slim disc approach but their worries had been already answered in details by Abramowicz et al. (1997). There is nothing wrong with the slim-disc vertical equilibrium equation in spherical coordinates. Cylindrical coordinates, however, introduce artificial singularities, noticed by Gu & Lu (2007), but all slim disc models in the Kerr geometry have been calculated in the spherical coordinates in which the problems discussed in their paper are absent.
4. Global radiation − MHD models
The methods discussed so far make significant assumptions about disc vertical structure and viscosity. They separate the radial and vertical dimensions. Only for very thin discs this is not constraining. To solve geometrically thick accretion flows consistently, one has to perform numerical simulations in at least 2D. It is a relatively simple task for optically thin ADAFs, for which the evolution of gas is independent of the radiative field. In case of optically thick (super-Eddington) discs, however, the radiation field must be evolved in parallel to the gas, as it significantly affects its dynamics. Initial, pioneering work (e.g. Ohsuga et al. 2005) used the Newtonian approximation but recently, numerical methods for handling radiation magnetohydrodynamics (RMHD) in general relativity have been developed and applied to global simulations of accretion discs (Fragile et al. 2014; McKinney et al. 2014; Sa¸dowski et al. 2015). In this work we use solutions for non-rotating BHs presented in Sa¸dowski et al. (2015), who performed axisymmetric, long duration simulations using a mean-field dynamo model to maintain turbulent magnetic field6. For a detailed discussion of these simulations we refer the reader to the original paper. Below we only briefly summarize their properties.
The simulations were initiated as equilibrium tori threaded by multiple loops of a weak poloidal field. The Magnetorotational Instability (MRI) quickly breaks the equilibrium and makes the gas and magnetic field turbulent. This leads to reconnections heating the gas, which in turn cools itself emitting photons. Because the simulations were axisymmetric (which allowed for high resolution and long duration), a mean-field model of the magnetic dynamo has been incorporated to prevent the magnetic field from decaying. In this model the poloidal and toroidal components are modified (conserving energy and momentum, and preserving divergence-free condition) to drive the magnetic field towards the prescribed configuration described by the mean magnetic field angle  and the magnetic to gas pressure ratio β′ = 0.1. It can be shown that the product of these quantities determines the order of magnitude of the viscosity parameter
and the magnetic to gas pressure ratio β′ = 0.1. It can be shown that the product of these quantities determines the order of magnitude of the viscosity parameter 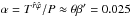 . The actual values of that parameter at radius R = 30 M are given in the fourth column of Table 1.
. The actual values of that parameter at radius R = 30 M are given in the fourth column of Table 1.
For our purposes, we consider five models from Sa¸dowski et al. (2015) that are listed in Table 1. They all exceed the critical accretion rate and span between 2.1ṀEdd and 558.8ṀEdd. We have chosen as representative R = 30 M because it is well inside the equilibrium region (outflows can be neglected) and far enough from the horizon so that the effects of disc’s puffing-up by magnetic support can be neglected (these magnetic effects cannot be represented by the slim-disc approximation). Figure 3 presents snapshots of the density for the three models with intermediate accretion rates (from top to bottom: 9.6, 24.3, and 73.1ṀEdd). It is clear that higher accretion rates imply higher densities of the gas. The disc density scale height, however, does not increase significantly, despite the order of magnitude difference in accretion rates. This fact is discussed quantitatively below.
 |
Fig. 3 Snapshots of logarithm of density for GRRMHD discs with ṁ = 9.6, 24.3, and 73.1ṀEdd. Density is given in g/cm3. |
GRRMHD models (Sa¸dowski et al. 2015).
We compare those results now with the properties of stationary slim-disc simulations (Sect. 3). These comparisons are done in two ways: by comparing the disc thickness (described by the hρ/R ratio), and by comparing locations of the solutions on the ṁ–Σ diagram. These comparisons must be qualitative, since the effective value of α varies between GRRMHD solutions (see Table 1) and is only of the same order of magnitude as α assumed for the slim discs (α = 0.01).
Figure 1 shows the density scale height for slim disc (blue diamonds) and GRRMHD solutions (orange circles). Their respective values are very close and in both cases the disc thickness saturates with accretion rate, i.e., going to highest accretion rate does not make both discs thicker. The difference in the actual values comes from the fact that the slim disc model assumes the vertical structure a priori, which does not exactly reflect the outcome of the turbulent discs. The disc thickness saturation effect is generic, independent of R.
 |
Fig. 4 Thermal equilibrium (ṁ–Σ) diagram for R = 30 M. Solutions based on different assumptions are compared. Black lines show analytical S-curves for Keplerian motion in the Paczyński-Wiita potential with ξ = 1 and α = 1;0.1;0.01;0.001 (left to right). Red dots represent stationary numerical slim discs for different accretion rates, with α = 0.01 (Sect. 3). Blue crosses correspond to GRRMHD simulations (see Table 1 and Sect. 4). All solutions have M = 10 M⊙. |
Another way to compare these two models is by means of a local ṁ–Σ diagram shown in Fig. 4 corresponding to R = 30 M, zero BH spin, and M = 10 M⊙. The previously obtained analytical S-curves (obtained from the Paczyński-Wiita potential assuming Keplerian angular velocity and ξ = 1) are shown with solid lines, and numerical slim disc solutions with red points. The GRRMHD solutions discussed in this section are denoted by blue crosses and show proportionality between the accretion rate and local surface density, which is a characteristic feature of the top, advection-dominated branch (see Sect. 2). What is more, these points lie almost on top of the slim disc solutions (red dots). This (almost) exact correspondence is, to some extent, a coincidence because the effective viscosity parameters in the two-dimensional, GRRMHD simulations are not exactly equal to the value assumed in the slim disc solutions (α = 0.01).
However, since α does not vary much (it is consistent to a factor of 4), it is fair to say that GRRMHD solutions belong to the same advection-dominated, slim disc branch. This is confirmed by the fact that for both models, the disc thickness saturates with accretion rate.
This agreement between the turbulent discs and the simplified model of slim discs is not unexpected. Numerical solutions show significant photon trapping inside the disc, which effectively cools the disc by advection. They also show outflows which, for non-rotating BHs, start only from outside radii R ≳ 30 (Sa¸dowski et al. 2015; Sadowski et al. 2016), and which are not accounted for in the slim disc model. Similarly to photon trapping, one may consider the outflowing gas as another way of cooling the disc. Both factors make numerical solutions radiatively inefficient.
It should be stressed that the relation between the hydrostatic shape of the disc and the transfer of radiation is not straightforward. In all GRRMHD models, hρ is well inside the disc’s photosphere, but for ṁ = 24.3 the base of the optically thin funnel is already far from the black hole at z = 1000 M. For accretion rates ṁ = 73.1 and ṁ = 558.8, the whole domain out to Rmax = 5000 M is optically thick at all θ, so that these two models have no optically thin funnel within the simulation box (Sa¸dowski et al. 2015)7.
5. Polish doughnuts
Polish doughnut (PD), also known as “thick accretion disc”, is a term describing a model of axisymmetric, stationary accretion structure around a black hole, developed in the early days of accretion astrophysics by the Warsaw group around Bohdan Paczyński (Abramowicz et al. 1978; Paczyński & Wiita 1980; Jaroszyński et al. 1980; see also Fishbone & Moncrief 1976)8. PDs are defined basically by the following three properties:
-
1.
These optically thick structures radiate locally at the Eddington rate, i.e., the local effective gravity at the photosphere is balanced by the radiation pressure exerted by radiative flux from the photosphere.
-
2.
The shape H(R) of a PD resembles a huge spheroid with long and narrow funnels along the rotation axis. Narrow funnels can collimate radiation to super-Eddington luminosities (λ ≡ L/LEdd> 10), as was realized long ago by Sikora (1981) and Abramowicz & Piran (1980; see Sa¸dowski & Narayan 2015, for numerical verification). They are presently of interest for modelling ULXs, (ultra-luminous X-ray sources, e.g. King 2009; King & Lasota 2014; Lasota et al. 2015). In such funnels, the relative vertical thickness of a PD must be necessarily large, χ ≡ (H/R)max ≫ 1 and large PD’s thickness is thus unavoidable.
-
3.
All the observable properties of a PD are derived from a single ad hoc assumed function, ℓ = ℓ(R): the specific angular momentum distribution at the PD’s photosphere. The specific angular momentum is assumed to be Keplerian, ℓ(Rin) = ℓK(Rin), at the inner PD edge Rin located between the ISCO and IBCO9, which implies a saddle point in the equipressure surfaces there (a cusp). This forces the angular momentum to be Keplerian also at the PD’s “centre” corresponding to the pressure maximum. From the assumed ℓ(R) one calculates the PD shape H(R), the flux of radiation at the surface f(R), the total luminosity L = ∫f·dS and finally the accretion rate is deduced from the luminosity: Ṁ = L/ (c2η), where η = η(Rin) is the radiative accretion efficiency. All these are given in terms of analytic (algebraic) formulae. No physical properties of the PD interior need to be considered. Indeed, one must stress that the PD models do not assume anything specific about their interiors, not even about the equation of state, p = p(ρ,T). In particular, the pressure (gas and radiation) p, the density ρ, the temperature T and the (non-azimuthal) velocity v do not appear in the model.
In the PD models it was assumed that H(R) corresponds to the photosphere location, however, as checked by Abramowicz et al. (1983), this in general is not the case. Therefore, as in the case of GRRMHD simulations discussed above, but for different reasons, the relation between the shape of the accretion flow and the radiation transfer is not straightforward.
The PD formalism has the advantage of allowing constructing thick disc models without having to deal with the largely unknown (especially when they were devised) physics of their interiors. This advantage turns into a drawback when physical processes in accretion flows are better understood and numerical models representing structures analogous to PDs become available. For example, the strength of advective cooling in a PD cannot be calculated from properties 1–3 above and no previously calculated analytic models of PDs contained advection. Although numerical models reproduce many properties of analytic PDs (e.g. De Villiers & Hawley 2003; Qian et al. 2009), as noticed by Abramowicz & Fragile (2013) pressure gradients in PDs are shallower than those in the corresponding numerical simulations. This should mean that numerical models including advection are thinner than analytical PD models with no advection. To test this conclusion Wielgus et al. (2015) generalized the PD formalism by including an advection-cooling parameter 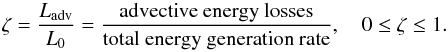 (19)The accretion rate is then obtained from
(19)The accretion rate is then obtained from 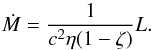 (20)
(20)
The relative thickness of these generalized, advective PDs is plotted in Fig. 6 which shows the slimming effects of advection on Polish doughnuts.
A toy model by Paczyński (1998) illustrates the properties of an extreme PD. In this model no energy is advected because all of it is used to inflate the disc through the pdV work (see also Abramowicz et al. 2000)10. Since the pdV work appears in the advective term of the energy conservation equation, Paczyński called his solution “advection-dominated” because radiative cooling was put strictly equal to zero, but obviously advective-cooling is also equal to zero (ζ = 0). There is also no outflow of matter. Although of great heuristic interest, it is unlikely that Paczyński’s toy-model can represent any realistic accretion flow since it requires the angular momentum to be almost constant and strongly sub-Keplerian everywhere except near the outer edge, where it rapidly joins the local Keplerian value. For example, numerical simulations show that whenever efficient MRI viscosity appears in a constant angular-momentum accretion flow, the angular momentum very quickly relaxes to Keplerian (see, e.g., Hawley 2000).
A new version of PDs was recently proposed by Coughlin & Begelman (2014) who considered low angular–momentum super-Eddington accretion flow appearing during so-called tidal disruption events (TDEs), when stars are captured by a supermassive black hole in a galactic centre. As in the case of Paczyński’s toy model, the accretion energy inflates the flow into a weakly bound, quasi-spherical structure. When the flow is maximally inflated, it escapes in form of powerful jets. Also in these ZEBRA (zero Bernoulli accretion) flows the angular momentum distribution must have a specific non-Keplerian form. It still not clear if and how ZEBRAs form and what is their evolution and therefore it is too early to decide if their thickness can be reduced by advection.
6. Discussion
Since the inner (R ≲ 30 M) regions of super-Eddington accretion flows onto black holes are likely to always be advection-dominated (cf. Sadowski et al. 2016), the very narrow funnels, that are supposed to produce strong radiation beaming near the black hole, most probably do not exist in actually observed accreting systems. Nevertheless such strong beaming might be necessary to explain X-ray sources such as SS 433 (Begelman et al. 2006) and ULXs (King 2009; King & Lasota 2014; Lasota et al. 2015) if they are radiating at super-Eddington luminosities. Strong radiation beaming is certainly necessary to explain the confirmed super-Eddington luminosity of the neutron-star ULX-2 in the galaxy M82 (Kluźniak & Lasota 2015; King & Lasota 2016). It might also be the case of the ultraluminous supersoft source ULS-1 in M81 (Liu et al. 2015). However, as mentioned above, we do not know how radiation is emitted from very (ṁ ≳ 30) super-Eddington accretion flows, since in this case the emitting surface is located outside the computational grid. One can only speculate that the beaming is determined by the vertical size of the outflow at the so-called spherization radius R ~ 7ṁM (Shakura & Sunyaev 1973), in other words by the “walls” formed by the outflows, as suggested by King (2008).
 |
Fig. 5 Effect of advection on the thickness of PDs. The maximum value of the relative height of a PD and the accretion rate are shown on the vertical and horizontal axes, respectively. (From Wielgus et al. 2015.) |
7. Conclusions
Since the seminal Shakura & Sunyaev (1973) paper various approaches have been used to describe accretion flows for which the geometrical thinness (H/R ≪ 1) cannot be assumed. With respect to geometrical thickness the resulting models could be divided into two classes: “slim” (H/R ≲ 1; this class also includes optically thin ADAFs) and “thick” (H/R> 1) but the relation between the two was not clear. It was implicitly assumed that by increasing the accretion rate slim discs will inflate to become thick. However, this could not be right because the thickness of slim discs is independent of the accretion rate. Slim discs never become thick. In obtaining this conclusion one assumes that accretion flows are stationary and driven by local viscosity. It might not apply to flows forming in TDEs (see e.g., Coughlin & Begelman 2014; Shiokawa et al. 2015) or to some flows that are dominated by large-scale magnetic fields such as ion-tori of Rees et al. (1982)11. But it seems that standard accretion discs are never obese. Whatever the accretion rate.
For very low accretion rates, Rees et al. (1982) suggested the existence of optically-thin, radiatively inefficient, ion-supported tori, whose rotational energy is extracted by large-scale magnetic fields.
In GRRMHD simulations (see Sect. 4) hρ is calculated in spherical coordinates as 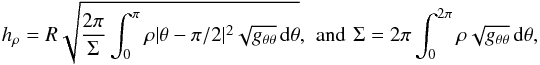 where gθθ is the θθ component of the metric tensor gμν. Time averaged data are used to perform the integral.
where gθθ is the θθ component of the metric tensor gμν. Time averaged data are used to perform the integral.
We are using here the form of this equation from Kato et al. (2008) – see their Eq. (3.38), however, for consistency with solutions of the transfer equation the factor “64” should be “16” (see Lasota 2015).
These solutions are in qualitative agreement with most recent, fully three-dimensional models (Sadowski & Narayan 2016).
For an excellent pedagogical explanation of PDs see Frank et al. (2002), for a review of relevant recent papers Abramowicz & Fragile (2013), or Rezzolla & Zanotti (2013). Komissarov (2006) constructed models of magnetized PDs.
MAD configurations, however, compress accretion flows making them thin (see e.g. Tchekhovskoy et al. 2011; McKinney et al. 2012).
Acknowledgments
We are grateful to Włodek Kluźniak for helpful comments. We thank Maciek Wielgus for his help with PDs and Fig. 6. The anonymous referee’s report was very helpful. This research was supported by the Polish NCN grants UMO-2013/08/A/ST9/00795 and DEC-2012/04/A/ST9/00083. J.P.L. was supported in part by a grant from the French Space Agency CNES. R.S.S.V. was supported by Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP), grants 2010/00487-9, 2013/01001-0 and 2015/10577-9. R.S.S.V. is grateful for the hospitality at Harvard-Smithsonian Center for Astrophysics and at Nicolaus Copernicus Astronomical Center. A.S. acknowledges support for this work by NASA through Einstein Postdoctoral Fellowship number PF4-150126 awarded by the Chandra X-ray Center, which is operated by the Smithsonian Astrophysical Observatory for NASA under contract NAS8-03060. A.S. acknowledges computational support from NSF via XSEDE resources (grant TG-AST080026N), and from NASA via the High-End Computing (HEC) Program through the NASA Advanced Supercomputing (NAS) Division at Ames Research Center.
References
- Abolmasov, P., & Chashkina, A. 2015, MNRAS, 454, 3432 [NASA ADS] [CrossRef] [Google Scholar]
- Abramowicz, M. A. 1981, Nature, 294, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Abramowicz, M. A. 1985, PASJ, 37, 727 [NASA ADS] [Google Scholar]
- Abramowicz, M. A. 2005, in Growing Black Holes: Accretion in a Cosmological Context, eds. A. Merloni, S. Nayakshin, & R. A. Sunyaev, ESO Astrophysics Symposia (Berlin: Springer), 257 [Google Scholar]
- Abramowicz, M. A., & Fragile, P. C. 2013, Liv. Rev. Relat., 16, 1 [Google Scholar]
- Abramowicz, M. A., & Piran, T. 1980, ApJ, 241, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Abramowicz, M., Jaroszyński, M., & Sikora, M. 1978, A&A, 63, 221 [NASA ADS] [Google Scholar]
- Abramowicz, M. A., Henderson, P. F., & Ghosh, P. 1983, MNRAS, 203, 323 [NASA ADS] [Google Scholar]
- Abramowicz, M. A., Czerny, B., Lasota, J. P., & Szuszkiewicz, E. 1988, ApJ, 332, 646 [NASA ADS] [CrossRef] [Google Scholar]
- Abramowicz, M. A., Chen, X., Kato, S., Lasota, J.-P., & Regev, O. 1995, ApJ, 438, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Abramowicz, M. A., Lanza, A., & Percival, M. J. 1997, ApJ, 479, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Abramowicz, M. A., Lasota, J.-P., & Igumenshchev, I. V. 2000, MNRAS, 314, 775 [NASA ADS] [CrossRef] [Google Scholar]
- Abramowicz, M. A., Jaroszyński, M., Kato, S., et al. 2010, A&A, 521, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Begelman, M. C. 1979, MNRAS, 187, 237 [NASA ADS] [Google Scholar]
- Begelman, M. C., King, A. R., & Pringle, J. E. 2006, MNRAS, 370, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, X., Abramowicz, M. A., Lasota, J.-P., Narayan, R., & Yi, I. 1995, ApJ, 443, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Coughlin, E. R., & Begelman, M. C. 2014, ApJ, 781, 82 [NASA ADS] [CrossRef] [Google Scholar]
- De Villiers, J.-P., & Hawley, J. F. 2003, ApJ, 592, 1060 [NASA ADS] [CrossRef] [Google Scholar]
- Dotan, C., & Shaviv, N. J. 2011, MNRAS, 413, 1623 [NASA ADS] [CrossRef] [Google Scholar]
- Ichimaru, S. 1977, ApJ, 214, 840 [NASA ADS] [CrossRef] [Google Scholar]
- Fishbone, L. G., & Moncrief, V. 1976, ApJ, 207, 962 [NASA ADS] [CrossRef] [Google Scholar]
- Fragile, P. C., Olejar, A., & Anninos, P. 2014, ApJ, 796, 22 [Google Scholar]
- Frank, J., King, A., & Raine, D. J. 2002, Accretion Power in Astrophysics (Cambridge: Cambridge University Press) [Google Scholar]
- Gu, W.-M. 2012, ApJ, 753, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Gu, W.- M., & Lu, J.-F. 2007, ApJ, 660, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Hawley, J. F. 2000, ApJ, 528, 462 [NASA ADS] [CrossRef] [Google Scholar]
- Jaroszyński, M., Abramowicz, M. A., & Paczyński, B. 1980, Acta Astron., 30, 1 [NASA ADS] [Google Scholar]
- Kato, S., Fukue, J., & Mineshige, S. 2008, Black-Hole Accretion discs – Towards a New Paradigm, (Kyoto: Kyoto University Press) [Google Scholar]
- Kawaguchi, T. 2003, ApJ, 593, 69 [NASA ADS] [CrossRef] [Google Scholar]
- King, A. 2008, New A Rev., 51, 775 [NASA ADS] [CrossRef] [Google Scholar]
- King, A. R. 2009, MNRAS, 393, L41 [NASA ADS] [Google Scholar]
- King, A., & Lasota, J.-P. 2014, MNRAS, 444, L30 [NASA ADS] [CrossRef] [Google Scholar]
- King, A., & Lasota, J.-P. 2016, MNRAS, in press [Google Scholar]
- Kluźniak, W., & Lasota, J.-P. 2015, MNRAS, 448, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Komissarov, S. S. 2006, MNRAS, 368, 993 [NASA ADS] [CrossRef] [Google Scholar]
- Lasota, J.-P. 2015, Black Accretion Discs, in Astrophysical Black Holes – From fundamental aspects to latest developments, ed. C. Bambi (Springer, Astrophysics and Space Science Library), in press [arXiv::1505.02172] [Google Scholar]
- Lasota, J.-P., King, A. R., Dubus, G., 2015, ApJ, 801, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, J.-F., Bai, Y., Wang, S., et al. 2015, Nature, 528, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Lynden-Bell, D., & Pringle, J. E. 1974, MNRAS, 168, 603 [NASA ADS] [CrossRef] [Google Scholar]
- McKinney, J. C., Tchekhovskoy, A., & Blandford, R. D. 2012, MNRAS, 423, 3083 [NASA ADS] [CrossRef] [Google Scholar]
- McKinney, J. C., Tchekhovskoy, A., Sądowski, A., & Narayan, R. 2014, MNRAS, 441, 3177 [NASA ADS] [CrossRef] [Google Scholar]
- Narayan, R., & Yi, I. 1994, ApJ, 428, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Narayan, R., & Yi, I. 1995, ApJ, 452, 710 [NASA ADS] [CrossRef] [Google Scholar]
- Novikov, I. D., & Thorne, K. S. 1973, in Black Holes, Les Astres Occlus, eds. C. Dewitt, & B. S. Dewitt (New York: Gordon and Breach), 343 [Google Scholar]
- Ohsuga, K., Mori, M., Nakamoto, T., & Mineshige, S. 2005, ApJ, 628, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Paczyński, B. 1998, Acta Astron., 48, 667 [NASA ADS] [Google Scholar]
- Paczyński, B., & Bisnovatyi-Kogan, G. 1981, Acta Astron., 31, 283 [NASA ADS] [Google Scholar]
- Paczyński, B., & Wiita, P. J. 1980, A&A, 88, 23 [NASA ADS] [Google Scholar]
- Qian, L., Abramowicz, M. A., Fragile, P. C., et al. 2009, A&A, 498, 471 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rees, M. J., Begelman, M. C., Blandford, R. D., & Phinney, E. S. 1982, Nature, 295, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Rezzolla, L., & Zanotti, O. 2013, Relativistic Hydrodynamics, (Oxford: Oxford University Press) [Google Scholar]
- Sądowski, A. 2009, ApJS, 183, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Sa¸dowski, A. 2011, Slim discs around Black Holes, Ph.D. thesis, [arXiv:1108.0396] [Google Scholar]
- Sądowski, A., & Narayan, R. 2015, MNRAS, 453, 3213 [NASA ADS] [CrossRef] [Google Scholar]
- Sadowski, A., & Narayan, R. 2016, MNRAS, 456, 3929 [NASA ADS] [CrossRef] [Google Scholar]
- Sądowski, A., Abramowicz, M., Bursa, M., et al. 2011, A&A, 527, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sądowski, A., Narayan, R., Tchekhovskoy, A., et al. 2015, MNRAS, 447, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Sadowski, A., Lasota, J.-P., Abramowicz, M. A., & Narayan, R. 2016, MNRAS, 456, 3915 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Shiokawa, H., Krolik, J. H., Cheng, R. M., Piran, T., & Noble, S. C. 2015, ApJ, 804, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Sikora, M. 1981, MNRAS, 196, 257 [Google Scholar]
- Tchekhovskoy, A., Narayan, R., & McKinney, J. C. 2011, MNRAS, 418, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Wielgus, M., Yan, W., Lasota J.-P., & Abramowicz M. A. 2015, A&A, in press [arXiv:1512.00749] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Aspect ratio hρ/R as a function of accretion rate ṁ. Solid black line: calculated at R = 30 M for the analytical model described in Sect. 2 assuming M = 10 M⊙, ξ = 1 and α = 0.01. Markers: the corresponding aspect ratio for numerical slim disc solutions (blue diamonds, Sect. 3) and GRRMHD simulations (orange circles, Sect. 4). |
| In the text | |
 |
Fig. 2 Thermal equilibrium (ṁ–Σ) diagram for slim-disc solutions at R = 30 M. Red dots: Numerical solutions from the slim-disc code (Sa¸dowski 2011). Black line: analytical S-curve, obtained from the Paczyński-Wiita potential. Both sets have M = 10 M⊙ and α = 0.01. The analytical S-curve has also ξ = 1, Ω/ΩK = 1. Green crosses: obtained from the Paczyński-Wiita potential but with the same ξ, Ω/ΩK values as the corresponding slim-disc simulations. Although the black line does deviate from the red points, we see that when the above corrections are taken into account, the analytical pseudo-Newtonian slim discs agree with the stationary, general relativistic, “1+1” simulations with great precision. |
| In the text | |
 |
Fig. 3 Snapshots of logarithm of density for GRRMHD discs with ṁ = 9.6, 24.3, and 73.1ṀEdd. Density is given in g/cm3. |
| In the text | |
 |
Fig. 4 Thermal equilibrium (ṁ–Σ) diagram for R = 30 M. Solutions based on different assumptions are compared. Black lines show analytical S-curves for Keplerian motion in the Paczyński-Wiita potential with ξ = 1 and α = 1;0.1;0.01;0.001 (left to right). Red dots represent stationary numerical slim discs for different accretion rates, with α = 0.01 (Sect. 3). Blue crosses correspond to GRRMHD simulations (see Table 1 and Sect. 4). All solutions have M = 10 M⊙. |
| In the text | |
 |
Fig. 5 Effect of advection on the thickness of PDs. The maximum value of the relative height of a PD and the accretion rate are shown on the vertical and horizontal axes, respectively. (From Wielgus et al. 2015.) |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


