| Issue |
A&A
Volume 587, March 2016
|
|
|---|---|---|
| Article Number | A92 | |
| Number of page(s) | 36 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201527470 | |
| Published online | 23 February 2016 | |
Exploring molecular complexity with ALMA (EMoCA): Alkanethiols and alkanols in Sagittarius B2(N2)
1
I. Physikalisches Institut, Universität zu Köln,
Zülpicher Str. 77, 50937
Köln, Germany
e-mail: hspm@ph1.uni-koeln.de
2
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69, 53121
Bonn,
Germany
3
Centre for Laser, Atomic and Molecular Sciences (CLAMS),
Department of Physics, University of New Brunswick, Saint John, NB
E2L 4L5,
Canada
4
Departments of Chemistry and Astronomy, University of
Virginia, Charlottesville, VA
22904,
USA
5
Université de Toulouse, UPS-OMP, IRAP,
Toulouse,
France
6
CNRS, IRAP, 9
Av. colonel Roche, BP
44346, 31028
Toulouse Cedex 4,
France
7
Department of Chemistry, University of Manitoba,
Winnipeg, MB
R3T 2N2,
Canada
Received: 29 September 2015
Accepted: 24 November 2015
Context. Over the past five decades, radio astronomy has shown that molecular complexity is a natural outcome of interstellar chemistry, in particular in star forming regions. However, the pathways that lead to the formation of complex molecules are not completely understood and the depth of chemical complexity has not been entirely revealed. In addition, the sulfur chemistry in the dense interstellar medium is not well understood.
Aims. We want to know the relative abundances of alkanethiols and alkanols in the Galactic center source Sagittarius B2(N2), the northern hot molecular core in Sgr B2(N), whose relatively small line widths are favorable for studying the molecular complexity in space.
Methods. We investigated spectroscopic parameter sets that were able to reproduce published laboratory rotational spectra of ethanethiol and studied effects that modify intensities in the predicted rotational spectrum of ethanol. We used the Atacama Large Millimeter Array (ALMA) in its Cycles 0 and 1 for a spectral line survey of Sagittarius B2(N) between 84 and 114.4 GHz. These data were analyzed by assuming local thermodynamic equilibrium (LTE) for each molecule. Our observations are supplemented by astrochemical modeling; a new network is used that includes reaction pathways for alkanethiols for the first time.
Results. We detected methanol and ethanol in their parent 12C species and their isotopologs with one 12C atom substituted by 13C; the latter were detected for the first time unambiguously in the case of ethanol. The 12C/13C ratio is ~25 for both molecules. In addition, we identified CH318 OH with a 16O/18O ratio of ~180 and a 13CH3OH/CH318 OH ratio of ~7.3. Upper limits were derived for the next larger alkanols normal- and iso-propanol. We observed methanethiol, CH3SH, also known as methyl mercaptan, including torsionally excited transitions for the first time. We also identified transitions of ethanethiol (or ethyl mercaptan), though not enough to claim a secure detection in this source. The ratios CH3SH to C2H5SH and C2H5OH to C2H5SH are ≳21 and ≳125, respectively. In the process of our study, we noted severe discrepancies in the intensities of observed and predicted ethanol transitions and propose a change in the relative signs of the dipole moment components. In addition, we determined alternative sets of spectroscopic parameters for ethanethiol. The astrochemical models indicate that substantial quantities of both CH3SH and C2H5SH may be produced on the surfaces of dust grains, to be later released into the gas phase. The modeled ratio CH3SH/C2H5SH = 3.1 is lower than the observed value of ≳21; the model value appears to be affected most by the underprediction of CH3SH relative to CH3OH and C2H5OH, as judged by a very high CH3OH/CH3SH ratio.
Conclusions. The column density ratios involving methanol, ethanol, and methanethiol in Sgr B2(N2) are similar to values reported for Orion KL, but those involving ethanethiol are significantly different and suggest that the detection of ethanethiol reported toward Orion KL is uncertain. Our chemical model presently does not permit the prediction of sufficiently accurate column densities of alkanethiols or their ratios among alkanethiols and alkanols. Therefore, additional observational results are required to establish the level of C2H5SH in the dense and warm interstellar medium with certainty.
Key words: astrochemistry / line: identification / molecular data / radio lines: ISM / ISM: individual objects: Sagittarius B2(N) / ISM: molecules
© ESO, 2016
1. Introduction
The degree of chemical complexity observed toward star-forming regions known as “hot cores” is greater than that found thus far in any other portion of the interstellar medium (ISM), encompassing a range of organic molecules of up to 12 atoms (Belloche et al. 2014). The significance of these detections may go beyond the immediate chemistry of hot cores themselves; the apparent similarity between the abundances of complex interstellar molecules and the chemical composition of comets suggests that interstellar material may have been incorporated directly into cometary and/or planetary solids during the planet formation process. It is therefore critical to understand the depth and breadth of chemical complexity that may develop in the early stages of star formation, and which may influence the chemistry of later planetary systems and perhaps the ultimate emergence of life.
Sagittarius (Sgr for short) B2 is an especially well-suited source for studying saturated or nearly saturated organic molecules, and most of the larger ones have been detected toward this source for the first time (Belloche et al. 2013). Sgr B2(N) and Sgr B2(M) are the two main sites of star formation in the Sgr B2 molecular cloud complex, one of the most massive star-forming regions in our Galaxy located close to the Galactic center. Sgr B2(N) contains two dense, compact hot cores separated by about 5′′ (Belloche et al. 2008; Qin et al. 2011), the more prominent one is the so-called Large Molecule Heimat Sgr B2(N-LMH), also called Sgr B2(N)-SMA1 (Qin et al. 2011) or P1 (Belloche et al. 2008); the other is called Sgr B2(N)-SMA2 (Qin et al. 2011) or P2 (Belloche et al. 2008) and is to the north of the first. We propose that Sgr B2(N1) and Sgr B2(N2) be adopted because they are short and unambiguous names. Single-dish observations of Sgr B2(N) usually cover both sources, but differences in the local standard of rest (lsr) velocities provide the means to distinguish between the two sources.
In order to study the molecular complexity in Sgr B2, we used the IRAM 30 m telescope to carry out molecular line surveys toward Sgr B2(N) and Sgr B2(M) at 3 mm wavelengths with additional observations at 2 and 1.3 mm (Belloche et al. 2013). Even though each frequency setup was observed for a modest amount of time, line confusion was reached for a considerable part of the surveys, in particular toward Sgr B2(N). Nevertheless, in this study we detected aminoacetonitrile, a possible precursor of glycine (the simplest amino acid), for the first time in space (Belloche et al. 2008), as well as ethyl formate and n-propyl cyanide (Belloche et al. 2009), the 13C isotopologs of vinyl cyanide (Müller et al. 2008), and several other minor isotopic species and transitions in excited vibrational states (Belloche et al. 2013).
Other recent investigations into the molecular complexity of Sgr B2(N) include a line survey with the HIFI high-resolution spectrometer on board Herschel covering its entire frequency region (most of ~500 to ~1900 GHz) (Neill et al. 2014) or the PRIMOS Legacy Project (up to about 50 GHz) employing the 100 m GBT dish, which led to the detection of ethanimine (Loomis et al. 2013) and E-cyanomethanimine (Zaleski et al. 2013), among others. Among the less recent studies of Sgr B2, we note the 1.3 mm line survey of Nummelin et al. (1998, 2000) who studied three positions (M, N, and NW) using the SEST 15 m dish.
The Orion Molecular Cloud, and in particular the Kleinmann-Low Nebula (Orion KL), have also been studied extensively in the context of molecular complexity (Crockett et al. 2014). An IRAM 30 m molecular line survey led to the detection of several molecules including methyl acetate (Tercero et al. 2013) (an isomer of ethyl formate), and numerous minor isotopic species, such as methyl-deuterated methyl formate, HCO(O)CH2D (Coudert et al. 2013). The detection of methyl formate in its second excited torsional state was reported through different observations (Takano et al. 2012). In recent years, considerable levels of molecular complexity have also been investigated in other star-forming regions. Ethanediol, for example, which is also known as ethylene glycol, is a molecule with ten atoms. It was detected in the hot corinos associated with the lower mass Class 0 protostars NGC 1333-IRAS2A (Maury et al. 2014) and, tentatively, IRAS 16293-2422B (Jørgensen et al. 2012) after the first detection toward Sgr B2(N) (Hollis et al. 2002).
Following up on our observations with the IRAM 30 m telescope, we used the Atacama Large Millimeter Array (ALMA) in its Cycle 0 for a spectral line survey of Sagittarius B2(N) between 84 and 111 GHz with the aim of Exploring Molecular Complexity with ALMA (EMoCA). An additional setup in Cycle 1 extended the frequency range to 114.4 GHz. We expected a reduction in the line confusion through the spatial resolution of Sgr B2(N1) and Sgr B2(N2). In fact, we observed reduced line confusion toward the weaker source Sgr B2(N2) caused not only by the spatial separation of the two sources, but also by narrower lines. As a first result, we were able to detect the first branched alkyl molecule in space, iso-propyl cyanide and to determine a 1:2.5 ratio relative to the more abundant n-propyl cyanide in Sgr B2(N2) (Belloche et al. 2014). The line confusion is high in Sgr B2(N1), therefore, we focus our initial analyses on Sgr B2(N2). In the present work, we report on alkanols and alkanethiols in this source.
Methanol, CH3OH, is
the lightest alkanol and one of the most abundant organic molecules in the ISM. It was among
the first molecules to be detected in space, toward Sgr A and Sgr B2, by means of radio
astronomy (Ball et al. 1970). In fact, 13CH3OH and CH3OD were detected in Sgr B2 shortly
thereafter (Gottlieb et al. 1979). We note, however,
that the identification of CH3OD in that work has been questioned recently (Belloche et al. 2016). A few years later, Gardner et al. (1989) reported on the detection of
CH OH in Sgr B2. The great diagnostic value of
methanol lines has been pointed out several times (Leurini
et al. 2004, 2007; Müller et al. 2004; Wang et al.
2011). Rotational lines of 13CH3OH have been used frequently to derive proper column
densities because those of the main isotopic species are often saturated in dense molecular
clouds (Belloche et al. 2013; Neill et al. 2013).
OH in Sgr B2. The great diagnostic value of
methanol lines has been pointed out several times (Leurini
et al. 2004, 2007; Müller et al. 2004; Wang et al.
2011). Rotational lines of 13CH3OH have been used frequently to derive proper column
densities because those of the main isotopic species are often saturated in dense molecular
clouds (Belloche et al. 2013; Neill et al. 2013).
Ethanol, C2H5OH, the next heaviest alkanol, was also among the first molecules to be detected in space employing radio astronomy (Zuckerman et al. 1975). The detection was also made toward Sgr B2. Initially, it was observed only via its anti (or trans) low-energy conformer, the higher lying gauche conformer was first detected in Orion KL several years later (Pearson et al. 1997). Ethanol was not only detected in several hot cores, but also in kinetically moderately warm Galactic center clouds (Requena-Torres et al. 2006). In addition, there is evidence for the molecule in the molecular clouds surrounding the Class 0 protostars IRAS 16293-2422A and B (Bisschop et al. 2008). Ethanol with one 13C has not yet been detected with certainty, but we reported on a tentative detection in the course of the 30 m line survey of Sgr B2(N) (Belloche et al. 2013).
In the case of propanol, C3H7OH, there are two isomers, the straight chain normal- or n-propanol and the branched iso- or i-propanol. We are aware of two reports attempting to detect n-propanol in space (Requena-Torres et al. 2008; Tercero et al. 2015). There appears to be no published report on the search for i-propanol in space.
Replacing an O atom in an alkanol with an S atom yields an alkanethiol. The simplest one is methanethiol, CH3SH, also known as methyl mercaptan. It was among the early molecules detected in space by radio astronomical means, first tentatively (Turner 1977) and confirmed subsequently (Linke et al. 1979), again toward Sgr B2. It was also observed toward the hot core G327.3-0.6 (Gibb et al. 2000), the cold core B1 (Cernicharo et al. 2012), and the Orion KL hot core (Kolesniková et al. 2014). The last study also reported the detection of ethanethiol, C2H5SH, also known as ethyl mercaptan. Even though many spectral features were ascribed to the molecule, most of them are partially or completely blended with emission from other species. In addition, the column density ratio of ethanethiol with respect to methanethiol or ethanol appears somewhat higher than the column density ratios of the latter two molecules with respect to methanol. The puzzlingly high apparent abundance of C2H5SH in Orion KL motivates probing the abundances of alkanols and alkanethiols in other hot cores, in particular Sgr B2(N), in order to understand better the interstellar chemistry of these two families of organic molecules.
2. Laboratory spectroscopy
In this section, we present background information on the spectroscopy of the molecules in the present study. One general aspect concerns the partition function of organic molecules and the related abundances. These molecules often have low-lying vibrations, such as OH-, SH-, or CH3-torsions, which are not always considered in the derivation of the partition function. We comment on necessary corrections of the partition function and, equivalently, the column densities under local thermodynamic equilibrium (LTE). Similar corrections may be required if not all of the thermally populated conformations were considered in the derivation of the partition function.
The rotational spectrum of a saturated or nearly saturated organic molecule may differ considerably from that of a simple asymmetric top rotor because the torsion or inversion of functional groups such as CH3, NH2, OH, or SH may be hindered only slightly. These large amplitude motions may lead to additional splitting in the rotational transitions, which sometimes can be resolved in radio astronomical spectra.
Pickett (1972) proposed a reduced axis system (RAS)
for the treatment of inversion problems, i.e., tunneling between two equivalent minima. Its
main off-diagonal term of a-symmetry is Fbc {
Jb,Jc
} with {
Jb,Jc
} =
JbJc
+
JcJb.
Distortion corrections, such as 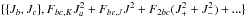 with J± =
Jb ±
iJc,
may also be required. Terms of b- and c-symmetry are
defined equivalently. The symmetry of the allowed terms in the Hamiltonian depends on the
symmetry of the inversion motion. The designation of the parameter as Fbc is fairly common, but
other designations also exist (e.g., Dbc). Parameters such as
F2bc may also be called
with J± =
Jb ±
iJc,
may also be required. Terms of b- and c-symmetry are
defined equivalently. The symmetry of the allowed terms in the Hamiltonian depends on the
symmetry of the inversion motion. The designation of the parameter as Fbc is fairly common, but
other designations also exist (e.g., Dbc). Parameters such as
F2bc may also be called
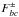 .
.
Reduced axis system Hamiltonians were employed successfully for a variety of molecules of interest for astrochemistry, including NH2D (Cohen & Pickett 1982), vinylamine (McNaughton & Evans 1999), aGg’-ethanediol (Christen & Müller 2003), NHD2 (Endres et al. 2006), H2DO+ (Müller et al. 2010), phenol (Kolesniková et al. 2013), and 1,3-propanediol (Smirnov et al. 2013).
A RAS Hamiltonian still appears to be well suited to describe the tunneling between two
equivalent conformations if a third minimum is sufficiently higher in energy. This third
minimum usually has a dihedral angle of ~0°
(syn) or ~180°
(anti); the two equivalent conformations have dihedral angles of about
±120° or of about ±60°, respectively. In either case, the conformations are frequently called
gauche. Examples are peroxynitric acid (Suenram et al. 1986a), fluoromethanol (Suenram et
al. 1986b), and propargyl alcohol (Pearson &
Drouin 2005). If a third minimum is closer in energy to the gauche
states, it may be necessary to include parameters of odd order into the Hamiltonian
to describe the tunneling between the gauche states. The lower order
parameters of a-symmetry are 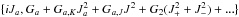 , those of b- and
c-symmetry are defined equivalently. This approach has been used, for
example, in the treatment of the rotation-tunneling spectrum of ethanol (Pearson et al. 1996, 2008).
, those of b- and
c-symmetry are defined equivalently. This approach has been used, for
example, in the treatment of the rotation-tunneling spectrum of ethanol (Pearson et al. 1996, 2008).
In the case of tunneling between two equivalent conformations if a third minimum is sufficiently higher in energy, the RAS interaction Hamiltonian with even order parameters, such as Fab, may be replaced by an interaction Hamiltonian with odd order parameters, such as Gc. Pearson & Drouin (2005) have shown that equivalent fits can be obtained with only even or with only odd order interaction parameters in the case of propargyl alcohol.
We note that the sign of the first off-diagonal interaction parameter of a given symmetry and between specific conformations or vibrational states is not determinable in a fit of field-free rest frequencies. This parameter is usually the one of lowest order, i.e., Gi or Fjk. However, the sign of any additional interaction parameter of the same symmetry and between those specific conformations or vibrational states are determinable with respect to that of the first parameter. Moreover, in the absence of off-diagonal interaction parameters, the signs of the dipole moment components are not determinable and do not matter. However, in the presence of off-diagonal interaction parameters and with their signs fixed, the relative signs of the dipole moment components may matter; in fact, it is the sign of the dipole moment component times the sign of the overlap integral that is determined. In that case, they may be determinable by Stark spectroscopy (Cohen & Pickett 1982; Suenram et al. 1986a,b). The relative signs of the dipole moment components may also lead to changes in the intensities of some transitions, and conversely, relative intensity measurements may lead to the determination of the relative signs of the dipole moment components (Christen & Müller 2003; Endres et al. 2006; Müller et al. 2010).
The treatment of torsional large amplitude motions (e.g., of CH3 groups) often requires more specialized Hamiltonian models (see, e.g., Herbst et al. 1984 or Kleiner 2010 for a review) because the regular K energy level structure of an asymmetric top rotor could be modified significantly by torsional contributions that oscillate as a function of K. The amplitude of this oscillation increases rapidly with excitation to torsional states of successively higher energy relative to the torsional barrier. The frequency of the K-variation depends on the ratio of the moment of inertia of the rotating top to that of the whole molecule, hence torsional contributions to the energies oscillate faster with K for heavy tops and light frames.
2.1. Methanol, CH3OH
The torsional energy for methanol varies rapidly with K because the moment of inertia of the CH3 group dominates that of the light OH frame. In addition, the intermediate-size barrier to rotation of the CH3 group leads to torsional contributions to the K energy level structure in the ground vibrational state that are of similar size to the K level splitting at low K. As a consequence, the origins of the b-type rotational transitions (with ΔK = 1) differ considerably from those expected for an asymmetric top rotor. In contrast, the patterns of the a-type rotational transitions (with ΔK = 0) resemble those of an asymmetric top in the absence of perturbations; this applies even to excited torsional states. The first excited torsional state straddles the barrier to internal rotation, and even higher torsional states display a K-level structure that increasingly approaches that of a free internal rotor.
We have used rotational transitions of 13CH3OH initially to infer the column density of methanol because of frequent saturation of lines pertaining to the main isotopic species. The spectroscopic line data were taken from the CDMS catalog1 (Müller et al. 2001, 2005). The first version is based on Xu et al. (1996) and Xu & Lovas (1997) with experimental transition frequencies in the range of our ALMA data from Kuriyama et al. (1986) and from the privately communicated methanol atlas of the Toyama University (Tsunekawa et al. 1995). An update of the CDMS entry is in preparation. It is based on extensive measurements taken in Cologne that extend up to ~1500 GHz and include data in the range of our survey (Xu et al. 2014). The magnitudes of the dipole moment components employed in the calculation are | μa | = 0.899 D and | μb | = 1.44 D from initial measurements on the main isotopic species (Ivash & Dennison 1953). Sastry et al. (1994) determined slightly different dipole moment components of 13CH3OH. The vibrational contributions to the partition function at 160 K are essentially converged by inclusion of νt = 2, a correction of the column density because of the population of vibrational states is not required.
We used the CDMS entry to evaluate the column density of
CH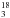 OH. The entry is based on Fisher et al. (2007) with extensive far-infrared data
from that work. Most of the rest frequencies determined with microwave accuracy are from
Hoshino et al. (1996) and from Ikeda et al. (1998). The dipole moment components are
slightly different from those of the main species and were taken from Sastry et al. (1996). As for 13CH3OH, vibrational corrections to
the partition function at 160 K are not needed.
OH. The entry is based on Fisher et al. (2007) with extensive far-infrared data
from that work. Most of the rest frequencies determined with microwave accuracy are from
Hoshino et al. (1996) and from Ikeda et al. (1998). The dipole moment components are
slightly different from those of the main species and were taken from Sastry et al. (1996). As for 13CH3OH, vibrational corrections to
the partition function at 160 K are not needed.
We used the JPL catalog2 (Pickett et al. 1998) entry to estimate the CH3OH column density because we expect to observe highly rotationally or torsionally excited CH3OH transitions with line widths much wider than in dark clouds. The entry is based on the extensive study of Xu et al. (2008) which extends to νt = 2 and high J and K quantum numbers. Rest frequencies in the range of our study were taken mainly from the methanol atlas of the Toyama University3 (Tsunekawa et al. 1995) with additional data from Lees & Baker (1968), Sastry et al. (1984), Müller et al. (2004), Xu et al. (2008). An older entry based on Xu & Lovas (1997) is available in the CDMS. Even though it covers only νt = 0 and 1 and has weaknesses for transitions with higher J and K values, it is frequently more accurate for lower energy transitions that may be important for dark cloud or maser observations, which require high frequency accuracy. This is achieved in part by merging corresponding laboratory data (Müller et al. 2004). The dipole moments were taken from Ivash & Dennison (1953). Very recently, determinations of the dipole moment components were reported by Mukhopadhyay & Sastry (2015) with very similar values. The small change in the a-dipole moment component upon torsional excitation probably has negligible effects for the strongest a-type transitions even in a perfect fit of astronomical data. There may be non-negligible effects in transitions in which contributions of the a- and b-dipole moment components almost cancel out. Vibrational corrections to the partition function at 160 K are again not needed.
We suspected that transitions pertaining to νt = 3 may be observable in our data. We took J = 2−1a-type transition frequencies from Tsunekawa et al. (1995), the lower state energies from Moruzzi et al. (1995), and estimated the line strengths from lower torsional states (Xu et al. 2008). It is worthwhile mentioning that substantial progress has been made recently in analyzing νt = 3 and higher vibrational states of methanol (Pearson et al. 2009, 2015).
2.2. Methanethiol, CH3SH
Replacing the O atom in methanol with an S atom yields methanethiol, reducing the moment of inertia ratio between the CH3 group and the SH frame compared to the OH frame in methanol. Overall, the torsional splitting in CH3SH is smaller than that in CH3OH. The splittings in the first excited torsional state of CH3SH are similar to the ones in the ground vibrational state of CH3OH.
Information on rest frequencies were taken from the CDMS. The entry is based on Xu et al. (2012). Extensive terahertz and far-IR data were combined with previous data, which include data in the range of our survey from Lees & Mohammadi (1980) with additional data mainly from Sastry et al. (1986) and Bettens et al. (1999). Dipole moment components of | μa | = 1.312 D and | μb | = 0.758 D were cited by Tsunekawa et al. (1989). The vibrational contributions to the partition function are quite well accounted for at 180 K, so no correction to the column density needs to be made.
2.3. Ethanol, C2H5OH
There are two large amplitude motions in ethanol, the internal rotation of the methyl group, whose rather small splitting is only rarely resolved in the laboratory and is frequently neglected, and the internal rotation of the OH group, which causes more prominent splitting. The anti conformer (also known as trans) with a dihedral HOCC angle of 180° is lowest in energy. The doubly degenerate gauche conformer with dihedral angles of about ± 60° is considerably higher in energy. Tunneling between the two equivalent gauche conformers causes them to split into the symmetric gauche+ and the antisymmetric gauche− states. The former is 56.82 K higher than the anti conformer and the latter 61.53 K (Pearson et al. 2008). Torsion-rotation interaction between the gauche conformers occurs even at low quantum numbers (Pearson et al. 1997). In contrast, such interaction can be neglected for the anti conformer up to moderate quantum numbers (J + 2Ka ≲ 30).
Pearson et al. (2008) reported extensively on the rotational spectra of the C2H5OH conformers and their mutual torsion-rotation interaction. Data associated with this work as well as resulting predictions of the ground state rotational spectrum are available in the JPL catalog. Transition frequencies in the range of our ALMA survey are from that work. Vibrational contributions to the partition function at 150 K are dominated by the two torsional modes (Durig & Larsen 1990). Combining anti and gauche conformers, the ground state partition function needs to be increased by a factor of 1.24; slight differences in the OH torsional energies of the two conformers are taken into account.
The entries of ethanol isotopologs with one 13C atom were taken from the CDMS catalog. They were based on Bouchez et al. (2012), which restricted the investigations to the anti conformers with J and Ka ranges in which interaction with the gauche conformers can be neglected. The contribution of the gauche conformers to the partition function increases the value at 150 K based on the anti conformer only by a factor of ~2.39 as estimated in the CDMS documentation from the main isotopic species. Vibrational contributions to the partition function were also derived from the main isotopic species.
The experimental dipole moment components of the ethanol conformers are given in Table 1 together with the proposed signs from Pearson et al. (2008), which are important because of the extensive torsion-rotation interaction. Pearson et al. (2008) discussed line strength issues in Sect. 5.2. They pointed out that intensities for a number of transitions are not correctly modeled by their Hamiltonian model and attributed this short-coming by the neglect of torsional corrections (sine and cosine functions) to the dipole moment components.
 |
Fig. 1 Sections of the continuum-subtracted spectrum recorded with ALMA toward Sgr B2(N2) in black. The synthetic spectrum of ethanol using the official JPL catalog entry is shown in red. Some lines are predicted to be much stronger than they appear in the spectrum, e.g., near 88 107 MHz and 91 059 MHz. A few other lines, e.g., near 90 354 MHz and 101 244 MHz, are stronger than predicted. Compare with Fig. 2. The central frequency of each panel is indicated below the x-axis in MHz; its width is given also in MHz in parentheses. The y-axis is labeled in brightness temperature units (K). |
 |
Fig. 2 Same as in Fig. 1 with the same LTE parameters, but the modeling was carried out with a modified catalog entry in which the sign of one dipole moment component was altered, see Table 1. |
As shown in Fig. 1, we noticed that several rather weak C2H5OH transitions in our line survey were predicted to be significantly too strong; these transitions are summarized in Table 2. We suspected that the sign choices of the dipole moment components relative to the interaction parameters could be responsible for the observed intensity issues. We changed the signs of the dipole moment components from Pearson et al. (2008) one at a time relative to μb of the anti conformer. The resulting predictions were compared with our ALMA observations. In addition, we inspected a laboratory spectrum of ethanol in the 3 mm wavelength region taken at the Universität zu Köln for educational purposes. Sign changes of either μa or μc of the gauche conformer yielded predictions that were compatible with our ALMA observations with a slight preference for a change in μa. The intensities in the laboratory spectrum were in support of this view; e.g., the gauche− transition 131,12−131,13 near 96716.5 MHz was about as strong as the g+−g− transition 399,31−3810,29 near 96746.9 MHz, and the gauche+ transition 131,12−130,13 near 93279.0 MHz was about twice as strong. Retaining the sign of μa and changing it in μc results in intensities of the two transitions with J = 13 lower by a factor of about 2. Changing the signs of the dipole moment components that are small in magnitude, μa of the anti conformer and μb of the gauche conformer, had very little effect on the predicted intensities, as is expected. Therefore, we refrain from any statement concerning their signs. Figure 2 shows the modeling of ethanol with the altered sign of the dipole moment component. Not only are there now no weak transitions predicted to be much stronger than observed, in some cases the lines, for which initially only part of the observed signal was assigned to C2H5OH, are now ascribed entirely to this molecule. Further details on the model are given in in Sect. 4.2; the entire model is presented in Appendix A.
Quantum numbers, conformers Conf., frequencies (MHz) of ethanol transitions appearing too strong in initial models, and Einstein A values (10-7 s-1) from the JPL catalog and new values proposed in the present study.
We should also point out that the choice of spectroscopic parameters may also affect the intensities. The intensities of ΔK = 3 transitions in the rotational spectrum of PH3 were discussed as a recent example (Müller 2013). Inclusion or omission of the ΔK = 6 term h3 or fixing it to an estimated value has profound effects on the value of the ΔK = 3 term ϵ in the fit which, in turn, affects the intensities of the weak ΔK = 3 transitions. Pearson et al. (2008) discussed the determinability of odd order parameters (e.g., Ga) simultaneously with even order parameters (e.g., Fbc) although not explicitly in relation to intensities in the rotational spectrum of C2H5OH.
We should emphasize that neglecting torsional corrections to the dipole moment components may also account for part of the intensity issues. Even though our dipole moment model was only studied in the 3 mm wavelength region, intensities may also be improved outside of this range. As indicated in this and the previous paragraphs, the proposed sign change does not necessarily resolve all intensity issues, even at 3 mm. Inspection of the existing laboratory spectral recordings, in particular outside the 3 mm range, or temperature dependent intensity measurements, such as those carried out for methanol (Fortman et al. 2014; McMillan et al. 2014), may help resolve the intensity issues in the rotational spectrum of ethanol overall.
2.4. Ethanethiol, C2H5SH: redetermination of spectroscopic parameters
Schmidt & Quade (1975) studied the microwave spectrum of ethanethiol, determined its dipole moment components, and estimated the anti conformer to have a higher energy than the gauche conformer by 204 ± 22 K. The spectroscopic analysis revealed gauche− to be higher than gauche+ by only 1754 MHz (or 0.084 K). The dipole moment components are μa = 1.48 ± 0.02 D and μb = 0.19 ± 0.10 D within the gauche conformers and μc = 0.59 ± 0.02 D between the gauche conformers. Values for the anti conformer are μa = 1.06 ± 0.03 D and μb = 1.17 ± 0.03 D.
Far-infrared and Raman spectroscopy were also employed to evaluate the energy separation between the gauche and the anti conformer. Values of 144 K (Smith et al. 1973), 121 K (Inagaki et al. 1973), 177 K (Manocha et al. 1973), and 160 K (Durig et al. 1975) were obtained. The last value may be a reasonable compromise among these values and the one from microwave measurements, but it should be viewed with caution because the uncertainty is at least 30 K, possibly more than 50 K. An energy difference of 160 K yields a population of 17 % for anti-C2H5SH at 180 K, considering the ground vibrational states only. Combining the energy difference with the vibrational data from Durig et al. (1975), including in particular the differences in the SH torsional energies, the combined conformational and vibrational correction is ~1.95 at 180 K.
Recently, Kolesniková et al. (2014) reported on the extension of the rotational spectrum up to 660 and 880 GHz for the anti and gauche conformers of the main isotopic species, respectively, and on measurements of the gauche conformer of the 34S isotopic species up to 300 GHz. Their Hamiltonian employed for the gauche conformers was very similar to the one used earlier for the gauche conformers of ethanol (Pearson et al. 1996). These data were used to create entries for the CDMS. We noted that the use of odd and even order interaction parameters resulted in very unstable fits for the gauche conformers. Therefore, we tried to fit the data using a RAS, as described at the beginning of Sect. 2, i.e., we tried to avoid using odd order parameters, such as Ga and Gb, in the fit. We note that these parameters were called Q and N, respectively, by Kolesniková et al. (2014). The magnitudes of 15.0 MHz and 6.3 MHz determined for the parent species are much smaller than the theoretically limiting values of ~2A (57494 MHz) and ~2B (10590 MHz), respectively, suggesting that both parameters have only fairly small effects in the fit. It is worthwhile mentioning that Schmidt & Quade (1975) did not use these parameters in their fits. In fact, they used Fbc and Fac for their more limited data set, which they named D+− and E+−, respectively.
We determined spectroscopic parameters as averages between both states and expressed the differences as rotational corrections of the energy difference, as described above and as was done for ethanediol (Christen & Müller 2003), for example. The advantage is that either parameter can be included in the fit without the other, whereas otherwise two distortion parameters are usually included in the fit, one for each state. We used Watson’s S reduction of the rotational Hamiltonian because it is more appropriate for asymmetric top rotors so close to the prolate case; κ = (2B−A−C) / (A−C) ≈ −0.95, close to the limiting case of −1. We employed in our first fits only the rotational and quartic distortion parameters, as well as E and Fbc. The last was expected to be very important as it connects the upper asymmetry component of gauche+ with the lower asymmetry component of gauche− with the same J and Ka. The largest perturbations are expected if the asymmetry splitting is similar to the energy splitting between gauche+ and gauche−. We note that the energy difference is called ΔE in Kolesniková et al. (2014) and equals 2E here by definition. At each stage of the fit, we searched among all reasonable parameters for the one that reduces the root mean square (rms) error as a measure of the quality of the fit most and which was determined with high significance. Neither Ga nor Gb was the parameter reducing the rms error most at any stage of the fit. Whenever one or the other was tried out in the fit, any appreciable reduction of the rms error made the fit highly unstable. This finding is hardly surprising as we do not have any indication that the transition frequencies of gauche-C2H5SH in the fit are affected by perturbation with the anti conformer. The final resulting parameters are given in Table 3.
We also determined new spectroscopic parameters for the gauche conformer
of C2H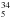 SH. To this end, we took the parameters of
the parent species and kept them fixed initially. Similarly to the fit of the parent
species, we searched for the reasonable parameter whose floating in the fit caused the
greatest reduction in the rms error until inclusion of new parameters caused only a minute
reduction of the rms error. As some parameters showed larger isotopic changes than
expected, we scaled the parameters, which were kept fixed, with appropriate powers of
B +
C, B−C, and E. The final set of
spectroscopic parameters for C2H
SH. To this end, we took the parameters of
the parent species and kept them fixed initially. Similarly to the fit of the parent
species, we searched for the reasonable parameter whose floating in the fit caused the
greatest reduction in the rms error until inclusion of new parameters caused only a minute
reduction of the rms error. As some parameters showed larger isotopic changes than
expected, we scaled the parameters, which were kept fixed, with appropriate powers of
B +
C, B−C, and E. The final set of
spectroscopic parameters for C2H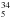 SH are also given in Table 3.
SH are also given in Table 3.
In addition, we redetermined the spectroscopic parameters of anti-C2H5SH. Kolesniková et al. (2014) used more centrifugal distortion parameters of eighth order for the anti conformer than for the gauche conformer even though fewer transition frequencies were determined extending to lower J and, in particular, Ka quantum numbers. We started with rotational and quartic centrifugal distortion parameters and weighted out lines that were difficult to reproduce. In the end, inclusion of only four additional sextic distortion parameters reproduced most of the transition frequencies well. The experimental line list is fairly sparse at higher Ka values (9 to 15), and they were difficult to fit at somewhat higher J (above 20). The residuals between observed and calculated frequencies showed only in some cases regular patterns. These residuals may be caused by perturbation of the rotational spectrum of the anti conformer or by blending of the assigned lines with other, unidentified lines. Therefore, we omitted these lines together with few lines having lower values of Ka which were also weak for the most part. Predictions beyond Ka = 8 or 9 should be viewed with caution because of these omissions. Transitions with such Ka values may not be so important for astronomical observations because the anti conformer is considerably higher in energy than the gauche conformer. Our resulting spectroscopic parameters are presented in Table 4. Associated line, parameter, and fit files along with additional auxiliary files will be available in the Fitting Spectra section of the CDMS4.
The experimental transition frequencies of the gauche conformers of the parent and 34S species of ethanethiol have been reproduced to 39.6 kHz and 38.1 kHz, respectively, about the same as in Kolesniková et al. (2014), where the rms values were 39 kHz and 41 kHz. However, we only required 34 parameters for the parent species whereas Kolesniková et al. (2014) used 41. In the case of the 34S isotopic species, 16 versus 19 parameters were floated. Therefore, we expect our parameters to describe the rotational spectrum better. Predictions much beyond the covered quantum number range (J ≤ 88, Ka ≤ 25 for the parent species) should be viewed with caution. Such transitions are likely well beyond the scope of astronomical observations.
We looked into intensity alterations dependent on sign changes of the dipole moment components and found these alterations to be much smaller and much rarer than in ethanol (see Sect. 2.3). Nevertheless, predicted intensities should be viewed with some caution.
Our values of EKK, EKKK, and EKKKK are fairly large in magnitude, possibly indicating perturbations of the spectrum by its lowest vibrational mode or by the anti conformer. Schmidt & Quade (1975) determined Fbc = 12.20 MHz and Fac = 139.34 MHz. The former agrees perfectly with our value, and the agreement for the latter is reasonable if we take into account that in our case the uncertainty is 0.69 MHz and in the case of Schmidt & Quade (1975) it is at least several megahertz.
We have also determined spectroscopic parameters of the anti conformer using Watson’s A reduction for comparison purposes with parameters of Kolesniková et al. (2014) and with values from quantum chemical calculations (Puzzarini et al. 2014). These parameters are given in Table 5.
The two sets of experimental rotational and quartic centrifugal distortion parameters agree well, the small, but significant differences in ΔK and δK are caused by larger differences between the higher order parameters. The agreement is also good for values calculated by quantum chemical means. The rotational parameters include first-order vibrational corrections and are commonly marginally larger than the experimental ones at that level of computation. Quantum chemically calculated distortion parameters usually do not include vibrational corrections. The deviations between calculated quartic centrifugal distortion parameters and the experimental values are largely caused by this neglect. The agreement between the two sets of experimental parameters is moderate to poor for the few sextic distortion parameters used in the present fit. The very large LK value in Kolesniková et al. (2014) is largely responsible for the much smaller value of ΦK. In fact, contributions of LK are larger than those of ΦK already at Ka = 5. The agreement is also poor between either set of sextic distortion parameters and those derived from quantum chemical calculations. Puzzarini et al. (2014) attributed these deviations entirely to errors in the experimental values. However, all three values (gauche- and anti-ethanethiol and dimethyl sulfide) of ΦK ≈ HK were reported as negative in that work. This is very unusual for an asymmetric top rotor close to the prolate limit, which usually has a positive value. For example, ~23 and ~18 Hz were obtained for the anti conformers of the two isotopomers of ethanol with one 13C (Bouchez et al. 2012), ~13.5 Hz for dimethyl ether with 0 (Endres et al. 2009), 1, and 2 13C atoms (Koerber et al. 2013), and 93 Hz for propargyl alcohol (Pearson & Drouin 2005). Therefore, we suspect that there are errors in the quantum chemical calculations of sextic distortion parameters in Puzzarini et al. (2014).
2.5. normal-Propanol, n-C3H7OH
Replacing one H atom at the terminal C atom in ethanol with a CH3 group yields the unbranched n-propanol. There are three possibilities for doing so with CCCO dihedral angles of 180° or ± 60°. As in the case of the HOCC dihedral, the conformations are called anti (or trans) and gauche, the latter being doubly degenerate. Orientations of the methyl group are designated by upper-case characters, those of the OH group by lower-case characters. The Ga conformer is lowest in energy, and the two non-equivalent Gg and Gg’ conformers are higher by 68.81 K and 73.17 K, respectively, as determined from perturbations in rotational transitions of Ga at high Ka quantum numbers and from perturbations between Gg and Gg’ (Kisiel et al. 2010). The energy of the Aa conformer relative to Ga is known only approximately, but it appears to be lower than that of either Gg and Gg’ (Kahn & Bruice 2005). The doubly degenerate Ag conformer is also quite close in energy to the other conformers (Kahn & Bruice 2005), and tunneling between the two equivalent conformers will likely lead to two distinguishable Ag+ and Ag− states. Uncertainties of the relative energies of the A conformers are difficult to estimate, but are probably at least 10 K if not a multiple thereof.
Predictions of the rotational spectrum of Ga-n-propanol were taken from the CDMS. The entry is based on the extensive data from Maeda et al. (2006a) with experimental data almost exclusively from that work. Frequencies of perturbed transitions were omitted. These transitions all have rather high values of Ka and will be of importance for astronomical observations only if lower energy transitions have been detected with very high signal-to-noise ratios and at high rotational temperatures. Dipole moment components of μa = 0.4914 (4) D, μb = 0.9705 (13) D, and μc = 0.9042 (12) D were determined by Kisiel et al. (2010) from a single state fit. Based on the relative energies of the n-propanol conformers, their total column density in the ground vibrational state at 150 K is about a factor of 3.3 higher than that determined for the Ga conformer; inclusion of thermal population of vibrational states (Fukushima & Zwolinski 1968) yields a combined factor of about 5.2.
2.6. iso-Propanol, i-C3H7OH
Replacing one H atom at the central C atom in ethanol by a CH3 group yields the branched i-propanol. The two positions are equivalent. There are again three orientations for the OH group: anti (or trans) and the doubly degenerate gauche. Tunneling between the two equivalent gauche conformers leads again to gauche+ and gauche−, which are separated by 2.236 K (Maeda et al. 2006b). There is consensus that the anti conformer is higher in energy than the gauche conformers, but the amount differs considerably. Intensity measurements at millimeter wavelengths (Maeda et al. 2006b) yielded a difference of ~120 K with an estimated uncertainty of 15 K. This value is in reasonable agreement with 81 K (Kahn & Bruice 2005) and with 227 ± 104 K from intensity measurements in the microwave region (Hirota 1979). A value of 12.5 K (Inagaki et al. 1973) appears to be too small. We have employed an energy difference of 100 K as the average of the two determinations judged to be most reliable. At 150 K rotational temperature, this leads to a column density correction factor of 1.26 from thermal population of the anti conformer. Taking into account vibrational data from Inagaki et al. (1973) and Dobrowolski et al. (2008) yields a combined conformational and vibrational correction factor to the partition function of ~1.86.
Predictions were generated from data summarized in Maeda et al. (2006b), which are based largely on measurements from that work covering most of the 115−360 GHz region. Hirota (1979) determined μa = 1.114 (15) D between the gauche substates and μb = 0.737 (25) D and μc = 0.8129 (49) D within the gauche substates.
3. Observations and data reduction
Part of the observations used in this article have been briefly described in Belloche et al. (2014). A detailed account of the observations, reduction, and analysis method of the full data set is reported in a companion paper (Belloche et al. 2016).
4. Results
4.1. Methanol CH3OH
Methanol is well detected toward Sgr B2(N2) in its vibrational ground state and in its first torsionally excited state νt = 1 (Figs. A.1 and A.2). The second torsionally excited state is relatively well detected as well, with about three detected lines and seven additional lines that contribute significantly to the detected signal (Fig. A.3). The six lines between 96.19 and 96.56 GHz are the a-type (ΔK = 0) transitions with J = 2−1. The remaining features are b-type transitions with J ≤ 21. The third torsionally excited state (νt = 3) cannot be considered as unambiguously detected; however, since it contributes significantly to the flux detected at 96 268 MHz (21−11 of E symmetry) according to our model that uses the same parameters as for the lower states, we include it in the full model (Fig. A.4).
The 13C isotopolog
of methanol is also clearly detected, both in its ground state and in νt = 1 (Figs. A.5 and A.6). Some
lines in the ground state are marginally optically thick (τmax = 1.3).
About eight lines of the 18O isotopolog are detected in its vibrational ground
state, which makes the assignment secure (Fig. A.7).
The J =
2−1a-type transitions occur at 91 958 MHz (not shown,
strongly blended), around 92 730 MHz, and at 93 506 MHz. The remainder are b-type transitions with low
values of K
and low to moderate values of J. Their emission is optically thin
(τmax =
0.14). Transitions from within νt = 1 are not unambiguously
detected for this isotopolog, but its emission contributes significantly to the line
detected at 97 069 MHz (Fig. A.8) which is why we
included it in the full model. Our model allows us to derive the following isotopic ratios
for methanol: 12C/13C ≈25 and 16O/18O ≈180. The 13CH3OH/CH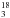 OH ratio is ~7.3.
OH ratio is ~7.3.
The fits to the integrated intensity maps of the detected methanol lines yield a source size that decreases with increasing energy level, from ~1.4″ at low energy to ~1.0″ at Eup≈1000 K. A similar behavior is found for the 13C isotopolog over a narrower energy range. The population diagrams of methanol (restricted to its transitions with an opacity lower than 2) and its isotopologs are very well fitted with a rotation temperature of about 140−160 K (Table 6 and Figs. A.9−A.11). The rotation temperature of the CH3OH ground vibrational state is constrained at low to moderate energies, for example, by the J-2−J1 transitions of E symmetry. The lines are very weak at low J (J = 2−4 near 101.1 GHz), but have substantial opacities at higher J; J = 17 at 111626.5 MHz is the last line in the region of our survey. On the higher energy side are the two asymmetry split 265−256 transitions of A symmetry around 97 210 MHz. The spectra of the optically thick lines of methanol require a large size and high temperature to be well fitted. Our LTE model thus assumes a source size of 1.4″ and a rotational temperature of 160 K. The fit is good for most lines of all three isotopologs, except for the shape of the very optically thick lines of methanol (with τ up to 19) and the likely masing lines at 84 521 and 95 169 MHz (5-1−40 of E symmetry and 80−71 of A+ symmetry, respectively; see, e.g., Müller et al. 2004).
Rotational temperatures derived from population diagrams of alkanols and alkanethiols toward Sgr B2(N2).
Parameters of our best-fit LTE model (or upper limit) of alkanols and alkanethiols toward Sgr B2(N2).
4.2. Ethanol C2H5OH
About 170 lines of ethanol are detected toward Sgr B2(N2) in its vibrational ground state (Fig. A.12). The fits to the integrated intensity maps of these lines yield a median source size of ~1.3′′, with no clear trend as a function of upper-level energy. The population diagram shown in Fig. A.13 yields a well-constrained rotational temperature (Table 6). We use a slightly higher temperature (150 K versus 140 K), still fully consistent with the intensities of the detected lines. With this source size and temperature, some lines turn out to be marginally optically thick (τmax = 1.2).
Both 13C isotopologs of ethanol are detected in their anti form with a few clearly detected lines each (Figs. A.14 and A.15). We derive a 12C/13C isotopic ratio of ~25 for ethanol, consistent with the one derived for methanol (see Sect. 4.1).
4.3. Propanol normal-C3H7OH and iso-C3H7OH
Propanol is not detected toward Sgr B2(N2) either in its straight chain form (normal) or in its branched form (iso). Assuming the same parameters as for ethanol, we derive upper limits to the column density of both forms (Table 7).
4.4. Methanethiol CH3SH
With about 12 lines clearly detected in its vibrational ground state, methanethiol is securely identified toward Sgr B2(N2) (Fig. A.16). We also identified torsionally excited transitions (νt = 1) belonging to the a-type J = 4−3 branch, which are shown in Fig. A.17. Even though they are slightly or heavily blended, two almost completely blended transitions, k = + 1 of E and 42,3−32,2 of A torsional symmetry near 100 806 MHz, account for essentially all of that emission feature. In addition, k = + 2 near 100 838 MHz and 41,3−31,2 of A torsional symmetry near 101522 MHz account for emission features that are part of a blend. The νt = 1 state is not unambiguously detected; however, since the synthetic spectrum computed with the same parameters as for the ground state is fully consistent with the observed spectrum, we consider this state as tentatively detected and we include it in the full model (Fig. A.17). The fits to the integrated intensity maps of the detected ground state lines yield a source size of ~1.4′′. The fit to the population diagram including both states is not well constrained (Trot = 210 ± 50 K, Table 6 and Fig. A.18). This fit is dominated by the more numerous lines in the vibrational ground state and tends to overestimate the intensities of the lines in the first vibrationally excited state. To avoid this overestimate when modeling the spectrum, we use a lower temperature of 180 K, still consistent with the fit result above. With this source size and temperature, the emission is optically thin (τmax = 0.3). The apparent discrepancy between the synthetic and observed spectra at 108 680 MHz is likely due to 13CN absorption produced by diffuse clouds along the line of sight, which we have not completely modeled so far. The small discrepancy at 110 342 MHz may be due to an overestimate of the level of the baseline. This frequency corresponds to the data point significantly below the model at Eu/kb ≈ 100 K (in red) in the population diagram.
4.5. Ethanethiol C2H5SH
Ethanethiol is not unambiguously detected toward Sgr B2(N2). Under the assumption of the same temperature, source size, linewidth, and velocity offset as for methanethiol (Sect. 4.4), the synthetic spectrum shown in Fig. A.19 is consistent with the observed spectrum, especially for the 114−104 multiplet near 111 647 MHz, but the lack of clearly detected lines prevents a secure identification. We consider this model as a 3σ upper limit to the column density of ethanethiol toward Sgr B2(N2) (Table 7).
5. Astrochemical modeling
In order to investigate the chemical formation and destruction mechanisms associated with CH3SH and C2H5SH, we incorporate a new set of reactions into the network presented by Belloche et al. (2014). This expanded network is used to simulate the coupled gas-phase and grain-surface chemistry occurring in Sgr B2(N2), using the kinetics model MAGICKAL (Garrod 2013).
Current astrochemical networks include relatively few sulfur-bearing molecules; with reference to the production of alkanethiols, none of them (to the authors’ knowledge) includes any treatment for the formation of sulfur-bearing molecules larger than H2CS. Here, in analogy with the dominant formation routes for methanol and ethanol in hot cores, as predicted by the chemical models, the new network concentrates on the production of alkanethiols solely on the surfaces of the dust grains. However, gas-phase destruction mechanisms for both molecules (as well as related intermediates) are included in the new network, the majority of which are ion-molecule processes or the subsequent dissociative recombination with electrons of the resultant molecular ions. Ion-molecule reactions are included for the major ionic species He+, H+, H3+, H3O+ and HCO+. Estimates for the rates of photo-dissociation of new molecules, as caused by cosmic ray-induced and (where extinction allows) external UV photons, are also included (see Garrod et al. 2008 and Garrod 2013).
For CH3SH, we assume the same grain-surface desorption/binding energy as for methanol (5534 K), which is based on the laboratory study of Collings et al. (2004). The weak hydrogen-bonding character of the thiol group is likely to result in a somewhat lower binding energy for methanethiol than for methanol in the amorphous water-dominated ices present on the dust grains; however, based on the greater observed rotational temperature for CH3SH than for CH3OH observed in our source (180 K versus 150 K), indicating a similar or greater desorption temperature for CH3SH, the adoption of the methanol-based value appears justified in the absence of appropriate laboratory data. In the case of C2H5SH, a binding energy of 6230 K is used − based on interpolation as detailed by Garrod (2013)− that is close to the value already adopted for ethanol (6259 K).
Methanethiol may form on grain surfaces through the addition of hydrogen atoms to H2CS. Both gas-phase and grain-surface formation routes already exist in the network for CS, HCS, and H2CS. The new network thus includes a chain of hydrogen addition reactions analogous to those for methanol, accounting for all hydrogenation states: CS, HCS, H2CS, CH3S/CH2SH and CH3SH. Methanethiol may also be formed via the addition of CH3 and HS, and other species in the chain may also be formed via alternative atomic additions, e.g., CH2 + S → H2CS. Ethanethiol may be formed by a selection of radical-radical and hydrogen-addition reactions on the grains, including CH3 + CH2SH and C2H5 + HS.
The physical model follows that detailed in previous papers where a cold collapse phase to maximum density (nH = 2 × 108 cm-3) and minimum dust-grain temperature (8 K) is followed by a warm-up from 8−400 K; during this phase, the gas and dust temperatures are assumed to be well coupled.
The initial chemical compositions used in the model follow those of Garrod (2013). Crucially, a standard, depleted sulfur abundance of 8 × 10-8 is used, which reproduces well the relative abundances of the sulfur-bearing molecules. The underlying reason for the anomalous depletion of atomic sulfur in dense regions (as compared to diffuse cloud values) is a long-standing problem (e.g., Anderson et al. 2013), and will not be addressed here.
5.1. Results of modeling
Figure 3 shows the results of the models, for CH3SH, C2H5SH, and a selection of related molecules (a), and their oxygen-substituted equivalents, each of which is a well-known hot-core molecule (b). The plots indicate the calculated time-dependent abundances of each molecule with respect to molecular hydrogen, during the warm-up phase of the chemistry. Solid lines indicate gas-phase abundances, while dotted lines of the same color indicate ice-mantle abundances for the same species.
Most of the CH3SH is formed early, during the cold collapse phase, when the CS accreted from the gas-phase is efficiently converted to H2CS via atomic hydrogen addition, and thence to CH3SH. In common with the methanol-producing series, the addition of H to CS and H2CS is expected in both cases to have an activation energy barrier. Previous networks have assumed a value of 1000 K for H + CS → HCS (e.g. Hasegawa et al. 1992), which is unaltered here. The hydrogenation of H2CS is a newly added process in this network, to which a barrier of 1000 K is also assigned. This reaction is allowed three product branches, each of which are given equal weight: CH3S, CH2SH, and HCS + H2 (corresponding to hydrogen abstraction). Most of the CS, that is accreted onto the grains during collapse, is ultimately converted into and stored as CH3SH in the ices.
Desorption of CH3SH from the dust grains becomes important above around 100 K; peak gas-phase abundance for this molecule occurs at a temperature of 119 K (see Table 8). In spite of the identical binding energy adopted for methanethiol as for methanol, CH3SH still reaches a gas-phase peak at a somewhat lower temperature than CH3OH; the large total abundance of methanol on the grains causes its release to take longer and peak later than for methanethiol. The peak gas-phase abundance of CH3SH is also lower than the peak value obtained on the grain surfaces; abstraction of hydrogen from methanethiol by surface radicals, including, most prominently, NH2, causes destruction of this molecule just prior to its release into the gas phase, reducing the overall peak by a factor of ~3. While similar H-abstraction processes also exist for methanol, the exothermicity of these reactions is low and results in larger activation energy barriers (and thus smaller rates). Barriers for abstraction reactions are based on experimental values where available, or calculated using the Evans-Polanyi relation (as detailed by Garrod 2013); barriers involving methanethiol are obtained with the last method.
Formation of C2H5SH is achieved through three main processes, occurring at ~20−30, 45, and 55 K. The first is the addition reaction CH3 + CH2SH → C2H5SH; this process is analogous to the dominant mechanism for ethanol formation in the model, and C2H5SH abundance in the ices shows similar behavior to that of ethanol in the 20−40 K temperature range.
At around 45 K, the addition of atomic H to the C2H5S radical becomes more important, contributing an abundance of a few 10-10 × n(H2). The C2H5S radical is itself formed by the addition of S atoms to C2H5, which is produced when acetylene in the bulk ice mantles becomes mobile, allowing it to be hydrogenated on the ice surface.
At 55 K, the main C2H5SH-producing event occurs, when H2S becomes mobile, dredges up from the bulk ice mantle, and desorbs from the ice surface. While most H2S is desorbed into the gas phase, some reacts with atomic H, which abstracts a hydrogen atom to give HS. This radical may then quickly react with C2H5 to produce ethanethiol. C2H5SH ultimately desorbs, reaching peak gas-phase abundance at a similar temperature to the alcohols. It should be noted that essentially all H2S in the ices is converted to C2H5SH through this mechanism, as can be clearly seen in Fig. 3a. However, there is no analogous conversion of H2S into CH3SH, as the CH3 radical is no longer present in significant abundance when H2S and HS become mobile on the grains. Neither does the addition of the OH radical to CH3/C2H5 provide any significant formation route for methanol/ethanol, analogous to the HS-related mechanisms. While the photodissociation of water ice provides abundant OH, its mobility is relatively low at these temperatures.
By the end of the model run, at 400 K, CS and H2CS comprise more than 50% of the sulfur budget; the remainder resides mostly in SO and SO2 (not shown).
5.2. Discussion of modeling
For the alcohols, the CH3OH/C2H5OH ratio of 78 produced by the models, comparing peak abundances, is a reasonable match to the observed value of ~20. In spite of the approximate nature of the overall sulfur abundance in the models due to the uncertainty in initial atomic sulfur budget, the modeled C2H5OH/C2H5SH ratio of 225 is in line with the observed lower limit of 125.
Peak abundance for CH3SH produced by the model is somewhat lower than the observations demand. A modeled ratio of CH3SH/C2H5SH = 3.1 is obtained, compared with the observed value of >21. Similarly, the ratio of methanol to methanethiol is around 50 times larger (~5700 versus 120) than the observed ratio, suggesting that the low CH3SH/C2H5SH ratio is caused more by an underprediction of CH3SH relative to the other three molecules rather than by an overprediction of C2H5SH. However, it should be noted that CH3SH is released from the grains at lower temperatures than either methanol or ethanethiol in the models. This would tend to produce a somewhat larger spatial extent for methanethiol under a three-dimensional treatment of the core, and would likely result in a greater average column density than is indicated when comparing peak abundances for each molecule. The differing sublimation characteristics of CH3SH may therefore improve its column density ratio with other molecules. Direct laboratory determination of the methanethiol binding energy on a water/methanol surface would give greater confidence to the comparison with observed column density values.
The low initial abundance of sulfur assumed in this model allows room for the methanethiol abundance to be increased through this variable; however, alternative model runs indicate that ethanethiol abundances also scale in this way. Lower efficiency in the early-stage formation of H2S on the grains could reduce the C2H5SH abundance, as could lower acetylene production. Acetylene abundances ultimately rely on the quantity of ice-mantle methane formed during the cold collapse stage, which is released into the gas phase at temperatures around 25 K, producing a range of hydrocarbons.
 |
Fig. 3 Chemical model abundances for a selection of sulfur-bearing molecules a) and their oxygen-bearing analogs b). Solid lines indicate gas-phase abundances; dotted lines of the same color indicate the grain-surface/ice abundances of the same species. |
Results of chemical kinetics modeling of alkanethiols and alkanols toward Sgr B2(N2).
6. Discussion
Column density ratios of alkanols and alkanethiols in different sources.
In light of the extensive number of emission features detected for CH3OH, C2H5OH, and CH3SH in our sensitive ALMA data toward Sgr B2(N2), it is noteworthy that we detect only a few, rather weak, and partially or completely blended lines that can be attributed to C2H5SH. Consequently, we are unable to claim even a tentative detection of the molecule. We consider the low upper limit to the column density of ethanethiol (Table 7) to be meaningful. In fact, comparing the Sgr B2(N2) column density ratios of alkanols and alkanethiols (or their lower limits) in Table 9, it is conceivable that the column density of C2H5SH is close to the upper limit. With so many potential ethanethiol lines partially or strongly blended in our ALMA data, additional observations at longer wavelengths may be more promising than more sensitive observations at 3 mm or observations at shorter wavelengths.
The non-detection of ethanethiol in Sgr B2(N2) is rather surprising in the context of the purported detection of the molecule in Orion KL at a column density that yields CH3SH/C2H5SH and C2H5OH/C2H5SH ratios that are much lower than our lower limits. The ratios (Table 9) are 5 and 20, respectively, ignoring the presence of the anti-conformer, or 4 and 16 if we assume a thermal (200 K) population of this conformer. Our numbers are ≳21 and ≳125, respectively. In contrast, the CH3OH/CH3SH ratios are identical, and the CH3OH/C2H5OH values are quite similar, 20 and 31, respectively. Inspection of the features reported in Kolesniková et al. (2014) as detected shows one isolated emission feature (near 243.58 GHz) assigned to ethanethiol. A small number of fairly isolated lines were assigned in part to the molecule. The majority of the potential C2H5SH lines, however, are strongly blended. More importantly, the model of all species excluding C2H5SH leaves no room for any ethanethiol contribution in the isolated emission feature near 263.90 GHz. The high abundance of C2H5SH relative to CH3SH and the alkanols in Orion KL compared to Sgr B2(N2), and the issues we pointed out concerning the identification of C2H5SH in the Orion KL spectrum suggest that the presence of ethanethiol in Orion KL is uncertain. Unfortunately, our chemical model calculations are not accurate enough, in particular for CH3SH, to support or dismiss the reported C2H5SH detection in Orion KL.
The column density of CH3SH is relatively high in G327.3−0.6, yielding a CH3OH/CH3SH ratio of 58 (Gibb et al. 2000), half the value in Sgr B2(N2) and Orion KL. On the other hand, the CH3OH/C2H5OH ratio is 82, higher than in Orion KL, and even higher than in Sgr B2(N2). On the basis of column density ratios alone, it is difficult to judge how promising a search for ethanethiol in G327.3−0.6 would be. We point out that we did not use the quoted column density of CH3OH from Gibb et al. (2000). Instead, we used the 13CH3OH column density and the quoted 12C/13C ratio of 40; the reported CH3OH/13CH3OH ratio was actually 10, suggesting substantial CH3OH opacities.
In their 1.3 mm line survey toward three positions in Sgr B2, Nummelin et al. (1998, 2000) detected CH3OH, C2H5OH, and CH3SH toward not only Sgr B2(N), but also toward Sgr B2(M). Judging from their 12C/13C ratios for methanol, these column densities are affected by substantial opacities. Emission of C2H5OH and CH3SH may be less prone to opacity biases. Their ratios are 3.8 and 1.4 for Sgr B2(N), whose emission is likely dominated by Sgr B2(N1), and Sgr B2(M), respectively. Both values are smaller than 5.9 for Sgr B2(N2), though not by much for Sgr B2(N). The Orion KL value is essentially identical to the one from Sgr B2(N), whereas the G327.3−0.6 value of 0.7 is even more extreme than the one from Sgr B2(M).
Our upper limit to the column density of normal-propanol is not very constraining in comparison to our CH3OH/C2H5OH ratio of 20, as it translates to a C2H5OH/n-C3H7OH ratio of ≳ 7.7. In the case of the Galactic center molecular cloud MC G+0.693−0.027, the column density ratio between CH3OH and C2H5OH is ~14 (Requena-Torres et al. 2008), lower than the Sgr B2(N2) value, but the lower limit to the C2H5OH to n-C3H7OH ratio is only ~4.5, which was derived from the CH3OH to C2H5OH and the CH3OH to n-C3H7OH ratios (Requena-Torres et al. 2008). In their paper on the tentative detection of ethyl methyl ether, Tercero et al. (2015) mention a ground state column density ratio of ≳60. Taking column density corrections by vibrational states for both molecules and by other conformers for n-propanol into account (see Table 7) the column density ratio becomes ≳14.3, slightly more constraining than ours. However, should our C2H5CN/n-C3H7CN ratio of ~55 (Belloche et al. 2016 and rescaled for the same source size of 1.2′′ in the case of n-C3H7CN, Belloche et al. 2014) be more appropriate for the estimation of the column density of n-C3H7OH, then all available observational results are not so meaningful. Our upper limit to the column density of iso-propanol translates to a C2H5OH/i-C3H7OH ratio of ≳ 21.5, which may be meaningful if the i-C3H7OH/n-C3H7OH ratio is considerably larger than the i-C3H7CN/n-C3H7CN ratio of ~0.4 in Sgr B2(N2) (Belloche et al. 2014).
Our tentative detection of torsionally excited methanethiol is the first such account; previously only ground state transitions had been identified. On the other hand, observations of CH3OH, νt = 2 and 13CH3OH, νt = 1 had been reported before, e.g., in Sgr B2(N) by Nummelin et al. (1998) and in Orion KL by Schilke et al. (2001).
We determined an isotopic ratio of ~25 for CH3OH/13CH3OH and for the ratio of parent ethanol to both of its isotopologs with one 13C. This value is slightly larger than our ratio determined for the main isotopic species of vinyl cyanide to all three of its singly 13C substituted species of 21 ± 1 (Müller et al. 2008). These ratios are in good to reasonable agreement with a value of ~20 in Galactic center sources (Wilson & Rood 1994; Milam et al. 2005) or the range of ~20 to 25 derived by Güsten et al. (1985).
Our CH3OH/CH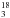 OH and 13CH3OH/CH
OH and 13CH3OH/CH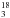 OH ratios of ~180 and ~7.3 are in very good agreement with
respective Sgr B2 values of 210 ±
40 and 7.5 ±
1.0 (Gardner et al. 1989) or with
~200 and 8.6 ± 1.2 for respective H2CO values in Sgr B2 and the
Galactic center source M−0.13−0.18
(Güsten et al. 1985). Wilson & Rood (1994) summarized isotopic ratios of ~250 and ~12.5 in the Galactic center ISM, in
reasonable agreement with our values.
OH ratios of ~180 and ~7.3 are in very good agreement with
respective Sgr B2 values of 210 ±
40 and 7.5 ±
1.0 (Gardner et al. 1989) or with
~200 and 8.6 ± 1.2 for respective H2CO values in Sgr B2 and the
Galactic center source M−0.13−0.18
(Güsten et al. 1985). Wilson & Rood (1994) summarized isotopic ratios of ~250 and ~12.5 in the Galactic center ISM, in
reasonable agreement with our values.
The isotopic ratios in the Galactic center ISM are rather different from the solar system values of about 89 and 490 for the 12C/13C and 16O/18O ratios, respectively. These changes reflect gradients in the isotopic ratios from the center of the Milky Way to its outer regions which, in addition, change with time. This aspect explains small, but non-negligible differences between the solar system values and those determined in the local ISM (e.g., Güsten et al. 1985; Wilson & Rood 1994; Milam et al. 2005).
7. Conclusion
Our sensitive ALMA data permitted clear detections of methanethiol with the first, albeit tentative, detection of lines in its first excited torsional state, ethanol, with the first unambiguous detection of the singly 13C substituted isotopomers, and three isotopologs of methanol; the main species was detected in several torsional states, including some evidence of its third excited torsional state. However, they were not sensitive enough for a clear detection of ethanethiol, though a comparison to CH3SH and alkanols suggests that its column density could be close to the upper limit derived here. We also obtained upper limits to the column densities of normal- and iso-propanol. Our values for the 12C/13C ratio obtained for methanol and ethanol and for the 16O/18O ratio obtained for methanol are in line with the values known for the ISM in the Galactic center region.
The column density ratios involving methanol, ethanol, and methanethiol in Sgr B2(N2) are similar to values reported for Orion KL, but those involving ethanethiol are significantly different and suggest that the detection of ethanethiol reported toward Orion KL is rather uncertain.
The chemical models presented here include new reactions for the formation and destruction of methanethiol and ethanethiol. This represents a step forward in the complexity of sulfur chemistry that can be treated with astrochemical models. The results indicate that adequate abundances of both alkanethiols may be formed in hot cores through dust-grain surface/ice-mantle chemistry. Methanethiol is formed at the low temperatures achieved during cold core collapse (on the order 10 K). Ethanethiol is produced on the grains at elevated temperatures (~45−55 K), with most of the surface H2S at those temperatures being converted almost entirely to ethanethiol. The modeled gas-phase ratio CH3SH/C2H5SH ≃ 3 is substantially lower than the observed value of >21. The strongest influence on this ratio is likely the underprediction of CH3SH (in comparison to CH3OH), although the efficient formation of C2H5SH from H2S on the grains is also a source of uncertainty.
In addition, more sensitive observations of Sgr B2(N), Orion KL, or other sources with ALMA or other interferometers are required to establish whether and possibly in what quantities ethanethiol, normal-propanol, and iso-propanol are present in the ISM. Such observations may be more promising at wavelengths longer than 3 mm for the first two molecules.
Acknowledgments
This paper makes use of the following ALMA data: ADS/JAO.ALMA#2011.0.00017.S, ADS/JAO.ALMA#2012.1.00012.S. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada), NSC and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ. The interferometric data are available in the ALMA archive at https://almascience.eso.org/aq/. This work has been supported by the Deutsche Forschungsgemeinschaft (DFG) through the collaborative research grant SFB 956 “Conditions and Impact of Star Formation”, project area B3. We thank Dr. Monika Koerber for making an ethanol spectrum available for inspection of the relative intensities. L.H.X. and R.M.L. acknowledge financial support from the Natural Sciences and Engineering Research Council (NSERC) of Canada. R.T.G. acknowledges support from the NASA Astrophysics Theory Program through grant NNX11AC38G. A.W. acknowledges financial support from the CNRS program “Physique et Chimie du Milieu Interstellaire (PCMI). Our research benefited from NASA’s Astrophysics Data System (ADS).
References
- Anderson, D. E., Bergin, E. A., Maret, S., Wakelam, V. 2013, ApJ, 779, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Ball, J. A., Gottlieb, C. A., Lilley, A. E., & Radford, H. E. 1970, ApJ, 162, L203 [NASA ADS] [CrossRef] [Google Scholar]
- Belloche, A., Menten, K. M., Comito, C., et al. 2008, A&A, 482, 179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belloche, A., Garrod, R. T., Müller, H. S. P., et al. 2009, A&A, 499, 215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belloche, A., Müller, H. S. P., Menten, K. M., Schilke, P., & Comito, C. 2013, A&A, 559, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belloche, A., Garrod, R. T., Müller, H. S. P., & Menten, K. M. 2014, Science, 345, 1584 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Belloche, A., Müller, H. S. P., Garrod, R. T., & Menten, K. M. 2016, A&A, 587, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bettens, F. L., Sastry, K. V. L. N., Herbst, E., et al. 1999, ApJ, 510, 789 [NASA ADS] [CrossRef] [Google Scholar]
- Bisschop, S. E., Jørgensen, J. K., van Dishoeck, E. F., & de Wachter, E. B. M. 2007, A&A, 465, 913 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bisschop, S. E., Jørgensen, J. K., Bourke, T. L., Bottinelli, S., & van Dishoeck, E. F. 2008, A&A, 488, 959 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouchez, A., Walters, A., Müller, H. S. P., et al. 2012, J. Quant. Spectr. Rad. Transf., 113, 1148 [NASA ADS] [CrossRef] [Google Scholar]
- Cernicharo, J., Marcelino, N., Roueff, E., et al. 2012, ApJ, 759, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Christen, D., & Müller, H. S. P. 2003, Phys. Chem. Chem. Phys., 5, 3600 [Google Scholar]
- Cohen, E. A., & Pickett, H. M. 1982, J. Mol. Spectr., 93, 83 [Google Scholar]
- Collings, M. P., Anderson, M. A., Chen, R., et al. 2004, MNRAS, 354, 1133 [NASA ADS] [CrossRef] [Google Scholar]
- Coudert, L. H., Drouin, B. J., Tercero, B., et al. 2013, ApJ, 779, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Crockett, N. R., Bergin, E. A., Neill, J. L., et al. 2014, ApJ, 787, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Dobrowolski, J. C., Ostrowski, S., Kołos, R., & Jamróz, M. H. 2008, Vib. Spectr., 48, 82 [CrossRef] [Google Scholar]
- Durig, J. R., & Larsen, R. A. 1990, J. Mol. Struct, 238, 195 [Google Scholar]
- Durig, J. R., Bucy, W. E., Wurrey, C. J., & Carreira, L. A. 1975, J. Phys. Chem., 79, 988 [CrossRef] [Google Scholar]
- Endres, C. P., Müller, H. S. P., Brünken, S., et al. 2006, J. Mol. Struct, 795, 242 [NASA ADS] [CrossRef] [Google Scholar]
- Endres, C. P., Drouin, B. J., Pearson, J. C., et al. 2009, A&A, 504, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fisher, J., Paciga, G., Xu, L.-H., et al. 2007, J. Mol. Spectr., 245, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Fortman, S. M., Neese, C. F., & De Lucia, F. C. 2014, ApJ, 782, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Fukushima, K., & Zwolinski, B. J. 1968, J. Mol. Spectr., 26, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Gardner, F. F., & Whiteoak, J. B. 1981, MNRAS, 194, 37P [NASA ADS] [Google Scholar]
- Gardner, F. F., Whiteoak, J. B., Reynolds, J., Peters, W. L., & Kuiper, T. B. H. 1989, MNRAS, 240, 35P [NASA ADS] [CrossRef] [Google Scholar]
- Garrod, R. T. 2013, ApJ, 765, 60 [Google Scholar]
- Garrod, R. T., Widicus Weaver, S. L., Herbst, E., 2008, ApJ, 682, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Gottlieb, C. A., Ball, J. A., Gottlieb, E. W., & Dickinson, D. F. 1979, ApJ, 227, 422 [NASA ADS] [CrossRef] [Google Scholar]
- Gibb, E., Nummelin, A., Irvine, W. M., Whittet, D. C. B., & Bergman, P. 2000, ApJ, 545, 309 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Güsten, R., Henkel, C., & Batrla, W. 1985, A&A, 149, 195 [NASA ADS] [Google Scholar]
- Henkel, C., Wilson, T. L., Walmsley, C. M., & Pauls, T. 1983, A&A, 127, 388 [NASA ADS] [Google Scholar]
- Hasegawa, T. I., Herbst, E. & Leung, C. M. 1992, ApJS, 82, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Herbst, E., Messer, J. K., De Lucia, F. C., & Helminger, P. 1984, J. Mol. Spectr., 108, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Hirota, E. 1979, J. Phys. Chem., 83, 1457 [Google Scholar]
- Hollis, J. M., Lovas, F. J., Jewell, P. R., & Coudert, L. H. 2002, ApJ, 571, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Hoshino, Y., Ohishi, M., Akabane, K., et al. 1996, ApJS, 104, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Ikeda, M., Duan, Y.-B., Tsunekawa, S., & Takagi, K. 1998, ApJS, 117, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Ikeda, M., Ohishi, M., Nummelin, A., et al. 2001, ApJ, 560, 792 [NASA ADS] [CrossRef] [Google Scholar]
- Inagaki, F., Harada, I., & Shimanouchi, T. 1973, J. Mol. Spectr., 46, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Ivash, E. V., & Dennison, D. M. 1953, J. Chem. Phys., 21, 1804 [NASA ADS] [CrossRef] [Google Scholar]
- Jørgensen, J. K., Favre, C., Bisschop, S. E., et al. 2012, ApJ, 757, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Kakar, R. K., & Quade, C. R. 1980, J. Chem. Phys., 72, 4300 [NASA ADS] [CrossRef] [Google Scholar]
- Kahn, K., & Bruice, T. C. 2005, Chem. Phys. Chem., 6, 487 [Google Scholar]
- Kisiel, Z., Dorosh, O., Maeda, A., et al. 2010, Phys. Chem. Chem. Phys., 12, 8329 [CrossRef] [Google Scholar]
- Kleiner, I. 2010, J. Mol. Spectr., 260, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Koerber, M., Bisschop, S. E., Endres, C. P., et al. 2013, A&A, 558, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kolesniková, L., Daly, A. M., Alonso, J. L., Tercero, B., & Cernicharo, J. 2013, J. Mol. Spectr., 289, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Kolesniková, L., Tercero, B., Cernicharo, J., et al. 2014, ApJ, 784, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Kuriyama, H., Takagi, K., Takeo, H., & Matsumura, C. 1986, ApJ, 311, 1073 [NASA ADS] [CrossRef] [Google Scholar]
- Lees, R. M., & Baker, J. G. 1968, J. Chem. Phys., 48, 5299 [NASA ADS] [CrossRef] [Google Scholar]
- Lees, R. M., & Mohammadi, M. A. 1980, Can. J. Phys., 58, 1640 [NASA ADS] [Google Scholar]
- Leurini, S., Schilke, P., Menten, K. M., et al. 2004, A&A, 422, 573 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leurini, S., Schilke, P., Wyrowski, F., & Menten, K. M. 2007, A&A, 466, 215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Linke, R. A., Frerking, M. A., & Thaddeus, P. 1979, ApJ, 234, L139 [NASA ADS] [CrossRef] [Google Scholar]
- Loomis, R. A., Zaleski, D. P., Steber, A. L., et al. 2013, ApJ, 765, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Maeda, A., De Lucia, F. C., Herbst, E., et al. 2006a, ApJS, 162, 428 [NASA ADS] [CrossRef] [Google Scholar]
- Maeda, A., Medvedev, I. R., De Lucia, F. C., & Herbst, E. 2006b, ApJS, 166, 650 [NASA ADS] [CrossRef] [Google Scholar]
- Manocha, A. S., Fateley, W. G., & Shimanouchi, T. 1973, J. Phys. Chem., 77, 1977 [CrossRef] [Google Scholar]
- Maury, A. J., Belloche, A., André, P., et al. 2014, A&A, 563, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McMillan, J. P., Fortman, S. M., Neese, C. F., & De Lucia, F. C. 2014, ApJ, 795, 56 [NASA ADS] [CrossRef] [Google Scholar]
- McNaughton, D., & Evans, C. J. 1999, J. Mol. Spectr., 196, 274 [NASA ADS] [CrossRef] [Google Scholar]
- Milam, S. N., Savage, C., Brewster, M. A., Ziurys, L. M., & Wyckoff, S. 2005, ApJ, 634, 1126 [NASA ADS] [CrossRef] [Google Scholar]
- Moruzzi, G., Winnewisser, B. P., Winnewisser, M., Mukhopadhyay, I., & Strumia, F. 1995, Microwave, infrared & laser transitions of methanol: Atlas of assigned lines from 0 to 1258 cm-1 (Boca Raton, FL, USA: CRC Press) [Google Scholar]
- Müller, H. S. P. 2013, J. Quant. Spectr. Rad. Transf., 130, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, H. S. P., Thorwirth, S., Roth, D. A., & Winnewisser, G. 2001, A&A, 370, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, H. S. P., Menten, K. M., Mäder, H. 2004, A&A, 428, 1019 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct, 742, 215 [CrossRef] [Google Scholar]
- Müller, H. S. P., Belloche, A., Menten, K. M., et al. 2008, J. Mol. Spectr., 251, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, H. S. P., Dong, F., Nesbitt, D. J., Furuya, T., & Saito, S. 2010, Phys. Chem. Chem. Phys., 12, 8362 [CrossRef] [Google Scholar]
- Mukhopadhyay, I., & Sastry, K. V. L. N. 2015, J. Mol. Spectr., 312, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Neill, J. L., Crockett, N. R., Bergin, E. A., Pearson, J. C., & Xu, L.-H. 2013, ApJ, 777, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Neill, J. L., Bergin, E. A., Lis, D. C., et al. 2014, ApJ, 789, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Nummelin, A., Bergman, P., Hjalmarson, Å., et al. 1998, ApJS, 117, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Nummelin, A., Bergman, P., Hjalmarson, Å., et al. 2000, ApJS, 128, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Pearson, J. C., & Drouin, B. J. 2005, J. Mol. Spectr., 234, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Pearson, J. C., Sastry, K. V. L. N., Herbst, E., & De Lucia, F. C. 1996, J. Mol. Spectr., 175, 246 [NASA ADS] [CrossRef] [Google Scholar]
- Pearson, J. C., Sastry, K. V. L. N., Herbst, E., & De Lucia, F. C. 1997, ApJ, 480, 420 [NASA ADS] [CrossRef] [Google Scholar]
- Pearson, J. C., Brauer, C. S., & Drouin, B. J. 2008, J. Mol. Spectr., 251, 394 [NASA ADS] [CrossRef] [Google Scholar]
- Pearson, J. C., Brauer, C. S., Drouin, B. J., & Xu, L.-H. 2009, Can. J. Phys., 87, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Pearson, J. C., Daly, A. M., & Lees, R. M. 2015, J. Mol. Spectr., 318, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Pickett, H. M. 1972, J. Chem. Phys., 56, 1715 [NASA ADS] [CrossRef] [Google Scholar]
- Pickett, H. M. 1991, J. Mol. Spectr., 148, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Pickett, H. M., Poynter, R. L., Cohen, E. A., et al. 1998, J. Quant. Spectr. Rad. Transf., 60, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Puzzarini, C., Senent, M. L., Domínguez-Gómez, R., et al. 2014, ApJ, 796, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Qin, S.-L., Schilke, P., Rolffs, R., et al. 2011, A&A, 530, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Requena-Torres, M. A., Martín-Pintado, J., Rodríguez-Franco, A., et al. 2006, A&A, 455, 971 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Requena-Torres, M. A., Martín-Pintado, J., Martín, S., & Morris, M. R. 2008, ApJ, 672, 352 [NASA ADS] [CrossRef] [Google Scholar]
- Sastry, K. V. L. N., Lees, R. M., & De Lucia, F. C. 1984, J. Mol. Spectr., 103, 486 [Google Scholar]
- Sastry, K. V. L. N., Herbst, E., Booker, R. A., & De Lucia, F. C. 1986, J. Mol. Spectr., 116, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Sastry, K. V. L. N., Vanderlinde, J., Donovan, D., Mukhopadhyay, I., & Gupta, P. K. 1994, J. Mol. Spectr., 168, 374 [NASA ADS] [CrossRef] [Google Scholar]
- Sastry, K. V. L. N., Mukhopadhyay, I., Gupta, P. K., & VanderLinde, J. 1996, J. Mol. Spectr., 176, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Schilke, P., Benford, D. J., Hunter, T. R., Lis, D. C., & Phillips, T. G. 2001, ApJS, 132, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, R. E., & Quade, C. R. 1975, J. Chem. Phys., 62, 3864 [NASA ADS] [CrossRef] [Google Scholar]
- Smirnov, I. A., Alekseev, E. A., Piddyachiy, V. I., Ilyushin, V. V., & Motiyenko, R. A. 2013, J. Mol. Spectr., 293, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, D., Devlin, J. P., & Scott, D. W. 1968, J. Mol. Spectr., 25, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Snyder, L. E., Kuan, Y.-J., & Miao, Y. 1994, Lect. Notes Phys., 439, 187 [Google Scholar]
- Suenram, R. D., Lovas, F. J., & Pickett, H. M. 1986a, J. Mol. Spectr., 116, 406 [NASA ADS] [CrossRef] [Google Scholar]
- Suenram, R. D., Lovas, F. J., & Pickett, H. M. 1986b, J. Mol. Spectr., 119, 446 [NASA ADS] [CrossRef] [Google Scholar]
- Takano, M., Sasada, Y., & Satoh, T. 1968, J. Mol. Spectr., 26, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Takano, S., Sakai, Y., Kakimoto, S., Sasaki, M., & Kobayashi, K. 2012, PASJ, 64, 89 [NASA ADS] [Google Scholar]
- Tercero, B., Kleiner, I., Cernicharo, J., et al. 2013, ApJ, 770, L13 [Google Scholar]
- Tercero, B., Cernicharo, J., López, A., et al. 2015, A&A, 582, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tsunekawa, S., Taniguchi, I., Tambo, A., et al. 1989, J. Mol. Spectr., 134, 63 [Google Scholar]
- Tsunekawa, S., Ukai, T. Toyama, A., & Takagi, K. 1995, Microwave frequencies of the CH3OH molecule in the frequency range 7 to 200 GHz, unpublished report, Dep. of Physics, Toyama University, Toyama, Japan [Google Scholar]
- Turner, B. E. 1977, ApJ, 213, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, S., Bergin, E. A., Crockett, N. R., et al. 2011, A&A, 527, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilson, T. L., & Rood, R. 1994, ARA&A, 32, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, L.-H., & Lovas, F. J. 1997, J. Phys. Chem. Ref. Data, 26, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, L.-H., Walsh, M. S., & Lees, R. M. 1996, J. Mol. Spectr., 179, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, L.-H., Fisher, J., Lees, R. M., et al. 2008, J. Mol. Spectr., 251, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, L.-H., Lees, R. M., Crabbe, G. T., et al. 2012, J. Chem. Phys., 137, 104313 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, L.-H., Lees, R. M., Hao, Y., et al. 2014, J. Mol. Spectr., 303, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Zaleski, D. P., Seifert, N. A., Steber, A. L., et al. 2013, ApJ, 765, L10 [Google Scholar]
- Zuckerman, B., Turner, B. E., Johnson, D. R., et al. 1975, ApJ, 196, L99 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Additional figures
 |
Fig. A.1 Transitions of CH3OH, ν= 0 covered by our ALMA survey. The best-fit LTE synthetic spectrum of CH3OH is displayed in red and overlaid on the observed spectrum of Sgr B2(N2) shown in black. The green synthetic spectrum contains the contributions of all molecules identified in our survey so far including the species shown in red. The central frequency of each panel is indicated below the x-axis in MHz; its width is given also in MHz in parentheses. The angular resolution is also indicated. The y-axis is labeled in brightness temperature units (K). The dotted line marks the 3σ noise level. |
 |
Fig. A.1 continued. |
 |
Fig. A.5 continued. |
 |
Fig. A.9 Population diagram of CH3OH, ν= 0, νt = 1, and νt = 2 toward Sgr B2(N2). Only the lines that are clearly detected, do not suffer too much from contamination from other species, and have an opacity below 2 are displayed. The observed data points are shown in black while the synthetic populations are shown in red. No correction is applied in panel a). In panel b), the optical depth correction has been applied to both the observed and synthetic populations and the contamination from all other species included in the full model has been removed from the observed data points. The straight line is a linear fit to the observed populations (in linear-logarithmic space). The rotational temperature derived in this way is reported in Table 6. |
 |
Fig. A.12 continued. |
 |
Fig. A.12 continued. |
 |
Fig. A.12 continued. |
 |
Fig. A.12 continued. |
 |
Fig. A.12 continued. |
 |
Fig. A.12 continued. |
 |
Fig. A.12 continued. |
 |
Fig. A.19 Same as Fig. A.1 for gauche-C2H5SH, ν= 0, but here, the green synthetic spectrum does not contain the contribution of gauche-C2H5SH that is shown in red. |
All Tables
Quantum numbers, conformers Conf., frequencies (MHz) of ethanol transitions appearing too strong in initial models, and Einstein A values (10-7 s-1) from the JPL catalog and new values proposed in the present study.
Rotational temperatures derived from population diagrams of alkanols and alkanethiols toward Sgr B2(N2).
Parameters of our best-fit LTE model (or upper limit) of alkanols and alkanethiols toward Sgr B2(N2).
Results of chemical kinetics modeling of alkanethiols and alkanols toward Sgr B2(N2).
All Figures
 |
Fig. 1 Sections of the continuum-subtracted spectrum recorded with ALMA toward Sgr B2(N2) in black. The synthetic spectrum of ethanol using the official JPL catalog entry is shown in red. Some lines are predicted to be much stronger than they appear in the spectrum, e.g., near 88 107 MHz and 91 059 MHz. A few other lines, e.g., near 90 354 MHz and 101 244 MHz, are stronger than predicted. Compare with Fig. 2. The central frequency of each panel is indicated below the x-axis in MHz; its width is given also in MHz in parentheses. The y-axis is labeled in brightness temperature units (K). |
| In the text | |
 |
Fig. 2 Same as in Fig. 1 with the same LTE parameters, but the modeling was carried out with a modified catalog entry in which the sign of one dipole moment component was altered, see Table 1. |
| In the text | |
 |
Fig. 3 Chemical model abundances for a selection of sulfur-bearing molecules a) and their oxygen-bearing analogs b). Solid lines indicate gas-phase abundances; dotted lines of the same color indicate the grain-surface/ice abundances of the same species. |
| In the text | |
 |
Fig. A.1 Transitions of CH3OH, ν= 0 covered by our ALMA survey. The best-fit LTE synthetic spectrum of CH3OH is displayed in red and overlaid on the observed spectrum of Sgr B2(N2) shown in black. The green synthetic spectrum contains the contributions of all molecules identified in our survey so far including the species shown in red. The central frequency of each panel is indicated below the x-axis in MHz; its width is given also in MHz in parentheses. The angular resolution is also indicated. The y-axis is labeled in brightness temperature units (K). The dotted line marks the 3σ noise level. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.2 Same as Fig. A.1 for CH3OH, νt = 1. |
| In the text | |
 |
Fig. A.3 Same as Fig. A.1 for CH3OH, νt = 2. |
| In the text | |
 |
Fig. A.4 Same as Fig. A.1 for CH3OH, νt = 3. |
| In the text | |
 |
Fig. A.5 Same as Fig. A.1 for 13CH3OH, ν= 0. |
| In the text | |
 |
Fig. A.5 continued. |
| In the text | |
 |
Fig. A.6 Same as Fig. A.1 for 13CH3OH, νt = 1. |
| In the text | |
 |
Fig. A.7 Same as Fig. A.1 for
CH |
| In the text | |
 |
Fig. A.8 Same as Fig. A.1 for
CH |
| In the text | |
 |
Fig. A.9 Population diagram of CH3OH, ν= 0, νt = 1, and νt = 2 toward Sgr B2(N2). Only the lines that are clearly detected, do not suffer too much from contamination from other species, and have an opacity below 2 are displayed. The observed data points are shown in black while the synthetic populations are shown in red. No correction is applied in panel a). In panel b), the optical depth correction has been applied to both the observed and synthetic populations and the contamination from all other species included in the full model has been removed from the observed data points. The straight line is a linear fit to the observed populations (in linear-logarithmic space). The rotational temperature derived in this way is reported in Table 6. |
| In the text | |
 |
Fig. A.10 Same as Fig. A.9 for 13CH3OH, ν= 0 and νt = 1. |
| In the text | |
 |
Fig. A.11 Same as Fig. A.9 for
CH |
| In the text | |
 |
Fig. A.12 Same as Fig. A.1 for C2H5OH, ν= 0. |
| In the text | |
 |
Fig. A.12 continued. |
| In the text | |
 |
Fig. A.12 continued. |
| In the text | |
 |
Fig. A.12 continued. |
| In the text | |
 |
Fig. A.12 continued. |
| In the text | |
 |
Fig. A.12 continued. |
| In the text | |
 |
Fig. A.12 continued. |
| In the text | |
 |
Fig. A.12 continued. |
| In the text | |
 |
Fig. A.13 Same as Fig. A.9 for C2H5OH, ν= 0. |
| In the text | |
 |
Fig. A.14 Same as Fig. A.1 for 13CH3CH2OH, ν= 0. |
| In the text | |
 |
Fig. A.15 Same as Fig. A.1 for
CH |
| In the text | |
 |
Fig. A.16 Same as Fig. A.1 for CH3SH, ν= 0. |
| In the text | |
 |
Fig. A.17 Same as Fig. A.1 for CH3SH, νt = 1. |
| In the text | |
 |
Fig. A.18 Same as Fig. A.9 for CH3SH, ν= 0 and νt = 1. |
| In the text | |
 |
Fig. A.19 Same as Fig. A.1 for gauche-C2H5SH, ν= 0, but here, the green synthetic spectrum does not contain the contribution of gauche-C2H5SH that is shown in red. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.