| Issue |
A&A
Volume 587, March 2016
|
|
|---|---|---|
| Article Number | A34 | |
| Number of page(s) | 11 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201527333 | |
| Published online | 12 February 2016 | |
Eclipsing time variations in close binary systems: Planetary hypothesis vs. Applegate mechanism
1 Hamburger Sternwarte, Universität Hamburg, Gojenbergsweg 112, 21029 Hamburg, Germany
e-mail: marcel.voelschow@hs.uni-hamburg.de
2 Departamento de Astronomía, Facultad Ciencias Fìsicas y Matemàticas, Universidad de Concepción, Av. Esteban Iturra s/n Barrio Universitario, Casilla 160-C, Concepción, Chile
Received: 8 September 2015
Accepted: 6 December 2015
The observed eclipsing time variations in post-common-envelope binaries (PCEBs) can be interpreted as potential evidence for massive Jupiter-like planets, or as a result of magnetic activity, leading to quasi-periodic changes in the quadrupole moment of the secondary star. The latter is commonly referred to as the Applegate mechanism. We employ an improved version of Applegate’s model including the angular momentum exchange between a finite shell and the core of the star. The framework is employed to derive the general conditions under which the Applegate mechanism can work, and is subsequently applied to a sample of 16 close binary systems with potential planets, including eleven PCEBs. Further, we present a detailed derivation and study of analytical models that allow for an straightforward extension to other systems. Using our full numerical framework, we show that the Applegate mechanism can clearly explain the observed eclipsing time variations in four of the systems, while the required energy to produce the quadrupole moment variations is too high in at least eight systems. In the remaining four systems, the required energy is comparable to the available energy produced by the stars, which we consider borderline cases. Therefore, the Applegate mechanism cannot uniquely explain the observed period time variations for this entire population. Even in systems where the required energy is too high, the Applegate mechanism may provide an additional scatter, which needs to be considered in the derivation and analysis of planetary models.
Key words: stars: activity / binaries: eclipsing / stars: interiors / planetary systems / stars: AGB and post-AGB / planets and satellites: detection
© ESO, 2016
1. Introduction
Short period binaries with dwarf components have proven to be ideal systems to constrain stellar structure and evolution models with precise mass and radius data. White dwarf/red dwarf (hereafter WD+RD) binaries are of particular relevance, as their large differences, both in radius and luminosity, results in accurate light curves very close to ideal predictions, allowing for high precision timing measurements (see, e.g., Parsons et al. 2010b).
These binary systems form as a result of a common envelope (CE) phase. The CE model was originally put forward by Paczynski (1976) and assumes that the primary star in an originally wider (~ 1 AU) binary system has reached the giant branch, and the secondary has been engulfed by the envelope of the giant. As a result, both the energy and angular momentum of the secondary are deposited into the envelope of the giant, causing the secondary to spiral inward toward scales of about a solar radius. These models have been refined in subsequent studies, e.g., Meyer & Meyer-Hofmeister (1979), Iben & Livio (1993), Taam & Sandquist (2000), Webbink (2008) and Taam & Ricker (2010). The CE phase has been simulated by Passy et al. (2012) using both smoothed-particle-hydrodynamics (SPH) and grid-based techniques, and a review of the current state of the art is provided by Ivanova et al. (2013). The systems resulting from this CE phase consist of a white dwarf resulting from the core of the giant and a red dwarf on a narrow orbit of ~ 1R⊙. They are referred to as post-common-envelope binaries (PCEBs).
The evolution of close binary systems is predominantly governed by angular momentum loss, which can be driven by gravitational wave emission for binaries with very short periods (Porb< 3 h) (Kraft et al. 1962; Faulkner 1971) or magnetic breaking for binaries with Porb> 3 h (Verbunt & Zwaan 1981). While the resulting angular momentum loss implies a continuous decrease of the orbital period over time, a number of systems is known showing regular quasiperiodic modulations on the order ΔP/Pbin ~ 3 × 10-5 with periods of several decades in Algols, RS Canum Venaticorum (RS CVn), W Ursae Majoris, and cataclysmic variable (CV) stars (Ibanoglu 1991). These variations are studied employing O−C diagrams, in which O denotes the observed orbital phase of the binary at a given time, from which a correction C is subtracted based on the zero- and first-order terms in the expansion of the angular velocity, i.e., assuming 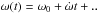 . A diagram showing O−C vs. time provides information on the quasiperiodic modulations, corresponding to fluctuations including a regular increase accompanied by a subsequent decrease in the orbital period. The period variation is related to the amplitude in the O−C diagram via (Applegate 1992)
. A diagram showing O−C vs. time provides information on the quasiperiodic modulations, corresponding to fluctuations including a regular increase accompanied by a subsequent decrease in the orbital period. The period variation is related to the amplitude in the O−C diagram via (Applegate 1992) 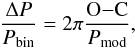 (1)where Pmod denotes the period of the modulation. In the case of eclipsing binaries, these fluctuations can be accurately measured with transit timing variations (TTVs) to constrain the underlying physical mechanism.
(1)where Pmod denotes the period of the modulation. In the case of eclipsing binaries, these fluctuations can be accurately measured with transit timing variations (TTVs) to constrain the underlying physical mechanism.
A potential mechanism to explain the eclipsing time variations has been proposed by Applegate (1992), in which the period variations are explained as a result of quasiperiodic changes in the quadrupole moment of the secondary star as a result of magnetic activity. It is thus assumed that a sufficiently strong magnetic field is regularly produced during a dynamo cycle, leading to a redistribution of the angular momentum within the star and, therefore, a change in its quadrupole moment. This model was motivated from a sample of 101 Algols studied by Hall (1989), showing a strong connection between the orbital period variations and the presence of magnetic activity.
To sufficiently change the stellar structure to drive the quasiperiodic period oscillation, a certain amount of energy is required to build up a strong magnetic field, which is subsequently dissipated and again built up in the next dynamo cycle. Ultimately, such energy should be extracted from the convective energy of the star, which is powered by the nuclear energy production (Marsh & Pringle 1990). While sufficient energy appears to be available in the case of Algols, it has been shown by Lanza (2005) that the Applegate scenario needs to be rejected for RS CVns, and independently Brinkworth et al. (2006) have reported that the orbital period variations of the PCEB system NN Ser cannot be explained with Applegate’s model.
In fact, the orbital period variations in NN Ser were shown to be consistent with a two-planet solution, which was shown to be dynamically stable (Beuermann et al. 2010, 2013; Horner et al. 2012; Marsh et al. 2014). Similarly, the planetary solution of HW Vir was shown to be secularly stable (Beuermann et al. 2012b), while a final conclusion on HU Aqr (Qian et al. 2011; Goździewski et al. 2012, 2015; Hinse et al. 2012; Wittenmyer et al. 2012) is pending. The eclipsing time variations in QS Vir, on the other hand, are currently not understood, and appear to be incompatible both with the planetary hypothesis as well as the Applegate scenario (Parsons et al. 2010b). A summary of PCEB systems potentially hosting planets has been compiled by Zorotovic & Schreiber (2013), including the properties of the planetary systems. The latter correspond to massive giant planets of several Jupiter masses on planetary orbits of a few AU. It has been suggested that at least some of these planets may have a second-generation origin (Völschow et al. 2014; Schleicher & Dreizler 2014; Bear & Soker 2014; Schleicher et al. 2015).
However, the discussion of whether the planets are real is still ongoing. In this respect, the proposed brown dwarf in V471 Tau has not been found via direct imaging (Hardy et al. 2015; but see comments by Vaccaro et al. 2015). In this paper, we in fact show that the period time variations in V471 Tau could also be produced by an Applegate mechanism.
The original Applegate model linking magnetic activity to period time variations has subsequently been improved by various authors. For instance, the analysis by Lanza et al. (1998) provided an improved treatment of the mechanical equilibrium, including the impact of rotational and magnetic energy on the quadrupole moment, leading to an improved estimate of the energy requirements. While the original framework was based on a thin-shell approximation, Brinkworth et al. (2006) considered a finite shell around the inner core and a change of the quadrupole moment of the core due to the exchange of angular momentum. An even more detailed formulation has been provided by Lanza (2006). It was proposed by Lanza & Rodonò (1999) that an energetically more favorable scenario may occur in the presence of an α2 dynamo, which was however shown to require strong assumptions concerning the operation of the dynamo, including a dynamo restricted to the star’s equatorial plane and a magnetic field of 105 G (Rüdiger et al. 2002).
In this paper, we adopt the formulation by Brinkworth et al. (2006) and apply it to realistic stellar profiles. Based on this analysis, we systematically assess whether the Applegate mechanism is feasible in a sample of 16 close binary systems with potential planets, including eleven PCEBs. We further provide analytical scaling relations that can reproduce our main results, provide further insights into the Applegate mechanism, and allow for an extension of this analysis to additional systems.
2. Systems investigated in this paper
2.1. Classification
Our sample consists of a total of 16 close binary systems with observed period variations potentially indicating the presence of planets. Eleven of these are the PCEB systems previously described by Zorotovic et al. (2011) and Zorotovic & Schreiber (2013); four RS CVn binaries, RU Cnc, AW Her (Tian et al. 2009), HR 1099 (Fekel 1983; García-Alvarez et al. 2003; Frasca & Lanza 2004), and SZ Psc (Jakate et al. 1976; Popper 1988; Wang et al. 2010); and the RR-Lyr type binary BX DRA (Park et al. 2013). The detailed properties of these systems, including binary type and spectral class, are listed in Table 1.
2.2. Period variations and the LTV effect
In the presence of a planet, close binary system, and companion revolve around their common barycenter resulting in variations of the observed eclipse timings referred to as the light travel time variation (LTV) effect.
In the binary eclipse O−C diagram, the expected signature of a single planet on a circular orbit is sinusoidal with semi-amplitude K and period Pplan. Treating the binary as a point mass and further assuming an edge-on binary (i.e., i = 90deg), we can approximate the semi-amplitude of the LTV K caused by the accompanying object via ![\begin{equation} K = \frac{ M_{\rm plan} G^{1/3}}{c} \left[\frac{P_{\rm plan}}{2 \pi (M_{\rm pri}+M_{\rm sec})} \right]^{2/3}, \end{equation}](/articles/aa/full_html/2016/03/aa27333-15/aa27333-15-eq36.png) (2)where Mpri and Msec denote the eclipsing binary component masses, Mplan the planetary mass, Pplan the planetary orbital period, c the speed of light, and G the gravitational constant (see Pribullaet al. (2012) for a more detailed description). Relative to the binary’s period, we have a period change of (see, e.g., Goździewski et al. 2015)
(2)where Mpri and Msec denote the eclipsing binary component masses, Mplan the planetary mass, Pplan the planetary orbital period, c the speed of light, and G the gravitational constant (see Pribullaet al. (2012) for a more detailed description). Relative to the binary’s period, we have a period change of (see, e.g., Goździewski et al. 2015) 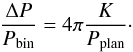 (3)In Table 2 we summarize the LTV properties of the proposed planetary systems as given in the literature we refer to in Table 1.
(3)In Table 2 we summarize the LTV properties of the proposed planetary systems as given in the literature we refer to in Table 1.
Summary of the TTV data.
3. Applegate’s mechanism
In the following, we introduce the framework to assess the feasibility of Applegate’s mechanism. For this purpose, we refer to the original Applegate framework and the resulting energy requirement to drive quadrupole moment variations of the secondary star. This is contrasted with the finite shell model by Brinkworth et al. (2006), which considers the angular momentum exchange between the core and a finite shell and accounts for the back reaction of the core. Using this framework, we derive three different approximations of increasing accuracy: an analytical Applegate model assuming a constant density throughout the star, an analytical two-zone model employing different densities in the core and the shell, and a numerical model employing a full stellar density profile. Finally, we present an analytical two-zone model, which precisely reproduces the results of the numerical model and leads to new insights into the limitations of the Applegate mechanism.
3.1. Thin shell model by Applegate (1992)
We consider a close PCEB system with a binary separation abin consisting of a white dwarf, and a red dwarf secondary with mass Msec and radius Rsec. According to Applegate (1992), the relative period change ΔP/Pbin is related to the secondary’s change in quadrupole moment ΔQ by 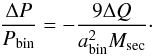 (4)As a result of the secondary’s magnetic activity, angular momentum can be transferred between the core and its outer regions leading to a change in their respective angular velocities, causing a change in the oblateness of both the core and outer shell and modulating the secondary’s quadrupole moment. For the sake of simplicity, Applegate considered a thin homogeneous shell and neglected the change of the core’s oblateness.
(4)As a result of the secondary’s magnetic activity, angular momentum can be transferred between the core and its outer regions leading to a change in their respective angular velocities, causing a change in the oblateness of both the core and outer shell and modulating the secondary’s quadrupole moment. For the sake of simplicity, Applegate considered a thin homogeneous shell and neglected the change of the core’s oblateness.
We divide the star into an inner core with radius Rcore and initial orbital velocity Ω1, and an adjacent outer shell with outer radius Rsec and orbital velocity Ω2, which both rotate as rigid objects. Under these assumptions, the required energy ΔE to drive a given period change via an exchange of angular momentum ΔJ between core and shell is given as 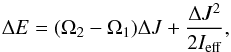 (5)with effective moment of inertia Ieff = IcoreIshell/ (Icore + Ishell (see, e.g., Applegate 1992; Parsons et al. 2010b). Assuming a thin shell, one obtains
(5)with effective moment of inertia Ieff = IcoreIshell/ (Icore + Ishell (see, e.g., Applegate 1992; Parsons et al. 2010b). Assuming a thin shell, one obtains 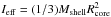 . A given period change ΔP and an angular momentum exchange are connected via
. A given period change ΔP and an angular momentum exchange are connected via 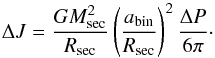 (6)Following Parsons et al. (2010b), one fixes the shell mass and evaluates Eq. (5) for varying core radii and, hence, angular momentum exchange to solve for the energy minimum.
(6)Following Parsons et al. (2010b), one fixes the shell mass and evaluates Eq. (5) for varying core radii and, hence, angular momentum exchange to solve for the energy minimum.
Combining the framework of Applegate (1992) with an improved model for the variation of the quadrupole moment considering both the rotation and magnetic energy (Lanza et al. 1998), Tian et al. (2009) derived an approximate formula for the relation between the required energy to drive Applegate’s mechanism and the observed eclipsing time variations, i.e., 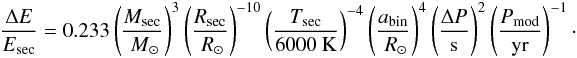 (7)Both this approximative formula and Applegate’s original work only consider angular momentum exchange between a thin outer shell and a dominating core. Moreover, they do not take into account the core’s rotational counter-reaction as a result of angular momentum conservation, i.e., an opposite change in the oblateness compensating a fraction of the change of the quadrupole moment. Thus, the energy required to power a certain level of period variation increases and a more realistic description of Applegate’s mechanism must include both components.
(7)Both this approximative formula and Applegate’s original work only consider angular momentum exchange between a thin outer shell and a dominating core. Moreover, they do not take into account the core’s rotational counter-reaction as a result of angular momentum conservation, i.e., an opposite change in the oblateness compensating a fraction of the change of the quadrupole moment. Thus, the energy required to power a certain level of period variation increases and a more realistic description of Applegate’s mechanism must include both components.
3.2. Finite shell model by Brinkworth et al. (2006)
In contrast to the original work by Applegate (1992), Brinkworth et al. (2006) derived an analytic expression for the effective change of the secondary’s quadrupole moment ΔQ for a given change of core rotation ΔΩ1 and shell rotation ΔΩ2, which reads ![\begin{equation} \label{eq:omega2equa} \Delta Q = Q' _1 \, \left[2 \Omega _1 \Delta \Omega _1 + ( \Delta \Omega _1 )^{2} \right] + Q' _2 \, \left[2 \Omega _2 \Delta \Omega _2 + ( \Delta \Omega _2 )^{2} \right] \comequa \end{equation}](/articles/aa/full_html/2016/03/aa27333-15/aa27333-15-eq73.png) (8)where the coefficients
(8)where the coefficients 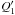 and
and 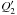 are (imposing spherical symmetry) given by integrals of the form
are (imposing spherical symmetry) given by integrals of the form 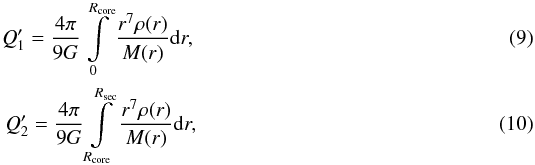 where the secondary’s radial density profile ρ(r) and M(r) are the total mass inside a radius r. Solving Eq. (8) for ΔΩ2 and using
where the secondary’s radial density profile ρ(r) and M(r) are the total mass inside a radius r. Solving Eq. (8) for ΔΩ2 and using ![\begin{equation} \label{eq:deltaE} \Delta E = ( \Omega _2 - \Omega _1 ) \cdot I_2 \Delta \Omega _2 + \frac{1}{2} \left[\frac{1}{I_1} + \frac{1}{I_2} \right] ( I_2 \, \Delta \Omega _2 ) ^{2} \end{equation}](/articles/aa/full_html/2016/03/aa27333-15/aa27333-15-eq80.png) (11)with the moment of inertia
(11)with the moment of inertia  gives the total amount of energy needed to perform the angular momentum transfer.
gives the total amount of energy needed to perform the angular momentum transfer.
The total number of parameters can be reduced by imposing angular momentum conservation, i.e., a lossless exchange 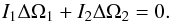 (14)Following Brinkworth et al. (2006), the minimum energy required to drive Applegate’s mechanism is achieved assuming no initial differential rotation or
(14)Following Brinkworth et al. (2006), the minimum energy required to drive Applegate’s mechanism is achieved assuming no initial differential rotation or 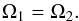 (15)Altogether, we can now solve Eq. (8) for ΔΩ2 and find
(15)Altogether, we can now solve Eq. (8) for ΔΩ2 and find![\begin{equation} \label{eq:solutionOmega2} ( \Delta \Omega _2) = -\Omega_2 \, \frac{\beta}{\alpha} \pm \sqrt{ \, \left[\Omega _2 \, \frac{\beta}{\alpha} \right]^{2} + \frac{\Delta Q}{\alpha} } \comequa \end{equation}](/articles/aa/full_html/2016/03/aa27333-15/aa27333-15-eq84.png) (16)where we defined
(16)where we defined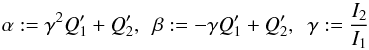 (17)for convenience and as a preparation for the next sections.
(17)for convenience and as a preparation for the next sections.
3.3. The case of a constant density profile
As a zero-order approximation, the framework introduced by Brinkworth et al. (2006) can be evaluated assuming a constant density throughout the star. While this is clearly an approximation, it already gives rise to some phenomenological scaling relations to illustrate how the required energy for the Applegate mechanism depends on the binary separation and the mass of the secondary. Employing this approximation, the density in the secondary is now given as 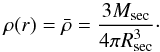 (18)Given this and defining ξ = Rsec/Rcore, we can calculate explicit expressions for the coefficients in Eq. (16):
(18)Given this and defining ξ = Rsec/Rcore, we can calculate explicit expressions for the coefficients in Eq. (16): 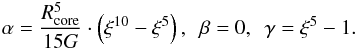 In this context, ΔΩ2 is given as
In this context, ΔΩ2 is given as ![\begin{equation} \Delta \Omega _2 = \pm \sqrt{\frac{15G \, \Delta Q}{R_{\rm core} ^{5} \, [\xi ^{10} - \xi ^{5}]}} \cdot \end{equation}](/articles/aa/full_html/2016/03/aa27333-15/aa27333-15-eq89.png) (19)Inserting this into Eq. (11) eliminates both the dependence on Rcore and Ω2 and finally yields
(19)Inserting this into Eq. (11) eliminates both the dependence on Rcore and Ω2 and finally yields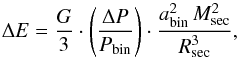 (20)or in a more practical form
(20)or in a more practical form 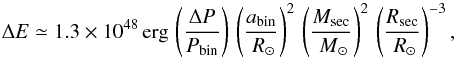 (21)which can also be expressed in terms of a relative Applegate threshold energy via division by the energy provided over one modulation period by the secondary:
(21)which can also be expressed in terms of a relative Applegate threshold energy via division by the energy provided over one modulation period by the secondary: 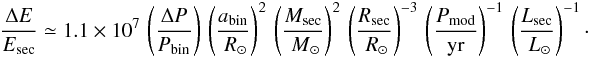 (22)The main goal of these calculations is a simple model to give rough order of magnitude estimates as well as the basic scaling properties of the Applegate mechanism. This zero-order estimate is independent of the angular velocity of the star and does not require an assumption of stellar rotation. The results of this estimate, along with those for the improved models, are given in Table 4. In the two-zone model presented in the next subsection, the required energy includes a dependence on the rotation rate, which can be estimated from the assumption of tidal locking.
(22)The main goal of these calculations is a simple model to give rough order of magnitude estimates as well as the basic scaling properties of the Applegate mechanism. This zero-order estimate is independent of the angular velocity of the star and does not require an assumption of stellar rotation. The results of this estimate, along with those for the improved models, are given in Table 4. In the two-zone model presented in the next subsection, the required energy includes a dependence on the rotation rate, which can be estimated from the assumption of tidal locking.
3.4. An analytical two-zone model
3.4.1. Derivation
While the model above already provides an interesting scaling relation, including the dependence on binary separation and the mass of the secondary, it is instructive to further understand the dependence on the stellar structure and the rotation of the secondary. For this purpose, we now consider a stellar density profile with a density ρ1 in the core and ρ2 in the shell. We denote the size of the core as Rcore. The density profile is then given as 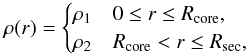 (23)and the main parameters can be summarized as
(23)and the main parameters can be summarized as 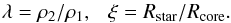 (24)We can calculate that
(24)We can calculate that ![\begin{eqnarray*} \alpha &=& \frac{\lambda R_{\rm core}^{5}}{15 G} \cdot \left( \lambda [\xi ^{5} -1]^{2} + f(\xi, \lambda) \right), \\ \beta &=& \frac{\lambda R_{\rm core}^{5}}{15 G} \cdot \left( f(\xi,\lambda) - \gamma \right), \\ \gamma &=& \lambda \left[\xi ^{5} - 1 \right], \end{eqnarray*}](/articles/aa/full_html/2016/03/aa27333-15/aa27333-15-eq97.png) where the function f is given by
where the function f is given by 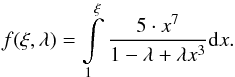 (25)The two solutions for the angular velocity change are given as
(25)The two solutions for the angular velocity change are given as 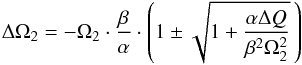 (26)with
(26)with 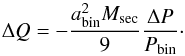 (27)We assume now that the star is tidally locked, implying that the orbital period of the secondary is given as the orbital period of the binary system, i.e., Ω2 = 2π/Pbin. Explicitly, we then have
(27)We assume now that the star is tidally locked, implying that the orbital period of the secondary is given as the orbital period of the binary system, i.e., Ω2 = 2π/Pbin. Explicitly, we then have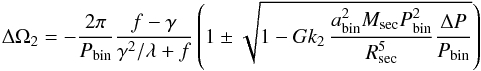 (28)with the coefficient
(28)with the coefficient 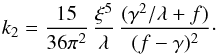 (29)The energy required to drive the angular momentum exchange is
(29)The energy required to drive the angular momentum exchange is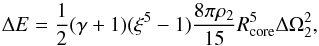 (30)which together with the identity
(30)which together with the identity 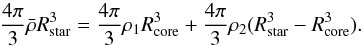 (31)results in
(31)results in 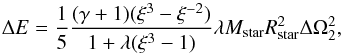 (32)or with Eq. (28)
(32)or with Eq. (28) 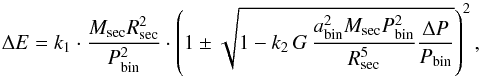 (33)where we define the coefficient
(33)where we define the coefficient 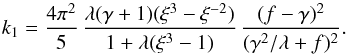 (34)According to the last section, we can relate Eq. (33) to the energy provided over one modulation period, i.e.,
(34)According to the last section, we can relate Eq. (33) to the energy provided over one modulation period, i.e., 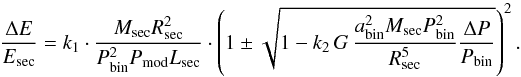 (35)For low-mass stars, typical values are ξ ~ 4/3 and λ ~ 1/100 (see Sect. 5). As the inverse zone transition parameter ξ shows just negligible variations for typical PCEB systems, we can fix it to ξ = 4/3 to find the zone density contrast parameter λ that is most compatible with the systems we examined (see Table 1). We set λ = 0.00960, implying f ~ 5.57. Given that, we can numerically evaluate the coefficients yielding
(35)For low-mass stars, typical values are ξ ~ 4/3 and λ ~ 1/100 (see Sect. 5). As the inverse zone transition parameter ξ shows just negligible variations for typical PCEB systems, we can fix it to ξ = 4/3 to find the zone density contrast parameter λ that is most compatible with the systems we examined (see Table 1). We set λ = 0.00960, implying f ~ 5.57. Given that, we can numerically evaluate the coefficients yielding 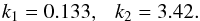 (36)
(36)
3.4.2. A critical condition
In contrast to the constant density approximation, the two-zone model incorporates all essential physics involved in the Applegate process. In particular, the two-zone model accounts for the orbital period of the binary resulting in two different energy branches just as in the full treatment (see Sect. 3.2). Here, the lower energy branch corresponds to the negative solution. Another implication results from the term inside the root. Restricting us to real-valued solutions raises the critical condition 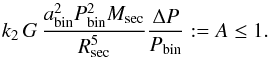 (37)Mathematically, systems that do not satisfy Eq. (37) (hereafter, we refer to the left-hand side as the Applegate parameter A) cannot drive the observed period change independent of energetic arguments as no real-valued solution exists. On the other hand, one can show that in the case of a critical system for which the Applegate parameter is unity, the two-zone model and the constant density model converge. In such a system, the energy to drive the Applegate process is given by
(37)Mathematically, systems that do not satisfy Eq. (37) (hereafter, we refer to the left-hand side as the Applegate parameter A) cannot drive the observed period change independent of energetic arguments as no real-valued solution exists. On the other hand, one can show that in the case of a critical system for which the Applegate parameter is unity, the two-zone model and the constant density model converge. In such a system, the energy to drive the Applegate process is given by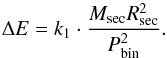 (38)Substituting Eq. (37) for the binary period leads to
(38)Substituting Eq. (37) for the binary period leads to 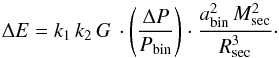 (39)In the case of constant density, λ = 1, which means that f = ξ5−1 = γ and we end up at k1·k2 = 1/3, proving that the two-zone model and the constant density model give identical Applegate energies for critical systems. Using this result, we can understand the physical meaning of critical systems by looking into the angular momentum budget of the star and its rotational state. For a critical system, the change of the outer shell’s angular velocity (cf. Eq. (28)) is given by
(39)In the case of constant density, λ = 1, which means that f = ξ5−1 = γ and we end up at k1·k2 = 1/3, proving that the two-zone model and the constant density model give identical Applegate energies for critical systems. Using this result, we can understand the physical meaning of critical systems by looking into the angular momentum budget of the star and its rotational state. For a critical system, the change of the outer shell’s angular velocity (cf. Eq. (28)) is given by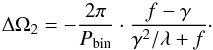 (40)Now, let λ → 1, which implies f → γ because for critical systems the two-zone model and the constant density model converge, as shown above. Non-zero solutions impose ξ → 1 and we arrive at
(40)Now, let λ → 1, which implies f → γ because for critical systems the two-zone model and the constant density model converge, as shown above. Non-zero solutions impose ξ → 1 and we arrive at 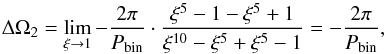 (41)proving that the constant density model is the limit of a two-zone calculation for the extreme case that the outer shell and its angular velocity vanish.
(41)proving that the constant density model is the limit of a two-zone calculation for the extreme case that the outer shell and its angular velocity vanish.
3.4.3. Quality of the approximation
The quality of the analytical two-zone model becomes clear from Fig. 1, in which we compare the estimates as calculated with the two-zone model with the full calculations described in the next subsection. The full model considers a white dwarf primary with 0.5 M⊙ accompanied by a fairly evolved secondary star with t ~ 5 Gyr, while the two-zone model employs λ = 0.0096 and ξ = 4/3, consistent with the typical structure of a low-mass star. In both calculations, we assume a relative period change of ΔP/Pbin = 10-7 with a modulation period of Pmod = 14 yr, corresponding to a Jupiter-like planet with mass ~ 3 MJup and semi-major axis ~ 5 au, and we investigate the results for varying Applegate parameters A. As one can see, the typical deviation of the required energy for the Applegate mechanism corresponds to less than 10% between the two models, provided that the Applegate condition (Eq. (37)) is satisfied with a left-hand side much smaller than unity. We adopt A ≲ 0.5 as a typical fiducial limit.
 |
Fig. 1 Relative difference between the two-zone model described in Sect. 3.4 with the full model considering a realistic stellar density profile as outlined in Sect. 4.1. The model assumes a white dwarf mass of 0.5M⊙ and an age of the secondary of 5 Gyr. We employ λ = 0.0096 and ξ = 4/3 as parameters in the two-zone model. The relative deviation of the results is shown as a function of the Applegate parameter A and for different secondary masses. A good approximation requires A ≲ 0.5. |
Finally, in Fig. 2, we compare the computational results of all three models described in the last two sections: namely, the constant density approximation, the two-zone model, and the full model for the same general system configuration as in Fig. 1, and varying binary separation. Here, we fixed the secondary mass to Msec = 0.3 M⊙, allowing us to compare the models for varying Applegate parameter. Over almost the entire parameter range, the two-zone model precisely resembles the full calculations with absolute deviations of less than 10%, while the constant density model lies off by several orders of magnitude. Both the full calculations and the two-zone model fail beyond A ~ 1 (corresponding to abin ~ 3.5 R⊙), which is predicted exactly by Eq. (37).
We therefore conclude that the two-zone model provides a valuable and sufficient approximation to estimate the required energy for the case of PCEBs with main-sequence low-mass companions in the range of 0.1 M⊙ to 0.6 M⊙ that satisfy the Applegate condition Eq. (37). Nevertheless, we evaluate our main results in what follows with the more detailed numerical framework that includes full stellar density profiles and varying core radii.
 |
Fig. 2 Comparison of the constant density and two-zone analytical models, as described in Sects. 3.3 and 3.4, with the full calculations as described in Sect. 4.1 in terms of the predicted relative Applegate threshold energy. We consider the same general system configuration as in Fig. 1 and described in Sect. 3.4, but fixed the secondary mass to Msec = 0.3 M⊙, which enabled us to plot the calculated energies as functions of the Applegate parameter A (see Eq. (37)). The analytical two-zone model closely follows the full calculations with typical deviations of less than 10%, while the simple constant density model overestimates the energy threshold by several magnitudes except for the critical region close to unity. |
4. Full calculations with a stellar density profile
4.1. Recipe
In addition to the constant density profile and the two-zone model, we present here the framework to derive the required energy to drive Applegate’s mechanism based on detailed and realistic density profiles. The latter require numerical solutions for the coefficients involved in Eq. (16). In this section, we describe our general framework and apply it to NN Ser. The results for the additional systems are given in Sect. 5.
From Eq. (16), we expect that the effective change of the shell’s angular velocity ΔΩ2 is an explicit function of its initial angular velocity Ω2 and an implicit function of the core radius Rcore via the moments of inertia I1,2 and the 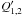 coefficients. We describe our procedure in the following.
coefficients. We describe our procedure in the following.
First we calculate I1,2 and 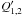 for a given core radius Rcore utilizing a radial density profile provided by Evolve ZAMS1 (Paxton 2004), but rescaled to the secondary’s radius and normalized to its mass as inferred by Parsons et al. (2010a) to resemble the measurements. We adopt an age value of ~ 2 Gyr, which is roughly the main-sequence lifetime of the 2 M⊙ WD progenitor (see Beuermann et al. 2010). Unless stated otherwise, we assume a solar metallicity in the following.
for a given core radius Rcore utilizing a radial density profile provided by Evolve ZAMS1 (Paxton 2004), but rescaled to the secondary’s radius and normalized to its mass as inferred by Parsons et al. (2010a) to resemble the measurements. We adopt an age value of ~ 2 Gyr, which is roughly the main-sequence lifetime of the 2 M⊙ WD progenitor (see Beuermann et al. 2010). Unless stated otherwise, we assume a solar metallicity in the following.
Based on that, we can calculate the two solutions for ΔΩ2 for a given initial rotation Ω2, named 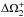 for the positive sign and
for the positive sign and 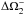 , respectively. These two solutions finally give two different corresponding energies ΔE+ and ΔE−.
, respectively. These two solutions finally give two different corresponding energies ΔE+ and ΔE−.
According to Haefner et al. (2004), the NN Ser system is tidally locked, constraining the inital angular velocities to 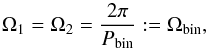 (42)with Pbin the orbital period of the binary (see, e.g., Brinkworth et al. 2006; Lanza 2006). Given the condition of tidal locking, the only remaining parameter is the core radius Rcore. We do not restrict it to equal the nuclear burning zone as typical red dwarfs are fully convective (see, e.g., Engle & Guinan 2011), but rather explore the minimum energy that can be obtained depending on the core radius. The relative period change ΔP/Pbin of the binary is calculated assuming sinusoidal perturbance by planets on circular orbits via
(42)with Pbin the orbital period of the binary (see, e.g., Brinkworth et al. 2006; Lanza 2006). Given the condition of tidal locking, the only remaining parameter is the core radius Rcore. We do not restrict it to equal the nuclear burning zone as typical red dwarfs are fully convective (see, e.g., Engle & Guinan 2011), but rather explore the minimum energy that can be obtained depending on the core radius. The relative period change ΔP/Pbin of the binary is calculated assuming sinusoidal perturbance by planets on circular orbits via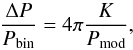 (43)with semi-amplitude K and modulation period Pmod (see, e.g., Applegate 1992; Goździewski et al. 2015), neglecting small variations due to orbital eccentricity in both the binary or the planet.
(43)with semi-amplitude K and modulation period Pmod (see, e.g., Applegate 1992; Goździewski et al. 2015), neglecting small variations due to orbital eccentricity in both the binary or the planet.
 |
Fig. 3 Angular velocity change normalized by the angular velocity of the binary both in the core (ΔΩ1) and shell (ΔΩ2) for our reference system NN Ser as a function of the size of the core. For both quantities, there are two solutions, denoted with + and –. The calculation is based on the full numerical model described in Sect. 4.1. |
 |
Fig. 4 Required energy to drive the eclipsing time observations for the solutions denoted with + and – in Fig. 3. The calculation is based on the full numerical model described in Sect. 4.1. |
As one can see from Fig. 3, we have two possible solutions corresponding to two different angular momentum transfer modes that are compatible with the boundary conditions. Both modes correspond to different energies. We plot them in Fig. 4 as a function of the fractional core radius δ: = rcore/rsec, showing that the two branches converge, as δ runs to either 0.3 or 0.9, but typically feature a prominent spread of several magnitudes in between. Outside this parameter space, only complex-valued solutions exist. The minimum energy for the modified Applegate mechanism (hereafter ΔEmin) is achieved at a fractional core radius of δmin ~ 0.75 for the lower branch.
Finally, we compare the energy needed to drive the Applegate mechanism over one modulation period Pmod with the total energy generated by the secondary, i.e., 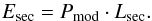 (44)In order to be viable, we require
(44)In order to be viable, we require 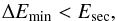 (45)knowing that a more realistic condition would require ΔEmin ≪ Esec, as the energy required for the quadrupole moment oscillations should correspond to a minor fraction of the available energy produced by the star.
(45)knowing that a more realistic condition would require ΔEmin ≪ Esec, as the energy required for the quadrupole moment oscillations should correspond to a minor fraction of the available energy produced by the star.
In Tables 1 and 2, we summarize the basic properties of all systems investigated in this paper. Our sample is based on the compilation of PCEBs with potential planets described by Zorotovic & Schreiber (2013); four RS CVn binaries, RU Cnc, AW Her (Tian et al. 2009), HR 1099 (Fekel 1983; García-Alvarez et al. 2003; Frasca & Lanza 2004), and SZ Psc (Jakate et al. 1976; Popper 1988; Wang et al. 2010); and the RR-Lyr type binary BX Dra (Park et al. 2013).
4.2. How does the age affect our results?
Because of their low mass and luminosity, typical red dwarfs of ~ 0.1 M⊙ have main-sequence lifetimes of several 100Gyr (see, e.g., Engle & Guinan 2011). On timescales of tens of Gyr, their fundamental properties and internal structures remain virtually constant.
Even for more massive dwarfs, such as in QS Vir with a mass of 0.43 M⊙, the radial density profile calculated with Evolve ZAMS shows little variation even for the two extreme cases of t ~ 1 Gyr and t ~ 14 Gyr: while the star’s radius increased by ~ 1 %, the core density increased by slightly more than ~ 10 %, concentrating more mass in the center (see Fig. 5). Calculating the relative energy threshold to drive the Applegate process, as described in Sect. 4.1, assuming ΔP/Pbin = 10-6, we find
-
t = 1 Gyr:ΔEmin/Esec = 0.615 at δ = 0.729
-
t = 14 Gyr: ΔEmin/Esec = 0.692 at δ = 0.713.
As both results differ by just ~ 10%, we conclude that the age of the system is a higher-order effect for the typical systems examined in this paper. We therefore adopt a canonical value of t = 5 Gyr if no age estimates are given in the literature. For the binaries with evolved components, we estimate the age with Evolve ZAMS by solving for the measured stellar radii.
 |
Fig. 5 Density profile of a red dwarf with 0.1M⊙ for a lifetime of 1 Gyr and 14 Gyr. The variation in the core density as a result of the different lifetimes corresponds to only about 10%. The calculation assumes a solar metallicity. |
4.3. Dependence on metallicity variations
Here we explore how much the model results can be affected by uncertainties in the metallicity variation. Using Evolve ZAMS, we have calculated the stellar density profile for the secondary in NN Ser for metallicities between 10-4 and 3 × 10-2, assuming a generic age of 5 Gyr. The resulting density profile is given in Fig. 6, showing a maximum variation in the core density of about 20%.
We further summarize the resulting changes in the stellar luminosity, radius, and surface temperature in Table 3. While the maximum variations in radius and surface temperature correspond to about 20%, the variation in the luminosity corresponds to a factor of 2 between the extreme cases. Considering that the metallicity is varied by more than two orders of magnitude, the latter still corresponds to a minor uncertainty.
Fundamental calculated secondary parameters for varying metallicity values.
 |
Fig. 6 Density profile of a red dwarf with 0.1M⊙ for metallicities between 10-4 and 3 × 10-2. The maximum variation in the core density corresponds to about 20%. The calculation assumes a generic age of 5 Gyr. |
Using the calculated stellar density profiles as input, we can now use the formalism developed in Sect. 4.1 to determine the required energy to drive the eclipsing time variations ΔEmin and compare them to the energy Esec produced by the secondary within one modulation period. For the metallicities investigated here, we find the following results:
-
Z = 0.0001: ΔEmin/Esec = 0.593
-
Z = 0.004:ΔEmin/Esec = 0.502
-
Z = 0.03:ΔEmin/Esec = 0.649.
Again, the scatter in the ratio ΔEmin/Esec is in the 10−20% level even for the large range of metallicities considered here. The metallicity contributes to the overall uncertainty, but an incorrect metallicity estimate cannot significantly affect the question whether the Applegate mechanism is feasible or not.
5. Results
In this section, we apply the framework from the previous section. This includes the detailed model presented in Sect. 4.1 to investigate how the feasibility of the Applegate model depends on the properties of the binary system. We further apply this framework to the sample presented in Sect. 2 to assess for which of these systems the eclipsing time observations can be explained with the Applegate mechanism.
5.1. Parameter study
In the following, we consider a close binary system with varying separation consisting of a 0.5 M⊙ white dwarf and a red dwarf companion with different masses in the range of 0.15 M⊙ to 0.6 M⊙. We assume a fixed relative period variation ΔP/Pbin = 10-7 with a modulation period of Pmod = 14 yr, corresponding to a Jupiter-like planet with mass ~ 3 MJup and semimajor axis ~ 5 au.
Using the model presented in Sect. 4.1, we determine the required energy to drive the Applegate mechanism as a function of binary separation for different masses of the secondary. The results of this calculation are presented in Fig. 7. For all secondary masses, the Applegate threshold energy scales positively with increasing binary separation, as a larger quadrupole moment variation must be generated with increasing binary separation for the same period variation to be produced. The ratio Emin/Esec decreases with increasing mass of the secondary, as more massive secondaries produce higher stellar luminosities and more energy that is potentially available to drive Applegate’s mechanism. This mechanism implies that more massive secondaries are particularly well suited to produce quadrupole moment variations, while it is more difficult for low-mass companions as observed in NN Ser.
Qualitatively, we can understand the scaling behavior seen in Fig. 7 utilizing the constant-density model. Normalized to the energy provided by the secondary over one planetary orbit, we obtain 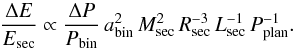 (46)From Demircan & Kahraman (1991), we adopt
(46)From Demircan & Kahraman (1991), we adopt 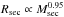 and
and 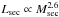 , while the relative period change and the planetary period are virtually constant. Combined we get
, while the relative period change and the planetary period are virtually constant. Combined we get 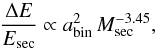 (47)resembling the fact that the relative Applegate threshold energy raises for increasing binary separation and decreases for increasing secondary mass.
(47)resembling the fact that the relative Applegate threshold energy raises for increasing binary separation and decreases for increasing secondary mass.
 |
Fig. 7 Relative Applegate energy calculated for varying secondary masses and binary separations according to Sect. 5.1. Typical PCEBs with extremly low-mass secondarys do not provide enough energy to power the Applegate process or do not even satisfy the Applegate condition. Rather, typical Applegate systems are both relatively massive and extremely compact. |
5.2. Application to our sample
We applied the calculations as described in Sect. 4.1 on the systems introduced and characterized in Sect. 2. In all our calculations, we assumed solar metallicity, and we rescaled and normalized the calculated radial density profile to resemble the (mean) observed mass and radius values. A summary of the main results is given in Table 4.
In total, we investigated 16 systems. Considering the numerical model based on realistic density profiles from Sect. 4.1, the Applegate formalism can safely explain the period variations of four systems (QS Vir, DP Leo, V471 Tau, BX Dra). However, this may be an underestimate for QS Vir, which contains variations in the O−C diagram that are much steeper than the average variation within one modulation time. For the other 12 systems, the relative threshold energy is greater than unity or no solution exists at all, implying that more than the total energy generated by the secondary is necessary to power the binary’s period variations or the system’s architecture is not capable of driving such a high level of period variation via the Applegate mechanism. For four of these systems, in particular, HU Aqr, UZ For, HR 1099, and SZ Psc, the ratio ΔE/Esec is of order 1. Given the uncertainties regarding metallicity and age, as discussed in the previous Sects. 4.2 and 4.3, these systems may still be able to drive an Applegate mechanism. However, for the remaining eight systems, the ratio ΔE/Esec is considerably larger than 1, implying that the observed eclipsing time variations cannot be explained by magnetic activitiy, particularly not in the wider, more massive and evolving RS CVn systems.
For comparison, we show the results from our constant density model, which tends to produce higher estimates of ΔE/Esec, leading to an overestimate of the required energy. The two-zone model yields results close to the numerical values. For comparison, we also show the results adopting the original framework by Applegate (1992) as presented by Parsons et al. (2010b) as well as the fit by Tian et al. (2009). Both cases tend to significantly underestimate the energy required to drive the eclipsing time variations due to the thin-shell approximation and its inherent negligence of the core’s back reaction. We therefore emphasize that an assessment of the Applegate mechanism needs to be based at least on a two-zone model.
5.3. Activity of the likely candidates
In order to test the hypothesis of an Applegate mechanism, we have checked for the presence of magnetic activity those systems where the Applegate mechanism can be expected to produce period time variations of the observed magnitude, i.e., BX Dra, V471 Tau, DP Leo, QS Vir, and RU Cnc. In principle, all systems show signs of strong magnetic activity.
Park et al. (2013) found strong changes in the light curves of BX Dra, which can only be explained by large spots. Its coronal activity, however, cannot be examined due to the large distance of 230 pc. V471 Tau, on the other hand, exhibits photometric variability, flaring events, and Hα emission along with a strong X-ray signal (Kamiński et al. 2007; Pandey & Singh 2008).
The X-ray flux of DP Leo has been studied extensively, e.g., by Schwope et al. (2002) and the magnetic activity of QS Vir could be detected via Ca II H&K emission, Doppler Imaging (Ribeiro et al. 2010), and coronal emission (Matranga et al. 2012). RU Cnc is a known ROSAT All Sky Survey (RASS) source (Zickgraf et al. 2003).
In general, it is very likely that the secondaries in these systems show magnetic activity as the red dwarfs are fully convective and rapidly rotating because of the tidal locking to the primary star. The stars therefore likely fulfill the conditions to drive a dynamo and produce magnetic fields. The question is thus whether the activity can drive sufficiently large changes in the quadrupole moment to explain the eclipsing time variations. At least for eight of the systems in our sample, the latter appears difficult on energetic grounds.
5.4. Further implications
Employing a detailed model for the Applegate mechanism in eclipsing binaries, we have checked here whether quadrupole moment variations driven by magnetic energy can explain the observed eclipsing time variations in a sample of PCEB systems. We found that at least in eight of these systems, this possibility can be ruled out.
However, this does not mean that these systems are not magnetically active, it only implies that magnetic activity is not the only or main cause of the observed period time variations. For instance in NN Ser, the required energy to drive the Applegate process exceeds the available energy by about a factor of 64. Considering that the period time variations scale proportionally to the available energy, an Applegate mechanism could nevertheless contribute to additional scatter in the eclipsing time variations at a level of ≲ 1%. While this effect may be neglected in the case of NN Ser, it may play an important role in other systems with Applegate energies closer to the energy provided by the secondary. It is therefore necessary to further investigate their possible contribution and to distinguish Applegate period variations from the potential influence of a companion in order to calculate realistic fits of planetary systems.
6. Conclusions and discussion
In this paper, we have systematically assessed the feasibility of the Applegate model in PCEB systems. For this purpose, we have adopted the formulation by Brinkworth et al. (2006) considering a finite shell around a central core, and including the change of the quadrupole moment both in the shell and the core. As these contributions partly balance each other, the core is energetically more expensive than the thin-shell model by Applegate (1992), i.e., it requires more energy per orbital period to drive the eclipsing time oscillations.
We apply the Brinkworth model here in different approximations, including a constant density approximation where the required energy is independent of stellar rotation, a two-zone model assuming different densities in the shell and the core, as well as a detailed numerical model where the framework is applied to realistic stellar density profiles. We show that the two-zone model reproduces the results of the most detailed framework with a deviation of less than 25%. We have explored the general dependence of the required energy. In particular, the Applegate mechanism becomes energetically more feasible for smaller binary separations, as in that case, a smaller change in the quadrupole moment is sufficient to drive the observed oscillations. In addition, the mechanism becomes more feasible with increasing mass of the secondary star, as the nuclear energy production increases with stellar mass. An ideal Applegate PCEB system consists therefore of a very tight binary (~ 0.5 R⊙) with a secondary star of ~ 0.5 M⊙.
This formalism is applied to a sample of close binaries with observed eclipsing time variations, including the PCEB sample provided by Zorotovic & Schreiber (2013), as well as four RS CVn binaries.
For most systems in our sample, the energy required to drive the Applegate process is considerably larger than the energy provided by the star. In these cases, the observed period variations cannot be explained in the context of the Applegate model. The situation is similar if we consider only the eleven PCEBs. Therefore, alternative interpretations such as the planetary hypothesis need to be investigated in more detail, and we also encourage direct imaging attempts as pursued by Hardy et al. (2015) particularly in those cases where the Applegate mechanism turns out to be unfeasible.
Our conclusions do not imply the absence of magnetic activity for binaries where the Applegate model is not able to produce the observed period variations. Rather, it only means that the magnetic activity is not strong enough to be the dominant mechanism. However, as many of these systems have rapidly rotating secondaries with a convective envelope, we expect signs of dynamo activity, which can contribute to the period time variations on some level. Assuming a contribution scaling linearly with the relative Applegate threshold energy, the Applegate process might provide a significant additional scatter that needs to be taken into account when inferring potential planetary orbits from the observed data.
Webpage Evolve ZAMS: http://www.astro.wisc.edu/~townsend/static.php?ref=ez-web
Acknowledgments
M.V. and R.B. gratefully acknowledge funding from the Deutsche Forschungsgemeinschaft via Research Training Group (GrK) 1351 Extrasolar Planets and their Host Stars. M.V. is thankful for funding from the Studienstiftung des Deutschen Volkes via a travel grant. We thank Klaus Beuermann, Stefan Dreizler, Rick Hessman, Ronald Mennickent, and Matthias Schreiber for stimulating discussions on the topic. We also would like to thank the referee Ed Devinney for helpful comments that improved our manuscript.
References
- Almeida, L. A., Jablonski, F., Tello, J., & Rodrigues, C. V. 2012, MNRAS, 423, 478 [NASA ADS] [CrossRef] [Google Scholar]
- Applegate, J. H. 1992, ApJ, 385, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Bailey, J., & Cropper, M. 1991, MNRAS, 253, 27 [NASA ADS] [Google Scholar]
- Bear, E., & Soker, N. 2014, MNRAS, 444, 1698 [NASA ADS] [CrossRef] [Google Scholar]
- Beuermann, K., Hessman, F. V., Dreizler, S., et al. 2010, A&A, 521, L60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beuermann, K., Buhlmann, J., Diese, J., et al. 2011, A&A, 526, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beuermann, K., Breitenstein, P., Debski, B., et al. 2012a, A&A, 540, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beuermann, K., Dreizler, S., Hessman, F. V., & Deller, J. 2012b, A&A, 543, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beuermann, K., Dreizler, S., & Hessman, F. V. 2013, A&A, 555, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brinkworth, C. S., Marsh, T. R., Dhillon, V. S., & Knigge, C. 2006, MNRAS, 365, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Demircan, O., & Kahraman, G. 1991, Ap&SS, 181, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Drake, J. J., Garraffo, C., Takei, D., & Gaensicke, B. 2014, MNRAS, 437, 3842 [NASA ADS] [CrossRef] [Google Scholar]
- Drechsel, H., Heber, U., Napiwotzki, R., et al. 2001, A&A, 379, 893 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Engle, S. G., & Guinan, E. F. 2011, in 9th Pacific Rim Conference on Stellar Astrophysics, eds. S. Qain, K. Leung, L. Zhu, & S. Kwok, ASP Conf. Ser., 451, 285 [Google Scholar]
- Faulkner, J. 1971, ApJ, 170, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Fekel, Jr., F. C. 1983, ApJ, 268, 274 [NASA ADS] [CrossRef] [Google Scholar]
- Frasca, A., & Lanza, A. F. 2004, VizieR Online Data Catalog: J/A+A/429/309 [Google Scholar]
- Frasca, A., & Lanza, A. F. 2005, A&A, 429, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García-Alvarez, D., Barnes, J. R., Collier Cameron, A., et al. 2003, A&A, 402, 1073 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gianninas, A., Bergeron, P., & Ruiz, M. T. 2011, ApJ, 743, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Goździewski, K., Nasiroglu, I., Słowikowska, A., et al. 2012, MNRAS, 425, 930 [NASA ADS] [CrossRef] [Google Scholar]
- Goździewski, K., Słowikowska, A., Dimitrov, D., et al. 2015, MNRAS, 448, 1118 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, R. O., Corbally, C. J., Garrison, R. F., et al. 2006, AJ, 132, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Haefner, R., Fiedler, A., Butler, K., & Barwig, H. 2004, A&A, 428, 181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hall, D. S. 1989, Space Sci. Rev., 50, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Hardy, A., Schreiber, M. R., Parsons, S. G., et al. 2015, ApJ, 800, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Hinse, T. C., Lee, J. W., Goździewski, K., et al. 2012, MNRAS, 420, 3609 [NASA ADS] [CrossRef] [Google Scholar]
- Horner, J., Wittenmyer, R. A., Hinse, T. C., & Tinney, C. G. 2012, MNRAS, 425, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Hussain, G. A. J., Allen de Prieto, C., Saar, S. H., & Still, M. 2006, MNRAS, 367, 1699 [NASA ADS] [CrossRef] [Google Scholar]
- Ibanoglu, C. 1991, The Observatory, 111, 257 [Google Scholar]
- Iben, Jr., I., & Livio, M. 1993, PASP, 105, 1373 [Google Scholar]
- Ivanova, N., Justham, S., Chen, X., et al. 2013, A&ARv, 21, 59 [Google Scholar]
- Jakate, S., Bakos, G. A., Fernie, J. D., & Heard, J. F. 1976, AJ, 81, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Kamiński, K. Z., Ruciński, S. M., Matthews, J. M., et al. 2007, AJ, 134, 1206 [NASA ADS] [CrossRef] [Google Scholar]
- Kilkenny, D., O’Donoghue, D., Koen, C., Lynas-Gray, A. E., & van Wyk, F. 1998, MNRAS, 296, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Kraft, R. P., Mathews, J., & Greenstein, J. L. 1962, ApJ, 136, 312 [NASA ADS] [CrossRef] [Google Scholar]
- Lanza, A. F. 2005, MNRAS, 364, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Lanza, A. F. 2006, MNRAS, 369, 1773 [NASA ADS] [CrossRef] [Google Scholar]
- Lanza, A. F., & Rodonò, M. 1999, A&A, 349, 887 [NASA ADS] [Google Scholar]
- Lanza, A. F., Rodono, M., & Rosner, R. 1998, MNRAS, 296, 893 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J. W., Kim, S.-L., Kim, C.-H., et al. 2009, AJ, 137, 3181 [NASA ADS] [CrossRef] [Google Scholar]
- Marsh, T. R., & Pringle, J. E. 1990, ApJ, 365, 677 [NASA ADS] [CrossRef] [Google Scholar]
- Marsh, T. R., Parsons, S. G., Bours, M. C. P., et al. 2014, MNRAS, 437, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Matranga, M., Drake, J. J., Kashyap, V., & Steeghs, D. 2012, ApJ, 747, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Maxted, P. F. L., O’Donoghue, D., Morales-Rueda, L., Napiwotzki, R., & Smalley, B. 2007, MNRAS, 376, 919 [NASA ADS] [CrossRef] [Google Scholar]
- Meng, X., Chen, X., & Han, Z. 2008, A&A, 487, 625 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meyer, F., & Meyer-Hofmeister, E. 1979, A&A, 78, 167 [NASA ADS] [Google Scholar]
- O’Brien, M. S., Bond, H. E., & Sion, E. M. 2001, ApJ, 563, 971 [NASA ADS] [CrossRef] [Google Scholar]
- O’Donoghue, D., Koen, C., Kilkenny, D., et al. 2003, MNRAS, 345, 506 [NASA ADS] [CrossRef] [Google Scholar]
- Paczynski, B. 1976, in Structure and Evolution of Close Binary Systems, eds. P. Eggleton, S. Mitton, & J. Whelan, IAU Symp., 73, 75 [Google Scholar]
- Pandey, J. C., & Singh, K. P. 2008, MNRAS, 387, 1627 [NASA ADS] [CrossRef] [Google Scholar]
- Park, J.-H., Lee, J. W., Kim, S.-L., Lee, C.-U., & Jeon, Y.-B. 2013, PASJ, 65, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Parsons, S. G., Marsh, T. R., Copperwheat, C. M., et al. 2010a, MNRAS, 402, 2591 [NASA ADS] [CrossRef] [Google Scholar]
- Parsons, S. G., Marsh, T. R., Copperwheat, C. M., et al. 2010b, MNRAS, 407, 2362 [NASA ADS] [CrossRef] [Google Scholar]
- Passy, J.-C., De Marco, O., Fryer, C. L., et al. 2012, ApJ, 744, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Paxton, B. 2004, PASP, 116, 699 [NASA ADS] [CrossRef] [Google Scholar]
- Popper, D. M. 1988, AJ, 96, 1040 [NASA ADS] [CrossRef] [Google Scholar]
- Potter, S. B., Romero-Colmenero, E., Ramsay, G., et al. 2011, MNRAS, 416, 2202 [NASA ADS] [CrossRef] [Google Scholar]
- Pourbaix, D., Tokovinin, A. A., Batten, A. H., et al. 2004, A&A, 424, 727 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pribulla, T., Vaňko, M., Ammler-von Eiff, M., et al. 2012, Astron. Nachr., 333, 754 [NASA ADS] [CrossRef] [Google Scholar]
- Qian, S.-B., Liu, L., Liao, W.-P., et al. 2011, MNRAS, 414, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Qian, S.-B., Zhu, L.-Y., Dai, Z.-B., et al. 2012, ApJ, 745, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Ribeiro, T., Kafka, S., Baptista, R., & Tappert, C. 2010, AJ, 139, 1106 [NASA ADS] [CrossRef] [Google Scholar]
- Rüdiger, G., Elstner, D., Lanza, A. F., & Granzer, T. 2002, A&A, 392, 605 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schleicher, D. R. G., & Dreizler, S. 2014, A&A, 563, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schleicher, D. R. G., Dreizler, S., Völschow, M., Banerjee, R., & Hessman, F. V. 2015, Astron. Nachr., 336, 458 [NASA ADS] [CrossRef] [Google Scholar]
- Schwope, A. D., Hambaryan, V., Schwarz, R., Kanbach, G., & Gänsicke, B. T. 2002, A&A, 392, 541 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schwope, A. D., Horne, K., Steeghs, D., & Still, M. 2011, A&A, 531, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taam, R. E., & Ricker, P. M. 2010, New A Rev., 54, 65 [Google Scholar]
- Taam, R. E., & Sandquist, E. L. 2000, ARA&A, 38, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Tian, Y. P., Xiang, F. Y., & Tao, X. 2009, Ap&SS, 319, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Vaccaro, T. R., Wilson, R. E., Van Hamme, W., & Terrell, D. 2015, ApJ, 810, 157 [CrossRef] [Google Scholar]
- Verbunt, F., & Zwaan, C. 1981, A&A, 100, L7 [NASA ADS] [Google Scholar]
- Völschow, M., Banerjee, R., & Hessman, F. V. 2014, A&A, 562, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, X.-L., Xiang, F.-Y., Tian, Y.-P., & Shi, X.-M. 2010, PASJ, 62, 671 [NASA ADS] [Google Scholar]
- Webbink, R. F. 2008, in Astrophys. Space Sci. Libr. 352, eds. E. F. Milone, D. A. Leahy, & D. W. Hobill, 233 [Google Scholar]
- Wittenmyer, R. A., Horner, J., Marshall, J. P., Butters, O. W., & Tinney, C. G. 2012, MNRAS, 419, 3258 [NASA ADS] [CrossRef] [Google Scholar]
- Wood, J. H., & Saffer, R. 1999, MNRAS, 305, 820 [NASA ADS] [CrossRef] [Google Scholar]
- Zickgraf, F.-J., Engels, D., Hagen, H.-J., Reimers, D., & Voges, W. 2003, A&A, 406, 535 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zorotovic, M., & Schreiber, M. R. 2013, A&A, 549, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zorotovic, M., Schreiber, M. R., Gänsicke, B. T., et al. 2011, A&A, 536, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Relative difference between the two-zone model described in Sect. 3.4 with the full model considering a realistic stellar density profile as outlined in Sect. 4.1. The model assumes a white dwarf mass of 0.5M⊙ and an age of the secondary of 5 Gyr. We employ λ = 0.0096 and ξ = 4/3 as parameters in the two-zone model. The relative deviation of the results is shown as a function of the Applegate parameter A and for different secondary masses. A good approximation requires A ≲ 0.5. |
| In the text | |
 |
Fig. 2 Comparison of the constant density and two-zone analytical models, as described in Sects. 3.3 and 3.4, with the full calculations as described in Sect. 4.1 in terms of the predicted relative Applegate threshold energy. We consider the same general system configuration as in Fig. 1 and described in Sect. 3.4, but fixed the secondary mass to Msec = 0.3 M⊙, which enabled us to plot the calculated energies as functions of the Applegate parameter A (see Eq. (37)). The analytical two-zone model closely follows the full calculations with typical deviations of less than 10%, while the simple constant density model overestimates the energy threshold by several magnitudes except for the critical region close to unity. |
| In the text | |
 |
Fig. 3 Angular velocity change normalized by the angular velocity of the binary both in the core (ΔΩ1) and shell (ΔΩ2) for our reference system NN Ser as a function of the size of the core. For both quantities, there are two solutions, denoted with + and –. The calculation is based on the full numerical model described in Sect. 4.1. |
| In the text | |
 |
Fig. 4 Required energy to drive the eclipsing time observations for the solutions denoted with + and – in Fig. 3. The calculation is based on the full numerical model described in Sect. 4.1. |
| In the text | |
 |
Fig. 5 Density profile of a red dwarf with 0.1M⊙ for a lifetime of 1 Gyr and 14 Gyr. The variation in the core density as a result of the different lifetimes corresponds to only about 10%. The calculation assumes a solar metallicity. |
| In the text | |
 |
Fig. 6 Density profile of a red dwarf with 0.1M⊙ for metallicities between 10-4 and 3 × 10-2. The maximum variation in the core density corresponds to about 20%. The calculation assumes a generic age of 5 Gyr. |
| In the text | |
 |
Fig. 7 Relative Applegate energy calculated for varying secondary masses and binary separations according to Sect. 5.1. Typical PCEBs with extremly low-mass secondarys do not provide enough energy to power the Applegate process or do not even satisfy the Applegate condition. Rather, typical Applegate systems are both relatively massive and extremely compact. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


