| Issue |
A&A
Volume 587, March 2016
|
|
|---|---|---|
| Article Number | A23 | |
| Number of page(s) | 16 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201527299 | |
| Published online | 15 February 2016 | |
Prospects for high-z cluster detections with Planck, based on a follow-up of 28 candidates using MegaCam at CFHT⋆
1
Laboratoire AIM, IRFU/Service d’Astrophysique − CEA/DSM − CNRS − Université
Paris Diderot,
Bât. 709, Saclay,
91191
Gif-sur-Yvette Cedex,
France
e-mail:
remco.van-der-burg@cea.fr
2
DSM/IRFU/SPP, CEA-Saclay, 91191
Gif-sur-Yvette Cedex,
France
3
Institut d’Astrophysique Spatiale, CNRS (UMR 8617) Université
Paris-Sud 11, Bâtiment
121, 91405
Orsay Cedex,
France
4
Instituto de Astrofísica de Canarias, C/vía Láctea s/n, 38205,
La Laguna, Tenerife,
Spain
5
Dpto. Astrofísica, Universidad de La Laguna (ULL),
38206, La Laguna, Tenerife, Spain
6
Institute of Theoretical Astrophysics, University of
Oslo, PO Box 1029,
Blindern, 0315
Oslo,
Norway
7
Departments of Physics, Carnegie Mellon University,
5000 Forbes Ave., Pittsburgh, PA
15217,
USA
8
Leiden Observatory, Leiden University,
PO Box 9513, 2300 RA
Leiden, The
Netherlands
9
Laboratoire de Physique Subatomique et de Cosmologie, Université
Joseph Fourier Grenoble I, CNRS/IN2P3, Institut National Polytechnique de
Grenoble, 53 rue des
Martyrs, 38026
Grenoble Cedex,
France
10
Université de Toulouse, UPS-OMP, IRAP, 31028
Toulouse Cedex 4,
France
11
CNRS, IRAP, 9
Av. colonel Roche, BP
44346, 31028
Toulouse Cedex 4,
France
Received: 3 September 2015
Accepted: 1 December 2015
The Planck catalogue of SZ sources limits itself to a significance threshold of 4.5 to ensure a low contamination rate by false cluster candidates. This means that only the most massive clusters at redshift z> 0.5, and in particular z> 0.7, are expected to enter into the catalogue, with a large number of systems in that redshift regime being expected around and just below that threshold. In this paper, we follow-up a sample of SZ sources from the Planck SZ catalogues from 2013 and 2015. In the latter maps, we consider detections around and at lower significance than the threshold adopted by the Planck Collaboration. To keep the contamination rate low, our 28 candidates are chosen to have significant WISE detections, in combination with non-detections in SDSS/DSS, which effectively selects galaxy cluster candidates at redshifts z ≳ 0.5. By taking r- and z-band imaging with MegaCam at CFHT, we bridge the 4000 Å rest-frame break over a significant redshift range, thus allowing accurate redshift estimates of red-sequence cluster galaxies up to z ~ 0.8. After discussing the possibility that an overdensity of galaxies coincides -by chance- with a Planck SZ detection, we confirm that 16 of the candidates have likely optical counterparts to their SZ signals, 13 (6) of which have an estimated redshift z> 0.5 (z> 0.7). The richnesses of these systems are generally lower than expected given the halo masses estimated from the Planck maps. However, when we follow a simplistic model to correct for Eddington bias in the SZ halo mass proxy, the richnesses are consistent with a reference mass-richness relation established for clusters detected at higher significance. This illustrates the benefit of an optical follow-up, not only to obtain redshift estimates, but also to provide an independent mass proxy that is not based on the same data the clusters are detected with, and thus not subject to Eddington bias.
Key words: galaxies: clusters: general / galaxies: photometry
Reduced images are available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/587/A23
© ESO, 2016
1. Introduction
Our fiducial Lambda-cold-dark-matter (ΛCDM) cosmological paradigm provides a model in which structures form hierarchically. The most massive gravitationally collapsed systems in this picture, called galaxy clusters, provide insights into the physics at play in the extremely hot and highly ionised intra-cluster medium (ICM), constitute unique laboratories to study the evolution of galaxies as a function of their environment, and are of particular interest for understanding structure formation through the statistical study of the cluster population. Furthermore, the abundance of galaxy clusters, as a function of mass and redshift, is sensitive to the underlying cosmology (e.g. Allen et al. 2011, and references therein), and thus provides a means of verifying the cosmological model (e.g. Vikhlinin et al. 2009; Rozo et al. 2010; Mantz et al. 2010b; Sehgal et al. 2011; Benson et al. 2013; Planck Collaboration XXIV 2015).
An observationally selected mass-limited sample of galaxy clusters would be ideal, as it would allow for a straightforward comparison with theoretical predictions when probing cluster formation physics or cosmology. In practice, such a selection cannot be made, since halo mass is not a direct observable. Historically, baryonic tracers such as galaxies and X-ray emitting gas have been used as mass proxies to construct samples of galaxy clusters (e.g. Abell et al. 1989; Ebeling et al. 1998; Gladders & Yee 2000; Böhringer et al. 2000, 2004; Gilbank et al. 2011; Gettings et al. 2012). However, due to differences in assembly histories, and the complexity of the physics involved, these detection methods potentially bias a cluster sample towards a specific dynamical state, or are particularly subject to projection effects along the line of sight. Cluster samples constructed in such ways still require significant corrections to link the observables to the halo mass, before comparing the data to theoretical predictions. This also complicates a cosmological analysis that is based on the abundance of clusters, since that requires a precise knowledge of the selection function and catalogue completeness.
A detection method proposed several decades ago, based on the Sunyaev-Zeldovich (SZ, Sunyaev & Zeldovich 1980) effect, is expected to yield cluster samples that are closer to being mass-selected (e.g. da Silva et al. 2004; Hoekstra et al. 2012). Over the last few years, SZ-based cluster samples have been provided over areas of 100s to 1000s of sq. deg by the South Pole Telescope (SPT, Reichardt et al. 2013; Bleem et al. 2015), and the Atacama Cosmology Telescope (ACT, Hasselfield et al. 2013). The first all-sky SZ-detected cluster catalogue is provided by Planck, which released three catalogues during the course of its lifetime. The first contained 189 clusters and was based on about a third of the final data set (Planck Collaboration VIII 2011). A more extensive catalogue, containing SZ detections down to a significance of signal-to-noise ratio S/N = 4.5, was released after about half of the survey lifetime in 2013 (Planck Collaboration XXIX 2014, hereafter PSZ1). The final Planck maps and SZ catalogues, based on the full mission, were published recently (Planck Collaboration XXVII 2015, hereafter PSZ2).
In practice, any catalogue down to sufficiently low S/N includes false detections. Although the average purity can be estimated statistically (Planck Collaboration XXIX 2014; Planck Collaboration XXVII 2015), a full exploitation of the catalogue requires one to identify bona fide clusters and to measure their redshifts. By cross-matching Planck SZ detections with existing cluster catalogues, and by identifying galaxy overdensities in existing survey data around the SZ sources, the Planck Collaboration has confirmed clusters as part of their analysis (Planck Collaboration XXIX 2015; Planck Collaboration XXVII 2015). As described in detail in these papers, the catalogue validation process also includes the results from several studies that are published independently (e.g. Rozo et al. 2015; Liu et al. 2015) and dedicated validation follow-up (e.g. Planck Collaboration XI 2011; Planck Collaboration Int. XXVI 2015). This verification work is still ongoing, and is now focussed on a systematic follow-up of remaining SZ candidates, such as the recent work of Planck Collaboration XXXVI (2015). Since the purity decreases (i.e. the number of false candidates increases) with decreasing S/N, systematic follow-up is less and less efficient at unravelling new clusters. Another difficulty, which is more severe at low S/N, is the ambiguity in SZ source confirmation, i.e. in assessing whether a galaxy overdensity is the real counterpart, or a chance association that is spatially coincident with the ~5′Planck beam.
Nevertheless, there is an interest to go to even lower S/N than the published Planck catalogues. For instance, going to lower S/N than a given limit may help to understand the completeness above that limit. More importantly for the present paper, the all-sky nature of the Planck catalogue allows us to probe the rarest objects that populate the high-mass end of the mass function. This is a unique capability of Planck, of particular importance in the high-redshift regime. The previous All-Sky Survey, performed in X-ray by the ROSAT satellite, had a limited depth and even the MACS survey (Ebeling et al. 2007), based on a systematic follow-up of the ROSAT Bright Source Catalogue, detected only 12 objects at z> 0.5, all of which lie at z< 0.7. However, the prospects to construct sizeable samples of massive clusters (M500 ≳ 5 × 1014 M⊙)1 spread over a range of high redshifts (0.5 <z< 1.0), is still limited. With a significance threshold of S/N = 4.5, the published PSZ2 catalogue is ~80% complete for M500 ≳ 7.5 × 1014 M⊙ at z ≳ 0.5, but its completeness decreases to 20% for M500 ≳ 5.0 × 1014 M⊙ (Fig. 26 in Planck Collaboration XXVII 2015). By lowering the significance threshold, one quickly gains in completeness and thus unveils more of these high-z massive clusters, a gain amplified by the fact that we are at the exponential end of the halo mass function at these redshifts. The main challenge is that these clusters have to be identified among an increasing number of candidates, the majority being at low redshift, together with an increasing fraction of false candidates as the detection significance (i.e. purity) decreases. A fully systematic follow-up of all these candidates would not only be very inefficient, but no longer feasible. However, in this paper we explore the use of existing optical and near-infrared survey data to pre-select likely massive high-z clusters among the candidates, before performing the deeper follow-up observations.
This study focuses on a sample of 28 cluster candidates, which are either part of the PSZ1 catalogue, the PSZ2 catalogue, or are detected at lower SZ significance in the final Planck maps. It therefore contributes to the general systematic validation of Planck cluster candidates in the public catalogues, but also takes a first step towards the construction of a sample of massive high-z samples beyond the standard detection limit. Specifically, this is a pilot study to (1) investigate how existing (optical and near-infrared) survey data allow us to study detections at lower SZ significance, while maintaining a high purity of detecting real clusters in general, and redshift z ≳ 0.5 clusters in particular; (2) illustrate the importance of a quantitative way to characterise optical counterparts of cluster candidates in deeper follow-up data to verify if it is expected for a halo corresponding to the measured SZ signal and, related to this; (3) study the effect of Eddington bias on the SZ mass proxy at low detection significance.
The present work concerns an inhomogeneously selected sample of cluster candidates that does not have a clearly defined selection function. As such it is inappropriate for cosmological studies. The eventual goal of the project is to obtain a representative sample of the most massive clusters at z> 0.5 (and particularly z> 0.7). Representativity is key for the study of the statistical properties of clusters (e.g. their baryon fractions and profiles, or their total mass profiles), as a probe of the physics of structure formation. In this context, a sample does not have to be complete or to have a precisely quantified selection function, such as is necessary for cosmological applications, so long as it is representative of the underlying population.
The structure of this paper is as follows. The cluster candidate sample we considered for follow-up is presented in Sect. 2, while the follow-up data and optical catalogues are presented in Sect. 3. In Sect. 4 we describe the red-sequence model that we use to find galaxy overdensities close to the Planck SZ detections and measure their redshifts and richnesses. We discuss the likelihood that these counterparts are truly associated with a given SZ detection in Sect. 5, and discuss the relation between mass and richness for this sample. In particular, we discuss the effect of Eddington bias in the SZ mass proxy in Sect. 5.1, which is important for interpreting our measured mass-richness relation. Section 6 contains a discussion of individual candidates, for which pseudo-colour images are shown in Appendix A. We summarise and conclude in Sect. 7.
All magnitudes we quote are in the AB magnitudes system, and we adopt ΛCDM cosmology with Ωm = 0.3, ΩΛ = 0.7 and H0 = 70 km s-1 Mpc-1.
2. Planck sample
2.1. Candidate selection
The Planck PSZ1 catalogue consists of extended sources detected at a significance of S/N> 4.5 in the first release (i.e. based on about half of the final data set). Candidates which were not yet validated to be a cluster at that time were sorted into CLASS1-3 according to their likelihood of being a real cluster (from high to low). This classification scheme was based on an SZ-quality assessment combined with information from external data from the ROSAT All Sky Survey (RASS) and the Wide-field Infrared Survey Explorer (WISE, Wright et al. 2010). In semesters 2013A and 2013B we targeted a total of 16 CLASS1 and CLASS2 candidates in the northern hemisphere (δJ2000> −25°) with MegaCam. We note that the follow-up of these candidates is part of a larger validation programme which aims at verifying all candidates of the PSZ1 catalogue. The ones we pursue in this paper were not (yet) confirmed to be actual clusters at that time, and were picked because they were possibly z ≳ 0.5 clusters as they did not show any obvious counterpart in the Digitized Sky Survey (DSS2), nor in SDSS (where available). The targets are presented in Table 1, where PSZ1 entry numbers and associated classifications are listed.
During semester 2014B, we targeted another 12 candidates with MegaCam, this time selected from the final maps and SZ catalogue (PSZ2). We improved our preferential selection of high-z cluster candidates for semester 2014B by combining information from WISE and the DSS in the following way. Massive cluster galaxies with redshifts z ≳ 0.5 are expected to be detected significantly in the WISE 3.4 μm channel, while showing no significant detection in the relatively shallow optical DSS images (e.g. Fassbender et al. 2011). We exploit this information by searching for overdensities of such galaxies within ~4′ from all Planck SZ detections down to a significance of S/N> 4.0 in the final maps, which did not correspond to known clusters. This way we selected, by visual inspection, 12 candidates in the Northern hemisphere (δJ2000> −25°) that are likely coincident with a system of high-z galaxies. An overview of the full list of targeted candidates is given in Table 1, with entries in the PSZ1 and PSZ2 catalogues (if applicable).
The PSZ2 catalogue, and also the updated version of the PSZ1 catalogue (Planck Collaboration XXIX 2015), contain a classification of SZ detections based on a supervised neural network. As described in Aghanim et al. (2015), the quality flag Q_NEURAL (or QN for PSZ1) provides a condensed one-dimensional description of the contribution of components other than the SZ effect to the spectral energy distribution (SED) measured by Planck. Physical sources of contamination include the cosmic microwave background (CMB), infrared emission from Galactic dust, molecular Galactic CO emission, and a radio component from Galactic free-free, synchrotron, and thermal dust emission. A high value of Q_NEURAL≳ 0.4 indicates that a source has an SED that is dominated by the SZ effect, whereas a lower value suggests a distorted SED, and thus a likely false candidate. We list Q_NEURAL parameters from Aghanim et al. (2015) in Table 1, and discuss our candidates in this context in Sect. 5.4.
The sample of 28 cluster candidates studied here.
 |
Fig. 1 Illustration of the background residual correction, showing a 15′ × 15′ part of the PSZ2 G048.21-65.00 z-band stack before (left panel), and after (right panel) the correction. The median improvement in the effective depth of the z-band images in a 2′′ aperture is approximately 0.4 mag. |
2.2. Homogenisation of SZ detections
Given that the PSZ1 catalogue was constructed from the maps of about half the final depth, we remeasure the SZ signal for each candidate consistently in the final maps (including those PSZ1 candidates that did not end up in the PSZ2 catalogue). We perform a consistent blind search of the SZ signal around the selected locations in the final version of the Planck maps (column S/Nblind in Table 1). We use the Matched Multi-Filter 3 (MMF3, Melin et al. 2006) detection method to search and extract SZ parameters from the Planck maps. We note that the MMF3 detection method resamples the Planck frequency maps centred on a given location, which may slightly affect the significance with which clusters are blindly detected.
Eight of the PSZ1 entries we considered in 2013A and 2013B are not part of the PSZ2 catalogue since they fall below the significance of S/N = 4.5 in the final Planck maps. Their S/N drop to even below 3 (except for one at S/N ~ 4), which suggests that they may have been noise fluctuations in the PSZ1 catalogue. It is informative to perform all processing steps on the available data for these PSZ1-only detections too, and to compare them to other candidates in the final sample as an extra test of our validation method. We will make these comparisons in Sect. 5.4.
3. Optical data and catalogues
To confirm the optical counterparts of these cluster candidates by estimating photometric redshifts and optical richnesses, we observed each through the r- and z-filters using MegaCam mounted on the Canada-France-Hawaii Telescope (CFHT). These filters cover wavelengths such that we expect to obtain reasonably precise photometric redshift estimates over a redshift baseline up to z ~ 0.8. The data are pre-processed using the Elixir pipeline (Magnier & Cuillandre 2004). After this standard reduction, there are still residual background patterns due to, for example, scattered light, fringe residuals, and amplifier drift. Given that these patterns are reasonably stable over time, and that most of the data for a given field and filter are taken during the same night, we can correct for these background effects. We do this by using the dithered pattern of observations to differentiate signals that are on a fixed position on the CCD array from sky-bound signals, similar to our approach in van der Burg et al. (2013, 2015). An example of this procedure is shown in Fig. 1. We remove cosmic rays on a frame-by-frame basis by using the Laplacian Cosmic Ray Identification method (van Dokkum 2001).
Astrometric solutions for the data are obtained using SCAMP (Bertin 2006), based on the USNO-B1 reference catalogue. We combine all exposures taken with a given filter for each semester to effectively increase the source density and obtain highly precise solutions with an internal scatter between filters of <0.05′′. Relative photometric zeropoints between exposures are estimated based on overlapping sources between different frames.
Although the exposures for a given field and filter are generally taken consecutively during the same night and therefore have a similar image quality (IQ), there can be a substantial difference between the image quality of the r- and z-band images of a given field, see Table 2. To measure colours on the same intrinsic part of the galaxies in both filters, we have to account for these differences. The approach we take is to use PSFEx (Bertin 2011) to determine a shapelet-based convolution kernel for each filter, to make the PSF homogeneous between the two stacks. As target PSF we choose a Moffat profile with a FWHM that is 10% larger than the largest IQ of the r- and z-band stacks, with a Moffat-β parameter of 2.5. These choices ensure that the target PSF has sufficiently broad wings that no deconvolution is required.
The exposure times of our images are chosen such that we probe the red-sequence galaxies, which dominate the cluster galaxy population, to a similar limit in the r- and z-band. We choose to use the original, unconvolved z-band image for source detection, as it probes the rest-frame galaxy redward of the 4000 Å break for redshifts up to z ~ 1, and thus provides catalogues that are closest to being stellar-mass selected. We measure colours using circular apertures with a diameter of 2′′ on the seeing-homogenised stacks. At this stage we re-evaluate the photometric zeropoints in several steps. First, for the images that overlap with the SDSS DR9 (Ahn et al. 2012) footprint (19 out of 28 fields), we compare the z-band MAG_AUTO magnitude from MegaCam with the model magnitude z-band magnitude from SDSS, and adjust our zeropoint to match this reference. We do the same for the r-band, based on the difference between the r − z aperture colour measured from the MegaCam data, and the SDSS model r − z colour. While making these comparisons, we apply the linear colour terms between the SDSS and MegaCam filters, as listed on the CFHT website3. Typical corrections are on the order of 0.05 mag, and are largest in the case of non-photometric observing conditions (which mostly occurred in semester 2013A).
We exploit the colour−colour distribution of stars as a second reliable photometric calibrator. To be able to calibrate the data against a universal stellar locus, we require a third photometric band. Because the number of stars that are bright enough in 2MASS, but unsaturated in the deep MegaCam exposures, is limited, we find that the WISE 3.4 μm band serves as a better reference. Therefore we construct an empirical r − z vs. z −3.4 μm colour−colour diagram of bright stars, combining all fields that suffer from little Galactic dust extinction (Schlegel et al. 1998) and that have been calibrated against SDSS. Subsequently, we re-calibrate the remaining fields (nine out of 28 fields) by comparing the measured colours with this r − z vs. z −3.4 μm reference stellar locus. Again, corrections are on the order of 0.05 mag. We estimate the remaining systematic uncertainty on the r − z colour, especially for fields with significant Galactic dust extinction, to be on the order of 0.05. We reach a median 5σ aperture magnitude depth of 25.0 and 23.8 in the r- and z-band stacks, respectively. Table 2 gives an overview of the basic properties of the data per field.
Characteristics of the MegaCam imaging data taken for the 28 fields.
4. Redshift and richness estimates
4.1. Red-sequence model
Our analysis is based on the properties of red-sequence galaxies, which are highly abundant in galaxy clusters, at least up to z ~ 1, and thus provide a signal with a high contrast against the background. To interpret our data, we first construct an empirical model that predicts the colour of red-sequence galaxies as a function of magnitude and redshift. We exploit the 30-band photometric data from the COSMOS/UltraVISTA field (Muzzin et al. 2013b), from which we select galaxies over a range of redshifts with similar properties as our cluster red-sequence galaxies. By combining the excellent photometric redshifts from this field with U − V and V − J rest-frame colour measurements, we select red-sequence galaxies down to faint magnitudes (ztot ≈ 24.0), in redshift bins up to z = 1.1 (e.g. Williams et al. 2009; van der Burg et al. 2013). Note that the r + and z + Subaru filters, which have been used in the UltraVISTA catalogue, are significantly different from the r- and z-band MegaCam filters used in this analysis. To make the model applicable to our data set, we thus match the COSMOS/UltraVISTA catalogue to the CFHTLS D2 field catalogue (Erben et al. 2009; Hildebrandt et al. 2009), which overlaps with the COSMOS field. By selecting galaxies from the 30-band catalogue, while using the flux measurements from the CFHTLS catalogue, we obtain a catalogue of quiescent galaxies with MegaCam r − z-colours as a function of total z-band magnitude and redshift.
Next we fit a linear relation to these colours, in overlapping redshift bins with width 0.04 and stepsize of 0.01. We remove outliers, especially with bluer colours (since cluster red-sequence galaxies are expected to be the oldest and thus reddest at a given redshift). For each redshift bin we thus obtain a slope, intersect (at a magnitude of ztot = 22.0 to reduce covariance between estimated slope and intersect), and scatter around the sequence. We subsequently fit a polynomial relation to each of these three parameters as a function of redshift to obtain smoothly varying functions, which we find to describe the colours of these quiescent galaxies well. The derived red-sequence model in the MegaCam r- and z-band filters is shown in Fig. 2.
 |
Fig. 2 Left panel: empirical model of the red sequence (black lines). At each redshift, the lines run from m∗−2 <m<m∗ + 2. Right panel: three model lines with galaxy colours and magnitudes overplotted from field PSZ2 G119.30-64.68 (zspec = 0.557), within 2 arcmin from the centre of the overdensity. For clarity, error bars are not shown on individual points, but these increase in size from lower-left to upper-right. The inset illustrates the statistical error on the colour measurement around the location of the red sequence at this redshift (offset from the z = 0.55 model for clarity). |
When using this model to estimate redshifts, the highest precision can be obtained in the regime where the 4000 Å break is located between the observed r- and z-band filters, which is in the redshift range 0.35 ≲ z ≲ 0.80. Outside this range, the r- and z-bands lose their constraint on the redshift, although the apparent z-band magnitude distribution of cluster galaxies may still be used as a rough measure of the distance modulus.
Besides the choice of filters, the depth of the data also limits the detectability of high-redshift clusters. We estimate 80% detection completeness limits for the z-band stacks, based on the recovery of simulated galaxies which we inject in our images. We assume Sérsic light profiles with a constant Sérsic parameter of n = 4. We draw sizes from a uniform distribution with effective radii between 1−3 kpc (assuming an angular diameter distance corresponding to redshift z = 0.6), which is appropriate for sources around our detection limit. We note that the recovery of simulated sources is only mildly dependent on these parameter choices since they are poorly resolved in our ground-based images, which results in a recovery rate that is primarily dependent on the PSF size. In Table 2, we show the faintest magnitudes at which 80% of injected sources are still detected. We define corresponding redshift limits as the redshift at which this magnitude limit reaches down to magnitude 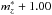 . We base our estimate of
. We base our estimate of 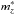 , the characteristic magnitude in the z-band, on the stellar mass functions that are measured in Muzzin et al. (2013a); Ilbert et al. (2013), which suggest that the characteristic mass of quiescent galaxies in our redshift range is approximately described by
, the characteristic magnitude in the z-band, on the stellar mass functions that are measured in Muzzin et al. (2013a); Ilbert et al. (2013), which suggest that the characteristic mass of quiescent galaxies in our redshift range is approximately described by 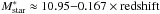 . The characteristic z-band magnitude we use corresponds to the magnitude of a quiescent galaxy formed at zform = 3 that has a stellar mass of
. The characteristic z-band magnitude we use corresponds to the magnitude of a quiescent galaxy formed at zform = 3 that has a stellar mass of 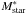 . The conservative limit of
. The conservative limit of 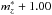 ensures that we can estimate richness without depending too much on an extrapolation of the luminosity function below the detection limit (see Sect. 4.3).
ensures that we can estimate richness without depending too much on an extrapolation of the luminosity function below the detection limit (see Sect. 4.3).
We perform an automated search for red-sequence galaxies in the colour−magnitude diagram (de-reddened for Galactic dust) as a function of redshift, by comparing the observed r − z colour of galaxies with this empirical red-sequence model. For each redshift from z = 0.05 to the limiting redshift per field, with dz = 0.01, we create a map of galaxies with r − z colours that are consistent with this model, allowing for an increase in photometric scatter towards the faint end. This does not (yet) provide a complete census of the galaxy population in these systems, but these maps contain a near-optimal signal for an overdensity of red-sequence galaxies at a given redshift (e.g. Gladders & Yee 2000). We then consider, as a possible centre of the galaxy overdensity, those galaxies (independent of colour) which are (1) located within 4′ from the SZ detection; and (2) brighter than m<m∗ at this redshift. Around each of these possible centres, we count the number of possible red-sequence galaxies within a radius of 0.5 Mpc, and perform a statistical background subtraction by performing the same colour selection on the regions around the overdensities. We then select the location of the most significant overdensity for each field. These coordinates are listed in Table 1. We verify that these centres are generally close to the locations of visually confirmed galaxy overdensities.
4.2. Photometric redshift estimates
The method described above is inadequate for measuring precise redshifts of the galaxy overdensities. The exact vertical location of the red sequence (which best constrains the photometric redshift) is washed out by the relatively large width of the search box (which was chosen to optimise the signal of the detection). To improve the redshift estimate, we repeat the above procedure, but fix the location and perform a search in a narrower colour box to specifically determine the location of the red sequence. We use a box with a fixed width of 0.05, which roughly equals the systematic uncertainty left in our r − z colour calibration. Our best redshift estimate is the one that provides the model that maximizes the number of galaxies in the box around it. In Table 1 we provide these values, together with a 68% error estimate. This uncertainty interval corresponds to redshift values for which the number drops by less than 1σ compared to the number of galaxies in the box that corresponds to the best redshift. For the clusters that have a spectroscopically confirmed redshift, we find overall consistency, within the uncertainties, between these redshifts and our photometric estimates, as illustrated in Fig. 3.
 |
Fig. 3 Spectroscopic versus photometric redshifts for the systems that have been confirmed spectroscopically. The grey area highlights the redshift interval within which we can estimate photometric redshifts precisely, because of our choice for the r- and z-bands. Blue triangles indicate the approximate redshift depth of the data (cf. Sect 4.1 and Table 2). |
4.3. Richness estimates
In both methods described above, the selection box we used is too small to account for all galaxies that appear to be offset from the red-sequence model owing to photometric (and intrinsic) scatter. Since this renders these galaxy numbers inaccurate, we perform a third and final analysis in which we fix the location and redshift of the model, and expand the width of the selection box around the model to obtain a more complete sampling of red-sequence galaxies that are associated with the cluster. As we do this, the statistical background correction becomes more uncertain and imprints a larger component on the overall error of the richness estimate. We expand the box until it has a width of two times the estimated (intrinsic+statistical) scatter of galaxies around the red sequence. We make a small correction to account for galaxies with a larger scatter, which is expected to be ~5% of the total, assuming Gaussian scatter.
To be able to compare these results to the mass-richness relation of Rykoff et al. (2014); Rozo et al. (2015), we make our richness measure comparable to the richness estimator λ used in those studies. Therefore we (1) consider galaxies with magnitudes brighter than m<m∗ + 1.75; and (2) make the radius (Rc) deviate from 0.5 Mpc and increase it until 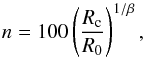 (1)where R0 = 1.0h-1 Mpc, and β = 0.2, following Eq. (4) in Rykoff et al. (2014). Note that, although we do not assume a radial profile for the galaxy population, in some cases we have to extrapolate the richness measurement from the detection limit to m = m∗ + 1.75. Measurements of the luminosity function of cluster galaxies have indicated that the slope of the distribution is quite shallow up to that magnitude limit (α ≈ −1.2, e.g. Barkhouse et al. 2007; Moretti et al. 2015). Completeness correction factors are therefore generally small, and only mildly dependent on the exact slope of the luminosity function. Two notable exceptions are PLCK G087.58-41.63 and PSZ2 G141.77+14.19, for which we have to correct the richness for incompleteness using correction factors of 2.1 and 1.8, respectively.
(1)where R0 = 1.0h-1 Mpc, and β = 0.2, following Eq. (4) in Rykoff et al. (2014). Note that, although we do not assume a radial profile for the galaxy population, in some cases we have to extrapolate the richness measurement from the detection limit to m = m∗ + 1.75. Measurements of the luminosity function of cluster galaxies have indicated that the slope of the distribution is quite shallow up to that magnitude limit (α ≈ −1.2, e.g. Barkhouse et al. 2007; Moretti et al. 2015). Completeness correction factors are therefore generally small, and only mildly dependent on the exact slope of the luminosity function. Two notable exceptions are PLCK G087.58-41.63 and PSZ2 G141.77+14.19, for which we have to correct the richness for incompleteness using correction factors of 2.1 and 1.8, respectively.
The richnesses are listed in Table 1. The associated uncertainties we give are purely statistical; they are the quadratic sum of the Poisson errors on the pure cluster+background counts, and Poisson errors on the subtracted background. It does not include a propagation of the redshift uncertainty on the richness measurement, nor the uncertainty on the correction factor (which we applied in 7 of the 28 fields). The statistical uncertainty we account for dominates over the other sources of uncertainty, except for two systems which we later confirm as clusters: PSZ2 G071.82-56.55, which has a relatively small statistical uncertainty on the richness measurement, but a relatively uncertain (high) redshift, and PSZ2 G141.77+14.19, which also has a relatively uncertain high redshift and a large correction factor. However, we note that including the systematic uncertainty would not have an effect on this analysis, since it does not change the sample of clusters we confirm in Sect. 5.3.
 |
Fig. 4 Illustrating the effect of Eddington bias on the measured SZ-based masses, after a significance cut of S/N> 4.5 (left) or S/N> 3.5 (right) is applied. Red: measured mass distribution of sources as a function of mass and redshift in 30 000 sq. deg. Black: true mass distribution of the same systems. |
5. Likelihood of counterparts
Galaxy overdensities appear on a range of different scales, from low-mass groups to massive galaxy clusters. Even if spectroscopic information indicates that a system of galaxies is physically associated, it is important to define quantitative criteria to assess whether a given system is consistent with what we expect for a halo that is responsible for the measured SZ signal. The measured SZ signal provides a halo mass estimate through the procedure introduced in Arnaud et al. (in prep.), as was already applied in Planck Collaboration XXIX (2014); Planck Collaboration XXVII (2015) to estimate masses for clusters with confirmed redshifts in the PSZ1 and PSZ2 catalogues, respectively. Before we exploit the relationship between richness and halo mass, we study how noise in the Planck maps affects the SZ-based halo mass proxy, especially in the low significance regime at which we are detecting clusters.
5.1. Eddington bias in the SZ halo mass proxy
Due to the presence of noise in the Planck maps, relatively low-mass haloes may scatter over the SZ-significance threshold and make it into the catalogue. Owing to the steepness of the halo mass function (e.g. Tinker et al. 2008; Bocquet et al. 2016), it is expected that more low-mass haloes scatter upwards than high-mass haloes scatter downwards. This results in a distorted view of the underlying halo distribution after applying a cut in significance (Eddington 1913 bias). We note that this bias is purely statistical (see e.g. Appendix A in Mantz et al. 2010a, for an illustration of the effect of this type of statistical bias). The cosmological analysis based on Planck cluster number counts restricts itself to the most significant SZ detections (S/N> 6), and the Eddington bias is moderate for this high S/N cut (e.g. Appendix A.2 of Planck Collaboration XX 2014). However, we consider SZ detections down to S/N = 4 and even below, which brings us to the regime where this type of bias starts to play a significant role.
A full account of the effect of Eddington bias on our analysis would require us to insert modelled SZ profiles in simulated Planck maps with representative noise properties, and we leave this to a future study. We provide, instead, the following estimate of the effect, in which we assume that haloes are spatially independent, i.e. non-overlapping. We simulate a list with masses and redshifts of all haloes with mass M500> 1014 M⊙ up to a redshift of z = 1.25 in a representative lightcone that spans 30 000 sq. deg on the sky. For this we follow the Tinker et al. (2008) halo mass function and the redshift-dependent comoving volume element for our assumed cosmology. Given the noise properties of the Planck maps, the next step is to estimate at what significance a source with a given M500 and redshift would be detected. For this we first use Eqs. (7) and (8) in Planck Collaboration XXIV (2015) to relate these masses and redshifts to a Y500 and θ500. A hydrostatic mass bias of 1-b = 0.8 is assumed here, which is the baseline value used in Planck Collaboration XXIV (2015), and is supported by, for example, a weak-lensing study of Hoekstra et al. (2015). We take, from the Planck noise maps, the average noise value σY500 over the SZ catalogue region (i.e. the final version of Fig. 4 in Planck Collaboration XX 2014). This noise value depends on the aperture considered, θ500, and was shown as being approximated by a Gaussian distribution (Sect. 3.3 in Planck Collaboration XXIV 2015). By combining Y500 and the appropriate noise value, we obtain a significance for each halo. When we compare relations between mass and significance, for a given redshift, we find that these are in excellent agreement with values of S/N and M500 in the published PSZ2 catalogue, as they should be.
In the presence of noise, this “true” significance deviates from the measured significance, which we model by adding a random variable drawn from a standard normal distribution to the “true” significance. If we apply a cut to the measured significance of S/N> 4.5, we obtain a total of 1359 sources. Given that the PSZ2 catalogue used this significance threshold, it is reassuring that this number is comparable to the number of detections reported in PSZ2 (1653), and has a roughly similar redshift distribution. After converting this measured significance back into a measured mass, following the same equations as before, we obtain the red points in Fig. 4. There is a sharp line below which no clusters are detected, which results from the direct relationship between significance and estimated mass. In the real data, this sharp edge is slightly diluted because the noise properties are not completely isotropic, and in some studies the SZ signal is remeasured at the location of an optical overdensity, which slightly reduces the SZ-based mass at fixed blind significance. When we compare these measured masses to the true masses of the same haloes (black points in Fig. 4), the nature of the Eddington bias becomes apparent. If we lower the significance cut from 4.5 to 3.5, the bias becomes more severe, as seen in the right-hand panel.
In Fig. 5 we quantify the magnitude of the bias as a function of measured significance. The magnitude of the bias depends on the steepness of the halo mass function around a given significance and is thus redshift-dependent. For this plot, we repeat the experiment 10 times and thus consider 300 000 sq. deg to improve the statistics on these numbers. Given the nature of this effect, it would be useful to estimate masses in a way that is not affected by Eddington bias. This illustrates the necessity of deeper follow-up data in cases of detections near the survey limit. Although mass proxies based on optical or X-ray follow-up data are considered less accurate than those that are SZ-based, they provide measurements that are independent of the detection and are thus not subject to the bias.
 |
Fig. 5 Magnitude of Eddington bias in the Planck SZ mass proxy as a function of measured significance and redshift. Shown is the mean fractional difference between the measured mass and the true mass. Since we only consider haloes in the mass range M500> 1014 M⊙, this is a lower limit to the true bias. Given this skewed distribution, the mean is higher than the median by up to ~50%. |
5.2. Mass-richness relation
One way to verify our candidates is to compare the measured richness to the SZ-based halo mass proxy, as was done in Rozo et al. (2015); Planck Collaboration XXVII (2015). Note that we searched within a radius of 4′ for the most significant galaxy overdensities around each SZ peak. For a galaxy overdensity that is found far away from the SZ maximum, the SZ signal at that location may be significantly lower. Before we estimate the SZ-based mass, we therefore re-extract the SZ signal at the location of the galaxy overdensity. This decreases the significance compared to the significance of the blind detection (by definition, see Table 1), where the given distance is an integer number of pixels (1 pixel = 1.72′) on this two-dimensional grid between the blind detection and the optical centre. This distance and the difference in S/N of the blind detection and the re-extracted value may also serve as a check on the identified counterpart. We note, however, that some of the clusters in our sample are multimodal in their galaxy distribution, as also suggested by the figures in Appendix A, where white circles mark the centres of the assumed optical position.
Figure 6 shows the resulting comparison between mass and richness. The black dashed line is the best-fitting relation from Rozo et al. (2015), which is based on a comparison between Planck and the redMaPPer cluster catalogue. Rozo et al. (2015) estimated an intrinsic scatter of ~25% around this relation. The low-mass end of the relation is constrained using haloes at low redshift, which are thus still significantly detected in the Planck maps. This assumes that the richness-mass relation of galaxy clusters does not evolve over this redshift range (e.g. Andreon & Congdon 2014). We note however that at higher redshift (z ≳ 1.0), an increasingly large population of galaxies may not yet be part of the red sequence, which complicates the use of a richness-based mass proxy.
 |
Fig. 6 Comparison between Planck SZ halo mass proxy, and richness (similar to the definition of Rykoff et al. (2014). The mass-richness relation from Rozo et al. (2015) is overplotted. The grey + symbols show the distribution of a simulated sample with redshift z> 0.5 and measured significance S/N> 3.5, and is thus similar to the population from which our candidates have been selected. Both intrinsic and statistical scatter in the richness have been included, but most of the scatter in the grey distribution is caused by statistical uncertainties in the SZ mass proxy. The effect of Eddington bias is apparent, since it causes the observed points to deviate from the intrinsic relation. Our criteria to confirm cluster counterparts (solid error bars) are described in Sect. 5.3, and are largely based on the grey dashed line. Three Planck detections are highlighted in colour, and these are discussed in detail in Sect. 6. |
When we compare the mass and associated richness for our candidates with the reference relation, the effect of Eddington bias is apparent. The SZ-based mass is likely to overestimate the true mass, which is probed in an unbiased way by the richness. This can be illustrated further using the simulations detailed in Sect. 5.1. We apply a cut on the measured significance of S/N> 3.5, and consider the redshift range z> 0.5, which yields 511 detections in our simplified simulation. Assuming that the richness is a proxy of the true mass, though with a 25% intrinsic scatter for a given mass, and Poisson uncertainties on the richness measurement, these 511 systems are shown by the grey points in Fig. 6. The richnesses measured for the targeted candidates are thus roughly consistent with what we expect in the presence of Eddington bias. This illustrates again that, when approaching the detection limit of Planck, deeper auxiliary data (whether it be X-ray, SZ or optical) are required to obtain an accurate mass estimate. In the present case, the richness thus serves as a more accurate estimator of the halo mass than the SZ mass proxy from the survey data, even though it suffers from a ~25% intrinsic scatter.
5.3. Quantifying criteria for cluster confirmation
Due to the role noise fluctuations in the Planck maps play in defining a cluster sample at low SZ significance, it is a priori unclear where to draw a line between confirmation and invalidation of an SZ cluster candidate using optical data. A reasonable criterion is to require that a measured SZ signal is dominated by the inverse Compton scattering of CMB photons of a halo, rather than by noise in the Planck maps. We can rephrase this by requiring the richness-based halo mass to be more than 50% of the SZ-based mass, or that candidates should lie above the grey dashed line in Fig. 6.
This criterion alone, however, is not necessarily sufficient, because we have specifically selected our 28 candidates based on a visual inspection of ~1000 WISE and DSS images. These ~1000 locations are coincident with SZ detections, but even if they were completely randomly spread on the sky, some would fall, by chance, on galaxy overdensities. We considered overdensities in WISE (and corresponding non-detections in DSS) within radii of 4′ from ~1000 SZ detections. This corresponds to a total considered area of ~14 sq. deg. As a very conservative comparison, we estimate the richness distribution of the 28 richest systems that are expected in a randomly chosen 14 sq. deg. For this we use the same simulation as before, but select haloes in the redshift range 0.4 <z< 1.0, and add 25% intrinsic scatter on the richness at a given mass. The results are the dashed and dotted lines in Fig. 7. The solid line shows the measured cumulative richness distribution of the 28 candidates studied here, where we used the mass-richness relation from Rozo et al. (2015) to obtain a mass for a given richness. Even though we only followed-up 3% of the ~1000 candidates, we find that the measured cumulative distribution is already in significant excess of the expected distributions for masses Mrichness> 2 × 1014 M⊙, corresponding to a richness estimator of λ ≳ 40. For systems with a richness-based mass in excess of this limit, we are therefore confident that these are likely part of our sample because of their SZ signal, and not just because they are a rich system coincident with a pure noise peak. It is important to note that this is a very conservative comparison, since only 3% of the ~1000 SZ detections have been chosen for the present follow-up with deep MegaCam imaging. A full follow-up of all candidates, which would allow for a more realistic comparison, is likely to raise the measured cumulative distribution substantially, especially around richness-masses of ~2−4 × 1014 M⊙. Since a full estimate of the sample completeness is beyond the scope of this work, we choose to follow this rather conservative limit with this word of caution.
In summary, we require successful candidates to (1) have a richness estimate in excess of 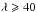 ; and (2) have a richness-based halo mass estimate that is, within 1σ, more than 50% of the SZ-based mass. Cluster candidates that fail to meet one of these criteria are shown with a dotted error bar in Fig. 6. Three candidates are marked in colour, and these are discussed in particular in Sect. 6. First we discuss some general characteristics of the sample of Planck clusters that were confirmed based on the two main criteria, which are shown with solid error bars in Fig. 6, and which are listed in the upper part of Table 1.
; and (2) have a richness-based halo mass estimate that is, within 1σ, more than 50% of the SZ-based mass. Cluster candidates that fail to meet one of these criteria are shown with a dotted error bar in Fig. 6. Three candidates are marked in colour, and these are discussed in particular in Sect. 6. First we discuss some general characteristics of the sample of Planck clusters that were confirmed based on the two main criteria, which are shown with solid error bars in Fig. 6, and which are listed in the upper part of Table 1.
 |
Fig. 7 Cumulative distribution of richness-based halo masses measured for our sample of 28 SZ detections, selected from a total area of 14 sq. deg (solid). Expected cumulative distribution of the richness-based halo mass of the 28 richest systems between 0.4 <z< 1.0 (dashed) per a random area of 14 sq. deg, in our assumed cosmology. Same but for a Planck CMB cosmology with WMAP polarisation Planck Collaboration XVI (2014; dotted). A 25% lognormal scatter on the richness at fixed halo mass is assumed, and each curve includes hydrostatic mass bias. |
5.4. Remarks on confirmed clusters
To confirm Planck cluster candidates, we exploit only two main criteria, which are primarily based on the measured richness (see above). There is more information available on these candidates, some of which is also compiled in Table 1. Based on this, the following remarks can be made:
-
Out of the 16 Planck detections that were listed in the PSZ1 catalogue, eight were also included in PSZ2. Each of the five PSZ1 sources that we confirm as being associated with a cluster is also included in the PSZ2, whereas most PSZ1 sources that turn out to be false candidates (8/11) dropped out of the PSZ2 catalogue. This is expected from noise arguments when the depth of the data increases.
-
Seven (nine) of the 16 PSZ1 sources are listed as CLASS1 (CLASS2) in the catalogue. Each of the five confirmed PSZ1 sources was listed as CLASS1, which illustrates the value of such a classification in cleaning the sample a priori.
-
The 13 candidates that are present in the PSZ2 catalogue have an SZ quality described by the Q_NEURAL parameter; see Aghanim et al. (2015) for details, and Table 1 for their values. All 10/13 confirmed have a Q_NEURAL> 0.8, whereas 3/13 invalidated candidates have a Q_NEURAL< 0.1. This illustrates the potential of using this neural network classification to pre-select the most promising SZ candidates for follow-up studies. This classification is less diagnostic in the case of a noise-dominated Planck SED, as illustrated by the QN parameter in the updated PSZ1 catalogue (Planck Collaboration XXIX 2015). From the eight SZ detections in PSZ1 that dropped out of PSZ2, only two have a classification of QN< 0.78, while none are confirmed as corresponding to real clusters.
-
The richness peaks that turn out to be associated with false candidates are found to be roughly uniformly spread around the SZ detections in the 4′ search-disk. In particular, the distance between the blind SZ detections and the optical positions (Distance in Table 1) of confirmed candidates is typically smaller than for invalidated candidates.
-
Candidates that were not part of PSZ1 (and were thus observed with MegaCam in 2014B), have a higher probability of corresponding to significant clusters. This illustrates the benefit of strengthening our WISE and DSS selection criteria to select the most promising candidates, thereby keeping the purity relatively high at low SZ detection significance.
We note that there are several cases where we find a significant overdensity of galaxies, but their richness still indicates that their intrinsic SZ signal is likely too small to contribute significantly to the SZ detection. We discuss some individual candidates in Sect. 6.
5.5. Representativity and completeness
By pre-selecting candidates optically, we are able to preferentially target clusters in the interesting z ≳ 0.5 range, while increasing the purity of the sample. The price to pay is an a priori more complex selection function. The low significance of the SZ detection is not an issue per se. That is because the completeness of the catalogue, i.e. the fraction of detected clusters as a function of detection threshold and intrinsic properties, can be quantified with Monte Carlo simulations, in which clusters are injected in real maps, as well as taken from analytical assumptions. These are performed extensively for the published catalogues (Planck Collaboration XXIX 2014; Planck Collaboration XXVII 2015).
We note, however, that the preselection of candidates provides a catalogue that is not purely SZ-selected. True clusters may be rejected by the preselection, for example because of uncertainties in the estimated redshift. The exact quantification of this additional incompleteness requires sophisticated modelling of the optical properties of the clusters, and this may be difficult. It introduces a systematic uncertainty in the catalogue selection function, which may hamper the use of such a cluster sample for precision cosmology. However, for statistical studies of the cluster population, as a probe of structure formation, the key requirement is the representativity of the sample, i.e. that the optical preselection does not introduce s specific bias as compared to the parent SZ-selected sample. This is a much less stringent constraint, which can also be studied a posteriori using multiwavelength data. Therefore, with Planck being the only all-sky SZ survey for the foreseeable future, such an approach may be the only way towards a sizeable, yet representative, sample of the most massive clusters at z ≳ 0.5.
6. Notes on individual candidates
We present our candidates in Table 1 and show colour images, mostly of confirmed candidates, in Appendix A. Below we discuss some special cases of confirmed and invalidated candidates, in turn.
6.1. Confirmed
PSZ2 G042.32+17.48 was also confirmed by Planck Collaboration XXXVI (2015), who find an optical counterpart around this position of zspec = 0.458 (3 galaxies). We confirm this overdensity based on a richness estimate, which is consistent with what we expect for a massive galaxy cluster. Our photometric redshift is fully consistent with the reported spectroscopic redshift.
PLCK G087.58-41.63. Galaxy cluster candidate, potentially at high redshift (z ≳ 1), but the r − z colour loses its constraint on the redshift in that regime. Deeper follow-up data in the near-IR are required to estimate the redshift and make a better richness estimate. We had to correct the richness for incompleteness by a factor of 2.1.
PSZ2 G141.77+14.19 shows a significant overdensity close in position to the centre of the SZ detection. After fixing the redshift to the spectroscopic value (zspec = 0.821), we had to correct the richness for incompleteness by a factor of 1.8, in part because of a substantial dust extinction in the field (E(B − V) = 0.30).
PLCK G191.75-21.78 shows a significant galaxy overdensity, with a z ~ 0.6 extended structure that spans several Mpc on the sky.
6.2. Invalidated
PSZ2 G037.67+15.71 is part of PSZ1 and PSZ2, with a highly significant (S/N = 6.61) SZ detection in the final maps. It was classified as CLASS1 source in the PSZ1, but no significant galaxy overdensity is found. A larger search radius around the peak of the SZ detection also does not result in a significant overdensity. A closer inspection of the individual frequency maps indicates the presence of an infrared source which, given that it is located only 15° from the Galactic plane, might well be related to Galactic dust. The Q_NEURAL parameter indicates, along the same lines, that the SED has a different shape than is expected for a pure SZ signal.
PSZ1 G038.25-58.36. A significant overdensity of galaxies found. However, the source dropped out of the PSZ2 catalogue and, after re-extraction, the SZ-based mass is consistent with zero. This source has likely ended up in the PSZ1 catalogue by chance.
PSZ2 G071.67-42.76 is another example that illustrates the possible contribution of other emission mechanisms than the SZ decrement to the measured Planck SED, just like PSZ2 G037.67+15.71. This source is a strong emitter at 353GHz, which boosts the significance of the SZ signal (=8.37, cf. Table 1). The Q_NEURAL parameter of this source indicates that this is a likely false cluster candidate. Indeed we do not find a significant overdensity of galaxies around this location. Both this source and PSZ2 G037.67+15.71 illustrate the fact that the Planck catalogue is not 100% pure, even at high S/N (this is expected, see, e.g. Fig. 11 in Planck Collaboration XXVII 2015). Note also that the purity is lower in regions of strong dust emission (the dust mask), where these two candidates are located.
PSZ1 G092.41-37.39. Around this SZ detection, Planck Collaboration XXXVI (2015) found a galaxy overdensity of three galaxies around zspec = 0.114. We also find a mild galaxy overdensity, centred on the same position, with a redshift that is consistent with theirs (though the r- and z-band filters give a poor precision at such low-z). We expect ROSAT, which is relatively deep at this position, to probe down to lower masses than Planck at this redshift; however, no significant source is detected in the RASS maps. We measure an X-ray luminosity at this position in the ROSAT [0.1−2.4] keV band, assuming a redshift of z = 0.114, of LX = 5.7 ± 4.9 × 1042 erg s-1. Using the LX − M500 relation from Pratt et al. (2009), we estimate a 1σ upper limit to the mass of M500< 5 × 1013 M⊙. Given that this is significantly lower than the mass-detection threshold of Planck at this redshift, we conclude that this is likely to be a noise fluctuation in the PSZ1 catalogue. We note that the source is detected at lower SZ significance in the final maps (S/N = 2.43).
7. Summary and conclusions
This paper presents a detailed analysis of deep r- and z-band follow-up imaging of 28 SZ cluster candidates that were detected in the Planck maps. The candidates were selected as being likely at z> 0.5, based on external survey data from DSS and WISE. The follow-up imaging data allow us to search for overdensities of red-sequence galaxies around the SZ detections, to estimate precise photometric redshifts over a redshift range of 0.35 ≲ z ≲ 0.80, and to measure richnesses for the overdensities. The richness measurement is an important step in the validation process, since it allows us to assess quantitatively if a system is as massive/rich as expected, given the strength of its SZ decrement. As such, it provides a means to also re-evaluate confirmed candidates in the literature, even if these are supported by spectroscopic redshifts.
Given that we consider sources down to an SZ detection significance of S/N ~ 3 and even below, the SZ-based mass proxy is particularly subject to Eddington bias. In this regime of low-S/N Planck detections, the richness provides a mass estimate that is independent of the SZ mass proxy, and thus not affected by Eddington bias.
We define quantitative criteria based on which we validate the optical counterparts of SZ detections. These criteria are based primarily on a comparison between the SZ-based mass and the richness-based mass. To confirm the optical identification of an SZ counterpart, we (1) require that a measured SZ signal is dominated by the inverse Compton scattering of CMB photons of a halo, rather than by noise in the Planck maps, and (2) require that the richness is sufficiently high that it is unlikely that the galaxy overdensity is overlapping, by chance, with an SZ source. Following these criteria, we confirm 16 galaxy clusters as likely counterparts to SZ detections, 13 (6) having an estimated redshift of z> 0.5 (z> 0.7). Their richnesses indicate masses that are typically 2 × 1014 ≲ M500/M⊙ ≲ 1015.
This work illustrates the potential of the Planck maps to provide SZ samples of the most massive galaxy clusters at high redshift (z ≳ 0.5), selected from the whole sky. It shows that the approach we have adopted, to pre-select candidates based on WISE and (S)DSS, indeed increases the efficiency with which we can construct samples of representative clusters in this redshift regime. It demonstrates the need for deep ancillary data to provide a secondary, Eddington-unbiased, mass proxy, and shows that additional information, e.g. from optical surveys, can be exploited to keep the purity high at low SZ detection significance. In combination with ongoing and future large optical and near-IR surveys such as PanSTARRS, WISE, Euclid and LSST, and X-ray survey missions such as eROSITA, the final Planck maps can thus be explored down to lower significance to provide a more complete accounting of haloes in the z ≳ 0.5 regime.
The Digitized Sky Surveys were produced at the Space Telescope Science Institute under US Government grant NAG W-2166. The images of these surveys are based on photographic data obtained using the Oschin Schmidt Telescope on Palomar Mountain and the UK Schmidt Telescope. The plates were processed into the present compressed digital form with the permission of these institutions.
Acknowledgments
We thank Emanuele Daddi and Adam Muzzin for insightful discussions, and an anonymous referee for detailed suggestions that led to a substantial clarification of the paper. The research leading to these results has received funding from the European Research Council under the European Union’s Seventh Framework Programme (FP7/2007-2013)/ERC grant agreement n° 340519. R.B., A.F. and A.S. acknowledge financial support from the Spanish Ministry of Economy and Competitiveness (MINECO) under the 2011 Severo Ochoa Program MINECO SEV-2011-0187. H.D. acknowledges support from the Research Council of Norway. R.H. acknowledges support from the European Research Council FP7 grant number 279396. E.P. acknowledges the support of the French Agence Nationale de la Recherche under grant ANR-11-BS56-015. Based on observations obtained with MegaPrime/MegaCam, a joint project of CFHT and CEA/DAPNIA, at the Canada-France-Hawaii Telescope (CFHT) which is operated by the National Research Council (NRC) of Canada, the Institute National des Sciences de l’Univers of the Centre National de la Recherche Scientifique of France, and the University of Hawaii. This article is based on observations made with the Gran Telescopio Canarias (GTC), installed in the Spanish Observatorio del Roque de los Muchachos (ORM) of the Instituto de Astrofísica de Canarias (IAC), in the island of La Palma. This research used telescope time awarded by the CCI International Time Programme at the Canary Islands Observatories (ITP13-8). The development of Planck has been supported by: ESA; CNES and CNRS/INSU-IN2P3-INP (France); ASI, CNR, and INAF (Italy); NASA and DoE (USA); STFC and UKSA (UK); CSIC, MICINN and JA (Spain); Tekes, AoF and CSC (Finland); DLR and MPG (Germany); CSA (Canada); DTU Space (Denmark); SER/SSO (Switzerland); RCN (Norway); SFI (Ireland); FCT/MCTES (Portugal); and The development of Planck has been supported by: ESA; CNES and CNRS/INSU-IN2P3-INP (France); ASI, CNR, and INAF (Italy); NASA and DoE (USA); STFC and UKSA (UK); CSIC, MICINN and JA (Spain); Tekes, AoF and CSC (Finland); DLR and MPG (Germany); CSA (Canada); DTU Space (Denmark); SER/SSO (Switzerland); RCN (Norway); SFI (Ireland); FCT/MCTES (Portugal); and PRACE (EU). This research made use of the following databases: the NED and IRSA databases, operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the NASA; SIMBAD, operated at CDS, Strasbourg, France; SZ-cluster database operated by IDOC at IAS under contract with CNES and CNRS.
References
- Abell, G. O., Corwin, Jr., H. G., & Olowin, R. P. 1989, ApJS, 70, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aghanim, N., Hurier, G., Diego, J.-M., et al. 2015, A&A, 580, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ahn, C. P., Alexandroff, R., Allen de Prieto, C., et al. 2012, ApJS, 203, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Alam, S., Albareti, F. D., Allen de Prieto, C., et al. 2015, ApJS, 219, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Allen, S. W., Evrard, A. E., & Mantz, A. B. 2011, ARA&A, 49, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Andreon, S., & Congdon, P. 2014, A&A, 568, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barkhouse, W. A., Yee, H. K. C., & López-Cruz, O. 2007, ApJ, 671, 1471 [NASA ADS] [CrossRef] [Google Scholar]
- Benson, B. A., de Haan, T., Dudley, J. P., et al. 2013, ApJ, 763, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E. 2006, in Astronomical Data Analysis Software and Systems XV, eds. C. Gabriel, C. Arviset, D. Ponz, & S. Enrique, ASP Conf. Ser., 351, 112 [Google Scholar]
- Bertin, E. 2011, in Astronomical Data Analysis Software and Systems XX, eds. I. N. Evans, A. Accomazzi, D. J. Mink, & A. H. Rots, ASP Conf. Ser., 442, 435 [Google Scholar]
- Bleem, L. E., Stalder, B., de Haan, T., et al. 2015, ApJS, 216, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Bocquet, S., Saro, A., Dolag, K., & Mohr, J. J. 2016, MNRAS, 456, 2361 [Google Scholar]
- Böhringer, H., Voges, W., Huchra, J. P., et al. 2000, ApJS, 129, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Böhringer, H., Schuecker, P., Guzzo, L., et al. 2004, A&A, 425, 367 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- da Silva, A. C., Kay, S. T., Liddle, A. R., & Thomas, P. A. 2004, MNRAS, 348, 1401 [NASA ADS] [CrossRef] [Google Scholar]
- Ebeling, H., Edge, A. C., Bohringer, H., et al. 1998, MNRAS, 301, 881 [NASA ADS] [CrossRef] [Google Scholar]
- Ebeling, H., Barrett, E., Donovan, D., et al. 2007, ApJ, 661, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Eddington, A. S. 1913, MNRAS, 73, 359 [Google Scholar]
- Erben, T., Hildebrandt, H., Lerchster, M., et al. 2009, A&A, 493, 1197 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fassbender, R., Böhringer, H., Nastasi, A., et al. 2011, New J. Phys., 13, 125014 [NASA ADS] [CrossRef] [Google Scholar]
- Gettings, D. P., Gonzalez, A. H., Stanford, S. A., et al. 2012, ApJ, 759, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Gilbank, D. G., Gladders, M. D., Yee, H. K. C., & Hsieh, B. C. 2011, AJ, 141, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Gladders, M. D., & Yee, H. K. C. 2000, AJ, 120, 2148 [NASA ADS] [CrossRef] [Google Scholar]
- Hasselfield, M., Hilton, M., Marriage, T. A., et al. 2013, J. Cosmol. Astropart. Phys., 7, 8 [Google Scholar]
- Hildebrandt, H., Pielorz, J., Erben, T., et al. 2009, A&A, 498, 725 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hoekstra, H., Mahdavi, A., Babul, A., & Bildfell, C. 2012, MNRAS, 427, 1298 [NASA ADS] [CrossRef] [Google Scholar]
- Hoekstra, H., Herbonnet, R., Muzzin, A., et al. 2015, MNRAS, 449, 685 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., McCracken, H. J., Le Fèvre, O., et al. 2013, A&A, 556, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kirk, B., Hilton, M., Cress, C., et al. 2015, MNRAS, 449, 4010 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, J., Hennig, C., Desai, S., et al. 2015, MNRAS, 449, 3370 [NASA ADS] [CrossRef] [Google Scholar]
- Magnier, E. A., & Cuillandre, J.-C. 2004, PASP, 116, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Mantz, A., Allen, S. W., Ebeling, H., Rapetti, D., & Drlica-Wagner, A. 2010a, MNRAS, 406, 1773 [NASA ADS] [Google Scholar]
- Mantz, A., Allen, S. W., Rapetti, D., & Ebeling, H. 2010b, MNRAS, 406, 1759 [NASA ADS] [Google Scholar]
- Melin, J.-B., Bartlett, J. G., & Delabrouille, J. 2006, A&A, 459, 341 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moretti, A., Bettoni, D., Poggianti, B. M., et al. 2015, A&A, 581, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muzzin, A., Marchesini, D., Stefanon, M., et al. 2013a, ApJ, 777, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Muzzin, A., Marchesini, D., Stefanon, M., et al. 2013b, ApJS, 206, 8 [Google Scholar]
- Planck Collaboration VIII. 2011, A&A, 536, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XI. 2011, A&A, 536, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XVI. 2014, A&A, 571, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XX. 2014, A&A, 571, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXIX. 2014, A&A, 571, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXIV. 2015, ArXiv e-prints [arXiv:1502.01597] [Google Scholar]
- Planck Collaboration XXVII. 2015, ArXiv e-prints [arXiv:1502.01598] [Google Scholar]
- Planck Collaboration XXIX 2015, ArXiv e-prints [arXiv:1502.00543] [Google Scholar]
- Planck Collaboration XXXVI 2015, ArXiv e-prints [arXiv:1504.04583] [Google Scholar]
- Planck Collaboration Int. XXVI. 2015, A&A, 582, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pratt, G. W., Croston, J. H., Arnaud, M., & Böhringer, H. 2009, A&A, 498, 361 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reichardt, C. L., Stalder, B., Bleem, L. E., et al. 2013, ApJ, 763, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Rozo, E., Wechsler, R. H., Rykoff, E. S., et al. 2010, ApJ, 708, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Rozo, E., Rykoff, E. S., Bartlett, J. G., & Melin, J.-B. 2015, MNRAS, 450, 592 [Google Scholar]
- Rykoff, E. S., Rozo, E., Busha, M. T., et al. 2014, ApJ, 785, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Sehgal, N., Trac, H., Acquaviva, V., et al. 2011, ApJ, 732, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Sunyaev, R. A., & Zeldovich, I. B. 1980, ARA&A, 18, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Tinker, J., Kravtsov, A. V., Klypin, A., et al. 2008, ApJ, 688, 709 [NASA ADS] [CrossRef] [Google Scholar]
- van der Burg, R. F. J., Muzzin, A., Hoekstra, H., et al. 2013, A&A, 557, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van der Burg, R. F. J., Hoekstra, H., Muzzin, A., et al. 2015, A&A, 577, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Dokkum, P. G. 2001, PASP, 113, 1420 [NASA ADS] [CrossRef] [Google Scholar]
- Vikhlinin, A., Kravtsov, A. V., Burenin, R. A., et al. 2009, ApJ, 692, 1060 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, R. J., Quadri, R. F., Franx, M., van Dokkum, P., & Labbé, I. 2009, ApJ, 691, 1879 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: r – z-colour images for the targeted systems with an optical counterpart
 |
Fig. A.1 Circles are centred on the position that maximizes the richness and have a radius of 0.5 Mpc at the estimated redshift. |
 |
Fig. A.2 Circles are centred on the position that maximizes the richness and have a radius of 0.5 Mpc at the estimated redshift. |
 |
Fig. A.3 Circles are centred on the position that maximizes the richness and have a radius of 0.5 Mpc at the estimated redshift. |
All Tables
All Figures
 |
Fig. 1 Illustration of the background residual correction, showing a 15′ × 15′ part of the PSZ2 G048.21-65.00 z-band stack before (left panel), and after (right panel) the correction. The median improvement in the effective depth of the z-band images in a 2′′ aperture is approximately 0.4 mag. |
| In the text | |
 |
Fig. 2 Left panel: empirical model of the red sequence (black lines). At each redshift, the lines run from m∗−2 <m<m∗ + 2. Right panel: three model lines with galaxy colours and magnitudes overplotted from field PSZ2 G119.30-64.68 (zspec = 0.557), within 2 arcmin from the centre of the overdensity. For clarity, error bars are not shown on individual points, but these increase in size from lower-left to upper-right. The inset illustrates the statistical error on the colour measurement around the location of the red sequence at this redshift (offset from the z = 0.55 model for clarity). |
| In the text | |
 |
Fig. 3 Spectroscopic versus photometric redshifts for the systems that have been confirmed spectroscopically. The grey area highlights the redshift interval within which we can estimate photometric redshifts precisely, because of our choice for the r- and z-bands. Blue triangles indicate the approximate redshift depth of the data (cf. Sect 4.1 and Table 2). |
| In the text | |
 |
Fig. 4 Illustrating the effect of Eddington bias on the measured SZ-based masses, after a significance cut of S/N> 4.5 (left) or S/N> 3.5 (right) is applied. Red: measured mass distribution of sources as a function of mass and redshift in 30 000 sq. deg. Black: true mass distribution of the same systems. |
| In the text | |
 |
Fig. 5 Magnitude of Eddington bias in the Planck SZ mass proxy as a function of measured significance and redshift. Shown is the mean fractional difference between the measured mass and the true mass. Since we only consider haloes in the mass range M500> 1014 M⊙, this is a lower limit to the true bias. Given this skewed distribution, the mean is higher than the median by up to ~50%. |
| In the text | |
 |
Fig. 6 Comparison between Planck SZ halo mass proxy, and richness (similar to the definition of Rykoff et al. (2014). The mass-richness relation from Rozo et al. (2015) is overplotted. The grey + symbols show the distribution of a simulated sample with redshift z> 0.5 and measured significance S/N> 3.5, and is thus similar to the population from which our candidates have been selected. Both intrinsic and statistical scatter in the richness have been included, but most of the scatter in the grey distribution is caused by statistical uncertainties in the SZ mass proxy. The effect of Eddington bias is apparent, since it causes the observed points to deviate from the intrinsic relation. Our criteria to confirm cluster counterparts (solid error bars) are described in Sect. 5.3, and are largely based on the grey dashed line. Three Planck detections are highlighted in colour, and these are discussed in detail in Sect. 6. |
| In the text | |
 |
Fig. 7 Cumulative distribution of richness-based halo masses measured for our sample of 28 SZ detections, selected from a total area of 14 sq. deg (solid). Expected cumulative distribution of the richness-based halo mass of the 28 richest systems between 0.4 <z< 1.0 (dashed) per a random area of 14 sq. deg, in our assumed cosmology. Same but for a Planck CMB cosmology with WMAP polarisation Planck Collaboration XVI (2014; dotted). A 25% lognormal scatter on the richness at fixed halo mass is assumed, and each curve includes hydrostatic mass bias. |
| In the text | |
 |
Fig. A.1 Circles are centred on the position that maximizes the richness and have a radius of 0.5 Mpc at the estimated redshift. |
| In the text | |
 |
Fig. A.2 Circles are centred on the position that maximizes the richness and have a radius of 0.5 Mpc at the estimated redshift. |
| In the text | |
 |
Fig. A.3 Circles are centred on the position that maximizes the richness and have a radius of 0.5 Mpc at the estimated redshift. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


