| Issue |
A&A
Volume 587, March 2016
|
|
|---|---|---|
| Article Number | A29 | |
| Number of page(s) | 6 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201527217 | |
| Published online | 15 February 2016 | |
Meridional motions and Reynolds stress from SDO/AIA coronal bright points data⋆
1
Hvar Observatory, Faculty of Geodesy, Kačićeva 26, University of
Zagreb,
10000
Zagreb,
Croatia
e-mail:
davor.sudar@gmail.com
2
Harvard-Smithsonian Center for Astrophysics, 60 Garden
Street, Cambridge,
MA
02138,
USA
3
Astronomical Institute of the Czech Academy of
Sciences, Fričova
298, 251 65
Ondřejov, Czech
Republic
4
Department of Physics, University of Rijeka,
Radmile Matejčić 2,
51000
Rijeka,
Croatia
Received: 19 August 2015
Accepted: 16 December 2015
Context. It is possible to detect and track coronal bright points (CBPs) in Solar Dynamics Observatory/Atmospheric Imaging Assembly (SDO/AIA) images. A combination of high resolution and high cadence provides a wealth of data that can be used to determine velocity flows on the solar surface with very high accuracy.
Aims. We derived a very accurate solar rotation profile and investigated meridional flows, torsional oscillations, and horizontal Reynolds stress based on ≈6 months of SDO/AIA data.
Methods. We used a segmentation algorithm to detect CBPs in SDO/AIA images. We also used invariance of the solar rotation profile with central meridian distance (CMD) to determine the height of CBPs in the 19.3 nm channel.
Results. The best fit solar rotation profile is given by ω(b) = (14.4060 ± 0.0051 + (−1.662 ± 0.050)sin2b + (−2.742 ± 0.081)sin4b)° day-1. The height of CBPs in the SDO/AIA 19.3 nm channel was found to be ≈6500 km. Meridional motion is predominantly poleward for all latitudes, while solar velocity residuals show signs of torsional oscillations. Horizontal Reynolds stress was found to be smaller than in similar works, but still showed transfer of angular momentum towards the solar equator.
Conclusions. Most of the results are consistent with Doppler measurements rather than tracer measurements. The fairly small calculated value of horizontal Reynolds stress might be due to the particular phase of the solar cycle. Accuracy of the calculated rotation profile indicates that it is possible to measure changes in the profile as the solar cycle evolves. Analysis of further SDO/AIA CBP data will also provide a better understanding of the temporal behaviour of the rotation velocity residuals, meridional motions, and Reynolds stress.
Key words: Sun: rotation / Sun: corona / Sun: activity
Table 1 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/587/A29
© ESO, 2016
1. Introduction
Studies of the solar rotation profile, torsional oscillations, and meridional velocities are based on the specific features traced on or above the photosphere or on Doppler measurements. The oldest known tracers for measuring the solar rotation profile are sunspots, which have been used for a long time (Newton & Nunn 1951; Howard et al. 1984; Balthasar et al. 1986; Brajša et al. 2002a; Sudar et al. 2014). The biggest advantage of sunspots is that they have been observed for more than a century. Coronal bright points (CBPs) have also been used very frequently by using the data obtained by different satellites. For example, Brajša et al. (2001, 2002b, 2004); Vršnak et al. (2003); Wöhl et al. (2010) used SOHO/EIT data, Hara (2009) analysed Yohkoh/SXT measurements, while Kariyappa (2008) used both Yohkoh and Hinode data. Recently, Sudar et al. (2015) have used SDO/AIA measurements in the 19.3 nm channel.
Doppler measurements give similar results for rotation (Howard & Harvey 1970; Ulrich et al. 1988; Snodgrass & Ulrich 1990), but analyses of meridional motions and torsional oscillation differ significantly between tracer and Doppler measurements. Analyses of tracer data show that meridional flow is going out of the centre of activity (Howard & Gilman 1986; Wöhl & Brajša 2001), while Doppler measurements usually show poleward meridional flow for all latitudes (Duvall 1979; Hathaway 1996). Of course, there have been studies that show the opposite. For example, Howard (1991) pointed out that solar plages show flow towards the centre of solar activity, unlike other tracer measurements. In contrast to other Doppler measurements, Pérez Garde et al. (1981) found motion towards the equator from their analysis of Doppler data. Olemskoy & Kitchatinov (2005) have pointed out that for tracer measurements it is critical to take into account the distribution of the tracers in latitude in order not to detect false flows. Recently, Sudar et al. (2014) have analysed sunspot group data from Greenwich Photoheliographic Results and, by using the arguments from Olemskoy & Kitchatinov (2005), find that the meridional flow is towards the centre of solar activity.
Based on Doppler data, Howard & Labonte (1980) reported that the Sun is a torsional oscillator. This was later confirmed by Ulrich et al. (1988), again with Doppler measurements, and Howe et al. (2000) with helioseismic measurements. While many later papers found the torsional oscillation pattern in such measurements, Sudar et al. (2014) were unable to detect anything like it in 150 yr of sunspot group data.
Tracer data is very useful for the analysis of horizontal Reynolds stress because both velocity components can be measured separately (Schröter 1985). There are a number of papers (Ward 1965; Schröter & Wöhl 1976; Gilman & Howard 1984; Pulkkinen & Tuominen 1998; Vršnak et al. 2003; Sudar et al. 2014) that have found the value of Reynolds stress in agreement with transfer of the angular momentum towards the equator which could explain the observed solar rotation profile.
Sudar et al. (2015) used SDO/AIA 19.3 nm channel to trace CBPs for two days. Their results show that the combination of high cadence/high resolution satellite measurements can provide a wealth of data that can be used to analyse variations of the solar rotation profile and all the associated phenomena mentioned above. Analysis of meridional flow, torsional oscillations, and horizontal Reynolds stress with SDO/AIA CBP data is the main goal of this paper.
2. Data and reduction methods
In this work we used measurements from Atmospheric Imaging Assembly (AIA) instrument which is on board the Solar Dynamics Observatory (SDO) satellite (Lemen et al. 2012). We used a similar procedure to that used in our previous paper (Sudar et al. 2015) to obtain CBP positions. The segmentation algorithm is a modification of similar algorithms described in McIntosh & Gurman (2005) and Martens et al. (2012). In Table 1, available at CDS, we provide the following information. Column 1 lists the Julian date of each observation, Col. 2 contains the identification number of CBP, Cols. 3 and 4 give the x and y coordinates for each CBP in pixels, respectively.
In order to obtain better accuracy than in Sudar et al. (2015) where we used observational data from 2 days, in this work we analysed more than 5 months of AIA/SDO observations with a 10-min cadence from 2011 January 1 to 2011 May 19. We removed data points near the limb (>0.95 R⊙) in order to avoid potential problems with inaccuracies in position for those points. Choosing only CBPs with ten or more data points to calculate velocities by linear fitting, we obtained 82 341 velocity measurements, which were converted from synodic to sidereal velocities (Skokić et al. 2014).
In Sudar et al. (2015) we showed a change in position over time of one CBP in Fig. 2. Apart from the trend line, CBPs also exhibit apparently random fluctuations around the fitted line. Such fluctuations might be the result of displacements associated with the evolution of CBP photospheric footpoints (Karachik et al. 2014). Another cause might be due to image pixelation or changes in intensity distribution of CBPs. Given that the spatial resolution of SDO/AIA is ≈0.6′′/pixel, we can estimate that the error in position induced by CBP apparently changing position by 1 pixel is about 0.04° in solar coordinates around the equator. This is much smaller than observed by Sudar et al. (2015). The error in velocity between two subsequent images would be less than 1 m s-1. In our case, where we actually make a straight line fit through positions measured in at least ten images where the same CBP is detected, the error is even smaller than that. Therefore, we assume that the observed fluctuations in CBP position are most likely caused by the evolution of CBP photospheric footpoints described by Karachik et al. (2014). Since these fluctuations do not have a preferred direction on the solar surface, we can assume that this effect averages out with a large number of data points.
With such a large number of data points obtained by an automatic method, it is very likely that some velocities are incorrect because of misidentification in subsequent images or some similar problems. It is quite common to filter out such outliers by selecting a fixed range of acceptable rotational velocity (Brajša et al. 2002b; Vršnak et al. 2003; Sudar et al. 2014, 2015). This approach neglects the fact that the solar rotation varies with latitude and that such a fixed cut-off does not have a uniform effect on all latitudes. This in turn can affect the calculated rotation profile. Although, this effect is probably negligible for the solar rotation, it might create problems for derived quantities such as rotation velocity residuals or Reynolds stress.
Brajša et al. (2001) and Wöhl et al. (2010) adopted a different, two-step approach where they first applied the fixed filter, calculated the solar rotation profile, and then eliminated all measurements which differed by more than 2° day-1 from the calculated profile. Finally, the new profile was calculated with a truncated dataset. This approach takes into account the variation of the rotation with latitude and performs a cut-off on rotation velocity residuals.
In an attempt to remove all arbitrariness from the procedure, we also developed a method which removes the outliers based on the rotation velocity residuals. The method we used is based on interquartile range. First we calculate solar rotation profile from all data, 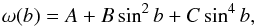 (1)where b is the latitude, and then we calculate rotation velocity residuals. Then we determine the lower quartile, Q1, and upper quartile, Q3, for the rotation velocity residuals distribution. We exclude all datapoints outside of the range
(1)where b is the latitude, and then we calculate rotation velocity residuals. Then we determine the lower quartile, Q1, and upper quartile, Q3, for the rotation velocity residuals distribution. We exclude all datapoints outside of the range ![\begin{equation} [Q_{1} - k(Q_{3} - Q{1}), Q_{3}+k(Q_{3} - Q{1})], \end{equation}](/articles/aa/full_html/2016/03/aa27217-15/aa27217-15-eq14.png) (2)where we have chosen k = 3.5, which removes the so-called hard outliers. With the reduced dataset we calculate solar rotation profile again and repeat the process iteratively until no datapoints are removed by interquartile criterion. In each iteration we removed the outliers by looking at meridional velocity distribution with the same method. The whole process is finished after only a few iterations.
(2)where we have chosen k = 3.5, which removes the so-called hard outliers. With the reduced dataset we calculate solar rotation profile again and repeat the process iteratively until no datapoints are removed by interquartile criterion. In each iteration we removed the outliers by looking at meridional velocity distribution with the same method. The whole process is finished after only a few iterations.
Since CBPs are situated above the photosphere at unknown height, we are actually measuring their apparent (projected) heliographic coordinates (Roša et al. 1995, 1998). To correct this problem we considered that the solar rotation profile is invariant to the central meridian distance (CMD). We divided the solar disk into bins that are 10° wide in CMD and calculated the rotation profile for each bin. We obtained a series of rotation profile coefficients – Ai, Bi, and Ci – that can be compared with the profile in the −5° to 5° CMD range defined by coefficients A, B, and C. We can calculate these coefficients for a number of different heights above photosphere and request that the function 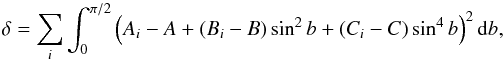 (3)is lowest for some trial height, h. The integral is taken from the equator to the pole so that the full profile is taken into account. This integral can be evaluated since coefficients do not depend on the latitude, b, so function δ becomes
(3)is lowest for some trial height, h. The integral is taken from the equator to the pole so that the full profile is taken into account. This integral can be evaluated since coefficients do not depend on the latitude, b, so function δ becomes 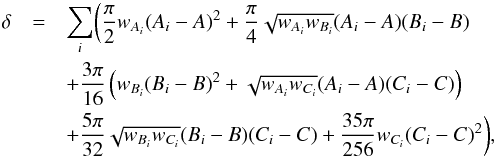 (4)where we have introduced weights for coefficients wAi, wBi, and wCi, which are calculated from their errors obtained by fitting the solar rotation profile in each CMD bin. This height correction procedure was performed together with the iterative outlier removal process described above.
(4)where we have introduced weights for coefficients wAi, wBi, and wCi, which are calculated from their errors obtained by fitting the solar rotation profile in each CMD bin. This height correction procedure was performed together with the iterative outlier removal process described above.
 |
Fig. 1 Calculated δ as a function of height, h, clearly shows a minimum value at around 6500 km above the photosphere. |
By following the reasoning in Roša et al. (1995) we can transform the apparent coordinates into the deprojected ones by assuming that CBP are at some height, h. This task is performed in polar coordinates obtained from pixel coordinates (Roša et al. 1995) so that both heliographic coordinates, CMD and latitude, are corrected for height. We can then simply plot δ as a function of h and from the minimum detect the best fit height. This plot is given in Fig. 1. We can clearly see that the minimum of function δ is located around 6500 km giving us the average height of CBPs seen in the SDO/AIA 19.3 nm channel. By fitting the parabolic function to δ(h) we get the average height, h = 6331 ± 239 km.
In the final run after all the filtering and with the best fit height we had 80 966 velocities in our dataset. For the analysis of rotation velocity residuals and meridional motion we transformed the velocities to units of m s-1. We calculated meridional velocities on the southern hemisphere with vmer = −∂b/∂t and assigned them symmetrical positive latitudes. This means that a negative value of meridional velocity represents motion towards the solar equator on both hemispheres.
3. Results
3.1. Solar rotation profile and rotation velocity residuals
In our previous paper (Sudar et al. 2015) we estimated that with 5−6 months of SDO/AIA data we could obtain a sufficient number of velocity measurements and that the accuracy of the solar rotation profile would be comparable with the most accurate tracer results obtained so far. Fitting the standard rotation profile (Eq. (1)) to 80 966 measurements for the coefficients we obtain A = 14.4060 ± 0.0051° day-1, B = −1.662 ± 0.050°day-1, and C = −2.742 ± 0.081° day-1. It is important to point out that previous studies needed decades of measurements to achieve this level of accuracy.
As Snodgrass & Howard (1985) explained, it is not straightforward to compare the results of the solar rotation profile from different sources when expressed as an expansion series of sin2b (Eq. (1)). To avoid a crosstalk problem between coefficients, it is better to express the result as Gegenbauer polynomials, which are orthogonal on the disk. Our solar rotation profile, expressed with Gegenbauer polynomials is given by the coefficients AG = 13.8386°day-1, BG = −0.698°day-1, and CG = −0.131°day-1.
Our result for the rotation profile is the most similar to the value calculated by Hara (2009) who found the coefficients to be A = 14.39°day-1, B = −1.91°day-1, and C = −2.45°day-1, or expressed with Gegenbauer coefficients AG = 13.80°day-1, BG = −0.709°day-1, and CG = −0.117°day-1. Hara (2009) analysed X-ray bright points observed by the Yohkoh soft X-ray telescope in the period 1994−1998. This time period starts close to the end of cycle 22 and ends soon after the beginning of cycle 23 (see Table 1 in Brajša et al. 2009).
Perhaps the similarity between our results and those of Hara (2009) are related to the low solar activity in both works. For example, Brajša et al. (2004) found a slightly higher value of the equatorial rotation A = 14.454 ± 0.027°day-1 in the period from 1998−1999 which is closer to the solar activity maximum. Wöhl et al. (2010) found even faster equatorial rotation A = 14.499 ± 0.006°day-1 with CBP data covering most of cycle 23 around its activity maximum. If such variations in the solar rotation profile are indeed due to the changing activity of the sun, given the coefficient uncertainties we calculated above, we should be able to detect and track these changes during the solar activity cycle with the expanded SDO/AIA CBP dataset.
 |
Fig. 2 Average solar rotation profile in 2° bins of latitude, b, is shown with filled black squares and error bars. The best fit solar rotation profile is shown with a solid black line. |
In Fig. 2 we show the best fit rotation profile, ω(b), with a solid black line. We also show average values of ω in 2° bins of latitude, b, with with black squares and error bars. We see that the bin averaged values are fairly well determined up to high latitudes (70°), which is very promising for further CBP studies based on the SDO/AIA data. The small size of the error bars also illustrates how well the rotation profile is determined.
 |
Fig. 3 Distribution of rotation velocity residuals, Δvrot, in 20 m s-1 bins. |
Rotation velocity residuals, Δvrot, are calculated by subtracting the actual rotation velocity of each CBP from the mean profile given by the coefficient of the fit above. The residuals are further transformed from units of ° day-1 to m s-1 where we took into account the latitude of each CBP. In Fig. 3 we show a distribution of rotation velocity residuals, Δvrot. Since Δvrot was used to eliminate the outliers, it is important to check whether there are any unusual features in their distribution, which would indicate that something went wrong with our procedure. The distribution in Fig. 3 looks fairly normal and well behaved so we assume that the method used is acceptable.
Tlatov & Pevtsov (2013) proposed an interesting idea that the torsional oscillation pattern, associated with rotation velocity residuals, could – at least partially – be an artefact of binning in latitude b. The authors have been successful in simulating the torsional oscillation pattern by assuming drifting of the tracers towards the solar equator during the solar activity cycle. This is most notable for sunspots with a characteristic butterfly diagram, but could also be visible for CBPs. Moreover, the authors suggest that this effect is present in Doppler and helioseismology measurements.
In Fig. 4 we show the values of rotation velocity residuals, Δvrot, grouped into 5° bins of latitude b with a thick black solid line and black squares with error bars. In order to address the problem of binning in latitude, we also calculated Δvrot averages in shifted bins, where the first bin is in the range from 0° to 2.5° and all subsequent bins are 5° wide (shown with a grey solid line and filled circles with error bars in Fig. 4). In addition, we calculated Δvrot averages in bins with a constant number of data points (n = 5000) and show the results in the same graph with a dotted line and stars with error bars. We also calculated average latitude,  , instead of using a middle value of b for each bin. This process should alleviate the binning problem described by Tlatov & Pevtsov (2013), because the value of
, instead of using a middle value of b for each bin. This process should alleviate the binning problem described by Tlatov & Pevtsov (2013), because the value of  is much more appropriate in the case of uneven distribution of data points in the bin.
is much more appropriate in the case of uneven distribution of data points in the bin.
From Fig. 4 we can conclude that all three of the binning techniques we used show practically the same behaviour. We also note that the values of  do not differ significantly from the middle value of b for each bin. The difference is lower than 0.2° for all but one bin. This suggests that the distribution of tracers in each bin is not far from uniform. In Fig. 4 we see positive values of Δvrot averages in the range between 10° and 20°, which might correspond to a branch of torsional oscillation pattern towards the equator. Another branch might be visible above 50°, even though the errors are becoming large in that region of latitudes. This type of result is more consistent with Doppler measurements than with sunspot data where Sudar et al. (2014) found no stable pattern that resembles torsional oscillations.
do not differ significantly from the middle value of b for each bin. The difference is lower than 0.2° for all but one bin. This suggests that the distribution of tracers in each bin is not far from uniform. In Fig. 4 we see positive values of Δvrot averages in the range between 10° and 20°, which might correspond to a branch of torsional oscillation pattern towards the equator. Another branch might be visible above 50°, even though the errors are becoming large in that region of latitudes. This type of result is more consistent with Doppler measurements than with sunspot data where Sudar et al. (2014) found no stable pattern that resembles torsional oscillations.
 |
Fig. 4 Rotation velocity residuals, Δvrot, in 5° bins in latitude, b, are shown with a thick black solid line and filled squares with error bars. Values calculated with bins of the same width, but with the first bin in the range 0°–2.5°, are shown with a grey solid line and filled circles with error bars. Δvrot averages in bins with constant number of data points (n = 5000) are shown with a dotted line and stars with error bars. |
3.2. Meridional velocities
In order not to detect false meridional flows due to uneven distribution of tracers across different latitudes, it is necessary to assign calculated velocities to the latitude of the first measurements of position for each CBP (Olemskoy & Kitchatinov 2005; Sudar et al. 2014).
 |
Fig. 5 Distribution of meridional velocities, vmer, in 20 m s-1 bins. |
As with Δvrot, it is wise to take a look at the distribution of meridional velocities, vmer (Fig. 5), because they were also used in outlier identification and elimination from the raw dataset. Again, there are no unexpected features in the distribution, which leads us to believe that the method used was valid and correctly implemented.
 |
Fig. 6 Average meridional velocity, vmer in 5° bins of latitude, b, are shown with a thick black solid line and filled squares with error bars. Values calculated with bins of the same width, but with the first bin in the range 0°–2.5°, are shown with a grey solid line and filled circles with error bars. vmer averages in bins with constant number of data points (n = 5000) are shown with a dotted line and stars with error bars. |
In Fig. 6 we show average meridional velocity, vmer, as a function of latitude, b. As in the case with Δvrot, we used three different binning techniques and show the results with the same symbols as in Fig. 4. From the image we can see that the meridional velocity is almost always positive, meaning towards the poles, for all latitudes. This result is in contrast to what was found with sunspot groups (Sudar et al. 2014) where the authors detected flow towards the centre of solar activity for all latitudes and for all phases of the solar cycle. Predominantly poleward flow was not found in other works dealing with tracers (Howard & Gilman 1986; Wöhl & Brajša 2001; Vršnak et al. 2003).
On the other hand, poleward flow for all latitudes has been detected by using the Doppler method (Duvall 1979; Hathaway 1996). There is a small indication that for latitudes near the equator the flow is towards the equator. Snodgrass & Dailey (1996) already reported that this feature is present in their analysis of Mt. Wilson magnetograms. Moreover, they found that this low latitude behaviour actually changes over the course of the solar cycle. It will be very interesting to check if this behaviour is present in the expanded SDO/AIA CBP dataset.
3.3. Horizontal Reynolds stress
The horizontal Reynolds stress is simply defined as a product of rotation velocity residuals and meridional velocities averaged over longitudes for a given latitude band: 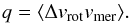 (5)In our convention, if the value of q is negative it means that the angular momentum is transported towards the solar equator.
(5)In our convention, if the value of q is negative it means that the angular momentum is transported towards the solar equator.
 |
Fig. 7 Horizontal Reynolds stress in bins of 10° in latitude, b, is shown with filled black squares with error bars. |
In Fig. 7 we show the value of the horizontal Reynolds stress, q, as a function of latitude, b, with black squares. The bins are 10° wide and the error bars are also shown. We can see that the Reynolds stress is zero for almost all latitudes, b. The only notable exception is the bin at 25° where q ≈ −1500 m2 s-2 and possibly the bin at 15°. Sudar et al. (2014) found the minimum at the same latitude, but about twice as deep. They also found negative values of q for all latitudes below 35°. Latitudes above 35° were out of reach for sunspot groups measurements.
The minimum at 25° seems unexpected when we look at the behaviour of average meridional velocity, vmer, and rotation velocity residuals, Δvrot, at the same latitude. The two velocities show a positive average value, while the horizontal Reynolds stress is negative. If we take into account that the average of the product is not equal to the product of averages, ⟨ vmerΔvrot ⟩ ≠ ⟨ vmer ⟩ ⟨ Δvrot ⟩, we see that the negative Reynolds stress we obtained actually means that the two velocities are not independent, but correlated.
4. Summary and conclusion
By using just under six months of SDO/AIA observations we have calculated the solar rotation profile with an accuracy comparable to other tracer measurements that needed a much longer time span of observations. The calculated solar rotation profile and comparison with other works indicates that our result is connected with a low solar activity in the observed phase of the current solar cycle. Further work with more SDO/AIA data might provide some valuable insight into the behaviour of the solar rotation during the solar cycle.
We found that CBPs observed by SDO/AIA in the 19.3 nm channel are located at an average height of ≈6300 km above the solar photosphere. This is slightly lower than in previous studies: Simon & Noyes (1972)≈11 000 km, Brajša et al. (2004) 8000−12 000 km, and Hara (2009)≈12 000 km. On the other hand, Karachik et al. (2006) suggest the value of 80 000 km, which is the height at which the Fe xiv λ195 line forms (Zhang & et al. 2000). Rotation velocity residuals show indications of torsional oscillations and further studies of the evolution of observed features might be very helpful for comparison with other methods.
Meridional velocities are almost always towards the solar poles, which is the direction often seen in helioseismology measurements (Zhao & Kosovichev 2004; González Hernández et al. 2008, 2010). Observations of sunspot groups, on the other hand, show a different meridional velocity pattern (Sudar et al. 2014). However, Sudar et al. (2014) have pointed out that meridional velocity residuals in helioseismology measurements show a striking similarity with sunspot groups observations. The difference between CBPs and sunspot groups can be explained with similar arguments to those in Sudar et al. (2014) who have suggested that sunspot observations show motions related to active regions, while the mostly poleward flow is observed outside of those regions (Zhao & Kosovichev 2004, Fig. 5). Our segmentation algorithm has difficulties in detecting CBPs over bright active regions, so the CBPs results are more similar to time-distance heliosiesmology studies than to sunspot measurements.
Reynolds stress shows a minimum at around 25° in latitude similar to the results from Sudar et al. (2014), but with lower magnitude (q(25°) ≈ −1500 m2 s-2, compared to ≈−3000 m2 s-2 in Sudar et al. 2014). We are not sure whether the reason for this result is the same as for the meridional velocities or whether this is some peculiarity of the phase of the solar cycle or even the whole cycle 24.
Further work on the expanded SDO/AIA dataset and even the possible application of the segmentation algorithm to previous satellite measurements (e.g. from SOHO/EIT) will be very helpful for our understanding of the dynamics on and above the photosphere. Such research can be considered complementary to helioseismology measurements which probe the behaviour below the solar surface.
Acknowledgments
This work has been supported in part by the Croatian Science Foundation under the project 6212 “Solar and Stellar Variability”. It has also received funding from the SOLARNET project (312495, 2013−2017), which is an Integrated Infrastructure Initiative (I3) supported by FP7 Capacities Programme. S.S. was supported by NASA Grant NNX09AB03G to the Smithsonian Astrophysical Observatory and contract SP02H1701R from Lockheed-Martin to SAO.
References
- Balthasar, H., Vázquez, M., & Wöhl, H. 1986, A&A, 155, 87 [NASA ADS] [Google Scholar]
- Brajša, R., Wöhl, H., Vršnak, B., et al. 2001, A&A, 374, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brajša, R., Wöhl, H., Vršnak, B., et al. 2002a, Sol. Phys., 206, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Brajša, R., Wöhl, H., Vršnak, B., et al. 2002b, A&A, 392, 329 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brajša, R., Wöhl, H., Vršnak, B., et al. 2004, A&A, 414, 707 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brajša, R., Wöhl, H., Hanslmeier, A., et al. 2009, A&A, 496, 855 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duvall, Jr., T. L. 1979, Sol. Phys., 63, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Gilman, P. A., & Howard, R. 1984, Sol. Phys., 93, 171 [NASA ADS] [Google Scholar]
- González Hernández, I., Kholikov, S., Hill, F., Howe, R., & Komm, R. 2008, Sol. Phys., 252, 235 [NASA ADS] [CrossRef] [Google Scholar]
- González Hernández, I., Howe, R., Komm, R., & Hill, F. 2010, ApJ, 713, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Hara, H. 2009, ApJ, 697, 980 [Google Scholar]
- Hathaway, D. H. 1996, ApJ, 460, 1027 [Google Scholar]
- Howard, R. F. 1991, Sol. Phys., 135, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Howard, R., & Gilman, P. A. 1986, ApJ, 307, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Howard, R., & Harvey, J. 1970, Sol. Phys., 12, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Howard, R., & Labonte, B. J. 1980, ApJ, 239, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Howard, R., Gilman, P. I., & Gilman, P. A. 1984, ApJ, 283, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Howe, R., Christensen-Dalsgaard, J., Hill, F., et al. 2000, ApJ, 533, L163 [NASA ADS] [CrossRef] [Google Scholar]
- Karachik, N., Pevtsov, A. A., & Sattarov, I. 2006, ApJ, 642, 562 [NASA ADS] [CrossRef] [Google Scholar]
- Karachik, N. V., Minenko, E., Sattarov, I., Pevtsov, A. A., & Sherdonov, C. T. 2014, Astron. Nachr., 335, 1037 [NASA ADS] [CrossRef] [Google Scholar]
- Kariyappa, R. 2008, A&A, 488, 297 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lemen, J. R., Title, A. M., Akin, D. J., et al. 2012, Sol. Phys., 275, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Martens, P. C. H., Attrill, G. D. R., Davey, A. R., et al. 2012, Sol. Phys., 275, 79 [NASA ADS] [CrossRef] [Google Scholar]
- McIntosh, S. W., & Gurman, J. B. 2005, Sol. Phys., 228, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Newton, H. W., & Nunn, M. L. 1951, MNRAS, 111, 413 [NASA ADS] [Google Scholar]
- Olemskoy, S. V., & Kitchatinov, L. L. 2005, Astron. Lett., 31, 706 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez Garde, M., Vázquez, M., Schwan, H., & Wöhl, H. 1981, A&A, 93, 67 [NASA ADS] [Google Scholar]
- Pulkkinen, P., & Tuominen, I. 1998, A&A, 332, 755 [NASA ADS] [Google Scholar]
- Roša, D., Vršnak, B., & Božić, H. 1995, Hvar Observatory Bulletin, 19, 23 [NASA ADS] [Google Scholar]
- Roša, D., Vršnak, B., Božić, H., et al. 1998, Sol. Phys., 179, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Schröter, E. H. 1985, Sol. Phys., 100, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Schröter, E. H., & Wöhl, H. 1976, Sol. Phys., 49, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, G. W., & Noyes, R. W. 1972, Sol. Phys., 26, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Skokić, I., Brajša, R., Roša, D., Hržina, D., & Wöhl, H. 2014, Sol. Phys., 289, 1471 [NASA ADS] [CrossRef] [Google Scholar]
- Snodgrass, H. B., & Dailey, S. B. 1996, Sol. Phys., 163, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Snodgrass, H. B., & Howard, R. 1985, Sol. Phys., 95, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Snodgrass, H. B., & Ulrich, R. K. 1990, ApJ, 351, 309 [Google Scholar]
- Sudar, D., Skokić, I., Ruždjak, D., Brajša, R., & Wöhl, H. 2014, MNRAS, 439, 2377 [NASA ADS] [CrossRef] [Google Scholar]
- Sudar, D., Skokić, I., Brajša, R., & Saar, S. H. 2015, A&A, 575, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tlatov, A. G., & Pevtsov, A. A. 2013, in Fifty Years of Seismology of the Sun and Stars, eds. K. Jain, S. C. Tripathy, F. Hill, J. W. Leibacher, & A. A. Pevtsov, ASP Conf. Ser., 478, 297 [Google Scholar]
- Ulrich, R. K., Boyden, J. E., Webster, L., Padilla, S. P., & Snodgrass, H. B. 1988, Sol. Phys., 117, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Vršnak, B., Brajša, R., Wöhl, H., et al. 2003, A&A, 404, 1117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ward, F. 1965, ApJ, 141, 534 [NASA ADS] [CrossRef] [Google Scholar]
- Wöhl, H., & Brajša, R. 2001, Sol. Phys., 198, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Wöhl, H., Brajša, R., Hanslmeier, A., & Gissot, S. F. 2010, A&A, 520, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, M., & et al. 2000, in IAU Joint Discussion, 7 [Google Scholar]
- Zhao, J., & Kosovichev, A. G. 2004, ApJ, 603, 776 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Calculated δ as a function of height, h, clearly shows a minimum value at around 6500 km above the photosphere. |
| In the text | |
 |
Fig. 2 Average solar rotation profile in 2° bins of latitude, b, is shown with filled black squares and error bars. The best fit solar rotation profile is shown with a solid black line. |
| In the text | |
 |
Fig. 3 Distribution of rotation velocity residuals, Δvrot, in 20 m s-1 bins. |
| In the text | |
 |
Fig. 4 Rotation velocity residuals, Δvrot, in 5° bins in latitude, b, are shown with a thick black solid line and filled squares with error bars. Values calculated with bins of the same width, but with the first bin in the range 0°–2.5°, are shown with a grey solid line and filled circles with error bars. Δvrot averages in bins with constant number of data points (n = 5000) are shown with a dotted line and stars with error bars. |
| In the text | |
 |
Fig. 5 Distribution of meridional velocities, vmer, in 20 m s-1 bins. |
| In the text | |
 |
Fig. 6 Average meridional velocity, vmer in 5° bins of latitude, b, are shown with a thick black solid line and filled squares with error bars. Values calculated with bins of the same width, but with the first bin in the range 0°–2.5°, are shown with a grey solid line and filled circles with error bars. vmer averages in bins with constant number of data points (n = 5000) are shown with a dotted line and stars with error bars. |
| In the text | |
 |
Fig. 7 Horizontal Reynolds stress in bins of 10° in latitude, b, is shown with filled black squares with error bars. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


