| Issue |
A&A
Volume 587, March 2016
|
|
|---|---|---|
| Article Number | A108 | |
| Number of page(s) | 38 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201527021 | |
| Published online | 26 February 2016 | |
Effects of environmental gas compression on the multiphase ISM and star formation
The Virgo spiral galaxies NGC 4501 and NGC 4567/68
1
CDS, Observatoire astronomique de Strasbourg, Université de Strasbourg,
CNRS, UMR 7550, 11 rue de l’Université,
67000
Strasbourg,
France
e-mail: Bernd.Vollmer@astro.unistra.fr
2
Univ. Bordeaux, Laboratoire d’Astrophysique de Bordeaux, UMR
5804, 33270
Floirac,
France
Received: 21 July 2015
Accepted: 26 December 2015
The cluster environment can affect galaxy evolution in different ways: via ram pressure stripping or by gravitational perturbations caused by galactic encounters. Both kinds of interactions can lead to the compression of the interstellar medium (ISM) and its associated magnetic fields, causing an increase in the gas surface density and the appearance of asymmetric ridges of polarized radio continuum emission. New IRAM 30m HERA CO(2−1) data of NGC 4501, a Virgo spiral galaxy currently experiencing ram pressure stripping, and NGC 4567/68, an interacting pair of galaxies in the Virgo cluster, are presented. We find an increase in the molecular fraction where the ISM is compressed. The gas is close to self-gravitation in compressed regions. This leads to an increase in gas pressure and a decrease in the ratio between the molecular fraction and total ISM pressure. The overall Kennicutt Schmidt relation based on a pixel-by-pixel analysis at ~1.5 kpc resolution is not significantly modified by compression. However, we detected continuous regions of low molecular star formation efficiencies in the compressed parts of the galactic gas disks. The data suggest that a relation between the molecular star formation efficiency SFEH2 = SFR/M(H2) and gas self-gravitation (Rmol/Ptot and Toomre Q parameter) exists. Both systems show spatial variations in the star formation efficiency with respect to the molecular gas that can be related to environmental compression of the ISM. An analytical model was used to investigate the dependence of SFEH2 on self-gravitation. The model correctly reproduces the correlations between Rmol/Ptot, SFEH2, and Q if different global turbulent velocity dispersions are assumed for the three galaxies. We found that variations in the NH2/ICO conversion factor can mask most of the correlation between SFEH2 and the Toomre Q parameter. Dynamical simulations were used to compare the effects of ram pressure and tidal ISM compression. These models give direct access to the volume density. We conclude that a gravitationally induced ISM compression has the same consequences as ram pressure compression: (i) an increasing gas surface density; (ii) an increasing molecular fraction; and (iii) a decreasing Rmol/Ptot in the compressed region due to the presence of nearly self-gravitating gas. The response of SFEH2 to compression is more complex. While in the violent ISM-ISM collisions (e.g., Taffy galaxies and NGC 4438) the interaction makes star formation drop by an order of magnitude, we only detect an SFEH2 variation of ~50% in the compressed regions of the three galaxies. We suggest that the decrease in star formation depends on the ratio between the compression timescale and the turbulent dissipation timescale. In NGC 4501 and NGC 4567/68 the compression timescale is comparable to the turbulent dissipation timescale and only leads to minor changes in the molecular star formation efficiency.
Key words: galaxies: evolution / galaxies: interactions / galaxies: clusters: individual: NGC 4501 / galaxies: star formation / galaxies: clusters: individual: NGC 4567/68
© ESO, 2016
1. Introduction
Environment plays an important role in galaxy evolution, affecting the gas content and star formation of cluster galaxies. Wide statistical studies of galaxy evolution in group and cluster environments (Peng et al. 2010) have pointed out that a dense environment quenches the star formation rate (SFR) on long timescales (several Gyr). Nevertheless, on a shorter timescale (hundreds of Myr) the interstellar medium (ISM) can be compressed by the interactions and thus the SFR can be enhanced during this relatively short timescale.
Two types of interactions that can modify the SFR in dense environments can be distinguished. The first type includes gravitational interactions such as flybys, galaxy-galaxy encounters, or galaxy harassment (Moore et al. 1996, 1999). This class of interactions affects both the stellar and the gaseous contents of galaxies. Tidal interactions can be compressing, and in this way can enhance both the gas and the stellar surface densities. The second type includes hydrodynamical interactions between the tenuous and hot (n ~ 10-4 cm-3, T ~ 107 K; Sarazin 1986) intra-cluster gas and ISM of galaxies, known as ram pressure striping (Gunn & Gott 1972). This interaction is most efficient when the galaxy enters the central part of a cluster where its velocity relative to the cluster mean is highest and the intra-cluster medium is dense (Vollmer et al. 2001).
The nearby Virgo cluster is an ideal laboratory to study the effect of a dense environment on galaxies and thus to explore the physical process of star formation. The distance of 17 Mpc allows us to reach a resolution of about 1 kpc with radio telescopes. The spiral population in the Virgo cluster shows disturbed and truncated Hi disks (Cayatte et al. 1990, 1994; Chung et al. 2009) caused by tidal interactions and ram pressure stripping. Ram pressure stripping naturally leads to truncated gas disks. During a ram pressure stripping event the ISM can be compressed (e.g., Vollmer 2009), especially when ram pressure increases and the vector of the galaxy’s motion is parallel to the galactic disk, i.e., the ram pressure wind is edge-on.
Otmianowska-Mazur & Vollmer et al. (2003) have shown that the polarized radio continuum emission increases significantly whenever the ISM is compressed or sheared. In most cases shear motions can be detected in the Hi velocity field (e.g., NGC 4535, Chung et al. 2009). Therefore, a ridge of enhanced polarized emission located at the outer edge of the gas disk in the absence of a sheared velocity field is a clear sign of gas compression (Vollmer et al. 2007, 2012, 2013). We identified such ridges in the Virgo spiral galaxies NGC 4501 and NGC 4568. Whereas NGC 4501 is affected by ram pressure (Vollmer et al. 2008), NGC 4568 is tidally interacting with its close neighbor, NGC 4567.
 |
Fig. 1 NGC 4501: 6 cm polarized emission Vollmer et al. 2003 on Hα emission (from GOLDMINE Gavazzi et al. 2003). |
Vollmer et al. (2008) has found an enhanced polarized emission in the southeastern region of NGC 4501 (see Fig. 1) due to a nearly edge-on intracluster medium (ICM)-ISM ram pressure stripping event. The compressed region is oriented toward M87 indicating that this galaxy is falling into the dense region of the cluster for the first time. Contrary to gravitational perturbations, ram pressure stripping does not perturb the stellar disk. The stellar disk of NGC 4501 shows symmetric spiral arms with obscured dust inter arm features (Fig. 4).
NGC 4567/68 are two close Virgo spiral galaxies. The centers of NGC 4567 and NGC 4568 are separated in projection by ~6 kpc and have comparable radial velocities (vr = 2255 km s-1) suggesting that they are gravitationally bound. The absence of any obvious large-scale optical tidal features in either galaxy prompted Iono et al. (2005) to qualify this system as a young interacting pair. The stellar component of NGC 4568 (Fig. 6) is only mildly disturbed and that of NGC 4567 has a faint external ring structure, indicating that the interaction is in an early stage. The interaction has not destroyed the inner spiral structures of NGC 4568 and NGC 4567, but does affect the outer stellar disk. In the northern interaction region the Hi velocities of NGC 4567 and NGC 4568 are comparable. A low surface brightness Hi tail extending to the north is detected in NGC 4568 (Chung et al. 2009). While NGC 4567 has a fairly normal symmetric large scale magnetic field structure (Fig. 2), NGC 4568 shows an asymmetric 6 cm polarized emission with its maximum in the south and northwest of the galaxy center (Vollmer et al. 2013). The tidal compression region with an enhanced surface brightness of Hi and 6cm polarized emission is located northwest of the galaxy center.
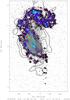 |
Fig. 2 NGC 4567/68: 6 cm polarized emission (Vollmer et al. 2013) on Hα emission (from GOLDMINE Gavazzi et al. 2003). |
Integrated properties NGC 4501 and NGC 4567/68
In this article we investigate the influence of large-scale (~1 kpc) compression on ISM properties (density and molecular fraction) and its efficiency in forming stars based on new IRAM 30m CO(2−1) observations of NGC 4501 and NGC 4567/68 and existing GALEX, Spitzer, and Herschel data. The basic properties of the two systems are given in Tables 1 and 2.
Basic properties of NGC 4501, NGC 4567/68, and NGC 4321
This article is organized in the following way. In Sect. 2 the IRAM 30m CO(2−1) observations of NGC 4501 and NGC 4567/68 and the data reduction process are presented. The observational results are given in Sect. 3 and discussed in Sect. 4. In Sect. 5 the analytical model of Vollmer & Leroy (2011) is used to interpret our observations. In Sect. 6 the results of a dynamical model of NGC 4501 and NGC 4567/68 are compared to all existing observations. We give our conclusions in Sect. 7. We use a distance of D = 17 Mpc for the Virgo cluster.
2. Observations and data reduction
NGC 4501 and NGC 4567/68 CO(2−1) were observed in December 2012 at the IRAM 30m single-dish telescope at Pico Veleta, Spain. The CO(2−1) emission line was mapped with the HERA multi-beam heterodyne receiver (Schuster et al. 2004) in on-the-fly mode. The scans were realized along the minor and major axes of the galaxies with a scanning speed of 5″s-1. The scans were done with two derotator positions (+90 and −90 deg), thus the same position in the sky was scanned with two different pixels of HERA. The resulting maps were oversampled with spectra taken at least every 3.8″.
The WILMA backend autocorrelator with a spectral resolution of 2 MHz and a bandwidth of 1024 MHz was used. Four 2.6 km s-1 velocity channels were binned together yielding a 10.4 km s-1 channel separation. We observed each system for about 20 h, to reach an average rms noise level of 8 mK and 7 mK in the 10.4 km s-1 channel for NGC 4501 and NGC 4567/68, respectively. The calibration was done with MIRA, using the TIME mode calibration, which decreases the rms noise level compared to the default calibration mode AVER. Bad spectra were filtered by comparing the theoretical system temperature 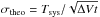 (ΔV = 10.4 km s-1 the channel separation and t = 0.5 s the integration time) to the real noise level. Spectra with an rms noise in excess of 1.1 × σtheo were rejected. A velocity window was selected for NGC 4501 (1950−2700 km s-1) and for NGC 4567/68 (2000−2550 km s-1). A constant baseline was adjusted outside the velocity window and subtracted from the spectrum. A data cube at a resolution of 12′′ was created using the CLASS GILDAS xy_map routine with a pixel size of 3″.
(ΔV = 10.4 km s-1 the channel separation and t = 0.5 s the integration time) to the real noise level. Spectra with an rms noise in excess of 1.1 × σtheo were rejected. A velocity window was selected for NGC 4501 (1950−2700 km s-1) and for NGC 4567/68 (2000−2550 km s-1). A constant baseline was adjusted outside the velocity window and subtracted from the spectrum. A data cube at a resolution of 12′′ was created using the CLASS GILDAS xy_map routine with a pixel size of 3″.
In order to compute the total intensity map, the atomic Hi data from VIVA (Chung et al. 2009) was used. For each spectrum, we selected the velocity window where the Hi flux was higher than 4.5 times the rms of the Hi spectrum. For NGC 4501, no Hi emission was detected near the galactic center. In this case, the CO(2−1) window was computed by fitting a Gaussian to the CO spectra and selecting a spectral window from μ − 3.2σ to μ + 3.2σ , where σ and μ are the standard deviation and peak position of the Gaussian. At the center of NGC 4501, the CO(2−1) emission is strong and a Gaussian shape fits the CO(2−1) line well. After windowing the CO(2−1) line, a third-order baseline was subtracted from the CO spectra. First- and second-order baseline subtractions were tried on both NGC 4501 and NGC 4567/68 and gave a higher rms noise than the third-order baseline subtraction. The rms maps of NGC 4501 and 4567/68 did not show any systematic residuals (Fig. A.1).
For comparison with a symmetric spiral galaxy, we used the face-on Virgo spiral galaxy NGC 4321 since both CO(2−1) and VLA Hi data were available. The CO(2−1) data cube is taken from the HERACLES data (Leroy et al. 2009) with a spatial resolution of 13″ and a typical rms of 20−40 mK in the 10.4 km s-1 channel. The Hi data are from the VIVA survey (Chung et al. 2009) with a beam size of 30′′.
3. Results
3.1. Molecular gas
Following Leroy et al. (2008) the molecular gas surface density ΣH2 was derived using a galactic CO-to-H2 conversion factor Xco = 2 × 1020 cm-2 or αco = 4.4M⊙ (K km s-1 pc2)-1 and a fixed line ratio ICO(2−1) /ICO(1−0) = 0.8 (see Eq. (1)). A factor of 1.36 was included to take the presence of helium into account, 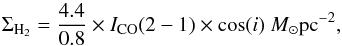 (1)where ICO(2−1) is the integrated intensity of the CO(2−1) in K km s-1 and i the inclination angle of the galaxy. The typical uncertainties in the molecular gas surface density are about ~1M⊙pc-2, which corresponds to the 3σ level per 10 km s-1 channel. The implications of using a Xco factor is discussed in Sect. 4.1.
(1)where ICO(2−1) is the integrated intensity of the CO(2−1) in K km s-1 and i the inclination angle of the galaxy. The typical uncertainties in the molecular gas surface density are about ~1M⊙pc-2, which corresponds to the 3σ level per 10 km s-1 channel. The implications of using a Xco factor is discussed in Sect. 4.1.
 |
Fig. 3 NGC 4501: CO(2−1) emission map. Contour levels are 1.0, 2.25, 4.0, 6.25, 9.0, 12.25, 16.0, 20.25, 25.0, and 30.25 K km s-1. The white contour corresponds to 0.1 K km s-1. |
For NGC 4501 the CO(2−1) emission extends over a radius of ~2.5′ = 11 kpc (Fig. 3). This is over half the optical radius R25 = 4.35′. In Fig. 4 the molecular gas is presented on the g′-band emission from SDSS. The emission map shows a well-defined southwestern edge, compared to the more diffuse northeastern side of the galactic disk. The inner disk of NGC 4501 has surface densities in excess of 30 M⊙ pc-2 (light blue contours in Fig. 3). In this region two spiral arm structures are present, the first one extending to the south and curved toward the southwestern edge, the second extending to the north and curved to the northeast. At the compressed western side a region of high surface density is found west of the galaxy center with surface density of 40−60M⊙ pc-2. The southeastern quadrant of the disk has an overall lower surface density than the northwestern quadrant.
 |
Fig. 4 NGC 4501: CO(2−1) emission on SDSS g′-band image. Contour levels are 1.0, 2.25, 4.0, 6.25, 9.0, 12.25, 16.0, 20.25, 25.0, and 30.25) K km s-1. |
The CO(2−1) emission distribution of NGC 4567 (Fig. 5) shows two spiral arms with high molecular gas surface densities. The first extends to the southwest and is curved to the north; the second is shorter, extends to the north, and bends toward NGC 4568.
 |
Fig. 5 NGC 4567/68: CO(2−1) emission map. Contours are 1.0, 2.25, 4.0, 6.25, 9.0, 12.25, 16.0, 20.25, 25.0, 30.25, 36.0, 42.25, 49.0, 56.25, and 64.0) K km s-1. The white contour corresponds to 0.1 K km s-1. |
The southern part of the CO(2−1) emission of NGC 4568 is more extended than the northern part. The northern part of the disk has higher molecular gas surface densities than the more extended southern part. A peculiar molecular gas arm is observed in NGC 4568. It extends to the south and curves to the west. The northern arm first extends to the northeast and then bends to the west, toward NGC 4567. The latter part of the northern arm might well be associated with the eastern spiral arm of NGC 4567. The molecular gas map of NGC 4567/68 is presented over the g’ SDSS band emission in Fig. 6.
 |
Fig. 6 NGC 4567/68: CO(2−1) emission on SDSS g′-band image. Contour levels are 1.0, 2.25, 4.0, 6.25, 9.0, 12.25, 16.0, 20.25, 25.0, 30.25, 36.0, 42.25, 49.0, 56.25, and 64.0 K km s-1. |
3.2. Total gas
Total gas surface density maps Σg were computed by combining the atomic gas surface density ΣHI and the molecular gas surface density Σg = ΣHI + ΣH2. The atomic gas surface density ΣHI was computed for these two galactic systems using VLA HI data from Chung et al. 2008. Following Leroy et al. (2008), 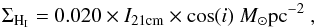 (2)where I21cm is the integrated intensity of the 21 cm line in K km s-1 and i the inclination angle of the galaxy. Equation (2) includes a factor of 1.36 to reflect the presence of helium. The typical uncertainties in the atomic gas surface density obtained here are ~0.5 M⊙ pc-2, which corresponds to the 3σ level per 10 km s-1 channel. Before summing, the CO observations of NGC 4501 and NGC 4567/68 were convolved to the Hi resolution (17″ for NGC 4501 and NGC 4567/68, 30″ for NGC 4321).
(2)where I21cm is the integrated intensity of the 21 cm line in K km s-1 and i the inclination angle of the galaxy. Equation (2) includes a factor of 1.36 to reflect the presence of helium. The typical uncertainties in the atomic gas surface density obtained here are ~0.5 M⊙ pc-2, which corresponds to the 3σ level per 10 km s-1 channel. Before summing, the CO observations of NGC 4501 and NGC 4567/68 were convolved to the Hi resolution (17″ for NGC 4501 and NGC 4567/68, 30″ for NGC 4321).
The total gas surface density maps of NGC 4501 (Fig. 7) shows three low surface density spirals arms on the eastern side of the disk, curved to the northwest. Moreover, the southwestern side of NGC 4501 has a well-defined edge as seen in ΣH2. The northern part of the NGC 4501 outer disk shows higher gas surface density then the southern part.
 |
Fig. 7 NGC 4501 total gas surface density Σg = ΣHI + ΣH2. The thin black contour levels are 4.0, 4.36, 5.44, 7.24, 9.76, 13.0, 16.96, 21.64, 27.04, 33.16, 40.0, 47.56, 55.84, 64.84, and 74.56 M⊙ pc-2. The resolution is 17″. Blue contour: high atomic gas surface density regions. Green contour: southern “U” shaped region with low SFEH2. Orange contour: northern low SFEH2 region. Red contour: high Rmol/Ptot region. Purple contour: central region defined from the stellar surface density excluded from the fit. The beam size is shown in the lower right corner. |
NGC 4567/68 total gas surface density is dominated by the molecular gas surface density inside R ~ 0.5 × R25. Therefore, the total gas surface density distribution of NGC 4567 and NGC 4568 show the same spiral arms as in molecular gas (Fig. 8).
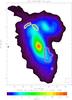 |
Fig. 8 NGC 4567/68 total gas surface density map. The thin black contours are 4, 5, 8, 13, 20, 29, 40, 53, 68, 85, 104, 125, 148, 173, and 200 M⊙ pc-2. The resolution is 17″. Yellow contour: northern low SFEH2 region. Purple contour: southern low SFEH2 region. The beam size is shown in the lower right corner. |
 |
Fig. 9 NGC 4501 molecular fraction Rmol = ΣH2/ ΣHI. The resolution is 17″. Contour levels are 0.04, 0.06, 0.1, 0.16, 0.25, 0.4, 0.63, 1, 1.58, 2.51, 3.98, 6.31, 10, 15.84, and 25.11. |
The total gas surface density of NGC 4568 is more extended to the south; it has a high surface density southern arm curved to the west and a southern low surface density component curved to the east, which causes an east-west asymmetry in the south of NGC 4568.
The northern low surface density (~2M⊙ pc-2) tail of NGC 4567/68 does not have a detected CO counterpart.
3.3. Molecular fraction
The molecular fraction Rmol = ΣH2/ ΣHI was derived using the convolved 17″ resolution data sets. This ratio is presented for NGC 4501 and NGC 4567/68 in Figs. 9 and 10.
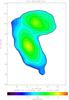 |
Fig. 10 NGC 4567/68 molecular fraction Rmol = ΣH2/ ΣHI. The resolution is 17″. Contour levels are 0.04, 0.06, 0.1, 0.16, 0.25, 0.4, 0.63, 1, 1.58, 2.51, 3.98, 6.31, 10, 15.84, and 25.11. |
For NGC 4501 the molecular fraction increases toward the center where no atomic gas is present. The molecular fraction is significantly higher in the western ridge of compressed gas (Rmol ~ 1) than at similar radii in the northeast, east, and southwest of the galaxy (Rmol ~ 0.1).
In NGC 4567/68 the molecular fraction increases toward the center of the disk, where the molecular gas surface density is about 10 times that of the atomic gas surface density. Between the two galaxies the molecular fraction is high (about one). However, in this region the molecular fraction is sensitive to projection effects. In NGC 4567 the molecular fraction is higher in the spiral arms. The southern outer gas disk has a very low molecular fraction (Rmol< 0.1).
3.4. Interstellar gas pressure Pext
Elmegreen (1989) derived the total mid-plane gas pressure Ptot from the numerical solution of hydrostatic equilibrium for a gas plus star disk, 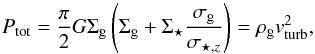 (3)where ρg is the gas density, vturb the gas velocity dispersion, G the gravitational constant, Σ⋆ the stellar surface density, σg the gas velocity dispersion, and σ⋆,z the vertical stellar velocity dispersion. This expression is accurate to within 10% (Elmegreen 1989).
(3)where ρg is the gas density, vturb the gas velocity dispersion, G the gravitational constant, Σ⋆ the stellar surface density, σg the gas velocity dispersion, and σ⋆,z the vertical stellar velocity dispersion. This expression is accurate to within 10% (Elmegreen 1989).
The 3.6μm emission, observed with the IRAC instrument on the Spitzer spatial telescope, was used to compute the stellar surface density of these two galactic systems. Following Leroy et al. (2008), 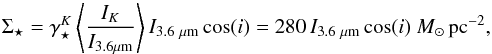 (4)where
(4)where 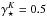 M⊙/L⊙ ,K is the K-band mass-to-light ratio, IK is the K-band intensity in MJy ster-1, and I3.6 μm is the 3.6μm intensity in MJy ster-1. A fixed ratio IK/I3.6μm = 1.818 and a solar K-band magnitude of 3.28 mag (Binney & Merrifield 1998) were assumed. The vertical stellar velocity dispersion can be derived from the stellar scale length l⋆ (following Leroy et al. (2008) and reference therein):
M⊙/L⊙ ,K is the K-band mass-to-light ratio, IK is the K-band intensity in MJy ster-1, and I3.6 μm is the 3.6μm intensity in MJy ster-1. A fixed ratio IK/I3.6μm = 1.818 and a solar K-band magnitude of 3.28 mag (Binney & Merrifield 1998) were assumed. The vertical stellar velocity dispersion can be derived from the stellar scale length l⋆ (following Leroy et al. (2008) and reference therein): 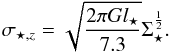 (5)Equation (5) assumes (1) a constant exponential stellar scale height hstar within the disk; (2) l⋆/h⋆ = 7.3 ± 2.2 (Kregel et al. 2002); and (3) an isothermal disk in the vertical direction (see van der Kruit 1988, van der Kruit & Searle 1981). We derived the stellar scale length of NGC 4501, NGC 4567/68, and NGC 4321 from radial profiles of their stellar surface density. The inner bulge component was excluded for the fit. We found l⋆ = 3.3 kpc for NGC 4501, l⋆ = 1.6 kpc for NGC 4567, l⋆ = 2.1 kpc for NGC 4568, and l⋆ = 4.9 for NGC 4321.
(5)Equation (5) assumes (1) a constant exponential stellar scale height hstar within the disk; (2) l⋆/h⋆ = 7.3 ± 2.2 (Kregel et al. 2002); and (3) an isothermal disk in the vertical direction (see van der Kruit 1988, van der Kruit & Searle 1981). We derived the stellar scale length of NGC 4501, NGC 4567/68, and NGC 4321 from radial profiles of their stellar surface density. The inner bulge component was excluded for the fit. We found l⋆ = 3.3 kpc for NGC 4501, l⋆ = 1.6 kpc for NGC 4567, l⋆ = 2.1 kpc for NGC 4568, and l⋆ = 4.9 for NGC 4321.
For all four galaxies, the ISM pressure Ptot was computed with deprojected data. Since both, the ISM pressure (Eq. (3)) and the molecular fraction mainly depend on the gas density (see, e.g., Leroy et al. 2008), we expect a close correlation between these parameters. Indeed, Blitz & Rosolowsky (2006) found 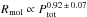 . The molecular fraction divided by the ISM pressure (Rmol/Ptot) maps are presented in the upper panels of Figs. 11−13 for NGC 4501, NGC 4567/68, and NGC 4321, respectively. Error maps of Rmol/Ptot are presented in the lower panels of Figs. 11, 12, and 13. The thick black contours indicate errors greater than 0.5 dex (a factor of ~3).
. The molecular fraction divided by the ISM pressure (Rmol/Ptot) maps are presented in the upper panels of Figs. 11−13 for NGC 4501, NGC 4567/68, and NGC 4321, respectively. Error maps of Rmol/Ptot are presented in the lower panels of Figs. 11, 12, and 13. The thick black contours indicate errors greater than 0.5 dex (a factor of ~3).
 |
Fig. 11 NGC 4501. Upper panel: molecular fraction divided by the ISM pressure Rmol/Ptot. The resolution is 17″. The ISM pressure and the molecular fraction are deprojected. Contour levels are (2, 2.5, 3.2, 4, 5, 6.3, 7.9, 10, 12.6, 15.8) × 10-5 cm3 K-1. Lower panel: error on Rmol/Ptot (in dex). The thick black contour corresponds to 0.5 dex. Contour levels are 0.3, 0.33, 0.37, 0.4, 0.43, 0.47, 0.5, 0.53, 0.57, and 0.6 dex. |
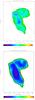 |
Fig. 12 NGC 4567/68. Upper panel: molecular fraction divided by the ISM pressure Rmol/Ptot. The resolution is 17″. The ISM pressure and the molecular fraction are deprojected. Contour levels are (1.2, 1.4, 1.7, 2.1, 2.5, 3, 3.6, 4.4, 5.2, 6.3) × 10-5 cm3 K-1. Lower panel: error on Rmol/Ptot (in dex). The thick black contour corresponds to 0.5 dex. Contour levels are 0.3, 0.33, 0.37, 0.4, 0.43, 0.47, 0.5, 0.53, 0.57, and 0.6 dex. |
 |
Fig. 13 NGC 4321. Upper panel: molecular fraction divided by the ISM pressure Rmol/Ptot. The resolution is 17″. The ISM pressure and the molecular fraction are deprojected. Contour levels are (1.2, 1.4, 1.7, 2.1, 2.5, 3, 3.6, 4.4, 5.2, 6.3) × 10-5 cm3 K-1. Lower panel: error on Rmol/Ptot (in dex). The thick black contour corresponds to 0.5 dex. Contour levels are 0.1, 0.13, 0.17, 0.2, 0.23, 0.27, 0.3, 0.33, 0.36, and 0.4 dex. |
For NGC 4501, Rmol/Ptot is nearly constant all over the disk. Nevertheless, some regions deviate from the average value; Rmol/Ptot is significantly lower in the west of the galaxy center (blue region) and in three distinct northern regions where the atomic gas surface density is also high. Moreover, in the southeastern part of NGC 4501 we detect a region where Rmol/Ptot is high (although with a high associated error). In NGC 4568 (Fig. 12) a clear north-south asymmetry is detected, Rmol/Ptot being lower in the northern part of the disk. In NGC 4567 the spiral arms have a lower Rmol/Ptot than the inter-arm regions. In NGC 4321 (Fig. 13) the spirals arms show a ~0.2 dex lower Rmol/Ptot than inter-arm regions as in NGC 4567.
To investigate the role of self-gravitating gas, we determined the ratio of gas pressure due to the gravitational potential of the gas 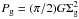 to that due to the stellar potential Ps = (π/ 2)GΣg(σg/σ⋆,z)Σ⋆. The ratio Pg/Ps> 1 indicates that the gravitational potential of the gas disk dominates that of the stellar disk. For Pg/Ps ≫ 1 the ISM is self-gravitating. The pressure ratio maps Pg/Ps of NGC 4501 and NGC 4567/68 are presented in Figs. 14 and 15.
to that due to the stellar potential Ps = (π/ 2)GΣg(σg/σ⋆,z)Σ⋆. The ratio Pg/Ps> 1 indicates that the gravitational potential of the gas disk dominates that of the stellar disk. For Pg/Ps ≫ 1 the ISM is self-gravitating. The pressure ratio maps Pg/Ps of NGC 4501 and NGC 4567/68 are presented in Figs. 14 and 15.
 |
Fig. 14 NGC 4501: ISM pressure due to the gravitational potential of the gas divided by the ISM pressure due to the stellar potential (Pg/Ps). The resolution is 17″. Contour levels are (0.33, 0.67, 1, 1.33, 1.67, 2, 2.33, 2.67, 3, 3.33, 3.67, 4, 4.33, 4.67, 5, 5.33, 5.67, 6, 6.33, 6.67) × 10-1. |
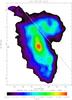 |
Fig. 15 NGC 4567/68: ISM pressure due to the gravitational potential of the gas divided by the ISM pressure due to the stellar potential (Pg/Ps). The resolution is 17″. Contour levels are (0.33, 0.67, 1, 1.33, 1.67, 2, 2.33, 2.67, 3, 3.33, 3.67, 4, 4.33, 4.67, 5, 5.33, 5.67, 6, 6.33, 6.67, 7, 7.33, 7.67, 8, 8.33) × 10-1. |
In NGC 4501 the ISM pressure is mostly dominated by the stellar potential. However, west of the galaxy center, within the ridge of compressed gas, the gravitational potential of the gas becomes more important than the stellar potential. Moreover, in the eastern region of the disk the pressure due to the stellar component dominates the ISM pressure budget. Contrary to the inner regions of NGC 4501, the central part of NGC 4568 has a high pressure ratio Pg/Ps> 0.7, i.e., the gas is almost self-gravitating. The spiral arms of NGC 4567 and NGC 4568 also show a higher Pg/Ps ~ 0.6 than the inter-arm or more external regions where Pg/Ps ~ 0.3.
3.5. SFR and SFEH2
For both galaxy systems, the star formation rate surface density (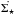 ) was computed with the Galaxy Evolution Explorer (GALEX, Martin et al. 2005) far-ultraviolet (FUV) emission and the 24 μm emission from Spitzer (Werner et al. 2004) following Leroy et al. (2008),
) was computed with the Galaxy Evolution Explorer (GALEX, Martin et al. 2005) far-ultraviolet (FUV) emission and the 24 μm emission from Spitzer (Werner et al. 2004) following Leroy et al. (2008), 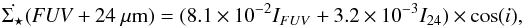 (6)where both intensities IFUV and I24 are given in MJy ster-1 and
(6)where both intensities IFUV and I24 are given in MJy ster-1 and 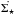 (FUV+24 μm) is given in M⊙ kpc-2 yr-1. While the FUV flux traces unobscured star formation from O, B, and A stars, the 24 μm emission is related to the UV heated dust. Thus, adding the 24 μm to the FUV emission fills the gap of shielded O and B stars. The FUV heated dust emission can also be tracked using the total infrared (TIR) emission (see Hao et al. 2011; Galametz et al. 2013; and Boquien et al. 2013).
(FUV+24 μm) is given in M⊙ kpc-2 yr-1. While the FUV flux traces unobscured star formation from O, B, and A stars, the 24 μm emission is related to the UV heated dust. Thus, adding the 24 μm to the FUV emission fills the gap of shielded O and B stars. The FUV heated dust emission can also be tracked using the total infrared (TIR) emission (see Hao et al. 2011; Galametz et al. 2013; and Boquien et al. 2013).
We tried three different ways of computing the TIR emission and concluded that 24 μm traces the TIR within 0.09 dex. This motivated our choice to use 24 μm to trace the obscured star formation (see discussion in Appendix B.1). We also made sure that the SFR computed with the Hα does not deviate significantly from the SFR computed with the FUV (see Appendix B.2 for the detailed study). Finally, we chose the FUV+24 μm for an easier comparison with other studies of nearby galaxies (e.g., Leroy et al. 2008; Bigiel et al. 2008). In the following 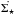 refers to
refers to 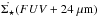 .
.
For the two galactic systems, the star formation efficiency maps with respect to the molecular gas 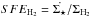 are presented in the upper panels of Figs. 16 and 17. The corresponding errors maps of SFEH2 are presented in the lower panels for NGC 4501 and NGC 4567/68, respectively.
are presented in the upper panels of Figs. 16 and 17. The corresponding errors maps of SFEH2 are presented in the lower panels for NGC 4501 and NGC 4567/68, respectively.
 |
Fig. 16 NGC 4501. Upper panel: star formation efficiency with respect to the molecular gas (SFEH2 = SFR/ ΣH2). Contour levels are (6, 12, 18, 24, 29, 36, 42, 48, 53, 59, 65, 72, 78, 84, 90, 96, 102, 107, 113, 119) × 10-2 Gyr-1. The white contour corresponds to SFEH2 = 0.5 Gyr-1 or a molecular gas depletion time of 2 Gyr. Lower panel: error of the star formation efficiency with respect to the molecular gas (dex). |
 |
Fig. 17 NGC 4567/6. Upper panel: NGC 4567/68 star formation efficiency with respect to the molecular gas (SFEH2 = SFR/ ΣH2. Contour levels are (6, 12, 18, 24, 29, 36, 42, 48, 53, 59, 65, 72, 78, 84, 90, 96, 102, 107, 113, 119) × 10-2 Gyr-1. The white contour corresponds to SFEH2 = 0.5 Gyr-1 or a molecular gas depletion time of 2 Gyr. Lower panel: error of the star formation efficiency with respect to the molecular gas (dex). |
The SFEH2 of NGC 4501 shows spatial variations within the disk from ~0.2 to ~1.5 Gyr-1 with most of the disk being close to the standard value of ~0.5 Gyr-1 (H2 consumption time of 2 Gyr). The high molecular SFEH2 regions correspond to regions where the molecular surface density is high, except in the very center of NGC 4501 where the SFEH2 is low and ΣH2 is high, as found by Sandstrom et al. (2013) in other nearby star-forming spiral galaxies. Most probably, the molecular gas surface density in the central region is overestimated by the assumed constant Xco factor (see Sect. 4.1 for details on Xco issues). At the northeastern edge, the SFEH2 is high with a low ΣH2. The southern edge of the disk shows a low SFEH2. This U-shaped region corresponds to regions of low ΣH2. Within the compressed western region, the region west of the galaxy center has an average SFEH2, whereas the northwestern part shows a low SFEH2.
The SFEH2 of NGC 4567/68 is on average higher than that of NGC 4501. The SFEH2 is lower in the northwestern tidally interacting part of the disk and in the southwest of NGC 4568. The SFEH2 is higher in the eastern part of NGC 4568 than in the western part of the disk. In the center and in the spirals arms of NGC 4567, the SFEH2 is lower than in the inter-arm regions.
The molecular star formation efficiency of NGC 4321 is almost constant over the entire galactic disk.
4. Discussion
4.1. XCO conversion factor
It has been found that techniques for estimating the H2 gas density according to CO emission are tricky as they rely mainly on three key theoretical assumptions (Dickman et al. 1986): (1) all GMCs have the same mean surface density (overlapping clouds can lead to a smaller value of ICO, which means that H2 mass can be underestimated); (2) the mean brightness temperature of the CO is well defined and does not vary with cloud size (CO emission is assumed to be optically thick); and (3) GMCs have a known mass spectrum and follow a size-linewidth relation. Moreover, the conversion factor is both expected and observed to vary with metallicity (van Dishoeck & Black 1988; Wolfire et al. 2010) leading to lower value at higher metallicity. Thus, in spiral galaxies the well-known metallicity gradient (Shaver et al. 1983, Pilkington et al. 2012 and references therein) may lead to an overestimation of ΣH2 in the central regions where the metallicity is expected to be higher. Sandstrom et al. (2013) investigated the radial variations of the conversion factor in a sample of 26 nearby star-forming galaxies. These authors found a significantly lower conversion factor in the nuclear regions of their sample. However, they found only a weak dependency of the conversion factor on metallicity. The conversion factor is also observed to sharply increase at metallicities below one-half solar. Nevertheless, the variation of XCO with metallicity is still poorly constrained, thus we prefer to use a simpler, first-order description of XCO. Bolatto et al. (2013) recommend the use of XCO(1−0) = 2 × 1020 cm-2(αCO(1−0) = 4.4 M⊙ (K km s-1 pc2)-1) with an estimated ± 30% uncertainty. Assuming a line ratio R21 = 0.8, this gives a value of αCO(2−1) = 5.5 M⊙ (K km s-1 pc2)-1 including He.
4.1.1. Star formation efficiency
The Kennicutt-Schmidt relation (KS) (Schmidt 1959, 1963 and Kennicutt 1989; 1998) links the gas reservoir of galaxies to the SFR using integrated values of SFR and Σg = ΣHI + ΣH2. Kennicutt (1998) found a non-linear relation (considering disk averages SFR and gas densities) 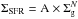 with N = 1.4 ± 0.15 from a sample of normal star-forming spirals and starburst galaxies. Many other works found N in the range of 1.0−2.0. Nevertheless, the use of Σg = ΣHI + ΣH2 in this relation is puzzling since stars form in molecular clouds and thus the information of the transition from HI to H2 is hidden when using Σg. These studies consider average SFR and gas surface densities.
with N = 1.4 ± 0.15 from a sample of normal star-forming spirals and starburst galaxies. Many other works found N in the range of 1.0−2.0. Nevertheless, the use of Σg = ΣHI + ΣH2 in this relation is puzzling since stars form in molecular clouds and thus the information of the transition from HI to H2 is hidden when using Σg. These studies consider average SFR and gas surface densities.
Other studies have found shallower power laws (N ~ 1) using only the molecular gas and SFR (Wong & Blitz 2002; Kennicutt et al. 2007; Bigiel et al. 2008; Leroy et al. 2008, 2013), Wong & Blitz (2002) consider azimuthally averaged surface densities, while Kennicutt et al. (2007), Bigiel et al. (2008), and Leroy et al. (2008; 2013) have studied the KS law at kpc or sub-kpc resolution.
A weaker correlation, or even no correlation, between atomic gas and SFR is found by Bigiel et al. (2008) in their sample of 18 nearby galaxies. Moreover, they observe that the atomic gas surface density in spirals and dwarf galaxies saturates at ~10M⊙ pc2 so that the correlation between atomic gas and SFR shows the saturation of the Hi line (Blitz & Rosolowsky 2006; Krumholz et al. 2009).
We investigated the spatially resolved SFR-Σg, SFR-ΣHI, and SFR-ΣH2 relations for the four galaxies (Fig. 18). Each point corresponds to a resolution element of 17″ or ~1.5 kpc. The resulting plots for each galaxy are presented in Appendix C (Fig. C.1−C.4 for NGC 4501, NGC 4567, NGC 4568, and NGC 4321, respectively).
 |
Fig. 18 NGC 4501, NGC 4567/8, and NGC 4321. Upper left panel: SFR as a function of ΣH2. Upper right panel: SFR as a function of total gas surface density. Lower left panel: SFR as a function of atomic gas surface density. Lower right: molecular fraction as a function of the ISM pressure Ptot. Typical errors bars are given for each relation. |
As expected, we do not see any clear correlation between SFR and ΣHI for NGC 4501 and NGC 4321. Instead, for NGC 4567/68 and NGC 4321 two regimes can be seen: (1) where log10(ΣHI) < 0.9 (8 M⊙ pc-2) and (2) where log10(ΣHI) > 0.9. The first regime shows a shallower slope than the second. In the central part of NGC 4501 the Hi surface density decreases radially to the center where no Hi is detected. Thus, the correlation between Hi and SFR breaks down in the central part of NGC 4501. This behavior is also observed in the field spiral galaxy NGC 628 (Leroy et al. 2008); the Hi surface density also strongly decreases toward the galaxy center where the gas is mostly molecular.
A power law was fitted to the SFR-ΣH2 and the SFR-Σg relations: 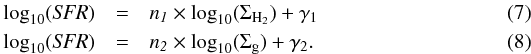 We used an MCMC approach for a linear regression with errors on both X and Y data (IDL routine LINMIX_ERR). This Bayesian approach gives the probability density distribution of both the slope and the offset of the fit. We also computed the Spearman rank correlation ρ for the two relations (Table 3). The uncertainty in the Spearman rank correlation ρ was estimated via the bootstrap method and by redistributing the data within the uncertainties. The errors obtained with the two methods agree within a factor of three. To be conservative, we only present the maximum of these error estimates.
We used an MCMC approach for a linear regression with errors on both X and Y data (IDL routine LINMIX_ERR). This Bayesian approach gives the probability density distribution of both the slope and the offset of the fit. We also computed the Spearman rank correlation ρ for the two relations (Table 3). The uncertainty in the Spearman rank correlation ρ was estimated via the bootstrap method and by redistributing the data within the uncertainties. The errors obtained with the two methods agree within a factor of three. To be conservative, we only present the maximum of these error estimates.
Results of fitting analysis I.
For NGC 4501 the central area was excluded from the fit since the conversion factor is not reliable and no Hi is detected in the center. For all three galaxies we found a power law index n1 for the molecular KS relation (ΣH2-SFR) in the range of 0.9−1, as has been found in other non-interacting galaxies. For the Σg-SFR relation a power law index n2 of 1.1−1.5 has been found. Moreover, the rms of the molecular and total gas KS relations are less then 20%. Those two results suggest that gas compression, either from ram pressure or from gravitational interaction, do not significantly change the KS relation.
For a direct comparison between galaxies, the SFR-ΣH2, SFR-ΣHI, SFR-Σg, and Rmol-Ptot relations are presented in Fig. 18. NGC 4321 shows a ~0.2 dex lower molecular SFEH2 and total SFEg. In the inner galactic disks (at high Ptot) of NGC 4567 and entire gas disk of NGC 4568 the molecular fraction is lower than that of the other galaxies.
4.1.2. Molecular fraction
Wong & Blitz (2002) and Blitz & Rosolowsky (2006; BR06) investigated the ISM pressure-molecular fraction relation with a pixel-by-pixel analysis . They fitted a relation between log (Ptot/kB) and log (Rmol), where kB is the Boltzmann constant. These authors find that the molecular fraction is correlated with the ISM pressure mostly in regions where Rmol> 1, 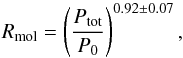 (9)with P0/kB = 3.5 ± 0.6 × 104 cm-3 K the pressure of the interstellar medium, where Rmol = 1. They found that P0 shows an offset for Hi-poor systems, such as interacting galaxies. The index of the power law does not show any systematic behavior when comparing the interacting to the non-interacting population in their sample. Blitz & Rosolowsky (2006) computed the ISM pressure in the following way:
(9)with P0/kB = 3.5 ± 0.6 × 104 cm-3 K the pressure of the interstellar medium, where Rmol = 1. They found that P0 shows an offset for Hi-poor systems, such as interacting galaxies. The index of the power law does not show any systematic behavior when comparing the interacting to the non-interacting population in their sample. Blitz & Rosolowsky (2006) computed the ISM pressure in the following way: 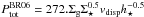 , with a mean gas velocity dispersion vdisp = 8 km s-1. We added the
, with a mean gas velocity dispersion vdisp = 8 km s-1. We added the 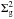 term to take the self-gravitation of the gas into account, and took vdisp = 10 km s-1. As did BR06, we used a constant conversion factor αco = 4.4 M⊙ (K km s-1 pc2)-1.
term to take the self-gravitation of the gas into account, and took vdisp = 10 km s-1. As did BR06, we used a constant conversion factor αco = 4.4 M⊙ (K km s-1 pc2)-1.
We investigated the spatially resolved molecular fraction-ISM pressure relation for NGC 4501, NGC 4567/68, and NGC 4321. The resulting relations are presented in Figs. C.1−C.4. We fitted the following power law to these relations: 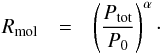 (10)The results of the fit and Spearman correlation coefficient ρ are given in Table 3. For NGC 4501 the power law index (α = 1.02 ± 0.27) is higher than (but within the uncertainty) the values of NGC 4567 (α = 0.70 ± 0.40), NGC 4568 (α = 0.76 ± 0.15), and NGC 4321 (α = 0.86 ± 0.09). Nevertheless, the rms is higher and the Spearman coefficient lower for NGC 4501 (ρ = 0.85) than that of the three other galaxies (ρ = 0.96, ρ = 0.91, ρ = 0.92). Our derived power law indices are in agreement with α = 0.8−0.9 found in other studies (Leroy et al. 2008; Wong & Blitz 2002; BR06).
(10)The results of the fit and Spearman correlation coefficient ρ are given in Table 3. For NGC 4501 the power law index (α = 1.02 ± 0.27) is higher than (but within the uncertainty) the values of NGC 4567 (α = 0.70 ± 0.40), NGC 4568 (α = 0.76 ± 0.15), and NGC 4321 (α = 0.86 ± 0.09). Nevertheless, the rms is higher and the Spearman coefficient lower for NGC 4501 (ρ = 0.85) than that of the three other galaxies (ρ = 0.96, ρ = 0.91, ρ = 0.92). Our derived power law indices are in agreement with α = 0.8−0.9 found in other studies (Leroy et al. 2008; Wong & Blitz 2002; BR06).
Pressure where ΣH2 = ΣHI.
Leroy et al. (2008) find a large scatter in both α and P0 in their sample when looking at galaxies individually. Considering the errors, the α and P0 values we find are in agreement with the values found by Wong & Blitz (2002), BR06 and Leroy et al. (2008).
By calculating the ISM pressure with the BR06 recipe (P = Ps and vturb = 8 km s-1), we find similar values for P0 in NGC 4501 and a somewhat higher but still compatible value of P0 for NGC 4321 (see Table 4). Nevertheless, when computing the ISM pressure using Ptot = Pg + Ps, we systematically find significantly higher values of P0 compared to the calculation with Ptot = Ps: P0 = 1.6 × 104 cm-3 K for NGC 4321 and NGC 4501, P0 = 2.5 × 104 cm-3 K for NGC 4567, and P0 = 3.2 × 104 cm-3 K for NGC 4568. We thus conclude that the gravitational potential of the gas is often significant compared to the stellar potential. In unperturbed gas-rich galaxies this typically occurs at R> 0.5 × R25. The values of P0 of the tidally interacting galaxies are significantly higher than those of NGC 4321 and NGC 4501.
The molecular fraction can be linked to the stellar and gas surface density. A linear relation between Rmol and Σ⋆ has been found by Leroy et al. (2008). These authors stated that “the simplest explanation is that present-day star formation roughly follows past star formation. A more aggressive interpretation is that the stellar potential well or feedback is critical to bring gas to high densities.” Moreover, we investigated the dependence of the molecular fraction Rmol on the total gas surface density Σg. We show the Rmol-Σ⋆ and Rmol-Σg relations in the upper panels of Fig. 19 for all four galaxies and in Appendix D for the individual galaxies (Figs. D.1−D.4 for NGC 4501, NGC 4567/68, and NGC 4321, respectively).
 |
Fig. 19 Upper left panel: molecular fraction as a function of stellar surface density. Upper right panel: molecular fraction as a function of the total gas surface density. Lower left panel: total gas as a function of molecular fraction divided by ISM pressure. Lower right: pressure due to the gravitational potential of the gas divided by the pressure due to the potential of the stellar disk (Pg/Ps) as a function of the molecular fraction divided by ISM pressure. Typical errors bars are given for each relation. |
The following power laws were fitted to the data: 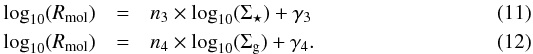 The results of these fits and the corresponding Spearman coefficients are presented in Table 5.
The results of these fits and the corresponding Spearman coefficients are presented in Table 5.
As has been found by Leroy et al. (2008), we observe an approximately linear correlation between the molecular fraction Rmol and the stellar surface density Σ⋆. A slightly steeper slope of n3 = 1.24 ± 0.26 is found for NGC 4501 compared to n3 = 1.03 ± 0.55 and n3 = 1.00 ± 0.22 for NGC 4567 and NGC 4568, respectively. We find somewhat, but not significantly higher Spearman coefficients and a lower rms for the Rmol-Σ⋆ relations compared to the Rmol-Σg relations (mean ⟨ ρ ⟩ sample = 0.930 for Rmol − Σ⋆ compared to a mean ⟨ ρ ⟩ sample = 0.895 for Rmol-Σg ). Thus, as found by Leroy et al. (2008) the best prediction of Rmol is determined by using Σ⋆ or Ptot.
4.1.3. Correlations implying ratios
Because a linear correlation exists between Rmol and Ptot, the correlations between the ratio Rmol/Ptot and observed quantities can be studied. Using the Toomre Q parameter defined as 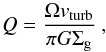 (13)where Ω = v(R) /R is the angular velocity and vturb the velocity dispersion of the gas. Substituting vturb = (QπGΣg) / Ω in Eq. (3) leads to
(13)where Ω = v(R) /R is the angular velocity and vturb the velocity dispersion of the gas. Substituting vturb = (QπGΣg) / Ω in Eq. (3) leads to 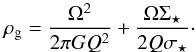 (14)Thus, ρg increases for decreasing Q or increasing gas self-gravitation. Since both Rmol and Ptot depend on ρg (see Eq. (3)), we expect to find a correlation between Rmol/Ptot and Q ∝ Ω / Σg if a constant velocity dispersion of the gas is assumed: Rmol/Ptot ∝ Q1.4 (see Sect. 5).
(14)Thus, ρg increases for decreasing Q or increasing gas self-gravitation. Since both Rmol and Ptot depend on ρg (see Eq. (3)), we expect to find a correlation between Rmol/Ptot and Q ∝ Ω / Σg if a constant velocity dispersion of the gas is assumed: Rmol/Ptot ∝ Q1.4 (see Sect. 5).
 |
Fig. 20 Rotation curves of the four galaxies from CO(2−1) data for NGC 4501 and NGC 4567/68 and from the two-parameter fit from Leroy et al. 2013 for NGC 4321. |
Results of fitting analysis II.
The rotation curves are derived from the IRAM CO(2−1) data along the major axis of the galaxies for NGC 4501 and NGC 4567/68. For NGC 4321 we used a two-parameter fit of the rotation curve from HERACLES and THINGS data vrot = vflat × (1−exp(−Rgal/lflat)) with Vflat = 283.7 km s-1 and lflat = 1.8 kpc (Leroy et al. 2013). These rotation curves are presented in Fig. 20.
We show Rmol/Ptot as a function of Q (assuming a turbulent velocity dispersion of 10 km s-1 for the gas) in the four galaxies (see Fig. 21). For the individual galaxies the plots are presented in Figs. E.1−E.4 for NGC 4501, NGC 4567, NGC 4568, and NGC 4321, respectively. We found a correlation in the four galaxies (Spearman coefficient 0.6 <ρ< 0.9). The mean slope is 1.0 and the typical rms of the correlations are less then 0.1 dex (a factor of 1.26). Thus, as expected, Rmol/Ptot is low where the gas is more self-gravitating and Q is low.
In a second step we looked at the relation between Rmol/Ptot and Pg/Ps to investigate the importance of self-gravitating gas (see Figs. D.1−D.4). We find an anti-correlation (Spearman ρ< −0.7 for NGC 4501 and NGC 4567/68) indicating that when the gas is at the limit of self-gravitation (high Pg/Ps), Rmol/Ptot is low because the increase in total pressure is more important than the increase in the molecular fraction. For NGC 4321 the pressure due to gravitational potential of the gas dominates everywhere (Pg/Ps> 1). The correlation is thus less well defined (Spearman ρ = 0.53).
The relation between the Toomre Q parameter and the molecular SFEH2 is shown in the lower panels of Figs. E.1−E.4. We find Spearman ρ coefficients of less then 0.1 (see Table 6) indicating that these quantities are not correlated within the galaxies.
For completeness we correlated Rmol/Ptot with Σg. We find no correlation for NGC 4501 and NGC 4321 (Spearman ρ ~ −0.3). For NGC 4567 and NGC 4568 we find an anti-correlation (Spearman ρ ~ −0.8). However, Rmol/Ptot is better correlated to the Toomre Q parameter than to Σg.
Finally, we tested the correlation between the two ratios SFEH2 and Rmol/Ptot. We find no clear sign of correlation when looking at galaxies individually (see left panel of Figs. E.1−E.4 and Table 6 for Spearman ρ coefficients).
We conclude that the ratio Rmol/Ptot is approximately proportional to the Toomre Q parameter. In regions of low Rmol/Ptot the ISM is self-gravitating. The ratio Rmol/Ptot can thus be used to detect regions where self-gravitation of the ISM is important.
Results of fitting analysis III.
4.2. Continuous regions deviating from the correlations
Continuous regions within the galaxies which deviate from the established correlations can potentially give insight into the physics of the ISM and the associated star formation. In NGC 4501, three spatial regions were selected with the following criteria (see Fig. 7):
-
regions with high atomic gas surface densities where ΣHI> 8 M⊙ pc-2 compared to the mean Hi surface density of 5 M⊙ pc-2 (blue squares in Fig. C.1 and blue contours in Fig. 7). These regions are located in the western and northwestern part of the disk and show (i) a higher SFEH2 (~1 Gyr-1) than the mean molecular SFEH2 of 0.61 Gyr-1 and (ii) a lower ratio of molecular fraction to ISM pressure (higher P0). The molecular fraction in this region is not lower than the mean at this radius. Within these regions the gas is nearly self-gravitating (see Fig. 14).
-
two low molecular SFE regions were selected with a SFEH2 below 0.49 Gyr-1, corresponding to 1σ below the average SFEH2 of NGC 4501: (i) a U-shaped region with a low SFEH2 in the southeast (green triangles and green contours in Fig. 7 and (ii) a northwestern low SFEH2 region (orange diamonds in Fig. C.1 and orange contours in Fig. 7). These two regions do not deviate from the SFR-Σg and the Rmol-Ptot relations, but show a ~0.1 dex higher Toomre Q (see lower panel of Fig. E.1) than the regions of high atomic gas surface density.
-
a high Rmol/Ptot region in the southwestern quadrant (red crosses in Fig. C.1 and red contours in Fig. 7). In this region Rmol deviates by more than 1σ from the Rmol-Ptot relation. The molecular SFEH2 is slightly but not significantly lower than the mean in this region. The ISM pressure is dominated by the stellar gravitational potential as Σg ~ 20M⊙ pc-2 (see Fig. 14)
In NGC 4568 two regions were selected with a molecular SFEH2 that is at least 1σ below the established correlation (SFEH2< 0.61 Gyr-1 compared to the mean SFEH2 of 0.74 Gyr-1):
-
the first region is located in the northwestern ridge of the interaction between the two galaxies (yellow contours and diamonds in Fig. 8 and C.3);
-
the second region is located in the south of NGC 4568 (purple triangles and contours in Figs. 8 and C.3).
Both regions have Hi surface densities of ~8.M⊙ pc-2. They do not deviate from the SFR-Σg or from the Rmol-Ptot relation. We note that the second low molecular SFEH2 region has a rather high Toomre Q (lower panel of Fig. E.3).
We conclude that continuous low SFEH2 regions show a somewhat higher Q compared to the mean, but they do not deviate from the Rmol/Ptot relation. On the other hand, regions where the gas is nearly self-gravitating have a lower Q, a higher molecular SFEH2, and a lower Rmol/Ptot with respect to the mean.
5. Analytical model
In the previous sections we investigate correlations of physical parameters within the galaxies. In a further step we now compare the correlations between the galaxies. The relations Rmol/Ptot-Q, SFEH2-Q, and SFEH2-Rmol/Ptot for the four galaxies are presented in the left panels of Fig. 21.
Results of fitting analysis VI.
 |
Fig. 21 Left (from top to bottom) for NGC 4501, NGC 4567/68, and NGC 4321: SFEH2-Rmol/Ptot, Q-Rmol/Ptot, and SFEH2-Q. Middle: relations corrected for the unknown velocity dispersion (see text). Right: with the SFEH2 of NGC 4501 corrected for the external pressure (leading to a 0.1 dex lower SFEH2). The dotted lines correspond to the correlations predicted by the analytical model: log (SFEH2) / log (Rmol/Ptot = −1, log (Rmol/Ptot) / log (Q) = 1.4, and log (SFEH2) / log (Q) = −1.5. The dashed lines correspond to correlations fitted to the data: log (SFEH2) / log (Rmol/Ptot = −0.5, log (Rmol/Ptot) / log (Q) = 1.5, and log (SFEH2) / log (Q) = −0.9. |
In NGC 4321 nearly half of the galaxy has values below Q = 1 indicating that either the turbulent velocity dispersion is underestimated (see Eq. (13)) or that the gas surface density, i.e., the CO-H2 conversion factor, is overestimated. Since the metallicity of NGC 4321 is comparable to that of NGC 4501 (Skillman et al. 1996), we do not expect a variation of the CO-H2 conversion factor between the galaxies. Thus, NGC 4321 most probably has a velocity dispersion in excess of 10 km s-1.
A clear correlation between Rmol/Ptot and Q is found in all galaxies individually where Rmol/Ptot increases with Q. Whereas NGC 4501 and NGC 4568 follow approximately the same relation, NGC 4321 and NGC 4567 show offsets of ~0.3 dex in opposite directions. We do not detect clear signs of correlation between the SFE and Q within the individual galaxies. The molecular SFE of NGC 4321 is about 0.2 dex lower than that of NGC 4501, NGC 4567, and NGC 4568. The resulting SFEH2-Rmol/Ptot is dominated by the offset of NGC 4321.
We used the analytical model described in Vollmer & Leroy (2011) to investigate these relations in detail. This analytical model considers the ISM (warm, cold, and molecular phases) as a single turbulent gas. This gas is assumed to be in vertical hydrostatic equilibrium (Eq. (3)). In this picture, the warm, cold, and molecular phases of the ISM are a single entity. Locally, the phase of the gas may depend on the local pressure, metallicity, stellar radiation field, stellar winds, and shocks. These factors are viewed as secondary by making a few simplifying assumptions.
The equilibrium between the different phases of the ISM and the equilibrium between turbulence and star formation depends on three local timescales: the turbulent crossing time tturb, the molecule formation timescale tmol, and the local free-fall timescale tff of a gas cloud.
The free-fall tff and the H2 formation timescale tmol are  with ρ the average gas density, φv the volume filling factor, G the gravitational constant, and Z ∝ 1 /α the metallicity computed assuming a closed box model:
with ρ the average gas density, φv the volume filling factor, G the gravitational constant, and Z ∝ 1 /α the metallicity computed assuming a closed box model: 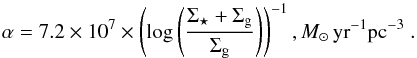 (17)The molecular fraction can be written as
(17)The molecular fraction can be written as 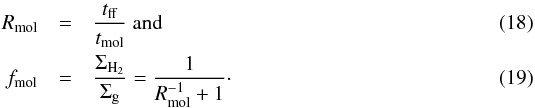 This gives ΣH2 = fmol × Σg and ΣHI = (1 − fmol) × Σg. In addition, we assumed a conversion factor NH2/ICO ∝ α ∝ Z-1.
This gives ΣH2 = fmol × Σg and ΣHI = (1 − fmol) × Σg. In addition, we assumed a conversion factor NH2/ICO ∝ α ∝ Z-1.
The model assumes that the gas is turbulent, so that the turbulent velocity dispersion exceeds the sound speed throughout the disk. This turbulence is driven by SNe which input their energy in turbulent eddies that have a characteristic length scale, ldriv, and a characteristic velocity, vturb. It is assumed that the energy input rate into the ISM due to SNe is cascaded to smaller scales without losses caused by turbulence. At scales smaller than the size of the largest self-gravitating clouds the energy is dissipated via cloud contraction and star formation. One can connect the energy input into the ISM by SNe directly to the SFR assuming a constant initial mass function independent of environment (Eq. (20)). In addition, we assume energy flux conservation (Eq. (20)), an SFR recipe (Eq. (21)), and a prescription for the turbulent viscosity (Eq. (23)):  Here vturb is the gas turbulent velocity dispersion, ldriv the turbulent driving length scale, ρ the disk mid-plane gas density, H the thickness of the gas disk, ξ = 4.6 × 10-8 (pc2 yr-1) the constant relating SN energy input into star formation, ν the viscosity, and
Here vturb is the gas turbulent velocity dispersion, ldriv the turbulent driving length scale, ρ the disk mid-plane gas density, H the thickness of the gas disk, ξ = 4.6 × 10-8 (pc2 yr-1) the constant relating SN energy input into star formation, ν the viscosity, and 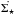 the star formation rate.
the star formation rate.
The resulting properties of the galactic gas disk depend on the stellar surface density Σ∗, the angular velocity Ω, the disk radius R, and three free parameters: (1) the mass accretion rate Ṁ = 2πνΣg of the disk; (2) the unknown scaling factor δ relating ldriv to the size of gravitationally bound clouds; and (3) the Toomre Q parameter of the disk. In addition, we allow for a varying Xco conversion factor.
This set of equations was solved radially and the relations Rmol/Ptot-Q, SFEH2-Q, and SFEH2-Rmol/Ptot) were computed. We assumed a constant turbulent velocity dispersion vturb and thus Q ∝ Ω / Σg. This assumption will be dropped later.
Leroy et al. (2008) and Schruba et al. (2011) observed variations in the molecular SFEH2 among galaxies in the HERACLES sample. Overall variations of the CO to H2 conversion factor can significantly affect the measured molecular SFEH2. To investigate the effect of XCO variations on the model results, we varied XCO by a factor of ± 0.3 dex. We assume a radial profile of Q, which is constant over most of the galactic disk and increases toward the center and at the edge of the disk (see Fig. 9 of Leroy et al. 2008 and Fig. 2 of Vollmer & Leroy 2011). For the CO-H2 conversion factor, we varied Q by a factor of ±0.3 dex. The model results are presented in Fig. 22.
 |
Fig. 22 Analytical model. Top left panel: SFEH2-Rmol/Ptot for three different values of Q (colors) and variation of Xco (dotted and dash-dotted lines). Top right: SFEH2-Q. Lower left: Q-Rmol/Ptot. Lower right: SFEH2-Q. |
In the framework of this model, we note that Rmol/Ptot is relatively insensitive to Xco variations. The scatter due to Xco variations is perpendicular to the SFE-Q relations, whereas it is highly inclined with respect to the Rmol/Ptot-Q relation. Thus, the scatter due to Xco variations easily masks an underlying correlation between SFE and Q. We found the following model slopes: log (SFEH2) / log (Q) = −1.5, log (Rmol/Ptot) / log (Q) = 1.4, and log (SFEH2) / log (Rmol/Ptot) = −1.0.
The analytical model helps to interpret the observed relations. The slopes of the individual observed Rmol/Ptot-Q relations are in agreement within the error bars with the prediction of the analytical model (middle panels of Figs. E.1−E.4). Except for NGC 4567, the individual observed SFE-Rmol/Ptot relations show the trend predicted by the analytical model (upper panels of Figs. E.1−E.4). However, the predicted slope of the SFE-Q relation is not observed in our data, because it is masked by variations of the CO-H2 conversion factor (lower panels of Figs. E.1−E.4). Thus, the slope of the observed Rmol/Ptot-Q relation (Fig. 21) is comparable to that of the analytical model for all galaxies (Fig. 22): Rmol/Ptot increases with increasing Toomre Q. However, there are global offsets between the galaxies in the Rmol/Ptot-Q relation (Fig. 21).
These offsets can be explained by the variation of the second free parameter of the analytical model, the mass accretion rate within the gas disk Ṁ. With increasing Ṁ the turbulent velocity dispersion of the disk vturb increases. To investigate the influence of the mass accretion rate on the observed relations, we varied the mass accretion rate by ± 0.3 dex (Fig. 23). The associated velocity dispersions are vturb = 10.7, 13.2, and 14.8 km s-1.
 |
Fig. 23 Analytical model. Top panel: molecular SFEH2 as a function of Rmol/Ptot for different mass accretion rates. The solid line corresponds to y = −0.65x + 1.92. Middle panel: Rmol/Ptot as a function of the turbulent velocity. The solid line corresponds to y = −2.8x + 13.58. Lower panel: SFEH2 as a function of the turbulent velocity. The solid line corresponds to y = 1.9x + 10.84. |
A linear fit to the model results yields log (Rmol/Ptot) = −2.8log (vturb) + 13.58, log (SFEH2) = 1.9log (vturb) + 10.84, and log (SFEH2) = −0.65log (Rmol/Ptot) + 1.92. Thus, for increasing vturb the SFEH2 increases and Rmol/Ptot decreases.
To correct the observed relations for the unknown velocity dispersion, we assumed a 0.1 dex higher velocity dispersion for NGC 4321 (so that the observed Toomre Q exceeds unity) and a 0.1 dex lower vturb for NGC 4567. These assumptions are chosen to align all galaxies in the Rmol/Ptot-Q relation (middle panels of Fig. 21). By doing this, the SFE of NGC 4321 increases and that of NGC 4567 decreases and a correlation between the SFEH2 − Q and SFEH2-Rmol/Ptot appears. As previously noted, the latter correlation is partially masked by variations of the CO-H2 conversion factor.
In the upper panel of Fig. 21 NGC 4501 seems to have a 0.1 dex higher molecular SFE than the other galaxies. This can be explain by adding an external pressure in the model (see Fig. 24).
 |
Fig. 24 Analytical model. Molecular SFEH2 as a function of Rmol/Ptot. The dashed line is for a galaxy with an external isotropic pressure applied to the ISM. |
By adding an external isotropic pressure P0 = 7 × 10-12 erg cm-3 the molecular SFE increases by 0.1 dex whereas Rmol/Ptot stays almost unchanged. Thus, if we assume an addition external pressure for NGC 4501 the observed correlations are reasonably close to the analytical predictions (right panels of Fig. 21): log (Rmol/Ptot) / log (Q) = 1.5, log (SFEH2) / log (Q) = −0.9, and log (SFEH2) / log (Rmol/Ptot) = −0.5.
We thus conclude that our observations are consistent with the prediction of the analytical model if different global velocity dispersions are assumed for the galaxies.
Is an external isotropic pressure of P0 = 7 × 10-12 erg cm-3 realistic for NGC 4501? The thermal pressure of the ICM can be estimated from the dynamical model. At the time of interest NGC 4501 is located at a distance of ~420 kpc from the cluster center. At this distance the ICM density is nICM ~ 3 × 10-4 cm-3. With an ICM temperature of TICM ~ 3 × 107 K, the thermal pressure of the ICM is Ptherm ~ 3 × 10-12 erg cm-3. In addition, ram pressure exerts an isotropic pressure on the windward face of the galaxy P0 ~ Pramsin(i), where i = 30° is the angle between the disk plane and the ram pressure wind direction. The dynamical model yields a ram pressure at the time of interest Pram = 10-11 erg cm-3 and thus P0 = 5 × 10-12 erg cm-3. To remove the gas from the outer edge of the gas disk a ram pressure of Pram ~ 2 × 10-10 erg cm-3 is needed. An isotropic pressure of P0 = 7 × 10-12 erg cm-3 is thus plausible for NGC 4501.
6. Dynamical model
In the following the relations discussed in the previous section are studied using a dynamical model for NGC 4501 and NGC 4567/68. We used the N-body code described in Vollmer et al. (2001), which consists of two components: a non-collisional component that simulates the stellar bulge/disk and the dark halo, and a collisional component that simulates the ISM. A scheme for star formation was implemented where stars were formed during cloud collisions and then evolved as non-collisional particles (see Vollmer et al. 2012).
The non-collisional component consists of 81 920 particles that simulate the galactic halo, bulge, and disk. The characteristics of the different galactic components are adapted to the observed properties. We adopted a model where the ISM is simulated as a collisional component, i.e., as discrete particles that possess a mass and a radius and can have inelastic collisions (sticky particles). The 20 000 particles of the collisional component represent gas cloud complexes that evolve in the gravitational potential of the galaxy. During the disk evolution, the particles can have inelastic collisions, the outcome of which (coalescence, mass exchange, or fragmentation) is simplified following Wiegel (1994). This results in an effective gas viscosity in the disk.
As the galaxy moves through the ICM, its clouds are accelerated by ram pressure. Within the galaxy’s inertial system, its clouds are exposed to a wind coming from a direction opposite to that of the galaxy’s motion through the ICM. The temporal ram pressure profile has the form of a Lorentzian, which is realistic for galaxies on highly eccentric orbits within the Virgo cluster (Vollmer et al. 2001). The effect of ram pressure on the clouds is simulated by an additional force on the clouds in the wind direction. Only clouds that are not protected by other clouds against the wind are affected. Since the gas cannot develop instabilities, the influence of turbulence on the stripped gas is not included in the model. The mixing of the intracluster medium into the ISM is very crudely approximated by a finite penetration length of the intracluster medium into the ISM, i.e., up to this penetration length the clouds undergo an additional acceleration caused by ram pressure.
The 3D dynamical model has the advantage of giving direct access to the volume density and velocity dispersion, two quantities that are very difficult to observe. The analytical model (Eqs. (15) and (19)) was used to compute ΣH2 and ΣHI in the simulations. In this dynamical model, there is no explicit energy dissipation and a large-scale compression is adiabatic.
In the simulations the SFR is traced by cloud-cloud collisions. When a collision between gas particles occurs, a new stellar particle is created and the information of the time of creation is stored. The FUV emission of a stellar particle is reconstructed using single stellar population models from STARBURST99 (Leitherer et al. 1999). Once the SFR derived from FUV flux and the molecular fraction are computed, the observable parameters (ΣHI, ΣH2, Σ⋆, Rmol, Ptot, Toomre Q, SFR, SFEH2) can be determined and model images and data cubes can be produced with the resolution of the observations.
6.1. NGC 4501 dynamical simulation
For NGC 4501, we made two simulations with identical temporal ram pressure profiles and different times of peak ram pressure (simulations A and B). With the delayed time of peak ram pressure we want to investigate the influence of galactic structure, i.e., spiral arms, on the resulting disturbed gas distribution. The resulting gas distribution of simulation A, molecular fraction, Rmol/Ptot, and molecular SFEH2 maps are presented in Figs. 25 and 26, respectively. The gas distribution and molecular fraction of simulation B are presented in Fig. 27.
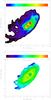 |
Fig. 25 NGC 4501 simulation A. Upper panel: total gas distribution. Lower panel: molecular fraction. |
 |
Fig. 26 NGC 4501 simulation A. Upper panel: SFEH2. Lower panel: Rmol/Ptot. |
 |
Fig. 27 NGC 4501 simulation B. Upper panel: total gas distribution. Lower panel: molecular fraction. |
As expected, the overall gas distribution of simulation B (Fig. 27) is very close to that of simulation A (Fig. 25). In simulation A a prominent gas spiral arm is found in the compressed region leading to a high surface density west of galaxy center; however, this is not the case for simulation B where only a small enhancement of the gas surface density is observed northwest of the galaxy center. We thus conclude that the detailed observed gas distribution depends on galactic structure, i.e., whether a spiral arm is located in the compressed region.
The simulated gas surface density of simulation A reproduces (i) the well-defined compressed western edge; (ii) the three low surface density spiral arms in the eastern part of the disk extending to the north; (iii) the regions of high gas surface density in the northern part of the disk; and (vi) the high molecular fraction in the western compressed side of the disk. The SFEH2 map is quantitatively reproduced, the higher SFEH2 in the northwestern quadrant of the disk is present in the simulation as is the U-shaped low SFEH2 region in the south. Moreover, the modeled SFEH2 is lower in the north of the compressed region as has been observed. However, the model does not reproduce the observed higher SFEH2 west of the center.
Within the western compression region, the reason for the low molecular star formation efficiency in the low surface density gas is the following. In a quiet model without interaction, the velocity dispersion of the gas particles is proportional to the square root of the gas density. Once the gas is compressed, it adapts its velocity dispersion to the new situation within a gas particle collision timescale. In the compressed regions of low surface density the particle density and thus the cloud collision frequency is smaller than the compression timescale and the equilibrium  is not yet reached at the time of interest. The molecular star formation efficiency is thus lower. On the other hand, in the high surface density region the collision timescale is short and the equilibrium is reached rapidly, i.e., the molecular star formation efficiency is unchanged. We believe that, in reality, the molecular star formation efficiency decreases once the compression becomes adiabatic, i.e., once the turbulent dissipation timescale tturb ~ ldriv/vturb is longer than the compression timescale tcomp = ρ/ (∂ρ/∂t). Even if the physics in the model and in reality that lead to a decreasing molecular star formation efficiency are quite different, the mechanisms are similar because in a collisional model the dissipation timescale is proportional to the collision timescale. Therefore, our simple dynamical model is able to predict regions of decreased molecular star formation efficiency due to adiabatic compression. In the future, we will test this prediction with simulations of NGC 4438 and the Taffy galaxies, where adiabatic compression decreases SFEmol by a factor of four to five (Braine et al. 2003; Vollmer et al. 2009, 2012).
is not yet reached at the time of interest. The molecular star formation efficiency is thus lower. On the other hand, in the high surface density region the collision timescale is short and the equilibrium is reached rapidly, i.e., the molecular star formation efficiency is unchanged. We believe that, in reality, the molecular star formation efficiency decreases once the compression becomes adiabatic, i.e., once the turbulent dissipation timescale tturb ~ ldriv/vturb is longer than the compression timescale tcomp = ρ/ (∂ρ/∂t). Even if the physics in the model and in reality that lead to a decreasing molecular star formation efficiency are quite different, the mechanisms are similar because in a collisional model the dissipation timescale is proportional to the collision timescale. Therefore, our simple dynamical model is able to predict regions of decreased molecular star formation efficiency due to adiabatic compression. In the future, we will test this prediction with simulations of NGC 4438 and the Taffy galaxies, where adiabatic compression decreases SFEmol by a factor of four to five (Braine et al. 2003; Vollmer et al. 2009, 2012).
The global model Rmol/Ptot is higher than observed. Nevertheless, we reproduce the main observational characteristics: (i) a low Rmol/Ptot in the northwestern quadrant and in the compressed region and (ii) a high Rmol/Ptot in the northwestern quadrant.
A pixel-by-pixel analysis was made for the NGC 4501 simulation A. The fitting results and the Spearman rank correlation coefficients ρ are presented in Table 8.
We find slopes in agreement with observations for the following relations: SFR−ΣH2, SFR−Σg, Rmol − Ptot, Rmol − Σ⋆, Rmol − Σg, and Rmol/Ptot − Q. However, the slope of the Rmol − Ptot relation is lower in our simulation of NGC 4501 (0.7) than the observed slope of 1.0. We found a correlation between Rmol/Ptot − Q (Spearman ρ = 0.9) with a slope of ~0.7 in agreement with the observed slope 0.84 ± 0.36.
We thus conclude that the dynamical simulation of NGC 4501 is in good agreement with observations.
6.2. NGC 4567/68 dynamical simulation
For simulations of colliding galaxies the parameter space (impact parameter, relative velocity, disk inclinations, prograde/retrograde encounter) is huge and degenerated. Our aim was to simulate NGC 4568 in a first place.
Results of the fitting analysis for the dynamical simulations of NGC 4501 and NGC 4567/68.
The size and rotation velocity of the model galaxies were adapted to the observed properties of NGC 4567 and NGC 4568. For the search of the orbit of NGC 4567 with respect to NGC 4568 we made several dozens of test simulations without a collisional component. We aimed at reproducing the position of NGC 4567 with respect to NGC 4568 together with a western compression ridge in NGC 4568. We have chosen a retrograde encounter with respect to NGC 4568. To produce a visible effect, the impact parameter is small (Δx = 6 kpc). The relative velocity at closest approach is Δv = 460 km s-1. NGC 4567 approaches NGC 4568 from the south/southwest. The time of interest is 10 Myr after the closest approach. In this stage the stellar disks overlap and a compression region forms in the western half of the disk of NGC 4568 and in the eastern half of the disk of NGC 4567. To avoid the overlap of the gas disk, we truncated the gas disk of NGC 4567. We are aware that this simulation does not perfectly reproduce the observed properties of the system. However, it can serve as a guideline to interpret observations.
The 3D simulations have the advantage that the two galaxies can be separated properly avoiding superposition effects. The maps of the gas distribution, molecular fraction, Rmol/Ptot, and molecular SFEH2 are presented in Figs. 28 and 29.
 |
Fig. 28 NGC 4567/68 simulation. Upper left panel: total gas distribution of both galaxies. Middle left panel: total gas distribution of NGC 4568m. Lower left panel: total gas distribution of NGC 4567m. Upper right panel: molecular fraction of both galaxies. Middle right panel: molecular fraction of NGC 4568m. Lower right panel: molecular fraction of NGC 4567m. |
 |
Fig. 29 NGC 4567/68 simulation. Upper left panel: SFEH2 of NGC 4567m. Lower left panel: molecular SFEH2 of NGC 4568m. Upper right panel: Rmol/Ph of NGC 4567m. Lower right panel: Rmol/Ph of NGC 4568m. |
In the following we name the model galaxies NGC 4567m and NGC 4568m. NGC 4568m shows a southern spiral arm curved to the west and an east-west asymmetry within the southern half of the disk; the southeastern part of the disk shows lower surface densities than the southwestern part. Thus, the southern part of the galactic disk of NGC 4568 (Fig. 8) is reproduced well by the model. The northern spiral arm of NGC 4568 is also reproduced by the model, but located somewhat farther to the west. The simulated gas surface density in the center of NGC 4568m is lower than the observed value by a factor of ~2. The total gas distribution of NGC 4567m does not show the observed spiral arms. The highest gas surface densities of NGC 4567m are not found in the center as in NGC 4567, but east of the center, where the gas is compressed by the tidal field. The overall gas surface density of NGC 4567m is significantly higher than that of NGC 4567.
The simulated overall distribution of the molecular fraction of NGC 4568m (middle right panel of Fig. 28) is in rough agreement with observations (Fig. 10): it is symmetric in the inner parts of the galactic disks. In addition, there is an excess of the molecular fraction in the southwestern part of the disk of NGC 4568m. The region between the galaxies shows a higher molecular fraction in the simulation than in the observations. The molecular fractions of NGC 4567m and NGC 4568m do not show the observed high values in the galaxy centers. This is due to a gas hole in the simulated galaxies that we introduced for computational reasons.
The simulated overall distribution of the molecular star formation efficiency of NGC 4568m (lower left panel of Fig. 29) is also in rough agreement with observations (Fig. 17). Only the model SFEH2 of the galaxy centers is significantly higher than observed. As observed, the SFEH2 distribution of NGC 4568m shows regions of higher SFEH2 on the eastern side of the galactic disk than on the western side. However, the absolute values of these regions are significantly lower in the model than in the observed galaxy. The observed low SFEH2 region in the southwestern edge of NGC 4568 is also present in the simulation.
The Rmol/Ptot distribution of NGC 4568m (lower right panel of Fig. 29) shows (i) a lower Rmol/Ptot in the center as has been observed and (ii) low Rmol/Ptot in the western part of NGC 4568m where the gas is compressed by the tidal field. The minimum Rmol/Ptot is located in the south of the compression ridge in NGC 4568m, whereas it is located in the northwest of the galactic disk in NGC 4568. The local minimum of Rmol/Ptot west of the center of NGC 4568m is not present in the observations. As has been observed, the region with the lowest Rmol/Ptot in the compression ridge has a normal molecular star formation efficiency. Owing to a strong tidal compression, the molecular fraction of NGC 4567m is much higher than that of NGC 4567. In addition, NGC 4567m lacks the observed spiral structure with a low molecular fraction in the spiral arms. In the light of the dynamical simulation we conclude that the relatively low molecular fraction of NGC 4567 and NGC 4568 compared to that of NGC 4321 is probably caused by tidal compression of the two galactic disks. The fact that the western side of the molecular fraction distribution of NGC 4568m does not reproduce the observed structure might again be due to galactic structure, as in NGC 4501. We will test this hypothesis within a subsequent project.
Thus, NGC 4567/68 is similar to NGC 4501 with respect to gas compression: the compression of the ISM increases the gas surface density and the molecular fraction, and makes Rmol/Ptot decrease. Moreover, the SFEH2 is normal, i.e., ~2 Gyr in high surface density compressed regions and somewhat lower (~0.2 dex) than the mean in regions of low gas surface density.
A pixel-by-pixel analysis was preformed in the same way as for the observations. The results of the fit and the Spearman rank correlation coefficient ρ are presented in Table 8.
We found steeper slopes of the molecular KS relation for NGC 4567 (1.5 compared to an observed slope of 0.9 ± 0.1) and for NGC 4568 (1.3 compared to 1.0 ± 0.1). For the SFR-Σg relation the model slopes are also steeper for NGC 4567 (1.5 compared to an observed slope of 1.1 ± 0.2) and for NGC 4568 (1.8 compared to 1.3 ± 0.1). The slope of the Rmol-Ptot correlation of NGC 4568 is reproduced well (slopes of ~0.7). For the Rmol − Σ⋆ and Rmol − Σg relations the slopes are on the lower side, but within the errors of the observed values. As observed, we found a correlation between Q − Rmol/Ptot with a comparable slope for NGC 4567 (0.8 compared to the observed slope of 0.7) and a much steeper slope for NGC 4568 (1.4 compared to 0.7).
We conclude that our observations are in reasonable agreement with observations.
6.3. What can be learned from the dynamical models
The standard slopes of the SFR-ΣH2, Rmol-Ptot, and Rmol-Σ∗ relations (e.g., Bigiel et al. 2008; Leroy et al. 2008; Blitz & Rosolowsky 2006) are reproduced by the dynamical models for NGC 4501 and NGC 4568. This makes us confident that the model predictions are reliable.
Furthermore, the dynamical models correctly reproduce the enhancement of the molecular fraction in the compressed regions of NGC 4501 and NGC 4568. Since in the analytical model the molecular fraction mainly depends on the gas density, we conclude that the dynamical model correctly predicts the enhancement of the gas density due to large-scale tidal or ram pressure compression.
As observed, the ratio between the molecular fraction divided by the total ISM pressure increases with Q: Rmol/Ptot ∝ Q1.5 in the dynamical models of NGC 4501 and NGC 4568 (Fig. 21). The model SFEH2 − Rmol/Ptot relation is also broadly consistent with our observations: SFEH2 ∝ (Rmol/Ptot)-0.5. However, the expected SFEH2 − Q correlation is not present in the dynamical models.
The dynamical model of NGC 4501 correctly reproduces the spatial distribution of all observed quantities; however, the model of NGC 4568 reproduces only the main characteristics of our observations without a good match between the modeled and observed spatial distribution. Nevertheless, both simulations show the same trends. A gravitationally induced ISM compression thus has the same consequences as the ram pressure compression that can also be observed in galactic spiral arms (NGC 4321): (i) an increasing gas surface density; (ii) an increasing molecular fraction; and (iii) a decreasing Rmol/Ptot in the compressed region due to the presence of nearly self-gravitating gas. The response of star formation and thus SFEH2 to compression is more complex. In regions of high gas surface density the molecular star formation efficiency stays close to the mean, whereas in regions of low gas surface density, SFEH2 decreases. We suggest that partial adiabatic compression is responsible for this behavior: in the high surface density gas the turbulent dissipation timescale is shorter than the compression timescale, the excess energy injected by compression can be dissipated, and the molecular star formation efficiency stays constant. On the other hand, in a compressed low surface density gas the compression timescale is shorter than the turbulent dissipation timescale, the molecular clouds become overpressured, and the star formation activity decreases leading to a decrease in SFEH2. Since we only observe a mild decrease in SFEH2 in the compressed low surface density gas, we conclude that in NGC 4501 and NGC 4568 the turbulent dissipation and compression timescales are not very different.
7. Summary and conclusions
New IRAM 30m HERA CO(2−1) observations of the Virgo spiral galaxies NGC 4501 and NGC 4567/68 are presented. The average rms noise level is less then 8 mK in the 10.4 km s-1 velocity channel at a resolution of 12″.
NGC 4501 shows signs of ongoing nearly edge-on ram pressure stripping. Molecular gas is detected extending over almost the entire optical disk (R25 = 4.35′). Moreover, the molecular gas distribution shows a well-defined southwestern edge where ram pressure compresses the ISM and a more diffuse northeastern edge. NGC 4501 shows a higher molecular fraction (Rmol = ΣH2/ ΣHI) in the compressed southwestern edge. In this particular region the compressed gas is at the limit of self-gravitation. The compression of the ISM does not change the overall molecular or the total gas Schmidt-Kennicutt relation at a kpc resolution (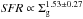 and
and 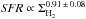 ). However, continuous regions of low molecular star formation efficiency are present in the disk: the molecular star formation efficiency (SFEH2) map is 0.2 dex lower in a U-shaped southeastern region and in the western part of the disk.
). However, continuous regions of low molecular star formation efficiency are present in the disk: the molecular star formation efficiency (SFEH2) map is 0.2 dex lower in a U-shaped southeastern region and in the western part of the disk.
For the gravitationally interacting Virgo spiral galaxy NGC 4568, we find that the southern molecular gas distribution is more extended than the northern distribution. Moreover, a peculiar spiral arm is detected in the south curving toward its companion, NGC 4567. Within the latter galaxy the molecular gas distribution shows a symmetric two-arm spiral structure. The molecular fraction increases in the region between the two galaxies. However, this could be due to projection effects. As in NGC 4501, the overall Schmidt-Kennicutt relations at ~1.5 kpc resolution are not affected by the compression of the ISM, but continuous regions of low/high molecular star formation efficiency are present in the disk: the SFEH2 is significantly higher than the mean in the eastern part of NGC 4568 and somewhat lower in the northwestern interacting part and in the southwestern edge of NGC 4568.
We note that when computing the total ISM pressure Ptot the self-gravitating gas term is not negligible in gas-rich galaxies and has been taken into account. The molecular fraction of the galaxies is correlated with the total ISM pressure 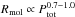 . The offset of the molecular fraction-ISM pressure relation is sensitive to the gas content of the galaxies. In agreement with Leroy et al. (2008), we found that the molecular fraction is better predicted by the stellar surface density than by the total gas surface density. We introduced a new parameter Rmol/Ptot, which is related to the gas self-gravitation and is poorly sensitive to variations of the CO-H2 conversion factor. For all galaxies in our sample Rmol/Ptot is correlated with the Toomre Q parameter Rmol/Ptot ∝ Q1.4−1.6. We found that galactic regions which are at the limit of self-gravitation (low Toomre Q and low Rmol/Ptot) tend to have higher SFEH2.
. The offset of the molecular fraction-ISM pressure relation is sensitive to the gas content of the galaxies. In agreement with Leroy et al. (2008), we found that the molecular fraction is better predicted by the stellar surface density than by the total gas surface density. We introduced a new parameter Rmol/Ptot, which is related to the gas self-gravitation and is poorly sensitive to variations of the CO-H2 conversion factor. For all galaxies in our sample Rmol/Ptot is correlated with the Toomre Q parameter Rmol/Ptot ∝ Q1.4−1.6. We found that galactic regions which are at the limit of self-gravitation (low Toomre Q and low Rmol/Ptot) tend to have higher SFEH2.
The analytical model described in Vollmer & Leroy (2011) was used to investigate the dependence of the molecular star formation efficiency on self-gravitation. The model correctly reproduces the correlations between Rmol/Ptot, SFEH2, and Q if different global turbulent velocity dispersions are assumed for the different galaxies. In addition, an isotropic external pressure might increase the molecular star formation efficiency slightly. We found that variations in the conversion factor can mask most of the correlation between SFEH2 and the Toomre Q parameter.
Dynamical simulations were used to compare the effects of ram pressure and tidal ISM compression. These models give direct access to the volume density.
The gas distribution of NGC 4501 is reproduced well by the model, as is the increase in the molecular fraction in the compressed part of the disk. We found that the gas distribution at the time of interest is sensitive to galactic structure, i.e., the position of the spiral arms with respect to the gas compression. The gas surface density is highest if a spiral arm is present in the compressed region. The simulated Rmol/Ptot map reproduces the observed map fairly well, with lower values in the compressed regions where the gas becomes almost self-gravitating. The model successfully reproduces the lower SFEH2 in the northwest and in the southwestern part of the compressed region. In these regions the collisional timescale is longer than the compression timescale. Thus, the gas cannot adapt its turbulent velocity fast enough to the new conditions in the compressed region. The effect of adiabatic compression is similar to this mechanism in our collisional model. We therefore suggest that adiabatic compression quenches star formation in low surface density parts of the compressed region by making the gas clouds overpressured.
For the gravitationally interacting system NGC 4567/68, the simulation correctly reproduces the gas distribution of NGC 4568. The model shows a small increase in the molecular fraction in the western compressed side of the disk as NGC 4501. The gravitationally induced compression increases the gas density and lowers Rmol/Ptot. Moreover, the lower SFEH2 in the southwestern part of the disk is reproduced in NGC 4568. In the light of the dynamical model, we confirm that NGC 4567/68 is a young interacting pair with a compression region west of the center of NGC 4568.
We conclude that, a gravitationally induced ISM compression has the same consequences as ram pressure compression, which can also be observed in galactic spiral arms: (i) an increasing gas surface density; (ii) an increasing molecular fraction; and (iii) a decreasing Rmol/Ptot in the compressed region due to the presence of nearly self-gravitating gas. The response of star formation and thus SFEH2 to compression is more complex. While in violent ISM-ISM collisions (Taffy galaxies, NGC 4438) the interaction decreases star formation by a factor of 4−5 (Braine et al. 2003; Vollmer et al. 2009, 2012), we only detect an SFEH2 variation of ~50% in the compressed regions of NGC 4501 and NGC 4568. We suggest that partial adiabatic compression is responsible for the quenched molecular star formation efficiency in all systems. The compression timescale is much smaller than the turbulent dissipation timescale in violent ISM-ISM collisions leading to a strong quenching of the star formation activity, whereas the two timescales are not very different in NGC 4501 and NGC 4568.
Acknowledgments
Based on IRAM observations. IRAM is supported by INSU/CNRS (France), MPG (Germany), and IGN (Spain).
References
- Bigiel, F., Leroy, A., Walter, F., et al. 2008, AJ, 136, 2846 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J., & Merrifield, M. 1998, Galactic Astronomy (Princeton University Press) [Google Scholar]
- Blitz, L., & Rosolowsky, E. 2006, ApJ, 650, 933 [NASA ADS] [CrossRef] [Google Scholar]
- Bolatto, A. D., Wolfire, M., & Leroy, A. K. 2013, ARA&A, 51, 207 [Google Scholar]
- Boquien, M., Boselli, A., Buat, V., et al. 2013, A&A, 554, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Braine, J., Davoust, E., Zhu, M., et al. 2003, A&A, 408, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cayatte, V., van Gorkom, J. H., Balkowski, C., & Kotanyi, C. 1990, AJ, 100, 604 [NASA ADS] [CrossRef] [Google Scholar]
- Cayatte, V., Kotanyi, C., Balkowski, C., & van Gorkom, J. H. 1994, AJ, 107, 1003 [NASA ADS] [CrossRef] [Google Scholar]
- Chung, A., van Gorkom, J. H., Kenney, J. D. P., Crowl, H., & Vollmer, B. 2009, AJ, 138, 1741 [NASA ADS] [CrossRef] [Google Scholar]
- Dickman, R. L., Snell, R. L., & Schloerb, F. P. 1986, ApJ, 309, 326 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G. 1989, ApJ, 338, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Galametz, M., Kennicutt, R. C., Calzetti, D., et al. 2013, MNRAS, 431, 1956 [NASA ADS] [CrossRef] [Google Scholar]
- Gavazzi, G., Boselli, A., Donati, A., Franzetti, P., & Scodeggio, M. 2003, A&A, 400, 451 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gunn, J. E., & Gott, III, J. R. 1972, ApJ, 176, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Hao, C.-N., Kennicutt, R. C., Johnson, B. D., et al. 2011, ApJ, 741, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Iono, D., Yun, M. S., & Ho, P. T. P. 2005, ApJS, 158, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, Jr., R. C. 1989, ApJ, 344, 685 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, Jr., R. C. 1998, ApJ, 498, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, Jr., R. C., Calzetti, D., Walter, F., et al. 2007, ApJ, 671, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, Jr., R. C., Lee, J. C., Funes José, G. S. J., Sakai, S., & Akiyama, S. 2008, ApJS, 178, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Kregel, M., van der Kruit, P. C., & de Grijs, R. 2002, MNRAS, 334, 646 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., McKee, C. F., & Tumlinson, J. 2009, ApJ, 693, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Leitherer, C., Schaerer, D., Goldader, J. D., et al. 1999, ApJS, 123, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Walter, F., Brinks, E., et al. 2008, AJ, 136, 2782 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Walter, F., Bigiel, F., et al. 2009, AJ, 137, 4670 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Walter, F., Sandstrom, K., et al. 2013, AJ, 146, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, D. C., Fanson, J., Schiminovich, D., et al. 2005, ApJ, 619, L1 [Google Scholar]
- Moore, B., Katz, N., Lake, G., Dressler, A., & Oemler, A. 1996, Nature, 379, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Moore, B., Lake, G., Quinn, T., & Stadel, J. 1999, MNRAS, 304, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Otmianowska-Mazur, K., & Vollmer, B. 2003, A&A, 402, 879 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peng, Y.-j., Lilly, S. J., Kovač, K., et al. 2010, ApJ, 721, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Pilkington, K., Few, C. G., Gibson, B. K., et al. 2012, A&A, 540, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sandstrom, K. M., Leroy, A. K., Walter, et al. 2013, ApJ, 777, 5S [NASA ADS] [CrossRef] [Google Scholar]
- Sarazin, C. L. 1986, Rev. Mod. Phys., 58, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, M. 1959, ApJ, 129, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, M. 1963, ApJ, 137, 758 [NASA ADS] [CrossRef] [Google Scholar]
- Schruba, A., Leroy, A. K., Walter, F., et al. 2011, AJ, 142, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Schuster, K.-F., Boucher, C., Brunswig, W., et al. 2004, A&A, 423, 1171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shaver, P. A., McGee, R. X., Newton, L. M., Danks, A. C., & Pottasch, S. R. 1983, MNRAS, 204, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Skillman, E. D., Kennicutt, Jr., R. C., Shields, G. A., & Zaritsky, D. 1996, ApJ, 462, 147 [NASA ADS] [CrossRef] [Google Scholar]
- van der Kruit, P. C. 1988, A&A, 192, 117 [NASA ADS] [Google Scholar]
- van der Kruit, P. C., & Searle, L. 1981, A&A, 95, 105 [NASA ADS] [Google Scholar]
- van Dishoeck, E. F., & Black, J. H. 1988, ApJ, 334, 771 [NASA ADS] [CrossRef] [Google Scholar]
- Vollmer, B. 2009, A&A, 502, 427 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vollmer, B., & Leroy, A. K. 2011, AJ, 141, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Vollmer, B., Cayatte, V., Balkowski, C., & Duschl, W. J. 2001, ApJ, 561, 708 [NASA ADS] [CrossRef] [Google Scholar]
- Vollmer, B., Soida, M., Beck, R., et al. 2007, A&A, 464, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vollmer, B., Soida, M., Chung, A., et al. 2008, A&A, 483, 89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vollmer, B., Braine, J., & Soida, M. 2012, A&A, 547, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vollmer, B., Soida, M., Beck, R., et al. 2013, A&A, 553, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Werner, M. W., Roellig, T. L., Low, F. J., et al. 2004, ApJS, 154, 1 [Google Scholar]
- Wolfire, M. G., Hollenbach, D., & McKee, C. F. 2010, ApJ, 716, 1191 [NASA ADS] [CrossRef] [Google Scholar]
- Wong, T., & Blitz, L. 2002, ApJ, 569, 157 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: CO(2−1) observations: rms
We computed the rms of the CO(2−1) spectra for each position. The CO(2−1) emission line signal in each spectrum was excluded from the rms calculation. The rms of the column density was defined as 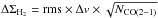 , where rms is the noise level of the CO spectra, Δv the spectral velocity resolution (10.4 km s-1), and NCO(2−1) the number of channels containing a CO(2−1) line signal. The CO(2−1) noise maps of NGC 4501 and NGC 4567/68 (Fig. A.1) do not show any systematic behavior.
, where rms is the noise level of the CO spectra, Δv the spectral velocity resolution (10.4 km s-1), and NCO(2−1) the number of channels containing a CO(2−1) line signal. The CO(2−1) noise maps of NGC 4501 and NGC 4567/68 (Fig. A.1) do not show any systematic behavior.
 |
Fig. A.1 CO(2−1) rms noise maps of NGC 4501 (upper panel) and NGC 4567/68 (lower panel). The color bar is in units of mK. The spectral velocity resolution is 10.4 km s-1. |
Appendix B: SFR comparison
Appendix B.1: Total IR
The FUV heated dust emission can be traced using the total infrared emission (TIR; see Hao et al. 2011 and Galametz et al. 2013). We tried three different recipes to compute the TIR emission:
-
TIR1 based on the 3.6, 8, 24, and 70 μm from Spitzer (Eqs. (B.1)−(B.3));
-
TIR2 based on the 3.6, 24 μm from Spitzer and 100, 160 μm from Herschel PACS (Eq. (B.4));
-
TIR3 based on the 3.6, 24, and 70 μm from Spitzer and 100, 160 μm from Herschel PACS (Eq. (B.5)).
 The TIR1, TIR2, and TIR3 recipes of NGC 4501, NGC 4567/68, and NGC 4321 were compared in a pixel-by-pixel analysis with the 24 μm emission (Fig. B.1). The three TIR recipes tightly correlate with the 24 μm emission (Iν(24 μm)). The rms of these correlations are smaller than 0.09 dex.
The TIR1, TIR2, and TIR3 recipes of NGC 4501, NGC 4567/68, and NGC 4321 were compared in a pixel-by-pixel analysis with the 24 μm emission (Fig. B.1). The three TIR recipes tightly correlate with the 24 μm emission (Iν(24 μm)). The rms of these correlations are smaller than 0.09 dex.
 |
Fig. B.1 Total infrared (TIR) correlations with Iν(24 μm) for NGC 4567/68, NGC 4501, and NGC 4321. The pixel size is 18″. Residuals of the relations Iν(24 μm) × 3.2 × 10-3/ 8.1 × 10-2 (see Eq. (6)) as a function of TIR1 × 0.46, TIR2 × 0.46, and TIR3 × 0.46 (see Eq. (B.6)). The dashed and dotted lines are at ± 1 × rms in the same color as the corresponding galaxy. |
Appendix B.2: SFR from Hα
We calculated the star formation rate based on Hα emission: 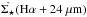 (Eq. (B.7)),
(Eq. (B.7)), 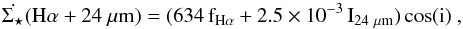 (B.7)where fHα is the Hα flux density (ergs s-1 cm-2 Å-1) corrected for Nii line contamination (NII / Hα ratio of 0.54; see Kennicutt et al. 2008). The Hα data for NGC 4501, NGC 4567/68, and NGC 4321 are part of the GOLD-mine database (Gavazzi et al. 2003).
(B.7)where fHα is the Hα flux density (ergs s-1 cm-2 Å-1) corrected for Nii line contamination (NII / Hα ratio of 0.54; see Kennicutt et al. 2008). The Hα data for NGC 4501, NGC 4567/68, and NGC 4321 are part of the GOLD-mine database (Gavazzi et al. 2003).  and
and 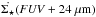 were compared pixel-by-pixel (see Fig. B.2). A significant deviation is found in the center of NGC 4501 where the
were compared pixel-by-pixel (see Fig. B.2). A significant deviation is found in the center of NGC 4501 where the  derived from Hα exceeds that derived from the FUV. The rms of the linear relations are 0.056 dex, 0.023 dex, and 0.054 dex for NGC 4501, NGC 4567/68, and NGC 4321, respectively.
derived from Hα exceeds that derived from the FUV. The rms of the linear relations are 0.056 dex, 0.023 dex, and 0.054 dex for NGC 4501, NGC 4567/68, and NGC 4321, respectively.
 |
Fig. B.2 Comparison of star formation rates computed with FUV+24 μm and Hα+24 μm. Residuals of the relations in dex for NGC 4501, NGC 4567/68, and NGC 4321. The continuous line corresponds to a linear relation between the two SFR indicators, while the dashed and dotted lines correspond to ± 1σ for each galaxy. |
Appendix C: Individual plots I
 |
Fig. C.1 NGC 4501. Upper left panel: SFR as a function of ΣH2. Upper right panel: SFR as a function of total gas surface density. Lower left panel: SFR as a function of atomic gas surface density. Lower right: molecular fraction versus ISM pressure Ptot. The orange error bars take into account systematic uncertainties in the calibration of the SFR (0.1 dex) and the NH2/ICO conversion factor (0.3 dex). |
 |
Fig. C.2 NGC 4567. Upper left panel: SFR as a function of ΣH2. Upper right panel: SFR as a function of total gas surface density. Lower left panel: SFR as a function of atomic gas surface density. Lower right panel: molecular fraction versus the ISM pressure Ptot. The orange error bars take into account systematic uncertainties in the calibration of the SFR (0.1 dex) and the NH2/ICO conversion factor (0.3 dex). |
 |
Fig. C.3 NGC 4568. Upper left panel: SFR as a function of ΣH2. Upper right panel: SFR as a function of total gas surface density. Lower left panel: SFR as a function of atomic gas surface density. Lower right panel: molecular fraction versus the ISM pressure Ptot. The orange error bars take into account systematic uncertainties in the calibration of the SFR (0.1 dex) and the NH2/ICO conversion factor (0.3 dex). |
 |
Fig. C.4 NGC 4321. Upper left panel: SFR as a function of ΣH2. Upper right panel: SFR as a function of total gas surface density. Lower left panel: SFR as a function of atomic gas surface density. Lower right panel: molecular fraction versus the ISM pressure Ptot. The orange error bars take into account systematic uncertainties in the calibration of the SFR (0.1 dex) and the NH2/ICO conversion factor (0.3 dex). |
Appendix D: Individual plots II
 |
Fig. D.1 NGC 4501. Upper left panel: molecular fraction as a function of stellar surface density. Upper right panel: molecular fraction as a function of the total gas surface density. Lower left panel: total gas as a function of molecular fraction divided by ISM pressure. Lower right panel: pressure due to the gravitational potential of the gas divided by the pressure due to the potential of the stellar disk (Pg/Ps) as a function of the molecular fraction divided by ISM pressure. For clarity we only show a few errors bars. |
 |
Fig. D.2 NGC 4567. Same panels as in Fig. D.1. |
 |
Fig. D.3 NGC 4568. Same panels as in Fig. D.1. |
 |
Fig. D.4 NGC 4321. Same panels as in Fig. D.1 |
Appendix E: Individual plots III
 |
Fig. E.1 NGC 4501. Upper panel: SFEH2 as a function of the molecular fraction over ISM pressure. Middle panel: Toomre Q as a function of Rmol/Ptot. Lower panel: SFEH2 as a function of Toomre Q. |
All Tables
Results of the fitting analysis for the dynamical simulations of NGC 4501 and NGC 4567/68.
All Figures
 |
Fig. 1 NGC 4501: 6 cm polarized emission Vollmer et al. 2003 on Hα emission (from GOLDMINE Gavazzi et al. 2003). |
| In the text | |
 |
Fig. 2 NGC 4567/68: 6 cm polarized emission (Vollmer et al. 2013) on Hα emission (from GOLDMINE Gavazzi et al. 2003). |
| In the text | |
 |
Fig. 3 NGC 4501: CO(2−1) emission map. Contour levels are 1.0, 2.25, 4.0, 6.25, 9.0, 12.25, 16.0, 20.25, 25.0, and 30.25 K km s-1. The white contour corresponds to 0.1 K km s-1. |
| In the text | |
 |
Fig. 4 NGC 4501: CO(2−1) emission on SDSS g′-band image. Contour levels are 1.0, 2.25, 4.0, 6.25, 9.0, 12.25, 16.0, 20.25, 25.0, and 30.25) K km s-1. |
| In the text | |
 |
Fig. 5 NGC 4567/68: CO(2−1) emission map. Contours are 1.0, 2.25, 4.0, 6.25, 9.0, 12.25, 16.0, 20.25, 25.0, 30.25, 36.0, 42.25, 49.0, 56.25, and 64.0) K km s-1. The white contour corresponds to 0.1 K km s-1. |
| In the text | |
 |
Fig. 6 NGC 4567/68: CO(2−1) emission on SDSS g′-band image. Contour levels are 1.0, 2.25, 4.0, 6.25, 9.0, 12.25, 16.0, 20.25, 25.0, 30.25, 36.0, 42.25, 49.0, 56.25, and 64.0 K km s-1. |
| In the text | |
 |
Fig. 7 NGC 4501 total gas surface density Σg = ΣHI + ΣH2. The thin black contour levels are 4.0, 4.36, 5.44, 7.24, 9.76, 13.0, 16.96, 21.64, 27.04, 33.16, 40.0, 47.56, 55.84, 64.84, and 74.56 M⊙ pc-2. The resolution is 17″. Blue contour: high atomic gas surface density regions. Green contour: southern “U” shaped region with low SFEH2. Orange contour: northern low SFEH2 region. Red contour: high Rmol/Ptot region. Purple contour: central region defined from the stellar surface density excluded from the fit. The beam size is shown in the lower right corner. |
| In the text | |
 |
Fig. 8 NGC 4567/68 total gas surface density map. The thin black contours are 4, 5, 8, 13, 20, 29, 40, 53, 68, 85, 104, 125, 148, 173, and 200 M⊙ pc-2. The resolution is 17″. Yellow contour: northern low SFEH2 region. Purple contour: southern low SFEH2 region. The beam size is shown in the lower right corner. |
| In the text | |
 |
Fig. 9 NGC 4501 molecular fraction Rmol = ΣH2/ ΣHI. The resolution is 17″. Contour levels are 0.04, 0.06, 0.1, 0.16, 0.25, 0.4, 0.63, 1, 1.58, 2.51, 3.98, 6.31, 10, 15.84, and 25.11. |
| In the text | |
 |
Fig. 10 NGC 4567/68 molecular fraction Rmol = ΣH2/ ΣHI. The resolution is 17″. Contour levels are 0.04, 0.06, 0.1, 0.16, 0.25, 0.4, 0.63, 1, 1.58, 2.51, 3.98, 6.31, 10, 15.84, and 25.11. |
| In the text | |
 |
Fig. 11 NGC 4501. Upper panel: molecular fraction divided by the ISM pressure Rmol/Ptot. The resolution is 17″. The ISM pressure and the molecular fraction are deprojected. Contour levels are (2, 2.5, 3.2, 4, 5, 6.3, 7.9, 10, 12.6, 15.8) × 10-5 cm3 K-1. Lower panel: error on Rmol/Ptot (in dex). The thick black contour corresponds to 0.5 dex. Contour levels are 0.3, 0.33, 0.37, 0.4, 0.43, 0.47, 0.5, 0.53, 0.57, and 0.6 dex. |
| In the text | |
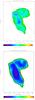 |
Fig. 12 NGC 4567/68. Upper panel: molecular fraction divided by the ISM pressure Rmol/Ptot. The resolution is 17″. The ISM pressure and the molecular fraction are deprojected. Contour levels are (1.2, 1.4, 1.7, 2.1, 2.5, 3, 3.6, 4.4, 5.2, 6.3) × 10-5 cm3 K-1. Lower panel: error on Rmol/Ptot (in dex). The thick black contour corresponds to 0.5 dex. Contour levels are 0.3, 0.33, 0.37, 0.4, 0.43, 0.47, 0.5, 0.53, 0.57, and 0.6 dex. |
| In the text | |
 |
Fig. 13 NGC 4321. Upper panel: molecular fraction divided by the ISM pressure Rmol/Ptot. The resolution is 17″. The ISM pressure and the molecular fraction are deprojected. Contour levels are (1.2, 1.4, 1.7, 2.1, 2.5, 3, 3.6, 4.4, 5.2, 6.3) × 10-5 cm3 K-1. Lower panel: error on Rmol/Ptot (in dex). The thick black contour corresponds to 0.5 dex. Contour levels are 0.1, 0.13, 0.17, 0.2, 0.23, 0.27, 0.3, 0.33, 0.36, and 0.4 dex. |
| In the text | |
 |
Fig. 14 NGC 4501: ISM pressure due to the gravitational potential of the gas divided by the ISM pressure due to the stellar potential (Pg/Ps). The resolution is 17″. Contour levels are (0.33, 0.67, 1, 1.33, 1.67, 2, 2.33, 2.67, 3, 3.33, 3.67, 4, 4.33, 4.67, 5, 5.33, 5.67, 6, 6.33, 6.67) × 10-1. |
| In the text | |
 |
Fig. 15 NGC 4567/68: ISM pressure due to the gravitational potential of the gas divided by the ISM pressure due to the stellar potential (Pg/Ps). The resolution is 17″. Contour levels are (0.33, 0.67, 1, 1.33, 1.67, 2, 2.33, 2.67, 3, 3.33, 3.67, 4, 4.33, 4.67, 5, 5.33, 5.67, 6, 6.33, 6.67, 7, 7.33, 7.67, 8, 8.33) × 10-1. |
| In the text | |
 |
Fig. 16 NGC 4501. Upper panel: star formation efficiency with respect to the molecular gas (SFEH2 = SFR/ ΣH2). Contour levels are (6, 12, 18, 24, 29, 36, 42, 48, 53, 59, 65, 72, 78, 84, 90, 96, 102, 107, 113, 119) × 10-2 Gyr-1. The white contour corresponds to SFEH2 = 0.5 Gyr-1 or a molecular gas depletion time of 2 Gyr. Lower panel: error of the star formation efficiency with respect to the molecular gas (dex). |
| In the text | |
 |
Fig. 17 NGC 4567/6. Upper panel: NGC 4567/68 star formation efficiency with respect to the molecular gas (SFEH2 = SFR/ ΣH2. Contour levels are (6, 12, 18, 24, 29, 36, 42, 48, 53, 59, 65, 72, 78, 84, 90, 96, 102, 107, 113, 119) × 10-2 Gyr-1. The white contour corresponds to SFEH2 = 0.5 Gyr-1 or a molecular gas depletion time of 2 Gyr. Lower panel: error of the star formation efficiency with respect to the molecular gas (dex). |
| In the text | |
 |
Fig. 18 NGC 4501, NGC 4567/8, and NGC 4321. Upper left panel: SFR as a function of ΣH2. Upper right panel: SFR as a function of total gas surface density. Lower left panel: SFR as a function of atomic gas surface density. Lower right: molecular fraction as a function of the ISM pressure Ptot. Typical errors bars are given for each relation. |
| In the text | |
 |
Fig. 19 Upper left panel: molecular fraction as a function of stellar surface density. Upper right panel: molecular fraction as a function of the total gas surface density. Lower left panel: total gas as a function of molecular fraction divided by ISM pressure. Lower right: pressure due to the gravitational potential of the gas divided by the pressure due to the potential of the stellar disk (Pg/Ps) as a function of the molecular fraction divided by ISM pressure. Typical errors bars are given for each relation. |
| In the text | |
 |
Fig. 20 Rotation curves of the four galaxies from CO(2−1) data for NGC 4501 and NGC 4567/68 and from the two-parameter fit from Leroy et al. 2013 for NGC 4321. |
| In the text | |
 |
Fig. 21 Left (from top to bottom) for NGC 4501, NGC 4567/68, and NGC 4321: SFEH2-Rmol/Ptot, Q-Rmol/Ptot, and SFEH2-Q. Middle: relations corrected for the unknown velocity dispersion (see text). Right: with the SFEH2 of NGC 4501 corrected for the external pressure (leading to a 0.1 dex lower SFEH2). The dotted lines correspond to the correlations predicted by the analytical model: log (SFEH2) / log (Rmol/Ptot = −1, log (Rmol/Ptot) / log (Q) = 1.4, and log (SFEH2) / log (Q) = −1.5. The dashed lines correspond to correlations fitted to the data: log (SFEH2) / log (Rmol/Ptot = −0.5, log (Rmol/Ptot) / log (Q) = 1.5, and log (SFEH2) / log (Q) = −0.9. |
| In the text | |
 |
Fig. 22 Analytical model. Top left panel: SFEH2-Rmol/Ptot for three different values of Q (colors) and variation of Xco (dotted and dash-dotted lines). Top right: SFEH2-Q. Lower left: Q-Rmol/Ptot. Lower right: SFEH2-Q. |
| In the text | |
 |
Fig. 23 Analytical model. Top panel: molecular SFEH2 as a function of Rmol/Ptot for different mass accretion rates. The solid line corresponds to y = −0.65x + 1.92. Middle panel: Rmol/Ptot as a function of the turbulent velocity. The solid line corresponds to y = −2.8x + 13.58. Lower panel: SFEH2 as a function of the turbulent velocity. The solid line corresponds to y = 1.9x + 10.84. |
| In the text | |
 |
Fig. 24 Analytical model. Molecular SFEH2 as a function of Rmol/Ptot. The dashed line is for a galaxy with an external isotropic pressure applied to the ISM. |
| In the text | |
 |
Fig. 25 NGC 4501 simulation A. Upper panel: total gas distribution. Lower panel: molecular fraction. |
| In the text | |
 |
Fig. 26 NGC 4501 simulation A. Upper panel: SFEH2. Lower panel: Rmol/Ptot. |
| In the text | |
 |
Fig. 27 NGC 4501 simulation B. Upper panel: total gas distribution. Lower panel: molecular fraction. |
| In the text | |
 |
Fig. 28 NGC 4567/68 simulation. Upper left panel: total gas distribution of both galaxies. Middle left panel: total gas distribution of NGC 4568m. Lower left panel: total gas distribution of NGC 4567m. Upper right panel: molecular fraction of both galaxies. Middle right panel: molecular fraction of NGC 4568m. Lower right panel: molecular fraction of NGC 4567m. |
| In the text | |
 |
Fig. 29 NGC 4567/68 simulation. Upper left panel: SFEH2 of NGC 4567m. Lower left panel: molecular SFEH2 of NGC 4568m. Upper right panel: Rmol/Ph of NGC 4567m. Lower right panel: Rmol/Ph of NGC 4568m. |
| In the text | |
 |
Fig. A.1 CO(2−1) rms noise maps of NGC 4501 (upper panel) and NGC 4567/68 (lower panel). The color bar is in units of mK. The spectral velocity resolution is 10.4 km s-1. |
| In the text | |
 |
Fig. B.1 Total infrared (TIR) correlations with Iν(24 μm) for NGC 4567/68, NGC 4501, and NGC 4321. The pixel size is 18″. Residuals of the relations Iν(24 μm) × 3.2 × 10-3/ 8.1 × 10-2 (see Eq. (6)) as a function of TIR1 × 0.46, TIR2 × 0.46, and TIR3 × 0.46 (see Eq. (B.6)). The dashed and dotted lines are at ± 1 × rms in the same color as the corresponding galaxy. |
| In the text | |
 |
Fig. B.2 Comparison of star formation rates computed with FUV+24 μm and Hα+24 μm. Residuals of the relations in dex for NGC 4501, NGC 4567/68, and NGC 4321. The continuous line corresponds to a linear relation between the two SFR indicators, while the dashed and dotted lines correspond to ± 1σ for each galaxy. |
| In the text | |
 |
Fig. C.1 NGC 4501. Upper left panel: SFR as a function of ΣH2. Upper right panel: SFR as a function of total gas surface density. Lower left panel: SFR as a function of atomic gas surface density. Lower right: molecular fraction versus ISM pressure Ptot. The orange error bars take into account systematic uncertainties in the calibration of the SFR (0.1 dex) and the NH2/ICO conversion factor (0.3 dex). |
| In the text | |
 |
Fig. C.2 NGC 4567. Upper left panel: SFR as a function of ΣH2. Upper right panel: SFR as a function of total gas surface density. Lower left panel: SFR as a function of atomic gas surface density. Lower right panel: molecular fraction versus the ISM pressure Ptot. The orange error bars take into account systematic uncertainties in the calibration of the SFR (0.1 dex) and the NH2/ICO conversion factor (0.3 dex). |
| In the text | |
 |
Fig. C.3 NGC 4568. Upper left panel: SFR as a function of ΣH2. Upper right panel: SFR as a function of total gas surface density. Lower left panel: SFR as a function of atomic gas surface density. Lower right panel: molecular fraction versus the ISM pressure Ptot. The orange error bars take into account systematic uncertainties in the calibration of the SFR (0.1 dex) and the NH2/ICO conversion factor (0.3 dex). |
| In the text | |
 |
Fig. C.4 NGC 4321. Upper left panel: SFR as a function of ΣH2. Upper right panel: SFR as a function of total gas surface density. Lower left panel: SFR as a function of atomic gas surface density. Lower right panel: molecular fraction versus the ISM pressure Ptot. The orange error bars take into account systematic uncertainties in the calibration of the SFR (0.1 dex) and the NH2/ICO conversion factor (0.3 dex). |
| In the text | |
 |
Fig. D.1 NGC 4501. Upper left panel: molecular fraction as a function of stellar surface density. Upper right panel: molecular fraction as a function of the total gas surface density. Lower left panel: total gas as a function of molecular fraction divided by ISM pressure. Lower right panel: pressure due to the gravitational potential of the gas divided by the pressure due to the potential of the stellar disk (Pg/Ps) as a function of the molecular fraction divided by ISM pressure. For clarity we only show a few errors bars. |
| In the text | |
 |
Fig. D.2 NGC 4567. Same panels as in Fig. D.1. |
| In the text | |
 |
Fig. D.3 NGC 4568. Same panels as in Fig. D.1. |
| In the text | |
 |
Fig. D.4 NGC 4321. Same panels as in Fig. D.1 |
| In the text | |
 |
Fig. E.1 NGC 4501. Upper panel: SFEH2 as a function of the molecular fraction over ISM pressure. Middle panel: Toomre Q as a function of Rmol/Ptot. Lower panel: SFEH2 as a function of Toomre Q. |
| In the text | |
 |
Fig. E.2 NGC 4567. Same panels as in Fig. E.1. |
| In the text | |
 |
Fig. E.3 NGC 4568. Same panels as in Fig. E.1. |
| In the text | |
 |
Fig. E.4 NGC 4321. Same panels as in Fig. E.1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


