| Issue |
A&A
Volume 587, March 2016
|
|
|---|---|---|
| Article Number | A21 | |
| Number of page(s) | 10 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201526745 | |
| Published online | 11 February 2016 | |
Laue lens for astrophysics: Extensive comparison between mosaic, curved, and quasi-mosaic crystals
Department of Physics and Earth Science, INFNUniversity of
Ferrara, and National Institute of Optics CNR INO-sensor, via Saragat 1/c, 44122 Ferrara Italy
Received: 15 June 2015
Accepted: 5 December 2015
With the aim of concentrating hard X- and γ-rays coming from celestial sources in the 100–1000 keV energy range, the concept of Laue lens was introduced more than 50 years ago. Crystals are the core of a Laue lens, since they focus the incoming X-rays through Bragg diffraction. For concrete applications, crystals characterized by high diffraction reflectivity are needed along with high-resolution focusing of diffracted photons. Here, an extensive comparison of the types of crystals proposed so far is presented. In order to quantify the focusing capability of a Laue lens based on these crystals, a simulation of a single-ring Laue lens based on the considered optical elements is presented. Finally, the breakthrough in the panorama of diffracting crystals is discussed.
Key words: techniques: high angular resolution / telescopes / techniques: imaging spectroscopy
© ESO, 2016
1. Introduction
Manipulation and focusing of hard X- and γ-rays in the 100–1000 keV energy range represents an increasingly significant topic for the astrophysics community. However, it is not trivial to focalize X-rays with good efficiency, and the modalities of implementation of an X-ray concentrator still represents an open issue. One non-focusing method, which has already been proposed for X-ray detection, consists in the usage of geometrical optics, such as collimators or coded masks (Ubertini et al. 2003). However, since the total cross section for γ-rays attains its minimum within 100–1000 keV, the efficiency of geometrical optics decreases while at the same time the background noise increases with respect to the signal. This is because of the growing importance of shield leakage and/or nβ activation. Another non-focusing solution consists of quantum optics based on Compton effect and tracking detectors (Von Ballmoos et al. 2005).
Focusing methods through Bragg diffraction have greater potential because they would be capable of concentrating the signal from a large collector onto a small spot on the detector and beating the instrumental background that may hamper the observation. If X-ray diffraction occurs traversing the crystal (the Laue scheme), the problem of focusing hard X-rays can be approached via a Laue lens (Smither 1982). The usage of high-efficiency crystals is a key point to make the experiments involving a Laue lens within reach.
In fact, X-ray astrophysics would broaden its horizons with the possibility of exploiting such an X-ray concentrator. The emission of γ-rays takes place in several places in the Universe; these span from our Sun to the cosmic γ-rays that originate locally in solar flares, and within our Galaxy in compact binary systems, pulsars, supernova remnants, and in extremely distant objects such as active galactic nuclei, γ-ray bursts (GRBs) at redshifts z> 8, and to the cosmic γ-ray background radiation of the early Universe. Moreover, the study of the origin of the positrons annihilating in the Galactic centre could be visible through the e+/e− annihilation line at 511 keV. A study of the distribution of this emission line would thus bring new clues concerning the still elusive sources of anti-matter.
An X-ray concentrator could also be used as an imager for high-quality imaging in nuclear medicine (Roa et al. 2005). In particular, this imager would improve γ-ray detection by providing better scan resolution with respect to traditional single photon emission computed tomography (SPECT) and positron emission tomography (PET; Paternò et al. 2015).
Starting from the initial proposals of Laue lenses (Lindquist & Webber 1968; Smither 1982; Lund 1992), significant progress has been made. Since then several γ-ray astronomy themes have motivated various mission concept studies, such as the advanced Compton telescope (ACT, Boggs 2006), the gamma-ray imager (GRI, Knödlseder et al. 2009), CLAIRE (von Ballmoos et al. 2005), MAX (Barrière et al. 2006), and the hard X-ray telescope (HAXTEL, Frontera et al. 2006). In these missions, mosaic crystals (Zachariasen 1945) were proposed as optical elements for Laue lenses. Crystals with curved diffracting planes (CDP crystals) represent an alternative to mosaic crystals (Authier & Malgrange 1998). Within the framework of bent crystals, it has recently been proposed the usage of the quasi-mosaic (QM) effect (Sumbaev 1957; Camattari et al. 2015a) for fabricating diffracting crystals for focusing X-rays (Guidi et al. 2011).
In this paper, an extended analysis of the focusing capability of a Laue lens composed of these different crystal types is shown. In particular, the performances of mosaic, CDP, and QM crystals are discussed and compared, highlighting their advantages and disadvantages. The aspects that are taken into account for the comparison are: integrated efficiency, point spread function, effective area, sensitivity, and signal-to-noise ratio for the three cases. Finally, an analysis of the possible breakthroughs in the framework of the discussed diffracting crystals is proposed.
2. Laue lens: The diffracting crystals
It is possible to use a so-called Laue lens to focus X- and γ-rays. A Laue lens is conceived as an ensemble of many crystals arranged in such a way that as much radiation as possible is diffracted onto the lens focusing point over a selected energy band (see Fig. 1). The photons are focused through Bragg diffraction: 2dsin(θB) = nλ, where d is the spacing between atomic planes, θB the angle subtended by the incoming γ-ray trajectory and the diffracting planes, n the order of diffraction, and λ the wavelength of the radiation. The inner radius of the Laue lens diffracts the highest energies, while the outer radius diffracts the lowest energies.
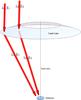 |
Fig. 1 Schematic representation of a Laue lens: E1<E2. |
Keitel et al. (1999), Barrière et al. (2010), Bellucci et al. (2011) recently proposed and demonstrated the high reflectivity of CDP crystals disposed with respect to impinging photons as shown in Fig. 2a, hereinafter named geometry 1. Since it is not possible to bend crystals thicker than a few mm, it is possible to stack together several CDP crystals, as in Neri et al. (2013). Thus, CDP crystals with arbitrary acceptance areas can be fabricated.
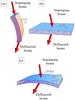 |
Fig. 2 Red arrows represent an X-ray beam, while tiles represent crystals. The crystallographic orientation used in the simulation is reported. If no orientation is reported, it means that it is indifferent for diffraction; a) indicates CDP crystal, geometry 1; b) mosaic crystal, geometry 2; and c) QM crystal, geometry 2. |
Alternatively, geometry 2 (Figs. 2b and c) can be employed in such a way as to expose the larger crystal surface to the photon flux. To exploit geometry 2, the diffracting planes have to be perpendicular to the crystal surface. A typical optical element of this type is the mosaic crystal (Fig. 2b). Such crystals have been proposed since the first proposals for Laue lens, however, growing an effective mosaic crystal is not simple and obtaining a reproducible energy bandpass is still an open issue.
Another kind of diffracting crystal, which relies on the QM effect, has recently been proposed (Fig. 2c). Quasi-mosaicity is an effect driven by crystalline anisotropy. For particular crystallographic orientations, a bending that results in a primary curvature may generate a QM curvature within the crystal due to crystal anisotropy. This effect can be used to fabricate curved crystals in geometry 2 for focusing X-rays (see Fig. 3). It was shown that bent crystals that present the QM effect allow very high-resolution focusing of hard X-rays with respect to mosaic crystals (Guidi et al. 2011; Camattari et al. 2013b, 2014b). Indeed, using QM crystals, it is possible to encompass the focusing action due to the primary curvature with the high diffraction reflectivity given by CDP built up by quasi-mosaicity.
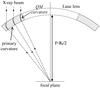 |
Fig. 3 Schematic representation of a cross section of a Laue lens based on QM crystals. Grey rectangles represent the crystals. The primary curvature leads to a secondary curvature of the planes affected by quasi-mosaicity. In this configuration, the QM diffracting planes are perpendicular to the main surface of the plates. The primary curvature facilitates focalizing diffracted radiation onto the focal plane, while the QM curvature increases the integrated diffraction efficiency. |
Here, a comparison between mosaic crystals, CDP crystals disposed in geometry 1, and QM crystals disposed in geometry 2 is shown. The following abbreviations have been used:
-
case 1: mosaic crystals disposed in geometry 2;
-
case 2: CDP crystals disposed in geometry 1;
-
case 3: QM crystals disposed in geometry 2.
3. Laue lens: Diffraction reflectivity
The high-efficiency focusing of the diffracted photons is an important requirement in all the applications involving a Laue lens. Perfect and flat mono-crystals diffract within a very narrow energy range, so they are not adequate for a Laue lens (Fig. 4a) both in the case of a monochromatic and polychromatic Laue lens. Indeed, in the first case the lens angular acceptance for the incident photons would be excessively selective. In the second case, the integrated reflectivity would be very low.
3.1. Case 1: Mosaic crystals
One of the components currently under investigation by the scientific community is the mosaic crystal. This type of crystal consists of an aggregation of crystallites whose angular distribution is a Gaussian spread about a nominal direction (Zachariasen 1945) (Fig. 4b). For a mosaic crystal, reflectivity is given by ![\begin{equation} \label{eq:refmosaic} \eta_{\rm M} = \frac{1}{2}\left[1-{\rm e}^{-2W_{\rm M}(\Delta\theta)QT_0}\right]{\rm e}^{\frac{-\mu T_0}{\cos \theta _{\rm B}}}, \end{equation}](/articles/aa/full_html/2016/03/aa26745-15/aa26745-15-eq12.png) (1)where T0 is the crystal thickness traversed by radiation, Δθ is the difference between the angle of incidence and the Bragg angle θB, μ the linear absorption coefficient within the crystal, and WM(Δθ) the distribution function of the crystallite orientations, that is, a normal distribution. This normal distribution can be written as follows:
(1)where T0 is the crystal thickness traversed by radiation, Δθ is the difference between the angle of incidence and the Bragg angle θB, μ the linear absorption coefficient within the crystal, and WM(Δθ) the distribution function of the crystallite orientations, that is, a normal distribution. This normal distribution can be written as follows: 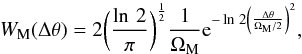 (2)where ΩM is called mosaicity, or mosaic spread, and represents the full width at half maximum (FWHM) of the angular distribution of the crystallites. Finally, considering the kinematical theory approximation (Malgrange 2002), Q is given by
(2)where ΩM is called mosaicity, or mosaic spread, and represents the full width at half maximum (FWHM) of the angular distribution of the crystallites. Finally, considering the kinematical theory approximation (Malgrange 2002), Q is given by 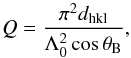 (3)where Λ0 is the extinction length as defined in Authier (2001) for the Laue symmetric case.
(3)where Λ0 is the extinction length as defined in Authier (2001) for the Laue symmetric case.
The integrated reflectivity HM depends on the energy of the beam that is considered. It can be written as follows: ![\begin{equation} H_{\rm M}=\frac{\int_{E_{\min}}^{E_{\max}} \left[1-{\rm e}^{-2W(\Delta\theta)QT_0}\right]{\rm e}^\frac {-\mu T_0}{\cos \theta _{\rm B}}\, {\rm d}E}{2(E_{\max}-E_{\min})}, \end{equation}](/articles/aa/full_html/2016/03/aa26745-15/aa26745-15-eq23.png) (4)where Emin and Emax are the minimum and the maximum energy considered, and
(4)where Emin and Emax are the minimum and the maximum energy considered, and 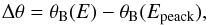 (5)where θB(E) is the Bragg angle for the energy E, and Epeack is the energy at which the mosaic crystal offers the maximum reflectivity.
(5)where θB(E) is the Bragg angle for the energy E, and Epeack is the energy at which the mosaic crystal offers the maximum reflectivity.
 |
Fig. 4 Diffraction capability with different kind of crystals disposed in geometry 2, considering a white X-ray beam impinging on the plate. a) Perfect crystal. If the Bragg condition is satisfied, a precise wave length is diffracted and the efficiency is dependent on the thickness traversed. The integrated reflectivity is very low. b) Mosaic crystal. The integrated diffraction efficiency is higher with respect to case a), though the diffraction efficiency is limited at 50% and the spatial resolution of the diffracted photons is limited by the mosaic defocusing effect. c) Bent crystal but without QM curvature. The primary curvature allows the focalization of the diffracted photons, however, the flat diffracting planes reduce the integrated intensity. d) Bent crystal with QM curvature. QM sample combines the focusing action due to the primary curvature with the high reflectivity of CDP built up by quasi-mosaicity. |
3.2. Case 2: CDP crystals
The peak reflectivity can be written, for case 2, as in Malgrange (2002): ![\begin{equation} \label{eq:refc} \eta_{\rm C} = \left[1-{\rm e}^{\frac{-\pi^2T_0d_{\rm hkl}}{\Omega_{\rm P}\Lambda^2_0}}\right]{\rm e}^{\frac{-\mu T_0}{\cos \theta _{\rm B}}}, \end{equation}](/articles/aa/full_html/2016/03/aa26745-15/aa26745-15-eq30.png) (6)where, in this case, ΩP represents the bending angle of the curved diffracting planes, which rely on the primary curvature of the crystal plate. The angular distribution of the diffracting planes WC(Δθ) turns out to be a box with the width as the angular spread ΩP. The angular spread is
(6)where, in this case, ΩP represents the bending angle of the curved diffracting planes, which rely on the primary curvature of the crystal plate. The angular distribution of the diffracting planes WC(Δθ) turns out to be a box with the width as the angular spread ΩP. The angular spread is 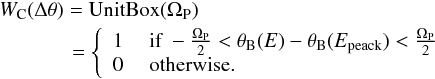 (7)Thus, the integrated reflectivity HC results
(7)Thus, the integrated reflectivity HC results ![\begin{equation} H_{\rm C}=\frac{\int_{E_{\min}}^{E_{\max}} \left[1-{\rm e}^{\frac{-\pi^2T_0d_{\rm hkl}}{\Omega_{\rm P}\Lambda^2_0}}\right]W_{\rm C}(\Delta\theta){\rm e}^{\frac{-\mu T_0}{\cos \theta _{\rm B}}}\ {\rm d}E}{E_{\max}-E_{\min}}\cdot \end{equation}](/articles/aa/full_html/2016/03/aa26745-15/aa26745-15-eq35.png) (8)
(8)
3.3. Case 3: QM crystals
The QM crystals are a subclass of CDP crystals. Thus, for case 3 (Fig. 4d), the peak reflectivity can be written as ![\begin{equation} \label{eq:refqm} \eta_{\rm QM} = \left[1-{\rm e}^{\frac{-\pi^2T_0d_{\rm hkl}}{\Omega_{\rm QM}\Lambda^2_0}}\right]{\rm e}^{\frac{-\mu T_0}{\cos \theta _{\rm B}}}. \end{equation}](/articles/aa/full_html/2016/03/aa26745-15/aa26745-15-eq36.png) (9)Here, the angular distribution WQM(Δθ) of the diffracting planes consist in the convolution between the primary curvature of the plate and the QM curvature, given by
(9)Here, the angular distribution WQM(Δθ) of the diffracting planes consist in the convolution between the primary curvature of the plate and the QM curvature, given by 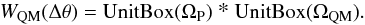 (10)The integrated reflectivity HQM results
(10)The integrated reflectivity HQM results ![\begin{equation} H_{\rm QM}=\frac{\int_{E_{\min}}^{E_{\max}} \left[1-{\rm e}^{\frac{-\pi^2T_0d_{\rm hkl}}{\Omega_{\rm QM}\Lambda^2_0}}\right]W_{\rm QM}(\Delta\theta){\rm e}^{\frac{-\mu T_0}{\cos \theta _{\rm B}}}\, {\rm d}E}{E_{\max}-E_{\min}}\cdot \end{equation}](/articles/aa/full_html/2016/03/aa26745-15/aa26745-15-eq40.png) (11)Since the focusing capability of a Laue lens mostly depends on the photon distribution that it can yield on the focal plane, a Monte Carlo code similar as that used in Camattari & Guidi (2014) was used to simulate a Laue lens based on such crystals. The difference between the three different cases are highlighted.
(11)Since the focusing capability of a Laue lens mostly depends on the photon distribution that it can yield on the focal plane, a Monte Carlo code similar as that used in Camattari & Guidi (2014) was used to simulate a Laue lens based on such crystals. The difference between the three different cases are highlighted.
4. Diffracting crystal comparison
A comparison between the focusing capability of a Laue lens based on the described crystals was performed. In particular, the comparison was worked out to evaluate advantages and drawbacks of a Laue lens alternately composed of mosaic, CDP, or QM crystals. The crystal features are the state-of-the-art of those features that currently exist. The simulations thus represent the actual Laue lenses that could be fabricated with current technology. However, a look at the scenario of the new methods that should be achieved in the future is proposed in Sect. 6.
4.1. Parameter selection
For sake of comparison, the simulation have been performed limiting as much as possible the differences between the three cases. Indeed, for the three cases, a Laue lens composed of a single ring filled with germanium crystals has been considered: Ge was chosen because it is a material usually employed for hard X-ray diffraction and it can be fabricated either as perfect or mosaic crystal. Silicon is a very similar crystal and its cost is sensibly lower with respect to Ge crystals. However, the diffraction efficiency for Si is centred at lower energies with respect to Ge crystals, i.e. about 100 keV. On the other hand, Ge can be considered more representative for evaluating the performance of a Laue lens because its energy range of diffraction at high efficiency is wider and shifts towards higher energies with respect to Si. Moreover, Ge crystals can be produced with a controlled mosaicity, while Si crystals can be produced principally as a perfect crystal. The diffracting planes taken into account were (111) planes, because their diffraction efficiency is very high. All the crystals were chosen with the same tile size 10 × 10 mm2, which is a typical size for diffracting crystals. The energy range of the photons was chosen centred at 200 keV, since Ge crystals diffract 200 keV photons at high efficiency. Since the differences between mosaic, CDP, and QM crystals vary with energy approximately in the same manner, the results of the simulations also hold for different photon energies. Finally, the focal length of the lens was fixed at f = 20 m, which is a value usually taken into account for the design of a Laue lens for astronomical purposes. The radius of the crystal ring turned out to be fixed by the Bragg law at 379.6 mm to obtain X-ray diffraction. Since this ring can be filled with 235 crystals, the resulting geometric area was 235 cm2.
Also, the angular spread of the diffracting planes was fixed for all three cases. For cases 1 and 2, the angular spread of the diffracting planes can be adjusted. In case 3, instead, the angular spread is determined by the size and curvature of the crystals (Camattari et al. 2015a). In fact, focusing is provided by bending the crystals along the lens radial direction to a primary curvature equal to 2f for a Laue lens made by QM crystals. Thus, for case 3, the primary radius of curvature along the radial direction (the [111] direction of Fig. 2b) is fixed by this geometrical constrain at R = 2f = 40 m.
Although the primary curvature along the radial direction is fixed to obtain the focalization of the diffracted photons, the primary curvature along the tangential direction (the [110] direction of Fig. 2b) is a free parameter. It was shown in Camattari et al. (2015a) that the QM curvature can be adjusted by properly setting the two perpendicular primary curvatures of the crystal. Here, a tangential radius of curvature of 11.5 m was chosen to obtain an angular spread of the QM planes of 30 arcsec, if the thickness of the QM crystal is 5 mm (calculation performed through the software AniCryDe (Camattari et al. 2015b). As a result of the convolution between the primary and the QM curvature, the FWHM of the angular distribution of the diffracting planes for a 10 × 10 mm2 QM sample turned out to be 51.57 arcsec. As a consequence, for case 1 the mosaicity ΩM was set 51.57 arcsec, and for case 2 the angular spread ΩP of the CDP was fixed at 51.57 arcsec.
Since the angular spread was fixed at 51.57 arcsec, an X-ray beam with energy between 192 and 208 keV was considered to impinge onto the crystal rings, parallel to the axis of the lens. Indeed, this energy spread guarantees that all the photons can be diffracted for all three considered cases. The simulated beam was constituted of 106 photons because it was a good compromise between precision and computational time.
The angular spread of the diffracting planes is a very important parameter. To work out a comparison between the crystal features, 51.57 arcsec was fixed by the geometrical constrains, as explained above. This angular spread can be achieved through the manufacturing techniques of these very different types of crystals. It is important to note that the angular spread is strictly linked to the focal length of the Laue lens and to the detector size. A focal distance of f = 20 m permits to design a Laue lens that is a good compromise between payload and efficiency. The results shown in this paper would qualitatively also hold for different focal lengths, since the features of the crystals change similarly as a function of f. With regard to the detector size, its diameter determines the field of view of the Laue lens for off-axis sources. Actually, the detector volume is of relevance for the detection efficiency. To compare the different types of diffracting crystals, the simulations deal with a Laue lens with fixed geometrical parameters. As a consequence, the detector would be the same for the three cases and the comparison can only be focused on the features of the crystals.
The thickness of the samples traversed by the photons (T0) was set similarly for the three cases. For cases 1 and 2, the best thicknesses can be calculated following the procedure reported in Barrière et al. (2009). It results in 5.33 mm for case 1 and 5.00 mm for case 2, imposing a radius of curvature of RP = T0/ ΩP = 20.0 m for the crystals of case 2. For case 3, T0 affects both the focusing capability and the integrated reflectivity of the lens. A high value of T0 leads to a higher reflectivity and a lower spatial resolution on the focal plane, while a lower value of T0 causes a decrease of the reflectivity and an increase of the focusing capability. The value T0 equal to 5.00 mm can be a good compromise to guarantee high reflectivity and high focalization of the diffracted photons (Bellucci et al. 2013). It is possible to use very hard tensile films to obtain a radius of curvature down to tens of meters for crystals that are 5 mm thick. Examples are reported in Camattari et al. (2014a) and in Mazzolari et al. (2015). All the selected parameters are listed in Tables 1 and 2.
Lens features.
Ge crystal features.
4.2. Simulation results
Firstly, the effective area was evaluated. The effective area of an optics at a certain energy is defined as its geometric area, as seen by the X-ray beam, multiplied by the diffraction reflectivity at that energy. The effective area and the integrated reflectivity of the rings were calculated both analytically and with the Monte Carlo code and reported in Table 3. The results for the three cases are shown in Fig. 5.
 |
Fig. 5 Effective area of the simulated rings. a) Case 1: mosaic crystals disposed in geometry 2. b) Case 2: CDP crystals disposed in geometry 1. c) Case 3: QM crystals disposed in geometry 2. The continuous lines represent the analytical result, while the histograms were obtained through the Monte Carlo simulation. |
As one could expect, the effective area for the mosaic ring follows a Gaussian distribution, since the orientation of the crystallites follows the same distribution. Regarding case 2, the effective area has a rectangular shape, in accordance with the angular distribution of the diffracting planes. Using QM crystals (case 3), the effective area turned out to be smaller with respect to case 2. Indeed, fixed a photon energy, the Bragg condition can be met in a relatively small region of a QM crystal. However, the small effective area is compensated by the strong focusing action exerted by this type of crystal. Indeed, the property of a QM crystal is to focus a parallel X-ray beam on a spot smaller than the size of the diffracting crystal itself. This is a peculiarity that cannot be obtained in cases 1 and 2.
The focusing capabilities were analyzed through the Monte Carlo code taking the photon distributions on the focal plane into account. The simulations results are shown in Figs. 6 and 7.
 |
Fig. 6 Photon distribution on the focal plane of the lens. a) Case 1: mosaic crystals disposed in geometry 2. b) Case 2: CDP crystals disposed in geometry 1. c) Case 3: QM crystals disposed in geometry 2. Bin width: 0.75 mm. |
 |
Fig. 7 Cross section of the photon distribution on the focal plane of the lens for the three cases. |
As an estimator of the focusing capabilities, the fractions of enclosed photons as a function of the radius Rspot of the focal spot enclosing the photons were calculated. The results are shown in Fig. 8. The performances of the rings are summarized in Table 3.
 |
Fig. 8 Fraction of enclosed photons as a function of the radius of the focal spot enclosing the photons (Rspot). |
Rings performances.
5. Discussion
 |
Fig. 9 a) Focusing factor of the simulated rings. b) Predicted 3σ detection sensitivities for continuum emission, assuming an exposure time of ΔT = 100 ks and ΔE/E = 1 / 2. The background was set at 1.5 × 10-4 counts cm-2 s-1 keV-1, taking into account the average detection efficiency ηd = 0.5 and the average attenuation factor fat = 0.9. |
Mosaic crystals were the first to be proposed with the aim of hard X-ray concentration. They are the simplest crystals to be positioned on a Laue lens because of their broad angular acceptance. The drawbacks of these crystals consist in a limited diffraction efficiency, corresponding to a maximum of 50% in peak reflectivity at zero absorption, and in a limitation on the spatial resolution of the diffracted photons as a result of the so-called mosaic defocusing effect (Halloin & Bastie 2005).
To overcome the drawbacks of mosaic crystals, crystals with curved diffracting planes (CDP crystals) were proposed. Indeed, their diffraction efficiency can exceed 50% because the continuous change of the incidence angle on bent crystalline planes prevents re-diffraction of a diffracted beam. Moreover, their energy bandpass can be controlled very well because it is proportional to the angular distribution of the diffracting planes (Malgrange 2002).
Within the framework of bent crystals for focusing X-rays, the use of the quasi-mosaic (QM) effect has recently been proposed (Guidi et al. 2011). In fact, by exploiting the QM effect, it is possible to obtain the curvatures of two perpendicular families of crystallographic planes (Sumbaev 1957). As a result, it is possible to combine high diffraction efficiency of the diffracted beam with its focalization (Camattari et al. 2013b). The QM effect was selected for the production of part of the crystals used for building a Laue lens prototype within the Laue project (Camattari et al. 2013a; Liccardo et al. 2014; Virgilli et al. 2013).
As can be seen by the performed simulation, the highest integrated reflectivity can be recorded with CDP crystals, which is case 2. A scheme based on this geometry is certainly a viable route for building a Laue lens. However, the use of diffracting crystals disposed in geometry 1 requires the fabrication and positioning of a large number of samples to cover the whole Laue lens because the crystals must be oriented with their major faces parallel to the photon direction, and it is not possible to produce bent crystals thicker than a few millimeters. A solution to this problem is to layer the samples one over the other to form a stack, as in Neri et al. (2013). In fact, a stack of bent crystals can be assembled as a single optical element for X-ray focusing. The relative alignment of the curved diffracting planes in the stack proposed in Neri et al. (2013) was tested by hard X-ray diffractometry using a polychromatic and divergent beam. The stacks exhibited a single and well-defined spot under X-ray diffraction, highlighting that the plates were sufficiently aligned to behave as a single crystal (Guidi et al. 2013).
As a result of the stacking, it would be possible to realize optical elements with arbitrarily large size, improving the problem of positioning. However, the number of crystals needed to cover a whole Laue lens still remains very large. Moreover, the process of fine alignment may be complicated and very expensive. To overcome these problems, geometry 2 (Fig. 2b) can be employed in such a way as to expose the larger crystal surface to the photon flux, as in cases 1 and 3. Especially regarding case 1, the crystals positioning can be accomplished more easily because of the large angular acceptance typical of mosaic crystals. Better focusing capability can be obtained with QM crystal owing to their focusing action.
Finally, the focusing capabilities of the simulated Laue lenses were quantified by means of three parameters, given by the focusing factor G(E), the sensitivity S(E), and the signal-to-noise ratio (S/N).
The focusing factor G(E) allows to estimate the number of events that an ideal detector located on the focus of the Laue lens would count under exposure to a certain photon flux. The factor G(E) is thus a quantifier of the focusing capability, defined as 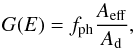 (12)where Aeff is the effective area of the lens and Ad is the area of the focal spot that contains a fraction fph of photons reflected by the lens. Physically, it represents the number of photons enclosed in a focal spot divided by the area of the focal spot and normalized with respect to the photon flux impinging on the lens. Thus, G(E) represents the gain of the lens, i.e. it is a geometrical parameter related to the array of the diffracting crystals. The compared Laue lenses are designed to be equal each other to directly compare the different types of diffracting crystals, i.e. the lenses have the same geometrical properties and only differ for the crystals used. Thus, the detector for collecting the signal would be the same for the three cases, and the comparison can only be worked out for the crystal differences.
(12)where Aeff is the effective area of the lens and Ad is the area of the focal spot that contains a fraction fph of photons reflected by the lens. Physically, it represents the number of photons enclosed in a focal spot divided by the area of the focal spot and normalized with respect to the photon flux impinging on the lens. Thus, G(E) represents the gain of the lens, i.e. it is a geometrical parameter related to the array of the diffracting crystals. The compared Laue lenses are designed to be equal each other to directly compare the different types of diffracting crystals, i.e. the lenses have the same geometrical properties and only differ for the crystals used. Thus, the detector for collecting the signal would be the same for the three cases, and the comparison can only be worked out for the crystal differences.
To calculate the focusing factor, the radius of the focal spot Rspot was chosen to enclose 90% of the photons, cutting the tails of the distribution (see Table 3). Figure 9a shows the focusing factor of the lenses as a function of the energy of the impinging photons. The best focusing factor is achieved for case 3.
Here, Rspot is a parameter related to the point spread function, i.e. it is a figure of merit of the focusing capability of the lens. Actually, the point spread function recorded by a real detector could be larger with respect to the photon distribution on the focal plane because of the Compton scattering within the detector, especially for high photon energies. Other effects that may degrade the resolution in a pixel detector concern the collection of the signal generated by the photons and the charge sharing. Since a pixel detector may reach a resolution of some hundreds of μm for these photon energies (Caroli et al. 2005; Khalil et al. 2015), the point spread function recorded in a detector would be approximately as wide as the photon distribution at the focal plane for the cases considered in this paper.
In fact, depending on the purpose of the experiment, the detector characteristics may vary widely. Thus, in the simulations reported in this paper, all the effects that may alter Rspot in the detector have been neglected to conduct a pure analysis of the focusing capability for the different types of optical elements.
The performance of the lens has also been expressed in terms of the sensitivity, which is the most often acknowledged quantifier recognized by the community of astrophysicists, that is, the lowest flux detectable with nσ = 3 sigma significance for cases of continuum-line emissions, i.e. ΔE/E = 1 / 2. The value Rspot was fixed to enclose 90% of the diffracted photons (see Table 3). The background B was 1.5 × 10-4 ph/(cm2 s keV) constant over the entire considered energy range. An on/off scheme for background subtraction has been assumed. To give a realistic estimation of the final sensitivity of the whole satellite-borne system for X-ray detection, some technical parameters, which do not depend on the lens concerned, have been taken into account. In particular, the average detection efficiency ηd for the energy band of interest can be estimated at 50%. Furthermore, an average attenuation factor fat at 0.9 has been set to account for the absorption of passive materials, e.g. the lens frame and satellite housing. The sensitivity S(E) was calculated as follows: 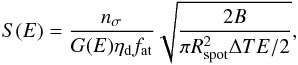 (13)where ΔT is the exposure time, set at 100 ks. The results for the sensitivities are shown in Fig. 9b. The best sensitivities are achieved for cases 2 and 3.
(13)where ΔT is the exposure time, set at 100 ks. The results for the sensitivities are shown in Fig. 9b. The best sensitivities are achieved for cases 2 and 3.
Finally, to compare the three focal spots, it was resorted to the S/N, as in Guidi et al. (2011), 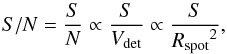 (14)where S is the signal count within a specified encircled area with radius Rspot, N is the background of the area, and Vdet is the useful volume of the detector. For a Laue lens, the size of the detector determines its field of view for off-axis sources. Here, an on-axis source was simulated and the noise of the detector was considered proportional to the focal spot size. In particular, Rspot was chosen to enclose 90% of the diffracted photons (see Table 3) in the focal plane and S the signal within this area. Thus, the background was taken proportional to the volume of the detector, which faced the incoming X-rays with a surface as large as the encircled area. Because of different focalization properties, the obtained S/N for the three cases were significantly different.
(14)where S is the signal count within a specified encircled area with radius Rspot, N is the background of the area, and Vdet is the useful volume of the detector. For a Laue lens, the size of the detector determines its field of view for off-axis sources. Here, an on-axis source was simulated and the noise of the detector was considered proportional to the focal spot size. In particular, Rspot was chosen to enclose 90% of the diffracted photons (see Table 3) in the focal plane and S the signal within this area. Thus, the background was taken proportional to the volume of the detector, which faced the incoming X-rays with a surface as large as the encircled area. Because of different focalization properties, the obtained S/N for the three cases were significantly different.
As a result of the simulation, the quotient between the S/Ns for the three cases turned out to be as follows: 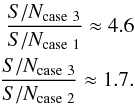 (15)Thus, QM crystals are also the most efficient in terms of the signal-to-noise ratio.
(15)Thus, QM crystals are also the most efficient in terms of the signal-to-noise ratio.
The comparison worked out in this paper is based on a photon beam with energy centred at 200 keV. This is mainly because of the high diffraction efficiency of Ge in this energy range. The obtained results also hold for different energies. For low energy, such as 100 keV, Si crystals can be used. For photons with energy greater than ≃600 keV, the diffraction efficiency of Si and Ge crystals decreases. With the aim of focusing such high energy photons at high efficiency, crystals with high Z, such as silver, gold, lead, etc. (Barrière et al. 2009), are needed. These materials cannot be fabricated as perfect crystals, but only as mosaic crystals. Thus, CDP and QM crystals would be not available if high Z material are used, and a comparison between these types of crystal would be impossible. In this case, it would be important to take into account that metal crystals have particular mechanical and chemical properties, which make them very difficult to cut, align, and carry out the gluing and polishing process.
In this paper, a comparison between different types of diffracting crystals has been worked out. Actually, the feasibility of a Laue lens depends on several criteria that have to be taken into account. With regard to the crystals, important parameters are the availability of crystalline materials, reproducibility of the crystal manufacturing, and alignment and mounting of the crystals on the lens frame. Moreover, in the context of a space-borne Laue lens, additional criteria must be considered, such as payload, mechanical robustness to shocks and vibrations, and long-time reliability with respect to chemical and temperature cycling.
A simulation for taking possible errors into account during alignment and mounting process of the crystals on the lens frame was worked out. In particular, a parameter for including that the crystals can be randomly misaligned with respect to their theoretical position has been considered in the simulation code. Each crystal was misaligned from its ideal position with three random angles within a certain range, each of them starting from ±5 arcsec to ±60 arcsec. The crystal misalignment resulted in an increased energy spread of the diffracted photons and in a defocusing of the signal on the focal plane.
In Fig. 10a, the radius of the focal spot Rspot, which encloses 90% of the diffracted photons, is plotted as a function of the crystal misalignment. The figure shows that, for each misalignment angle, the smallest focal spot is achievable in the case of QM crystals. In Fig. 10b, the detection sensitivity for continuum emission, centred at 200 keV, is plotted as a function of the crystal misalignment. In this case, a Laue lens made of QM crystals is the best example if the crystal misalignment is lower than ±30 arcsec. Beyond this threshold, the CDP case results to be the better in terms of sensitivity. Indeed, the QM case is more sensitive to the crystal alignment and an excessive misalignment would lead to a serious decrease of its focusing power.
 |
Fig. 10 a) Radius of the focal spot Rspot for enclosing 90% of the diffracted photons as a function of the crystal misalignment. b) Detection sensitivities for continuum emission at 200 keV as a function of the crystal misalignment. |
6. Breakthrough in the diffracting crystal scenario
This paper is aimed to be an exhaustive analysis of the state-of-the-art concerning the crystals that could be involved in the fabrication of a Laue lens for astrophysics. Mosaic, CDP, and QM crystals were taken into account, highlighting advantages and drawbacks of the different crystal types. Some improvements that may reduce the size of the focal spot are under development. In fact, by reducing the spot in the focal plane, it would be possible to improve the sensitivity of a Laue lens and the signal-to-noise ratio recorded by the detector. Indeed, since the sensitivity is roughly proportional to the radius Rspot of the focal spot enclosing the photons, it would be linearly improved by a reduction of the focal spot. Since the signal-to-noise ratio is proportional to 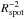 , a reduction of the focal spot would produce a quadratic increase of the S/N.
, a reduction of the focal spot would produce a quadratic increase of the S/N.
6.1. Case 1: Bent mosaic crystals
The focal spot of a traditional mosaic crystal is the result of a convolution of the footprint of the crystal tile and the so-called mosaic defocusing. Roughly speaking, because of the mosaic defocusing, the divergence of the diffracted beam is twice the mosaic spread of the crystal (Halloin & Bastie 2005). However, if a mosaic crystal was bent (as proposed in Ferrari et al. 2013) to a radius of curvature equal to twice the focal length of the lens, as for the case of QM crystals, a focusing effect would be achieved. The focal spot of a bent mosaic crystal would decrease to a rectangle with the longest side corresponding to the tangential side of the crystal and the shortest side ideally only caused by mosaic defocusing, which is given by 2FdetΩM, where Fdet is the distance from the lens to the detector and ΩM is the mosaicity.
6.2. Case 2: Stacked CDP crystals
The technology to bend and directly bond Si crystals to produce self-standing X-ray optics is under development by Cosine (Ackermann et al. 2013). This technology in named Silicon Pore Optics (SPO), while the final product is named Silicon Laue lens Components (SiLC). The key idea of this technique is to produce crystals with two independent curvatures. Since these curvature can be strong, the crystal thickness does not exceed 300 μm. However, these crystals can be bonded to each other. The first curvature is along the radial direction, i.e. the crystals are bent to fit the rings of the lens. This curvature strongly improves the focusing properties of a Laue lens. Indeed, as a result, the size of the focal spot would no longer be determined by the footprint of the individual single crystals, but by the accuracy of the applied curvature. Furthermore, a wedge is incorporated in each individual Si crystal to ensure that all crystals are confocal in the radial direction. The second curvature is along the axial direction of the lens. This curvature improves the reflectivity of each crystal, since it permits the exploitation of CDP for high efficiency diffraction.
6.3. Case 3: Shaped QM crystals
The focalization along the lens radial direction of the diffracted photons is achieved with QM crystals. Thus, the focal spot of each crystal has the form of a rectangle with its longest side corresponding to the footprint of the tangential side of the QM crystal, while the shortest side is due to the QM spread of the diffracting planes, which is given by 2FdetΩQM. It can be deduced that if a QM crystal was shaped with the tangential side shortened, the focal spot would decrease. It would be reasonable to achieve a squared focal spot. Thus, the tangential side should be reduced to obtain Ltan = 2FdetΩQM.
Take as an example the QM crystals reported for case 3. They are 10 × 10 mm2 tiles with a QM spread of 30 arcsec. The QM crystals should be 10 × 5.8 mm2 tiles to reduce the focal spot of each QM crystal to a square of 5.8 × 5.8 mm2. If the QM spread was 10 arcsec, tiles 10 × 1.9 mm2 would produce a spot that is 1.9 × 1.9 mm2 large.
7. Conclusions
The first idea of a Laue lens to focalize X- and γ-rays was based on a scheme entirely based on mosaic crystals. Compared to the initial formulation, significant progress has been made, which can bring the concept of a Laue lens within reach. The usage of CDP crystals disposed in geometry 1 would increase the integrated reflectivity, though the number of samples that have to be produced is very large. Moreover, it has been demonstrated that, by using crystals with two curvatures, i.e. exploiting the QM effect, it is possible to decrease the focal spot and thus increase the collected photons in a very narrow point spread function. As a result, the principal figures of merit, i.e. focusing factor, sensitivity, and signal-to-noise ratio, attain their maximum values using QM crystals.
A high effective area and a high signal-to-noise ratio of the collected photons are key factors towards a concrete realization of such a lens for astrophysical purposes. Since the brightness of the sky in the 100–1000 keV energy range is very limited, several innovations have still to be conceived for the fabrication of the optical elements and for the assembly process because the needed accuracies are very high. This means that the technological progresses recorded so far are still not sufficient to permit the realization of an optics that has to be launched in a satellite. Starting from the work carried out on mosaic crystals, the introduction of curved crystals, and from the proposal of using the QM effect, several steps forwards have been made, as shown in this paper. To further improve the effective area of a Laue lens, different materials with different crystallographic orientations must be used, even if in this way the lens weight would increase significantly (Bellucci et al. 2013; Camattari et al. 2014c).
Acknowledgments
The author is grateful to INFN for financial support through the LAUPER project.
References
- Ackermann, M., Barrière, N., Collon, M. J., et al. 2013, Proc. SPIE, 8861, 88610G [CrossRef] [Google Scholar]
- Authier, A. 2001, Dynamical theory of X-ray diffraction (Oxford University Press) [Google Scholar]
- Authier, A., & Malgrange, C. 1998, Acta Cryst. A, 54, 806 [CrossRef] [Google Scholar]
- Barrière, N., Ballmoos, P., Halloin, H., et al. 2006, in Focusing Telescopes in Nuclear Astrophysics, ed. P. Von Ballmoos (Springer), 269 [Google Scholar]
- Barrière, N., Rousselle, J., von Ballmoos, P., et al. 2009, J. App. Cryst., 42, 834 [CrossRef] [Google Scholar]
- Barrière, N., Guidi, V., Bellucci, V., et al. 2010, J. Appl. Cryst., 43, 1519 [CrossRef] [Google Scholar]
- Bellucci, V., Camattari, R., Guidi, V., Neri, I., & Barrière, N. 2011, Exp. Astron., 31, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Bellucci, V., Camattari, R., & Guidi, V. 2013, A&A, 560, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boggs, S. E. 2006, N. Astron. Rev., 50, 604 [NASA ADS] [CrossRef] [Google Scholar]
- Camattari, R., & Guidi, V. 2014, A&A, 570, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Camattari, R., Battelli, A., Bellucci, V., & Guidi, V. 2013a, Exp. Astron., 37, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Camattari, R., Guidi, V., Bellucci, V., Neri, I., & Jentschel, M. 2013b, Rev. Sci. Instr., 84, 053110 [NASA ADS] [CrossRef] [Google Scholar]
- Camattari, R., Dolcini, E., Bellucci, V., Mazzolari, A., & Guidi, V. 2014a, J. Appl. Cryst., 47, 1762 [CrossRef] [Google Scholar]
- Camattari, R., Paternò, G., Battelli, A., et al. 2014b, J. Appl. Cryst., 47, 799 [CrossRef] [Google Scholar]
- Camattari, R., Paternò, G., Bellucci, V., & Guidi, V. 2014c, Exp. Astron., 38, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Camattari, R., Guidi, V., Bellucci, V., & Mazzolari, A. 2015a, J. Appl. Cryst., 107, 064102 [Google Scholar]
- Camattari, R., Lanzoni, L., Bellucci, V., & Guidi, V. 2015b, J. Appl. Cryst., 48, 943 [CrossRef] [Google Scholar]
- Caroli, E., Auricchio, N., Bertuccio, G., et al. 2005, Exp. Astron., 20, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrari, C., Buffagni, E., Bonnini, E., & Korytar, D. 2013, J. Appl. Cryst., 46, 1576 [CrossRef] [Google Scholar]
- Frontera, F., Pisa, A., Loffredo, G., et al. 2006, in Focusing Telescopes in Nuclear Astrophysics, ed. P. Von Ballmoos (Springer), 241 [Google Scholar]
- Guidi, V., Bellucci, V., Camattari, R., & Neri, I. 2011, J. Appl. Cryst., 44, 1255 [CrossRef] [Google Scholar]
- Guidi, V., Bellucci, V., Camattari, R., & Neri, I. 2013, Nucl. Instr. Meth. B, 309, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Halloin, H., & Bastie, P. 2005, Exp. Astron., 20, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Keitel, S., Malgrange, C., Niemöller, T., & Schneider, J. R. 1999, Acta Crystallogr. A, A55, 855 [CrossRef] [Google Scholar]
- Khalil, M., Frontera, F., Caroli, E., Virgilli, E., & Valsan, V. 2015, Nucl. Instr. Meth. A, 786, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Knödlseder, J., von Ballmoos, P., Frontera, F., et al. 2009, Exp. Astron., 23, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Liccardo, V., Virgilli, E., Frontera, F., et al. 2014, Exp. Astron., 38, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Lindquist, T. R., & Webber, W. R. 1968, Can. J. Phys., 46, S1103 [CrossRef] [Google Scholar]
- Lund, N. 1992, Exp. Astron., 2, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Malgrange, C. 2002, Cryst. Res. Tech., 37, 654 [CrossRef] [Google Scholar]
- Mazzolari, A., Camattari, R., Bellucci, V., et al. 2015, Nucl. Instr. Meth. B, 355, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Neri, I., Camattari, R., Bellucci, V., Guidi, V., & Bastie, P. 2013, J. Appl. Cryst., 46, 953 [CrossRef] [Google Scholar]
- Paternò, G., Bellucci, V., Camattari, R., & Guidi, V. 2015, J. Appl. Cryst., 48, 125 [CrossRef] [Google Scholar]
- Roa, D., Smither, R., Zhang, X., et al. 2005, Exp. Astron., 20, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Smither, R. K. 1982, Rev. Sci. Instr., 53, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Sumbaev, O. 1957, Soviet Phys. JETP, 27, 1042 [Google Scholar]
- Ubertini, P., Lebrun, F., Di Cocco, G., et al. 2003, A&A, 411, L131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Virgilli, E., Frontera, F., Valsan, V., et al. 2013, Proc. SPIE, 8861, 886107 [CrossRef] [Google Scholar]
- Von Ballmoos, P., Güdel, M., Kahn, S. M., & Sunjaev, R. 2005, High energy spectroscopic astrophysics (Springer) [Google Scholar]
- von Ballmoos, P., Halloin, H., Evrad, J., et al. 2005, Exp. Astron., 20, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Zachariasen, W. H. 1945, Theory of X-ray diffraction in crystals (New York: J. Wiley and Sons, Inc.) [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Schematic representation of a Laue lens: E1<E2. |
| In the text | |
 |
Fig. 2 Red arrows represent an X-ray beam, while tiles represent crystals. The crystallographic orientation used in the simulation is reported. If no orientation is reported, it means that it is indifferent for diffraction; a) indicates CDP crystal, geometry 1; b) mosaic crystal, geometry 2; and c) QM crystal, geometry 2. |
| In the text | |
 |
Fig. 3 Schematic representation of a cross section of a Laue lens based on QM crystals. Grey rectangles represent the crystals. The primary curvature leads to a secondary curvature of the planes affected by quasi-mosaicity. In this configuration, the QM diffracting planes are perpendicular to the main surface of the plates. The primary curvature facilitates focalizing diffracted radiation onto the focal plane, while the QM curvature increases the integrated diffraction efficiency. |
| In the text | |
 |
Fig. 4 Diffraction capability with different kind of crystals disposed in geometry 2, considering a white X-ray beam impinging on the plate. a) Perfect crystal. If the Bragg condition is satisfied, a precise wave length is diffracted and the efficiency is dependent on the thickness traversed. The integrated reflectivity is very low. b) Mosaic crystal. The integrated diffraction efficiency is higher with respect to case a), though the diffraction efficiency is limited at 50% and the spatial resolution of the diffracted photons is limited by the mosaic defocusing effect. c) Bent crystal but without QM curvature. The primary curvature allows the focalization of the diffracted photons, however, the flat diffracting planes reduce the integrated intensity. d) Bent crystal with QM curvature. QM sample combines the focusing action due to the primary curvature with the high reflectivity of CDP built up by quasi-mosaicity. |
| In the text | |
 |
Fig. 5 Effective area of the simulated rings. a) Case 1: mosaic crystals disposed in geometry 2. b) Case 2: CDP crystals disposed in geometry 1. c) Case 3: QM crystals disposed in geometry 2. The continuous lines represent the analytical result, while the histograms were obtained through the Monte Carlo simulation. |
| In the text | |
 |
Fig. 6 Photon distribution on the focal plane of the lens. a) Case 1: mosaic crystals disposed in geometry 2. b) Case 2: CDP crystals disposed in geometry 1. c) Case 3: QM crystals disposed in geometry 2. Bin width: 0.75 mm. |
| In the text | |
 |
Fig. 7 Cross section of the photon distribution on the focal plane of the lens for the three cases. |
| In the text | |
 |
Fig. 8 Fraction of enclosed photons as a function of the radius of the focal spot enclosing the photons (Rspot). |
| In the text | |
 |
Fig. 9 a) Focusing factor of the simulated rings. b) Predicted 3σ detection sensitivities for continuum emission, assuming an exposure time of ΔT = 100 ks and ΔE/E = 1 / 2. The background was set at 1.5 × 10-4 counts cm-2 s-1 keV-1, taking into account the average detection efficiency ηd = 0.5 and the average attenuation factor fat = 0.9. |
| In the text | |
 |
Fig. 10 a) Radius of the focal spot Rspot for enclosing 90% of the diffracted photons as a function of the crystal misalignment. b) Detection sensitivities for continuum emission at 200 keV as a function of the crystal misalignment. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


