| Issue |
A&A
Volume 586, February 2016
|
|
|---|---|---|
| Article Number | L4 | |
| Number of page(s) | 4 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201527768 | |
| Published online | 27 January 2016 | |
The NH2D hyperfine structure revealed by astrophysical observations⋆
1 Univ. Grenoble Alpes, IPAG, 38000 Grenoble, France
e-mail: fabien.daniel@obs.ujf-grenoble.fr
2 CNRS, IPAG, 38000 Grenoble, France
3 LISA, UMR 7583 CNRS-Universités Paris Est Créteil et Paris Diderot, 61 avenue du Général de Gaulle, 94010 Créteil, France
4 Max-Planck Institute for Extraterrestrial Physics (MPE), Giessenbachstr. 1, 85748 Garching, Germany
5 Department of Physics, PO Box 64, University of Helsinki, 00014 Helsinki, Finland
6 LERMA, Observatoire de Paris, PSL Research University, CNRS, UMR 8112, 75014 Paris, France
7 Max-Planck Institute for Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
8 Department of Physics and Astronomy, The University of Western Ontario, London, N6A 3K7, Canada
Received: 17 November 2015
Accepted: 28 December 2015
Context. The 111–101 lines of ortho- and para-NH2D (o/p-NH2D) at 86 and 110 GHz, respectively, are commonly observed to provide constraints on the deuterium fractionation in the interstellar medium. In cold regions, the hyperfine structure that is due to the nitrogen (14N) nucleus is resolved. To date, this splitting is the only one that is taken into account in the NH2D column density estimates.
Aims. We investigate how including the hyperfine splitting caused by the deuterium (D) nucleus affects the analysis of the rotational lines of NH2D.
Methods. We present 30 m IRAM observations of the above mentioned lines and APEX o/p-NH2D observations of the 101–000 lines at 333 GHz. The hyperfine patterns of the observed lines were calculated taking into account the splitting induced by the D nucleus. The analysis then relies on line lists that either neglect or include the splitting induced by the D nucleus.
Results. The hyperfine spectra are first analyzed with a line list that only includes the hyperfine splitting that is due to the 14N nucleus. We find inconsistencies between the line widths of the 101–000 and 111–101 lines, the latter being larger by a factor of ~1.6 ± 0.3. Such a large difference is unexpected because the two sets of lines probably originate from the same region. We next employed a newly computed line list for the o/p-NH2D transitions where the hyperfine structure induced by both nitrogen and deuterium nuclei was included. With this new line list, the analysis of the previous spectra leads to compatible line widths.
Conclusions. Neglecting the hyperfine structure caused by D leads to overestimating the line widths of the o/p-NH2D lines at 3 mm. The error for a cold molecular core is about 50%. This error propagates directly to the column density estimate. We therefore recommend to take the hyperfine splittings caused by both the 14N and D nuclei into account in any analysis that relies on these lines.
Key words: line: profiles / molecular processes / methods: data analysis / ISM: abundances
© ESO, 2016
1. Introduction
The first firm identification of singly deuterated interstellar ammonia, NH2D, was reported by Olberg et al. (1985) toward three molecular clouds at 86 and 110 GHz, the frequencies of the JKa,Kc = 111–101 lines of o/p-NH2D, respectively. The identification was unambiguous thanks to the narrow line widths, which allowed resolving the hyperfine splitting that is due to the nitrogen nucleus. These two lines have since been detected in a variety of cold astronomical sources, and they are routinely employed to derive the (D/H) ratio in ammonia (see, e.g., Roueff et al. 2005). This ratio is a sensitive tracer of the physical conditions and provides strong constraints to deuterium fractionation models.
In the previous studies by Coudert & Roueff (2006, 2009) and in the current spectroscopic databases (JPL1 and CDMS2), the line lists of the NH2D microwave spectra are based on the measurements by De Lucia & Helminger (1975), Cohen & Pickett (1982), and Fusina et al. (1988). These data sets only consider the nitrogen quadrupole hyperfine structure. In this letter, we present a new theoretical analysis of the NH2D hyperfine structure. This analysis takes the nitrogen quadrupole interaction, the deuteron quadrupole interaction, and the nitrogen spin-rotation interaction into account. It is based on the measurements by Kukolich (1968), Cohen & Pickett (1982), and Fusina et al. (1988). We show that by including the three coupling terms in the analysis, the origin of different line widths in the 101–000 and 111–101 lines of NH2D, as observed recently toward the prestellar core H-MM1, can be explained quite easily. Historically, the first astronomical observation resolving the hyperfine splitting caused by the D quadrupole coupling was presented by Caselli & Dore (2005) for DCO+.
The paper is organized as follows. In Sect. 2 we describe the IRAM and APEX observations of the o/p-NH2D lines detected toward H-MM1. Section 3 details the spectroscopy calculations. In Sect. 4 we discuss the effect of the new line list on the derivation of radiative transition parameters, and we conclude in Sect. 5.
2. Observations
The target of the present NH2D observations is the dense, starless core H-MM1 lying in the eastern part of Lynds 1688 in Ophiuchus (Johnstone et al. 2004; Parise et al. 2011). The position observed, 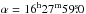 , δ = −24°33′33″, was chosen as the H2 column density peak, as derived from pipeline-reduced Herschel far-infrared maps. These were downloaded from the Herschel Science Archive3.
, δ = −24°33′33″, was chosen as the H2 column density peak, as derived from pipeline-reduced Herschel far-infrared maps. These were downloaded from the Herschel Science Archive3.
2.1. APEX 12 m
The ground-state 101–000 transitions of o/p-NH2D at ~333 GHz were observed using the upgraded version of the First Light APEX4 Submillimeter Heterodyne instrument (FLASH; Heyminck et al. 2006) on APEX (Güsten et al. 2006). The two lines separated by about 40 MHz were covered by one of the MPIfR Fast Fourier Transform Spectrometers (XFTTS) connected to the 0.8 mm receiver. The original spectral resolution at 333 GHz is about 35 m s-1; the spectra shown in this paper are Hanning smoothed to a resolution of 69 m s-1 (76 kHz). The APEX beam size (FWHM) is ~20″ at 333 GHz. The observations were carried out between 29 and 31 May, 2015, in stable and fairly good weather conditions (PWV 0.7–1.2 mm), using position switching for sky subtraction. The average system temperature at 333 GHz was 260 K. The resulting rms noise at a resolution of 69 m s-1 is 0.017 K on the 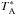 scale.
scale.
2.2. IRAM 30 m
The 111–101 lines of o/p-NH2D at ~86 and ~110 GHz were observed at the IRAM 30m telescope using the EMIR 090 receiver5 and the VESPA autocorrelator. The spectral resolution of this instrument, 20 kHz, is 68 m s-1 at 86 GHz and 53 m s-1 at 110 GHz. At these frequencies, the beam sizes of the telescope are 29″ and 23″, respectively. The observations were performed on July 5, 2015, in acceptable weather conditions (PWV 8–10 mm). The observing mode was position switching. The integration times for the o/p-NH2D lines were 15 and 22 min, and the average system temperatures at 86 and 110 GHz were 170 K and 250 K, respectively. The resulting rms noise levels of the o/p-NH2D spectra were 0.07 K and 0.08 K on the 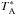 scale.
scale.
3. Hyperfine pattern calculations
Just like in NH3, the nitrogen nucleus in NH2D can tunnel across the plane made by the H and D nuclei. Each rotational transition is thus split into a doublet by this inversion motion. The resulting rotation-inversion levels are either symmetric or antisymmetric under the exchange of the two protons, and they will either correspond to para or ortho level.
Hyperfine patterns were calculated from a fit of high-resolution data that can be divided into three sets. The first set consists of microwave and far-infrared transitions involving the two inversion substates of the ground vibrational state. This first set includes 174 microwave transitions (Cohen & Pickett 1982) and 297 far-infrared transitions (Fusina et al. 1988) for which no hyperfine structure is resolved. The second set involves the 76 microwave transitions listed in Table IX of Cohen & Pickett (1982) for which the nitrogen atom quadrupole coupling structure is resolved. The last data set comprises the 21 hyperfine components measured by Kukolich (1968) for the para 414–404 rotation-inversion transition at 25 023.8 MHz. For this last data set, the quadrupole coupling structure that is due to both the nitrogen and deuterium atoms is resolved.
Rotation-inversion energies were computed with the help of a semi-rigid rotator Hamiltonian for both inversion substates and a second-order Coriolis coupling term between these substates (Cohen & Pickett 1982). Molecule-fixed components of the hyperfine coupling tensors are written using the IAM axis system of this reference. Quadrupole and magnetic spin-rotation hyperfine couplings were taken into account, leading to a hyperfine Hamiltonian depending on four coupling constants: two for the quadrupole coupling of the nitrogen and deuterium atoms, and two for the magnetic spin-rotation coupling of the same atoms. By using equations similar to Eqs. (3) and (17) of Thaddeus et al. (1964), we can express these four constants as diagonal matrix elements of four operators involving four rank-two hyperfine coupling tensors: the zero trace χN and χD, describing quadrupole coupling of the nitrogen and deuterium atoms, respectively, and CN and CD, corresponding to the magnetic spin-rotation coupling of the same atoms.
Hyperfine energies were calculated with the coupling scheme J + IN = F1 and F1 + ID = F, where J is the rotational angular momentum, and IN and ID are angular momenta of the nitrogen and deuterium nuclei, respectively. The corresponding coupled basis set functions | J,IN;F1,ID;F,MF ⟩ were used to set up the hyperfine Hamiltonian matrix. Matrix elements were taken from Thaddeus et al. (1964).
The inversion-rotation transitions belonging to the first data set were analyzed first, allowing us to determine a set of spectroscopic parameters analogous to the set listed in Table III of Cohen & Pickett (1982). Components of the four hyperfine coupling tensors were then fitted to the frequencies of transitions belonging to the second and third data sets, evaluating the hyperfine coupling constants with the eigenfunctions retrieved in the first analysis. For lines belonging to the first (second) data set, an experimental uncertainty value of 0.1 MHz (1 kHz) was assumed, and this compares well with a root mean square deviation of the observed minus calculated residual of 8.4 kHz (1.5 kHz). Table 1 reports the values obtained for fitted components of the hyperfine coupling tensors. These components are given in the axis system of Cohen & Pickett (1982). Because the rotation-inversion transition measured by Kukolich (1968) is characterized by ΔJ = 0, calculated hyperfine frequencies mainly depend on the sum 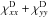 . For this reason, only
. For this reason, only 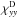 was varied in the analysis and
was varied in the analysis and 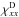 was constrained to a value retrieved from the deuteron coupling constant (eqξQ)D reported by Kukolich (1968) and using the fact that the angle between the ND bond and the z-axis (Cohen & Pickett 1982) is 78.98°. Magnetic spin-rotation coupling effects could only be retrieved for the nitrogen atom. Because we were unable to determine all three diagonal components of the corresponding tensor separately, they were constrained to be equal, as for the normal species (Kukolich 1967).
was constrained to a value retrieved from the deuteron coupling constant (eqξQ)D reported by Kukolich (1968) and using the fact that the angle between the ND bond and the z-axis (Cohen & Pickett 1982) is 78.98°. Magnetic spin-rotation coupling effects could only be retrieved for the nitrogen atom. Because we were unable to determine all three diagonal components of the corresponding tensor separately, they were constrained to be equal, as for the normal species (Kukolich 1967).
The results of this analysis were used to predict hyperfine patterns of other rotation-inversion transitions, evaluating hyperfine intensities with Eq. (29) of Thaddeus et al. (1964). We note that hyperfine effects due to the two hydrogen atoms may be important for ortho transitions. These effects were evaluated taking into account the spin-spin coupling, calculated from the equilibrium structure of the molecule, and the spin-rotation coupling, evaluating the coupling constant for J = 1 from Kukolich (1967) and Garvey et al. (1976). When these additional hyperfine couplings were included, they were found to marginally affect the line parameters. In particular, the line width is at most altered by a few percents (see Sect. 4). Therefore, these effects are neglected below.
Hyperfine parameters.
4. Modeling
The HFS method of the CLASS software6 allows quickly analyzing hyperfine spectra. In particular, it gives some basic parameters of the lines, such as the width Δv of the individual transitions or the opacity summed over all the hyperfine components τtot. The total column density of a molecule can be inferred from the parameters obtained with the HFS fit using the relation (see, e.g., Bacmann et al. 2010; Mangum & Shirley 2015) 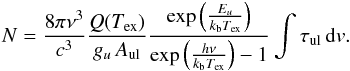 (1)As explained in Bacmann et al. (2010), the integration of the opacity over velocity for the u → l component can be related to the total opacity τtot given by the HFS fit through
(1)As explained in Bacmann et al. (2010), the integration of the opacity over velocity for the u → l component can be related to the total opacity τtot given by the HFS fit through 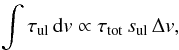 (2)where sul is the line-strength associated with the isolated hyperfine transition. The line width that enters this expression is associated with thermal and nonthermal processes, that is, with the motion of molecules at microscopic (temperature) and macroscopic (turbulence) scales. This expression is routinely used in astrophysical applications. In the particular case of NH2D, this relation is often applied to the analysis of the 86 or 110 GHz lines, with the aim to place constraints on the deuterium fraction (see, e.g., Olberg et al. 1985; Tiné et al. 2000; Roueff et al. 2005; Busquet et al. 2010; Fontani et al. 2015).
(2)where sul is the line-strength associated with the isolated hyperfine transition. The line width that enters this expression is associated with thermal and nonthermal processes, that is, with the motion of molecules at microscopic (temperature) and macroscopic (turbulence) scales. This expression is routinely used in astrophysical applications. In the particular case of NH2D, this relation is often applied to the analysis of the 86 or 110 GHz lines, with the aim to place constraints on the deuterium fraction (see, e.g., Olberg et al. 1985; Tiné et al. 2000; Roueff et al. 2005; Busquet et al. 2010; Fontani et al. 2015).
In the case of NH2D, the hyperfine structure induced by the D nucleus is not resolved in astrophysical media since the broadening of the lines due to non-thermal motions is larger than the hyperfine splitting. Hence, it seems reasonable to analyze the lines just taking into account the hyperfine structure induced by the 14N nucleus. Doing so, the HFS method applied to the H-MM1 observations described in the previous section leads to these parameters for the p-NH2D lines:
-
110 GHz: τtot = 2.2 ± 0.6 and Δv = 0.33 ± 0.02 km s-1
-
333 GHz: τtot = 2.0 ± 0.8 and Δv = 0.20 ± 0.02 km s-1
and for the o-NH2D lines, to
-
86 GHz: τtot = 5.1 ± 0.3 and Δv = 0.37 ± 0.01 km s-1
-
333 GHz: τtot = 2.2 ± 0.3 and Δv = 0.24 ± 0.01 km s-1.
Different transitions of a molecule should have similar intrinsic line widths if they originate from the same region of the cloud. In astrophysical sources, this condition is not necessarily fulfilled: if the source harbors density or temperature gradients, lines with different critical densities are formed in different parts of the cloud. The factor ~1.6 ± 0.3 found between the line widths of the 111–101 and 101–000 transitions of o/p-NH2D is puzzling, however, because all four transitions have high critical densities (7 × 104–7 × 105 cm-3), all the observations have similar spatial resolutions (see Sect. 2), and finally, because NH2D should be strongly concentrated in the center of the core for chemical reasons. We would thus expect these lines to probe the same volume of gas, and we should, in principle, derive similar values for Δv.
Line list of the 111–101 o/p-NH2D transitions, with the hyperfine structure that is due to the nitrogen and deuterium nuclei.
 |
Fig. 1 Left panels: fit of the o-NH2D lines at 86 GHz (upper panel) and 333 GHz (lower panel) with the hyperfine structure caused by the D nucleus. Right panels: fit of the p-NH2D lines at 110 GHz (upper panel) and 333 GHz (lower panel). Note that fits of similar quality are obtained if the hyperfine structure caused by D is omitted. |
 |
Fig. 2 Line-strengths, normalized and centered on rest frequencies, for the 86 GHz and 333 GHz lines of o-NH2D. The spectroscopy shown in black accounts for the coupling with D, the spectroscopy shown in red only accounts for N. |
By taking into account the splitting induced by the D nucleus (see Tables 2 and 3), the parameters derived from the HFS method are for p–NH2D
-
110 GHz: τtot = 2.2 ± 0.7 and Δv = 0.23 ± 0.02 km s-1
-
333 GHz: τtot = 1.4 ± 0.8 and Δv = 0.19 ± 0.02 km s-1
and for the o-NH2D
-
86 GHz: τtot = 5.2 ± 0.5 and Δv = 0.24 ± 0.01 km s-1
-
333 GHz: τtot = 2.3 ± 0.4 and Δv = 0.23 ± 0.01 km s-1.
The corresponding fits of the o/p-NH2D hyperfine transitions are compared to the observations in Fig. 1. For both spin isomers, we find that the differences between the line widths are largely reduced, they are now at most ~20%. In particular, we find that the effect is strongest for the 86 and 110 GHz lines, while the two lines at 333 GHz have similar line widths regardless of whether the hyperfine structure induced by the D nucleus is taken into account or not. This difference between the lines comes from the spectroscopy and is illustrated in Fig. 2 for the o-NH2D spin isomer (the description that follows would be similar for p-NH2D). This figure shows that the number of hyperfine components is limited for the 101–000 transitions. Additionally, for these lines, the spread in velocity of the hyperfine components is reduced by comparison to the spread of hyperfine components in the 111–101 transitions. For the latter transitions, a reduced Δv therefore results when the coupling with D is taken into account. Finally, for the 86 and 110 GHz transitions, the estimates of τtot are similar for the two sets of line lists. As a result, according to Eqs. (1) and (2), the error made in the line width estimate will translate directly into the column density estimate. For the H-MM1 observations, the two estimates will typically differ by a factor of ~1.5, which is well above calibration errors.
5. Conclusion
We have observed the 111–101 and 101–000 lines of o/p-NH2D toward the prestellar core H-MM1 and calculated the hyperfine patterns of the observed transitions. We found that when the hyperfine splitting induced by the D nucleus is neglected (as done in previous studies), the line analysis leads to inconsistent results for the line widths of the two transitions of o/p-NH2D. For the two spin isomers, the widths of the 111–101 and 101–000 lines differ by a factor of 1.6 ± 0.3 if the D coupling is not taken into account. In contrast, the new line list gives similar line widths for all the transitions. An error in the line width will be transferred to the column density estimate, and the effect is particularly pronounced for the 111–101 lines of ortho- and para-NH2D at 86 and 110 GHz. The column density estimates derived from these lines when the hyperfine structure caused by D is taken into account or not differ by a factor of ~1.5 for H-MM1.
The HFS acronym stands for HyperFine Structure and a description of the method is available at www.iram.es/IRAMES/otherDocuments/postscripts/classHFS.ps
Acknowledgments
This work has been supported by the Agence Nationale de la Recherche (ANR-HYDRIDES), contract ANR-12-BS05-0011-01 and by the CNRS national program “Physico-Chimie du Milieu Interstellaire”. A.P., P.C. and J.P. acknowledge the financial support of the European Research Council (ERC; project PALs 320620). J.H. acknowledges support from the MPE and the Academy of Finland grant 258769. Partial salary support for A.P. was provided by a Canadian Institute for Theoretical Astrophysics (CITA) National Fellowship.
References
- Bacmann, A., Caux, E., Hily-Blant, P., et al. 2010, A&A, 521, L42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Busquet, G., Palau, A., Estalella, R., et al. 2010, A&A, 517, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caselli, P., & Dore, L. 2005, A&A, 433, 1145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cohen, E. A., & Pickett, H. M. 1982, J. Mol. Spectr., 93, 83 [Google Scholar]
- Coudert, L. H., & Roueff, E. 2006, A&A, 449, 855 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coudert, L. H., & Roueff, E. 2009, A&A, 499, 347 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Lucia, F. C., & Helminger, P. 1975, J. Mol. Spectr., 54, 200 [Google Scholar]
- Fontani, F., Busquet, G., Palau, A., et al. 2015, A&A, 575, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fusina, L., Di Lonardo, G., Johns, J. W. C., & Halonen, L. 1988, J. Mol. Spectr., 127, 240 [NASA ADS] [CrossRef] [Google Scholar]
- Garvey, R. M., Lucia, F. C. D., & Cederberg, J. W. 1976, Molec. Phys., 31, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Güsten, R., Nyman, L. Å., Schilke, P., et al. 2006, A&A, 454, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heyminck, S., Kasemann, C., Güsten, R., de Lange, G., & Graf, U. U. 2006, A&A, 454, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johnstone, D., Di Francesco, J., & Kirk, H. 2004, ApJ, 611, L45 [Google Scholar]
- Kukolich, S. G. 1967, Phys. Rev., 156, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Kukolich, S. G. 1968, J. Chem. Phys., 49, 5523 [Google Scholar]
- Mangum, J. G., & Shirley, Y. L. 2015, PASP, 127, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Olberg, M., Bester, M., Rau, G., et al. 1985, A&A, 142, L1 [NASA ADS] [Google Scholar]
- Parise, B., Belloche, A., Du, F., Güsten, R., & Menten, K. M. 2011, A&A, 528, C2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roueff, E., Lis, D. C., van der Tak, F. F. S., Gerin, M., & Goldsmith, P. F. 2005, A&A, 438, 585 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thaddeus, P., Krisher, L. C., & Loubser, J. H. N. 1964, J. Chem. Phys., 40, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Tiné, S., Roueff, E., Falgarone, E., Gerin, M., & Pineau des Forêts, G. 2000, A&A, 356, 1039 [NASA ADS] [Google Scholar]
All Tables
Line list of the 111–101 o/p-NH2D transitions, with the hyperfine structure that is due to the nitrogen and deuterium nuclei.
All Figures
 |
Fig. 1 Left panels: fit of the o-NH2D lines at 86 GHz (upper panel) and 333 GHz (lower panel) with the hyperfine structure caused by the D nucleus. Right panels: fit of the p-NH2D lines at 110 GHz (upper panel) and 333 GHz (lower panel). Note that fits of similar quality are obtained if the hyperfine structure caused by D is omitted. |
| In the text | |
 |
Fig. 2 Line-strengths, normalized and centered on rest frequencies, for the 86 GHz and 333 GHz lines of o-NH2D. The spectroscopy shown in black accounts for the coupling with D, the spectroscopy shown in red only accounts for N. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


