| Issue |
A&A
Volume 586, February 2016
|
|
|---|---|---|
| Article Number | A108 | |
| Number of page(s) | 24 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201527441 | |
| Published online | 03 February 2016 | |
New and updated convex shape models of asteroids based on optical data from a large collaboration network
1
Centre National d’Études Spatiales, 2 place Maurice Quentin, 75039
Paris Cedex 01,
France
e-mail: hanus.home@gmail.com
2
Laboratoire Lagrange, UMR7293, Université de la Côte d’Azur, CNRS,
Observatoire de la Côte d’Azur, Blvd de l’Observatoire, CS
34229, 06304
Nice Cedex 4,
France
3
Astronomical Institute, Faculty of Mathematics and Physics,
Charles University in Prague, V
Holešovičkách 2, 18000
Prague, Czech
Republic
4
Astronomical Observatory Institute, Faculty of Physics, A.
Mickiewicz University, Słoneczna
36, 60-286
Poznań,
Poland
5
Geneva Observatory, 1290
Sauverny,
Switzerland
6
Aix Marseille Université, CNRS, OHP (Observatoire de Haute
Provence), Institut Pythéas (UMS 3470), 04870
Saint-Michel-l’Observatoire,
France
7
Centre for Science at Extreme Conditions, The University of
Edinburgh, Erskine Williamson
Building, Peter Guthrie Tait Road, Edinburgh, EH9
3FD, UK
8
Association T60, Observatoire du Pic du Midi,
65200
Bagnères-de-Bigorre,
France
9
Observatoire des Hauts Patys, 84410
Bédoin,
France
10
Observatoire de Chinon, Mairie de Chinon, 37500
Chinon,
France
11 Villefagnan
Observatory, France
12 Harfleur Observatory,
France
13
490 chemin du gonnet,
38440
Saint Jean de Bournay,
France
14
Observatoire des Engarouines, 1606 chemin de Rigoy, 84570
Malemort-du-Comtat,
France
15
Collonges Observatory, 90 allée des résidences, 74160
Collonges,
France
16
SUPA, School of Physics & Astronomy,
North Haugh, St Andrews, KY16 9SS, UK
17
Via Capote Observatory, Thousand Oaks, CA
91320,
USA
18
Le Florian, Villa 4, 880 chemin de Ribac-Estagnol,
06600
Antibes,
France
19
Observatoire de Dauban, 04150
Banon,
France
20
Levendaal Observatory, Uiterstegracht 48, 2312 TE
Leiden, The
Netherlands
21
European Southern Observatory, La Silla, Coquimbo, Chile
22
Eurac Observatory, Bolzano/Bozen,
Italy
23
Vallemare di Bordona, Rieti, Italy
24
Observatorio Astronómico Caimari, 07144
Costitx,
Spain
25
Observatoire de Durtal, 49430
Durtal,
France
26
OAM - Mallorca, 07144
Costitx,
Spain
27
20 parc des Pervenches,
13012
Marseille,
France
28
Agrupación Astronómica de Sabadell, Apartado de Correos 50, PO Box 50, 08200
Sabadell, Barcelona, Spain
29
Observatorio El Vendrell, 1193
Trragona,
Spain
30
AFOEV (Association Française des Observateurs d’Etoiles
Variables), Observatoire de
Strasbourg 11, rue de l’Université, 67000
Strasbourg,
France
31
Observatori d’Ager, 08014
Barcelona,
Spain
32
Stazione Astronomica di Sozzago, 28060
Sozzago,
Italy
33
Santa Lucia Stroncone, 05039
Stroncone,
Italy
34
Institut d’Astrophysique de l’Université Liège,
Allèe du 6 Aout 17,
4000
Liège,
Belgium
35 Haleakala-Faulkes Telescope
North, Hawaii,
USA
36
Seine-Maritime, Le Havre, 76600
Haute-Normandie,
France
37
Village-Neuf Observatory, 9bis rue du Sauvage, 68300
Saint-Louis,
France
38
Mt. Suhora Observatory, Pedagogical University.
Podchorążych 2, 30-084, Cracow, Poland
39
Shed of Science Observatory, 5213 Washburn Ave. S, Minneapolis, MN
55410,
USA
40 Waterlooville,
UK
41
Observatoire St-Martin, 31 grande rue, 25330
Amathay Vésigneux,
France
42
Observatorio CEAM, Caimari, Canary Islands, Spain
43
Florida Gulf Coast University, 10501 FGCU Boulevard South, Fort Myers, FL
33965,
USA
44
Observatoire du Bois de Bardon, 16110
Taponnat,
France
45
Association T60, 14 avenue Edouard Belin, 31400
Toulouse,
France
46
Osservatorio l’Ampolla, Tarragona, Spain
47
International Occultation Timing Association,
Montgomery, AL, USA
48
Club d’Astronomie de Lyon Ampere (CALA),
Place de la Nation,
69120
Vaulx-en-Velin,
France
49 LinhaceiraObservatory,
Portugal
50
Hong Kong Space Museum, Tsimshatsui, Hong Kong, PR China
51
Institute of Planetary Research, German Aerospace Center, Rutherfordstrasse 2,
12489
Berlin,
Germany
52
Astroqueyras, Mairie, 05350
Saint-Véran,
France
53
51 Centre astronomique de la Couyère, La Ville
d’ABas, 35320
La Couyère,
France
54
Hunters Hill Observatory, 7 Mawalan Street, Ngunnawal
ACT
2913,
Australia
55
Observatoire des Terres Blanches, 04110
Reillanne,
France
56
Department of Physics, University of Strathclyde,
16 Richmond Street,
Glasgow
G1 1XQ,
UK
57
Guitalens Observatory, 5 chemin d’En Combes, 81220
Guitalens,
France
58
Observatoire Les Makes, G. Bizet 18, 97421
La Rivière,
France
59
980 Antelope Drive West,
Bennett, CO
80102,
USA
60 Institute of Astronomy of Kharkiv
Karazin National University, Kharkiv 61022, Sumska Str. 35, Ukraine
61
Severní 765, 50003
Hradec Králové, Czech
republic
62
Uranoscope, Avenue Carnot 7, 77220
Gretz-Armainvilliers,
France
63 Observatoire OPERA,
France
64
Instituto de Astrofísica de Andalucía,
CSIC, Apdo. 9481, 08080
Barcelona,
Spain
65 Mulheim-Ruhr,
Germany
66 Tzec Maun Foundation
Observatory, Mayhill,
New Mexico,
US
67
Observatorio Montcabrer, C/Jaume Balmes nb 24, Cabrils
08348
Barcelona,
Spain
68
Kingsgrove, NSW, Australia
69
Sant Gervasi Observatory, 08022
Barcelona,
Spain
70
4438 Organ Mesa Loop,
Las Cruces, NM
88011,
USA
71
Rue des Ecoles 2,
34920
Le Crès,
France
72
11 rue François-Nouteau,
49650
Brain-sur-Allonnes,
France
73
Ottmarsheim Observatory, 5 rue du Lièvre, 68490
Ottmarsheim,
France
74
Université Claude BERNARD Lyon 1. Observatoire de Pommier,
POMMIER, 63230
Chapdes-Beaufort,
France
75
4 rue de la Bruyère,
37500
La Roche Clermault,
France
76
Observatoire de Blauvac, 293 chemin de St Guillaume, 84570
Blauvac,
France
77
Shadowbox Observatory, 12745
Crescent Drive, Carmel, IN
46032,
USA
78
Lowell Observatory, Flagstaff, AZ
86001,
USA
79 Savigny-le-Temple,
France
80
Observatorio Amanecer de Arrakis, MPC274 Alcalá de Guadaíra, Sevilla, Spain
81
Gnosca Observatory, 6525
Gnosca,
Switzerland
82
DeKalb Observatory, 2507 CR 60, Auburn, IN
46706,
USA
83
Center for Solar System Studies, 9302 Pittsburgh Ave, Suite 105, Rancho Cucamonga, CA
91730,
USA
84
School of Physics and Astronomy, University of
Edinburgh, James Clerk Maxwell
Building, Peter Guthrie Tait Road, Edinburgh, EH9
3FD, UK
85
European Space Astronomy Centre, ESA, PO Box 78, 28691
Villanueva de la Cañada,
Madrid,
Spain
86 Ironwood North,
Hawaii,
USA
87 Centre de Recherche en Astronomie,
Astrophysique et Géophysique, BP
63
Bouzereah,
Algiers
88
Astronomical Observatory of Jagiellonian University,
ul. Orla 171, 30-244
Kraków,
Poland
Received: 24 September 2015
Accepted: 22 October 2015
Context. Asteroid modeling efforts in the last decade resulted in a comprehensive dataset of almost 400 convex shape models and their rotation states. These efforts already provided deep insight into physical properties of main-belt asteroids or large collisional families. Going into finer detail (e.g., smaller collisional families, asteroids with sizes ≲20 km) requires knowledge of physical parameters of more objects.
Aims. We aim to increase the number of asteroid shape models and rotation states. Such results provide important input for further studies, such as analysis of asteroid physical properties in different populations, including smaller collisional families, thermophysical modeling, and scaling shape models by disk-resolved images, or stellar occultation data. This provides bulk density estimates in combination with known masses, but also constrains theoretical collisional and evolutional models of the solar system.
Methods. We use all available disk-integrated optical data (i.e., classical dense-in-time photometry obtained from public databases and through a large collaboration network as well as sparse-in-time individual measurements from a few sky surveys) as input for the convex inversion method, and derive 3D shape models of asteroids together with their rotation periods and orientations of rotation axes. The key ingredient is the support of more that 100 observers who submit their optical data to publicly available databases.
Results. We present updated shape models for 36 asteroids, for which mass estimates are currently available in the literature, or for which masses will most likely be determined from their gravitational influence on smaller bodies whose orbital deflections will be observed by the ESA Gaia astrometric mission. Moreover, we also present new shape model determinations for 250 asteroids, including 13 Hungarias and three near-Earth asteroids. The shape model revisions and determinations were enabled by using additional optical data from recent apparitions for shape optimization.
Key words: minor planets, asteroids: general / techniques: photometric / methods: observational / methods: numerical
© ESO, 2016
1. Introduction
Asteroid modeling efforts in the last decade resulted in an extensive dataset of almost 400 convex shape models and rotation states (see the review by Ďurech et al. 2015a). The majority of these models was determined by the lightcurve inversion method (LI) developed by Kaasalainen & Torppa (2001) and Kaasalainen et al. (2001). About 100 models are based on disk-integrated, dense-in-time optical data (e.g., Torppa et al. 2003; Slivan et al. 2003; Michałowski et al. 2005; Marciniak et al. 2009, 2011). Combining dense-in-time data with sparse-in-time measurements from large sky surveys, or using only sparse-in-time data, increased the number of available shape models by a factor of 4 (Ďurech et al. 2009; Hanuš et al. 2011, 2013a,c). Future data from Gaia, Panoramic Survey Telescope and Rapid Response System (PanSTARRS), and Large Synoptic Survey Telescope (LSST) should result in an increase of shape models by an order of at least one magnitude (Ďurech et al. 2005). The methods that will be used for analysis of these future data of unprecedented amount and quality, by the means of complex shape modeling, are similar to those applied here and developed within the scope of our recent studies.
Most asteroid shape models derived by the LI method and their optical data are available in the Database of Asteroid Models from Inversion Techniques (DAMIT1; Ďurech et al. 2010).
We would like to emphasize and acknowledge that the shape modeling stands on the shoulders of hundreds of observers, often amateurs, who regularly obtain photometric data with their small and mid-sized telescopes. These observations have significantly contributed to the great progress of the shape modeling field in the last decade. Although there is much more sparse than dense data available, the latter will always remain important because their much higher photometric accuracy and rotation coverage leads to higher quality shape models. This is a typical example of the great interaction between the professional and amateur community (Mousis et al. 2014).
Knowing the rotational parameters and shapes of asteroids is very important for numerous applications. The large amount of currently known asteroid models already provided a deep insight into physical properties of main-belt asteroids (MBAs) and large collisional families: (i) an excess of prograde rotators within (MBAs) larger than ~50 km in diameter, predicted by numerical simulations (Johansen & Lacerda 2010), was confirmed by Kryszczyńska et al. (2007), Hanuš et al. (2011); (ii) an excess of retrograde rotators within near-Earth asteroids (NEAs) is consistent with the fact that most of the NEAs come from the ν6 resonance (La Spina et al. 2004). To enter the ν6 resonance via Yarkovsky effect2, the object must be a retrograde rotator; (iii) an anisotropy of spin-axis directions of MBAs asteroids with diameters ≲30 km and NEAs was revealed and explained by the YORP effect3, collisions, and mass shedding (Hanuš et al. 2011; Pravec et al. 2012); (iv) a bimodality of prograde and retrograde rotators symmetric with respect to the center of the family is caused by the combined Yarkovsky, YORP, and collisional dynamical evolution (Kryszczyńska 2013; Hanuš et al. 2013a); (v) the larger dispersion of spin-axis directions of smaller (D ≲ 50 km) prograde than retrograde asteroids suggests that spin states of prograde rotators are affected by resonances (Hanuš et al. 2013c); or (vi) the disruption of asteroid pairs4 was most likely the outcome of the YORP effect that spun up the original asteroid (Polishook 2014).
With the use of convex shape models in combination with asteroidal stellar occultations and disk-resolved images obtained by space telescopes or ground-based telescopes equipped with adaptive optics (AO) systems, the size of the model can be constrained, making it possible to determine the asteroid volume. Even when the object is considerably nonconvex, the scaled convex model from occultations and AO data tends to compensate by average fitting to the disk-resolved data. As a result, the overestimation of the volume is smaller than would correspond to the convex hull. The volume can then provide, in combination with mass estimates, realistic values of bulk densities (Ďurech et al. 2011; Hanuš et al. 2013b).
The mass is one of the most challenging parameters to measure for an asteroid. Mass estimates are now available for 280 asteroids, but only 113 of these are more precise than 20% (Carry 2012; Scheeres et al. 2015). However, the situation is expected to improve significantly in the near future. The observations of the ESA Gaia astrometric satellite will provide masses accurate to better than 50% for ≈150 asteroids (and for ≈50 with an accuracy better than 10%; Mouret et al. 2007, 2008) by the orbit deflection method. The advantage of the masses determined by Gaia is in the uniqueness of the mission: we should obtain a comprehensive sample with well-described biases (e.g., the current mass estimates are currently strongly biased toward the inner main belt).
To maximize the possible outcome by means of density determinations, we focus on determination of shape models for asteroids for which accurate mass estimates are available or will most likely be determined by Gaia. Moreover, it is also important to update shape models for such asteroids using recently obtained optical data. By doing this, we can provide better constraints on the rotational phase (i.e., on the asteroid orientation, which is important for scaling the size) of these asteroids due to the improvement of the rotation period, and more accurate rotation state and shape parameters.
Convex models, together with thermal infrared observations, have also been used as inputs for thermophysical modeling, enabling the determination of geometric visible albedo, size, and surface properties (e.g., Müller et al. 2011; Hanuš et al. 2015). This application is particularly important because it can make use of the large sample of infrared data for more than 100 000 asteroids acquired by the NASA’s Wide-field Infrared Survey Explorer (WISE). The missing input here is shape models of sufficient quality (Delbo et al. 2015).
Moreover, convex models or at least rotational states are usually necessary inputs for more complex shape modeling, which can be performed if additional data, such as stellar occultations, AO images or interferometry containing information about the nonconvexities, (Kaasalainen & Viikinkoski 2012; Carry et al. 2010a,b, 2012; Viikinkoski et al. 2015; Tanga et al. 2015) are available.
Finally, large flat areas/facets on convex shape models, represented by polyhedra, usually indicate possible concavities (Devogèle et al. 2015). Candidates for highly irregular bodies can be identified for further studies.
In Sect. 2, we introduce the dense- and sparse-in-time optical disk-integrated data, which we used for the shape model determinations. We describe the lightcurve (convex) inversion method in Sect. 3, present updated and new shape model determinations in Sects. 4.1 and 4.2, comment on several individual solutions in Sect. 4.3, and conclude our work in Sect. 5.
2. Optical disk-integrated photometry
Similar to Hanuš et al. (2011, 2013a,c), we use two different types of optical disk-integrated data: (i) dense-in-time photometry, i.e., classical continuous multihour observations; and (ii) sparse-in-time photometry consisting of a few hundred individual calibrated measurements from several astrometric observatories, typically covering ~15 years.
Dense photometry was acquired from publicly available databases, from those of our collaborators, or directly from several individual observers. The historical data from the second half of the twentieth Century are mainly stored in the Asteroid Photometric Catalogue (APC5; Piironen et al. 2001). Currently, the common practice, which is used mostly by observers from the United States, is a regular data submission to the Minor Planet Center in the Asteroid Lightcurve Data Exchange Format (ALCDEF6; Warner et al. 2011). These data are publicly available and often also published in the Minor Planet Bulletin7, where the synodic rotation period is reported. Many European observers send their data to the Courbes de rotation d’astéroïdes et de comètes database (CdR8), maintained by Raoul Behrend at Observatoire de Genève. Composite lightcurves with best-fitting synodic rotation periods are then published on the web page.
We obtained the first type of sparse-in-time photometric data for this study from the AstDyS site (Asteroids – Dynamic Site9) and processed the data according to Hanuš et al. (2011). We solely employ sparse data from the USNO-Flagstaff station (IAU code 689) and the Catalina Sky Survey Observatory (IAU code 703, Larson et al. 2003), weighting them with respect to dense data (unity weight) by 0.3 and 0.15, respectively. As an alternative to this type of sparse-in-time data, we use the Lowell Photometric Database (Oszkiewicz et al. 2011; Bowell et al. 2014). The photometry from several astrometric surveys, including both USNO-Flagstaff and Catalina Sky Survey, reported to the Minor Planet Center (MPC), was reprocessed; e.g., systematic effects in the magnitude calibration were removed. This enormous dataset typically consists of several hundreds of individual measurements for each of the ~320 000 asteroids that were processed so far. Although the accuracy of the recalibrated photometry is improved, the dataset for each asteroid is still a mixture of measurements from several observatories with different photometric quality. Compared to the data of USNO-Flagstaff and Catalina observatories downloaded from AstDyS, Lowell data provide an increased quantity of measurements from more observing geometries. These data, however, are, on average, of poor photometric quality, as they also contain measurements from observatories that were originally rejected in Hanuš et al. (2011) owing to low accuracy. We assigned to Lowell data the weight of 0.1. A subset of Lowell data was already analyzed by Ďurech et al. (2013) and a complex analysis of the reliability of shape models, based solely on these data, is underway (Ďurech et al. 2016). On top of that, the volunteer project Asteroids at home10, which makes use of distributed computing and runs in the framework of Berkeley Open Infrastructure for Network Computing (BOINC), currently employs shape model computations based on Lowell data (Ďurech et al. 2015b). Thousands of individual home computational stations of volunteers are currently participating in the project.
Tables 1 and A.1 include the information about the optical data used for the shape model determination, such as the number of dense-in-time lightcurves and apparitions covered by dense-in-time observations and the number of sparse-in-time measurements from corresponding astrometric surveys. Table A.2 provides references to the dense data used for the shape model determinations and Table A.3 links the observers to their observatories.
Rotational states and summary of used photometry for asteroids for which we updated their shape models based on new disk-integrated optical data.
3. Convex inversion and reproducibility
In this work, we use the lightcurve inversion method of Kaasalainen & Torppa (2001) and Kaasalainen et al. (2001), which is already a well-documented, investigated, and employed technique for asteroid shape modeling (for more details, see the review by Ďurech et al. 2015a).
The main advantage of using convex inversion is that convex models are usually the only stable or unambiguous inversion result (Ďurech & Kaasalainen 2003); they best portray the resolution level or information content of disk-integrated photometry. To demonstrate this more intuitively, consider an asteroid with a large planar region (or many regions) on the surface (e.g., an ellipsoid with a sizable chunk or chunks chopped off), and a large crater (say, half the size of the plane) at one end of the plane. Then it is impossible to tell from lightcurve data (no matter how large solar phase angles, i.e., shadows) where the crater is in the plane, or whether it is two craters half the size, or even myriads of small craters on the surface that have the same combined area as the big one (even if the crater filled most of the plane). In other words, one simply cannot say whether the lightcurves are caused just by small-scale surface roughness on a convex shape, or by huge nonconvexities that would be obvious in any disk-resolved data. Hence, any nonconvex model from disk-integrated photometric data is inevitably ambiguous, while the convex model is unambiguous. This also explains why the assumption of the nonconvexity represented by a large plane in the convex model (e.g., Devogèle et al. 2015), while often a good guess because of physical constraints, cannot usually be more than an assumption.
Convex inversion was successfully used for shape model determinations of almost 400
asteroids. On top of that, several convex models were validated by disk-resolved and
delay-Doppler images or by direct comparison with images obtained by space probes (e.g.,
Kaasalainen et al. 2001; Carry et al. 2012). The parameter space of shape, rotation period, spin
vector orientation, and scattering properties (simple three-parameter empirical model) is
systematically investigated in the means of a χ2-metric 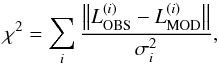 (1)where the ith brightness measurement
(1)where the ith brightness measurement
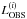 (with an uncertainty of σi) is compared to the
corresponding modeled brightness
(with an uncertainty of σi) is compared to the
corresponding modeled brightness 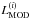 . The best-fitting parameter set is searched
for.
. The best-fitting parameter set is searched
for.
A significant minimum in the parameter space indicates a unique solution. Visual examination of the fit in the period subspace is performed as well as the comparison between observed and modeled lightcurves. Additionally, the pole-ecliptic latitudes should be similar within the two pole solutions, which are typically determined as a result of the ambiguity (symmetry) presented in most lightcurve inversion models (Kaasalainen & Lamberg 2006). On the other hand, the pole-ecliptic longitudes of these so-called mirror solutions should differ by ~180 degrees. The pole ambiguity is present in the majority of our shape models.
Moreover, we also compute the principal moments of inertia of each shape model, assuming a homogeneous mass distribution, and compare these moments with the moment of inertia along the rotation axis. A reliable solution should rotate within ~10–20 degrees of the axis with the largest moment of inertia.
If available, we use a priori information about the rotation period of the asteroid from the Minor Planet Lightcurve Database11 (Warner et al. 2009) to significantly reduce, usually by at least two orders of magnitude, computation requirements. Hence, we investigate the parameter space only in the proximity of the expected rotation period.
It should be kept in mind that none of the shape models should be taken as granted, i.e., each asteroid model contains an uncertainty (both in shape and rotation state), which increases with decreasing amount, variety, and quality of the optical data. It was already shown in Hanuš et al. (2015) that by varying a shape model within its uncertainty, one can obtain significantly different fits to the thermal infrared data by the thermophysical modeling. Thus, the shape uncertainty plays an important role for the interpretation of the thermal infrared data. This demonstrates the need of accounting for the shape model uncertainties in all further shape model applications. Also, the overall shape model based mostly on sparse data usually contains many flat facets (areas) with rather sharp edges, thus most of the low-detail topography is hidden (i.e., we have a large uncertainty in the shape). As we use more dense data, the shape becomes smoother and has more details. This limits the application of the lower-resolution shape models based mostly on sparse data.
In the ecliptic coordinate frame, the typical pole direction uncertainties are: (i) ≲5° in latitude β and ≲5°/cosβ in longitude λ for asteroid models based on large multiapparition dense lightcurve datasets; (ii) ~5−10° in β and ~5−10°/cosβ in λ for models based on combined multiapparition dense data and sparse-in-time measurements; and finally; (iii) ~10−30° in β and ~10−30°/cosβ in λ for models based on combined few-apparition dense data with sparse-in-time measurements or only sparse-in-time data.
To sum up, we follow the same procedure for the shape model determinations as in Hanuš et al. (2011, 2013a,c). Finally, we would like to emphasize that our work can be easily reproduced by anyone who is interested. The LI code and the lightcurve data are available in DAMIT, as well as the user manual.
4. Results and discussions
4.1. Updated shape models
We updated shape models of 36 asteroids with known mass estimates or for which masses will be most likely determined by the orbit deflection method from the Gaia astrometric observations (Mouret et al. 2007, 2008, and personal communication with François Mignard). For each one of these asteroids, there were new available optical dense data (see Table A.2). We combined these new data with Lowell data and the already available dense photometry from DAMIT. If applicable, we replaced the original sparse data from AstDyS with the Lowell data.
In most cases, rotational states of updated shape models are similar to those of the original models in the DAMIT database. The only exceptions, which we individually commented on in Sect. 4.3, are asteroids (27) Euterpe, and (532) Herculina. We performed the LI independently from any previous shape modeling results (e.g., we did not use information about the spin axis).
Updated models provide better constraints on the rotational phase, thus these models allow us, for example, to better link recently obtained AO and occultation profiles with the orientation of the shape model at the time of the observation. This is essential for a potential scaling of the sizes of shape models to compute the volume, and consequently bulk densities. Obviously, the uncertainties in rotation period, spin axis direction, and shape model should be improved as there are more data used for the modeling.
Optimized rotation state parameters and information about optical data are listed in Table 1. References to the optical dense-in-time data can be found in Table A.2.
4.2. New shape models
The majority of our new shape model determinations is obtained by combining dense-in-time data with sparse-in-time measurements from the Lowell database. However, the fact that Lowell data contain for each asteroid a mixture of measurements from several observatories makes it difficult to find a representative weight with respect to the dense data. Indeed, a specific single value of the weight can result in an overestimation for some asteroids, while it can underestimate others. Despite these issues, we decided to use a weight of 0.1 for the Lowell data as a whole and to present corresponding shape models. As a consequence, we sometimes obtained a unique shape solution if we combined dense data and the sparse data from AstDyS (i.e., from USNO and Catalina), but not if we used the Lowell data instead. We present these shape models as well.
Moreover, 57 out of 250 shape models are based only on sparse data from USNO-Flagstaff and Catalina Sky Survey observatories. That these models can nevertheless be reliable was already shown in Hanuš & Ďurech (2012) and Hanuš et al. (2013c). As suggested there, we ran the LI search for shape and rotation state parameters with two different shape resolutions: (i) standard one; and (ii) lower one, which serves as a test of the solution stability. For this case, the asteroid’s synodic rotation period is also available in the Minor Planet Lightcurve Database (LCDB, Warner et al. 2009), an additional test for the reliability can be performed. A rotation period derived by the LI (a period interval of 2–1000 h is typically scanned), which matches that already reported, points to a secure solution. In practice, all shape solutions based solely on sparse data that fulfilled our stability tests had rotation periods in an agreement with synodic periods from LCDB. This also demonstrates that our other unique solutions, for which a previous period estimate is not available, are reliable. We present nine of these shape and rotation state solutions; these are labeled in Table A.1.
We present shape models of three NEAs, which all have negative values of their pole latitudes β, and obliquities larger than 90°. The fact that they all show retrograde rotation supports the consensus that about half of the NEAs migrated through the ν6 secular resonance, which causes an observed excess of retrograde rotators (La Spina et al. 2004).
We further present shape models of 13 asteroids that are classified as Hungarias. The majority of them (10 out of 13) exhibit retrograde rotation, which is in an agreement with the findings of Warner et al. (2014), who reported, in a sample of 53 Hungarias, a 75% representation of retrograde rotators.
Thirty-one of the derived shape models are those asteroids whose density will be measured in future or was already obtained. While for some of them, estimations on their masses are already available, the masses of the others will be determined from Gaia astrometric measurements. Constraining the model sizes of these asteroids using disk-resolved images, stellar occultation data, or thermophysical modeling will directly facilitate estimation of bulk densities.
Rotation state parameters and information about used optical data for all new shape model determinations are listed in Table A.1. References to the optical dense-in-time data can be found in Table A.2.
4.3. Individual asteroids
(27) Euterpe. The lightcurve amplitude of this asteroid is very low (≲0.1 mag) and the dense data cover multiple apparitions. Thus, we decided to exclude the Lowell data from the shape modeling because they were dominated by noise. Our derived rotation period (10.40193 h) is slightly different than that derived by Stephens et al. (2012) (10.40825 h), which resulted in a different pole solution of (λ, β) = (82, 44)° and (λ, β) = (265, 39)° for the mirror solution. The solution in longitude λ is similar to that of Stephens et al. (2012), but their latitude has a different sign (−39 and −30, respectively).
(532) Herculina. Our (single) pole solution only differs by ~180° in longitude λ from that reported by Kaasalainen et al. (2002), thus it corresponds to their mirror solution. In contrast to their solution, our model is based on additional data from 2005 and 2010 apparitions.
(537) Pauly. The rotation period of 14.15 h from the LCDB is in contradiction with our shape modeling result: our period of 16.2961 h fits the data significantly better and thus is preferred.
(596) Scheila. The observations taken on December 11th, 2010 with the Catalina Schmidt telescope exhibited a comet-like appearance (Larson 2010). This behavior was later confirmed by Jewitt et al. (2011) from the HST observations on December 27th, 2010 and on January 4th, 2011 and interpreted as caused most likely by a collision with a 35m asteroid. All photometric data used for the shape modeling date prior to this event, so the shape model does not reflect any potential changes in the shape, period, or spin orientation induced by the collision (Bodewits et al. 2014).
(8567) 1996 HW1. The shape model of this NEAs was already determined by Magri et al. (2011) from a combination of dense lightcurves and radar Doppler images. We derived a consistent shape model and rotational state solution from combined dense and sparse data. The main difference between these two models is the fact that the Doppler images contain nonconvex signatures that were translated into their shape model. Even if our shape model is purely convex, it reliably represents the overall shape of the real asteroid. This case once again demonstrates the reliability of the convex inversion method.
(9563) Kitty. We derived the shape model of this asteroid without knowledge of a previous period estimate. However, Chang et al. (2015) recently reported period P = 5.35 ± 0.03 h based on the optical data from the Intermediate Palomar Transient Factory that is in perfect agreement with our independent determination of P = 5.38191 ± 0.00005 h.
5. Conclusions
In this work, we updated shape models of 36 asteroids with mass estimates by including new optical dense-in-time data in the shape modeling. For 250 asteroids, including 13 Hungarias and three NEAs, we derived their convex shape models and rotation states from combined disk-integrated dense- and sparse-in-time photometric data or from only sparse-in-time data. This effort was achieved with the help of the community of ~100 individual observers who shared their lightcurves. All new models are now included in the DAMIT database and are available to anyone for additional studies. For nine asteroids, we provide, together with shape models and pole orientations, their first rotation period estimates.
Our work is a typical example in which a contribution of hundreds of observers, who are regularly obtaining photometric data with their small and mid-sized telescopes, was necessary to achieve presented results. The initial motivation of the observers is to derive the synodic rotation period (sometimes this is an object of a publication in the Minor Planet Bulletin), however, the shape modeling provides a welcome additional opportunity for the usage of their optical data. We acknowledge all the observers who submit their observations to the public databases and invite others to do so as well. This practice allows us an easy and straightforward access to the data and largely avoids an overlook of the precious data.
The shape models can be used as inputs for various studies, such as spin-vector analysis, detection of concavities, thermophysical modeling with the varied-shape approach by Hanuš et al. (2015), nonconvex modeling, size optimization by disk-resolved images or occultation data, or density determinations.
Shape models based only on sparse data (or combined with a few dense lightcurves) are convenient candidates for follow-up observations, both to confirm the rotation periods and to improve the shape models, which is necessary, e.g., for thermophysical modeling. Finally, we maintain a web page with a list of asteroids, for which mass estimates are available and the shape model determination still requires additional photometric data (Hanuš 2015). These objects are candidates for accurate density determination and any lightcurve support is welcome.
A thermal recoil force affecting rotating asteroids (Bottke et al. 2001).
Yarkovsky–O’Keefe–Radzievskii–Paddack effect, a torque caused by the recoil force from anisotropic thermal emission, can alter the rotational periods and orientation of spin axes; see, e.g., Rubincam (2000), Vokrouhlický et al. (2003).
Acknowledgments
J.H. greatly appreciates the CNES post-doctoral fellowship program. J.H. and M.D. were supported by the project under the contract 11-BS56-008 (SHOCKS) of the French Agence National de la Recherche (ANR), JD by grant GACR 15-04816S of the Czech Science Foundation, DO by the grant NCN 2012/S/ST9/00022 of Polish National Science Center, and A. Marciniak by grant 2014/13/D/ST9/01818 of Polish National Science Center. We thank the referee, Mikko Kaasalainen, for his thorough review of our manuscript and his constructive comments and suggestions that led to a significant improvement of the text. The computations have been carried out on the “Mesocentre” computers, hosted by the Observatoire de la Côte d’Azur, and on the computational cluster Tiger at the Astronomical Institute of Charles University in Prague (http://sirrah.troja.mff.cuni.cz/tiger). Data from Pic du Midi Observatory were partly obtained with the 0.6 m telescope, a facility operated by observatoire Midi-Pyrénées and Association T60, an amateur association. The Joan Oró Telescope (TJO) of the Montsec Astronomical Observatory (OAdM) is owned by the Catalan Government and operated by the Institute for Space Studies of Catalonia (IEEC). We thank Franck Pino (INO-AZ) and Lech Mankiewicz (EU-HOU/Comenius) for the remote access to Ironwood North.
References
- Alkema, M. S. 2013a, Minor Planet Bulletin, 40, 133 [NASA ADS] [Google Scholar]
- Alkema, M. S. 2013b, Minor Planet Bulletin, 40, 68 [NASA ADS] [Google Scholar]
- Alton, K. B. 2011, Minor Planet Bulletin, 38, 8 [NASA ADS] [Google Scholar]
- Benishek, V. 2014, Minor Planet Bulletin, 41, 126 [NASA ADS] [Google Scholar]
- Berthier, J., Vachier, F., Marchis, F., Ďurech, J., & Carry, B. 2014, Icarus, 239, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Bodewits, D., Vincent, J.-B., & Kelley, M. S. P. 2014, Icarus, 229, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Bottke, W. F., Vokrouhlický, D., Brož, M., Nesvorný, D., & Morbidelli, A. 2001, Science, 294, 1693 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bowell, E., Oszkiewicz, D. A., Wasserman, L. H., et al. 2014, Meteor. Planet. Sci., 49, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Brinsfield, J. W. 2007a, Minor Planet Bulletin, 34, 58 [NASA ADS] [Google Scholar]
- Brinsfield, J. W. 2007b, Minor Planet Bulletin, 34, 108 [NASA ADS] [Google Scholar]
- Brinsfield, J. W. 2008a, Minor Planet Bulletin, 35, 179 [NASA ADS] [Google Scholar]
- Brinsfield, J. W. 2008b, Minor Planet Bulletin, 35, 86 [NASA ADS] [Google Scholar]
- Brinsfield, J. W. 2009, Minor Planet Bulletin, 36, 64 [NASA ADS] [Google Scholar]
- Brinsfield, J. W. 2010a, Minor Planet Bulletin, 37, 19 [NASA ADS] [Google Scholar]
- Brinsfield, J. W. 2010b, Minor Planet Bulletin, 37, 50 [NASA ADS] [Google Scholar]
- Brinsfield, J. W. 2011, Minor Planet Bulletin, 38, 73 [NASA ADS] [Google Scholar]
- Brinsfield, J. W. 2012, Minor Planet Bulletin, 39, 55 [NASA ADS] [Google Scholar]
- Buchheim, R. K. 2005, Minor Planet Bulletin, 32, 79 [NASA ADS] [Google Scholar]
- Buchheim, R. K. 2007, Minor Planet Bulletin, 34, 13 [Google Scholar]
- Buchheim, R. K. 2014, Minor Planet Bulletin, 41, 241 [NASA ADS] [Google Scholar]
- Cantu, S., Adolphson, M., Montgomery, K., & Renshaw, T. 2015, Minor Planet Bulletin, 42, 28 [NASA ADS] [Google Scholar]
- Carry, B. 2012, Planet. Space Sci., 73, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Carry, B., Dumas, C., Kaasalainen, M., et al. 2010a, Icarus, 205, 460 [NASA ADS] [CrossRef] [Google Scholar]
- Carry, B., Kaasalainen, M., Leyrat, C., et al. 2010b, A&A, 523, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carry, B., Kaasalainen, M., Merline, W. J., et al. 2012, Planet. Space Sci., 66, 200 [Google Scholar]
- Chang, C.-K., Ip, W.-H., Lin, H.-W., et al. 2015, ApJS, 219, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, M. 2010, Minor Planet Bulletin, 37, 89 [NASA ADS] [Google Scholar]
- Delbo, M., Mueller, M., Emery, J., Rozitis, B., & Capria, M. T. 2015, Asteroids IV, in press [Google Scholar]
- Descamps, P., Marchis, F., Durech, J., et al. 2009, Icarus, 203, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Devogèle, M., Rivet, J. P., Tanga, P., et al. 2015, MNRAS, 453, 2232 [NASA ADS] [Google Scholar]
- Ďurech, J., & Kaasalainen, M. 2003, A&A, 404, 709 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ďurech, J., Grav, T., Jedicke, R., Denneau, L., & Kaasalainen, M. 2005, Earth Moon Planets, 97, 179 [Google Scholar]
- Ďurech, J., Kaasalainen, M., Marciniak, A., et al. 2007, A&A, 465, 331 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ďurech, J., Kaasalainen, M., Warner, B. D., et al. 2009, A&A, 493, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ďurech, J., Sidorin, V., & Kaasalainen, M. 2010, A&A, 513, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ďurech, J., Kaasalainen, M., Herald, D., et al. 2011, Icarus, 214, 652 [NASA ADS] [CrossRef] [Google Scholar]
- Ďurech, J., Hanuš, J., Vančo, R., Oszkiewicz, D., & Bowell, E. 2013, in AAS/Division for Planetary Sciences Meeting Abstracts, 45, 304.05 [Google Scholar]
- Ďurech, J., Carry, B., Delbo, M., Kaasalainen, M., & Viikinkoski, M. 2015a, Asteroids IV, in press [Google Scholar]
- Ďurech, J., Hanuš, J., & Vančo, R. 2015b, Astronomy and Computing, 13, 80 [Google Scholar]
- Ďurech, J., Hanuš, J., Oszkiewicz, D., & Vančo, R. 2016, A&A, in press, DOI: 10.1051/0004-6361/201527573 [Google Scholar]
- Ferrero, A., Klinglesmith, III, D. K., & Pilcher, F. 2014, Minor Planet Bulletin, 41, 33 [NASA ADS] [Google Scholar]
- Hanuš, J. 2015, Minor Planet Bulletin, 42, 208 [NASA ADS] [Google Scholar]
- Hanuš, J., & Ďurech, J. 2012, Planet. Space Sci., 73, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Hanuš, J., Ďurech, J., Brož, M., et al. 2011, A&A, 530, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hanuš, J., Brož, M., Ďurech, J., et al. 2013a, A&A, 559, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hanuš, J., Marchis, F., & Ďurech, J. 2013b, Icarus, 226, 1045 [NASA ADS] [CrossRef] [Google Scholar]
- Hanuš, J., Ďurech, J., Brož, M., et al. 2013c, A&A, 551, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hanuš, J., Delbo, M.,Ďurech, J., & Alí-Lagoa, V. 2015, Icarus, 256, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Higgins, D. 2008, Minor Planet Bulletin, 35, 30 [NASA ADS] [Google Scholar]
- Higgins, D., & Goncalves, R. M. D. 2007, Minor Planet Bulletin, 34, 16 [NASA ADS] [Google Scholar]
- Higgins, D., & Pilcher, F. 2009, Minor Planet Bulletin, 36, 143 [NASA ADS] [Google Scholar]
- Higgins, D., & Warner, B. D. 2009, Minor Planet Bulletin, 36, 159 [NASA ADS] [Google Scholar]
- Higgins, D., Pravec, P., Kusnirak, P., et al. 2006a, Minor Planet Bulletin, 33, 89 [NASA ADS] [Google Scholar]
- Higgins, D., Pravec, P., Kusnirak, P., et al. 2006b, Minor Planet Bulletin, 33, 8 [NASA ADS] [Google Scholar]
- Higgins, D., Pravec, P., Kusnirak, P., Reddy, V., & Dyvig, R. 2006c, Minor Planet Bulletin, 33, 64 [NASA ADS] [Google Scholar]
- Jehin, E., Gillon, M., Queloz, D., et al. 2011, The Messenger, 145, 2 [NASA ADS] [Google Scholar]
- Jewitt, D., Weaver, H., Mutchler, M., Larson, S., & Agarwal, J. 2011, ApJ, 733, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Johansen, A., & Lacerda, P. 2010, MNRAS, 404, 475 [NASA ADS] [Google Scholar]
- Kaasalainen, M., & Lamberg, L. 2006, Inverse Problems, 22, 749 [Google Scholar]
- Kaasalainen, M., & Torppa, J. 2001, Icarus, 153, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Kaasalainen, M., & Viikinkoski, M. 2012, A&A, 543, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaasalainen, M., Torppa, J., & Muinonen, K. 2001, Icarus, 153, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Kaasalainen, M., Torppa, J., & Piironen, J. 2002, Icarus, 159, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Klinglesmith, III, D. A., Hanowell, J., Risley, E., et al. 2014, Minor Planet Bulletin, 41, 139 [NASA ADS] [Google Scholar]
- Klinglesmith, D. A., DeHart, A., Hanowell, J., & Hendrickx, S. 2015, Minor Planet Bulletin, 42, 101 [NASA ADS] [Google Scholar]
- Koff, R. A. 2001, Minor Planet Bulletin, 28, 77 [NASA ADS] [Google Scholar]
- Koff, R. A. 2002, Minor Planet Bulletin, 29, 25 [NASA ADS] [Google Scholar]
- Koff, R. A. 2004, Minor Planet Bulletin, 31, 58 [NASA ADS] [Google Scholar]
- Koff, R. A. 2005, Minor Planet Bulletin, 32, 32 [NASA ADS] [Google Scholar]
- Koff, R. A. 2006, Minor Planet Bulletin, 33, 31 [NASA ADS] [Google Scholar]
- Koff, R. A., & Brincat, S. M. 2000, Minor Planet Bulletin, 27, 49 [NASA ADS] [Google Scholar]
- Koff, R. A., & Brincat, S. M. 2001, Minor Planet Bulletin, 28, 67 [NASA ADS] [Google Scholar]
- Koff, R. A., Brincat, S. M., Stephens, R. D., & Pravec, P. 2001, Minor Planet Bulletin, 28, 46 [NASA ADS] [Google Scholar]
- Kryszczyńska, A. 2013, A&A, 551, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kryszczyńska, A., La Spina, A., Paolicchi, P., et al. 2007, Icarus, 192, 223 [NASA ADS] [CrossRef] [Google Scholar]
- La Spina, A., Paolicchi, P., Kryszczyńska, A., & Pravec, P. 2004, Nature, 428, 400 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Larson, S. M. 2010, IAU Circ., 9188, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, S., Beshore, E., Hill, R., et al. 2003, in BAAS, 35, AAS/Division for Planetary Sciences Meeting Abstracts 35, 982 [Google Scholar]
- Magri, C., Howell, E. S., Nolan, M. C., et al. 2011, Icarus, 214, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Marchis, F., Lainey, V., Descamps, P., et al. 2010, Icarus, 210, 635 [NASA ADS] [CrossRef] [Google Scholar]
- Marciniak, A., Michałowski, T., Hirsch, R., et al. 2009, A&A, 498, 313 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marciniak, A., Michałowski, T., Polińska, M., et al. 2011, A&A, 529, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marciniak, A., Bartczak, P., Santana-Ros, T., et al. 2012, A&A, 545, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martinez, L. E. 2012, Minor Planet Bulletin, 39, 25 [NASA ADS] [Google Scholar]
- Michałowski, T., Kaasalainen, M., Marciniak, A., et al. 2005, A&A, 443, 329 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miles, R., & Warner, B. D. 2009, Minor Planet Bulletin, 36, 66 [NASA ADS] [Google Scholar]
- Mouret, S., Hestroffer, D., & Mignard, F. 2007, A&A, 472, 1017 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mouret, S., Hestroffer, D., & Mignard, F. 2008, Planet. Space Sci., 56, 1819 [NASA ADS] [CrossRef] [Google Scholar]
- Mousis, O., Hueso, R., Beaulieu, J.-P., et al. 2014, Exp. Astron., 38, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, T. G., Ďurech, J., Hasegawa, S., et al. 2011, A&A, 525, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oey, J. 2006, Minor Planet Bulletin, 33, 96 [NASA ADS] [Google Scholar]
- Oey, J. 2008, Minor Planet Bulletin, 35, 132 [NASA ADS] [Google Scholar]
- Oey, J. 2009a, Minor Planet Bulletin, 36, 4 [NASA ADS] [Google Scholar]
- Oey, J. 2009b, Minor Planet Bulletin, 36, 162 [NASA ADS] [Google Scholar]
- Oey, J., Vilagi, J., Gajdos, S., Kornos, L., & Galad, A. 2007, Minor Planet Bulletin, 34, 81 [NASA ADS] [Google Scholar]
- Oey, J., Pilcher, F., Benishek, V., Higgins, D., & Pravec, P. 2012, Minor Planet Bulletin, 39, 86 [NASA ADS] [Google Scholar]
- Oszkiewicz, D. A., Muinonen, K., Bowell, E., et al. 2011, J. Quant. Spectr. Rad. Transf., 112, 1919 [NASA ADS] [CrossRef] [Google Scholar]
- Owings, L. E. 2009, Minor Planet Bulletin, 36, 51 [NASA ADS] [Google Scholar]
- Owings, L. E. 2013a, Minor Planet Bulletin, 40, 104 [NASA ADS] [Google Scholar]
- Owings, L. E. 2013b, Minor Planet Bulletin, 40, 8 [NASA ADS] [Google Scholar]
- Piironen, J., Lagerkvist, C., Torppa, J., Kaasalainen, M., & Warner, B. 2001, in BAAS, 33, 1562 [Google Scholar]
- Pilcher, F. 2008a, Minor Planet Bulletin, 35, 51 [NASA ADS] [Google Scholar]
- Pilcher, F. 2008b, Minor Planet Bulletin, 35, 71 [NASA ADS] [Google Scholar]
- Pilcher, F. 2008c, Minor Planet Bulletin, 35, 135 [NASA ADS] [Google Scholar]
- Pilcher, F. 2009a, Minor Planet Bulletin, 36, 133 [Google Scholar]
- Pilcher, F. 2009b, Minor Planet Bulletin, 36, 25 [NASA ADS] [Google Scholar]
- Pilcher, F. 2009c, Minor Planet Bulletin, 36, 100 [NASA ADS] [Google Scholar]
- Pilcher, F. 2010a, Minor Planet Bulletin, 37, 98 [NASA ADS] [Google Scholar]
- Pilcher, F. 2010b, Minor Planet Bulletin, 37, 167 [NASA ADS] [Google Scholar]
- Pilcher, F. 2010c, Minor Planet Bulletin, 37, 119 [NASA ADS] [Google Scholar]
- Pilcher, F. 2010d, Minor Planet Bulletin, 37, 148 [Google Scholar]
- Pilcher, F. 2010e, Minor Planet Bulletin, 37, 45 [NASA ADS] [Google Scholar]
- Pilcher, F. 2010f, Minor Planet Bulletin, 37, 21 [NASA ADS] [Google Scholar]
- Pilcher, F. 2011a, Minor Planet Bulletin, 38, 183 [NASA ADS] [Google Scholar]
- Pilcher, F. 2011b, Minor Planet Bulletin, 38, 76 [NASA ADS] [Google Scholar]
- Pilcher, F. 2011c, Minor Planet Bulletin, 38, 50 [NASA ADS] [Google Scholar]
- Pilcher, F. 2011d, Minor Planet Bulletin, 38, 156 [NASA ADS] [Google Scholar]
- Pilcher, F. 2012a, Minor Planet Bulletin, 39, 57 [NASA ADS] [Google Scholar]
- Pilcher, F. 2012b, Minor Planet Bulletin, 39, 220 [NASA ADS] [Google Scholar]
- Pilcher, F. 2013a, Minor Planet Bulletin, 40, 33 [NASA ADS] [Google Scholar]
- Pilcher, F. 2013b, Minor Planet Bulletin, 40, 189 [NASA ADS] [Google Scholar]
- Pilcher, F. 2013c, Minor Planet Bulletin, 40, 85 [Google Scholar]
- Pilcher, F. 2013d, Minor Planet Bulletin, 40, 161 [NASA ADS] [Google Scholar]
- Pilcher, F. 2014a, Minor Planet Bulletin, 41, 155 [NASA ADS] [Google Scholar]
- Pilcher, F. 2014b, Minor Planet Bulletin, 41, 47 [NASA ADS] [Google Scholar]
- Pilcher, F. 2014c, Minor Planet Bulletin, 41, 250 [NASA ADS] [Google Scholar]
- Pilcher, F. 2015a, Minor Planet Bulletin, 42, 190 [NASA ADS] [Google Scholar]
- Pilcher, F. 2015b, Minor Planet Bulletin, 42, 280 [NASA ADS] [Google Scholar]
- Pilcher, F. 2015c, Minor Planet Bulletin, 42, 91 [NASA ADS] [Google Scholar]
- Pilcher, F., & Franco, L. 2014, Minor Planet Bulletin, 41, 35 [NASA ADS] [Google Scholar]
- Pilcher, F., & Higgins, D. 2011, Minor Planet Bulletin, 38, 32 [NASA ADS] [Google Scholar]
- Pilcher, F., & Jardine, D. 2009, Minor Planet Bulletin, 36, 52 [NASA ADS] [Google Scholar]
- Pilcher, F., Benishek, V., Delos, S., et al. 2012a, Minor Planet Bulletin, 39, 46 [NASA ADS] [Google Scholar]
- Pilcher, F., Delos, S., Ahrendts, G., & Barker, T. 2012b, Minor Planet Bulletin, 39, 204 [NASA ADS] [Google Scholar]
- Pilcher, F., Ferrero, A., & Oey, J. 2012c, Minor Planet Bulletin, 39, 228 [NASA ADS] [Google Scholar]
- Pilcher, F., Alvarez, E. M., Ferrero, A., et al. 2014, Minor Planet Bulletin, 41, 70 [NASA ADS] [Google Scholar]
- Pilcher, F., Ferrero, A., Klinglesmith, III, D. A., & Hanowell, J. 2015, Minor Planet Bulletin, 42, 90 [NASA ADS] [Google Scholar]
- Polishook, D. 2009, Minor Planet Bulletin, 36, 119 [NASA ADS] [Google Scholar]
- Polishook, D. 2014, Icarus, 241, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Polishook, D., Ofek, E. O., Waszczak, A., et al. 2012, MNRAS, 421, 2094 [NASA ADS] [CrossRef] [Google Scholar]
- Pravec, P., Wolf, M., & Šarounová, L. 1998, Icarus, 136, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Pravec, P., Scheirich, P., Vokrouhlický, D., et al. 2012, Icarus, 218, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Pray, D. P. 2004a, Minor Planet Bulletin, 31, 34 [NASA ADS] [Google Scholar]
- Pray, D. P. 2004b, Minor Planet Bulletin, 31, 6 [NASA ADS] [Google Scholar]
- Rubincam, D. P. 2000, Icarus, 148, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Ruthroff, J. C. 2010, Minor Planet Bulletin, 37, 158 [NASA ADS] [Google Scholar]
- Ruthroff, J. C. 2011, Minor Planet Bulletin, 38, 86 [NASA ADS] [Google Scholar]
- Scheeres, D. J., Britt, D., Carry, B., & Holsapple, K. A. 2015, Asteroids IV. In press [Google Scholar]
- Shevchenko, V. G., Chiorny, V. G., Gaftonyuk, N. M., et al. 2008, Icarus, 196, 601 [NASA ADS] [CrossRef] [Google Scholar]
- Skiff, B. A., Bowell, E., Koehn, B. W., et al. 2012, Minor Planet Bulletin, 39, 111 [NASA ADS] [Google Scholar]
- Slivan, S. M., Binzel, R. P., Crespo da Silva, L. D., et al. 2003, Icarus, 162, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Stephens, R. D. 2001, Minor Planet Bulletin, 28, 5 [NASA ADS] [Google Scholar]
- Stephens, R. D. 2003, Minor Planet Bulletin, 30, 1 [NASA ADS] [Google Scholar]
- Stephens, R. D. 2005, Minor Planet Bulletin, 32, 2 [NASA ADS] [Google Scholar]
- Stephens, R. D. 2006, Minor Planet Bulletin, 33, 100 [NASA ADS] [Google Scholar]
- Stephens, R. D. 2007a, Minor Planet Bulletin, 34, 31 [NASA ADS] [Google Scholar]
- Stephens, R. D. 2007b, Minor Planet Bulletin, 34, 102 [NASA ADS] [Google Scholar]
- Stephens, R. D. 2007c, Minor Planet Bulletin, 34, 64 [NASA ADS] [Google Scholar]
- Stephens, R. D. 2008, Minor Planet Bulletin, 35, 60 [NASA ADS] [Google Scholar]
- Stephens, R. D. 2009, Minor Planet Bulletin, 36, 59 [NASA ADS] [Google Scholar]
- Stephens, R. D. 2010a, Minor Planet Bulletin, 37, 28 [NASA ADS] [Google Scholar]
- Stephens, R. D. 2010b, Minor Planet Bulletin, 37, 122 [NASA ADS] [Google Scholar]
- Stephens, R. D. 2012, Minor Planet Bulletin, 39, 226 [NASA ADS] [Google Scholar]
- Stephens, R. D. 2013, Minor Planet Bulletin, 40, 92 [NASA ADS] [Google Scholar]
- Stephens, R. D. 2014a, Minor Planet Bulletin, 41, 92 [NASA ADS] [Google Scholar]
- Stephens, R. D. 2014b, Minor Planet Bulletin, 41, 226 [NASA ADS] [Google Scholar]
- Stephens, R. D. 2014c, Minor Planet Bulletin, 41, 171 [Google Scholar]
- Stephens, R. D. 2015a, Minor Planet Bulletin, 42, 70 [NASA ADS] [Google Scholar]
- Stephens, R. D. 2015b, Minor Planet Bulletin, 42, 104 [NASA ADS] [Google Scholar]
- Stephens, R. D., & Warner, B. D. 2008, Minor Planet Bulletin, 35, 84 [NASA ADS] [Google Scholar]
- Stephens, R. D., & Warner, B. D. 2013, Minor Planet Bulletin, 40, 93 [NASA ADS] [Google Scholar]
- Stephens, R. D., Malcolm, G., Koff, R. A., Brincat, S. M., & Warner, B. 2001, Minor Planet Bulletin, 28, 1 [NASA ADS] [Google Scholar]
- Stephens, R. D., Warner, B. D., Megna, R., & Coley, D. 2012, Minor Planet Bulletin, 39, 2 [NASA ADS] [Google Scholar]
- Stephens, R. D., Coley, D., & Warner, B. D. 2014, Minor Planet Bulletin, 41, 8 [NASA ADS] [Google Scholar]
- Strabla, L., Quadri, U., & Girelli, R. 2011, Minor Planet Bulletin, 38, 169 [NASA ADS] [Google Scholar]
- Strabla, L., Quadri, U., & Girelli, R. 2012, Minor Planet Bulletin, 39, 177 [NASA ADS] [Google Scholar]
- Strabla, L., Quadri, U., & Girelli, R. 2013, Minor Planet Bulletin, 40, 232 [NASA ADS] [Google Scholar]
- Tanga, P., Carry, B., Colas, F., et al. 2015, MNRAS, 448, 3382 [NASA ADS] [CrossRef] [Google Scholar]
- Torppa, J., Kaasalainen, M., Michałowski, T., et al. 2003, Icarus, 164, 346 [NASA ADS] [CrossRef] [Google Scholar]
- Viikinkoski, M., Kaasalainen, M., & Durech, J. 2015, A&A, 576, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vokrouhlický, D., Nesvorný, D., & Bottke, W. F. 2003, Nature, 425, 147 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Warner, B. D. 1999, Minor Planet Bulletin, 26, 31 [NASA ADS] [Google Scholar]
- Warner, B. 2000, Minor Planet Bulletin, 27, 4 [Google Scholar]
- Warner, B. 2001, Minor Planet Bulletin, 28, 4 [NASA ADS] [Google Scholar]
- Warner, B. D. 2005a, Minor Planet Bulletin, 32, 29 [NASA ADS] [Google Scholar]
- Warner, B. D. 2005b, Minor Planet Bulletin, 32, 54 [NASA ADS] [Google Scholar]
- Warner, B. D. 2005c, Minor Planet Bulletin, 32, 4 [NASA ADS] [Google Scholar]
- Warner, B. D. 2006a, Minor Planet Bulletin, 33, 82 [NASA ADS] [Google Scholar]
- Warner, B. D. 2006b, Minor Planet Bulletin, 33, 58 [NASA ADS] [Google Scholar]
- Warner, B. D. 2006c, Minor Planet Bulletin, 33, 85 [NASA ADS] [Google Scholar]
- Warner, B. D. 2006d, Minor Planet Bulletin, 33, 35 [NASA ADS] [Google Scholar]
- Warner, B. D. 2007a, Minor Planet Bulletin, 34, 72 [NASA ADS] [Google Scholar]
- Warner, B. D. 2007b, Minor Planet Bulletin, 34, 104 [Google Scholar]
- Warner, B. D. 2008a, Minor Planet Bulletin, 35, 56 [NASA ADS] [Google Scholar]
- Warner, B. D. 2008b, Minor Planet Bulletin, 35, 163 [NASA ADS] [Google Scholar]
- Warner, B. D. 2009a, Minor Planet Bulletin, 36, 109 [NASA ADS] [Google Scholar]
- Warner, B. D. 2009b, Minor Planet Bulletin, 36, 7 [NASA ADS] [Google Scholar]
- Warner, B. D. 2009c, Minor Planet Bulletin, 36, 172 [NASA ADS] [Google Scholar]
- Warner, B. D. 2010a, Minor Planet Bulletin, 37, 112 [NASA ADS] [Google Scholar]
- Warner, B. D. 2010b, Minor Planet Bulletin, 37, 24 [NASA ADS] [Google Scholar]
- Warner, B. D. 2010c, Minor Planet Bulletin, 37, 57 [NASA ADS] [Google Scholar]
- Warner, B. D. 2010d, Minor Planet Bulletin, 37, 127 [NASA ADS] [Google Scholar]
- Warner, B. D. 2011a, Minor Planet Bulletin, 38, 142 [NASA ADS] [Google Scholar]
- Warner, B. D. 2011b, Minor Planet Bulletin, 38, 25 [NASA ADS] [Google Scholar]
- Warner, B. D. 2011c, Minor Planet Bulletin, 38, 63 [NASA ADS] [Google Scholar]
- Warner, B. D. 2012a, Minor Planet Bulletin, 39, 158 [NASA ADS] [Google Scholar]
- Warner, B. D. 2012b, Minor Planet Bulletin, 39, 16 [NASA ADS] [Google Scholar]
- Warner, B. D. 2012c, Minor Planet Bulletin, 39, 69 [NASA ADS] [Google Scholar]
- Warner, B. D. 2012d, Minor Planet Bulletin, 39, 245 [NASA ADS] [Google Scholar]
- Warner, B. D. 2013a, Minor Planet Bulletin, 40, 71 [NASA ADS] [Google Scholar]
- Warner, B. D. 2013b, Minor Planet Bulletin, 40, 137 [NASA ADS] [Google Scholar]
- Warner, B. D. 2014a, Minor Planet Bulletin, 41, 27 [NASA ADS] [Google Scholar]
- Warner, B. D. 2014b, Minor Planet Bulletin, 41, 144 [NASA ADS] [Google Scholar]
- Warner, B. D. 2015a, Minor Planet Bulletin, 42, 54 [NASA ADS] [Google Scholar]
- Warner, B. D. 2015b, Minor Planet Bulletin, 42, 115 [Google Scholar]
- Warner, B. D. 2015c, Minor Planet Bulletin, 42, 132 [NASA ADS] [Google Scholar]
- Warner, B. D., Shepard, M. K., Harris, A. W., et al. 2006, Minor Planet Bulletin, 33, 102 [NASA ADS] [Google Scholar]
- Warner, B. D., Behrend, R., Poncy, R., & Coliac, J.-F. 2008a, Minor Planet Bulletin, 35, 25 [NASA ADS] [Google Scholar]
- Warner, B. D., Durech, J., Fauerbach, M., & Marks, S. 2008b, Minor Planet Bulletin, 35, 167 [NASA ADS] [Google Scholar]
- Warner, B. D., Harris, A. W., & Pravec, P. 2009, Icarus, 202, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Warner, B. D., Stephens, R. D., & Harris, A. W. 2011, Minor Planet Bulletin, 38, 172 [Google Scholar]
- Warner, B. D., Harris, A. W., Stephens, R. D., & Coley, D. 2014, in AAS/Division for Planetary Sciences Meeting Abstracts, 46, 509.12 [Google Scholar]
Appendix A: Additional tables
New asteroid shape model determinations from disk-integrated optical data.
New observations used for updating the shape models and observations that are not included in the UAPC used for new shape model determinations.
Observers, observatory code and observatory name.
All Tables
Rotational states and summary of used photometry for asteroids for which we updated their shape models based on new disk-integrated optical data.
New observations used for updating the shape models and observations that are not included in the UAPC used for new shape model determinations.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


