| Issue |
A&A
Volume 586, February 2016
|
|
|---|---|---|
| Article Number | A67 | |
| Number of page(s) | 8 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201527439 | |
| Published online | 27 January 2016 | |
First high-precision differential abundance analysis of extremely metal-poor stars⋆
1 Universidade de São Paulo, Insituto de Astronomia, Geofísica e Ciências Atmosféricas, IAG, Departamento de Astronomia, Rua do Matão 1226, Cidade Universitária, 05508-900 São Paulo, SP, Brazil
e-mail: hreggiani@gmail.com
2 The Australian National University, Research School of Astronomy and Astrophysics, Weston, ACT 2611, Australia
3 University of Texas at Austin, McDonald Observatory and Department of Astronomy, TX, USA
Received: 23 September 2015
Accepted: 7 December 2015
Context. Studies of extremely metal-poor stars indicate that chemical abundance ratios [X/Fe] have a root mean square scatter as low as 0.05 dex (12%). It remains unclear whether this reflects observational uncertainties or intrinsic astrophysical scatter arising from physical conditions in the interstellar medium at early times.
Aims. We measure differential chemical abundance ratios in extremely metal-poor stars to investigate the limits of precision and to understand whether cosmic scatter or observational errors are dominant.
Methods. We used high-resolution (R ~ 95 000) and high signal-to-noise (S/N = 700 at 5000 Å) HIRES/Keck spectra to determine high-precision differential abundances between two extremely metal-poor stars through a line-by-line differential approach. We determined stellar parameters for the star G64-37 with respect to the standard star G64-12. We performed EW measurements for the two stars for the lines recognized in both stars and performed spectral synthesis to study the carbon abundances.
Results. The differential approach allowed us to obtain errors of σ(Teff) = 27 K, σ(log g) = 0.06 dex, σ( [Fe/H] ) = 0.02 dex and σ(vt) = 0.06 km s-1. We estimated relative chemical abundances with a precision as low as σ([X/Fe]) ≈ 0.01 dex. The small uncertainties demonstrate that there are genuine abundance differences larger than the measurement errors. The observed Li difference cannot be explained by the difference in mass because the less massive star has more Li.
Conclusions. It is possible to achieve an abundance precision around ≈ 0.01−0.05 dex for extremely metal-poor stars, which opens new windows on the study of the early chemical evolution of the Galaxy.
Key words: stars: abundances / stars: evolution / stars: Population II / Galaxy: abundances / Galaxy: evolution / Galaxy: halo
Table A.1 is also available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/586/A67
© ESO, 2016
1. Introduction
Extremely metal-poor (EMP) stars (i.e. stars with [Fe/H] < −3) are relics of the early universe and can provide us with precious clues about the chemical evolution and formation of the Galaxy. These objects arguably offer the most powerful insights into the evolution, nucleosynthetic yields, and properties of the first supernovae (Audouze & Silk 1995; Ryan et al. 1996; Shigeyama & Tsujimoto 1998; Chieffi & Limongi 2002; Umeda & Nomoto 2002).
The most accurate abundance measurements in EMP stars come from Cayrel et al. (2004) and Arnone et al. (2005) with errors for [X/Fe] as low as 0.05 dex. A key open question is whether the observed scatter in abundance ratios reflects genuine cosmic scatter or measurement uncertainties. Higher precision abundance studies of EMP stars are needed to clarify this issue, but such measurements are challenging as they require long exposures using 8 m class telescopes to obtain high-resolution and high signal-to-noise ratio (S/N) data. To improve our precision we employed the differential technique in our analysis. Recently, the differential technique in twin stars, meaning stars with similar stellar parameters, made it possible to considerably improve the precision achieved in spectroscopic studies because many error sources, such as imprecise log(gf) values, largely cancel out, allowing a much better precision in the determination of relative stellar parameters and abundances. Studies with this technique have been used to recognize planet signatures on the chemical composition of stars (Meléndez et al. 2009; Ramírez et al. 2009; Tucci Maia et al. 2014; Biazzo et al. 2015), stellar evolution effects (Monroe et al. 2013; Tucci Maia et al. 2015), chemical evolution in the solar neighborhood (Nissen 2015), abundance anomalies in globular clusters (Yong et al. 2013), and distinct populations in the metal-rich halo (Nissen & Schuster 2010).
Here we explore, for the first time, the chemical composition of two EMP turn-off stars through a strictly differential analysis, achieving an unprecedented precision (0.01 dex) for a few of the analyzed species.
2. Observations and data reduction
Spectra of G64-12 and G64-37 were obtained with the High Resolution Echelle Spectrometer (HIRES; Vogt et al. 1994), on the Keck 10 m telescope at Mauna Kea. The star G64-12 was observed on June 16, 2005, and G64-37 on January 19, 2006. The observations were performed with the same setup using the slit E4 (0.4″ × 7″), resulting in a resolving power of R ~ 95 000, with a S/N = 700 at 5000 Å and S/N = 900 around the Li 6707 Å line. The spectra have a wavelength coverage ranging from ~3900 Å to 8300 Å.
The orders were extracted using the Mauna Kea Echelle Extraction (MAKEE1) package, especially written to reduce HIRES spectra. We performed the Doppler correction and continuum normalization via IRAF.
3. Analysis
We used a line-by-line differential approach to obtain stellar parameters and chemical abundances, as described in our previous works (e.g. Meléndez et al. 2012; Yong et al. 2013; Ramírez et al. 2015). The 2014 version of the local thermodynamic equilibrium (LTE) analysis code MOOG (Sneden 1973) was employed with the Castelli et al. (1997) atmospheric models.
The linelist was created by inspecting each feature to verify that each chosen line could be measured on both spectra. The log(gf) values and energy levels are from Vienna Atomic Line Database (VALD). The Fe I lines were updated using data from Den Hartog et al. (2014) and transition probabilities for the Fe II lines are from Meléndez & Barbuy (2009). The Ti II values were updated using Lawler et al. (2013). We note that the choice of log(gf) values is inconsequential in a differential analysis.
The equivalent widths (EWs) were measured by hand with the splot task in IRAF, using Gaussian profile fits. In order to determine the local continuum we compared each line in the two stars by overplotting the spectra in a 6 Å window.
The complete linelist, including the EWs for both objects, is presented in Table A.1.
G64-12 is used as the standard star for the analysis with the following stellar parameters: Teff = 6463 K from the infrared flux method (IRFM; Meléndez et al. 2010), log g = 4.26 dex from the absolute magnitude (Nissen et al. 2007)2 and, using our EWs, we obtained [Fe/H] = −3.20 dex and vt = 1.65 km s-1. We then employed a strictly line-by-line differential approach to obtain the stellar parameters of G64-37. Using the Fe I and Fe II abundances from G64-12 as references we determined Teff = 6570 K through differential excitation equilibrium (Fig. 1), consistent with the IRFM value (Teff = 6583 ± 50 K, Meléndez et al. 2010). We obtained a log g = 4.40 dex through differential ionization equilibrium, consistent with Nissen et al. (2007) (log g = 4.24 ± 0.15). We obtained vt = 1.74 km s-1 by allowing no trend in the differential Fe I line abundances with reduced EWs (Fig. 1), and found [Fe/H] = −3.00 dex. The errors for the atmospheric parameters are σ(Teff) = 27 K, σ(log g) = 0.06 dex, σ( [Fe/H] ) = 0.02 dex, and σ(vt = 0.06) km s-1. They include the degeneracy of stellar parameters and were determined strictly through a differential approach.
 |
Fig. 1 Differential abundances versus lower excitation potential (top panel) and reduced equivalent widths (lower panel). |
Once the stellar parameters of G64-37 were determined through the iron lines, we determined the abundance of the other elements recognized in both spectra: Li, O, Na, Mg, Al, Si, Ca, Sc, Ti, Cr, Mn, Fe, Co Ni, Zn, Sr, and Ba. For the elements Li, Mn, Co, and Ba, hyperfine splitting was accounted for. For Li we used the linelist described in Meléndez & Ramírez (2004). For Mn and Co we employed the linelists from Kurucz3 and for Ba we employed the linelist from McWilliam (1998). We present the final differential abundances in Table 1, along with the errors from propagating the stellar parameter errors and the observational error. The total errors were calculated by quadratically adding both observational and systematic errors. In the last column of Table 1 we also show the ratio between differential abundances and total errors. This column reveals there are genuine abundance differences, greater than 2σ significance for Δ[X/H], for all elements (except oxygen and silicon) between the two stars.
To demonstrate the importance of the differential technique in this work we analyzed the [Mg/H] ratio for star G64-12 in a non-differential way (classic analysis), achieving a much higher total error. The observational error ( ) alone (0.059 dex) is higher than the total error obtained by using the differential analysis; when added to the parameter uncertainties (0.021 dex) the final error associated with the measurement is ≈ 0.083 dex, much higher than the 0.026 dex achieved using the differential technique.
) alone (0.059 dex) is higher than the total error obtained by using the differential analysis; when added to the parameter uncertainties (0.021 dex) the final error associated with the measurement is ≈ 0.083 dex, much higher than the 0.026 dex achieved using the differential technique.
We also present the differential abundance results relative to Fe (Δ[X/Fe]). In this case the errors were derived considering how the error for each stellar parameter behaves in relation to the same error in the iron differential abundance. After this step, we quadratically added the new parameter errors with the observational errors (defined as  , where N is the number of measured lines) presented in Table 1. We can see through the significance of our results (Table 2, Col. 4) that working with [X/Fe] has decreased the confidence in the result of some elements when compared to the results of [X/H] (Table 1). Eleven out of 17 species exhibit abundance differences (greater than 2σ significance) between the two stars for Δ[X/Fe]. For the remaining six elements, the majority are heavy elements for which the total error is dominated by observational uncertainties arising from the small numbers of weak spectral lines, as can be seen in Table A.1.
, where N is the number of measured lines) presented in Table 1. We can see through the significance of our results (Table 2, Col. 4) that working with [X/Fe] has decreased the confidence in the result of some elements when compared to the results of [X/H] (Table 1). Eleven out of 17 species exhibit abundance differences (greater than 2σ significance) between the two stars for Δ[X/Fe]. For the remaining six elements, the majority are heavy elements for which the total error is dominated by observational uncertainties arising from the small numbers of weak spectral lines, as can be seen in Table A.1.
To further show the improvement that the differential technique offers, in Fig. 2 we compare our errors with those obtained by Cayrel et al. (2004, Table 9) using a classical analysis. The dashed line represents the median value of the ratios between the two errors showing that our results are about four times more precise than the aforementioned work.
Relative abundances (G64-37 minus G64-12) and associated uncertainties due to errors in stellar parameters and observations.
For carbon it was more appropriate to determine the abundances by spectral synthesis of the CH band. First, we estimated the macro-turbulent (Vmacro) velocity of the stars by visually fitting four different iron lines (3920.2 Å, 4005.2 Å, 4045.8 Å, 4063.6 Å). We determined Vmacro = 3.8 km s-1 for G64-12 and Vmacro = 3.7 km s-1 for G64-37.
 |
Fig. 2 Ratio between measurement errors from Cayrel et al. (2004) (σC) and the errors obtained in this work (σ) for a number of elements. |
We prepared a linelist, spanning from 4290 Å to 4335 Å, specifically for the carbon synthesis using CH data from Masseron et al. (2014) along with atomic blends for the region from VALD. For each star we synthesized three different regions of the CH band, 4299 Å to 4302 Å, 4308 Å to 4315 Å, and 4322 Å to 4327 Å. An example of a best fit for one of the regions, for star G64-12, can be seen in Fig. 3. We averaged the abundance determination for the three regions and determined the abundance difference between the stars. We determined the parameter errors by synthesizing the three regions for each different parameter uncertainty.
Δ[X/Fe] differential abundances (G64-37 – G64-12).
We also estimated ages and masses, using the q2 code (Ramírez et al. 2014). The code fits Y2 isochrones (Yi et al. 2001; Kim et al. 2002) with the adopted stellar parameters. The method estimates the age and mass through a probability distribution approach, as described in Ramírez et al. (2013). For G64-12 we estimated an age of 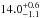 Gyr with a mass
Gyr with a mass 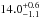 M⊙. The best solution for star G64-37 is an age of
M⊙. The best solution for star G64-37 is an age of 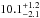 Gyr with a mass
Gyr with a mass 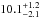 M⊙. The error bars represent the 68% confidence threshold.
M⊙. The error bars represent the 68% confidence threshold.
It is important to note that we derived the stellar ages through a probability density function (PDF) and obtained that star G64-12 is older than 12.9 Gyr with 68% certainty, and older than about 11.5 Gyr with 92% certainty. The probability of star G64-12 being as young as star G64-37 (10 Gyr) is as low as 0.3%. Star G64-37 is younger than 11.3 Gyr with 68% certainty, and younger than 12.3 with 92% certainty.
The masses of both stars were also derived trough a PDF and we obtain that star G64-12 is less massive than 0.77 M⊙ with 68% certainty and less massive than 0.78 M⊙ with 92% certainty. Star G64-37 is more massive than 0.78 M⊙ with 68% certainty and more massive than 0.77 M⊙ with 92% certainty. The chance of star G64-12 being as massive as G64-37 is only about 4.5%.
Based on our PDF we can say that star G64-12 is older and less massive than star G64-37 with a very high degree of confidence. We note that the difference in age between our pair is similar to the difference in age between “low-alpha” and “high-alpha” halo stars at [Fe/H] >−2 (Schuster et al. 2012).
We checked our stellar parameters and our abundance results using the q2 code, using MARCS model atmospheres (Gustafsson et al. 2008), and the 2014 version of MOOG to compute the curves of growth and obtained consistent results.
4. Discussion and conclusions
In Fig. 4 we show our differential abundances. This figure demonstrates that the differential technique is capable of revealing subtle differences in the abundance pattern of metal-poor stars due to the small errors of ≈ 0.01−0.02 dex. The precision achieved shows that the pair G64-12/G64-37 have distinct abundance patterns. To compare our results we searched the literature for works that analyzed both stars and have similar S/N and resolution to ours. We found a work from Nissen et al. (2007) and they measured Δ [Zn/H] = 0.19 ± 0.20, in good agreement with our results. Fabbian et al. (2009) also found similar stellar parameters, Δ [C/H] = + 0.04 ± 0.21 and Δ [O/H] = −0.03 ± 0.21. The difference in carbon abundances might be due to the different techniques used for the determinations; we synthesized CH molecular bands, while Fabbian et al. (2009) measured EWs for CI lines (not available in our spectral coverage), but the values are consistent within the analysis errors. The oxygen abundance agrees with our data, within the errors. Our study, using high-quality observation demonstrates that it is possible to study, for example, the separation of the halo population via the abundance pattern of alpha elements Mg, Si, and Ti, shown to exist by Nissen & Schuster (2010) in more metal-rich halo stars.
 |
Fig. 3 Best fit of one of the regions synthesized to determine the carbon abundances (star G64-12). The dashed lines are a ±0.1 dex difference in C abundance. |
 |
Fig. 4 Top panel: Δ[X/H] abundances. Lower panel: Δ[X/Fe] abundances. Filled circles are the values corrected for Galactic chemical evolution, while the open circles represent the uncorrected abundances (G64-37–G64-12). |
The differential abundances presented in Table 1 are indicative that these two stars belong to two different populations as there is a significant difference in the abundances of all analyzed elements. In the last column of Table 1 we show the significance of our results and it can be seen that all of our results can be trusted with over 2σ confidence, with the exception of oxygen.
By analyzing the α-elements, it is possible to see how small the errors must be to separate the stars via differential abundances: Δ [Ti/H] = 0.142 ± 0.035, Δ [O/H] = 0.007 ± 0.053, Δ [Mg/H] = 0.072 ± 0.026, and Δ [Si/H] = 0.047 ± 0.024 are very small. Thus, to distinguish a clear difference we have to achieve errors on the order of (0.01−0.02 dex). There is a small abundance difference between the stars, which indicates that they might belong to distinct halo populations.
As in Nissen & Schuster (2010) and Ramírez et al. (2012), we can analyze the possibility of distinct halo populations through [α/Fe] ratios. As can be seen in Table 2, when compared to iron, the differential abundances between these stars are more prominent (Δ[O/Fe]=−0.173 ± 0.065, Δ[Mg/Fe]=−0.108 ± 0.023, Δ[Si/Fe]=−0.133 ± 0.009, and Δ[Ti/Fe]=−0.046 ± 0.011), which also indicates that they belong to distinct halo populations. It is important to emphasize that for all the α-elements the significance of our results are all above 2σ, including for [O/Fe]. With this data we find that G64-37, the younger halo star, has lower [α/Fe], which is in agreement with the results of Schuster et al. (2012).
In order to exclude differences that might arise from Galactic chemical evolution (GCE) we performed linear regressions to the data published in Bonifacio et al. (2009), who performed abundance analyses for stars with similar stellar parameters to the ones used here, but in a wider range of metallicities. Then, we corrected our [X/Fe] ratios for the predicted ratio of the linear regression. We present the corrected differential abundances, Δ[X/Fe]C, for trends in Galactic chemical evolution (GCE) in the last column of Table 2. We note that the GCE corrections are within the error bars of our results and do not change our interpretation, as can also be seen in Fig. 4.
We also estimated the velocity components for the two stars, using an estimated distance from the absolute magnitude by Nissen et al. (2007), proper motion data from van Leeuwen (2007), and radial velocity from Latham et al. (2002). For star G64-12 we obtained ULSR = 21 km s-1, VLSR = −352 km s-1, and WLSR = −400 km s-1 and for star G64-37 ULSR = 231 km s-1, VLSR = −369 km s-1, and WLSR = −77 km s-14. We found that both stars have extreme kinematics, falling outside Fig. 3 from Nissen & Schuster (2010). However, it is important to point out that their study present stars with metallicities [Fe/H] > −1.5, which are much higher than the stars in this work.
With the small errors achieved, it is also possible to revisit the Li plateau (Spite & Spite 1982). Meléndez et al. (2010) demonstrated the existence of two plateaus with a break at [Fe/H] ≈ −2.5. With an error of ~ 0.021 on our Li differential abundance it will be possible to study a larger sample of stars and determine with higher precision where the break of the Li plateau is. As the two stars have metallicities that place them on the same plateau, we can compare the absolute differential abundance with the scatter found by Meléndez et al. (2010). The differential Δ[Li/H] abundance found in this study (0.098 dex) is higher than the average scatter (0.04 dex) previously found among stars in that range ([Fe/H] < −2.5).
In Meléndez et al. (2010) it was argued that the difference in Li is due to the differences in mass between the stars, as stars with lower masses deplete more lithium (Richard et al. 2005). However, the pair studied here behave unexpectedly: the more metal-poor, older, and less massive star seems to have a higher Li content. To check the result we also performed non-LTE abundance corrections (Lind et al. 2009) and arrived at a differential non-LTE abundance of Δ [Li/H] = −0.10 dex, which shows the consistency of our results. Presently there are only Li diffusion models for [Fe/H] ≥ −2 (Richard et al. 2005). It would be important to extend these models to lower metallicities to test against our high-precision Li abundances.
The results presented here illustrate how a differential study can help indicate whether lithium is, in fact, being depleted in stars or if physics beyond the primordial nucleosynthesis model is necessary (Fields et al. 2014).
Even after GCE corrections, clear abundance differences remain even among chemical elements produced via similar processes. For example, oxygen is more enhanced than carbon in G64-12, as is also the case of barium and strontium. The difference in the abundance patterns of these stars can give us important information on the environments in which these two stars formed and on the supernovae that enriched them.
We attempted to determine possible supernovae progenitors for our stars. To this end we employed the STARFIT5 code (Chan et al., in prep.) with the absolute abundances calculated for our standard star (G64-12) and the absolute values for the standard star plus the differential abundances (Table 1) to study a possible progenitor for star G64-37.
We found no extreme difference between the possible polluting supernovae. The results from STARFIT indicate that the star G64-12 had a progenitor with mas M = 18 M⊙, log (mixing) = −1.0 dex and a remnant of 3.9 M⊙. The results of G64-37 implied a supernovae with M = 11 M⊙, log (mixing) = −1.6 dex and a remnant of 1.6 M⊙.
Our study demonstrates that the advent of precision spectroscopy can open new windows on the study of the early Galaxy, supernovae yields, and the chemical evolution of the Galaxy. With a larger sample of very metal-poor stars we will be able to assess additional questions such as cosmic scatter in the Galactic halo and how the first supernovae enriched our Galaxy.
The package was created by T. A. Barlow and is freely available at http://www.astro.caltech.edu/~tb/makee/
The parallax is too uncertain, and so we adopted the photometric MV from Nissen et al. (2007)
Acknowledgments
H.R. thanks the CAPES fellowship program. J.M. is grateful for support by FAPESP (2010/50930-6 and 2012/24392-2). D.Y. was supported through an Australian Research Council Future Fellowship (FT140100554). M.A. has been supported by the Australian Research Council grant (FL110100012).
References
- Arnone, E., Ryan, S. G., Argast, D., et al. 2005, A&A, 430, 507 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Audouze, J., & Silk, J. 1995, AJ, 451, L9 [Google Scholar]
- Biazzo, K., Gratton, R., Desidera, S., et al. 2015, A&A, 583, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonifacio, P., Spite, M., Cayrel, R., et al. 2009, A&A, 501, 519 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cayrel, R., Depagne, E., Spite, M., et al. 2004, A&A, 416, 1117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castelli, F., Gratton, R. G., & Kurucz, R. L. 1997, A&A, 318, 841 [NASA ADS] [Google Scholar]
- Chieffi, A., & Limongi, M. 2002, AJ, 577, 281 [Google Scholar]
- Collet, R., Asplund, M., & Trampedach, R. 2007, A&A, 469, 687 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Den Hartog, E. A., Ruffoni, M. P., et al. 2014, AJ, 215, 23 [Google Scholar]
- Fabbian, D., Nissen, P. E., Asplund, M., et al. 2009, A&A, 500, 1143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fields, B. D., Molaro, P., & Sarkar, S. 2014, Chin. Phys., C38, 339 [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kim, Y-C., Demarque, P., Yi, S., & Alexander, D. 2002, ApJS, 143, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Latham, D. W., Mazeh, T., Carney, B. W., et al. 2002, AJ, 124, 1144 [NASA ADS] [CrossRef] [Google Scholar]
- Lawler, J. E., Guzman, A., Wood, M. P., et al. 2013, AJ, 205, 11 [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lind, K., Asplund, M., & Barklem, P. S. 2009, A&A, 503, 541 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masseron, T., Plez, B., Van Eck, S., et al. 2014, A&A, 571, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McWilliam, A. 1998, AJ, 115, 1640 [NASA ADS] [CrossRef] [Google Scholar]
- Meléndez, J., & Barbuy, B. 2009, A&A, 497, 611 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meléndez, J., & Ramírez, I. 2004, AJ, 615, L33 [Google Scholar]
- Meléndez, J., Asplund, M., Gustafsson, B., & Yong, D. 2009, AJ, 704, L66 [Google Scholar]
- Meléndez, J., Casagrande, L., Ramírez, I., et al. 2010, A&A, 515, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meléndez, J., Bergemann, M., Cohen, J. G., et al. 2012, A&A, 543, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Monroe, T., Meléndez, J., Ramírez, I., et al. 2013, AJ, 774, L32 [Google Scholar]
- Nissen, P. E. 2015, A&A, 579, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nissen, P. E., & Schuster, W. 2010, A&A, 511, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nissen, P. E., Akerman, C., Asplund, M., et al. 2007, A&A, 469, 319 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramírez, I., Meléndez, J., & Asplund, M. 2009, A&A, 508, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramírez, I., Meléndez, J., & Chanamé, J. 2012, ApJ, 757, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez, I., Allen de Prieto, C., & Lambert, D. L. 2013, AJ, 764, 78 [CrossRef] [Google Scholar]
- Ramírez, I., Meléndez, J., Bean, J., et al. 2014, A&A, 572, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramírez, I., Khanal, S., & Aleo, P. 2015, ApJ, 808, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Richard, O., Michaud, G., & Richer, J. 2005, ApJ, 619, 538 [NASA ADS] [CrossRef] [Google Scholar]
- Ryan, S. G., Norris, J., & Beers, T. C. 1996, AJ, 471, 254 [Google Scholar]
- Schuster, W. J., Moreno, E., Nissen, P. E., & Pichardo, B. 2012, A&A, 538, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shigeyama, T., & Tsujimoto, T. 1998, AJ, 507, L135 [NASA ADS] [CrossRef] [Google Scholar]
- Sneden, C. A. 1973, Ph.D. Thesis, Univ. Texas [Google Scholar]
- Spite, F., & Spite, M. 1982, A&A, 115, 357 [NASA ADS] [Google Scholar]
- Tucci Maia, M., Meléndez, J., & Ramírez, I. 2014, AJ, 790, L25 [Google Scholar]
- Tucci Maia, M., Meléndez, J., Castro, M., et al. 2015, A&A, 576, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Umeda, H., & Nomoto, K. 2002, AJ, 565, 385 [Google Scholar]
- Vogt, S. S., Allen, S. L., Bigelow, B. C., et al. 1994, Proc. SPIE, 2198, 362 [Google Scholar]
- Yi, S., Demarque, P., Kim, Y.-C., et al. 2001, AJ, 136, 417 [Google Scholar]
- Yong, D., Meléndez, J., Grundah, L., et al. 2013, MNRAS, 434, 3542 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Additional table
Linelist used for the abundances determinations.
All Tables
Relative abundances (G64-37 minus G64-12) and associated uncertainties due to errors in stellar parameters and observations.
All Figures
 |
Fig. 1 Differential abundances versus lower excitation potential (top panel) and reduced equivalent widths (lower panel). |
| In the text | |
 |
Fig. 2 Ratio between measurement errors from Cayrel et al. (2004) (σC) and the errors obtained in this work (σ) for a number of elements. |
| In the text | |
 |
Fig. 3 Best fit of one of the regions synthesized to determine the carbon abundances (star G64-12). The dashed lines are a ±0.1 dex difference in C abundance. |
| In the text | |
 |
Fig. 4 Top panel: Δ[X/H] abundances. Lower panel: Δ[X/Fe] abundances. Filled circles are the values corrected for Galactic chemical evolution, while the open circles represent the uncorrected abundances (G64-37–G64-12). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


