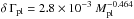| Issue |
A&A
Volume 586, February 2016
|
|
|---|---|---|
| Article Number | A105 | |
| Number of page(s) | 16 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201527194 | |
| Published online | 02 February 2016 | |
Planet filtering at the inner edges of dead zones in protoplanetary disks
Astronomy Unit, Queen Mary University of London, Mile end Road, London, E1 4NS, UK
e-mail: j.faure@qmul.ac.uk; r.p.nelson@qmul.ac.uk
Received: 14 August 2015
Accepted: 11 November 2015
Context. The interface between the dead zone and the inner active zone in a protoplanetary disk provides a promising region where the inward migration of planets may be halted owing to the existence of strong corotation torques. Recent work has indicated that this region may be prone to supporting a vortex cycle, during which vortices form at the dead-active zone interface and migrate into the active region before being destroyed, after which a new vortex forms and the cycle repeats.
Aims. The aim of this paper is to examine the interaction between migrating planets and this vortex cycle, and to determine the conditions under which planets are able to remain trapped at the dead-active zone interface.
Methods. We use the magnetohydrodynamics (MHD) codes PLUTO and RAMSES to perform 2D viscous disk simulations and 3D MHD simulations of protoplanetary disks containing migrating planets. A temperature switch is used to control the effective viscosity at the dead-active zone interface.
Results. We find that both low mass and non-gap forming higher mass planets are able to escape from the planet trap at the inner edge of the dead zone as a result of their interaction with the migrating vortices, whereas intermediate mass planets remain trapped for the duration of simulation run times.
Conclusions. Our results indicate that the vortex cycle causes the dead zone inner edge to act as an effective and mass-dependent planet filter, allowing some planets to pass through this region and others to remain there over long timescales.
Key words: accretion, accretion disks / hydrodynamics / planet-disk interactions / protoplanetary disks
© ESO, 2016
1. Introduction
At the time of writing there are almost 2000 confirmed extrasolar planets that have been discovered by a variety of techniques, and more than 3000 unconfirmed candidate planets that have been detected by the Kepler spacecraft1. Among the most interesting of these exoplanets are the short-period systems, such as the hot Jupiters exemplified by 51 Peg b (Mayor & Queloz 1995), hot Neptunes such as Gliese 436b (Butler et al. 2004), and the numerous compact systems of super-Earths and Neptunes discovered by radial velocity measurements and by the Kepler spacecraft such as Gliese 581 (Udry et al. 2007; Mayor et al. 2011) and Kepler 11 (Lissauer et al. 2011). Given the difficulties of forming such planets in situ, either because the high temperatures do not favour the existence of planetary building blocks in solid form during the epoch of planet formation or because the amount of solid material required to explain some of the planetary systems is significantly larger than would be expected to occur locally in most protoplanetary disk models, it is generally believed that these planets formed at larger orbital radii and migrated into their currently observed orbits. If this migration occurred while the protoplanetary disk was present then the planets would have likely migrated through disk regions where the dynamical evolution of the disk displayed highly diverse properties.
Disk-driven migration occurs in two basic flavours (e.g. Kley & Nelson 2012). Type II migration occurs for planets that are massive enough to form deep gaps, and these planets migrate at speeds close to the viscous evolution rate of the disk (Lin & Papaloizou 1986; Ward 1997; Nelson et al. 2000). Type I migration occurs for low mass planets that cannot form deep gaps, and is driven by a combination of Lindblad and corotation torques (Goldreich & Tremaine 1980), the former arising through the excitation of spiral waves at Lindblad resonances and the latter from interaction with material that undergoes horseshoe orbits in the planet coorbital zone (Ward 1991; Masset et al. 2006a). Recent work has focussed on the question of how entropy and vortensity gradients in a protoplanetary disk can prevent the very rapid inward migration of protoplanets by balancing the negative Lindblad torque experienced by the planet with the positive corotation torque (Masset 2001, 2002; Baruteau & Lin 2010; Baruteau et al. 2011; Pierens et al. 2012; Masset et al. 2006a; Paardekooper & Mellema 2006; Kley & Crida 2008; Paardekooper et al. 2011; Pierens et al. 2012).
The concept of a planet trap was introduced by Masset et al. (2006b), where a disk location with a positive gradient in the surface density can trap a migrating planet because the vortensity related corotation torque is expected to have a large positive value in such a region. There are a number of hypothetical reasons why a planet trap may arise within a protoplanary disk, but an oft cited one is that regions between orbital radii 0.5 ≲ R ≲ 10 au are expected to host a dead zone where the effective disk viscosity is small due to poor coupling between the gas and magnetic fields (e.g. Gammie 1996), whereas regions closer to the star maintain a large effective viscosity because thermal ionisation of gas-phase potassium and thermoionic emission from grains allows strong coupling between the gas and magnetic fields (Umebayashi & Nakano 1988; Desch & Turner 2015). These more highly ionised regions are likely to sustain vigorous magnetohydrodynamics (MHD) turbulence driven by the magnetorotational instability (MRI) (Balbus & Hawley 1991), and the larger inward mass flow in this inner region is expected to create a sharp change in the surface density profile that can act as a planet trap.
The presence of density jumps or bumps at disk interfaces, such as at opacity transitions or in transitions between flow regimes (turbulent to laminar as described above), has been the subject of significant research because of its promise as a method to stop or slow down rapid planet migration (Matsumura et al. 2007; Hasegawa & Pudritz 2011; Bitsch et al. 2014, 2015; Baillié et al. 2015). In particular, the accretion mismatch at the inner edge of the dead zone and the subsequent formation of a density maximum has been intensively studied in the last few years using both hydrodynamic (Varnière & Tagger 2006; Lyra et al. 2008; Regály et al. 2012) and MHD simulations (Dzyurkevich et al. 2010, 2013). It appears that the flow around the density bump is not stable, but is prone to the Rossby wave instability (RWI; Lovelace et al. 1999), which produces large coherent vortices (Li et al. 2000; Meheut et al. 2010; Lin 2012; Lyra & Mac Low 2012). While a full understanding of the stability of giant vortices remains elusive (Lesur & Papaloizou 2009; Chang & Oishi 2010; Mizerski & Lyra 2012), these structure are thought to play an important role in planet formation (Barge & Sommeria 1995; Tanga et al. 1996; Johansen et al. 2004; Klahr & Bodenheimer 2006; Inaba & Barge 2006; Meheut et al. 2012a,b). This interest has intensified since the discovery of asymmetric features in high angular resolution imaging of protoplanetary disks (Brown et al. 2009; Casassus et al. 2012; van der Marel et al. 2013; Isella et al. 2013; Pérez et al. 2014); in particular, models able to account for the observed orbital location of these structures remain to be found.
Moreover, it has been demonstrated (Faure et al. 2015) that vortices, which are supposed to stay at the top of the density bump where they formed (Paardekooper et al. 2010b), are in fact subject to inward migration in a non-locally isothermal context. In MHD simulations of disk regions covering the dead zone inner edge, the migrating vortex is seen to be mass loaded (by virtue of arising at a density maximum) and to penetrate inside the turbulent region. It survives over a great distance as soon as the feedback of temperature onto the ionisation fraction is taken into account. The vortex is finally destroyed by turbulent fluctuations, and this releases its mass back into the disk, which then spreads to form a new pressure maximum and vortex at the initial formation location. The second generation vortex will follow the same cycle as its predecessor. It has been argued that the vortex cycle may have strong consequences on the planetesimal formation scenario via the gas friction onto small dust grains, but the potential effect of the cycle on planet migration at the interface has not yet been explored.
The gravitational interaction between a massive vortex and a planetary mass body has been addressed by Regály et al. (2013), Ataiee et al. (2014). They found that under some circumstances a vortex can capture a planet at its front or at its back and cause it to migrate with the vortex. This result, combined with the vortex cycle, may reduce the ability of the dead zone inner edge to trap planets.
In this paper we calculate directly the effect of the vortex cycle on planet migration within a non-locally isothermal viscous disk. As expected from Ataiee et al. (2014), we find that the vortex drags the planet with it during its migration, and when the vortex is destroyed it leaves the planet at some radius closer to the star. The subsequent evolution then depends on the planet mass and the disk mass, providing an effective filter for planets arriving at the dead zone inner edge. One of the main aims of this paper is to delineate the planet behaviour and explain the physical reasons for the different modes of planet evolution observed in the simulations. Using the simulation results we identify regions of parameter space where planets are able to remain in the planet trap zone, and parameters for which we expect planets to escape from this zone.
The paper is organised as follows. We describe our viscous disk model, the evolution equations, and list the physical ingredients required to reproduce the vortex cycle in Sect. 2. In Sect. 3 we present the results of the simulations, and describe the mutual influence of the vortex and the planet as a function of model parameters. In Sect. 4 we use customised simulations to examine in detail the nature of the interaction that maintains the joint evolution of the planet and the vortex, and identify the main physical mechanisms that have an impact on the fate of the planet. From this understanding we are able to derive a simple scaling for the range of planet masses that are stopped by the dead zone inner edge. We finally present a validation of these results using an MHD simulation of the dead zone inner edge region including a planet. The important implications and perspectives introduced by the results presented here are summarised in Sect. 5.
2. Simulation setup
We undertake hydrodynamic simulations to examine the interaction between a migrating planet and a vortex cycle. As discussed in the introduction, the vortex cycle is induced in the inner regions of a protoplanetary disk where there is a transition between the dead zone and the inner active zone. The inner active zone exists because the temperature there is high enough for gas-phase potassium to be ionised, hence allowing the development of magnetorotational turbulence. This transition leads to the formation of a surface density transition, and a pressure bump that is unstable to the formation of a vortex because of the RWI. In the non-locally isothermal situation, the vortex migrates inwards towards the hotter turbulent region. The vortex, however, keeps its temperature cooler than the surrounding medium and below the ionization temperature such that the MRI cannot develop inside. This protection from internal disruption enables its penetration deep inside the active zone. During the migration phase, the change in flow regime at the vortex edge drives a mass inflow such that the initial density bump is significantly modified. The vortex is at the same time eroded at its surface by the turbulent fluctuations. The vortex cycle arises because the vortex is finally destroyed and releases its mass into the disk, which then reforms the surface density transition, pressure bump, and migrating vortex. It has been demonstrated by Faure et al. (2015) that this vortex cycle can be reproduced in simple 2D simulations of a viscous disk model, and this allows us to take advantage of their low computational cost (compared to 3D MHD simulations) so that a full parameter survey can be undertaken. In this section we describe the 2D viscous disk model we use to investigate the effect of the vortex cycle on the dynamics of low and intermediate mass planets at the dead zone inner edge.
2.1. Disk model equations
The evolution of the disk model described below is calculated using the PLUTO code (Mignone et al. 2007). We used the cylindrical coordinates (R,φ) with units vectors (eR,eφ) to solve the following set of equations
![\begin{eqnarray} && \frac{\partial \Sigma}{\partial t} + \del \bcdot (\Sigma \bb{v}) = 0 \label{cont_eq}\\ && \frac{\partial \Sigma \bb{v}}{\partial t} + \del \bcdot (\Sigma \bb{v} \bb{v}) + \del P = -\Sigma \del \Phi + \del \tau \label{mom_eq}\\ && \frac{\partial E}{\partial t} + \del \bcdot \left[(E+P) \bb{v} \right] = -\Sigma\bb{v}\cdot \del \Phi -{\cal L} + \del \bcdot (\tau \cdot \bb{v})\label{energy_eq}\\ && \Phi = \Phi_\star+\Phi_{\rm pl} \end{eqnarray}](/articles/aa/full_html/2016/02/aa27194-15/aa27194-15-eq4.png) where v is the velocity, τ the Navier-Stokes stress tensor, and Σ the disk surface density. The quantities P and E are the vertically integrated pressure and total energy (the sum of the kinetic and thermal energy). The parameter Φ⋆ is the gravitational potential of the star. In the cylindrical approximation, it is given by Φ⋆ = − GM⋆/R, where G is the gravitational constant and M⋆ is the stellar mass. When present, the planet exerts a gravitational force on the gas according to the potential
where v is the velocity, τ the Navier-Stokes stress tensor, and Σ the disk surface density. The quantities P and E are the vertically integrated pressure and total energy (the sum of the kinetic and thermal energy). The parameter Φ⋆ is the gravitational potential of the star. In the cylindrical approximation, it is given by Φ⋆ = − GM⋆/R, where G is the gravitational constant and M⋆ is the stellar mass. When present, the planet exerts a gravitational force on the gas according to the potential 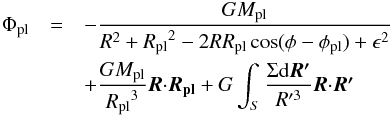 (5)where S is the simulation domain surface, Mpl is the planet mass, Rpl = (Rpl,φpl) is its position, and ϵ = 0.2H(R) is the softening length. As we are mainly interested in studying the influence of a surface density transition and its associated corotation torque on planet migration, we neglect the thermal diffusion process that is required to unsaturate the entropy contribution to the corotation torque (Paardekooper & Mellema 2006; Kley & Crida 2008; Paardekooper et al. 2011; Pierens et al. 2012). The second and third terms in the planet potential are indirect terms that arise because we work in a frame of reference centred on the host star (Nelson et al. 2000). All the details of the evolution of the planet through the disk action are given in Sect. 2.2.1. We use a perfect gas equation of state to close the above set of equations. The vertically integrated thermal energy is related to P via the relation Eth = P/ (γ − 1) in which γ = 1.4. We use the same gas cooling function ℒ as in Faure et al. (2015),
(5)where S is the simulation domain surface, Mpl is the planet mass, Rpl = (Rpl,φpl) is its position, and ϵ = 0.2H(R) is the softening length. As we are mainly interested in studying the influence of a surface density transition and its associated corotation torque on planet migration, we neglect the thermal diffusion process that is required to unsaturate the entropy contribution to the corotation torque (Paardekooper & Mellema 2006; Kley & Crida 2008; Paardekooper et al. 2011; Pierens et al. 2012). The second and third terms in the planet potential are indirect terms that arise because we work in a frame of reference centred on the host star (Nelson et al. 2000). All the details of the evolution of the planet through the disk action are given in Sect. 2.2.1. We use a perfect gas equation of state to close the above set of equations. The vertically integrated thermal energy is related to P via the relation Eth = P/ (γ − 1) in which γ = 1.4. We use the same gas cooling function ℒ as in Faure et al. (2015), 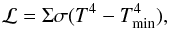 (6)where T is temperature and Tmin is the temperature associated with radiative equilibrium. We use the viscous prescription as a crude model of both turbulent angular momentum transport and heating. The kinematic viscosity radial profile is calibrated by the result of an identical 3D ideal MHD simulation of a fully turbulent disk model (without a dead zone) of Faure et al. (2015),
(6)where T is temperature and Tmin is the temperature associated with radiative equilibrium. We use the viscous prescription as a crude model of both turbulent angular momentum transport and heating. The kinematic viscosity radial profile is calibrated by the result of an identical 3D ideal MHD simulation of a fully turbulent disk model (without a dead zone) of Faure et al. (2015), 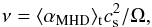 (7)where ⟨ αMHD ⟩ t is the stress tensor normalised by local pressure (TRφ/P) azimuthally, vertically, and time averaged over 200 orbits. The viscosity parameter takes the value ⟨ αMHD ⟩ t ≃ 0.04 at the inner edge of the domain and decreases to ⟨ αMHD ⟩ t ≃ 0.015 at the outer edge of the active region. Here, cs and Ω are the local sound speed and the orbital angular frequency.
(7)where ⟨ αMHD ⟩ t is the stress tensor normalised by local pressure (TRφ/P) azimuthally, vertically, and time averaged over 200 orbits. The viscosity parameter takes the value ⟨ αMHD ⟩ t ≃ 0.04 at the inner edge of the domain and decreases to ⟨ αMHD ⟩ t ≃ 0.015 at the outer edge of the active region. Here, cs and Ω are the local sound speed and the orbital angular frequency.
In all simulations the computational domain is R ∈ [R0,8 R0] and φ ∈ [0,2π] and has a resolution of [480,640]. To limit the reflection of waves at the domain boundaries, we add two buffer zones (de Val-Borro et al. 2006) extending on R ∈ [R0,1.5 R0] and R ∈ [7.7R0,8 R0] where physical quantities are damped towards their initial radial profile.
2.2. Notation and units
In the following X0 denotes the value of any quantity X at the inner edge of the domain. Units are identical to those defined in Faure et al. (2014) and chosen such that 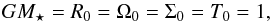 where Ω stands for the gas angular velocity. Time is measured in units of the inner orbital period.
where Ω stands for the gas angular velocity. Time is measured in units of the inner orbital period.
Density and temperature profiles are initialised with radial power laws, 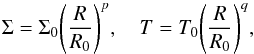 (8)where p = − 1.5 and q = − 0.75.
(8)where p = − 1.5 and q = − 0.75.
In the cooling function, Eq. (6), we chose σ to fix the disk aspect ratio to the desired value. In order to ease the comparison between the results presented here and the results of the MHD simulations of Faure et al. (2015), we chose H0/R0 ~ 0.12 in our two main cases. This corresponds to a disk cooling time of about 25 local orbits. This large value of H0/R0 is required to resolve the magnetorotational turbulence in MHD simulations.
2.2.1. Planet evolution
The evolution equation of the planet position is 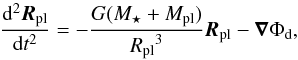 (9)where the gravitational potential of the disk is given by
(9)where the gravitational potential of the disk is given by 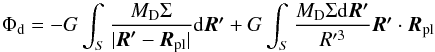 (10)and MD is a dimensionless parameter that scales the disk mass. The second term of the disk potential is the indirect term. Equation (9)is integrated explicitly at each time step. The gas surface density considered here is the averaged density
(10)and MD is a dimensionless parameter that scales the disk mass. The second term of the disk potential is the indirect term. Equation (9)is integrated explicitly at each time step. The gas surface density considered here is the averaged density 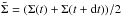 over the time step duration dt.
over the time step duration dt.
In most of the cases, the planet mass is set to a small enough value to prevent the formation of a gap in the disk. Only a few runs of our parameter survey (Sect. 3.3) included a planet able to open a small gap with relative density perturbation less than 10%. None of the planets considered are able to carve a deep gap since, for the most massive case 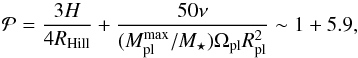 (11)where Ωpl is the rotation frequency at R = Rpl and RHill is the Hill radius of the planet (Crida et al. 2006). The individual numbers on the right hand side of Eq. (11) show the contributions of the viscous and pressure-related terms. For gap formation we require
(11)where Ωpl is the rotation frequency at R = Rpl and RHill is the Hill radius of the planet (Crida et al. 2006). The individual numbers on the right hand side of Eq. (11) show the contributions of the viscous and pressure-related terms. For gap formation we require 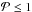 .
.
For the smallest planet mass considered (Mpl = 1.5 × 10-4), the horseshoe half-width is (Paardekooper et al. 2011) 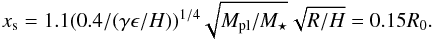 (12)This is then resolved by about 10 cells in the radial direction, similar to the resolution used in studies of the corotation region (Baruteau & Lin 2010; Baruteau et al. 2011; Pierens et al. 2012; Paardekooper 2014). In our fiducial run MD = 1.8 × 10-4. That sets the disk mass within 100 au equal to 2.3% of the stellar mass if R0 = 1 au.
(12)This is then resolved by about 10 cells in the radial direction, similar to the resolution used in studies of the corotation region (Baruteau & Lin 2010; Baruteau et al. 2011; Pierens et al. 2012; Paardekooper 2014). In our fiducial run MD = 1.8 × 10-4. That sets the disk mass within 100 au equal to 2.3% of the stellar mass if R0 = 1 au.
2.3. Disk model
In our viscous disk model, the feedback loop between angular momentum transport via viscosity and temperature is included by imposing 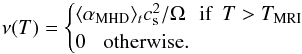 (13)The temperature threshold TMRI is a free parameter that sets the location of the transition between the viscous region and the inviscid region (Latter & Balbus 2012; Faure et al. 2014). We choose TMRI = 0.41, which places the dead zone inner edge around RDZ = 3.4 R0. The inner edge location is put far from the outer boundary of the domain to limit the wave reflection. Indeed, the reflection on the inner boundary of the domain of waves emitted by a planet or a vortex located at the dead zone inner edge is not an issue since waves propagating inside the active region are damped by viscosity. This is not the case for outward propagating waves that are only damped by shocks and numerical diffusion.
(13)The temperature threshold TMRI is a free parameter that sets the location of the transition between the viscous region and the inviscid region (Latter & Balbus 2012; Faure et al. 2014). We choose TMRI = 0.41, which places the dead zone inner edge around RDZ = 3.4 R0. The inner edge location is put far from the outer boundary of the domain to limit the wave reflection. Indeed, the reflection on the inner boundary of the domain of waves emitted by a planet or a vortex located at the dead zone inner edge is not an issue since waves propagating inside the active region are damped by viscosity. This is not the case for outward propagating waves that are only damped by shocks and numerical diffusion.
At the viscous jump, a density bump forms with a growth rate similar to the growth measured in MHD simulations of Faure et al. (2015). As soon as the density bump has reached five times the initial local density (which occurs at t = 3000), we add a random velocity perturbation at the position of the bump to trigger the RWI. The perturbation amplitude equals 10% of the sound speed. A vortex forms at the top of the density perturbation in a few tens of orbits and the vortex cycle is established. The average temperature radial profile when we introduce the perturbation is shown by the black dashed line in Fig. 2. The temperature exceeds the temperature threshold at R ≃ 3.2, slightly closer to the star than expected from looking at the initial profile. The average temperature radial profile outside the vortex in the middle of a cycle (red dashed line in Fig. 2) shows that the dead zone inner edge does not move during the vortex migration. The temperature radial profile at the same time (red plain line in the same figure) indicates that the vortex interior is not prone to the MRI since its temperature is kept below TMRI. We also ran a simulation of an identical disk model except that we used the locally isothermal approximation. The viscosity then becomes a function of position only. In this context, Faure et al. (2015) have shown that vortices formed at the dead zone inner edge do not migrate and, consequently, the vortex cycle does not develop.
 |
Fig. 1 Radial position of the density perturbation maximum (red curve, vortex position) and orbital evolution of planets A (green curve, top panel) and B (green curve, bottom panel). The black lines show the theoretical orbital evolution of the same planets in a power law disk model. The grey area corresponds to the positive total torque region around the vortex and the blue area shows the vortex Hill sphere in the vortex-point-mass model. The blue line shows the evolution of the same planets in the locally isothermal disk model. |
3. Planet orbital evolution at the dead-active zone interface
The planet is introduced during the middle of the 4th vortex cycle at (Rpl = 3.5,φpl = π/ 4). Two different planet masses have been considered: Mpl = 1.5 × 10-4 (case A) and Mpl = 3 × 10-4 (case B). These two planets are much lighter than the vortices observed in the simulations (by about an order of magnitude). The orbital evolution of the heavy planet is shown in the bottom panel of Fig. 1, while the lighter case is shown in the top panel. Surprisingly, the planets are not trapped at the dead zone inner edge as predicted by Masset et al. (2006b). However, the orbital evolution of the same planet in the locally isothermal disk model, where the vortex cycle does not develop, is consistent with the trapping of planets at the dead zone inner edge. This strongly suggests that the vortex cycle plays a major role in the dynamics of planets at the dead zone inner edge. In this section, we study both the vortex and the planet dynamics and their mutual interaction.
3.1. The two phases of the planet-vortex interaction
Our analysis of the mutual influence of the planet and the vortex is based on the determination of the vortex characteristics (mass, size, and position) and the background density profile (ΣBG). They are deduced from the fit (Σfit) of the average radial density profile for each output. The reader interested in the technical details of the analysis procedure is invited to refer to Appendix A. An example of a density radial profile and its fit is given in Fig. 3. The green solid line shows the corresponding density background ΣBG that is composed of the initial power law and what remains of the density bump after the formation of the vortex. The determination of the vortex size and location in this example at t = 4242 (1242 orbits after planet introduction) can be seen in the map of density perturbation (Σ − ΣBG) in Fig. 4. We also highlight two other coherent overdensities in this figure. They are in fact smaller vortices following the same inward migration as the primary vortex. This figure reveals an almost axisymmetric distribution of material behind the vortex, suggesting a sheared-out trailing tail following the vortex rotation. We call this density perturbation to the background density outside the vortex the vortex tail density perturbation. Figure 3 shows that the vortex tail changes the average radial surface density structure and in particular creates a steep positive density gradient. In this example, the mass of the primary vortex is Mv = 2.6 × 10-3 M⋆.
The Hill radius associated with the vortex when considered as a point mass of mass Mv is indicated by the blue shaded area in Fig. 1; it is about one scale height H at t = 4242. It roughly indicates the gravitational sphere of influence of the vortex, and as such it also represents the radii where a planet orbiting in the disk is likely to experience horseshoe dynamics when interacting gravitationally with the vortex. The grey area in Fig. 1 shows the width of the positive total torque region associated with the positive density gradient produced by the vortex tail. This positive torque arises because of a strong corotation torque. The total torque is evaluated using our fit Σfit to the density profile and the formula (47) given by Paardekooper et al. (2010a) where β = 0 and 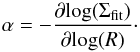 (14)The extension of the positive torque region at the 4242th orbit of case A is shown by the grey shaded area in Fig. 3. The theoretical migration of planet B calculated using the formula (47) but taking β = − q = 0.75 and α = − p = 1.5 is shown in Fig. 1, and agrees well with the simulation results when the planet is observed to be undergoing inward migration in the absence of a vortex.
(14)The extension of the positive torque region at the 4242th orbit of case A is shown by the grey shaded area in Fig. 3. The theoretical migration of planet B calculated using the formula (47) but taking β = − q = 0.75 and α = − p = 1.5 is shown in Fig. 1, and agrees well with the simulation results when the planet is observed to be undergoing inward migration in the absence of a vortex.
It is clear in both panels of Fig. 1 that the planet migration is changed when the vortex approaches. We distinguish two regimes:
-
When the planet is below the inner border of the positive torqueregion (R<RPT), the influence of the vortex is weak and the average density profile is close to the initial power law profile. In this case the planet migrates as in a power law disk without a dead zone.
-
When the planet orbital radius is inside the region of width equal to the vortex Hill radius, the vortex and planet migrate together with the same velocity.
At the end of a cycle, the vortex leaves the planet at the radius where it is destroyed. When a new vortex forms its migration is faster and it catches up with the planet during its inward motion. The planet is pulled back when it enters the positive torque region of the vortex tail (when R = RPT), and its evolution becomes locked to the vortex orbital evolution again.
3.2. Planet-vortex concomitant migration
 |
Fig. 2 Red dashed line: average density radial profile at t = 4242 in the simulation of case A outside the vortex. Red plain line: temperature profile at the vortex azimuth at the same time. Black plain line: initial temperature profile; black dashed line: steady state temperature radial profile before the introduction of the velocity perturbation. The temperature threshold TMRI is indicated by the vertical blue line. The two hatched areas show the buffer zones used in the simulation, the inner and outer regions where physical quantities are damped to the initial power law profile. |
The details of the interaction between the planet and the vortex when they become locked together can be seen in Fig. 5. The oscillations of the planet orbit around the vortex orbit (top panel) evoke the horseshoe motion of a small body (the planet in that case) interacting with a heavy body (the vortex). At this stage of the simulation, the mass ratio Mpl/Mv ~ 0.1. However, the range of the planet-vortex angular distance Δφ = φpl − φv (bottom panel) never approaches 2π as would be expected for the pure restricted three-body problem. The planet never follows an entire horseshoe orbit. It is always truncated before the planet reaches the other side of the vortex.
A close look at a plot of the coorbital evolution of the planet and the vortex reveals that the planet slowly moves outward after each U-turn in front of the vortex (associated with fast inward motions). To identify the physical origin of this outward migration, we ran two additional test simulations called RELAX-1 and RELAX-2. These are simulations of a similar disk model including planet A, but where the density is relaxed to either the density background profile (ΣBG, RELAX-1) and the density fit (Σfit, RELAX-2) measured at t = 4242 of the simulation of case A (see Fig. 3). In these simulations, the temperature threshold switch is also turned off in order to get fully viscous disks. The two steady radial density profiles obtained in these two simulations are shown in Fig. 3. The planet experiences a positive theoretical torque for both density distributions and migrates outwards in the two disks. The orbital evolution of planet A in the simulations RELAX-1 and RELAX-2 is shown on the top panel of Fig. 5.
The comparison of the orbital evolutions shows that the outward migration is much faster than expected in a disk with an average density radial profile corresponding to ΣBG described above. It is, in fact, as fast as the migration in a disk with an average density radial profile given by Σfit. We deduce that the horseshoe motion in azimuth of the planet in the frame of the vortex rotation is shortened by the outward migration induced by the vortex tail.
The vortex tail is thus the positive torque region that pulls the planet back during every cycle, and also enables the planet-vortex concomitant migration. In case B the outward migration of the planet is consistently faster and its horseshoe motion is shortened even more. In summary, we can see that the strongly coupled orbital evolution of the planet and vortex is assisted by the strong outward migration of the planet. The differential migration of planet and vortex in these cases leads to a shorter synodic period that reduces the azimuthal drift associated with the horseshoe motion. This reduced horseshoe motion is illustrated in the lower panel of Fig. 5.
3.3. The planet’s fate: parameter study
 |
Fig. 3 Red line: average density radial profile at t = 4242 in the simulation of case A. Black plain line: fit (Σfit) of the average density profile. Green plain line: density background profile (ΣBG) deduced from the fit. Green dashed line and black dashed lines: average equilibrium density radial profiles reached in the simulations RELAX-1 and RELAX-2, respectively. The grey area shows theoretical positive total torque region considering the reconstructed density profile with the density fit. The position of the inner boundary of this area (RPT) is indicated by a vertical blue line. The two hatched areas show the buffer zones used in the simulation: the inner and outer regions where physical quantities are damped to the initial power law profile. |
 |
Fig. 4 Map of density perturbation Σ − ΣBG at t = 4242 of the simulation of case A. The vortex contour is delimited by the black line and the vortex position is is indicated by the black cross. The white cross indicates the planet position. The two squares indicate the secondary vortices. |
 |
Fig. 5 Evolution of the planet orbit (green curve, top panel), the radial position of the density perturbation maximum (vortex orbit, red line, top panel), and the planet-vortex angular distance (bottom panel) in the simulation of planet A. The black dashed and plain lines show the orbital evolution of the same planet in the RELAX-1 and RELAX-2 simulations, respectively. |
The mutual influence between the vortex and planet found in the previous section raises a question about the actual efficiency of the dead zone inner edge trap. In this section we investigate the effect of varying the planet and disk masses on the ability of the planet to cross the dead zone inner edge border and escape the planet trap altogether.
In the previous runs, when the planets approached the inner boundary of the domain, their migration is polluted by boundary effects, preventing us from drawing any firm conclusion about their fates. For this parameter survey, we have therefore moved the dead zone inner edge outwards (RDZ = 5R0) setting TMRI = 0.2. Finally, we limited the vortex migration distance by tuning the viscosity for two reasons: 1) we want the planet to stay far from the inner boundary and 2) shortening the vortex cycle period means that a planet will experience more vortex cycles for the same computational time. We then scaled the ⟨αMHD⟩ parameter such that the viscosity interior to R = RDZ is about 1.5 times larger than the viscosity in the disk model with the dead zone inner edge close to the inner boundary. This sets the vortex migration distance between formation and destruction around Δ R ~ 1.6R0 ~ 4H(4R0). The average vortex cycle period tcycle is found to be about 550 inner orbits. The average vortex migration velocity over one cycle is then Vv = Δ R/tcycle ~ 4.6 × 10-4R0Ω0. We note that the migration speed may vary by 20% from one cycle to another. The planet is introduced at the beginning of the second cycle (cases starting at t = 3500) and/or at the end of the second cycle (cases starting at t = 4000).
List of all runs of the parameter study sample.
 |
Fig. 6 Synthetic summary of runs that sample the parameter space. The point size is directly related to the planet escaping time by |
All cases run are listed in Table 1. For a visual representation, see Fig. 6 where each run is shown by a point on the (Mpl/MD,Mpl × MD) plane. We have numbered six runs that will be used below to discuss the simulation outcomes. The stars in Fig. 6 indicate the (Mpl/MD,Mpl × MD) runs corresponding to cases A and B of the previous section. To account for the stochastic component in the evolution of these experiments, we ran the same simulation changing only the initial relative position of the planet and the vortex for a few of the (Mpl/MD,Mpl × MD) cases (see the relevant runs in the Table 1). Red points indicate runs for which the planet does not escape before the integration is stopped. On the other hand, a parameter set (Mpl/MD,Mpl × MD) for which at least one simulation exhibits an escaping planet is denoted by a black dot. In this last situation, the point size is a function of the time the planet spends following the vortex cycle before escaping from the dead zone inner edge trap (tesc). When multiple runs with different initial conditions for the same physical parameters (Mpl,MD) were realised, the escaping time is the averaged value over the escaping cases only. In cases where no planets escape the planet trap, the point size is set by the simulation run time tsim. This gives a lower limit on the time the planet is captured in those specific cases.
Our lightest planet case (labelled #6 in Fig. 6) is the smallest planet mass we can reasonably consider. In this case, the resolution is such that the horseshoe width extends over seven cells. We noticed in a test simulation of the viscous disk model where the viscous jump has been inhibited that a small gap develops with a density perturbation below 10% through the action of the planet labelled #1 in Fig. 6.
We compute the theoretical planet migration speed (assuming the planet remains on a circular Keplerian orbit) 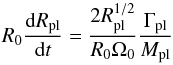 (15)in our power law disk (without dead zone) usingthe expression (47) given by Paardekooper et al. (2010a) of the total torque acting on the planet (Γpl) with β = − q = 0.75 and α = − p = 1.5:
(15)in our power law disk (without dead zone) usingthe expression (47) given by Paardekooper et al. (2010a) of the total torque acting on the planet (Γpl) with β = − q = 0.75 and α = − p = 1.5: 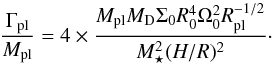 (16)This migration speed of a planet, free from the vortex influence, equals the average vortex migration speed at the dead zone inner edge if
(16)This migration speed of a planet, free from the vortex influence, equals the average vortex migration speed at the dead zone inner edge if 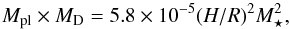 (17)that is to say
(17)that is to say 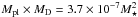 and Mpl = 2.1 × 10-3 M⋆ in our main disk model. The parameter space is then divided horizontally into two parts: points above the broad green region in Fig. 6 refer to simulations where the theoretical planet migration in a power law disk is faster than the vortex, while points below the region are simulations where the planet migration is theoretically slower than the vortex. The thickness of the green region arises because of the observed variation of the vortex migration speed between cycles.
and Mpl = 2.1 × 10-3 M⋆ in our main disk model. The parameter space is then divided horizontally into two parts: points above the broad green region in Fig. 6 refer to simulations where the theoretical planet migration in a power law disk is faster than the vortex, while points below the region are simulations where the planet migration is theoretically slower than the vortex. The thickness of the green region arises because of the observed variation of the vortex migration speed between cycles.
In this figure, it appears that planets in the highest parts of the diagram (Mpl × MD> 10-6 M⋆) all escape from the trap very rapidly. It also seems that planet capture is favoured on the right side of the plane (higher Mpl/MD), while planets escape faster when moving to the left side.
The red line of constant MD = 10-3 on the sample map crosses the parameter space from the bottom left to the top right corner. We take the simulations 1, 2, 3, 4, 5, and 6, spread along this line to illustrate the different behaviours of the planet-vortex evolution in the different parts of this diagram. The co-evolution of the planet and the vortex migration in these cases is shown in Fig. 7.
 |
Fig. 7 Same as Fig. 1 for the six cases highlighted in Fig. 6. They are ordered from top to bottom by increasing number (or equivalently by decreasing planet mass). |
For these six cases, and all others in the simulation sample, we recover the two phases described above: most of the time, the planet and the vortex are locked and migrate together. When the vortex is destroyed, the planet is free to migrate inward. A few differences between these cases deserve to be highlighted here.
-
First of all, as shown in Table 1 andFig. 6, the escaping time is not a monotonicfunction of planet mass.
-
The fluctuations of the planet orbits induced by density fluctuations in the disk (see below) are stronger for the two lightest planets. The planets escape in simulations #5 and #6 because these fluctuations kick the planets out of the positive torque region.
-
The vortex migration distance is shorter for higher planet masses.
-
For the most massive cases (#1, #2, and #3), the migration after vortex destruction is slower than expected theoretically in a power law disk. When the migration is compatible with the “theoretical free migration”, it is in general too late to outrun the new vortex. In case #3, the planet finally manages to escape after a long vortex cycle that leaves it deep inside the viscous region. In case #1, and all other cases with such a high mass, the altered migration velocity is faster than the vortex migration speed and so the planet escapes at the end of the first cycle.
-
Case #4 lies at the bottom of the green region in Fig. 6. This planet escapes during a slower cycle where the planet migration speed exceeds the vortex migration speed.
4. Discussion
4.1. The vortex tail and planet-vortex locking
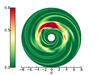 |
Fig. 8 Density map of perturbation to the flat background density at t = 150 of the inviscid simulation where Γ = 1.4 and k = 2. |
 |
Fig. 9 Evolution of the planet orbit (top panel) and the planet-vortex angular distance (bottom panel) in simulations of the inviscid disk model. Red line: MI1 case, green line MI2 case, and blue line MI3 case. The dashed area indicates the first U-turn of the planet in the MI1 case and in the MI2 case (respectively from left to right). The horizontal dashed line indicates the vortex orbital distance and the vertical line shows when the planet crosses the vortex orbit in the MI1 case. |
We have suggested that the planet-vortex locking mechanism can be modelled by a gravitational interaction between two point masses (the planet and the vortex) plus a positive corotation torque exerted by the quasi-axisymmetric vortex tail on the planet. The shape of the tail suggests that its origin is due to mass being expelled by the mass-loaded vortex that forms at the peak of the pressure bump. Mass spreading by internal viscous dissipation is probably too slow because the viscosity inside the vortex is null. Indeed, the temperature in the vortex core is below the temperature threshold for switching on viscosity, and the vortex is only eroded by viscous processes at its edge (Faure et al. 2015).
To test the validity of our two point mass model, we realised a few additional test simulations of a simple inviscid disk model with a flat temperature and density background (p = q = 0). In this disk, the energy equation is replaced by a polytropic evolution equation, 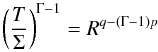 (18)with Γ the polytropic index that is a free parameter. To generate a vortex, a vorticity perturbation δω is introduced as a patch of circular perturbation of velocity and density. In order to maintain the vortex mass close to the initial value, we found it necessary to introduce density relaxation
(18)with Γ the polytropic index that is a free parameter. To generate a vortex, a vorticity perturbation δω is introduced as a patch of circular perturbation of velocity and density. In order to maintain the vortex mass close to the initial value, we found it necessary to introduce density relaxation 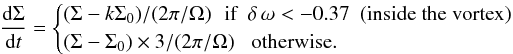 (19)with k a free parameter. After one vortex orbit (t ~ 5), the vorticity perturbation has relaxed to a quasi-steady state. The fact that mass has to be added constantly to the vortex to maintain its quasi-steady structure implies that the vortex expels mass or loses it via the action of residual numerical dissipation. The main differences between this disk model and the disk including a dead zone is the absence of the background density bump and the absence of explicit viscosity.
(19)with k a free parameter. After one vortex orbit (t ~ 5), the vorticity perturbation has relaxed to a quasi-steady state. The fact that mass has to be added constantly to the vortex to maintain its quasi-steady structure implies that the vortex expels mass or loses it via the action of residual numerical dissipation. The main differences between this disk model and the disk including a dead zone is the absence of the background density bump and the absence of explicit viscosity.
First we ran a batch of simulations without a planet with various k and polytropic indexes: 1.4 (locally adiabatic case), 1 (locally isothermal case), and 0.6. We discovered that, in most cases, vortices are not stable structures; they eventually split into a big vortex and a few smaller child-vortices because of the vortex mass loading. As an example, we show the density map (Fig. 8) of the disk with Γ = 1.4 and k = 2 at t = 150. At this stage, two child-vortices have detached from the primary one. It seems that the timescale associated to the vortex splitting is very sensitive to the vortex mass perturbation k and the disk thermodynamics. In fact, this phenomenon of vortex-splitting is also observed in the viscous simulations where the viscosity gradient at the vortex edge drives a mass inflow inside the vortex (Faure et al. 2015). These simulations show that the vortices do not necessarily require viscous erosion at their edges to eject the mass needed to build up a tail. However, the viscous process, that is more efficient on smaller structures, may ease the formation of the tail by dissipating child-vortices on short timescales.
While most simulations have shown that child-vortices are not massive enough to significantly affect the planet angular momentum, they may have an indirect impact on the planet migration by increasing the mass in the tail. Addressing the detailed reasons for the splitting of the vortices goes beyond the scope of this paper, but will be addressed in future work.
After choosing a disk model with a relatively long-lived vortex (described below), we ran three simulations with different initial locations of the planet Mpl = 3 × 10-4 that is introduced five orbits after the beginning of the simulation:
-
Case MI1: the planet initially leads the vortex in azimuth byΔ φ = 1.7, and orbits further from the star than the vortex with Rpl − Rv = 0.4.
-
Case MI2: The planet initially leads the vortex in azimuth (Δ φ = 1.7), and the planet and vortex orbit at the same distance from the star.
-
Case MI3: The planet and vortex orbit initially at the same distance from the star, but now the vortex leads the planet in azimuth with Δ φ = 5.
We chose k = 1.2 for these simulations. This leaves a window of a few hundred orbits to study the interaction between vortices and planets before vortices start to split. Choosing MD = 6. × 10-4 M⋆, we get a vortex mass about two times higher (Mv ~ 6 × 10-4 M⋆) than the planet mass (Mpl = 3 × 10-4 M⋆). We also opt for a locally isothermal disk model (Γ = 1) to prevent the vortex migration (Paardekooper et al. 2010b; Faure et al. 2015), as our intention here is to focus on the horseshoe dynamics. We note, however, that the planet is able to migrate relative to the vortex and this plays an important role in the evolution. The evolution of the planet in these cases is shown in Fig. 9.
For the run MI1, the planet is initially further from the star than the vortex is, and leads in azimuth. The vortex orbits faster and catches up with the planet. When the planet enters the gravitational influence of the vortex, it makes a U-turn at t = 20 orbits, such that it orbits closer to the star than the vortex does. The planet now orbits faster than the vortex and runs away from it. At t ≃ 75, when the planet has a conjunction with the vortex, the gravitational effect on the planet is weak since the planet orbital distance from the vortex is greater than the Hill sphere radius of the vortex by virtue of the planet’s inward migration. The planet thus escapes from vortex influence and continues migrating inwards.
Case MI2 is identical, except that the planet initially orbits closer to the star than the vortex does. It runs away from the vortex without experiencing a U-turn. When it has a conjunction with the vortex the migration has moved it outside of the horseshoe region and it continues to migrate inwards.
In the last case (MI3), the planet is constantly following the vortex rotation. When the planet approaches the vortex, it makes a U-turn that places it on an orbit that is further from the star than the vortex is. Because of its inward migration, it then catches up the vortex again, and the cycle repeats without end (or at least for the lifetime of the vortex). This demonstrates how migration can shorten the horseshoe motion in azimuth. The planet remains captured behind the vortex.
These numerical experiments confirm that the planet initiates horseshoe motion when it encounters the vortex, just as a small body enters the gravitational sphere of influence of a larger one orbiting around the star. Consistently with our model for the planet-vortex locking, the outward motion of the planet after a vortex-planet encounter has not been observed in the MI simulations since the vortex tail is damped by our density relaxation (so a strong positive corotation torque is not present). However, the simulation MI3 shows that a vortex migrating slower than a planet can capture the planet behind it. By symmetry, this suggests that a vortex migrating inwards faster than the planet should be able to capture the planet in front of it, with the migration speed difference playing the role of the vortex tail in shortening the horseshoe motion in azimuth.
4.2. Planet filtering
From the parameter study presented in section 3.3 it seems that either low mass planets or more massive planets escape from the planet trap, while intermediate mass planets remain trapped at the inner edge of the dead zone.
Apparently planets are able to fully escape from the trap during a vortex cycle as soon as they can migrate across this zone before the vortex created in the next cycle attracts them back. In other words, the planet migration has to be faster than that of the vortex. This translates into the criterion Eq. (17)involving the product of the disk and planet mass. Taking that the vortex migration speed scales with R− 1 / 2 (as the Keplerian velocity) and with (H/R)2 (Paardekooper et al. 2010b), we can rewrite the criterion as 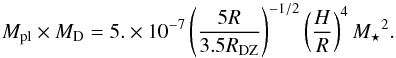 (20)Hence, for reasonable values of disk scale height (H/R = 0.05), disk mass (MD = 10-3, Mdisk ~ 10%M⋆), and dead zone inner edge position (RDZ = 0.5 au), the limiting mass is Mpl = 10-4 M⋆ (i.e. approximately Neptune’s mass).
(20)Hence, for reasonable values of disk scale height (H/R = 0.05), disk mass (MD = 10-3, Mdisk ~ 10%M⋆), and dead zone inner edge position (RDZ = 0.5 au), the limiting mass is Mpl = 10-4 M⋆ (i.e. approximately Neptune’s mass).
The lower mass limit where fluctuations free the planet from the inner edge trap cannot be estimated so easily. These fluctuations reflect the torque variability induced by density waves (excited by the vortex) and small structures in the disk that arise when a vortex is disrupted at the end of a cycle. We have measured the standard deviation of the torque for different disk and planet masses. As expected, the torque fluctuations linearly depend on the disk mass. This is not the case for the planet mass dependence as shown in Figs. 10 and 11. The measure of the torque deviation on case #6 is very uncertain since the planet escapes rapidly. Measurement errors indicated in the Fig. 11 have been taken into account. We fitted the data with a power law to obtain a scaling of the torque fluctuation amplitude with the planet mass. We found that the torque deviation scales with planet mass as 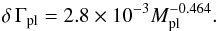 (21)Isocontours of the torque deviation normalised by that measured in case #6 (δ Γpl,#6) are shown in Fig. 6. Reasons for the dependence of the fluctuating torque on the planet mass are described below.
(21)Isocontours of the torque deviation normalised by that measured in case #6 (δ Γpl,#6) are shown in Fig. 6. Reasons for the dependence of the fluctuating torque on the planet mass are described below.
Planets on the left part of the (Mpl/MD,Mpl × MD) plane are more prone to being kicked out of the planet trap region by torque fluctuations. Taking the torque fluctuations amplitude measured in case #4 (isocontour δ Γpl/δ Γpl,#6 = 0.385) as the limit below which the planet always escapes, whatever its migration speed, we can derive a lower mass limit for the fiducial disk model mentioned above. We obtain Mpl = 3. × 10-5 M⋆ (i.e. about ten times Earth’s mass). Since the vortex lifetime and (more importantly) the fragments lifetime should be shortened by an interior residual viscosity, the stochastic torque given by our calculations is sensitive to numerical resolution that sets the dissipation in the inactive regions. Hence, this tentative result of the minimum mass should be confirmed by simulations with the appropriate higher resolution of a disk model with an explicit low viscosity inside the dead zone.
Hence, only intermediate mass planets can be kept at the inner edge of the dead zone; low mass planets are ejected by torque fluctuations at vortex destruction and high mass ones migrate too fast (provided they cannot form a gap).
 |
Fig. 10 Torque evolution (top panel) and its standard deviation to average value (bottom panel) in runs 2, 4, 5, and 6 (red, blue, green, and black curves, respectively). |
 |
Fig. 11 Variation of the average torque standard deviation with planet mass for the late escaping planets of the sample (more than 10 000 orbits): red crosses. The black dot with error bars corresponds to case 6. The green curve shows the best fit by a power law: |
Moreover, the maximum mass criterion seems to be elevated for higher Mpl/MD ratios because more massive planets destabilise the vortex. This effect can be seen in plots of the evolution of relative maximum density for different planet masses. We show an example for cases #2 (higher mass) and #4 (lower mass) in Fig. 12. The vortex cycle in case #2 is always interrupted prematurely. The vortex is cut into fragments as the density map of Fig. 13 shows. No real primary vortex can be identified, each element has roughly the planet mass. The vortical structure is broken by the waves emitted by the planet, which are stronger for heavier planets. The breaking is observed in lighter planet cases, but at a later stage when viscosity has weakened the vortex sufficiently. The planet interacts with all the pieces of the broken vortex, delaying its free migration. However, the viscous spreading of the vortex mass is speeded up significantly because it breaks up, and this shortens the vortex cycle. A new cycle will begin as soon as this material has viscously spread back to the dead zone inner edge. In order to escape from the planet trap, these more massive vortex-destroying planets need the vortex cycle to be sufficiently prolonged that they can migrate inwards faster than a single coherent vortex. The feedback of the planet onto the vortex behaviour is more and more pronounced moving towards the right in the (Mpl/MD,Mpl × MD) plane shown in Fig. 6: the more massive the planet, the more exceptional the cycle has to be. A second consequence is that the vortex in the small planet case has time to grow so that it becomes increasingly mass loaded. When the vortex breaks up at the end of the vortex migration cycle then the vortex fragments are themselves more massive and induce stronger torque fluctuations that can kick the low mass planets out of the trap region before a new vortex forms and migrates. This is the origin of the relation between planet mass and torque fluctuation amplitude discussed above. This also implies that the torque fluctuations amplitude is probably a function of the disk H/R. This has, however, been ignored in the estimation of the lower limit planet mass in a fiducial disk.
 |
Fig. 12 Evolution of the maximum of the density perturbation in cases 2 (red line) and 4 (green line) of the sample. |
Finally, we ran the locally isothermal counterparts for most simulations in our sample, where vortex migration and the vortex cycles do not occur. We find that all planets stay at the dead zone inner edge. This highlights the fact that the vortex cycle inhibits the dead zone inner edge trapping capability for either low mass planets and more massive planets. This result complements the predictions for planet trapping from Masset et al. (2006b).
4.3. Role of the vortex gravitational potential
The planet trapping by the vortex can be partly interpreted by viewing it in the context of the restricted three-body problem since the planet is considerably lighter than the vortex in the simulations presented here. The vortex is consequently quite massive while its gravitational influence on the rest of the disk has been neglected (self-gravity ignored). The most massive vortices have been found in the viscous simulations denoted as A and B. In this section, we evaluate a posteriori the potential influence of the vortex on the disk itself.
We first compute the Toomre number Q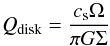 (22)for disk stability. An example of Q-values obtained in the simulations is shown in Fig. 14. Even in the vortex, where the rotation is slower and the density higher, the minimum value is Qdisk = 9.04. We then calculated the average value of the Toomre number Q for the vortex itself, treating the vortex as a local sub-disk to test against internal fragmentation
(22)for disk stability. An example of Q-values obtained in the simulations is shown in Fig. 14. Even in the vortex, where the rotation is slower and the density higher, the minimum value is Qdisk = 9.04. We then calculated the average value of the Toomre number Q for the vortex itself, treating the vortex as a local sub-disk to test against internal fragmentation 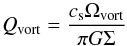 (23)with a rotation frequency evaluated from vorticity perturbation
(23)with a rotation frequency evaluated from vorticity perturbation 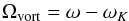 (24)where ωK is the Keplerian vorticity at the vortex centre. In the example, the 4242nd orbit of case A, the average value is ⟨Qvort⟩ = 5.4. At all times of the viscous simulations, the values of Qdisk and ⟨Qvort⟩ remain above unity.
(24)where ωK is the Keplerian vorticity at the vortex centre. In the example, the 4242nd orbit of case A, the average value is ⟨Qvort⟩ = 5.4. At all times of the viscous simulations, the values of Qdisk and ⟨Qvort⟩ remain above unity.
We finally evaluate the possibility for the vortex to open a gap since that would change the picture presented above completely. Using Eq. (11), we checked that 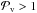 for all outputs in the two viscous simulations with a dead zone inner edge close to the inner boundary.
for all outputs in the two viscous simulations with a dead zone inner edge close to the inner boundary. 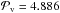 at t = 4242 in the simulation of case A.
at t = 4242 in the simulation of case A.
We conclude that the disk and the vortex are gravitationally stable, and the vortex is also not massive enough to carve a deep gap if the self-gravity is included. For the simulations of the disk model with a dead zone inner edge located further from the inner boundary and a high disk mass MD = 1 × 10-3, the vortex remains lighter than in the simulations of cases A and B since it forms in a less dense region.
4.4. Runs with MHD turbulence
The last effect on the trapping of planets that has not yet been mentioned is the viscosity value we used. Viscosity weakens the vortex during its migration and sets the cycle maximum amplitude. This effect is very sensitive. We ran a single 3D MHD simulation of a turbulent version of our disk model to test the validity of our results.
This simulation was performed using a uniform grid version of the code RAMSES (Teyssier 2002; Fromang et al. 2006). We solved the MHD equations in cylindrical coordinates (R,φ,Z) with units vectors (eR,eφ,ez)![\begin{eqnarray} &&\frac{\partial \rho}{\partial t}+\del \bcdot (\rho \bb{v}) = 0 ,\\ &&\frac{\partial \rho \bb{v}}{\partial t}+\del \bcdot (\rho \bb{v} \bb{v} - \bb{B} \bb{B}) + \del P = -\rho \del \Phi ,\\ &&\frac{\partial E}{\partial t}+\del \bcdot \left[(E+P) \bb{v} - \bb{B} (\bb{B} \bcdot \bb{v}) + {\cal F_{\eta}} \right] = -\rho\bb{v}\cdot\nabla \Phi -{\cal L} \label{energy_eq2} ,\\ &&\frac{\partial \vec{B}}{\partial t} - \bb{\nabla} \btimes (\bb{v} \times \bb{B}) = - \bb{\nabla} \btimes (\eta \bb{\nabla} \btimes \bb{B}) \label{induc} , \end{eqnarray}](/articles/aa/full_html/2016/02/aa27194-15/aa27194-15-eq253.png)
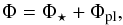 (29)where ρ is the volume density, v is the velocity, and B is the magnetic field. The extensive variables (like P, E, ℒ) are the volumetric version of the 2D quantities with the same name. The magnetic diffusivity is denoted by η and is responsible for the resistive flux ℱη that appears in Eq. (27)(see Balbus & Hawley 1998). We captured the turbulent heating by solving the equation of total energy conservation. The initial magnetic field configuration is purely toroidal. Its vertical profile is such that the integrated magnetic flux through a vertical slice of the disk vanishes. The computational domain is R ∈ [R0,8 R0], φ ∈ [0,2π], and Z ∈ [ − 0.3 R0,0.3 R0] and has a resolution of [480,640,80]. In this simulation, a resistive buffer extends over Δ R = 0.5 on both sides of the domain to damp the magnetic fluctuations at the boundary and ensure numerical stability. A viscous buffer extends between the inner edge of the domain and R = 2. This has been found necessary by Faure et al. (2015) to ensure the continuity of angular momentum transport at the inner boundary of the domain.
(29)where ρ is the volume density, v is the velocity, and B is the magnetic field. The extensive variables (like P, E, ℒ) are the volumetric version of the 2D quantities with the same name. The magnetic diffusivity is denoted by η and is responsible for the resistive flux ℱη that appears in Eq. (27)(see Balbus & Hawley 1998). We captured the turbulent heating by solving the equation of total energy conservation. The initial magnetic field configuration is purely toroidal. Its vertical profile is such that the integrated magnetic flux through a vertical slice of the disk vanishes. The computational domain is R ∈ [R0,8 R0], φ ∈ [0,2π], and Z ∈ [ − 0.3 R0,0.3 R0] and has a resolution of [480,640,80]. In this simulation, a resistive buffer extends over Δ R = 0.5 on both sides of the domain to damp the magnetic fluctuations at the boundary and ensure numerical stability. A viscous buffer extends between the inner edge of the domain and R = 2. This has been found necessary by Faure et al. (2015) to ensure the continuity of angular momentum transport at the inner boundary of the domain.
 |
Fig. 13 Map of relative density perturbation to the azimuthal average density at t = 4780 of the 2nd simulation of the sample. The vortex contour is delimited by the black line and the vortex position is located at the black cross. The planet position is shown by a white cross. |
We first ran an ideal MHD simulation of this disk model (η = 0) that sets the initial conditions for our non-ideal MHD runs we discuss below. A dead zone (or resistive region) is introduced in the disk when the turbulence has developed into a steady state and the temperature has reached a stable profile. We then take into account the feedback of the temperature on the ionization fraction setting, 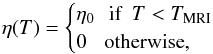 (30)as we did previously for the viscosity in the viscous disk model. The temperature threshold and the dead zone inner edge position are set to identical values as in the cases A and B of our viscous disk: TMRI = 0.41 and RDZ = 3.4 R0. As in the viscous simulations, a vortex forms and starts to migrate through the active region. Figure 15 shows the orbital evolution of the vortex and the planet (Mpl = 1.5 × 10-4) that is introduced at the beginning of the first vortex cycle. While the planet orbit is occasionally shifted up, the planet closely follows the vortex migration. In this simulation, the turbulent fluctuations of density are not strong enough to disrupt the vortex-planet coupled evolution and stop their concomitant migration.
(30)as we did previously for the viscosity in the viscous disk model. The temperature threshold and the dead zone inner edge position are set to identical values as in the cases A and B of our viscous disk: TMRI = 0.41 and RDZ = 3.4 R0. As in the viscous simulations, a vortex forms and starts to migrate through the active region. Figure 15 shows the orbital evolution of the vortex and the planet (Mpl = 1.5 × 10-4) that is introduced at the beginning of the first vortex cycle. While the planet orbit is occasionally shifted up, the planet closely follows the vortex migration. In this simulation, the turbulent fluctuations of density are not strong enough to disrupt the vortex-planet coupled evolution and stop their concomitant migration.
While the vortex migration distance is very sensitive to the value of αMHD in the viscous simulations, the vortex cycle obtained in the MHD simulation shows that the turbulence self-adjusts to enable the vortex penetration in the active zone over a large distance.
 |
Fig. 14 Map of the Toomre number for the disk gravitational stability at t = 4242 of the simulation of case A. The vortex contour is delimited by the black line and the vortex position is located at the black cross. |
 |
Fig. 15 Radial position of the density perturbation maximum (red curve, vortex position) and orbital evolution of the planet (green curve). |
5. Conclusion
In this paper we have presented a series of simulations of viscous disk models, centred on the vicinity of the dead zone inner edge, with embedded migrating planets. Previous work (Faure et al. 2015) has shown that the dramatic change in the effective viscosity at this interface leads to the formation of a sharp transition in the surface density, the formation of a pressure bump that is unstable to the formation of a vortex, and a repeating vortex-cycle that is driven by the migration, destruction, and reformation of the vortex. The main aim of this work is to examine in detail the interaction between the planet and the vortex cycle, and to determine its influence on the ability of the dead zone inner edge to act as a planet trap (Masset et al. 2006b). The main results and conclusions to be drawn from this study can be summarised as follows:
-
The interaction between the planet and the inward migratingvortex always causes the planet to be dragged inwards by thevortex. In agreement with Ataieeet al. (2014), we find that this occursbecause the planet and vortex undergo horseshoe interaction thatcauses the vortex and planet to migrate together.
-
The inward migration of the vortex into the inner viscous region of the disk causes its eventual destruction, and this releases the planet. The subsequent evolution can then result in the planet remaining trapped in the region of the dead zone inner edge or completely escaping from this region by migrating inwards. The outcome depends on the planet mass.
-
Massive (but non-gap forming) planets tend to escape from the planet trap. This is because they migrate inwards and away from the planet trap region rapidly when released by the vortex.
-
Low mass planets also tend to escape from the planet trap because they experience strong stochastic torques from both the spiral waves excited by the migrating vortex and from the vortex fragments when it is disrupted, and these tend to kick the planet out of the planet trap region.
-
Intermediate mass planets migrate too slowly to escape the influence of the next incoming vortex in the cycle, and so remain trapped in the region centred on the dead zone inner edge through horseshoe interaction with the subsequent generations of vortices. These planets are also less affected by the stochastic torques that are responsible for allowing the low mass planets to escape the trap. Consequently, we find that the vortex cycle causes the dead zone inner edge to act as a mass-dependent planet filter.
-
We estimate that the range of masses for which the planet trap operates effectively is approximately in the range 3 × 10-5 M⋆<Mpl< 10-4 M⋆, although we caution that this needs to be confirmed by more sophisticated MHD simulations than we have presented here.
The simulations that we have presented are by necessity simplified 2D viscous disk simulations that employ a rather unsophisticated temperature dependent switch to model the transition between the dead zone and the magnetically active inner region of the disk. Performing a suite of 3D MHD simulations to examine this problem, with the requirement of undertaking a parameter study in order to understand the physics of the vortex-planet interaction, would require computational resources that are beyond those that we have at our disposal. Nonetheless, the study presented here provides a clear proof of concept that the interaction between planets and vortices at the dead zone inner edge is important, and should be taken into account when modelling the migration of short period planets. Future work will focus on developing more sophisticated models to validate those that we have presented here, including the effects of MHD turbulence, non-ideal MHD effects, and the heating of the disk by stellar irradiation and turbulent dissipation so that the physics of the dead zone inner edge are captured more accurately. The effect of planet growth should also be investigated since the results presented above involve planets already massive enough to undergo gas accretion. These models will automatically incorporate the stochastic torques from the MHD turbulence as well as the disrupting vortex, hence placing firmer limits on which planets remain at the planet trap and which ones can escape inwards.
Finally, we note that the vortex-planet interactions that we have examined in this work may also be relevant for regions of the disk that lie far beyond the dead zone inner edge. It has been suggested that planet traps may arise at large orbital radii from the star, such as at the location of the ice line(s) (e.g. Ida & Lin 2008; Lyra et al. 2010; Hasegawa & Pudritz 2011; Kretke & Lin 2012), and it is clear that if vortices located at these radii form and migrate then the processes that we have examined in this work may also be relevant in this broader context. It is clear that the interaction between planets and vortices in regions of protoplanetary disks where pressure bumps lead to vortex formation is likely to play an important role in the migration history of forming planets.
Acknowledgments
This research was supported by an STFC Consolidated grant awarded to the QMUL Astronomy Unit 2012-2016. This work used the DiRAC Complexity system, operated by the University of Leicester IT Services, which forms part of the STFC DiRAC HPC Facility (www.dirac.ac.uk). This equipment is funded by BIS National E-Infrastructure capital grant ST/K000373/1 and STFC DiRAC Operations grant ST/K0003259/1. DiRAC is part of the National E-Infrastructure.
References
- Ataiee, S., Dullemond, C. P., Kley, W., Regály, Z., & Meheut, H. 2014, A&A, 572, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baillié, K., Charnoz, S., & Pantin, E. 2015, A&A, 577, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Balbus, S. A., & Hawley, J. F. 1991, ApJ, 376, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Balbus, S. A., & Hawley, J. F. 1998, Rev. Mod. Phys., 70, 1 [Google Scholar]
- Barge, P., & Sommeria, J. 1995, A&A, 295, L1 [NASA ADS] [Google Scholar]
- Baruteau, C., & Lin, D. N. C. 2010, ApJ, 709, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Baruteau, C., Fromang, S., Nelson, R. P., & Masset, F. 2011, A&A, 533, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Morbidelli, A., Lega, E., Kretke, K., & Crida, A. 2014, A&A, 570, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Johansen, A., Lambrechts, M., & Morbidelli, A. 2015, A&A, 575, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, J. M., Blake, G. A., Qi, C., et al. 2009, ApJ, 704, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Butler, R. P., Vogt, S. S., Marcy, G. W., et al. 2004, ApJ, 617, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Casassus, S., Perez, M. S., Jordán, A., et al. 2012, ApJ, 754, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Chang, P., & Oishi, J. S. 2010, ApJ, 721, 1593 [NASA ADS] [CrossRef] [Google Scholar]
- Crida, A., Morbidelli, A., & Masset, F. 2006, Icarus, 181, 587 [Google Scholar]
- Desch, S. J., & Turner, N. J. 2015, ApJ, 811, 156 [NASA ADS] [CrossRef] [Google Scholar]
- de Val-Borro, M., Edgar, R. G., Artymowicz, P., et al. 2006, MNRAS, 370, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Dzyurkevich, N., Flock, M., Turner, N. J., Klahr, H., & Henning, T. 2010, A&A, 515, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dzyurkevich, N., Turner, N. J., Henning, T., & Kley, W. 2013, ApJ, 765, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Faure, J., Fromang, S., & Latter, H. 2014, A&A, 564, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Faure, J., Fromang, S., Latter, H., & Meheut, H. 2015, A&A, 573, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fromang, S., Hennebelle, P., & Teyssier, R. 2006, A&A, 457, 371 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gammie, C. F. 1996, ApJ, 457, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Tremaine, S. 1980, ApJ, 241, 425 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Hasegawa, Y., & Pudritz, R. E. 2011, MNRAS, 417, 1236 [NASA ADS] [CrossRef] [Google Scholar]
- Ida, S., & Lin, D. N. C. 2008, ApJ, 685, 584 [NASA ADS] [CrossRef] [Google Scholar]
- Inaba, S., & Barge, P. 2006, ApJ, 649, 415 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Isella, A., Pérez, L. M., Carpenter, J. M., et al. 2013, ApJ, 775, 30 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Johansen, A., Andersen, A. C., & Brandenburg, A. 2004, A&A, 417, 361 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klahr, H., & Bodenheimer, P. 2006, ApJ, 639, 432 [NASA ADS] [CrossRef] [Google Scholar]
- Kley, W., & Crida, A. 2008, A&A, 487, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kley, W., & Nelson, R. P. 2012, ARA&A, 50, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Kretke, K. A., & Lin, D. N. C. 2012, ApJ, 755, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Latter, H. N., & Balbus, S. 2012, MNRAS, 424, 1977 [NASA ADS] [CrossRef] [Google Scholar]
- Lesur, G., & Papaloizou, J. C. B. 2009, A&A, 498, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, H., Finn, J. M., Lovelace, R. V. E., & Colgate, S. A. 2000, ApJ, 533, 1023 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, M.-K. 2012, ApJ, 754, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, D. N. C., & Papaloizou, J. 1986, ApJ, 309, 846 [NASA ADS] [CrossRef] [Google Scholar]
- Lissauer, J. J., Fabrycky, D. C., Ford, E. B., et al. 2011, Nature, 470, 53 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lovelace, R. V. E., Li, H., Colgate, S. A., & Nelson, A. F. 1999, ApJ, 513, 805 [NASA ADS] [CrossRef] [Google Scholar]
- Lyra, W., & Mac Low, M.-M. 2012, ApJ, 756, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Lyra, W., Johansen, A., Klahr, H., & Piskunov, N. 2008, A&A, 491, L41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lyra, W., Paardekooper, S.-J., & Mac Low, M.-M. 2010, ApJ, 715, L68 [NASA ADS] [CrossRef] [Google Scholar]
- Masset, F. S. 2001, ApJ, 558, 453 [Google Scholar]
- Masset, F. S. 2002, A&A, 387, 605 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masset, F. S., D’Angelo, G., & Kley, W. 2006a, ApJ, 652, 730 [NASA ADS] [CrossRef] [Google Scholar]
- Masset, F. S., Morbidelli, A., Crida, A., & Ferreira, J. 2006b, ApJ, 642, 478 [NASA ADS] [CrossRef] [Google Scholar]
- Matsumura, S., Pudritz, R. E., & Thommes, E. W. 2007, ApJ, 660, 1609 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Marmier, M., Lovis, C., et al. 2011, A&A, submitted [arXiv:1109.2497] [Google Scholar]
- Meheut, H., Casse, F., Varniere, P., & Tagger, M. 2010, A&A, 516, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meheut, H., Keppens, R., Casse, F., & Benz, W. 2012a, A&A, 542, A9 [Google Scholar]
- Meheut, H., Meliani, Z., Varniere, P., & Benz, W. 2012b, A&A, 545, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mignone, A., Bodo, G., Massaglia, S., et al. 2007, ApJS, 170, 228 [Google Scholar]
- Mizerski, K. A., & Lyra, W. 2012, J. Fluid Mech., 698, 358 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, R. P., Papaloizou, J. C. B., Masset, F., & Kley, W. 2000, MNRAS, 318, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Paardekooper, S.-J. 2014, MNRAS, 444, 2031 [NASA ADS] [CrossRef] [Google Scholar]
- Paardekooper, S.-J., & Mellema, G. 2006, A&A, 459, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paardekooper, S.-J., Baruteau, C., Crida, A., & Kley, W. 2010a, MNRAS, 401, 1950 [NASA ADS] [CrossRef] [Google Scholar]
- Paardekooper, S.-J., Lesur, G., & Papaloizou, J. C. B. 2010b, ApJ, 725, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Paardekooper, S.-J., Baruteau, C., & Kley, W. 2011, MNRAS, 410, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez, L. M., Isella, A., Carpenter, J. M., & Chandler, C. J. 2014, ApJ, 783, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Pierens, A., Baruteau, C., & Hersant, F. 2012, MNRAS, 427, 1562 [NASA ADS] [CrossRef] [Google Scholar]
- Regály, Z., Juhász, A., Sándor, Z., & Dullemond, C. P. 2012, MNRAS, 419, 1701 [NASA ADS] [CrossRef] [Google Scholar]
- Regály, Z., Sándor, Z., Csomós, P., & Ataiee, S. 2013, MNRAS, 433, 2626 [NASA ADS] [CrossRef] [Google Scholar]
- Tanga, P., Babiano, A., Dubrulle, B., & Provenzale, A. 1996, Icarus, 121, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Teyssier, R. 2002, A&A, 385, 337 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Udry, S., Bonfils, X., Delfosse, X., et al. 2007, A&A, 469, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Umebayashi, T., & Nakano, T. 1988, Prog. Theor. Phys. Suppl., 96, 151 [NASA ADS] [CrossRef] [Google Scholar]
- van der Marel, N., van Dishoeck, E. F., Bruderer, S., et al. 2013, Science, 340, 1199 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Varnière, P., & Tagger, M. 2006, A&A, 446, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ward, W. R. 1991, in Lun. Plan. Inst. Tech. Rep., 22, 1463 [Google Scholar]
- Ward, W. R. 1997, Icarus, 126, 261 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Analysis procedure and definitions
In order to evaluate the vortex mass and position, for each output we fit the average of the radial profile of density perturbation to the initial power law by a two-Gaussian function, 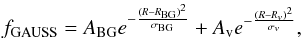 (A.1)where ABG, RBG, σBG, Ah, Rh, and σh are free parameters of the fit. An example of a density radial profile reconstructed (Σfit) with such a fit is given in Fig. 3, black curve.
(A.1)where ABG, RBG, σBG, Ah, Rh, and σh are free parameters of the fit. An example of a density radial profile reconstructed (Σfit) with such a fit is given in Fig. 3, black curve.
We define the vortex position and the vortex size using the density perturbation δ Σ = Σ − Σfit. The vortex position is the
location of the maximum of the density perturbation δ Σ where we also excluded the density perturbation inside the planet’s Hill sphere. The vortex contour is given by δ Σ = max(δ Σ) / 2. For the example of t = 4242, we show the vortex contour and position on the density maps of Fig. 4.
We call the background density ΣBG at time t the reconstructed density profile from the fit without the density perturbation associated with the vortex (δ Σv = Avexp( − (R − Rv)2/σv)).
Following these analysis steps, we can finally deduce the vortex mass Mv. It is defined as the total gas mass inside the vortex contour reduced by the background density.
All Tables
All Figures
 |
Fig. 1 Radial position of the density perturbation maximum (red curve, vortex position) and orbital evolution of planets A (green curve, top panel) and B (green curve, bottom panel). The black lines show the theoretical orbital evolution of the same planets in a power law disk model. The grey area corresponds to the positive total torque region around the vortex and the blue area shows the vortex Hill sphere in the vortex-point-mass model. The blue line shows the evolution of the same planets in the locally isothermal disk model. |
| In the text | |
 |
Fig. 2 Red dashed line: average density radial profile at t = 4242 in the simulation of case A outside the vortex. Red plain line: temperature profile at the vortex azimuth at the same time. Black plain line: initial temperature profile; black dashed line: steady state temperature radial profile before the introduction of the velocity perturbation. The temperature threshold TMRI is indicated by the vertical blue line. The two hatched areas show the buffer zones used in the simulation, the inner and outer regions where physical quantities are damped to the initial power law profile. |
| In the text | |
 |
Fig. 3 Red line: average density radial profile at t = 4242 in the simulation of case A. Black plain line: fit (Σfit) of the average density profile. Green plain line: density background profile (ΣBG) deduced from the fit. Green dashed line and black dashed lines: average equilibrium density radial profiles reached in the simulations RELAX-1 and RELAX-2, respectively. The grey area shows theoretical positive total torque region considering the reconstructed density profile with the density fit. The position of the inner boundary of this area (RPT) is indicated by a vertical blue line. The two hatched areas show the buffer zones used in the simulation: the inner and outer regions where physical quantities are damped to the initial power law profile. |
| In the text | |
 |
Fig. 4 Map of density perturbation Σ − ΣBG at t = 4242 of the simulation of case A. The vortex contour is delimited by the black line and the vortex position is is indicated by the black cross. The white cross indicates the planet position. The two squares indicate the secondary vortices. |
| In the text | |
 |
Fig. 5 Evolution of the planet orbit (green curve, top panel), the radial position of the density perturbation maximum (vortex orbit, red line, top panel), and the planet-vortex angular distance (bottom panel) in the simulation of planet A. The black dashed and plain lines show the orbital evolution of the same planet in the RELAX-1 and RELAX-2 simulations, respectively. |
| In the text | |
 |
Fig. 6 Synthetic summary of runs that sample the parameter space. The point size is directly related to the planet escaping time by |
| In the text | |
 |
Fig. 7 Same as Fig. 1 for the six cases highlighted in Fig. 6. They are ordered from top to bottom by increasing number (or equivalently by decreasing planet mass). |
| In the text | |
 |
Fig. 8 Density map of perturbation to the flat background density at t = 150 of the inviscid simulation where Γ = 1.4 and k = 2. |
| In the text | |
 |
Fig. 9 Evolution of the planet orbit (top panel) and the planet-vortex angular distance (bottom panel) in simulations of the inviscid disk model. Red line: MI1 case, green line MI2 case, and blue line MI3 case. The dashed area indicates the first U-turn of the planet in the MI1 case and in the MI2 case (respectively from left to right). The horizontal dashed line indicates the vortex orbital distance and the vertical line shows when the planet crosses the vortex orbit in the MI1 case. |
| In the text | |
 |
Fig. 10 Torque evolution (top panel) and its standard deviation to average value (bottom panel) in runs 2, 4, 5, and 6 (red, blue, green, and black curves, respectively). |
| In the text | |
 |
Fig. 11 Variation of the average torque standard deviation with planet mass for the late escaping planets of the sample (more than 10 000 orbits): red crosses. The black dot with error bars corresponds to case 6. The green curve shows the best fit by a power law: |
| In the text | |
 |
Fig. 12 Evolution of the maximum of the density perturbation in cases 2 (red line) and 4 (green line) of the sample. |
| In the text | |
 |
Fig. 13 Map of relative density perturbation to the azimuthal average density at t = 4780 of the 2nd simulation of the sample. The vortex contour is delimited by the black line and the vortex position is located at the black cross. The planet position is shown by a white cross. |
| In the text | |
 |
Fig. 14 Map of the Toomre number for the disk gravitational stability at t = 4242 of the simulation of case A. The vortex contour is delimited by the black line and the vortex position is located at the black cross. |
| In the text | |
 |
Fig. 15 Radial position of the density perturbation maximum (red curve, vortex position) and orbital evolution of the planet (green curve). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.