| Issue |
A&A
Volume 586, February 2016
|
|
|---|---|---|
| Article Number | A42 | |
| Number of page(s) | 14 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201527158 | |
| Published online | 25 January 2016 | |
Polarized radiative transfer in discontinuous media
1 Istituto Ricerche Solari Locarno (IRSOL), via Patocchi 57–Prato Pernice, 6605 Locarno-Monti, Switzerland
e-mail: steiner@kis.uni-freiburg.de, fzueger@irsol.ch; belluzzi@irsol.ch
2 Kiepenheuer-Institut für Sonnenphysik (KIS), Schöneckstrasse 6, 79104 Freiburg, Germany
Received: 10 August 2015
Accepted: 2 November 2015
Context. Observations of the solar atmosphere of ever increasing spatial resolution reveal steep gradients in the magnetic field and in thermal states. Likewise, numerical simulations of the solar atmosphere show contact discontinuities and shock fronts. This asks for the development of robust methods for computing the radiative transfer of polarized light in discontinuous media.
Aims. Here, we propose a new concept for dealing with discontinuities in the radiative transfer of polarized light and carry out a few basic test calculations. While in the past, the focus was on interpolating the source function with ever-increasing accuracy and smoothness, we propose to take the opposite approach by reconstructing it with piecewise continuous functions, taking discontinuities on purpose into account. This concept is known from computational fluid dynamics.
Methods. Test calculations were carried out for (i) a Milne-Eddington atmosphere; (ii) an atmosphere featuring a single discontinuity that is shifted across one grid cell; and (iii) a two-layered atmosphere with discontinuities in the source function, the velocity, and the magnetic field.
Results. It is shown that the method of piecewise continuous reconstruction is a viable approach to solving the radiative transfer equation for polarized light. In the special case where a discontinuity coincides with a computational cell interface, the method is capable of producing the exact solution. Overall, the assessment of the piecewise continuous reconstruction method turns out to be cautiously positive, but it does not lead to an order-of-magnitude improvement in accuracy over conventional methods for the examples considered here. More realistic model atmospheres need to be considered for judging practical applicability.
Key words: radiative transfer / polarization / methods: numerical / Sun: atmosphere / Sun: magnetic fields
© ESO, 2016
1. Introduction
The transfer and polarization of a beam of light traveling across an atmosphere is a problem that needs to be routinely solved in solar and stellar physics. The partial polarization of light in solar and stellar atmospheres is generated by magnetic fields, scattering processes, and atomic polarization, and it therefore bears a great deal of information about the physical state of the atmosphere from which the light emerges. In astrophysical research one can only remotely sense these atmospheres, which is why radiative transfer computations are an indispensable tool for recovering their physical state.
In general terms, the problem of the transfer of partially polarized light can be described by the following system of coupled first-order, ordinary differential equations, 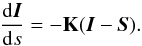 (1)Here, K and S are, in the simplest case of local thermodynamic equilibrium (LTE), known functions of the coordinate s along the ray path. The intensity vector I = (I,Q,U,V)T is termed as the Stokes vector, where I stands for the total intensity of the light beam, Q for the intensity difference of the linearly polarized light in two orthogonal axes in the plane perpendicular to the light beam, U for the corresponding intensity difference in the two axes rotated by 45° in the same plane, and V for the intensity difference between the righthanded and lefthanded circularly polarized light. Furthermore, S = (SI,SQ,SU,SV)T is the source function for the four Stokes parameters and K the 4 × 4 propagation matrix that can be written in the form (see Landi Degl’Innocenti & Landolfi 2004, for a general derivation of the equations and the symmetry properties of K)
(1)Here, K and S are, in the simplest case of local thermodynamic equilibrium (LTE), known functions of the coordinate s along the ray path. The intensity vector I = (I,Q,U,V)T is termed as the Stokes vector, where I stands for the total intensity of the light beam, Q for the intensity difference of the linearly polarized light in two orthogonal axes in the plane perpendicular to the light beam, U for the corresponding intensity difference in the two axes rotated by 45° in the same plane, and V for the intensity difference between the righthanded and lefthanded circularly polarized light. Furthermore, S = (SI,SQ,SU,SV)T is the source function for the four Stokes parameters and K the 4 × 4 propagation matrix that can be written in the form (see Landi Degl’Innocenti & Landolfi 2004, for a general derivation of the equations and the symmetry properties of K) 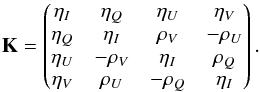 (2)The coefficients ηQ, ηU, and ηV define the absorption with respect to the different polarization states of the light beam, ρQ, ρU, and ρV describe the coupling of the Stokes parameters owing to anomalous dispersion effects, while ηI is the usual absorption coefficient irrespective of the polarization state (Landi Degl’Innocenti & Landi Degl’Innocenti 1985; Landi Degl’Innocenti 1987). The seven independent coefficients that appear in the matrix K are functions of the wavelength and of other parameters describing the atmosphere. In the case of spectral lines formed in the presence of a magnetic field, these parameters depend, among others, on the strength and orientation of the magnetic field with respect to the ray of propagation. In the case of nonlocal thermodynamic equilibrium (non-LTE), the source function S and the propagation matrix K depend in a complicated manner on the Stokes vector I so that the equation system (1) becomes nonlinear. In this case, the radiative transfer Eq. (1) must be supplemented by rate equations describing the electron transition between atomic energy states. When atomic polarization is neglected and only the Zeeman effect is considered, the source function vector has a particularly simple form (see Sect. 4.1), and Eq. (1) is referred to as the Unno-Rachkovsky equation (Unno 1956; Rachkovsky 1962a,b).
(2)The coefficients ηQ, ηU, and ηV define the absorption with respect to the different polarization states of the light beam, ρQ, ρU, and ρV describe the coupling of the Stokes parameters owing to anomalous dispersion effects, while ηI is the usual absorption coefficient irrespective of the polarization state (Landi Degl’Innocenti & Landi Degl’Innocenti 1985; Landi Degl’Innocenti 1987). The seven independent coefficients that appear in the matrix K are functions of the wavelength and of other parameters describing the atmosphere. In the case of spectral lines formed in the presence of a magnetic field, these parameters depend, among others, on the strength and orientation of the magnetic field with respect to the ray of propagation. In the case of nonlocal thermodynamic equilibrium (non-LTE), the source function S and the propagation matrix K depend in a complicated manner on the Stokes vector I so that the equation system (1) becomes nonlinear. In this case, the radiative transfer Eq. (1) must be supplemented by rate equations describing the electron transition between atomic energy states. When atomic polarization is neglected and only the Zeeman effect is considered, the source function vector has a particularly simple form (see Sect. 4.1), and Eq. (1) is referred to as the Unno-Rachkovsky equation (Unno 1956; Rachkovsky 1962a,b).
In this article, we consider the so called formal solution of Eq. (1) only for which S and K are supposed to be known. The formal solution is an essential part of iterative schemes for solving the nonlinear problem and is therefore of fundamental practical relevance. Section 2 reviews various methods of the formal solution for the transfer of partially polarized light. In Sect. 3, we then propose an alternative method for the formal solution in the case of a discontinuous medium and give details of it in Sect. 4. Section 5 presents a few examples and compares between different solution procedures. Summary, conclusions, and future plans are given in Sect. 6.
2. Formal solution
Generally, the formal solution of Eq. (1) can be written in terms of the evolution operator (or Stokes attenuation operator) O as 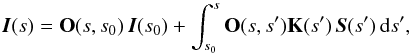 (3)where O(s,s′) is a 4 × 4 matrix obeying the differential equation
(3)where O(s,s′) is a 4 × 4 matrix obeying the differential equation 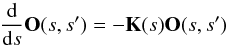 (4)and the limiting condition
(4)and the limiting condition 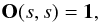 (5)where 1 is the 4 × 4 identity matrix. Equation (4) is as difficult to solve as Eq. (1), which is why early attempts to solve the radiative transfer for polarized light numerically was done by means of Runge-Kutta integration of Eq. (1) directly (Beckers 1969; Wittmann 1974; Landi Degl’Innocenti 1976). Alternatively, Eq. (1) can be recast to a second-order differential equation for the sum of inward and outward propagating intensities (method of Feautrier 1964) and solved with a second-order finite difference scheme (Auer et al. 1977; Rees et al. 1989).
(5)where 1 is the 4 × 4 identity matrix. Equation (4) is as difficult to solve as Eq. (1), which is why early attempts to solve the radiative transfer for polarized light numerically was done by means of Runge-Kutta integration of Eq. (1) directly (Beckers 1969; Wittmann 1974; Landi Degl’Innocenti 1976). Alternatively, Eq. (1) can be recast to a second-order differential equation for the sum of inward and outward propagating intensities (method of Feautrier 1964) and solved with a second-order finite difference scheme (Auer et al. 1977; Rees et al. 1989).
In the following two sections, we take a closer look at two different analytical methods for solving the radiative transfer equation across an atmospheric slab of finite spatial and optical thickness.
2.1. Analytical form of the evolution operator
A particular case for which the evolution operator O(s,s′) for an atmospheric slab of finite thickness can be written in a closed analytical form is the one where the propagation matrix K is constant with s (or, more general K(s) = f(s)K′ with K′ = const.). Thus, K at a particular point s1 commutes with the same matrix at any other point s2, so that we can expand ![\begin{equation} \label{eq:evolution_operator_exp} {{\bf O}}(s,s') = \exp[-\mathbf{K}(s-s')], \; {\rm where}\; \exp(\mathbf{K}) = \sum_{n=0}^{\infty}\frac{(-1)^n}{n!}\mathbf{K}^n, \end{equation}](/articles/aa/full_html/2016/02/aa27158-15/aa27158-15-eq32.png) (6)making use of the commutative property of K. Starting from here and decomposing K in terms of the unitary matrix and three complex and corresponding conjugate complex matrices, the evolution operator can finally be expressed in closed analytical form as was shown by Landi Degl’Innocenti & Landi Degl’Innocenti (1985) as
(6)making use of the commutative property of K. Starting from here and decomposing K in terms of the unitary matrix and three complex and corresponding conjugate complex matrices, the evolution operator can finally be expressed in closed analytical form as was shown by Landi Degl’Innocenti & Landi Degl’Innocenti (1985) as ![\begin{eqnarray} \label{eq:evolution_operator_anal} {{\bf O}}(s,s') &=& \exp(-\eta_I x) \left\{ \frac{1}{2}\left[\cosh(\Lambda_1 x) + \cos(\Lambda_2 x)\right]\mathbf{M}_1 \right. \nonumber\\ &&\quad - \sin(\Lambda_2 x)\mathbf{M}_2 - \sinh(\Lambda_1 x)\mathbf{M}_3 \nonumber\\ &&\quad+\left. \frac{1}{2}\left[\cosh(\Lambda_1 x) - \cos(\Lambda_2 x)\right]\mathbf{M}_4 \right\}, \end{eqnarray}](/articles/aa/full_html/2016/02/aa27158-15/aa27158-15-eq33.png) (7)where x = (s−s′), M1 the unitary matrix, and M2...M4 and Λ1,2 real 4 × 4 matrices and real scalars, respectively, consisting of combinations of the coefficients of the propagation matrix.
(7)where x = (s−s′), M1 the unitary matrix, and M2...M4 and Λ1,2 real 4 × 4 matrices and real scalars, respectively, consisting of combinations of the coefficients of the propagation matrix.
Since K = const. across the finite path from s1 to s2, and since it commutes with the evolution operator O(s,s′), we can take it out of the integral so that Eq. (3) now reads 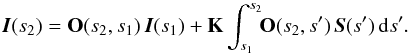 (8)Subdividing the ray of propagation into a sequence of paths (short characteristics), each having constant but in general different propagation matrix K and integrable source transmission O(s2,s′) S(s′), we can thus integrate the transfer equation piece by piece analytically, using the emergent Stokes vector of the preceding path as the boundary condition of the subsequent path. We are going to make use of this solution strategy in Sect. 5.
(8)Subdividing the ray of propagation into a sequence of paths (short characteristics), each having constant but in general different propagation matrix K and integrable source transmission O(s2,s′) S(s′), we can thus integrate the transfer equation piece by piece analytically, using the emergent Stokes vector of the preceding path as the boundary condition of the subsequent path. We are going to make use of this solution strategy in Sect. 5.
2.2. From DELO to DELOPAR and BESSER
Currently, the most widely applied method for the numerical integration of the radiative transfer equation for polarized light is the “diagonal element lambda operator”, DELO (Rees et al. 1989), and variations of it. Noting that the diagonal elements of the propagation matrix are all identical, Eq. (1) can be written as 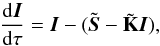 (9)where dτ = −ηIds,
(9)where dτ = −ηIds, 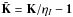 , and
, and 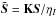 . The formal solution of Eq. (9) across the finite optical path from τi + 1 to τi is then
. The formal solution of Eq. (9) across the finite optical path from τi + 1 to τi is then 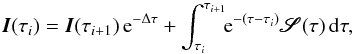 (10)where
(10)where 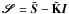 is called the effective source function and Δτ = τi + 1−τi. We notice that optical depths are measured in the opposite direction with respect to the ray path so that τ(i + 1) >τ(i). Thus, the evolution operator (commonly referred to as Λ-operator in ordinary radiative transfer) of this pseudo formal solution derives only from the unity diagonal elements of the matrix K/ηI, hence the name DELO. All the rest, consisting of the off-diagonal elements, makes part of the effective source function. Since
is called the effective source function and Δτ = τi + 1−τi. We notice that optical depths are measured in the opposite direction with respect to the ray path so that τ(i + 1) >τ(i). Thus, the evolution operator (commonly referred to as Λ-operator in ordinary radiative transfer) of this pseudo formal solution derives only from the unity diagonal elements of the matrix K/ηI, hence the name DELO. All the rest, consisting of the off-diagonal elements, makes part of the effective source function. Since 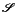 depends on I(τ), Eq. (10) really is an integral equation for I(τ), which reduces to the common formal solution in the absence of polarization when
depends on I(τ), Eq. (10) really is an integral equation for I(τ), which reduces to the common formal solution in the absence of polarization when 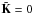 . To obtain an explicit formula for I(τi), Rees et al. (1989) linearly interpolated
. To obtain an explicit formula for I(τi), Rees et al. (1989) linearly interpolated  between τi + 1 and τi so that
between τi + 1 and τi so that ![\begin{equation} \label{eq:delo_interpol} \pmb{\mathscr{S}(\tau)} = \left[(\tau_{i+1} - \tau)\pmb{\mathscr{S}}_{i} + (\tau - \tau_{i})\pmb{\mathscr{S}}_{i+1}\right]/\Delta\tau. \end{equation}](/articles/aa/full_html/2016/02/aa27158-15/aa27158-15-eq57.png) (11)Then, Eq. (10) can be integrated analytically, yielding an explicit formula for I(τi). The crucial point here is that the effective source function
(11)Then, Eq. (10) can be integrated analytically, yielding an explicit formula for I(τi). The crucial point here is that the effective source function 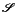 is linearly interpolated and continuous at nodes i.
is linearly interpolated and continuous at nodes i.
Trujillo Bueno (2003) realized that the DELO method can be improved by using parabolic interpolation between τi−1, τi, and τi + 1 for the source function 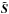 , while maintaining linear interpolation for
, while maintaining linear interpolation for 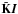 . Both interpolants are continuous but not differentiable at the nodes τi. Trujillo Bueno (2003) called this improved version DELOPAR and stated that it was “substantially more accurate than the original DELO method”.
. Both interpolants are continuous but not differentiable at the nodes τi. Trujillo Bueno (2003) called this improved version DELOPAR and stated that it was “substantially more accurate than the original DELO method”.
Because parabolic interpolation can be non-monotonic between otherwise monotonic node values, Štěpán & Trujillo Bueno (2013) went even one step further (drawing from an idea of Auer 2003), using quadratic Bézier splines for 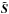 (but still linear interpolation for
(but still linear interpolation for 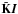 ). In this case, the interpolant of the source function is strictly monotone for a monotonic sequence of node values and it can be made one times differentiable and it remains continuous as is the interpolant for
). In this case, the interpolant of the source function is strictly monotone for a monotonic sequence of node values and it can be made one times differentiable and it remains continuous as is the interpolant for 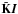 . Štěpán & Trujillo Bueno (2013) called this method of integration enthusiastically BESSER (BEzier Spline SolvER, which is also German for better) and performed some accuracy tests proving the superiority of it.
. Štěpán & Trujillo Bueno (2013) called this method of integration enthusiastically BESSER (BEzier Spline SolvER, which is also German for better) and performed some accuracy tests proving the superiority of it.
De la Cruz Rodríguez & Piskunov (2013) used quadratic and cubic Bézier splines for the interpolation of the effective source function and provided detailed comparisons of the accuracy between these methods, the linear and parabolic DELO method, and the Hermitian interpolation method of Bellot Rubio et al. (1998). The latter method is not based on DELO but belongs to an own class of formal solution methods introduced to radiative transfer by Auer (1976) and extended to Stokes radiative transfer by Bellot Rubio et al. (1998). In the Hermitian method, the Stokes vector at si is obtained by Taylor expansion to fourth-order around si−1, where I(si−1) is known. Using its first and second derivative and the transfer Eq. (1), I(si) can then be expressed in terms of I(si−1) and the propagation matrix and source function and first derivatives of S and K, which both are obtained from quadratic interpolation of these quantities. De la Cruz Rodríguez & Piskunov (2013) concluded that the “DELO-Bezier schemes outperform all other algorithms when the density of depth points is low and the structure of the medium includes steep gradients”. A Bézier type interpolation for the formal solution of the polarized radiative transfer equation was also employed by Holzreuter & Solanki (2012). Steffen (1990) introduced an interpolation method based on third-order polynomials that produces a smooth and strictly monotonic interpolant with continuous first-order derivatives. This method is applied for the interpolation of absorption coefficients in one of the radiative transfer modules (based on the Feautrier scheme and long characteristics) of the (magneto-)hydrodynamics code CO5BOLD (Freytag et al. 2012).
3. From BESSER back to simple
When DELO is good and BESSER better, what then is best? The answer to this question, we surmise, depends on the application. It is remarkable that De la Cruz Rodríguez & Piskunov (2013) also state that for very coarse grids with just one node per decade of optical depth “it is hard to beat the DELO-linear solution, which keeps the errors under control despite the strong gradients and poorly sampled stellar atmosphere”. Such poorly sampled model atmospheres are of practical relevance, for example for the Stokes inversion problem1, for which it is difficult and expensive to deal with a large number of grid nodes. Other applications where low-order methods may be advisable include discontinuous atmospheres, which feature shock fronts and contact discontinuities. This is actually also the strategy pursued by shock capturing hydrodynamical schemes, which switch to low-order at locations of a discontinuity. Standard non-LTE radiative transfer codes notoriously show difficulties to converge when applied to the post-processing of data from numerical simulations because of the steep gradients and discontinuities that occur in such atmospheres. In the following, we therefore propose a method specifically aimed at dealing with discontinuous atmospheres.
3.1. Learning from computational fluid dynamics
Very often in solar and stellar physics, one is confronted with the task of computing (synthesizing) spectral lines from model atmospheres that are the result of numerical simulations. Such atmospheres frequently show steep gradients, shock fronts, contact discontinuities, or intermittent peaks in temperature. Furthermore, it is important to realize that a physical quantity, qi, from a finite volume numerical scheme represents the spatial average over the finite volume Vi = ΔxΔyΔz of the computational cell which qi refers to, not the exact node value (see, e.g., Toro 2009; LeVeque 2002). This is in particular true for the conserved quantities: mass density, momentum density, and total energy density. Similarly, the numerical magnetic field components represent spatial averages over computational cell interfaces. Therefore, the reconstruction step of a hydrodynamical scheme comprises the interpolation of these quantities under the constraint of conservation, i.e., 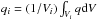 , where q is the reconstruction (interpolant) over volume Vi. While an interpolation function goes usually through its discrete node points, a reconstruction does not necessarily adopt the node value at the node location but assumes this value when integrated over the corresponding computational cell. This additional constraint may imply that the reconstruction is discontinuous at the cell boundaries.
, where q is the reconstruction (interpolant) over volume Vi. While an interpolation function goes usually through its discrete node points, a reconstruction does not necessarily adopt the node value at the node location but assumes this value when integrated over the corresponding computational cell. This additional constraint may imply that the reconstruction is discontinuous at the cell boundaries.
The most basic reconstruction scheme, known under the name “Godunov scheme”, is the piecewise constant reconstruction. In this case q(x) = qi,x ∈ Vi. This implies that discontinuities occur at cell interfaces from one volume element to the neighboring one. In a continuous medium, these discontinuities are small, but they can become large at real discontinuities in the medium, which is indeed what we want to allow for. Yet, the piecewise constant reconstruction may be too inaccurate for representing the continuous, smooth parts of an atmosphere. The next higher-order reconstruction, still allowing for discontinuities, is the “van Leer scheme” (Van Leer 1979) consisting of the piecewise linear reconstruction. Thus, we write q = qi + σσσ(x−xi),x ∈ Vi, where 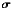 defines the slopes of the linear reconstruction in each coordinate direction and xi refers to the volume center. Note that this reconstruction still obeys the conservation requirement and still allows for discontinuities at cell interfaces but leaves now the freedom of choosing the components of
defines the slopes of the linear reconstruction in each coordinate direction and xi refers to the volume center. Note that this reconstruction still obeys the conservation requirement and still allows for discontinuities at cell interfaces but leaves now the freedom of choosing the components of 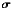 for obtaining a best reconstruction in parts where the atmosphere is continuous. Moreover, the slopes
for obtaining a best reconstruction in parts where the atmosphere is continuous. Moreover, the slopes 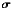 can be chosen, or limited, such that the reconstruction is monotonic, meaning that local extremes are avoided as was the purpose of the Bézier-spline method. Moving one order of accuracy higher, one can use the piecewise parabolic reconstruction (PPM) of Colella & Woodward (1984), which still is conservative, preserves monotonicity, and allows for discontinuities.
can be chosen, or limited, such that the reconstruction is monotonic, meaning that local extremes are avoided as was the purpose of the Bézier-spline method. Moving one order of accuracy higher, one can use the piecewise parabolic reconstruction (PPM) of Colella & Woodward (1984), which still is conservative, preserves monotonicity, and allows for discontinuities.
 |
Fig. 1 Definition of optical depth, ray path, and grid indices for cells, nodes, and cell interfaces. |
3.2. Slope limiters
There exists a large number of different types of slope limiters for the van Leer reconstruction scheme. We choose for our purpose symmetric limiters, i.e., limiters that do not differentiate between upwind or downwind direction. Given node values qi−1, qi, and qi + 1, where q is a general expression for quantities like the source function, or the effective source function, or absorption coefficients, or optical depth, etc., we consider the local ray path from 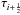 to
to 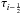 , where
, where 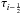 is half way from τi−1 to τi, and
is half way from τi−1 to τi, and 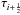 half way from τi to τi + 1 (see Fig. 1). We then compute the slope σi for the reconstruction in the computational cell i by
half way from τi to τi + 1 (see Fig. 1). We then compute the slope σi for the reconstruction in the computational cell i by 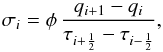 (12)where φ is the slope limiter. For φ ≡ 0, we recover the piecewise constant reconstruction. Given
(12)where φ is the slope limiter. For φ ≡ 0, we recover the piecewise constant reconstruction. Given 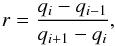 (13)which represents the ratio of successive gradients on the solution mesh, the minmod limiter of Roe (1986) is given by
(13)which represents the ratio of successive gradients on the solution mesh, the minmod limiter of Roe (1986) is given by 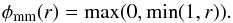 (14)It selects for the slope in cell i, σi = 0 whenever the grid function has a a local minimum or a local maximum at node i. In the case of a monotonic grid function, it selects either
(14)It selects for the slope in cell i, σi = 0 whenever the grid function has a a local minimum or a local maximum at node i. In the case of a monotonic grid function, it selects either 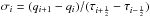 or
or 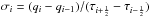 , i.e., the slope with respect to the node value to the left or to the right, whichever of their moduli is smaller. This choice minimizes the total variation of the reconstruction q and keeps it locally monotone so that no local minima or maxima can occur. Another slope limiter that is going to be used in the following section is the Van Leer limiter (Van Leer 1974) given by
, i.e., the slope with respect to the node value to the left or to the right, whichever of their moduli is smaller. This choice minimizes the total variation of the reconstruction q and keeps it locally monotone so that no local minima or maxima can occur. Another slope limiter that is going to be used in the following section is the Van Leer limiter (Van Leer 1974) given by 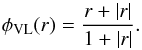 (15)Again, this slope limiter becomes zero in case that the grid function possesses a local minimum or maximum but it allows for twice as large gradients as with the minmod limiter in the case when r is large. Additionally, we will use the superbee limiter of Roe (1986), given by
(15)Again, this slope limiter becomes zero in case that the grid function possesses a local minimum or maximum but it allows for twice as large gradients as with the minmod limiter in the case when r is large. Additionally, we will use the superbee limiter of Roe (1986), given by 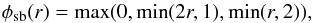 (16)which, once again, allows for steeper gradients than both the minmod and the Van Leer limiter.
(16)which, once again, allows for steeper gradients than both the minmod and the Van Leer limiter.
The behavior of the different slope limiters can be appreciated with the help of Fig. 2. Panel (a) shows an initial function that is piecewise linear and continuous, except of a jump at the interface from cell 4 to cell 5. The black dots indicate discrete node values (discrete grid function) representing the average of the initial function over the corresponding computational cell, thereby satisfying the requirement of conservation. The nodes are located in the center of each computational cell and constitute the only available data for the subsequent reconstructions of the initial function in panels (c)–(f). Panel (b) shows a simple linear interpolation between the discrete node values, which violates conservation. Panel (c), shows the piecewise constant reconstruction, which, obviously, satisfies conservation. Panel (d), (e), and (f) show the piecewise linear reconstruction using the minmod, Van Leer, and superbee slope limiters, respectively. As can be expected from the comments on Eqs. (14)–(16), slopes get increasingly steeper from panel (c)–(f) in the third to fifth computational cells. Superbee in panel (f) reproduces the slopes of the original function exactly in the third and the fifth cell, but this on the expense of monotonicity. In fact, already the Van Leer reconstruction shows at the interface from the third to the fourth cell non-monotonic behavior, and this is accentuated by superbee in panel (f) at the same location. We note that for the piecewise constant reconstruction (panel c), a local change of a discrete value affects the corresponding local cell alone, while for all other reconstructions, it also changes the slopes in the next neighbor cells.
 |
Fig. 2 a) Initial, piecewise linear function with a single discontinuity at the interface from cell 4 to cell 5. The black dots indicate its conservative discretization (discrete grid function); b) non-conservative, continuous linear interpolation of the discrete grid function. Linear extrapolation is applied in half of the first and half of the last computational cell. c) Piecewise constant reconstruction of the discrete grid function; d) piecewise linear reconstruction using the minmod slope limiter of Eq. (14); e) piecewise linear reconstruction using the Van Leer slope limiter of Eq. (15); f) piecewise linear reconstruction using the superbee slope limiter of Eq. (16). Panels b)–f) replicate the discrete grid function (black dots) from panel a). |
Figure 3 shows the function φ(r) for the three chosen limiters. The gray domain is the admissible codomain of φ(r), for which the total variation of the resulting reconstruction does not surpass the total variation of the original, discrete grid function. Its derivation and the definition of total variation and total variation diminishing (TVD) is given in the Appendix A. All limiters assume unity value for r = 1, which means that for a linear grid function (qi−qi−1 = qi + 1−qi), the piecewise linear reconstruction assumes the same linearity as the grid function. Alone the minmod limiter is within the domain of total variation diminishing reconstruction and follows exactly the maximal admissible values. From this graph it also becomes clear that superbee is the most aggressive reconstruction allowing for steeper gradients than Van Leer, which in turn is more aggressive than minmod. For r< 0, φ(r) = 0 for all limiters, which reduces the method to piecewise constant reconstruction in the case of local maxima or minima in the grid function. We conjecture that smooth limiters, such as the Van Leer limiter for r> 0, may potentially be advantageous when applying them to problems where convergence is sought such as in iterative solution schemes for non-LTE and Stokes inversion problems, or when repetitively computing the formal solution as part of a hydrodynamic scheme.
4. Radiative transfer with piecewise continuous reconstruction
In the following, the methods of piecewise continuous reconstruction and slope limiters is applied to the source function. All other physical quantities, in particular the propagation matrix, are left either entirely constant or piecewise constant. We opt for this simplification because it keeps the assessment of the method transparent and permits a first proof of concept of the new approach.
 |
Fig. 3 Three different slope-limiter functions: minmod (Eq. (14), solid curve), Van Leer (Eq. (15), dot-dashed curve), and superbee (Eq. (16), dashed curve). The grey area indicates the admissible codomain of the function φ(r) for which the total variation of the resulting reconstruction does not surpass the total variation of the original, discrete grid function (see Appendix A). |
4.1. Transfer of polarized radiation in the Zeeman regime
We are interested in the radiative transfer at wavelengths of a magnetically sensitive spectral line and consider polarization introduced by the Zeeman effect alone. No scattering polarization or atomic polarization is taken into account. In this case, distinguishing between line and continuum processes, and assuming the continuum to be unpolarized, Eq. (1) can be written in the form (see Sect. 9.4 of Landi Degl’Innocenti & Landolfi 2004) 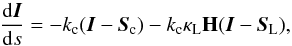 (17)where Sc = (Sc,0,0,0)T and SL = (SL,0,0,0)T are the continuum and line source functions, respectively. We note that under the above-mentioned assumptions both source functions are unpolarized. The quantity κL is the ratio between the frequency-integrated line absorption coefficient, kL, expressed in Doppler width units, and the continuum absorption coefficient, kc,
(17)where Sc = (Sc,0,0,0)T and SL = (SL,0,0,0)T are the continuum and line source functions, respectively. We note that under the above-mentioned assumptions both source functions are unpolarized. The quantity κL is the ratio between the frequency-integrated line absorption coefficient, kL, expressed in Doppler width units, and the continuum absorption coefficient, kc, 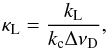 (18)where ΔνD is the Doppler width of the line (in frequency units). It can be observed that kL/ ΔνD and kc have the dimensions of the inverse of a length (true absorptions), while κL is a dimensionless quantity. The dimensionless propagation matrix H, due to line processes alone, is given by
(18)where ΔνD is the Doppler width of the line (in frequency units). It can be observed that kL/ ΔνD and kc have the dimensions of the inverse of a length (true absorptions), while κL is a dimensionless quantity. The dimensionless propagation matrix H, due to line processes alone, is given by 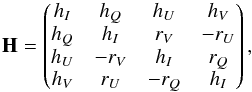 (19)where
(19)where 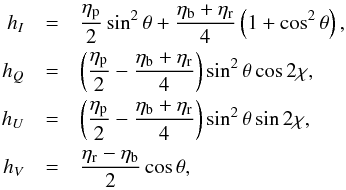 (20)and rQ, rU, and rV, are computed analogously to hQ, hU, and hV but with the absorption profiles ηp, ηb, and ηr replaced by the corresponding anomalous dispersion profiles ρp, ρb, and ρr, respectively (see, e.g., Eq. (9.32) of Landi Degl’Innocenti & Landolfi 2004).
(20)and rQ, rU, and rV, are computed analogously to hQ, hU, and hV but with the absorption profiles ηp, ηb, and ηr replaced by the corresponding anomalous dispersion profiles ρp, ρb, and ρr, respectively (see, e.g., Eq. (9.32) of Landi Degl’Innocenti & Landolfi 2004).
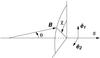 |
Fig. 4 Angles θ and χ that specify the magnetic field direction with respect to the coordinate system ê1 and ê2 and the direction of the line-of-sight s. Adapted from Landi Degl’Innocenti & Landolfi (2004). |
The angles θ and χ determine the orientation of the magnetic field with respect to the line-of-sight as shown in Fig. 4. The quantities ηq with q = −1,0, + 1, corresponding to “b” (blue), “p” (parallel) and “r” (red), respectively, are the absorption profiles associated with the various Zeeman components. The “b” component (also referred to as σb) is characterized by ΔM = Mu−Mℓ = 1, and is generally shifted in frequency to the blue side with respect to the unperturbed line, the “r” component (also referred to as σr) has ΔM = −1 and is generally shifted to the red, while the “p” component (also referred to as π) has ΔM = 0 and falls in between the σb and σr components. As usual, Mu and Mℓ are the magnetic quantum numbers of the upper and lower sublevel, respectively. The explicit expressions of the profiles are 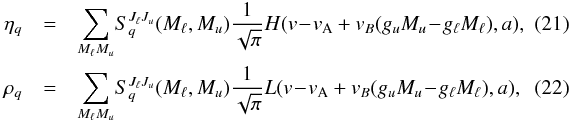 with H and L the Voigt function and the associated dispersion profile, respectively, as given in Eq. (5.45) in Landi Degl’Innocenti & Landolfi (2004).
with H and L the Voigt function and the associated dispersion profile, respectively, as given in Eq. (5.45) in Landi Degl’Innocenti & Landolfi (2004).
The reduced frequency, v, is defined as v = (ν0−ν)/ΔνD where ν0 is the line-center frequency and ΔνD the Doppler width of the line. Indicating with wT the random velocity of the atoms owing to thermal and, eventually, micro turbulent motions, then ΔνD = ν0wT/c, where c is the speed of light. The quantity vA is the normalized frequency shift due to a bulk motion of velocity wA in the medium: vA = wA/wT = ν0wA/ (cΔνD). The quantity vB is the normalized Zeeman splitting: vB = νL/ ΔνD, with νL the Larmor frequency (νL = 1.3996 × 106B, where B expressed in G and νL in s-1) and gu and gℓ are the Landé factors of the upper and lower sublevels, respectively, of the Zeeman components under consideration.
The parameter a is the damping constant taking line broadening (natural and collisional) into account. The quantity 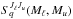 , is the relative strength of the Zeeman component q connecting the upper sublevel (JuMu) and the lower sublevel (JℓMℓ), where J is the total angular momentum quantum number. Using Wigner 3-j symbols, its explicit expression is given by
, is the relative strength of the Zeeman component q connecting the upper sublevel (JuMu) and the lower sublevel (JℓMℓ), where J is the total angular momentum quantum number. Using Wigner 3-j symbols, its explicit expression is given by 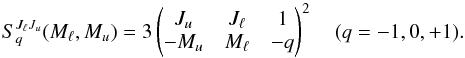 (23)For the examples shown in Sect. 5, we consider a normal Zeeman triplet corresponding to a transition between an upper level with Ju = 1 and gu = 1, and a lower level with Jℓ = 0. From Eq. (23), it can be easily shown that in this case the relative strength is unity for all the three Zeeman components.
(23)For the examples shown in Sect. 5, we consider a normal Zeeman triplet corresponding to a transition between an upper level with Ju = 1 and gu = 1, and a lower level with Jℓ = 0. From Eq. (23), it can be easily shown that in this case the relative strength is unity for all the three Zeeman components.
For our purpose, we now rewrite the transfer Eq. (17) using optical depth instead of geometrical depth and we assume that the atmosphere is in LTE so that Sc = SL = S = (B,0,0,0)T, where B is the Planck function. Then 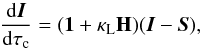 (24)where
(24)where 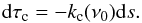 (25)Here is kc(ν0) the continuum absorption-coefficient at the line-center frequency ν0.
(25)Here is kc(ν0) the continuum absorption-coefficient at the line-center frequency ν0.
With Eqs. (19)−(24) and the textual equations in between, the radiative transfer problem for a Zeeman triplet is well defined given the parameters κL, vB, vA, θ, χ, and a, and defining the source function B(τc) and boundary intensities. The values for the standard case used in the following section are κL = 20, vA = 0, vB = 1.5, θ = 60°, χ = 0, and a = 0.05, which are the identical ones that are used by Landi Degl’Innocenti & Landolfi (2004) in Chap. 9.
4.2. Construction of piecewise continuous and strictly continuous source functions
Next, we define a computational grid on the axis of continuum optical depth, τc. We choose two possibilities; (i) a grid equidistant in τc; and (ii) a grid equidistant in log (τc). Since stellar atmospheres are gravitationally stratified, case (ii) can be expected to approximately correspond to an equidistant grid in the space coordinate s for a line-of-sight parallel to the gravitational acceleration. It then resembles the situation of computational grids in hydrodynamic simulations for stellar atmospheres, which often are equidistant in space.
For the definition of the source function values, we proceed as follows. First, we define an analytical expression for S(τc). Here, S denotes the normalized source function S(τc) = B(τc) /B0 so that we obtain intensities normalized to some reference value, B0. For B0 ~ B(τc = 1), we then expect intensities on the order of 1. To get an idea, we choose 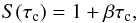 (26)which is known as the Milne-Eddington model in conjunction with depth-independent constants κL, ΔνD, vB, vA, θ, χ, a and a semi-infinite atmosphere2. In this case, Eq. (24) can be solved analytically (Rachkovsky 1962b), which circumstance we conveniently use for testing our program (see also Landi Degl’Innocenti & Landolfi 2004, Chap. 9.7 and 9.8). For the continuum intensity, the Milne-Eddington model produces Ic(τc = 0) = 1 + β. Another, more productive example for the present investigation is given by
(26)which is known as the Milne-Eddington model in conjunction with depth-independent constants κL, ΔνD, vB, vA, θ, χ, a and a semi-infinite atmosphere2. In this case, Eq. (24) can be solved analytically (Rachkovsky 1962b), which circumstance we conveniently use for testing our program (see also Landi Degl’Innocenti & Landolfi 2004, Chap. 9.7 and 9.8). For the continuum intensity, the Milne-Eddington model produces Ic(τc = 0) = 1 + β. Another, more productive example for the present investigation is given by 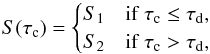 (27)which exhibits a discontinuity at continuum optical depth τc = τd, where the source function jumps from S1 to S2. Despite that the source function is constant elsewhere, the jump alone gives rise to the production of a spectral line.
(27)which exhibits a discontinuity at continuum optical depth τc = τd, where the source function jumps from S1 to S2. Despite that the source function is constant elsewhere, the jump alone gives rise to the production of a spectral line.
Having defined the analytical form of S(τc), we then map this function to the discrete node values at τi, by averaging over the corresponding computational cell according to 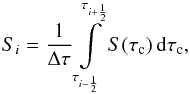 (28)where Δτ = τi + 1/2−τi−1/2 and where we use the index convention of Fig. 1. We then have a grid function similar to that presented to us in tables of stellar atmospheres, or produced by numerical simulations, or solved for in case of the inversion problem.
(28)where Δτ = τi + 1/2−τi−1/2 and where we use the index convention of Fig. 1. We then have a grid function similar to that presented to us in tables of stellar atmospheres, or produced by numerical simulations, or solved for in case of the inversion problem.
Having defined the discrete grid function Si, we then reconstruct a continuous or piecewise continuous source function 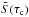 as was explained in Sect. 3, where we observe conservation of the source,
as was explained in Sect. 3, where we observe conservation of the source, 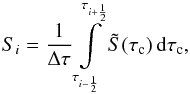 (29)whenever possible. This condition is trivially fulfilled for the piecewise constant reconstruction
(29)whenever possible. This condition is trivially fulfilled for the piecewise constant reconstruction 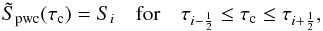 (30)and it is also fulfilled for the piecewise linear reconstruction
(30)and it is also fulfilled for the piecewise linear reconstruction 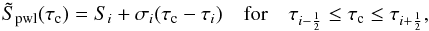 (31)provided that τi is halfway between
(31)provided that τi is halfway between 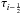 and
and 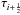 , independent of the value of the slope σi that can be freely chosen or determined by the selected slope limiter (see Sect. 3.2).
, independent of the value of the slope σi that can be freely chosen or determined by the selected slope limiter (see Sect. 3.2).
Condition (29) can be less easily satisfied for reconstructions that are both piecewise linear and strictly continuous (i.e., also continuous at the cell boundaries). Forcing the conservation condition for such reconstructions leads potentially to excessive variation of the reconstruction even when constrained to minimize it, or, the reconstruction may be ill defined in the sense that it strongly depends on the boundary values, which are normally least significant in the radiative transfer problem. For the present investigation, however, a strictly continuous interpolation is sought for comparison with the here proposed piecewise continuous reconstructions. A continuous interpolation is thought to approximately represent the DELO method in which the effective source function is linearly interpolated in between discrete node values. We choose two different continuous interpolations, both violating the conservation principle, Eq. (29). In a first method, we keep the variation least by simply connecting node values with linear interpolations. Thus, 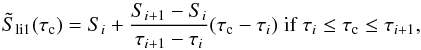 (32)which defines a piecewise linear continuous function. In the boundary cell 1, we extrapolate the linear source function of the interval [τ1,τ2] to the interval [τ1−1/2,τ1] and in the boundary cell N from [τN−1,τN] to [τN,τN + 1/2]. The propagation matrix κLH for the interval [τi,τi + 1] is evaluated at τi + 1/2.
(32)which defines a piecewise linear continuous function. In the boundary cell 1, we extrapolate the linear source function of the interval [τ1,τ2] to the interval [τ1−1/2,τ1] and in the boundary cell N from [τN−1,τN] to [τN,τN + 1/2]. The propagation matrix κLH for the interval [τi,τi + 1] is evaluated at τi + 1/2.
Second, we define source-function values at the cell boundaries by taking the average of the corresponding cell-center values, i.e., S(τi + 1/2) = 0.5(Si + Si + 1), and linearly interpolate between these values. Thus, we have 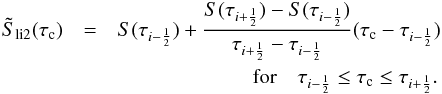 (33)In this case, the propagation matrix in the interval
(33)In this case, the propagation matrix in the interval ![\hbox{$[\tau_{i-\frac{1}{2}}, \tau_{i+\frac{1}{2}}]$}](/articles/aa/full_html/2016/02/aa27158-15/aa27158-15-eq217.png) is given by the data on node i. Equations (32) and (33) provide us with two continuous, piecewise linear interpolations, which can be considered rough equivalences to the DELO interpolation.
is given by the data on node i. Equations (32) and (33) provide us with two continuous, piecewise linear interpolations, which can be considered rough equivalences to the DELO interpolation.
Having defined the reconstruction (or interpolation in case of Eqs. (32) and (33)), we solve the transfer Eq. (24) within one single computational cell using the analytical solution of Landi Degl’Innocenti & Landi Degl’Innocenti (1985) given by Eqs. (7) and (8), keeping all quantities κL, ΔνD, vB, vA, θ, χ, a constant within that cell. Thereby, the boundary Stokes vector (I(s1) in Eq. (8)) is given by the solution in the preceding computational cell. In practice, we start at a sufficiently large optical depth τN with the outwardly directed boundary Stokes vector I(τN + 1/2), which is computed using the analytical Unno-Rachkovsky solution for a semi-infinite atmosphere given by ![\begin{equation} \label{eq:unno_rachkovsky} {\vec{I}}(\tau_{N+1/2}) = B_{0}\left[(1 + \beta\tau_{N+1/2}){\vec{1}} +\beta{{\bf C}}^{-1}\right]{\vec{U}}\; \end{equation}](/articles/aa/full_html/2016/02/aa27158-15/aa27158-15-eq221.png) (34)where
(34)where 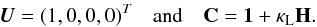 (35)Then, the analytical integration of the transfer equation is carried out over cell N, yielding I(τN−1/2), which is used for the boundary Stokes vector for cell N−1, and so on until cell 1 for which τ1−1/2 = 0 or some small value in case of a logarithmic τ scale.
(35)Then, the analytical integration of the transfer equation is carried out over cell N, yielding I(τN−1/2), which is used for the boundary Stokes vector for cell N−1, and so on until cell 1 for which τ1−1/2 = 0 or some small value in case of a logarithmic τ scale.
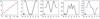 |
Fig. 5 a) Source function S(τc) using any of Eqs. (31)−(33) (red, solid) and using the piecewise constant reconstruction of Eq. (30) (blue, dotted) as a function of continuum optical depth τc. The corresponding resulting Stokes profiles are given in panels b)−e) as functions of the reduced frequency v: (black, solid) for the source function of Eqs. (31)−(33) and (blue, dotted) for the piecewise constant reconstruction of Eq. (30). b) Stokes I; c) Stokes Q; d) Stokes U; e) Stokes V. |
Errors in the Stokes profiles of three different examples with different reconstructions of the source function.
5. Examples, validation and comparisons
We have created a simple GNU Octave program for solving Eq. (17) for the normal Zeeman triplet and the various reconstruction and interpolation schemes for arbitrary atmospheres that has served us for a comparison of the different methods.
As a first example, let us compute the solution for a Milne-Eddington atmosphere. We take the source function of Eq. (26) with β = 5 and compute on an equidistant grid in τc that extends from τ1−1/2 = 0 to τN + 1/2 = 2 subdivided into N = 5 computational cells so that the optical depth changes by Δτc = 0.4 in each cell. Here, and in the following examples, we intentionally choose a very coarse grid to obtain perceivably different solutions for the different methods. The outwardly propagating, incident intensity at τN + 1/2 = 2 is computed using the Unno-Rachkovsky solution, Eq. (34). The propagation matrix is determined using the standard values for the parameters κL, vB, vA, θ, χ, and a given at the end of Sect. 4.1. In frequency space, we compute from v = (ν0−ν)/ΔνD = −5 to 5 with a frequency resolution of Δv = 0.1.
All the linear schemes, i.e., the piecewise continuous linear reconstruction of Eq. (31) and the continuous linear interpolations of Eqs. (32), (33), reproduce this linear source function in τc exactly. In theses cases the numerical solution of the emerging Stokes vector at τc = 0 is identical to the analytical Unno-Rachkovsky solution. We checked for any discrepancies and found that the agreement is to machine accuracy. Only with the piecewise constant reconstruction, one obtains, as expected, a substantial deviation from the analytical solution.
Figure 5 shows the comparison. Figure 5a shows in solid red the source function from any of the reconstructions or interpolations of Eqs. (31)−(33), which is identical to the Milne-Eddington source function S(τc) = 1 + 5τc and in dotted blue the piecewise constant reconstruction of Eq. (30). Panels (b)–(e) show the four Stokes parameters I, Q, U, and V as a function of reduced frequency v for the linear reconstruction and interpolations of Eqs. (31)–(33) (solid black curves) and for the piecewise constant reconstruction of Eq. (30) (dotted blue curves). It is worth mentioning that Stokes U would be identically zero in the absence of the magneto-optical effect because of χ = 0.
 |
Fig. 6 Second example. Source function (first row) and Stokes I, Q, U, and V as a function of reduced frequency v (second to fifth row, respectively) at five different positions of the discontinuity, τc = 0.6, 0.675, 0.75, 0.825, and 0.9 shown in this sequence from the first column to the last column. Each panel shows the curves for the continuous interpolation according to Eq. (32) (light blue), the piecewise constant reconstruction according to Eq. (30) (blue), the piecewise linear reconstruction with minmod slope limiter according to Eqs. (31) and (14) (red), and the reference solution (orange, dashed). |
Recalling that we use a very coarse grid, it is remarkable that the differences are not dramatic, also not in the continuum. For the computation of the errors, we compute the maximal difference in the frequency range [ν0−5,ν0 + 5] between the actual solution and the reference solution relative to the continuum intensity of the reference solution, thus 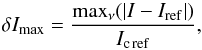 (36)and correspondingly for δQmax, δUmax, and δVmax. Iref refers to a numerical solution obtained with a large number of grid cells, typically 1000. In the present case, it is identical to the analytical solution of Unno-Rachkovsky. We also define the rms of the error,
(36)and correspondingly for δQmax, δUmax, and δVmax. Iref refers to a numerical solution obtained with a large number of grid cells, typically 1000. In the present case, it is identical to the analytical solution of Unno-Rachkovsky. We also define the rms of the error, 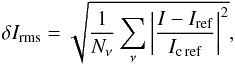 (37)where Nν is the number of frequency points, and correspondingly for δQrms, δUrms, and δVrms, and the error in the continuum of Stokes I,
(37)where Nν is the number of frequency points, and correspondingly for δQrms, δUrms, and δVrms, and the error in the continuum of Stokes I, 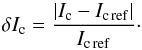 (38)Table 1 gives the relative errors in percents according to Eqs. (36)–(38) for the different examples presented in this section. The top three rows refers to the first example, i.e., Fig. 5. From it we can see that the piecewise constant reconstruction leads to an error of 1% in the continuum intensity, and to a maximal error in Stokes I of 5.6%, while Q and V have maximal deviations of 3% and 2.5%, respectively. Because all linear reconstructions reproduce the Rachkovsky solution exactly, the first and third rows of Table 1 have zero errors.
(38)Table 1 gives the relative errors in percents according to Eqs. (36)–(38) for the different examples presented in this section. The top three rows refers to the first example, i.e., Fig. 5. From it we can see that the piecewise constant reconstruction leads to an error of 1% in the continuum intensity, and to a maximal error in Stokes I of 5.6%, while Q and V have maximal deviations of 3% and 2.5%, respectively. Because all linear reconstructions reproduce the Rachkovsky solution exactly, the first and third rows of Table 1 have zero errors.
In a second example, we consider a single discontinuity in the source function as given by Eq. (27), where we choose S1 = 0 and S2 = 5 and shift the discontinuity from τd = 0.6 to τd = 0.9 in steps of 0.075 across one grid cell of width Δτc = 0.3. At the same time, κL = 0.5 ahead of the discontinuity, i.e., for τc<τd, and κL = 20 behind the discontinuity, i.e., for τc>τd. With this choice, the spectral line and continuum are confined to form close to the discontinuity for obtaining maximal impact from it, not being attenuated or diluted by opacity and source ahead of it. All other parameter values are equal to those of the first example. Because of the small line opacity ahead of the discontinuity, the line depression of Stokes I is, with about 10% of the continuum intensity, weak, at the advantage that differences between the various reconstruction methods become the more visible. The computational domain in τc extends from τ1−1/2 = 0 to τN + 1/2 = 1.5 subdivided into N = 5 computational cells so that the optical depth changes by Δτc = 0.3 in each cell. The outwardly propagating, incident intensity at τN + 1/2 = 1.5 is equal to S2 = 5.
 |
Fig. 7 Third example. Source function (first row) and Stokes I, Q, U, and V as a function of reduced frequency v (second to fifth row, respectively) at four different positions of the discontinuity, τc = 0.6, 0.7, 0.8, and 0.9 shown in this sequence from the first column to the last column. Each panel shows the curves for the continuous interpolation according to Eq. (32) (light blue), the piecewise constant reconstruction according to Eq. (30) (blue), the piecewise linear reconstruction with minmod slope limiter according to Eqs. (31) and (14) (red), and the reference solution (orange, dashed). |
Figure 6 shows in the first row in orange, dashed the original and, in solid, the reconstructed and the interpolated source functions as the discontinuity moves from τc = 0.6 to τc = 0.9 (from left to right) across one grid cell. Here, we recall that a discrete source function is derived from the original (orange, dashed) one with the help of Eq. (28), which then is the starting point for all reconstructed and interpolated (solid) source functions. This is also true for the line opacity κL for which we then always use the piecewise constant reconstruction to obtain a constant propagation matrix for each grid cell.
The second to fifth rows show the resulting Stokes-I to Stokes-V profiles, respectively. At τc = 0.6 (first column) and τc = 0.9 (rightmost column), the discontinuity of the original source function exactly coincides with a cell boundary. In these cases, the piecewise continuous reconstructions exactly reproduce the original source function and therefore also exactly match with the reference solution in all Stokes profiles. This is also reflected in Table 1, which lists vanishing errors at τd = 0.6 and τd = 0.9 for all the piecewise continuous reconstruction schemes. The continuous interpolation, on the other hand, shows substantial deviations from the reference solution in all Stokes parameters (light blue curves)3.
When the discontinuity is located in the middle of the cell at τc = 0.75 (middle column), none of the reconstruction methods perform particularly well; the continuous interpolation (light blue curves) is slightly better than all the piecewise continuous reconstructions (blue and red curves). In between cell boundary and cell center at τc = 0.675 and τc = 0.825, the piecewise continuous reconstructions again outperform the continuous interpolation, where it is the piecewise constant reconstruction (blue curve) that performs best. This good performance of the piecewise constant reconstruction is certainly due to the fact that in this example, the original source function is constant everywhere with exception of the discontinuity, while all other reconstruction methods show gradients across at least one grid cell, to which the formation of spectral lines is sensibly reacting on.
From Table 1, one can see that for the piecewise constant reconstruction, the maximal errors grow up to 1% in the continuum intensity, and up to 16%, 9.6%, and 8.5% in Stokes I, Q, and V, respectively. These numbers are 1.4%, 22%, 13%, and 11.5%, respectively, for the continuous interpolation. Although the piecewise continuous reconstruction method reproduces the exact solution when τd = 0.6 and τd = 0.9, the over-all improvement over the strictly continuous method is not dramatic.
The third example, is a bit more complicated then the first two and produces asymmetric Stokes profiles. The source function is given by 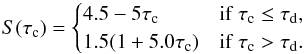 (39)The line opacity κL = 10 is the same in both layers, but the bulk velocity and the normalized Zeeman splitting change from vA = 0 and vB = 1.5 ahead of the discontinuity, i.e., for τc<τd (top layer), to vA = 2.0 and vB = 0 behind the discontinuity, i.e., for τc>τd (bottom layer). All other parameters are kept constant and assume the standard values given in Sect. 4.1. Notice that only the outer (canopy) layer contains a magnetic field, which is illuminated by a medium beneath it that moves with vA = 2.0 in the upward direction. With this choice, the illumination of the top layer at frequencies of the two Zeeman components is asymmetric because the absorption line in the bottom layer is shifted to the frequency of the blue Zeeman component, which produces asymmetric Stokes-profiles (Grossmann-Doerth et al. 1988; Steiner 2000).
(39)The line opacity κL = 10 is the same in both layers, but the bulk velocity and the normalized Zeeman splitting change from vA = 0 and vB = 1.5 ahead of the discontinuity, i.e., for τc<τd (top layer), to vA = 2.0 and vB = 0 behind the discontinuity, i.e., for τc>τd (bottom layer). All other parameters are kept constant and assume the standard values given in Sect. 4.1. Notice that only the outer (canopy) layer contains a magnetic field, which is illuminated by a medium beneath it that moves with vA = 2.0 in the upward direction. With this choice, the illumination of the top layer at frequencies of the two Zeeman components is asymmetric because the absorption line in the bottom layer is shifted to the frequency of the blue Zeeman component, which produces asymmetric Stokes-profiles (Grossmann-Doerth et al. 1988; Steiner 2000).
Figure 7 shows from the second to the last column the Stokes profiles as the discontinuity moves from τd = 0.6 to τd = 0.9 in steps of Δτ = 0.1. Different from the former two examples, at τd = 0.6 and τd = 0.9, when the discontinuity exactly coincides with a cell boundary, the piecewise continuous reconstructions do not reproduce the reference solution exactly anymore, but still, they match it closely. On the other hand, when the discontinuity straddles the cell at τd = 0.7, the piecewise continuous reconstructions are not substantially better than the continuous interpolation but over-all, they perform not bad. At τd = 0.8, the continuous interpolation performs definitely better than the piecewise continuous reconstructions. It is remarkable that the piecewise constant and the piecewise linear reconstructions are very similar despite that the corresponding source functions (top row) look distinctly different.
The modest performance of the piecewise-continuous reconstructions in this case is probably due to the inexact tracing of the local minimum of the source function immediately ahead of the discontinuity. Since it is a local minimum, TVD-schemes discard it and replace it by a locally flat function. At least for the important Stokes V, the maximal deviation of the piecewise continuous reconstructions from the reference solution is always less than that of the continuous interpolation (see Table 1).
6. Conclusions
This paper deals with the problem of computing the formal solution of the radiative transfer equation for polarized light across an atmosphere that harbors discontinuities. Discontinuities may arise, e.g., at the interface of media at different physical states or at shock fronts of ideal fluids. In the case of a nonideal fluid, one still deals with a quasi discontinuity when the jump in physical states occurs on a spatial scale much smaller than that of the numerical discretization. Given the physical quantities that characterize the atmosphere on a discrete grid by discrete grid functions, we reconstruct corresponding functions that define these quantities at any point along a line-of-sight, which is needed for the integration of the radiative transfer equation. In the past, this reconstruction has been achieved with polynomials of ever higher degree and smoothness. For example, for the effective source function of the DELO method, linear, then quadratic interpolation, and finally quadratic and cubic Bézier splines have been employed.
Here, we propose to take the opposite path, reconstructing the source function with piecewise continuos functions, accepting discontinuities at computational cell interfaces. As was the purpose of the Bézier splines, the piecewise continuous reconstruction is chosen such that it remains strictly positive and monotone. This is trivially fulfilled for the piecewise constant reconstruction and, as shown in Appendix A, it is fulfilled for the piecewise linear reconstruction using the minmod function as a slope limiter. This approach for solving the radiative transfer equation for polarized light may be considered similar in spirit to previously designed codes by Dykema et al. (1996) and Korčáková & Kubát (2003) for the radiative transfer in moving media that made use of the discontinuous finite element method (see also Castor 2004,Sect. 11.9). There however, the piecewise continuous reconstruction applies to the intensity itself, not only to the source function as we do here and slopes are determined by the Galerkin formalism.
The performance of the new method is assessed with three simple test cases. An atmosphere featuring a single discontinuity at an arbitrary position is first discretized in a conservative manner as expressed by Eq. (28) (and analogous for other quantities that exhibit a jump at the same location as the source function). Next, the source function is reconstructed using (i) a strictly continuous linear interpolation; (ii) the piecewise constant reconstruction; and (iii) the piecewise linear reconstruction with a variety slope limiters. For other discontinuous quantities, piecewise constant reconstruction is always used. From these reconstructions, the emergent Stokes vector is computed and the Stokes profiles are compared with the reference solution obtained with very high resolution in optical depth. The strictly continuous linear interpolation (i) represents here the classical DELO method, which also uses linear interpolation. However, different from DELO, we always use the formal solution of Landi Degl’Innocenti & Landi Degl’Innocenti (1985) for the integration across one computational cell and do not deal with the effective source function used by the original DELO method of Rees et al. (1989).
For a Milne-Eddington atmosphere (source function linear with optical depth), all methods, with the exception of the piecewise constant reconstruction, reproduce the analytical solution exactly. The piecewise constant reconstruction leads to an error of 1% in the continuum intensity, and to a maximal error in Stoke I of 5.6%, while Q and V have maximal deviations of 3% and 2.5%, respectively (see Table 1). These errors are relatively small considering that the chosen computational grid is very coarse with a constant optical depth step of Δτc = 0.4.
The piecewise constant reconstruction in turn performs best in the case of a step source function, which exhibits a single jump, otherwise being constant. In fact, all piecewise continuous reconstruction methods reproduce the exact solution when the jump of the original source function coincides with a computational cell-interface, while the DELO-like linear interpolation shows an error of 0.3% in the continuum intensity and maximal errors of 22%, 13%, 2.4%, and 11.5% in Stokes I, Q, U, and V, respectively. When the discontinuity of the original source function is located somewhere within a computational cell, then the piecewise constant reconstruction performs still best: the maximal errors grow to 1% in the continuum intensity, and to 16%, 9.6%, and 8.5% in Stokes I, Q, and V, respectively. In turn, these numbers are 1.4%, 22%, 13%, and 11.5%, respectively, for the DELO-like continuous interpolation. The piecewise linear reconstruction with minmod limiter shows slightly worse behavior than the piecewise constant reconstruction (with corresponding maximal errors of 0.6%, 18.8%, 10.3%, and 8.9% for the continuum intensity and Stokes I, Q, and V, respectively). When using piecewise linear reconstruction with Van Leer and superbee limiter, the fidelity to the reference solution further deteriorates but remains over all still better than the continuous interpolation.
The last test case consists in a step source function with linear (Milne-Eddington like) behavior away from the discontinuity. Together with the source function, also the magnetic field strength (normalized Zeeman splitting) and the line-of-sight bulk velocity jumps at the location of the discontinuity, which produces asymmetric Stokes profiles. In this case, none of the reconstructions reproduce the reference solution exactly anymore, even when the jump of the original source function coincides with a cell interface. In these instances, the reconstructions still perform considerably better than the linear interpolation. But as the jump moves sufficiently far into the cell, the linear interpolation starts to outperform the piecewise continuous reconstructions.
Over all, the assessment of the piecewise continuous reconstruction method turns out cautiously positive but does not lead to an order-of-magnitude improvement over conventional methods for the examples considered here. For a better and more meaningful assessment we plan to first improve the piecewise continuous reconstruction method by applying it also to the
propagation matrix, not only to the source function. This is still possible within the analytical formalism of Landi Degl’Innocenti & Landi Degl’Innocenti (1985). Next, we plan to implement the true DELO method in our test code in replacement of the current approximative DELO representative for better comparison. Finally, the new method will be applied to real life atmospheres from numerical, three-dimensional magnetohydrodynamic simulations.
The Stokes inversion problem consists in the determination of the kernel of the integral Eq. (3) and with it of the physical state of the atmosphere, given the emergent intensity I(0).
Here and in the following, we use Eq. (32) as the interpolation scheme.
Acknowledgments
This work has benefited from discussions within the international team “Heating of the magnetized chromosphere” (B. De Pontieu & S. McIntosh, conveners) at the International Space Science Institute (ISSI). Special thanks are extended to J. de la Cruz Rodriguez and J. C. del Toro Iniesta for explaining to us details of the DELO approach, to M. Steffen for pointing us to the work of Korčáková & Kubát (2003), and to J. M. Borrero and G. Janett for reading and commenting on a previous version of the manuscript. We thank the anonymous referee for careful reading and helping us improving legibility of the text.
References
- Auer, L. 1976, J. Quant. Spec. Radiat. Transf., 16, 931 [NASA ADS] [CrossRef] [Google Scholar]
- Auer, L. 2003, in Stellar Atmosphere Modeling, eds. I. Hubeny, D. Mihalas, & K. Werner, ASP Conf. Ser., 288, 3 [Google Scholar]
- Auer, L. H., Heasley, J. N., & House, L. L. 1977, ApJ, 216, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Beckers, J. M. 1969, Sol. Phys., 9, 372 [NASA ADS] [CrossRef] [Google Scholar]
- Bellot Rubio, L. R., Ruiz Cobo, B., & Collados, M. 1998, ApJ, 506, 805 [NASA ADS] [CrossRef] [Google Scholar]
- Castor, J. I. 2004, Radiation Hydrodynamics (Cambridge University Press), 368 [Google Scholar]
- Colella, P., & Woodward, P. R. 1984, J. Comp. Phys., 54, 174 [Google Scholar]
- De la Cruz Rodríguez, J., & Piskunov, N. 2013, ApJ, 764, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Dykema, P. G., Klein, R. I., & Castor, J. I. 1996, ApJ, 457, 892 [NASA ADS] [CrossRef] [Google Scholar]
- Feautrier, P. 1964, Comptes Rendus de L’Académie des Sciences, 258, 3189 [Google Scholar]
- Freytag, B., Steffen, M., Ludwig, H.-G., et al. 2012, J. Comp. Phys., 231, 919 [Google Scholar]
- Grossmann-Doerth, U., Schüssler, M., & Solanki, S. K. 1988, A&A, 206, L37 [NASA ADS] [Google Scholar]
- Harten, A. 1983, J. Comp. Phys., 49, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Holzreuter, R., & Solanki, S. K. 2012, A&A, 547, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Korčáková, D., & Kubát, J. 2003, A&A, 401, 419 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Landi Degl’Innocenti, E. 1976, A&AS, 25, 379 [NASA ADS] [Google Scholar]
- Landi Degl’Innocenti, E. 1987, in Numerical Radiative Transfer, ed. W. Kalkofen (Cambridge University Press), 265 [Google Scholar]
- Landi Degl’Innocenti, E., & Landi Degl’Innocenti, M. 1985, Sol. Phys., 97, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Landi Degl’Innocenti, E., & Landolfi, M. 2004, Polarization in Spectral Lines (Dordrecht: Kluwer Academic Publishers), Astrophys. Space Sci. Library, 307 [Google Scholar]
- LeVeque, R. 2002, Finite Volume Methods for Hyperbolic Problems (Cambridge University Press) [Google Scholar]
- Rachkovsky, D. N. 1962a, Izvestiya Ordena Trudovogo Krasnogo Znameni Krymskoj Astrofizicheskoj Observatorii, 27, 148 [Google Scholar]
- Rachkovsky, D. N. 1962b, Izvestiya Ordena Trudovogo Krasnogo Znameni Krymskoj Astrofizicheskoj Observatorii, 28, 259 [Google Scholar]
- Rees, D. E., Durrant, C. J., & Murphy, G. A. 1989, ApJ, 339, 1093 [NASA ADS] [CrossRef] [Google Scholar]
- Roe, P. L. 1986, Ann. Rev. Fluid Mech., 18, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Steffen, M. 1990, A&A, 239, 443 [NASA ADS] [Google Scholar]
- Steiner, O. 2000, Sol. Phys., 196, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Štěpán, J., & Trujillo Bueno, J. 2013, A&A, 557, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sweby, P. K. 1984, SIAM J. Num. Analysis, 21, 995 [Google Scholar]
- Toro, E. F. 2009, Riemann Solvers and Numerical Methods for Fluid Dynamics, (Springer) [Google Scholar]
- Trujillo Bueno, J. 2003, in Stellar Atmosphere Modeling, eds. I. Hubeny, D. Mihalas, & K. Werner, ASP Conf. Ser., 288, 551 [Google Scholar]
- Unno, W. 1956, PASJ, 8, 108 [NASA ADS] [Google Scholar]
- Van Leer, B. 1974, J. Comp. Phys., 14, 361 [CrossRef] [Google Scholar]
- Van Leer, B. 1979, J. Comp. Phys., 32, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Wittmann, A. 1974, Sol. Phys., 35, 11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Total variation diminishing codomain
Figure A.1 shows the computational cell i with discrete value qi and neighboring values qi−1 and qi + 1 and the piecewise linear reconstruction (dashed, red) with slope σi in cell i and slopes σi−1 and σi + 1 in the neighboring cells i−1 and i + 1, respectively. The reconstruction in cell i−1 ends on the left interface of cell i with value 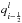 and the reconstruction in cell i + 1 on the right interface of cell i with value
and the reconstruction in cell i + 1 on the right interface of cell i with value 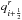 . Slope σi is, according to Eq. (12), given by
. Slope σi is, according to Eq. (12), given by 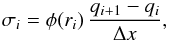 (A.1)where ri is the ratio of successive gradients,
(A.1)where ri is the ratio of successive gradients, 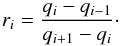 (A.2)Corresponding equations exist for σi−1 and σi + 1 and ri−1 and ri + 1.
(A.2)Corresponding equations exist for σi−1 and σi + 1 and ri−1 and ri + 1.
In the following, we seek finding the admissible codomain of the function φ(ri) that constrains the slope σi within bounds such that the reconstruction stays monotone for monotone discrete values qi−1, qi, and qi + 1. Thus, we demand that ![\appendix \setcounter{section}{1} \begin{equation} \label{eq:appa3} q_{i-1/2}^{l} \le q_{i} + \sigma_{i}(x-x_{i}) \le q_{i+1/2}^{r} \quad \mbox{for}\; x\in [x_{i-\frac{1}{2}}, x_{i+\frac{1}{2}}], \end{equation}](/articles/aa/full_html/2016/02/aa27158-15/aa27158-15-eq290.png) (A.3)where we assume without loss of generality that qi−1 ≤ qi ≤ qi + 1. In case that the sequence qi−1, qi, qi + 1 is non-monotone, then ri< 1. In this case, we demand that φ(ri) = 0, hence, σi = 0. Also φ(r) ≥ 0∀r ∈R, else the slope σ would be contrarian to the monotonic trend of the discrete values. Condition (A.3) implies that the reconstruction is also monotone in the interval [xi−1,xi + 1]4.
(A.3)where we assume without loss of generality that qi−1 ≤ qi ≤ qi + 1. In case that the sequence qi−1, qi, qi + 1 is non-monotone, then ri< 1. In this case, we demand that φ(ri) = 0, hence, σi = 0. Also φ(r) ≥ 0∀r ∈R, else the slope σ would be contrarian to the monotonic trend of the discrete values. Condition (A.3) implies that the reconstruction is also monotone in the interval [xi−1,xi + 1]4.
From the first relation of condition (A.3), where we just need to consider 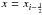 , and using that
, and using that 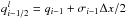 and substituting σi−1 with the corresponding right hand side of Eq. (A.1), it follows that
and substituting σi−1 with the corresponding right hand side of Eq. (A.1), it follows that 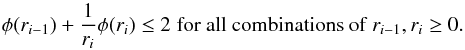 (A.4)Correspondingly, from the second relation of condition (A.3) it follows
(A.4)Correspondingly, from the second relation of condition (A.3) it follows 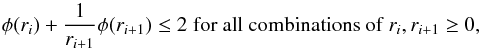 (A.5)which is equivalent to Eq. (A.4).
(A.5)which is equivalent to Eq. (A.4).
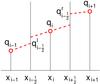 |
Fig. A.1 Computational cell i with discrete value qi and neighboring values qi−1 and qi + 1. The piecewise linear reconstruction (dashed, red lines) assumes value |
We can further postulate that φ(1) = 1, since then, with ri = 1, the reconstruction in cell i assumes the same linearity as the grid function for the values qi−1,qi, and qi + 1, which in this case fall all on a straight line because qi−qi−1 = qi + 1−qi.
Setting ri = 1, we then obtain from Eq. (A.4) φ(ri−1) ≤ 1∀ri−1 ≥ 0, hence, we must have φ(r) ≤ 1∀r ≥ 0. Setting ri−1 = 1, we obtain from the same equation (1 /ri)φ(ri) ≤ 1∀ri ≥ 0, and hence, we must also have φ(r) ≤ r∀r ≥ 0. Both together, and recalling that φ(r) = 0forr< 0 and φ(r) ≥ 0∀r ∈R, can be expressed as 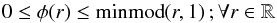 (A.6)where the function minmod(.,.) is defined as
(A.6)where the function minmod(.,.) is defined as 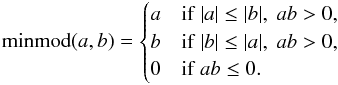 (A.7)Next, we can show that any continuous, single valued function φ(r) that satisfies Eq. (A.6) also fulfills condition (A.4) (or condition (A.5)) for any combination of ri, ri−1, ri + 1. Considering Eq. (A.4), we have only to deal with ri and ri−1, in which case we have the only combinations (i) ri,ri−1 ∈ [0,1], (ii) ri−1 ∈ [0,1] ,ri ≥ 1; (iii) ri ∈ [0,1] ,ri−1 ≥ 1, and (iv) ri,ri−1 ≥ 1. For combination (i), Eq. (A.6) implies that
(A.7)Next, we can show that any continuous, single valued function φ(r) that satisfies Eq. (A.6) also fulfills condition (A.4) (or condition (A.5)) for any combination of ri, ri−1, ri + 1. Considering Eq. (A.4), we have only to deal with ri and ri−1, in which case we have the only combinations (i) ri,ri−1 ∈ [0,1], (ii) ri−1 ∈ [0,1] ,ri ≥ 1; (iii) ri ∈ [0,1] ,ri−1 ≥ 1, and (iv) ri,ri−1 ≥ 1. For combination (i), Eq. (A.6) implies that ![\appendix \setcounter{section}{1} \begin{eqnarray*} \phi(r_{i-1}) \le r_{i-1} ;\; \phi(r_{i}) \le r_{i}\; \textrm{for}\; r_{i}, r_{i-1} \in [0,1]. \end{eqnarray*}](/articles/aa/full_html/2016/02/aa27158-15/aa27158-15-eq318.png) Using these inequalities in Eq. (A.4) leads to an inequality, which is unconditionally fulfilled. Likewise, for combination (ii), Eq. (A.6) implies that
Using these inequalities in Eq. (A.4) leads to an inequality, which is unconditionally fulfilled. Likewise, for combination (ii), Eq. (A.6) implies that ![\appendix \setcounter{section}{1} \begin{eqnarray*} \phi(r_{i-1}) \le r_{i-1};\; \phi(r_{i}) = 1\; \textrm{for}\; r_{i-1} \in [0,1] ,\;r_{i}\ge 1 , \end{eqnarray*}](/articles/aa/full_html/2016/02/aa27158-15/aa27158-15-eq319.png) which again, when inserting in Eq. (A.4), leads to an inequality that is always fulfilled. For combination (iii), Eq. (A.6) implies that
which again, when inserting in Eq. (A.4), leads to an inequality that is always fulfilled. For combination (iii), Eq. (A.6) implies that ![\appendix \setcounter{section}{1} \begin{eqnarray*} \phi(r_{i-1}) \le 1 ;\; \phi(r_{i}) \le r_{i}\; \textrm{for}\; r_{i} \in [0,1] ,\;r_{i-1} \ge 1 , \end{eqnarray*}](/articles/aa/full_html/2016/02/aa27158-15/aa27158-15-eq320.png) again leading to an unconditional inequality when inserting in Eq. (A.4), and the same is true for combination (iv) when Eq. (A.6) implies that
again leading to an unconditional inequality when inserting in Eq. (A.4), and the same is true for combination (iv) when Eq. (A.6) implies that 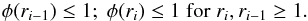 Likewise, the same exercise can be performed for condition (A.5) so that any curve with 0 ≤ φ(r) ≤ minmod(r,1),r ≥ 0 fulfills conditions (A.5) and (A.6) for any combinations of ri, ri−1, ri + 1, qed. Thus, together with φ(r) = 0 for r ≤ 0, the grey area in Fig. 3 defines the codomain of limiters φ(r) that guarantee monotonicity of the reconstruction.
Likewise, the same exercise can be performed for condition (A.5) so that any curve with 0 ≤ φ(r) ≤ minmod(r,1),r ≥ 0 fulfills conditions (A.5) and (A.6) for any combinations of ri, ri−1, ri + 1, qed. Thus, together with φ(r) = 0 for r ≤ 0, the grey area in Fig. 3 defines the codomain of limiters φ(r) that guarantee monotonicity of the reconstruction.
The total variation of a grid function qi or an arbitrary, differentiable function (or distribution) q(x) is, respectively, defined as 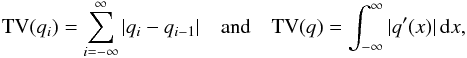 (A.8)where qi or q(x) must approach constant values q± as x,i → ± ∞. The step from the discrete grid function qi to the reconstruction q(x) is called total variation nonincreasing (TVNI) or short TVD for total variation diminishing if
(A.8)where qi or q(x) must approach constant values q± as x,i → ± ∞. The step from the discrete grid function qi to the reconstruction q(x) is called total variation nonincreasing (TVNI) or short TVD for total variation diminishing if 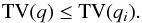 (A.9)According to Harten (1983), the transition from qi to q(x) is TVD if it is monotonicity preserving, which is the condition from which Eq. (A.6) was derived, i.e., Eq. (A.3) with corollary proven in footnote 4. Thus, piecewise linear reconstructions with limiters satisfying Eq. (A.6) are TDV.
(A.9)According to Harten (1983), the transition from qi to q(x) is TVD if it is monotonicity preserving, which is the condition from which Eq. (A.6) was derived, i.e., Eq. (A.3) with corollary proven in footnote 4. Thus, piecewise linear reconstructions with limiters satisfying Eq. (A.6) are TDV.
We can also derive Eq. (A.6) from condition (A.9) directly. For that we first write the reconstruction in the interval ] xi−3/2,xi + 3/2 [ in terms of the unit step distribution 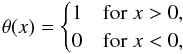
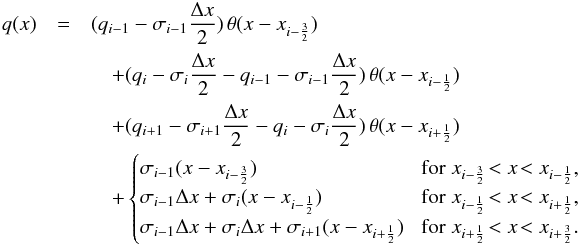 (A.10)For to evaluate the total variation of this function, we need its derivative, which is
(A.10)For to evaluate the total variation of this function, we need its derivative, which is 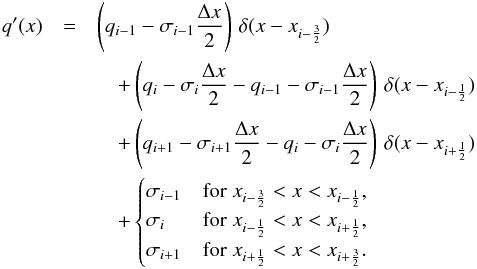 (A.11)The total variation of q(x) in the interval [xi−1,xi + 1] is then according to the right expression in Eq. (A.8)
(A.11)The total variation of q(x) in the interval [xi−1,xi + 1] is then according to the right expression in Eq. (A.8) ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{eq:qTV} \mathrm{TV}_{[x_{i-1}, x_{i+1}]}(q) &=& \int_{x_{i-1}}^{x_{i+1}} |q^{\prime}(x)|\, {\rm d} x\nonumber \\ &=& \left|q_{i} - \sigma_{i}\frac{\Delta x}{2} - \left(q_{i-1} + \sigma_{i-1}\frac{\Delta x}{2}\right)\right|\nonumber \\ &&{}+\left|q_{i+1} - \sigma_{i+1}\frac{\Delta x}{2} - \left(q_{i} + \sigma_{i}\frac{\Delta x}{2}\right)\right|\nonumber \\ &&{}+\left|\sigma_{i-1}\right|\frac{\Delta x}{2} + \left|\sigma_{i}\right|\Delta x + \left|\sigma_{i+1}\right|\frac{\Delta x}{2} , \end{eqnarray}](/articles/aa/full_html/2016/02/aa27158-15/aa27158-15-eq333.png) (A.12)which simply is the sum of the two jumps at
(A.12)which simply is the sum of the two jumps at 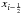 and
and 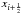 plus the variation of the reconstruction in cell i and half of cells i−1 and i + 1. The corresponding expression for the grid function qi is according to the left expression in Eq. (A.8)
plus the variation of the reconstruction in cell i and half of cells i−1 and i + 1. The corresponding expression for the grid function qi is according to the left expression in Eq. (A.8)![\appendix \setcounter{section}{1} \begin{eqnarray} \label{eq:qiTV} \mathrm{TV}_{[x_{i-1}, x_{i+1}]}(q_{i}) &=& |q_{i+1} - q_{i}| + |q_{i} - q_{i-1}|\nonumber \\ &=& |q_{i+1} - q_{i}| + |r_{i}||q_{i+1} - q_{i}|\nonumber \\ &=& |q_{i+1} - q_{i}| (1 + |r_{i}|). \end{eqnarray}](/articles/aa/full_html/2016/02/aa27158-15/aa27158-15-eq336.png) (A.13)Using Eq. (A.1) and corresponding expressions for σi−1 and σi + 1 in Eq. (A.12) and rearranging terms and using Eq. (A.13), condition (A.9) then becomes
(A.13)Using Eq. (A.1) and corresponding expressions for σi−1 and σi + 1 in Eq. (A.12) and rearranging terms and using Eq. (A.13), condition (A.9) then becomes  (A.14)In the same way as for Eqs. (A.4) and (A.5), this inequality must be satisfied for all possible combinations of ri, ri−1, ri + 1. Postulating φ(r) = 0 for r< 0, φ(r) ≥ 0 for r ≥ 0, and φ(1) = 1 as done in the previous derivation, we then can again derive Eq. (A.6). Likewise, having condition (A.6), we can check if Eq. (A.14) is satisfied for all possible combinations of ri, ri−1, ri + 1.
(A.14)In the same way as for Eqs. (A.4) and (A.5), this inequality must be satisfied for all possible combinations of ri, ri−1, ri + 1. Postulating φ(r) = 0 for r< 0, φ(r) ≥ 0 for r ≥ 0, and φ(1) = 1 as done in the previous derivation, we then can again derive Eq. (A.6). Likewise, having condition (A.6), we can check if Eq. (A.14) is satisfied for all possible combinations of ri, ri−1, ri + 1.
In the numerical analysis of advection schemes, a similar gray shaded region as shown in Fig. 3 is known as the (first-order) Sweby region (see Sweby 1984; LeVeque 2002) but it comprises the (larger) region 0 ≤ φ(r) ≤ minmod(2,2r). The reason for this difference is that we consider here exclusively the reconstruction step, i.e., the step from the grid function qi to the reconstruction q(x), while Sweby regions are derived for the full sequence of advection-scheme steps consisting of reconstruction, evolution, and averaging. Especially the averaging step has a diffusive character, which relaxes conditions for the slope limiter in the reconstruction step, admitting a larger codomain for φ(r) than when considering the reconstruction step alone.
All Tables
Errors in the Stokes profiles of three different examples with different reconstructions of the source function.
All Figures
 |
Fig. 1 Definition of optical depth, ray path, and grid indices for cells, nodes, and cell interfaces. |
| In the text | |
 |
Fig. 2 a) Initial, piecewise linear function with a single discontinuity at the interface from cell 4 to cell 5. The black dots indicate its conservative discretization (discrete grid function); b) non-conservative, continuous linear interpolation of the discrete grid function. Linear extrapolation is applied in half of the first and half of the last computational cell. c) Piecewise constant reconstruction of the discrete grid function; d) piecewise linear reconstruction using the minmod slope limiter of Eq. (14); e) piecewise linear reconstruction using the Van Leer slope limiter of Eq. (15); f) piecewise linear reconstruction using the superbee slope limiter of Eq. (16). Panels b)–f) replicate the discrete grid function (black dots) from panel a). |
| In the text | |
 |
Fig. 3 Three different slope-limiter functions: minmod (Eq. (14), solid curve), Van Leer (Eq. (15), dot-dashed curve), and superbee (Eq. (16), dashed curve). The grey area indicates the admissible codomain of the function φ(r) for which the total variation of the resulting reconstruction does not surpass the total variation of the original, discrete grid function (see Appendix A). |
| In the text | |
 |
Fig. 4 Angles θ and χ that specify the magnetic field direction with respect to the coordinate system ê1 and ê2 and the direction of the line-of-sight s. Adapted from Landi Degl’Innocenti & Landolfi (2004). |
| In the text | |
 |
Fig. 5 a) Source function S(τc) using any of Eqs. (31)−(33) (red, solid) and using the piecewise constant reconstruction of Eq. (30) (blue, dotted) as a function of continuum optical depth τc. The corresponding resulting Stokes profiles are given in panels b)−e) as functions of the reduced frequency v: (black, solid) for the source function of Eqs. (31)−(33) and (blue, dotted) for the piecewise constant reconstruction of Eq. (30). b) Stokes I; c) Stokes Q; d) Stokes U; e) Stokes V. |
| In the text | |
 |
Fig. 6 Second example. Source function (first row) and Stokes I, Q, U, and V as a function of reduced frequency v (second to fifth row, respectively) at five different positions of the discontinuity, τc = 0.6, 0.675, 0.75, 0.825, and 0.9 shown in this sequence from the first column to the last column. Each panel shows the curves for the continuous interpolation according to Eq. (32) (light blue), the piecewise constant reconstruction according to Eq. (30) (blue), the piecewise linear reconstruction with minmod slope limiter according to Eqs. (31) and (14) (red), and the reference solution (orange, dashed). |
| In the text | |
 |
Fig. 7 Third example. Source function (first row) and Stokes I, Q, U, and V as a function of reduced frequency v (second to fifth row, respectively) at four different positions of the discontinuity, τc = 0.6, 0.7, 0.8, and 0.9 shown in this sequence from the first column to the last column. Each panel shows the curves for the continuous interpolation according to Eq. (32) (light blue), the piecewise constant reconstruction according to Eq. (30) (blue), the piecewise linear reconstruction with minmod slope limiter according to Eqs. (31) and (14) (red), and the reference solution (orange, dashed). |
| In the text | |
 |
Fig. A.1 Computational cell i with discrete value qi and neighboring values qi−1 and qi + 1. The piecewise linear reconstruction (dashed, red lines) assumes value |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


